Пределы функций: Примеры на пределы функций

Примеры на пределы функций

Продолжаем изучать правила раскрытия неопределенностей в пределах. Сегодня рассмотрим 5 примеров и проанализируем ход вычислений.

Пример 6. Вычислить предел последовательности:

Решение: При подстановке бесконечности получим неопределенность вида бесконечность поделить на бесконечность (∞/∞).
Раскрыть особенность возможно двумя способами: по правилу Лопиталя или выделением множителей, которые вносят наибольший вклад в числителе и знаменателе дроби.
По правилу Лопиталя получим

По второй методике предел последовательности равен

Значения совпадают, как первая схема так и вторая не тяжелые для применения.
Однако часто в одних задачах требуют вычислить предел последовательности по правилу Лопиталя.
В других наоборот – не используя правило Лопиталя найти предел.

 

Пример 7. Вычислить предел последовательности:

Решение: Имеем разницу двух корней, которые при подстановке переменной дают особенность вида бесконечность минус бесконечность (∞-∞).
Для устранения особенности умножим и разделим корневую зависимость на сопряженное выражение (сумму корней). В результате придем к разности квадратов в числителе.
Повторная подстановка дает особенность вида бесконечность разделить на бесконечность.
Чтобы избавиться от особенности выделяем доминантные множители в числителе и знаменателе и оцениваем, что в итоге перевешивает (доминирует).

Получили, что в числителе старший степень чем в знаменателе, поэтому предел стремится к бесконечности. Но важно еще выяснить к плюс бесконечности или к минус бесконечности. Для этого следует проанализировать вклад слагаемых в скобках.

 

Пример 8. Найти предел функции:

Решение: При подстановке единицы получаем особенность вида ноль разделить на ноль {0/0}.
Для ее раскрытия разницу корней в числителе умножим на сумму корней, чтобы избавиться от иррациональности. На ту же сумму корней следует умножить знаменатель, чтобы манипуляциями не изменить значение предела.
Далее анализируем знаменатель – он содержит полином, который в свою очередь имеет в разложении множитель (x-1) (как особенность).
Разложим полином на простые множители и заменим ими соответствующую часть дроби.

Далее упрощаем числитель и знаменатель на общий множитель (x-1), и методом подстановки находим предел функции, что осталась.

 

Пример 9. Найти предел функции:

Решение: В заданиях, где переменная стремится к нулю и имеем дробь, содержащий логарифмы или тригонометрические функции следует искать возможность получить первую замечательный предел, следствия второго и первого лимита или сочетание обоих вариантов. Этот пример сочетает все возможное, что может Вас ждать на практике.
Простая подстановка показывает, что имеем лимит с неопределенностью вида {0/0}. Для устранения неопределенности и возведения сперва логарифма к виду ln(1+y)/y, делим и умножаем на sin(3x). Чтобы этот же синус в числителе свести под некую формулу, разделим и умножим на (3x).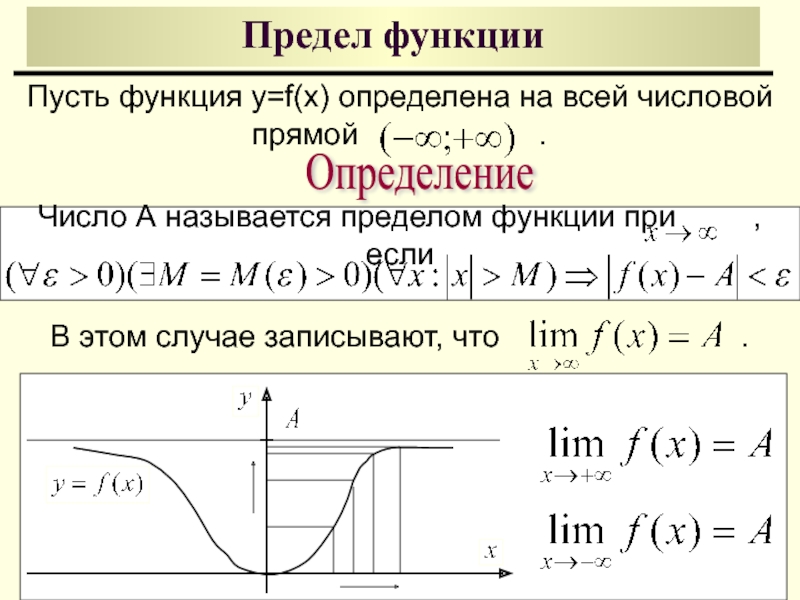 ∞. А это означает, что имеем дело со вторым замечательным пределом.
Для устранения особенности в скобках и показателе выделим выражения, содержащие (x-1). После этого делаем замену переменных, t=x-1, при этом новая переменная стремится к нулю. Далее в показателе выделяем множитель, который является обратно пропорциональным к слагаемому в дужках (1/4t), это даст нам экспоненту.

Все, что останется множителем в показателе даст степень экспоненты в предельном переходе (12).

Хорошо проанализируйте приведенный пример, он на самом деле не такой тяжелый, если внимательно разобраться.
В новых публикациях Вы получите ответы на другие вопросы, которые могли у Вас возникнуть в связи с тем, что рассмотрено всего 5 примеров.

Односторонние пределы функций задачи с решением и примерами по высшей математике

Односторонние пределы функций

Если отыскивается предел функции при условии, что стремясь к , т. е. , может принимать только такие значения, которые меньше , то этот предел, если он существует, называется левосторонним пределом функции . Левосторонний предел функции обозначается символом:

или .

Если отыскивается предел функции при условии, что стремясь к , т. е. , может принимать только такие значения, которые больше , то этот предел, если он существует, называется правосторонним пределом функции . Правосторонний предел функции обозначается символом:

или .

Очевидно, что предел функции при существует только тогда, когда существуют и равны между собой её левосторонний и правосторонний пределы, т. е. .

Функция называется непрерывной при , если её левосторонний и правосторонний пределы существуют, равны между собой и равны значению функции в этой точке, т. е.

Если это равенство не выполняется, то точка является точкой разрыва.

Если существуют левосторонний и правосторонний пределы функции, но не равны между собой, т. е. , то точка называется точкой разрыва первого рода.

Величина называется скачком функции в точке .

Если в точке не существует левосторонний или правосторонний предел функции или не существуют оба предела одновременно, то эта точка называется точкой разрыва второго рода. Во всех этих случаях функция терпит разрыв второго рода.

Если в точке функция имеет левосторонний и правосторонний пределы и эти пределы между собой равны, но их значения не совпадают со значением функции в точке , т. е.

, то точка называется точкой устранимого разрыва.

Разрыв «устраняется» тем, что полагают равным и , т. е. принимают, что .

Задача №45.

Показать, что функция

имеет разрыв в точке .

Решение:

При . Найдём односторонние пределы функции в точке .

Имеем: . Условие непрерывности не выполнено. В точке функция имеет разрыв. Это точка разрыва первого рода.

Задача №46.

Какого рода разрыв имеет функция в точке ?

Решение:

Функция терпит разрыв в точке . Левосторонний предел функции . Правосторонний предел функции .

Здесь не существует ни предела слева, ни предела справа, а поэтому точка — точка разрыва второго рода.

Задача №47.

Непрерывна ли функция ? Если нет, то в какой точке непрерывна, и какого рода эта точка имеет разрыв?

Решение:

Функция не является непрерывной, так как она неопределена в точке .

Известно, что , т. е. существуют левосторонний и правосторонний пределы и равны 1, но — не существует. Если условимся, что при функция , то разрыв будет «устранён». Точка является точкой устранимого разрыва, так как и функция в этой точке может быть доопределена так, что можно взять .

Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Пределы функций. Понятие, основные определения, свойства, методы вычислений

1. Пределы функций

Понятие, основные
определения,
свойства, методы
вычислений

2. План

I Понятие предела функции
II Геометрический смысл предела
III Бесконечно малые и большие функции и их
свойства
IV Вычисления пределов:
1) Некоторые наиболее употребительные
пределы;
2) Пределы непрерывных функций;
3) Пределы сложных функций;
4) Неопределенности и методы их решений

3.

Понятие предела функции Определение:
Пределом
функции y= f(x)
называется
некоторое
число b при x→a.
И записывается
это так : lim f ( x) b
x a

4. Геометрический смысл предела

Определение: Для любого
ε>0 можно указать δ-
окрестность точки а на
оси Ох ,такую что для
всех х из этой
окрестности кроме х=а,
соответствующее
значение y лежат в εокрестности точки b
Математическая запись:
При
|x-a|
-δ
a-δ
xЄ(a-δ;a+δ) ↔ f(x)Є(b-ε; b+ε)

5. Геометрический смысл предела (продолжение)

Если число b1 есть предел функции y= f(x)
при x→a, так что x
левым односторонним пределом точки а: lim f ( x) b1
x a 0
Если число b2 есть предел функции y= f(x) при
x→a, так что x>0 то число b2 называется
правым односторонним пределом точки а:
lim f ( x) b2
x a 0
Если b1=b2=b, то число b есть предел этой
функции при x→a: lim f ( x) b
x a

6.

Бесконечно малые и большие функции и их свойства Определение: Функция f(x) называется
бесконечно малой при x→a x если
предел этой функции
lim f ( x) 0
x a( x )
Определение: Функция f(x) называется
бесконечно большой при x→a x 0 если
предел этой функции
lim f ( x)
x a ( x 0 )

7. Свойства бесконечно малых и больших функции

Функция обратная по величине бесконечно
большой, есть бесконечно малая
lim x 0
x 0
1
lim
x 0 x
Функция обратная по величине бесконечно
малой, но отличная от 0, есть бесконечно

малая
lim x lim 1 0
x
x x

8. Основные теоремы о пределах

Теорема 1: Для того, чтобы число А было пределом функции f(x)
при x a , необходимо и достаточно, чтобы эта функция
была представлена в виде f ( x) A ( x) , где (x ) бесконечно малая.
Следствие 1: Функция не может в одной точке иметь 2 различных
предела.
Теорема 2: Предел постоянной величины равен самой постоянной
Теорема 3: Если функция f ( x) 0( f ( x) 0) для всех x в некоторой
окрестности точки a, кроме, быть может, самой точки a, и в
точке a имеет предел , то lim f ( x) 0 lim f ( x) 0
x a
x a

9.

Основные теоремы о пределах (продолжение) Теорема 4: Если функция f1(x) и f2(x) имеют пределы при x a,
то при x a, имеет пределы также их сумма f1(x)+f2(x),
произведение f1(x)*f2(x), и при условии lim f 2 ( x) 0 частное
f1(x)/f2(x), причем lim ( f1 ( x) f 2 ( x)) lim f1 ( x) lim f 2 ( x),
x a
x a
x a
lim ( f1 ( x) f 2 ( x)) lim f1 ( x) lim f 2 ( x),
x a
lim
x a
x a
x a
f1 ( x)
lim f1 ( x) / lim f 2 ( x).
x a
f 2 ( x) x a
Следствие 2: Если функция f(x) имеет предел при x a , то
lim ( f ( x)) n (lim f ( x)) n ,где n – натуральное число.
x a
x a
Следствие 3: Постоянный множитель можно выносить за знак
предела lim Cf ( x ) C lim f ( x ), C – const
x a
x a

10. Неопределенности и методы их решений Неопределенность вида

Неопределенности и методы их решений
0
Неопределенность вида
0
Методы:
1.
2.
3.
Разложение числителя и знаменателя
на множители с последующим
сокращением
Устранение иррациональных разностей.
Домножение на сопряженное.
Первый замечательный предел.
lim
0
sin
1

11. Неопределенности и методы их решений Неопределенность вида

Методы: Деление на наибольшую степень
Предел отношения двух многочленов (при условии,
что аргумент стремится к ∞) равен пределу
отношения их старших членов.
a0 x m a1 x m 1 … am
a0 x m
lim
lim
n
n
1
x b x b x
x b x n
…
b
0
1
n
0
Здесь a 0 0 и b 0 0
0 (m n)
a0
(m n)
b0
(m n)

12. Примеры:

x 3x 2
lim
x 1
x 1
3
1 x 1 x
lim
x 0
1 x 1
sin 7 x
lim
x 0 sin 14 x
2
3n n 1
lim 4
n n 2n
3

Урок Пределы функций

План–конспект занятия

Конкурсант (ФИО) Москалева Наталия Владиславовна

Дисциплина ЕН.01 Математика

Тема: Предел функции

Тим занятия Изучения нового материала

Длительность: 90 минут

Цель учебного занятия:

А. Учебные цели (для обучающихся):

1) формировать у обучающихся общие компетенции: ОК-1,2,9;

2) определить основные понятия: предел функции, бесконечно большие и бесконечно малые величины, неопределенность; научиться вычислять пределы и раскрывать неопределенности различных видов; закрепить новые понятия на практических задачах;

3) развивать качества мышления, умение наблюдать, обобщать, анализировать, совершенствовать пространственное воображение;

4) воспитывать математическую культуру, взаимопомощь, умение слушать товарища, чувство ответственности за коллектив в процессе творческой работы.

Б. Методические цели (для преподавателя):

1) формировать у обучающихся общие компетенции: ОК-1,2,9;

2) формировать представление о пределе функции;

3) организовать самостоятельную работу учащихся;

4) учить сравнивать, обобщать, анализировать ответы товарищей.

Задачи учебного занятия:

Образовательные:

ввести понятие предела числа, предела функции;

дать понятия о видах неопределенности;

научиться вычислять пределы функции;

научиться систематизировать и применять полученные знания, активизировать самоконтроль, взаимоконтроль.

Развивающие:

развивать  математическое мышление, развивать навыки коммуникативной культуры, развивать умения обучающихся четко, кратко излагать свои мысли, делать выводы, обобщения, анализировать;

Воспитательная:

воспитывать интерес к математике и к дисциплинам умственного труда.

Формирование общих компетенций (над которыми идет работа на учебном занятии)

ОК 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.

ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности.

ОК 09. Использовать информационные технологии в профессиональной деятельности.

Формирование профессиональных компетенций (над которыми идет работа на учебном занятии)

Используемые образовательные технологии:

Объяснительно-иллюстративная

Информационно-коммуникационные технологии (testpad)

Игровые (найди пару, кроссворд)

Технология обучение в сотрудничестве (работа в паре, работа в группе)

Разноуровневое обучение (дифференцированный подход к обучающимся)

Материалы и оборудование:

Мультимедийный проектор, экран, компьютер, доска, мел, карточки с упражнениями.

Этапы учебного занятия

1. Организационный момент – 2 мин.

2. Актуализация опорных знаний – 5 мин.

3. Изучение нового материала – 40 мин.

4. Закрепление материала – 35 мин.

5. Итоги урока – 3 мин.

6. Домашнее задание – 2 мин.

Ход учебного занятия

1. Организационный момент

Приветствие учителя, проверка готовности обучающихся к уроку.

В дальнейшем все задания выводятся на экран с компьютера.

– самостоятельность, способность к коллективной работе.

Определение темы задания с помощью кроссворда.

Озвучивание целей урока.

2. Актуализация опорных знаний

Что означает слово предел, функция, область определения функции

3. Изучение нового материала

Знакомство с теорией предела.

Предел функции в заданной точке— такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом: 

Рассмотрим различные графики функций и определим по ним предел функции:

Вычислим предел в точке (устно): 

1). ;

2) ;

3). ;

З аметим, что предел числа равен самому числу. Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).

Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.

Основные виды неопределенностей:  

Раскрытие неопределенностей

Для раскрытия неопределенностей 0/0 используют следующее:

упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул.

домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;

используют свойства замечательных пределов

Для раскрытия неопределенностей ∞/∞ необходимо разделить числитель и знаменатель на старшую степень знаменателя

Для раскрытия неопределенностей I и II замечательных пределов использую свойства тригонометрических и степенных функций.

Если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.

Рассмотрим примеры нахождения разного типа пределов:

4. Закреплнние материала

 Пример 1. Вычислите предел функции: 

При прямой подстановке, получается неопределенность:

Разложим на множители числитель и знаменатель и вычислим предел.

Пример 2. Вычислите предел функции: 

При прямой подстановке, получается неопределенность.

Помножим и числитель,  и знаменатель на .

Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично  

Пример 3. Вычислите предел функции: 

При прямой подстановке, получается неопределенность.

Помножим и числитель,  и знаменатель на .

Мы учли, что 

4. Самостоятельные упражнения

Вычислите пределы:

https://uchi.ru/b2t/teacher/check/3250313

5. Подведение итогов урока

Данный урок первый  по теме: «Предел функции». На уроке рассмотрены способы нахождения пределов. Разобрано что такое неопределенность, как раскрывать неопределенности.

6. Домашнее задание

Домашнее задание раздается на карточках каждому ученику.

https://uchi.ru/homeworks/teacher/new ?stage=jobs&s=1&p=5&t=199&c=22352

Свойства пределов функции

Предел функции является в математическом анализе одним из основных понятий. Функция f(x) в точке х₀ предел имеет L. Если все значения х достаточно близки к х₀, то близко к L и значение f(x).

На бесконечности предел функции описывает поведение значения самой функции, когда аргумент ее становится бесконечно большим.

Предел функции обозначается в виде f(x) → L в случае, если х→а

К основным свойствам пределов функции относят:

• предел постоянной величины, который равен самой постоянной величины;
• предел суммы, который равен сумме пределов самих функций. Также по аналогии и предел разности функций равен разности пределов данных функций;
• предел суммы множества функций равен также сумме пределов таких функций. По аналогии рассчитывает и предел нескольких функций, который равен разности пределов данных функций;
• повышение предела произведения функции (постоянного коэффициента) на знак предела;
• произведению пределов функций равен предел произведения двух функций;
• расширенное свойство предела произведения, которое в том заключается, что предел произведения функций равен и произведению пределов данных функций;
• предел частного функций равен отношению пределов данных функций, но только в том случае, если предел знаменателя нулю не равен;
• предел функции степенной, где действительным числом является степень р;
• предел функции показательной, при которой основание b больше 0;
• предел функции логарифмической, в которой основание b больше 0;
• теорема «двух милиционеров», при которой «зажатой» остается функция f(x)между другими двумя функции, которые также стремятся к пределу А.

Все перечисленные свойства пределов позволяют исходный предел функции свести к уже известному, чтобы получить ответ.

Определение и свойства пределов

Число b называется пределом функции f(x) при x → a, если для любого ε > 0 сущестувует δ > 0 такое, что для любого x из δ-окрестности a (|x – a|

Запись: ∀ ε > 0 ∃ δ > 0 : |x – a| |f(x) – f(a)|

Обозначение

Свойства пределов

lim x → a (f(x) + g(x) – h(x)) =   lim x → a f(x) +   lim x → a g(x) –   lim x → a h(x)

lim x → a (f(x) * g(x)) =   lim x → a f(x) *   lim x → a g(x)

lim x → a (cf(x)) = c *   lim x → a f(x)

lim x → a ( f(x) g(x) ) =    (   lim x → a g(x) ≠ 0)

Замечательные пределы

lim x → ∞ (1 +  1  x ) x   =   lim α → 0 (1 + α)  1  α     = e

e = 2,718281828459045235360287471352662497757. ..

Связь между десятичными и натуральными логарифмами

lg(x) = M ln(x),

где M = lg(e) = 0,43429448190325182765112891891666…

Свойства пределов

Обозначение предела

Предел функции обозначается \ (f \ left (x \ right) \ to L \) как \ (x \ to a \) или с использованием обозначения предела: \ (\ lim \ limits_ {x \ to a } f \ left (x \ right) = L. \)

Ниже мы предполагаем, что пределы функций \ (\ lim \ limits_ {x \ to a} f \ left (x \ right), \) \ (\ lim \ limits_ {x \ to a} g \ left (x \ справа), \) \ (\ lim \ limits_ {x \ to a} {f_1} \ left (x \ right), \) \ (\ ldots, \) \ (\ lim \ limits_ {x \ to a} { f_n} \ left (x \ right) \) существуют.

Правило суммы

Это правило гласит, что предел суммы двух функций равен сумме их пределов:

\ [\ lim \ limits_ {x \ to a} \ left [{f \ left (x \ right) + g \ left (x \ right)} \ right] = \ lim \ limits_ {x \ to a} f \ left (x \ right) + \ lim \ limits_ {x \ to a} g \ left (x \ right). \]

Правило расширенной суммы

\ [\ lim \ limits_ {x \ to a} \ left [{{f_1} \ left (x \ right) + \ ldots + {f_n} \ left (x \ right)} \ right] = \ lim \ limits_ {x \ to a} {f_1} \ left (x \ right) + \ ldots + \ lim \ limits_ {x \ to a} {f_n} \ left (x \ right).\]

Правило постоянной функции

Предел постоянной функции – это константа:

\ [\ lim \ limits_ {x \ to a} C = C. \]

Постоянное множественное правило

Предел умножения константы на функцию равен произведению константы на предел функции:

\ [\ lim \ limits_ {x \ to a} kf \ left (x \ right) = k \ lim \ limits_ {x \ to a} f \ left (x \ right). \]

Правило продукта

Это правило гласит, что предел произведения двух функций является произведением их пределов (если они существуют):

\ [\ lim \ limits_ {x \ to a} \ left [{f \ left (x \ right) g \ left (x \ right)} \ right] = \ lim \ limits_ {x \ to a} f \ left (x \ right) \ cdot \ lim \ limits_ {x \ to a} g \ left (x \ right). \]

Правило расширенного продукта

\ [\ lim \ limits_ {x \ to a} \ left [{{f_1} \ left (x \ right) {f_2} \ left (x \ right) \ cdots {f_n} \ left (x \ right)} » \ right] = \ lim \ limits_ {x \ to a} {f_1} \ left (x \ right) \ cdot \ lim \ limits_ {x \ to a} {f_2} \ left (x \ right) \ cdots \ lim \ limits_ {x \ to a} {f_n} \ left (x \ right). \]

Правило частного

Предел частного двух функций – это частное их пределов, при условии, что предел в функции знаменателя не равен нулю:

\ [\ lim \ limits_ {x \ to a} \ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} = \ frac {{\ lim \ limits_ {x \ to a} f \ left (x \ right)}} {{\ lim \ limits_ {x \ to a} g \ left (x \ right)}}, \; \; \; \ text {if} \; \; \ lim \ limits_ {x \ to a} g \ left (x \ right) \ ne 0.{\ lim \ limits_ {x \ to a} f \ left (x \ right)}}, \]

, где основание \ (b \ gt 0. \)

Предел логарифма функции

\ [\ lim \ limits_ {x \ to a} \ left [{\ log _b f \ left (x \ right)} \ right] = \ log_b \ left [{\ lim \ limits_ {x \ to a} f \ left (x \ right)} \ right], \]

, где основание \ (b \ gt 0. 3}} \ right).2}}} {{1 + \ sqrt 9}} = 81. \]

См. Другие проблемы на странице 2.

Лимиты | Функции Salesforce | Разработчики Salesforce

Функции

выполняются «вне» вашей организации в эластичной вычислительной инфраструктуре, которая избавляет вас от необходимости беспокоиться о многих ограничениях организации Salesforce. Кроме того, при вызове функции некоторые ограничения на стороне Salesforce, например ограничения вызовов API, корректируются, чтобы обеспечить возможность масштабирования функций в соответствии с вашими потребностями. Однако есть некоторые ограничения функций Salesforce, о которых вам все же нужно помнить при разработке функции.

Пределы и функции вершины

Код

Apex, вызывающий функции, по-прежнему выполняется в вашей организации, и к нему по-прежнему применяются обычные ограничения Apex. Следующие ограничения Apex требуют особого внимания при применении кода Apex, вызывающего функции:

на несколько функций Максимальное количество вызовов асинхронных функций из Apex

Описание	Предел	Соображения
Максимальное время ожидания ответа от синхронно запущенной функции	2 минуты	Рассмотрите возможность использования асинхронного вызова вместо синхронного или разделения	Без ограничений	Вызовы асинхронных функций не учитываются при максимальном количестве выполнений асинхронных методов Apex для организации. Обратные вызовы Apex для асинхронных вызовов функций в остальном идентичны другим ограничениям использования асинхронного Apex (например, future аннотации) во время выполнения.
Максимальное количество одновременных синхронных длительных (более 5 секунд) вызовов функций	10 на организацию	время выполнения включает время выполнения функции. Рассмотрите возможность использования асинхронных вызовов вместо синхронных.

Дополнительные сведения об ограничениях Apex см. В разделе «Пределы регулятора Apex».

Пределы выполнения функции

В следующей таблице перечислены ограничения для функций, развернутых и запущенных в вычислительных средах.

Описание	Лимит	Соображения
Время выполнения	15 минут	Рассмотрите возможность разделения работы вашей функции на отдельные функции или отдельные фазы рабочего процесса, который вы пытаетесь выполнить. выполнить.В настоящее время это ограничение не применяется. В будущем для функций будет применяться ограничение времени ожидания. Рекомендуется избегать работы функций дольше 15 минут.
Память процесса	1 ГБ	Рассмотрите возможность разделения работы вашей функции на отдельные функции или отдельные фазы общего рабочего процесса, который вы пытаетесь выполнить.
Размер полезной нагрузки	Синхронизация 6 МБ, асинхронность 12 МБ	Большие файлы данных, такие как файлы изображений или видео, не должны передаваться как часть полезной нагрузки функции.Вместо этого сохраните данные извне до вызова и ссылайтесь на данные по URL-адресу.
Размер ответа	Синхронизация 6 МБ, асинхронность 12 МБ	Это применимо только к данным ответа от функции, отправленным обратно в Apex, а не к общему объему данных, который может быть записан обратно в организацию

Ограничения API для функций

Следующие ограничения применяются к вызовам API веб-службы Salesforce, которые ваш код функции делает для организации, которая вызвала функцию. Имейте в виду, что если вы используете пакеты SDK функций, такие как пакеты SDK для Node.js или Java, методы API данных в пакетах SDK также используют API веб-служб Salesforce.

Описание	Лимит	Соображения
Всего запросов функций за 24-часовой период	235 000 запросов	Организациям, использующим функции, предоставляется 235 000 запросов API в день для единственного использования функциями Salesforce.
Одновременные длительные запросы API	То же, что и ограничения API	Долговременные запросы – это запросы, которые занимают 20 секунд или дольше. Рассмотрите возможность перемещения длительно выполняемых запросов в организацию – например, переместите сложную операцию с данными в Apex и попросите функцию использовать этот код через Apex REST или выполнить сложную операцию с данными в коде обратного вызова Apex из асинхронного вызова.

Нормальные ограничения платформы применяются к «нисходящим» действиям, вызываемым через API.Например, ограничение времени ЦП Apex будет применяться к операциям DML, которые вызывают триггеры.

Обратите внимание, что класс UnitOfWork в пакетах SDK для Node.js и Java использует API Composite Graph для вызовов вашей организации и, следовательно, имеет те же ограничения, что и ограничения API Composite Graph. Например, код вашей функции может ссылаться максимум на 15 различных узлов / объектов в одной транзакции UnitOfWork.

Дополнительные сведения об ограничениях API см. В разделе «Ограничения и распределение запросов API».

См. Шаблоны функций и Рекомендации по работе в пределах.

квот Lambda – AWS Lambda

Вычисления и хранилище

Lambda устанавливает квоты на количество вычислительных ресурсов и ресурсов хранения, которые вы можете использовать. для запуска и хранения функций. Следующие квоты применяются для каждого региона AWS и могут быть увеличены.Для дополнительной информации, см. Запрос квоты увеличение Service Quotas User Guide .

Новые учетные записи AWS могут начинаться с лимитов ниже этих значений по умолчанию. Лямбда контролирует использование и повышает ваши лимиты автоматически зависят от вашего использования.

Ресурс	Квота по умолчанию	Можно увеличить до
Одновременные исполнения	1 000	Десятки тысяч
Хранилище для загруженных функций (. zip-архивы) и слои. Каждая версия функции и слой версия потребляет память. Передовой опыт управления хранилищем кода см. В разделе Мониторинг хранилища лямбда-кода в Lambda. Руководство оператора .	75 ГБ	Терабайт
Хранилище для функций, определенных как образы контейнеров. Эти изображения хранятся в Amazon ECR.	См. Сервис Amazon ECR квоты.
эластичных сетевых интерфейсов на виртуальное частное облако (VPC) Эта квота используется совместно с другими сервисами, такими как Amazon Elastic File System (Amazon EFS). См. Квоты Amazon VPC.	250	сот

Подробные сведения о параллелизме и о том, как Lambda масштабирует параллелизм функций в ответ для трафика, см. Масштабирование лямбда-функции.

Функциональная конфигурация, развертывание и исполнение

Следующие квоты применяются к настройке, развертыванию и выполнению функций. Они не может быть измененный.

В документации, сообщениях журнала и консоли Lambda используется сокращение MB (скорее чем MiB) для обозначения 1024 КБ.

Ресурс	Квота
Распределение памяти функций	от 128 МБ до 10240 МБ с шагом 1 МБ.
Функция тайм-аут	900 секунд (15 минут)
Переменные среды функции	4 КБ, для всех переменных среды, связанных с функцией, в совокупности
Функция политики на основе ресурсов	20 КБ
Функциональные уровни	пять слоев
Параллелизм пакетов функций	500 – 3000 (зависит от региона)
Полезные данные вызова (запрос и ответ)	6 МБ (синхронно) 256 КБ (асинхронный)
Пакет развертывания (. zip-архив) размер	50 МБ (в архиве, для прямой загрузки) 250 МБ (разархивировано) Эта квота применяется ко всем загружаемым вами файлам, включая слои и пользовательские среды выполнения. 3 МБ (консольный редактор)
Размер пакета кода изображения контейнера	10 ГБ
Тестовые события (редактор консоли)	10
/ tmp хранилище каталогов	512 Мб
Дескрипторы файлов	1,024
Процессы / потоки выполнения	1,024

Лямбда-запросы API

Следующие квоты связаны с запросами Lambda API.

Ресурс	Квота
запросов на вызов на регион (запросов в секунду)	Квота на 10 одновременных выполнений (синхронно, все источники) Квота на 10 одновременных выполнений (асинхронные источники, не относящиеся к AWS)
запросов на вызов на регион (запросов в секунду) для асинхронных источников сервисов AWS	Принято неограниченное количество запросов. Скорость выполнения зависит от параллелизма, доступного для функция. Видеть Асинхронный вызов.
запросов на вызов для каждой версии функции или псевдонима (запросов в секунду)	10 выделенных подготовленных параллельных операций Эта квота применяется только к функциям, использующим подготовленный параллелизм.
запросов API GetFunction	100 запросов в секунду
запросов API GetPolicy	15 запросов в секунду
Остальные запросы API плоскости управления (исключая вызов, GetFunction и GetPolicy Запросы)	15 запросов в секунду

Прочие услуги

квоты для других сервисов, таких как AWS Identity and Access Management (IAM), Amazon CloudFront (Lambda @ Edge) и Amazon Virtual Private Cloud (Amazon VPC) могут влияют на ваши лямбда-функции. Для получения дополнительной информации см. AWS. квоты на сервисы в Общем справочнике Amazon Web Services и Использование AWS Lambda с другими сервисами.

квот | Документация по облачным функциям | Google Cloud

В этом документе описаны ограничения квот для функций Google Cloud.

Чтобы увеличить квоты выше значений по умолчанию, перечисленных здесь, перейдите к Страница квот облачных функций, выберите квоты, которые вы хотите изменить, нажмите ИЗМЕНИТЬ КВОТЫ , предоставьте информацию о пользователе, если будет предложено, и введите новый предел квоты для каждой выбранной квоты.

Квоты для облачных функций Google охватывают 3 области:

• Лимиты ресурсов

  Они влияют на общий объем ресурсов, которые могут потреблять ваши функции.

• Сроки

  Они влияют на то, как долго вещи могут работать.

• Пределы скорости

  Они влияют на скорость, с которой вы можете вызывать API облачных функций, и / или скорость, с которой могут использоваться ресурсы. Вы можете думать о тарифных квотах как о «ресурсах с течением времени».”

Различные типы ограничений более подробно описаны ниже.

Лимиты ресурсов

Ограничения ресурсов влияют на общий объем ресурсов, которые могут потреблять ваши функции. Региональный масштаб определяется для каждого проекта, и каждый проект поддерживает свои собственные ограничения.

Квота	Описание	Предел	Можно увеличить	Область применения
Количество функций	Общее количество функций, которые можно развернуть на регион	1 000	№	на регион
Максимальный размер развертывания	Максимальный размер развертывания одной функции	100 МБ (сжатый) для исходников. 500 МБ (без сжатия) для исходников и модулей.	№	на функцию
Максимальный размер несжатого HTTP-запроса	Данные, отправленные функциям HTTP в запросе HTTP	10 МБ	№	за вызов
Максимальный размер несжатого ответа HTTP	Данные, отправленные функциями HTTP в ответе HTTP	10 МБ	№	за вызов
Максимальный размер события для фоновых функций	Данные, отправленные в событиях фоновым функциям	10 МБ	№	за событие
Максимальный объем памяти функций	Объем памяти, который может использовать каждый экземпляр функции	8192МиБ	№	на функцию

Примечание: Если вы запускаете функцию с помощью Pub / Sub, либо через событийно-управляемые функции или в качестве цели HTTP для push-уведомлений подписки, имейте в виду, что сообщения Pub / Sub кодируются в кодировке base64. Сообщение Pub / Sub размером 10 МБ – максимальный размер. поддерживается – его размер после кодирования превышает 10 МБ, и поэтому он может превышать Ограничение максимального размера Cloud Functions.

Сроки

Квота	Описание	Предел	Можно увеличить	Область применения
Максимальная продолжительность функции	Максимальное время, в течение которого функция может работать до принудительного завершения	540 секунд	№	за вызов

Пределы скорости

Квота	Описание	Предел	Можно увеличить	Область применения
Вызовы API (ЧТЕНИЕ)	Вызовы для описания или перечисления функций через API облачных функций	5000 за 100 секунд	Есть	по проекту
Вызовы API (ЗАПИСЬ)	Вызовы для развертывания или удаления функций через API облачных функций	80 за 100 секунд	№	по проекту
API-вызовы (CALL)	Обращения к «вызову» API	16 за 100 секунд	№	по проекту

Масштабируемость

Облачные функции, вызываемые HTTP, быстро масштабируются для обработки входящего трафика, в то время как фоновые функции масштабируются более постепенно. Возможность масштабирования функции вверх продиктовано несколькими факторами, в том числе:

• Время, необходимое для завершения выполнения функции (краткосрочные функции обычно можно масштабировать для обработки большего количества одновременных Запросы).
• Время, необходимое для инициализации функции. холодный запуск.
• Ограничения скорости, как описано выше.
• Коэффициент ошибок вашей функции.
• Переходные факторы, такие как региональная нагрузка и емкость центра обработки данных.

Фоновые функции имеют дополнительные пределы, как объяснено ниже. Эти ограничения не применяются к HTTP. функции.

Дополнительные квоты для фоновых функций

Квота	Описание	Предел	Можно увеличить	Область применения
Максимальное количество одновременных вызовов	Максимальное количество одновременных вызовов одной функции Пример: если обработка каждого события занимает 100 секунд, вызов скорость будет ограничена 30 в секунду в среднем	3 000	№	на функцию
Макс. частота вызовов	Максимальная частота событий, обрабатываемых одной функцией Пример: , если обработка события занимает 100 мс, вызов скорость будет ограничена до 1000 в секунду, даже если всего 100 запросов, в среднем обрабатываются параллельно	1000 в секунду	№	на функцию
Максимальный размер данных одновременного события	Максимальный общий размер входящих событий для одновременных вызовов одна функция Пример: , если размер событий составляет 1 МБ, и их обработка занимает 10 секунд, средняя скорость будет 1 событие в секунду, потому что 11-е событие не будет обработано до тех пор, пока не будет обработано одно из первых 10 событий отделки	10 МБ	№	на функцию
Макс. Пропускная способность входящих событий	Максимальная пропускная способность входящих событий для одной функции Пример: если события имеют размер 1 МБ, то частота вызовов может быть максимум 10 в секунду, даже если функции завершаются в течение 100 мс	10 МБ в секунду	№	на функцию

При достижении лимита квоты

Когда функция потребляет весь выделенный ресурс, ресурс становится недоступно, пока квота не будет обновлена ​​или увеличена. Это может означать, что ваш function и все другие функции в том же проекте до этого момента работать не будут. Функция возвращает код ошибки HTTP 500, когда один из ресурсов превышена квота, и функция не может быть выполнена.

Чтобы увеличить квоты сверх значений по умолчанию, перечисленных здесь, перейдите к Страница квот облачных функций, выберите квоты, которые вы хотите изменить, нажмите ИЗМЕНИТЬ КВОТЫ , укажите информацию о пользователе, если будет предложено, и введите новый предел квоты для каждой выбранной квоты.

Расчет пределов функции

Чтобы вычислить предел функции, важно помнить об основных свойствах пределов.

Свойства границ

Пусть $$ f (x) $$ – функция, поэтому:

1. $$ \ displaystyle \ lim_ {x \ to p} {x} = p \\ $$
2. $$ \ displaystyle \ lim_ {x \ to p} {k \ cdot f (x)} = k \ cdot \ lim_ {x \ to p} {f (x)} $$, где $$ k $$ – целое число.
3. $$ \ displaystyle \ lim_ {x \ to p} {(f (x) + g (x))} = \ lim_ {x \ to p} {f (x)} + \ lim_ {x \ to p} {g (x)} \\ $$
4. $$ \ displaystyle \ lim_ {x \ to p} {(f (x) -g (x))} = \ lim_ {x \ to p} {f (x)} – \ lim_ {x \ to p} {g (x)} \\ $$
5. $$ \ Displaystyle \ lim_ {x \ to p} {(f (x) \ cdot g (x))} = \ lim_ {x \ to p} {f (x)} \ cdot \ lim_ {x \ to p} {g (x)} \\ $$
6. $$ \ displaystyle \ lim_ {x \ to p} {\ dfrac {f (x)} {g (x)}} = \ dfrac {\ displaystyle \ lim_ {x \ to p} {f (x)}} {\ displaystyle \ lim_ {x \ to p} {g (x)}} $$ si $$ g (x) \ neq0 $$

Здесь мы можем увидеть пример каждого свойства:

1. $$ \ Displaystyle \ lim_ {x \ to 2} {x} = 2 \\ $$
2. $$ \ displaystyle \ lim_ {x \ to 1} {2x ^ 2} = 2 \ cdot \ lim_ {x \ to 1} {x ^ 2} = 2 \ cdot1 ^ 2 = 2 \\ $$
3. $$ \ displaystyle \ lim_ {x \ to 4} {(x ^ 2 + 3x)} = \ lim_ {x \ to 4} {x ^ 2} + \ lim_ {x \ to 4} {3x} = 4 ^ 2 + 3 \ cdot4 = 16 + 12 = 28 \\ $$
4. $$ \ displaystyle \ lim_ {x \ to 3} {(x-5x)} = \ lim_ {x \ to 3} {x} – \ lim_ {x \ to 3} {5x} = 3-5 \ cdot3 = 3-15 = -12 \\ $$
5. $$ \ displaystyle \ lim_ {x \ to 2} {x ^ 2} = \ lim_ {x \ to 2} {x} \ cdot \ lim_ {x \ to 2} {x} = 2 \ cdot2 = 4 \ \ $$
6. $$ \ displaystyle \ lim_ {x \ to 1} {\ dfrac {x + 1} {x}} = \ dfrac {\ displaystyle \ lim_ {x \ to 1} {x + 1}} {\ displaystyle \ lim_ {x \ to 1} {x}} = \ dfrac {1 + 1} {1} = 2 $$

Операции с бесконечностью

Мы знаем, что некоторые пределы могут оказаться бесконечными. \ infty, \ ldots $$$

Вы можете узнать, как решать эти ситуации в следующем блоке (расчет пределов-неопределенностей).

Теперь мы можем вычислить предел функции.

Чтобы вычислить предел функции $$ f (x) $$ в $$ x = p $$, мы просто должны заменить $$ x $$ на $$ p $$ в выражении предела. При выполнении этого шага может быть получено конкретное значение (число, бесконечное значение или неопределенность. В последнем случае нам придется изменить выражение предела на другое эквивалентное выражение, чтобы очистить неопределенность.Этот шаг объясняется в следующем разделе (расчет пределов-неопределенностей).

В случае, когда функции определены частями или прерывистыми функциями, нам придется установить боковые ограничения в зависимости от точки, в которой предел должен быть вычислен. Мы выберем подходящее выражение функции для установки в пределе, если мы подойдем справа или слева. У нас есть пример:

Рассмотрим $$ f (x) = \ left \ {\ begin {array} {c} x + 1 \ \ text {si} x

$$$ L ^ – = \ lim_ {x \ to 1 ^ -} {f (x)} = \ lim_ {x \ to 1 ^ -} {x + 1} = 1 + 1 = 2 $$$

$$$ L ^ + = \ lim_ {x \ to 1 ^ +} {f (x)} = \ lim_ {x \ to 1 ^ +} {x-1} = 1-1 = 0 $$$

Когда мы выполняем ограничение функции в бесконечности, необходимо действовать так же, как если бы мы выполняли ограничение в точке, но заменяя значение конкретной точки бесконечностью. 2} = \ lim_ {x \ to – \ infty} {x} \ cdot \ lim_ {x \ to – \ infty} {x} = (- \ infty) \ cdot (- \ infty) = + \ infty $$ $

Как рассчитать, примеры, практические задачи, рисунки

Ошибка: Нажмите «Не робот», затем повторите попытку.

Краткий обзор

Если $$ x $$ приближается к одной из точек перехода функции, вам необходимо проверить оба односторонних предела.

Примеры

Пример 1

Определите $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) $$, если $$ f $$ определен, как показано ниже.

$$ е (х) = \ влево \ {% \ begin {array} {ll} 2x + 3, & x

Шаг 1

Оцените односторонние пределы. +} (5x-9) = 5 (4) -9 = 11 \ end {выровнять *} $$

Шаг 2

Если односторонние ограничения совпадают, ограничение существует.

Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) = 11 $$, если $$ f $$ определен, как указано выше.

Пример 2

Вычислить $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$, когда $$ f $$ определен следующим образом. 2 + 4, & х

Шаг 1

Изучите односторонние пределы.+} \ sqrt x = \ sqrt 0 = 0 \ end {выровнять *} $$

Шаг 2

Если односторонние ограничения различны, ограничение не существует.

Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

Пример 3

Предположим, что $$ f $$ определен, как показано ниже.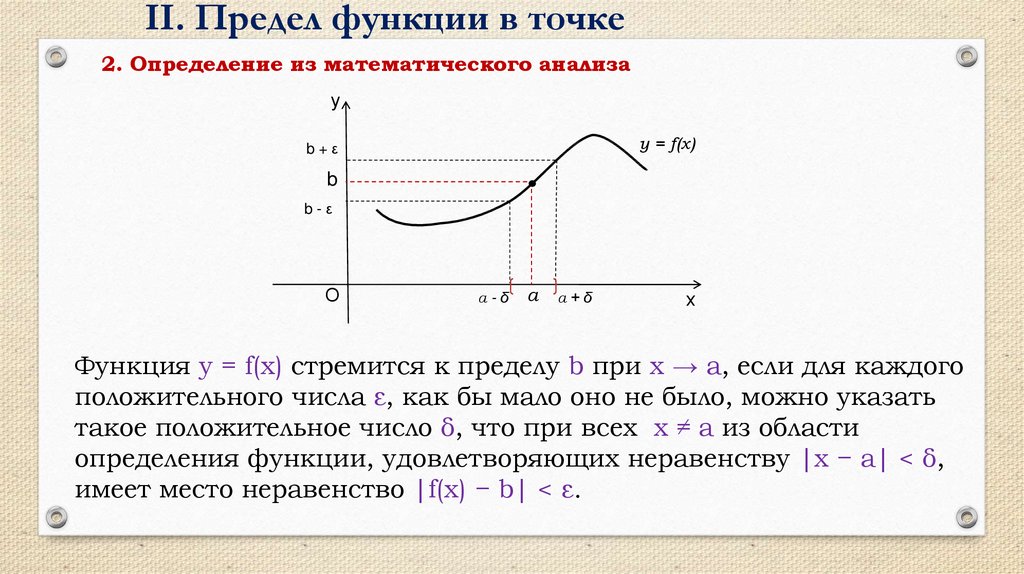 +} \ left (\ frac 2 3 x + b \ right) = \ frac {2 (5)} 3 + b = \ frac {10} 3 + b \ end {выровнять *} $$

Шаг 2

Установите два предела равными друг другу и решите.

$$ \\ \ begin {align *} \ frac {10} 3 + b & = 7 \\ [6pt] b & = 7 – \ frac {10} 3 \\ [6pt] b & = \ frac {11} 3 \ end {выровнять *} \\ $$

Ответ: $$ b = \ frac {11} 3 $$

Практические задачи

Задача 1

Вычислить $$ \ displaystyle \ lim_ {x \ to 2} f (x) $$, если $$ f $$ определен следующим образом. +} \ left (3x + 4 \ right) = 3 (2) +4 = 10 \ end {выровнять *} $$

Шаг 2 Отвечать

Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to2} f (x) = 10 $$, если $$ f $$ определен, как указано выше.

Задача 2

Вычислить $$ \ displaystyle \ lim_ {x \ to 4} f (x) $$, если $$ f $$ определен следующим образом. +} \ frac 1 4 x = \ frac 4 4 = 1 \ end {выровнять *} $$

Шаг 2 Отвечать

Ответ: $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 1 $$, если $$ f $$ определен, как указано выше.

Задача 3

Вычислить $$ \ displaystyle \ lim_ {x \ to 1} f (x) $$, когда $$ f $$ определен следующим образом. +} \ frac 1 {x-1} = \ frac 1 0 \ qquad \ mbox {Деление на ноль!} \ end {выровнять *} $$

Шаг 2 Отвечать

Ответ: $$ \ displaystyle \ lim_ {x \ to1} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

Задача 4

Вычислить $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$, когда $$ f $$ определен, как показано ниже. +} \ left (2x + \ frac 8 3 \ right) = 2 (-5) + \ frac 8 3 = – \ frac {22} 3 \ end {выровнять *} $$

Шаг 2 Отвечать

Ответ: $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$ не существует, если $$ f $$ определен, как указано выше.

Задача 5

Определите значение $$ b $$, чтобы $$ \ displaystyle \ lim_ {x \ to-6} f (x) $$ существовал, когда $$ f $$ определен, как показано ниже. +} \ left (\ frac 1 2 x + 9 \ right) = \ frac {-6} 2 + 9 = -3 + 9 = 6 \ end {выровнять *} $$

Шаг 2

Установите два односторонних предела равными друг другу и решите.

Отвечать

$$ \ begin {align *} 36 + b & = 6 \\ b & = -30 \ end {выровнять *} $$

Ответ: $$ b = -30 $$

Задача 6

Определите значение $$ m $$, чтобы $$ \ displaystyle \ lim_ {x \ to3} f (x) $$ существовал, когда $$ f $$ определяется следующим образом. +} (mx-4) = 3m-4 \ end {выровнять *} $$

Шаг 2

Приравняйте два предела и решите.

Отвечать

$$ \\ \ begin {align *} 3–4 & = 13 \\ [6pt] 3м & = 17 \\ [6pt] m & = \ frac {17} 3 \ end {выровнять *} \\ $$

Ответ: $$ m = \ frac {17} 3 $$

Задача 7

Определите значение (я) $$ m $$ и $$ b $$, поэтому $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 10 $$, когда $$ f $$ определен, как показано ниже. +} (5x + b) = 20 + b. \ end {выровнять *} $$

Шаг 2

Поскольку оба предела должны равняться 10, составьте систему уравнений и решите.

Отвечать

$$ \\ \ begin {align *} 4m + 2b & = 10 \\ 20 + b & = 10 \\ [12pt] % 4m + 2b & = 10 \\ b & = -10 && \ mbox {Решите относительно \ (b \) во втором уравнении. } \\ [12pt] % 4m + 2 (-10) & = 10 && \ mbox {Подставьте значение \ (b \) в другое уравнение.} \\ 4м – 20 & = 10 \\ 4 м & = 30 \\ [6 пт] m & = \ frac {30} 4 \\ [6pt] m & = \ frac {15} 2 \ end {выровнять *} \\ $$

Ответ: $$ m = \ frac {15} 2 $$ и $$ b = -10 $$.

Ошибка: Нажмите «Не робот», затем повторите попытку.

Math Nspired – Исчисление – Пределы функций от Texas Instruments

Управление настройками файлов cookie

Вы можете управлять своими предпочтениями в отношении того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.

Категория	Описание	Разрешить
Аналитические и рабочие файлы cookie	Эти файлы cookie, включая файлы cookie Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI, а также видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте).
Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
Функциональные файлы cookie	Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, включая более персонализированный и релевантный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: