Пределы. Понятие пределов. Вычисление пределов.
Понятие пределов рассмотрим на показательных примерах.
Пусть х – числовая переменная величина, Х – область ее изменения. Если каждому числу х, принадлежащему Х, поставлено в соответствие некоторое число у, то говорят, что на множестве Х определена функция, и записывают у = f(x).
Множество Х в данном случае – плоскость, состоящая из двух координатных осей – 0X и 0Y. Для примера изобразим функцию у = х2. Оси 0X и 0Y образуют Х – область ее изменения. На рисунке прекрасно видно, как ведет себя функция. В таком случае говорят, что на множестве Х определена функция у = х2.
Совокупность Y всех частных значений функции называется множеством значений f(x). Другими словами, множество значений – это промежуток по оси 0Y, где определена функция. Изображенная парабола явно показывает, что f(x) > 0 , т.к. x2 > 0.
Совокупность всех х называется областью определения f(x). Множество определений смотрим по 0X и в нашем случае областью допустимых значений является [-; +].
Точка а (а принадлежит или Х) называется предельной точкой множества Х, если в любой окрестности точки а имеются точки множества Х, отличные от а.
Пришла пора понять – что же такое предел функции?
Чисто b, к которому стремится функция при стремлении х к числу а, называется пределом функции. Записывается это следующим образом:
Например, f(x) = х2. Нам надо узнать, к чему стремится (не равна) функция при х 2. Сначала запишем предел:
Посмотрим на график.
Проведем параллельно оси 0Y линию через точку 2 на оси 0X. Она пересечет наш график в точке (2;4). Опустим из этой точки на ось 0Y перпендикуляр – и попадем в точку 4. Вот к чему стремится наша функция при х 2. Если теперь подставить в функцию f(x) значение 2, то ответ будет таким же.
Если теперь подставить в функцию f(x) значение 2, то ответ будет таким же.
Теперь прежде чем перейти к вычислению пределов, введем базовые определения.
Понятие пределов введено французским математиком Огюстеном Луи Коши в XIX веке.
Допустим, функция f(x) определена на некотором интервале, в котором содержится точка x = A, однако совсем не обязательно, чтобы значение f(А) было определено.
Тогда, согласно определению Коши, пределом функции f(x) будет некое число B при x, стремящимся к А, если для каждого C > 0 найдется число D > 0, при котором
Т.е. если функция f(x) при x А ограничена пределом В, это записывается в виде
.
Пределом последовательности называется некое число А, если для любого сколь угодно малого положительного числа В > 0 найдется такое число N, при котором все значения в случае n > N удовлетворяют неравенству
Такой предел имеет вид .
Последовательность, у которой есть предел, будем называть сходящейся, если нет – расходящейся.
Как Вы уже заметили, пределы обозначаются значком lim, под которым записывается некоторое условие для переменной, и далее уже записывается сама функция. Такой набор будет читаться, как «предел функции при условии…». Например:
– предел функции при х, стремящимся к 1.
Выражение «стремящимся к 1» означает, что х последовательно принимает такие значения, которые бесконечно близко приближаются к 1.
Теперь становится ясно, что для вычисления данного предела достаточно подставить вместо х значение 1:
Ответ: -3.
Кроме конкретного числового значения х может стремиться и к бесконечности. Например:
Выражение х означает, что х постоянно возрастает и неограниченно близко приближается к бесконечности. Поэтому подставив вместо х бесконечность станет очевидно, что функция 1- х будет стремиться к , но с обратным знаком:
Таким образом, вычисление пределов сводится к нахождению его конкретного значения либо определенной области, в которую попадает функция, ограниченная пределом.
Исходя из вышеизложенного следует, что при вычислении пределов важно пользоваться несколькими правилами:
- Сперва попытаемся подставить в функцию число. Результат вычисление и будет ответом.
- Если х стремиться не к числу, например в пределах вида или , то такие пределы решаются сразу, т.к число деленное на бесконечность всегда дает ноль, а деленное на 0 всегда бесконечность. Если у вас затруднено понимание понятий бесконечность и 0 в пределах, то вы можете подставлять вместо бесконечности – бесконечно большое число – например 1000 000, или вместо 0 – бесконечно малое – к примеру 0,000001 и прикинуть к чему будет стремиться ответ.
- Есть еще одна интересная группа пределов, где мы и в числите и в знаменателе при подстановке получаем или 0 или бесконечность. Так называемые пределы с неопределенностью, часть из которых замечательные. Их мы рассматриваем отдельно в статьях “Вычисление пределов. Пределы с неопределенностью” и “Замечательные пределы: Первый и второй замечательный предел”.

Понимая сущность предела и основные правила вычисления пределов, вы получите ключевое представление о том, как их решать. Если какой предел будет вызывать у вас затруднения, то пишите в комментарии и мы обязательно вам поможем.
Заметка: Юриспруденция – наука о законах, помогающее в конфлитных и других жизненных трудностях.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Внутренняя ошибка сервера
Дополнительная отладочная информация URL: https://www.khanacademy.org/math/ap-calculus-ab/ab-limits-new/ab-1-15/v/limits-at- положительная и отрицательная бесконечность
Заголовки:
{
"host": "www.khanacademy.org",
"x-forwarded-for": "85.249.26.246, 157.52.95.61, 157.52.75.71, 169.254.1.1",
"x-forwarded-host": "www.
khanacademy.org, www.khanacademy.org",
"x-forwarded-proto": "https",
"переадресовано": "for = \" 157.52.75.71 \ "; proto = https",
"user-agent": "Mozilla / 5.0 (X11; Linux x86_64; rv: 33.0) Gecko / 20100101 Firefox / 33.0",
"accept": "text / html, application / xhtml + xml, application / xml; q = 0.9, * / *; q = 0.8",
"accept-language": "en-US, en; q = 0,5",
"accept-charset": "windows-1251, utf-8; q = 0,7, *; q = 0,7",
"content-type": "application / x-www-form-urlencoded; charset = UTF-8",
"fastly-ssl": "1",
"fastly-client-ip": "85.249.26.246",
"x-forwarded-server": "cache-bma1672-BMA, cache-mdw17328-MDW",
"fastly-soc-x-request-id": "8c0e55389bb961a741ec33ee4ce98e18a13dfcf762a67168ffa2751a1c508e8b",
"x-fastly-tls": "1",
"x-ka-deadline": "2021-11-16T17: 35: 20Z",
"x-ka-bingo-id": "kaid_873830987125 62569511",
"x-ka-tmp-set-bingo-id-cookie": "! $ - GK5WOy7Xn9Qv_di4jCtgjI_mU0lDffnalLrwROVxZs.~ r2odqj ~ 1 $ a2FpZF84NzM4MzA5ODcxMjU5MDQ1MzYyNTY5NTEx ",
"x-ka-use-render-gateway": "правда",
«х-лак»: «210965496, 4176516382, 1825617000, 10 784766, VS0, VS0",
"x-fastly-country": "RU",
"x-fastly-region": "TA",
"x-ka-curriculum": "",
"x-ka-orig-url": "/ math / ap-Calculus-ab / ab-limits-new / ab-1-15 / v / limits-at-positive-and-negative-infinity",
"x-ka-orig-host": "www.khanacademy.org",
"x-ka-is-e2e": "ложь",
"x-ka-is-bot": "ложь",
"x-ka-is-ios": "ложь",
"x-ka-is-phone": "ложь",
"x-ka-is-tablet": "ложь",
"x-ka-is-unsupported-browser": "правда",
"x-ka-browser": "Firefox",
"x-ka-browser-os": "Linux",
"x-ka-lang": "en",
"x-ka-locale": "en",
«х-ка-прокси-обновление-каал»: «0»,
"x-ka-published-content-version": "b362d19b0dbcd4aa7eda60a240dc38f6c0053bc0",
"x-ka-static-version": "211116-0736-da62641532e1",
"x-ka-at-post-gateway-proxy-edge": "0",
"fastly-client": "1",
"Fastly-ФФ":!!!!! «LtsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1672-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1661-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = ОМП кэш-mdw17328- MDW, ltsxTZVz3 / qY + PjkowxBUBQDaDchBm1aPceAyytMsr4 =! MDW! Cache-mdw17371-MDW ",
"cdn-loop": "Быстро, Быстро, Быстро, Быстро",
"x-cloud-trace-context": "58ce4dff9d3b0a06cc81faabfba0700a / 865
784766, VS0, VS0",
"x-fastly-country": "RU",
"x-fastly-region": "TA",
"x-ka-curriculum": "",
"x-ka-orig-url": "/ math / ap-Calculus-ab / ab-limits-new / ab-1-15 / v / limits-at-positive-and-negative-infinity",
"x-ka-orig-host": "www.khanacademy.org",
"x-ka-is-e2e": "ложь",
"x-ka-is-bot": "ложь",
"x-ka-is-ios": "ложь",
"x-ka-is-phone": "ложь",
"x-ka-is-tablet": "ложь",
"x-ka-is-unsupported-browser": "правда",
"x-ka-browser": "Firefox",
"x-ka-browser-os": "Linux",
"x-ka-lang": "en",
"x-ka-locale": "en",
«х-ка-прокси-обновление-каал»: «0»,
"x-ka-published-content-version": "b362d19b0dbcd4aa7eda60a240dc38f6c0053bc0",
"x-ka-static-version": "211116-0736-da62641532e1",
"x-ka-at-post-gateway-proxy-edge": "0",
"fastly-client": "1",
"Fastly-ФФ":!!!!! «LtsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1672-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1661-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = ОМП кэш-mdw17328- MDW, ltsxTZVz3 / qY + PjkowxBUBQDaDchBm1aPceAyytMsr4 =! MDW! Cache-mdw17371-MDW ",
"cdn-loop": "Быстро, Быстро, Быстро, Быстро",
"x-cloud-trace-context": "58ce4dff9d3b0a06cc81faabfba0700a / 865 19464204952; o = 3",
"x-appengine-region": "я",
"x-appengine-citylatlong": "43. 517766, -70.377291 ",
"x-appengine-country": "США",
"x-appengine-city": "старый фруктовый сад",
"x-google-apps-metadata": "domain = gmail.com, host = www.khanacademy.org",
"x-appengine-default-namespace": "gmail.com",
"traceparent": "00-58ce4dff9d3b0a06cc81faabfba0700a-782b603c05f5ba98-03",
"x-appengine-timeout-ms": "599999",
"x-appengine-https": "включено",
"x-appengine-user-ip": "157.52.75.71",
"x-appengine-api-ticket": "ChBlMGY2MmZiZjZiZjZhNDBjEKHVnxUQp9WfFRoTCP6t95 + znfQCFbyBtQEdieEGaw ==",
"x-appengine-request-log-id": "6193e96300ff0af83ed2f8382a0001737e6b68616e2d61636164656d7
517766, -70.377291 ",
"x-appengine-country": "США",
"x-appengine-city": "старый фруктовый сад",
"x-google-apps-metadata": "domain = gmail.com, host = www.khanacademy.org",
"x-appengine-default-namespace": "gmail.com",
"traceparent": "00-58ce4dff9d3b0a06cc81faabfba0700a-782b603c05f5ba98-03",
"x-appengine-timeout-ms": "599999",
"x-appengine-https": "включено",
"x-appengine-user-ip": "157.52.75.71",
"x-appengine-api-ticket": "ChBlMGY2MmZiZjZiZjZhNDBjEKHVnxUQp9WfFRoTCP6t95 + znfQCFbyBtQEdieEGaw ==",
"x-appengine-request-log-id": "6193e96300ff0af83ed2f8382a0001737e6b68616e2d61636164656d7 72656e6465722d676174657761793a3231313130382d303632332d62101333163632",
"x-appengine-default-version-hostname": "khan-academy.appspot.com "
} Шлюз рендеринга Стек:
https://cdn.kastatic.org/genwebpack/prod/en/chunk-map.ba8bb3a76bd8a5e39be6.js:4
window ["kaJsonAssets"] ["chunkMap"] = {"chunks": {"1422": ["/ genwebpack / prod / en / 1422. 5c46a3e83acdeae8c4fd.js"], "./ javascript / app-shell-package / app -entry ": [" / genwebpack / prod / en / javascript / app-shell-package / app-entry.95aab4ab037c6d9a4bd5.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / страница-пакет / заголовок-запись ~./javascript/sat-mis~d7d3c7de":["/genwebpack/prod/en/javascript/app-shell-package/app-entry~./javascript/page-package/header-entry~./javascript/sat-mis ~ d7d3c7de.32357580f3eea36789d4.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript / app- shell-package / app-entry ~. / javascript / student-package / student-entry.c0d0f7ae67f1c1f5cfe5.css "," / genwebpack / prod / en / javascript / app-shell-package / app-entry ~. / javascript / student -пакет / студенческий вход.9e6aedcc2285f31f4fe1.js "]," ./ javascript / badges-package / viewbadges-entry ": [" / genwebpack / prod / en / javascript / badges-package / viewbadges-entry.
5c46a3e83acdeae8c4fd.js"], "./ javascript / app-shell-package / app -entry ": [" / genwebpack / prod / en / javascript / app-shell-package / app-entry.95aab4ab037c6d9a4bd5.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / страница-пакет / заголовок-запись ~./javascript/sat-mis~d7d3c7de":["/genwebpack/prod/en/javascript/app-shell-package/app-entry~./javascript/page-package/header-entry~./javascript/sat-mis ~ d7d3c7de.32357580f3eea36789d4.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript / app- shell-package / app-entry ~. / javascript / student-package / student-entry.c0d0f7ae67f1c1f5cfe5.css "," / genwebpack / prod / en / javascript / app-shell-package / app-entry ~. / javascript / student -пакет / студенческий вход.9e6aedcc2285f31f4fe1.js "]," ./ javascript / badges-package / viewbadges-entry ": [" / genwebpack / prod / en / javascript / badges-package / viewbadges-entry. 4195517f08e0ebddaf4a.css "/ pro / genwebpack ru / javascript / badges-package / viewbadges-entry.4af1c080d9702352c2c5.js "]," ./ javascript / devadmin-package / award-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / award -badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / award-badge-entry.765e3cbecbf1bb15e03d.js "]," ./ javascript / devadmin-package / create-custom-badge -entry ": [" / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.9f5e83716c78a36456d8.js "]," ./ javascript / devadmin-package / download-csv-entry ": [ "/genwebpack/prod/en/javascript/devadmin-package/download-csv-entry.38691c3d6f738f3344a2.js"pting,"./javascript/devadmin-package/download-csv-entry./javascript~devadmin-package/translation -linter-de ~ 7c7b793f ": [" / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~.
4195517f08e0ebddaf4a.css "/ pro / genwebpack ru / javascript / badges-package / viewbadges-entry.4af1c080d9702352c2c5.js "]," ./ javascript / devadmin-package / award-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / award -badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / award-badge-entry.765e3cbecbf1bb15e03d.js "]," ./ javascript / devadmin-package / create-custom-badge -entry ": [" / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.9f5e83716c78a36456d8.js "]," ./ javascript / devadmin-package / download-csv-entry ": [ "/genwebpack/prod/en/javascript/devadmin-package/download-csv-entry.38691c3d6f738f3344a2.js"pting,"./javascript/devadmin-package/download-csv-entry./javascript~devadmin-package/translation -linter-de ~ 7c7b793f ": [" / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.c88c5344428c6e9e48b7.css "," / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.7017266bcdc848240746.js "]. javascript / devadmin-package / translation-linter-debugging-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / translation-linter-debugging-entry.82aa7738576225311f69.js "]," ./ javascript / devadmin -package / update-custom-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.8069f4c9a068b52ec276.js "]," ./ javascript / devpanel-package / abort-pipelines-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / abort-pipelines-entry.6ab5862b9cc3329f3318.js "]," ./ javascript / devpanel-package / content-analytics-oauth-entry ": [" / genwebpack / prod / en /javascript/devpanel-package/content-analytics-oauth-entry.
/ javascript / devadmin-package / translation-linter-de ~ 7c7b793f.c88c5344428c6e9e48b7.css "," / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.7017266bcdc848240746.js "]. javascript / devadmin-package / translation-linter-debugging-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / translation-linter-debugging-entry.82aa7738576225311f69.js "]," ./ javascript / devadmin -package / update-custom-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.8069f4c9a068b52ec276.js "]," ./ javascript / devpanel-package / abort-pipelines-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / abort-pipelines-entry.6ab5862b9cc3329f3318.js "]," ./ javascript / devpanel-package / content-analytics-oauth-entry ": [" / genwebpack / prod / en /javascript/devpanel-package/content-analytics-oauth-entry. dfb95926e34ea7354d19.css","/genwebpack/prod/en/javascript/devpanel-package/content-analytics-oauth-entry.29f4296a91c33e6d061e.js "]," ./ javascript / devpanel-package / edit-learn-menu-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / edit-learn-menu-entry.96788deff06387dc5db2.js "]," ./ javascript / devpanel-package / email-preview-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / email-preview-entry.9473911a47a0fadd4f43.js "]," ./ javascript /devpanel-package/standard-mapping-entry":["/genwebpack/prod/en/javascript/devpanel-package/standard-mapping-entry.acc7781344410030db08.css","/genwebpack/prod/en/javascript/devpanel- пакет / стандарт-сопоставление-запись.e70cc5c9aea7e6fc2f76.js "]," ./ javascript / devpanel-package / start-mapreduce-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / start-mapreduce-entry.a7ce035dbc8daafa1699.js "," ./javascript/devpanel-package/test-emails-entry":["/genwebpack/prod/en/javascript/devpanel-package/test-emails-entry.
dfb95926e34ea7354d19.css","/genwebpack/prod/en/javascript/devpanel-package/content-analytics-oauth-entry.29f4296a91c33e6d061e.js "]," ./ javascript / devpanel-package / edit-learn-menu-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / edit-learn-menu-entry.96788deff06387dc5db2.js "]," ./ javascript / devpanel-package / email-preview-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / email-preview-entry.9473911a47a0fadd4f43.js "]," ./ javascript /devpanel-package/standard-mapping-entry":["/genwebpack/prod/en/javascript/devpanel-package/standard-mapping-entry.acc7781344410030db08.css","/genwebpack/prod/en/javascript/devpanel- пакет / стандарт-сопоставление-запись.e70cc5c9aea7e6fc2f76.js "]," ./ javascript / devpanel-package / start-mapreduce-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / start-mapreduce-entry.a7ce035dbc8daafa1699.js "," ./javascript/devpanel-package/test-emails-entry":["/genwebpack/prod/en/javascript/devpanel-package/test-emails-entry. 2b5b241365737f3b1dbf.js" ],"./javascript/devpanel-package /thumbnails-entry":["/genwebpack/prod/en/javascript/devpanel-package/thumbnails-entry.f563e2a2a57dab92e593.js"pting,"./javascript/discussion-package/mod-entry":["/genwebpack/ prod / en / javascript / обсуждение-пакет / мод-запись.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсудить-пакет / mod-entry.4b6a73a0594b32556dee.js "]," ./ javascript / обсуждение-пакет / модерация-журналы-запись ": [" / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.e388870b0b9099d849f9.js "]," ./ javascript / donate-package / recurring-donation-cancel-entry ": [" / genwebpack / prod / en / javascript / donate-package / recurring-donation-cancel-entry.fc66bf5e2742c821bbb3.js "]," ./ javascript / editor-package / content-tags-entry ": [" / genwebpack / prod / en / javascript / editor-package / content-tags-entry.
2b5b241365737f3b1dbf.js" ],"./javascript/devpanel-package /thumbnails-entry":["/genwebpack/prod/en/javascript/devpanel-package/thumbnails-entry.f563e2a2a57dab92e593.js"pting,"./javascript/discussion-package/mod-entry":["/genwebpack/ prod / en / javascript / обсуждение-пакет / мод-запись.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсудить-пакет / mod-entry.4b6a73a0594b32556dee.js "]," ./ javascript / обсуждение-пакет / модерация-журналы-запись ": [" / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.e388870b0b9099d849f9.js "]," ./ javascript / donate-package / recurring-donation-cancel-entry ": [" / genwebpack / prod / en / javascript / donate-package / recurring-donation-cancel-entry.fc66bf5e2742c821bbb3.js "]," ./ javascript / editor-package / content-tags-entry ": [" / genwebpack / prod / en / javascript / editor-package / content-tags-entry. b410dd841acd270f6ef7.css "," / genwebpack / prod / en / javascript / editor-package / content-tags-entry.abf91db444ac83a110b1.js "]," ./ javascript / moderator-flag-queue-package / flag-queue-shell-entry ": [" / genwebpack /prod/en/javascript/moderator-flag-queue-package/flag-queue-shell-entry.27cd8706601b558ad57c.css","/genwebpack/prod/en/javascript/moderator-flag-queue-package/flag-queue- оболочка.06df4e16de2d5ed40956.js "]," ./ javascript / offensive-terms-package / offensive-terms-entry ": [" / genwebpack / prod / en / javascript / offensive-terms-package / offensive-terms-entry.b8cb8c30891a5d7e4090.js "]," ./ javascript / page-package / footer-entry ": [" / genwebpack / prod / en / javascript / page-package / footer-entry.e897c238c206b9677856.js "]," ./ javascript / page-package /header-entry":["/genwebpack/prod/en/javascript/page-package/header-entry.c2ed6ae24bb62d5b8d5e.js" visible,"./javascript/page-template-package/infra-entry":["/ genwebpack / prod / en / javascript / page-template-package / infra-entry.
b410dd841acd270f6ef7.css "," / genwebpack / prod / en / javascript / editor-package / content-tags-entry.abf91db444ac83a110b1.js "]," ./ javascript / moderator-flag-queue-package / flag-queue-shell-entry ": [" / genwebpack /prod/en/javascript/moderator-flag-queue-package/flag-queue-shell-entry.27cd8706601b558ad57c.css","/genwebpack/prod/en/javascript/moderator-flag-queue-package/flag-queue- оболочка.06df4e16de2d5ed40956.js "]," ./ javascript / offensive-terms-package / offensive-terms-entry ": [" / genwebpack / prod / en / javascript / offensive-terms-package / offensive-terms-entry.b8cb8c30891a5d7e4090.js "]," ./ javascript / page-package / footer-entry ": [" / genwebpack / prod / en / javascript / page-package / footer-entry.e897c238c206b9677856.js "]," ./ javascript / page-package /header-entry":["/genwebpack/prod/en/javascript/page-package/header-entry.c2ed6ae24bb62d5b8d5e.js" visible,"./javascript/page-template-package/infra-entry":["/ genwebpack / prod / en / javascript / page-template-package / infra-entry. 585659fb68561ea58d52.js "]," ./ javascript / perseus-admin-package / perseus-admin-entry ": [" / genwebpack / prod / en / javascript / perseus-admin-package / perseus-admin-entry.8ab0420e4582737a7173.js "]," ./ javascript / perseus-all-package / perseus-item-entry ": [" / genwebpack / prod / en / javascript / perseus-all-package / perseus-item-entry.643d5b363ddc411202c8.js "], "./javascript/perseus-merged-editor-package/demo-perseus-entry":["/genwebpack/prod/en/javascript/perseus-merged-editor-package/demo-perseus-entry.5e366604784e7778de81.js "]," ./ javascript / sat-mission-package / sat-mission-entry ": [" / genwebpack / prod / en / javascript / sat-mission-package / sat-mission-entry.dbc2527d345f941a709a.css ", "/genwebpack/prod/en/javascript/sat-mission-package/sat-mission-entry.828c827b611cda1191fe.js" visible,"./javascript/scratchpads-package/code-entry":["/genwebpack/prod/en /javascript/scratchpads-package/code-entry.224277a0452876dae984.js"pting,"./javascript/scratchpads-package/exec-pjs-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec- pjs-запись.
585659fb68561ea58d52.js "]," ./ javascript / perseus-admin-package / perseus-admin-entry ": [" / genwebpack / prod / en / javascript / perseus-admin-package / perseus-admin-entry.8ab0420e4582737a7173.js "]," ./ javascript / perseus-all-package / perseus-item-entry ": [" / genwebpack / prod / en / javascript / perseus-all-package / perseus-item-entry.643d5b363ddc411202c8.js "], "./javascript/perseus-merged-editor-package/demo-perseus-entry":["/genwebpack/prod/en/javascript/perseus-merged-editor-package/demo-perseus-entry.5e366604784e7778de81.js "]," ./ javascript / sat-mission-package / sat-mission-entry ": [" / genwebpack / prod / en / javascript / sat-mission-package / sat-mission-entry.dbc2527d345f941a709a.css ", "/genwebpack/prod/en/javascript/sat-mission-package/sat-mission-entry.828c827b611cda1191fe.js" visible,"./javascript/scratchpads-package/code-entry":["/genwebpack/prod/en /javascript/scratchpads-package/code-entry.224277a0452876dae984.js"pting,"./javascript/scratchpads-package/exec-pjs-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec- pjs-запись. 821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-pjs-entry.8e4298bd94576a50ee32.js "]," ./ javascript / scratchpads-package / exec-sql-entry ": [" / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.f3c6b98aa6ef8d7842e9.js "] ./javascript/scratchpads-package/exec-webpage-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec-webpage-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-webpage-entry.1132cc1fe1fe36ff1d5f.js "]," ./ javascript / shared-package / page-template-mini-entry ": [" / genwebpack / prod / en / javascript / shared-package / page-template-mini-entry.538a2a3317957b775c3c.js "]," ./ javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript /student-package/student-entry.6234febc0f2c282c53b2.js"pting,"./javascript/topicsadmin-package/topics-admin-entry":["/genwebpack/prod/en/javascript/topicsadmin-package/topics-admin- Вход.
821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-pjs-entry.8e4298bd94576a50ee32.js "]," ./ javascript / scratchpads-package / exec-sql-entry ": [" / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.f3c6b98aa6ef8d7842e9.js "] ./javascript/scratchpads-package/exec-webpage-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec-webpage-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-webpage-entry.1132cc1fe1fe36ff1d5f.js "]," ./ javascript / shared-package / page-template-mini-entry ": [" / genwebpack / prod / en / javascript / shared-package / page-template-mini-entry.538a2a3317957b775c3c.js "]," ./ javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript /student-package/student-entry.6234febc0f2c282c53b2.js"pting,"./javascript/topicsadmin-package/topics-admin-entry":["/genwebpack/prod/en/javascript/topicsadmin-package/topics-admin- Вход. b29d425eb22e28cee37f.css "," / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry.96663ff0d8398ada0775.js "]," ./ javascript / themesadmin-package / themes-admin-entry ~. / javascript / пакет-редактора-перевода / видео-тр ~ 3029e3e6 ": [" / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry ~. / javascript / translation-editor-package / video-tr ~ 3029e3e6. e8e618eab
b29d425eb22e28cee37f.css "," / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry.96663ff0d8398ada0775.js "]," ./ javascript / themesadmin-package / themes-admin-entry ~. / javascript / пакет-редактора-перевода / видео-тр ~ 3029e3e6 ": [" / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry ~. / javascript / translation-editor-package / video-tr ~ 3029e3e6. e8e618eab635113.js "]," ./ javascript / themesadmin-package / themes-admin-entry ~. / javascript / translations-dashboard-package / tran ~ 59637777 ": [" / genwebpack / prod / en / javascript / themesadmin-package / темы-админ-запись ~./javascript/translations-dashboard-package/tran~59637777.883163af512601ab641c.js" ],"./javascript/translation-editor-package/all-videos-csv-entry":["/genwebpack/prod/en/javascript/translation -editor-package / all-videos-csv-entry.e0cacf86e4c35775efd7.js "]," ./ javascript / translation-editor-package / video-translation-table-entry ": [" / genwebpack / prod / en / javascript / пакет-редактора-перевода / видео-перевод-таблица-запись. 39a58caa9300173b5176.css "," / genwebpack / prod / en / javascript / translation-editor-package / video-translation-table-entry.f2292a5e63b89fba6f21.js "]," ./ javascript / translations-dashboard-package / translations-dashboard-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / translations-dashboard-entry.0d3ab659da641a0585e1.js "]," ./ javascript / translations-dashboard-package / video-subtitle-data-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.27cd8706601b558ad57c. css "," / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.709bf28b0b0f6607d2a1.js "]," ./ javascript / tutorial-editor-package / video-editor-entry ": [" / genwebpack / prod / en / javascript / tutorial-editor-package / video-editor-entry.dee1bfdfe3fe7016371a.js "] , "./ javascript / tutorial-scratchpad-package / scratchpad-page-entry": ["/ genwebpack / prod / en / javascript / tutorial-scratchpad-package / scratchpad-page-entry.
39a58caa9300173b5176.css "," / genwebpack / prod / en / javascript / translation-editor-package / video-translation-table-entry.f2292a5e63b89fba6f21.js "]," ./ javascript / translations-dashboard-package / translations-dashboard-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / translations-dashboard-entry.0d3ab659da641a0585e1.js "]," ./ javascript / translations-dashboard-package / video-subtitle-data-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.27cd8706601b558ad57c. css "," / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.709bf28b0b0f6607d2a1.js "]," ./ javascript / tutorial-editor-package / video-editor-entry ": [" / genwebpack / prod / en / javascript / tutorial-editor-package / video-editor-entry.dee1bfdfe3fe7016371a.js "] , "./ javascript / tutorial-scratchpad-package / scratchpad-page-entry": ["/ genwebpack / prod / en / javascript / tutorial-scratchpad-package / scratchpad-page-entry. 6570ecceb7b41ea7bf90.js"], ". /javascript/video-package/video-lite-entry":["/genwebpack/prod/en/javascript/video-package/video-lite-entry.b0940d69f99a4dea9527.css","/genwebpack/prod/en/javascript/ видео-пакет / видео-лайт-запись.e54cb77b4051a220494c.js "]," 0isi ": [" / genwebpack / prod / en / 0isi.24361e8119fcb896222f.js "]," 10RM ": [" / genwebpack / prod / en / 10RM.1ff438807fbd5138a] ": [" / genwebpack / prod / en / 11pb.22229c77cba5dc5dd306.js "]," 121I ": [" / genwebpack / prod / en / 121I.518843d16186aab971f7.js "]," 12uO ": [" / genwebpack / prod /en/12uO.e7ee6f20bf68cce09364.js"pting,"13UF":["/genwebpack/prod/en/13UF.42c4de53ee81c80c6d5b.js" ],"13Vt":["/genwebpack/prod/en/2.13b2a82ac68fd/en/2.13bt.1ec68f "]," 14Lx ": [" / genwebpack / prod / en / 14Lx.5e23c2554d3671cb3eeb.js "]," 14Rr ": [" / genwebpack / prod / en / 14Rr.a6bac93f2932b9232591.js "]," 14en ": [" / genwebpack / prod / en / 14en.adee2b2af03fab9571da.js "]," 15HC ": ["/genwebpack/prod/en/15HC.97f4eea4380b0f6a1ffd.
6570ecceb7b41ea7bf90.js"], ". /javascript/video-package/video-lite-entry":["/genwebpack/prod/en/javascript/video-package/video-lite-entry.b0940d69f99a4dea9527.css","/genwebpack/prod/en/javascript/ видео-пакет / видео-лайт-запись.e54cb77b4051a220494c.js "]," 0isi ": [" / genwebpack / prod / en / 0isi.24361e8119fcb896222f.js "]," 10RM ": [" / genwebpack / prod / en / 10RM.1ff438807fbd5138a] ": [" / genwebpack / prod / en / 11pb.22229c77cba5dc5dd306.js "]," 121I ": [" / genwebpack / prod / en / 121I.518843d16186aab971f7.js "]," 12uO ": [" / genwebpack / prod /en/12uO.e7ee6f20bf68cce09364.js"pting,"13UF":["/genwebpack/prod/en/13UF.42c4de53ee81c80c6d5b.js" ],"13Vt":["/genwebpack/prod/en/2.13b2a82ac68fd/en/2.13bt.1ec68f "]," 14Lx ": [" / genwebpack / prod / en / 14Lx.5e23c2554d3671cb3eeb.js "]," 14Rr ": [" / genwebpack / prod / en / 14Rr.a6bac93f2932b9232591.js "]," 14en ": [" / genwebpack / prod / en / 14en.adee2b2af03fab9571da.js "]," 15HC ": ["/genwebpack/prod/en/15HC.97f4eea4380b0f6a1ffd. js" visible,"179z":["/genwebpack/prod/en/179z.35514fd3cab2564674c7.js" ],"18dX":["/genwebpack/prod/prod/prod/ /18dX.190d0fb7d4c2bef520c4.js"pting,"193f":["/genwebpack/prod/en/193f.899ec8d8070ca64b645a.js"pting,"19mY":["/genwebpack/prod/en/19mY114.ca69b1] , «19 мл»: [«/ genwebpack / prod / en / 19ml.e50030a703146692ebbc.js»], «1APQ»: [«/ genwebpack / prod / en / 1APQ.c3856c68bc621551f9f3.js "]," 1ARw ": [" / genwebpack / prod / en / 1ARw.7bddbd5e6dab22bab50f.js "]," 1Apj ": [" / genwebpack / prod / en / 1Apj.1a38b47f52b54f39 ": [" / genwebpack / prod / en / 1BNf.43ebc442f64f7369a9ef.js "]," 1CZn ": [" / genwebpack / prod / en / 1CZn.333d2cc462adf30d4a98.js "],« 1Chp ": /en/1Chp.1f55519c75613e84097f.js"pting,"1DPW":["/genwebpack/prod/en/1DPW.66ea27723628cbd96d4c.js" ],"1FEV":["/genwebpack/prod/en/1FEV.907f24sa9 "]," 1HtF ": [" / genwebpack / prod / en / 1HtF.f389ec9f925bd10ae92c.js "]," 1IOE ": [" / genwebpack / prod / en / 1IOE.0c5aa1189d6a85e5b8e6.js "]," 1Ixv ": [" / genwebpack / prod / en / 1Ixv.799795c0c7d8b8e57857.JsT3 "]," ["/genwebpack/prod/en/1JT3.42337f0638f663c0eebe.css","/genwebpack/prod/en/1JT3.dee6925dc90ae3fed61b.js" ],"1KNP":["/genwebpack/prod/enfa/facn25c2d4dd0ddd/enfajfcd4d4 "]," 1KcS ": [" / genwebpack / prod / en / 1KcS.755d0dc6455d01f2a5a9.js "]," 1KcS5 ": [" / genwebpack / prod / en / 1KcS5.cbf0735ad22893bfcc18. 1Lsq "]," ["] "/genwebpack/prod/en/1Lqt.0018b3ec5b8d6cd2a6b0.js" visible,"1MTk":["/genwebpack/prod/en/1MTk.0cc5a5cae922535cbd92.js "]," 1Ps6 ": [" / genwebpack / prod / en / 1Ps6.948efbd2bd6d39b634c2.js "]," 1QYc ": [" / genwebpack / prod / en / 1QYc.4b13f70bdc6 /prod/en/1QYc.af18a462a031f1362e81.js"pting,"1RSY":["/genwebpack/prod/en/1RSY.acac8e519565b63f2179.js"pting,"1RWy":["/genwebpackae/prod/en/1RW4406356ac7 .js "]," 1Rdk ": [" / genwebpack / prod / en / 1Rdk.d966fcda4e23074b76df.js "]," 1Ssk ": [" / genwebpack / prod / en / 1Ssk.d75cf0adf54f5a3601d1.js "N], "1TN : ["/ genwebpack / prod / en / 1TNN.8f9ad792204f250f6d5f.js"], "1Vc5": ["/ genwebpack / prod / en / 1Vc5.8f68f93c9d3289b956e4.js "]," 1VjB ": [" / genwebpack / prod / en / 1VjB.aeddd83bcfc3f8ff095e.js "]," 1Vny ": [" / genwebpack / prod / en / 1Vny14cb42sp3f] ": [" / genwebpack / prod / en / 1Vpd.d8e28876328ad22a57ee.js "]," 1W80 ": [" / genwebpack / prod / en / 1W80.ebbd1f9bfb2d400a8e7b.js "]," 1XtT ": [/ prod / genweb /en/1XtT.07babde83b5822beb7dd.js"pting,"1YsT":["/genwebpack/prod/en/1YsT.96e48a31335f94f6b87b.js"pting,"1Z2M":["/genwebpackd/prod/en/1Z2M.0cdae184 "]," 1ZAq ": [" / genwebpack / prod / en / 1ZAq.e4033e39ccfd7bd2b1df.js "]," 1ZoN ": [" / genwebpack / prod / en / 1ZoN.03c639a16af30d773299.js "]," 1a8C ": [" / genwebpack / prod / en / 1a8C.b8e416ea840a05a93d9e.js "]," ["/genwebpack/prod/en/1a9J.c94c5ef6bde1b59612a4.js" visible,"1aEw":["/genwebpack/prod/en/1aEw.990d57e623849420d091.js" ],"1bEx":["/genwebpack/prod /1bEx.32a8cba2844f9a00ab78.js"pting,"1bJ6":["/genwebpack/prod/en/1bJ6.0bb24069af2659acc9ea.js"pting,"1cVY":["/genwebpack/prod/en/1cVY.9f586681743] , «1cnO»: [«/ genwebpack / prod / en / 1cnO.ae6e4a1eaea573438376.js»], «1d7P»: [«/ genwebpack / prod / en / 1d7P.2352b893e8b550e075f3.js "]," 1dp5 ": [" / genwebpack / prod / en / 1dp5.2f7ac2e98c77337465ad.js "]," 1fgW ": [" / genwebpack / prod / en / 1fgW.b39605Kadedab2.f. ": [" / genwebpack / prod / en / 1h2K.ef3dd108141adf8244db.js "]," 1igT ": [" / genwebpack / prod / en / 1igT.7d5511f75e62dda397a1.css "," / genwebpack / prod / enad199. .js "]," 1jDv ": [" / genwebpack / prod / en / 1jDv.810c08eeada0b7c55418.js "]," 1k1o ": [" / genwebpack / prod / en / 1k1o.793e1e7d3a70b345d965. 1js "] : ["/ genwebpack / prod / en / 1lam.3ca7eeb607a0de899ba8.js"], "1mwh": ["/ genwebpack / prod / en / 1mwh.56f21189a29dedb41560.js "]," 1nPp ": [" / genwebpack / prod / en / 1nPp.4eb89ca5f22cae307faf.js "]," 1nZL ": [" / genwebpack / prod / en / 1nZL.7def940ccb59c65s. ": [" / genwebpack / prod / en / 1qGO.37c17f50e72786b69d45.js "]," 1qGz ": [" / genwebpack / prod / en / 1qGz.0ac308e9e27d48e06b7a.js "]," 1qIab ": [" / genweb /en/1qIa.e97aa0e02ca35b05f591.js"pting,"1r3U":["/genwebpack/prod/en/1r3U.3ec4fac3874326a0d9e4.js"pting,"1rSG":["/genwebpack/prod/en20ar2c03.0.0.0/ru "]," 1u2V ": [" / genwebpack / prod / en / 1u2V.203d0c62f0de22575400.js "]," 1urj ": [" / genwebpack / prod / en / 1urj.36c2cddd9e86cc0815bb.js "]," 1vDA ": [" / genwebpack / prod / en / 1vDA.e872d09fbeeb96995127.js "]," 1vWt " ["/genwebpack/prod/en/1vWt.f2261d57d7ec095fc12f.js" visible,"1vry":["/genwebpack/prod/en/1vry.680a2a28db9b74a90bd4.js" ],"1w6N":["/genwebpack/ /1w6N.dd29f189080ba9e4d355.js "]," 1xMX ": [" / genwebpack / prod / en / 1xMX.27cd8706601b558ad57c.css "," / genwebpack / prod / en / 1xMX.d380b08d10daW1b996f7. " "/genwebpack/prod/en/1xW1.80aedf8990a196adac76.js"pting,"1xq9":["/genwebpack/prod/en/1xq9.d5d6a645df79e516fd48.js "]," 1yEK ": [" / genwebpack / prod / en / 1yEK.a4b5797f4f95fb2e02de.js "]," 1yJd ": [" / genwebpack / prod / en / 1yJ4yd.7ef7285 ": [" / genwebpack / prod / en / 1yxG.8e87c72f94d335d81bfa.js "]," 1yxy ": [" / genwebpack / prod / en / 1yxy.2bababdb2115263b3311.js "]," 1z4c ": [" / prodwebpack / /en/1z4c.ddd4e5062fd3e323d6f5.js" visible,"1z5B":["/genwebpack/prod/en/1z5B.74a7f9f76fc2d609fdb4.css","/genwebpack/prod/en/1z5B.c63da2a",c50a2a",,,,,??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? : ["/ genwebpack / prod / en / 1zsz.1b72254e792a7b814493.js"], "20ED": ["/ genwebpack / prod / en / 20ED.a4b61be1c993b1abf648.js "]," 21RN ": [" / genwebpack / prod / en / 21RN.aae1c1e6768eeef409ca.js "]," 21xc ": [" / genwebpack / prod / en / 21xc.7d5511f75acbda39, / /prod/en/21xc.65d513ac168e0b46c01a.js"pting,"23IL":["/genwebpack/prod/en/23IL.bb2b683b2988d9c49201.js" provided,"23Pc":["/genwebpack/prod/en/23Pc15.0bc72 .js "]," 23uO ": [" / genwebpack / prod / en / 23uO.eb8f1d4a8d692b1f763f.js "]," 244e ": [" / genwebpack / prod / en / 244e.def12064fe92d244c5ac.jsj "]," 244e.def12064fe92d244c5ac.jsj "] : ["/ genwebpack / prod / en / 245j.352b3b588f2fd9a298f0.js"], "24CB": ["/ genwebpack / prod / en / 24CB.fc516a269ea7cc336789.js "]," 26Fy ": [" / genwebpack / prod / en / 26Fy.6d73c9580f5f3ac0bb9a.js "]," 279q ": [" / genwebpack / prod / en / 279q.2d0cefbcec71b1b1 ": [" / genwebpack / prod / en / 27qs.b246eac722ebc4391f1c.js "]," 28I1 ": [" / genwebpack / prod / en / 28I1.887a949aeda5609fe8ae.js "]," 28OZ ": [" / genwebpack / prod /en/28OZ.ccf600950c62d1041d63.js"pting,"28nD":["/genwebpack/prod/en/28nD.da7f72c232c7c26f27de.js" visible,"29Wk":["/genwebpack/prod/en/29Wk.486s2154690 "]," 29i2 ": [" / genwebpack / prod / en / 29i2.d03aa8eca3248a8432af.js "]," 2B5d ": [" / genwebpack / prod / en / 2B5d.783ba78352289a6d83f6.js "]," 2Bu7 ": [" / genwebpack / prod / en / 2Bu7.94f56daa513725ede19f.js "]," 2CLP " ["/genwebpack/prod/en/2CLP.e0fbd05d1a46ef3131f8.js"] ],"2Cp5":["/genwebpack/prod/en/2Cp5.baf6d10730e7ea44ffcf.js" ],"2Cwm":pack/genwebpack/genwebpack/prod/genwebpack/prod/genwebpack/prod/genwebpack/ /2Cwm.dfddd314e99fe8285964.js" visible,"2EQr":["/genwebpack/prod/en/2EQr.460c28028161009cc952.js"pting,"2EaT":["/genwebpack/prod/en/2EaT.b04683b , «2FX7»: [«/ genwebpack / prod / en / 2FX7.9bb9851d1bf8354d2efd.js»], «2GxB»: [«/ genwebpack / prod / en / 2GxB.994555d9dedd7b712575.css "," / genwebpack / prod / en / 2GxB.1ff95ecae75bd2087c80.js "]," 2HCt ": [" / genwebpack / prod / en / 2HCt.01dad59cf3068b8a5c79.js "],« 2HCt. /prod/en/2HKw.8adc9ea1fc87bd619377.css","/genwebpack/prod/en/2HKw.8eae231ec7b4c569b9e6.js" ],"2HYH":["/genwebpack/prod/en/2HYF28.917.a79f 2Ikv ": [" / genwebpack / prod / en / 2Ikv.75793b428da9c28.js "]," 2J2c ": [" / genwebpack / prod / en / 2J2c.6436cd1ec59f811a76a1.js "]," 2KyNwebpack ": [/" prod / en / 2KyN.12e23a4121029944369b.js "]," 2Lqu ": [" / genwebpack / prod / en / 2Lqu.0dd199cb760b197.js "]," 2MQA ": [" / genwebpack / prod / en / 2MQA.5f17d329eaf378de8ed3.js "]," 2MwD ": [" / genwebpack / prod / en / 2MwD.e2cae10eze234c1 ": [" / genwebpack / prod / en / 2Nrz.e046eb28af390e7d6ac1.js "]," 2PSY ": [" / genwebpack / prod / en / 2PSY.8559e57a9f971d776d56.css "," / genwebpack / prod / en / 2aPSY .js "]," 2QK7 ": [" / genwebpack / prod / en / 2QK7.e2051ce4cf851c9ecefe.css "," / genwebpack / prod / en / 2QK7.703195163649aaa19cf3.js "]," 2QW5 ": [/ / genwebpack prod / en / 2QW5.21c40ab5e511db226a08.js "]," 2RMK ": [" / genwebpack / prod / en / 2RMK.bf00889c696e6223dfd4.js "]," 2Rvf ": [" / genwebpack / prod / en / 2Rvf.87567382100cff2ccca3.js "]," 2SNV ": [" / genwebpack / prod / en / 2SNV.345d5ea75c929b. ": [" / genwebpack / prod / en / 2SdV.6b1ef603c0478837bc75.js "]," 2Sin ": [" / genwebpack / prod / en / 2Sin.8ae3ec2940569b614452.js "]," 2TCQ ": [" / genwebpack / prod /en/2TCQ.2234f9687251fba02039.js"pting,"2Uus":["/genwebpack/prod/en/2Uus.334f730bca942a7c1539.js"pting,"2Vse":["/genwebpack/prod/en/2Vse.e96b4c0a "]," 2X2X ": [" / genwebpack / prod / en / 2X2X.e8ea894cc7db366683a7.js »],« 2Xlo »: [« / genwebpack / prod / en / 2Xlo.e5fc51c0815927158700.css »,« / genwebpack / prod / en / 2Xlo.31d6294666f7c507b835.js »],« 2Yeu »: [/ prod / genwebpack /en/2Yeu.63db4e3b8b00cb6b8206.js"pting,"2aBZ":["/genwebpack/prod/en/2aBZ.7be61a2b8fcac69b4924.js" ],"2aia":["/genwebpack/prod/ru68c03/2aia "," / genwebpack / prod / en / 2aia.32fd64718bd9a617373e.js "]," 2cnn ": [" / genwebpack / prod / en / 2cnn.2eaaf633d663000537ca.js "]," 2dVQ ": [" / genwebpack / prod en / 2dVQ.73822f6a51381e100621.js "]," 2gJR ": [" / genwebpack / prod / en / 2gJR.444a818d8f12103867b3.js "]," 2hbS ": [" / genwebpack / prod / en / 2hbS.5eb872e21d766cb1aa72.js "]," 2iHJ ": [" / genwebpack / prod / en / 2iHJ.dfa7cfda1f /prod/en/2iHJ.97a8672cfba211a8a6e8.js"pting,"2iOq":["/genwebpack/prod/en/2iOq.acdbef3d7b6a0e74abb7.js" ],"2iXX":["/genwebpack2/prod4/prod .js "]," 2jSl ": [" / genwebpack / prod / en / 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "]," 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "] : ["/ genwebpack / prod / en / 2lOt.1ff08964f6c77ff596c5.js"], "2m0x": ["/ genwebpack / prod / en / 2m0x.efa28362307d5af47b40.css "," / genwebpack / prod / en / 2m0x.0fa9a67410bd4673bc0a.js "]," 2mTh ": [" / genwebpack / prod / en / 2mTh.bc3ccf1d22e920f522df. ", 2mTh.bc3ccf1d22e920f522df.js /prod/en/2nMR.2558326fc96438a96989.js"pting,"2pPD":["/genwebpack/prod/en/2pPD.7e77a3cc66405918d863.js" ],"2pZY":["/genwebpack/prod16.d3fa4de4d4d3d3d4d3d3d3d4b5/ .js "]," 2prj ": [" / genwebpack / prod / en / 2prj.31856cec826592510353.js "]," 2qoD ": [" / genwebpack / prod / en / 2qoD.3e22ff098d72f5d6021a.js "]," 2rHT " : ["/ genwebpack / prod / en / 2rHT.b763f55a47ea52e4f629.js"], "2rso": ["/ genwebpack / prod / en / 2rso.3425679bf76c759ac725.css "," / genwebpack / prod / en / 2rso.4b28b9a29147f3a93be7.js "]," 2sHZ ": [" / genwebpack / prod / en / 2sHZ.e0f5a4fec3e8b2a3aeb2.js "/ /prod/en/2snA.3bec1fd07d4c2d5dfbcc.js"pting,"2teg":["/genwebpack/prod/en/2teg.7895c5d3d7e0dff380b4.js" ],"30A8":["/genwebpack30/prod.4d/en .js "]," 30RW ": [" / genwebpack / prod / en / 30RW.6c6416ace108b66f4e47.css "," / genwebpack / prod / en / 30RW.027de18a57ec67e2fac5.js "]," 30wi ": [" / genwebpack / prod / en / 30wi.ad707bfed5b6209329e8.js "]," 31FY ": [" / genwebpack / prod / en / 31FY.75b0c6a961988dca672f.js "]," 31e4 ": [" / genwebpack / prod / en / 31e4.7cdbc8ec756077361960.js "]," 31jp ": [" / genwebpack / prod / en / 31jp.5a992361b5395js "], 326hd63", 326hd63 ", 326hd63. ": [" / genwebpack / prod / en / 326h.e00d12f7fefb8b00524d.js "]," 32Sy ": [" / genwebpack / prod / en / 32Sy.18c8132f4993c34d3d0d.js "]," 32q8 ": [" / prod / genwebpack / /en/32q8.8efbc50ea3c43be649a5.js"pting,"34uh":["/genwebpack/prod/en/34uh.b4a80e2538c28eee8555.js"pting,"35BT":["/genwebpack/prod/en/35BT39.js85e5) "]," 36AW ": [" / genwebpack / prod / en / 36AW.ba6b36c7cd0a5ddfad21.js »],« 379K »: [« / genwebpack / prod / en / 379K.aaeadfc858e15d50d8c5.js »],« 37Vm »: [« / genwebpack / prod / en / 37Vm.904c77b2fb8c0d6a9ff7.css »,« / genwebpack »/ genwebpack /en/37Vm.e2134f7295285f100241.js" Survival "," / genwebpack / prod / en / 39EU.e2e8851dca936e35176a.js "]," 39il ": [" / genwebpack / prod / en / 39il.294443516cb884c76787.js "]," 3C1J ": [" / genwebpack / prod / en / 3C1J.73550690b1f2bbdc6270.js "]," 3Cmw ": [" / genwebpack / prod / en / 3Cmw.f8d20d392a38665185da.css "," / genwebpack / prod / en / 3Cmw.b6ba737fdce36e6a22c4.js "]," 3Eux ": [" / genwebpack / prod / en / 3Eux.c4ae89869ae0dFC7bd98./ /prod/en/3FC7.8c67dfa280fd40a64c54.js"pting,"3Fde":["/genwebpack/prod/en/3Fde.c423a076d3a6e4b78215.js" ],"3G70":["/genwebpack/ce38d/en/3G70 " .js "]," 3ITe ": [" / genwebpack / prod / en / 3ITe.3d52f15dd2520e730488.js "]," 3KTd ": [" / genwebpack / prod / en / 3KTd.623d4d983e9aaab5be6c.js "]," 3L8 : ["/ genwebpack / prod / en / 3L8X.3ea888b98536ff1d0203.js"], "3LDP": ["/ genwebpack / prod / en / 3LDP.6406829f4ba1d9ac4a0b.js "]," 3LDf ": [" / genwebpack / prod / en / 3LDf.4e17e540cb5f7800fd1e.js "]," 3NVp ": [" / genwebpack / prod / en / 3NVp23a9e9481 ": [" / genwebpack / prod / en / 3Nju.ebc351c24a428bf743a9.js "]," 3NmD ": [" / genwebpack / prod / en / 3NmD.6bfebf201e56fcb42f0b.js "]," 3Pml ": [" / genweb. /en/3Pml.1b973ab850d1adab7aa8.js" visible,"3Qw5":["/genwebpack/prod/en/3Qw5.cd6a69f9769cc8de0ffd.js"pting,"3SWN":["/genwebpack/prod/en/3SWN":["/genwebpack/prod/en/6S11fsWN.6D) "]," 3TWR ": [" / genwebpack / prod / en / 3TWR.7b1e748ff4697b4424a5.js "]," 3Tdt ": [" / genwebpack / prod / en / 3Tdt.768262c5db31f6d54f4c.js "]," 3UBJ ": [" / genwebpack / prod / en / 3UBJ.3bb351e25d6e48fe64d7.js "]," 3Uys ": ["/genwebpack/prod/en/3Uys.70ec59ff2553aa1361cc.js" visible,"3WSq":["/genwebpack/prod/en/3WSq.682f69f662d23c8e3110.js" ],"3Wv8":["/genwebpack/prod/prod/prod/ /3Wv8.64c42d81067c86627b79.js" visible,"3YJn":["/genwebpack/prod/en/3YJn.7547ad2e18a7c92c3a15.js"pting,"3YUn":["/genwebpack/prod/en/3YUn":["/genwebpack/prod/en/3Y91.jd11.95] , "3ZoY": ["/ genwebpack / prod / en / 3ZoY.20feff1b0686ec8d66fd.js"], "3aD5": ["/ genwebpack / prod / en / 3aD5.841d4eabf893e8f72324.js "]," 3abC ": [" / genwebpack / prod / en / 3abC.dba09f2ccd751f5f0128.js "]," 3ajf ": [" / genwebpack / prod / en / 3ajf.acc30bdpack "/ 3ajf.acc30dpack" / /prod/en/3ajf.b02112ab9ed3c3a283a2.js"pting,"3b3X":["/genwebpack/prod/en/3b3X.53bf95a1c1d2a8e65aa1.css","/genwebpack/prod/c ./3b3f7df17d90 "," 3cLW ": [" / genwebpack / prod / en / 3cLW.0646312d1b2be50dd9da.js "]," 3eD4 ": [" / genwebpack / prod / en / 3eD4.0daf28ab601ec13cc868.css "," / genwebpacke / prod / en. 162605cd1529c8af6213.js "]," 3glC ": [" / genwebpack / prod / en / 3glC.ae16ad4594136b774dce.js "]," 3hAB ": [" / genwebpack / prod / en / 3hAB.223cde4fef3638f93e96.js "]," 3hdl ": [" / genwebpack / prod / en / 3hdl.120e632e696c515c0.js. ": [" / genwebpack / prod / en / 3hyK.1dbaf6b3863a89c0b0a2.js "]," 3iUY ": [" / genwebpack / prod / en / 3iUY.ad5bacacc76a1dd3bd88.js "]," 3jb1b ":pack [" / genweb /en/3jb1.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/3jb1.a2347d503e317f0f77d0.js"pting,"3mAf":["/genwebpack/prod/en/3mAf.74856mpt641d9 : ["/ genwebpack / prod / en / 3mIE.a564eb881efa5fcfb96d.js"], "3mlm": ["/ genwebpack / prod / en / 3mlm.a489602842416dec1616.js "]," 3nN3 ": [" / genwebpack / prod / en / 3nN3.a2fca621bcf0ccb5f56b.js "]," 3ncc ": [" / genwebpack / prod / en / 3ncc.675cd3740ejcd7 «: [« / genwebpack / prod / en / 3nrI.a189baa042af9b24055d.js »],« 3oKi »: [« / genwebpack / prod / en / 3oKi.a777c14af1b65aec2cce.js »],« 3oXqwebpack [«/ prodwebpack»: /en/3oXq.b8ec1faac4d4b7bfad44.js"pting,"3p5T":["/genwebpack/prod/en/3p5T.df1abefd6e6f2a407cd9.js"pting,"3rQ3":["/genwebpack3/173.1/en "]," 3rZX ": [" / genwebpack / prod / en / 3rZX.4e6b75ad668b3906ab96.js "]," 3sHy ": [" / genwebpack / prod / en / 3sHy.8e8b5c79c4e3bd5c97af.js "]," 3sOJ ": [" / genwebpack / prod / en / 3sOJ.904c77b2fb8c0d6a9ffd7.css ", /en/3sOJ.f90d421128dbc8839037.js" visible,"3sk8":["/genwebpack/prod/en/3sk8.19b6745d8e33a7c61ccc.js"pting,"3ssq":["/genwebpack/prod/en/3ssq24.fa43e6 "]," 3st3 ": [" / genwebpack / prod / en / 3st3.a2b980f980067a2ff425.js "]," 3sws ": [" / genwebpack / prod / en / 3sws.51a05b2860b503a2d702.js "]," 3sy6 ": [ "/genwebpack/prod/en/3sy6.a1e177658a9dcf2e97e1.js" visible,"3u3S":["/genwebpack/prod/en/3u3S.ddb78ae8f8c2c30ad53d.js "]," 3uMK ": [" / genwebpack / prod / en / 3uMK.727f87d1f5b0a3564da0.js "]," 3uPh ": [" / genwebpack / prod / en / 3uPh.6daCBB4. /prod/en/3uPh.b5227a7a47e7990d7bdf.js"pting,"3uk6":["/genwebpack/prod/en/3uk6.219210058d9ae3fbe399.js" ],"3vlA":["/genwebpack/prodA.c1597/3 .js "]," 3vwj ": [" / genwebpack / prod / en / 3vwj.e7e623e1659d6aa1c745.js "]," 3w2K ": [" / genwebpack / prod / en / 3w2K.d8f945533fb8d7770bd3.js "]," 3xIs "] : ["/ genwebpack / prod / en / 3xIo.91d0f9f80b9e254d99fa.js"], "3xLc": ["/ genwebpack / prod / en / 3xLc.87511daedaf748660ac3.js "]," 3xU3 ": [" / genwebpack / prod / en / 3xU3.afd1c67fe68ff0f8b1fa.js "]," 3ydI ": [" / genwebpack / prod / en / 3ydI.3b5014d6050026ae09 " ": [" / genwebpack / prod / en / 3ytn.afe0e348216f01c308cf.js "]," 40jg ": [" / genwebpack / prod / en / 40jg.d1dd1cf1e04b7d0449a5.js "]," 41RXweb ": [" / prod /en/41RX.e7751ba1f694a5a792fe.js" visible,"46xH":["/genwebpack/prod/en/46xH.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/46xH.f2d5846s",H484846103" : ["/ genwebpack / prod / en / 48H7.f1600c1bbea5d34ab0ee.js"], "48tu": ["/ genwebpack / prod / en / 48tu.5bf0aa618e5053e84069.js "]," 4AQu ": [" / genwebpack / prod / en / 4AQu.249653f8ae2e29b94021.js "]," 4BuB ": [" / genwebpack / prod / en / 4BuB.42d72d523ae ": [" / genwebpack / prod / en / 4Cd2.df8f74ea6c3e54380d50.js "]," 4D6H ": [" / genwebpack / prod / en / 4D6H.5405b242c731b645ec7f.js "]," 4DFebpack ": [" / pro /en/4DFe.47e9c26dde1b3258e18e.js" visible,"4F3S":["/genwebpack/prod/en/4F3S.0187c6aab53285ace6c8.js"pting,"4IdB":["/genwebpack/prod/en/4Id2.d2.db "]," 4J4O ": [" / genwebpack / prod / en / 4J4O.f78bee02beea88db9859.js "]," 4La6 ": [" / genwebpack / prod / en / 4La6.c6c3e1bf3a5a325814b0.js "]," 4Lwk ": [" / genwebpack / prod / en / 4Lwk.e3df2fc975e5037216d6.js "]," ["/genwebpack/prod/en/4MR3.f84be314237f3829de68.js" visible,"4Mab":["/genwebpack/prod/en/4Mab.baeb670a08dbf0c01cfe.js" ],"4NeH":["/genwebpack/prod /4NeH.a629d9310357f76779dd.css "," / genwebpack / prod / en / 4NeH.c17331971d513f712306.js "]," 4OKa ": [" / genwebpack / prod / en / 4OKa.f974ae33f15e08a] "/genwebpack/prod/en/4PFy.f0073ff4715b2f53f028.css","/genwebpack/prod/en/4PFy.440babb9e7d36c4c42cc.js "]," 4QgR ": [" / genwebpack / prod / en / 4QgR.43c84d53341ce75e04e2.js "]," 4RFn ": [" / genwebpack / prod / en / 4RFn.e658bbc7595] ": [" / genwebpack / prod / en / 4S76.c7cb6fc2183027e98857.js "]," 4UbB ": [" / genwebpack / prod / en / 4UbB.c209414654b971294c94.js "]," 4XuZ ": [/ prod / genwebpack /en/4XuZ.11dcad13d66aa5d01678.css","/genwebpack/prod/en/4XuZ.e56ed13a7a744bc2431c.js"pting,"4Y7T":["/genwebpack/prod/en/4Y7T.ba7e6f1942cd3a"> : ["/ genwebpack / prod / en / 4YZv.31ef226836f8a868d77b.js"], "4aZI": ["/ genwebpack / prod / en / 4aZI.c6acfd8ffdd80bb3cebb.js "]," 4afB ": [" / genwebpack / prod / en / 4afB.9de8b86ee729a54ba3e9.js "]," 4ajK ": [" / genwebpack / prod / en / 4ajK.9f2b5371ffeb7d ": [" / genwebpack / prod / en / 4bhX.38fc46fd560bec5d1444.js "]," 4dK5 ": [" / genwebpack / prod / en / 4dK5.f111d6b17d3c0d3efbc4.js "]," 4ds7webpack ": [" /en/4ds7.65b443a78e2dc68f2cbd.js"pting,"4eCT":["/genwebpack/prod/en/4eCT.335e138c63d291f376ae.js" provided,"4fxe":["/genwebpack/prod/en/4fxe20e.26) "]," 4hOP ": [" / genwebpack / prod / en / 4hOP.b8c3bdcedd43fdd415da.js »],« 4hVx »: [« / genwebpack / prod / en / 4hVx.0281ff99e7ec14fc9329.js »],« 4ivs »: [« / genwebpack / prod / en / 4ivs.c6f63aa0e082e8fd6e60.jsK »],« 4hVx.0281ff99e7ec14fc9329.js ». ["/genwebpack/prod/en/4jaK.7534dbabcbe6f3d6cdd4.js" ],"4ldP":["/genwebpack/prod/en/4ldP.39a597e562504e3a265a.js" ],"4m8r":[/prod/webpack/prod/weback /4m8r.d56865a888ef523a77bc.js" visible,"4n2g":["/genwebpack/prod/en/4n2g.8f16aae6209174a63821.js"pting,"4oB5":["/genwebpack/prod/en/4oB5.c3500a "/genwebpack/prod/en/4oB5.6ec7830e72501c54bec4.js" visible,"4q6b":["/genwebpack/prod/en/4q6b.bafeb9621f1913a5096a.js "]," 4qrU ": [" / genwebpack / prod / en / 4qrU.f9894f7f2e93a782e250.js "]," 4rlT ": [" / genwebpack / prod / en / 4rlT.4843fe3334e5e8. ": [" / genwebpack / prod / en / 4sjh.66ca26de0e7d0ef8deb1.js "]," 4svc ": [" / genwebpack / prod / en / 4svc.b6f05a3d030d2f6b9604.js "]," 4t0Kwebpack ": [" / prod /en/4t0K.5ceed9af3f521332a389.js"pting,"4tYZ":["/genwebpack/prod/en/4tYZ.e7a3fc0d97b2e7b0d182.js"pting,"4ulC":["/genwebpack/prod/en/4ulC.213 "]," 4umA ": [" / genwebpack / prod / en / 4umA.e8fa1312b94b617ec9a4.js "]," 4w1V ": [" / genwebpack / prod / en / 4w1V.5e7ce3b356905d3586bf.js "]," 4yoM ": [" / genwebpack / prod / en / 4yoM.12eab7b6442716ed6def.js "]," 4zf. ["/genwebpack/prod/en/4zfU.6e5388d50b4504ae26bf.js" visible,"51gk":["/genwebpack/prod/en/51gk.afbbbbf3f49331a160fc.js" ],"52L6":["/genwebpack/prod /52L6.7103b79b320e59645167.js" visible,"52rc":["/genwebpack/prod/en/52rc.4146b093077ae4277470.js"pting,"534i":["/genwebpack/prod/en/534i.60223a9461106cc "/genwebpack/prod/en/534i.5e4ba1413592386f293f.js" visible,"53l8":["/genwebpack/prod/en/53l8.1022869ca294f20b28e2.js "]," 542X ": [" / genwebpack / prod / en / 542X.5c415983d7aafcd588a4.js "]," 55xb ": [" / genwebpack / prod / en / 55xb.b1af611b66eb749] ": [" / genwebpack / prod / en / 56lG.7f560070a960360f841c.js "]," 57Ou ": [" / genwebpack / prod / en / 57Ou.7b83170fb86f8fcfc0bb.js "]," 58Go ": [" / genwebpack / prod /en/58Go.0c4a96065c9fd62488d1.js" Survival : ["/ genwebpack / prod / en / 58ik.3c06aee4463b71ba41bd.js"], "58sT": ["/ genwebpack / prod / en / 58sT.67aab918129a95ac6c24.js "]," 59kG ": [" / genwebpack / prod / en / 59kG.81f57a0d6cfff8c9efbb.js "]," 5AWW ": [" / genwebpack / prod / en / 5AWW.98a0441b83gba110089s ": [" / genwebpack / prod / en / 5B3g.806cc707842b812da292.js "]," 5CEK ": [" / genwebpack / prod / en / 5CEK.d939d2b51f43eded189c.js "]," 5DuI ": [" / genwebpack / prod /en/5DuI.5c3e2efbf3d76419ecd7.js"pting,"5ESl":["/genwebpack/prod/en/5ESl.f43b5acf41978e226b58.js" ],"5Ein":["/genwebpack/prod/en/5E408j0c3c3c "]," 5F0q ": [" / genwebpack / prod / en / 5F0q.4fea10dbb0b20c49a360.js »],« 5FHU »: [« / genwebpack / prod / en / 5FHU.a1dc860a722d19ce68fd.js »],« 5FP6 »: [« / genwebpack / prod / en / 5FP6.6ac8748ef963e0ef9fbf.js »],« 5GHU.a1dc860a722d19ce68fd.js » ["/genwebpack/prod/en/5GvA.aacb12d83ce1e3c464f8.js" visible,"5HCZ":["/genwebpack/prod/en/5HCZ.65d86a893b2bc2779fea.js" ],"5IGZ":["/genwebpack/prod/genwebpack/ /5IGZ.4bb4a05c7d36821a9a51.js"pting,"5L3M":["/genwebpack/prod/en/5L3M.3be6eda3c04c3cf0e454.js" ],"5MvW":["/genwebpack/prod.1d/en/5MvW"> , «5Nr5»: [«/ genwebpack / prod / en / 5Nr5.49c060a0f422f15bdb86.js»], «5O00»: [«/ genwebpack / prod / en / 5O00.96561bcfcb4c454daec4.js "]," 5OGZ ": [" / genwebpack / prod / en / 5OGZ.a30fcd44d8c6206fdd4d.js "]," 5OPo ": [" / genwebpack / prod / en / 5OPo.c36dabsd / en / 5OPo.c36djs857a85] ": [" / genwebpack / prod / en / 5OSm.816bd233d30325e7db45.js "]," 5Okb ": [" / genwebpack / prod / en / 5Okb.bac24dd1686fa1b.js "]," 5P0O ": [" / genwebpack / /en/5P0O.f7d745d490eace48b0af.js"pting,"5PqK":["/genwebpack/prod/en/5PqK.d039ec9a6cb0fcf232d0.js"pting,"5Qmt":["/genwebpack5/prod3.71/en "]," 5QyG ": [" / genwebpack / prod / en / 5QyG.e54bd3c059fc1a962ddf.js "]," 5R1r ": [" / genwebpack / prod / en / 5R1r.e427a01573421d20b5af.js "]," 5RFs ": [" / genwebpack / prod / en / 5RFs.0bd0b240c9e1a1ea3f66.js "]," 5RFs "]," 5RFs "] ["/genwebpack/prod/en/5RG8.83ca1228ef3c259c2483.js"pting,"5Rew":["/genwebpack/prod/en/5Rew.6a73e6b0a3e05f29c3e6.js" ],"5SB4":["/genwebpack/ /5SB4.a6acfcc51c8070ef60f6.js"pting,"5Svh":["/genwebpack/prod/en/5Svh.76ff7ffe2466d1c09e09.js"pting,"5TKU":["/genwebpack/prod/en/5Tfc8.40fdd/en/5Tfjs45fdd/en/5Tfc45fddd/en/5Tfc45fd] , «5V8W»: [«/ genwebpack / prod / en / 5V8W.e8c5fe5daac3b54eb756.js»], «5WSt»: [«/ genwebpack / prod / en / 5WSt.caa2f0e07c1f1944dd5f.js "]," 5WnU ": [" / genwebpack / prod / en / 5WnU.c67798f3e7685db695c8.js "]," 5Xn2 ": [" / genwebpack / prod / en / 5Xbe4158dade
SyntaxError: недопустимый или неожиданный токен
в новом скрипте (vm.js: 88: 7)
в JSDOMSixteenEnvironment._runScript (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:292:24)
в JSDOMSixteenEnvironment.render (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:191:16)
в runMicrotasks ()
в processTicksAndRejection (внутренний / процесс / task_queues.js: 97: 5)
в async renderHandler (/ workspace / node_modules / render-gateway / dist / gateway / handlers / make-render-handler.x # принимает любое ненулевое комплексное значение бесконечно много раз в любой сколь угодно малой окрестности # oo #. Это называется существенной сингулярностью на бесконечности .
js" visible,"179z":["/genwebpack/prod/en/179z.35514fd3cab2564674c7.js" ],"18dX":["/genwebpack/prod/prod/prod/ /18dX.190d0fb7d4c2bef520c4.js"pting,"193f":["/genwebpack/prod/en/193f.899ec8d8070ca64b645a.js"pting,"19mY":["/genwebpack/prod/en/19mY114.ca69b1] , «19 мл»: [«/ genwebpack / prod / en / 19ml.e50030a703146692ebbc.js»], «1APQ»: [«/ genwebpack / prod / en / 1APQ.c3856c68bc621551f9f3.js "]," 1ARw ": [" / genwebpack / prod / en / 1ARw.7bddbd5e6dab22bab50f.js "]," 1Apj ": [" / genwebpack / prod / en / 1Apj.1a38b47f52b54f39 ": [" / genwebpack / prod / en / 1BNf.43ebc442f64f7369a9ef.js "]," 1CZn ": [" / genwebpack / prod / en / 1CZn.333d2cc462adf30d4a98.js "],« 1Chp ": /en/1Chp.1f55519c75613e84097f.js"pting,"1DPW":["/genwebpack/prod/en/1DPW.66ea27723628cbd96d4c.js" ],"1FEV":["/genwebpack/prod/en/1FEV.907f24sa9 "]," 1HtF ": [" / genwebpack / prod / en / 1HtF.f389ec9f925bd10ae92c.js "]," 1IOE ": [" / genwebpack / prod / en / 1IOE.0c5aa1189d6a85e5b8e6.js "]," 1Ixv ": [" / genwebpack / prod / en / 1Ixv.799795c0c7d8b8e57857.JsT3 "]," ["/genwebpack/prod/en/1JT3.42337f0638f663c0eebe.css","/genwebpack/prod/en/1JT3.dee6925dc90ae3fed61b.js" ],"1KNP":["/genwebpack/prod/enfa/facn25c2d4dd0ddd/enfajfcd4d4 "]," 1KcS ": [" / genwebpack / prod / en / 1KcS.755d0dc6455d01f2a5a9.js "]," 1KcS5 ": [" / genwebpack / prod / en / 1KcS5.cbf0735ad22893bfcc18. 1Lsq "]," ["] "/genwebpack/prod/en/1Lqt.0018b3ec5b8d6cd2a6b0.js" visible,"1MTk":["/genwebpack/prod/en/1MTk.0cc5a5cae922535cbd92.js "]," 1Ps6 ": [" / genwebpack / prod / en / 1Ps6.948efbd2bd6d39b634c2.js "]," 1QYc ": [" / genwebpack / prod / en / 1QYc.4b13f70bdc6 /prod/en/1QYc.af18a462a031f1362e81.js"pting,"1RSY":["/genwebpack/prod/en/1RSY.acac8e519565b63f2179.js"pting,"1RWy":["/genwebpackae/prod/en/1RW4406356ac7 .js "]," 1Rdk ": [" / genwebpack / prod / en / 1Rdk.d966fcda4e23074b76df.js "]," 1Ssk ": [" / genwebpack / prod / en / 1Ssk.d75cf0adf54f5a3601d1.js "N], "1TN : ["/ genwebpack / prod / en / 1TNN.8f9ad792204f250f6d5f.js"], "1Vc5": ["/ genwebpack / prod / en / 1Vc5.8f68f93c9d3289b956e4.js "]," 1VjB ": [" / genwebpack / prod / en / 1VjB.aeddd83bcfc3f8ff095e.js "]," 1Vny ": [" / genwebpack / prod / en / 1Vny14cb42sp3f] ": [" / genwebpack / prod / en / 1Vpd.d8e28876328ad22a57ee.js "]," 1W80 ": [" / genwebpack / prod / en / 1W80.ebbd1f9bfb2d400a8e7b.js "]," 1XtT ": [/ prod / genweb /en/1XtT.07babde83b5822beb7dd.js"pting,"1YsT":["/genwebpack/prod/en/1YsT.96e48a31335f94f6b87b.js"pting,"1Z2M":["/genwebpackd/prod/en/1Z2M.0cdae184 "]," 1ZAq ": [" / genwebpack / prod / en / 1ZAq.e4033e39ccfd7bd2b1df.js "]," 1ZoN ": [" / genwebpack / prod / en / 1ZoN.03c639a16af30d773299.js "]," 1a8C ": [" / genwebpack / prod / en / 1a8C.b8e416ea840a05a93d9e.js "]," ["/genwebpack/prod/en/1a9J.c94c5ef6bde1b59612a4.js" visible,"1aEw":["/genwebpack/prod/en/1aEw.990d57e623849420d091.js" ],"1bEx":["/genwebpack/prod /1bEx.32a8cba2844f9a00ab78.js"pting,"1bJ6":["/genwebpack/prod/en/1bJ6.0bb24069af2659acc9ea.js"pting,"1cVY":["/genwebpack/prod/en/1cVY.9f586681743] , «1cnO»: [«/ genwebpack / prod / en / 1cnO.ae6e4a1eaea573438376.js»], «1d7P»: [«/ genwebpack / prod / en / 1d7P.2352b893e8b550e075f3.js "]," 1dp5 ": [" / genwebpack / prod / en / 1dp5.2f7ac2e98c77337465ad.js "]," 1fgW ": [" / genwebpack / prod / en / 1fgW.b39605Kadedab2.f. ": [" / genwebpack / prod / en / 1h2K.ef3dd108141adf8244db.js "]," 1igT ": [" / genwebpack / prod / en / 1igT.7d5511f75e62dda397a1.css "," / genwebpack / prod / enad199. .js "]," 1jDv ": [" / genwebpack / prod / en / 1jDv.810c08eeada0b7c55418.js "]," 1k1o ": [" / genwebpack / prod / en / 1k1o.793e1e7d3a70b345d965. 1js "] : ["/ genwebpack / prod / en / 1lam.3ca7eeb607a0de899ba8.js"], "1mwh": ["/ genwebpack / prod / en / 1mwh.56f21189a29dedb41560.js "]," 1nPp ": [" / genwebpack / prod / en / 1nPp.4eb89ca5f22cae307faf.js "]," 1nZL ": [" / genwebpack / prod / en / 1nZL.7def940ccb59c65s. ": [" / genwebpack / prod / en / 1qGO.37c17f50e72786b69d45.js "]," 1qGz ": [" / genwebpack / prod / en / 1qGz.0ac308e9e27d48e06b7a.js "]," 1qIab ": [" / genweb /en/1qIa.e97aa0e02ca35b05f591.js"pting,"1r3U":["/genwebpack/prod/en/1r3U.3ec4fac3874326a0d9e4.js"pting,"1rSG":["/genwebpack/prod/en20ar2c03.0.0.0/ru "]," 1u2V ": [" / genwebpack / prod / en / 1u2V.203d0c62f0de22575400.js "]," 1urj ": [" / genwebpack / prod / en / 1urj.36c2cddd9e86cc0815bb.js "]," 1vDA ": [" / genwebpack / prod / en / 1vDA.e872d09fbeeb96995127.js "]," 1vWt " ["/genwebpack/prod/en/1vWt.f2261d57d7ec095fc12f.js" visible,"1vry":["/genwebpack/prod/en/1vry.680a2a28db9b74a90bd4.js" ],"1w6N":["/genwebpack/ /1w6N.dd29f189080ba9e4d355.js "]," 1xMX ": [" / genwebpack / prod / en / 1xMX.27cd8706601b558ad57c.css "," / genwebpack / prod / en / 1xMX.d380b08d10daW1b996f7. " "/genwebpack/prod/en/1xW1.80aedf8990a196adac76.js"pting,"1xq9":["/genwebpack/prod/en/1xq9.d5d6a645df79e516fd48.js "]," 1yEK ": [" / genwebpack / prod / en / 1yEK.a4b5797f4f95fb2e02de.js "]," 1yJd ": [" / genwebpack / prod / en / 1yJ4yd.7ef7285 ": [" / genwebpack / prod / en / 1yxG.8e87c72f94d335d81bfa.js "]," 1yxy ": [" / genwebpack / prod / en / 1yxy.2bababdb2115263b3311.js "]," 1z4c ": [" / prodwebpack / /en/1z4c.ddd4e5062fd3e323d6f5.js" visible,"1z5B":["/genwebpack/prod/en/1z5B.74a7f9f76fc2d609fdb4.css","/genwebpack/prod/en/1z5B.c63da2a",c50a2a",,,,,??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? : ["/ genwebpack / prod / en / 1zsz.1b72254e792a7b814493.js"], "20ED": ["/ genwebpack / prod / en / 20ED.a4b61be1c993b1abf648.js "]," 21RN ": [" / genwebpack / prod / en / 21RN.aae1c1e6768eeef409ca.js "]," 21xc ": [" / genwebpack / prod / en / 21xc.7d5511f75acbda39, / /prod/en/21xc.65d513ac168e0b46c01a.js"pting,"23IL":["/genwebpack/prod/en/23IL.bb2b683b2988d9c49201.js" provided,"23Pc":["/genwebpack/prod/en/23Pc15.0bc72 .js "]," 23uO ": [" / genwebpack / prod / en / 23uO.eb8f1d4a8d692b1f763f.js "]," 244e ": [" / genwebpack / prod / en / 244e.def12064fe92d244c5ac.jsj "]," 244e.def12064fe92d244c5ac.jsj "] : ["/ genwebpack / prod / en / 245j.352b3b588f2fd9a298f0.js"], "24CB": ["/ genwebpack / prod / en / 24CB.fc516a269ea7cc336789.js "]," 26Fy ": [" / genwebpack / prod / en / 26Fy.6d73c9580f5f3ac0bb9a.js "]," 279q ": [" / genwebpack / prod / en / 279q.2d0cefbcec71b1b1 ": [" / genwebpack / prod / en / 27qs.b246eac722ebc4391f1c.js "]," 28I1 ": [" / genwebpack / prod / en / 28I1.887a949aeda5609fe8ae.js "]," 28OZ ": [" / genwebpack / prod /en/28OZ.ccf600950c62d1041d63.js"pting,"28nD":["/genwebpack/prod/en/28nD.da7f72c232c7c26f27de.js" visible,"29Wk":["/genwebpack/prod/en/29Wk.486s2154690 "]," 29i2 ": [" / genwebpack / prod / en / 29i2.d03aa8eca3248a8432af.js "]," 2B5d ": [" / genwebpack / prod / en / 2B5d.783ba78352289a6d83f6.js "]," 2Bu7 ": [" / genwebpack / prod / en / 2Bu7.94f56daa513725ede19f.js "]," 2CLP " ["/genwebpack/prod/en/2CLP.e0fbd05d1a46ef3131f8.js"] ],"2Cp5":["/genwebpack/prod/en/2Cp5.baf6d10730e7ea44ffcf.js" ],"2Cwm":pack/genwebpack/genwebpack/prod/genwebpack/prod/genwebpack/prod/genwebpack/ /2Cwm.dfddd314e99fe8285964.js" visible,"2EQr":["/genwebpack/prod/en/2EQr.460c28028161009cc952.js"pting,"2EaT":["/genwebpack/prod/en/2EaT.b04683b , «2FX7»: [«/ genwebpack / prod / en / 2FX7.9bb9851d1bf8354d2efd.js»], «2GxB»: [«/ genwebpack / prod / en / 2GxB.994555d9dedd7b712575.css "," / genwebpack / prod / en / 2GxB.1ff95ecae75bd2087c80.js "]," 2HCt ": [" / genwebpack / prod / en / 2HCt.01dad59cf3068b8a5c79.js "],« 2HCt. /prod/en/2HKw.8adc9ea1fc87bd619377.css","/genwebpack/prod/en/2HKw.8eae231ec7b4c569b9e6.js" ],"2HYH":["/genwebpack/prod/en/2HYF28.917.a79f 2Ikv ": [" / genwebpack / prod / en / 2Ikv.75793b428da9c28.js "]," 2J2c ": [" / genwebpack / prod / en / 2J2c.6436cd1ec59f811a76a1.js "]," 2KyNwebpack ": [/" prod / en / 2KyN.12e23a4121029944369b.js "]," 2Lqu ": [" / genwebpack / prod / en / 2Lqu.0dd199cb760b197.js "]," 2MQA ": [" / genwebpack / prod / en / 2MQA.5f17d329eaf378de8ed3.js "]," 2MwD ": [" / genwebpack / prod / en / 2MwD.e2cae10eze234c1 ": [" / genwebpack / prod / en / 2Nrz.e046eb28af390e7d6ac1.js "]," 2PSY ": [" / genwebpack / prod / en / 2PSY.8559e57a9f971d776d56.css "," / genwebpack / prod / en / 2aPSY .js "]," 2QK7 ": [" / genwebpack / prod / en / 2QK7.e2051ce4cf851c9ecefe.css "," / genwebpack / prod / en / 2QK7.703195163649aaa19cf3.js "]," 2QW5 ": [/ / genwebpack prod / en / 2QW5.21c40ab5e511db226a08.js "]," 2RMK ": [" / genwebpack / prod / en / 2RMK.bf00889c696e6223dfd4.js "]," 2Rvf ": [" / genwebpack / prod / en / 2Rvf.87567382100cff2ccca3.js "]," 2SNV ": [" / genwebpack / prod / en / 2SNV.345d5ea75c929b. ": [" / genwebpack / prod / en / 2SdV.6b1ef603c0478837bc75.js "]," 2Sin ": [" / genwebpack / prod / en / 2Sin.8ae3ec2940569b614452.js "]," 2TCQ ": [" / genwebpack / prod /en/2TCQ.2234f9687251fba02039.js"pting,"2Uus":["/genwebpack/prod/en/2Uus.334f730bca942a7c1539.js"pting,"2Vse":["/genwebpack/prod/en/2Vse.e96b4c0a "]," 2X2X ": [" / genwebpack / prod / en / 2X2X.e8ea894cc7db366683a7.js »],« 2Xlo »: [« / genwebpack / prod / en / 2Xlo.e5fc51c0815927158700.css »,« / genwebpack / prod / en / 2Xlo.31d6294666f7c507b835.js »],« 2Yeu »: [/ prod / genwebpack /en/2Yeu.63db4e3b8b00cb6b8206.js"pting,"2aBZ":["/genwebpack/prod/en/2aBZ.7be61a2b8fcac69b4924.js" ],"2aia":["/genwebpack/prod/ru68c03/2aia "," / genwebpack / prod / en / 2aia.32fd64718bd9a617373e.js "]," 2cnn ": [" / genwebpack / prod / en / 2cnn.2eaaf633d663000537ca.js "]," 2dVQ ": [" / genwebpack / prod en / 2dVQ.73822f6a51381e100621.js "]," 2gJR ": [" / genwebpack / prod / en / 2gJR.444a818d8f12103867b3.js "]," 2hbS ": [" / genwebpack / prod / en / 2hbS.5eb872e21d766cb1aa72.js "]," 2iHJ ": [" / genwebpack / prod / en / 2iHJ.dfa7cfda1f /prod/en/2iHJ.97a8672cfba211a8a6e8.js"pting,"2iOq":["/genwebpack/prod/en/2iOq.acdbef3d7b6a0e74abb7.js" ],"2iXX":["/genwebpack2/prod4/prod .js "]," 2jSl ": [" / genwebpack / prod / en / 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "]," 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "] : ["/ genwebpack / prod / en / 2lOt.1ff08964f6c77ff596c5.js"], "2m0x": ["/ genwebpack / prod / en / 2m0x.efa28362307d5af47b40.css "," / genwebpack / prod / en / 2m0x.0fa9a67410bd4673bc0a.js "]," 2mTh ": [" / genwebpack / prod / en / 2mTh.bc3ccf1d22e920f522df. ", 2mTh.bc3ccf1d22e920f522df.js /prod/en/2nMR.2558326fc96438a96989.js"pting,"2pPD":["/genwebpack/prod/en/2pPD.7e77a3cc66405918d863.js" ],"2pZY":["/genwebpack/prod16.d3fa4de4d4d3d3d4d3d3d3d4b5/ .js "]," 2prj ": [" / genwebpack / prod / en / 2prj.31856cec826592510353.js "]," 2qoD ": [" / genwebpack / prod / en / 2qoD.3e22ff098d72f5d6021a.js "]," 2rHT " : ["/ genwebpack / prod / en / 2rHT.b763f55a47ea52e4f629.js"], "2rso": ["/ genwebpack / prod / en / 2rso.3425679bf76c759ac725.css "," / genwebpack / prod / en / 2rso.4b28b9a29147f3a93be7.js "]," 2sHZ ": [" / genwebpack / prod / en / 2sHZ.e0f5a4fec3e8b2a3aeb2.js "/ /prod/en/2snA.3bec1fd07d4c2d5dfbcc.js"pting,"2teg":["/genwebpack/prod/en/2teg.7895c5d3d7e0dff380b4.js" ],"30A8":["/genwebpack30/prod.4d/en .js "]," 30RW ": [" / genwebpack / prod / en / 30RW.6c6416ace108b66f4e47.css "," / genwebpack / prod / en / 30RW.027de18a57ec67e2fac5.js "]," 30wi ": [" / genwebpack / prod / en / 30wi.ad707bfed5b6209329e8.js "]," 31FY ": [" / genwebpack / prod / en / 31FY.75b0c6a961988dca672f.js "]," 31e4 ": [" / genwebpack / prod / en / 31e4.7cdbc8ec756077361960.js "]," 31jp ": [" / genwebpack / prod / en / 31jp.5a992361b5395js "], 326hd63", 326hd63 ", 326hd63. ": [" / genwebpack / prod / en / 326h.e00d12f7fefb8b00524d.js "]," 32Sy ": [" / genwebpack / prod / en / 32Sy.18c8132f4993c34d3d0d.js "]," 32q8 ": [" / prod / genwebpack / /en/32q8.8efbc50ea3c43be649a5.js"pting,"34uh":["/genwebpack/prod/en/34uh.b4a80e2538c28eee8555.js"pting,"35BT":["/genwebpack/prod/en/35BT39.js85e5) "]," 36AW ": [" / genwebpack / prod / en / 36AW.ba6b36c7cd0a5ddfad21.js »],« 379K »: [« / genwebpack / prod / en / 379K.aaeadfc858e15d50d8c5.js »],« 37Vm »: [« / genwebpack / prod / en / 37Vm.904c77b2fb8c0d6a9ff7.css »,« / genwebpack »/ genwebpack /en/37Vm.e2134f7295285f100241.js" Survival "," / genwebpack / prod / en / 39EU.e2e8851dca936e35176a.js "]," 39il ": [" / genwebpack / prod / en / 39il.294443516cb884c76787.js "]," 3C1J ": [" / genwebpack / prod / en / 3C1J.73550690b1f2bbdc6270.js "]," 3Cmw ": [" / genwebpack / prod / en / 3Cmw.f8d20d392a38665185da.css "," / genwebpack / prod / en / 3Cmw.b6ba737fdce36e6a22c4.js "]," 3Eux ": [" / genwebpack / prod / en / 3Eux.c4ae89869ae0dFC7bd98./ /prod/en/3FC7.8c67dfa280fd40a64c54.js"pting,"3Fde":["/genwebpack/prod/en/3Fde.c423a076d3a6e4b78215.js" ],"3G70":["/genwebpack/ce38d/en/3G70 " .js "]," 3ITe ": [" / genwebpack / prod / en / 3ITe.3d52f15dd2520e730488.js "]," 3KTd ": [" / genwebpack / prod / en / 3KTd.623d4d983e9aaab5be6c.js "]," 3L8 : ["/ genwebpack / prod / en / 3L8X.3ea888b98536ff1d0203.js"], "3LDP": ["/ genwebpack / prod / en / 3LDP.6406829f4ba1d9ac4a0b.js "]," 3LDf ": [" / genwebpack / prod / en / 3LDf.4e17e540cb5f7800fd1e.js "]," 3NVp ": [" / genwebpack / prod / en / 3NVp23a9e9481 ": [" / genwebpack / prod / en / 3Nju.ebc351c24a428bf743a9.js "]," 3NmD ": [" / genwebpack / prod / en / 3NmD.6bfebf201e56fcb42f0b.js "]," 3Pml ": [" / genweb. /en/3Pml.1b973ab850d1adab7aa8.js" visible,"3Qw5":["/genwebpack/prod/en/3Qw5.cd6a69f9769cc8de0ffd.js"pting,"3SWN":["/genwebpack/prod/en/3SWN":["/genwebpack/prod/en/6S11fsWN.6D) "]," 3TWR ": [" / genwebpack / prod / en / 3TWR.7b1e748ff4697b4424a5.js "]," 3Tdt ": [" / genwebpack / prod / en / 3Tdt.768262c5db31f6d54f4c.js "]," 3UBJ ": [" / genwebpack / prod / en / 3UBJ.3bb351e25d6e48fe64d7.js "]," 3Uys ": ["/genwebpack/prod/en/3Uys.70ec59ff2553aa1361cc.js" visible,"3WSq":["/genwebpack/prod/en/3WSq.682f69f662d23c8e3110.js" ],"3Wv8":["/genwebpack/prod/prod/prod/ /3Wv8.64c42d81067c86627b79.js" visible,"3YJn":["/genwebpack/prod/en/3YJn.7547ad2e18a7c92c3a15.js"pting,"3YUn":["/genwebpack/prod/en/3YUn":["/genwebpack/prod/en/3Y91.jd11.95] , "3ZoY": ["/ genwebpack / prod / en / 3ZoY.20feff1b0686ec8d66fd.js"], "3aD5": ["/ genwebpack / prod / en / 3aD5.841d4eabf893e8f72324.js "]," 3abC ": [" / genwebpack / prod / en / 3abC.dba09f2ccd751f5f0128.js "]," 3ajf ": [" / genwebpack / prod / en / 3ajf.acc30bdpack "/ 3ajf.acc30dpack" / /prod/en/3ajf.b02112ab9ed3c3a283a2.js"pting,"3b3X":["/genwebpack/prod/en/3b3X.53bf95a1c1d2a8e65aa1.css","/genwebpack/prod/c ./3b3f7df17d90 "," 3cLW ": [" / genwebpack / prod / en / 3cLW.0646312d1b2be50dd9da.js "]," 3eD4 ": [" / genwebpack / prod / en / 3eD4.0daf28ab601ec13cc868.css "," / genwebpacke / prod / en. 162605cd1529c8af6213.js "]," 3glC ": [" / genwebpack / prod / en / 3glC.ae16ad4594136b774dce.js "]," 3hAB ": [" / genwebpack / prod / en / 3hAB.223cde4fef3638f93e96.js "]," 3hdl ": [" / genwebpack / prod / en / 3hdl.120e632e696c515c0.js. ": [" / genwebpack / prod / en / 3hyK.1dbaf6b3863a89c0b0a2.js "]," 3iUY ": [" / genwebpack / prod / en / 3iUY.ad5bacacc76a1dd3bd88.js "]," 3jb1b ":pack [" / genweb /en/3jb1.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/3jb1.a2347d503e317f0f77d0.js"pting,"3mAf":["/genwebpack/prod/en/3mAf.74856mpt641d9 : ["/ genwebpack / prod / en / 3mIE.a564eb881efa5fcfb96d.js"], "3mlm": ["/ genwebpack / prod / en / 3mlm.a489602842416dec1616.js "]," 3nN3 ": [" / genwebpack / prod / en / 3nN3.a2fca621bcf0ccb5f56b.js "]," 3ncc ": [" / genwebpack / prod / en / 3ncc.675cd3740ejcd7 «: [« / genwebpack / prod / en / 3nrI.a189baa042af9b24055d.js »],« 3oKi »: [« / genwebpack / prod / en / 3oKi.a777c14af1b65aec2cce.js »],« 3oXqwebpack [«/ prodwebpack»: /en/3oXq.b8ec1faac4d4b7bfad44.js"pting,"3p5T":["/genwebpack/prod/en/3p5T.df1abefd6e6f2a407cd9.js"pting,"3rQ3":["/genwebpack3/173.1/en "]," 3rZX ": [" / genwebpack / prod / en / 3rZX.4e6b75ad668b3906ab96.js "]," 3sHy ": [" / genwebpack / prod / en / 3sHy.8e8b5c79c4e3bd5c97af.js "]," 3sOJ ": [" / genwebpack / prod / en / 3sOJ.904c77b2fb8c0d6a9ffd7.css ", /en/3sOJ.f90d421128dbc8839037.js" visible,"3sk8":["/genwebpack/prod/en/3sk8.19b6745d8e33a7c61ccc.js"pting,"3ssq":["/genwebpack/prod/en/3ssq24.fa43e6 "]," 3st3 ": [" / genwebpack / prod / en / 3st3.a2b980f980067a2ff425.js "]," 3sws ": [" / genwebpack / prod / en / 3sws.51a05b2860b503a2d702.js "]," 3sy6 ": [ "/genwebpack/prod/en/3sy6.a1e177658a9dcf2e97e1.js" visible,"3u3S":["/genwebpack/prod/en/3u3S.ddb78ae8f8c2c30ad53d.js "]," 3uMK ": [" / genwebpack / prod / en / 3uMK.727f87d1f5b0a3564da0.js "]," 3uPh ": [" / genwebpack / prod / en / 3uPh.6daCBB4. /prod/en/3uPh.b5227a7a47e7990d7bdf.js"pting,"3uk6":["/genwebpack/prod/en/3uk6.219210058d9ae3fbe399.js" ],"3vlA":["/genwebpack/prodA.c1597/3 .js "]," 3vwj ": [" / genwebpack / prod / en / 3vwj.e7e623e1659d6aa1c745.js "]," 3w2K ": [" / genwebpack / prod / en / 3w2K.d8f945533fb8d7770bd3.js "]," 3xIs "] : ["/ genwebpack / prod / en / 3xIo.91d0f9f80b9e254d99fa.js"], "3xLc": ["/ genwebpack / prod / en / 3xLc.87511daedaf748660ac3.js "]," 3xU3 ": [" / genwebpack / prod / en / 3xU3.afd1c67fe68ff0f8b1fa.js "]," 3ydI ": [" / genwebpack / prod / en / 3ydI.3b5014d6050026ae09 " ": [" / genwebpack / prod / en / 3ytn.afe0e348216f01c308cf.js "]," 40jg ": [" / genwebpack / prod / en / 40jg.d1dd1cf1e04b7d0449a5.js "]," 41RXweb ": [" / prod /en/41RX.e7751ba1f694a5a792fe.js" visible,"46xH":["/genwebpack/prod/en/46xH.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/46xH.f2d5846s",H484846103" : ["/ genwebpack / prod / en / 48H7.f1600c1bbea5d34ab0ee.js"], "48tu": ["/ genwebpack / prod / en / 48tu.5bf0aa618e5053e84069.js "]," 4AQu ": [" / genwebpack / prod / en / 4AQu.249653f8ae2e29b94021.js "]," 4BuB ": [" / genwebpack / prod / en / 4BuB.42d72d523ae ": [" / genwebpack / prod / en / 4Cd2.df8f74ea6c3e54380d50.js "]," 4D6H ": [" / genwebpack / prod / en / 4D6H.5405b242c731b645ec7f.js "]," 4DFebpack ": [" / pro /en/4DFe.47e9c26dde1b3258e18e.js" visible,"4F3S":["/genwebpack/prod/en/4F3S.0187c6aab53285ace6c8.js"pting,"4IdB":["/genwebpack/prod/en/4Id2.d2.db "]," 4J4O ": [" / genwebpack / prod / en / 4J4O.f78bee02beea88db9859.js "]," 4La6 ": [" / genwebpack / prod / en / 4La6.c6c3e1bf3a5a325814b0.js "]," 4Lwk ": [" / genwebpack / prod / en / 4Lwk.e3df2fc975e5037216d6.js "]," ["/genwebpack/prod/en/4MR3.f84be314237f3829de68.js" visible,"4Mab":["/genwebpack/prod/en/4Mab.baeb670a08dbf0c01cfe.js" ],"4NeH":["/genwebpack/prod /4NeH.a629d9310357f76779dd.css "," / genwebpack / prod / en / 4NeH.c17331971d513f712306.js "]," 4OKa ": [" / genwebpack / prod / en / 4OKa.f974ae33f15e08a] "/genwebpack/prod/en/4PFy.f0073ff4715b2f53f028.css","/genwebpack/prod/en/4PFy.440babb9e7d36c4c42cc.js "]," 4QgR ": [" / genwebpack / prod / en / 4QgR.43c84d53341ce75e04e2.js "]," 4RFn ": [" / genwebpack / prod / en / 4RFn.e658bbc7595] ": [" / genwebpack / prod / en / 4S76.c7cb6fc2183027e98857.js "]," 4UbB ": [" / genwebpack / prod / en / 4UbB.c209414654b971294c94.js "]," 4XuZ ": [/ prod / genwebpack /en/4XuZ.11dcad13d66aa5d01678.css","/genwebpack/prod/en/4XuZ.e56ed13a7a744bc2431c.js"pting,"4Y7T":["/genwebpack/prod/en/4Y7T.ba7e6f1942cd3a"> : ["/ genwebpack / prod / en / 4YZv.31ef226836f8a868d77b.js"], "4aZI": ["/ genwebpack / prod / en / 4aZI.c6acfd8ffdd80bb3cebb.js "]," 4afB ": [" / genwebpack / prod / en / 4afB.9de8b86ee729a54ba3e9.js "]," 4ajK ": [" / genwebpack / prod / en / 4ajK.9f2b5371ffeb7d ": [" / genwebpack / prod / en / 4bhX.38fc46fd560bec5d1444.js "]," 4dK5 ": [" / genwebpack / prod / en / 4dK5.f111d6b17d3c0d3efbc4.js "]," 4ds7webpack ": [" /en/4ds7.65b443a78e2dc68f2cbd.js"pting,"4eCT":["/genwebpack/prod/en/4eCT.335e138c63d291f376ae.js" provided,"4fxe":["/genwebpack/prod/en/4fxe20e.26) "]," 4hOP ": [" / genwebpack / prod / en / 4hOP.b8c3bdcedd43fdd415da.js »],« 4hVx »: [« / genwebpack / prod / en / 4hVx.0281ff99e7ec14fc9329.js »],« 4ivs »: [« / genwebpack / prod / en / 4ivs.c6f63aa0e082e8fd6e60.jsK »],« 4hVx.0281ff99e7ec14fc9329.js ». ["/genwebpack/prod/en/4jaK.7534dbabcbe6f3d6cdd4.js" ],"4ldP":["/genwebpack/prod/en/4ldP.39a597e562504e3a265a.js" ],"4m8r":[/prod/webpack/prod/weback /4m8r.d56865a888ef523a77bc.js" visible,"4n2g":["/genwebpack/prod/en/4n2g.8f16aae6209174a63821.js"pting,"4oB5":["/genwebpack/prod/en/4oB5.c3500a "/genwebpack/prod/en/4oB5.6ec7830e72501c54bec4.js" visible,"4q6b":["/genwebpack/prod/en/4q6b.bafeb9621f1913a5096a.js "]," 4qrU ": [" / genwebpack / prod / en / 4qrU.f9894f7f2e93a782e250.js "]," 4rlT ": [" / genwebpack / prod / en / 4rlT.4843fe3334e5e8. ": [" / genwebpack / prod / en / 4sjh.66ca26de0e7d0ef8deb1.js "]," 4svc ": [" / genwebpack / prod / en / 4svc.b6f05a3d030d2f6b9604.js "]," 4t0Kwebpack ": [" / prod /en/4t0K.5ceed9af3f521332a389.js"pting,"4tYZ":["/genwebpack/prod/en/4tYZ.e7a3fc0d97b2e7b0d182.js"pting,"4ulC":["/genwebpack/prod/en/4ulC.213 "]," 4umA ": [" / genwebpack / prod / en / 4umA.e8fa1312b94b617ec9a4.js "]," 4w1V ": [" / genwebpack / prod / en / 4w1V.5e7ce3b356905d3586bf.js "]," 4yoM ": [" / genwebpack / prod / en / 4yoM.12eab7b6442716ed6def.js "]," 4zf. ["/genwebpack/prod/en/4zfU.6e5388d50b4504ae26bf.js" visible,"51gk":["/genwebpack/prod/en/51gk.afbbbbf3f49331a160fc.js" ],"52L6":["/genwebpack/prod /52L6.7103b79b320e59645167.js" visible,"52rc":["/genwebpack/prod/en/52rc.4146b093077ae4277470.js"pting,"534i":["/genwebpack/prod/en/534i.60223a9461106cc "/genwebpack/prod/en/534i.5e4ba1413592386f293f.js" visible,"53l8":["/genwebpack/prod/en/53l8.1022869ca294f20b28e2.js "]," 542X ": [" / genwebpack / prod / en / 542X.5c415983d7aafcd588a4.js "]," 55xb ": [" / genwebpack / prod / en / 55xb.b1af611b66eb749] ": [" / genwebpack / prod / en / 56lG.7f560070a960360f841c.js "]," 57Ou ": [" / genwebpack / prod / en / 57Ou.7b83170fb86f8fcfc0bb.js "]," 58Go ": [" / genwebpack / prod /en/58Go.0c4a96065c9fd62488d1.js" Survival : ["/ genwebpack / prod / en / 58ik.3c06aee4463b71ba41bd.js"], "58sT": ["/ genwebpack / prod / en / 58sT.67aab918129a95ac6c24.js "]," 59kG ": [" / genwebpack / prod / en / 59kG.81f57a0d6cfff8c9efbb.js "]," 5AWW ": [" / genwebpack / prod / en / 5AWW.98a0441b83gba110089s ": [" / genwebpack / prod / en / 5B3g.806cc707842b812da292.js "]," 5CEK ": [" / genwebpack / prod / en / 5CEK.d939d2b51f43eded189c.js "]," 5DuI ": [" / genwebpack / prod /en/5DuI.5c3e2efbf3d76419ecd7.js"pting,"5ESl":["/genwebpack/prod/en/5ESl.f43b5acf41978e226b58.js" ],"5Ein":["/genwebpack/prod/en/5E408j0c3c3c "]," 5F0q ": [" / genwebpack / prod / en / 5F0q.4fea10dbb0b20c49a360.js »],« 5FHU »: [« / genwebpack / prod / en / 5FHU.a1dc860a722d19ce68fd.js »],« 5FP6 »: [« / genwebpack / prod / en / 5FP6.6ac8748ef963e0ef9fbf.js »],« 5GHU.a1dc860a722d19ce68fd.js » ["/genwebpack/prod/en/5GvA.aacb12d83ce1e3c464f8.js" visible,"5HCZ":["/genwebpack/prod/en/5HCZ.65d86a893b2bc2779fea.js" ],"5IGZ":["/genwebpack/prod/genwebpack/ /5IGZ.4bb4a05c7d36821a9a51.js"pting,"5L3M":["/genwebpack/prod/en/5L3M.3be6eda3c04c3cf0e454.js" ],"5MvW":["/genwebpack/prod.1d/en/5MvW"> , «5Nr5»: [«/ genwebpack / prod / en / 5Nr5.49c060a0f422f15bdb86.js»], «5O00»: [«/ genwebpack / prod / en / 5O00.96561bcfcb4c454daec4.js "]," 5OGZ ": [" / genwebpack / prod / en / 5OGZ.a30fcd44d8c6206fdd4d.js "]," 5OPo ": [" / genwebpack / prod / en / 5OPo.c36dabsd / en / 5OPo.c36djs857a85] ": [" / genwebpack / prod / en / 5OSm.816bd233d30325e7db45.js "]," 5Okb ": [" / genwebpack / prod / en / 5Okb.bac24dd1686fa1b.js "]," 5P0O ": [" / genwebpack / /en/5P0O.f7d745d490eace48b0af.js"pting,"5PqK":["/genwebpack/prod/en/5PqK.d039ec9a6cb0fcf232d0.js"pting,"5Qmt":["/genwebpack5/prod3.71/en "]," 5QyG ": [" / genwebpack / prod / en / 5QyG.e54bd3c059fc1a962ddf.js "]," 5R1r ": [" / genwebpack / prod / en / 5R1r.e427a01573421d20b5af.js "]," 5RFs ": [" / genwebpack / prod / en / 5RFs.0bd0b240c9e1a1ea3f66.js "]," 5RFs "]," 5RFs "] ["/genwebpack/prod/en/5RG8.83ca1228ef3c259c2483.js"pting,"5Rew":["/genwebpack/prod/en/5Rew.6a73e6b0a3e05f29c3e6.js" ],"5SB4":["/genwebpack/ /5SB4.a6acfcc51c8070ef60f6.js"pting,"5Svh":["/genwebpack/prod/en/5Svh.76ff7ffe2466d1c09e09.js"pting,"5TKU":["/genwebpack/prod/en/5Tfc8.40fdd/en/5Tfjs45fdd/en/5Tfc45fddd/en/5Tfc45fd] , «5V8W»: [«/ genwebpack / prod / en / 5V8W.e8c5fe5daac3b54eb756.js»], «5WSt»: [«/ genwebpack / prod / en / 5WSt.caa2f0e07c1f1944dd5f.js "]," 5WnU ": [" / genwebpack / prod / en / 5WnU.c67798f3e7685db695c8.js "]," 5Xn2 ": [" / genwebpack / prod / en / 5Xbe4158dade
SyntaxError: недопустимый или неожиданный токен
в новом скрипте (vm.js: 88: 7)
в JSDOMSixteenEnvironment._runScript (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:292:24)
в JSDOMSixteenEnvironment.render (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:191:16)
в runMicrotasks ()
в processTicksAndRejection (внутренний / процесс / task_queues.js: 97: 5)
в async renderHandler (/ workspace / node_modules / render-gateway / dist / gateway / handlers / make-render-handler.x # принимает любое ненулевое комплексное значение бесконечно много раз в любой сколь угодно малой окрестности # oo #. Это называется существенной сингулярностью на бесконечности . Mathway | Популярные задачи
1
Найдите производную - d / dx
натуральное бревно x
2
Оцените интеграл
интеграл натурального логарифма x относительно x
3
Найдите производную - d / dx
е ^ х
4
Оцените интеграл
интеграл e ^ (2x) относительно x
5
Найдите производную - d / dx
1 / х
6
Найдите производную - d / dx
х ^ 2
7
Найдите производную - d / dx
1 / (х ^ 2)
8
Найдите производную - d / dx
грех (х) ^ 2
9
Найдите производную - d / dx
сек (x)
10
Оцените интеграл
интеграл e ^ x относительно x
11
Оцените интеграл
интеграл x ^ 2 относительно x
12
Оцените интеграл
интеграл квадратного корня x относительно x
13
Найдите производную - d / dx
cos (x) ^ 2
14
Оцените интеграл
интеграл 1 / x относительно x
15
Оцените интеграл
интеграл sin (x) ^ 2 относительно x
16
Найдите производную - d / dx
х ^ 3
17
Найдите производную - d / dx
сек (x) ^ 2
18
Оцените интеграл
интеграл cos (x) ^ 2 относительно x
19
Оцените интеграл
интеграл от sec (x) ^ 2 относительно x
20
Найдите производную - d / dx
е ^ (х ^ 2)
21
Оцените интеграл
интеграл от 0 до 1 кубического корня из 1 + 7x относительно x
22
Найдите производную - d / dx
грех (2x)
23
Найдите производную - d / dx
загар (x) ^ 2
24
Оцените интеграл
интеграл от 1 / (x ^ 2) относительно x
25
Найдите производную - d / dx
2 ^ х
26
График
натуральное бревно из
27
Найдите производную - d / dx
cos (2x)
28
Найдите производную - d / dx
хе ^ х
29
Оцените интеграл
интеграл 2x относительно x
30
Найдите производную - d / dx
(натуральный логарифм x) ^ 2
31
Найдите производную - d / dx
натуральный логарифм (x) ^ 2
32
Найдите производную - d / dx
3x ^ 2
33
Оцените интеграл
интеграл xe ^ (2x) относительно x
34
Найдите производную - d / dx
2e ^ х
35
Найдите производную - d / dx
натуральное бревно 2х
36
Найдите производную - d / dx
-sin (х)
37
Найдите производную - d / dx
4x ^ 2-x + 5
38
Найдите производную - d / dx
y = 16 корень четвертой степени из 4x ^ 4 + 4
39
Найдите производную - d / dx
2x ^ 2
40
Оцените интеграл
интеграл e ^ (3x) относительно x
41
Оцените интеграл
интеграл cos (2x) относительно x
42
Найдите производную - d / dx
1 / (квадратный корень из x)
43
Оцените интеграл
интеграл e ^ (x ^ 2) относительно x
44
Оценить
e ^ бесконечность
45
Найдите производную - d / dx
х / 2
46
Найдите производную - d / dx
-cos (x)
47
Найдите производную - d / dx
грех (3x)
48
Найдите производную - d / dx
1 / (х ^ 3)
49
Оцените интеграл
интеграл tan (x) ^ 2 относительно x
50
Оцените интеграл
интеграл 1 по x
51
Найдите производную - d / dx
х ^ х
52
Найдите производную - d / dx
x натуральное бревно x
53
Найдите производную - d / dx
х ^ 4
54
Оцените предел
предел, когда x приближается к 3 из (3x-5) / (x-3)
55
Оцените интеграл
интеграл x ^ 2 натуральный логарифм x относительно x
56
Найдите производную - d / dx
f (x) = квадратный корень из x
57
Найдите производную - d / dx
х ^ 2sin (х)
58
Оцените интеграл
интеграл sin (2x) относительно x
59
Найдите производную - d / dx
3e ^ х
60
Оцените интеграл
интеграл xe ^ x относительно x
61
Найдите производную - d / dx
у = х ^ 2
62
Найдите производную - d / dx
квадратный корень из x ^ 2 + 1
63
Найдите производную - d / dx
грех (x ^ 2)
64
Оцените интеграл
интеграл e ^ (- 2x) относительно x
65
Оцените интеграл
интеграл натурального логарифма квадратного корня x относительно x
66
Найдите производную - d / dx
e ^ 2
67
Найдите производную - d / dx
х ^ 2 + 1
68
Оцените интеграл
интеграл sin (x) относительно x
69
Найдите производную - d / dx
арксин (х)
70
Оцените предел
предел, когда x приближается к 0 из (sin (x)) / x
71
Оцените интеграл
интеграл e ^ (- x) относительно x
72
Найдите производную - d / dx
х ^ 5
73
Найдите производную - d / dx
2 / х
74
Найдите производную - d / dx
натуральное бревно 3х
75
Найдите производную - d / dx
х ^ (1/2)
76
Найдите производную - d / d @ VAR
f (x) = квадратный корень из x
77
Найдите производную - d / dx
cos (x ^ 2)
78
Найдите производную - d / dx
1 / (х ^ 5)
79
Найдите производную - d / dx
кубический корень из x ^ 2
80
Оцените интеграл
интеграл cos (x) относительно x
81
Оцените интеграл
интеграл e ^ (- x ^ 2) относительно x
82
Найдите производную - d / d @ VAR
е (х) = х ^ 3
83
Оцените интеграл
интеграл от 0 до 10 из 4x ^ 2 + 7 относительно x
84
Оцените интеграл
интеграл (натуральный логарифм x) ^ 2 относительно x
85
Найдите производную - d / dx
бревно х
86
Найдите производную - d / dx
арктан (x)
87
Найдите производную - d / dx
натуральное бревно 5х
88
Найдите производную - d / dx
5e ^ х
89
Найдите производную - d / dx
cos (3x)
90
Оцените интеграл
интеграл x ^ 3 относительно x
91
Оцените интеграл
интеграл x ^ 2e ^ x относительно x
92
Найдите производную - d / dx
16 корень четвертой степени из 4x ^ 4 + 4
93
Найдите производную - d / dx
х / (е ^ х)
94
Оценить предел
Предел , когда x приближается к 3 от arctan (e ^ x)
95
Оцените интеграл
интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x
96
Найдите производную - d / dx
3 ^ х
97
Оцените интеграл
интеграл xe ^ (x ^ 2) относительно x
98
Найдите производную - d / dx
2sin (х)
99
Оценить
сек (0) ^ 2
100
Найдите производную - d / dx
натуральный логарифм x ^ 2
Предел функции при стремлении x к бесконечности
Предел функции
x стремится к бесконечности
В этом модуле мы объясняем, что это означает, когда Предел функции стремится к бесконечности, по крайней мере, к бесконечности или к истинной связи, в то время как x стремится к бесконечности или бесконечности.Мы также объясняем, что означает, что функция стремится быть действительной, а x стремится к определенному действительному числу.
В любом случае мы приводим пример функции, которая не достигает предела. Чтобы освоить описанные здесь техники, важно, чтобы вы выполняли много упражнений, чтобы это стало второй натурой.
В этом примере мы используем программирование на Python, чтобы проверить предел, когда x стремится к бесконечности. Предел - это значение, к которому функция «приближается», потому что вход приближается к некоторому значению. Пределы являются неотъемлемой частью исчисления и определяются с помощью непрерывности, производных и интегралов.
В этой статье использовались различные библиотеки Python. Теперь давайте посмотрим, как найти предел для данной функции, когда x стремится к бесконечности в коде Python.
1. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (sin (1 / x), x, oo, '+'))
сюжет (sin (1 / x))
Выход: 0
Предел функции, когда x стремится к бесконечности
2.Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (1) / x, x, oo, '+'))
сюжет (exp (1) / x)
Выход: 0
Предел функции, когда x стремится к бесконечности
3. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (-1) / x, x, oo))
сюжет (exp (-1) / x)
Выход: 0
Предел функции, когда x стремится к бесконечности
4. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (x) / x, x, oo))
сюжет (exp (x) / x)
Вывод: oo
Предел функции, когда x стремится к бесконечности
5. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (exp (-x) / x, x, oo))
сюжет (exp (-x) / x))
Предел функции, когда x стремится к бесконечности
6.Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (x ** 2 * sin (1 / x), x, oo, '+'))
сюжет (x ** 2 * sin (1 / x))
Вывод: oo Предел функции, когда x стремится к бесконечности
7. Обсудите предел следующей функции, когда x → ∞
импортировать numpy как np
из sympy import *
x = символы ('x')
init_printing (use_unicode = True)
print (предел (x / (1 + x), x, oo, '+'))
участок (x / (1 + x))
Выход: 1
Предел функции, когда x стремится к бесконечности
пределов бесконечности: что нужно знать - Матено.com
Вы работаете с задачами «Предел в бесконечности» в Calculus? Давайте разберем их и разовьем ваше понимание, чтобы вы могли решать их самостоятельно.
I. Как думать о «уходе в бесконечность»
• Когда вы видите $ \ displaystyle {\ lim_ {x \ to \, \ infty}} $, подумайте:
«Предел x увеличивается и растет, и растет, и растет,…, в положительном направлении, навсегда ».
• Когда вы видите $ \ displaystyle {\ lim_ {x \ to \, - \ infty}} $, подумайте:
«Предел x растет и растет, и растет, и растет,…, в отрицательное направление, навсегда.n} = 0} \ text {for} n> 0} $
Например, $ \ displaystyle {\ lim_ {x \ to \, - \ infty} \ frac {1} {x} = 0} $: As x увеличивается и увеличивается в отрицательном направлении по мере того, как мы движемся по оси x влево, навсегда, $ y = \ dfrac {1} {x} $ становится все ближе и ближе к 0. Следовательно, «предел при отрицательная бесконечность »равна 0. Нужно быстро построить график функции, чтобы проверить предел? Нам нравится веб-сайт Desmos - он бесплатный и очень простой в использовании!
III. 3.3 $ растет и растет вниз, в отрицательном направлении
y , навсегда. Следовательно, мы записываем предел как $ - \ infty. $ Краткое словарное примечание : когда мы пишем, что предел «равен» $ \ infty $ или $ - \ infty $, помните, что на самом деле мы имеем в виду, что функция растет и растет и РАСТЕТ вечно, никогда не достигая определенного значения. (Опять же: бесконечность - это не конкретное место или какое-то «магическое число»; вместо этого это процесс бесконечного роста.) Следовательно, в этих случаях предел не существует (DNE).
В некоторых ситуациях, например, в вопросе с несколькими вариантами ответов (среди прочего, на экзамене AP Calculus) правильный ответ может быть указан как «не существует», «DNE» или «undefined», а не «$ \ infty $ »или« $ - \ infty $ ».
IV. Полиномы: преобладает наибольшая степень
Что происходит, когда x растет, растет и растет, когда у нас есть многочлен, который по определению имеет разные степени x в нем? Давайте рассмотрим конкретный пример для исследования.N} $$
Если вы хотите более тщательно доказать свой результат, начните с вынесения x -в наибольшую степень. Затем перейдите к поиску предела, как показано в примерах выше.
V. Доля многочленов (также известная как «Рациональные функции»)
Если у вас есть один многочлен, разделенный на другой многочлен (технически называемый рациональной функцией ), тогда:
Шаг 1. Определите термин в числителе с наибольшей степенью, а член в знаменателе с наибольшей степенью.Затем вы можете игнорировать все остальные члены, как мы это сделали для многочленов в предыдущем разделе.
Шаг 2. Сравните степень в числителе со степенью в знаменателе. Есть три возможности: (1) наибольшая степень в числителе такая же, как и в знаменателе; (2) наибольшая степень в знаменателе больше, чем в числителе; (3) наибольшая степень в числителе больше, чем в знаменателе. Рассмотрим каждый:
• Возможность 1: Равные степени.2} = 0} $ и так далее.
[свернуть]
Мы можем проверить результат, посмотрев на график функции. Обратите внимание, что он приближается к линии $ y = \ dfrac {2} {5} $ как $ x \ to \ infty. $
На графике в примере 3 показана горизонтальная асимптота : Если $ \ displaystyle {\ lim_ {x \ to \ infty} f (x) = L} $, где L - действительное число, тогда график f (x) становится сколь угодно близко к линии $ y = L $ как $ x \ to \ infty . $ Эта линия $ y = L $ называется горизонтальной асимптотой графика f .2} = 0}. $
[свернуть]
Мы можем проверить результат, посмотрев на график функции. Обратите внимание, что кривая $ y = f (x) $ приближается к прямой $ y = - \ dfrac {1} {2} $ как $ x \ to \, - \ infty $, и поэтому эта линия является горизонтальной асимптотой для этого функция.
• Возможность 2: Знаменатель преобладает. Если наибольшая степень в знаменателе больше , чем наибольшая степень в числителе, то предел равен 0. Это правило выполняется как для $ x \ to \ infty $, так и для $ x \ to \, - \ infty.$
$$ \ bbox [желтый, 5px] {\ lim_ {x \ to \ infty} \ frac {\ text {(некоторый многочлен)}} {\ text {(многочлен, высшая степень которого> числителя)}} = 0} $$
$$ \ bbox [желтый, 5px] {\ lim_ {x \ to \, - \ infty} \ frac {\ text {(некоторый многочлен)}} {\ text {(многочлен, максимальная степень которого> числителя)} } = 0} $$
Концептуально рост знаменателя «побеждает» рост в числителе, то есть знаменатель увеличивается быстрее, чем числитель, и поэтому дробь стремится к нулю как x растет, растет и растет либо в положительном, либо в отрицательном направлении.4} = 0} $ и так далее.
[свернуть]
Мы можем проверить результат, посмотрев на график функции. Обратите внимание, что кривая $ y = f (x) $ приближается к линии $ y = 0 $ как $ x \ to \, - \ infty $, и поэтому эта линия (горизонтальная ось) является горизонтальной асимптотой для этой функции.
• Возможность 3: числитель преобладает. Если наибольшая степень в числителе больше , чем наибольшая степень в знаменателе, то предел равен либо $ \ infty $, либо $ - \ infty $, и, следовательно, не существует (DNE).Это правило выполняется как для $ x \ to \ infty $, так и для $ x \ to \, - \ infty. $
$$ \ bbox [yellow, 5px] {\ lim_ {x \ to \ infty} \ frac {\ text { (многочлен, высшая степень которого> знаменателя)}} {\ text {(некоторый многочлен)}} = \ infty \ text {или} - \ infty} $$
$$ \ bbox [yellow, 5px] {\ lim_ {x \ to \, - \ infty} \ frac {\ text {(многочлен, максимальная степень которого> знаменателя)}} {\ text {(некоторый многочлен)}} = \ infty \ text {или} - \ infty} $$
Концептуально , рост числителя «побеждает» рост знаменателя, что означает, что числитель увеличивается быстрее, чем знаменатель, и поэтому дробь становится все больше и больше x растет и растет и растет в любом положительное или отрицательное направление.4} \\ [8px]
& = \ lim_ {x \ to \ infty} \ frac {x} {3} \\ [8px]
& = \ infty \ quad \ cmark
\ end {align *} \]
Вторая строка в решении показывает, что функция приближается к $ \ dfrac {x} {3} $ по мере увеличения x , что соответствует графику показывает. 4} \\ [8px]
& = \ lim_ {x \ to \, - \ infty} \ frac {x} {3} \\ [8px]
& = - \ infty \ quad \ cmark
\ end {align *} \] Вторая строка в решении показывает, что функция приближается к $ \ dfrac {x} {3} $ по мере увеличения x , что соответствует график показывает.«Предел на отрицательной бесконечности» равен отрицательному $ \ infty $, потому что функция постоянно растет в отрицательном направлении y по мере того, как x увеличивается, а значение больше - в отрицательном направлении. Между прочим, линия $ y = \ dfrac {x} {3} $ представляет собой наклонную асимптоту (как в положительном, так и в отрицательном направлениях) для этой функции, поскольку график функции сколь угодно близко к этой линии при увеличении x (в обоих направлениях).
Обращаюсь к вам:
- Или какие у вас есть вопросы?
- Какими советами вы могли бы поделиться по решению задач Limit at Infinity?
- Как продвигается ваше изучение математики?
Прокомментируйте, пожалуйста, ниже!
Как найти предел, когда x стремится к бесконечности математики класса 11 CBSE
Подсказка: При любом x стремится к бесконечности значение $ \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ зависит от старшей степени x в f (x) и старшей степени g (x), где f и g являются алгебраическими функциями x.Если f имеет более высокую степень, чем g, то значение $ \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ будет стремиться к бесконечности, когда x стремится к бесконечности. Если g имеет более высокую степень, тогда значение $ \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ будет стремиться к 0, когда x стремится к бесконечности. Если оба имеют одинаковую наивысшую степень, тогда значение $ \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ будет стремиться к $ \ dfrac {\ text {коэффициенту наивысшей степени x in f}} {\ text {коэффициент наивысшей степени x в g}} $, когда x стремится к бесконечности.{3}}} {3x} $ стремится к бесконечности. Примечание: В задаче $ \ displaystyle \ lim_ {x \ to 0} \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ вышеупомянутое правило отменено. Если функция f имеет более высокую степень, тогда $ \ displaystyle \ lim_ {x \ to 0} \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ будет равно 0. Если функция g имеет более высокую степень, чем функция f, то $ \ displaystyle \ lim_ {x \ to 0} \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ будет стремиться к бесконечности. Если оба имеют одинаковую наивысшую мощность, то $ \ displaystyle \ lim_ {x \ to 0} \ dfrac {f \ left (x \ right)} {g \ left (x \ right)} $ равно $ \ dfrac {\ text {константа} \ текст {присутствует} \ текст {in} \ текст {функция} \ текст {f}} {\ текст {константа} \ текст {присутствует} \ текст {in} \ текст {функция} \ текст {g} } $.
Видеоурок: Пределы бесконечности
стенограмма видео
В этом видео мы узнаем
о пределах на бесконечности и неограниченных пределах. Ранее мы узнали о
смысл предела 𝑓 числа 𝑥, когда 𝑥 приближается к некоторому действительному числу 𝑐. Если значение этого лимита равно 𝐿,
это означает, что если мы выберем достаточно близко к, то мы можем сделать из как
близко к 𝐿, как хотелось бы.Мы можем получить значение 𝑓 из 𝑥
сколь угодно близко к 𝐿. В этом видео мы собираемся
интерпретировать пределы формы как предел 𝑓 из 𝑥, когда 𝑥 приближается к бесконечности. Что это значит для таких лимитов
иметь значение 𝐿?
Можно попробовать просто заменить 𝑐 в
приведенное выше определение бесконечностью. Итак, мы интерпретируем это как
что если мы выберем достаточно близким к бесконечности, то сможем сделать 𝑓 из 𝑥 как можно ближе к
𝐿 как хотим.Но что это значит для 𝑥 быть
достаточно близко к бесконечности, когда бесконечность бесконечно далеко от любого значения 𝑥
что мы могли выбрать? Оказывается, вместо того, чтобы сказать
что 𝑥 достаточно близко к бесконечности, мы должны сказать, что достаточно велико. Итак, предел 𝑓 элемента при
стремится к бесконечности, равно 𝐿 означает, что если мы выберем достаточно большим, то мы сможем
сделайте 𝑓 из 𝑥 как можно ближе к 𝐿.
Глядя на график
обратная функция, мы можем видеть, что если мы выберем 𝑥 достаточно большим, то мы можем сделать
обратная функция, единица над 𝑥, как можно ближе к нулю. Итак, мы говорим, что предел
единица над 𝑥, когда 𝑥 стремится к бесконечности, равна нулю. Значение этого предельного нуля - это
значение, которое функция, перешедшая на единицу, становится все ближе и ближе к какому-либо значению.
без ограничений.
Еще можно подумать о пределе
из 𝑓 из 𝑥, когда стремится к отрицательной бесконечности. Этот предел равен 𝐿 означает, что если
мы выбираем 𝑥 большой и достаточно отрицательный, другими словами отрицательный, но большой
достаточно по величине, тогда мы можем сделать из настолько близким к 𝐿, насколько захотим. Как и в случае с пределом, когда приближается
положительная бесконечность, мы можем думать об этом значении 𝐿 по-другому. Это значение 𝐿 - это значение, которое 𝑓
становится все ближе и ближе к по мере того, как 𝑥 неограниченно убывает.
Итак, какой предел
𝑥 как 𝑥 приближается к отрицательной бесконечности? Так как 𝑥 убывает без
границ, один над 𝑥 становится все ближе и ближе к нулю. Итак, значение этого лимита, опять же,
равно нулю. Эти два ограничения очень полезны
пределы знать. Оказывается, что предельные законы мы
изученные для конечных пределов, правильно интерпретированные, работают так же хорошо для бесконечных
пределы.Используя эти законы пределов вместе
с пределами обратной функции при стремлении к бесконечности и отрицательных
бесконечность, которую мы только что нашли, мы можем найти значение многих других ограничений. Давайте посмотрим на пример.
Найдите предел отрицательных четырех
более 𝑥 в квадрате плюс пять на 𝑥 плюс восемь, когда 𝑥 приближается к бесконечности.
У нас есть предел как 𝑥
здесь приближается к бесконечности, но по-прежнему действуют все обычные правила ограничений.Например, предел суммы
функций равно сумме пределов. Итак, мы можем разделить наш лимит
до трех. Это равно пределу
отрицательные четыре на 𝑥 в квадрате, когда 𝑥 приближается к бесконечности плюс предел пяти
больше, когда 𝑥 приближается к бесконечности, плюс предел восьми, когда 𝑥 приближается
бесконечность.
Что уж говорить об этом
предел? Что ж, мы знаем, что предел
константа 𝐾, когда 𝑥 приближается к некоторому числу 𝑐, равна.А что касается предыдущего лимита
закон, это верно, даже если 𝑐 не является действительным числом, но бесконечным или отрицательным
бесконечность. Значение этого последнего лимита равно
всего восемь.
А как насчет двух других
пределы? Мы можем использовать тот факт, что
предел постоянного кратного функции - это постоянное кратное
предел функции. Таким образом, первый предел равен
отрицательное в четыре раза больше предела в в квадрате по мере приближения
бесконечность.А второй - пять раз
предел единицы над при стремлении к бесконечности. И наконец, добавляем
восемь.
Теперь предел
обратная функция один над, когда 𝑥 приближается к бесконечности, является чем-то, что мы
должен знать. Его значение равно нулю. Но как насчет предела одного
больше 𝑥 в квадрате, когда 𝑥 приближается к бесконечности? Что ж, мы можем использовать тот факт, что
предел мощности функции - это мощность предела
функция.Этот предел является пределом
обратная функция на единицу больше в квадрате, так как один больше в квадрате равняется единице больше
𝑥 все в квадрате. И по нашему предельному закону это
предел единицы над, когда 𝑥 стремится к бесконечности во всем квадрате. Этот предел известен как
нуль. Итак, наш предел, предел
единица больше 𝑥 в квадрате при стремлении к бесконечности также равна нулю.
Мы можем обобщить то, что вы
получить другой предельный закон, что предел единицы больше 𝑥 в степени, поскольку 𝑥
стремится к бесконечности, равно нулю, по крайней мере, если 𝑛 больше нуля.Наш исходный предел:
следовательно, отрицательное четыре раза ноль плюс пять раз ноль плюс восемь, то есть,
конечно, всего восемь.
Давайте посмотрим на другой пример.
Найдите предел отрицательных двух
𝑥 на отрицательные четыре плюс восемь 𝑥 на отрицательные три минус 𝑥 на отрицательные
отрицательные два плюс девять 𝑥 к отрицательному минус четыре всего два 𝑥 на
отрицательные четыре минус шесть 𝑥 к отрицательным трем плюс семь к отрицательным
два плюс шесть 𝑥 к минусу один плюс три, поскольку 𝑥 стремится к бесконечности.
Это предел частного
функций. И мы знаем, что предел
частное функций есть частное их пределов. Итак, мы можем найти пределы
числитель и знаменатель отдельно, если они существуют. И как предел суммы
функции - это сумма их пределов, мы можем найти пределы поэтапно.
Теперь у нас есть много ограничений на
оценивать, но все они состоят из очень простых терминов.И мы можем сделать их проще,
вывод констант за пределы. Как предел постоянной
умноженная на эту константу, умноженная на предел функции. А теперь подавляющее большинство
наши пределы имеют вид предел 𝑥 в степени некоторого отрицательного числа
когда 𝑥 приближается к бесконечности.
Какова стоимость таких
пределы? Что ж, мы можем написать 𝑥 в
отрицательный 𝑛 как один над 𝑥 к 𝑛.А для 𝑛 больше нуля
значение равно нулю. Тогда все эти ограничения равны
нуль. И нам осталось только
два предела, о которых нужно беспокоиться, оба из которых являются пределами констант четыре и
три. Предел постоянной
функция - это как раз та константа. Итак, соблюдая осторожность
Включите этот знак минус, мы увидим, что ответ будет отрицательным - четыре из трех.
Решение этой проблемы было
просто, потому что у нас были только константы и отрицательные степени в
числитель и знаменатель. И мы знаем, что предел
отрицательная сила такова, как 𝑥 приближается к бесконечности; это ноль.
Давайте посмотрим на пример, в котором мы
не иметь отрицательных сил.
Найдите предел 𝑥 в квадрате
плюс три все больше восьми 𝑥 в кубе плюс девять 𝑥 плюс один при приближении 𝑥
бесконечность.
Наша первая мысль могла бы быть
используйте тот факт, что предел частного - это частное от пределов. Это дает нам предел 𝑥
в квадрате плюс три, когда стремится к бесконечности сверх предела восьми 𝑥 в кубе
плюс девять 𝑥 плюс один, когда 𝑥 приближается к бесконечности. Но мы сталкиваемся с проблемами
потому что ни один предел не определен. В числителе как 𝑥
приближается к бесконечности, 𝑥 в квадрате плюс три не приближается к реальному значению, это
просто становится все больше и больше без ограничений.И то же самое происходит в
знаменатель. Поскольку 𝑥 неограниченно возрастает,
кубическая восемь 𝑥 в кубе плюс девять 𝑥 плюс один также неограниченно увеличивается.
Или, может быть, вы думаете, что оба предела
должна быть бесконечность. Итак, предел левой
сторона бесконечность над бесконечностью. Но это, как ноль
ноль, - неопределенная форма. И это не говорит нам
значение нашего лимита.Нам нужно использовать другой
подход.
Уловка в этом вопросе
найти наибольшую степень, которая появляется в числителе или
знаменатель. Здесь в кубе. И найдя это высшее
мощность, мы делим на нее числитель и знаменатель. Что мы получим? 𝑥 в квадрате делится на 𝑥 в кубе
к отрицательному. И три разделены на 𝑥 в кубе
равняется трем 𝑥 отрицательным трем.А в знаменателе восемь
в кубе делится на 𝑥 в кубе - это всего восемь. Девять 𝑥, разделенное на 𝑥 в кубе, равно
девять 𝑥 к отрицательным двум. И один, разделенный на 𝑥 в кубе, равен
𝑥 к отрицательной тройке.
Итак, теперь у нас просто отрицательный
степени и постоянная в числителе и знаменателе. И в результате, когда мы применяем
этого предельного закона, мы находим, что пределы в числителе и знаменателе теперь соответствуют
существовать.Давайте выясним их ценности. Мы можем использовать тот факт, что
предел суммы функций - это сумма их пределов. Это позволяет нам найти
лимит каждого срока в отдельности. Мы также можем взять
коэффициент вне пределов.
А теперь, кроме одного лимита,
который является пределом постоянной функции, и значение которого, следовательно, должно быть
восемь, все остальные пределы имеют вид предела в степени
отрицательный 𝑛, когда 𝑥 приближается к бесконечности.Где 𝑛, конечно, больше
чем ноль. И мы знаем цену таких
пределы. Значение всегда равно нулю.
Итак, это ноль, а это
ноль, и это ноль, и это ноль. Итак, упрощая, наш ответ:
ноль больше восьми, что, конечно, просто ноль.
Теперь, при первой неудачной попытке
решая эту задачу, мы сказали, что пределы числителя и знаменателя
индивидуально были либо неопределенными, либо бесконечными.Что мы имеем в виду, говоря, что
значение таких лимитов может быть бесконечным. Давайте разберемся.
Если предел 𝑓 из 𝑥, как 𝑥
стремится к бесконечности, является бесконечностью, это означает, что мы можем сделать значение 𝑓 из 𝑥
произвольно большим, выбрав 𝑥 достаточно большим. Предположим, вы хотите, чтобы 𝑓 из было
больше миллиарда. Что ж, есть такая ценность, что
если мы выберем 𝑥 больше, чем это значение, то 𝑓 из 𝑥 будет больше, чем
миллиард по мере необходимости.Другой способ подумать об этом -
что после определенного момента, когда неограниченно возрастает, из также увеличивается
без ограничений.
Аналогично, предел 𝑓 из 𝑥,
когда 𝑥 приближается к бесконечности, отрицательная бесконечность означает, что при увеличении
неограниченно, из неограниченно убывает. И для полноты записываем
значения, когда 𝑥 также стремится к отрицательной бесконечности.Давайте посмотрим на пример.
Найдите предел шести 𝑥
в квадрате больше минус шесть, когда 𝑥 стремится к бесконечности.
Есть разные способы найти
этот предел. Один из способов - посмотреть на график
из равно шести 𝑥 в квадрате над 𝑥 минус шесть. Похоже, что по мере увеличения 𝑥
без ограничений, шесть 𝑥 в квадрате над 𝑥 минус шесть также увеличивается без
граница. В результате можно сказать, что
этот предел бесконечен.Но вы можете не убедиться
этим. Возможно, график
что-то немного другое дальше по оси.
Мы также можем выполнить
полиномиальное деление в столбик, чтобы найти шесть 𝑥 в квадрате над 𝑥 минус шесть, равняется шести
𝑥 плюс 36 плюс 216 больше 𝑥 минус шесть. И это просто
возьмите ограничения с правой стороны. Мы можем сделать это
посменно.Предел шести 𝑥, так как 𝑥
приближается к бесконечности, должна быть бесконечность. Поскольку 𝑥 неограниченно возрастает,
шесть 𝑥 тоже неограниченно возрастают. Предел 36, поскольку 𝑥
приближается к бесконечности, всего 36. Это предел
постоянный.
И последний предел может быть
немного сложнее. Делим числитель и
знаменатель по наибольшей степени, которую мы видим; это 𝑥.Предел частного - это
частное пределов. И предел в числителе
просто ноль, а в знаменателе только единица. Итак, значение этого лимита равно
нуль. Итак, наш предел - бесконечность плюс
36. И когда мы имеем дело с
ограничений, совершенно нормально сказать, что бесконечность плюс 36 - это просто бесконечность, что
дает другой путь к этому ответу.
Хорошо, давай посмотрим финал
проблема.
Найдите предел девяти минус
восемь 𝑥 плюс шесть 𝑥 в квадрате минус два 𝑥 в кубе, когда 𝑥 приближается к отрицательному
бесконечность.
Первое, чем мы можем быть
возникает соблазн записать этот предел суммы как сумму некоторых пределов. Затем мы можем оценить каждый из
эти ограничения один за другим. Предел постоянной
функция девять - это всего лишь девять.Что уж говорить о лимите
из восьми 𝑥, когда 𝑥 приближается к отрицательной бесконечности? Что ж, с графиком 𝑦
равно восьми 𝑥, мы можем видеть, что, когда 𝑥 неограниченно убывает, также
убывает неограниченно. Итак, предел в восемь 𝑥,
когда 𝑥 приближается к отрицательной бесконечности, это отрицательная бесконечность.
Как насчет лимита в шесть 𝑥
в квадрате, когда 𝑥 приближается к отрицательной бесконечности? Опять же, у нас есть график в
ум, и мы видим, что, когда неограниченно убывает, возрастает без ограничений.
граница.Итак, этот предел бесконечен. И, наконец, предел двух
в кубе, когда 𝑥 приближается к отрицательной бесконечности, мы знаем, как выглядит кубическая кривая
нравиться. И мы видим это как 𝑥
приближается к отрицательной бесконечности, 𝑦 также приближается к отрицательной бесконечности. Этот предел отрицательный
бесконечность.
Итак, похоже, наш предел
девять минус отрицательная бесконечность плюс бесконечность минус отрицательная бесконечность.И если мы будем относиться к бесконечности как к
число, мы можем записать минус отрицательную бесконечность как плюс бесконечность, получив девять плюс
бесконечность плюс бесконечность плюс бесконечность. И эта сумма равна
бесконечность. Теперь мы должны быть немного
осторожно относитесь к манипулированию бесконечностью таким образом. Но оказывается, что все
эти шаги допустимы в этой ситуации. Нам повезло, что мы
в конце не осталось минусовых знаков, так как бесконечность минус бесконечность
неопределенный.
Значит, по разным причинам
Возможно, стоит посмотреть, как решить эту проблему другим способом. Вместо этого мы учитываем
из максимальной степени, т. е. 𝑥 в кубе, изнутри предела. Это дает нам предел 𝑥
умножить на девять 𝑥 в кубе на три минус восемь 𝑥 на два минус
плюс шесть 𝑥 к отрицательному минус два, когда 𝑥 приближается к отрицательному
бесконечность.Предел продукта - это
произведение пределов.
А теперь, каков предел 𝑥
в кубе, когда 𝑥 приближается к отрицательной бесконечности? Что ж, можно немного доработать
наш график и назовем его графиком равно 𝑥 в кубе. И мы увидим, что этот предел
отрицательная бесконечность. Как насчет этого лимита? Ну эти термины с минусом
степени 𝑥 ничего не дают, поэтому остается только предел
отрицательные два, когда 𝑥 приближается к отрицательной бесконечности.И это, конечно, просто
отрицательные два. Единственный кусочек бесконечности
манипуляция, которую нам нужно сделать, - это умножить отрицательную бесконечность на отрицательные два. Знак минус отменяет. И получаем просто бесконечность.
В качестве альтернативы мы могли бы
факторизовал весь член отрицательными двумя 𝑥 в кубе вне предела. Затем значение
второй предел в нашем продукте будет всего один. Легко показать, что
первый предел в произведении - бесконечность.И вы могли бы быть более готовы
поверить, что бесконечность, умноженная на единицу, есть бесконечность, чем вы должны были поверить, что
отрицательная бесконечность, умноженная на два, равна бесконечности.
Используя этот метод, мы можем показать
что предел многочлена, когда 𝑥 приближается к положительной или отрицательной бесконечности,
является просто пределом члена наивысшей степени этого многочлена при приближении
положительная или отрицательная бесконечность.Тогда все, что нам нужно сделать, это посмотреть
на или представьте себе график этой мономиальной функции.
Давайте посмотрим на ключевые моменты, которые мы
рассматривается в этом видео. Мы можем рассматривать пределы вида
предел 𝑓 из 𝑥, когда 𝑥 стремится к положительной или отрицательной бесконечности. И в этих случаях предельные законы
все еще применяются. Предел обратного
функция единица над, когда 𝑥 приближается либо к положительной, либо к отрицательной бесконечности, равна
нуль.А значит, комбинируя это с одним
предельных законов, мы видим, что предел единицы над 𝑥 в степени, при
стремится к положительной или отрицательной бесконечности, также равно нулю, если 𝑛 больше, чем
нуль.
Мы можем найти пределы рационального
функции, разделив числитель и знаменатель на наибольшую степень 𝑥 и используя
приведенный выше результат. Аналогичным образом мы можем показать
что предел многочлена, когда 𝑥 приближается к положительной или отрицательной бесконечности, равен
только предел его высшей степени.Нам нужно быть осторожными, когда
играя с бесконечностью. Но, за некоторыми исключениями, для
Например, неопределенное образует бесконечность над бесконечностью и бесконечность минус бесконечность,
бесконечностью можно манипулировать как действительным числом в контексте ограничений.
.


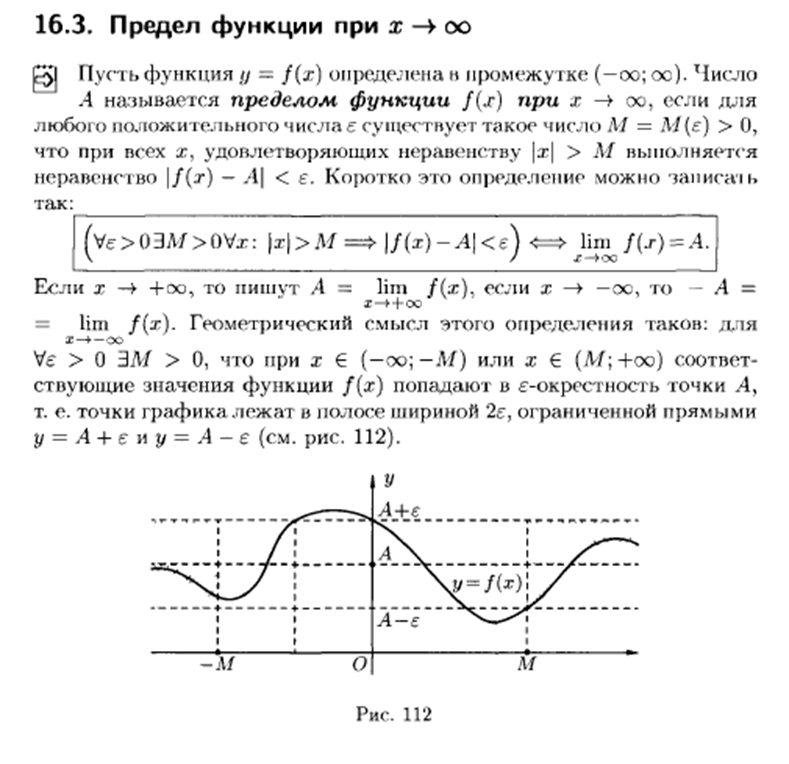
 784766, VS0, VS0",
"x-fastly-country": "RU",
"x-fastly-region": "TA",
"x-ka-curriculum": "",
"x-ka-orig-url": "/ math / ap-Calculus-ab / ab-limits-new / ab-1-15 / v / limits-at-positive-and-negative-infinity",
"x-ka-orig-host": "www.khanacademy.org",
"x-ka-is-e2e": "ложь",
"x-ka-is-bot": "ложь",
"x-ka-is-ios": "ложь",
"x-ka-is-phone": "ложь",
"x-ka-is-tablet": "ложь",
"x-ka-is-unsupported-browser": "правда",
"x-ka-browser": "Firefox",
"x-ka-browser-os": "Linux",
"x-ka-lang": "en",
"x-ka-locale": "en",
«х-ка-прокси-обновление-каал»: «0»,
"x-ka-published-content-version": "b362d19b0dbcd4aa7eda60a240dc38f6c0053bc0",
"x-ka-static-version": "211116-0736-da62641532e1",
"x-ka-at-post-gateway-proxy-edge": "0",
"fastly-client": "1",
"Fastly-ФФ":!!!!! «LtsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1672-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1661-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = ОМП кэш-mdw17328- MDW, ltsxTZVz3 / qY + PjkowxBUBQDaDchBm1aPceAyytMsr4 =! MDW! Cache-mdw17371-MDW ",
"cdn-loop": "Быстро, Быстро, Быстро, Быстро",
"x-cloud-trace-context": "58ce4dff9d3b0a06cc81faabfba0700a / 865
784766, VS0, VS0",
"x-fastly-country": "RU",
"x-fastly-region": "TA",
"x-ka-curriculum": "",
"x-ka-orig-url": "/ math / ap-Calculus-ab / ab-limits-new / ab-1-15 / v / limits-at-positive-and-negative-infinity",
"x-ka-orig-host": "www.khanacademy.org",
"x-ka-is-e2e": "ложь",
"x-ka-is-bot": "ложь",
"x-ka-is-ios": "ложь",
"x-ka-is-phone": "ложь",
"x-ka-is-tablet": "ложь",
"x-ka-is-unsupported-browser": "правда",
"x-ka-browser": "Firefox",
"x-ka-browser-os": "Linux",
"x-ka-lang": "en",
"x-ka-locale": "en",
«х-ка-прокси-обновление-каал»: «0»,
"x-ka-published-content-version": "b362d19b0dbcd4aa7eda60a240dc38f6c0053bc0",
"x-ka-static-version": "211116-0736-da62641532e1",
"x-ka-at-post-gateway-proxy-edge": "0",
"fastly-client": "1",
"Fastly-ФФ":!!!!! «LtsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1672-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = BMA кэш-bma1661-BMA, ltsxTZVz3 / Qy + PjkowxBUBQDaDchBm1aPceAyytMsr4 = ОМП кэш-mdw17328- MDW, ltsxTZVz3 / qY + PjkowxBUBQDaDchBm1aPceAyytMsr4 =! MDW! Cache-mdw17371-MDW ",
"cdn-loop": "Быстро, Быстро, Быстро, Быстро",
"x-cloud-trace-context": "58ce4dff9d3b0a06cc81faabfba0700a / 865 517766, -70.377291 ",
"x-appengine-country": "США",
"x-appengine-city": "старый фруктовый сад",
"x-google-apps-metadata": "domain = gmail.com, host = www.khanacademy.org",
"x-appengine-default-namespace": "gmail.com",
"traceparent": "00-58ce4dff9d3b0a06cc81faabfba0700a-782b603c05f5ba98-03",
"x-appengine-timeout-ms": "599999",
"x-appengine-https": "включено",
"x-appengine-user-ip": "157.52.75.71",
"x-appengine-api-ticket": "ChBlMGY2MmZiZjZiZjZhNDBjEKHVnxUQp9WfFRoTCP6t95 + znfQCFbyBtQEdieEGaw ==",
"x-appengine-request-log-id": "6193e96300ff0af83ed2f8382a0001737e6b68616e2d61636164656d7
517766, -70.377291 ",
"x-appengine-country": "США",
"x-appengine-city": "старый фруктовый сад",
"x-google-apps-metadata": "domain = gmail.com, host = www.khanacademy.org",
"x-appengine-default-namespace": "gmail.com",
"traceparent": "00-58ce4dff9d3b0a06cc81faabfba0700a-782b603c05f5ba98-03",
"x-appengine-timeout-ms": "599999",
"x-appengine-https": "включено",
"x-appengine-user-ip": "157.52.75.71",
"x-appengine-api-ticket": "ChBlMGY2MmZiZjZiZjZhNDBjEKHVnxUQp9WfFRoTCP6t95 + znfQCFbyBtQEdieEGaw ==",
"x-appengine-request-log-id": "6193e96300ff0af83ed2f8382a0001737e6b68616e2d61636164656d7 5c46a3e83acdeae8c4fd.js"], "./ javascript / app-shell-package / app -entry ": [" / genwebpack / prod / en / javascript / app-shell-package / app-entry.95aab4ab037c6d9a4bd5.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / страница-пакет / заголовок-запись ~./javascript/sat-mis~d7d3c7de":["/genwebpack/prod/en/javascript/app-shell-package/app-entry~./javascript/page-package/header-entry~./javascript/sat-mis ~ d7d3c7de.32357580f3eea36789d4.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript / app- shell-package / app-entry ~. / javascript / student-package / student-entry.c0d0f7ae67f1c1f5cfe5.css "," / genwebpack / prod / en / javascript / app-shell-package / app-entry ~. / javascript / student -пакет / студенческий вход.9e6aedcc2285f31f4fe1.js "]," ./ javascript / badges-package / viewbadges-entry ": [" / genwebpack / prod / en / javascript / badges-package / viewbadges-entry.
5c46a3e83acdeae8c4fd.js"], "./ javascript / app-shell-package / app -entry ": [" / genwebpack / prod / en / javascript / app-shell-package / app-entry.95aab4ab037c6d9a4bd5.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / страница-пакет / заголовок-запись ~./javascript/sat-mis~d7d3c7de":["/genwebpack/prod/en/javascript/app-shell-package/app-entry~./javascript/page-package/header-entry~./javascript/sat-mis ~ d7d3c7de.32357580f3eea36789d4.js "]," ./ javascript / app-shell-package / app-entry ~. / javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript / app- shell-package / app-entry ~. / javascript / student-package / student-entry.c0d0f7ae67f1c1f5cfe5.css "," / genwebpack / prod / en / javascript / app-shell-package / app-entry ~. / javascript / student -пакет / студенческий вход.9e6aedcc2285f31f4fe1.js "]," ./ javascript / badges-package / viewbadges-entry ": [" / genwebpack / prod / en / javascript / badges-package / viewbadges-entry. 4195517f08e0ebddaf4a.css "/ pro / genwebpack ru / javascript / badges-package / viewbadges-entry.4af1c080d9702352c2c5.js "]," ./ javascript / devadmin-package / award-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / award -badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / award-badge-entry.765e3cbecbf1bb15e03d.js "]," ./ javascript / devadmin-package / create-custom-badge -entry ": [" / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.9f5e83716c78a36456d8.js "]," ./ javascript / devadmin-package / download-csv-entry ": [ "/genwebpack/prod/en/javascript/devadmin-package/download-csv-entry.38691c3d6f738f3344a2.js"pting,"./javascript/devadmin-package/download-csv-entry./javascript~devadmin-package/translation -linter-de ~ 7c7b793f ": [" / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~.
4195517f08e0ebddaf4a.css "/ pro / genwebpack ru / javascript / badges-package / viewbadges-entry.4af1c080d9702352c2c5.js "]," ./ javascript / devadmin-package / award-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / award -badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / award-badge-entry.765e3cbecbf1bb15e03d.js "]," ./ javascript / devadmin-package / create-custom-badge -entry ": [" / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / create-custom-badge-entry.9f5e83716c78a36456d8.js "]," ./ javascript / devadmin-package / download-csv-entry ": [ "/genwebpack/prod/en/javascript/devadmin-package/download-csv-entry.38691c3d6f738f3344a2.js"pting,"./javascript/devadmin-package/download-csv-entry./javascript~devadmin-package/translation -linter-de ~ 7c7b793f ": [" / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.c88c5344428c6e9e48b7.css "," / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.7017266bcdc848240746.js "]. javascript / devadmin-package / translation-linter-debugging-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / translation-linter-debugging-entry.82aa7738576225311f69.js "]," ./ javascript / devadmin -package / update-custom-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.8069f4c9a068b52ec276.js "]," ./ javascript / devpanel-package / abort-pipelines-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / abort-pipelines-entry.6ab5862b9cc3329f3318.js "]," ./ javascript / devpanel-package / content-analytics-oauth-entry ": [" / genwebpack / prod / en /javascript/devpanel-package/content-analytics-oauth-entry.
/ javascript / devadmin-package / translation-linter-de ~ 7c7b793f.c88c5344428c6e9e48b7.css "," / genwebpack / prod / en / javascript / devadmin-package / download-csv-entry ~. / javascript / devadmin-package / translation-linter-de ~ 7c7b793f.7017266bcdc848240746.js "]. javascript / devadmin-package / translation-linter-debugging-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / translation-linter-debugging-entry.82aa7738576225311f69.js "]," ./ javascript / devadmin -package / update-custom-badge-entry ": [" / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / devadmin-package / update-custom-badge-entry.8069f4c9a068b52ec276.js "]," ./ javascript / devpanel-package / abort-pipelines-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / abort-pipelines-entry.6ab5862b9cc3329f3318.js "]," ./ javascript / devpanel-package / content-analytics-oauth-entry ": [" / genwebpack / prod / en /javascript/devpanel-package/content-analytics-oauth-entry. dfb95926e34ea7354d19.css","/genwebpack/prod/en/javascript/devpanel-package/content-analytics-oauth-entry.29f4296a91c33e6d061e.js "]," ./ javascript / devpanel-package / edit-learn-menu-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / edit-learn-menu-entry.96788deff06387dc5db2.js "]," ./ javascript / devpanel-package / email-preview-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / email-preview-entry.9473911a47a0fadd4f43.js "]," ./ javascript /devpanel-package/standard-mapping-entry":["/genwebpack/prod/en/javascript/devpanel-package/standard-mapping-entry.acc7781344410030db08.css","/genwebpack/prod/en/javascript/devpanel- пакет / стандарт-сопоставление-запись.e70cc5c9aea7e6fc2f76.js "]," ./ javascript / devpanel-package / start-mapreduce-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / start-mapreduce-entry.a7ce035dbc8daafa1699.js "," ./javascript/devpanel-package/test-emails-entry":["/genwebpack/prod/en/javascript/devpanel-package/test-emails-entry.
dfb95926e34ea7354d19.css","/genwebpack/prod/en/javascript/devpanel-package/content-analytics-oauth-entry.29f4296a91c33e6d061e.js "]," ./ javascript / devpanel-package / edit-learn-menu-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / edit-learn-menu-entry.96788deff06387dc5db2.js "]," ./ javascript / devpanel-package / email-preview-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / email-preview-entry.9473911a47a0fadd4f43.js "]," ./ javascript /devpanel-package/standard-mapping-entry":["/genwebpack/prod/en/javascript/devpanel-package/standard-mapping-entry.acc7781344410030db08.css","/genwebpack/prod/en/javascript/devpanel- пакет / стандарт-сопоставление-запись.e70cc5c9aea7e6fc2f76.js "]," ./ javascript / devpanel-package / start-mapreduce-entry ": [" / genwebpack / prod / en / javascript / devpanel-package / start-mapreduce-entry.a7ce035dbc8daafa1699.js "," ./javascript/devpanel-package/test-emails-entry":["/genwebpack/prod/en/javascript/devpanel-package/test-emails-entry.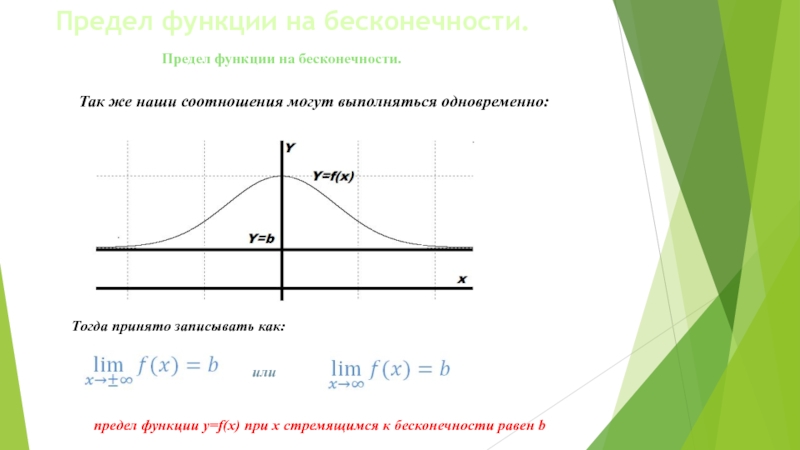 2b5b241365737f3b1dbf.js" ],"./javascript/devpanel-package /thumbnails-entry":["/genwebpack/prod/en/javascript/devpanel-package/thumbnails-entry.f563e2a2a57dab92e593.js"pting,"./javascript/discussion-package/mod-entry":["/genwebpack/ prod / en / javascript / обсуждение-пакет / мод-запись.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсудить-пакет / mod-entry.4b6a73a0594b32556dee.js "]," ./ javascript / обсуждение-пакет / модерация-журналы-запись ": [" / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.e388870b0b9099d849f9.js "]," ./ javascript / donate-package / recurring-donation-cancel-entry ": [" / genwebpack / prod / en / javascript / donate-package / recurring-donation-cancel-entry.fc66bf5e2742c821bbb3.js "]," ./ javascript / editor-package / content-tags-entry ": [" / genwebpack / prod / en / javascript / editor-package / content-tags-entry.
2b5b241365737f3b1dbf.js" ],"./javascript/devpanel-package /thumbnails-entry":["/genwebpack/prod/en/javascript/devpanel-package/thumbnails-entry.f563e2a2a57dab92e593.js"pting,"./javascript/discussion-package/mod-entry":["/genwebpack/ prod / en / javascript / обсуждение-пакет / мод-запись.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсудить-пакет / mod-entry.4b6a73a0594b32556dee.js "]," ./ javascript / обсуждение-пакет / модерация-журналы-запись ": [" / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.27cd8706601b558ad57c.css "," / genwebpack / prod / en / javascript / обсуждение-пакет / moderation-logs-entry.e388870b0b9099d849f9.js "]," ./ javascript / donate-package / recurring-donation-cancel-entry ": [" / genwebpack / prod / en / javascript / donate-package / recurring-donation-cancel-entry.fc66bf5e2742c821bbb3.js "]," ./ javascript / editor-package / content-tags-entry ": [" / genwebpack / prod / en / javascript / editor-package / content-tags-entry. b410dd841acd270f6ef7.css "," / genwebpack / prod / en / javascript / editor-package / content-tags-entry.abf91db444ac83a110b1.js "]," ./ javascript / moderator-flag-queue-package / flag-queue-shell-entry ": [" / genwebpack /prod/en/javascript/moderator-flag-queue-package/flag-queue-shell-entry.27cd8706601b558ad57c.css","/genwebpack/prod/en/javascript/moderator-flag-queue-package/flag-queue- оболочка.06df4e16de2d5ed40956.js "]," ./ javascript / offensive-terms-package / offensive-terms-entry ": [" / genwebpack / prod / en / javascript / offensive-terms-package / offensive-terms-entry.b8cb8c30891a5d7e4090.js "]," ./ javascript / page-package / footer-entry ": [" / genwebpack / prod / en / javascript / page-package / footer-entry.e897c238c206b9677856.js "]," ./ javascript / page-package /header-entry":["/genwebpack/prod/en/javascript/page-package/header-entry.c2ed6ae24bb62d5b8d5e.js" visible,"./javascript/page-template-package/infra-entry":["/ genwebpack / prod / en / javascript / page-template-package / infra-entry.
b410dd841acd270f6ef7.css "," / genwebpack / prod / en / javascript / editor-package / content-tags-entry.abf91db444ac83a110b1.js "]," ./ javascript / moderator-flag-queue-package / flag-queue-shell-entry ": [" / genwebpack /prod/en/javascript/moderator-flag-queue-package/flag-queue-shell-entry.27cd8706601b558ad57c.css","/genwebpack/prod/en/javascript/moderator-flag-queue-package/flag-queue- оболочка.06df4e16de2d5ed40956.js "]," ./ javascript / offensive-terms-package / offensive-terms-entry ": [" / genwebpack / prod / en / javascript / offensive-terms-package / offensive-terms-entry.b8cb8c30891a5d7e4090.js "]," ./ javascript / page-package / footer-entry ": [" / genwebpack / prod / en / javascript / page-package / footer-entry.e897c238c206b9677856.js "]," ./ javascript / page-package /header-entry":["/genwebpack/prod/en/javascript/page-package/header-entry.c2ed6ae24bb62d5b8d5e.js" visible,"./javascript/page-template-package/infra-entry":["/ genwebpack / prod / en / javascript / page-template-package / infra-entry. 585659fb68561ea58d52.js "]," ./ javascript / perseus-admin-package / perseus-admin-entry ": [" / genwebpack / prod / en / javascript / perseus-admin-package / perseus-admin-entry.8ab0420e4582737a7173.js "]," ./ javascript / perseus-all-package / perseus-item-entry ": [" / genwebpack / prod / en / javascript / perseus-all-package / perseus-item-entry.643d5b363ddc411202c8.js "], "./javascript/perseus-merged-editor-package/demo-perseus-entry":["/genwebpack/prod/en/javascript/perseus-merged-editor-package/demo-perseus-entry.5e366604784e7778de81.js "]," ./ javascript / sat-mission-package / sat-mission-entry ": [" / genwebpack / prod / en / javascript / sat-mission-package / sat-mission-entry.dbc2527d345f941a709a.css ", "/genwebpack/prod/en/javascript/sat-mission-package/sat-mission-entry.828c827b611cda1191fe.js" visible,"./javascript/scratchpads-package/code-entry":["/genwebpack/prod/en /javascript/scratchpads-package/code-entry.224277a0452876dae984.js"pting,"./javascript/scratchpads-package/exec-pjs-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec- pjs-запись.
585659fb68561ea58d52.js "]," ./ javascript / perseus-admin-package / perseus-admin-entry ": [" / genwebpack / prod / en / javascript / perseus-admin-package / perseus-admin-entry.8ab0420e4582737a7173.js "]," ./ javascript / perseus-all-package / perseus-item-entry ": [" / genwebpack / prod / en / javascript / perseus-all-package / perseus-item-entry.643d5b363ddc411202c8.js "], "./javascript/perseus-merged-editor-package/demo-perseus-entry":["/genwebpack/prod/en/javascript/perseus-merged-editor-package/demo-perseus-entry.5e366604784e7778de81.js "]," ./ javascript / sat-mission-package / sat-mission-entry ": [" / genwebpack / prod / en / javascript / sat-mission-package / sat-mission-entry.dbc2527d345f941a709a.css ", "/genwebpack/prod/en/javascript/sat-mission-package/sat-mission-entry.828c827b611cda1191fe.js" visible,"./javascript/scratchpads-package/code-entry":["/genwebpack/prod/en /javascript/scratchpads-package/code-entry.224277a0452876dae984.js"pting,"./javascript/scratchpads-package/exec-pjs-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec- pjs-запись. 821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-pjs-entry.8e4298bd94576a50ee32.js "]," ./ javascript / scratchpads-package / exec-sql-entry ": [" / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.f3c6b98aa6ef8d7842e9.js "] ./javascript/scratchpads-package/exec-webpage-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec-webpage-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-webpage-entry.1132cc1fe1fe36ff1d5f.js "]," ./ javascript / shared-package / page-template-mini-entry ": [" / genwebpack / prod / en / javascript / shared-package / page-template-mini-entry.538a2a3317957b775c3c.js "]," ./ javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript /student-package/student-entry.6234febc0f2c282c53b2.js"pting,"./javascript/topicsadmin-package/topics-admin-entry":["/genwebpack/prod/en/javascript/topicsadmin-package/topics-admin- Вход.
821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-pjs-entry.8e4298bd94576a50ee32.js "]," ./ javascript / scratchpads-package / exec-sql-entry ": [" / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-sql-entry.f3c6b98aa6ef8d7842e9.js "] ./javascript/scratchpads-package/exec-webpage-entry":["/genwebpack/prod/en/javascript/scratchpads-package/exec-webpage-entry.821f55994e62be8390ab.css "," / genwebpack / prod / en / javascript / scratchpads-package / exec-webpage-entry.1132cc1fe1fe36ff1d5f.js "]," ./ javascript / shared-package / page-template-mini-entry ": [" / genwebpack / prod / en / javascript / shared-package / page-template-mini-entry.538a2a3317957b775c3c.js "]," ./ javascript / student-package / student-entry ": [" / genwebpack / prod / en / javascript /student-package/student-entry.6234febc0f2c282c53b2.js"pting,"./javascript/topicsadmin-package/topics-admin-entry":["/genwebpack/prod/en/javascript/topicsadmin-package/topics-admin- Вход.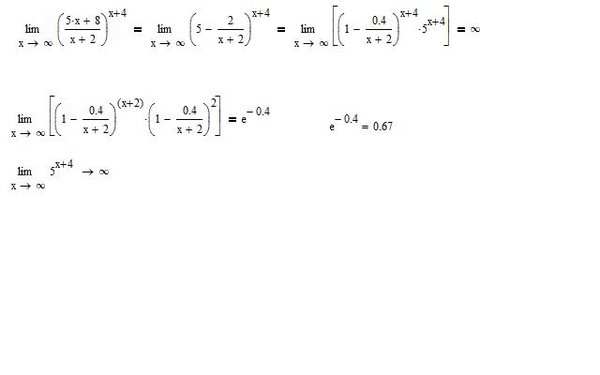 b29d425eb22e28cee37f.css "," / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry.96663ff0d8398ada0775.js "]," ./ javascript / themesadmin-package / themes-admin-entry ~. / javascript / пакет-редактора-перевода / видео-тр ~ 3029e3e6 ": [" / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry ~. / javascript / translation-editor-package / video-tr ~ 3029e3e6. e8e618eab
b29d425eb22e28cee37f.css "," / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry.96663ff0d8398ada0775.js "]," ./ javascript / themesadmin-package / themes-admin-entry ~. / javascript / пакет-редактора-перевода / видео-тр ~ 3029e3e6 ": [" / genwebpack / prod / en / javascript / themesadmin-package / themes-admin-entry ~. / javascript / translation-editor-package / video-tr ~ 3029e3e6. e8e618eab 39a58caa9300173b5176.css "," / genwebpack / prod / en / javascript / translation-editor-package / video-translation-table-entry.f2292a5e63b89fba6f21.js "]," ./ javascript / translations-dashboard-package / translations-dashboard-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / translations-dashboard-entry.0d3ab659da641a0585e1.js "]," ./ javascript / translations-dashboard-package / video-subtitle-data-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.27cd8706601b558ad57c. css "," / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.709bf28b0b0f6607d2a1.js "]," ./ javascript / tutorial-editor-package / video-editor-entry ": [" / genwebpack / prod / en / javascript / tutorial-editor-package / video-editor-entry.dee1bfdfe3fe7016371a.js "] , "./ javascript / tutorial-scratchpad-package / scratchpad-page-entry": ["/ genwebpack / prod / en / javascript / tutorial-scratchpad-package / scratchpad-page-entry.
39a58caa9300173b5176.css "," / genwebpack / prod / en / javascript / translation-editor-package / video-translation-table-entry.f2292a5e63b89fba6f21.js "]," ./ javascript / translations-dashboard-package / translations-dashboard-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / translations-dashboard-entry.0d3ab659da641a0585e1.js "]," ./ javascript / translations-dashboard-package / video-subtitle-data-entry ": [" / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.27cd8706601b558ad57c. css "," / genwebpack / prod / en / javascript / translations-dashboard-package / video-subtitle-data-entry.709bf28b0b0f6607d2a1.js "]," ./ javascript / tutorial-editor-package / video-editor-entry ": [" / genwebpack / prod / en / javascript / tutorial-editor-package / video-editor-entry.dee1bfdfe3fe7016371a.js "] , "./ javascript / tutorial-scratchpad-package / scratchpad-page-entry": ["/ genwebpack / prod / en / javascript / tutorial-scratchpad-package / scratchpad-page-entry. 6570ecceb7b41ea7bf90.js"], ". /javascript/video-package/video-lite-entry":["/genwebpack/prod/en/javascript/video-package/video-lite-entry.b0940d69f99a4dea9527.css","/genwebpack/prod/en/javascript/ видео-пакет / видео-лайт-запись.e54cb77b4051a220494c.js "]," 0isi ": [" / genwebpack / prod / en / 0isi.24361e8119fcb896222f.js "]," 10RM ": [" / genwebpack / prod / en / 10RM.1ff438807fbd5138a] ": [" / genwebpack / prod / en / 11pb.22229c77cba5dc5dd306.js "]," 121I ": [" / genwebpack / prod / en / 121I.518843d16186aab971f7.js "]," 12uO ": [" / genwebpack / prod /en/12uO.e7ee6f20bf68cce09364.js"pting,"13UF":["/genwebpack/prod/en/13UF.42c4de53ee81c80c6d5b.js" ],"13Vt":["/genwebpack/prod/en/2.13b2a82ac68fd/en/2.13bt.1ec68f "]," 14Lx ": [" / genwebpack / prod / en / 14Lx.5e23c2554d3671cb3eeb.js "]," 14Rr ": [" / genwebpack / prod / en / 14Rr.a6bac93f2932b9232591.js "]," 14en ": [" / genwebpack / prod / en / 14en.adee2b2af03fab9571da.js "]," 15HC ": ["/genwebpack/prod/en/15HC.97f4eea4380b0f6a1ffd.
6570ecceb7b41ea7bf90.js"], ". /javascript/video-package/video-lite-entry":["/genwebpack/prod/en/javascript/video-package/video-lite-entry.b0940d69f99a4dea9527.css","/genwebpack/prod/en/javascript/ видео-пакет / видео-лайт-запись.e54cb77b4051a220494c.js "]," 0isi ": [" / genwebpack / prod / en / 0isi.24361e8119fcb896222f.js "]," 10RM ": [" / genwebpack / prod / en / 10RM.1ff438807fbd5138a] ": [" / genwebpack / prod / en / 11pb.22229c77cba5dc5dd306.js "]," 121I ": [" / genwebpack / prod / en / 121I.518843d16186aab971f7.js "]," 12uO ": [" / genwebpack / prod /en/12uO.e7ee6f20bf68cce09364.js"pting,"13UF":["/genwebpack/prod/en/13UF.42c4de53ee81c80c6d5b.js" ],"13Vt":["/genwebpack/prod/en/2.13b2a82ac68fd/en/2.13bt.1ec68f "]," 14Lx ": [" / genwebpack / prod / en / 14Lx.5e23c2554d3671cb3eeb.js "]," 14Rr ": [" / genwebpack / prod / en / 14Rr.a6bac93f2932b9232591.js "]," 14en ": [" / genwebpack / prod / en / 14en.adee2b2af03fab9571da.js "]," 15HC ": ["/genwebpack/prod/en/15HC.97f4eea4380b0f6a1ffd. js" visible,"179z":["/genwebpack/prod/en/179z.35514fd3cab2564674c7.js" ],"18dX":["/genwebpack/prod/prod/prod/ /18dX.190d0fb7d4c2bef520c4.js"pting,"193f":["/genwebpack/prod/en/193f.899ec8d8070ca64b645a.js"pting,"19mY":["/genwebpack/prod/en/19mY114.ca69b1] , «19 мл»: [«/ genwebpack / prod / en / 19ml.e50030a703146692ebbc.js»], «1APQ»: [«/ genwebpack / prod / en / 1APQ.c3856c68bc621551f9f3.js "]," 1ARw ": [" / genwebpack / prod / en / 1ARw.7bddbd5e6dab22bab50f.js "]," 1Apj ": [" / genwebpack / prod / en / 1Apj.1a38b47f52b54f39 ": [" / genwebpack / prod / en / 1BNf.43ebc442f64f7369a9ef.js "]," 1CZn ": [" / genwebpack / prod / en / 1CZn.333d2cc462adf30d4a98.js "],« 1Chp ": /en/1Chp.1f55519c75613e84097f.js"pting,"1DPW":["/genwebpack/prod/en/1DPW.66ea27723628cbd96d4c.js" ],"1FEV":["/genwebpack/prod/en/1FEV.907f24sa9 "]," 1HtF ": [" / genwebpack / prod / en / 1HtF.f389ec9f925bd10ae92c.js "]," 1IOE ": [" / genwebpack / prod / en / 1IOE.0c5aa1189d6a85e5b8e6.js "]," 1Ixv ": [" / genwebpack / prod / en / 1Ixv.799795c0c7d8b8e57857.JsT3 "]," ["/genwebpack/prod/en/1JT3.42337f0638f663c0eebe.css","/genwebpack/prod/en/1JT3.dee6925dc90ae3fed61b.js" ],"1KNP":["/genwebpack/prod/enfa/facn25c2d4dd0ddd/enfajfcd4d4 "]," 1KcS ": [" / genwebpack / prod / en / 1KcS.755d0dc6455d01f2a5a9.js "]," 1KcS5 ": [" / genwebpack / prod / en / 1KcS5.cbf0735ad22893bfcc18. 1Lsq "]," ["] "/genwebpack/prod/en/1Lqt.0018b3ec5b8d6cd2a6b0.js" visible,"1MTk":["/genwebpack/prod/en/1MTk.0cc5a5cae922535cbd92.js "]," 1Ps6 ": [" / genwebpack / prod / en / 1Ps6.948efbd2bd6d39b634c2.js "]," 1QYc ": [" / genwebpack / prod / en / 1QYc.4b13f70bdc6 /prod/en/1QYc.af18a462a031f1362e81.js"pting,"1RSY":["/genwebpack/prod/en/1RSY.acac8e519565b63f2179.js"pting,"1RWy":["/genwebpackae/prod/en/1RW4406356ac7 .js "]," 1Rdk ": [" / genwebpack / prod / en / 1Rdk.d966fcda4e23074b76df.js "]," 1Ssk ": [" / genwebpack / prod / en / 1Ssk.d75cf0adf54f5a3601d1.js "N], "1TN : ["/ genwebpack / prod / en / 1TNN.8f9ad792204f250f6d5f.js"], "1Vc5": ["/ genwebpack / prod / en / 1Vc5.8f68f93c9d3289b956e4.js "]," 1VjB ": [" / genwebpack / prod / en / 1VjB.aeddd83bcfc3f8ff095e.js "]," 1Vny ": [" / genwebpack / prod / en / 1Vny14cb42sp3f] ": [" / genwebpack / prod / en / 1Vpd.d8e28876328ad22a57ee.js "]," 1W80 ": [" / genwebpack / prod / en / 1W80.ebbd1f9bfb2d400a8e7b.js "]," 1XtT ": [/ prod / genweb /en/1XtT.07babde83b5822beb7dd.js"pting,"1YsT":["/genwebpack/prod/en/1YsT.96e48a31335f94f6b87b.js"pting,"1Z2M":["/genwebpackd/prod/en/1Z2M.0cdae184 "]," 1ZAq ": [" / genwebpack / prod / en / 1ZAq.e4033e39ccfd7bd2b1df.js "]," 1ZoN ": [" / genwebpack / prod / en / 1ZoN.03c639a16af30d773299.js "]," 1a8C ": [" / genwebpack / prod / en / 1a8C.b8e416ea840a05a93d9e.js "]," ["/genwebpack/prod/en/1a9J.c94c5ef6bde1b59612a4.js" visible,"1aEw":["/genwebpack/prod/en/1aEw.990d57e623849420d091.js" ],"1bEx":["/genwebpack/prod /1bEx.32a8cba2844f9a00ab78.js"pting,"1bJ6":["/genwebpack/prod/en/1bJ6.0bb24069af2659acc9ea.js"pting,"1cVY":["/genwebpack/prod/en/1cVY.9f586681743] , «1cnO»: [«/ genwebpack / prod / en / 1cnO.ae6e4a1eaea573438376.js»], «1d7P»: [«/ genwebpack / prod / en / 1d7P.2352b893e8b550e075f3.js "]," 1dp5 ": [" / genwebpack / prod / en / 1dp5.2f7ac2e98c77337465ad.js "]," 1fgW ": [" / genwebpack / prod / en / 1fgW.b39605Kadedab2.f. ": [" / genwebpack / prod / en / 1h2K.ef3dd108141adf8244db.js "]," 1igT ": [" / genwebpack / prod / en / 1igT.7d5511f75e62dda397a1.css "," / genwebpack / prod / enad199. .js "]," 1jDv ": [" / genwebpack / prod / en / 1jDv.810c08eeada0b7c55418.js "]," 1k1o ": [" / genwebpack / prod / en / 1k1o.793e1e7d3a70b345d965. 1js "] : ["/ genwebpack / prod / en / 1lam.3ca7eeb607a0de899ba8.js"], "1mwh": ["/ genwebpack / prod / en / 1mwh.56f21189a29dedb41560.js "]," 1nPp ": [" / genwebpack / prod / en / 1nPp.4eb89ca5f22cae307faf.js "]," 1nZL ": [" / genwebpack / prod / en / 1nZL.7def940ccb59c65s. ": [" / genwebpack / prod / en / 1qGO.37c17f50e72786b69d45.js "]," 1qGz ": [" / genwebpack / prod / en / 1qGz.0ac308e9e27d48e06b7a.js "]," 1qIab ": [" / genweb /en/1qIa.e97aa0e02ca35b05f591.js"pting,"1r3U":["/genwebpack/prod/en/1r3U.3ec4fac3874326a0d9e4.js"pting,"1rSG":["/genwebpack/prod/en20ar2c03.0.0.0/ru "]," 1u2V ": [" / genwebpack / prod / en / 1u2V.203d0c62f0de22575400.js "]," 1urj ": [" / genwebpack / prod / en / 1urj.36c2cddd9e86cc0815bb.js "]," 1vDA ": [" / genwebpack / prod / en / 1vDA.e872d09fbeeb96995127.js "]," 1vWt " ["/genwebpack/prod/en/1vWt.f2261d57d7ec095fc12f.js" visible,"1vry":["/genwebpack/prod/en/1vry.680a2a28db9b74a90bd4.js" ],"1w6N":["/genwebpack/ /1w6N.dd29f189080ba9e4d355.js "]," 1xMX ": [" / genwebpack / prod / en / 1xMX.27cd8706601b558ad57c.css "," / genwebpack / prod / en / 1xMX.d380b08d10daW1b996f7. " "/genwebpack/prod/en/1xW1.80aedf8990a196adac76.js"pting,"1xq9":["/genwebpack/prod/en/1xq9.d5d6a645df79e516fd48.js "]," 1yEK ": [" / genwebpack / prod / en / 1yEK.a4b5797f4f95fb2e02de.js "]," 1yJd ": [" / genwebpack / prod / en / 1yJ4yd.7ef7285 ": [" / genwebpack / prod / en / 1yxG.8e87c72f94d335d81bfa.js "]," 1yxy ": [" / genwebpack / prod / en / 1yxy.2bababdb2115263b3311.js "]," 1z4c ": [" / prodwebpack / /en/1z4c.ddd4e5062fd3e323d6f5.js" visible,"1z5B":["/genwebpack/prod/en/1z5B.74a7f9f76fc2d609fdb4.css","/genwebpack/prod/en/1z5B.c63da2a",c50a2a",,,,,??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? : ["/ genwebpack / prod / en / 1zsz.1b72254e792a7b814493.js"], "20ED": ["/ genwebpack / prod / en / 20ED.a4b61be1c993b1abf648.js "]," 21RN ": [" / genwebpack / prod / en / 21RN.aae1c1e6768eeef409ca.js "]," 21xc ": [" / genwebpack / prod / en / 21xc.7d5511f75acbda39, / /prod/en/21xc.65d513ac168e0b46c01a.js"pting,"23IL":["/genwebpack/prod/en/23IL.bb2b683b2988d9c49201.js" provided,"23Pc":["/genwebpack/prod/en/23Pc15.0bc72 .js "]," 23uO ": [" / genwebpack / prod / en / 23uO.eb8f1d4a8d692b1f763f.js "]," 244e ": [" / genwebpack / prod / en / 244e.def12064fe92d244c5ac.jsj "]," 244e.def12064fe92d244c5ac.jsj "] : ["/ genwebpack / prod / en / 245j.352b3b588f2fd9a298f0.js"], "24CB": ["/ genwebpack / prod / en / 24CB.fc516a269ea7cc336789.js "]," 26Fy ": [" / genwebpack / prod / en / 26Fy.6d73c9580f5f3ac0bb9a.js "]," 279q ": [" / genwebpack / prod / en / 279q.2d0cefbcec71b1b1 ": [" / genwebpack / prod / en / 27qs.b246eac722ebc4391f1c.js "]," 28I1 ": [" / genwebpack / prod / en / 28I1.887a949aeda5609fe8ae.js "]," 28OZ ": [" / genwebpack / prod /en/28OZ.ccf600950c62d1041d63.js"pting,"28nD":["/genwebpack/prod/en/28nD.da7f72c232c7c26f27de.js" visible,"29Wk":["/genwebpack/prod/en/29Wk.486s2154690 "]," 29i2 ": [" / genwebpack / prod / en / 29i2.d03aa8eca3248a8432af.js "]," 2B5d ": [" / genwebpack / prod / en / 2B5d.783ba78352289a6d83f6.js "]," 2Bu7 ": [" / genwebpack / prod / en / 2Bu7.94f56daa513725ede19f.js "]," 2CLP " ["/genwebpack/prod/en/2CLP.e0fbd05d1a46ef3131f8.js"] ],"2Cp5":["/genwebpack/prod/en/2Cp5.baf6d10730e7ea44ffcf.js" ],"2Cwm":pack/genwebpack/genwebpack/prod/genwebpack/prod/genwebpack/prod/genwebpack/ /2Cwm.dfddd314e99fe8285964.js" visible,"2EQr":["/genwebpack/prod/en/2EQr.460c28028161009cc952.js"pting,"2EaT":["/genwebpack/prod/en/2EaT.b04683b , «2FX7»: [«/ genwebpack / prod / en / 2FX7.9bb9851d1bf8354d2efd.js»], «2GxB»: [«/ genwebpack / prod / en / 2GxB.994555d9dedd7b712575.css "," / genwebpack / prod / en / 2GxB.1ff95ecae75bd2087c80.js "]," 2HCt ": [" / genwebpack / prod / en / 2HCt.01dad59cf3068b8a5c79.js "],« 2HCt. /prod/en/2HKw.8adc9ea1fc87bd619377.css","/genwebpack/prod/en/2HKw.8eae231ec7b4c569b9e6.js" ],"2HYH":["/genwebpack/prod/en/2HYF28.917.a79f 2Ikv ": [" / genwebpack / prod / en / 2Ikv.75793b428da9c28.js "]," 2J2c ": [" / genwebpack / prod / en / 2J2c.6436cd1ec59f811a76a1.js "]," 2KyNwebpack ": [/" prod / en / 2KyN.12e23a4121029944369b.js "]," 2Lqu ": [" / genwebpack / prod / en / 2Lqu.0dd199cb760b197.js "]," 2MQA ": [" / genwebpack / prod / en / 2MQA.5f17d329eaf378de8ed3.js "]," 2MwD ": [" / genwebpack / prod / en / 2MwD.e2cae10eze234c1 ": [" / genwebpack / prod / en / 2Nrz.e046eb28af390e7d6ac1.js "]," 2PSY ": [" / genwebpack / prod / en / 2PSY.8559e57a9f971d776d56.css "," / genwebpack / prod / en / 2aPSY .js "]," 2QK7 ": [" / genwebpack / prod / en / 2QK7.e2051ce4cf851c9ecefe.css "," / genwebpack / prod / en / 2QK7.703195163649aaa19cf3.js "]," 2QW5 ": [/ / genwebpack prod / en / 2QW5.21c40ab5e511db226a08.js "]," 2RMK ": [" / genwebpack / prod / en / 2RMK.bf00889c696e6223dfd4.js "]," 2Rvf ": [" / genwebpack / prod / en / 2Rvf.87567382100cff2ccca3.js "]," 2SNV ": [" / genwebpack / prod / en / 2SNV.345d5ea75c929b. ": [" / genwebpack / prod / en / 2SdV.6b1ef603c0478837bc75.js "]," 2Sin ": [" / genwebpack / prod / en / 2Sin.8ae3ec2940569b614452.js "]," 2TCQ ": [" / genwebpack / prod /en/2TCQ.2234f9687251fba02039.js"pting,"2Uus":["/genwebpack/prod/en/2Uus.334f730bca942a7c1539.js"pting,"2Vse":["/genwebpack/prod/en/2Vse.e96b4c0a "]," 2X2X ": [" / genwebpack / prod / en / 2X2X.e8ea894cc7db366683a7.js »],« 2Xlo »: [« / genwebpack / prod / en / 2Xlo.e5fc51c0815927158700.css »,« / genwebpack / prod / en / 2Xlo.31d6294666f7c507b835.js »],« 2Yeu »: [/ prod / genwebpack /en/2Yeu.63db4e3b8b00cb6b8206.js"pting,"2aBZ":["/genwebpack/prod/en/2aBZ.7be61a2b8fcac69b4924.js" ],"2aia":["/genwebpack/prod/ru68c03/2aia "," / genwebpack / prod / en / 2aia.32fd64718bd9a617373e.js "]," 2cnn ": [" / genwebpack / prod / en / 2cnn.2eaaf633d663000537ca.js "]," 2dVQ ": [" / genwebpack / prod en / 2dVQ.73822f6a51381e100621.js "]," 2gJR ": [" / genwebpack / prod / en / 2gJR.444a818d8f12103867b3.js "]," 2hbS ": [" / genwebpack / prod / en / 2hbS.5eb872e21d766cb1aa72.js "]," 2iHJ ": [" / genwebpack / prod / en / 2iHJ.dfa7cfda1f /prod/en/2iHJ.97a8672cfba211a8a6e8.js"pting,"2iOq":["/genwebpack/prod/en/2iOq.acdbef3d7b6a0e74abb7.js" ],"2iXX":["/genwebpack2/prod4/prod .js "]," 2jSl ": [" / genwebpack / prod / en / 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "]," 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "] : ["/ genwebpack / prod / en / 2lOt.1ff08964f6c77ff596c5.js"], "2m0x": ["/ genwebpack / prod / en / 2m0x.efa28362307d5af47b40.css "," / genwebpack / prod / en / 2m0x.0fa9a67410bd4673bc0a.js "]," 2mTh ": [" / genwebpack / prod / en / 2mTh.bc3ccf1d22e920f522df. ", 2mTh.bc3ccf1d22e920f522df.js /prod/en/2nMR.2558326fc96438a96989.js"pting,"2pPD":["/genwebpack/prod/en/2pPD.7e77a3cc66405918d863.js" ],"2pZY":["/genwebpack/prod16.d3fa4de4d4d3d3d4d3d3d3d4b5/ .js "]," 2prj ": [" / genwebpack / prod / en / 2prj.31856cec826592510353.js "]," 2qoD ": [" / genwebpack / prod / en / 2qoD.3e22ff098d72f5d6021a.js "]," 2rHT " : ["/ genwebpack / prod / en / 2rHT.b763f55a47ea52e4f629.js"], "2rso": ["/ genwebpack / prod / en / 2rso.3425679bf76c759ac725.css "," / genwebpack / prod / en / 2rso.4b28b9a29147f3a93be7.js "]," 2sHZ ": [" / genwebpack / prod / en / 2sHZ.e0f5a4fec3e8b2a3aeb2.js "/ /prod/en/2snA.3bec1fd07d4c2d5dfbcc.js"pting,"2teg":["/genwebpack/prod/en/2teg.7895c5d3d7e0dff380b4.js" ],"30A8":["/genwebpack30/prod.4d/en .js "]," 30RW ": [" / genwebpack / prod / en / 30RW.6c6416ace108b66f4e47.css "," / genwebpack / prod / en / 30RW.027de18a57ec67e2fac5.js "]," 30wi ": [" / genwebpack / prod / en / 30wi.ad707bfed5b6209329e8.js "]," 31FY ": [" / genwebpack / prod / en / 31FY.75b0c6a961988dca672f.js "]," 31e4 ": [" / genwebpack / prod / en / 31e4.7cdbc8ec756077361960.js "]," 31jp ": [" / genwebpack / prod / en / 31jp.5a992361b5395js "], 326hd63", 326hd63 ", 326hd63. ": [" / genwebpack / prod / en / 326h.e00d12f7fefb8b00524d.js "]," 32Sy ": [" / genwebpack / prod / en / 32Sy.18c8132f4993c34d3d0d.js "]," 32q8 ": [" / prod / genwebpack / /en/32q8.8efbc50ea3c43be649a5.js"pting,"34uh":["/genwebpack/prod/en/34uh.b4a80e2538c28eee8555.js"pting,"35BT":["/genwebpack/prod/en/35BT39.js85e5) "]," 36AW ": [" / genwebpack / prod / en / 36AW.ba6b36c7cd0a5ddfad21.js »],« 379K »: [« / genwebpack / prod / en / 379K.aaeadfc858e15d50d8c5.js »],« 37Vm »: [« / genwebpack / prod / en / 37Vm.904c77b2fb8c0d6a9ff7.css »,« / genwebpack »/ genwebpack /en/37Vm.e2134f7295285f100241.js" Survival "," / genwebpack / prod / en / 39EU.e2e8851dca936e35176a.js "]," 39il ": [" / genwebpack / prod / en / 39il.294443516cb884c76787.js "]," 3C1J ": [" / genwebpack / prod / en / 3C1J.73550690b1f2bbdc6270.js "]," 3Cmw ": [" / genwebpack / prod / en / 3Cmw.f8d20d392a38665185da.css "," / genwebpack / prod / en / 3Cmw.b6ba737fdce36e6a22c4.js "]," 3Eux ": [" / genwebpack / prod / en / 3Eux.c4ae89869ae0dFC7bd98./ /prod/en/3FC7.8c67dfa280fd40a64c54.js"pting,"3Fde":["/genwebpack/prod/en/3Fde.c423a076d3a6e4b78215.js" ],"3G70":["/genwebpack/ce38d/en/3G70 " .js "]," 3ITe ": [" / genwebpack / prod / en / 3ITe.3d52f15dd2520e730488.js "]," 3KTd ": [" / genwebpack / prod / en / 3KTd.623d4d983e9aaab5be6c.js "]," 3L8 : ["/ genwebpack / prod / en / 3L8X.3ea888b98536ff1d0203.js"], "3LDP": ["/ genwebpack / prod / en / 3LDP.6406829f4ba1d9ac4a0b.js "]," 3LDf ": [" / genwebpack / prod / en / 3LDf.4e17e540cb5f7800fd1e.js "]," 3NVp ": [" / genwebpack / prod / en / 3NVp23a9e9481 ": [" / genwebpack / prod / en / 3Nju.ebc351c24a428bf743a9.js "]," 3NmD ": [" / genwebpack / prod / en / 3NmD.6bfebf201e56fcb42f0b.js "]," 3Pml ": [" / genweb. /en/3Pml.1b973ab850d1adab7aa8.js" visible,"3Qw5":["/genwebpack/prod/en/3Qw5.cd6a69f9769cc8de0ffd.js"pting,"3SWN":["/genwebpack/prod/en/3SWN":["/genwebpack/prod/en/6S11fsWN.6D) "]," 3TWR ": [" / genwebpack / prod / en / 3TWR.7b1e748ff4697b4424a5.js "]," 3Tdt ": [" / genwebpack / prod / en / 3Tdt.768262c5db31f6d54f4c.js "]," 3UBJ ": [" / genwebpack / prod / en / 3UBJ.3bb351e25d6e48fe64d7.js "]," 3Uys ": ["/genwebpack/prod/en/3Uys.70ec59ff2553aa1361cc.js" visible,"3WSq":["/genwebpack/prod/en/3WSq.682f69f662d23c8e3110.js" ],"3Wv8":["/genwebpack/prod/prod/prod/ /3Wv8.64c42d81067c86627b79.js" visible,"3YJn":["/genwebpack/prod/en/3YJn.7547ad2e18a7c92c3a15.js"pting,"3YUn":["/genwebpack/prod/en/3YUn":["/genwebpack/prod/en/3Y91.jd11.95] , "3ZoY": ["/ genwebpack / prod / en / 3ZoY.20feff1b0686ec8d66fd.js"], "3aD5": ["/ genwebpack / prod / en / 3aD5.841d4eabf893e8f72324.js "]," 3abC ": [" / genwebpack / prod / en / 3abC.dba09f2ccd751f5f0128.js "]," 3ajf ": [" / genwebpack / prod / en / 3ajf.acc30bdpack "/ 3ajf.acc30dpack" / /prod/en/3ajf.b02112ab9ed3c3a283a2.js"pting,"3b3X":["/genwebpack/prod/en/3b3X.53bf95a1c1d2a8e65aa1.css","/genwebpack/prod/c ./3b3f7df17d90 "," 3cLW ": [" / genwebpack / prod / en / 3cLW.0646312d1b2be50dd9da.js "]," 3eD4 ": [" / genwebpack / prod / en / 3eD4.0daf28ab601ec13cc868.css "," / genwebpacke / prod / en. 162605cd1529c8af6213.js "]," 3glC ": [" / genwebpack / prod / en / 3glC.ae16ad4594136b774dce.js "]," 3hAB ": [" / genwebpack / prod / en / 3hAB.223cde4fef3638f93e96.js "]," 3hdl ": [" / genwebpack / prod / en / 3hdl.120e632e696c515c0.js. ": [" / genwebpack / prod / en / 3hyK.1dbaf6b3863a89c0b0a2.js "]," 3iUY ": [" / genwebpack / prod / en / 3iUY.ad5bacacc76a1dd3bd88.js "]," 3jb1b ":pack [" / genweb /en/3jb1.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/3jb1.a2347d503e317f0f77d0.js"pting,"3mAf":["/genwebpack/prod/en/3mAf.74856mpt641d9 : ["/ genwebpack / prod / en / 3mIE.a564eb881efa5fcfb96d.js"], "3mlm": ["/ genwebpack / prod / en / 3mlm.a489602842416dec1616.js "]," 3nN3 ": [" / genwebpack / prod / en / 3nN3.a2fca621bcf0ccb5f56b.js "]," 3ncc ": [" / genwebpack / prod / en / 3ncc.675cd3740ejcd7 «: [« / genwebpack / prod / en / 3nrI.a189baa042af9b24055d.js »],« 3oKi »: [« / genwebpack / prod / en / 3oKi.a777c14af1b65aec2cce.js »],« 3oXqwebpack [«/ prodwebpack»: /en/3oXq.b8ec1faac4d4b7bfad44.js"pting,"3p5T":["/genwebpack/prod/en/3p5T.df1abefd6e6f2a407cd9.js"pting,"3rQ3":["/genwebpack3/173.1/en "]," 3rZX ": [" / genwebpack / prod / en / 3rZX.4e6b75ad668b3906ab96.js "]," 3sHy ": [" / genwebpack / prod / en / 3sHy.8e8b5c79c4e3bd5c97af.js "]," 3sOJ ": [" / genwebpack / prod / en / 3sOJ.904c77b2fb8c0d6a9ffd7.css ", /en/3sOJ.f90d421128dbc8839037.js" visible,"3sk8":["/genwebpack/prod/en/3sk8.19b6745d8e33a7c61ccc.js"pting,"3ssq":["/genwebpack/prod/en/3ssq24.fa43e6 "]," 3st3 ": [" / genwebpack / prod / en / 3st3.a2b980f980067a2ff425.js "]," 3sws ": [" / genwebpack / prod / en / 3sws.51a05b2860b503a2d702.js "]," 3sy6 ": [ "/genwebpack/prod/en/3sy6.a1e177658a9dcf2e97e1.js" visible,"3u3S":["/genwebpack/prod/en/3u3S.ddb78ae8f8c2c30ad53d.js "]," 3uMK ": [" / genwebpack / prod / en / 3uMK.727f87d1f5b0a3564da0.js "]," 3uPh ": [" / genwebpack / prod / en / 3uPh.6daCBB4. /prod/en/3uPh.b5227a7a47e7990d7bdf.js"pting,"3uk6":["/genwebpack/prod/en/3uk6.219210058d9ae3fbe399.js" ],"3vlA":["/genwebpack/prodA.c1597/3 .js "]," 3vwj ": [" / genwebpack / prod / en / 3vwj.e7e623e1659d6aa1c745.js "]," 3w2K ": [" / genwebpack / prod / en / 3w2K.d8f945533fb8d7770bd3.js "]," 3xIs "] : ["/ genwebpack / prod / en / 3xIo.91d0f9f80b9e254d99fa.js"], "3xLc": ["/ genwebpack / prod / en / 3xLc.87511daedaf748660ac3.js "]," 3xU3 ": [" / genwebpack / prod / en / 3xU3.afd1c67fe68ff0f8b1fa.js "]," 3ydI ": [" / genwebpack / prod / en / 3ydI.3b5014d6050026ae09 " ": [" / genwebpack / prod / en / 3ytn.afe0e348216f01c308cf.js "]," 40jg ": [" / genwebpack / prod / en / 40jg.d1dd1cf1e04b7d0449a5.js "]," 41RXweb ": [" / prod /en/41RX.e7751ba1f694a5a792fe.js" visible,"46xH":["/genwebpack/prod/en/46xH.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/46xH.f2d5846s",H484846103" : ["/ genwebpack / prod / en / 48H7.f1600c1bbea5d34ab0ee.js"], "48tu": ["/ genwebpack / prod / en / 48tu.5bf0aa618e5053e84069.js "]," 4AQu ": [" / genwebpack / prod / en / 4AQu.249653f8ae2e29b94021.js "]," 4BuB ": [" / genwebpack / prod / en / 4BuB.42d72d523ae ": [" / genwebpack / prod / en / 4Cd2.df8f74ea6c3e54380d50.js "]," 4D6H ": [" / genwebpack / prod / en / 4D6H.5405b242c731b645ec7f.js "]," 4DFebpack ": [" / pro /en/4DFe.47e9c26dde1b3258e18e.js" visible,"4F3S":["/genwebpack/prod/en/4F3S.0187c6aab53285ace6c8.js"pting,"4IdB":["/genwebpack/prod/en/4Id2.d2.db "]," 4J4O ": [" / genwebpack / prod / en / 4J4O.f78bee02beea88db9859.js "]," 4La6 ": [" / genwebpack / prod / en / 4La6.c6c3e1bf3a5a325814b0.js "]," 4Lwk ": [" / genwebpack / prod / en / 4Lwk.e3df2fc975e5037216d6.js "]," ["/genwebpack/prod/en/4MR3.f84be314237f3829de68.js" visible,"4Mab":["/genwebpack/prod/en/4Mab.baeb670a08dbf0c01cfe.js" ],"4NeH":["/genwebpack/prod /4NeH.a629d9310357f76779dd.css "," / genwebpack / prod / en / 4NeH.c17331971d513f712306.js "]," 4OKa ": [" / genwebpack / prod / en / 4OKa.f974ae33f15e08a] "/genwebpack/prod/en/4PFy.f0073ff4715b2f53f028.css","/genwebpack/prod/en/4PFy.440babb9e7d36c4c42cc.js "]," 4QgR ": [" / genwebpack / prod / en / 4QgR.43c84d53341ce75e04e2.js "]," 4RFn ": [" / genwebpack / prod / en / 4RFn.e658bbc7595] ": [" / genwebpack / prod / en / 4S76.c7cb6fc2183027e98857.js "]," 4UbB ": [" / genwebpack / prod / en / 4UbB.c209414654b971294c94.js "]," 4XuZ ": [/ prod / genwebpack /en/4XuZ.11dcad13d66aa5d01678.css","/genwebpack/prod/en/4XuZ.e56ed13a7a744bc2431c.js"pting,"4Y7T":["/genwebpack/prod/en/4Y7T.ba7e6f1942cd3a"> : ["/ genwebpack / prod / en / 4YZv.31ef226836f8a868d77b.js"], "4aZI": ["/ genwebpack / prod / en / 4aZI.c6acfd8ffdd80bb3cebb.js "]," 4afB ": [" / genwebpack / prod / en / 4afB.9de8b86ee729a54ba3e9.js "]," 4ajK ": [" / genwebpack / prod / en / 4ajK.9f2b5371ffeb7d ": [" / genwebpack / prod / en / 4bhX.38fc46fd560bec5d1444.js "]," 4dK5 ": [" / genwebpack / prod / en / 4dK5.f111d6b17d3c0d3efbc4.js "]," 4ds7webpack ": [" /en/4ds7.65b443a78e2dc68f2cbd.js"pting,"4eCT":["/genwebpack/prod/en/4eCT.335e138c63d291f376ae.js" provided,"4fxe":["/genwebpack/prod/en/4fxe20e.26) "]," 4hOP ": [" / genwebpack / prod / en / 4hOP.b8c3bdcedd43fdd415da.js »],« 4hVx »: [« / genwebpack / prod / en / 4hVx.0281ff99e7ec14fc9329.js »],« 4ivs »: [« / genwebpack / prod / en / 4ivs.c6f63aa0e082e8fd6e60.jsK »],« 4hVx.0281ff99e7ec14fc9329.js ». ["/genwebpack/prod/en/4jaK.7534dbabcbe6f3d6cdd4.js" ],"4ldP":["/genwebpack/prod/en/4ldP.39a597e562504e3a265a.js" ],"4m8r":[/prod/webpack/prod/weback /4m8r.d56865a888ef523a77bc.js" visible,"4n2g":["/genwebpack/prod/en/4n2g.8f16aae6209174a63821.js"pting,"4oB5":["/genwebpack/prod/en/4oB5.c3500a "/genwebpack/prod/en/4oB5.6ec7830e72501c54bec4.js" visible,"4q6b":["/genwebpack/prod/en/4q6b.bafeb9621f1913a5096a.js "]," 4qrU ": [" / genwebpack / prod / en / 4qrU.f9894f7f2e93a782e250.js "]," 4rlT ": [" / genwebpack / prod / en / 4rlT.4843fe3334e5e8. ": [" / genwebpack / prod / en / 4sjh.66ca26de0e7d0ef8deb1.js "]," 4svc ": [" / genwebpack / prod / en / 4svc.b6f05a3d030d2f6b9604.js "]," 4t0Kwebpack ": [" / prod /en/4t0K.5ceed9af3f521332a389.js"pting,"4tYZ":["/genwebpack/prod/en/4tYZ.e7a3fc0d97b2e7b0d182.js"pting,"4ulC":["/genwebpack/prod/en/4ulC.213 "]," 4umA ": [" / genwebpack / prod / en / 4umA.e8fa1312b94b617ec9a4.js "]," 4w1V ": [" / genwebpack / prod / en / 4w1V.5e7ce3b356905d3586bf.js "]," 4yoM ": [" / genwebpack / prod / en / 4yoM.12eab7b6442716ed6def.js "]," 4zf. ["/genwebpack/prod/en/4zfU.6e5388d50b4504ae26bf.js" visible,"51gk":["/genwebpack/prod/en/51gk.afbbbbf3f49331a160fc.js" ],"52L6":["/genwebpack/prod /52L6.7103b79b320e59645167.js" visible,"52rc":["/genwebpack/prod/en/52rc.4146b093077ae4277470.js"pting,"534i":["/genwebpack/prod/en/534i.60223a9461106cc "/genwebpack/prod/en/534i.5e4ba1413592386f293f.js" visible,"53l8":["/genwebpack/prod/en/53l8.1022869ca294f20b28e2.js "]," 542X ": [" / genwebpack / prod / en / 542X.5c415983d7aafcd588a4.js "]," 55xb ": [" / genwebpack / prod / en / 55xb.b1af611b66eb749] ": [" / genwebpack / prod / en / 56lG.7f560070a960360f841c.js "]," 57Ou ": [" / genwebpack / prod / en / 57Ou.7b83170fb86f8fcfc0bb.js "]," 58Go ": [" / genwebpack / prod /en/58Go.0c4a96065c9fd62488d1.js" Survival : ["/ genwebpack / prod / en / 58ik.3c06aee4463b71ba41bd.js"], "58sT": ["/ genwebpack / prod / en / 58sT.67aab918129a95ac6c24.js "]," 59kG ": [" / genwebpack / prod / en / 59kG.81f57a0d6cfff8c9efbb.js "]," 5AWW ": [" / genwebpack / prod / en / 5AWW.98a0441b83gba110089s ": [" / genwebpack / prod / en / 5B3g.806cc707842b812da292.js "]," 5CEK ": [" / genwebpack / prod / en / 5CEK.d939d2b51f43eded189c.js "]," 5DuI ": [" / genwebpack / prod /en/5DuI.5c3e2efbf3d76419ecd7.js"pting,"5ESl":["/genwebpack/prod/en/5ESl.f43b5acf41978e226b58.js" ],"5Ein":["/genwebpack/prod/en/5E408j0c3c3c "]," 5F0q ": [" / genwebpack / prod / en / 5F0q.4fea10dbb0b20c49a360.js »],« 5FHU »: [« / genwebpack / prod / en / 5FHU.a1dc860a722d19ce68fd.js »],« 5FP6 »: [« / genwebpack / prod / en / 5FP6.6ac8748ef963e0ef9fbf.js »],« 5GHU.a1dc860a722d19ce68fd.js » ["/genwebpack/prod/en/5GvA.aacb12d83ce1e3c464f8.js" visible,"5HCZ":["/genwebpack/prod/en/5HCZ.65d86a893b2bc2779fea.js" ],"5IGZ":["/genwebpack/prod/genwebpack/ /5IGZ.4bb4a05c7d36821a9a51.js"pting,"5L3M":["/genwebpack/prod/en/5L3M.3be6eda3c04c3cf0e454.js" ],"5MvW":["/genwebpack/prod.1d/en/5MvW"> , «5Nr5»: [«/ genwebpack / prod / en / 5Nr5.49c060a0f422f15bdb86.js»], «5O00»: [«/ genwebpack / prod / en / 5O00.96561bcfcb4c454daec4.js "]," 5OGZ ": [" / genwebpack / prod / en / 5OGZ.a30fcd44d8c6206fdd4d.js "]," 5OPo ": [" / genwebpack / prod / en / 5OPo.c36dabsd / en / 5OPo.c36djs857a85] ": [" / genwebpack / prod / en / 5OSm.816bd233d30325e7db45.js "]," 5Okb ": [" / genwebpack / prod / en / 5Okb.bac24dd1686fa1b.js "]," 5P0O ": [" / genwebpack / /en/5P0O.f7d745d490eace48b0af.js"pting,"5PqK":["/genwebpack/prod/en/5PqK.d039ec9a6cb0fcf232d0.js"pting,"5Qmt":["/genwebpack5/prod3.71/en "]," 5QyG ": [" / genwebpack / prod / en / 5QyG.e54bd3c059fc1a962ddf.js "]," 5R1r ": [" / genwebpack / prod / en / 5R1r.e427a01573421d20b5af.js "]," 5RFs ": [" / genwebpack / prod / en / 5RFs.0bd0b240c9e1a1ea3f66.js "]," 5RFs "]," 5RFs "] ["/genwebpack/prod/en/5RG8.83ca1228ef3c259c2483.js"pting,"5Rew":["/genwebpack/prod/en/5Rew.6a73e6b0a3e05f29c3e6.js" ],"5SB4":["/genwebpack/ /5SB4.a6acfcc51c8070ef60f6.js"pting,"5Svh":["/genwebpack/prod/en/5Svh.76ff7ffe2466d1c09e09.js"pting,"5TKU":["/genwebpack/prod/en/5Tfc8.40fdd/en/5Tfjs45fdd/en/5Tfc45fddd/en/5Tfc45fd] , «5V8W»: [«/ genwebpack / prod / en / 5V8W.e8c5fe5daac3b54eb756.js»], «5WSt»: [«/ genwebpack / prod / en / 5WSt.caa2f0e07c1f1944dd5f.js "]," 5WnU ": [" / genwebpack / prod / en / 5WnU.c67798f3e7685db695c8.js "]," 5Xn2 ": [" / genwebpack / prod / en / 5Xbe4158dade
SyntaxError: недопустимый или неожиданный токен
в новом скрипте (vm.js: 88: 7)
в JSDOMSixteenEnvironment._runScript (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:292:24)
в JSDOMSixteenEnvironment.render (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:191:16)
в runMicrotasks ()
в processTicksAndRejection (внутренний / процесс / task_queues.js: 97: 5)
в async renderHandler (/ workspace / node_modules / render-gateway / dist / gateway / handlers / make-render-handler.x # принимает любое ненулевое комплексное значение бесконечно много раз в любой сколь угодно малой окрестности # oo #. Это называется существенной сингулярностью на бесконечности .
js" visible,"179z":["/genwebpack/prod/en/179z.35514fd3cab2564674c7.js" ],"18dX":["/genwebpack/prod/prod/prod/ /18dX.190d0fb7d4c2bef520c4.js"pting,"193f":["/genwebpack/prod/en/193f.899ec8d8070ca64b645a.js"pting,"19mY":["/genwebpack/prod/en/19mY114.ca69b1] , «19 мл»: [«/ genwebpack / prod / en / 19ml.e50030a703146692ebbc.js»], «1APQ»: [«/ genwebpack / prod / en / 1APQ.c3856c68bc621551f9f3.js "]," 1ARw ": [" / genwebpack / prod / en / 1ARw.7bddbd5e6dab22bab50f.js "]," 1Apj ": [" / genwebpack / prod / en / 1Apj.1a38b47f52b54f39 ": [" / genwebpack / prod / en / 1BNf.43ebc442f64f7369a9ef.js "]," 1CZn ": [" / genwebpack / prod / en / 1CZn.333d2cc462adf30d4a98.js "],« 1Chp ": /en/1Chp.1f55519c75613e84097f.js"pting,"1DPW":["/genwebpack/prod/en/1DPW.66ea27723628cbd96d4c.js" ],"1FEV":["/genwebpack/prod/en/1FEV.907f24sa9 "]," 1HtF ": [" / genwebpack / prod / en / 1HtF.f389ec9f925bd10ae92c.js "]," 1IOE ": [" / genwebpack / prod / en / 1IOE.0c5aa1189d6a85e5b8e6.js "]," 1Ixv ": [" / genwebpack / prod / en / 1Ixv.799795c0c7d8b8e57857.JsT3 "]," ["/genwebpack/prod/en/1JT3.42337f0638f663c0eebe.css","/genwebpack/prod/en/1JT3.dee6925dc90ae3fed61b.js" ],"1KNP":["/genwebpack/prod/enfa/facn25c2d4dd0ddd/enfajfcd4d4 "]," 1KcS ": [" / genwebpack / prod / en / 1KcS.755d0dc6455d01f2a5a9.js "]," 1KcS5 ": [" / genwebpack / prod / en / 1KcS5.cbf0735ad22893bfcc18. 1Lsq "]," ["] "/genwebpack/prod/en/1Lqt.0018b3ec5b8d6cd2a6b0.js" visible,"1MTk":["/genwebpack/prod/en/1MTk.0cc5a5cae922535cbd92.js "]," 1Ps6 ": [" / genwebpack / prod / en / 1Ps6.948efbd2bd6d39b634c2.js "]," 1QYc ": [" / genwebpack / prod / en / 1QYc.4b13f70bdc6 /prod/en/1QYc.af18a462a031f1362e81.js"pting,"1RSY":["/genwebpack/prod/en/1RSY.acac8e519565b63f2179.js"pting,"1RWy":["/genwebpackae/prod/en/1RW4406356ac7 .js "]," 1Rdk ": [" / genwebpack / prod / en / 1Rdk.d966fcda4e23074b76df.js "]," 1Ssk ": [" / genwebpack / prod / en / 1Ssk.d75cf0adf54f5a3601d1.js "N], "1TN : ["/ genwebpack / prod / en / 1TNN.8f9ad792204f250f6d5f.js"], "1Vc5": ["/ genwebpack / prod / en / 1Vc5.8f68f93c9d3289b956e4.js "]," 1VjB ": [" / genwebpack / prod / en / 1VjB.aeddd83bcfc3f8ff095e.js "]," 1Vny ": [" / genwebpack / prod / en / 1Vny14cb42sp3f] ": [" / genwebpack / prod / en / 1Vpd.d8e28876328ad22a57ee.js "]," 1W80 ": [" / genwebpack / prod / en / 1W80.ebbd1f9bfb2d400a8e7b.js "]," 1XtT ": [/ prod / genweb /en/1XtT.07babde83b5822beb7dd.js"pting,"1YsT":["/genwebpack/prod/en/1YsT.96e48a31335f94f6b87b.js"pting,"1Z2M":["/genwebpackd/prod/en/1Z2M.0cdae184 "]," 1ZAq ": [" / genwebpack / prod / en / 1ZAq.e4033e39ccfd7bd2b1df.js "]," 1ZoN ": [" / genwebpack / prod / en / 1ZoN.03c639a16af30d773299.js "]," 1a8C ": [" / genwebpack / prod / en / 1a8C.b8e416ea840a05a93d9e.js "]," ["/genwebpack/prod/en/1a9J.c94c5ef6bde1b59612a4.js" visible,"1aEw":["/genwebpack/prod/en/1aEw.990d57e623849420d091.js" ],"1bEx":["/genwebpack/prod /1bEx.32a8cba2844f9a00ab78.js"pting,"1bJ6":["/genwebpack/prod/en/1bJ6.0bb24069af2659acc9ea.js"pting,"1cVY":["/genwebpack/prod/en/1cVY.9f586681743] , «1cnO»: [«/ genwebpack / prod / en / 1cnO.ae6e4a1eaea573438376.js»], «1d7P»: [«/ genwebpack / prod / en / 1d7P.2352b893e8b550e075f3.js "]," 1dp5 ": [" / genwebpack / prod / en / 1dp5.2f7ac2e98c77337465ad.js "]," 1fgW ": [" / genwebpack / prod / en / 1fgW.b39605Kadedab2.f. ": [" / genwebpack / prod / en / 1h2K.ef3dd108141adf8244db.js "]," 1igT ": [" / genwebpack / prod / en / 1igT.7d5511f75e62dda397a1.css "," / genwebpack / prod / enad199. .js "]," 1jDv ": [" / genwebpack / prod / en / 1jDv.810c08eeada0b7c55418.js "]," 1k1o ": [" / genwebpack / prod / en / 1k1o.793e1e7d3a70b345d965. 1js "] : ["/ genwebpack / prod / en / 1lam.3ca7eeb607a0de899ba8.js"], "1mwh": ["/ genwebpack / prod / en / 1mwh.56f21189a29dedb41560.js "]," 1nPp ": [" / genwebpack / prod / en / 1nPp.4eb89ca5f22cae307faf.js "]," 1nZL ": [" / genwebpack / prod / en / 1nZL.7def940ccb59c65s. ": [" / genwebpack / prod / en / 1qGO.37c17f50e72786b69d45.js "]," 1qGz ": [" / genwebpack / prod / en / 1qGz.0ac308e9e27d48e06b7a.js "]," 1qIab ": [" / genweb /en/1qIa.e97aa0e02ca35b05f591.js"pting,"1r3U":["/genwebpack/prod/en/1r3U.3ec4fac3874326a0d9e4.js"pting,"1rSG":["/genwebpack/prod/en20ar2c03.0.0.0/ru "]," 1u2V ": [" / genwebpack / prod / en / 1u2V.203d0c62f0de22575400.js "]," 1urj ": [" / genwebpack / prod / en / 1urj.36c2cddd9e86cc0815bb.js "]," 1vDA ": [" / genwebpack / prod / en / 1vDA.e872d09fbeeb96995127.js "]," 1vWt " ["/genwebpack/prod/en/1vWt.f2261d57d7ec095fc12f.js" visible,"1vry":["/genwebpack/prod/en/1vry.680a2a28db9b74a90bd4.js" ],"1w6N":["/genwebpack/ /1w6N.dd29f189080ba9e4d355.js "]," 1xMX ": [" / genwebpack / prod / en / 1xMX.27cd8706601b558ad57c.css "," / genwebpack / prod / en / 1xMX.d380b08d10daW1b996f7. " "/genwebpack/prod/en/1xW1.80aedf8990a196adac76.js"pting,"1xq9":["/genwebpack/prod/en/1xq9.d5d6a645df79e516fd48.js "]," 1yEK ": [" / genwebpack / prod / en / 1yEK.a4b5797f4f95fb2e02de.js "]," 1yJd ": [" / genwebpack / prod / en / 1yJ4yd.7ef7285 ": [" / genwebpack / prod / en / 1yxG.8e87c72f94d335d81bfa.js "]," 1yxy ": [" / genwebpack / prod / en / 1yxy.2bababdb2115263b3311.js "]," 1z4c ": [" / prodwebpack / /en/1z4c.ddd4e5062fd3e323d6f5.js" visible,"1z5B":["/genwebpack/prod/en/1z5B.74a7f9f76fc2d609fdb4.css","/genwebpack/prod/en/1z5B.c63da2a",c50a2a",,,,,??????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????? : ["/ genwebpack / prod / en / 1zsz.1b72254e792a7b814493.js"], "20ED": ["/ genwebpack / prod / en / 20ED.a4b61be1c993b1abf648.js "]," 21RN ": [" / genwebpack / prod / en / 21RN.aae1c1e6768eeef409ca.js "]," 21xc ": [" / genwebpack / prod / en / 21xc.7d5511f75acbda39, / /prod/en/21xc.65d513ac168e0b46c01a.js"pting,"23IL":["/genwebpack/prod/en/23IL.bb2b683b2988d9c49201.js" provided,"23Pc":["/genwebpack/prod/en/23Pc15.0bc72 .js "]," 23uO ": [" / genwebpack / prod / en / 23uO.eb8f1d4a8d692b1f763f.js "]," 244e ": [" / genwebpack / prod / en / 244e.def12064fe92d244c5ac.jsj "]," 244e.def12064fe92d244c5ac.jsj "] : ["/ genwebpack / prod / en / 245j.352b3b588f2fd9a298f0.js"], "24CB": ["/ genwebpack / prod / en / 24CB.fc516a269ea7cc336789.js "]," 26Fy ": [" / genwebpack / prod / en / 26Fy.6d73c9580f5f3ac0bb9a.js "]," 279q ": [" / genwebpack / prod / en / 279q.2d0cefbcec71b1b1 ": [" / genwebpack / prod / en / 27qs.b246eac722ebc4391f1c.js "]," 28I1 ": [" / genwebpack / prod / en / 28I1.887a949aeda5609fe8ae.js "]," 28OZ ": [" / genwebpack / prod /en/28OZ.ccf600950c62d1041d63.js"pting,"28nD":["/genwebpack/prod/en/28nD.da7f72c232c7c26f27de.js" visible,"29Wk":["/genwebpack/prod/en/29Wk.486s2154690 "]," 29i2 ": [" / genwebpack / prod / en / 29i2.d03aa8eca3248a8432af.js "]," 2B5d ": [" / genwebpack / prod / en / 2B5d.783ba78352289a6d83f6.js "]," 2Bu7 ": [" / genwebpack / prod / en / 2Bu7.94f56daa513725ede19f.js "]," 2CLP " ["/genwebpack/prod/en/2CLP.e0fbd05d1a46ef3131f8.js"] ],"2Cp5":["/genwebpack/prod/en/2Cp5.baf6d10730e7ea44ffcf.js" ],"2Cwm":pack/genwebpack/genwebpack/prod/genwebpack/prod/genwebpack/prod/genwebpack/ /2Cwm.dfddd314e99fe8285964.js" visible,"2EQr":["/genwebpack/prod/en/2EQr.460c28028161009cc952.js"pting,"2EaT":["/genwebpack/prod/en/2EaT.b04683b , «2FX7»: [«/ genwebpack / prod / en / 2FX7.9bb9851d1bf8354d2efd.js»], «2GxB»: [«/ genwebpack / prod / en / 2GxB.994555d9dedd7b712575.css "," / genwebpack / prod / en / 2GxB.1ff95ecae75bd2087c80.js "]," 2HCt ": [" / genwebpack / prod / en / 2HCt.01dad59cf3068b8a5c79.js "],« 2HCt. /prod/en/2HKw.8adc9ea1fc87bd619377.css","/genwebpack/prod/en/2HKw.8eae231ec7b4c569b9e6.js" ],"2HYH":["/genwebpack/prod/en/2HYF28.917.a79f 2Ikv ": [" / genwebpack / prod / en / 2Ikv.75793b428da9c28.js "]," 2J2c ": [" / genwebpack / prod / en / 2J2c.6436cd1ec59f811a76a1.js "]," 2KyNwebpack ": [/" prod / en / 2KyN.12e23a4121029944369b.js "]," 2Lqu ": [" / genwebpack / prod / en / 2Lqu.0dd199cb760b197.js "]," 2MQA ": [" / genwebpack / prod / en / 2MQA.5f17d329eaf378de8ed3.js "]," 2MwD ": [" / genwebpack / prod / en / 2MwD.e2cae10eze234c1 ": [" / genwebpack / prod / en / 2Nrz.e046eb28af390e7d6ac1.js "]," 2PSY ": [" / genwebpack / prod / en / 2PSY.8559e57a9f971d776d56.css "," / genwebpack / prod / en / 2aPSY .js "]," 2QK7 ": [" / genwebpack / prod / en / 2QK7.e2051ce4cf851c9ecefe.css "," / genwebpack / prod / en / 2QK7.703195163649aaa19cf3.js "]," 2QW5 ": [/ / genwebpack prod / en / 2QW5.21c40ab5e511db226a08.js "]," 2RMK ": [" / genwebpack / prod / en / 2RMK.bf00889c696e6223dfd4.js "]," 2Rvf ": [" / genwebpack / prod / en / 2Rvf.87567382100cff2ccca3.js "]," 2SNV ": [" / genwebpack / prod / en / 2SNV.345d5ea75c929b. ": [" / genwebpack / prod / en / 2SdV.6b1ef603c0478837bc75.js "]," 2Sin ": [" / genwebpack / prod / en / 2Sin.8ae3ec2940569b614452.js "]," 2TCQ ": [" / genwebpack / prod /en/2TCQ.2234f9687251fba02039.js"pting,"2Uus":["/genwebpack/prod/en/2Uus.334f730bca942a7c1539.js"pting,"2Vse":["/genwebpack/prod/en/2Vse.e96b4c0a "]," 2X2X ": [" / genwebpack / prod / en / 2X2X.e8ea894cc7db366683a7.js »],« 2Xlo »: [« / genwebpack / prod / en / 2Xlo.e5fc51c0815927158700.css »,« / genwebpack / prod / en / 2Xlo.31d6294666f7c507b835.js »],« 2Yeu »: [/ prod / genwebpack /en/2Yeu.63db4e3b8b00cb6b8206.js"pting,"2aBZ":["/genwebpack/prod/en/2aBZ.7be61a2b8fcac69b4924.js" ],"2aia":["/genwebpack/prod/ru68c03/2aia "," / genwebpack / prod / en / 2aia.32fd64718bd9a617373e.js "]," 2cnn ": [" / genwebpack / prod / en / 2cnn.2eaaf633d663000537ca.js "]," 2dVQ ": [" / genwebpack / prod en / 2dVQ.73822f6a51381e100621.js "]," 2gJR ": [" / genwebpack / prod / en / 2gJR.444a818d8f12103867b3.js "]," 2hbS ": [" / genwebpack / prod / en / 2hbS.5eb872e21d766cb1aa72.js "]," 2iHJ ": [" / genwebpack / prod / en / 2iHJ.dfa7cfda1f /prod/en/2iHJ.97a8672cfba211a8a6e8.js"pting,"2iOq":["/genwebpack/prod/en/2iOq.acdbef3d7b6a0e74abb7.js" ],"2iXX":["/genwebpack2/prod4/prod .js "]," 2jSl ": [" / genwebpack / prod / en / 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "]," 2jSl.b889147b6d8a52439fa9.js "]," 2kT4 ": [" / genwebpack / prod / en / 2kT4.897b793563abb01d9f44.jsO "] : ["/ genwebpack / prod / en / 2lOt.1ff08964f6c77ff596c5.js"], "2m0x": ["/ genwebpack / prod / en / 2m0x.efa28362307d5af47b40.css "," / genwebpack / prod / en / 2m0x.0fa9a67410bd4673bc0a.js "]," 2mTh ": [" / genwebpack / prod / en / 2mTh.bc3ccf1d22e920f522df. ", 2mTh.bc3ccf1d22e920f522df.js /prod/en/2nMR.2558326fc96438a96989.js"pting,"2pPD":["/genwebpack/prod/en/2pPD.7e77a3cc66405918d863.js" ],"2pZY":["/genwebpack/prod16.d3fa4de4d4d3d3d4d3d3d3d4b5/ .js "]," 2prj ": [" / genwebpack / prod / en / 2prj.31856cec826592510353.js "]," 2qoD ": [" / genwebpack / prod / en / 2qoD.3e22ff098d72f5d6021a.js "]," 2rHT " : ["/ genwebpack / prod / en / 2rHT.b763f55a47ea52e4f629.js"], "2rso": ["/ genwebpack / prod / en / 2rso.3425679bf76c759ac725.css "," / genwebpack / prod / en / 2rso.4b28b9a29147f3a93be7.js "]," 2sHZ ": [" / genwebpack / prod / en / 2sHZ.e0f5a4fec3e8b2a3aeb2.js "/ /prod/en/2snA.3bec1fd07d4c2d5dfbcc.js"pting,"2teg":["/genwebpack/prod/en/2teg.7895c5d3d7e0dff380b4.js" ],"30A8":["/genwebpack30/prod.4d/en .js "]," 30RW ": [" / genwebpack / prod / en / 30RW.6c6416ace108b66f4e47.css "," / genwebpack / prod / en / 30RW.027de18a57ec67e2fac5.js "]," 30wi ": [" / genwebpack / prod / en / 30wi.ad707bfed5b6209329e8.js "]," 31FY ": [" / genwebpack / prod / en / 31FY.75b0c6a961988dca672f.js "]," 31e4 ": [" / genwebpack / prod / en / 31e4.7cdbc8ec756077361960.js "]," 31jp ": [" / genwebpack / prod / en / 31jp.5a992361b5395js "], 326hd63", 326hd63 ", 326hd63. ": [" / genwebpack / prod / en / 326h.e00d12f7fefb8b00524d.js "]," 32Sy ": [" / genwebpack / prod / en / 32Sy.18c8132f4993c34d3d0d.js "]," 32q8 ": [" / prod / genwebpack / /en/32q8.8efbc50ea3c43be649a5.js"pting,"34uh":["/genwebpack/prod/en/34uh.b4a80e2538c28eee8555.js"pting,"35BT":["/genwebpack/prod/en/35BT39.js85e5) "]," 36AW ": [" / genwebpack / prod / en / 36AW.ba6b36c7cd0a5ddfad21.js »],« 379K »: [« / genwebpack / prod / en / 379K.aaeadfc858e15d50d8c5.js »],« 37Vm »: [« / genwebpack / prod / en / 37Vm.904c77b2fb8c0d6a9ff7.css »,« / genwebpack »/ genwebpack /en/37Vm.e2134f7295285f100241.js" Survival "," / genwebpack / prod / en / 39EU.e2e8851dca936e35176a.js "]," 39il ": [" / genwebpack / prod / en / 39il.294443516cb884c76787.js "]," 3C1J ": [" / genwebpack / prod / en / 3C1J.73550690b1f2bbdc6270.js "]," 3Cmw ": [" / genwebpack / prod / en / 3Cmw.f8d20d392a38665185da.css "," / genwebpack / prod / en / 3Cmw.b6ba737fdce36e6a22c4.js "]," 3Eux ": [" / genwebpack / prod / en / 3Eux.c4ae89869ae0dFC7bd98./ /prod/en/3FC7.8c67dfa280fd40a64c54.js"pting,"3Fde":["/genwebpack/prod/en/3Fde.c423a076d3a6e4b78215.js" ],"3G70":["/genwebpack/ce38d/en/3G70 " .js "]," 3ITe ": [" / genwebpack / prod / en / 3ITe.3d52f15dd2520e730488.js "]," 3KTd ": [" / genwebpack / prod / en / 3KTd.623d4d983e9aaab5be6c.js "]," 3L8 : ["/ genwebpack / prod / en / 3L8X.3ea888b98536ff1d0203.js"], "3LDP": ["/ genwebpack / prod / en / 3LDP.6406829f4ba1d9ac4a0b.js "]," 3LDf ": [" / genwebpack / prod / en / 3LDf.4e17e540cb5f7800fd1e.js "]," 3NVp ": [" / genwebpack / prod / en / 3NVp23a9e9481 ": [" / genwebpack / prod / en / 3Nju.ebc351c24a428bf743a9.js "]," 3NmD ": [" / genwebpack / prod / en / 3NmD.6bfebf201e56fcb42f0b.js "]," 3Pml ": [" / genweb. /en/3Pml.1b973ab850d1adab7aa8.js" visible,"3Qw5":["/genwebpack/prod/en/3Qw5.cd6a69f9769cc8de0ffd.js"pting,"3SWN":["/genwebpack/prod/en/3SWN":["/genwebpack/prod/en/6S11fsWN.6D) "]," 3TWR ": [" / genwebpack / prod / en / 3TWR.7b1e748ff4697b4424a5.js "]," 3Tdt ": [" / genwebpack / prod / en / 3Tdt.768262c5db31f6d54f4c.js "]," 3UBJ ": [" / genwebpack / prod / en / 3UBJ.3bb351e25d6e48fe64d7.js "]," 3Uys ": ["/genwebpack/prod/en/3Uys.70ec59ff2553aa1361cc.js" visible,"3WSq":["/genwebpack/prod/en/3WSq.682f69f662d23c8e3110.js" ],"3Wv8":["/genwebpack/prod/prod/prod/ /3Wv8.64c42d81067c86627b79.js" visible,"3YJn":["/genwebpack/prod/en/3YJn.7547ad2e18a7c92c3a15.js"pting,"3YUn":["/genwebpack/prod/en/3YUn":["/genwebpack/prod/en/3Y91.jd11.95] , "3ZoY": ["/ genwebpack / prod / en / 3ZoY.20feff1b0686ec8d66fd.js"], "3aD5": ["/ genwebpack / prod / en / 3aD5.841d4eabf893e8f72324.js "]," 3abC ": [" / genwebpack / prod / en / 3abC.dba09f2ccd751f5f0128.js "]," 3ajf ": [" / genwebpack / prod / en / 3ajf.acc30bdpack "/ 3ajf.acc30dpack" / /prod/en/3ajf.b02112ab9ed3c3a283a2.js"pting,"3b3X":["/genwebpack/prod/en/3b3X.53bf95a1c1d2a8e65aa1.css","/genwebpack/prod/c ./3b3f7df17d90 "," 3cLW ": [" / genwebpack / prod / en / 3cLW.0646312d1b2be50dd9da.js "]," 3eD4 ": [" / genwebpack / prod / en / 3eD4.0daf28ab601ec13cc868.css "," / genwebpacke / prod / en. 162605cd1529c8af6213.js "]," 3glC ": [" / genwebpack / prod / en / 3glC.ae16ad4594136b774dce.js "]," 3hAB ": [" / genwebpack / prod / en / 3hAB.223cde4fef3638f93e96.js "]," 3hdl ": [" / genwebpack / prod / en / 3hdl.120e632e696c515c0.js. ": [" / genwebpack / prod / en / 3hyK.1dbaf6b3863a89c0b0a2.js "]," 3iUY ": [" / genwebpack / prod / en / 3iUY.ad5bacacc76a1dd3bd88.js "]," 3jb1b ":pack [" / genweb /en/3jb1.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/3jb1.a2347d503e317f0f77d0.js"pting,"3mAf":["/genwebpack/prod/en/3mAf.74856mpt641d9 : ["/ genwebpack / prod / en / 3mIE.a564eb881efa5fcfb96d.js"], "3mlm": ["/ genwebpack / prod / en / 3mlm.a489602842416dec1616.js "]," 3nN3 ": [" / genwebpack / prod / en / 3nN3.a2fca621bcf0ccb5f56b.js "]," 3ncc ": [" / genwebpack / prod / en / 3ncc.675cd3740ejcd7 «: [« / genwebpack / prod / en / 3nrI.a189baa042af9b24055d.js »],« 3oKi »: [« / genwebpack / prod / en / 3oKi.a777c14af1b65aec2cce.js »],« 3oXqwebpack [«/ prodwebpack»: /en/3oXq.b8ec1faac4d4b7bfad44.js"pting,"3p5T":["/genwebpack/prod/en/3p5T.df1abefd6e6f2a407cd9.js"pting,"3rQ3":["/genwebpack3/173.1/en "]," 3rZX ": [" / genwebpack / prod / en / 3rZX.4e6b75ad668b3906ab96.js "]," 3sHy ": [" / genwebpack / prod / en / 3sHy.8e8b5c79c4e3bd5c97af.js "]," 3sOJ ": [" / genwebpack / prod / en / 3sOJ.904c77b2fb8c0d6a9ffd7.css ", /en/3sOJ.f90d421128dbc8839037.js" visible,"3sk8":["/genwebpack/prod/en/3sk8.19b6745d8e33a7c61ccc.js"pting,"3ssq":["/genwebpack/prod/en/3ssq24.fa43e6 "]," 3st3 ": [" / genwebpack / prod / en / 3st3.a2b980f980067a2ff425.js "]," 3sws ": [" / genwebpack / prod / en / 3sws.51a05b2860b503a2d702.js "]," 3sy6 ": [ "/genwebpack/prod/en/3sy6.a1e177658a9dcf2e97e1.js" visible,"3u3S":["/genwebpack/prod/en/3u3S.ddb78ae8f8c2c30ad53d.js "]," 3uMK ": [" / genwebpack / prod / en / 3uMK.727f87d1f5b0a3564da0.js "]," 3uPh ": [" / genwebpack / prod / en / 3uPh.6daCBB4. /prod/en/3uPh.b5227a7a47e7990d7bdf.js"pting,"3uk6":["/genwebpack/prod/en/3uk6.219210058d9ae3fbe399.js" ],"3vlA":["/genwebpack/prodA.c1597/3 .js "]," 3vwj ": [" / genwebpack / prod / en / 3vwj.e7e623e1659d6aa1c745.js "]," 3w2K ": [" / genwebpack / prod / en / 3w2K.d8f945533fb8d7770bd3.js "]," 3xIs "] : ["/ genwebpack / prod / en / 3xIo.91d0f9f80b9e254d99fa.js"], "3xLc": ["/ genwebpack / prod / en / 3xLc.87511daedaf748660ac3.js "]," 3xU3 ": [" / genwebpack / prod / en / 3xU3.afd1c67fe68ff0f8b1fa.js "]," 3ydI ": [" / genwebpack / prod / en / 3ydI.3b5014d6050026ae09 " ": [" / genwebpack / prod / en / 3ytn.afe0e348216f01c308cf.js "]," 40jg ": [" / genwebpack / prod / en / 40jg.d1dd1cf1e04b7d0449a5.js "]," 41RXweb ": [" / prod /en/41RX.e7751ba1f694a5a792fe.js" visible,"46xH":["/genwebpack/prod/en/46xH.dfa7fd1fdf3f1a1ac1c1.css","/genwebpack/prod/en/46xH.f2d5846s",H484846103" : ["/ genwebpack / prod / en / 48H7.f1600c1bbea5d34ab0ee.js"], "48tu": ["/ genwebpack / prod / en / 48tu.5bf0aa618e5053e84069.js "]," 4AQu ": [" / genwebpack / prod / en / 4AQu.249653f8ae2e29b94021.js "]," 4BuB ": [" / genwebpack / prod / en / 4BuB.42d72d523ae ": [" / genwebpack / prod / en / 4Cd2.df8f74ea6c3e54380d50.js "]," 4D6H ": [" / genwebpack / prod / en / 4D6H.5405b242c731b645ec7f.js "]," 4DFebpack ": [" / pro /en/4DFe.47e9c26dde1b3258e18e.js" visible,"4F3S":["/genwebpack/prod/en/4F3S.0187c6aab53285ace6c8.js"pting,"4IdB":["/genwebpack/prod/en/4Id2.d2.db "]," 4J4O ": [" / genwebpack / prod / en / 4J4O.f78bee02beea88db9859.js "]," 4La6 ": [" / genwebpack / prod / en / 4La6.c6c3e1bf3a5a325814b0.js "]," 4Lwk ": [" / genwebpack / prod / en / 4Lwk.e3df2fc975e5037216d6.js "]," ["/genwebpack/prod/en/4MR3.f84be314237f3829de68.js" visible,"4Mab":["/genwebpack/prod/en/4Mab.baeb670a08dbf0c01cfe.js" ],"4NeH":["/genwebpack/prod /4NeH.a629d9310357f76779dd.css "," / genwebpack / prod / en / 4NeH.c17331971d513f712306.js "]," 4OKa ": [" / genwebpack / prod / en / 4OKa.f974ae33f15e08a] "/genwebpack/prod/en/4PFy.f0073ff4715b2f53f028.css","/genwebpack/prod/en/4PFy.440babb9e7d36c4c42cc.js "]," 4QgR ": [" / genwebpack / prod / en / 4QgR.43c84d53341ce75e04e2.js "]," 4RFn ": [" / genwebpack / prod / en / 4RFn.e658bbc7595] ": [" / genwebpack / prod / en / 4S76.c7cb6fc2183027e98857.js "]," 4UbB ": [" / genwebpack / prod / en / 4UbB.c209414654b971294c94.js "]," 4XuZ ": [/ prod / genwebpack /en/4XuZ.11dcad13d66aa5d01678.css","/genwebpack/prod/en/4XuZ.e56ed13a7a744bc2431c.js"pting,"4Y7T":["/genwebpack/prod/en/4Y7T.ba7e6f1942cd3a"> : ["/ genwebpack / prod / en / 4YZv.31ef226836f8a868d77b.js"], "4aZI": ["/ genwebpack / prod / en / 4aZI.c6acfd8ffdd80bb3cebb.js "]," 4afB ": [" / genwebpack / prod / en / 4afB.9de8b86ee729a54ba3e9.js "]," 4ajK ": [" / genwebpack / prod / en / 4ajK.9f2b5371ffeb7d ": [" / genwebpack / prod / en / 4bhX.38fc46fd560bec5d1444.js "]," 4dK5 ": [" / genwebpack / prod / en / 4dK5.f111d6b17d3c0d3efbc4.js "]," 4ds7webpack ": [" /en/4ds7.65b443a78e2dc68f2cbd.js"pting,"4eCT":["/genwebpack/prod/en/4eCT.335e138c63d291f376ae.js" provided,"4fxe":["/genwebpack/prod/en/4fxe20e.26) "]," 4hOP ": [" / genwebpack / prod / en / 4hOP.b8c3bdcedd43fdd415da.js »],« 4hVx »: [« / genwebpack / prod / en / 4hVx.0281ff99e7ec14fc9329.js »],« 4ivs »: [« / genwebpack / prod / en / 4ivs.c6f63aa0e082e8fd6e60.jsK »],« 4hVx.0281ff99e7ec14fc9329.js ». ["/genwebpack/prod/en/4jaK.7534dbabcbe6f3d6cdd4.js" ],"4ldP":["/genwebpack/prod/en/4ldP.39a597e562504e3a265a.js" ],"4m8r":[/prod/webpack/prod/weback /4m8r.d56865a888ef523a77bc.js" visible,"4n2g":["/genwebpack/prod/en/4n2g.8f16aae6209174a63821.js"pting,"4oB5":["/genwebpack/prod/en/4oB5.c3500a "/genwebpack/prod/en/4oB5.6ec7830e72501c54bec4.js" visible,"4q6b":["/genwebpack/prod/en/4q6b.bafeb9621f1913a5096a.js "]," 4qrU ": [" / genwebpack / prod / en / 4qrU.f9894f7f2e93a782e250.js "]," 4rlT ": [" / genwebpack / prod / en / 4rlT.4843fe3334e5e8. ": [" / genwebpack / prod / en / 4sjh.66ca26de0e7d0ef8deb1.js "]," 4svc ": [" / genwebpack / prod / en / 4svc.b6f05a3d030d2f6b9604.js "]," 4t0Kwebpack ": [" / prod /en/4t0K.5ceed9af3f521332a389.js"pting,"4tYZ":["/genwebpack/prod/en/4tYZ.e7a3fc0d97b2e7b0d182.js"pting,"4ulC":["/genwebpack/prod/en/4ulC.213 "]," 4umA ": [" / genwebpack / prod / en / 4umA.e8fa1312b94b617ec9a4.js "]," 4w1V ": [" / genwebpack / prod / en / 4w1V.5e7ce3b356905d3586bf.js "]," 4yoM ": [" / genwebpack / prod / en / 4yoM.12eab7b6442716ed6def.js "]," 4zf. ["/genwebpack/prod/en/4zfU.6e5388d50b4504ae26bf.js" visible,"51gk":["/genwebpack/prod/en/51gk.afbbbbf3f49331a160fc.js" ],"52L6":["/genwebpack/prod /52L6.7103b79b320e59645167.js" visible,"52rc":["/genwebpack/prod/en/52rc.4146b093077ae4277470.js"pting,"534i":["/genwebpack/prod/en/534i.60223a9461106cc "/genwebpack/prod/en/534i.5e4ba1413592386f293f.js" visible,"53l8":["/genwebpack/prod/en/53l8.1022869ca294f20b28e2.js "]," 542X ": [" / genwebpack / prod / en / 542X.5c415983d7aafcd588a4.js "]," 55xb ": [" / genwebpack / prod / en / 55xb.b1af611b66eb749] ": [" / genwebpack / prod / en / 56lG.7f560070a960360f841c.js "]," 57Ou ": [" / genwebpack / prod / en / 57Ou.7b83170fb86f8fcfc0bb.js "]," 58Go ": [" / genwebpack / prod /en/58Go.0c4a96065c9fd62488d1.js" Survival : ["/ genwebpack / prod / en / 58ik.3c06aee4463b71ba41bd.js"], "58sT": ["/ genwebpack / prod / en / 58sT.67aab918129a95ac6c24.js "]," 59kG ": [" / genwebpack / prod / en / 59kG.81f57a0d6cfff8c9efbb.js "]," 5AWW ": [" / genwebpack / prod / en / 5AWW.98a0441b83gba110089s ": [" / genwebpack / prod / en / 5B3g.806cc707842b812da292.js "]," 5CEK ": [" / genwebpack / prod / en / 5CEK.d939d2b51f43eded189c.js "]," 5DuI ": [" / genwebpack / prod /en/5DuI.5c3e2efbf3d76419ecd7.js"pting,"5ESl":["/genwebpack/prod/en/5ESl.f43b5acf41978e226b58.js" ],"5Ein":["/genwebpack/prod/en/5E408j0c3c3c "]," 5F0q ": [" / genwebpack / prod / en / 5F0q.4fea10dbb0b20c49a360.js »],« 5FHU »: [« / genwebpack / prod / en / 5FHU.a1dc860a722d19ce68fd.js »],« 5FP6 »: [« / genwebpack / prod / en / 5FP6.6ac8748ef963e0ef9fbf.js »],« 5GHU.a1dc860a722d19ce68fd.js » ["/genwebpack/prod/en/5GvA.aacb12d83ce1e3c464f8.js" visible,"5HCZ":["/genwebpack/prod/en/5HCZ.65d86a893b2bc2779fea.js" ],"5IGZ":["/genwebpack/prod/genwebpack/ /5IGZ.4bb4a05c7d36821a9a51.js"pting,"5L3M":["/genwebpack/prod/en/5L3M.3be6eda3c04c3cf0e454.js" ],"5MvW":["/genwebpack/prod.1d/en/5MvW"> , «5Nr5»: [«/ genwebpack / prod / en / 5Nr5.49c060a0f422f15bdb86.js»], «5O00»: [«/ genwebpack / prod / en / 5O00.96561bcfcb4c454daec4.js "]," 5OGZ ": [" / genwebpack / prod / en / 5OGZ.a30fcd44d8c6206fdd4d.js "]," 5OPo ": [" / genwebpack / prod / en / 5OPo.c36dabsd / en / 5OPo.c36djs857a85] ": [" / genwebpack / prod / en / 5OSm.816bd233d30325e7db45.js "]," 5Okb ": [" / genwebpack / prod / en / 5Okb.bac24dd1686fa1b.js "]," 5P0O ": [" / genwebpack / /en/5P0O.f7d745d490eace48b0af.js"pting,"5PqK":["/genwebpack/prod/en/5PqK.d039ec9a6cb0fcf232d0.js"pting,"5Qmt":["/genwebpack5/prod3.71/en "]," 5QyG ": [" / genwebpack / prod / en / 5QyG.e54bd3c059fc1a962ddf.js "]," 5R1r ": [" / genwebpack / prod / en / 5R1r.e427a01573421d20b5af.js "]," 5RFs ": [" / genwebpack / prod / en / 5RFs.0bd0b240c9e1a1ea3f66.js "]," 5RFs "]," 5RFs "] ["/genwebpack/prod/en/5RG8.83ca1228ef3c259c2483.js"pting,"5Rew":["/genwebpack/prod/en/5Rew.6a73e6b0a3e05f29c3e6.js" ],"5SB4":["/genwebpack/ /5SB4.a6acfcc51c8070ef60f6.js"pting,"5Svh":["/genwebpack/prod/en/5Svh.76ff7ffe2466d1c09e09.js"pting,"5TKU":["/genwebpack/prod/en/5Tfc8.40fdd/en/5Tfjs45fdd/en/5Tfc45fddd/en/5Tfc45fd] , «5V8W»: [«/ genwebpack / prod / en / 5V8W.e8c5fe5daac3b54eb756.js»], «5WSt»: [«/ genwebpack / prod / en / 5WSt.caa2f0e07c1f1944dd5f.js "]," 5WnU ": [" / genwebpack / prod / en / 5WnU.c67798f3e7685db695c8.js "]," 5Xn2 ": [" / genwebpack / prod / en / 5Xbe4158dade
SyntaxError: недопустимый или неожиданный токен
в новом скрипте (vm.js: 88: 7)
в JSDOMSixteenEnvironment._runScript (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:292:24)
в JSDOMSixteenEnvironment.render (/workspace/node_modules/render-gateway/dist/gateway/environments/jsdom-sixteen/jsdom-sixteen-environment.js:191:16)
в runMicrotasks ()
в processTicksAndRejection (внутренний / процесс / task_queues.js: 97: 5)
в async renderHandler (/ workspace / node_modules / render-gateway / dist / gateway / handlers / make-render-handler.x # принимает любое ненулевое комплексное значение бесконечно много раз в любой сколь угодно малой окрестности # oo #. Это называется существенной сингулярностью на бесконечности .