примеры пределов с экспонентой
Пределы/ Предел функции
примеры пределов с е
| → | ↑ Функция f(x) ? |
|---|
Примеры
Для конечных точек:
———Слева (x0-)Справа (x0+)
График:
от до
Ввести:
{ кусочно-заданную функцию можно здесь.
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- ctg(x)
- Функция – Котангенс от x
- arcctg(x)
- Функция – Арккотангенс от x
- arcctgh(x)
- Функция – Гиперболический арккотангенс от x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- 15/7
- – дробь
3Другие функции:
- asec(x)
- Функция – арксеканс от x
- acsc(x)
- Функция – арккосеканс от x
- sec(x)
- Функция – секанс от
- csc(x)
- Функция – косеканс от x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция – округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция – гиперболический арксеканс от x
- csch(x)
- Функция – гиперболический косеканс от
- sech(x)
- Функция – гиперболический секанс от x
- acsch(x)
- Функция – гиперболический арккосеканс от x
Постоянные:
- pi
- Число “Пи”, которое примерно равно ~3. 14159..
- e
- Число e – основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- Символ бесконечности – знак для бесконечности
14159..Что такое экспонента: определение, формула, свойства, график
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Экспонента: определение, формула, свойства, график
В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Свойства экспоненциальной функции
Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
f (x) = exp(x) = e x
где e – число Эйлера.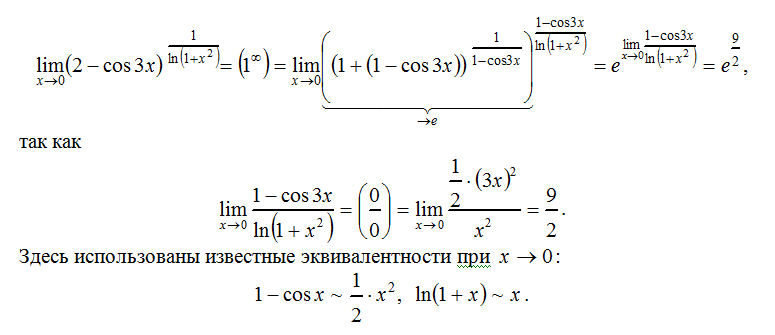
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:
График экспоненты
Ниже представлен график экспоненциальной функции y = e x.
Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y.
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке (0, 1), так как e0 = 1.
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Свойства экспоненциальной функции
- Экспонента определена для всех x, причем функция везде возрастает, и ее значение всегда больше нуля. То есть:
- область определения: – ∞ < x + ∞;
- область значений: 0 < y < + ∞.
- Обратная к экспоненте функция – это натуральный логарифм (ln x).
- ln e x = x;
- e ln x = x, где x > 0.
- Для экспоненты применимы правила операций с показателями, например: e (a + b)
- Производная экспоненты:
- (e x)‘ = e x.
- если вместо x – сложная функция u: (e u)‘ = e u + u‘.
- Интеграл экспоненты: ∫ e x dx = e x + C, где C – константа интегрирования.
То есть:ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Пределы для тригонометрических, экспоненциальных и логарифмических функций
на
Тригонометрические функции непрерывны во всех точках
Тангенс и секанс равномерно текут повсюду в своей области, которая является комбинацией всех точных чисел.
Пусть a – действительное число в области определения данной тригонометрической функции, тогда
- $\lim _{x\to a}\sin x=\sin a$
- $\lim _{x\ к a}\cos x=\cos a$
- $\lim _{x\to a}\tan x=\tan a$
- $\lim _{x\to a}\cot x=\cot a$
- $\lim _{x\to a}\sec x=\sec a$
- $\lim _{x\to a}\csc x=\csc a$
Особые случаи:
- $\lim _{x\to 0}\ frac{\sin x}{x}=1$
- $\lim _{x\to 0}\frac{1-cos x}{x}=0$
Отсюда можно получить
$\lim _{x\to 0}\frac{\tan x}{x}=(\lim _{x\to 0}\frac{\sin x}{x})(\lim _{x\to 0}\ frac{1}{\cos x})=(1)(1)=1$
9{+}}\ln x=-\infty $, так как мы не можем помещать отрицательные значения x в функцию логарифмирования. Это означает, что нормальный предел не может существовать, потому что x справа и слева от рассматриваемой точки должны быть оценены, в то время как x слева от нуля отрицательны. Мы можем видеть, что если аргумент журнала стремится к нулю справа (т.
Примечание: Когда не так много места по вертикали (например, в экспоненте), мы часто пишем «$$x \to a$$» в пределе сбоку, а не под «$$». \лим$$”.
$$ \textstyle \lim_{x\to a} f(x) = \displaystyle \lim_{x\to a} f(x) $$ 9+} \ синий {\ грех х} \ cdot \красный{% \ln х } % = \синий 0\, \красный{% (-\infty) } $$
Это неопределенная форма, которую мы изучали на предыдущем уроке.
Обратите внимание, что в предыдущих уроках мы показывали $$ \lim\limits_{x\to0} \ гидроразрыва {\ греха х} х = 1 $$ Вы также можете использовать правило Лопиталя для его оценки.
Шаг 6
Оцените исходный предел, используя найденные нами значения.
9Икс = 1 $$Для справки, вот график функции и предельного значения.
Определение числа $$e$$
Число $$ e $$, которое используется в качестве основания натуральных экспоненциальных и логарифмических функций, часто определяется с использованием следующего предела:
$$
\displaystyle\lim_{x \to \infty}
\левый(%
1 + \фракция 1 х
\справа)^х.
{%
\ синий х
}
%
& = \lim_{x \to \infty}
\синий х\,
\красный{%
\ln\слева(%
1 + \фракция 1 х
\верно)
}
&& \text{Свойство логарифмов}
\\[6pt]
%
& = \синий \infty
\cdot\красный{%
\ln 1
}
&& \text{Оценка}
\\[6pt]
%
& = \синий \infty
\cdot\красный 0
\конец{выравнивание*}
$$
Шаг 4
Перепишите предел так, чтобы он имел форму $$ \frac 0 0 $$.
$$ \displaystyle\lim_{x \to \infty} \синий х\, \красный{% \ln\слева(% 1 + \фракция 1 х \верно) } % = \displaystyle\lim_{x \to \infty} \ гидроразрыв {% \красный{% \ln\слева(% 1 + \фракция 1 х \верно) } } {% \синий{1/x} } = \ гидроразрыв {% \красный{% \ln 1 } } {% \синий{% 1/\infty } } % = \ гидроразрыв {% \ красный 0 } {% \ синий 0 } $$
Шаг 5
Примените правило Лопиталя и повторно оцените предел.
0
\\[6pt]
%
& = 1
\конец{выравнивание*}
$$
9\infty$$
.
Покажите, что предел равен 90 305, а не 90 306 неопределенным.
Шаг 1
Давайте определим две функции, о которых мы знаем только их пределы:
$$ \начать{выравнивать*} \text{Определить} и(х) \text{ так что } \lim_{х\к} и и = 0 \\[6pt] % \text{Определить} v(x) \text{ так что } \lim_{х\к} & v = \infty \\[6pt] % \конец{выравнивание*} $$ 9{% \lim_{х\к} v\cdot \в ты } $$
Шаг 3
Теперь оцените предел в показателе степени.
$$ \begin{выравнивание*}% \lim_{х\к} u \cdot \ln v % & = \lim_{х\к а} \ синий ты \cdot\ln \ красный v % = \lim_{х\к а} \ синий \ бесконечный \cdot\ln \ красный 0 % = \lim_{х\к а} \ синий \ бесконечный \cdot \красный{% (-\infty) } % = -\infty \конец{выравнивание*} $$ 9{-\infty} $$ имеют несколько иной результат (хотя и НЕ неопределенный). В вопросах в конце урока мы проработаем этот вариант.
Продолжайте практиковать Проблемы
Реклама
Ultimate Math Solver (бесплатно)
Free Algebra Solver .