Пределы с логарифмами примеры решения: Пределы с логарифмами, примеры решений

как решать пределы с логарифмами примеры решения

Вы искали как решать пределы с логарифмами примеры решения? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и предел логарифма, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение. Например, «как решать пределы с логарифмами примеры решения».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как решать пределы с логарифмами примеры решения,предел логарифма,предел логарифма натурального,предел натурального логарифма,пределы примеры решения с логарифмами,пределы с логарифмами,пределы с логарифмами примеры решения,пределы с натуральными логарифмами примеры решения.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как решать пределы с логарифмами примеры решения. Просто введите задачу в окошко и нажмите «решить» здесь (например, предел логарифма натурального).

Где можно решить любую задачу по математике, а так же как решать пределы с логарифмами примеры решения Онлайн?

Решить задачу как решать пределы с логарифмами примеры решения вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Метод логарифмирования раскрытия неопределенностей.

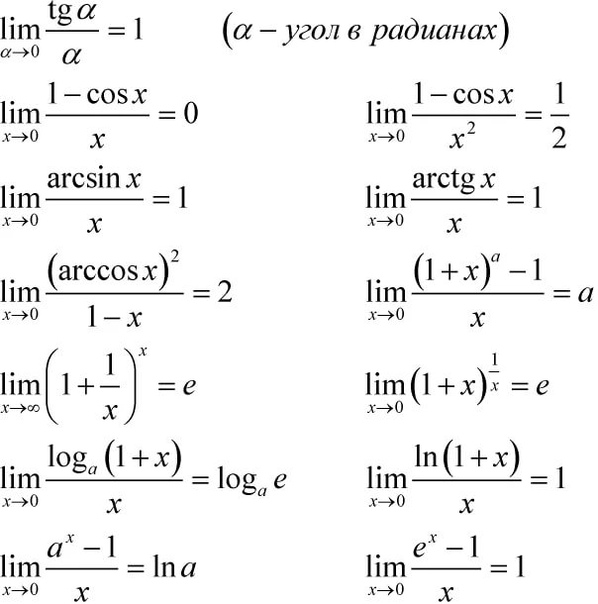2) →1 когда x→0, то предел равен 7/3.

 

Пример 26 Согласно алгоритму, чтобы раскрыть неопределенность ∞/∞ дважды применяем правило Лопиталя.

 

Пример 27 Переходим от неопределенности вида ноль умножить на бесконечность к неопределенности бесконечность разделить на бесконечность, которую раскрываем по правилу Лопиталя через дифференцирование числителя и знаменателя дроби. Внимательно посмотрите схему перехода от одной неопределенности к другой и запомните, что когда имеем произведение логарифма на другую функцию, то в знаменатель переносим последнюю, а не логарифм.

Пример 28 Прямая подстановка дает неопределенность ноль умножить на бесконечность 0*∞

Чтобы свести пример к применению правила Лопиталя в искусственный способ котангенс переносим в знаменатель дроби, а далее заменяем 1/ctg(x)=tg(x). Таким образом получаем особенность в виде доли бесконечно малых функций, раскрываем дифференцированием по Лопиталю и подстановкой x=0.

Раскрытие неопределенностей ∞-∞

Пределы с неопределенностью ∞-∞ также раскрываем по правилу Лопиталя, но предварительно проводим определенные элементарные действия над слагаемыми, чтобы перейти от разности бесконечно больших функций к дроби.
Пример 29 Формулы ниже хорошо иллюстрируют как дважды применяли дифференцирование числителя и знаменателя дроби, чтобы избавиться от неопределенности 0/0.

Пример 30 Имеем неопределенность вида ∞-∞, которую раскрываем путем сведения дробей к общему знаменателю. Далее по правилу Лопиталя вычисляем производные числителя и знаменателя, и так дважды.

И только когда избавляемся неопределенности выполняем подстановку аргумента в предел. Считаем, чтобы начать решать примеры на правило Лопиталя, 30 приведенных примеров вполне достаточно. Если есть проблемы с расчетными или модулями, то всегда можете обращаться к нам за помощью!

Сложные пределы и методы их решения

В этой статье собраны наиболее интересные и сложные случаи пределов, решение которых требует определенных навыков и знаний. В большинстве случаев, пределы, изучаемые в

базовом курсе высшей математики, просты и решаются в одно-два действия. Однако иногда приходится сталкиваться со сложными примерами пределов, которые чтобы решить
нужно знать хитростные способы. Рассмотрим же их!

Пример 1. Решить предел

Чтобы решить данный предел, необходимы знания по теме первый замечательный предел и эквивалентные бесконечно малые функции. Ну а в начале долгого пути, нам предстоит сделать преобразования в числителе, используя свойства тригонометрических функций, и в знаменателе, используя обманный ход, но обо всем по порядку. Начнем с числителя, представим

в равнозначной записи и запишем числитель уже в новой форме:

Тот факт, что x стремится к нулю, позволяет нам считать что в будущем можно будет использовать свойства эквивалентных бесконечно малых. Поэтому, обращаем внимание на
логарифм, стоящий в знаменателе. Если его немного «отредактировать» и привести к нужному виду, то его смело можно будет использовать для получения эквивалентных
значений. Обращаемся к таблице эквивалентных бесконечно малых величин и видим, что для счастья нам не хватает единицы. Вот здесь-то мы и используем способ (как я его
называю) «искусственного добавления» числа:

Все довольно просто, мы не нарушая баланса выражения, добавили и убавили единицу к косинусу. С учетом всех знаков , преобразуем выражение:

В результате наших действий, мы получили идеальных кандидатов на эквивалентные замены. В числителе вынесли знак минус за скобки, получив тем самым

в знаменателе подготовили выражение с логарифмом. С ними все понятно, что же делать в синусом? Все просто, используем первый замечательный предел и получаем законную
единицу. Вычисляем:

Краткие пояснения к тому, какие эквивалентные замены были произведены, а также как был использован первый предел:

— первый предел, при

Отдельной строкой хотелось бы остановиться на третьей формуле. Как известно, эквивалентная малая для логарифма выглядит следующим образом:

ln(1+x) ~x

В нашем случае, в роли х выступала вся скобка (-(1-cos(5x))).

Далее, мы повторно используем правило, но только уже для случая с косинусом:

при

В нашем случае, cos(x) — это cos(5x) и соответствующая замена была такой:

при

Ну вот и все. Предел был непростым, но интересным, и его решение, надеюсь, было вам понятным.

Замечательные пределы. Примеры решений

Продолжаем наш разговор на тему Пределы и способы их решения. Перед изучением материалов данной страницы настоятельно рекомендую ознакомиться со статьей Пределы. Примеры решений. Из вышеуказанной статьи Вы сможете узнать, что же такое предел, и с чем его едят – это ОЧЕНЬ важно. Почему? Можно не понимать, что такое определители и успешно их решать, можно совершенно не понимать, что такое производная и находить их на «пятёрку». Но вот если Вы не понимаете, что такое предел, то с решением практических заданий придется туго. Также не лишним будет ознакомиться с образцами оформления решений и моими рекомендациями по оформлению. Вся информация изложена в простой и доступной форме.

А для целей данного урока нам потребуются следующие методические материалы:Замечательные пределы и Тригонометрические формулы. Их можно найти на страницеМатематические формулы, таблицы и справочные материалы. Лучше всего методички распечатать – это значительно удобнее, к тому же к ним часто придется обращаться в оффлайне.

Чем же замечательны замечательные пределы? Замечательность данных пределов состоит в том, что они доказаны величайшими умами знаменитых математиков, и благодарным потомкам не приходиться мучаться страшными пределами с нагромождением тригонометрических функций, логарифмов, степеней. То есть при нахождении пределов мы будем пользоваться готовыми результатами, которые доказаны теоретически.

Замечательных пределов существует несколько, но на практике у студентов-заочников в 95% случаев фигурируют два замечательных предела: Первый замечательный предел,Второй замечательный предел. Следует отметить, что это исторически сложившиеся названия, и, когда, например, говорят о «первом замечательном пределе», то подразумевают под этим вполне определенную вещь, а не какой-то случайный, взятый с потолка предел.

Начнем.

Первый замечательный предел

Рассмотрим следующий предел:   (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала).

Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида  , которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что:

 

Данный математический факт носит название Первого замечательного предела.

Нередко в практических  заданиях функции могут быть расположены по-другому, это ничего не меняет:

 – тот же самый первый замечательный предел.

! Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде , то и решать его нужно в таком же виде, ничего не переставляя.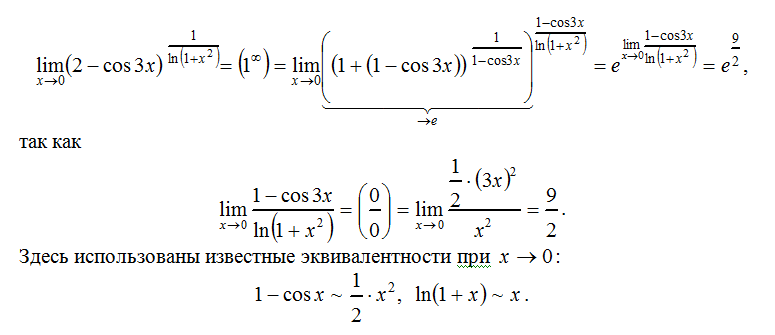

На практике в качестве параметра   может выступать не только переменная  , но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.

Примеры: ,  ,  , 

Здесь  ,  ,  ,  , и всё гуд – первый замечательный предел применим.

А вот следующая запись – ересь:

Почему? Потому-что многочлен   не стремится к нулю, он стремится к пятерке.

Кстати, вопрос на засыпку, а чему равен предел  ? Ответ можно найти в конце урока.

На практике не все так гладко, почти никогда студенту не предложат решить халявный предел   и получить лёгкий зачет. Хммм… Пишу эти строки и пришла в голову очень важная мысль – все-таки «халявные» математические определения и формулы вроде    лучше помнить наизусть, это может оказать неоценимую помощь на зачете, когда вопрос будет решаться между «двойкой» и «тройкой», и преподаватель решит задать студенту какой-нибудь простой вопрос или предложить решить простейший пример («а может он (а) все-таки знает чего?!»).

Переходим к рассмотрению практических примеров:

Пример 1

Найти предел 

Если мы замечаем в пределе синус, то это нас сразу должно наталкивать на мысль о возможности применения первого замечательного предела.

Сначала пробуем подставить 0 в выражение под знак предела (делаем это мысленно или на черновике):

Итак, у нас есть неопределенность вида  , ее обязательно указываем в оформлении решения. Выражение под знаком предела у нас похоже на первый замечательный предел, но это не совсем он, под синусом находится  , а в знаменателе  .

В подобных случаях первый замечательный предел нам нужно организовать самостоятельно, используя искусственный прием. Ход рассуждений может быть таким: «под синусом у нас  , значит, в знаменателе нам тоже нужно получить  ».  А делается это очень просто:

То есть, знаменатель искусственно умножается в данном случае на 7 и делится на ту же семерку. Теперь запись у нас приняла знакомые очертания. Когда задание оформляется от руки, то первый замечательный предел желательно пометить простым карандашом:

Что произошло? По сути, обведенное выражение у нас превратилось в единицу и исчезло в произведении: Теперь только осталось избавиться от трехэтажности дроби: Готово. Окончательный ответ: 

Если не хочется использовать пометки карандашом, то решение можно оформить так:

“ Используем первый замечательный предел  “

Пример 2

Найти предел 

Опять мы видим в пределе дробь и синус. Пробуем подставить в числитель и знаменатель ноль:

Действительно, у нас неопределенность   и, значит, нужно попытаться организовать первый замечательный предел. На уроке Пределы. Примеры решений мы рассматривали правило, что когда у нас есть неопределенность  , то нужно разложить числитель и знаменатель на множители. Здесь – то же самое, степени мы представим в виде произведения (множителей):

Далее, по уже знакомой схеме организовываем первые замечательные пределы. Под синусами у нас  , значит, в числителе тоже нужно получить  :

Аналогично предыдущему примеру, обводим карандашом замечательные пределы (здесь их два), и указываем, что они стремятся к единице:

Собственно, ответ готов:

В следующих примерах, я не буду заниматься художествами в Пэйнте, думаю, как правильно оформлять решение в тетради – Вам уже понятно.

Пример 3

Найти предел 

Подставляем ноль в выражение под знаком передела:

Получена неопределенность  , которую нужно раскрывать. Если в пределе есть тангенс, то почти всегда его превращают в синус и косинус по известной тригонометрической формуле   (кстати, с котангенсом делают примерно то же самое, см. методический материалГорячие тригонометрические формулы на странице Математические формулы, таблицы и справочные материалы).

 В данном случае:

Косинус нуля равен единице, и от него легко избавиться (не забываем пометить, что он стремится к единице):

Таким образом, если в пределе косинус является МНОЖИТЕЛЕМ, то его, грубо говоря, нужно превратить в единицу, которая исчезает в произведении.

Дальше по накатанной схеме, организуем первый замечательный предел:

Здесь все вышло проще, без всяких домножений и делений. Первый замечательный предел тоже превращается в единицу и исчезает в произведении:

В итоге получена бесконечность, бывает и такое.

Пример 4

Найти предел 

Пробуем подставить ноль в числитель и знаменатель:

Получена неопределенность   (косинус нуля, как мы помним, равен единице)

Используем тригонометрическую формулу  . Возьмите на заметку! Пределы с применением этой формулы почему-то встречаются очень часто.

Постоянные множители вынесем за значок предела:

 

Организуем первый замечательный предел:

Здесь у нас только один замечательный предел, который превращается в единицу и исчезает в произведении:

Избавимся от трехэтажности:

Предел фактически решен, указываем, что оставшийся синус стремится к нулю:

Пример 5

Найти предел 

Этот пример сложнее, попробуйте разобраться самостоятельно:

 

Второй замечательный предел

В теории математического анализа доказано, что:

Данный факт носит название второго замечательного предела.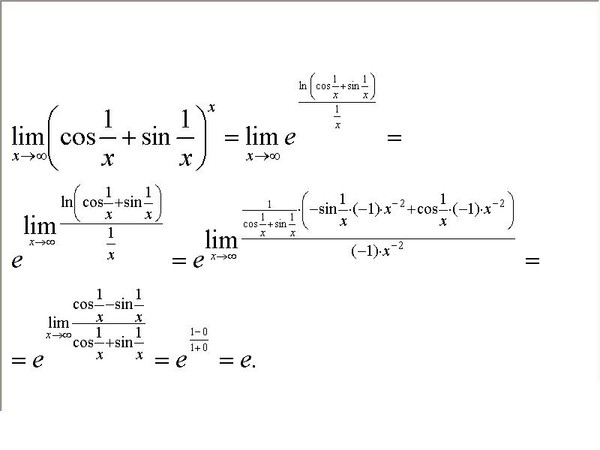

Справка:  – это иррациональное число.

В качестве параметра   может выступать не только переменная  , но и сложная функция.Важно лишь, чтобы она стремилась к бесконечности.

Пример 6

Найти предел 

Когда выражение под знаком предела находится в степени – это первый признак того, что нужно попытаться применить второй замечательный предел.

Но сначала, как всегда, пробуем подставить бесконечно большое число в выражение   , по какому принципу это делается, разобрано на уроке Пределы. Примеры решений.

Нетрудно заметить, что при   основание степени  , а показатель – , то есть имеется, неопределенность вида  :

Данная неопределенность как раз и раскрывается с помощью второго замечательного предела. Но, как часто бывает, второй замечательный предел не лежит на блюдечке с голубой каемочкой, и его нужно искусственно организовать. Рассуждать можно следующим образом: в данном примере параметр  , значит, в показателе нам тоже нужно организовать   . Для этого возводим основание в степень  , и, чтобы выражение не изменилось – возводим в степень  :

Когда задание оформляется от руки, карандашом помечаем:

Практически всё готово, страшная степень превратилась в симпатичную букву  :

При этом сам значок предела перемещаем в показатель.

Далее, отметки карандашом я не делаю, принцип оформления, думаю, понятен.

Пример 7

Найти предел 

Внимание! Предел подобного типа встречается очень часто, пожалуйста, очень внимательно изучите данный пример.

Пробуем подставить бесконечно большое число в выражение, стоящее под знаком предела:

В результате получена неопределенность  . Но второй замечательный предел применим к неопределенности вида  . Что делать? Нужно преобразовать основание степени. Рассуждаем так: в знаменателе у нас  , значит, в числителе тоже нужно организовать  :

Теперь можно почленно разделить числитель на знаменатель:

Вроде бы основание стало напоминать  , но у нас знак «минус» да и тройка какая-то вместо единицы. Поможет следующее ухищрение, делаем дробь трехэтажной:

Таким образом, основание приняло вид  , и, более того, появилась нужная нам неопределенность  . Организуем второй замечательный предел  . Легко заметить, что в данном примере  . Снова исполняем наш искусственный прием: возводим основание степени в  , и, чтобы выражение не изменилось – возводим в обратную дробь  :

Наконец-то долгожданное   устроено, с чистой совестью превращаем его в букву  :

Но на этом мучения не закончены, в показателе у нас появилась неопределенность вида  , раскрывать такую неопределенность мы научились на уроке Пределы. Примеры решений. Делим числитель и знаменатель на  :

Готово.

А сейчас мы рассмотрим модификацию второго замечательного предела. Напомню, что второй замечательный предел выглядит следующим образом:  . Однако на практике время от времени можно встретить его «перевёртыш», который в общем виде записывается так:

Пример 8

Найти предел 

Сначала (мысленно или на черновике) пробуем подставить ноль (бесконечно малое число) в выражение, стоящее под знаком предела:

В результате получена знакомая неопределенность  . Очевидно, что в данном примере  . С помощью знакомого искусственного приема организуем в показателе степени конструкцию  :

Выражение   со спокойной душой превращаем в букву  :

Еще не всё, в показателе у нас появилась неопределенность вида  . Раскладываем тангенс на синус и косинус (ничего не напоминает?):

Косинус нуля стремится к единице (не забываем помечать карандашом), поэтому он просто пропадает в произведении:

А что такое   и к чему оно стремится, нужно уже знать, иначе «двойка»!

Как видите, в практических заданиях на вычисление пределов нередко требуется применять сразу несколько правил и приемов.

В 90-95% на зачете, экзамене Вам встретится первый замечательный предел или второй замечательный предел. Как быть, если попался «экзотический» замечательный предел? (со списком всех замечательных пределов можно ознакомиться в соответствующей методичке). Ничего страшного, практически все выкладки, приёмы решения для первого замечательного предела справедливы и для остальных замечательных пределов. Нужно решать их по аналогии.

Да, так чему же равен предел  ?

Если у Вас получился ответ  , значит в понимании высшей математики не всё так безнадежно = ). 2 = 0 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ$$ lim_limits frac <arcsin x>= 0 $$

В пределе получаем неопределенность ноль делить на ноль $[frac<0><0>]$. Замечаем, что числитель похож на формулу из таблицы эквивалентности пределов. Подставим в него точку $x=0$.

$$ 1- cos (4 cdot 0) = 1-cos 0 = 1 – 1 = 0 $$

Получили, что числитель равен нулю при $x=0$, а это значит допустима замена на бесконечно малую функцию.

Возвращаемся к пределу, подставляя в него полученное выражение для числителя.

Пример 2

Заменяя эквивалентными бесконечно малыми найдите предел $ lim_limits frac<1-cos 4x> $

Решение

Ответ

$$ lim_limits frac<1-cos 4x> = 0 $$

Подставив $x=1$ получаем неопределенность $[ frac<0> <0>] $. 2 = (a-b)(a+b)$ для знаменателя упрощаем его.

Метод решения

Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).

Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.

Применяемые определения и теоремы

Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.

Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым

Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство

Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй. Разумеется, можно менять не все функции а только одну или некоторые из них.

Таблица эквивалентных функций

Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .

Пример 3

Вычислить предел функции используя эквивалентно малые величины $lim_limits frac<sin (x-1)> $

Решение

Эквивалентность при

Равенство при

Предостережение

Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.

В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x , то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0 . Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.

Примеры

Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.

Пример 1

Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 2

Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.

Пример 3

Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0 . Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0 .

Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;

.

Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.

Пример 4

При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞ .

Преобразуем ее к неопределенности вида 0/0 . Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.

В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.

В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .

Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .

Теперь заменим множители эквивалентными функциями:
.

Примечание. Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили ln (1+x) на x, то получили бы ошибку.

Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.

Автор: Олег Одинцов . Опубликовано: 10-05-2019

Функции вида α ( x ) и β ( x ) называются бесконечно малыми, если значение x → x 0 , а lim x → x 0 α ( x ) = 0 и lim x → x 0 β ( x ) = 0 .

Функции вида α ( x ) и β ( x ) называются эквивалентно бесконечно малыми, если значение x → x 0 , а lim x → x 0 α ( x ) β ( x ) = 1 .

Для нахождения пределов используют замены эквивалентных бесконечно малых. Их проводят, основываясь на данных таблицы.

Таблица эквивалентных бесконечно малых

Когда имеем α ( x ) как бесконечно малую функцию со значением x → x 0 .

sin ( α ( x ) )	эквивалентна	α ( x )
t g ( α ( x ) )	эквивалентна	α ( x )
a r c sin ( α ( x ) )	эквивалентна	α ( x )
a r c t g ( α ( x ) )	эквивалентна	α ( x )
1 – cos ( α ( x ) )	эквивалентна	α ( x ) 2 2
ln ( 1 + α ( x ) )	эквивалентна	α ( x )
α α ( x ) – 1	эквивалентна	α ( x ) ln α
1 + α ( x ) p – 1	эквивалентна	p α ( x )
1 + α ( x ) 1 p – 1	эквивалентна	α ( x ) p

Для доказательства эквивалентности основываются на равенстве lim x → x 0 α ( x ) β ( x ) = 1 .

Доказать эквивалентность бесконечно малых величин ln ( 1 + α ( x ) ) и α ( x ) .

Необходимо вычислить предел отношения данных величин lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) .

При использовании одно свойства логарифмов, получаем, что

lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) = 1 α ( x ) ln ( 1 + α ( x ) ) = ln ( 1 + α ( x ) ) 1 α ( x )

Запишем предел вида

lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) = ln ( 1 + α ( x ) ) 1 α ( x )

Логарифмическая функция считается непрерывной на своей области определения, тогда необходимо применять свойство предела непрерывных функций, причем сменить знак перед предельным переходом и логарифмом. Получаем, что

lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) = ln ( 1 + α ( x ) ) 1 α ( x ) = ln lim x → x 0 1 + α ( x ) 1 a ( x )

Необходимо произвести замену переменных t = α ( x ) . Имеем, что α ( x ) является бесконечно малой функцией с x → x 0 , тогда lim x → x 0 a ( x ) = 0 . Отсюда следует, что t → 0 .

Предел принимает вид

lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) = ln ( 1 + α ( x ) ) 1 α ( x ) = ln lim x → x 0 1 + α ( x ) 1 a ( x ) = = ln lim t → 0 ( 1 + t ) 1 t = ln ( e ) = 1

Ответ: lim x → x 0 ln ( 1 + α ( x ) ) α ( x ) = 1

Получение 1 говорит о том, что заданные бесконечно малые функции эквивалентны. При последнем переходе применяли второй замечательный предел.

Таблица эквивалентных бесконечно малых необходима для ускорения процесса вычисления.

Вычислить предел функции lim x → 0 1 – cos 4 x 2 16 x 4 .

Производится подстановка значений

lim x → 0 1 – cos 4 x 2 16 x 4 = 1 – cos ( 4 · 0 2 ) 16 · 0 4 = ” open=” 0 0

Полученная неопределенность говорит о том, что функция бесконечно малая и для ее разрешения необходимо обратиться к таблице эквивалентных бесконечно малых. Тогда получаем, что функция 1 – cos α ( x ) является эквивалентной α ( x ) 2 2 , тогда имеем, что 1 – cos ( 4 x 2 ) является эквивалентной 4 x 2 2 2 .

После того, как была произведена замена бесконечно малой функции на ее эквивалентную, предел запишется так:

lim x → 0 1 – cos 4 x 2 16 x 4 = ” open=” 0 0 = lim x → 0 ( 4 x 2 ) 2 2 16 x 4 = lim x → 0 16 x 4 32 x 4 = 1 2

Без таблицы эквивалентных бесконечно малых не имели бы возможность воспользоваться правилом Лопиталя. Получаем, что

lim x → 0 1 – cos 4 x 2 16 x 4 = ” open=” 0 0 = lim x → 0 1 – cos ( 4 x 2 ) ‘ 16 x 4 ‘ = lim x → 0 8 x sin ( 4 x 2 ) 64 x 3 = = lim x → 0 sin ( 4 x 2 ) 8 x 2 = ” open=” 0 0 = lim x → 0 sin 4 x 2 ‘ 8 x 2 ‘ = lim x → 0 8 x cos ( 4 x 2 ) 16 x = 1 2 lim x → 0 cos ( 4 x 2 ) = 1 2

Можно было произвести преобразование функции с применением тригонометрических формул с применением первого замечательного предела. Запишем, что

lim x → 0 1 – cos ( 4 x 2 ) 16 x 4 = ” open=” 0 0 = lim x → 0 2 sin 2 ( 2 x 2 ) 16 x 4 = = lim x → 0 1 2 · sin ( 2 x 2 ) 2 x 2 · sin ( 2 x 2 ) 2 x 2 = 1 2 lim x → 0 sin ( 2 x 2 ) 2 x 2 · lim x → 0 sin ( 2 x 2 ) 2 x 2 = = п у с т ь t = 2 x 2 , t → 0 п р и x → 0 = 1 2 lim t → 0 sin ( t ) t · lim t → 0 sin ( t ) t = 1 2 · 1 · 1 = 1 2

Первый замечательный предел. Решение первого замечательного предела. Примеры

Первый замечательный предел (основной тригонометрический предел) имеет вид \lim\limits_{x \to 0} \frac{{\sin x}}{x} = 1. Используя данный предел, можно получить ряд других тригонометрических пределов: {\lim\limits_{x \to 0} \frac{{\tg x}}{x} = 1,\;\;\;} {\lim\limits_{x \to 0} \frac{{\arcsin x}}{x} = 1,\;\;\;} {\lim\limits_{x \to 0} \frac{{\arctg x}}{x} = 1.}

Пример 1

Вычислить предел \lim\limits_{x \to 0} \large\frac{{7x}}{{\sin 5x}}\normalsize .

Решение.
L = {\lim\limits_{x \to 0} \frac{{7x}}{{\sin 5x}} } = {\lim\limits_{x \to 0} \frac{{5 \cdot 7x}}{{5\sin 5x}} } = {\frac{7}{5}\lim\limits_{x \to 0} \frac{{5x}}{{\sin 5x}} } = {\frac{7}{5}\lim\limits_{x \to 0} \frac{1}{{\large\frac{{\sin 5x}}{{5x}}\normalsize}} } = {\frac{7}{5}\frac{{\lim\limits_{x \to 0} 1}}{{\lim\limits_{x \to 0} \large\frac{{\sin 5x}}{{5x}}\normalsize}}.2}}} } = {- 2\lim\limits_{x \to 0} \frac{{\sin x}}{x} \cdot \lim\limits_{x \to 0} \frac{{\sin 4x}}{x} } = {- 2 \cdot 1 \cdot \lim\limits_{2x \to 0} \frac{{4\sin 4x}}{{4x}} } = {- 2 \cdot 4\lim\limits_{x \to 0} \frac{{\sin 4x}}{{4x}} = — 8.}

Пример 3

Вычислить предел \lim\limits_{x \to 0} \large\frac{{\sin7x — \sin 5x}}{{\sin x}}\normalsize .

Решение.
Используем следующее тригонометрическое тождество: \sin x — \sin y = 2\sin \frac{{x — y}}{2}\cos \frac{{x + y}}{2}. Получаем \lim\limits_{x \to 0} \frac{{\sin7x — \sin 5x}}{{\sin x}} = {\lim\limits_{x \to 0} \frac{{2\sin \large\frac{{7x — 5x}}{2}\normalsize\cos \large\frac{{7x + 5x}}{2}\normalsize}}{{\sin x}} } = {\lim\limits_{x \to 0} \frac{{2\sin x\cos 6x}}{{\sin x}} } = {\lim\limits_{x \to 0} \left( {2\cos 6x} \right).} Поскольку \cos{6x} является непрерывной функцией при x = 0 , то \lim\limits_{x \to 0} \left( {2\cos 6x} \right) = {2\lim\limits_{x \to 0} \cos 6x } = {2 \cdot \cos \left( {4 \cdot 0} \right) = 2 \cdot 1 = 2.2}} = \frac{1}{{\sqrt 2 }}.} Здесь мы учли, что предел остается неизменным при замене предельного перехода x \to 0 на \large\frac {x}{2}\normalsize \to 0 .

график, основание, функции, предел, формулы и область определения

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.

Если , то .

Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.

Вконтакте

Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:

Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.

Приведем некоторые тождества:

Приведем основные алгебраические выражения:

;

.

Внимание! может существовать только при x>0, x≠1, y>0.

Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.

Обозначения:

• lg x — десятичный;
• ln x — натуральный.

Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.

График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:

Для удобства мы можем взять пять опорных точек:

;

;

.

;

.

Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.

Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .

Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .

Предел натурального log

Изучая график, возникает вопрос — как ведет себя функция при y

Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х

Предел натурального log можно записать таким образом:

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством (только вместо «с» у нас выражение):

Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1 . Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то , получаем:

Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если , то , получаем:

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0) &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество a log a b = b (a > 0, a ≠ 1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического “тождества” при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм произведения и логарифм частного log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании “слева направо” происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного – расширение ОДЗ.

Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

Log a (f (x) 2 = 2 log a f (x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).

Таблица формул, связанных с логарифмами

a log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)

Натуральный логарифм

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x ).

Натуральный логарифм – это логарифм по основанию , где e – иррациональная константа, равная приблизительно 2,718281 828 . Натуральный логарифм обычно обозначают как ln(x ), log e (x ) или иногда просто log(x ), если основание e подразумевается.

Натуральный логарифм числа x (записывается как ln(x) ) – это показатель степени , в которую нужно возвести число e , чтобы получить x . Например, ln(7,389…) равен 2, потому что e 2 =7,389… . Натуральный логарифм самого числа e (ln(e) ) равен 1, потому что e 1 = e , а натуральный логарифм 1 (ln(1) ) равен 0, поскольку e 0 = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a . Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа , о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции :

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности . Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

История

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia , опубликованной в 1668 году , хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. Ранее его называли гиперболическим логарифмом, поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.

Конвенции об обозначениях

Натуральный логарифм принято обозначать через «ln(x )», логарифм по основанию 10 – через «lg(x )», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x )» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln 2 ln 3 4x 5 = [ ln( 3 )] 2 .

Англо-американская система

Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 – «log 10 (x )».

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x )» (или изредка «log e (x )»), когда они имеют в виду натуральный логарифм, а запись «log(x )» у них означает log 10 (x ).

log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:

Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.

Определение

Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т. е. как интеграл :

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x −1)/(x +1) и x > 0.

Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n – число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) – вычислительная сложность умножения двух n -значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e x для любого произвольного комплексного числа x , при этом используется бесконечный ряд с комплексным x . Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .

Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным – любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.

См. также

• Джон Непер – изобретатель логарифмов

Примечания

1. Mathematics for physical chemistry . – 3rd. – Academic Press, 2005. – P. 9. – ISBN 0-125-08347-5 , Extract of page 9
2. J J O”Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
3. Cajori Florian A History of Mathematics, 5th ed . – AMS Bookstore, 1991. – P. 152. – ISBN 0821821024
4. Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.

Что такое логарифм?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно “не очень…”
И для тех, кто “очень даже…”)

Что такое логарифм? Как решать логарифмы? Эти вопросы многих выпускников вводят в ступор. Традиционно тема логарифмов считается сложной, непонятной и страшной. Особенно – уравнения с логарифмами.

Это абсолютно не так. Абсолютно! Не верите? Хорошо. Сейчас, за какие-то 10 – 20 минут вы:

1. Поймете, что такое логарифм .

2. Научитесь решать целый класс показательных уравнений. Даже если ничего о них не слышали.

3. Научитесь вычислять простые логарифмы.

Причём для этого вам нужно будет знать только таблицу умножения, да как возводится число в степень…

Чувствую, сомневаетесь вы… Ну ладно, засекайте время! Поехали!

Для начала решите в уме вот такое уравнение:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся – с интересом!)

можно познакомиться с функциями и производными.

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) “b” по его основанию “a” считается степень “c”, в которую необходимо возвести основание “a”, чтобы в итоге получить значение “b”. Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное – понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание “a” всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь “1” и “0” в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и “с” должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел – это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени – это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема “логарифмы”. Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 – оно является логарифмическим неравенством, так как неизвестное значение “х” находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример – логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 – log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула “свойством степени логарифма”. Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов – примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 – как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы “Натуральные логарифмы”.

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Исчисление I – Пределы бесконечности, часть II

Показать общее уведомление Показать мобильное уведомление Показать все заметки Скрыть все заметки

Это немного заранее, но я хотел сообщить всем, что мои серверы будут проходить техническое обслуживание 17 и 18 мая с 8:00 AM CST до 14:00 PM CST.Будем надеяться, что единственное неудобство будет заключаться в периодической потере / разрыве соединения, которую следует исправить, просто перезагрузив страницу. В остальном обслуживание (скрестив пальцы) должно быть «невидимым» для всех.

Пол
6 мая 2021 г.

Похоже, вы используете устройство с “узкой” шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-8: Пределы на бесконечности, Часть II

В предыдущем разделе мы рассмотрели пределы бесконечности многочленов и / или рационального выражения, включающего многочлены.{- x}} = \ infty \]

Суть этого примера заключалась в том, чтобы указать, что если показатель экспоненты стремится к бесконечности в пределе, то экспоненциальная функция также стремится к бесконечности в пределе. Точно так же, если показатель степени стремится к минус бесконечности в пределе, тогда экспонента стремится к нулю в пределе.

Также обратите внимание, что в последнем разделе значение лимита не зависело от того, перешли мы на плюс или минус бесконечность. В приведенном выше примере мы уже видели, что изменение знака бесконечности может изменить ответ, поэтому не зацикливайтесь на каких-либо предположениях, которые вы могли сделать из работы в предыдущем разделе!

Вот несколько примеров, иллюстрирующих эти идеи.{- 15x}}} \ right) \) Показать все решения Скрыть все решения

Итак, единственное различие между этими двумя пределами заключается в том, что в первом мы берем предел, когда идем к плюсовой бесконечности, а во втором – к минус бесконечности. К этому моменту мы смогли «повторно использовать» работу из первого предела, по крайней мере, в части второго предела. С экспонентами, которые часто не выполняются, мы будем рассматривать каждую из этих задач как отдельные проблемы.{- 15x}}} \ right) = \ infty – \ infty + \ infty + 0 – 0 \]

Последние два термина не представляют проблемы (однако они будут в следующей части; вы это понимаете?). Однако первые три представляют собой проблему, поскольку представляют нам еще одну неопределенную форму.

При работе с полиномами мы вычленили член с наибольшим показателем в нем. Давайте сделаем то же самое здесь. Однако теперь нам нужно иметь дело как с положительными, так и с отрицательными показателями, а также с тем, что мы подразумеваем под «наибольшим» показателем.{- 25x}}} \ right)} \ right] \]

Обратите внимание, что при выполнении этого факторизации все оставшиеся экспоненты теперь имеют отрицательные показатели, и мы знаем, что для этого предела (, т. {- 15x}}} \ right) = 0 – 0 + 0 + \ infty – \ infty \]

Итак, последние два члена представляют собой проблему, поскольку они снова оставляют нам неопределенную форму.{- 15x}}} \ right) = – \ infty \]

Итак, имея дело с суммами и / или разностями экспоненциальных функций, мы ищем экспоненту с «наибольшим» показателем и помним здесь, что «наибольший» означает показатель, наиболее удаленный от нуля. Также помните, что если мы смотрим на предел на плюс бесконечность, только экспоненты с положительными показателями будут вызывать проблемы, поэтому это единственные термины, на которые мы обращаем внимание при определении наибольшего показателя. Точно так же, если мы смотрим на предел на минус бесконечности, тогда только экспоненты с отрицательными показателями будут вызывать проблемы, и поэтому только они рассматриваются при определении наибольшего показателя.

Наконец, как вы могли догадаться из предыдущего примера, имея дело с суммой и / или разностью экспонент, все, что нам нужно сделать, это посмотреть на наибольшую экспоненту, чтобы определить поведение всего выражения. Опять же, помня, что если предел равен плюс бесконечности, мы смотрим только экспоненты с положительными показателями, а если мы смотрим на предел минус бесконечности, мы смотрим только экспоненты с отрицательными показателями.

Давайте теперь рассмотрим некоторые рациональные функции, включающие экспоненты.{- x}}}} \) Показать решение

Основная концепция, используемая при работе с этой проблемой, такая же, как и в случае с рациональными выражениями в предыдущем разделе. Мы смотрим на знаменатель и определяем экспоненциальную функцию с «наибольшим» показателем, которую затем вычтем из числителя и знаменателя. Мы будем использовать те же рассуждения, что и в предыдущем примере, для определения «наибольшего» показателя. В этом случае, поскольку мы смотрим на предел на плюс бесконечность, мы смотрим только на экспоненты с положительными показателями.{- x}}}} \) Показать решение

В этом случае мы собираемся в пределе минус бесконечность, и поэтому мы будем смотреть на экспоненты в знаменателе с отрицательными показателями при определении «наибольшего» показателя. Однако в этой проблеме есть только один, поэтому мы будем его использовать.

Опять же, не забывайте смотреть только на знаменатель. НЕ используйте экспоненту в числителе, даже если она «больше», чем экспонента в знаменателе. Мы всегда смотрим только на знаменатель, когда определяем, какой член вычитать вне зависимости от того, что происходит в числителе.+}} \ ln x = – \ infty \ hspace {0,5 дюйма} \ hspace {0,25 дюйма} \ mathop {\ lim} \ limits_ {x \ to \ infty} \ ln x = \ infty \]

Обратите внимание, что нам пришлось установить правостороннее ограничение для первого, поскольку мы не можем подставить отрицательные \ (x \) в логарифм. Это означает, что нормального предела не будет, поскольку мы должны смотреть на \ (x \) ’с обеих сторон рассматриваемой точки, а \ (x \)’ слева от нуля отрицательны.

Из предыдущего примера мы видим, что если аргумент журнала (то, что мы берем журнал) стремится к нулю справа ( i.е. {- 1}} x \) Показать решение

Как отмечалось выше, все, что нам действительно нужно сделать, это посмотреть на график обратной тангенса.{- 1}} \ left ({\ frac {1} {x}} \ right) = – \ frac {\ pi} {2} \]

Чтобы увидеть точное и математическое определение этого вида предела, см. Раздел «Определение предела» в конце этой главы.

Натуральные логарифмы

Логарифмы с основанием \ (e, \), где \ (e \) – иррациональное число, значение которого равно \ (2.718281828 \ ldots, \), называются натуральными логарифмами. Натуральный логарифм \ (x \) обозначается \ (\ ln x. \) Натуральные логарифмы широко используются в математике, физике и технике.y} = \ ln x, \; \;} \ Rightarrow
{y \ ln a = \ ln x, \; \;} \ Rightarrow
{y = \ frac {1} {{\ ln a}} \ ln x, \; \;} \ Rightarrow
{{\ log _a} x = \ frac {{\ ln x}} {{\ ln a}}.}
\]

Последняя формула выражает логарифм числа \ (x \) с основанием \ (a \) через натуральный логарифм этого числа. Положив \ (x = e, \), мы имеем

\ [{\ log _a} e = \ frac {1} {{\ ln a}} \ ln e = \ frac {1} {{\ ln a}}. \]

Если \ (a = 10, \), получаем:

\ [{{\ log _ {10}} x = \ lg x = M \, {\ ln x}, \; \; \;} \ kern-0.3pt
{\ text {where} \; \; M = \ frac {1} {{\ ln a}} = \ lg e} \ приблизительно {0,43429 \ ldots}
\]

Обратная связь:

\ [{\ ln x = \ frac {1} {M} \ lg x, \; \; \;} \ kern-0.3pt
{\ text {where} \; \; \ frac {1} {M }} = {\ ln 10} \ приблизительно {2.30258 \ ldots}
\]

Графики функций \ (y = \ ln x \) и \ (y = \ lg x \) показаны на рисунке \ (1. \)

Рисунок 1.

---

Решенные проблемы

Щелкните или коснитесь проблемы, чтобы увидеть решение.

Пример 1

Вычислите \ (\ ln {\ large \ frac {1} {{\ sqrt e}} \ normalsize}.\)

Пример 2

Запишем одним логарифмом: \ ({\ large \ frac {1} {3} \ normalsize} \ ln \ left ({x – 1} \ right) – {{\ large \ frac {1} {2} \ normalsize} \ ln \ left ({x + 1} \ right)} + {2 \ ln x}. \)

Пример 3

Нарисуйте график функции \ (y = \ ln \ left ({x + 1} \ right) – 1. \)

Пример 4

Нарисуйте график функции \ (y = \ left | {\ ln x} \ right |. \)

Пример 5

Нарисуйте график функции \ (y = \ left | {\ ln \ left | x \ right |} \ right |.2} \ sqrt [3] {{x – 1}}}} {{\ sqrt {x + 1}}}.}
\]

1.5 Экспоненциальные и логарифмические функции – Исчисление Том 1

Цели обучения

• Определите форму экспоненциальной функции.
• Объясните разницу между графиками и.
• Осознайте значение числа.
• Определите форму логарифмической функции.
• Объясните связь между экспоненциальными и логарифмическими функциями.
• Опишите, как вычислить логарифм с различным основанием.
• Укажите гиперболические функции, их графики и основные тождества.

В этом разделе мы исследуем экспоненциальные и логарифмические функции. Мы используем свойства этих функций для решения уравнений, включающих экспоненциальные или логарифмические члены, и изучаем значение и важность числа. Мы также определяем гиперболические и обратные гиперболические функции, которые включают комбинации экспоненциальных и логарифмических функций. (Обратите внимание, что мы представляем альтернативные определения экспоненциальных и логарифмических функций в главе «Применение интеграций» и доказываем, что функции имеют одинаковые свойства в обоих определениях.)

Экспоненциальные функции возникают во многих приложениях. Один из распространенных примеров – рост населения.

Например, если популяция начинается с особей, а затем растет с ежегодной скоростью, ее популяция через 1 год составляет

. .

Население через 2 года –

.

В целом его население по прошествии лет

. ,

, который является экспоненциальной функцией. В более общем смысле, любая функция вида, где, является экспоненциальной функцией с основанием и экспонентой .Показательные функции имеют постоянные основания и переменные показатели. Обратите внимание, что функция формы для некоторой константы – это не экспоненциальная функция, а степенная функция.

Чтобы увидеть разницу между экспоненциальной функцией и степенной функцией, мы сравниваем функции и. На (Рисунок) мы видим, что оба и приближаются к бесконечности как. В конце концов, однако, становится больше чем и растет быстрее, чем. В обратном направлении, как, тогда как. Линия представляет собой горизонтальную асимптоту для.

На (рис.) Мы построили график обоих, чтобы показать, чем графики различаются.

Вычисление экспоненциальных функций

Напомним свойства показателя степени: если это положительное целое число, то мы определяем (с множителем). Если это отрицательное целое число, то для некоторого положительного целого числа и мы определяем. Кроме того, определяется как 1. Если – рациональное число, то, где и – целые числа и. Например, . Однако как определяется, если это иррациональное число? Например, что мы подразумеваем под? Это слишком сложный вопрос, чтобы мы могли полностью ответить прямо сейчас; однако мы можем сделать приближение.На (Рисунок) мы перечисляем некоторые подходящие рациональные числа, а также представлены значения для каждого рационального числа. Мы утверждаем, что если мы выбираем рациональные числа, которые становятся все ближе и ближе к, значения становятся все ближе и ближе к некоторому числу. Мы определяем это число как.

Значения для списка рациональных чисел, аппроксимирующих

	1,4	1,41	1,414	1,4142	1,41421	1.414213
	2,639	2.65737	2,66475	2,665119	2,665138	2,665143

Рост бактерий

Решение

Количество бактерий через 6 часов определяется бактериями. Количество бактерий через 10 часов определяется бактериями. Количество бактерий через 24 часа определяется бактериями.

Учитывая экспоненциальную функцию, вычислить и.

Решение

.

Особый тип экспоненциальной функции часто появляется в реальных приложениях. Чтобы описать это, рассмотрим следующий пример экспоненциального роста, который возникает из-за начисления сложных процентов на сберегательный счет. Предположим, человек вкладывает доллары на сберегательный счет с годовой процентной ставкой, начисляемой ежегодно. Сумма через 1 год

.

Сумма денег через 2 года

.

В более общем плане сумма по прошествии лет составляет

.

Если деньги накапливаются 2 раза в год, сумма денег через полгода составляет

.

Сумма денег через 1 год

.

По прошествии лет количество денег на счету

.

В более общем смысле, если деньги накапливаются раз в год, сумма денег на счете через несколько лет определяется функцией

.

Что происходит как? Для ответа на этот вопрос допустим и пишем

,

и изучите поведение as, используя таблицу значений ((рисунок)).

Значения as

	10	100	1000	10 000	100 000	1 000 000
	2,5937	2,7048	2,71692	2,71815	2,718268	2,718280

Глядя на эту таблицу, кажется, что число приближается к числу от 2,7 до 2,8 as. На самом деле, действительно приближается к некоторому числу как.Мы звоним по этому номеру. С точностью до шести знаков после запятой,

.

Буква была впервые использована для обозначения этого числа швейцарским математиком Леонардом Эйлером в 1720-х годах. Хотя Эйлер не открыл число, он показал много важных связей между логарифмическими функциями. Мы до сих пор пользуемся этой нотацией, чтобы отдать дань уважения работе Эйлера, поскольку она встречается во многих областях математики и потому, что мы можем использовать ее во многих практических приложениях.

Возвращаясь к нашему примеру со сберегательным счетом, мы можем сделать вывод, что если человек кладет доллары на счет с годовой процентной ставкой, непрерывно начисляемой, тогда.Эта функция может быть вам знакома. Поскольку в приложениях часто возникают функции, включающие основание, мы называем функцию естественной экспоненциальной функцией . Эта функция интересна не только из-за определения числа, но также, как обсуждается далее, ее график имеет важное свойство.

Так как мы знаем, увеличивается. На (Рисунок) мы показываем график вместе с касательной линии к графику at. Мы дадим точное определение касательной в следующей главе; но неформально мы говорим, что касательная линия к графику at – это линия, которая проходит через точку и имеет тот же «наклон», что и в этой точке.Функция является единственной экспоненциальной функцией с касательной, имеющей наклон 1. Как мы увидим позже в тексте, наличие этого свойства делает естественную экспоненциальную функцию простейшей экспоненциальной функцией для использования во многих случаях.

Рис. 3. График имеет касательную с наклоном 1 при.

Используя наше понимание экспоненциальных функций, мы можем обсудить их обратные, то есть логарифмические функции. Они пригодятся, когда нам нужно рассмотреть любое явление, которое варьируется в широком диапазоне значений, например pH в химии или децибелы в уровнях звука.

Показательная функция взаимно однозначна, с доменом и диапазоном. Следовательно, у него есть обратная функция, называемая логарифмической функцией с основанием . Для любого логарифмическая функция с основанием, обозначенная, имеет домен и диапазон и удовлетворяет

если и только если .

Например,

Кроме того, поскольку и являются обратными функциями,

.

Наиболее часто используемая логарифмическая функция – это функция. Поскольку в основе этой функции лежит натуральное число, она называется натуральным логарифмом .Здесь мы используем обозначения или для обозначения. Например,

.

Поскольку функции и противоположны друг другу,

,

и их графики симметричны относительно линии ((Рисунок)).

Рис. 4. Функции и инвертируются друг с другом, поэтому их графики симметричны относительно линии.

На этом сайте вы можете увидеть пример десятичной логарифмической шкалы.

В общем, для любого основания функция симметрична относительно линии с функцией. Используя этот факт и графики экспоненциальных функций, мы построим графики функций для нескольких значений ((Рисунок)).

Рисунок 5: Графики показаны для.

Прежде чем решать некоторые уравнения, включающие экспоненциальные и логарифмические функции, давайте рассмотрим основные свойства логарифмов.

Правило: свойства логарифмов

Если, и – любое действительное число, то

Решение уравнений с экспоненциальными функциями

Решите каждое из следующих уравнений относительно.

Решить.

Решение

Решение уравнений с логарифмическими функциями

Решите каждое из следующих уравнений относительно.

Решить.

Решение

Оценивая логарифмическую функцию с помощью калькулятора, вы могли заметить, что единственными параметрами являются или log, называемый десятичным логарифмом , или ln, который является натуральным логарифмом. Однако экспоненциальные функции и логарифмические функции могут быть выражены с помощью любого желаемого основания. Если вам нужно использовать калькулятор для вычисления выражения с другой базой, вы можете сначала применить формулы замены базы.Используя это изменение основания, мы обычно записываем данную экспоненциальную или логарифмическую функцию в терминах естественных экспоненциальных и натуральных логарифмических функций.

Проба

Для первой формулы замены основания мы начнем с использования степенного свойства логарифмических функций. Мы знаем это по любой базе. Следовательно,

.

Кроме того, мы знаем, что и являются обратными функциями. Следовательно,

.

Объединяя эти два последних равенства, мы заключаем, что.

Чтобы доказать второе свойство, покажем, что

.

Пусть, и. Мы это покажем. По определению логарифмических функций мы знаем, что и. Из предыдущих уравнений мы видим, что

.

Следовательно,. Поскольку экспоненциальные функции взаимно однозначны, мы можем заключить, что.

□

Пеленальные столики

Используйте вычислительную утилиту для вычисления с использованием формулы изменения базы, представленной ранее.

Решение

Используйте второе уравнение с и:

.

Используйте формулу замены базы и вычислительную утилиту для оценки.

Вступление к главе: Шкала Рихтера для землетрясений

Рисунок 6: (кредит: модификация работы Робба Ханнавакера, NPS)

В 1935 году Чарльз Рихтер разработал шкалу (ныне известную как шкала Рихтера ) для измерения силы землетрясения. Шкала представляет собой логарифмическую шкалу с основанием 10, и ее можно описать следующим образом: Рассмотрим одно землетрясение с магнитудой по шкале Рихтера и второе землетрясение с магнитудой по шкале Рихтера. Предположим, это означает, что землетрясение магнитуды сильнее, но насколько оно сильнее, чем другое землетрясение? Одним из способов измерения интенсивности землетрясения является использование сейсмографа для измерения амплитуды сейсмических волн.Если – амплитуда, измеренная для первого землетрясения, и – это амплитуда, измеренная для второго землетрясения, то амплитуды и магнитуды двух землетрясений удовлетворяют следующему уравнению:

.

Рассмотрим землетрясение силой 8 баллов по шкале Рихтера и землетрясение силой 7 баллов по шкале Рихтера. Затем

.

Следовательно,

,

, что подразумевает или. Поскольку это в 10 раз больше, мы говорим, что первое землетрясение в 10 раз сильнее второго землетрясения.С другой стороны, если одно землетрясение силой 8 баллов по шкале Рихтера, а другое – 6 баллов, то относительная интенсивность двух землетрясений удовлетворяет уравнению

.

Следовательно,. То есть первое землетрясение в 100 раз сильнее второго.

Как мы можем использовать логарифмические функции для сравнения относительной силы землетрясения магнитудой 9 баллов в Японии в 2011 году и землетрясения магнитудой 7,3 на Гаити в 2010 году?

Решение

Для сравнения землетрясений в Японии и на Гаити мы можем использовать уравнение, представленное ранее:

.

Таким образом, и мы делаем вывод, что землетрясение в Японии было примерно в 50 раз более интенсивным, чем землетрясение на Гаити.

Сравните относительную силу землетрясения магнитудой 8,4 и землетрясения магнитудой 7,4.

Землетрясение магнитудой 8,4 примерно в 10 раз сильнее землетрясения магнитудой 7,4.

Гиперболические функции определены в терминах определенных комбинаций и. Эти функции естественным образом возникают в различных инженерных и физических приложениях, включая изучение волн на воде и колебаний упругих мембран.Другое распространенное использование гиперболической функции – это представление висящей цепи или троса, также известного как цепная связь ((рисунок)). Если мы введем систему координат так, чтобы нижняя точка цепи лежала вдоль оси -оси, мы можем описать высоту цепи в терминах гиперболической функции. Сначала мы определяем гиперболические функции.

Рис. 7. Форму шелковой нити в паутине можно описать с помощью гиперболической функции. Такая же форма применима к цепи или тросу, подвешенным на двух опорах только под собственным весом.(Источник: «Mtpaley», Wikimedia Commons)

Определение

Гиперболический косинус

Гиперболический синус

Гиперболический тангенс

Гиперболический косеканс

Гиперболический секанс

Гиперболический котангенс

Имя cosh рифмуется со словом «gosh», тогда как имя sinh произносится как «cinch». Tanh , sech , csch и coth произносятся как tanch, seech, coseech и cotanch соответственно.

Используя определение и принципы физики, можно показать, что высота подвесной цепи, такой как показанная на (Рисунок), может быть описана функцией для определенных констант и.

Но почему эти функции называются гиперболическими функциями ? Чтобы ответить на этот вопрос, подумайте о количестве. Используя определение и, мы видим, что

.

Это тождество является аналогом тригонометрического тождества. Здесь для заданного значения точка лежит на единичной гиперболе ((Рисунок)).

Рисунок 8 – Гипербола единиц.

Обратные гиперболические функции

Из графиков гиперболических функций мы видим, что все они взаимно однозначны, кроме и. Если мы ограничим области определения этих двух функций интервалом, тогда все гиперболические функции взаимно однозначны, и мы сможем определить обратные гиперболические функции. Поскольку сами гиперболические функции включают экспоненциальные функции, обратные гиперболические функции включают логарифмические функции.

Определение

Обратные гиперболические функции

Давайте посмотрим, как вывести первое уравнение.Остальные следуют аналогичным образом. Предполагать . Тогда, и, по определению функции гиперболического синуса,. Следовательно,

.

Умножая это уравнение на, получаем

.

Это можно решить как квадратное уравнение с решением

.

Так как единственное решение – это решение с положительным знаком. Применяя натуральный логарифм к обеим частям уравнения, мы заключаем, что

.

Вычисление обратных гиперболических функций

Оцените каждое из следующих выражений.

Решение

Оценить.

Решение

.

Для следующих упражнений оцените указанные экспоненциальные функции с точностью до двух значащих цифр после запятой.

Решение

а. 125 г. 2.24 с. 9,74

Решение

а. 0,01 б. 10000 с. 46,42

Для следующих упражнений сопоставьте экспоненциальное уравнение с правильным графиком.

5. 6. 7. 8. 9. 10.

Для следующих упражнений нарисуйте график экспоненциальной функции. Определите область, диапазон и горизонтальную асимптоту.

11.

Решение

Область: все действительные числа, Диапазон:, Горизонтальная асимптота на

12.

13.

Решение

Область: все действительные числа, Диапазон:, Горизонтальная асимптота на

14.

15.

Решение

Область: все действительные числа, Диапазон:, Горизонтальная асимптота на

16.

17.

Решение

Область: все действительные числа, Диапазон:, Горизонтальная асимптота на

Для следующих упражнений запишите уравнение в эквивалентной экспоненциальной форме.

18.

19.

Решение

20.

21.

Решение

22.

23.

Решение

24.

25.

Решение

Для следующих упражнений запишите уравнение в эквивалентной логарифмической форме.

26.

27.

Решение

28.

29.

Решение

30.

31.

Решение

32.

33.

Решение

34.

35.

Решение

Для следующих упражнений используйте данные графики логарифмических функций, чтобы определить их область определения, диапазон и вертикальную асимптоту.

36.

38.

40.

В следующих упражнениях используйте свойства логарифмов, чтобы записать выражения в виде суммы, разности и / или произведения логарифмов.

42.

43.

Решение

44.

45.

Решение

46.

47.

Решение

Для следующих упражнений точно решите экспоненциальное уравнение.

48.

49.

Решение

50.

51.

Решение

52.

53.

Решение

54.

55.

Решение

Для следующих упражнений решите точно логарифмическое уравнение, если это возможно.

56.

57.

Решение

58.

59.

Решение

60.

61.

Решение

62.

63.

Решение

В следующих упражнениях используйте формулу замены основы и основание 10 или основание для вычисления заданных выражений. Ответьте в точной и приблизительной форме с округлением до четырех знаков после запятой.

64.

65.

Решение

66.

67.

Решение

68.

69.

Решение

70. Перепишите следующие выражения в экспонентах и ​​упростите.

а.

г.

г.

г.

71. [T] Число бактерий в культуре через несколько дней можно смоделировать с помощью функции. Определите количество присутствующих бактерий через 15 дней.

Решение

72. [T] Спрос (в миллионах баррелей) на нефть в богатой нефтью стране задается функцией, где – цена (в долларах) барреля нефти. Найдите требуемое количество нефти (с округлением до миллиона баррелей) при цене от 15 до 20 долларов.

73. [T] Накопленная сумма инвестиций в размере 100 000 долларов США, проценты по которым непрерывно складываются в течение многих лет, определяется как. Найдите сумму, накопленную за 5 лет.

Решение

Приблизительно 131 653 доллара будет накоплено за 5 лет.

74. [T] Инвестиции накапливаются ежемесячно, ежеквартально или ежегодно и задаются функцией, где – стоимость инвестиции во время, – это первоначальный принцип, который был инвестирован, – это годовая процентная ставка, и количество раз в год начисляются проценты.При годовой процентной ставке 3,5% и начальном принципе в 100 000 долларов найдите сумму, накопленную за 5 лет для начисляемых процентов: a. ежедневно, б., ежемесячно, в. ежеквартально и d. ежегодно.

Решение

и. а. pH = 8 б. База ii. а. pH = 3 б. Кислота iii. а. pH = 4 б. Кислота

76. [T] Йод-131 – это радиоактивное вещество, которое распадается в соответствии с функцией, где – начальное количество пробы вещества в днях.Определите, за сколько времени (с точностью до ближайшего дня) разложится 95% количества.

78. [T] Сумма, накопленная после того, как 1000 долларов инвестируется в течение многих лет с процентной ставкой 4%, моделируется функцией.

1. Найдите сумму, накопленную за 5 лет и 10 лет.
2. Определите, сколько времени потребуется, чтобы первоначальные вложения утроились.

79. [T] Известно, что бактериальная колония, выращенная в лаборатории, удваивается за 12 часов.Предположим, что изначально присутствует 1000 бактерий.

1. Используйте экспоненциальную функцию, чтобы определить значение, которое представляет собой скорость роста бактерий. Округлить до четырех знаков после запятой.
2. Определите приблизительно, сколько времени нужно для роста 200 000 бактерий.

Решение

а. б. часы

80. [T] Популяция кроликов в заповеднике удваивается каждые 6 месяцев. Предположим, изначально было 120 кроликов.

1. Используйте экспоненциальную функцию, чтобы определить константу скорости роста.Округлить до четырех знаков после запятой.
2. Используйте функцию в части a. чтобы приблизительно определить, сколько времени нужно, чтобы поголовье кроликов достигло 3500.

81. [T] Землетрясение 1906 года в Сан-Франциско имело магнитуду 8,3 балла по шкале Рихтера. В то же время в Японии землетрясение магнитудой 4,9 нанесло лишь незначительный ущерб. Насколько приблизительно больше энергии было выделено землетрясением в Сан-Франциско, чем землетрясением в Японии?

Решение

Землетрясение в Сан-Франциско имело или в несколько раз больше энергии, чем землетрясение в Японии.

Исчисление

– Предел функций журнала

исчисление – Предел функций журнала – Обмен стеками по математике

Сеть обмена стеком

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 6 лет, 1 месяц назад

Просмотрено 1к раз

$ \ begingroup $ Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.

---

Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме форума Mathematics Stack Exchange.

Закрыт 4 года назад.

Мне нужна помощь в решении этой проблемы.

$$ \ displaystyle \ lim _ {x \ to 0} \ frac {\ log \ left (1 + 7x \ right)} {5x} $$

Создан 16 мар.

$ \ endgroup $ 1 $ \ begingroup $

подсказка : $ Q = \ dfrac {7} {5} \ cdot \ dfrac {\ log (1 + 7x)} {7x} $

Создан 16 мар.

$ \ endgroup $ $ \ begingroup $

$ \ lim_ {x \ to 0} \ frac {\ log (1 + 7x)} {5x} = \ frac {0} {0}.$

Поскольку предел неопределенного типа, мы можем применить правило L’Hospitals. То есть просто дифференцируйте верхнюю часть и дифференцируйте нижнюю часть, а затем повторно оцените предел.

$ \ lim_ {x \ to 0} \ frac {\ log (1 + 7x)} {5x} = \ frac {0} {0} \; \; \; \Правая стрелка \;\;\; \ lim_ {x \ to 0} {\ frac {\ frac {1} {1 + 7x} \ cdot 7} {5}} = \ frac {7} {5}

долл. США

Создан 16 мар.

$ \ endgroup $ $ \ begingroup $

$$ \ lim _ {x \ to 0} \ frac {\ log \ left (1 + 7x \ right)} {5x} = \ lim_ {x \ to 0} \ frac {7} {5} \ frac { 1} {7x} \ log {(1 + 7x)} = $$ $$ = \ frac {7} {5} \ log {\ left (\ lim_ {x \ to 0} (1 + 7x) ^ {\ frac {1} {7x}} \ right)} = \ frac {7 } {5} \ log e = \ frac {7} {5} $$

Создан 16 мар.

Ади ДаниАди Дани

16.2k44 золотых знака2525 серебряных знаков4848 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Подсказка

Также можно использовать тот факт, что если $ y << 1 $, то $ \ log (1 + y) \ приблизительно y $. Замените $ y $ на $ 7x $, и вы получите ответ.

Создан 16 мар.

Клод ЛейбовичиКлод Лейбовичи

189k5151 золотой знак8080 серебряных знаков172172 бронзовых знака

$ \ endgroup $ $ \ begingroup $

Используйте определение производной журнала и установите $ 7x = t $: $$ \ frac {7} {5} \ lim_ {t \ to 0} \ lim_ {v \ to 1} \ frac {\ log (v + t) – \ log v} {t} = \ frac {7} {5 } \ lim_ {v \ to 1} \ lim_ {t \ to 0} \ frac {\ log (v + t) – \ log v} {t} = \ frac {7} {5} \ lim_ {v \ to 1} \ frac {1} {v} = \ frac {7} {5}

$

Создан 16 мар.

AlexAlex

18.5k44 золотых знака2323 серебряных знака3838 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Я думаю, вы можете решить эту проблему, используя следующую формулу:
$$ \ lim _ {x \ to 0} \ frac {\ log (1 + x)} {x} = 1 $$

Итак, просто разделите и умножьте на 7 долларов, вы получите ответ как 7 долларов / 5 долларов

эгрег

217k1717 золотых знаков117117 серебряных знаков280280 бронзовых знаков

Создан 16 мар.

$ \ endgroup $ $ \ begingroup $

Мы можем расширить $ \ log (1 + x) $ для $ | x | \ lt1 $ как:

$$ \ log (1 + x) = x- \ frac {x ^ 2} 2+ \ frac {x ^ 3} 3- \ dots $$

Следовательно:

$$ \ lim_ \ limits {x \ to0} \ frac {\ log (1 + 7x)} {5x} $$ $$ = \ lim_ \ limits {x \ to0} \ frac {7x- \ frac {49x ^ 2} 2+ \ dots} {5x} $$ $$ = \ frac75 $$

Создан 08 ноя.

JMPJMP

16.4k5050 золотых знаков2929 серебряных знаков4646 бронзовых знаков

$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Как использовать правило L’Hôpital с экспоненциальными формами

Краткий обзор

• Неопределенные формы экспоненты: $$ 0 ^ 0 $$, $$ 1 ^ \ infty $$ и $$ \ infty ^ 0 $$. {\ sin x} $$, используя уравнение, описанное выше, и упростите, используя свойства логарифмов.+} \ sin x \ cdot \ ln x } && \ text {Переведите предел в экспоненту.} \ end {выровнять *} $$

  Примечание: Когда вертикального пространства не так много (например, в экспоненте), мы часто пишем «$$ x \ to $$» в ограничении сбоку, а не под «$$». \ lim $$ “.

  $$ \ textstyle \ lim_ {х \ к а} е (х) = \ Displaystyle \ lim_ {х \ к а} е (х) $$

  Шаг 3

  Сузьте фокус до экспоненты и оцените предел.+} \ синий {\ sin x} \ cdot \красный{% \ ln x } % = \ синий 0 \, \красный{% (- \ infty) } $$

  Это неопределенная форма, которую мы изучали на предыдущем уроке. +} 1 \ cdot 0 \\ [6pt] % & = 0 \ end {выровнять *} $$

  Обратите внимание, что в предыдущих уроках мы показали $$ \ lim \ limits_ {x \ to0} \ frac {\ sin x} х = 1 $$ Вы также можете использовать правило L’Hôpital для его оценки.

  ШАГ 6

  Оцените исходный предел, используя найденные нами значения.

  Напомним, что на шаге 2 мы переписали предел, используя экспоненциальный и натуральный логарифмы. Затем на шаге 3 мы сузили фокус до экспоненты. Теперь нам нужно вернуться к проблеме в целом.

  $$ \ begin {align *} \ lim_ {х \ to0 ^ +} \оставил(% \ грех х \ справа) ^ х % & = e ^ {% \синий{% \ lim_ {x \ to 0 ^ +} Икс\, \ ln (\ грех х) } } && \ text { из шага 2 } \\ [6pt] % & = e ^ {\ blue 0} && \ text { из шага 3 } \\ [6pt] % & = 1 \ end {выровнять *} $$

  Отвечать

  $$ \ Displaystyle \ lim_ {х \ to0 ^ +} \оставил(% \ грех х \ справа) ^ x = 1 $$

  Для справки, вот график функции и предельного значения. {% \ синий x } % & = \ lim_ {x \ to \ infty} \ синий х \, \красный{% \ ln \ left (% 1 + \ гидроразрыва 1 х \верно) } && \ text {Свойство логарифмов} \\ [6pt] % & = \ синий \ infty \ cdot \ red {% \ ln 1 } && \ text {Оценка} \\ [6pt] % & = \ синий \ infty \ cdot \ красный 0 \ end {выровнять *} $$

  Шаг 4

  Перепишите предел так, чтобы он имел форму $$ \ frac 0 0 $$.

  $$ \ Displaystyle \ lim_ {х \ к \ infty} \ синий х \, \красный{% \ ln \ left (% 1 + \ гидроразрыва 1 х \верно) } % = \ Displaystyle \ lim_ {х \ к \ infty} \ frac {% \красный{% \ ln \ left (% 1 + \ гидроразрыва 1 х \верно) } } {% \ синий {1 / x} } = \ frac {% \красный{% \ ln 1 } } {% \синий{% 1 / \ infty } } % = \ frac {% \ красный 0 } {% \ синий 0 } $$

  Шаг 5

  Примените правило L’Hôpital и повторно оцените лимит. {- 1} } \\ [6pt] % & = \ lim_ {x \ to \ infty} \ frac 1 {% 1 + \ гидроразрыва 1 х } \\ [6pt] % & = \ frac 1 {1 + 0} \\ [6pt] % & = 1 \ end {выровнять *} $$

  ШАГ 6

  Оцените исходный предел.Икс = e $$.

  НЕ ИМЕЕТ РЕАКЦИИ КОЛЕННОГО РОДКА!

  Иногда вопрос о ограничении будет выглядеть как как неопределенная форма, но на самом деле его просто нужно немного упростить. Рассмотрим следующий пример.

  Пример 4

  Оценивать $$ \ Displaystyle \ lim_ {x \ to \ infty} \оставил(% е ^ х \ right) ^ {% 1 / х ^ 2 } $$. 2 } = 1 $$.\ infty $$ . Покажите, что предел , а не неопределенных.

  Шаг 1

  Давайте определим две функции, где все, что мы знаем о них, – это их пределы:

  $$ \ begin {align *} \ text {Определить} u (x) \ text {так что} \ lim_ {x \ to a} & u = 0 \\ [6pt] % \ text {Определить} v (x) \ text {так что} \ lim_ {x \ to a} & v = \ infty \\ [6pt] % \ end {выровнять *} $$

  где $$ a $$ – любое число, ИЛИ $$ \ infty $$.{% \ lim_ {x \ to a} v \ cdot \ ln u } $$

  Шаг 3

  Теперь оцените предел в экспоненте. \ infty $$, конечный результат всегда будет равен $$ 0 $$.{- \ infty} $$ дают несколько иной результат (хотя и НЕ неопределенный). В вопросах в конце урока мы проработаем этот вариант.

  Продолжить практические задачи

  Ошибка: Нажмите «Не робот», затем повторите попытку.

  Логарифмические функции

  Логарифмические функции являются обратными экспоненциальными функциями, и любая экспоненциальная функция может быть выражена в логарифмической форме. Точно так же все логарифмические функции можно переписать в экспоненциальной форме. Логарифмы действительно полезны, поскольку позволяют нам работать с очень большими числами, манипулируя числами гораздо более управляемого размера.

  Если x = 2 ^y должны были быть решены для y , чтобы его можно было записать в функциональной форме, необходимо было бы ввести новое слово или символ.Если x = 2 ^y , тогда y = (степень на базе 2), чтобы равняться x . Слово логарифм, сокращенно журнал, введено для удовлетворения этой потребности.

  y = (степень на базе 2) равно x

  Это уравнение переписывается как y = log ₂ x .

  Это читается как « y равно логарифму x , основание 2» или « y равно логарифму, основание 2, x .”

  Логарифмическая функция является функцией вида

  , который читается как « y равно логарифму x , основание b » или « y равно логарифму, основанию b , x ».

  В обеих формах x > 0 и b > 0, b ≠ 1. Нет никаких ограничений для y .

  Пример 1

  Перепишите каждое экспоненциальное уравнение в его эквивалентной логарифмической форме.Решения следующие.

  1. 5 ² = 25

  Пример 2

  Перепишите каждое логарифмическое уравнение в эквивалентной экспоненциальной форме. Решения следующие.

  1. журнал ₆ 36 = 2

  2. бревно _a м = p

  Пример 3

  По возможности решите следующие уравнения.

  1. журнал ₇ 49 = y

  3. журнал _y 8 = 3

  4. журнал ₄ y = –2

  5. журнал ₃ (–9) = y

  5. Это невозможно, так как 3 ^y всегда будет положительным результатом.Напомним, что логарифмы имеют только положительную область значений; следовательно, –9 не входит в область логарифма.

  Чаще всего при работе с логарифмами используются основания с основанием 10 и основанием e . (Буква e представляет собой иррациональное число, которое имеет множество применений в математике и естественных науках. Значение e составляет приблизительно 2,718281828…) Логарифм с основанием 10, log ₁₀ , известен как десятичный логарифм и записывается как журнал, при этом база не записывается, но считается равной 10.Логарифм с основанием e , log _e , известен как натуральный логарифм и записывается как ln.

  Пример 5

  Найдите следующие логарифмы.

  1. журнал 100

  2. журнал 10,000

  3. журнал 0,1

  4. ln e

  5. пер. э ²

  Решение логарифмических функций – объяснение и примеры

  В этой статье мы узнаем, как вычислять и решать логарифмические функции с неизвестными переменными.

  Логарифмы и показатели – две тесно связанные между собой темы в математике. Поэтому полезно сделать краткий обзор показателей степени.

  Показатель степени – это форма записи многократного умножения числа на само себя. Показательная функция имеет вид f (x) = b ^y , где b> 0

  Например, , 32 = 2 × 2 × 2 × 2 × 2 = 2 ² .

  Показательная функция 2 ² читается как « два в возведении в степень пяти » или « два в возведении в пятерку » или « два в пятой степени. ”

  С другой стороны, логарифмическая функция определяется как функция, обратная возведению в степень. Рассмотрим снова экспоненциальную функцию f (x) = b ^y , где b> 0

  y = log _b x

  Тогда логарифмический функция задается;

  f (x) = log _b x = y, где b – основание, y – показатель степени, а x – аргумент.

  Функция f (x) = log _b x читается как «log base b of x». Логарифмы полезны в математике, потому что они позволяют нам выполнять вычисления с очень большими числами.

  Как решать логарифмические функции?

  Для решения логарифмических функций важно использовать экспоненциальные функции в данном выражении. Натуральный логарифм или ln является обратной величиной e . Это означает, что один может отменить другой, т.е.

  ln (e ^x ) = x

  e ^{ln x} = x

  Чтобы решить уравнение с логарифмом (ами), важно знать их свойства.

  Свойства логарифмических функций

  Свойства логарифмических функций – это просто правила для упрощения логарифмов, когда входные данные имеют форму деления, умножения или экспоненты логарифмических значений.

  Некоторые из объектов недвижимости перечислены ниже.

  Правило произведения логарифма гласит, что логарифм произведения двух чисел, имеющих общее основание, равен сумме отдельных логарифмов.

  ⟹ log _a (p q) = log _a p + log _a q.

  Правило частного логарифмов утверждает, что логарифм отношения двух чисел с одинаковыми основаниями равен разности каждого логарифма.

  ⟹ log _a (p / q) = log _a p – log _a q

  Правило логарифма степени утверждает, что логарифм числа с рациональной степенью равен произведению экспоненты и его логарифм.

  ⟹ log _a (p ^q ) = q log _a p

  log _a p = log _x p ⋅ log _a x

  ⟹ log _q p = log _x п / лог _x q

  ⟹ лог _п 1 = 0.

  Другие свойства логарифмических функций включают:

  • Основания экспоненциальной функции и ее эквивалентной логарифмической функции равны.
  • Логарифмы положительного числа по основанию того же числа равны 1.

  log _a a = 1

  • Логарифмы 1 до любого основания равны 0.

  log _a 1 = 0

  • Log _a 0 не определено
  • Логарифмы отрицательных чисел не определены.
  • Основание логарифма никогда не может быть отрицательным или 1.
  • Логарифмическая функция с основанием 10 называется десятичным логарифмом. Всегда принимайте основание 10 при решении с помощью логарифмических функций без маленького индекса для основания.

  Сравнение экспоненциальной функции и логарифмической функции

  Всякий раз, когда вы видите логарифмы в уравнении, вы всегда думаете о том, как отменить логарифм, чтобы решить уравнение. Для этого вы используете экспоненциальную функцию .Обе эти функции взаимозаменяемы.

  В следующей таблице показан способ записи и замены экспоненциальных функций и логарифмических функций местами. В третьем столбце рассказывается о том, как читать обе логарифмические функции.

  9352 Давайте воспользуемся этими свойствами для решения пары задач, связанных с логарифмическими функциями.

  Пример 1

  Перепишите экспоненциальную функцию 7 ² = 49 в ее эквивалентную логарифмическую функцию.

  Решение

  Дано 7 ² = 64.

  Здесь основание = 7, показатель степени = 2 и аргумент = 49. Следовательно, 7 ² = 64 в логарифмической функции;

  ⟹ log ₇ 49 = 2

  Пример 2

  Запишите логарифмический эквивалент 5 ³ = 125.

  Решение

  База = 5;

  показатель степени = 3;

  и аргумент = 125

  5 ³ = 125 ⟹ log ₅ 125 = 3

  Пример 3

  Решить относительно x в журнале ₃ x = 2

  Решение

  25

  log ₃ x = 2
  3 ² = x
  ⟹ x = 9

  Пример 4

  Если 2 log x = 4 log 3, найдите значение ‘x’.

  Решение

  2 log x = 4 log 3

  Разделите каждую сторону на 2.

  log x = (4 log 3) / 2

  log x = 2 log 3

  log x = log 3 ²

  log x = log 9

  x = 9

  Пример 5

  Найдите логарифм 1024 по основанию 2.

  Решение

  1024 = 2 ¹⁰

  log ₂ 1024 = 10

  Пример 6

  Найдите значение x в журнале ₂ ( x ) = 4

  Решение

  Перепишите логарифмическую функцию log 08 x ) = 4 в экспоненциальной форме.

  2 ⁴ = x

  16 = x

  Пример 7

  Решите относительно x в следующем логарифмическом журнале функций ₂ (x – 1) = 5.

  43

  Решение
  Запишите логарифм в экспоненциальной форме как;

  log ₂ (x – 1) = 5 ⟹ x – 1 = 2 ⁵

  Теперь решите относительно x в алгебраическом уравнении.
  ⟹ x – 1 = 32
  x = 33

  Пример 8

  Найдите значение x в логарифме x 900 = 2.

  Решение

  Запишите логарифм в экспоненциальной форме как;

  x ² = 900

  Найдите квадратный корень из обеих частей уравнения, чтобы получить;

  x = -30 и 30

  Но поскольку основание логарифмов никогда не может быть отрицательным или 1, правильный ответ равен 30.

  Пример 9

  Решите относительно данного x, log x = log 2 + log 5

  Решение

  Используя правило продукта Log _b (mn) = log _b m + log _b n получаем;

  ⟹ журнал 2 + журнал 5 = журнал (2 * 5) = журнал (10).

  Следовательно, x = 10.

  Пример 10

  Логарифм решения _x (4x – 3) = 2

  Решение

  Перепишите логарифм в экспоненциальной форме, чтобы получить;

  x ² = 4x – 3

  Теперь решите квадратное уравнение.
  x ² = 4x – 3
  x ² – 4x + 3 = 0
  (x -1) (x – 3) = 0

  x = 1 или 3

  Поскольку основание логарифма никогда не может быть 1, тогда единственное решение – 3.

  Практические вопросы

  1. Выразите следующие логарифмы в экспоненциальной форме.

  а. 1ог ₂ 6

  б. журнал ₉ 3

  c. журнал ₄ 1

  д. журнал ₆ 6

  e. журнал ₈ 25

  ф. log ₃ (-9)

  2. Найдите x в каждом из следующих логарифмов

  a. журнал ₃ (x + 1) = 2

  b. журнал ₅ (3x – 8) = 2

  c.журнал (x + 2) + журнал (x – 1) = 1

  d. log x ⁴ – log 3 = log (3x ² )

  3. Найдите значение y в каждом из следующих логарифмов.

  а. журнал ₂ 8 = y

  b. журнал ₅ 1 = y

  c. журнал ₄ 1/8 = y

  d. log y = 100000

  4. Решите относительно xif log _x (9/25) = 2.

  5. Решите log ₂ 3 – log ₂ 24

  6. Найдите значение x в следующий логарифм log ₅ (125x) = 4

  7.

  Оставить комментарий Отменить ответ

  Для отправки комментария вам необходимо авторизоваться.

  Меню

  Поиск:

  Экспоненциальная функция	Логарифмическая функция	Считывается как
  8 2 = 64	логарифм по основанию 8 64328	10 3 = 1000	log 1000 = 3	log с основанием 10 из 1000
  10 0 = 1	log 1 = 0	log с основанием 10 из 1
  25 2 = 625	log 25 625 = 2	log base 25 из 625
  12 2 = 144	log 12 144 = 2	log base 12 из 144