Пределы триг. функций стремящиеся к бесконечности : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| Spider84 |
| ||
29/01/14 |
| ||
| |||
| ex-math |
| |||
24/02/12 |
| |||
| ||||
функций стремящиеся к бесконечности| tatkuz1990 |
| |||
30/12/13 |
| |||
| ||||
функций стремящиеся к бесконечности
| ||||
18/01/13 |
| |||
| ||||
функций стремящиеся к бесконечности| arseniiv |
| |||
27/04/09 |
| |||
| ||||
функций стремящиеся к бесконечности
| Otta |
| |||
09/05/13 |
| |||
| ||||
| g______d |
| |||
08/11/11 |
| |||
| ||||
Поэтому если написана любая формула, содержащая , предела автоматически не существует, даже для функции или . Нужно говорить слова вроде “давайте устраним все устранимые разрывы” или “давайте доопределим функцию естественным образом”, а если они не сказаны, то я бы тоже вешался на месте программы.| Spider84 |
| ||
29/01/14 |
| ||
| |||
| bot |
| |||
21/12/05 |
| |||
| ||||
01.2014, 07:08 | ИСН |
| |||
18/05/06 |
| |||
| ||||
функций стремящиеся к бесконечности| Spider84 |
| ||
29/01/14 |
| ||
| |||
функций стремящиеся к бесконечности| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Пределы с иррациональностями.
3-8}=\frac{5}{384}$.Пример №6
Найти $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}$.
Решение
Так как $\lim_{x\to 2}(\sqrt[5]{3x-5}-1)=0$ и $\lim_{x\to 2}(\sqrt[3]{3x-5}-1)=0$, то мы имеем дело с неопределенностью $\frac{0}{0}$. В таких ситуациях, когда выражения под корнями одинаковы, можно использовать способ замены. Требуется заменить выражение под корнем (т.е. $3x-5$), введя некоторую новую переменную. Однако простое использование новой буквы ничего не даст. Представьте, что мы просто заменили выражение $3x-5$ буквой $t$. Тогда дробь, стоящая под пределом, станет такой: $\frac{\sqrt[5]{t}-1}{\sqrt[3]{t}-1}$. Иррациональность никуда не исчезла, – лишь несколько видоизменилась, что нисколько не облегчило задачу.
Здесь уместно вспомнить, что корень может убрать лишь степень. Но какую именно степень использовать? Вопрос не тривиален, ведь у нас два корня. Один корень пятого, а другой – третьего порядка. Степень должна быть такой, чтобы одновременно убрать оба корня! Нам нужно натуральное число, которое одновременно делилось бы на $3$ и на $5$.
2+1+1}=\frac{3}{5}.
$$
Ответ: $\lim_{x\to 2}\frac{\sqrt[5]{3x-5}-1}{\sqrt[3]{3x-5}-1}=\frac{3}{5}$.
Первая часть
Вторая часть
Третья часть
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Объяснение урока: Пределы в бесконечности
В этом объяснении мы узнаем, как оценивать пределы функции, когда 𝑥 стремится к бесконечности.
Предел функции на бесконечности описывает поведение выходных значений функции как 𝑥 стремится до бесконечности. В отличие от предела функции в конечной точке, метод прямой подстановки не годится для этих целей. пределы, так как бесконечность не является числом. Вместо этого нам нужно рассмотреть поведение значения функции как 𝑥 становится больше без ограничений.
Давайте рассмотрим пример из реальной жизни относительно радиоактивного элемента в объекте. Мы знаем, что радиоактивные элементы распадаются
(экспоненциально) во времени; следовательно, радиоактивный элемент в объекте со временем постепенно исчезает.
Если мы обозначим
𝑓(𝑡) количество (по массе) радиоактивного элемента в объекте в момент времени 𝑡,
это означает, что значение 𝑓(𝑡) будет приближаться к нулю, когда 𝑡 стремится к положительной бесконечности. Это мотивирует определение предела на бесконечности.
Определим формально предел на бесконечности.
Определение: предел на бесконечности
Если значения 𝑓(𝑥) приближаются к некоторому конечному значению 𝐿 как значение 𝑥 стремится к бесконечности, то говорят, что предел 𝑓(𝑥) при 𝑥 приближается к положительной бесконечности, существует и равен 𝐿, и мы обозначаем это как lim→∞𝑓(𝑥)=𝐿.
Если значения 𝑓(𝑥) неограниченно увеличиваются (или уменьшаются) по мере того, как 𝑥 стремится к бесконечности, то говорят, что предел 𝑓(𝑥) на бесконечности равен положительному (или отрицательному) бесконечность соответственно.
Заметим, что все предельные законы относительно предела суммы, разности, произведения и частных пары функций
применить точно так же для предела на бесконечности.
Правило: законы пределов
Пусть 𝑓(𝑥) и 𝑔(𝑥) функции, области определения которых простираются до положительных бесконечность, и пусть 𝑐 — ненулевая константа. Тогда следующие тождества выполняются до тех пор, пока правая часть сторона уравнения не является неопределенной формой, 00,∞∞,0⋅∞, или ∞−∞: limlimlimlimlimlimlimlimlim, если правая часть определена корректно )=𝑐𝑓(𝑥),(𝑓(𝑥)𝑔(𝑥))=𝑓(𝑥)𝑔(𝑥),(𝑓(𝑥)±𝑔(𝑥))=𝑓(𝑥)±𝑔(𝑥),( 𝑓(𝑥))=𝑓(𝑥),𝑓(𝑥)𝑔(𝑥)=𝑓(𝑥)𝑔(𝑥)𝑔(𝑥)≠0.
Рассмотрим, как изображается предел на бесконечности на графике функции 𝑓(𝑥).
Чтобы найти предел этой функции на бесконечности, нам нужно найти значение 𝑓(𝑥), приближающееся к 𝑥 стремится к бесконечности. Это означает, что мы рассматриваем 𝑦-координаты точек на графике по мере продвижения к правому краю графика. Следуя заданному графику таким образом, 𝑦-координаты точек на графике ведут к числу 2. Это говорит нам о том, что lim→∞𝑓(𝑥)=2.
Этот предел на бесконечности тесно связан с горизонтальной асимптотой графика функции, которая представляет собой горизонтальную линию
график приближается по мере того, как мы движемся вправо или влево от графика.
Определение: Предел на бесконечности и горизонтальные асимптоты
Предположим, что предел функции 𝑓(𝑥) на бесконечности существует и определяется выражением lim→∞𝑓(𝑥)=𝐿.
Тогда график 𝑦=𝑓(𝑥) имеет горизонтальную асимптоту 𝑦=𝐿.
Поскольку ранее мы обнаружили, что lim→∞𝑓(𝑥)=2, мы можем заключить, что 𝑦=2 — это горизонтальная асимптота этой функции, как показано ниже.
Мы также можем понять предел на бесконечности, взглянув на таблицу значений функции по мере увеличения 𝑥. Например, рассмотрим таблицу значений функции 1𝑥 для больших значений.
| 𝑥 | 1 | 10 | 100 | 1 000 |
|---|---|---|---|---|
| 1𝑥 | 1 | 0.1 | 0.01 | 0.001 |
From the table above, we can see that значение функции 1𝑥 стремится к нулю, когда 𝑥 стремится к положительной бесконечности. Это ведет к lim→∞1𝑥=0.
Этот предел также говорит нам о том, что граф 𝑦=1𝑥 имеет горизонтальную асимптоту
𝑦=0, как мы видим ниже.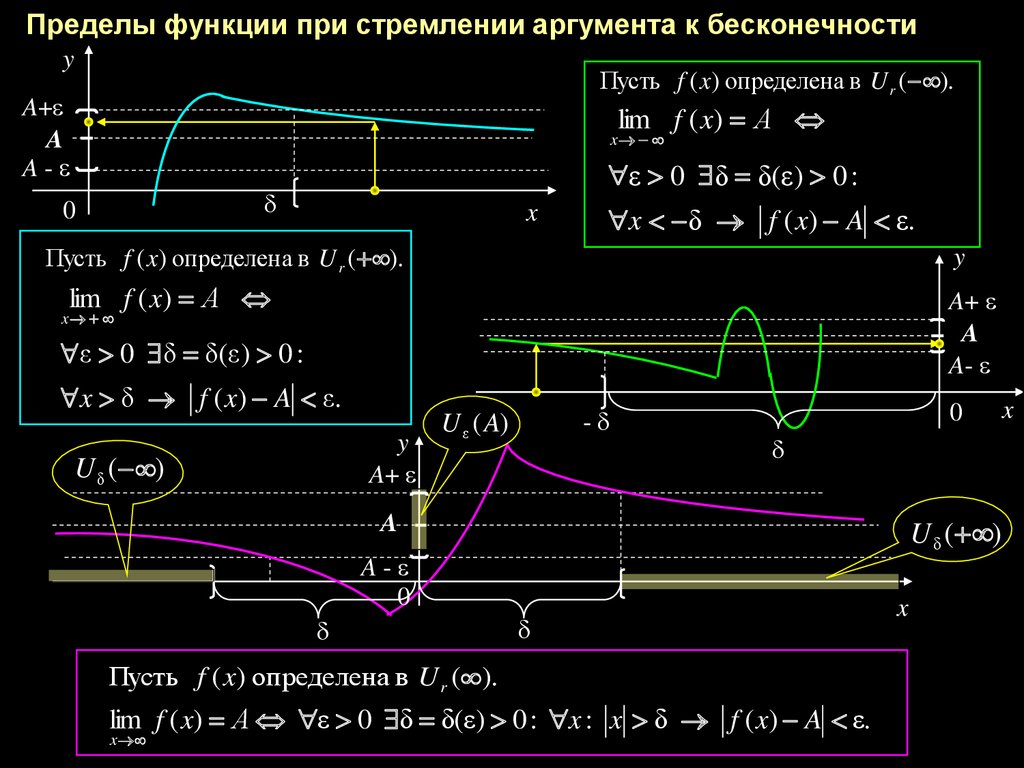
Хотя в основном мы будем рассматривать пределы на положительной бесконечности, мы должны помнить, что пределы на отрицательной бесконечности аналогично можно определить и вычислить. Для пределов на отрицательной бесконечности нам нужно следить за точками на графике, когда мы движемся к левому краю графика.
Например, мы можем рассмотреть левую часть графика 𝑦=1𝑥.
Из этого графика можно сделать вывод, что 𝑦-координаты точек на графике стремятся к 0 как 𝑥 стремится к отрицательной бесконечности. Мы можем выразить это как lim→∞1𝑥=0.
Заметим, что предел на отрицательной бесконечности этой функции совпадает с пределом на положительной бесконечности. Когда пределы на как положительные, так и отрицательные бесконечности одинаковы, мы можем записать предел как 𝑥→±∞. Например, мы обнаружили, что lim→±∞1𝑥=0.
Также для любой константы 𝑎 и натурального числа 𝑛 можно применить предельный закон для степеней
и скалярные умножения для записи
limlimlimlim→∞→∞→∞→∞𝑎𝑥=𝑎1𝑥=𝑎1𝑥=𝑎1𝑥=𝑎×0=0.
Мы видим, что вывод будет таким же, если мы применим предел на отрицательной бесконечности. Это приводит к более общему правилу, которые мы будем использовать для решения различных задач предела на бесконечности.
Правило: предел на бесконечности обратных функций
Для любого действительного числа 𝑎 и натурального числа 𝑛, lim→±∞𝑎𝑥=0.
Как мы увидим, это правило очень полезно при нахождении предела на бесконечности для самых разных функций. Чтобы изобразить главное Для того, чтобы применить это правило, мы рассмотрим предел на бесконечности полиномиальной функции в нашем первом примере.
Пример 1: вычисление пределов многочленов на бесконечности
Рассмотрим многочлен 𝑓(𝑥)=5𝑥+9𝑥−2𝑥−𝑥+11.
- Что из следующего равно lim→∞𝑓(𝑥)?
- LIM → ∞11
- −𝑥Lim → ∞
- −2𝑥Lim → ∞
- 5𝑥Lim → ∞
- Отсюда, найдите LIM → ∞𝑓 (𝑥).
Ответ
Часть 1
В этой части нам нужно найти предел многочлена на бесконечности.
Напомним, что предел функции при
бесконечность описывает поведение значений функции при неограниченном увеличении 𝑥. Когда мы
рассмотрите возможность замены 𝑥 очень большим значением, скажем, 𝑥=1000000, первый член
5𝑥 будет иметь наибольшую величину из пяти членов этого многочлена. Это потому что
этот термин содержит множитель с наибольшей степенью 𝑥, то есть 𝑥. В
по сравнению с этим членом, остальные четыре члена этого полинома будут пренебрежимо малы. Это приводит к
представление о том, что предел этой функции на бесконечности будет вести себя как предел 5𝑥 на
положительная бесконечность.
Мы можем сделать эту идею более строгой, обосновав такое поведение алгебраически. Начнем с факторизации 𝑥 из многочлена. Мы можем написать 5𝑥+9𝑥−2𝑥−𝑥+11=𝑥5+9𝑥−2𝑥−1𝑥+11𝑥.
Напомним, что предельные законы применимы к пределу на бесконечности таким же образом. Используя предельные законы относительно суммы,
разность и произведение пары функций можно написать
limlimlimlimlim→∞→∞→∞→∞→∞→∞5𝑥+9𝑥−2𝑥−𝑥+11=𝑥5+9𝑥−2𝑥+1𝑥−1 .
Напомним также, что для любого действительного числа 𝑎 и натурального числа 𝑛 lim→∞𝑎𝑥=0.
Это означает, что limlimlim→∞→∞→∞→∞9𝑥=0,2𝑥=0,1𝑥=0,11𝑥=0.
Это приводит к limlim→∞→∞5𝑥+9𝑥−2𝑥−𝑥+11=5𝑥.
Это вариант D.
Часть 2
В предыдущей части мы обнаружили, что данный предел на бесконечности совпадает с 5𝑥.lim→∞
Этот предел описывает поведение функции 𝑥 при неограниченном увеличении 𝑥. Если мы рассмотрим подстановку больших значений 𝑥 в это выражение, мы увидим, что результирующее значение будет расти без ограничений. Напомним, что когда значение функции становится больше по мере того, как 𝑥 стремится к бесконечности, мы говорим, что предел функции на бесконечности равен бесконечности. Следовательно, 5𝑥=5×∞=∞.lim→∞
Это означает lim→∞5𝑥+9𝑥−2𝑥−𝑥+11=∞.
В предыдущем примере мы нашли предел полиномиальной функции на бесконечности, выделив на множитель наивысшую степень
𝑥 из полинома и применяя пределы обратных функций на бесконечности.
В результате мы нашли
что предел этого многочлена совпадает с пределом старшего члена, который является членом, содержащим наибольшую степень
из 𝑥. Мы можем обобщить этот результат для любого многочлена, следуя аналогичным рассуждениям.
Правило: предел на бесконечности полиномиальной функции
Пусть 𝑝(𝑥) — полиномиальная функция, заданная формулой 𝑝(𝑥)=𝑎𝑥+𝑎𝑥+⋯+𝑎𝑥+𝑎,𝑎≠0.
Тогда limlim→∞→∞𝑝(𝑥)=𝑎𝑥.
Этот предел равен положительной или отрицательной бесконечности, если знак 𝑎 положительный или отрицательный соответственно.
Важная идея, вытекающая из этого правила, заключается в том, что многочлен на бесконечности растет как старший член или член, содержащий высшая сила 𝑥. Используя эту идею, мы также можем найти предел рациональной функции на бесконечности, как мы увидим в следующем примере.
Пример 2. Вычисление пределов рациональных функций на бесконечности
Рассмотрим рациональную функцию 𝑓(𝑥)=3𝑥−8𝑥9−2𝑥.
- Что из следующего равно lim→∞𝑓(𝑥)?
- 3-89-2лим→∞→∞
- 3+89+2лимлим→∞→∞ 8-лим 3 ∞
- 3−89+2lim→∞
- 3−89−2lim→∞
Ответ
Часть 1
В этой части нам нужно найти предел рациональной функции на отрицательной бесконечности. Так как рациональная функция есть частное многочленов, мы можем найти этот предел, рассматривая свойство многочленов относительно числителя и знаменателя рациональная функция. Напомним, что предел полинома на бесконечности контролируется старшим членом или членом с высшая сила. В числителе данной рациональной функции старший член равен 3𝑥, а старший член знаменателя равен −2𝑥. Следовательно, данная рациональная функция должна вести себя одинаково при бесконечность как частное 3𝑥−2𝑥, которое можно привести к константе 3−2.
Давайте сделаем эту идею более строгой, используя алгебру.
Начнем с деления числителя и знаменателя частного
высшей степенью 𝑥, которая равна 𝑥. Это ведет к
3𝑥−8𝑥9−2𝑥=3𝑥−8𝑥×(9−2𝑥)×=3−−2.
Это вариант А.
Часть 2
В предыдущей части мы получили, что заданный предел на бесконечности равен 3−89−2.limlim→∞→∞
Напомним, что для любого действительного числа 𝑎 и натурального числа 𝑛 lim→±∞𝑎𝑥=0.
Это означает, что limlim→∞→∞1𝑥=0,1𝑥=0.
Подставляя эти пределы выше, мы получаем 3−8×09×0−2=3−2=−32.
Следовательно, lim→∞𝑓(𝑥)=−32.
В предыдущем примере мы нашли предел рациональной функции, разделив числитель и знаменатель частного
по высшей степени 𝑥 и применяя предел на бесконечности обратных функций.
Этот метод может быть
применяется для многих различных функций при нахождении предела на бесконечности.
Практическое руководство. Нахождение предела рациональной функции на бесконечности
Пусть 𝑝(𝑥) и 𝑞(𝑥) — многочлены, и пусть 𝑚 быть степенью знаменателя 𝑞(𝑥). Чтобы найти предел lim→±∞𝑝(𝑥)𝑞(𝑥), нужно
- умножить числитель и знаменатель частного на 1𝑥,
- упростить числитель и знаменатель частного,
- применить правило lim →±∞𝑎𝑥=0 и найдите ответ.
Заметим, что мы умножаем числитель и знаменатель частного на обратную величину наибольшей степени знаменателя. В предыдущем примере это не повлияло на наш метод, так как и числитель, и знаменатель частного имели одинаковые значения. степень. Когда у нас есть рациональная функция с разными степенями, лучше умножить на обратную величину наибольшая степень знаменателя, чтобы избежать ситуации, когда мы получим ноль в знаменателе.
В следующем примере мы рассмотрим предел на бесконечности рациональной функции, где числитель и знаменатель
частные являются полиномами разных степеней.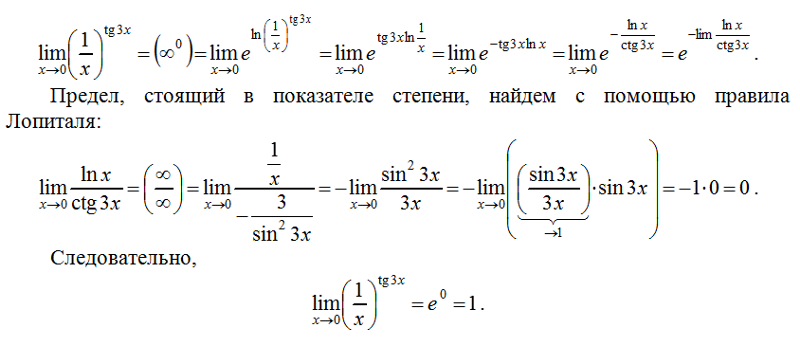
Пример 3. Нахождение предела рациональной функции на бесконечности
Найти lim→∞−5𝑥−9−2𝑥+5.
Ответ
В этом примере нам нужно найти предел на бесконечности рациональной функции. Напомним, что для нахождения предела рациональной функции, мы можем начать с умножения числителя и знаменателя частного на величину, обратную наибольшая степень 𝑥 в знаменателе. В заданной рациональной функции высшая степень 𝑥 в знаменателе равно 𝑥, поэтому мы можем умножить числитель и знаменатель частное на 1𝑥. Это ведет к −5𝑥−9−2𝑥+5=(−5𝑥−9)×(−2𝑥+5)×=−−2+.
Применяя предельные законы, могу написать limlimlim→∞→∞→∞→∞−5𝑥−9−2𝑥+5=−−−2+.
Напомним, что для любого действительного числа 𝑎 и натуральное число 𝑛, lim→∞𝑎𝑥=0.
Это означает, что limlim→∞→∞→∞5𝑥=0,9𝑥=0,5𝑥=0.
Подставляя эти пределы выше, мы получаем
lim→∞−5𝑥−9−2𝑥+5=−0−0−2+0=0.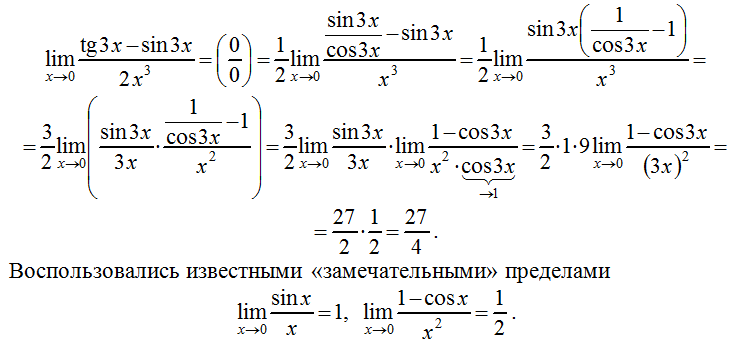
Следовательно, lim→∞−5𝑥−9−2𝑥+5=0.
В следующем примере мы найдем предел на бесконечности рациональной функции, где числитель имеет большее степень.
Пример 4. Нахождение предела рациональной функции на бесконечности
Найти lim→∞−𝑥−7𝑥+3𝑥+7𝑥+4−8𝑥−6𝑥−6𝑥+4.
Ответ
В этом примере нам нужно найти предел на бесконечности рациональной функции. Напомним, что для нахождения предела рациональной функции на бесконечности, мы можем начать с умножения числителя и знаменателя частного на обратную наибольшей степени 𝑥 для знаменателя. В заданной рациональной функции высшая степень 𝑥 в знаменателе равно 𝑥, поэтому мы можем умножить числитель и знаменатель частное на 1𝑥. Это ведет к −𝑥−7𝑥+3𝑥+7𝑥+4−8𝑥−6𝑥−6𝑥+4=−𝑥−7𝑥+3𝑥+7𝑥+4×(−8𝑥−6𝑥−6𝑥+4)×=−𝑥−7++ +−8−−+.
Применяя предельные законы, мы можем написать
limlimlimlimlimlimlim→∞→∞→∞→∞→∞→∞→∞→∞−+7𝑥 +4−8𝑥−6𝑥−6𝑥+4=−𝑥−7+++−8−−+.
Напомним, что для любого действительного числа 𝑎 и натурального числа 𝑛 lim→∞𝑎𝑥=0.
Это означает, что limlimlimlim→∞→∞→∞→∞→∞3𝑥=0,7𝑥=0,4𝑥=0,6𝑥=0,6𝑥=0.
Подставляя эти пределы выше, мы получаем limlim→∞→∞→∞−𝑥−7𝑥+3𝑥+7𝑥+4−8𝑥−6𝑥−6𝑥+4=−𝑥−7−8=𝑥+78.
Мы знаем, что lim→∞𝑥=∞; следовательно, lim→∞𝑥+78=∞+78=∞.
Это дает нам lim→∞−𝑥−7𝑥+3𝑥+7𝑥+4−8𝑥−6𝑥−6𝑥+4=∞.
В предыдущих примерах мы нашли предел на бесконечности различных рациональных функций. Более пристальное изучение нашего метода приводит к следующий общий вывод.
Правило: пределы на бесконечности рациональных функций
Пусть 𝑝(𝑥) и 𝑞(𝑥) — многочлены.
- Если 𝑝(𝑥) и 𝑞(𝑥) совпадают градусов, то lim→±∞𝑝(𝑥)𝑞(𝑥) определяется отношением старших коэффициентов, которые равны коэффициенты высшей степени 𝑥 как в числителе, так и в знаменателе частного.
- Если 𝑝(𝑥) имеет более низкую степень, чем 𝑞(𝑥),
тогда lim→±∞𝑝(𝑥)𝑞(𝑥)=0.
- Если 𝑝(𝑥) имеет более высокую степень, чем 𝑞(𝑥), тогда lim→±∞𝑝(𝑥)𝑞(𝑥) равно положительной или отрицательной бесконечности.
Мы могли бы использовать это свойство для более быстрого решения предыдущих примеров. Хотя это полезное правило, о котором следует помнить, находя предел алгебраически применим в более широком круге задач. Привыкание к алгебраическому методу нахождения предела на бесконечность также приведет к более конкретному пониманию этого предмета.
В следующем примере мы применим это правило для идентификации неизвестных констант в функции из заданного предела на бесконечности.
Пример 5. Нахождение неизвестных в рациональной функции с учетом ее предела на бесконечности
Найдите значения 𝑎 и 𝑏, учитывая, что lim→∞5𝑥−2𝑥+3(𝑎+4)𝑥+(1−𝑏)𝑥+5𝑥=∞.
Ответ
В этом примере нам дан предел рациональной функции на бесконечности. Мы знаем, что предел на бесконечности рационального
функция зависит от степеней многочленов в числителе и знаменателе функции.
Напомним правило для
предел на бесконечности рациональных функций.
Пусть 𝑝(𝑥) и 𝑞(𝑥) — многочлены.
- Если град 𝑝(𝑥)=𝑞(𝑥), то lim→±∞𝑝(𝑥)𝑞(𝑥) равно отношению старших коэффициентов.
- Если градус𝑝(𝑥)𝑞(𝑥), тогда lim→±∞𝑝(𝑥)𝑞(𝑥)=0.
- Если градус𝑝(𝑥)>𝑞(𝑥), тогда lim→±∞𝑝(𝑥)𝑞(𝑥)=±∞.
В частности, отметим, что предел на бесконечности равен конечному числу для первых двух случаев. Поскольку предел на бесконечности в этом примере бесконечна, наша рациональная функция должна принадлежать третьему случаю. Это степень многочлена в числителе больше степени многочлена в знаменателе. Рассмотрим степени этих многочленов в нашей функции.
Числитель нашей функции равен 5𝑥−2𝑥+3, который является многочленом
степени 5. Следовательно, степень многочлена в знаменателе
должно быть меньше 5. Знаменатель нашей функции равен (𝑎+4)𝑥+(1−𝑏)𝑥+5𝑥.
Если 𝑎+4 отлично от нуля, то степень этого многочлена будет равна 6, что больше 5. Таким образом, мы должны иметь
𝑎+4=0,
что приводит к 𝑎=−4. В этом случае первый коэффициент равен нулю, а значит, знаменатель
нашей функции записывается как (1−𝑏)𝑥+5𝑥. Точно так же, если 1−𝑏 не равно нулю,
степень этого полинома равна 5, что соответствует степени числителя. Это не может быть правдой на основании данного
предел на бесконечности. Следовательно, мы должны иметь
1−𝑏=0,
что приводит к 𝑏=1. Это означает, что знаменатель нашей функции равен 5𝑥,
степень которого равна 4. Заметим, что, поскольку 5 > 4, степень числителя больше степени
степень знаменателя. Это помещает нашу функцию в третью категорию указанного выше правила, вывод которого
согласуется с заданным пределом на бесконечности.
Следовательно, 𝑎=−4, 𝑏=1.
Мы рассмотрели пределы на бесконечности многочленов и рациональных функций.
В этих примерах мы использовали тот факт, что
многочлен на бесконечности ведет себя как член высшей степени. Эта идея оказалась полезной для оценки пределов на бесконечности
рациональные функции.
Аналогичную стратегию можно использовать в функции, в которой либо числитель, либо знаменатель содержит подкоренной корень. В этом случае, а не выбирать член высшей степени (который может находиться под корнем), нам нужно идентифицировать общее поведение числителя и знаменателя с учетом корня. Мы рассмотрим это в следующем примере.
Пример 6. Нахождение предела комбинации корней и многочленов на бесконечности
Найти lim→∞√6𝑥+95𝑥+1.
Ответ
В этом примере нам нужно найти предел в бесконечности частного. Мы знаем, что предел на положительной бесконечности описывает поведение значения функции при увеличении 𝑥. Рассмотрим поведение числителя и знаменатель частного отдельно для больших значений 𝑥.
Для числителя √6𝑥+9 — квадратный корень полиномиальной функции 6𝑥+9.
Мы знаем, что многочлен растет как старший член, который является членом с наибольшей степенью 𝑥. В этом случае старший член этого полинома равен 6𝑥. Используя эту идею с правилом мощности для пределов,
мы получаем
limlimlimlimlim→∞→∞→∞→∞→∞√6𝑥+9=6𝑥+9=6𝑥=√6𝑥=√6𝑥.
Это означает, что числитель ведет себя как функция √6𝑥 при 𝑥 приближается к бесконечности.
Далее рассмотрим знаменатель 5𝑥+1. Поскольку знаменатель представляет собой многочлен со старшим членом 5𝑥 ведет себя как 5𝑥 на бесконечности. Это приводит к выводу, что данное частное ведет себя как √6𝑥5𝑥, что упрощается до константы √65.
Мы можем сделать этот аргумент более строгим, используя алгебру. Мы видели, что и числитель, и знаменатель частного ведут себя как постоянные времена 𝑥. Значит, разделим числитель и знаменатель этого частного на 𝑥. Это ведет к √6𝑥+95𝑥+1=√6𝑥+9×(5𝑥+1)×=(6𝑥+9)×5+=6+5+.
Используя предельные законы, мы можем написать
limlim→∞→∞→∞√6𝑥+95𝑥+1=6+5+.
Напомним, что для любого действительного числа 𝑎 и натурального числа 𝑛 lim→∞𝑎𝑥=0.
Это означает, что limlim→∞→∞1𝑥=0,1𝑥=0.
Подставляя эти пределы выше, мы получаем lim→∞√6𝑥+95𝑥+1=√65.
В предыдущем примере мы нашли предел на бесконечности функции, числитель которой содержит функцию квадратного корня. Мы можно использовать ту же стратегию, чтобы найти предел на бесконечности функции, которая содержит разность квадратных корней. Сначала На первый взгляд, эти задачи не похожи друг на друга, так как не даются в виде частного. Но умножая на сопряженное выражения квадратного корня, мы можем записать эти функции в виде частного, что делает ранее установленный метод доступный. Мы рассмотрим такой предел в нашем последнем примере.
Пример 7. Нахождение предела функций корней на бесконечности с помощью рационализации
Определить lim→∞√16𝑥−5𝑥−4𝑥, если он существует.
Ответ
В этом примере нам нужно найти предел функции на бесконечности.
Наша функция задается как разность двух
функции, √16𝑥−5𝑥 и 4𝑥. Обе эти функции стремятся к бесконечности как
𝑥 стремится к бесконечности, что означает, что этот предел можно символически записать ∞−∞. Это тип неопределенной формы, что означает, что мы не можем определить значение
этот предел основан на текущей форме. Чтобы найти предел функции в неопределенной форме, мы должны алгебраически
упростим данную функцию, пока мы не сможем оценить предел.
Поскольку данная функция представляет собой разность функции извлечения квадратного корня и многочлена, мы можем думать о сопряженном методе, который часто используется для упрощения таких алгебраических выражений. Напомним, что выражение √𝑎−√𝑏 сопряжено с √𝑎+√𝑏; следовательно, сопряжение данной функции, √16𝑥−5𝑥−4𝑥 можно записать как √16𝑥−5𝑥+4𝑥.
Чтобы упростить данную функцию, начнем с умножения функции на частное, числитель и знаменатель которого равны
к этому сопряженному выражению:
Пример a .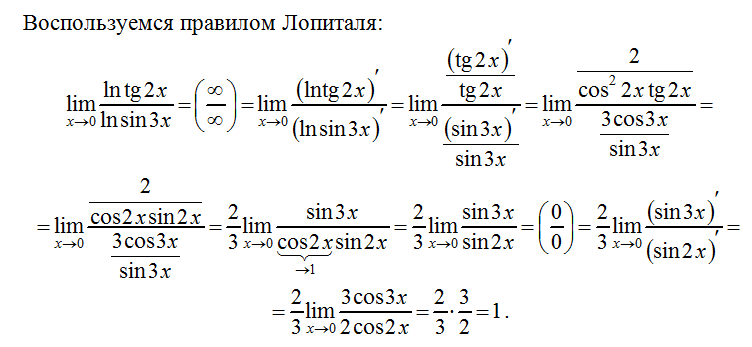
Чтобы умножить числитель этой дроби, мы можем использовать формулу разности квадратов: (𝑎−𝑏)(𝑎+𝑏)=𝑎−𝑏. Поскольку квадрат отменяет квадратный корень из первого члена, это выражение упрощается до 16𝑥 – 5𝑥- (4𝑥) √16𝑥 – 5𝑥+4𝑥 = 16𝑥 – 5𝑥 – 16𝑥√16𝑥 – 5𝑥+4𝑥 = −5𝑥√16𝑥 – 5𝑥+4𝑥.
Теперь, когда у нас есть упростив данную функцию, рассмотрим предел на бесконечности. Мы можем написать limlim→∞→∞√16𝑥−5𝑥−4𝑥=−5𝑥√16𝑥−5𝑥+4𝑥.
Мы знаем, что предел на положительной бесконечности описывает поведение значения функции при 𝑥 становится больше. Рассмотрим поведение числителя и знаменателя частного отдельно для больших значений из 𝑥.
Чтобы найти предел на бесконечности функции частного, мы умножаем числитель и знаменатель на величину, обратную
термин высшей степени. Числитель частного представляет собой многочлен, где член высшей степени равен 𝑥. В знаменателе у нас есть сумма функции квадратного корня, √16𝑥−5𝑥, и полинома,
4𝑥.
Хотя выражение квадратного корня содержит член второй степени 16𝑥, это
член находится под квадратным корнем, что означает, что он ведет себя как √16𝑥=4𝑥, который имеет то же самое
степень как полиномиальный член. Следовательно, член высшей степени знаменателя также равен 𝑥.
Таким образом, мы можем умножить числитель и знаменатель этого частного на 1𝑥, что приводит к −5𝑥√16𝑥−5𝑥+4𝑥=−5𝑥×√16𝑥−5𝑥+4𝑥×=−5×(16𝑥−5𝑥)+4=−516−+4.
Используя предельные законы, мы можем написать limlim→∞→∞−516−+4=−516−+4.
Напомним, что для любого действительного числа 𝑎 lim→∞𝑎𝑥=0.
Это означает, что lim→∞5𝑥=0.
Подставляя этот предел выше, мы получаем limlim→∞→∞√16𝑥−5𝑥−4𝑥=−516−+4=−5√16+4=−54+4=−58.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые моменты
- Если значения 𝑓(𝑥) приближаются к некоторому конечному значению 𝐿 как значения
𝑥 стремятся к бесконечности, то мы говорим, что существует предел 𝑓(𝑥) в бесконечности
и равно 𝐿, и мы обозначаем это как
lim→∞𝑓(𝑥)=𝐿. Аналогично определяется предел на отрицательной бесконечности.
- Если значения 𝑓(𝑥) неограниченно увеличиваются (или уменьшаются) при стремлении 𝑥 до бесконечности, то говорят, что предел 𝑓(𝑥) на бесконечности равен положительной (или отрицательной) бесконечности.
- Предельные законы применяются тем же образом к пределу в бесконечности, пока правая часть тождества не приводит в неопределенной форме: 00,∞∞,0⋅∞ или ∞−∞.
- Полиномиальная функция на бесконечности ведет себя как ее старший член, который является членом, содержащим наивысшую степень 𝑥.
- Для любой константы 𝑎 и положительного числа 𝑚, lim→±∞𝑎𝑥=0.
- Пусть 𝑝(𝑥) и 𝑞(𝑥) полиномы, и пусть 𝑚
быть степенью знаменателя 𝑞(𝑥). Чтобы найти предел lim→±∞𝑝(𝑥)𝑞(𝑥), нам нужно
- умножить числитель и знаменатель частного на 1𝑥,
- упростить числитель и знаменатель частного,
- применить правило lim→±∞𝑎𝑥=0 и найти ответ.
Аналогично определяется предел на отрицательной бесконечности.
Пределы в бесконечности: правила, комплекс и график
Вы становитесь больше или приближаетесь к тому, на что смотрите? Перспектива может изменить все! В этой статье вы увидите, что происходит, когда входные данные функции становятся достаточно большими.
Оценка пределов в бесконечности
Знаете ли вы, что существует несколько способов думать о бесконечных пределах и оценивать их? Один из способов — это то, что происходит, когда вы получаете вертикальную асимптоту. Для получения дополнительной информации о таком бесконечном пределе см. разделы «Односторонние пределы» и «Бесконечные пределы».
Другой вид бесконечного предела — это размышления о том, что происходит со значениями функции \(f(x)\), когда \(x\) становится очень большим, и это то, что исследуется здесь с использованием определения, полезных правил и графиков. . Итак, читайте дальше, чтобы узнать, как оценивать пределы на бесконечности!
Определение предела в бесконечности
Помните, что символ \(\infty\) не представляет действительное число.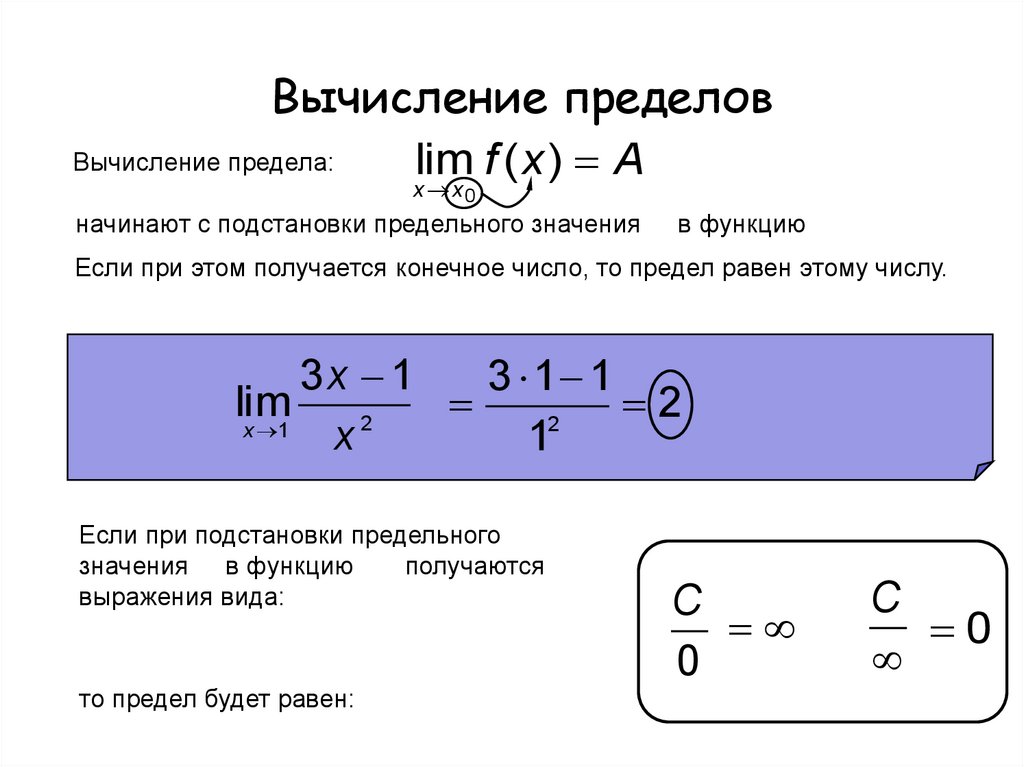
Вместо этого он описывает поведение значений функции, которые становятся все больше и больше, точно так же, как \(-\infty\) описывает поведение функции, которая становится все более и более отрицательной. Поэтому, если вы видите
\[\lim_{x\to\infty}f(x)=L,\]
, это не означает, что вы можете использовать \(\infty\) как значение функции ! Написание предела таким образом — это просто сокращение, чтобы дать вам лучшее представление о том, что делает функция. Итак, сначала давайте посмотрим на определение, а затем на пример. 9{-x}+1,\) и решить, существует ли
\[\lim_{x\to\infty}f(x)=L \]
.
Решение
Сначала давайте посмотрим на график функции. Из того, что вы знаете об экспоненциальных функциях (см. Экспоненциальные функции), хорошим кандидатом на предел является \(L=1\). Итак, на том же графике, что и функция, нарисуйте линии \(y=1\), \(y=1-\epsilon=0,98\) и \(y=1+\epsilon=1,02\). Хотя вы точно не знаете, какое значение имеет \(\epsilon\), вы знаете, что это небольшое положительное число.
Рис. 1. График функции для нахождения предела на бесконечности
Итак, вы можете видеть, что для приведенного выше графика, пока \(x>4\) график \(f(x)\) находится между линиями \(y=1-\epsilon\) и \(y=1+\epsilon\). Но что произойдет, если у вас есть еще меньшее значение \(\epsilon\)?
На приведенном ниже графике исходные линии присутствуют, но теперь есть две дополнительные линии, \(y=1-\epsilon_{1}=0,0993\) и \(y=1+\epsilon_{1}=1,007 \), где \(\epsilon_{1}\) — некоторое число, меньшее, чем \(\epsilon\).
Рис. 2. График с меньшим значением эпсилон для нахождения предела на бесконечности \(x>7\), чтобы функция попала в ловушку между \(y=1-\epsilon_{1}\) и \(y=1+\epsilon_{1}.\)
Обычно значение Вы обнаружите, что \(N\) будет зависеть как от функции, так и от значения \(\epsilon\), и поскольку вы берете меньшие \(\epsilon\) значения, вам потребуется большее значение для \(N\). 9{-x}+1=1.\]
Теперь может случиться так, что предел как \(x\to\infty\) не существует.
Рассмотрим функцию \(f(x)=\sin x\) . Существует ли
\[\lim_{x\to\infty}f(x)\]
?
Решение
Первое, что вам нужно сделать, если вы хотите найти предел, это выбрать кандидата на значение предела \(L\). Но если вы попытаетесь выбрать одно значение для \(L\), скажем, \(L=1\), вы всегда найдете значения функции для \(f(x)=\sin (x)\), которые превышают \ (\dfrac{1}{2}\) от \(L\), потому что функция синуса колеблется между \(-1\) и \(1\). На самом деле, для любого \(L\), который вы пытаетесь выбрать, колебание синусоидальной функции всегда будет проблемой. Так
\[\lim_{x\to\infty} \sin x\]
не существует.
Иногда при \(x\to \infty\) значения функции продолжают увеличиваться, как в случае с функцией \(f(x)=x\). Так как это происходит со многими функциями, для этого поведения существует специальное определение.
Мы говорим, что функция \(f(x)\) имеет бесконечный предел на бесконечности , и пишем
\[\lim_{x\to\infty}f(x)=\infty,\]
если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)>M\) для всех \(x>N.
\)
Это не то же самое, что сказать, что предел существует или что функция на самом деле “упирается” в бесконечность. Запись
\[\lim_{x\to\infty}f(x)=\infty\]
– это просто сокращение для того, чтобы сказать, что функция становится все больше и больше, когда вы берете \(x\), чтобы стать больше и больше.
Возьмите функцию \(f(x)=\sqrt{x}\) и покажите, что
\[\lim_{x\to\infty}f(x)=\infty.\]
Решение
Чтобы показать, что предел бесконечен, возьмем фиксированное \(M>0\). Вы хотите, чтобы \(x>N\) означало, что \(f(x)>M\), или, другими словами, что \(\sqrt{x}>M\). 92}=M,\]
, и все это верно, потому что вы знаете, что \(N\) и \(M\) положительны. Таким образом, вы показали, что
\[\lim_{x\to\infty}f(x)=\infty.\]
Пределы на отрицательной бесконечности
Подобно пределу на бесконечности, вы можете определить предел на отрицательной бесконечность.
Мы говорим, что функция \(f(x)\) имеет предел на отрицательной бесконечности , если существует действительное число \(L\) такое, что для всех \(\epsilon>0\) существует \( N>0\) такой, что
\[|f(x)-L|<\epsilon\]
для всех \(x<-N\), и мы пишем
\[\lim_{x\to -\infty}=L.
\]
Вы также можете определить функцию, имеющую предел в бесконечности, равный отрицательной бесконечности. Обратите внимание, что это очень похоже на определение выше.
Мы говорим, что функция \(f(x)\) имеет отрицательный бесконечный предел на бесконечности , и пишем
\[\lim_{x\to\infty}f(x)=-\infty, \]
, если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)<-M\) для всех \(x>N.\)
Конечно, то, что вы можете сделать в положительном направлении, вы можете сделать и в отрицательном.
Мы говорим, что функция \(f(x)\) имеет бесконечный предел на отрицательной бесконечности , и пишем
\[\lim_{x\to-\infty}f(x)=\infty,\]
если для всех \(M>0\) существует \(N>0\) такое, что \(f(x)>M\) для всех \(x<-N.\)
И, наконец, отрицательный бесконечный предел на отрицательной бесконечности.
Мы говорим, что функция \(f(x)\) имеет отрицательное число бесконечный предел на отрицательной бесконечности , и напишите
\[\lim_{x\to -\infty} f(x)=-\infty,\]
если для всех \(M>0\) существует такое \(N>0\), что \(f(x)<-M\) для всех \(x<-N.
\)
Нахождение бесконечного предела по графу
Иногда может быть очень полезно постройте график функции и посмотрите на таблицу значений при попытке найти бесконечный предел. Это особенно верно, когда у вас может быть не очень хорошее представление о том, как выглядит функция.
Используя функцию
\[f(x)=\frac{1}{x}\sin x,\]
найти
\[\lim_{x\to\infty} f(x).\ ]
Решение
Сначала сделайте график функции и таблицу значений функции. На графике ниже вы можете увидеть точки в таблице, нанесенные на функцию.
Рис. 3. Использование графика для нахождения предела функции.
| \(х\) | \(f(х)\) | ||||||||||
| \(10\) | \ (-0,0544 \) | ||||||||||
| \ (20 \) | \ (0,0456 \) | ||||||||||
| \ (30 \) | \ (-0,0329 \) | ||||||||||
| \ (-0,0329 \) | |||||||||||
| \ (-0,0329 \) | |||||||||||
| \ (-0,0329 \) | |||||||||||
| \ (0,0329 \) | \(0. 0186\) | ||||||||||
| \(50\) | \(-0.0052\) | ||||||||||
| \(60\) | \(-0.0050\) | ||||||||||
| \(70\) | \(0,0110\) | ||||||||||
| \(80\) | \(-0,0124\) | ||||||||||
| \(90\) | \(0,00943)| \ (100 \) | \ (-0,0050 \) | | ||||||||
| \ (200 \) | \ (-0,0043 \) | ||||||||||
| \ (300 \) | \ (-0,0033 \) | \ (300 \)\ (-0,0033 \) | \)|||||||||
| \(400\) | \(-0,0021\) | ||||||||||
| \(500\) | \(-0,0009\) |
| \ (x \) | \ (f (x) \) | ||||||||||
| \ (10 \) | \ (-0,0544 \) | ||||||||||
| \ (20 \) | \ (200043 | \ (20 \) | \ ( | \ (200043 | \ (20. | \ (200043 | \ (200043 | \ (200043 | \ (200043 | \ (200043 | |
| \. 0,0456 \) | |||||||||||
| \ (30 \) | \ (-0,0329 \) | ||||||||||
| \ (40 \) | \ (0,0186 \) | ||||||||||
| \ (50 \) | \ (50 \) | \ (50 \) | \ (50 \) | \ (50 \) | |||||||
| \ (50 \) | |||||||||||
| \ (50 \) | |||||||||||
| \. 0,0052\) | |||||||||||
| \(60\) | \(0,0050\) | ||||||||||
| (\70\) | \(0,0110\) | ||||||||||
| \ (80 \) | \ (-0,0124 \) | ||||||||||
| \ (90 \) | \ (0,0099 \) | ||||||||||
| \ (100 \) | \ (0,00505055059 \ (1003 \ (0,005055055039) | \ (100 \) | \ (0,00505505039 | \ (100 \) | \ (0,0050 | ||||||
\. |
Таблица 2.- Точки графика.
Сдвинув окно графика, намного легче увидеть, что значения функции приближаются к нулю как \(x\to\infty\). Теперь вы можете сказать, что
\[\lim_{x\to\infty}f(x)=0.\]
Давайте рассмотрим другой пример.
При поиске предела на бесконечности важно сочетать графики и таблицы. Например, если вы возьмете функцию \(f(x)=\sin x,\), вы можете составить следующую таблицу значений:
| \(x\) | \(\sin(x)\) |
| \(0\) | \(0\) | \(0\) |
| \(100\pi\) | \(0\) |
| \(1000 \pi\) | \(0\) | 90 Таблица значений функции. может привести вас к мысли, что предел на бесконечности равен нулю. Однако, если вы нарисуете функцию, вы увидите, что \(f(x)=\sin x\) продолжает колебаться независимо от того, насколько большими вы берете значения \(x\). Таким образом, просто просмотр таблицы может ввести в заблуждение, если вы не будете осторожны в выборе значений \(x\), которые вы в нее введете. Зная, что вы делаете с функцией синуса, вы можете с уверенностью сказать, что \[\lim_{x\to\infty}\sin x\]не существует.Обзор поведения функции синуса см. в разделе Тригонометрические функции. Примеры бесконечных пределовСуществует специальное название для случаев, когда существует предел на бесконечности или предел на отрицательной бесконечности функции. Если \[\lim_{x\to\pm\infty}f(x)=L,\] , где \(L\) – действительное число, то мы говорим, что строка \(y=L \) является горизонтальной асимптотой для \(f(x)\). Вы уже видели примеры функций с горизонтальными асимптотами в исчислении, это просто дает вам точное математическое определение. Давайте посмотрим на пример. 93}.\end{align}\] Используя то, что вы знаете о многочленах, вы можете видеть, что на самом деле эта функция обладает тем свойством, что \[\lim_{x\to\infty}f(x)=5 ,\] и что \[\lim_{x\to-\infty}f(x)=5,\] , поэтому эта функция имеет \(y=5\) в качестве горизонтальной асимптоты. Правила пределов в бесконечностиПодобно законам пределов, существуют свойства пределов, которые полезно знать, когда вы смотрите на \(x\to\infty\). Предположим, что \(L\), \(M\) и \(k\) — действительные числа, причем \(f\) и \(g\) — такие функции, что \[\lim_{x \to\pm\infty}f(x)=L\quad \text{and}\quad \lim_{x\to\pm\infty}g(x)=M.\] Тогда верно следующее, Правило суммы. \[\lim_{x\to\pm\infty}(f(x)+g(x))=L+M.\] Правило различия . \[\lim_{x\to\pm\infty} (f(x)-g(x))=L-M.\] Правило продукта . \[\lim_{x\to\pm\infty}(f(x)\cdot g(x))=L\cdot M.\] Постоянное множественное правило. \[\lim_{x\to\pm \infty}k\cdot f(x)=k\cdot L.\] Частное правило. Если \(M\neq 0\), то \[\lim_{x\to\pm\infty}\frac{f(x)}{g(x)}=\frac{L}{M} .\] Силовое правило. Можете ли вы применить приведенное выше правило частных, чтобы найти \[\lim_{x\to\infty}\dfrac{5x+\sin x}{x}? \] Решение Если вы попытаетесь взять \(f(x)=5x+\sin x\) и \(g(x)=x\), то обе эти функции имеют бесконечный предел на бесконечности , поэтому вы не можете применить правило частного. Вместо этого вы можете сначала сделать небольшую алгебру, \[\begin{align} \frac{5x+\sin x}{x} &=\frac{5x}{x}+\frac{1}{x}\ sin x\\ &=5+\frac{1}{x}\sin x. \конец{выравнивание}\] Если взять \(f(x)=5\) и \(g(x)=\frac{1}{x}\sin x\), то из приведенной выше работы известно, что \[\lim_{ x\to\infty}f(x)=\lim_{x\to\infty}5=5,\] и \[\lim_{x\to\infty}\frac{1}{x} \sin(x)=0,\] , так что вы можете использовать правило суммы, чтобы получить это, \[\begin{align} \lim_{x\to\infty}\frac{5x+\sin x}{ x} &=\lim_{x\to\infty}5+\lim_{x\to\infty}\frac{1}{x}\sin x \\ &=5+0\\ &=5. Так что нет, вы не можете использовать правило частного, но вы можете использовать немного алгебры, а затем правило суммы, чтобы найти предел. Один из наиболее важных результатов о пределах, Теорема Сжатия, также верен для пределов на бесконечности. Теорема сжатия для пределов в бесконечности. Предположим, что \[g(x)\le f(x)\le h(x),\] и \[\lim_{x\to\pm\infty}g(x)= \lim_{x\to\pm\infty}h(x)=L,\] , затем \[\lim_{x\to\pm\infty}f(x)=L.\] Примечание что на самом деле важно только то, что \(g(x)\le f(x) \le h(x)\) верно для очень больших значений \(x\), если вы пытаетесь найти предел как \(x \to\infty\), или что это верно для очень отрицательных значений, если вы пытаетесь найти предел как \(x\to -\infty.\) 92)+3\sin x-\cos x}{x}=0.\] Пределы тригонометрических функций на бесконечности Вы можете задаться вопросом о пределах тригонометрических функций. В разделах выше есть примеры с функциями синуса и косинуса. Бесконечные пределы – Ключевые выводы
|
r\) определено для всех \(x>0\), то 9г}\\ &=0. \end{align}\]
Если \(r,s\in\mathbb{Z}\), где \(s\neq 0\), то
\end{align}\]
Те же концепции могут быть применены к любой триггерной функции, обратной триггерной функции или гиперболической триггерной функции. Дополнительные сведения и примеры см. в статьях Тригонометрические функции, Гиперболические функции, Обратные функции и Обратные тригонометрические функции.