Пределы высшая математика: Элементы высшей математики: Раздел 1. Теория пределов

Свойства пределов в высшей математике с примерами

Свойства пределов справедливы как для пределов числовых последовательностей, так и для пределов функций. Свойства справедливы как для , так и для .

1. Предел суммы переменных равен сумме их пределов

2. Предел произведения переменных равен произведению их пределов

3. Предел дроби двух переменных равен дроби их пределу, если предел делителя отличен от нуля:

, если .

4. Постоянный множитель выносится за знак предела .

5. Предел постоянной равен самой постоянной, , где .

Примеры выполнения задания

Пример:

Найти пределы числовой последовательности (пункт а) и функций. В пункте б) воспользоваться первым замечательным пределом, в пункте в) — свойством эквивалентности бесконечно малых.

Решение:

Вычисление предела по каждому пункту рассмотрим на примерах

Пункт a)

.

Решение:

В задачах этого пункта имеет место неопределённость вида . Чтобы раскрыть неопределённость вида , нужно разделить числитель и знаменатель на наивысшую степень переменной, входящую в выражение. В результате, если многочлены числителя и знаменателя одинаковой степени, предел равен отношению старших коэффициентов числителя и знаменателя. Если в числителе степень многочлена выше, чем в знаменателе, то предел равен бесконечности. Если степень числителя ниже степени знаменателя, то предел равен нулю.

. При числитель и знаменатель дроби — бесконечно большие величины, неопределенность вида . Для раскрытия неопределённости разделим числитель и знаменатель на наибольшую степень переменной, то есть, разделим на .

Пункт б)

Примеры вычисления пределов с помощью первого замечательного предела:

Решение:

Вычисляя числитель и знаменатель заданных пределов при , получаем неопределенность вида .

. Умножив числитель и знаменатель на 2, получили первый замечательный предел.

Пункт в)

Используя эквивалентность бесконечно малых величин, вычислить пределы: .

Решение:

При величины . Алгебраическая сумма бесконечно малых эквивалентна бесконечно малой низшего порядка малости (). В числителе и знаменателе дробей — бесконечно малые величины. Согласно теореме 3, предел дроби двух бесконечно малых сохраняет своё значение при замене этих бесконечно малых им эквивалентными. Вычисляем пределы, заменяя бесконечно малые величины им эквивалентными, используя таблицу 1.

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Высшая математика для 1 курса

Возможно вам будут полезны эти страницы:

3 Функции. Пределы. Непрерывность – СтудИзба

Глава 3.  Функции. Пределы. Непрерывность.

§1. Множества. Логическая символика.

аÎА         аÏА        Æ                                АÌВ     “аÎА Þ аÎВ          А = В, если  АÌВ и ВÌА

1) А = {а₁,а₂,…а_к} – перечисление элементов        2) А = {хÎТ½a(х)} – с помощью свойства (формулы)

АÈВ = {хïхÎА или хÎВ}              АÇВ = {хïхÎА и хÎВ}                 А В = {хïхÎА, хÏВ}  

a,b – утверждения.         – отрицание.          aÞb – импликация.          aÛb – эквивалентность.

aÙb – конъюнкция.  aÚb – дизъюнкция.                      “хÎХ  a(х)          ” – квантор всеобщности

      $хÎХ  a(х)        $ – квантор существования                     $!хÎХ  a(х)    

Рекомендуемые файлы

        §2. Функции вещественной переменной.

D Ì R       x Î D           f ( x )          E = {yÎRïy = f ( x ), x Î D}         f : D ® E        y = f ( x )

f : D ® E             “x₁,x₂ÎD      x₁ ¹ x₂ Þ f ( x₁ ) ¹ f ( x₂ )                “yÎE   $!xÎD : f ( x ) = y     

  f^-1 : E ® D       x = f^-1 ( y )    обратная функция

f : X ® Y, g : Y ® Z.   Композиция ( сложная функция)  h = g

° f  : X ® Z       h ( x ) = g ( f ( x ))

Элементарные функции.   1. y = x^a, aÎ R.      2. y = a^x, a > 0, a ¹ 1.      3. y = log_ax,   a > 0, a ¹ 1.

4. y = sin x,  y = cos x,  y = tg x,  y = ctg x.  5. y = arcsin x,  y = arccos x,  y = arctg x,  y = arcctg x.

G = { ( x, y ) Î R² ï x Î D, y = f ( x ) }

§3. Предел последовательности вещественных чисел.

Последовательность   f : N ® R         f

( n ) = x_n– n-й член последовательности        { x_n } _nÎN

Число а называется пределом последовательности { x_n }_nÎN   ( = a ), если

         “e>0  $N(e):  “n> N(e)   ïx_n – a ï< e                                Сходящаяся последовательность

Геом.

смысл. Вне интервала ( а – e , а + e ) может находиться лишь конечное число x_n

Свойства. Если  = a,     = b, то  1.  = a ± b         2.  = a^.b

Последовательность:          

Число а называется пределом последовательности  , то есть  , если

  : .

Сходящаяся последовательность.

Геометрический смысл:

Вне интервала  может находиться лишь конечное число членов последовательности.

Свойства:

Если  , то

  – бесконечно малая, если  .

  – бесконечно большая, если

Число    – основание натурального логарифма.

Теорема 1 ( о сжатой последовательности).

Если   и  , то  .

 называется ограниченной, если 

Теорема 2.

Если    – ограничена и не убывает (т. е. ), то .

Следствие:

Если    – ограничена и не возрастает (т.е. ), то .

Теорема 3.

Если , то   – ограничена.

§4.  Предел функции.

Пусть функция  определена на множестве D. Число а называется пределом функции  в точке

x₀ (), если 

  такое, что  .

«Замечательные» пределы:

1. 

Свойства:

Если  , то

§5.  Непрерывные функции. Теоремы Коши и Вейерштрасса.

Односторонний предел справа (правосторонний предел)  

  такое, что  .

Односторонний предел слева (левосторонний предел)  

  такое, что  .

                             

y=f(x)   D   непрерывной в точке  x₀

а) х₀Î D          б)  $          в)

Разрывы

1) $ , но х₀ Ï D  или     –  устранимый разрыв.

2)  , но

а₊¹ а_–   или    – разрыв 1-го рода.

3) разрыв 2-го рода.

f Î C( a,b )   f( x ) непрерывна на интервале, если она непрерывна во всех его точках.

f Î C[ a,b ]   f( x ) непрерывна на отрезке, если она непрерывна на интервале ( a,b ) и

Теорема 1.  Если  f(x)  и  g(x)  непрерывны в точке х

0,  то функции   f(x) ± g(x),  f(x) ^. g(x),  f(x) / g(x)       ( при g(x₀)¹0 )  также непрерывны в точке х₀.

Теорема 2. Если   f Î C[ a,b],  f(a ) ^. f(b) < 0 , то $ cÎ (a,b): f(c) = 0.

Теорема 3. Если   f Î C< a,b>,

принимает  значения  A,B  ( A < B ) на промежутке  < a,b>, то “CÎ[A,B] $ cÎ(a,b): f(c) = C.

Теорема 4. Если   f Î C[ a,b],  то она ограничена на [ a,b] .

Теорема 5. Если   f Î C[ a,b],  то существуют точки, в которых достигаются наибольшее и наименьшее значения на отрезке.

§6.  Вычисление пределов. Практические советы.

1. Если  f(x) – бесконечно малая (б.м.) при x®x₀ , то 1/f(x) – бесконечно большая (б.б.) при  x®x₀.

2. Если  f(x) – б.б.  при x®x₀ , то 1/f(x) – б.м.  при  x®x₀.

3. Если  f(x) – б.м.  при x®x₀, g(x) – б.б.  при x®x₀, то 

4. Если  f(x) – б.м.  при x®x₀, ,  то 

                            f(x)/g(x) – б.м.  при x®x₀,  g(x)/f(x) – б.б.  при x®x₀.

5. Пусть  f(x) и g(x) – б.м.  при x®x₀, рассмотрим 

Если  р = 0, то  f(x) величина большего порядка малости, чем  g(x) при x®x₀            f(x)=o(g(x))

Если  р = ¥, то  f(x) величина меньшего порядка малости, чем  g(x) при x®x₀            g(x)=o(f(x))

Обратите внимание на лекцию “Название нашей страный и название русского народа”.

Если  р = С, то  f(x)  и g(x) величины одного порядка малости при x®x₀      

   g(x)=О(f(x))  или   f(x)» Cg(x). Таблица эквивалентностей.

Если x₀ ¹ 0, то можно сделать замену переменной   у = x–x₀® 0, откуда    х = у + х₀

При x®¥  предел отношения степенных функций зависит от старших степеней, при  x® 0  – от младших.

 

Высшая математика для чайников. Предел функции. by Виосагмир И.А.

2011

год

Виосагмир И.А. Предел функции 2011 год

Высшая математика для

чайников. Предел функции.

viosagmir@gmail

2011 год

Предел функции

Введение

Ну что же… Я приветствую Вас в своей первой книге, посвященной пределам функции. Это первая часть из моей будущей серии “высшая математика для чайников”. Название книги уже должно Вам многое о ней рассказать, но Вы его можете совершенно не так понять. Эта книга посвящена не “чайникам”, а всем тем, кому нелегко понять то, что творят профессоры в своих книгах. Я уверен, что Вы меня понимаете. Я сам находился и нахожусь в такой ситуации, что просто вынужден прочитывать одно и то же предложение несколько раз. Это нормально? Я думаю – нет.

Так чем же моя книга отличается от всех других? Во-первых, здесь нормальный язык, а не “заумный”; во-вторых здесь разобрана масса примеров, которая, кстати, наверняка, пригодится вам; в-третьих, текст имеет существенное различие между собой – главные вещи выделены определенными маркерами, и наконец, моя цель лишь одна – ваше понимание. От Вас требуется только одного: желания и умения. “Умения?” – спросите Вы. Да! Умения и .

Вообще рекомендуется завести отдельно тетрадку листов этак на 65, и все в ней писать. Все, что написано в этой книге. Результат будет впечатляющим, это я Вам обещаю. Так же лучше пользоваться разноцветными фломастерами. Ну что же, господа… Я хочу Вам пожелать успехов и понимания. Если Вы добьете эту книгу, Вы сможете многое!!!

В моей книге будут встречаться некоторые обозначения. Крайне рекомендую им следовать.

• учить обязательно! – рекомендуется попробовать сделать самим.

• можно не учить, но нужно понять!

2011 год

Глава 1. Предел функции.

Пусть ᡶ ㎘ числовая переменная величина, ᡐ ㎘ область ее изменения. Если каждому числу ᡶ ∈ ᡐ поставлено в соответствие некоторое число ᡷ, то говорят, что на множестве ᡐ определена функция, и пишут ᡷ 㐄 ᡘ䙦ᡶ䙧.

Надеюсь это Вам понятно, но я на всякий случай поясню. Множество ᡐ в данном случае – плоскость, состоящая из двух координатных осей – 0X и 0Y. Это вам должно быть известно еще со школы. Если Вы забыли это, открывайте класс 7 – 8 и повторяйте. Для примера, на рис. 1 изображена функция ᡷ 㐄 ᡶ⡰. Оси 0X и 0Y образуют ᡐ ㎘ область ее изменения. Мы прекрасно видим на рис. 1, как ведет себя функция. В таком случае говорят, что на множестве ᡐ определена функция ᡷ 㐄 ᡶ⡰.

Совокупность ᡑ всех частных значений функции называется множеством значений ᡘ䙦ᡶ䙧.

Другими словами, множество значений – это промежуток по оси OY, где определена функция. Для примера, рассмотрим рис. 1. ᡘ䙦ᡶ䙧㐄 ᡶ⡰ – отсюда сразу видно, что ᡘ䙦ᡶ䙧㐈 0, т.к. ᡶ⡰㐈 0. На рисунке это явно видно. В данном случае область значений 㐄 䙰0; ㎗∞䙱. Запомните, множество значений смотрим по 0Y!

Совокупность всех ᡶ называется областью определения ᡘ䙦ᡶ䙧.

Делаем вывод из предыдущих соображений и понимаем, что множество определений смотрим по 0ᡐ. В нашем случае ОДЗ = 䙰㎘∞;㎗∞䙱.

Точка ᡓ 䙦ᡓ ∈ ᡐ или ᡓ 㐅 ᡐ䙧 называется предельной точкой множества ᡐ, если в любой окрестности точки ᡓ имеются точки множества ᡐ, отличные от ᡓ.

Здесь я дополнять ничего не буду. И так все ясно. Можно лишь добавить, что в нашем случае ᡓ ㎘ предельная точка множества ᡐ ㎘ области определения функции ᡘ䙦ᡶ䙧.

Содержание:

1) Предел функции в точке 2) Теоремы о пределах 3) Односторонние пределы 4) Предел, при ᡶ → ∞ 5) Бесконечно большие функции 6) Графики элементарных функций

1. Предел функции в точке.

Рис. 1

ᡶ㎘независимая переменная (аргумент). ᡐ㎘область определения функции ᡘ䙦ᡶ䙧. ᡷ㎘частное значение функции ᡘ䙦ᡶ䙧 в точке.

2011 год

Так, давайте перед определением я в общих словах объясню, что такое предел функции. Число b, к которому стремится функция при стремлении x к числу ᡓ, называется пределом функции. Вот так это все записывается:

limけ→〨ᡘ䙦ᡶ䙧㐄 ᡔ

Например, ᡘ䙦ᡶ䙧㐄 ᡶ⡰. Нам нужно узнать, к чему стремится (не равна!) функция, при ᡶ → 2. Сначала запишем предел:

limけ→⡰ᡘ䙦ᡶ䙧㐄limけ→⡰ᡶ⡰

Теперь пришло время взглянуть на график. Проведем параллельно 0ᡑ линию через точку 2 на оси 0ᡐ. Она пересекла наш график в точке 䙦2;4䙧. Опустим из этой точки на ось 0ᡑ перпендикуляр и… опа! Какое там значение? Все правильно, 4. Вот к чему стремится наша функция, при ᡶ → 2.

Сложно? Ну, нет, конечно! Вы, наверное, заметили, что если подставить в функцию ᡘ䙦ᡶ䙧 значение 2, то ответ будет таким же. Совершенно верно. Так и решаются эти “сложные” лимиты. Не забывайте проверять на определенность! Определенность, это, когда у нас есть понятный

результат. Неопределенность, когда нет понятного результата. Например: 䙴⦘⦘䙵 или 䙴⡨⡨䙵 – все это

неопределенность. Это очень важно, никогда не забывайте про это! Следовательно, у Вас должна быть в тетради вот такая запись (не забудьте нарисовать и рисунок):

け→⡰limᡘ䙦ᡶ䙧㐄limけ→⡰ᡶ⡰㐄 䙰2⡰䙱 㐄 4

Ну, с этим, в общем, все понятно. Потренируйтесь и посчитайте вот такие вот пределы:

limけ→⡱㐶

1

ᡶ

㑀; limけ→⡰ᡶ⡱; limけ→⡩ᡶ䙦け⡸⡰䙧ㄘ; limけ→⡷√

ᡶ

ᡶ⡰

То же самое происходит и для случая, когда ᡶ → ㎗∞ или к другому бесконечному числу:

け→⡸⦘lim ᡘ䙦ᡶ䙧㐄䙰㎗∞⡰䙱㐄 ㎗∞

А вот пример, где есть неопределенность:

け→⡨lim

sinᡶ ᡶ

Если мы подставим под ᡶ значение, равное 0, то вот, что у нас получится: 䙴⡨⡨䙵. А это

неопределенность, следовательно, решать мы не имеем права! Потом я Вас научу, как раскрывать неопределенность. Сейчас же вы должны не забывать про это. Подставили и проверили. Решается? Значит – определенность. Не решается? Ну что же, тогда потом решите. Когда все пройдете.

Давайте перейдем к формальностям, то есть к определениям.

2011 год

Пусть – 㐈 0㎘ произвольно. Тогда

|ᡶ⡰㎘4|㐄|䙦ᡶ ㎘2䙧⡰㎗4䙦ᡶ ㎘2䙧|㐉|ᡶ ㎘2|⡰㎗4|ᡶ ㎘2|㐉 –,

как только 0 㐇|ᡶ ㎘2|㐇√4㎗–㎘2 㐄√⡲⡸やや⡸⡰. Последнее неравенство тем более будет выполняться, если – √4㎗–㎗

㐈

–

2 √4㎗–

㐈

–

2 √4㎗4– ㎗–⡰

㐄

–

2䙦2㎗–䙧㐄 ‒䙦–䙧㐈|ᡶ ㎘2|.

Так, давайте все-таки рассмотрим этот пример более подробно.

1) Распишем определение:

Число 4 называется пределом функции ᡘ䙦ᡶ䙧㐄 ᡶ⡰ в точке 2 (при ᡶ → 2), если ∀ – 㐈 0 ∃ ‒ 㐈 0 такое, что ∀ ᡶ, удовлетворяющего условиям ᡶ ‵ ᡐ, 0 㐇|ᡶ ㎘2|㐇 ‒, выполняется неравенство |ᡶ⡰㎘4|㐇 –.

2) Упростим: a) Условие:

0 㐇|ᡶ ㎘2|㐇 ‒ ⟺ ㎘‒ 㐇 ᡶ ㎘2 㐇 ‒ ⟺ 2 ㎘‒ 㐇 ᡶ 㐇 2㎗‒ b) неравенство:

|ᡶ⡰㎘4|㐇 – ⟺ ㎘– 㐇 ᡶ⡰㎘4 㐇 – ⟺ 4㎘– 㐇 ᡶ⡰㐇 4㎗– 3) Поймем:

Число 4 называется пределом функции ᡘ䙦ᡶ䙧㐄 ᡶ⡰ в точке 2 (при ᡶ → 2), если ∀ – 㐈 0 ∃ ‒ 㐈 0 такое, что ∀ ᡶ, удовлетворяющего условиям ᡶ ‵ ᡐ, 2㎘‒ 㐇 ᡶ 㐇 2㎗‒, выполняется неравенство 4㎘– 㐇 ᡶ⡰㐇 4㎗–.

Все! Прочтите последнее определение, которое мы написали, используя график. Верно? Ну конечно верно! Этот способ я написал специально для вас, для понимания. Ни в какой литературе вы такого не найдете. Поэтому, если хотите по-настоящему все это быстро решать – пожалуйста! Да, объяснить, как это делается аналитически, я не

2011 год

уверен, что смогу. Пример я вам написал, теперь вы должны в нем сами разобраться, используя мой графический способ. Все строится от понимания, господа. Сейчас попробую объяснить все на аналитическом уровне.

No3. Для закрепления.

Доказать, используя определение Коши предела функции, что

けlim→⡲

ᡶ⡰−

ᡶ⡰−4ᡶ=

Шаг 1:

Зададим функцию ᡘ(ᡶ), которая является у нас выражением, стоящим у нас под знаком предела:

ᡘ䙦ᡶ䙧=

ᡶ⡰−

ᡶ⡰−4ᡶ

Поскольку мы рассматриваем предел, стремящийся к 4, нужно рассмотреть некоторую окрестность 4-ки, которая для данной функции определена. Например, интервал от 2 до 5.

4 ‵ (2,5)

Но! Заметьте, что функция у нас определена не всюду! Она не определена в 0 и при ᡶ=4. Надеюсь, Вы это понимаете, но на всякий случай распишу: ᡶ⡰−4ᡶ≠0→ ᡶ䙦ᡶ−4䙧≠0→䙶ᡶᡶ≠0≠4. Надеюсь все понятно. Так, отвлеклись, так что быстро идем дальше. Мы можем в принципе рассмотреть любой интервал, но нам такой удобнее 4 ‵ (2,5).

Шаг 2:

Запишем определение предела функции ᡘ(ᡶ) по Коши.

∀–>0,∃‒>0: ∀ᡶ≠4,|ᡶ−4|<‒⇒|ᡘ䙦ᡶ䙧−2|<–

Это значит: для любого – мы должны найти такое ‒, что как только x у нас отлично от 4 и x-4 по модулю не превосходит ‒ ⇒ |ᡘ䙦ᡶ䙧−2| должно не превосходить –.

Шаг 3:

Преобразуем выражение |ᡘ䙦ᡶ䙧−2|, ᡶ≠4.

2011 год

учебник и посмотрите там материал. Соответственно, Вы ничего не поймете, если не напишете собственноручно решение + графики. Это Вам небольшая подсказка. Нарисуйте! И все сразу станет ясно.

No1. Я забегаю немного вперед, но хотелось бы решить этот предел:

limけ→⡲

ᡶ⡰㎘

ᡶ⡰㎘4ᡶ

Если мы подставим 4 под ᡶ, у нас получится неопределенность:

け→⡲lim

ᡶ⡰㎘

ᡶ⡰㎘4ᡶ

㐄㐨

0

0

㐲㎘неопределенность!

Что делать? Все просто. А давайте ка упростим дробь!

ᡶ⡰㎘ ᡶ⡰㎘4ᡶ

㐄

䙦ᡶ ㎘4䙧䙦ᡶ ㎗4䙧

ᡶ䙦ᡶ ㎘4䙧

㐄

ᡶ ㎗

ᡶ

Все! Теперь, если мы подставим 4, у нас будет определенность, а, следовательно, мы можем решать.

け→⡲lim

ᡶ⡰㎘

ᡶ⡰㎘4ᡶ

㐄 limけ→⡲

ᡶ ㎗

ᡶ

㐄㐨

8

4

㐲㐄 2

Вывод: от неопределенности мы избавляемся с помощью преобразований.

No2. Посчитать предел:

limけ→⡰

ᡶ⡰㎘

ᡶ⡰㎗6ᡶ ㎘

Здесь все очень просто. Разложим на множители числитель и знаменатель. Рассказываю первый и последний раз, как это делать.

Что бы разложить знаменатель на множители, мы должны приравнять его к нулю и просто решить уравнение. Давайте сделаем это.

ᡶ⡰㎗6ᡶ ㎘16 㐄 0

Что бы решить квадратное уравнение, прежде всего нужно найти дискриминант по формуле:

ᠰ 㐄 ᡔ⡰㎘4ᡓᡕ

2011 год

ᡓ,ᡔ,ᡕ− элементы квадратного уравнения. В общем виде квадратное уравнение выглядит так:

ᡓᡶ⡰+ᡔᡶ+ᡕ=

Следовательно, в нашем случае ᡓ=1,ᡔ=6,ᡕ=−16. Подставляем значения и находим дискриминант:

ᠰ=36+4∙1∙16=

Далее находим корни квадратного уравнения, используя формулу

ᡶ⡩,⡰=

−ᡔ±√ᠰ

2 ᡓ

Подставляем и получаем:

ᡶ⡩,⡰=

−6±

2

=㐢

ᡶ⡩=

−6+

2 =

ᡶ⡰=

−6−

2 =−

Корни нашли, а значит мы очень близки к разложению на множители квадратного многочлена. Сначала запишем формулу:

ᡓᡶ⡰+ᡔᡶ+ᡕ=(ᡶ−ᡶ⡩)(ᡶ−ᡶ⡰)

Заметим, что не всякий многочлен можно так расписать. В данном случае у нас нет никаких противоречий, и, следовательно, это можно делать. Таким образом:

ᡶ⡰+6ᡶ−16=(ᡶ−2)(ᡶ+8)

Вот эту вещь вы должны уметь делать очень быстро. Ну, максимум – минута. Так что, если есть проблемы, сразуже их решайте.

В числитиле можно тоже разложить на множители. Это сделать гораздо проще, так как там разность квадратов. Напоминаю формулу:

ᡓ⡰−ᡔ⡰=(ᡓ−ᡔ)(ᡓ+ᡔ)

Таким образом:

ᡶ⡰−4=(ᡶ−2)(ᡶ+2)

И получаем наш предел:

limけ→⡰

ᡶ⡰−

ᡶ⡰+6ᡶ−16= limけ→⡰

(ᡶ−2)(ᡶ+2)

(ᡶ−2)(ᡶ+8)= limけ→⡰

(ᡶ−2)(ᡶ+2)

(ᡶ−2)(ᡶ+8)= limけ→⡰

ᡶ+

ᡶ+8=

4

10 =

2

5

Как видите, в общем-то решение в одну строчку.

No3. Посчитать предел:

2011 год

Итого:

け→⡩lim

ᡶ⡳㎘ᡶ⡲㎗2ᡶ⡰㎘5ᡶ ㎗

ᡶ⡱㎗4ᡶ⡰㎘7ᡶ ㎗2 㐄 limけ→⡩

䙦ᡶ ㎘1䙧䙦ᡶ⡲㎗2ᡶ ㎘3䙧

䙦ᡶ ㎘1䙧䙦ᡶ⡰㎗5ᡶ ㎘2䙧㐄 limけ→⡩

ᡶ⡲㎗2ᡶ ㎘

ᡶ⡰㎗5ᡶ ㎘2㐄

1㎗2㎘

1㎗5㎘2㐄

0

4 㐄 0

No5. Посчитать предел:

lim け→ゕ⡲

sinᡶ ㎘cosᡶ tgᡶ ㎘1 㐄 limけ→ゕ⡲

sinᡶ ㎘cosᡶ sinᡶ cosᡶ㎘

cosᡶ cosᡶ

㐄 lim け→ゕ⡲

sinᡶ ㎘cosᡶ sinᡶ ㎘cosᡶ cosᡶ

㐄 lim け→ゕ⡲

䙦sinᡶ ㎘cosᡶ䙧cosᡶ sinᡶ ㎘cosᡶ 㐄 limけ→ゕ⡲cosᡶ

㐄

√ 2

2

Определение 2 (предел функции по Гейне)

Предел функции по Гейне редко можно встретить где-нибудь в практике. От Вас требуется лишь одно – выучить его на всякий случай. Может быть и пригодится.

Подчеркнем, что понятие предела функции в точке ᡓ вводится только для предельных точек ᡓ области определения функции. Отметим, что при этом функция может быть и не определена в точке ᡓ, т.е., вообще говоря, ᡓ не принадлежит ᡐ.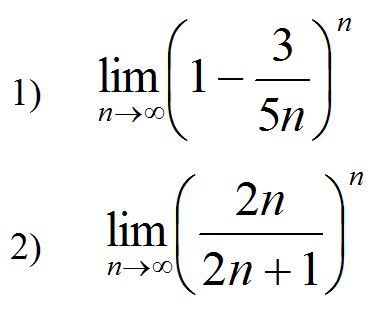

Число b называется пределом функции ᡘ䙦ᡶ䙧 в точке ᡓ, если для любой сходящейся к ᡓ последовательности 䙨ᡶぁ䙩 такой, что ᡶぁ∈ᡐ, ᡶぁ㐅ᡓ, соответствующая последовательность значений функции 䙨ᡘ䙦ᡶぁ䙧䙩 сходится к b.

Обозначение: limけ→〨ᡘ䙦ᡶ䙧㐄ᡔ или ᡘ䙦ᡶ䙧→ᡔ при ᡶ→ᡓ.

2011 год

Определения 1 и 2 предела функции эквивалентны.

Пусть ᡘ䙦ᡶ䙧 и ᡙ䙦ᡶ䙧 определены в некоторой окрестности точки ᡓ, кроме, может быть, самой точки ᡓ, и limけ→〨ᡘ䙦ᡶ䙧 㐄 ᡔ, limけ→〨ᡙ䙦ᡶ䙧 㐄 ᡕ. Тогда:

limけ→〨㐵ᡘ䙦ᡶ䙧㎗ᡙ䙦ᡶ䙧㐹㐄ᡔ㎗ᡕ; けlim→〨㐵ᡘ䙦ᡶ䙧㎘ᡙ䙦ᡶ䙧㐹㐄ᡔ㎘ᡕ

けlim→〨ᡘ䙦ᡶ䙧ᡙ䙦ᡶ䙧㐄ᡔᡕ; limけ→〨

ᡘ䙦ᡶ䙧

ᡙ䙦ᡶ䙧㐄

ᡔ

ᡕ при условии ᡕ㐅 0

Пусть ᡘ䙦ᡶ䙧, ᡙ䙦ᡶ䙧 и ᡠ䙦ᡶ䙧 определены в некоторой окрестности точки ᡓ, кроме, может быть, самой точки ᡓ, и удовлетворяют неравенствам ᡘ䙦ᡶ䙧㐉 ᡙ䙦ᡶ䙧㐉 ᡠ䙦ᡶ䙧. Пусть limけ→〨ᡘ䙦ᡶ䙧 㐄 limけ→〨ᡠ䙦ᡶ䙧㐄 ᡔ. Тогда limけ→〨ᡙ䙦ᡶ䙧 㐄 ᡔ.

Здесь, похоже, все понятно. Теоремы выражены четко и ясно, информация должна восприниматься легко. Если что-то не так, не волнуйтесь, примеры нас ждут впереди.

2. Теоремы о пределах

2011 год

Смотрим на график и видим, что функция при ᡶ → ㎗∞ стремится к 0.

け→⡸⦘lim

1

ᡶ

㐄㐨

1

㎗∞

㎘определенность㐲㐄 0 6) Если ᡶ → ㎘∞

Все то же самое:

け→⡹⦘lim

1

ᡶ㐄㐨

1

㎘∞㎘определенность㐲㐄 0

Последние два примера рекомендую запомнить. При раскрытии неопределенности, они нам потом очень понадобятся. Ну что, поняли суть? Ну, тогда формальности…

Определение 1 (предел функции по Коши)

Определение 2 (предел функции по Гейне)

В общем, добавить тут и нечего. Полная аналогия с предыдущими определениями по Коши и по Гейне, так что, если вы поняли, как доказываются пределы, то сможете доказать и односторонние. Структура доказательств та же.

Обозначения:

け→〨⡸⡨lim ᡘ䙦ᡶ䙧㐄 ᡔ && ᡘ䙦ᡓ ㎗0䙧㐄 ᡔ

Если существуют ᡘ䙦ᡓ ㎗0䙧 и ᡘ䙦ᡓ ㎘0䙧, причем ᡘ䙦ᡓ ㎗0䙧㐄 ᡘ䙦ᡓ ㎘0䙧㐄 ᡔ, то существует limけ→〨ᡘ䙦ᡶ䙧㐄 ᡔ.

Число b называется правым (левым) пределом функции ᡘ䙦ᡶ䙧 в точке a, если для любой сходящейся к a последовательности 䙨ᡶぁ䙩 такой, что ᡶぁ ‵ ᡐ,ᡶぁ㐈ᡓ 䙦ᡶぁ㐇ᡓ䙧, соответствующая последовательность значений функции 䙨ᡘ䙦ᡶぁ䙧䙩 сходится к b.

Число b называется правым (левым) пределом функции ᡘ䙦ᡶ䙧 в точке a, если ∀–㐈 0 ∃‒㐈 0 такое, что ∀ᡶ, удовлетворяющего условиям ᡶ‵ᡐ, ᡓ㐇ᡶ㐇ᡓ㎗‒ (ᡓ㎘‒㐇ᡶ㐇ᡓ䙧, выполняется неравенство |ᡘ䙦ᡶ䙧㎘ᡔ|㐇–.

2011 год

Если функция ᡘ䙦ᡶ䙧 определена в некоторой окрестности точки a, за исключением, быть может, самой точки a, и существует limけ→〨ᡘ䙦ᡶ䙧㐄 ᡔ, то существуют ᡘ䙦ᡓ ㎗0䙧 и ᡘ䙦ᡓ ㎘0䙧, причем ᡘ䙦ᡓ ㎗0䙧㐄 ᡘ䙦ᡓ ㎘0䙧㐄 ᡔ.

На всякий случай, рассмотрим пример на теорему 4. Давайте рассмотрим функцию ᡘ䙦ᡶ䙧㐄√ᡶ. Она изображена на рис. 4.

Давайте найдем пределы:

け→⡲⡸⡨lim √ᡶ㐄㐧√4㎗0㎘определенность㐱㐄 2

Почему 0 ни на что не повлиял? Да потому что ему незачем что-то менять. Функция определена в ᡶ 㐄 4, следовательно, нет никакой надобности брать ㎗0.

け→⡲⡹⡨lim √ᡶ㐄㐧√4㎗0㎘определенность㐱㐄 2

Все то же самое. Функция определена в ᡶ 㐄 4, следовательно, нет никакой надобности брать ㎘0. Этого никто не объясняет, потому что это вполне все логично.

Отсюда, по теореме 4:

け→⡲⡸⡨lim √ᡶ, limけ→⡲⡹⡨√ᡶ㎘существуют,причем limけ→⡲⡸⡨√ᡶ㐄 limけ→⡲⡹⡨√ᡶ㐄 2

Поэтому существует предел limけ→⡲√ᡶ㐄 2.

Так, это закрепили. А что, если мы рассмотрим ᡶ 㐄 0?

Ну, давайте проверять:

け→⡨⡸⡨lim √ᡶ㐄㐧√0㎗0㎘определенность㐱㐄 0

Этот предел существует. Посмотрите на функцию, и вы увидите, что она там определена.

け→⡨⡹⡨lim √ᡶ㐄㐧√0㎘0㎘неопределенность㐱㐄 предел не существует

Запомните раз и на всегда: корень не может быть отрицательным! Поэтому предела не существует! Но зато существует вот что:

け→⡨lim√ᡶ㐄㐧√ 0 ㎘определенность㐱㐄 0

Как видите, теорема 4 работает лишь в одну сторону. В ней нельзя поставить отрицание. Поэтому, друзья, будьте внимательны!

Рис. 4

2011 год

No4. Посчитать предел:

け→⦘lim

3ᡶ⡲㎘4ᡶ⡰㎗

2 ㎗5ᡶ ㎘2ᡶ⡲ 㐄 limけ→⦘

ᡶ⡲䙲3㎘ᡶ 4 ⡰㎗ᡶ 1 ⡲䙳

ᡶ⡲䙲ᡶ 2 ⡲㎗ᡶ 5 ⡱㎘2䙳

㐄 limけ→⦘

3㎘ᡶ 4 ⡰㎗ᡶ 1 ⡲

2

ᡶ⡲㎗

5

ᡶ⡱㎘

㐄㐨

3㎘0㎗

0㎗0㎘2㐲㐄 ㎘

3

2

No5. Посчитать предел:

け→⦘lim

2ᡶ⡱㎗ᡶ⡰㎘5ᡶ ㎗

6ᡶ⡰㎘ᡶ ㎗

㐄 limけ→⦘

ᡶ⡰䙲2ᡶ ㎗1㎘ 5 ᡶ㎗ᡶ 1 ⡰䙳

ᡶ⡰䙲6㎘ 1 ᡶ㎗ᡶ 1 ⡰䙳

㐄 limけ→⦘

2ᡶ ㎗1㎘ 5 ᡶ㎗ᡶ 1 ⡰

6 ㎘ 1 ᡶ㎗ᡶ 1 ⡰

㐄 limけ→⦘

2ᡶ ㎗

6

㐄 ∞

No6.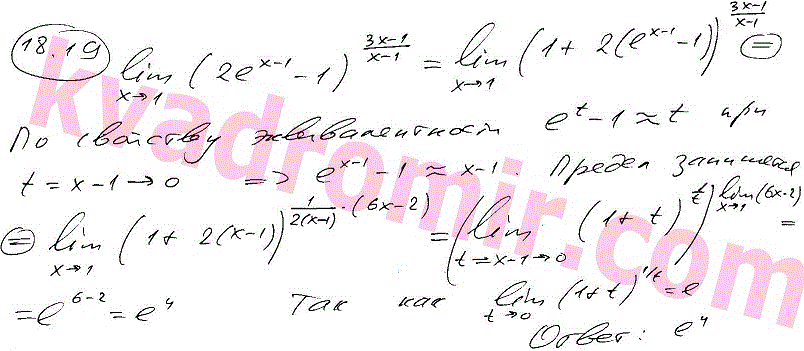 Посчитать предел:

け→⦘lim

1㎗2ᡶ⡱㎗4ᡶ⡳

4ᡶ⡰㎗ᡶ⡴

㐄 limけ→⦘

ᡶ⡴䙲ᡶ 1 ⡴㎗ᡶ 2 ⡱㎗ 4 ᡶ䙳

ᡶ⡴䙲ᡶ 4 ⡲㎗1䙳

㐄 limけ→⦘

1

ᡶ⡴㎗

2

ᡶ⡱㎗

4

ᡶ

4

ᡶ⡲㎗

㐄㐨

0㎗0㎗

0㎗1 㐲

㐄 0

Еще раз повторяю, когда дробь – тогда выносим!

Настало время поведать вам и вторую тайну. Если нам дано выражение вида ᠧ⡩㎙ᠧ⡰, не

поленитесь его помножить на 。。ㄗㄗ㎙。㎙。ㄘㄘ. Привожу пример:

け→⦘limᡶ⡰㎗ᡶ 㐄䙰∞㎗∞ ㎘неопределенность䙱㐄 limけ→⦘

䙦ᡶ⡰㎗ᡶ䙧∙䙦ᡶ⡰㎗ᡶ䙧

ᡶ⡰㎗ᡶ 㐄 limけ→⦘

ᡶ⡲㎗2ᡶ ㎗ᡶ⡰

ᡶ⡰㎗ᡶ

㐄 limけ→⦘

ᡶ⡰䙲ᡶ⡰㎗ 2 ᡶ㎗1䙳

ᡶ⡰䙲1㎗ 1 ᡶ䙳

㐄 limけ→⦘

ᡶ⡰㎗

1

㐄 limけ→⦘

ᡶ⡰䙲1㎗ᡶ 1 ⡰䙳

ᡶ⡰䙲ᡶ 1 ⡰䙳

㐄 limけ→⦘

1㎗ᡶ 1 ⡰

1

ᡶ⡰

㐄䙰 1 䙱㐄 1

Несомненно, в будущем вы так не будете все подробно расписывать. Вам будет достаточно нескольких действий, так что не волнуйтесь.

P. Как только встречаете

No1. Посчитать предел:

け→⦘lim㒓ᡶ⡲㎗8ᡶ⡰㎗3㎘㒓ᡶ⡲㎗ᡶ⡰

Сложно? Нет! На какой вид похоже? На ᠧ⡩㎙ᠧ⡰. Делаем сопряженное.

ᡓ㎘ᡔ㐄

䙦ᡓ㎘ᡔ䙧䙦ᡓ㎗ᡔ䙧

䙦ᡓ㎗ᡔ䙧

С О П Р Я Ж Е Н Н О Е

2011 год

けlim→⦘㒓ᡶ⡲+8ᡶ⡰+3−㒓ᡶ⡲+ᡶ⡰= limけ→⦘

㐵√ᡶ⡲+8ᡶ⡰+3−√ᡶ⡲+ᡶ⡰㐹㐵√ᡶ⡲+8ᡶ⡰+3+√ᡶ⡲+ᡶ⡰㐹

√ᡶ⡲+8ᡶ⡰+3−√ᡶ⡲+ᡶ⡰

= limけ→⦘

ᡶ⡲+8ᡶ⡰+3−ᡶ⡲−ᡶ⡰

√ᡶ⡲+8ᡶ⡰+3−√ᡶ⡲+ᡶ⡰

= limけ→⦘

7 ᡶ⡰+

ᡶ⡰㒕1+ᡶ 8 ⡰+ᡶ 3 ⡲+ᡶ⡰㒕1+ᡶ 1 ⡰

= limけ→⦘

ᡶ⡰䙲7+ᡶ 3 ⡰䙳

ᡶ⡰䙸㒕1+ᡶ 8 ⡰+ᡶ 3 ⡲+㒕1+ᡶ 1 ⡰䙹

= limけ→⦘

7+ᡶ 3 ⡰

㒕1+ᡶ 8 ⡰+ᡶ 3 ⡲+㒕1+ᡶ 1 ⡰

Вот то, что я вам говорил. Вы ВСЕ должны в конечном итоге получать дроби вида けс㊉, потому что

все они стремятся к 0!!! Продолжаем:

けlim→⦘

7+ᡶ 3 ⡰

㒕1+ᡶ 8 ⡰+ᡶ 3 ⡲+㒕1+ᡶ 1 ⡰

=㐨

7+

√1+0+0+√1+

㐲=

7

2

Страшно? Ну нет же☺. Медленно, не спеша, решайте пределы и вы достигните многого!

No2. Посчитать предел:

けlim→⡸⦘

㒕ᡶ+㒓ᡶ+√ᡶ

√ᡶ+

Страшно☺? Не волнуйтесь, все то же самое. Надо что-то сократить. Что и как? √ᡶ−это надо вынести и сократить. Если попытаемся вынести ᡶ, то мы с вами просто запутаемся, а ответ от этого не изменится. Разве что может быть неопределенность. То есть выносим x с самой старшей степенью в знаменателе.

けlim→⡸⦘

㒕ᡶ+㒓ᡶ+√ᡶ

√ᡶ+

= limけ→⡸⦘

√ᡶ∙㒗1+㒖 1 ᡶ+㒕ᡶ 1 ⡱

√ᡶ∙㒕1+ 1 ᡶ

= limけ→⡸⦘

㒗1+㒖 1

ᡶ+㒕

1

ᡶ⡱

㒕1+ 1 ᡶ

=

ᝃ

ᝂ

ᝂ

ᝂ

ᝂ

ᝂ

ᝂ

ᝁ

㒗1+㒖 1

0 +㒕

1

0 ⡱

㒕1+ 10

ᝆ

ᝅ

ᝅ

ᝅ

ᝅ

ᝅ

ᝅ

ᝄ

=

Трудность может состоять здесь лишь в одном: как вынести √ᡶ? Надеюсь, что это вы делать умеете.

No3. Посчитать предел:

けlim→⡸⦘

㐵ᡶ−√ᡶ⡰−1㐹

ぁ +㐵ᡶ+√ᡶ⡰−1㐹

ぁ

ᡶぁ

13.2: Пределы и непрерывность в высших измерениях

Итак, мы рассмотрели функции более чем одной переменной и увидели, как их изобразить. В этом разделе мы увидим, как взять предел функции более чем одной переменной и что означает непрерывность функции более чем одной переменной в точке ее области определения. Оказывается, у этих концепций есть аспекты, которые просто не встречаются с функциями одной переменной.

Предел функции двух переменных

Отзыв из раздела 2.5 что определение предела функции одной переменной:

Пусть \(f(x)\) определено для всех \(x≠a\) в открытом интервале, содержащем \(a\). Пусть \(L\) — действительное число. Затем

\[\lim_{x→a}f(x)=L\]

, если для каждого \(ε>0,\) существует \(δ>0\), такое что если \(0<|x−a|<δ\) для всех \(x\) в области \(f\), затем

\[|f(x)−L|<ε.\]

Прежде чем мы сможем адаптировать это определение для определения предела функции двух переменных, нам сначала нужно увидеть, как расширить идею открытого интервала одной переменной до открытого интервала двух переменных.2\}\]

, как показано на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): диск \(δ\) с центром вокруг точки \((2,1)\).

Идея круга \(δ\) появляется в определении предела функции двух переменных. Если \(δ\) мало, то все точки \((x,y)\) в круге \(δ\) близки к \((a,b)\). Это совершенно аналогично тому, как х близко к а в определении предела функции одной переменной. В одном измерении мы выражаем это ограничение как

.

\[a−δ

В более чем одном измерении мы используем диск \(δ\).

Определение: предел функции двух переменных

Пусть \(f\) — функция двух переменных, \(x\) и \(y\). Предел \(f(x,y)\) при приближении \((x,y)\) к \((a,b)\) равен \(L\), записанному как

\[\lim_{(x,y)→(a,b)}f(x,y)=L\]

, если для каждого \(ε>0\) существует достаточно малое \(δ>0\) такое, что для всех точек \((x,y)\) в \(δ\) круге вокруг \((a ,b)\), за исключением, возможно, самого \((a,b)\), значение \(f(x,y)\) не более чем на \(ε\) от \(L\) ( Рисунок \(\PageIndex{2}\)).2}<δ.\]

Рисунок \(\PageIndex{2}\): Предел функции с двумя переменными требует, чтобы \(f(x,y)\) находилось в пределах \(ε\) от \(L\) всякий раз, когда \((x, y)\) находится в пределах \(δ\) от \((a,b)\). Чем меньше значение \(ε\), тем меньше значение \(δ\).

Доказательство существования предела с использованием определения предела функции двух переменных может быть сложной задачей. Вместо этого мы воспользуемся следующей теоремой, которая поможет нам найти пределы. Формулы этой теоремы являются расширением формул теоремы о предельных законах из книги «Предельные законы».

Предельные законы для функций двух переменных

Пусть \(f(x,y)\) и \(g(x,y)\) определены для всех \((x,y)≠(a,b)\) в окрестности \((a ,b)\), и предположим, что окрестность полностью содержится внутри области определения \(f\). Предположим, что \(L\) и \(M\) — действительные числа такие, что

\[\lim_{(x,y)→(a,b)}f(x,y)=L\]

и

\[\lim_{(x,y)→(a,b)}g(x,y)=M,\]

и пусть \(с\) — константа. Тогда выполняется каждое из следующих утверждений:

Постоянный закон:

\[\lim_{(х,у)→(а,б)}с=с\]

Законы об идентичности:

\[\lim_{(х,у)→(а,б)}х=а\]

\[\lim_{(x,y)→(a,b)}y=b\]

Закон суммы:

\[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M\]

Закон о разнице:

\[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M\]

Постоянный кратный закон:

\[\lim_{(x,y)→(a,b)}(cf(x,y))=cL\]

Закон о продукте:

\[\lim_{(x,y)→(a,b)}(f(x,y)g(x,y))=LM\]

Частное право:

\[\lim_{(x,y)→(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{L}{M} \text{для} М≠0\]

Степенной закон:

\[\lim_{(x,y)→(a,b)}(f(x,y))^n=L^n\]

для любого положительного целого числа \(n\). 2−4x+3y−6)\)

\(\displaystyle \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y}\)

Раствор

а.2−4(2)+3(−1)−6 \\[4pt] =−6. \конец{выравнивание*}\]

б. Перед применением частного закона нам нужно убедиться, что предел знаменателя отличен от нуля. Используя разностный закон, постоянный множественный закон и закон тождества,

\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x,y)→(2,−1)}4x−\ lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2,−1)}x)−3(\lim_{(x ,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \конец{выравнивание*}\]

Поскольку предел знаменателя не равен нулю, применяется закон частного.Теперь мы вычисляем предел числителя, используя разностный закон, постоянный кратный закон и закон тождества:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\lim_ {(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x, y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \конец{выравнивание*}\]

Следовательно, согласно частному закону имеем

\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y )→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2,−1)}(4x−3y)} \\[4pt] =\dfrac{1 {11}. 2}=0 \не число\]

для любого значения \(x\).2}=\tfrac{1}{2}. \номер\]

Это верно для любой точки на прямой \(y=x\). Если мы позволим \(x\) приблизиться к нулю, оставаясь на этой линии, значение функции останется фиксированным на \(\tfrac{1}{2}\), независимо от того, насколько мал \(x\).

Выберите значение ε меньше \(1/2\) — скажем, \(1/4\). Тогда, независимо от того, насколько маленький диск \(δ\) мы нарисуем вокруг \((0,0)\), значения \(f(x,y)\) для точек внутри этого диска \(δ\) будут включают как \(0\), так и \(\tfrac{1}{2}\). Следовательно, определение предела в точке никогда не выполняется, и предел не существует.2}.\) Вдоль прямой \(y=0\) функция равна нулю; вдоль линии \(y=x\) функция равна \(\tfrac{1}{2}\).

б. Подобно а., мы можем приблизиться к началу координат по любой прямой, проходящей через начало координат. Если мы попытаемся использовать ось \(x\) (т. е. \(y=0\)), то функция останется фиксированной на нуле. То же верно и для оси \(y\). Предположим, мы приближаемся к началу координат по прямой линии наклона \(k\). 2)} \\ = 0.2\) (Рисунок \(\PageIndex{4}\)).

1. Точка \(P_0\) называется внутренней точкой \(S\), если существует диск \(δ\) с центром вокруг \(P_0\), полностью содержащийся в \(S\).
2. Точка \(P_0\) называется граничной точкой \(S\), если каждый \(δ\) круг с центром в \(P_0\) содержит точки как внутри, так и снаружи \(S\).

Рисунок \(\PageIndex{4}\): В показанном наборе \(S\) \((−1,1)\) является внутренней точкой, а \((2,3)\) является граничной точкой .2\) (Рисунок \(\PageIndex{4}\)).

1. \(S\) называется открытым множеством , если каждая точка \(S\) является внутренней точкой.
2. \(S\) называется замкнутым множеством , если оно содержит все свои граничные точки.

Примером открытого множества является диск \(δ\). Если мы включим границу диска, то он станет замкнутым множеством. Множество, которое содержит некоторые, но не все, его граничные точки, не является ни открытым, ни закрытым. Например, если мы включаем половину границы круга \(δ\), но не другую половину, то множество не является ни открытым, ни закрытым.2\) (Рисунок \(\PageIndex{4}\)).

1. Открытое множество \(S\) является связным множеством , если оно не может быть представлено как объединение двух или более непересекающихся, непустых открытых подмножеств.
2. Множество \(S\) является областью , если оно открыто, связно и непусто.

Определение предела функции двух переменных требует, чтобы диск \(δ\) содержался внутри области определения функции. Однако, если мы хотим найти предел функции в граничной точке области, \(δ\) круг не содержится внутри области.По определению некоторые точки диска \(δ\) находятся внутри области, а некоторые — снаружи. Поэтому нам нужно рассматривать только точки, которые находятся как внутри круга \(δ\), так и внутри области определения функции. Это приводит к определению предела функции в граничной точке.

Определение

Пусть \(f\) является функцией двух переменных, \(x\) и \(y\), и предположим, что \((a,b)\) находится на границе области определения \(f\) . Тогда предел \(f(x,y)\) при приближении \((x,y)\) к \((a,b)\) равен \(L\), записанному как

\[\lim_{(x,y)→(a,b)}f(x,y)=L,\]

, если для любого \(ε>0,\) существует число \(δ>0\) такое, что для любой точки \((x,y)\) внутри области определения \(f\) и в пределах подходящего небольшое положительное расстояние \(δ\) от \((a,b),\) значение \(f(x,y)\) не более чем на \(ε\) от \(L\) (рис. \(\PageIndex{2}\)).2} \номер\]

Непрерывность функций двух переменных

В разделе «Непрерывность» мы определили непрерывность функции одной переменной и увидели, как она зависит от предела функции одной переменной. В частности, необходимы три условия для непрерывности \(f(x)\) в точке \(x=a\)

1. \(f(a)\) существует.
2. \(\displaystyle \lim_{x→a}f(x)\) существует.
3. \(\displaystyle \lim_{x→a}f(x)=f(a).\)

Эти три условия необходимы и для непрерывности функции двух переменных.

Определение: непрерывные функции

Функция \(f(x,y)\) непрерывна в точке \((a,b)\) своей области определения, если выполняются следующие условия:

1. \(f(a,b)\) существует.
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\) существует.
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\)

Пример \(\PageIndex{4}\): демонстрация непрерывности функции двух переменных

Показать, что функция

\[f(x,y)=\dfrac{3x+2y}{x+y+1} \номер\]

непрерывна в точке \((5,−3).\)

Раствор

В соответствии с определением непрерывности должны быть выполнены три условия. В этом примере \(a=5\) и \(b=−3.\)

1. \(f(a,b)\) существует. Это верно, потому что область определения функции f состоит из тех упорядоченных пар, для которых знаменатель не равен нулю (т. 2}\номер \]

непрерывна в точке \((2,−3)\).2}<δ\) верно, \(|f(x,y)−f(a,b)|<ε.\) Это определение можно комбинировать с формальным определением (то есть эпсилон–дельта определение ) непрерывности функции одной переменной для доказательства следующих теорем:

Сумма непрерывных функций непрерывна

Если \(f(x,y)\) непрерывна в \((x_0,y_0)\), а \(g(x,y)\) непрерывна в \((x_0,y_0)\), то \(f(x,y)+g(x,y)\) непрерывен в \((x_0,y_0)\).

Произведение непрерывных функций непрерывно

Если \(g(x)\) непрерывна в \(x_0\) и \(h(y)\) непрерывна в \(y_0\), то \(f(x,y)=g(x) h(y)\) непрерывна в точке \((x_0,y_0).2\) в диапазон \(R⊆R.\) Предположим, что \(g\) непрерывна в некоторой точке \((x_0,y_0)∈D\) и определим \(z_0=g(x_0,y_0)\) . Пусть f будет функцией, которая отображает \(R\) в \(R\), так что \(z_0\) находится в области определения \(f\). Наконец, предположим, что \(f\) непрерывно в \(z_0\). Тогда \(f∘g\) непрерывен в \((x_0,y_0)\), как показано на рисунке \(\PageIndex{7}\). 2y−3z}{2x+5y−z}.\номер\]

Раствор

Прежде чем мы сможем применить частное, нам нужно убедиться, что предел знаменателя отличен от нуля. Используя разностный закон, закон тождества и постоянный закон,

\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z) =2(\lim_{(x,y,z)→ (4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y)−(\lim_{(x,y,z)→( 4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{align*}\]

Так как это не ноль, мы затем находим предел числителя.2}=2 \номер\]

Геометрическая интерпретация и пределы понимания

На ранних стадиях математического образования человеческие способности к геометрическому и пространственному мышлению имели первостепенное значение для понимания математических понятий. Числа символизировались с помощью цветных блоков, дроби как срезы круга, даже во вводных курсах математического анализа понятия интегрирования и дифференцирования вводятся с геометрической интерпретацией.Однако по мере того, как я продвигался в своем математическом образовании, я заметил, что более продвинутые темы, по-видимому, получают меньше пользы от острого чувства пространства и фигуры, что вызвало большие трудности в некоторых моих более продвинутых классах. Даже на таких курсах, как прикладной численный анализ, где геометрическое приложение считается довольно простым, я сбиваюсь с толку, пытаясь представить себе математическую деятельность мысленным взором.

Возможно, для кого-то это не так уж удивительно, я обнаружил, что у Локка есть кое-что интересное, что он может сказать по этой теме еще до изобретения исчисления бесконечно малых.Видите ли, я утверждаю, что эта трудность геометрической интерпретации в высшей математике возникает из-за того, что они часто включали величины, которые находятся за пределами того, что человеческий разум может правильно понять. Это не значит, что мы не можем рассуждать о бесконечных суммах и тому подобном, но когда мы это делаем, мы рассматриваем не само количество, а скорее процесс суммирования.

Как говорит сам Локк, «…как сложение, так и деление пространства или длительности, когда рассматриваемая идея становится очень большой или очень маленькой, ее точный объем становится очень неясным и запутанным; и только число повторных добавлений или делений остается ясным и отчетливым» (Ес. Конц. Гум. Поддр. 143). Это довольно крутой прием, особенно если учесть современный математический ландшафт, населенный как тяжелыми вычислениями, так и теоретиками, которые почти не терпят никаких вычислений. Это обнаруживает довольно неожиданный разрыв между методами действия численных методов (т. е. моделированием, вычислениями и т. д.) и более теоретическими видами работы, к которым склонны математики-люди.

Но, возможно, главный вывод из этого заключается в том, что когда люди работают с математикой, они не моделируют рассматриваемую систему так, как это делает компьютер, а используют эвристические устройства и тому подобное для получения информации о системе. в более общей и более абстрактной форме.Имея это в виду, гораздо более логично, что математические программы более высокого уровня, как правило, отвлекают внимание от попыток визуализировать рассматриваемые системы, поскольку это тип мышления, к которому чаще всего прибегают математики. Однако я подозреваю, что существует довольно большая разница между усердным моделированием всей топологии и простой мысленной визуализацией такой вещи, которая способствует визуальному решению задач. Я уверен, вы согласитесь. Отбрасывая простое объяснение того, что две идеи трудно визуализировать в голове, например, при работе в n-мерных пространствах и т. п., что может вызвать такое пространственное разъединение в задачах, которые в противном случае визуализируются мысленным взором?

Возможно, некоторые трудности с математическим визуальным мышлением могут быть освещены соответствующей записью Стэнфордской пластины (https://plato.stanford.edu/archives/spr2020/entries/epistemology-visual-thinking), в котором упоминается интересный факт о визуальных доказательствах, а именно то, что они часто могут чрезмерно обобщать или недообобщать доказательство при использовании. Поскольку здесь мы не говорим строго о силе визуального мышления в доказательстве, я в основном буду игнорировать части, которые непосредственно связаны с этой темой, но я нахожу, что многие из причин, по которым визуальное мышление может привести к ошибке в доказательстве, могут привести к ошибкам. объяснить его трудность использования в некоторых ситуациях. Причина, по которой визуальные доказательства часто чрезмерно или недостаточно обобщают, заключается в том, что должен быть идеальный баланс между минималистской элегантностью и подробными деталями, чтобы сформированное изображение идеально отражало математическую концепцию. Если есть лишняя детализация, изображение недообобщается, если недостаточно, то чрезмерно. Я предполагаю, что есть аналогичные причины, по которым наглядное мышление может быть такой задачей в высшей математике, где чрезвычайно точные определения, аксиомы и теоремы являются субстратом, из которого возникают наши визуальные представления.Эти математические объекты могут стать довольно сложными по мере продвижения к более сложной математике, что делает гораздо более сложной задачей для ума определить, что имеет непосредственное отношение к поставленной задаче, из всей другой посторонней информации, включенной в сеть определений. и теоремы. Это сильно отличается от типа геометрической интерпретации низшей математики, которая в основном связана с геометрическими отношениями величин, таких как длина, объем или площадь.

Принимая во внимание эти соображения, возможно, дело не в том, что геометрическую интерпретацию следует полностью игнорировать из высшей математики, когда это уместно, а в том, что ум не так естественно знаком с языком теорем и определений, как с модусами количество. Это послание я усвоил на собственном горьком опыте во время учебы в бакалавриате. Учитывая, что визуальное мышление может иметь своим содержанием любую математическую сущность, а не только числа, я считаю, что не должно быть неотъемлемого свойства высшей математики, которое должно было бы препятствовать использованию ею визуальных техник.Это, конечно, исключает те идеи, которые не подходят для трех- или двухмерных визуализаций, которые может производить человеческий разум.

курсов по математике | Университет Вирджинии Уэслиан

Курсы математики (MATH)

0 0 5  Алгебраические предварительные занятия (4)
Студенты развивают базовые вычислительные навыки и укрепляют свое понимание основ при подготовке к курсам, которые включают более сложные количественные понятия. Учащиеся с уровнем размещения D должны пройти этот курс с оценкой C или выше, прежде чем приступить к МАТЕМАТИКЕ 104. Темы включают операции с целыми числами и числами со знаком, дробями, десятичными знаками, показателями, переменными, линейными уравнениями и решением элементарных задач. Только традиционная оценка. Хотя студенты не получают кредита за этот курс, оценка за курс учитывается в их общем среднем балле, как если бы это был курс продолжительностью 4 семестра. Условие: размещение или согласие. Предлагается каждую весну.

1 0 4 Алгебра и ее приложения (4)
Представляет темы алгебры с помощью традиционных и прикладных методов. Темы включают функции, показатели степени и экспоненты, линейные, экспоненциальные, рациональные и квадратичные функции и графики, системы уравнений, а также квадратные и линейные неравенства. Условие: уровень размещения C, математика 005 с оценкой C или выше или согласие. Студенты должны иметь TI- Графический калькулятор ТИ-83 или ТИ-84. Предлагается каждый семестр.

1 3 5 Исчисление с предварительным исчислением, часть I (4)
Студенты изучают основные инструменты исчисления, почему они работают и как применять их в различных контекстах. Рассмотрены символьный, графический и численный подходы. Темы включают ограничения, производные и приложения. Включает достаточный охват функций и тригонометрии для поддержки изучения исчисления и других наук. Последовательность из двух курсов, МАТЕМАТИКА 135 и 136, является достаточной подготовкой к MATH 172 Исчисление II.Условие: уровень размещения B, МАТЕМАТИКА 104 с оценкой B или выше или согласие. Предлагается каждую осень.

1 3 6 Исчисление с предварительным исчислением, часть II (4)
Продолжение MATH 135. Темы включают приложения производных, интеграл Римана и основную теорему исчисления. Включает в себя достаточные инструкции по продвинутым алгебраическим методам для поддержки изучения исчисления. Требование: МАТЕМАТИКА 135 с оценкой C- или выше или согласие.Предлагается каждую весну.

1 5 0  Темы современной математики (4)
Знакомит учащихся с областями современной математики. Темы различаются, но могут включать теорию голосования, теорию игр, математику и искусство, элементарная теория чисел, теория графов и задачи планирования, управленческая наука и другие. Основное внимание уделяется навыкам критического мышления, устному и письменному общению по математике, а также применению в других дисциплинах. Условие: уровень размещения A или B.Предлагается каждый семестр.

1 7 1 Исчисление I (4)
Студенты изучают основные инструменты исчисления, почему они работают и как применять их в различных контекстах. Исчисление I развивается дифференциальное исчисление с помощью символического, графического и численного подходов. Темы включают дифференцирование алгебраических и трансцендентных функций, приложения в моделировании и оптимизации, основную теорему исчисления и введение в дифференциальные уравнения. Условие: уровень размещения A или согласие. Предлагается каждый семестр.

1 7 2 Исчисление II (4)
Продолжение исчисления I. Более продвинутые методы изучаются и используются для решения количественных задач в различных контекстах. Темы включают методы интегрирования, приложения определенного интегрирования, полярные координаты, параметрические уравнения, а также последовательности и ряды. Требование: МАТЕМАТИКА 136 или 171 с оценкой C- или выше или согласие.Предлагается каждый семестр.

2 0 5 Основы логики и доказательства (4)
Введение в абстрактное математическое мышление и навыки логического рассуждения, необходимые на курсах математики/информатики верхнего уровня. Темы включают логику, аргумент, доказательства, индукцию, множества и абстрактные функции и отношения. Уделяет внимание математическому письму. Идентичен CS 205. Предпосылки: MATH 217 с оценкой C- или выше или CS 212 с оценкой C или выше, или согласие. Рекомендуемая весна второго года обучения. Предлагается каждую весну.

2 1 0  Вводная статистика (4)
Знакомит учащихся с обучением на основе данных. Темы включают основы производства данных, анализ данных, вероятность, центральный Предельная теорема и статистический вывод. Статистическое программное обеспечение используется для управления данными, расчета и визуализации. Никаких предварительных знаний статистики не требуется. Учащиеся не могут получить зачет одновременно по MATH 210 и PSY 210.Требования: статус второкурсника или выше и уровень размещения H, A или B, или MATH 104 с оценкой C- или выше. Не подходит для первокурсников. Студенты должны иметь графический калькулятор TI-83 или TI-84. Предлагается каждый семестр.

2 1 7 Линейная алгебра (4)
Изучение векторных пространств и линейных уравнений с несколькими переменными. Темы включают системы линейных уравнений, векторные пространства, линейную зависимость векторов, основания, размерность, линейные преобразования, матрицы, определители и приложения.Требование: МАТЕМАТИКА 172 с оценкой C- или выше, или согласие. Предлагается каждую осень.

2 7 3 Многомерное исчисление (4)
Темы включают функции нескольких переменных, кривые, поверхности, частное дифференцирование, множественные интегралы и векторный анализ. Требование: МАТЕМАТИКА 172 с оценкой C- или выше, или согласие. Предлагается каждую весну.

2 7 4  Обыкновенные дифференциальные уравнения (4)
Исследует теорию и приложения обыкновенных дифференциальных уравнений и их решений.Темы включают линейные и нелинейные уравнения первого порядка, линейные уравнения более высокого порядка, решения рядов, системы линейных дифференциальных уравнений, преобразования Лапласа и численные методы. Требование: МАТЕМАТИКА 172 с оценкой C- или выше, или согласие. Предлагается каждую осень.

3 0 0 Программа помощника преподавателя по математике (1)
Квалифицированные студенты помогают преподавателям математики в проведении занятий. Зачисление осуществляется по приглашению кафедры MATH/CS.Студент может зарегистрироваться более одного раза, но может использовать не более 3 семестровых часов, заработанных таким образом, для окончания учебы. Не может использоваться для удовлетворения основных или второстепенных требований по математике. Один семестр требуется для студентов, желающих получить сертификат о среднем образовании; однако курс открыт для всех студентов. Предлагается каждый семестр.

3 1 0 Статистические модели (4) Вт
Курс прикладного анализа данных. Подчеркивает построение моделей для аутентичных наборов данных.Статистическое программное обеспечение широко используется для анализа реальных наборов данных из различных контекстов. Темы включают параметрические и непараметрические тесты, простую и множественную регрессию и ANOVA. Требования: ENG 105 с оценкой C или выше, MATH 172 с оценкой C или выше и MATH 210 с оценкой C или выше, или согласие. Подаренная весна четных лет.

3 1 6 Вероятность (4)
Подходы к вероятности как к дисциплине с приложениями в математике и естественных науках.Темы включают классические и аксиоматическая вероятность, случайные величины, общие распределения, функции плотности, математическое ожидание, условная вероятность, независимость, закон больших чисел и центральная предельная теорема. Требование: МАТЕМАТИКА 273 с оценкой C- или выше, или согласие. Предлагаем осень нечетных лет.

3 1 9 Алгебраические структуры I (4)
Введение в алгебраические структуры с упором на кольца и поля.Темы включают гомоморфизмы и изоморфизмы, кольцо структура, классы эквивалентности, фактор-структуры и полиномиальные кольца. Требования: MATH/CS 205 с оценкой C- или выше и MATH 217 с оценкой C- или выше. Предлагается каждую осень.

3 2 5 Теория элемской математики I (4)
Развивает профессиональные знания по математике, обычно преподаваемой в начальных школах (K-6). Часть I посвящена системам счисления, арифметике, теории чисел и алгебраическим понятиям.Не считается факультативом для любой специальности математики. Предварительные требования: Любой курс математики с кредитным рейтингом (настоятельно рекомендуется MATH 150), младший/старший статус и допуск к программе сертификации учителей начального или специального образования. Предлагается каждую весну.

3 2 6 Теория элемской математики II (4)
Развивает профессиональные знания по математике, обычно преподаваемой в начальной школе (K6). Часть II посвящена геометрии, вероятности и статистике.Не считается факультативом по любой специальности математики. Требования: МАТЕМАТИКА 325 (оценка C или выше). Предлагается каждую осень.

3 3 3 Теория чисел (4) W
Введение в изучение множества натуральных чисел. Темы могут включать линейную конгруэнтность, наибольший общий делитель, Функция Эйлера, китайская теорема об остатках, малая теорема Ферма, теорема Вильсона, символ Лежандра и квадратичная взаимность.Условие: ENG 105 с оценкой C или выше и MATH/CS 205 с оценкой C- или выше, или согласие. Предлагаем осень нечетных лет.

3 4 0 Современные геометрии (4)
Исследует евклидову и неевклидову геометрию и влияние неевклидовой геометрии на культуру. Темы могут включать геодезические, планиметрия, неевклидовы геометрии, конечные геометрии, комплексные числа и геометрические преобразования.Условие: MATH/CS 205 с оценкой C- или выше, MATH 217 с оценкой C- или выше или согласие. Предлагается весна нечетных лет.

3 5 0 Численные методы (4)
Изучает эффективные методы решения численных задач с помощью ЭВМ. Темы включают арифметику с плавающей запятой, интерполяцию и аппроксимацию, интегрирование, корни нелинейных уравнений, обыкновенные дифференциальные уравнения и системы линейных уравнений.Идентичен CS 350. Предпосылки: MATH 172 с оценкой C- или выше и CS 212 с оценкой C- или выше или согласие. Подаренная весна четных лет.

3 8 0 Дополнительные темы по математике (4)
Изучает область математики, которая не включена в учебную программу. Студенты могут повторить курс для получения кредита, поскольку тема меняется. Требование: МАТЕМАТИКА 217 с оценкой C- или выше и согласием.Предлагается с перерывами.

4 1 0  Математические модели (4) Вт
Введение в математические модели и анализ чувствительности. Особое внимание уделяется построению моделей для реальных приложений в различных областях. Математическое программное обеспечение широко используется для решения задач. Темы включают модели оптимизации, линейное и дискретное программирование, динамические модели и вероятностные модели. Требования: ENG 105 с оценкой C или выше, MATH 217 с оценкой C- или выше и MATH 273 с оценкой C- или выше.Предлагаем осень четных лет.

4 1 9 Алгебраические структуры II (4)
Продолжение «Алгебраических структур I» с акцентом на группы, теоремы о гомоморфизмах и теорию Галуа. Требование: МАТЕМАТИКА 319 с оценкой C- или выше. Подаренная весна четных лет.

4 7 0 Стажировка по математике (2 или 4)
Интенсивный математический проект, проводимый в профессиональной среде.Пройдено/не пройдено. Требования: статус юниор/старший, совокупный средний балл не менее 2,5 и согласие. Предлагается по запросу.

4 7 1 Реальный анализ (4)
Теоретическая трактовка непрерывности и вещественнозначных функций. Темы могут включать последовательности, ряды, пределы, производную и интеграл. Требование: МАТЕМАТИКА 319 с оценкой C- или выше. Предлагается весна нечетных лет.

4 8 7 Семинар по математике для старшеклассников (1)
Студенты читают и обсуждают текущие журнальные статьи по математике.Темы разные и могут включать решение проблем. Пройдено/не пройдено. Предварительное условие: заявленный статус по специальности «Математика» и «старший» или согласие. Предлагается каждую весну.

4 8 9 Исследования по математике (2 или 4)
Предлагает студентам возможность проводить оригинальные научные исследования в интересующей их области. Студенты тесно сотрудничают с одним или несколькими преподавателями факультета естественных наук для разработки и проведения исследовательского проекта, а затем устно представляют свои результаты на семестровом исследовательском симпозиуме для студентов и в качестве официальной исследовательской работы. Студентам предлагается представить свои выводы на конференции. Условие: младший/старший статус и специальность по математике, предварительное одобрение консультанта проекта и согласие преподавателя. Студенты могут записаться на 2 или 4 часа в данном семестре. Можно повторять максимум 8 семестровых часов. Идентично BIO 489, CHEM 489, CS 489 и EES 489. Предлагается каждый семестр и большинство январских сроков (только 2 семестровых часа).

Бюллетень бакалавриата

Stony Brook — весна 2022 г. BulletinMAT

МАТ 118: математическое мышление

Развитие количественного мышления и способности решать задачи посредством выбора математических тем: логика и рассуждение; числа, функции и моделирование; комбинаторика и вероятность; рост и изменение.Другие темы могут включать геометрию, статистику, теорию игр и теорию графов. Благодаря участию в решении задач учащиеся развивают понимание интеллектуальных возможностей математики и ее связи с другими дисциплинами.

Необходимое условие: C или выше по MAP 103 или уровень 2+ или выше на вступительном экзамене по математике

(Предварительное условие должно быть выполнено в течение одного года с начала этого курса.)

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 119: основы предварительного исчисления

Этот курс является дополнением к MAT 123: Предварительное исчисление и обеспечивает структурированную среду, в которой учащиеся могут освежить навыки алгебры, необходимые для успеха в предварительном исчислении. Эти темы включают понимание показателей (особенно дробных и отрицательных показателей), манипулирование математическими выражениями, решение уравнений и моделирование/словные задачи. Курс нельзя пройти с CHE 129.

Необходимое условие: 2+ при размещении или разрешении инструктора МАТ 123

Соответствие: MAT 123

1 кредит, оценка S/U

​

MAT 122: обзор исчисления с приложениями

Основы математического анализа в автономном односеместровом курсе.Свойства и приложения полиномиальных, экспоненциальных и логарифмических функций. Производные: наклоны, скорость изменения, оптимизация, интегралы, площадь, кумулятивное изменение и среднее значение. Основная теорема исчисления. Акцент на моделировании примеров из экономики. Студенты, которые впоследствии захотят поступить на MAT 125 или 131, должны будут набрать 4 балла на вступительном экзамене по математике, прежде чем приступить к любому курсу. Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше по MAP 103 или уровень 3 на вступительном экзамене по математике

(Условие должно быть выполнено в течение одного года до начала курса.)

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 123: предварительный расчет

Комплексная подготовка к последовательностям регулярного исчисления.Тщательная разработка рациональных, экспоненциальных, логарифмических и тригонометрических функций и их приложений. Асимптотика и построение кривых. Общие примеры моделирования. Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше по MAP 103 или уровень 3 на вступительном экзамене по математике или соответствующему MAT 119 (предварительные требования должны быть выполнены в течение одного года до начала курса.)

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 125: исчисление A

Дифференциальное исчисление с упором на концептуальное понимание, вычисления и приложения для учащихся, имеющих необходимые знания математики 12-го класса средней школы. Пределы и непрерывные функции.Дифференцирование элементарных алгебраических, тригонометрических, показательных и логарифмических функций; графическое изображение; моделирование; и максимизация. Правило Лопиталя. Не допускается зачет в дополнение к MAT 131, 141 или AMS 151. Этот курс был обозначен как курс с высоким спросом/контролируемым доступом (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше в MAT 123; или уровень 4 на вступительном экзамене по математике; или соответствующий MAT 130

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 126: Исчисление B

Продолжение MAT 125, охватывающее интегральное исчисление: суммы Римана, фундаментальная теорема, символические и числовые методы интегрирования, площадь под кривой, объем, приложения, такие как работа и вероятность, несобственные интегралы.Этот курс был обозначен как курс высокого спроса/контролируемого доступа (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше по MAT 125, или 131, или 141, или AMS 151, или уровень 6 на вступительном экзамене по математике

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 127: Исчисление C

Продолжение MAT 126, охватывающее: последовательности, ряды, ряды Тейлора, дифференциальные уравнения и моделирование.Не может быть зачтено в дополнение к MAT 132, MAT 142, MAT 171 или AMS 161. Этот курс был обозначен как курс с высоким спросом / контролируемым доступом (HD / CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше по MAT 126 или уровень 8 на вступительном экзамене по математике

DEC:     C
SBC: число запросов в секунду

3 кредита

​

MAT 130: тригонометрия и логарифмы

Обратные функции, экспоненциальные и логарифмические функции, радианная мера углов и тригонометрические функции. Преподается как компаньон к МАТ 125.

Необходимое условие: MAT 122 с оценкой C или выше, или уровнем 3+ или выше на вступительном экзамене, или разрешением инструктора

Дополнительный реквизит: MAT 125

1 кредит, оценка S/U

​

МАТ 131: Исчисление I

Дифференциальное и интегральное исчисление с упором на концептуальное понимание, вычисления и приложения для учащихся, имеющих необходимые знания по математике 12-го класса средней школы.Дифференциация элементарной алгебраической; тригонометрические, экспоненциальные и логарифмические функции; графическое изображение; моделирование и максимизация; правило Лопиталя; интеграл Римана; и Основная теорема исчисления. Не допускается зачет в дополнение к MAT 125, 141 или AMS 151. Этот курс был определен как курс с высоким спросом/контролируемым доступом (HD/CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: B или выше по MAT 123 или уровень 5 на вступительном экзамене по математике

DEC:     C
SBC: число запросов в секунду

4 кредита

​

МАТ 132: Исчисление II

Продолжение MAT 131, охватывающее символьные и числовые методы интегрирования; площадь под кривой; объем; приложения, такие как работа и вероятность; последовательности; ряд; ряд Тейлора; дифференциальные уравнения; и моделирование.Не может быть зачтено в дополнение к MAT 127, MAT 142, MAT 171 или AMS 161. Этот курс был обозначен как курс с высоким спросом / контролируемым доступом (HD / CA). Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше по AMS 151 или MAT 131 или 141, или уровень 7 на вступительном экзамене по математике

DEC:     C
SBC: число запросов в секунду

4 кредита

​

MAT 141: Анализ I

Тщательное изучение теории, лежащей в основе исчисления.Развитие системы действительных чисел, пределы и бесконечные последовательности, функции одной действительной переменной, непрерывность, дифференцируемость, интеграл Римана и основная теорема исчисления. Все внимание уделяется доказательствам. Включены все темы MAT131, хотя представление значительно отличается. Не может быть засчитан в дополнение к MAT 125, MAT 131 или AMS 151. Учащийся, успешно завершивший оба MAT 141 и MAT 142, получит эквивалент MAT 320. Этот курс был обозначен как High Demand/Controlled Access (HD). /CA) курс.Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: Уровень 5 на вступительном экзамене по математике; приоритет отдается студентам университетских программ с отличием

DEC:     C
SBC: число запросов в секунду

4 кредита

​

MAT 142: Анализ II

Продолжение МАТ 141 в том же духе, включая темы МАТ 132, но с акцентом на теорию и включая доказательства основных теорем: методы и приложения интегрирования, бесконечные ряды, ряды Тейлора, моделирование и элементарные дифференциальные уравнения.Учащийся, успешно завершивший как MAT 141, так и MAT 142, получит освобождение от требований к MAT 320. Не может быть засчитан в дополнение к MAT 127, MAT 171 или AMS 161. Этот курс был определен как курс с высоким спросом/контролируемым доступом. (HD/CA) курс. Студенты, регистрирующиеся на курсы HD/CA в первый раз, имеют приоритет.

Необходимое условие: C или выше в MAT 141 или разрешение Advanced Track Committee

СБК: число запросов в секунду

4 кредита

​

MAT 171: ускоренное вычисление одной переменной

Один семестр, курс с отличием, который рассматривает материал MAT 131 за несколько недель, затем концентрируется на темах, затронутых в MAT 132, с дополнительным вниманием, уделяемым основной теории.В первую очередь предназначен для учащихся, которые изучали исчисление в средней школе. Не может быть засчитан в дополнение к MAT 126, MAT 127, MAT 132, MAT 142 или AMS 161.

Предпосылки: Уровень 5 на экзамене AB Calculus AP, Уровень 3 на экзамене BC Calculus, A или A- в MAT 131 или AMS 151, MAT 141 или уровень 7 на вступительном экзамене по математике. Приоритет отдается студентам в программах с отличием университета.

DEC:     C
SBC: число запросов в секунду

4 кредита

​

MAT 200: логика, язык и доказательство

Базовый курс логики математики, построение доказательств и написание доказательств.Математическое содержание — это прежде всего логика и доказательства, теория множеств, комбинаторика, функции и отношения. Значительное внимание уделяется писательству. Не может быть принято в кредит в дополнение к MAT 250.

Необходимое условие: Уровень 4 на вступительном экзамене по математике или эквивалентном курсе или разрешение инструктора

СБК: STEM+

3 кредита

​

MAT 203: Исчисление III с приложениями

Векторная алгебра в двух и трех измерениях, многомерное дифференциальное и интегральное исчисление, оптимизация, векторное исчисление, включая теоремы Грина, Гаусса и Стокса. Приложения к экономике, технике и всем наукам с упором на численные и графические решения; использование графических калькуляторов или компьютеров. Не может быть принято в кредит помимо AMS 261.

Необходимое условие: C или выше по MAT 127, или 132, или 142, или AMS 161, или уровень 9 на вступительном экзамене по математике

СБК: STEM+

4 кредита

​

MAT 211: Введение в линейную алгебру

Введение в теорию линейной алгебры с некоторыми приложениями; векторы, векторные пространства, базисы и размерность, приложения к геометрии, линейные преобразования и ранги, собственные значения и собственные векторы, определители и скалярные произведения.Не могут быть приняты в кредит дополнительно к AMS 210.

Необходимое условие: C или выше по AMS 151, или MAT 131, или 141, или совместная регистрация по MAT 126, или уровень 7 на вступительном экзамене по математике

СБК: STEM+

3 кредита

​

MAT 220: линейная алгебра и геометрия

Векторы и векторная алгебра. Скалярное произведение. Перекрестное произведение и тройное произведение. Аналитическая геометрия. Векторные уравнения прямых и плоскостей. Кривые и поверхности второй степени. Комплексные числа. Линейные пространства и линейные отображения. Матрицы, системы линейных уравнений. Изоморфизмы векторных пространств, базисы и размерность. MAT 220 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 211 и не может приниматься в расчет в дополнение к MAT 211.

Необходимое условие: MAT 131 или эквивалентный курс или уровень 7 или выше на вступительном экзамене по математике или разрешение Advanced Track Committee

Необходимый компонент: MAT 250

СБК: STEM+

3 кредита

​

MAT 250: Введение в продвинутую математику

Введение в программу Advanced Track по математике. Обеспечивает основу основ логики высказываний, кванторов, доказательств, множеств, функций, мощности, отношений, отношений эквивалентности и частных множеств, отношений порядка, комбинаторики. Системы счисления: натуральные числа, целые числа, рациональные, действительные и комплексные числа. MAT 250 в первую очередь предназначен для учащихся программы Advanced Track. Он служит альтернативой MAT 200 и не может учитываться в дополнение к MAT 200. Ранее предлагался как MAT 150; не в кредит в дополнение к MAT 150.

Необходимое условие: MAT 131 или эквивалентный курс, или уровень 7 или выше на вступительном экзамене по математике или с разрешения Advanced Track Committee.

СБК: число запросов в секунду

4 кредита

​

MAT 260: Решение задач по математике

Учащиеся активно решают сложные задачи по плоской геометрии, основам теории чисел и математическому анализу и пишут точные аргументы. В ходе курса проводится соответствующая подготовка к решению задач.

Необходимое условие: Разрешение инструктора

1 кредит

​

MAT 303: Исчисление IV с приложениями

Однородные и неоднородные линейные дифференциальные уравнения; системы линейных дифференциальных уравнений; серийные решения; преобразования Лапласа; ряд Фурье.Приложения к экономике, технике и всем наукам с упором на численные и графические решения; использование компьютеров. Не может быть использовано для кредита в дополнение к AMS 361 или MAT 308.

Необходимое условие: C или выше по MAT 127, или 132, или 142, или AMS 161, или уровень 9 на вступительном экзамене по математике

СБК: STEM+

4 кредита

​

MAT 307: многомерное исчисление с помощью линейной алгебры

Введение в линейную алгебру: векторы, матрицы, системы линейных уравнений, основания и размерность, скалярное произведение, определители. Многомерное дифференциальное и интегральное исчисление, дивергенция и ротор, линейные и поверхностные интегралы, теоремы Грина, Гаусса и Стокса. Более теоретический и интенсивный, чем MAT 203, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 308 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 203, MAT 211 и MAT 303. Не может быть зачтено в дополнение к MAT 203 или AMS 261.

Необходимое условие: МАТ 127 или МАТ 132

СБК: STEM+

4 кредита

​

MAT 308: дифференциальные уравнения с линейной алгеброй

Линейная алгебра: определители, собственные значения и собственные векторы, диагонализация.Дифференциальные уравнения; существование и единственность решений. уравнения первого и второго порядка; линейные и нелинейные уравнения. Системы линейных уравнений. Преобразование Лапласа. Приложения к физике. Более теоретический и интенсивный, чем MAT 303, этот курс в первую очередь предназначен для математических специальностей. Вместе с MAT 307 он образует 2-семестровую последовательность, охватывающую тот же материал, что и 3-семестровую последовательность MAT 205, MAT 211 и MAT 305. Не может быть зачтено в дополнение к MAT 303 или AMS 361.

Необходимое условие: МАТ 307; или МАТ 203 и МАТ 211; или МАТ 132 и МАТ 220; или разрешение инструктора

СБК: STEM+

4 кредита

​

MAT 310: линейная алгебра

Конечномерные векторные пространства, линейные отображения, двойственные пространства, билинейные функции, скалярные произведения. Дополнительные темы, такие как канонические формы, полилинейная алгебра, численная линейная алгебра.

Необходимое условие: C или выше в MAT 211 или 308 или AMS 210 или MAT 220; C или выше в MAT 200 или MAT 250 или разрешение инструктора

4 кредита

​

MAT 311: Теория чисел

Сравнения, квадратичные вычеты, квадратичные формы, цепные дроби, диофантовы уравнения, теоретико-числовые функции и свойства простых чисел.

Предпосылки: C или выше в MAT 312 или 313; C или выше в MAT 200 или MAT 250 или разрешение инструктора

3 кредита

​

MAT 312: Прикладная алгебра

Разделы по алгебре: группы, неформальная теория множеств, отношения, гомоморфизмы. Приложения: коды с исправлением ошибок, теорема Бернсайда, вычислительная сложность, китайская теорема об остатках.Этот курс предлагается как AMS 351, так и MAT 312.

Необходимое условие: C или выше в AMS 210 или MAT 211 или MAT 220

Консультативное требование: MAT 200, или CSE 215, или CSE 150, или эквивалент

3 кредита

​

MAT 313: Абстрактная алгебра

Группы и кольца вместе с их гомоморфизмами и фактор-структурами.Уникальная факторизация, многочлены и поля.

Необходимое условие: C или выше в MAT 310 или MAT 312 или MAT 315; C или выше в MAT 200 или MAT 250 или разрешение инструктора

3 кредита

​

MAT 314: Абстрактная алгебра II

Этот курс является продолжением MAT 313, Абстрактная алгебра. Он охватывает модули над кольцами, включая структурную теорему для модулей над PID, теорию полей и расширений полей, а также введение в теорию Галуа.

Необходимое условие: МАТ 313 или разрешение инструктора

3 кредита

​

MAT 315: расширенная линейная алгебра

Конечномерные векторные пространства над полем, линейные отображения, изоморфизмы, дуальные пространства, фактор-векторные пространства, билинейные и квадратичные функции, скалярные произведения, канонические формы линейных операторов, полилинейная алгебра, тензоры.Этот курс служит альтернативой MAT 310. Это интенсивный курс, в первую очередь предназначенный для математических специальностей в программе Advanced Track.

Необходимое условие: B или выше по MAT 200 или MAT 250, и B или выше по MAT 220, или разрешение инструктора

4 кредита

​

MAT 319: основы анализа

Тщательное изучение теории, лежащей в основе тем в исчислении с одной переменной, с акцентом на те темы, которые возникают в старшей школе. Реальная система счисления. Пределы функций и последовательностей. Дифференциации, интегрирование и основная теорема. Бесконечная серия.

Необходимое условие: C или выше по MAT 200 или MAT 250 или с разрешения инструктора; C или выше в одном из следующих: MAT 203, 211, 220, 307, AMS 261 или A- или выше в MAT 127, 132, 142 или AMS 161

4 кредита

​

MAT 320: Введение в анализ

Тщательное изучение теории, лежащей в основе исчисления.Реальная система счисления. Основные свойства функций одной действительной переменной. Дифференцирование, интегрирование и обратная теорема. Бесконечные последовательности функций и равномерная сходимость. Бесконечная серия. Метрические пространства и компактность. Этот курс представляет собой более сложную альтернативу MAT 319, подходящую для студентов, которым удобно работать со строгими доказательствами.

Необходимое условие: B или выше по MAT 200 или MAT 250 или разрешение инструктора; C или выше в одном из следующих: MAT 203, 211, 220, 307, AMS 261 или A- или выше в MAT 127, 132, 142 или AMS 161

4 кредита

​

MAT 322: анализ в нескольких измерениях

Непрерывность, дифференцирование и интегрирование в евклидовом n-пространстве.Дифференцируемые карты. Теоремы о неявной и обратной функциях. Дифференциальные формы и общая теорема Стокса.

Предпосылки: C или выше в MAT 203, MAT 220, MAT 307 или AMS 261; C или выше в MAT 310 или MAT 315; B или выше в MAT 320

3 кредита

​

MAT 324: реальный анализ

Введение в меру Лебега и интегрирование. Аспекты рядов Фурье, функциональных пространств, гильбертовых пространств, банаховых пространств.

Предпосылки: B или выше в MAT 320

3 кредита

​

MAT 331: Компьютерное решение математических задач

Исследование использования компьютера в качестве инструмента для понимания сложных математических задач посредством проектно-ориентированного подхода.Учащиеся изучают как соответствующие математические концепции, так и способы использования компьютера (а иногда и неправильного использования) для их понимания. Конкретные проблемы могут варьироваться в зависимости от семестра; прошлые темы включали криптографию, фракталы и рекурсию, моделирование полета планера, подгонку кривой, брахистохрону и компьютерную графику. Предыдущий опыт работы с компьютерами не требуется.

Необходимое условие: C или выше в MAT 203 или 205 или 307 или AMS 261

СБК: ТЕХ

3 кредита

​

МАТ 336: История математики

Обзор истории математики с истоков до XIX века с особым вниманием к первоисточникам и взаимодействию между культурой и математикой.Акцент на темы, относящиеся к школьной программе. месопотамская, египетская и греческая математика; неевропейская математика; математика раннего Возрождения; рождение и расцвет исчисления; начало теории вероятностей; и происхождение неевклидовой геометрии и современной концепции числа.

Необходимое условие: MAT 200 или MAT 203 или или MAT 250 или MAT 307 или AMS 261

DEC:     H
SBC: СПК, СТАС, ВРТД

3 кредита

​

MAT 341: прикладной реальный анализ

Уравнения в частных производных математической физики: уравнения теплопроводности, волны и уравнения Лапласа. Решения с помощью таких методов, как разделение переменных с использованием ортогональных функций (например, ряды Фурье, функции Бесселя, полиномы Лежандра). Решение Даламбера волнового уравнения.

Предпосылки: C или выше в следующем: MAT 203 или 220 или 307 или AMS 261; MAT 303 или 305 или 308 или AMS 361

Консультативное условие: MAT 200 или MAT 250

3 кредита

​

MAT 342: Прикладной комплексный анализ

Комплексные числа, аналитические функции, уравнения Коши-Римана и Лапласа, интегральная формула Коши и приложения.Основная теорема алгебры и принцип максимума. Теорема Коши о вычетах и ​​приложения к вычислению действительных интегралов. Конформные отображения.

Необходимое условие: C или выше в следующем: MAT 203 или MAT 220 или MAT 307 или AMS 261

Консультативное условие: MAT 200 или MAT 250

3 кредита

​

MAT 351: дифференциальные уравнения: динамика и хаос

Исследование долговременного поведения решений обыкновенных дифференциальных уравнений или повторяющихся отображений, подчеркивающее различие между стабильностью, с одной стороны, и чувствительной зависимостью и хаотическим поведением, с другой.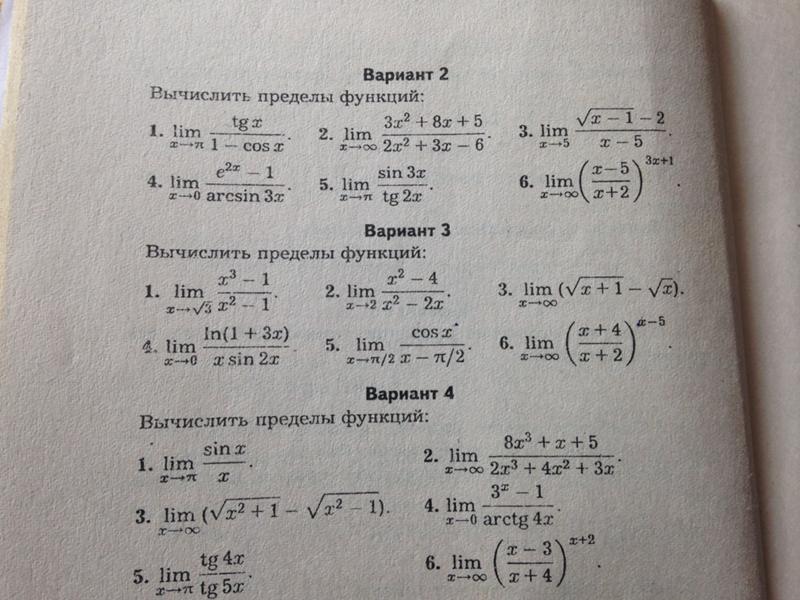 Курс описывает примеры хаотического поведения и фрактальных аттракторов, а также разрабатывает некоторые математические инструменты для их понимания.

Предпосылки: C или выше в следующем: MAT 203 или MAT 220 или MAT 307 или AMS 261; МАТ 303 или МАТ 308 или АМС 361; MAT 200 или MAT 250 или разрешение инструктора

3 кредита

​

MAT 360: геометрические структуры

Формальные геометрии и модели.Темы, выбранные из проективной, аффинной, евклидовой и неевклидовой геометрий.

Предварительное или необходимое: MAT 203, или 220, или 307, или AMS 261; MAT 200 или MAT 250 или разрешение инструктора

3 кредита

​

MAT 362: дифференциальная геометрия поверхностей

Локальная и глобальная геометрия поверхностей: геодезические, параллельный перенос, кривизна, изометрии, отображение Гаусса, теорема Гаусса-Бонне.

Необходимое условие: C или выше в MAT 319 или MAT 320 или MAT 364; MAT 203 или MAT 307 или MAT 322

3 кредита

​

MAT 364: топология и геометрия

Широкое введение в топологию и геометрию, математические теории формы, формы и жесткой конструкции.Темы включают интуитивную теорию узлов, решетки и мозаики, неевклидову геометрию, гладкие кривые и поверхности в евклидовом трехмерном пространстве, открытые множества и непрерывность, комбинаторные и алгебраические инварианты пространств, многомерные пространства.

Предпосылки: MAT 203, или 220, или 307, или AMS 261; МАТ 200 или 250

Консультативное условие: MAT 319 или 320

3 кредита

​

МАТ 371: Логика

Обзор логических основ математики: развитие исчисления высказываний и теории квантификации, понятия доказательства и модели, теорема о полноте, теорема Геделя о неполноте. Этот курс предлагается как CSE 371, так и MAT 371.

Необходимое условие: CSE 150 или CSE 215 или MAT 200 или MAT 250

3 кредита

​

MAT 373: анализ алгоритмов

Математический анализ различных компьютерных алгоритмов, включая поиск, сортировку, умножение матриц, быстрое преобразование Фурье и графовые алгоритмы.Сложность времени и пространства. Анализ верхней границы, нижней границы и среднего случая. Введение в полноту NP. Для реализации и сравнения алгоритмов требуются некоторые машинные вычисления. Этот курс предлагается как CSE 373 и MAT 373. Не засчитывается в дополнение к CSE 385.

Предпосылки: C или выше в MAT 211 или AMS 210; CSE 214 или CSE 260

3 кредита

​

MAT 401: Семинар по математике

Обсуждение конкретной области математики. Работа каждого семестра охватывает разные области математики. Можно повторять по мере изменения темы. Предварительные требования будут объявляться вместе с темой каждый раз, когда предлагается курс.

Необходимое условие: У3/У4; разрешение кафедры или преподавателя; дополнительные предварительные условия объявлены с темой

СБК: СПК

3 кредита

​

MAT 402: Семинар по математике

Обсуждение конкретной области математики.Работа каждого семестра охватывает разные области математики. Можно повторять по мере изменения темы. Предварительные требования будут объявляться вместе с темой каждый раз, когда предлагается курс.

Необходимое условие: У3/У4; разрешение кафедры или преподавателя; дополнительные предварительные условия объявлены с темой

СБК: СПК

3 кредита

​

MAT 425: как преподавать коррекционную математику

Предоставляет знания и навыки для преподавания дополнительных занятий по математике в колледже. Он включает анализ трудностей, с которыми сталкиваются студенты на курсах математического колледжа начальных уровней. В нем вновь обращается к довузовской математике, обсуждается ее использование в курсах колледжа, и на основе этого конкретного материала студентов учат, как выявлять и исправлять типичные ошибки и заблуждения, как составлять задачи и тесты, как анализировать и оценивать инициативные работы студентов, и как организовать уроки в среде студентов с разнообразные задачи и потребности.Студенты узнают, как представлять математику ясно и математически правильно как в устной, так и в письменной форме.

Необходимое условие: MAT 200 и степень B или выше в одном из классов исчисления

3 кредита

​

MAT 444: экспериментальное обучение

Этот курс предназначен для учащихся, которые участвуют в существенной, структурированной экспериментальной учебной деятельности в сочетании с другим классом. Экспериментальное обучение происходит, когда знания, полученные в ходе формального обучения и прошлого опыта, применяются к «реальным» условиям или проблемам для создания новых знаний посредством процесса размышлений, критического анализа, обратной связи и синтеза. Внеклассный опыт, который поддерживает экспериментальное обучение, может включать: сервисное обучение, исследования под руководством наставника, полевые работы или стажировку.

Необходимое условие: WRT 102 или эквивалент; разрешение инструктора и утверждение контракта EXP+ (http://sb.cc.stonybrook.edu/bulletin/current/policiesandregulations/grade_requirements/EXPplus.php)

СБК: опыт+

0 баллов, оценка S/U

​

MAT 458: Эффективно говорите перед аудиторией

Курс с нулевым кредитом, который можно пройти в сочетании с любым курсом MAT, дающим возможность достичь результатов обучения, предусмотренных учебной программой Stony Brook Curriculum SPK.

Предварительно или дополнительно: WRT 102 или эквивалент; разрешение инструктора

СБК: СПК

0 баллов, оценка S/U

​

MAT 459: эффективное письмо по математике

Курс с нулевым кредитом, который можно пройти вместе с любым курсом MAT 300 или 400 уровней с разрешения инструктора.Курс предоставляет возможность практиковать навыки и приемы эффективного академического письма и удовлетворяет результатам обучения в рамках учебной программы Stony Brook Curriculum WRTD.

Необходимое условие: ВРТ 102; разрешение инструктора

СБК: WRTD

0 баллов, оценка S/U

​

MAT 475: Практикум для студентов бакалавриата

Каждый учащийся помогает преподавать курс математики для младших классов или работает в Центре обучения математике. Работа студента регулярно контролируется преподавателем. Кроме того, еженедельно проводится семинар. В обязанности может входить подготовка материалов для использования и обсуждения учащимися, помощь учащимся в решении проблем и участие в «альтернативных» учебных проектах. Предназначен для студентов старших классов, которые преуспели в последовательности исчисления. Не может быть использован для крупного кредита.

Необходимое условие: Разрешение директора бакалавриата

СБК: опыт+

3 кредита, оценка S/U

​

MAT 487: независимое изучение специальных тем

Курс чтения для детей и взрослых.Темы могут быть выбраны студентом с одобрения курирующего члена факультета, который также берет на себя ответственность за оценку. Тема, которая освещается в курсе, регулярно предлагаемом кафедрой, не подходит для самостоятельного изучения. Может повторяться.

Необходимое условие: Разрешение директора бакалавриата

0-6 кредитов

​

MAT 495: Диссертация с отличием

Студент и курирующий преподаватель вместе выбирают тему по математике, и студент пишет содержательную статью, излагающую тему по-новому.

Необходимое условие: Разрешение директора бакалавриата

СБК: EXP+, WRTD

3 кредита

​

Математика 3325: Переход к высшей математике

***Это руководство по курсу. Студенты должны связаться с преподавателем для получения обновленной информации о текущей программе курса, учебниках и содержании курса***

Условие: МАТЕМАТИКА 1432

Описание курса:  Введение в доказательство в математике: логика, множества, отношения, функции и мощность, первый взгляд на эпсилон-дельта методы доказательства.Особое внимание будет уделено написанию и передаче математических идей

*Примечание. Этот курс является обязательным для всех математических специальностей. Ранее  MATH 3397 Переход к Advanced Math.

скачать Math4325 (pdf файл)

Назначение:

Этот курс представляет собой введение в доказательства и абстрактный подход, который характерен для курсов математики старшего уровня. Он служит переходом к продвинутой математике, и его следует проходить после начальной последовательности исчисления и до (или одновременно с) курсов математики среднего уровня. Цель состоит в том, чтобы дать учащимся навыки и методы, которые им понадобятся при изучении любого типа высшей математики, будь то чистая математика, прикладная математика или курсы, ориентированные на приложения. В частности, этот курс охватывает темы, широко распространенные в математике (например, логика, множества, функции, отношения), и помогает подготовить учащихся к таким предметам, как реальный анализ, абстрактная алгебра и расширенная линейная алгебра, которые необходимы для основных и дополнительных курсов.

Основной целью курса будет научить студентов читать, писать и понимать доказательства.На протяжении всего курса студенты познакомятся с обозначениями, языком и методами, используемыми математиками, и получат практику, используя их в своих собственных доказательствах. Кроме того, большое внимание будет уделяться письму и общению.

Предпосылки : Исчисление I и Исчисление II.

Требуемый текст:  Переход к высшей математике , 7-е изд. Дуглас Смит, Морис Эгген и Ричард Сент-Андре. ISBN : 9780495562023

Рекомендуемые тексты:

• Математические доказательства: переход к высшей математике , Гэри Чартранд, Альберт Д.Полимени и Пин Чжан
• Переход к высшей математике : Структура и доказательство Боба Дюма и Джона Маккарти
• Доказательства и основы : Первый курс абстрактной математики Итана Д. Блоха

Краткое содержание курса : Предполагается, что предметы I–VII и VIII (A и B) будут рассмотрены. Элемент VIII (C и D) не является обязательным.

I. Введение в высшую математику

А. Что такое математика?
Б.Индуктивное и дедуктивное рассуждение
C. Что такое доказательство?

II. Логика и доказательства

A. Таблицы истинности, кондиционалы (P ⇒ Q) и бикондиционалы (P ⇔ Q)
B. Отрицание, обратное и контрапозитивное
C. Экзистенциальные и универсальные кванторы (∀, ∃, ∃!)
D. Методы доказательства ( Противоположность, противоречие, индукция), контрпримеры и доказательство утверждений с помощью кванторов
E. Написание доказательств (условия, обозначения и стиль)

III.Теория множеств и ее аксиомы

A. Множества и обозначения множеств, пустое множество, степенное множество
B. Объединение, пересечение, дополнение, подмножества
C. Доказательство равенства множеств
D. Аксиомы наивной теории множеств
E. Аксиома выбора

IV. Натуральные числа

A. Натуральные числа и постулаты Пеано
B. Принцип математической индукции, принцип сильной математической индукции, принцип правильного порядка
C. Делимость, наибольшие общие делители, наименьшие общие кратные и алгоритм деления

В.Отношения

A. Декартовы произведения и отношения
B. Отношения эквивалентности и разбиения
C. Частичные упорядочения, наименьшие верхние границы и наибольшие нижние границы

VI. Функции

A. Определение функции, доменов и кодоменов
B. Композиция и инверсии
C. Проверка правильности определения функции
D. Инъективные, сюръективные и биективные функции
E. Обратимость функций

VII. Мощность

А.Взаимно-однозначные соответствия и эквивалентность множеств 90 599 B. Мощность конечных множеств (и принцип «голубиной норы») 90 599 C. Мощность бесконечных множеств 90 599 D. Счетные, счетные и несчетные множества 90 599 E. Частичный порядок кардинального числа Числа и теорема Кантора-Шредера-Бернштейна

VIII. Основные свойства действительных чисел

A. Аксиомы действительных чисел
B. Полнота вещественных чисел, супремумов и инфимумов
C. Пределы последовательностей ( необязательный )
D.(ε,δ)-определение пределов и непрерывности ( опционально )

 

CSD Размещение:

Академические корректировки/вспомогательные средства : Система Университета Хьюстона соответствует разделу 504 Закона о реабилитации от 1973 г. и Закону об американцах-инвалидах 1990 г. в отношении обеспечения разумных академических корректировок/вспомогательных средств для студентов с инвалидностью. . В соответствии с Разделом 504 и рекомендациями ADA Хьюстонский университет стремится предоставлять разумные академические корректировки/вспомогательные средства студентам, которые просят и требуют их.Если вы считаете, что у вас есть инвалидность, требующая академической корректировки/вспомогательной помощи, посетите веб-сайт Центра для учащихся с ограниченными возможностями (CSD) по адресу http://www.uh.edu/csd/ для получения дополнительной информации.

Формы размещения : Студенты, которым требуются академические корректировки/вспомогательные пособия, должны своевременно (обычно в начале семестра) предоставить своему преподавателю действующую Форму размещения студентов (SAF) (бумажную копию или онлайн-версию, как целесообразно) из офиса CSD до того, как утвержденное приспособление может быть реализовано.

Подробная информация об этой политике и соответствующих обязанностях учащегося изложена в документе «Политика академических корректировок/вспомогательных средств учащегося» (01.D.09) в разделе [ШАГ 4: Представление учащегося (5.4.1 и 5.4.2), стр. 6]. Для получения дополнительной информации посетите страницу ресурсов для учащихся Центра для учащихся с ограниченными возможностями .

Кроме того, если учащийся запрашивает (одобренное CSD) приспособление для прохождения тестирования, то учащийся также заполняет бумажную форму запроса на индивидуальное приспособление для прохождения тестирования (RITA), чтобы организовать проведение тестов в офисе CSD.CSD предлагает учащемуся встретиться со своим инструктором в рабочее время и/или договориться о встрече для заполнения формы RITA для обеспечения конфиденциальности.

*Примечание. Формы RITA необходимо заполнить как минимум за 48 часов до первоначальной даты тестирования. Пожалуйста, проконсультируйтесь со своим консультантом заранее, чтобы убедиться, что ваши тесты запланированы своевременно. Пожалуйста, имейте в виду, что если вы превысите согласованный лимит времени для вашего экзамена, вы будете оштрафованы пропорционально количеству дополнительного времени.

 

UH CAPS

Консультационные и психологические услуги (CAPS) могут помочь учащимся, которые испытывают трудности с преодолением стресса, приспосабливаются к колледжу или испытывают грусть и безнадежность. Вы можете связаться (CAPS), позвонив по телефону 713-743-5454 в рабочее и нерабочее время для обычных встреч или если вы или кто-то из ваших знакомых находится в кризисной ситуации. Для участия в программе «Поговорим» не требуется предварительной записи, которая представляет собой консультационную услугу в удобном месте и в удобное время на территории кампуса.

Курсы бакалавриата | Кафедра математики

МАТЕМАТИКА 1010 – Семинар Патнэма	(2 кредита) Целью этого курса является развитие способности решать математические задачи, требующие значительного элемента изобретательности и настойчивости. Обучение будет включать в себя изучение задач из предыдущих соревнований Патнэма, для которых этот курс можно рассматривать как полезную подготовку. Будет предпринята попытка поиска объединяющих математических идей.Также будут обсуждаться общие стратегии решения проблем.	Согласие инструктора
МАТЕМАТИКА 1020 – Прикладная элементарная теория чисел	(3 кредита) Этот курс раскроет ключевую роль теории чисел в развитии математики. В ходе курса будут рассмотрены некоторые приложения теории чисел. Пример программы	МАТЕМАТИКА 0430
МАТЕМАТИКА 1025 — Введение в математическую криптографию	(3 кредита) Курс охватывает теоретические основы криптосистем и анализ их ограничений и уязвимостей.Особое внимание будет уделено криптосистемам с открытым ключом, включая системы на основе эллиптических кривых. Будут обсуждаться приложения реального мира, такие как безопасность браузера и биткойн. Пример программы	МАТЕМАТИКА 0430
МАТЕМАТИКА 1050 – Комбинаторная математика	Рассматриваемые темы включают биномиальную теорему, принцип исключения включения, рекуррентные соотношения, производящие функции и проблемы раскраски.	МАТЕМАТИКА 0413 или 0450 или 1185
МАТЕМАТИКА 1070 – Численный математический анализ	(3 кредита) Этот курс вместе с MATH 1080 образует двухсеместровое введение в численный анализ на продвинутом уровне бакалавриата и включает в себя интерполяцию, численное дифференцирование и интегрирование, решение нелинейных уравнений, численное решение систем или обыкновенных дифференциальных уравнений, а также дополнительные темы, такие как время разрешает.Акцент делается на понимании алгоритмов, а не на подробном кодировании, хотя потребуется некоторое программирование. Пример программы	МАТЕМАТИКА 0240 и некоторый опыт программирования
МАТЕМАТИКА 1080 – Численная математика: линейная алгебра	(3 кредита) Этот курс представляет собой введение в числовую линейную алгебру, в котором рассматриваются численные методы решения линейных алгебраических систем и матричных задач на собственные числа, а также приложения к уравнениям в частных производных. Хотя курс будет подчеркивать вычислительную точку зрения, анализ сходимости и устойчивости алгоритмов будет исследован. Пример программы	(MATH 0240 или 0245) и (MATH 0250, 0280, 1180 или 1185) и некоторый опыт программирования
МАТЕМАТИКА 1100 – линейное программирование	(3 кредита) Рассматриваемые темы будут включать проблемы линейного программирования, симплекс-метод, качество, пересмотренный симплекс-метод и транспортную задачу.	МАТЕМАТИКА 0280 или 1180 ENGCMP 0200 или 0203 или 0205 и т. д.
МАТЕМАТИКА 1101 — Введение в оптимизацию	(3 кредита) Этот курс знакомит студентов с методами оптимизации. Особое внимание будет уделено приложениям, но будет рассмотрена некоторая теория и обсуждены доказательства. Кроме того, студентов научат, как использовать доступное программное обеспечение для ответов на вопросы. Темы курса будут включать линейное программирование, целочисленное программирование, нелинейное программирование, выпуклые и аффинные множества, выпуклые и вогнутые функции, оптимизацию без ограничений и комбинаторную оптимизацию (т. е. Проблемы с сетевым потоком). Пример программы	MATH 0240 и один из MATH 0280, 1180 или 1185
МАТЕМАТИКА 1103 – Математические задачи в бизнесе, промышленности и правительстве	(3 кредита) Курс семинара, посвященный проблемам бизнеса, промышленности и правительства. Пример программы	Математика 1101 или Математика 1360
МАТЕМАТИКА 1110 – Промышленная математика	(3 кредита) Этот курс посвящен приближенному численному решению задач, возникающих в производственной среде.Охватываемые темы включают физическую интерпретацию математической модели, использование библиотечного программного обеспечения, подготовку программного обеспечения, анализ результатов и отчет о результатах.	МАТЕМАТИКА 1180 и 1185
МАТЕМАТИКА 1121 – Актуарная математика II	(3 кредита) Этот курс будет охватывать материал, указанный в программе экзамена m (3) (математика непредвиденных обстоятельств жизни и финансовая экономика) общества актуариев. В частности, будут представлены актуальные темы страхования жизни и пожизненных аннуитетов, включая модели многократного уменьшения, а также ценообразование Блэка и Шоулза для производных ценных бумаг и анализ рисков. Материал будет представлен в традиционном академическом формате лекций и вспомогательных занятий, а также дополнительных занятий, специально направленных на подготовку студентов к экзамену SOA. Пример программы	МАТЕМАТИКА 0240 или 1120
МАТЕМАТИКА 1122 – Актуарная математика III	(3 кредита) Непредвиденные обстоятельства жизни Пример программы	(MATH 470 или 1121) и (MATH 1119 или STAT 1151)
МАТЕМАТИКА 1123 – Актуарная математика IV	(3 кредита) Непредвиденные обстоятельства жизни, часть 2 Пример программы	Математика 1122
МАТЕМАТИКА 1126 — Предиктивная аналитика 1	(3 балла) Это вводный курс по современной науке о данных, включая статистическое обучение и временные ряды. Будут затронуты следующие темы: линейная регрессия (проверка, методы повторной выборки, выбор модели и регуляризация, усадка, уменьшение размерности, основные компоненты), обобщенные линейные модели (модели логистической и пробит-регрессии, категориальный и подсчетный ответ, меры соответствия), Неконтролируемое обучение (деревья решений и случайные леса, начальная загрузка, бэггинг, основные компоненты, кластерный анализ), временные ряды (модели случайного блуждания, авторегрессионные модели, модели ARCH/GARCH, моделирование и прогнозирование Бокса-Дженкинса). Пример программы	МАТЕМАТИКА 0230 и 1119
МАТЕМАТИКА 1127 — Предиктивная аналитика 2	(3 балла) Этот курс с 3 кредитами является продолжением курса «Математика 1126», «Прогнозная аналитика 1». Он будет охватывать фундаментальные знания о науке о данных с приложениями к страхованию и бизнесу. Студенты познакомятся с Basic R, сбором данных, очисткой данных, исследованием и визуализацией данных, прогнозным моделированием и профессиональной отчетностью. Он также готовит студентов к экзамену SOA Exam PA. По завершении этого курса студенты разовьют навыки прогнозной аналитики, которые позволят им: (1) сформулировать типы проблем, которые могут быть решены с помощью прогнозного моделирования, определить бизнес-проблему и то, как имеющиеся данные соотносятся с возможным анализом, использовать информация для предложения моделей, таких как обобщенная линейная модель (GLM), деревья решений, кластерный анализ и анализ основных компонентов; (2) приобрести опыт использования R для прогнозной аналитики и уметь создавать эффективные графики в RStudio, работать с различными типами данных, понимать принципы проектирования данных и создавать различные общие визуализации для изучения данных; (3) оценивать качество данных, решать проблемы с данными и выявлять нормативные и этические проблемы; (4) эффективно сообщать о результатах применения прогнозной аналитики для решения бизнес-проблемы. Пример программы	МАТЕМАТИКА 1126
МАТЕМАТИКА 1128 – Актуарная математика V	(3 балла) Этот курс с 3 кредитами будет охватывать темы «Краткосрочной актуарной математики 1», который обеспечивает основу для последующего курса «Краткосрочная актуарная математика 2», а также готовит студентов к экзамену SOA STAM. Студенты познакомятся с различными моделями частоты, серьезности и агрегирования, которые полезны для краткосрочных актуарных приложений.Учащиеся узнают о шагах, связанных с процессом моделирования, и о том, как применять эти шаги. По окончании курса слушатели смогут: 1) анализировать данные из приложения в бизнес-контексте; 2) определить подходящую модель, включая значения параметров; 3) обеспечить меры доверия для решений, основанных на модели. Студенты познакомятся с различными инструментами для калибровки и оценки моделей. Пример программы	МАТЕМАТИКА 1119 и СТАТИСТИКА 1152
МАТЕМАТИКА 1129 – Актуарная математика VI	(3 балла) Этот курс с 3 кредитами будет охватывать темы «Краткосрочной актуарной математики 2» (STAM 2), который основан на темах STAM 1, а также подготовит студентов к экзамену SOA STAM.Студенты познакомятся с теорией достоверности: априорное распределение, апостериорное распределение, прогнозирующее распределение, байесовская премия, модель Бульмана, модели Бульмана-Штрауба, премия за достоверность, коэффициент достоверности и эмпирические байесовские методы. По окончании курса слушатели смогут: 1) понимать и оценивать потери, используя процедуры достоверности; 2) понимать фундаментальные принципы ценообразования и резервирования некоторых из наиболее распространенных краткосрочных страховых и перестраховочных покрытий: автострахования, домовладельцев, ответственности, здоровья, инвалидности и стоматологии.Студенты познакомятся с некоторыми методами и базовыми статистическими моделями, используемыми для оценки убытков, понесенных в результате краткосрочного страхования и перестрахования. Пример программы	МАТЕМАТИКА 1128
МАТЕМАТИКА 1180 – Линейная алгебра	(3 кредита) Этот курс подчеркивает теоретическое и строгое развитие линейной алгебры. Основные темы включают теорию векторных пространств, линейных преобразований, матриц, характеристических полиномов, базисов и канонических форм.Другие темы могут быть затронуты, если позволяет время. Пример программы	Необходимый компонент: МАТЕМАТИКА 0413 или МАТЕМАТИКА 0450
МАТЕМАТИКА 1185 — Линейная алгебра с отличием	(3 кредита) Введение в вычислительные и теоретические аспекты линейной алгебры. Программа включает исключение Гаусса, матричную алгебру, треугольную факторизацию, векторные пространства, линейную независимость, базис, размерность, ортогональность, скалярный продукт, грамм-Шмидт, разложение по сингулярным числам, определители, собственные значения, матричные экспоненты, унитарные матрицы, сходство, положительную определенность, минимум принципы, конечные элементы, норма и число обусловленности, вычисление собственных значений, итерационные решения линейных систем, линейные неравенства, симплекс-метод.	Согласие инструктора
МАТЕМАТИКА 1230 – Большие идеи математики	(3 кредита) Курс «Большие идеи» предназначен для того, чтобы предоставить студентам, изучающим математику, практический опыт. Он объединит текущие математические знания учащегося в единое целое посредством принятия исторической перспективы. Он особенно предназначен для математических специальностей, интересующихся математическим образованием или историей, философией и психологией математики. Учащиеся, выбравшие факультативную стажировку MATH 1231, узнают, как историческое развитие математики связано с математикой в ​​средней школе. Заключительный опыт завершится исследовательским проектом и презентацией.	МАТЕМАТИКА 0430
МАТЕМАТИКА 1231 – Стажировка в области математического образования	(1 кредит) Эта стажировка состоит из двух компонентов: 1) опыт работы в классе по наставничеству старшеклассника, разрабатывающего исследовательский проект, и 2) семинар, на котором обсуждаются «большие идеи» математики в MATH 1230 и то, как математика развивается в учебной программе начальной и средней школы. .Стажеры будут проводить один час каждые две недели, обучая старшеклассника в местной средней школе.	МАТЕМАТИКА 1230
МАТЕМАТИКА 1250 – Абстрактная алгебра	(3 кредита) В этом курсе довольно подробно изучаются основные алгебраические системы, группы и кольца. Темы включают: подгруппы, группы перестановок, гомоморфизмы, подкольца, идеалы и фактор-кольца. Акцент делается на теорию с примерами. Пример программы	МАТЕМАТИКА 0430
МАТЕМАТИКА 1270 – Обыкновенные дифференциальные уравнения 1	(3 кредита) Этот курс охватывает методы решения обыкновенных дифференциальных уравнений, которые часто встречаются в приложениях.Общие методы будут преподаваться для одиночных уравнений n-го порядка и систем нелинейных уравнений первого порядка. Это будет включать методы фазовой плоскости и анализ стабильности. Компьютерные эксперименты будут использованы для иллюстрации поведения решений различных уравнений. Пример программы	Один из MATH 0280, 1180 или 1185
МАТЕМАТИКА 1275 — Обыкновенные дифференциальные уравнения с отличием 1	(3 кредита) Этот курс обеспечивает более тщательное математическое рассмотрение теории, чем это возможно в курсе без дипломов (MATH 1270), а также охватывает некоторые более современные приложения. В дополнение к основному материалу о точных решениях будут даны математические доказательства теорем существования и единственности, что позволит лучше понять такие важные темы, как поведение на фазовой плоскости и теория устойчивости. Кроме того, будет рассмотрено больше тем, в том числе более подробное обсуждение серийных решений и специальных функций, чем это возможно в MATH 1270. Наконец, курсовой проект, обычно выполняемый в парах, по теме, которую студенты выбирают под руководством и одобрение от инструктора, будет ключевой особенностью. Пример программы	(MATH 0230 или 0235) и (MATH 1180 или 1185) CoREQ: МАТЕМАТИКА 413 или 0450
МАТЕМАТИКА 1280 – Обыкновенные дифференциальные уравнения 2	(3 кредита) Это курс устойчивости и качественных методов анализа обыкновенных дифференциальных уравнений, возникающих в реалистических моделях. Изучаются методы фазовой плоскости, методы возмущений и теория бифуркаций.	МАТЕМАТИКА 1270 или 1275
МАТЕМАТИКА 1290 – Разделы по геометрии	(3 кредита) Курс, призванный дать «современный» взгляд на геометрию. Возможные подходы включают (1) связь геометрий с абстрактными алгебраическими системами и (2) дедуктивное, синтетическое развитие евклидовой и неевклидовой геометрии. Пример программы	МАТЕМАТИКА 0240 и (МАТИКА 0413 или 0450)
МАТЕМАТИКА 1310 – Теория графов	(3 кредита) Концепция графа и изучение его теоретических свойств и приложений составляют основу этого курса.Темы включают пути, схемы, деревья, плоские графы, проблемы раскраски, орграфы, теорию соответствия и сетевые потоки.	МАТЕМАТИКА 0413 или 0450
МАТЕМАТИКА 1350 – Введение в дифференциальную геометрию	(3 кредита) Возможные темы: основные идеи топологии, описание кривых в пространстве, определение и локальное изучение гладких поверхностей в евклидовом пространстве (фундаментальные формы, геодезические и кривизна), глобальные свойства поверхностей, формула Гаусса-Бонне и приложения.	МАТЕМАТИКА 0240 и (МАТИКА 1180 или 1185)
МАТЕМАТИКА 1360 – Моделирование в прикладной математике	(3 кредита) Этот курс знакомит с некоторыми фундаментальными подходами прикладной математики. Акцент делается на процессе построения модели и на развитии понимания некоторых объединяющих тем прикладной математики, таких как равновесия, устойчивость, законы сохранения и т. д. Материал представлен в форме тематических исследований. Пример программы	МАТЕМАТИКА 0290 или МАТЕМАТИКА 1270 или МАТЕМАТИКА 1275
МАТЕМАТИКА 1370 — Введение в вычислительную нейронауку	(3 кредита) Этот курс представляет современные математические теории нейронауки, включая одиночные нейроны и нейронные сети. Внимание будет уделено 1451 динамике и функции нервной деятельности. Пример программы	МАТЕМАТИКА 0240 или МАТЕМАТИКА 0245 или МАТЕМАТИКА 0450
МАТЕМАТИКА 1380 – Математическая биология	(3 кредита) Этот курс представляет собой широкое введение в математические методы, обычно применяемые к проблемам биологии. Будут представлены модели, использующие исчисление, обыкновенные дифференциальные уравнения, уравнения в частных производных, дискретные динамические системы, стохастическую динамику или структуру клеточных автоматов, и будут описаны основные методы их анализа. Также будут рассмотрены вычислительные методы, включая вычислительные платформы, такие как XPPAUT. На протяжении всего курса у студентов будут широкие возможности для практики разработки и анализа моделей математической биологии. Пример программы	(MATH 0280 или 1180 или 1185) и (MATH 0290 или 1270 или 1275)
МАТЕМАТИКА 1410 – Введение в основы математики	(3 кредита) Этот курс знакомит с логическими основами математики; он охватывает исчисление высказываний и исчисление предикатов, формальную теорию чисел и первую теорему Гёделя о неполноте.Если позволит время, мы также рассмотрим начальную теорию множеств и начальную теорию моделей.	Математика 0413 или Математика 0450
МАТЕМАТИКА 1470 – Уравнения с частными производными 1	(3 кредита) Это первый член двучленной последовательности в элементарных УЧП. Цели курса – предоставить студентам методы, необходимые для постановки и решения задач, связанных с УЧП, и подготовиться к дальнейшему изучению УЧП.Изучаются три основных типа линейных УЧП второго порядка – параболические, эллиптические и гиперболические. Кроме того, вводятся инструменты, необходимые для решения уравнений в частных производных, такие как ряды Фурье и преобразования Лапласа.	МАТЕМАТИЧЕСКИЕ 0240 и {[(МАТИЧЕСКИЕ 0280 или 1180 или 1185) и (МАТИЧЕСКИЕ 0290 или 1270)] или МАТЕМАТИЧЕСКИЕ 0250}
Математика 1510 – Математическая теория вероятностей	(3 кредита) Этот курс является введением в математическую теорию вероятностей.Основные темы включают случайные величины, ожидания, характеристические функции, условную вероятность и введение в мартингалы и цепи Маркова.	(математика 0420 или 0450) и (математика 280, 1180 или 1185) или разрешение инструктора
МАТЕМАТИКА 1530 — Расширенное исчисление 1	(3 кредита) Этот курс содержит строгое развитие исчисления функций одной переменной, включая компактность на прямой, непрерывность, дифференцируемость, интегрирование и равномерную сходимость последовательностей и рядов функций. Могут быть включены и другие темы, такие как понятие пределов и непрерывности в метрических пространствах.	МАТЕМАТИКА 0420 или МАТЕМАТИКА 0450
МАТЕМАТИКА 1540 – Усовершенствованное исчисление 2	(3 кредита) В этом курсе, являющемся продолжением Fall Math 1530, будет строго разработана теория дифференцирования и интегрирования функций многих переменных. Темы будут включать теоремы об обратной и неявной функциях, теорему Фубини, замену переменных и теорему Стокса.	МАТЕМАТИКА 1530
МАТЕМАТИКА 1550 — векторный анализ и приложения	(3 кредита) Рассматриваемые темы включают: векторную алгебру, векторное дифференцирование и интегрирование, дивергенцию, градиент, завиток, теоремы Грина, Гаусса и Стокса и криволинейные системы координат. Особое внимание будет уделено решению проблем и приложениям в электромагнитной теории и потоках жидкости. Пример программы Расписание семестра	MATH 0240 и (MATH 250 или 0280 или 1180 или 1185)
МАТЕМАТИКА 1560 – Комплексные переменные и приложения	(3 кредита) Этот курс охватывает следующие темы: элементарные операции с комплексными числами, производные, интегралы, теорема Коши и следствия, такие как интегральная формула, степенной ряд, теорема о вычетах, приложения к действительным интегралам и рядам.	[MATH 0240 или 245 (с B или лучше)] или MATH 1550
МАТЕМАТИКА 1570 – Введение в анализ Фурье	(3 кредита) Курс представляет собой строгое введение в ряды и интегралы Фурье с приложениями к тепловому потоку, волновому движению, физике и теории чисел. Он предназначен для студентов с базовыми знаниями реального анализа, включая равномерную сходимость последовательностей и рядов функций. Знание интеграла Лебаска не предполагается. Пример программы	(Math 0420 или 0450) и (Math 0280 или 1180 или 1185)
МАТЕМАТИКА 1700 — Введение в топологию	(3 кредита) Будет изучена топология r1, а также топология общих метрических пространств. Основные понятия будут применены для получения фундаментальной теоремы существования для обыкновенных дифференциальных уравнений первого порядка. Курс будет построен на доказательстве теорем и решении задач.	МАТЕМАТИКА 0420 или 0450
МАТЕМАТИКА 1800 – Дополнительные темы по математике	(3 кредита) Это вводный курс продолжительностью один семестр по квантовой теории информации. Цель состоит в том, чтобы дать введение в парадигмы квантовых вычислений и математику, лежащую в основе квантовых алгоритмов. Мы увидим, что во многих случаях они намного эффективнее своих классических аналогов. Мы начнем с краткого введения в квантовую механику, а затем обсудим основы квантовых вычислений.Затем мы рассмотрим некоторые хорошо известные квантовые алгоритмы, такие как алгоритм Шора для простой факторизации. Мы также обсудим возможное влияние появления квантового компьютера на стандарты современной криптографии. Необходимая основа для курса – линейная алгебра. Знание квантовой механики полезно, но не обязательно.	МАТЕМАТИКА 0280 или 1180 или 1185
или MATH 1900 Стажировка	(1–3 кредита) Под руководством преподавателей учащийся участвует в опыте, проекте или работе, связанной с математикой.	Свяжитесь с директором бакалавриата для получения номера разрешения
МАТЕМАТИКА 1902 Направленное исследование	(1–3 кредита) Под руководством преподавателя студент изучает взаимно согласованную тему математики.	Свяжитесь с директором бакалавриата для получения номера разрешения

Вводные курсы по математике | Математика

Курсы по многомерной математике

Кафедра предлагает 3 последовательности по многомерной математике.Если вы использовали многомерное исчисление в другом месте, нажмите кнопку ниже:

Уже взялись за многомерное исчисление?

Серия 50:

См. подробный список тем.

Математика 51- Линейная алгебра, многомерное исчисление и современные приложения (5 единиц) охватывает линейную алгебру и многомерное дифференциальное исчисление унифицированным образом наряду с приложениями, связанными со многими количественными областями. Этот материал включает в себя базовую геометрию и алгебру векторов, матриц и линейных преобразований, а также методы оптимизации в любом количестве переменных (включая частные производные и множители Лагранжа).

Унифицированное рассмотрение как линейной алгебры (за пределами измерения 3 и включая собственные значения), так и оптимизации с несколькими переменными не рассматривается в одном курсе, доступном для неспециалистов где-либо еще. Многие студенты, которые изучают многомерное исчисление до поступления в Стэнфорд, находят Math 51 поучительным для изучения из-за его широкого охвата и синтеза концепций. Если вы хотите перевести баллы вместо математики 51, вам, скорее всего, понадобятся два курса (один по многомерному исчислению, один по линейной алгебре).

Математика 52- Интегральное исчисление нескольких переменных (5 единиц)   охватывает многомерную интеграцию и, в частности, теорему Грина и теорему Стокса. Здесь используется как линейная алгебра, так и матричный производный материал из Math 51.

Математика 53- Дифференциальные уравнения с линейной алгеброй, методы Фурье и современные приложения (5 единиц) развивает основные концепции, примеры и результаты для обыкновенных дифференциальных уравнений, а также охватывает важные уравнения в частных производных и методы Фурье для их решения.Здесь используется как линейная алгебра, так и матричный производный материал из Math 51.

Унифицированное рассмотрение как обыкновенных дифференциальных уравнений, так и уравнений в частных производных (УЧП) вместе с методами Фурье не рассматривается в одном курсе, доступном для неспециалистов где-либо еще. Для тех, кто изучал дифференциальные уравнения до поступления в Стэнфорд, Math 53 укрепит ваши навыки и расширит ваши знания за счет использования линейной алгебры и охвата методов PDE и Фурье. Если вы хотите перевести кредит взамен математики 53, вам, вероятно, понадобятся два курса (один по обыкновенным дифференциальным уравнениям и один по материалам PDE/Fourier).

** Математика 52 и Математика 53 можно проходить в любом порядке.

Эта серия обеспечивает необходимый математический фон для всех дисциплин, особенно для естественных наук, математики, математических и вычислительных наук, экономики и техники.

Учебник по математике 51 Учебник по математике 53

Оглавление и страница приложений в начале текстов курса предоставляют дополнительную информацию; эти тексты курсов находятся в свободном доступе для всех, у кого есть SUNetId.

Для тех, кто проявляет большой интерес к математике и предпочитает более концептуальное и теоретическое понимание, мы рекомендуем следующие две последовательности:

Серия 60CM

Математика 61CM-62CM-63CM- Современная математика: непрерывные методы   (по 5 единиц в каждой) Эта последовательность из трех четвертей, ориентированная на доказательство, охватывает материал 51, 52, 53, а также дополнительное расширенное исчисление, многомерную геометрию, обыкновенные дифференциальные уравнения и уравнения в частных производных.Это обеспечивает унифицированное рассмотрение исчисления с несколькими переменными, линейной алгебры и дифференциальных уравнений с другим порядком тем и акцентом по сравнению со стандартными курсами. Студенты должны очень хорошо знать исчисление с одной переменной и проявлять интерес к теоретическому подходу к предмету.

Эта серия обеспечивает необходимую математическую основу для всех дисциплин, особенно для естественных наук, математики, математических и вычислительных наук, экономики и инженерии.