При вычислении производной постоянный множитель можно: Правила дифференцирования

1.4. Простейшие правила вычисления производных

Теперь укажем ряд простых правил, с помощью которых станет возможным вычисление производной для любой функции составленной из элементарных при посредстве конечного числа арифметических действий и суперпозиций.

Теорема 1. Постоянный множитель можно выносить за знак производной, т.е. если у = с f(x), где с = const, то у’ = с f’(x).

Доказательство. Если независимая переменная х получит приращение , то новое значение функции у будет у + = с f(x+ ).

Отсюда и окончательно

Теорема 2. Производная суммы конечного числа функций, имеющих (в определенной точке) производную, равна соответствующей сумме производных этих функций (в той же точке).

Для случая, например, двух слагаемых, имеем:

y = u(x) + v(x), .

Заметим, что выражение y = u(x) – v(x) равносильно y = u(x) + (–1)v(x) и .

Доказательство. Придадим x приращение ∆x; тогда u, v и y получают приращения соответственно ∆u, ∆v и ∆y. Их новые значения u+∆u, v+∆v и y+∆y связаны тем же соотношением:

y + ∆y= (u+∆u) + (v+∆v).

Отсюда

∆y = ∆u + ∆v, и ,

так что .

Этот результат легко может быть распространен на любое число слагаемых (и притом, тем же методом).

Теорема 3. Производная произведения двух непрерывных функций, имеющих производную, равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции, т. е. если y = u(x)·v(x), то .

Доказательство. Приращению отвечают, как и выше, приращения ∆

u, ∆v и ∆y; при этом

y + ∆y = (u+∆u)·(v+∆v), так что

∆y = ∆u·v + u·∆v + ∆u·∆v и

.

Так как при ∆x  , в силу непрерывности v(x) и ∆v  , то

.

На основании доказанной теоремы легко получается правило дифференцирования произведения любого числа функций.

Так, если имеем произведение трех функций , то, представляя правую часть как произведение

u и , получим:

Таким приемом можем получить аналогичную формулу для произведения любого (конечного) числа функций. Именно, если y = u₁, u₂, .., u_n, то

.

Теорема 4. Производная дроби (т.е. частного от деления двух непрерывных функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, т.е. если (где ), то

Доказательство. При тех же обозначениях, что и выше, имеем

так что

и

Устремляя здесь к нулю (причем одновременно и ) убеждаемся, что

Теорема. Если функция в некоторой точке x = x₀ имеет (конечную) производную , то

1. приращение функции может быть представлено в виде

, (3.

6)

или, короче, , где  есть величина, зависящая от x и вместе с ним стремящаяся к нулю, т.е. ;

2. функция в этой точке необходимо непрерывна.

Доказательство. 1) Согласно определению производной, . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем

, где .

Определяя отсюда y, придем к формуле (3.6).

2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При x 

 сумма в правой части (3.6) обращается в нуль. Следовательно, , или , а это означает, что функция в точке x₀ непрерывна.

Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x₀= 1 функция y = |x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.

Тест по алгебре на тему Производная

Тест по алгебре производная

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях) », Ч.1.: Мордкович А. Г., Семенов П. В.; Ч.2.: Мордкович А. Г. и др., под ред. Мордковича А. Г.

Глава 5. Производная

Производная данной функции это

A) значение данной функции при x=0

B) новая функция, связанная с данной

C) максимальное значение данной функции

Найдите производную функции y=x+2x 2

B) +x

Найдите производную функции y=-4x 3 +8x-12

C) ) -12x 2 -8

Какая из формул является неверной?

A)

B)

C)

Чему равна производная суммы двух функций?

A) Произведению производных

B) Сумме производных

C) Разности производных

Найдите производную функции

A)

B)

C) нет правильного ответа

Найдите производную функции

B)

C)

Составьте уравнение касательной к графику функции y= в точке

Какой знак имеет производная функции на заданном отрезке, если сама функция возрастает?

A)

B)

C)

Точки экстремума функции — это.

A) точки минимума функции

B) точки максимума функции

C) точки, в которых производная функции не существует или равна нулю

Производная данной функции это.

Xn—j1ahfl. xn--p1ai

25.12.2017 4:08:06

2017-12-25 04:08:06

Источники:

Https://xn--j1ahfl. xn--p1ai/library/test_po_algebre_na_temu_proizvodnaya_231943.html

Тест по теме Производная функции » /> » /> .keyword { color: red; }

Тест по алгебре производная

Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.

В тесте содержатся вопросы на понятие производной, правила вычисления производной, примеры на вычисление производной.

Список вопросов теста

Вопрос 1

Что называется производной функции в точке х0?

Варианты ответов

Производной функции в точке х0 называется отношение приращения функции к приращению её аргумента при стремлении последнего к нулю. Производной функции в точке х0 называется предел отношения приращения функции к приращению её аргумента при стремлении последнего к нулю. Производной функции в точке х0 называется предел отношения значения функции к её аргументу при стремлении последнего к нулю. Нет правильного ответа.

Вопрос 2

Выберите из предложенных правил вычисления производных верные.

Варианты ответов

Производная произведения двух функций равна произведению производных. Производная константы равна самой константе. Производная суммы/разности нескольких функций равна сумме/разности производных этих функций. Постоянный множитель можно выносить за знак производной. Производная частного двух функций равна частному производных этих функций.

Вопрос 3

Найдите производную: У = 2х — 3.

Варианты ответов

Вопрос 4

Найдите производную функции У = х 2 — 6

Варианты ответов

Вопрос 5

Найдите производную функции У = sinx + cosx

Варианты ответов

sinx + cosx cosx — sinx 2cosx 2sinx

Вопрос 6

Как называется операция нахождения производной?

Варианты ответов

Дифференцирование Интегрирование Лимитирование Дебилирование

Вопрос 7

С помощью какого математического понятия даётся понятие производной?

Варианты ответов

С помощью предела функции в точке. С помощью предела на бесконечности. С помощью таблицы производных. Никакого математического понятия при определении производной не используется.

Вопрос 8

При вычислении производной степенной функции в резудьтате получается функция, степень которой.

Варианты ответов

на единицу меньше степени исходной функции. на единицу больше степени исходной функции. степень не меняется, меняется множитель перед функцией. нет правильного ответа.

Вопрос 9

Как можно по-другому назвать правила вычисления производных?

Варианты ответов

Правила дифференцирования. Правила интегрирования. Правила лимитирования. Правила вычисления.

Вопрос 10

Найдите производную функции У = -4х 2 + 3sinx + 7x — 1.

На единицу меньше степени исходной функции.

Videouroki. net

03.03.2020 0:36:46

2020-03-03 00:36:46

Источники:

Https://videouroki. net/tests/tiest-po-tiemie-proizvodnaia-funktsii-1.html

Тесты по теме Производная онлайн | Online Test Pad » /> » /> .

keyword { color: red; }

Тест по алгебре производная

Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.

Математический анализ. Вычисление производных.

Данный тест рассчитан на выпускников школ и первокурсников ВУЗов. Проверьте свои знания в теории производных.

Производная. Формулы.

Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.

Нахождение производной

Тренировочный тест на нахождение производной сложной функции, производная частного и произведения

Производная элементарных функций

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.

Производные элементарных функций

Тест рекомендуется использовать при изучении темы «Производные элементарных функций» по учебнику Ю. М. Колягина, 11 класс

Наибольшее и наименьшее значения функций

Контрольный тест по алгебре и началам анализа в 11 классе. По материалам профильного ЕГЭ 2019 года (№12)

Урок №6 «Признаки возрастания и убывания функции»

Данный тест предназначен для закрепления материала по теме «Признак возрастания и убывыания функции». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи.

Производная функции (высшая математика)

Тест по курсу высшей математики на тему «Производная функции». Тест создан с целью проверки элементарных теоретических знаний производной и умения решать простейшие задачи производной.

Тест «Вторая производная. Физический смысл производной»

Тест «Вторая производная. Физический смысл производной». Тест по теме «Вторая производная. Физический смысл производной» проверяет знание определения первой и второй производной, понимание физического смысла первой и второй производной функции, умения вычислять первую и вторую производные функций. умения вычислять значения производных функций в точке. Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа.

Производная. Геометрический смысл производной.

Алгебра и начала анализа. Тема «Производная» Тест по теме «Производная. Геометрический смысл производной».

Производная функции в школьном курсе математике

Тест состоит из 10 вопросов раскрывающих тему «Производная функции»

Математика тест для 11 класса по теме производная

Тест предназначен для учащихся 11 классов или студентов 1 и 2 курса. Содержит задания по теме «Производная и её приложения», «Интеграл», «Первообразная», «Пределы». Включает в себя 19 заданий

Тест для обучающихся 11 класс в форме ЕГЭ (профильный уровень)

Тест состоит из 12 вопросов 1 части ЕГЭ профильного уровня обучающихся 11 класса

Вычисление производной

Данный тест может быть использован в качестве контроля знаний учащихся после изучения темы «Производная»

Нахождение производной суммы.

Формулы дифференцирования.

Использование формул дифференцирования и правила суммы для нахождения производных.

Дифференцирование алгебраической суммы

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.

Дифференцирование произведения

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.

Нахождение значений производных в точке

Тест направлен на формирования навыков поиска производных различных функций и нахождение значений производных

Дифференцирование частного

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.

УД Математика Производная (вариант 2)

Тест по математике «Вычисление производной» для студентов 1 курса СПО

Производная тригонометрической функции

Тест предназначен для проверки зананий по теме «Производная тригонометрических функций и их комбинации с элементарными функциями»

Нахождение значения производной тригонометрической функции в точке

Тест предназначен для проверки зананий по теме «Нахождение значения производной тригонометрической функции в точке»

Производная и ее приложения

Тест предназначен для проверки знания физического и геометрического смысла производной, формул производных элементарных функций, правил вычисления производной, уения применять производную для составления уравнения касательной, исследования функции на монотонность и экстремумы

ОУД.

03 Математика. Итоговое тестирование

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части учебной дисциплины математика. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

Производная функции

Проверка усвоения учащимися темы «Производная функции», умение применять полученные знания на конкретных примерах и задачам физики и геометрии.

Применение производной к исследованию функций в заданиях ЕГЭ №1

Тест предназначен для обучающихся средней школы для подготовки к ЕГЭ и проверки уровня знаний по теме «Применение производной к исследованию функций и построению графиков».

Выполнение задания №7 формата ЕГЭ (профильный уровень)

В тесте представлены задания на применение геометрического, физического смыслов производной и при исследовании функции

Применение производной к исследованию функций в заданиях ЕГЭ №2

Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Физический, геометрический смысл призводной и применение производной к исследованию функций «.

Производная. Геометрический смысл производной

Данный тест предназначен для проверки знаний обучающихся по теме «Производная. Геометрический смысл производной»

Производная простейших функций

Тест по алгебре и началам математического анализа на применение знаний таблицы производных

Геометрический смысл производной в задачах ЕГЭ

Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Производная. Геометрический смысл производной».

Производные некоторых элементарных функций

Тест по теме «Производные некоторых элементарных функций» предназначен для проверки усвоения указанной темы обучающимися 11 класса

Механический смысл производной

Тест состоит из 7 вопросов по теме «Физический смысл производной», содержит прямые и обратные задания, аналогичные заданию №6 ЕГЭ.

Итоговый тест за 1 четверть, 11 класс, математика

Тест по математике 11 класса за 1 четверть по УМК Алимова Ш. А. (алгебра и начала анализа) и Атанасяна Л. С. (геометрия). Базовый уровень.

Производные функции

Тест для проработки темы — производная. Предназначен для решения и проработки темы учников и их родителей.

Производная сложной функции

Образовательный тест по теме «Производная сложной функции» позволяет проверить знания школьников или студентов. В тесте требуется как найти сложную функцию из предложенных, так и самостоятельно вычислить производную некоторой сложной функции. Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции. Тест одновариантный, состоит из 14 заданий.

Правила дифференцирования

Тест предназначен для проверки знаний по теме «Правила дифференцирования».

Применение производной к исследованию функций и построению графиков.

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части по теме производная. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

Тест по теме «Производная»

Тест по теме «Производная» состоит из четырнадцати вопросов, девять из которых тестовые, остальные с записью ответа

Примеры использования производной для нахождения наилучшего решения в прикладных задачах.

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Начала математического анализа». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

Производная. Понятие производной

Алгебра и начала анализа. Тема «Производная» Тест №1 по теме «Понятие производной. Физический смысл производной»

Тест «Правила дифференцирования»

Тест «Правила дифференцирования». Тест по теме «Правила дифференцирования» проверяет знание правил дифференцирования — правило дифференцирования суммы двух функций, правило вынесения постоянного множителя за знак производной, правило нахождения производной произведения функций, частного функций, нахождения производной сложной функции. Тест содержит 10 вопросов. В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа.

Тест «Производные элементарных функций»

Тест «Производные элементарных функций». Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций. Тест содержит 10 вопросов с единичным верным ответом.

Тест на соответствие «Производные элементарных функций»

Тест на соответствие «Производные элементарных функций». Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, тригонометрических функций, умения вычислять производные функций. Тест содержит 10 функций и 10 производных функций. При выполнении теста необходимо установить соотвтетствие между функцией и ее производной.

Тест «Геометрический смысл производной. Уравнение касательной и нормали»

Тест по теме «Геометрический смысл производной. Уравнение касательной и нормали» проверяет знание геометрического смысла производной, алгоритм нахождения уравнения касательной и нормали к графику функции в точке; умения составлять уравнение касательной и нормали к графику функции в заданной точке, находить угловой коэффициент касательной к графику функции, угол между касательной к графику и осью Ох. Тест содержит 10 вопросов с выбором единичного и верного ответа, установление верной последовательности и вопросы с вводом верного ответа в виде числа.

Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

2$ и получить нулевой ответ? 93$$

---

Это верно в общем случае, пусть $f(x) = a\cdot g(x)$, где $a$ — константа, а $f, g$ — дифференцируемые функции. Тогда, используя обозначение, что $f'(x)$ является производной от $f$ по x, и правило произведения, мы имеем $$f'(x) = g(x)\dfrac{\mathrm{d} }{\mathrm{d}x}\left(a\right) + a \cdot g'(x)$$

Применяя правило, что $\dfrac{\mathrm{d}}{\mathrm{d}x }\left(a\right) = 0$ упрощает вышесказанное до $$f'(x) = a\cdot g'(x)$$

---

В качестве примечания, хотя верно, что $$\dfrac {\ mathrm {d}} {\ mathrm {d} x} \ left (f (x) + g (x) \ right) = \ dfrac {\ mathrm {d}} {\ mathrm {d} x} \ left (f (x) \ right) + \ dfrac {\ mathrm {d}} {\ mathrm {d} x} \ left (g (x) \ right) = f ‘(x) + g’ (x) $ $

, что называется линейностью дифференциального оператора, мы имеем $$\dfrac{\mathrm{d}}{\mathrm{d}x}\left(f(x) \cdot g(x)\right) \ neq \ dfrac {\ mathrm {d}} {\ mathrm {d} x} \ left (f (x) \ right) \ cdot \ dfrac {\ mathrm {d}} {\ mathrm {d} x} \ left ( г(х)\справа) $$

$\endgroup$

6

$\begingroup$

Да, всегда можно убрать константу. {2}$ по правилу произведения имело лучше все же работать – это произведение функций и поэтому правило произведения должно работать. Это работает и должно работать, просто быстрее использовать правило, что константы можно вытащить из операции дифференцирования, но эти два метода всегда будут согласовываться, они эквивалентны. 9{2}$, и это произведение функций, здесь лучше работает правило произведения, и оно работает: $\frac{d}{dx}(x \cdot x) = x \cdot \frac{d}{dx } x + \frac{d}{dx}x \cdot x = x + x = 2x$.

Практически к любой функции можно применить несколько правил для получения производной. Производные правила — это полные математические теоремы, они никогда не перестанут работать.

Если вы хотите извлечь константу из дифференцирования, сделайте это, если вы хотите использовать правило произведения, сделайте это; оба являются действительными ходами. Обратите внимание, что использование правила произведения для постоянной функции и произведения произвольной функции доказывает, что извлечение константы всегда допустимо.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. Функция константы

: определение, график и примеры

Типы функций >

Содержание:

1. Что такое постоянная функция?
2. График постоянной функции
3. Производная константы
   • Правило постоянного коэффициента
   • Константа, умноженная на степенную функцию
4. Интеграл постоянной функции
5. Предел постоянной функции
6. Применение постоянной функции

Постоянная функция y(x) = 1,

Постоянная функция — это когда выходная переменная ( y ) не зависит от входной переменной ( x ). Как правило, это функция, которая всегда имеет одно и то же значение независимо от входных данных. Например:

• Если x = 0, y = 1
• Если х = 1, у = 1
• Если х = 2, у = 1

Мы можем записать этот тип функции как:

f(x) = c

Где:

• c — константа: число, которое не меняется при изменении x.

Примеры постоянных функций:

• f(x) = 99,
• f(x) = 0,1 и
• f(x)= -21

Поскольку f(x) равно константе, значение f(x) всегда будет одним и тем же, каким бы ни было значение x.

Наверх.

В двухмерной плоскости график функции этого типа представляет собой прямую горизонтальную линию. Он проходит через точки (0, c), (1, c) и (-1, c), где c — одно и то же число, а a — это любое число в числовой строке.

Например, график постоянной функции f(x) = 4 представляет собой прямую горизонтальную линию, проходящую через точки (2,4), (0,4) и (-2,4). Этот график показан ниже.

Наверх.

Посмотрите видео или прочитайте ниже:

Производная постоянной функции

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

В то время как большинство правил требуют от вас выполнения нескольких шагов, для получения производной константы требуется выполнить только 9 шагов. 0113 один шаг :

Измените константу на 0, потому что производная или наклон любой постоянной функции равна нулю.

Другими словами, если f(x) = c, то f′(x) = 0.

В виде формулы это:

Правило иногда называют правилом константы .

«Правило» на самом деле является сокращением ; его использование позволяет обойти необходимость использования предела для нахождения производной любой постоянной функции.

Примеры

Производная от y = 5 равна нулю.

Производная константы:

• Если f(x) = 5, то f&prime(x) = 0,
• Если f(x) = -2, то f′(x) = 0,
• Если f(x) = 10000000, то f′(x) = 0,
• Если f(x) = 55 1/3, то f′(x) = 0,
• Если f(x) = √9, то f′(x) = 0,

Производная от y = -2 равна 0.

Вот и все!

Совет : Вы можете использовать прямую замену, чтобы получить тот же ответ (т. е. что производная равна нулю).

Примечание об аналогичных функциях

Правило о том, что производная от константы применяется только , если брать производную от константы (она же полиномиальная функция нулевой степени), а не константы, которые также имеют показатели степени, константы, умноженные на х или что-то кроме числа. Хотя √9 — константа, √9x — нет. Если вы сомневаетесь, нарисуйте график вашей функции. Если результатом является горизонтальная линия, то ваша функция является константой.

Наверх.

Правило нахождения производных функций с постоянным множителем «с».
Правило постоянного множителя — это способ найти производную функции, имеющей постоянный множитель. Вы, вероятно, больше привыкли к тому, что постоянные факторы называются «коэффициентами». так что это правило можно было бы с таким же успехом назвать правилом коэффициентов .

Что такое постоянный коэффициент?

A Постоянный коэффициент (также называемый числовым коэффициентом или просто коэффициентом ) — это просто число (константа), которое стоит перед функцией.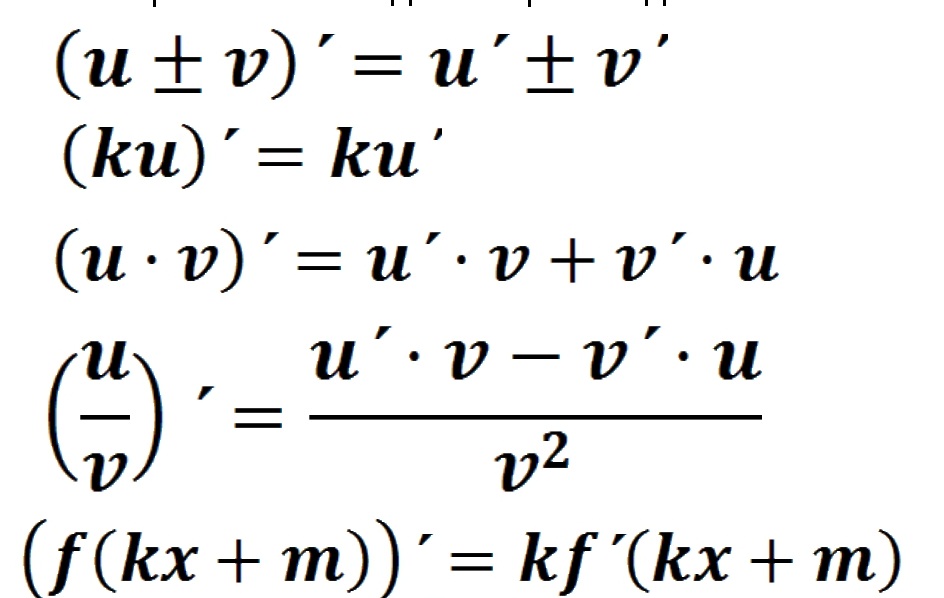 Это просто значение, которое не зависит от x (или любых других входных данных).

Постоянные множители довольно часто встречаются с тригонометрическими функциями и полиномиальными функциями. Например:

• f(x) = 3 sin x имеет постоянный коэффициент 3,
• f(x) = -6x ² имеет постоянный коэффициент -6.

Как использовать правило постоянного множителя

По сути, вы просто игнорируете постоянный множитель: вытащите его вперед и забудьте о нем. Вам нужно только найти производную части, которая равна не константа.

Пример, найдите первую производную f(x) = 3 sin(x)

• Запишите обозначение производной: f ^′ = 3 sinx(x)
• Вытяните константу впереди: 3 f ^′ = sinx(x)
• Найдите производную функции (без учета константы):
  3 f ^′ = cos(x)
• Поместите константу туда, где она была в начале:
  = 3 cos(x)

Формальное определение правила постоянного фактора

Формальное определение правила выглядит следующим образом (Simonds & Jordan, 2020):

Где:

• k = константа,
• &Ропф; = множество действительных чисел.

Наверх.

Производная константы всегда равна нулю, а производная функции зависит от типа функции (например, вы можете дифференцировать показатели с помощью степенного правила). Интуитивно вы можете подумать, что константа, умноженная на функцию, равна нулю, потому что производная константы равна нулю (0 * что угодно = 0). Однако дифференциация в исчислении не всегда интуитивно понятна; производная константы, умноженная на функцию степенного правила, фактически равна константе, умноженной на производную функции.

Пример Вопрос 1: Какова производная от 5x ³ ?

Шаг 1: Отделите константу от функции.
5
x ³

Шаг 2: Продифференцируем функцию , используя правила дифференцирования. Функция x ³ является показателем степени и поэтому дифференцируется по степенному правилу:
d/dx [x ³ ] = 3x ^{3 – 1} = 3x ²

Шаг 3: Поместите константу обратно перед производной функции из шага 2:
5(3 ^x2 )

Шаг 4: Используйте алгебру для умножения на:
5(3 ^x2 ) = 15x ² 5 9 Какая производная от -7x ^-4 ?

Шаг 1: Отделите константу от функции.
-7
x ^-4

Шаг 2: Продифференцируем функцию , используя правила дифференцирования. Функция х ^-4 является показателем степени и поэтому дифференцируется по степенному правилу:
d/dx [x ^-4 ] = -4x ^-4-1 = -4x ^-5

Шаг 3: Место константа перед производной функции из шага 2:
-7[-4x ^-5 ]

Шаг 4: Используйте алгебру для умножения на:
-7[-4x ^-5 ] = 28x ^-5 = 28/x ⁵

Вот оно!

Наверх.

Интеграл функции этого типа равен c x . Например, интеграл от f(x) = 10 равен 10x.

Ниже показан график зависимости f(x) = 10 и интеграла f(x) = 10x. Синий квадрат представляет интеграл при оценке от 0 до 1.

Вернуться к началу.

Предел постоянной функции (согласно свойствам пределов) равен константе. Например, если функция y = 5, то предел равен 5,9.0005

Хотя это один из самых простых типов функций, его можно использовать для моделирования ситуаций, когда определенный параметр является постоянным и не зависит от независимого параметра. Например, школьная столовая, где каждому ребенку давали по одному пончику, независимо от возраста, или экзамен, на котором каждому ученику ставили тройку, независимо от того, насколько усердно он работал.

Ссылки

Изображения, частично созданные с помощью графического калькулятора Symbolab.
Ларсон, Р. и Эдвардс, Б. (2008). Исчисление одной переменной. Cengage Learning.
Мильоре, Э. (2005). Обзор основных понятий алгебры.
Саймондс, С. Джордан, А. (2020). 5.4 Правило постоянного фактора. Лабораторное руководство по исчислению MTH 251 в Портлендском муниципальном колледже. Получено 27 июля 2020 г. с: http://spot.pcc.edu/math/clm/section-constant-factor-rule.html
Maplesoft Support. Онлайн-справка: Математические приложения: функции и отношения.