Волоконные брэгговские решетки Научно-исследовательский центр световодной фотоники – Университет ИТМО
Современный мир так же сложно представить без сети Интернет, как и системы связи без оптического волокна. Большинство сетей коммуникаций в настоящее время используют волоконные световоды как среду для передачи информации. Во второй половине прошлого века произошла настоящая революция в представлениях о будущем телекоммуникационных систем. Такой переворот стал возможным благодаря началу нового этапа в развитии волоконной оптики. Были найдены решения, позволившие использовать оптическое волокно для передачи информации.
На первый взгляд может показаться, что основным применением волоконных световодов является их использование в системах связи. В определенный момент времени, это стало правдой лишь отчасти.
Волоконные световоды условно можно разделить на две категории: специальные и телекоммуникационные. Как понятно из названия, телекоммуникационные световоды применяются в различных системах связи.
Эти устройства делятся на различные типы в зависимости от принципа их действия и особенностей конструкции. Довольно часто, для создания приборов на основе специальных оптических волокон применяются волоконные решетки Брэгга. Как правило, на их основе реализуются чувствительные элементы датчиков физических параметров и систем мониторинга, резонаторы волоконных лазеров, спектральные фильтры телекоммуникационных систем с уплотнением каналов (WDM системы) и т.д.
Волоконная решетка Брэгга (ВБР) – дифракционная решетка, локализованная в сердцевине оптического волокна, которая образована за счет периодического изменения показателя преломления кварцевого стекла под воздействием электромагнитного излучения (Рис.
 1). При прохождении излучения через оптическое волокно с записанной в него ВБР, происходит его частичное или полное отражение от решетки в определенном спектральном диапазоне. Условно можно сказать, что ВБР работает как зеркало, которое отражает свет с определенным спектром, а излучение, не попавшее в этот диапазон, продолжает свое распространение в первоначальном направлении. Таким образом, определенную ВБР можно характеризовать с помощью ее спектров отражения и пропускания.
1). При прохождении излучения через оптическое волокно с записанной в него ВБР, происходит его частичное или полное отражение от решетки в определенном спектральном диапазоне. Условно можно сказать, что ВБР работает как зеркало, которое отражает свет с определенным спектром, а излучение, не попавшее в этот диапазон, продолжает свое распространение в первоначальном направлении. Таким образом, определенную ВБР можно характеризовать с помощью ее спектров отражения и пропускания.
Рис.1 Фотографические изображения волоконных решеток Брэгга, полученные с помощью оптического микроскопа
Основным параметром ВБР является длина волны брэгговского резонанса λB, которая также является центральной длиной волны спектров отражения и пропускания решетки. Эта величина определяется выражением (1):
λB=2neffΛ, (1)
где neff – эффективный показатель преломления для длины волны брэгговского резонанса, Λ– период решетки.
Кроме того, важнейшей характеристикой ВБР является коэффициент отражения. Он показывает, какой процент мощности излучения, попадающего в спектральный диапазон решетки, отражается в обратном направлении в оптическом волокне.
Можно определить три основных метода записи ВБР: метод фазовой маски, запись в интерферометре Тальбота и метод пошаговой записи. На сегодняшний день на кафедре Световодной фотоники реализованы два первых способа получения волоконных брэгговских решеток.
УФ излучение, генерируемое лазерной системой Coherent COMPexPro 102, попадает на фазовую маску ФМ, за которой образуется интерференционная картина пучков +1 и -1 порядков дифракции. Оптическое волокно с удаленным защитным покрытием находится непосредственно за фазовой маской. Интерференционная картина осуществляет модуляцию показателя преломления в сердцевине световода. Цилиндрическая линза в схеме позволяет регулировать плотность записывающего излучения на оптическом волокне, что позволяет изменять коэффициент записываемой ВБР.

Рис.2 Принципиальная схема и фотографические изображения стенда записи ВБР методом фазовой маски
Излучение, генерируемое эксимерной лазерной системой Optosystems CL-7500, фокусируется цилиндрической линзой и падает на фазовую маску. Излучение +1 и -1 порядков дифракции отражается от зеркал, закрепленных на поворотных подвижках, которые сводят пучки в область расположения оптического волокна, где образуется интерференционная картина, которая осуществляет запись ВБР. Цилиндрическая линза, как и в предыдущем случае, позволяет изменять коэффициент отражения записываемой решетки, а поворот зеркал, выбирать необходимую длину волны брэгговского резонанса. Особенностью стенда записи ВБР в интерферометре Тальбота реализованного на кафедре Светводной фотоники является применение высококогерентного лазера Optosystems CL-7550 отечественного производства, имеющего уникальные характеристики генерируемого УФ излучения.
Рис. 3. Принципиальная схема и фотографическое изображение стенда записи ВБР в интерферометре Тальбота
3. Принципиальная схема и фотографическое изображение стенда записи ВБР в интерферометре Тальбота
Принимая в рассмотрение описанные выше характеристики, можно понять основные принципы работы волоконных решеток Брэгга в конструкции различных устройств.
Если говорить о системах WDM в сетях связи и коммуникаций, то возможность разделения излучения по спектральным диапазонам объясняет применение ВБР в конструкции спектральных фильтров. Данные системы успешно работают в телекоммуникационных сетях и позволяют существенно увеличить их пропускную способность.
Наличие способов получения волоконных решеток с необходимым коэффициентом и спектром отражения позволяют реализовать на их основе резонаторы для волоконных лазеров, которые находят все более широкое применение в различных областях науки и техники и используются для резки, гравировки и маркировки материалов, диагностики заболеваний и т.д.
Как известно, изменение внешних воздействий на материал (температуры, механический напряжений, давления и т. д.) приводит к изменению его геометрических параметров. Данное явление справедливо и для оптического волокна. Но кроме этого, изменение его геометрических характеристик приводит к изменению параметров записанных в него ВБР, в частности их периода. Как видно из выражения (1) это влечет за собой сдвиг длины волны брэгговского резонанса, а как следствие изменение спектров отражения и пропускания решеток. Анализируя данные изменения можно судить о характере внешних воздействий на оптическое волокно. Данные явления положены в основу многих приборов и устройств на основе специальных волоконных световодов.
д.) приводит к изменению его геометрических параметров. Данное явление справедливо и для оптического волокна. Но кроме этого, изменение его геометрических характеристик приводит к изменению параметров записанных в него ВБР, в частности их периода. Как видно из выражения (1) это влечет за собой сдвиг длины волны брэгговского резонанса, а как следствие изменение спектров отражения и пропускания решеток. Анализируя данные изменения можно судить о характере внешних воздействий на оптическое волокно. Данные явления положены в основу многих приборов и устройств на основе специальных волоконных световодов.
Выше приведена лишь часть из существующих применений волоконных решеток Брэгга. Системы, реализованные на их основе, продолжают свое активное развитие.
Студенты и аспиранты кафедры Световодной фотоники имеют уникальную возможность осуществлять свои научно-исследовательские работы в области записи волоконных решеток Брэгга и создания устройств на их основе на самом современном оборудовании, под руководством заслуженных преподавателей с огромным опытом и знаниями в данной области.
В нижеследующей таблице приведены возможности кафедры по записи волоконных брэгговских решеток:
| Параметр | Значение |
| Центральная длина волны при комнатной температуре, нм | 1450 ÷ 1620 |
| Отклонение от центральной длины волны, нм | ± 0,3 |
| Коэффициент отражения R, % | 1 ÷ 99 |
| Спектральная ширина резонанса на полувысоте (-3 дБ, FWHM), нм | 0,08 ÷ 7 (Для ВБР с постоянным периодом 0,08 ÷ 0,7) |
| Подавление боковых пиков, дБ | > 10 |
| Длина выходных концов оптического волокна, м | стандарт: 0,7 возможно изменение по договоренности с заказчиком |
| Восстановление акрилатного покрытия оптического волокна | возможно, по договоренности с заказчиком |
| Упаковка | по договоренности с заказчиком |
| Запись через покрытие | возможно |
| Запись массивов ВБР | возможно |
На рисунке 4 приведен спектр отражения массива ВБР из 16-ти решеток со спектральным интервалом 2,4 нм, изготовленный в нашей лаборатории. В нижеследующей таблице приведены подробные характеристики массива.
В нижеследующей таблице приведены подробные характеристики массива.
Рис. 4. Спектр отражения массива ВБР из 16-ти решеток
Паспорт массива из 16-ти ВБР.
Параметр | Значение | ||
|---|---|---|---|
Тип волокна: | одномодовое изотропное оптическое волокно с повышенной концентрацией германия | ||
Количество ВБР на одном волокне: | 16 шт.; | ||
Длина каждой ВБР: | 10 мм; | ||
Расстояние между центрами ВБР: | 50 мм; | ||
Длины волн и коэффициенты отражения отдельных ВБР массива: | № | Длина волны, нм | R, % |
ВБР1 | 1527,96 | 92 | |
ВБР2 | 1530,42 | 82 | |
ВБР3 | 1532,80 | 89 | |
ВБР4 | 1535,20 | 95 | |
ВБР5 | 1537,62 | 86 | |
ВБР6 | 1540,00 | 89 | |
ВБР7 | 1542,46 | 82 | |
ВБР8 | 1544,80 | 98 | |
ВБР9 | 1547,29 | 84 | |
ВБР10 | 1549,65 | 78 | |
ВБР11 | 1551,95 | 99 | |
ВБР12 | 1554,48 | 87 | |
ВБР13 | 1556,77 | 95 | |
ВБР14 | 1559,26 | 93 | |
ВБР15 | 1561,64 | 88 | |
ВБР16 | 1563,99 | 99 | |
Погрешность центральной длины волны каждой ВБР: | не более ±0,1 нм; | ||
Перепокрытие зачищенной зоны для каждой ВБР: | есть, акрилат; | ||
Длина хвостов оптического волокна (с каждой стороны): | не менее 1000 мм. | ||
На рисунке 5 представлен спектр отражения чирпированной ВБР, записанной в нашей лаборатории. Спектральная ширина резонанса на полувысоте 4,7 нм.
Рис. 5. Пример спектра чирпированной ВБР
Специальные структуры волоконных брэгговских решеток
Суперпозиции волоконных брэгговских решеток
Суперпозиция брэгговских решеток представляет собой запись нескольких ВБР с различными резонансными длинами волн в одну область оптического волокна таким образом, что каждая новая решетка суперпозиции записывается поверх уже существующих. На рисунке 6 представлены спектры суперпозиций ВБР со спектральным интервалом между отдельными решетками 0,4 нм (а) и 40 нм (б).
(а)
(б)
Рис. 6. Примеры спектров суперпозиций ВБР со спектральным интервалом между отдельными решетками 0,4 нм (а) и 40 нм (б)
Наклонные волоконные брэгговские решеток
Наклонные волоконные брэгговские решетки (НВБР) обладают периодической модуляцией показателя преломления вдоль оси волокна, однако отличаются от ВБР тем, что имеют определенный угол наклона между плоскостью решетки и поперечным сечением волокна, что приводит к возникновению более сложного модового взаимодействия. На рисунке 7 представлены спектры пропускания и отражения наклонной ВБР.
На рисунке 7 представлены спектры пропускания и отражения наклонной ВБР.
Рис. 7. Пример спектров пропускания и отражения наклонной ВБР
Волоконные брэгговские решетки с фазовым сдвигом
Внесение фазового сдвига в решётку показателя преломления приводит к появлению внутри полосы отражения узкой области пропускания, ширина которой может варьироваться в диапазоне от нескольких единиц до сотен пикометров. На рисунках 8(а,б) приведены примеры спектров отражения ВБР с фазовым сдвигом.
Рис. 8(а). Пример спектра отражения ВБР с фазовым сдвигом.
Длина решётки – 2*2,5 мм, ширина области пропускания в пике отражения
на полувысоте – 84 пм
Рис. 8(б). Пример спектра отражения ВБР с фазовым сдвигом.
Длина решётки – 2*5 мм, ширина области пропускания в пике отражения
на полувысоте – 42 пм
На рисунке 9 представлена зависимость ширины области пропускания в полосе отражения ВБР с фазовым сдвигом от длины решетки.
Рис. 9. Зависимость ширины области пропускания в полосе отражения ВБР с фазовым сдвигом от длины решетки
Волоконные брэгговские решетки в двулучепреломляющих оптических волокнах
На нашей установке по записи ВБР возможна запись решеток в анизотропном оптическом волокне любого типа (PANDA, Bow-tie, с эллиптической напрягающей оболочкой) с предварительной ориентацией оси двулучепреломления световода.
Во-первых, запись волоконных решеток Брэгга эффективнее при позиционировании оси двулучепреломления анизотропного оптического волокна определенным образом по отношению к штрихам интерференционной картины. Во-вторых, предварительная ориентация оси двулучепреломления анизотропного волоконного световода при записи ВБР позволяет снизить поляризационные преобразования на решетке.
Используемый нами метод выставления оси двулучепреломления анизотропного оптического волокна заключается в наблюдении за интерференционной картиной рассеивания вперёд при освещении боковой поверхности световода излучением когерентного источника (рис. 10).
10).
(а)
(б)
Рис. 10. а – схематичное изображение двулучепреломляющего оптического волокна с эллиптической напрягающей оболочкой, где 1 – сердцевина, 2 – изолирующая оболочка, 3 – напрягающая оболочка, 4 – защитная оболочка, 5 – конструктивная оболочка, φ – угол между направлением распространения пучка He-Ne лазера и медленной осью двулучепреломления световода, 6 – направление распространения пучка He-Ne лазера; б – коллаж из интерференционных картин рассеивания вперёд, каждая из которых представляет вертикально ориентированный набор минимумов и максимумов, значение угла φ соответствует ориентации волокна на рис. 10(а)
Волоконные брэгговские решетки типа II
Применение ВБР типа II позволяет получать высокоэффективные брэгговские зеркала, используя метод одноимпульсной записи. При этом глубина модуляции показателя преломления у ВБР типа II, индуцированная одиночным импульсом, может превосходить её у ВБР типа I более чем в 100 раз. Это позволяет осуществить технологию одноимпульсной записи брэгговских зеркал с коэффициентом отражения близким к 100% и сравнительно большой шириной пика отражения решетки на полувысоте (около 1 нм) без использования чирпированной фазовой маски.
При этом глубина модуляции показателя преломления у ВБР типа II, индуцированная одиночным импульсом, может превосходить её у ВБР типа I более чем в 100 раз. Это позволяет осуществить технологию одноимпульсной записи брэгговских зеркал с коэффициентом отражения близким к 100% и сравнительно большой шириной пика отражения решетки на полувысоте (около 1 нм) без использования чирпированной фазовой маски.
Кроме того, ВБР типа II характеризуются высокой термостойкостью. Они стабильны и не деградируют при длительном воздействии температур до 900 °С.
На рисунке 11 представлен спектр отражения ВБР типа II, записанной одиночным импульсом эксимерного лазера.
Рис. 11. Спектр отражения ВБР типа II, записанной одиночным импульсом эксимерного лазера
|
ПРОГРАММА-МИНИМУМкандидатского экзамена по специальности ВведениеНастоящая программа основана на следующих дисциплинах: электромагнитной теории света, геометрической оптике, физической оптике, взаимодействии света с веществом, оптике лазеров, прикладной оптике, спектроскопии, статистической и квантовой оптике. Программа разработана экспертным советом Высшей аттестационной комиссии Министерства образования Российской Федерации по физике при участии Московского государственного университета им. М. В. Ломоносова и Физического института им. П.Н. Лебедева РАН. 1. Электромагнитная теория света
2. Геометрическая оптика
3. Интерференция и дифракция световых волн
4. Теория излучения и взаимодействия световых волн с веществом
5. Статистическая оптика
6. Спектроскопия
7. Экспериментальная и прикладная оптика
8. Оптика лазеров
Основная литература
|
как это работает — Рамблер/новости
Изучение одного из самых распространенных физических явлений – дифракции – привело к возникновению такого устройства, как дифракционная решетка.
В России крупнейший производитель дифракционной оптики – «Швабе» Госкорпорации Ростех. Дифракционные решетки холдинга сегодня функционируют во многих оптических приборах, и не только у нас в стране, но и за рубежом.
Дифракционные решетки холдинга сегодня функционируют во многих оптических приборах, и не только у нас в стране, но и за рубежом.
Дифракционная решетка: как увидеть радугу
Дифракционная решетка – это оптический прибор, представляющий собой поверхность, на которую нанесено большое число параллельных, равноотстоящих друг от друга микроскопических штрихов (щелей или выступов). Уже из самого названия прибора понятно, что он работает по принципу дифракции света – явления отклонения света от прямолинейного распространения при встрече с препятствием.
У электромагнитных волн, составляющих свет, разный эффект интерференции, или по-простому способности огибать препятствия. Проходя через дифракционную решетку, световые волны огибают препятствия решетки (штрихи, щели или выступы) с разным углом отклонения. Для каждой длины волны существует свой угол дифракции, и белый свет раскладывается штрихами решетки в спектр, то есть в радугу. Кстати, эффект радуги основан на таком же принципе, только в роли решетки – капельки воды.
В природе можно обнаружить и множество других естественных дифракционных решеток. Примером грубой дифракционной решетки можно считать ресницы. Смотря на свет сквозь прищуренные веки, можно в какой-то момент увидеть спектральные линии. А физик Джеймс Грегори, который впервые применил дифракционную решетку, использовал в этом качестве птичье перо. Благодаря очень тонкой структуре через перо можно пропустить солнечный свет и увидеть его разложение на спектр.
Изготовление: 3600 штрихов на миллиметр
Сегодня дифракционную решетку можно сделать самому из более современных материалов, например DVD-диска. Шаг между штрихами такой решетки составляет 0,74 мкм. Это намного более впечатляющий результат по сравнению с самой первой искусственной дифракционной решеткой в мире, которая появилась в 1875 году: она состояла из 50 натянутых волосков с расстоянием между ними в 250 мкм.
Число штрихов современной дифракционной решетки может доходить до 3600 на один миллиметр, и процесс изготовления такого устройства требует очень высокой точности. Если хоть одна щель из множества будет нанесена с ошибкой, то решетка будет забракована. Нарезание решетки длится до 7 суток, хотя время нанесения штриха составляет 3 секунды.
Если хоть одна щель из множества будет нанесена с ошибкой, то решетка будет забракована. Нарезание решетки длится до 7 суток, хотя время нанесения штриха составляет 3 секунды.
Существуют два вида дифракционных решеток: прозрачные и отражательные. Прозрачная решетка – это стеклянная тонкая пластинка или пластинка из прозрачного пластика, на которую нанесены штрихи. Штрихи дифракционной решетки являются препятствием для света, через них он не может пройти. Оставшиеся между штрихами прозрачные зазоры играют роль щелей. При выполнении лабораторных работ чаще используют этот вид решеток.
Отражательная решетка – это металлическая или пластиковая отполированная пластинка, на которую вместо штрихов нанесены бороздки определенной глубины. Такие решетки часто используют при анализе спектров излучения. Вышеупомянутый DVD-диск – яркий пример этого вида дифракционной решетки: расположив его перед глазом, можно найти на нем спектр.
Практическое применение: от ДНК до далекой звезды
Дифракционные решетки широко применяются в различных оптических устройствах: спектральных приборах для получения монохроматического света (монохроматоры, спектрофотометры и др. ), в качестве оптических датчиков линейных и угловых перемещений, для поляризаторов и оптических фильтров и даже в так называемых антибликовых очках.
), в качестве оптических датчиков линейных и угловых перемещений, для поляризаторов и оптических фильтров и даже в так называемых антибликовых очках.
Дифракционные решетки нашли свое применение во многих научных исследованиях. Например, этот прибор лег в основу рентгеноструктурного анализа – самого распространенного метода определения структуры вещества. Этот способ заключается в измерении параметров кристаллической решетки посредством дифракции рентгеновских лучей. То есть в данном случае дифракционная решетка используется не для определения длины волны света, а для обратной задачи – нахождения по длине волны постоянной решетки (расстояния между штрихами).
В настоящее время широко используют рентгеноструктурный анализ биологических молекул и систем. Так, например, по данным, полученным этим методом, из нескольких возможных химических формул пенициллина была выбрана одна. В свое время этим методом были с успехом исследованы такие высокополимерные соединения, как каучук, целлюлоза, многие полиамиды и т. д. Именно с помощью рентгеноструктурного анализа американец Джеймс Уотсон и англичанин Френсис Крик установили структуру молекулы ДНК (двойная спираль), за что и были удостоены в 1962 году Нобелевской премии.
д. Именно с помощью рентгеноструктурного анализа американец Джеймс Уотсон и англичанин Френсис Крик установили структуру молекулы ДНК (двойная спираль), за что и были удостоены в 1962 году Нобелевской премии.
Сегодня изделия дифракционной оптики применяются для научных исследований в области экологии. Например, в составе гиперспектральных камер для оценки качества воздуха. С их помощью определяют состав и состояние объекта съемки, фиксируя спектральные характеристики каждого пикселя на изображении.
Государственный институт прикладной оптики (ГИПО) холдинга «Швабе» – крупнейший производитель дифракционной оптики в России – поставляет для этих целей решетки и за рубеж. Только за прошлый год было поставлено более 400 изделий в Германию, Ирландию, Норвегию, Словакию и другие страны.
Дифракционная решетка шагнула и далеко за пределы Земли. С ее помощью, например, можно узнать химический состав далеких звезд. Свет, идущий от звезды, собирают зеркалами и направляют на решетку. Таким образом можно узнать все длины волн спектра, а значит, и химические элементы, которые их излучают.
Таким образом можно узнать все длины волн спектра, а значит, и химические элементы, которые их излучают.
Анатолий Михайлович Балагуров
Дата и место рождения: 19 января 1945, Винницкая обл., СССР
Основные даты:
1968 – окончил Московский Государственный Университет им. М.В.Ломоносова, физический факультет.
1968 – 1993 – стажер-исследователь, младший научный сотрудник, научный сотрудник, старший научный сотрудник ЛНФ ОИЯИ.
1993 – 1999 – начальник отдела физики конденсированных сред ЛНФ ОИЯИ.
1999 – 2011 – начальник сектора дифракции ЛНФ ОИЯИ.
2006 – 2008 – начальник отдела нейтронных исследований конденсированных сред.
с 2011 – главный научный сотрудник ЛНФ ОИЯИ.
1979 – в ОИЯИ защитил диссертацию “Нейтронографические исследования структуры монокристаллов методом времени пролета” на соискание научной степени к.ф.-м.н.
1993 – в ОИЯИ защитил диссертацию “Структурная нейтронография моно- и поликристаллов на импульсных реакторах” на соискание научной степени д. ф.-м.н.
ф.-м.н.
2000 – присвоено звание профессора ВАК.
Основные научные интересы:
(I) Конструкция и развитие нейтронных дифрактометров по времени пролета для исследований моно- и поликристаллов.
(II) Применение корреляционного (Фурье) обратного метода времени пролета для дифракции нейтронов.
(III) Нейтронные дифракционные исследования атомной и магнитной структуры кристаллов, фазовых переходов, длиннопериодных мембранных структур и др.
(IV) Применение дифракции нейтронов высокого разрешения для изучения внутренних напряжений в объемных изделиях и материалах.
Премии:
А.М.Балагуров является заслуженным деятелем науки и техники Московской области (звание присуждено в 2005 г.), награжден медалью “В память 650-летия Москвы” (в 1997 г.), знаком “Ветеран атомной энергетики и промышленности” (в 2004 г.), премией и медалью “Имени С.И.Мосина” (в 2005 г.) и Золотой медалью “Имени Фельбера” Чешского политехнического университета в Праге (в 2005 г. ). Многократный лауреат премий ОИЯИ.
). Многократный лауреат премий ОИЯИ.
В 2000 г. в составе авторского коллектива получил Государственную премию Российской Федерации за цикл работ “Разработка и реализация новых методов структурной нейтронографии по времени пролета с использованием импульсных и стационарных реакторов”.
Опубликовал более 230 работ в периодической научной печати, включая обзоры в УФН и статьи в Физической энциклопедии. Многократно являлся приглашенным докладчиком на российских и международных конференциях и школах. Руководитель одиннадцати диссертационных работ на соискание ученой степени кандидата наук. Нейтронные эксперименты в основном осуществлял на импульсных реакторах в ЛНФ ОИЯИ, многократно участвовал в экспериментах на нейтронных источниках в ILL (Франция), LLB (Франция), ISIS (Великобритания), PSI (Швейцария).
Некоторые последние научные публикации:
- A.M. Balagurov “Neutron diffraction for science and applications” Priroda, 2012, v.
 6.
6. - A.M. Balagurov, L.G. Mamsurova, I.A. Bobrikov, To Than Loan, V.Yu. Pomjakushin, K.S. Pigalsky, N.G. Trusevich, A.A. Vishnev “Effects of structural disorder in fine-grained HTSC YBa2Cu3Oy” JETP, 2012, v. 141 (6), 1.
- V.V. Sumin, I.V. Papushkin, R.N. Vasin, А. Venter, А.М. Balagurov “Determination of the residual stress tensor in textured zirconium alloy by neutron diffraction” Journal of Nuclear Materials, 2012, v. 421, pp. 64 – 72.
- Yu.V.Taran, A.M.Balagurov, B.M.Sabirov, A.Evans, V. Davydov, A.Venter “Residual stresses in a stainless steel – titanium alloy joint made with the explosive technique” Journal of Physics: Conference Series, 2012, v. 340, pp. 012105 (1-8).
- Yu.V. taran, A.M. Balagurov, J. Schreiber, A. Evans, A.M. Venter “Residual stresses in biaxially fatigued austenitic stainless steel sample of cruciform geometry” Journal of Physics: Conference Series, 2012, v.
 340, pp. 012099 (1-9).
340, pp. 012099 (1-9). - Yu.V. taran, A.M. Balagurov “Correction of a neutron diffraction peak shift due to a partial immersion of a gauge volume in an unstressed sample” Nuclear Instruments and Methods in Physics Research A, 2012, v. 679, pp. 19 – 24.
- Yu.V. taran, A.M. Balagurov, J. Schreiber, A. Evans, A.M. Venter “Residual stresses in biaxially fatigued austenitic stainless steel sample of cruciform geometry” Physics of Elementary Particles and Atomic Nuclei, Letters, 2011, v.8, pp. 228-236.
- A.M. Balagurov, I.А. Bobrikov, V.Yu. Pomjakushin, E.V. Pomjakushina, D.V. Sheptyakov, I.O. Troyanchuk, “Low-Temperature Structural Anomalies in Pr0.5Sr0.5CoO3” JETP Letters, 2011, Vol. 93, No. 5, pp. 263–268.
- V. Yu. Kazimirov, M. B. Smirnov, L. Bourgeois, L. Guerlou-Demourgues, L. Servant, A. M. Balagurov, I. Natkaniec, N. R. Khasanova, E. V. Antipov “Lattice dynamics of Ni and Mg hydroxides” Solid State Ionics, 2010, v.
 181 (39-40), p. 1764 – 1770.
181 (39-40), p. 1764 – 1770. - N.Y. Ryabova, M.A. Kiselev, A.I. Beskrovnyi, A.M. Balagurov “Investigation of the Structure of Multilayer Lipid Membranes by Real-Time Neutron Diffraction” Physics of the Solid State, 2010, v.52(5), pp.1050-1058.
- N.Yu. Ryabova, M.A. Kiselev, A.M. Balagurov “Influence of Cholesterol and Ceramide VI on the Structure of Multilamellar Lipid Membranes at Water Exchange” Cryst. Reports, 2010, v.55(3), pp.479-487.
- G. Bruno, A.M. Efremov, B. Clausen, A.M. Balagurov, V. Simkin, B.R. Wheaton, J.E. Webb, D.W. Brown “On the Stress free Lattice Expansion of Cordierite” Acta Mater., 2010, v.58, pp.1994-2003.
- V.Yu. Pomjakushin, D.V. Sheptyakov, E.V. Pomjakushina, K.Conder, A.M. Balagurov “Evidence for strong effect of quenched correlated disorder on phase separation and magnetism in (La1−yPry)0.7Ca0.3MnO3” J.
 Phys.: Condens. Matter, 2010, v.22, p.115601 (1-5).
Phys.: Condens. Matter, 2010, v.22, p.115601 (1-5). - D.V. Sheptyakov, V.Yu. Pomjakushin, O.A. Drozhzhin, S.Ya. Istomin, E.V. Antipov, I.A. Bobrikov, A.M. Balagurov “Correlation of chemical coordination and magnetic ordering in Sr3YCo4O10.5+δ, δ=0.02 and 0.26” Phys. Rev. B, 2009, v.80(2), p. 024409 (1-9).
- I.O. Troyanchuk, M.V. Bushinskii, D.V. Karpinsky, V.M. Dobryanskii, V.V. Sikolenko, A.M. Balagurov “Positive magnetoresistance effect in rare earth cobaltites” JETP Letters, 2009, Vol. 89, No. 7, pp. 319–323.
- A.M. Balagurov, I.А. Bobrikov, D.V. Karpinsky, I.O. Troyanchuk, V.Yu. Pomjakushin, D.V. Sheptyakov “Successive Structural Phase Transitions in Pr0.5Sr0.5CoO3 in the Range 10–1120 K” JETP Letters, 2008, Vol. 88, No. 8, pp. 531–536.
- A.M.Balagurov, I.A.Bobrikov, V.Yu.Pomjakushin, D.V.Sheptyakov, N.
 A.Babushkina, O.Yu.Gorbenko, M.S.Kartavtseva, A.R.Kaul “Effect of Isotopic Composition and Microstructure on the Crystalline and Magnetic Phase States in R0.5Sr0.5MnO3” JETP, 2008, Vol. 106, No. 3, pp. 528–541.
A.Babushkina, O.Yu.Gorbenko, M.S.Kartavtseva, A.R.Kaul “Effect of Isotopic Composition and Microstructure on the Crystalline and Magnetic Phase States in R0.5Sr0.5MnO3” JETP, 2008, Vol. 106, No. 3, pp. 528–541. - Yu.V. Taran, A.M. Balagurov, S.G. Sheverev, J. Schreiber, A.M. Korsunsky, W.J.J. Vorster, H. Bomas, C. Stoeberl “Neutron diffraction investigation of an in-plane biaxial fatigued stainless steel sample of cruciform geometry” J. Phys.: Condens.Matter, 2008, v.20, p.104257 (6).
- Ivan V. Nikolaev, Hans D’Hondt, Artem M. Abakumov, Joke Hadermann, Anatoly M. Balagurov, Ivan A. Bobrikov, Denis V. Sheptyakov, Vladimir Yu. Pomjakushin, Konstantin V. Pokholok, Dmitry S. Filimonov, Gustaaf Van Tendeloo, Evgeny V. Antipov “ Crystal structure, phase transition and magnetic ordering in the perovskitelike Pb2-xBaxFe2O5 solid solutions”Phys.
 Rev. B, 2008, v.78, p. 024426 (1-12).
Rev. B, 2008, v.78, p. 024426 (1-12).
Интерференция и дифракция (1) (Реферат)
Интерференция и дифракция
Дифракция света. При внесении
тела в заданное электромагнитное поле
заряженные частицы начинают совершать
вынужденные колебания, излучение от
которых вносит искажения в исходное
распределение света. В случае тел,
размеры которых велики по сравнению с
длиной волны, эти процессы хорошо
описываются на языке геометрической
оптики (как отражение, преломленое и
поглощение света). В противном случае
принято говорить о явлении дифракции.
Строгое (в рамках волновой теории света)
решение задачи о дифракции существует
лишь для частного случая круглого
однородного тела в поле плоской
монохроматтической волны (теория Ми) и
дается весьма громозкими формулами.
Сравнительно простое приближенное
решение получается в случае бесконечной
поглощающей поверхности (экран) с
отверстиями заданной формы и с заданным
пропусканием света для точек, достаточно
удаленных от них (дифракция Френеля). Метод решения последней задачи был
“угадан” Гюйгенсом, уточнен Френелем
и лишь впоследствии был строго выведен
Кирхгофом на основе волновой теории и
уравнений Максвелла: электромагнитное
поле вдали от экрана может рассчитываться
как суперпозиция сферических волн,
испускаемых каждой его открытой точкой.
Метод решения последней задачи был
“угадан” Гюйгенсом, уточнен Френелем
и лишь впоследствии был строго выведен
Кирхгофом на основе волновой теории и
уравнений Максвелла: электромагнитное
поле вдали от экрана может рассчитываться
как суперпозиция сферических волн,
испускаемых каждой его открытой точкой.
В соответствии с принципом
Гюйгенса-Френеля плоский волновой фронт
волны, прошедший через большое отверстие,
остается плоским вдали от его краев и
изгибается у границы (рис. 18_1). Это
означает, что световые лучи (множество
нормалей к фронту) у границ отверстия
изгибаются (дифрагируют). При уменьшении
размеров отверстия роль дифракции
возрастает. Отверстия, размеры которого
сравнимы с длиной волны, превращает
плоскую волну в сферическую. При
прохождении света через такие отверстия
приближение геометрической оптики
становится неприменимым, основанные
на ее принципах оптические приборы
теряют свою работоспособность. Из-за
явления дифракции принципиально
невозможно получить оптическое
изображение объекта или его деталей,
размеры которых не превосходят длины
волны излучения.
Теория Кирхгофа. В основе теории дифракции Френеля лежит математическое тождество, позволяющее связать значения любой являющейся решением уравнения Д’Аламбера функции E(r) в произвольной точке внутри замкнутой области с ее значениями на поверхности, ограничивающей эту область (интеграл Кирхгофа):
(1) .
Правдоподбное (но не совсем точное) предположение о том, что поле электромагнитной волны за непрозрачным экраном равно нулю, а искажения, вносимые переизлученным полем на открытых отверстиях малы позволяют получить для поля во всех точках за экраном выражение, согласующееся с принципом Гюйгенса-Френеля. На рис 18_2 приведена фотография распределения интенсивности света, дифрагировавшего на небольшом отверстии прямоугольной формы, и результат расчетов интенсивности по формуле (1).
Интерференция. В
предельном случае дифракции на экране
с бесконечно-малыми отверстиями
(математически описываемыми при помощи
дельта-функций) говорят об интерференции,
наблюдаемой методом деления волнового
фронта. Христоматийным примером подобного
рода экспериментов является опыт Юнга
(рис. 18_3). В зависимости от разности хода вторичные сферические волны, возникающие
на отверстиях экрана 1 и 2 при дифракции
первичной сферической волны от точечного
монохроматического источника S, в точке
X происходит сложение или вычитание
электромагнитных колебаний. В результате
возникает интерференционная картинка
в виде чередующихся светлых и темных
полос. В 19 веке считалось, что опыты по
интерференции являются неопровержимым
свидетельством волновой природы света
(при прохождении пучка классических
частиц через два отверстия в экране
интерференционной картины, очевидно,
возникать не может).
Христоматийным примером подобного
рода экспериментов является опыт Юнга
(рис. 18_3). В зависимости от разности хода вторичные сферические волны, возникающие
на отверстиях экрана 1 и 2 при дифракции
первичной сферической волны от точечного
монохроматического источника S, в точке
X происходит сложение или вычитание
электромагнитных колебаний. В результате
возникает интерференционная картинка
в виде чередующихся светлых и темных
полос. В 19 веке считалось, что опыты по
интерференции являются неопровержимым
свидетельством волновой природы света
(при прохождении пучка классических
частиц через два отверстия в экране
интерференционной картины, очевидно,
возникать не может).
Другим примером сложения колебаний
является интерференция в тонких пленках
(метод деления волнового фронта), при
которой складываются электромагнитные
волны, отразившиеся от двух поверхностей
(рис. 18_4). В зависимости от соотношения
между толщиной пленки и длиной волны
излучения наблюдается усиление или
ослабление цвета. При освещении белым
светом (смесь с различными длинами волн)
возникает зависящая от толщины цветная
окраска пленки (например, радужные
разводы на пятне нефти в воде). Описанный
способ окраски используется в природе:
пестрая расцветка крыльев бабочек
обусловлена не наличием красящего
пигмента, а интерференцией света в
тонких прозрачных чашуйках крыльев. В
технике интерференционные покрытия
используются для создания зеркал с
высоким коэффициентом отражения
(“диэлектрические зеркала”) и для
просветления оптики (гашения волн,
отраженных от многочисленных поверхностей
линз сложных объективов).
При освещении белым
светом (смесь с различными длинами волн)
возникает зависящая от толщины цветная
окраска пленки (например, радужные
разводы на пятне нефти в воде). Описанный
способ окраски используется в природе:
пестрая расцветка крыльев бабочек
обусловлена не наличием красящего
пигмента, а интерференцией света в
тонких прозрачных чашуйках крыльев. В
технике интерференционные покрытия
используются для создания зеркал с
высоким коэффициентом отражения
(“диэлектрические зеркала”) и для
просветления оптики (гашения волн,
отраженных от многочисленных поверхностей
линз сложных объективов).
Интерфереметрические измерения. Высокая чувствительность наблюдаемой картины распределения интенсивностей к разности хода интерферирующих пучков лежит в основе целого класса сверх точных приборов, называемых интерферометрами.
На рис. 18_5 изображен интерферометр
Майкельсона, использованный в решающих
экспериментах по проверке постулата о
постоянстве скорости света. В приборе
сравниваются фазы двух волн,
распространяющихся во взаимно
перпендикулярных плечах интерферометра.
В зависимости от разности хода наблюдается
усиление или ослабление света на выходе
прибора. Этот прибор может использоваться
для прицезионных измерение длины: при
перемещении зеркала вдоль измеряемого
объекта подсчет “миганий”
интерференционной картины позволяет
определить длину пройденного пути с
точностью до четверти длины волны
источника света (около 100 нм). Другим
“впечатляющим” применением
интерферометра является измерение
сверх-малых скоростей движения (несколько
сантиметров в год): сползание ледников,
дрейф материков и т.д.
В приборе
сравниваются фазы двух волн,
распространяющихся во взаимно
перпендикулярных плечах интерферометра.
В зависимости от разности хода наблюдается
усиление или ослабление света на выходе
прибора. Этот прибор может использоваться
для прицезионных измерение длины: при
перемещении зеркала вдоль измеряемого
объекта подсчет “миганий”
интерференционной картины позволяет
определить длину пройденного пути с
точностью до четверти длины волны
источника света (около 100 нм). Другим
“впечатляющим” применением
интерферометра является измерение
сверх-малых скоростей движения (несколько
сантиметров в год): сползание ледников,
дрейф материков и т.д.
Поскольку время распространения света в плечах интерферометра зависит не только от их длин, но и от показателя преломления прозрачной среды, с помощью интерференции можно производить точный анализ наличия малых химических примесей в веществе, вызывающих изменеие показателя преломления.
Голография нашла применение не
только в производстве изопродукции, но
и в современной науке и технике. В отличии
от фотографии, на которой осуществляется
запись распределения интенсивности на
плоскости изображения, создаваемого
на пластинке методами геометрической
оптики, голограмма сохраняет информацию
не только об интенсивности слагающих
электромагнитное поле волн, но и их
фазе. Это позволяет практически полностью
восстанавливать электромагнитное поле,
создаваемое голографируемым объектом
и вызывать зрительное ощущение реального
объемного тела. В известном смысле
голограмма аналогична зеркалу,
продолжающему генерировать изображение
после ухода смотревшейся в него девушки).
В отличии
от фотографии, на которой осуществляется
запись распределения интенсивности на
плоскости изображения, создаваемого
на пластинке методами геометрической
оптики, голограмма сохраняет информацию
не только об интенсивности слагающих
электромагнитное поле волн, но и их
фазе. Это позволяет практически полностью
восстанавливать электромагнитное поле,
создаваемое голографируемым объектом
и вызывать зрительное ощущение реального
объемного тела. В известном смысле
голограмма аналогична зеркалу,
продолжающему генерировать изображение
после ухода смотревшейся в него девушки).
Производство высококачественных
гологамм стало возможным после создания
лазеров – мощных источников монохроматического
излучения, способных давать устойчивую
интерференционную картину даже при
больших разностях хода интерферииующих
пучков. При записи голограммы (рис. 18_6)
фотографируется сложная интерференционная
картина, возникающая при сложении идущей
непосредственно от лазера плоской
монохроматической волны (“опорной
волны”) с рассеяной объектом “предметной
волны”, фронты которой могут представлять
собой весьма сложные поверхности. Считывание проявленной голограммы
осуществляется при помощи того же лазера
(рис. 18_7). В результате дифракции опорной
волны на сложном узоре, возникшем при
фотографировании интерференционной
картины возникает две симметричные
волны, одна из которых практически
идентична предметной и формирует мнимое
изображение объекта. Вторая волна
создает “инвертированное”
изображение, которое в практических
приложениях стремятся подавить.
Считывание проявленной голограммы
осуществляется при помощи того же лазера
(рис. 18_7). В результате дифракции опорной
волны на сложном узоре, возникшем при
фотографировании интерференционной
картины возникает две симметричные
волны, одна из которых практически
идентична предметной и формирует мнимое
изображение объекта. Вторая волна
создает “инвертированное”
изображение, которое в практических
приложениях стремятся подавить.
В настоящее время широкое
использование нашли толстые голограммы,
со слоем фотоэмульсии, существенно
превосходящим длину волны записывающего
излучения. На такой голограмме
регистрируется пространственная
структура интерференционной картины.
Такая трехмерная структура пропускает
через себя только излучение с длиной
волны, совпадающей с той, на которой
записывалась голограмма. Т.о. для
восстановления изображения толстой
голограммой нет необходимости в освещении
монохроматичесим источником: пластинка
сама “выбирает” их белого света
составляющую, на которой она создавалась.
Комбинация из трех голограмм, записанныз в красных, зеленых и синих лучах создает цветное объемной изображение объекта.
Обращение волнового фронта и динамическая голография. Проблема обащения волнового вронта (ОВФ) возникла в связи с практически важной задачей фокусировки мощного лазерного излучения на небольших и возможно движущихся объектах (передача энергии, связь, “звездные войны” и т.д.). Задача еще более усложняется в случае, когда источник излучения и мишень разделены толстым слоем нестационарной атмосферы: статистические флуктуации плотности приводят, согласно принципу Ферма, к искривлению лучей света (или, точнее, к искажению волнового фронта) и расфокусировке пучка.
Поставленная проблема могла бы
быть решена в случае создания хорошо
отражающего свет зеркала, поверхность
которого принимала бы форму фронта
падающей на него волны (ОВФ – зеркала).
В этом случае мишень можно было бы
облучать сравнительно слабым источником
света с широкой диаграммой направленности
излучения. Часть фронита отраженной от
мишени и искаженной атмосферой волны
может быть пропущена через оптический
усилитель (слой вещества, усиливающего
проходящие через него световые волны,
но не изменяющего никаких их характеристик,
кроме амплитуды колебаний) и направлена
на ОВФ- зеркало (рис. 18_7), при отражении
от которого форма волнового фронта не
изменится, а направление его распространения
изменится на противоположное. После
еще одного усиления волна пройдет через
все искажающие неоднородности атмосферы
в обратном направлении (время
распространения света на расстояниях
порядка толщины атмосферы намного
меньше характерного времени
перераспределения неоднородностей) и
полностью сфокусируется на мишени.
Часть фронита отраженной от
мишени и искаженной атмосферой волны
может быть пропущена через оптический
усилитель (слой вещества, усиливающего
проходящие через него световые волны,
но не изменяющего никаких их характеристик,
кроме амплитуды колебаний) и направлена
на ОВФ- зеркало (рис. 18_7), при отражении
от которого форма волнового фронта не
изменится, а направление его распространения
изменится на противоположное. После
еще одного усиления волна пройдет через
все искажающие неоднородности атмосферы
в обратном направлении (время
распространения света на расстояниях
порядка толщины атмосферы намного
меньше характерного времени
перераспределения неоднородностей) и
полностью сфокусируется на мишени.
Существует несколько
подходов к созданию ОВФ – зеркала: гибкая
отражающая пленка, форма которой
расcчитывается
быстродействующим компьютером; обращение
волнового фронта, возникающее вследствие
нелинейного процесса вынужденного
комбинационного рассеяния, голографические
методы ОВФ (динамическая голография). Идея последнего подхода очевидна из
соображений симметрии: при облучении
тонкой голограммы считывающей волной,
направленной точно навстречу использованной
при записи опорной, одна из двух
дифрагированных волн будет распространяться
навстречу предметной, т.е. точно в
направлении объекта (рис. 18_8). Проблема
быстрого (по сравнению со скоростью
изменения атмосферы) создания голограммы
решается методами нелинейной оптики:
существуют вещества, практически
мгновенно становящиеся прозрачными
под воздействием возникающего в
максимумах интерференционной картины
излучения большой интенсивности, которые
и используются в качестве “фотопластинок”
в динамической голографии.
Идея последнего подхода очевидна из
соображений симметрии: при облучении
тонкой голограммы считывающей волной,
направленной точно навстречу использованной
при записи опорной, одна из двух
дифрагированных волн будет распространяться
навстречу предметной, т.е. точно в
направлении объекта (рис. 18_8). Проблема
быстрого (по сравнению со скоростью
изменения атмосферы) создания голограммы
решается методами нелинейной оптики:
существуют вещества, практически
мгновенно становящиеся прозрачными
под воздействием возникающего в
максимумах интерференционной картины
излучения большой интенсивности, которые
и используются в качестве “фотопластинок”
в динамической голографии.
ОВФ уже сейчас используется в
реально действующих экспериментальных
установках по управляемому лазерному
термоядерному синтезу, где приходится
решать задачу одновременной фокусировки
разогревающего излучения нескольких
сверх мощных лазеров на небольшой
дейтериевой мишени. С точки зрения
теории решение проблемы ОВФ представляет
самостоятельный интерес, поскольку
представляет собой пример восстановления
упорядоченного излучения после его
искажения на хаотической структуре. Иногда о процессе ОВФ говорят как об
обращении во времени классически
необратимого процесса или даже просто
об обращении времени.
Иногда о процессе ОВФ говорят как об
обращении во времени классически
необратимого процесса или даже просто
об обращении времени.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://study.online.ks.ua/
Дифракция – Основы, Приложения – Диафрагма, свет, узор и волны
5 минут чтения
Основы, Приложения
Дифракция — это отклонение от прямого пути, возникающее, когда волна, такая как свет или звук, проходит вокруг препятствия или через отверстие. Важность дифракции в любой конкретной ситуации зависит от относительного размера препятствия или отверстия и длины волны, падающей на него.Дифракционная решетка является важным устройством, использующим дифракцию света для получения спектров. Дифракция также имеет фундаментальное значение в других приложениях, таких как рентгеноструктурное исследование кристаллов и голография.
Все волны подвержены дифракции, когда встречают препятствие на своем пути. Рассмотрим тень флагштока, отбрасываемую Солнцем на землю. С расстояния затемненная зона тени создает впечатление, что свет, идущий по прямой от Солнца, блокируется полюсом.Но внимательное наблюдение за краем тени покажет, что переход от темного к светлому не резкий. Вместо этого вдоль края есть серая область, созданная светом, который был «изогнут» или преломлен на стороне полюса.
Когда источник волн, например электрическая лампочка, направляет луч через отверстие или апертуру, на экране, расположенном за апертурой, появляется дифракционная картина. Дифракционная картина будет выглядеть примерно как апертура (щель, круг , квадрат ), но она будет окружена некоторыми дифрагированными волнами, которые придают ей «нечеткий» вид.
Если и источник, и экран находятся далеко от апертуры, степень «размытости» определяется длиной волны источника и размером апертуры. При большой апертуре большая часть луча будет проходить прямо, только края апертуры вызывают дифракцию, и будет меньше «размытости». Но если размер апертуры сравним с длиной волны, дифракционная картина будет расширяться. Например, открытое окно может вызвать дифрагию звуковых волн под большими углами.
При большой апертуре большая часть луча будет проходить прямо, только края апертуры вызывают дифракцию, и будет меньше «размытости». Но если размер апертуры сравним с длиной волны, дифракционная картина будет расширяться. Например, открытое окно может вызвать дифрагию звуковых волн под большими углами.
Дифракция Френеля относится к случаю, когда либо источник, либо экран находятся близко к апертуре. Когда и источник, и экран находятся далеко от апертуры, используется термин дифракция Фраунгофера. В качестве примера последнего рассмотрим звездный свет, попадающий в телескоп . Дифракционная картина круглого зеркала телескопа или линзы известна как диск Эйри, который виден как яркий центральный диск в середине ряда более тусклых колец. Это указывает на то, что изображение звезды всегда будет расширено за счет дифракции.Когда оптические инструменты, такие как телескопы, не имеют дефектов, говорят, что наибольшая деталь, которую они могут наблюдать, ограничена дифракцией.
Решетки дифракционные
Преимущество дифракции света было искусно использовано для создания одного из самых важных инструментов науки — дифракционной решетки. Вместо одной апертуры в материале выгравировано большое количество тонких щелей или канавок — до 25 000 на дюйм. При изготовлении этих чувствительных устройств важно, чтобы канавки были параллельны , расположены на одинаковом расстоянии друг от друга и имели одинаковую ширину.
Дифракционная решетка преобразует падающий пучок света в спектр . Это происходит потому, что каждая канавка решетки дифрагирует луч, но поскольку все канавки параллельны, расположены на одинаковом расстоянии друг от друга и имеют одинаковую ширину, дифрагированные волны конструктивно смешиваются или интерферируют, так что различные компоненты можно рассматривать отдельно. Спектры, создаваемые дифракционными решетками, чрезвычайно полезны в приложениях от изучения структуры атомов, молекул до исследования состава звезд.
Рентгеновские лучи — это световые волны с очень короткой длиной волны. Когда они облучают твердый кристалл материал, они дифрагируют на атомах в кристалле. Но поскольку для кристаллов характерно состоять из атомов, расположенных на одинаковом расстоянии друг от друга, можно использовать полученные дифракционные картины для определения местоположений и расстояний между атомами. Простые кристаллы, состоящие из равноотстоящих друг от друга плоскостей атомов, преломляют рентгеновские лучи в соответствии с законом Брэгга.Текущие исследования с использованием дифракции рентгеновских лучей используют инструмент, называемый дифрактометром, для получения дифракционных картин, которые можно сравнить с картинами известных кристаллов для определения структуры новых материалов.
Голография
Когда два лазерных луча смешиваются под углом на поверхности фотопластинки или другого записывающего материала, они создают интерференционную картину чередующихся темных и ярких линий. Поскольку линии идеально параллельны, расположены на одинаковом расстоянии друг от друга и имеют одинаковую ширину, этот процесс используется для изготовления голографических дифракционных решеток высокого качества.На самом деле любую голограмму ( голо — целое: грамм — сообщение) можно рассматривать как сложную дифракционную решетку. Запись голограммы включает смешивание лазерного луча и несфокусированной дифракционной картины какого-либо объекта. Чтобы восстановить изображение объекта (голография также известна как реконструкция волнового фронта), освещающий луч дифрагирует на плоских поверхностей внутри голограммы, следуя закону Брэгга, так что наблюдатель может видеть изображение со всеми его тремя- габаритная деталь.
Поскольку линии идеально параллельны, расположены на одинаковом расстоянии друг от друга и имеют одинаковую ширину, этот процесс используется для изготовления голографических дифракционных решеток высокого качества.На самом деле любую голограмму ( голо — целое: грамм — сообщение) можно рассматривать как сложную дифракционную решетку. Запись голограммы включает смешивание лазерного луча и несфокусированной дифракционной картины какого-либо объекта. Чтобы восстановить изображение объекта (голография также известна как реконструкция волнового фронта), освещающий луч дифрагирует на плоских поверхностей внутри голограммы, следуя закону Брэгга, так что наблюдатель может видеть изображение со всеми его тремя- габаритная деталь.
Дополнительные темы
Научная энциклопедия Наука и философия: Зависимость — интеллектуальные корни зависимого мышления – Уравнение Дирака
Дифракция рентгеновских лучей – обзор
2.
 3.1.6 Дифракция рентгеновских лучей (XRD)
3.1.6 Дифракция рентгеновских лучей (XRD) Дифракция рентгеновских лучей (XRD) – это аналитический метод, основанный на дифракции рентгеновских лучей на веществе, особенно для кристаллических материалов. Рентгеновская дифракция представляет собой упругое рассеяние (без потери энергии фотонов), вызывающее усиление интерференции по мере анализа более упорядоченных материалов.Для некристаллических материалов более подходит термин «диффузия». Это мощный неразрушающий метод для характеристики кристаллических материалов, поскольку он предоставляет информацию о структурах, фазах, предпочтительных ориентациях кристаллов (текстуре) и других структурных параметрах, таких как средний размер зерна, кристалличность, напряжение и дефекты кристаллов. Этот метод имеет огромное значение в науке, технике и технике [61]. Интересно, что рентгеновская дифракция широко используется для характеристики целлюлозы и ее производных, а также для характеристики целлюлозы на основе нанокомпозитов [62].Структурные свойства нанокомпозитов (размер и показатель кристалличности кристаллита целлюлозы) можно охарактеризовать с помощью рентгеноструктурного анализа. XRD также используется для определения возможных изменений в кристаллической структуре матрицы после добавления наночастиц.
XRD также используется для определения возможных изменений в кристаллической структуре матрицы после добавления наночастиц.
Нипело и др. [63] изготовили несколько самостоятельных гибридных пленок с использованием нанокристаллов целлюлозы (CNC) и электропряденых композитных волокон с использованием CNC и поливинилового спирта с магнитными свойствами, обусловленными наночастицами оксида железа кобальта в матрице CNC.Характеристика этих материалов была проведена с помощью различных инструментов, таких как сканирующая электронная микроскопия, атомно-силовая микроскопия и рентгеновская дифракция. Из свойств, влияющих на магнитное поведение частиц неорганического железа, кристалличность и размер являются наиболее важными. XRD использовали для оценки кристаллической структуры и размера частиц. На рис. 2.15А показано, что дифракционные пики, исходящие от CNC, преобладают в неорганическом материале CNC. Вдобавок к этим дифракционным пикам результаты XRD смеси CNC-неорганическая показали сильные пики при 30, 34, 57 и 62 градусах. Углы дифракции Брэгга характерны для частиц феррита кобальта. Таким образом, они были удалены из рентгенограммы чистого CNC в рентгенограмму CNC-неорганического материала, и полученная картина была сопоставлена с картиной магнитных эталонных частиц, осажденных в отсутствие CNC (рис. 2.15B). Из измерений XRD (рис. 2.15) основное различие в магнитных свойствах частиц чистого феррита кобальта и неорганических систем CNC связано с размером и структурой.
Углы дифракции Брэгга характерны для частиц феррита кобальта. Таким образом, они были удалены из рентгенограммы чистого CNC в рентгенограмму CNC-неорганического материала, и полученная картина была сопоставлена с картиной магнитных эталонных частиц, осажденных в отсутствие CNC (рис. 2.15B). Из измерений XRD (рис. 2.15) основное различие в магнитных свойствах частиц чистого феррита кобальта и неорганических систем CNC связано с размером и структурой.
Рис. 2.15. (A) Профили XRD чистого CNC и CNC-неорганического материала, (B) спектр вклада неорганических частиц после извлечения данных, соответствующих CNC, из спектра магнитного CNC-неорганического материала, (C) спектр магнитного очищенный CNC-неорганический материал и (D) эталонный спектр феррита кобальта [63].
Пратип и Сингх [64] стремились получить три новых гибридных материала путем добавления слоистого силиката и микрокристаллической целлюлозы к термопластичному полимеру с использованием сополимера этилена и пропилена (ЭП) в качестве термопластичной полимерной матрицы и сополимера малеинированного ЭП (МЭП) в качестве агента совместимости. .Эти три типа нанокомпозитов были охарактеризованы с помощью рентгеновской дифракции, дифференциальной сканирующей калориметрии, термогравиметрического анализа и инфракрасной спектроскопии с преобразованием Фурье. Интеркаляция слоистого силиката в нанокомпозит была подтверждена методом XRD. На рис. 2.16 представлены рентгенограммы гибридных материалов, на которых пики сдвига в базисном пространстве 001 смещаются от большего угла (2 θ = 4°–6°) к меньшему углу (2 θ = 1,5°–3°), которое обычно представляет собой расстояние (d) между силикатными слоями.Более высокие d-расстояния связаны с макромолекулярными цепями, входящими в галерею слоистых силикатов, что обычно называют «чередованием», в то время как отслоение этих силикатных слоев от порядка галереи называется «расслаиванием», для которого пики будут не видно под меньшими углами. В случае волокон чистой кристаллической целлюлозы появляются пики около 16 и 23 градусов. Эти пики в других образцах трудно обнаружить, что может быть связано с разрушением кристаллической области целлюлозы во время обработки или в результате реакции с компатибилизатором.
.Эти три типа нанокомпозитов были охарактеризованы с помощью рентгеновской дифракции, дифференциальной сканирующей калориметрии, термогравиметрического анализа и инфракрасной спектроскопии с преобразованием Фурье. Интеркаляция слоистого силиката в нанокомпозит была подтверждена методом XRD. На рис. 2.16 представлены рентгенограммы гибридных материалов, на которых пики сдвига в базисном пространстве 001 смещаются от большего угла (2 θ = 4°–6°) к меньшему углу (2 θ = 1,5°–3°), которое обычно представляет собой расстояние (d) между силикатными слоями.Более высокие d-расстояния связаны с макромолекулярными цепями, входящими в галерею слоистых силикатов, что обычно называют «чередованием», в то время как отслоение этих силикатных слоев от порядка галереи называется «расслаиванием», для которого пики будут не видно под меньшими углами. В случае волокон чистой кристаллической целлюлозы появляются пики около 16 и 23 градусов. Эти пики в других образцах трудно обнаружить, что может быть связано с разрушением кристаллической области целлюлозы во время обработки или в результате реакции с компатибилизатором. Расстояние d промежуточного слоя в глине (MMT20A) составило около 232,3 нм (2 θ = 3,8 градуса).
Расстояние d промежуточного слоя в глине (MMT20A) составило около 232,3 нм (2 θ = 3,8 градуса).
Рис. 2.16. Рентгенограммы целлюлозных нанокомпозитов в диапазоне: (А) 2°–30° и (Б) 2°–10° [64].
Порошковая рентгеновская дифракция (XRD)
Barbara L Dutrow, Университет штата Луизиана
,Christine M. Clark, Университет Восточного Мичигана
Что такое порошковая рентгеновская дифракция (XRD)
идентификации кристаллического материала и может предоставить информацию о размерах элементарной ячейки.Исследуемый материал тонко измельчают, гомогенизируют и определяют средний сыпучий состав.
Основные принципы порошковой рентгеновской дифракции (XRD)
Макс фон Лауэ в 1912 году обнаружил, что кристаллические вещества действуют как трехмерные дифракционные решетки для длин волн рентгеновского излучения, аналогично расстоянию между плоскостями в кристаллической решетке. Рентгеновская дифракция в настоящее время является распространенным методом изучения кристаллических структур и межатомных расстояний.
Рентгеновская дифракция основана на конструктивной интерференции монохроматических рентгеновских лучей и кристаллического образца.Эти рентгеновские лучи генерируются электронно-лучевой трубкой, фильтруются для получения монохроматического излучения, коллимируются для концентрирования и направляются на образец. Взаимодействие падающих лучей с образцом создает конструктивную интерференцию (и дифрагированный луч), когда условия удовлетворяют закону Брэгга ( n λ=2 d sin θ). Этот закон связывает длину волны электромагнитного излучения с углом дифракции и периодом решетки в кристаллическом образце. Затем эти дифрагированные рентгеновские лучи обнаруживаются, обрабатываются и подсчитываются.При сканировании образца в диапазоне углов 2θ должны быть достигнуты все возможные направления дифракции решетки из-за случайной ориентации порошкообразного материала. Преобразование дифракционных пиков в d-расстояния позволяет идентифицировать минерал, поскольку каждый минерал имеет набор уникальных d-расстояний. Как правило, это достигается путем сравнения d-интервалов со стандартными эталонными шаблонами.
Как правило, это достигается путем сравнения d-интервалов со стандартными эталонными шаблонами.
Все методы дифракции основаны на генерации рентгеновских лучей в рентгеновской трубке. Эти рентгеновские лучи направляются на образец, и дифрагированные лучи собираются.Ключевым компонентом всей дифракции является угол между падающим и дифрагированным лучами. Помимо этого, порошковая и монокристаллическая дифракция различаются по приборам.
Приборы для порошковой рентгеновской дифракции (XRD) – как они работают? Рентгеновские дифрактометры
состоят из трех основных элементов: рентгеновской трубки, держателя образца и детектора рентгеновского излучения. Прибор Bruker для рентгеновской дифракции D8-Discover. Детали Рентгеновские лучи генерируются в электронно-лучевой трубке путем нагревания нити накала для производства электронов, ускорения электронов по направлению к цели путем подачи напряжения и бомбардировки материала мишени электронами.Когда электроны имеют достаточную энергию, чтобы вытеснить электроны внутренней оболочки материала мишени, создаются характеристические рентгеновские спектры. Эти спектры состоят из нескольких компонентов, наиболее распространенными из которых являются K α и K β . K α частично состоит из K α1 и K α2 . K α1 имеет немного более короткую длину волны и вдвое большую интенсивность, чем K α2 . Конкретные длины волн характерны для материала мишени (Cu, Fe, Mo, Cr).Фильтрация с помощью фольги или кристаллических монохроматоров необходима для получения монохроматических рентгеновских лучей, необходимых для дифракции. K α1 и K α2 достаточно близки по длине волны, поэтому используется их средневзвешенное значение. Медь является наиболее распространенным материалом-мишенью для монокристаллической дифракции с излучением CuK α = 1,5418 Å. Эти рентгеновские лучи коллимируются и направляются на образец. При вращении образца и детектора регистрируется интенсивность отраженного рентгеновского излучения.Когда геометрия падающих на образец рентгеновских лучей удовлетворяет уравнению Брэгга, возникает конструктивная интерференция и возникает пик интенсивности.
Эти спектры состоят из нескольких компонентов, наиболее распространенными из которых являются K α и K β . K α частично состоит из K α1 и K α2 . K α1 имеет немного более короткую длину волны и вдвое большую интенсивность, чем K α2 . Конкретные длины волн характерны для материала мишени (Cu, Fe, Mo, Cr).Фильтрация с помощью фольги или кристаллических монохроматоров необходима для получения монохроматических рентгеновских лучей, необходимых для дифракции. K α1 и K α2 достаточно близки по длине волны, поэтому используется их средневзвешенное значение. Медь является наиболее распространенным материалом-мишенью для монокристаллической дифракции с излучением CuK α = 1,5418 Å. Эти рентгеновские лучи коллимируются и направляются на образец. При вращении образца и детектора регистрируется интенсивность отраженного рентгеновского излучения.Когда геометрия падающих на образец рентгеновских лучей удовлетворяет уравнению Брэгга, возникает конструктивная интерференция и возникает пик интенсивности. Детектор записывает и обрабатывает этот рентгеновский сигнал и преобразует сигнал в скорость счета, которая затем выводится на устройство, такое как принтер или компьютерный монитор.
Рентгеновская порошковая дифрактограмма. Положения пиков возникают там, где рентгеновский луч дифрагирует на кристаллической решетке. Уникальный набор d-интервалов, полученный из этого шаблона, можно использовать для «отпечатков пальцев» минерала.Подробности
Детектор записывает и обрабатывает этот рентгеновский сигнал и преобразует сигнал в скорость счета, которая затем выводится на устройство, такое как принтер или компьютерный монитор.
Рентгеновская порошковая дифрактограмма. Положения пиков возникают там, где рентгеновский луч дифрагирует на кристаллической решетке. Уникальный набор d-интервалов, полученный из этого шаблона, можно использовать для «отпечатков пальцев» минерала.ПодробностиГеометрия рентгеновского дифрактометра такова, что образец вращается на пути коллимированного рентгеновского луча под углом θ, в то время как детектор рентгеновского излучения установлен на кронштейне для сбора дифрагированных рентгеновских лучей и вращается на угол 2θ. Инструмент, используемый для поддержания угла и вращения образца, называется гониометром . Для типичных рисунков порошка данные собираются при 2θ от ~ 5 ° до 70 °, углы, которые предварительно заданы в рентгеновском сканировании.
Области применения
Порошковая рентгеновская дифракция наиболее широко используется для идентификации неизвестных кристаллических материалов (например,г. минералы, неорганические соединения). Определение неизвестных твердых веществ имеет решающее значение для исследований в области геологии, наук об окружающей среде, материаловедения, инженерии и биологии.
минералы, неорганические соединения). Определение неизвестных твердых веществ имеет решающее значение для исследований в области геологии, наук об окружающей среде, материаловедения, инженерии и биологии.Другие приложения включают:
- характеристика кристаллических материалов
- идентификация тонкозернистых минералов, таких как глины и глины со смешанным слоем, которые трудно определить оптически
- определение размеров элементарной ячейки
- измерение чистоты образца
- определение кристаллических структур с использованием уточнения Ритвельда
- определение модальных количеств минералов (количественный анализ)
- характеризуют образцы тонких пленок по:
- определение несоответствия решеток между пленкой и подложкой и определение напряжений и деформаций
- определение плотности дислокаций и качества пленки путем измерения кривой качания
- измерение сверхрешеток в многослойных эпитаксиальных структурах
- определение толщины, шероховатости и плотности пленки с помощью измерения коэффициента отражения рентгеновских лучей при скользящем падении
- проводить текстурные измерения, такие как ориентация зерен, в поликристаллическом образце
Преимущества и недостатки порошковой рентгеновской дифракции (XRD)?
Сильные стороны
- Мощный и быстрый (< 20 мин) метод идентификации неизвестного минерала
- В большинстве случаев обеспечивает однозначное определение минералов
- Требуется минимальная подготовка проб
- Блоки XRD широко доступны
- Интерпретация данных относительно проста
Ограничения
- Гомогенный и однофазный материал лучше всего подходит для идентификации неизвестного
- Должен иметь доступ к стандартному справочному файлу неорганических соединений (d-расстояния, hkl s)
- Требуются десятые доли грамма материала, который необходимо измельчить в порошок
- Для смешанных материалов предел обнаружения ~ 2% от образца
- Для определения элементарных ячеек индексация структур неизометрических кристаллических систем затруднена
- Пиковое наложение может возникать и ухудшаться при «отражениях» под большим углом
Руководство пользователя.
 Сбор и подготовка проб
Сбор и подготовка пробДля определения неизвестного необходимы: материал, инструмент для измельчения и держатель проб.
- Получить несколько десятых долей грамма (или более) максимально чистого материала
- Измельчите образец в мелкий порошок, как правило, в жидкости, чтобы свести к минимуму дополнительную деформацию (поверхностную энергию), которая может смещать положения пиков, и чтобы сделать ориентацию случайной. Предпочтителен порошок размером менее ~10 мкм (или 200 меш)
- Поместите в держатель образца или на поверхность образца: упаковка мелкодисперсного порошка в держатель образца. Подробности
- равномерно нанести на предметное стекло, обеспечивая плоскую верхнюю поверхность
- упаковать в контейнер для проб
- посыпка на двойной клейкой ленте
- Необходимо соблюдать осторожность, чтобы создать плоскую верхнюю поверхность и добиться случайного распределения ориентаций решетки, если только не создается ориентированное пятно.

- Для анализа глин, требующих одной ориентации, USGS предоставляет специальные методы подготовки образцов глины.
Сбор данных, результаты и представление
Сбор данных Интенсивность дифрагированных рентгеновских лучей непрерывно регистрируется по мере того, как образец и детектор поворачиваются на соответствующие углы.Пик интенсивности возникает, когда минерал содержит плоскости решетки с интервалами d, подходящими для дифрагирования рентгеновских лучей при этом значении θ. Хотя каждый пик состоит из двух отдельных отражений (Kα 1 и Kα 2 ), при малых значениях 2θ положения пиков перекрываются с Kα 2 , проявляясь в виде горба со стороны Kα 1 . Большее разделение происходит при более высоких значениях θ. Обычно эти объединенные пики рассматриваются как один. Положение 2λ дифракционного пика обычно измеряется как центр пика при высоте пика 80%.
Обычно эти объединенные пики рассматриваются как один. Положение 2λ дифракционного пика обычно измеряется как центр пика при высоте пика 80%.
Результаты обычно представляются в виде положения пика при 2θ и количества рентгеновских лучей (интенсивности) в виде таблицы или графика x-y (показано выше). Интенсивность ( I ) указывается либо как интенсивность высоты пика, т. е. интенсивность выше фона, либо как интегрированная интенсивность, площадь под пиком. Относительную интенсивность записывают как отношение интенсивности пика к интенсивности самого интенсивного пика (относительная интенсивность = I/I 1 x 100 ).
Определение неизвестного Расстояние d каждого пика затем получают путем решения уравнения Брэгга для соответствующего значения λ. Как только все d-интервалы определены, автоматические процедуры поиска/сопоставления сравнивают d с неизвестных материалов с известными материалами. Поскольку каждый минерал имеет уникальный набор d-расстояний, сопоставление этих d-расстояний обеспечивает идентификацию неизвестного образца. Систематическая процедура используется для упорядочения d-расстояний с точки зрения их интенсивности, начиная с наиболее интенсивного пика.Файлы d-расстояний для сотен тысяч неорганических соединений доступны в Международном центре дифракционных данных в виде файла порошковой дифракции (PDF). Многие другие сайты содержат d-интервалы минералов, такие как База данных кристаллической структуры американского минералога. Обычно эта информация является неотъемлемой частью программного обеспечения, поставляемого с прибором.
Поскольку каждый минерал имеет уникальный набор d-расстояний, сопоставление этих d-расстояний обеспечивает идентификацию неизвестного образца. Систематическая процедура используется для упорядочения d-расстояний с точки зрения их интенсивности, начиная с наиболее интенсивного пика.Файлы d-расстояний для сотен тысяч неорганических соединений доступны в Международном центре дифракционных данных в виде файла порошковой дифракции (PDF). Многие другие сайты содержат d-интервалы минералов, такие как База данных кристаллической структуры американского минералога. Обычно эта информация является неотъемлемой частью программного обеспечения, поставляемого с прибором.
Для определения параметров элементарной ячейки каждое отражение должно быть проиндексировано определенным hkl .
Литература
Следующая литература может быть использована для дальнейшего изучения дифракции рентгеновских лучей (XRD)
- Bish, DL и Post, JE, редакторы.
 1989. Современная порошковая дифракция. Обзоры по миэнралогии, т. 20. Минералогическое общество Америки.
1989. Современная порошковая дифракция. Обзоры по миэнралогии, т. 20. Минералогическое общество Америки. - Каллити, Б. Д. 1978. Элементы дифракции рентгеновских лучей. 2-е изд. Аддисон-Уэсли, Рединг, Массачусетс,
- Клуг, Х. П. и Л. Э. Александр. 1974. Процедуры рентгеновской дифракции для поликристаллических и аморфных материалов.2-е изд. Уайли, Нью-Йорк.
- Мур, Д.М. и Р.К. Рейнольдс-младший, 1997. Рентгеновская дифракция, идентификация и анализ глинистых минералов. 2-е изд. Издательство Оксфордского университета, Нью-Йорк.
Дополнительные ссылки
Для получения дополнительной информации о порошковой рентгеновской дифракции (XRD) перейдите по ссылкам ниже.
Преподавательская деятельность и ресурсы
Преподавательская деятельность, лаборатории и ресурсы, относящиеся к порошковой рентгеновской дифракции (XRD).
- Лабораторные упражнения по рентгенологическим методам из коллекции SERC Teaching Mineralogy Collections
- Выветривание магматических, метаморфических и осадочных пород в полузасушливом климате.
 Инженерное применение петрологии. Эта задача развивает навыки рентгеноструктурного анализа применительно к минералогии глин, закрепляет лекционный материал по геохимии выветривания и демонстрирует роль петрологической характеристики в проектировании участка.
Инженерное применение петрологии. Эта задача развивает навыки рентгеноструктурного анализа применительно к минералогии глин, закрепляет лекционный материал по геохимии выветривания и демонстрирует роль петрологической характеристики в проектировании участка. - Учебное пособие по дифракции рентгеновских лучей в Кембридже
- Презентация в формате Powerpoint об использовании рентгеновской дифракции в почвоведении (PowerPoint, 1,6 МБ, 7 сентября 2007 г.) Мелоди Бержерон, Лаборатория изображений и химического анализа Университета штата Монтана.
- Брэди, Джон Б., и Бордман, Шелби Дж., 1995, Знакомство студентов-минералогов с дифракцией рентгеновских лучей посредством экспериментов по оптической дифракции с использованием лазеров. жур. геол. Образование, т. 43 № 5, 471-476.
- Брэди, Джон Б., Ньютон, Роберт М.и Бордман, Шелби Дж., 1995, Новое использование экспериментов по порошковой рентгеновской дифракции в учебной программе бакалавриата. жур. геол. Образование, т.
 43 № 5, 466–470.
43 № 5, 466–470. - Дутроу, Барб, 1997, Лучшая жизнь благодаря минералам. Дифракция рентгеновских лучей на предметах домашнего обихода, в: Брэди Дж., Могк Д. и Перкинс Д. (ред.) Преподавание минералогии, Минералогическое общество Америки, с. 349-359.
- Ховис, Гай, Л., 1997, Определение химического состава, состояния порядка, молярного объема и плотности моноклинного щелочного полевого шпата с помощью рентгеновской дифракции, в: Brady, J., Могк Д. и Перкинс Д. (ред.) Преподавание минералогии, Минералогическое общество Америки, с. 107-118.
- Брэди, Джон Б., 1997, Получение твердых растворов с помощью галогенидов щелочных металлов (и их разрушение), в: Брейди, Дж., Могк, Д. и Перкинс Д. (ред.) Преподавание минералогии, Минералогическое общество Америки, стр. . 91-95.
- Перкинс, Декстер, III, и Соренсен, Пол, Синтез минералов и эксперименты по дифракции рентгеновских лучей, в: Брейди, Дж., Могк, Д. и Перкинс Д. (ред.) Преподавание минералогии, Минералогическое общество Америки, стр.
 .81-90.
.81-90. - Холлечер, Курт, Долгосрочный практический экзамен по минералогии, в: Брейди, Дж., Могк, Д. и Перкинс Д. (ред.) Преподавание минералогии, Минералогическое общество Америки, с. 43-46.
- Мочер, Дэвид, 2004 г., Характеристика и идентификация неизвестных минералов: терминологический проект по минералогии, Jour. Геофизическое образование, т. 52, № 1, с. 5-9.
- Хлучи, М.М., 1999, Значение обучения студентов рентгеновским методам и минералогии глины, Jour. Геофизическое образование, т. 47, с.236-240.
Рентгеновская дифракция для исследования материалов: от основ к применению
Описание книги
Рентгеновская дифракция является полезным и мощным методом анализа для характеристики кристаллических материалов, обычно используемых в MSE, физике и химии. В этой информативной новой книге описываются принципы рентгеновской дифракции и ее применения для определения характеристик материалов. Он состоит из трех частей. Первый посвящен элементарной кристаллографии и оптике, что необходимо для понимания теории дифракции рентгеновских лучей, обсуждаемой во втором разделе книги. Часть 2 описывает, как дифракция рентгеновских лучей может быть применена для характеристики таких различных форм материалов, как тонкие пленки, монокристаллы и порошки. Третий раздел книги посвящен приложениям рентгеновской дифракции.
Часть 2 описывает, как дифракция рентгеновских лучей может быть применена для характеристики таких различных форм материалов, как тонкие пленки, монокристаллы и порошки. Третий раздел книги посвящен приложениям рентгеновской дифракции.
В книге представлен ряд примеров, помогающих читателям лучше понять предмет. Дифракция рентгеновских лучей для исследования материалов: от основ к приложениям , а также
• предоставляет базовые знания о дифракции, позволяющие неспециалистам ознакомиться с темами
• охватывает практические применения, а также основные принципы дифракции рентгеновских лучей
• представляет соответствующие примеры с ответами, чтобы помочь читателям легче понять содержание
• включает характеристику тонкой пленки с помощью рентгеновской дифракции с соответствующими экспериментальными методами
• содержит огромное количество искусно нарисованных графических изображений, помогающих проиллюстрировать содержание
Книга поможет читателям (студентам и исследователям в области материаловедения, физики и химии) разобраться в кристаллографии и кристаллических структурах, интерференции и дифракции, структурном анализе объемных материалов, характеристике тонких пленок и неразрушающем измерении внутренних напряжений и фазовых переходов.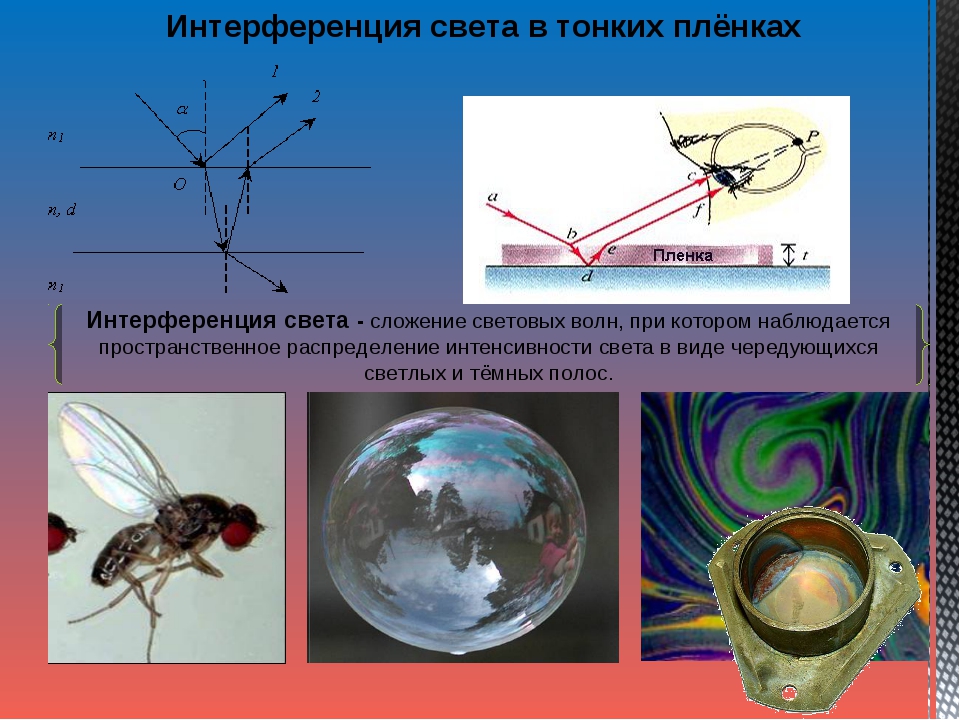
Дифракция является оптическим явлением и поэтому может быть лучше понята, если объяснить ее с помощью оптического подхода, которым пренебрегали в других книгах. Эта книга помогает восполнить этот пробел, предоставляя информацию, объясняющую концепцию дифракции рентгеновских лучей и то, как ее можно применять для анализа материалов.
Эта книга будет ценным справочником для исследователей в этой области и хорошим вводным пособием по дифракции рентгеновских лучей для студентов, изучающих материаловедение, физику и химию.
Содержание
Prefice
Часть I: X-Rays и Crystal Geometry
Электромагнитные волны и рентгеновские лучи
Геометрия кристаллов
Интерференция и дифракция
Часть II: Теория х Дифракция
Направления рентгеновских дифракций
интенсивности рентгеновской дифракции
Часть III: Применение рентгеновской дифракции
Характеристика тонких пленок с помощью рентгеновской дифракции
Метод Лауэ и определение ориентации монокристалла
Порошковая дифракция
Индекс
отзывов
“Эта книга представляет собой очень доступное введение в XRD для исследования материалов.
Написана лаконичной и ясной прозой. Текст создает целостную картину XRD. После прочтения этой книги исследователи смогут понять основы многих материаловедческих и инженерных исследовательских работ. . . . Рентгеновская дифракция (XRD) — это мощный неразрушающий метод характеризации для определения структуры, фазы, состава и деформации материалов. Это один из наиболее часто используемых методов для характеристики материалов. Эта книга отличается от других книг по этой теме упрощенным изложением и охватом анализа тонких пленок.Он в значительной степени сводит к минимуму математику и обильно иллюстрирован, что делает его хорошей отправной точкой для изучения основных принципов XRD. Определены и объяснены общие тонкопленочные структуры (случайные поликристаллические, текстурированные) и их отношения с подложкой (деформация, вращение в плоскости). Это делает его ценным для исследователей, изучающих осаждение тонких пленок. В книгу включены примеры задач для закрепления изученных понятий, а также задачи, которые можно задать в качестве домашнего задания».
—J.Х. Эдгар, Университет штата Канзас, США, для MRS BULLETIN, февраль 2017 г.
18. Методы рентгеновской дифракции | Кристаллические материалы | Введение в химию твердого тела | Материаловедение и инженерия
« Предыдущая | Следующая »
Обзор сессии
| Модули | Кристаллические материалы |
| Концепции | Закон Braggs, рентгеновская дифракция кристаллов: дифрактометрия, Laue, и Debye-Scherrer, кристаллическая симметрия правила отбора |
| Ключевые слова | рентгеновская дифракция, закон Брэггса, угол падения, угол отражения, конструктивная интерференция, деструктивная интерференция, гребень, впадина, амплитуда, длина волны, фаза, монохроматический, когерентный свет, некогерентный свет, порядок отражения, показатель преломления, коллиматор, дифракционный пик, вращательная симметрия, дифракция Лауэ, квазикристалл, трансляционная симметрия, дальний порядок, рентгеновская кристаллография, плитки Пенроуза, Уильям Генри Брэгг, Уильям Лоуренс Брэгг, Макс фон Лауэ , Роджер Пенроуз, Питер Дебай, Питер Шеррер, Дэн Шехтман |
| Химические вещества | медь (Cu), никель (Ni), кремний (Si), алюминиево-марганцевый сплав (Al-Mn) |
| Применение | выращивание монокристаллов Si, идентификация плоскости и симметрия в кристаллах, плитки Пенроуза |
Предварительные условия
Прежде чем приступить к этому занятию, вы должны ознакомиться с предыдущими темами этого модуля (занятия с 15 по 17), в частности:
- Индексы Миллера для направлений кристаллов и плоскости
- Кристаллические структуры SC, FCC и BCC
- Методы получения рентгеновских лучей и характеристические эмиссионные линии (Cu K α и т.
 д.)
д.)
Глядя в будущее
Рентгеновская дифракция — это популярный метод исследования структуры органических молекул, таких как белки (занятие 31) и ДНК (самое известное занятие) (занятие 32), а также неорганических кристаллов. Он также используется для определения степени дальнего порядка и симметрии, присутствующей в кристалле или отсутствующей в стекле, что является темой следующего модуля (Занятие 21: Введение в очки).
Цели обучения
После завершения этого занятия вы должны уметь:
- Зарисовать отражение падающего излучения от атомных плоскостей и вывести закон Брэггса для этой геометрии.
- Определите, какие плоскости дают рентгеновские дифракционные пики в кристаллах ГЦК и ОЦК.
- По графику зависимости интенсивности рентгеновского излучения от угла или значениям 2θ дифракционных пиков определите кристаллическую структуру и постоянную решетки образца.

- Объясните разницу между рентгеновской дифрактометрией и дифракцией по Лауэ .
- Определите типы симметрии , присутствующие в данном шаблоне мозаики.
чтение
Архивная Лекция Лекции № 5 (PDF), Разделы 4-6
| Книжные главы | Темы |
|---|---|
| [Selor] 12.3, «Структуры простых бинарных соединений». | Общие структуры бинарных соединений, рентгеновская дифракция |
| [JS] 3.7, «Рентгеновская дифракция». | Дифракция, закон Брэггса и правила отражения; методы монокристаллической, поликристаллической и порошковой дифракции |
Видео лекции
Ресурсы
Слайды лекции (PDF – 5.3MB)
Краткое изложение лекций
Рентгеновские лучи отражаются от каждой атомной плоскости в кристалле, создавая структуры деструктивных и созидательных интерференций в соответствии с законом Брэггса . Один популярный метод определения кристаллической структуры, рентгеновская дифрактометрия , включает монохроматические рентгеновские лучи, отражающиеся от вращающейся мишени; результирующие пиков указывают на идентичность и расстояние между плоскостями плотной упаковки, которые различны для FCC и BCC.Другой метод, дифракция по Лауэ , использует рентгеновские лучи с несколькими длинами волн и фиксированной мишенью, создавая структуру, отражающую симметрию , присутствующую в кристаллической структуре. Кубические решетки включают в себя плоскости, которые имеют 90 256 1-, 2-, 3- или 4-кратную вращательную симметрию 90 257, но 90 256 квазикристаллов 90 257, демонстрирующих 90 256 5-кратных 90 257 структур, наблюдались в экспериментах со сплавами Al-Mn и математически генерировались в виде плиток Пенроуза.
Один популярный метод определения кристаллической структуры, рентгеновская дифрактометрия , включает монохроматические рентгеновские лучи, отражающиеся от вращающейся мишени; результирующие пиков указывают на идентичность и расстояние между плоскостями плотной упаковки, которые различны для FCC и BCC.Другой метод, дифракция по Лауэ , использует рентгеновские лучи с несколькими длинами волн и фиксированной мишенью, создавая структуру, отражающую симметрию , присутствующую в кристаллической структуре. Кубические решетки включают в себя плоскости, которые имеют 90 256 1-, 2-, 3- или 4-кратную вращательную симметрию 90 257, но 90 256 квазикристаллов 90 257, демонстрирующих 90 256 5-кратных 90 257 структур, наблюдались в экспериментах со сплавами Al-Mn и математически генерировались в виде плиток Пенроуза.
Главная задание
Проблемы
Проблемы (PDF)
Решения (PDF)
Решения (PDF)
Учебные книги
[JS] Глава 3, Проблемы образца 20, 21
| [SELOR] Разделы | Conceptual | Численность | ||
|---|---|---|---|---|
[Сейлор] 12. 3, «Структуры простых бинарных соединений». 3, «Структуры простых бинарных соединений». | 8, 9 | 11, 12 | 11, 12 |
для дальнейшего изучения
Люди
Люди
Уильям Генри Брэгг, Уильям Лоуренс Брэгг – 1915 Нобелевская премия в физике
Max Von Laue – 1914 Нобелевская премия по физике
Дан Шехтман
Роджер Пенроуз
Питер Дебай – Нобелевская премия по химии 1936 года
Пауль Шеррер
Культура
Моцарт, Вольфганг.«Рондо Алла Турка». Соната для фортепиано No. 11 ля мажор , К. 331.
Другое содержание OCW и OER
« Предыдущая | Далее »
Явления оптической дифракции вокруг краев фотодетекторов: упрощенный метод для метрологических приложений
Понятие краевой дифракции
Оптическая дифракция очень часто относится к искривлению световых волн вокруг препятствия.На рисунке 1 схематично показана концепция создания оптической дифракционной картины из монохроматического света. Световая волна частично блокируется непрозрачным предметом, прежде чем попасть на экран, как показано на рис. 1. Согласно сложившимся геометрическим теориям оптики, острая кромка непрозрачного предмета отбрасывает тень, имеющую достаточно резкие очертания той же формы. как непрозрачный объект в точке P. Однако при ближайшем рассмотрении можно обнаружить, что край этой тени не является абсолютно резким, а показывает систему темных и светлых полос в непосредственной близости от края в точке P.Эти темные и яркие полосы называются картиной дифракции, как показано на рис. 1. Эта картина возникает из-за дифракции света вокруг нижнего края непрозрачного объекта и в результате интерференции прямых и дифрагированных лучей света. Если освещенность в какой-либо точке равна нулю или минимальна, это называется деструктивной интерференцией, которая представляет собой темную полосу, а если она максимальна, это называется конструктивной интерференцией, которая представляет собой яркую полосу. Дальнейшее рассмотрение этого традиционного метода дифракции доступно в учебнике по физике Serway and Jewett 21 .
Световая волна частично блокируется непрозрачным предметом, прежде чем попасть на экран, как показано на рис. 1. Согласно сложившимся геометрическим теориям оптики, острая кромка непрозрачного предмета отбрасывает тень, имеющую достаточно резкие очертания той же формы. как непрозрачный объект в точке P. Однако при ближайшем рассмотрении можно обнаружить, что край этой тени не является абсолютно резким, а показывает систему темных и светлых полос в непосредственной близости от края в точке P.Эти темные и яркие полосы называются картиной дифракции, как показано на рис. 1. Эта картина возникает из-за дифракции света вокруг нижнего края непрозрачного объекта и в результате интерференции прямых и дифрагированных лучей света. Если освещенность в какой-либо точке равна нулю или минимальна, это называется деструктивной интерференцией, которая представляет собой темную полосу, а если она максимальна, это называется конструктивной интерференцией, которая представляет собой яркую полосу. Дальнейшее рассмотрение этого традиционного метода дифракции доступно в учебнике по физике Serway and Jewett 21 . Традиционная краевая дифракционная картина и распределение интенсивности, показанные на рис. 1, используются далее в этой статье для сравнения предложенной нами концепции.
Традиционная краевая дифракционная картина и распределение интенсивности, показанные на рис. 1, используются далее в этой статье для сравнения предложенной нами концепции.
Схематическая диаграмма, иллюстрирующая явление дифракции на линейке.
Явление дифракции изучается в рамках двух классов, а именно теорий дифракции Френеля и Фраунгофера 22,23,24 . Дифракция Френеля представляет собой плохое приближение – случаи, когда один или оба источника и экрана наблюдения находятся достаточно близко к апертуре, поэтому необходимо учитывать кривизну волнового фронта.Работа, представленная в этой статье, посвящена дифракции Френеля. Дифракционная картина Френеля имеет математически сложный характер 13,25 .
Среди них хорошо известен подход Френеля, основанный на принципе Гюйгенса 26,27 . Он описывает дифракционное поле в терминах суперпозиции двух волн: одна волна распространяется через дифрагирующий объект без каких-либо возмущений (называется геометрической волной), а вторая волна исходит из каждой точки освещенной границы объекта или края (называется границей). дифрагированная волна).{2}\), он касается первого, когда cos( kδ ) = +1, и позже, когда cos( kδ ) = −1. Это показывает, что в плоскости наблюдения интерференционные полосы генерируются в области прямого освещения, где U (ж) интерферирует с U (г) , однако в области геометрической тени только U ( г) присутствует и, следовательно, помех не наблюдается. Контраст этих полос продолжает уменьшаться по мере удаления от границы тени.{1/2}]\,n=1,\,2,\,3,\ldots ,$$
дифрагированная волна).{2}\), он касается первого, когда cos( kδ ) = +1, и позже, когда cos( kδ ) = −1. Это показывает, что в плоскости наблюдения интерференционные полосы генерируются в области прямого освещения, где U (ж) интерферирует с U (г) , однако в области геометрической тени только U ( г) присутствует и, следовательно, помех не наблюдается. Контраст этих полос продолжает уменьшаться по мере удаления от границы тени.{1/2}]\,n=1,\,2,\,3,\ldots ,$$
(2)
, где r — расстояние между источником и непрозрачным краем, а b — расстояние между непрозрачным краем и экраном наблюдения. Уравнение (2) показывает, что ширина полосы β продолжает уменьшаться с увеличением порядка полосы n . Кроме того, для определенного порядка интерференционных полос n , β можно увеличить, уменьшив r .Уравнение (2) также показывает, что его можно использовать для описания явления на основе освещения точечным источником, а не на основе коллимированного источника света. Позже в разделе обсуждений мы расскажем, что в качестве источника света использовался диодный лазер. Он имеет микролинзу, прикрепленную к его излучающей головке, чтобы изменить форму луча от эллиптической до круглой, и имеет расходимость около 0,8 мрад. Мы не использовали никакую внешнюю оптику для коллимации лазерного луча в наших экспериментах. Следовательно, уравнение (2) все еще можно использовать для описания явления как лазерного источника с 0.Расходимость в 8 мрад все же можно аппроксимировать точечным источником. С другой стороны, расходимость играет решающую роль в дифракционных экспериментах, и поэтому ею нельзя пренебрегать, в отличие от интерференционных экспериментов. Однако достижимое изменение ширины полосы путем изменения х было бы незначительным, если расстояние между непрозрачным краем и экраном наблюдения х очень меньше по сравнению с х . В предлагаемом методе краевой дифракции b очень меньше по сравнению с r .
Позже в разделе обсуждений мы расскажем, что в качестве источника света использовался диодный лазер. Он имеет микролинзу, прикрепленную к его излучающей головке, чтобы изменить форму луча от эллиптической до круглой, и имеет расходимость около 0,8 мрад. Мы не использовали никакую внешнюю оптику для коллимации лазерного луча в наших экспериментах. Следовательно, уравнение (2) все еще можно использовать для описания явления как лазерного источника с 0.Расходимость в 8 мрад все же можно аппроксимировать точечным источником. С другой стороны, расходимость играет решающую роль в дифракционных экспериментах, и поэтому ею нельзя пренебрегать, в отличие от интерференционных экспериментов. Однако достижимое изменение ширины полосы путем изменения х было бы незначительным, если расстояние между непрозрачным краем и экраном наблюдения х очень меньше по сравнению с х . В предлагаемом методе краевой дифракции b очень меньше по сравнению с r .
Концепция дифракции вокруг края фотодетектора: одновременная генерация и детектирование
В этой работе оптическая дифракция устанавливается без поддержки какого-либо внешнего непрозрачного объекта.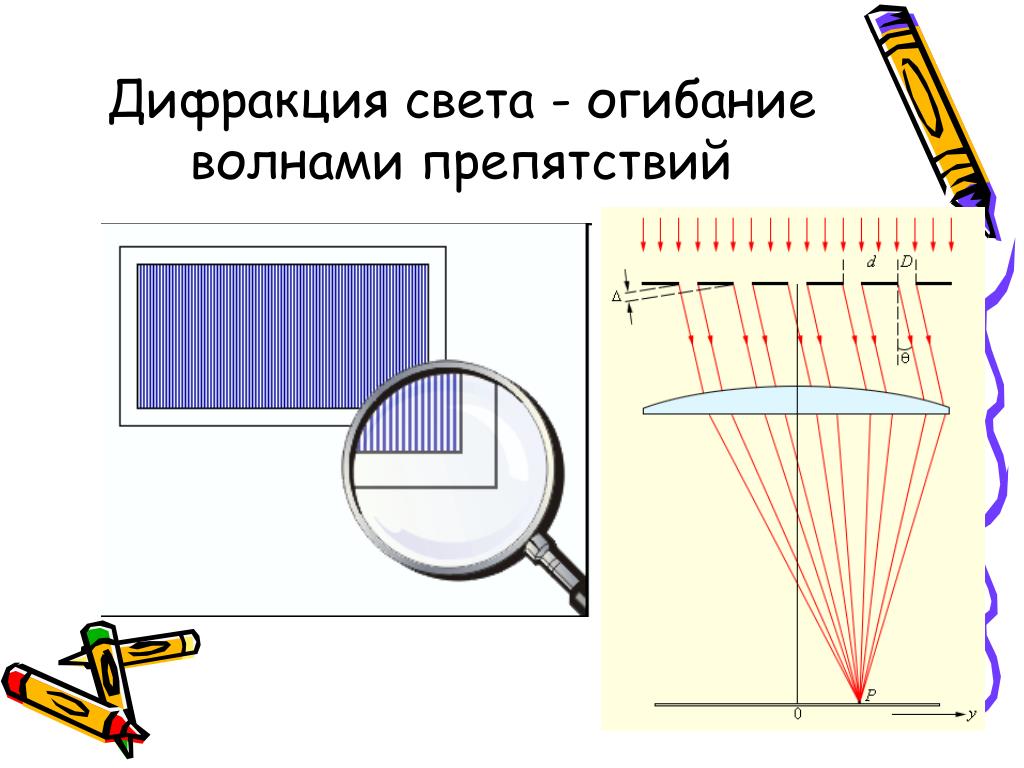 С другой стороны, в качестве непрозрачного объекта использовался край чувствительной области фотодетектора, который используется для регистрации дифракционной картины. Экспериментальная установка, используемая для одновременной генерации и обнаружения такой дифракционной картины, показана на рис. 2 (а). Дифракционная картина создается на фотодетекторе путем освещения фотодетектора таким образом, что световой луч, падающий на границу раздела между активной чувствительной и непрозрачной областями фотодетектора, как показано на рис.2(б). Дифракционная картина, сформированная на фотодетекторе, показана на рис. 2(в), а соответствующее распределение интенсивности, полученное вдоль центральной горизонтальной оси, показано на рис. 2(г). Одновременно фотодетектор генерирует электрический сигнал, соответствующий картине интерференционных полос в реальном времени. Поэтому этот метод называется одновременным.
С другой стороны, в качестве непрозрачного объекта использовался край чувствительной области фотодетектора, который используется для регистрации дифракционной картины. Экспериментальная установка, используемая для одновременной генерации и обнаружения такой дифракционной картины, показана на рис. 2 (а). Дифракционная картина создается на фотодетекторе путем освещения фотодетектора таким образом, что световой луч, падающий на границу раздела между активной чувствительной и непрозрачной областями фотодетектора, как показано на рис.2(б). Дифракционная картина, сформированная на фотодетекторе, показана на рис. 2(в), а соответствующее распределение интенсивности, полученное вдоль центральной горизонтальной оси, показано на рис. 2(г). Одновременно фотодетектор генерирует электрический сигнал, соответствующий картине интерференционных полос в реальном времени. Поэтому этот метод называется одновременным.
Дифракция вокруг края фотодетектора: ( a ) Экспериментальная схема для одновременной генерации и регистрации; ( b ) Освещение по краям; ( c ) Полученная дифракционная картина и ( d ) Полученное распределение интенсивности.
Изображения, представленные на рис. 2(b,c), записаны внешней цифровой зеркальной камерой Nikon D5600. Изображение, представленное на рис. 2(b), не может показать явление дифракции с деталями и диапазоном освещения непосредственно для глаза, но оно может указывать на общий характер эффекта. Изображение, показанное на рис. 2(c), представляет собой увеличенную часть краевой области дифракции на фотодетекторе. Впоследствии изображение, показанное на рис. 2(c), подвергается анализу с использованием программного обеспечения Matlab. Значения интенсивности преобразуются в цифровую информацию путем тщательного считывания координатных точек.Данные, представленные на рис. 2(d), получены путем извлечения значений интенсивности вдоль центральной горизонтальной оси рис. 2(c).
Полученная картина интерференционных полос и распределение интенсивности, показанное на рис. 2(в, г) с помощью предлагаемого метода, сравниваются с таковыми для традиционно установленной прямолинейной дифракции Френеля 21 , показанной на рис. 1. Сравнение подтверждает, что существуют сходство и близкое соответствие между традиционным и предлагаемым случаями краевой дифракции.Полосы, полученные предложенным методом, имеют искривленную форму, а чередующиеся полосы проявляют более высокую интенсивность, чем предыдущие. Причина такого изогнутого вида полос и изменения амплитуды чередующихся полос связана с тем, что край фотодетектора, использованного в этом исследовании, представляет собой не совсем один прямой край, а изогнутый край. Кривые ребра можно рассматривать как состоящие из бесконечного числа бесконечно малых прямых ребер, имеющих разную ориентацию. Из-за этого внутри фотодетектора в разных ориентациях формируются разные прямолинейные дифракционные картины, которые интерферируют между собой.Это чаще встречается в задачах дифракции и называется эффектом каустики 28,29 . Сравнение качественно показало, что сходства намного больше, чем различий, за исключением очевидной кривизны. Никакого другого прямого сравнения в традиционной литературе и искусстве не существует.
1. Сравнение подтверждает, что существуют сходство и близкое соответствие между традиционным и предлагаемым случаями краевой дифракции.Полосы, полученные предложенным методом, имеют искривленную форму, а чередующиеся полосы проявляют более высокую интенсивность, чем предыдущие. Причина такого изогнутого вида полос и изменения амплитуды чередующихся полос связана с тем, что край фотодетектора, использованного в этом исследовании, представляет собой не совсем один прямой край, а изогнутый край. Кривые ребра можно рассматривать как состоящие из бесконечного числа бесконечно малых прямых ребер, имеющих разную ориентацию. Из-за этого внутри фотодетектора в разных ориентациях формируются разные прямолинейные дифракционные картины, которые интерферируют между собой.Это чаще встречается в задачах дифракции и называется эффектом каустики 28,29 . Сравнение качественно показало, что сходства намного больше, чем различий, за исключением очевидной кривизны. Никакого другого прямого сравнения в традиционной литературе и искусстве не существует. Однако исследования, проведенные П. М. Ринаром 30 в 1976 г. на крупномасштабных дифракционных картинах от круглых объектов, также подтверждают данные, представленные на рис. 2(d). Чтобы еще больше подтвердить эти данные, можно рассмотреть эквивалентную муаровую картину, нарисовав на экране наблюдения разные полосы прямых краев вдоль всей ориентации изогнутого края, что приведет к данным, подобным показанным на рис.2(с).
Однако исследования, проведенные П. М. Ринаром 30 в 1976 г. на крупномасштабных дифракционных картинах от круглых объектов, также подтверждают данные, представленные на рис. 2(d). Чтобы еще больше подтвердить эти данные, можно рассмотреть эквивалентную муаровую картину, нарисовав на экране наблюдения разные полосы прямых краев вдоль всей ориентации изогнутого края, что приведет к данным, подобным показанным на рис.2(с).
Предлагаемая система краевой дифракции обладает многочисленными преимуществами по сравнению с другими традиционными методами, такими как интерферометры. Основным преимуществом этого метода является простота его реализации, когда нет необходимости в оптике. Традиционные методы включают использование высококачественных оптических элементов, таких как линза, светоделитель, зеркало, и, следовательно, существуют связанные с этим сложности, такие как оптические проблемы выравнивания, аберрации и астигматизма. Традиционные интерферометры требуют относительно мощных лазерных источников, поскольку свет проходит несколько путей через светоделители и, следовательно, связанные с этим потери интенсивности света неизбежны. Другими важными преимуществами являются (i) экономичность и меньшая чувствительность к экологическим и тепловым проблемам, поскольку не используется дополнительная оптика, (ii) возможность оценить радиус кривизны изогнутой дифракционной кромки, (iii) не зависит от свойства материала дифрагирующей кромки, независимо от того, является ли он проводящим или непроводящим, отражающим или поглощающим, металлическим или неметаллическим и т. д. Наиболее спонтанным неотъемлемым преимуществом является то, что предлагаемая система краевой дифракции имеет сравнимую более высокую интенсивность дифрагированной волны с прямой геометрической волной и следовательно, можно наблюдать четкие полосовые узоры, поскольку дифракционная кромка встроена в экран наблюдения фотодетектора.
Другими важными преимуществами являются (i) экономичность и меньшая чувствительность к экологическим и тепловым проблемам, поскольку не используется дополнительная оптика, (ii) возможность оценить радиус кривизны изогнутой дифракционной кромки, (iii) не зависит от свойства материала дифрагирующей кромки, независимо от того, является ли он проводящим или непроводящим, отражающим или поглощающим, металлическим или неметаллическим и т. д. Наиболее спонтанным неотъемлемым преимуществом является то, что предлагаемая система краевой дифракции имеет сравнимую более высокую интенсивность дифрагированной волны с прямой геометрической волной и следовательно, можно наблюдать четкие полосовые узоры, поскольку дифракционная кромка встроена в экран наблюдения фотодетектора.
Предлагаемый метод имеет дополнительные преимущества по сравнению с системой квадрантного детектора. Квадрантный детектор имеет четыре ячейки, разделенные промежутком. Основным требованием для использования этого детектора является то, что световой луч должен освещаться во всех четырех квадрантах одновременно. Это условие вводит определенные ограничения в чувствительности, точности, динамическом диапазоне и, следовательно, в приложениях.
Это условие вводит определенные ограничения в чувствительности, точности, динамическом диапазоне и, следовательно, в приложениях.
Метод, рассмотренный выше в этой статье, находит ряд метрологических, гражданских и оборонных применений.Некоторыми из наиболее важных и ярких примеров являются (i) дистанционный мониторинг акустического сигнала, (ii) аппаратура для работы в качестве оптического микрофона, (iii) бесконтактная аппаратура для измерения перемещений объектов, (iv) аппаратура для работы в качестве оптический гидрофон для подводного акустического обнаружения, (v) аппаратура для подслушивания, (vi) аппаратура для обнаружения поверхностных волн, внутренних волн и любых гидродинамических возмущений в океане, (vii) аппаратура для обнаружения гравитационных волн (viii) аппаратура для обнаружения колебаний давления в любой оптически прозрачной среде (ix) аппаратура для обнаружения выживших из труднодоступных завалов, образовавшихся в результате стихийных бедствий и т. д.
Что такое рентгеноструктурный анализ (XRD) и как он работает?
Рентгеноструктурный анализ (XRD) — это метод, используемый в материаловедении для определения кристаллографической структуры материала.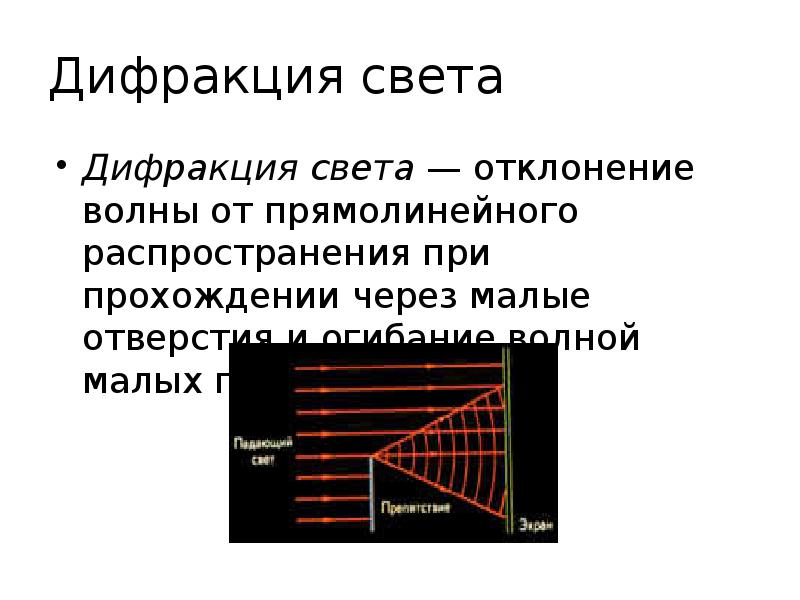 XRD работает, облучая материал падающими рентгеновскими лучами, а затем измеряя интенсивность и углы рассеяния рентгеновских лучей, которые покидают материал [1].
XRD работает, облучая материал падающими рентгеновскими лучами, а затем измеряя интенсивность и углы рассеяния рентгеновских лучей, которые покидают материал [1].
Нажмите здесь , чтобы посмотреть наши последние технические подкасты на YouTube .
Основным применением рентгеноструктурного анализа является идентификация материалов на основе их дифракционной картины.Помимо идентификации фаз, рентгеноструктурный анализ также дает информацию об отклонениях фактической структуры от идеальной из-за внутренних напряжений и дефектов [1].
Как это работает?
Кристаллы представляют собой регулярные массивы атомов, в то время как рентгеновские лучи можно рассматривать как волны электромагнитного излучения. Атомы кристаллов рассеивают падающие рентгеновские лучи, главным образом за счет взаимодействия с электронами атомов. Это явление известно как упругое рассеяние; электрон известен как рассеиватель.Регулярный массив рассеивателей создает регулярный массив сферических волн. В большинстве направлений эти волны компенсируют друг друга за счет деструктивной интерференции, однако они конструктивно складываются в нескольких конкретных направлениях, определяемых законом Брэгга:
В большинстве направлений эти волны компенсируют друг друга за счет деструктивной интерференции, однако они конструктивно складываются в нескольких конкретных направлениях, определяемых законом Брэгга:
2dsin θ = n λ
Где d — расстояние между дифрагирующими плоскостями, θ{\ displaystyle \ theta} — угол падения, n — целое число, а λ — длина волны луча.Определенные направления проявляются в виде пятен на дифракционной картине, называемых отражениями. Следовательно, картины дифракции рентгеновских лучей являются результатом электромагнитных волн, падающих на регулярную решетку рассеивателей.
Рентгеновские лучи используются для получения дифракционной картины, потому что их длина волны λ часто имеет тот же порядок величины, что и расстояние d между плоскостями кристалла (1-100 ангстрем).
Преимущества и области применения XRD
XRD — это неразрушающий метод, используемый для [2]:
Чем может помочь TWI?
TWI имеет долгую историю работы со своими членами в различных секторах промышленности по характеристике материалов, включая дифракцию рентгеновских лучей. Например, TWI поддержала компанию Wireline Technologies Ltd в разработке электронной упаковки для каротажа скважинных данных. Компания Wireline Technologies Ltd попросила TWI проанализировать образцы материалов, вышедших из строя. Этот анализ был выполнен с использованием рентгеновской дифракции и сканирующей электронной микроскопии и помог подтвердить характер и причину отказов, тем самым помогая Wireline Technologies выбрать наиболее подходящие материалы. для их приложений.
Например, TWI поддержала компанию Wireline Technologies Ltd в разработке электронной упаковки для каротажа скважинных данных. Компания Wireline Technologies Ltd попросила TWI проанализировать образцы материалов, вышедших из строя. Этот анализ был выполнен с использованием рентгеновской дифракции и сканирующей электронной микроскопии и помог подтвердить характер и причину отказов, тем самым помогая Wireline Technologies выбрать наиболее подходящие материалы. для их приложений.
В настоящее время TWI располагает современным усовершенствованным дифрактометром Bruker D8, который предлагает нашим членам следующие испытания и анализ:
- Идентификация фаз, качественная и количественная (XRPD)
– Анализ продуктов коррозии
– Анализ фаз в термически напыленных порошках
– Количественное определение фазового баланса (остаточный аустенит/дуплекс и т.д.) - Падение угла скольжения (GIXD) для анализа тонких слоев на поверхности.
– Фазы в тонких слоях
- XRR для измерения толщины слоя
– Неразрушающие измерения толщины
- Фазовые превращения при переменной влажности и температуре
- Измерения остаточных напряжений
– Измерения параметров решетки без напряжений
Пожалуйста, свяжитесь с нами, чтобы узнать больше о наших возможностях рентгеновской дифракции и о том, как мы можем удовлетворить потребности вашего бизнеса.


 04.05 “Оптика”
04.05 “Оптика”
 Продольный и поперечный эффекты
Допплера.
Продольный и поперечный эффекты
Допплера. Многослойные покрытия.
Многослойные покрытия.
 Релаксационные процессы. Уравнение
для матрицы плотности. Самосогласованные уравнения для поля,
поляризации и разности заселенностей. Эффект насыщения.
Релаксационные процессы. Уравнение
для матрицы плотности. Самосогласованные уравнения для поля,
поляризации и разности заселенностей. Эффект насыщения.
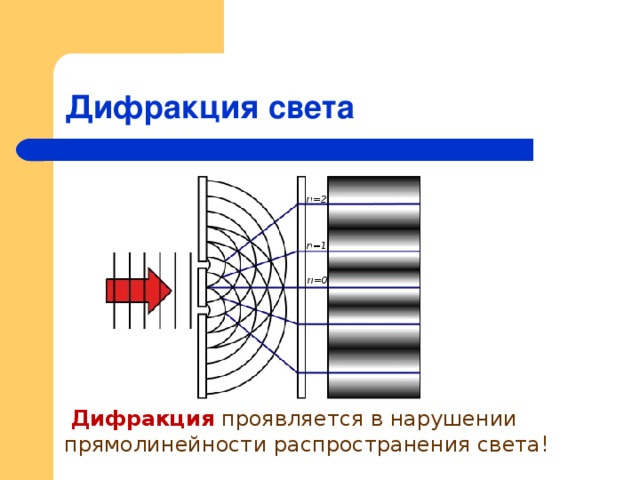 Параметрическое преобразование
частоты. Самофокусировка света. Вынужденное и комбинационное
рассеяние. Вынужденное рассеяние Мандельштама-Бриллюэна.
Четырехволновое взаимодействие. Обращение волнового фронта.
Вещество в сверхсильном световом поле.
Параметрическое преобразование
частоты. Самофокусировка света. Вынужденное и комбинационное
рассеяние. Вынужденное рассеяние Мандельштама-Бриллюэна.
Четырехволновое взаимодействие. Обращение волнового фронта.
Вещество в сверхсильном световом поле. Дробовой
шум.
Дробовой
шум.

 Поглощение в инфракрасной
области спектра и взаимодействие света с фононной
подсистемой. Переходы в электронной подсистеме. Поглощение
света в металлах. Запрещенная зона и область прозрачности в
диэлектриках. Экситоны Ванье-Мотта и Френкеля. Область
фундаментального поглощения. Переходы с остовных уровней.
Эффекты Оже и Фано. Эффекты на краях остовного поглощения:
EXAFS и XANES. Понятие о поляритонах. Спектроскопия
дефектных состояний в кристаллах. Автолокализация экситонов
и дырок в диэлектриках. Вторичные эффекты в кристаллах:
люминесценция, фотоэмиссия, дефектообразование под действием
света.
Поглощение в инфракрасной
области спектра и взаимодействие света с фононной
подсистемой. Переходы в электронной подсистеме. Поглощение
света в металлах. Запрещенная зона и область прозрачности в
диэлектриках. Экситоны Ванье-Мотта и Френкеля. Область
фундаментального поглощения. Переходы с остовных уровней.
Эффекты Оже и Фано. Эффекты на краях остовного поглощения:
EXAFS и XANES. Понятие о поляритонах. Спектроскопия
дефектных состояний в кристаллах. Автолокализация экситонов
и дырок в диэлектриках. Вторичные эффекты в кристаллах:
люминесценция, фотоэмиссия, дефектообразование под действием
света.
 Закон Вавилова. Триплетные состояния молекул и их
роль в процессах деградации и миграции энергии электронного
возбуждения. Схема Теренина-Льюиса. Тушение (температурное,
концентрационное, посторонними веществами) люминесценции.
Безызлучательный перенос энергии электронного возбуждения.
Люминесценция молекулярных кристаллов. Теория Давыдова.
Кооперативные процессы в люминесценции.
Закон Вавилова. Триплетные состояния молекул и их
роль в процессах деградации и миграции энергии электронного
возбуждения. Схема Теренина-Льюиса. Тушение (температурное,
концентрационное, посторонними веществами) люминесценции.
Безызлучательный перенос энергии электронного возбуждения.
Люминесценция молекулярных кристаллов. Теория Давыдова.
Кооперативные процессы в люминесценции.
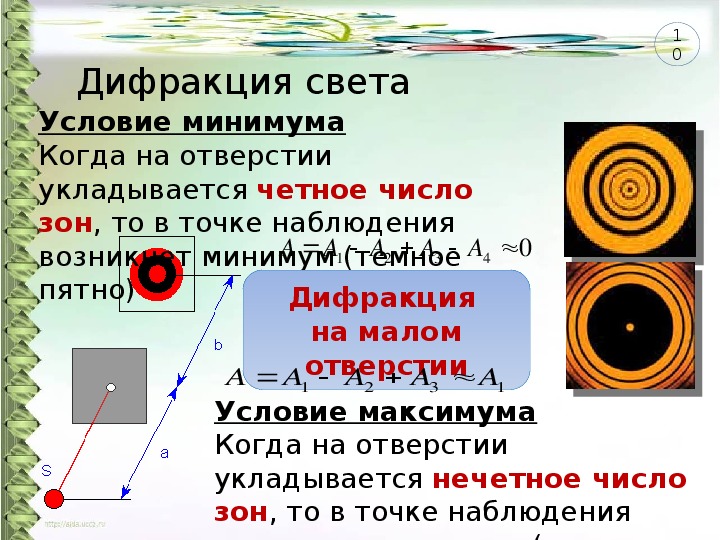 Приборы
с зарядовой связью (ПЗС) – линейки, матрицы.
Приборы
с зарядовой связью (ПЗС) – линейки, матрицы.
 Направленные
ответвители. Волоконные линии связи. Нелинейные эффекты в
оптических волокнах.
Направленные
ответвители. Волоконные линии связи. Нелинейные эффекты в
оптических волокнах.
 , Путхоф Г. Основы квантовой электроники. М.:
Мир, 1972.
, Путхоф Г. Основы квантовой электроники. М.:
Мир, 1972.

 М., 1999.
М., 1999.
 6.
6. 340, pp. 012099 (1-9).
340, pp. 012099 (1-9). 181 (39-40), p. 1764 – 1770.
181 (39-40), p. 1764 – 1770. Phys.: Condens. Matter, 2010, v.22, p.115601 (1-5).
Phys.: Condens. Matter, 2010, v.22, p.115601 (1-5). A.Babushkina, O.Yu.Gorbenko, M.S.Kartavtseva, A.R.Kaul “Effect of Isotopic Composition and Microstructure on the Crystalline and Magnetic Phase States in R0.5Sr0.5MnO3” JETP, 2008, Vol. 106, No. 3, pp. 528–541.
A.Babushkina, O.Yu.Gorbenko, M.S.Kartavtseva, A.R.Kaul “Effect of Isotopic Composition and Microstructure on the Crystalline and Magnetic Phase States in R0.5Sr0.5MnO3” JETP, 2008, Vol. 106, No. 3, pp. 528–541. Rev. B, 2008, v.78, p. 024426 (1-12).
Rev. B, 2008, v.78, p. 024426 (1-12).
 1989. Современная порошковая дифракция. Обзоры по миэнралогии, т. 20. Минералогическое общество Америки.
1989. Современная порошковая дифракция. Обзоры по миэнралогии, т. 20. Минералогическое общество Америки. Инженерное применение петрологии. Эта задача развивает навыки рентгеноструктурного анализа применительно к минералогии глин, закрепляет лекционный материал по геохимии выветривания и демонстрирует роль петрологической характеристики в проектировании участка.
Инженерное применение петрологии. Эта задача развивает навыки рентгеноструктурного анализа применительно к минералогии глин, закрепляет лекционный материал по геохимии выветривания и демонстрирует роль петрологической характеристики в проектировании участка. 43 № 5, 466–470.
43 № 5, 466–470. .81-90.
.81-90. Написана лаконичной и ясной прозой. Текст создает целостную картину XRD. После прочтения этой книги исследователи смогут понять основы многих материаловедческих и инженерных исследовательских работ. . . . Рентгеновская дифракция (XRD) — это мощный неразрушающий метод характеризации для определения структуры, фазы, состава и деформации материалов. Это один из наиболее часто используемых методов для характеристики материалов. Эта книга отличается от других книг по этой теме упрощенным изложением и охватом анализа тонких пленок.Он в значительной степени сводит к минимуму математику и обильно иллюстрирован, что делает его хорошей отправной точкой для изучения основных принципов XRD. Определены и объяснены общие тонкопленочные структуры (случайные поликристаллические, текстурированные) и их отношения с подложкой (деформация, вращение в плоскости). Это делает его ценным для исследователей, изучающих осаждение тонких пленок. В книгу включены примеры задач для закрепления изученных понятий, а также задачи, которые можно задать в качестве домашнего задания».
Написана лаконичной и ясной прозой. Текст создает целостную картину XRD. После прочтения этой книги исследователи смогут понять основы многих материаловедческих и инженерных исследовательских работ. . . . Рентгеновская дифракция (XRD) — это мощный неразрушающий метод характеризации для определения структуры, фазы, состава и деформации материалов. Это один из наиболее часто используемых методов для характеристики материалов. Эта книга отличается от других книг по этой теме упрощенным изложением и охватом анализа тонких пленок.Он в значительной степени сводит к минимуму математику и обильно иллюстрирован, что делает его хорошей отправной точкой для изучения основных принципов XRD. Определены и объяснены общие тонкопленочные структуры (случайные поликристаллические, текстурированные) и их отношения с подложкой (деформация, вращение в плоскости). Это делает его ценным для исследователей, изучающих осаждение тонких пленок. В книгу включены примеры задач для закрепления изученных понятий, а также задачи, которые можно задать в качестве домашнего задания».
 д.)
д.)