Контрольная работа по физике Применение законов Ньютона 10 класс
Контрольная работа по физике Применение законов Ньютона 10 класс с ответами. Контрольная работа включает 4 варианта, в каждом варианте по 6 заданий.
1 вариант
1. Рассчитайте силу, которая необходима для равномерного подъема вагонетки массой 600 кг по эстакаде с углом наклона 20°. Трением пренебречь.
2. Каков вес груза массой 10 кг, находящегося на подставке, движущейся вверх с ускорением 2,5 м/с2?
3. С сортировочной горки, высота которой равна 40 м, а длина — 400 м, начинает спускаться вагон. Определите скорость вагона в конце сортировочной горки, если коэффициент сопротивления движению вагона равен 0,05.
4. Мальчик массой 50 кг качается на качелях, длина подвеса которых равна 4 м. С какой силой он давит на сиденье при прохождении среднего положения со скоростью 6 м/с?
5. С наклонной плоскости, угол наклона которой 45°, соскальзывают два груза массой 2 кг (движется первым) и 1 кг, соединенные пружиной жесткостью 100 Н/м. Коэффициенты трения между грузами и плоскостью равны соответственно 0,2 и 0,5. Найдите растяжение пружины при соскальзывании грузов.
6. Брусок массой 400 г под действием груза массой 100 г (рис. 60) проходит из состояния покоя путь 80 см за 2 с. Найдите коэффициент трения.
2 вариант
1. Рассчитайте силу, которую необходимо приложить, чтобы поднять по наклонной плоскости тело массой 7 кг с ускорением 2,4 м/с2, если угол наклона наклонной плоскости к горизонту равен 15°. Трение не учитывать.
2. С какой силой космонавт массой 70 кг, находящийся в космическом корабле, движущемся вверх с ускорением 40 м/с2, давит на кресло кабины?
3. Лифт опускается равноускоренно и в первые 10 с проходит 10 м. На сколько уменьшится вес пассажира массой 70 кг, который находится в этом лифте?
4. Рассчитайте ускорение, с которым тело соскальзывает с наклонной плоскости, имеющей угол наклона 30°, если коэффициент трения равен 0,2.
5. Брусок начинает соскальзывать с вершины наклонной плоскости, имеющей высоту 10 ми угол наклона 30°. Какова скорость тела в конце спуска и продолжительность спуска, если коэффициент трения тела о плоскость равен 0,1?
6.Определите ускорение и силы натяжения нитей (рис. 61), если массы грузов равны m1 = 3 кг, m2 = 4 кг, m3 = 5 кг, а угол наклона α = 30°. Коэффициент трения равен 0,2.
3 вариант
1. Брусок начинает соскальзывать с наклонной плоскости, имеющей угол наклона 30°. Найдите ускорение, с которым движется тело. Трение не учитывать.
2. Определите массу тела, которое в лифте, движущемся вниз с ускорением 5 м/с2, имеет вес, равный 100 H.
3.Груз массой 50 кг находится на наклонной плоскости длиной 5 ми высотой 3 м. Найдите силу, необходимую для перемещения груза вверх по наклонной плоскости с ускорением 1 м/с2, зная, что коэффициент трения равен 0,2.
4. Велосипедист массой 80 кг двигается по аттракциону «мертвая петля» со скоростью 54 км/ч. Радиус петли равен 4,5 м. Найдите вес велосипедиста в верхней точке петли.
5. Тело брошено вверх по наклонной плоскости с углом 28°. Найдите время подъема тела до остановки и время спуска, если начальная скорость тела равна 13 м/с, а коэффициент трения — 0,2.
6. Определите путь, пройденный телом m1 за 0,2 с, если коэффициент трения его на наклонной плоскости равен 0,1 (рис. 62), m1 = 1 кг, m2 = 6 кг, α = 30°.
4 вариант
1. С наклонной плоскости, имеющей угол наклона 40°, соскальзывает тело массой 10 кг. Определите силу трения, если ускорение тела равно 2 м/с2.
2. Ракета на старте с поверхности Земли движется вертикально вверх с ускорением 20 м/с2. Каков вес космонавта массой 80 кг?
3.
4. Трамвайный вагон массой 15 т движется по выпуклому мосту радиусом кривизны 50 м. Определите скорость трамвая, если его вес на середине моста равен 102 кН.
5. Для удержания груза на наклонной плоскости, имеющей при основании угол 30°, необходимо приложить силу, равную 40 Н, направленную вдоль наклонной плоскости. А для равномерного подъема этого груза вверх по наклонной плоскости надо приложить силу, равную 80 Н. Рассчитайте коэффициент трения.
6. К концам невесомой нерастяжимой нити, перекинутой через невесомый неподвижный блок, подвешены два груза массами по 100 г каждый. На один из грузов положен перегрузок массой 50 г. При этом вся система приходит в движение. Найдите ускорение, с которым движутся грузы и перегрузок.
Какова сила натяжения нити?
Ответы на контрольную работу по физике Применение законов Ньютона 10 класс
1. ≈ 2050 Н
2. 125 Н
3. ≈ 20 м/с
4. 950 Н
5. ≈ 0,014 м
6. 0,2
2 вариант
1. 35 Н
2. 3,5 Кн
3. 14 Н
4. 3,4 м/с2
5. ≈ 13 м/с; ≈ 3 с
6. 0,25 м/с2; 47,75 Н; 20,5 Н
3 вариант
1. 5 м/с2
2. 20 кг
3. ≈ 430 Н
4. 3,2 кН
5. 2 с; ≈ 3 с
6. 15,5 см
4 вариант
1. ≈ 44 Н
2. 2,4 кН
3. ≈ 48 Н
4. 12,25 м/с
5. ≈ 0,19
6. 1,96 м/с2; 1,18 Н
PDF-версия
Контрольная работа Применение законов Ньютона 10 класс
(183 Кб, pdf)
Курс общей физики, Т.1
Курс общей физики, Т.1
ОглавлениеПРЕДИСЛОВИЕМЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ВВЕДЕНИЕ ЧАСТЬ 1.  ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ§ 2. Некоторые сведения о векторах § 3. Скорость § 4. Ускорение § 5. Кинематика вращательного движения ГЛАВА II. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 6. Классическая механика. Границы ее применимости § 7. Первый закон Ньютона. Инерциальные системы отсчета § 8. Масса и импульс тела § 9. Второй закон Ньютона § 10. Единицы и размерности физических величин § 11. Третий закон Ньютона § 12. Принцип относительности Галилея § 13. Силы § 14. Упругие силы § 15. Силы трения. § 16, Сила тяжести и вес § 17. Практическое применение законов Ньютона ГЛАВА III. ЗАКОНЫ СОХРАНЕНИЯ § 18. Сохраняющиеся величины § 19. Кинетическая энергия § 21. Консервативные силы § 22. Потенциальная энергия во внешнем поле сил § 23. Потенциальная энергия взаимодействия § 24. Закон сохранения энергии § 25. Энергия упругой деформации § 26. Условия равновесия механической системы § 27.  Закон сохранения импульса§ 28. Соударение двух тел § 29. Закон сохранения момента импульса § 30. Движение в центральном поле сил § 31. Задача двух тел ГЛАВА IV. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА § 32. Силы инерции § 33. Центробежная сила инерции § 34. Сила Кориолиса ГЛАВА V. МЕХАНИКА ТВЕРДОГО ТЁЛА § 36. Движение твердого тела § 37. Движение центра масс твердого тела § 38. Вращение тела вокруг неподвижной оси § 39. Момент инерции § 40. Понятие о тензоре инерции § 41. Кинетическая энергия вращающегося твердого тела § 42. Кинетическая энергия тела при плоском движении § 43. Применение закона динамики твердого тела § 44. Гироскопы ГЛАВА VI. ВСЕМИРНОЕ ТЯГОТЕНИЕ § 45. Закон всемирного тяготения § 46. Гравитационное поле § 47. Принцип эквивалентности § 48. Космические скорости ГЛАВА VII. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. Общие сведения о колебаниях  Малые колебания§ 51. Комплексные числа § 52. Линейные дифференциальные уравнения § 53. Гармонические колебания § 54. Маятник § 55. Векторная диаграмма § 56. Биения § 57. Сложение взаимно перпендикулярных колебаний § 58. Затухающие колебания § 59. Автоколебания § 60. Вынужденные колебания § 61. Параметрический резонанс ГЛАВА VIII. РЕЛЯТИВИСТСКАЯ МЕХАНИКА § 62. Специальная теория относительности § 63. Преобразования Лоренца § 64. Следствия из преобразований Лоренца § 65. Интервал § 66. Преобразование и сложение скоростей § 67. Релятивистское выражение для импульса § 69. Преобразования импульса и энергии § 70. Взаимосвязь массы и энергии § 71. Частицы с нулевой массой покоя ГЛАВА IX. ГИДРОДИНАМИКА § 72. Линии и трубки тока. Неразрывность струи § 73. Уравнение Бернулли § 74. Истечение жидкости из отверстия § 75. Силы внутреннего трения § 76.  Ламинарное и турбулентное течения§ 77. Течение жидкости в круглой трубе § 78. Движение тел в жидкостях и газах ЧАСТЬ 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 79. Статистическая физика и термодинамика § 80. Масса и размеры молекул § 82. Внутренняя энергия системы § 83. Первое начало термодинамики § 84. Работа, совершаемая телом при изменениях объема § 85. Температура § 86. Уравнение состояния идеального газа § 87. Внутренняя энергия и теплоемкость идеального газа § 88. Уравнение адиабаты идеального газа § 89. Политропические процессы § 90. Работа, совершаемая идеальным газом при различных процессах § 91. Ван-дер-ваальсовский газ § 92. Барометрическая формула ГЛАВА XI. СТАТИСТИЧЕСКАЯ ФИЗИКА § 93. Некоторые сведения из теории вероятностей § 94. Характер теплового движения молекул § 95. Число ударов молекул о стенку § 96. Давление газа на стенку § 98.  Распределение Максвелла§ 99. Экспериментальная проверка закона распределения Максвелла § 100. Распределение Больцмана § 101. Определение Перреном числа Авогадро § 102. Макро- и микросостояния. Статистический вес § 103. Энтропия ГЛАВА XII. ТЕРМОДИНАМИКА § 104. Основные законы термодинамики § 105. Цикл Карно § 106. Термодинамическая шкала температур § 107. Примеры на вычисление энтропии § 108. Некоторые применения энтропии § 109. Термодинамические потенциалы ГЛАВА XIII. КРИСТАЛЛИЧЕСКОЕ СОСТОЯНИЕ § 110. Отличительные черты кристаллического состояния § 111. Классификация кристаллов § 112. Физические типы кристаллических решеток § 113. Дефекты в кристаллах § 114. Теплоемкость кристаллов ГЛАВА XIV. ЖИДКОЕ СОСТОЯНИЕ § 115. Строение жидкостей § 116. Поверхностное натяжение § 117. Давление под изогнутой поверхностью жидкости § 118. Явления на границе жидкости и твердого тела § 119. Капиллярные явления ГЛАВА XV.  ФАЗОВЫЕ РАВНОВЕСИЯ И ПРЕВРАЩЕНИЯ§ 121. Испарение и конденсация § 122. Равновесие жидкости и насыщенного пара § 123. Критическое состояние § 124. Пересыщенный пар и перегретая жидкость § 125. Плавление и кристаллизация § 126. Уравнение Клапейрона—Клаузиуса § 127. Тройная точка. Диаграмма состояния ГЛАВА XVI. ФИЗИЧЕСКАЯ КИНЕТИКА § 128. Явления переноса § 129. Средняя длина свободного пробега § 130. Диффузия в газах § 131. Теплопроводность газов § 132. Вязкость газов § 133. Ультраразреженные газы § 134. Эффузия ПРИЛОЖЕНИЯ I. Вычисление некоторых интегралов II. Формула Стирлинга III. Симметричные тензоры второго ранга |
В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие.— 2-е изд., перераб.—М.: Наука. Главная редакция физико-математической литературы, 1982.— 432 с.
6: Применение законов Ньютона
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4005
- OpenStax
- OpenStax
Автомобильные гонки в последние годы стали очень популярными.
Когда каждая машина движется по криволинейной траектории вокруг поворота, ее колеса также быстро вращаются. Колеса совершают много оборотов, в то время как автомобиль совершает только часть одного (дуга окружности). Как мы можем описать скорости, ускорения и действующие силы? Какая сила удерживает гоночный автомобиль от разворота и удара о стену, граничащую с трассой? Что обеспечивает эту силу? Почему трек забанен? Мы ответим на все эти вопросы в этой главе, расширяя наше рассмотрение законов движения Ньютона.
-
- 6.1: Прелюдия к применению законов Ньютона
- Популярность автомобильных гонок в последние годы возросла. Когда каждая машина движется по криволинейной траектории вокруг поворота, ее колеса также быстро вращаются. Колеса совершают много оборотов, в то время как автомобиль совершает только часть одного (дуга окружности). Как мы можем описать скорости, ускорения и действующие силы? Какая сила удерживает гоночный автомобиль от разворота и удара о стену, граничащую с трассой? Что обеспечивает эту силу? Почему трек забанен? Мы ответим на все эти вопросы в этой главе, расширяя нашу с
-
- 6.
2: Решение задач с помощью законов Ньютона (часть 1) - Законы движения Ньютона можно применять во многих ситуациях для решения задач движения. Некоторые задачи содержат несколько векторов силы, действующих на объект в разных направлениях.
- 6.
-
- 6.3: Решение задач с законами Ньютона (часть 2)
- Некоторые задачи движения содержат несколько физических величин, таких как силы, ускорение, скорость или положение. Для их решения можно применить концепции кинематики и динамики.
-
- 6.4: Трение (Часть 1)
- Когда тело движется, оно испытывает сопротивление, потому что тело взаимодействует с окружающей средой. Это сопротивление есть сила трения. Трение препятствует относительному движению между соприкасающимися системами, но также позволяет нам двигаться — концепция, которая становится очевидной, если вы попытаетесь пройтись по льду. Трение — распространенная, но сложная сила, и ее поведение до сих пор полностью не изучено.
Тем не менее, можно понять обстоятельства, в которых он себя ведет.
-
- 6.5: Трение (Часть 2)
- Простое трение всегда пропорционально нормальной силе. Когда предмет находится не на горизонтальной поверхности, как в случае с наклонной плоскостью, необходимо найти силу, действующую на предмет, направленную перпендикулярно поверхности.
-
- 6.6: Центростремительная сила
- Центростремительная сила – это сила, направленная к центру, которая всегда направлена к центру вращения, поэтому она перпендикулярна линейной скорости. Вращающаяся и ускоренная системы отсчета неинерциальны. Силы инерции, такие как сила Кориолиса, необходимы для объяснения движения в таких системах отсчета.
-
- 6.7: Сила сопротивления и конечная скорость
- Силы сопротивления, действующие на объект, движущийся в жидкости, противодействуют движению. Для более крупных объектов (таких как бейсбольный мяч), движущихся со скоростью в воздухе, сила сопротивления определяется с использованием коэффициента сопротивления, площади объекта, обращенной к жидкости, и плотности жидкости.
Для небольших объектов (таких как бактерия), движущихся в более плотной среде, сила сопротивления определяется законом Стокса.
-
- 6.E: Применение законов Ньютона (упражнения)
-
- 6.S: Применение законов Ньютона (Резюме)
Миниатюра: серийные автомобили, участвовавшие в гонках Grand National Divisional на Iowa Speedway 2 мая 015. Автомобили часто развивают скорость до 200 миль в час. (320 км/ч).
Эта страница под названием 6: Применение законов Ньютона распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
-
- Теги
-
- [email protected]://openstax.
org/details/books/university-physics-volume-1
- [email protected]://openstax.
Применение законов Ньютона | Инженерная библиотека
На этой странице представлена глава о применении законов Ньютона из «Справочника по основам Министерства энергетики: классическая физика», DOE-HDBK-1010-92, Министерство энергетики США, июнь 1992 г.
Другие связанные главы из «Справочника по основам Министерства энергетики: классическая физика» можно увидеть справа.
Сила и вес
Силу можно рассматривать просто как толчок или тягу, но более четко ее можно определить как любое действие на тело, которое стремится изменить скорость тела. Вес — это сила, действующая на объект из-за положения объекта в гравитационном поле.
Введение
При изучении сил учащийся должен делать обоснованные предположения, требуемые при постановке реальных задач. Способность понимать и использовать правильные предположения при постановке и решении инженерных задач, безусловно, является одной из самых важных способностей успешного оператора.
Одна из целей данного пособия — предоставить возможность развить эту способность посредством изучения основ и анализа практических задач.
Необходим эффективный метод решения всех инженерных проблем. Выработка хороших привычек формулировать проблемы и представлять их решения окажется ценным активом. Каждое решение должно представлять собой логическую последовательность шагов от гипотезы к заключению, а его представление должно включать четкое изложение следующих частей, каждая из которых четко определена: а) данные, б) желаемые результаты, в) необходимые диаграммы, г) расчеты. д) ответы и выводы. Многие проблемы становятся ясными и прямолинейными, когда они начинаются с логического и дисциплинированного метода атаки.
Предмет классической физики основан на удивительно небольшом количестве фундаментальных понятий и включает главным образом применение этих основных соотношений к множеству ситуаций. Законы движения Ньютона являются одними из фундаментальных понятий, используемых при изучении силы и веса.
Сила
Сила определяется как векторная величина, стремящаяся вызвать ускорение тела в направлении его приложения. Изменение скорости тела вызывает ускорение тела. Следовательно, сила может быть математически определена как заданная вторым законом движения Ньютона (уравнение 4-1).
F = ма
(4-1)
где:
| Ф | = | сила, действующая на объект (Ньютон или фунт-сила) |
| м | = | масса объекта (кг или фунт) |
| и | = | ускорение объекта (м/сек 2 или фут/сек 2 ) |
Сила характеризуется точкой приложения, величиной и направлением. Сила, фактически распределенная по небольшому участку тела, на который она воздействует, может считаться сосредоточенной силой, если размеры затрагиваемой области малы по сравнению с другими соответствующими размерами.
Две или более сил могут действовать на объект, не влияя на его состояние движения.
Например, на книгу, лежащую на столе, действует направленная вниз сила, вызванная гравитацией, и восходящая сила, действующая на нее со стороны столешницы. Эти две силы компенсируются, и результирующая сила книги равна нулю. Этот факт можно проверить, заметив, что никакого изменения состояния движения не произошло.
Масса
Вес есть особое применение понятия силы. Он определяется как сила, действующая на объект со стороны гравитационного поля Земли, или, точнее, сила притяжения Земли к телу.
$$ W = {мг \над g_c} $$
(4-2)
где:
| Ш | = | вес (фунт) |
| м | = | масса (фунты) объекта |
| г | = | местное ускорение свободного падения (32,17 фут/сек 2 ) |
| г с | = | постоянная преобразования, используемая для облегчения использования второго закона Ньютона в английской системе единиц и равная 32,17 фут-фунт/фунт-сила-сек 2 |
Обратите внимание, что g c имеет то же числовое значение, что и ускорение свободного падения на уровне моря.
Масса тела одинакова, где бы оно ни находилось, будь то на Луне или на Земле. Однако вес тела зависит от местного ускорения силы тяжести. Таким образом, вес объекта на Луне меньше, чем на Земле, потому что локальное ускорение свободного падения на Луне меньше, чем на Земле.
Пример: 92 } } \номер \\ &=& 28,19 ~\text{фунт-сила} \end{эквнаррай} $$
Поняв идею массы и веса, особенно их различия, легче объяснить концепцию гравитационной силы. Любой брошенный объект будет ускоряться при падении, даже если он не находится в физическом контакте с каким-либо другим телом. Чтобы объяснить это, была разработана идея гравитационной силы, в результате чего появилось представление о том, что одно тело, такое как Земля, оказывает силу на другое тело, даже если они находятся далеко друг от друга. Гравитационное притяжение двух объектов зависит от массы каждого и расстояния между ними. Эта концепция известна как закон тяготения Ньютона, который был представлен в предыдущей главе.
У нас есть несколько структурных калькуляторов на выбор. Здесь только несколько:
- Калькулятор луча
- Калькулятор болтовых соединений
- Распределение силы болтового соединения
- Калькулятор зажимов
- Калькулятор потери устойчивости колонны
- Калькулятор роста усталостной трещины
Диаграммы свободного тела
При изучении действия сил на тело необходимо выделить тело и определить все силы, действующие на него. Этот метод использования диаграммы свободного тела необходим для понимания основных и сложных силовых задач.
При решении задачи, связанной с силами, необходимо тщательно помнить законы Ньютона и применять эти принципы буквально и точно. При применении этих принципов существенно, чтобы тело было изолировано от всех других тел, чтобы можно было рассмотреть полный и точный учет всех сил, действующих на это тело. Диаграмма такого изолированного тела с изображением всех внешних сил, действующих на него, называется диаграммой свободного тела 9019.
9 . Давно установлено, что метод диаграмм свободного тела является ключом к пониманию инженерных задач. Это потому, что изоляция тела — это инструмент, который четко разделяет причину и следствие и фокусирует наше внимание на буквальном применении принципа.
Пример:
Рассмотрим книгу, лежащую на столе на рис. 1. Хотя книга неподвижна, на нее действуют две силы, удерживающие ее в неподвижном состоянии. Одним из них является вес (W) книги, оказывающей давление на стол. Другая — это сила, с которой стол удерживает книгу на месте. Эта сила известна как нормальная сила (Н) и равна весу книги. Нормальная сила определяется как любая перпендикулярная сила, с которой любые две поверхности прижимаются друг к другу. Диаграмма свободного тела для этой ситуации, показанная справа на рисунке 1, изолирует книгу и представляет силы, действующие на объект.
Рисунок 1: Книга на столеПостроение диаграммы свободного тела
При построении диаграммы свободного тела обычно выполняются следующие шаги.
| Шаг 1. | Определите, какое тело или комбинацию тел следует изолировать. Выбранное тело обычно включает одну или несколько желаемых неизвестных величин. |
| Шаг 2. | Затем изолируйте выбранное тело или комбинацию тел с помощью диаграммы, представляющей его полные внешние границы. |
| Шаг 3. | Изобразите все силы, действующие на изолированное тело, приложенные удаленными контактирующими и притягивающими телами в их надлежащих положениях на схеме изолированного тела. Не показывайте силы, которые объект воздействует на что-либо еще, так как эти силы не действуют на сам объект. |
| Шаг 4. |
Укажите выбор координатных осей прямо на схеме. Соответствующие размеры также могут быть представлены для удобства. Обратите внимание, однако, что диаграмма свободного тела служит для того, чтобы сосредоточить внимание на действии внешних сил; поэтому схему не следует загромождать излишней информацией. Стрелки силы должны четко отличаться от других стрелок, чтобы избежать путаницы. Для этого можно использовать цветные карандаши.
|
Когда эти шаги будут выполнены, получится правильная диаграмма свободного тела, и учащийся может применить к диаграмме соответствующие уравнения, чтобы найти правильное решение.
Пример:
Автомобиль на рис. 2 буксируется силой некоторой величины. Постройте диаграмму свободного тела, показывающую все силы, действующие на автомобиль.
Рисунок 2: АвтомобильРешение:
Следуя шагам построения диаграммы свободного тела (показаны на рисунке 3), объект (автомобиль) выбирается и изолируется. Все силы, действующие на автомобиль, представлены с помощью соответствующих осей координат. Эти силы таковы:
| F Приложение | – | Сила, приложенная для буксировки автомобиля |
| Ф К | – | Сила трения, которая противодействует приложенной силе из-за веса автомобиля и характера поверхностей (автомобильных шин и дороги) |
| Ш | – | Вес автомобиля |
| Н | – | Нормальная сила, действующая на автомобиль со стороны дороги |
3: Схема свободного тела Сила трения (F K ) — это сила, противодействующая направлению движения. Эта сила объясняется более подробно в главе о типах сил.
Чтобы решить эту практическую задачу, учащийся присваивал значения каждой силе в соответствии с данными, приведенными в задаче. После назначения знака (например, + для сил, направленных вверх и вправо, – для сил, направленных вниз и влево), студент суммирует все силы, чтобы найти результирующую силу, действующую на тело. Используя эту информацию о результирующей силе и соответствующие уравнения, учащийся мог найти запрошенные неизвестные. В качестве варианта можно предложить учащемуся найти неизвестную силу, действующую на тело, при наличии достаточной информации о других силах, действующих на тело. Учащийся научится решать конкретные примеры с использованием диаграмм свободного тела в следующей главе.
Некоторые расширенные диаграммы свободного тела для различных типов систем показаны на рисунке 4.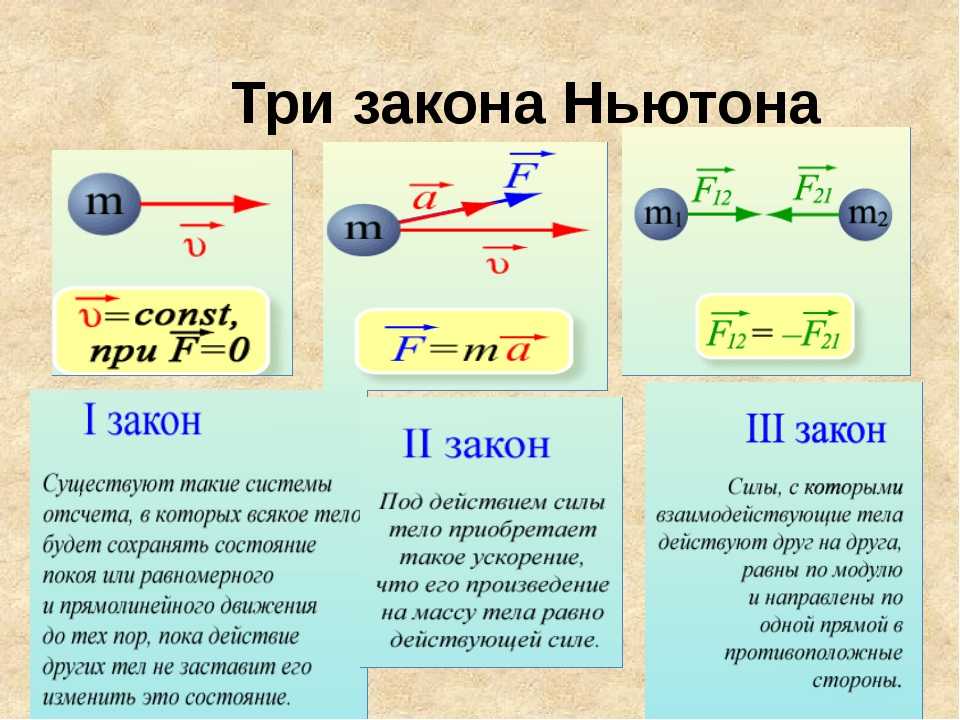
У нас есть несколько структурных калькуляторов на выбор. Здесь только несколько:
- Калькулятор луча
- Калькулятор болтовых соединений
- Распределение силы болтового соединения
- Калькулятор зажимов
- Калькулятор потери устойчивости колонны
- Калькулятор роста усталостной трещины
Равновесие сил
Знание сил, необходимых для поддержания объекта в равновесии, необходимо для понимания природы тел в состоянии покоя и в движении.
Чистая сила
Когда силы действуют на объект, результатом может быть изменение состояния движения объекта. Однако, если выполняются определенные условия, силы могут объединяться для поддержания состояния равновесия или баланса.
Чтобы определить, находится ли тело в равновесии, необходимо оценить суммарный эффект всех сил, действующих на него. Все силы, действующие на объект, в результате образуют по существу одну силу, влияющую на движение объекта.
Сила, являющаяся результатом всех сил, действующих на тело, определяется как чистая сила . Важно помнить, что силы являются векторными величинами. При анализе различных сил необходимо учитывать как величину (смещение) силы, так и направление приложения силы. Как описано в предыдущей главе, это лучше всего сделать с помощью диаграммы свободного тела.
Чтобы лучше понять это, рассмотрим книгу, лежащую на столе, в секции А на рис. 5.
Рисунок 5: Net Force
Книга остается неподвижной, опираясь на стол, потому что стол прикладывает нормальную силу, направленную вверх, равную весу книги. Следовательно, результирующая сила, действующая на книгу, равна нулю. Если к книге приложить силу (участок В на рис. 5) и пренебречь влиянием трения, результирующая сила будет равна приложенной силе, и книга будет двигаться в направлении приложенной силы. Диаграмма свободного тела в разделе C на рисунке 5 показывает, что вес (W) книги компенсируется нормальной силой (N) стола, поскольку они равны по величине, но противоположны по направлению.
Таким образом, результирующая (чистая) сила равна приложенной силе (F ПРИЛОЖЕНИЕ ).
Равновесие
Поскольку считается, что объект, находящийся в равновесии, находится в состоянии равновесия, можно предположить, что результирующая сила, действующая на объект, равна нулю. То есть, если векторная сумма всех сил, действующих на объект, равна нулю, то объект находится в равновесии.
Первый закон движения Ньютона описывает равновесие и действие силы на тело, находящееся в равновесии. Этот закон гласит: «Объект остается в покое (если изначально находился в покое) или движется по прямой линии с постоянной скоростью, если результирующая сила, действующая на него, равна нулю». Первый закон движения Ньютона также называют законом инерции. Инерция — это тенденция тела сопротивляться изменению состояния его движения.
Первое условие равновесия, являющееся следствием первого закона Ньютона, может быть записано в векторной форме: «Тело будет находиться в поступательном равновесии тогда и только тогда, когда векторная сумма сил, действующих на тело со стороны окружающей среды, равна нулю».
Например, если на тело действуют три силы, то для того, чтобы тело находилось в равновесии, необходимо, чтобы выполнялось следующее.
Ф 1 + F 2 + F 3 = 0
(4-3)
Это уравнение можно также записать следующим образом.
Σ F = 0
(4-4)
В эту сумму входят все силы, действующие на тело со стороны окружающей среды. Исчезновение этой векторной суммы является необходимым условием, называемым первым условием равновесия, которое должно быть выполнено, чтобы обеспечить поступательное равновесие. В трех измерениях (x, y, z) составные уравнения первого условия равновесия:
| Σ F X = 0 | Σ F Y = 0 | Σ F Z = 0 |
(4-5)
Это условие применяется к объектам, движущимся с постоянной скоростью, а также к телам, находящимся в покое или в статическом равновесии (называемым СТАТИКОЙ).
Применяя знание того, что объект, находящийся в равновесии, имеет результирующую силу, равную нулю, можно решить следующий пример:
Пример:
Объект на рисунке 6 имеет вес 125 фунтов силы.
Объект подвешен на тросах, как показано на рисунке. Рассчитайте натяжение (T 1 ) троса под углом 30° к горизонтали.
Натяжение кабеля — это сила, передаваемая кабелем. Натяжение в любой точке троса можно измерить, отрезав от него подходящую длину и вставив пружинную шкалу.
Рисунок 7: Диаграмма свободного телаРешение:
Поскольку объект и поддерживающие его тросы неподвижны (т. е. находятся в равновесии), мы знаем, что результирующая сила, действующая на пересечение тросов, равна нулю. Тот факт, что результирующая сила равна нулю, говорит нам, что сумма x-компонентов T 1 , T 2 и T 3 равна нулю, а сумма y-компонентов T 1 , T 2 и T 3 равно нулю.
Σ F x = T 1.x + T 2.x 9{\circ}) &=& 0 \номер \\ (T_1)(0.5) + (T_2)(0) + (125 ~\text{lbf})(-1) &=& 0 \nonumber \\ 0,5 ~T_1 – 125 ~\text{фунт-сила} &=& 0 \номер \\ 0,5 ~T_1 &=& 125 ~\text{lbf} \nonumber \\ T_1 &=& 250 ~\text{фунт-сила} \end{эквнаррай} $$
Более простой метод решения этой проблемы включает в себя присвоение знака диаграмме свободного тела и изучение направления сил.
Выбрав (+) в качестве восходящего направления и (-) в качестве нисходящего направления, учащийся может на экзамене определить, что 1) восходящая составляющая T 9{\circ}) – 125 ~\text{lbf} &=& 0 \nonumber \\ 0,5 ~T_1 &=& 125 ~\text{lbf} \nonumber \\ T_1 &=& 250 ~\text{фунт-сила} \end{эквнаррай} $$
Если сумма всех сил, действующих на тело, равна нулю, говорят, что тело находится в равновесии сил. Если сумма всех сил не равна нулю, любая сила или система сил, способная уравновесить систему, определяется как уравновешивающая .
Пример:
Автомобиль массой 2000 фунтов ускоряется (на поверхности без трения) со скоростью 2 фута/сек 2 . Какую силу необходимо приложить к автомобилю, чтобы он уравновешивал эту систему?
Решение:
а. Нарисуйте схему свободного тела.
Рисунок 8: Диаграмма свободного тела
б. Сила F 2 ДОЛЖНА быть приложена в направлении, противоположном F 1 , так, чтобы сумма всех сил, действующих на автомобиль, равнялась нулю.
Σ Усилия = F 1 +плюс; F 2 + Н + Вт = 0
в. Так как автомобиль остается на поверхности, силы N и W действуют равными и противоположными направлениями. Сила F 92} \номер \\ &=& 124 ~\text{фунт-сила} \end{эквнаррай} $$
У нас есть несколько структурных калькуляторов на выбор. Здесь только несколько:
- Калькулятор луча
- Калькулятор болтовых соединений
- Распределение силы болтового соединения
- Калькулятор зажимов
- Калькулятор потери устойчивости колонны
- Калькулятор роста усталостной трещины
Виды силы
При определении того, как объект реагирует на силу или силы, важно понимать различные типы сил, которые могут воздействовать на объект.
В предыдущем разделе обсуждалось равновесие сил, действующих на тела. Вспоминая, что сила определяется как векторная величина, стремящаяся вызвать ускорение тела в направлении своего приложения, становится очевидным, что учащийся должен быть знаком с различными типами существующих сил, чтобы построить правильную свободную модель.
-диаграмму тела и применить соответствующее уравнение. Сила прикладывается либо прямым механическим контактом, либо дистанционным действием.
Силы растяжения и сжатия
При обсуждении типов сил используется простое правило, чтобы определить, является ли сила растягивающей или сжимающей силой. Если сила, приложенная к элементу, стремится разорвать элемент, говорят, что он находится в состоянии натяжения . Если сила стремится сжать элемент, это сжатие . Следует также отметить, что канаты, тросы и т. д., прикрепленные к телам, могут воспринимать только растягивающие нагрузки, и поэтому такие объекты находятся в напряжении при размещении на диаграмме свободного тела. Кроме того, когда речь идет о жидкости, следует понимать, что силы жидкости почти всегда являются сжимающими силами.
Трение
Другой тип силы, часто используемый в классической физике, — это сила, возникающая в результате контакта двух поверхностей, когда одна из поверхностей пытается двигаться параллельно или над другой поверхностью.
Такие силы называются силами трения . Существует два типа сил трения: силы сухого трения, иногда называемые кулоновским трением, и силы трения жидкости.
Жидкостное трение возникает между слоями жидкости, движущимися с разными скоростями. Этот тип силы трения используется при рассмотрении задач, связанных с течением жидкости по трубам. Такие проблемы рассматриваются в Основном руководстве по течению жидкости. В этом разделе рассматриваются задачи о контакте твердых тел по сухим поверхностям.
Законы сухого трения лучше всего понять из следующего эксперимента. На горизонтальной плоской поверхности лежит брусок веса W (см. рис. 9). Силы, действующие на брусок, это его вес W и нормальная сила N поверхности. Поскольку у веса нет горизонтальной составляющей, нормальная сила поверхности также не имеет горизонтальной составляющей; поэтому реакция нормальна к поверхности и представлена буквой N в части (а) рисунка. Предположим теперь, что к блоку приложена горизонтальная сила P (см.
часть (b)). Если P мало, блок не будет двигаться. Следовательно, должна существовать какая-то другая горизонтальная сила, которая уравновешивает P. Эта другая сила есть сила трения покоя F, которая фактически является равнодействующей большого числа сил, действующих на всей поверхности контакта между бруском и плоскостью. Природа этих сил точно неизвестна, но обычно предполагается, что эти силы возникают из-за неровностей контактирующих поверхностей, а также из-за действия молекул.
Если усилие P увеличить, то сила трения F также увеличится, продолжая противодействовать P, пока ее величина не достигнет некоторого максимального значения F M (см. часть (c) рис. 9). При дальнейшем увеличении P сила трения уже не может его уравновешивать, и блок начинает скользить. Как только блок был приведен в движение, величина F падает с F M до меньшего значения F K . Это связано с меньшим взаимопроникновением между неровностями соприкасающихся поверхностей, когда эти поверхности движутся относительно друг друга.
С этого момента блок продолжает скользить с возрастающей скоростью (т. е. ускоряется), а сила трения, обозначаемая F K и называемая кинетической силой трения, остается приблизительно постоянной.
Экспериментальные данные показывают, что максимальное значение F M силы статического трения пропорционально нормальной составляющей N реакции поверхности, как показано в уравнении 4-5.
F M = μ S N
(4-5)
Термин μ S представляет собой константу, называемую коэффициентом статического трения. Точно так же звездная величина F K кинетической силы трения можно выразить в следующем виде.
F K = μ K N
(4-6)
Член μ K представляет собой константу, называемую коэффициентом кинетического трения. Коэффициенты трения µ S и µ K не зависят от площади соприкасающихся поверхностей. Однако оба коэффициента сильно зависят от характера контактирующих поверхностей.
Поскольку они также зависят от точного состояния поверхностей, их значение редко известно с точностью более 5%. Следует отметить, что силы трения всегда противоположны по направлению движению (или приближающемуся движению) объекта.
Центростремительная сила
Тело, движущееся с постоянной скоростью по окружности, не находится в равновесии. Хотя величина линейной скорости не меняется, направление скорости постоянно меняется. Поскольку изменение направления требует ускорения, объект, движущийся по круговой траектории, имеет постоянное ускорение по направлению к центру круговой траектории.
Вспоминая второй закон движения Ньютона, F = ma, требуется сила, чтобы вызвать ускорение. Следовательно, чтобы иметь постоянное ускорение по направлению к центру кругового пути, должна быть результирующая сила, действующая по направлению к центру. Эта сила известна как центростремительная сила. Без этой силы объект будет двигаться прямолинейно. На рис. 10 показана центростремительная сила.
Центробежная сила
Другая сила, которая кажется противоположной направлению движения, — это центробежная сила, действующая на объект, который движется по криволинейной траектории. Эта сила кажется силой, направленной от центра кругового пути. На самом деле это вымышленная сила, но это кажущаяся сила, которая используется для описания сил, возникающих из-за вращения объекта.
Чтобы лучше понять центростремительные и центробежные силы, представьте, что к плоскости на рисунке 10 прикреплена струна. Когда плоскость вращается вокруг центра, струна воздействует на плоскость центростремительной силой. Это приводит к тому, что скорость самолета изменяется в направлении, заставляя его двигаться по окружности.
Рисунок 11: Центробежная сила
Кажущаяся направленная наружу сила, центробежная сила, по-видимому, оттягивает плоскость от центра, показанного на рис. 11. Это та же самая видимая направленная наружу сила, которую человек ощущает, когда едет в машине, когда машина движется по кругу.