Пример 0: Умножение и деление 0 — урок. Математика, 3 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Действия с нулём

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

24 + 0 = 24

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

+ 0 =

Вычитание

При вычитании нуля из некоторого числа (целого, дробного, положительного или отрицательного) оставляет его полностью неизменным.

Пример 1

Две тысячи сто пятьдесят два минус ноль равняется две тысячи сто пятьдесят два.

2152 – 0 = 2152

Пример 2

Сорок одна целая три пятых минус ноль равняется сорок одна целая три пятых.

– 0 =

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль.

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль.

586 × 0 = 0

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль.

0 × 135 = 0

Пример 3

Ноль умножить на ноль равняется ноль.

0 × 0 = 0

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда

ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль.

0 : 265 = 0

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль.

0 :

596

= 0

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным.

Таким образом, теоретически оно может представлять собой абсолютно любое число.

0 : 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как деление нуля на ноль, не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в

ноль. Если это определено, то такому выражению, как ноль разделить на ноль, в подавляющем большинстве случаев можно придать некий смысл.

Семантическое Версионирование 2.0.0 | Semantic Versioning

Кратко

Учитывая номер версии МАЖОРНАЯ.МИНОРНАЯ.ПАТЧ, следует увеличивать:

МАЖОРНУЮ версию, когда сделаны обратно несовместимые изменения API.
МИНОРНУЮ версию, когда вы добавляете новую функциональность, не нарушая обратной совместимости.
ПАТЧ-версию, когда вы делаете обратно совместимые исправления.

Дополнительные обозначения для предрелизных и билд-метаданных возможны как дополнения к МАЖОРНАЯ.МИНОРНАЯ.ПАТЧ формату.

Вступление

В мире управления процессом разработки есть понятие «ад зависимостей» (dependency hell). Чем больше растёт ваша система и чем больше библиотек вы интегрируете в ваш проект, тем больше вероятность оказаться в этой ситуации.

В системе с множественными зависимостями выпуск новой версии может быстро превратиться в кошмар. Если спецификации зависимости слишком жесткие, вы находитесь в опасности блокирования выпуска новой версии (невозможность обновить пакет без необходимости выпуска новой версии каждой зависимой библиотеки). Если спецификация зависимостей слишком свободна, вас неизбежно настигнет версионное несоответствие (необоснованное предположение совместимости с будущими версиями).

В качестве решения данной проблемы я предлагаю простой набор правил и требований, которые определяют, как назначаются и увеличиваются номера версий. Для того чтобы эта система работала, вам необходимо определить публичный API. Он может быть описан в документации или определяться самим кодом. Главное, чтобы этот API был ясным и точным. Однажды определив публичный API, вы сообщаете об изменениях в нём особым увеличением номера версий. Рассмотрим формат версий X.Y.Z (мажорная, минорная, патч). Баг-фиксы, не влияющие на API, увеличивают патч-версию, обратно совместимые добавления/изменения API увеличивают минорную версию и обратно несовместимые изменения API увеличивают мажорную версию.

Я называю эту систему «Семантическое Версионирование» (Semantic Versioning). По этой схеме номера версий и то, как они изменяются, передают смысл содержания исходного кода и что было модифицировано от одной версии к другой.

Спецификация Семантического Версионирования (SemVer)

Слова «ДОЛЖЕН» (MUST), «НЕ ДОЛЖЕН» (MUST NOT), «ОБЯЗАТЕЛЬНО» (REQUIRED), «СЛЕДУЕТ» (SHOULD), «НЕ СЛЕДУЕТ» (SHOULD NOT), «РЕКОМЕНДОВАННЫЙ» (RECOMMENDED), «МОЖЕТ» (MAY) и «НЕОБЯЗАТЕЛЬНЫЙ» (OPTIONAL) в этом документе должны быть интерпретированы в соответствии с RFC 2119.

ПО, использующее Семантическое Версионирование, должно объявить публичный API. Этот API может быть объявлен самим кодом или существовать строго в документации. Как бы ни было это сделано, он должен быть точным и исчерпывающим.
Обычный номер версии ДОЛЖЕН иметь формат X.Y.Z, где X, Y и Z — неотрицательные целые числа и НЕ ДОЛЖНЫ начинаться с нуля. X — мажорная версия, Y — минорная версия и Z — патч-версия. Каждый элемент ДОЛЖЕН увеличиваться численно. Например: 1.9.0 ->1.10.0 -> 1.11.0.
После релиза новой версии пакета содержание этой версии НЕ ДОЛЖНО быть модифицировано. Любые изменения ДОЛЖНЫ быть выпущены как новая версия.
Мажорная версия ноль (0.y.z) предназначена для начальной разработки. Всё может измениться в любой момент. Публичный API не должен рассматриваться как стабильный.
Версия 1.0.0 определяет публичный API. После этого релиза номера версий увеличиваются в зависимости от того, как изменяется публичный API.
Патч-версия Z (x.y.Z | x > 0) ДОЛЖНА быть увеличена только если содержит обратно совместимые баг-фиксы. Определение баг-фикс означает внутренние изменения, которые исправляют некорректное поведение.
Минорная версия (x.Y.z | x > 0) ДОЛЖНА быть увеличена, если в публичном API представлена новая обратно совместимая функциональность. Версия ДОЛЖНА быть увеличена, если какая-либо функциональность публичного API помечена как устаревшая (deprecated). Версия МОЖЕТ быть увеличена в случае реализации новой функциональности или существенного усовершенствования в приватном коде. Версия МОЖЕТ включать в себя изменения, характерные для патчей. Патч-версия ДОЛЖНА быть обнулена, когда увеличивается минорная версия.
Мажорная версия X (X.y.z | X > 0) ДОЛЖНА быть увеличена, если в публичном API представлены какие-либо обратно несовместимые изменения. Она МОЖЕТ включать в себя изменения, характерные для уровня минорных версий и патчей.
Когда увеличивается мажорная версия, минорная и патч-версия ДОЛЖНЫ быть обнулены.
Предрелизная версия МОЖЕТ быть обозначена добавлением дефиса и серией разделённых точкой идентификаторов, следующих сразу за патч-версией. Идентификаторы ДОЛЖНЫ содержать только ASCII буквенно-цифровые символы и дефис [0-9A-Za-z-]. Идентификаторы НЕ ДОЛЖНЫ быть пустыми. Числовые идентификаторы НЕ ДОЛЖНЫ начинаться с нуля. Предрелизные версии имеют более низкий приоритет, чем соответствующая релизная версия. Предрелизная версия указывает на то, что эта версия не стабильна и может не удовлетворять требованиям совместимости, обозначенными соответствующей нормальной версией. Примеры: 1.0.0-alpha, 1.0.0-alpha.1, 1.0.0-0.3.7, 1.0.0-x.7.z.92.
Сборочные метаданные МОГУТ быть обозначены добавлением знака плюс и ряда разделённых точкой идентификаторов, следующих сразу за патчем или предрелизной версией. Идентификаторы ДОЛЖНЫ содержать только ASCII буквенно-цифровые символы и дефис [0-9A-Za-z-]. Идентификаторы НЕ ДОЛЖНЫ быть пустыми. Сборочные метаданные СЛЕДУЕТ игнорировать, когда определяется старшинство версий. Поэтому два пакета с одинаковой версией, но разными сборочными метаданными, рассматриваются как одна и та же версия. Примеры: 1.0.0-alpha+001, 1.0.0+20130313144700, 1.0.0-beta+exp.sha.5114f85.
Приоритет определяет, как версии соотносятся друг с другом, когда упорядочиваются. Приоритет версий ДОЛЖЕН рассчитываться путём разделения номеров версий на мажорную, минорную, патч и предрелизные идентификаторы. Именно в такой последовательности (сборочные метаданные не фигурируют в расчёте). Приоритет определяется по первому отличию при сравнении каждого из этих идентификаторов слева направо: Мажорная, минорная и патч-версия всегда сравниваются численно. Пример: 1.0.0 < 2.0.0 < 2.1.0 < 2.1.1. Когда мажорная, минорная и патч-версия равны, предрелизная версия имеет более низкий приоритет, чем нормальная версия. Пример: 1.0.0-alpha < 1.0.0. Приоритет двух предрелизных версий с одинаковыми мажорной, минорной и патч-версией ДОЛЖНЫ быть определены сравнением каждого разделённого точкой идентификатора слева направо до тех пор, пока различие не будет найдено следующим образом: идентификаторы, состоящие только из цифр, сравниваются численно; буквенные идентификаторы или дефисы сравниваются лексически в ASCII-порядке. Численные идентификаторы всегда имеют низший приоритет, чем символьные. Больший набор предрелизных символов имеет больший приоритет, чем меньший набор, если сравниваемые идентификаторы равны. Пример: 1.0.0-alpha < 1.0.0-alpha.1 < 1.0.0-alpha.beta < 1.0.0-beta < 1.0.0-beta.2 < 1.0.0-beta.11 < 1.0.0-rc.1 < 1.0.0.

Зачем использовать семантическое версионирование?

Это не новая или революционная идея. Вероятно, вы уже используете что-то подобное. Проблема в том, что «подобное» — не достаточно хорошо. Без соответствия формальной спецификации, номера версий практически бесполезны для управления зависимостями. Ясно определив и сформулировав идею версионирования, становится легче сообщать о намерениях пользователям вашего ПО. Когда эти намерения ясны, гибки (но не слишком), спецификации зависимостей наконец могут быть созданы.

Простой пример демонстрирует, как Семантическое Версионирование может сделать «ад зависимостей» вещью из прошлого. Представим библиотеку, названную «Firetruck».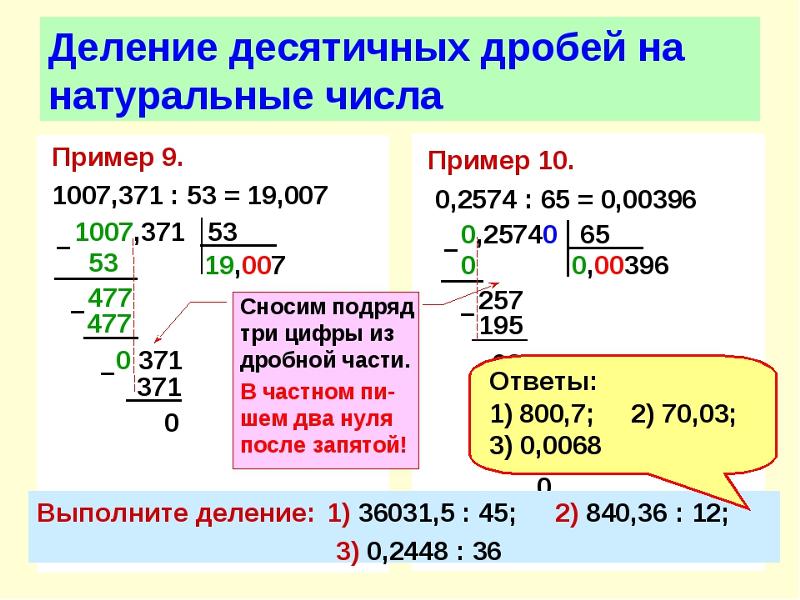 Она требует Семантически Версионированный пакет под названием «Ladder». Когда Firetruck был создан, Ladder был 3.1.0 версии. Так как Firetruck использует функциональность версии 3.1.0, вы спокойно можете объявить зависимость от Ladder версии 3.1.0, но менее чем 4.0.0. Теперь, когда доступен Ladder 3.1.1 и 3.2.0 версии, вы можете интегрировать его в вашу систему и знать, что он будет совместим с текущей функциональностью.

Как ответственный разработчик, вы, конечно, хотите быть уверены, что все обновления функционируют как заявлено. В реальном мире полный бардак и ничего нельзя с этим поделать. Что вы можете сделать — это дать Семантическому Версионированию предоставить способ выпуска релизов без выпуска новых версий зависимых пакетов и сохранить вам время и нервы.

Если это звучит соблазнительно, всё что вам нужно — это начать использовать Семантическое Версионирование, объявить, что вы его используете, и следовать правилам. Добавьте ссылку на этот сайт в вашем README, тогда пользователи будут знать правила и извлекать из этого пользу.

FAQ

Что я должен делать с ревизиями в 0.y.z на начальной стадии разработки?

Самое простое — начать разработку с 0.1.0 и затем увеличивать минорную версию для каждого последующего релиза.

Как я узнаю, когда пора делать релиз 1.0.0?

Если ваше ПО используется на продакшене, оно, вероятно, уже должно быть версии 1.0.0. Если у вас стабильный API, от которого зависят пользователи, версия должна быть 1.0.0. Если вы беспокоитесь за обратную совместимость, вероятно, версия вашего ПО уже 1.0.0.

Не препятствует ли это быстрой разработке и коротким итерациям?

Мажорная версия 0 как раз и означает быструю разработку. Если вы изменяете API каждый день, вы должны быть на версии 0.y.z или на отдельной ветке разработки работать над следующей главной версией.

Даже если малейшие обратно несовместимые изменения в публичном API требуют выпуска новой главной версии, не закончится ли это тем, что очень скоро версия станет 42.0.0?

Это вопрос ответственной разработки и предвидения. Несовместимые изменения не должны быть представлены как незначительные в ПО, имеющем много зависимого кода. Стоимость обновления может быть велика. Практика увеличения главных версий релизов с обратно несовместимыми изменениями означает, что вам придётся думать о последствиях ваших изменений и учитывать соотношение цена/качество.

Документирование всего API — слишком много работы!

Это ваша ответственность, как профессионального разработчика, правильно документировать ПО, предназначенное для широкого использования. Управление сложностью ПО очень важная часть поддержки высокой эффективности проекта. Это тяжело сделать, если никто не знает, как использовать ваше ПО или какой метод можно вызывать безопасно. В долгосрочной перспективе Семантическое Версионирование и настойчивость в качественном документировании публичного API поможет всем и всему работать слаженно.

Что мне делать, если я случайно зарелизил обратно несовместимые изменения как минорную версию?

Как только вы поняли, что нарушили спецификации Семантического Версионирования, исправьте проблему и выпустите новую минорную версию, которая исправляет проблему и восстанавливает обратную совместимость. Даже в таких обстоятельствах неприемлемо модифицировать уже выпущенные релизы. Если это необходимо, укажите в документации о нарушении обратной совместимости, версионирования и проинформируйте ваших пользователей, чтобы они знали о нарушении порядка версий.

Что я должен делать, если я обновляю свои собственные зависимости без изменения публичного API?

Это можно рассматривать как совместимые изменения, так как они не влияют на публичный API. ПО, которое явно зависит от тех же зависимостей что и ваш пакет, должно иметь собственные спецификации зависимостей и автор будет уведомлен о возможных конфликтах. Являются ли данные изменения уровня патча или минорного уровня, зависит от того, обновили ли вы свои зависимости чтобы исправить баг или реализовать новую функциональность. В последнем случае, как правило, добавляется некоторое количество дополнительного кода и как следствие, увеличивается минорная версия.

Что если я нечаянно изменил публичный API в несоответствии с изменением номера версии (т.

е. код содержит обратно несовместимые изменения в патч-релизе)?

На ваше усмотрение. Если у вас огромная аудитория, которая будет поставлена перед фактом возвращения прежнего поведения API, то лучше выпустить новый релиз с увеличением главной версии, даже несмотря на то, что фикс содержит исправления уровня патча. Запомните, в Семантическом Версионировании номера версий изменяются строго следуя спецификации. Если эти изменения важны для ваших пользователей, используйте номер версии, чтобы информировать их.

Что делать с устаревшей функциональностью?

Объявление функциональности устаревшей — это обычное дело в ходе разработки и часто необходимо для продвижения вперёд. Когда вы объявляете устаревшим часть публичного API, вы должны сделать две вещи: (1) обновить вашу документацию, чтобы дать пользователям узнать об этом изменении; (2) выпустить новый релиз с увеличением минорной версии. Прежде чем вы полностью удалите устаревшую функциональность в релизе с увеличением главной версии, должен быть как минимум один минорный релиз, содержащий объявление функциональности устаревшей, чтобы пользователи могли плавно перейти на новый API.

Есть ли в SemVer лимиты на длину строки версии?

Нет, но руководствуйтесь здравым смыслом. 255 символов в строке версии, пожалуй, перебор. Кроме того, определенные системы могут предъявлять свои собственные ограничения на размер строки.

Об авторе

Авторство спецификаций Семантического Версионирования принадлежит Тому Престон-Вернеру, основателю Gravatars и соучредителю GitHub.

Если вы хотите оставить отзыв, пожалуйста, создайте запрос на GitHub.

Лицензия

Creative Commons — CC BY 3.0

Что это такое и как его использовать

Цифра 0 уже давно ставит в тупик людей, изучающих математические понятия. Ноль это число? Как мы это используем? Хотя все мы на каком-то уровне знаем, что ноль означает ничего или ничего, это не всегда помогает нам включить его в математические задачи. Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.

Что такое число 0?

Является ли ноль числом? Ноль или 0 это 9Число 0009 и цифра, используемая для представления числа 0 , широко используются в математике и могут использоваться как самостоятельные числа или как заполнители в уравнениях.

История

Число 0 использовалось для представления идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при записи чисел и уравнений.

Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.

Современное использование

Ноль обычно используется в языке для выражения концепции отсутствия и используется в математике как целое число. Число 0 в сегодняшней математике может быть сложным; зачем что-то вычислять, когда на самом деле там ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.

Операции с 0

Хотя этот список функций с использованием нуля не охватывает все математические функции , эти основные арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.