Метод Крамера для решения системы двух линейных уравнений: алгоритм следования, примеры.
Квадратная матрица 2-го порядка и её определитель
Квадратной матрицей 2-го порядка A называется таблица из 4-х чисел вида: $$ A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix} $$
В квадратной матрице 2-го порядка две строки и два столбца.
Например: $ |A| = \begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} $
Определителем матрицы 2-го порядка называется число:
$$ A = \begin{vmatrix} a & b \\ c & d \\ \end{vmatrix} = ad-bc $$
Например: $\begin{vmatrix} 1 & -4 \\ 2,5 & 3 \\ \end{vmatrix} = 1\cdot3-2,5\cdot(-4) = 3+10 = 13$
Метод Крамера для решения системы 2-х линейных уравнений
Дана система 2-х линейных уравнений:
$$ {\left\{ \begin{array}{c} a_1 x+b_1 y=c_1 \\ a_2 x+b_2 y=c_2 \end{array} \right.} $$
Определим главный определитель системы:
$$ \Delta = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \\ \end{vmatrix} = a_1 b_2-a_2 b_1 $$
и вспомогательные определители:
$$ \Delta_x = \begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \\ \end{vmatrix} = c_1 b_2-c_2 b_1, \Delta_y = \begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \\ \end{vmatrix} = a_1 c_2-a_2 c_1 $$
Тогда решение системы:
$$ {\left\{ \begin{array}{c} x = \frac{\Delta_x}{\Delta} \\ y = \frac{\Delta_y}{\Delta} \end{array} \right. } $$
} $$
Соотношение коэффициентов уравнений, значений определителей, расположения прямых и количества решений:
$ \frac{a_1}{a_2} \neq \frac{b_1}{b_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} $
$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $
$ \Delta \neq 0 $
$ \Delta = 0, \Delta _x \neq 0, \Delta_y \neq 0 $
$ \Delta = \Delta_x = \Delta_y = 0$
Прямые пересекаются
Прямые параллельны
Прямые совпадают
Бесконечное множество решений
Внимание!
Метод Крамера используется в линейной алгебре для решения систем линейных уравнений произвольного порядка $N \ge 2$.
Главный определитель, вспомогательные определители и решения таких систем находятся аналогично.
Поэтому для метода Крамера несложно составить алгоритм и запрограммировать для решения прикладных задач.
Метод Крамера для N=3 (три уравнения, три переменных) рассмотрен в §49 данного справочника.
Примеры
Пример 1. Решите систему уравнений методом Крамера:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & -3 \\ \end{vmatrix} = 5\cdot(-3)-2\cdot(-4) = -15+8 =-7 $$
$$ \Delta_x = \begin{vmatrix} 3 & -4 \\ 4 & -3 \\ \end{vmatrix} = 3\cdot(-3)-4\cdot(-4) = -9+16 = 7 $$
$$ \Delta_y = \begin{vmatrix} 5 & 3 \\ 2 & 4 \\ \end{vmatrix} = 5\cdot4-2\cdot3 = 20-6 = 14 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{7}{-7} = -1, y = \frac{\Delta_y}{\Delta} = \frac{14}{-7} = -2 $$
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 4 & -3 \\ 3 & -4 \\ \end{vmatrix} = 4\cdot(-4)-3\cdot(-3) = -16+9 = -7 $$
$$ \Delta_x = \begin{vmatrix} 7 & -3 \\ 0 & -4 \\ \end{vmatrix} = 7\cdot(-4)-0\cdot(-3) = -28 $$
$$ \Delta_y = \begin{vmatrix} 4 & 7 \\ 3 & 0 \\ \end{vmatrix} = 4\cdot0-3\cdot7 = -21 $$
$$ x = \frac{\Delta_x}{\Delta} = \frac{-28}{-7} = 4, y = \frac{\Delta_y}{\Delta} = \frac{-21}{-7} = 3 $$
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right. } $
} $
$$ \Delta = \begin{vmatrix} 5 & -4 \\ 2 & 3 \\ \end{vmatrix} = 5\cdot3-2\cdot(-4) = 15+8 = 23 $$
$$ \Delta_a = \begin{vmatrix} 9 & -4 \\ -1 & -3 \\ \end{vmatrix} = 9\cdot3-(-1)\cdot(-4) = 27-4 = 23 $$
$$ \Delta_b = \begin{vmatrix} 5 & 9 \\ 2 & -1 \\ \end{vmatrix} = 5\cdot(-1)-2\cdot9 = -5-18 = -23 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{23}{23} = 1, b = \frac{\Delta_b}{\Delta} = \frac{-23}{23} = -1 $$
Ответ: (1;-1)
$ r) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} $
$$ \Delta = \begin{vmatrix} 7 & 4 \\ 3 & 2 \\ \end{vmatrix} = 7\cdot2-3\cdot4 = 14-12 = 2 $$
$$ \Delta_a = \begin{vmatrix} 5 & 4 \\ 1 & 2 \\ \end{vmatrix} = 5\cdot2-1\cdot4 = 10-4 = 6 $$
$$ \Delta_b = \begin{vmatrix} 7 & 5 \\ 3 & 1 \\ \end{vmatrix} = 7\cdot1-3\cdot5 = 7-15 = -8 $$
$$ a = \frac{\Delta_a}{\Delta} = \frac{6}{2} = 3, b = \frac{\Delta_b}{\Delta} = \frac{-8}{2} = -4 $$
Ответ: (3;-4)
Пример 2*. 2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
Ответ: 1) $a \neq \pm5$; 2) a = 5; 3) a = -5
Решение системы уравнений методом Крамера
Метод применим только в том случае, если число переменных совпадает с числом уравнений в этой системе линейных уравнений.
Необходимым условием является, чтобы определитель матрицы системы не равнялся нулю, то есть
D = det A≠0
Система из n уравнений с n неизвестными
Если определитель матрицы линейной системы не равен нулю, то система имеет единственное решение.
Решение находится по формулам:
i=0,1,2…n
D — главный определитель, составленный из числовых коэффициентов при неизвестных,
Di – вспомогательный определитель, получаемый из главного заменой i -го столбца столбцом свободных членов bi.
Допустим, дана система трех линейных уравнений с тремя неизвестными, вида
главный определитель находится по формуле:
а вспомогательные по формулам:
Далее по формулам Крамера находим корни искомой системы линейных уравнений:
Пример 1
Решить систему линейных уравнений с двумя неизвестными с помощью метода Крамера
$\left\{ {\begin{array}{*{20}{c}}{2{x_1}}& + &{3{x_2}}& = &{ — 1} \\ {3{x_1}}& + &{4{x_2}}& = &{ — 1} \end{array}} \right.$
Решение
$\left\{ {\begin{array}{*{20}{c}}{2{x_1}}& + &{3{x_2}}& = &{ — 1} \\ {3{x_1}}& + &{4{x_2}}& = &{ — 1} \end{array}} \right.$
Находим определитель матрицы второго порядка системы
$\Delta = \left| {\begin{array}{*{20}{c}}2&3 \\ 3&4 \end{array}} \right| = 8 — 9 = — 1 \ne 0$
Имеем:
${\Delta _{\,1}} = \left| {\begin{array}{*{20}{c}} { — 1}&3 \\ { — 1}&4 \end{array}} \right|=$
$= — 1 \cdot 4 — 3 \cdot ( — 1) = — 1$
${\Delta _2} = \left| {\begin{array}{*{20}{c}} 2&{ — 1} \\ 3&{ — 1} \end{array}} \right|=$
$= 2 \cdot ( — 1) — 3 \cdot ( — 1) = 1$
Следовательно, находим корни уравнения
${x_{\,1}} = \frac{{{\Delta _{\,1}}}}{\Delta } = \frac{{ — 1}}{{ — 1}} = 1$
${x_2} = \frac{{{\Delta _2}}}{\Delta } = \frac{1}{{ — 1}} = — 1$
Пример 2
Решить систему линейных уравнений с тремя неизвестными с помощью метода Крамера
$\left\{ {\begin{array}{*{20}{c}}{3{x_1} — {x_2} + {x_3} = 12} \\ {5{x_1} +{x_2} + 2{x_3} = 3} \\ {x{}_1 + {x_2} + 2{x_3} = 3} \end{array}{\text{ }}} \right. $
$
Решение
Найдем определитель матрицы третьего порядка, по формуле:
Определитель матрицы равен:
Определитель не равен нулю
Вычислим вспомогательные определители
Тогда получаем окончательное решение
${x_1} = \frac{{\Delta {x_1}}}{\Delta } = \frac{0}{{12}} = 0$
${x_2} = \frac{{\Delta {x_2}}}{\Delta } = — \frac{{84}}{{12}} = — 7$
${x_3} = \frac{{\Delta {x_3}}}{\Delta } = \frac{{60}}{{12}} = 5$
Ответ: x1=0; x2=-7; x3=5
Метод Крамера
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.

- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ – номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей – со знаком минус.

Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.

Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 – x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 3 = – 12 – 8 -12 -32 – 6 + 6 = – 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) – (-1) \cdot 2 \cdot 21 = – 84 – 40 – 36 – 160 – 18 + 42 = – 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = – 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 – (-2) \cdot 3 \cdot 10 – (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = – 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = – 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Формулы Крамера.
 Матричный способ решения систем линейных уравнений | Математика
Матричный способ решения систем линейных уравнений | МатематикаПусть задана система линейных уравнений, содержащая одинаковое число уравнений и неизвестных
| (1.19) |
Введем три матрицы
Матрица , составленная из коэффициентов системы, является квадратной матрицей порядка . Матрицы и являются столбцовыми и составлены соответственно из неизвестных и свободных членов системы.
Получить решение
Так как число столбцов матрицы равно числу строк матрицы , то существует произведение , являющееся столбцовой матрицей тех же размеров, что и матрица . Тогда систему уравнений (1.19) можно записать в форме одного матричного уравнения.
| (1.20) |
Для определения матрицы из (1.20) допустим, что матрица имеет обратную матрицу определяемую формулой (17). Тогда, умножая обе части (1.20) слева на , получим
Тогда, умножая обе части (1.20) слева на , получим
| (1.21) |
По определению обратной матрицы ,где единичная матрица порядка . Отсюда
Следовательно, уравнение (1.21) запишется в виде
| (1.22) |
Матричное равенство (1.22) определяет решение заданной системы уравнений в матричной форме. Для определения конкретных значений неизвестных перепишем (1.22) в виде
| , | (1.23) |
где определитель, соответствующий матрице ;
алгебраические дополнения элементов этой матрицы.
Перемножив матрицы в правой части (23), найдем
Отсюда, согласно условию равенства двух матриц, получим
(1. 24) 24) |
Формулы (1.24) и определяют матричный способ решения системы
Для запоминания этих формул и последующего их применения на практике введем группу определителей:
,
Заметим, что определитель получен из заменой его первого столбца на столбец свободных членов, определитель получен из заменой его второго столбца на столбец свободных членов и т.д.. Разложим каждый из определителей по столбцу из свободных членов Тогда
| (1.25) |
Из сравнения полученных результатов (1.25) с числителями равенств (1.24) следует, что решение системы (1.19) можно записать в виде
| (1.26) |
Формулы (1.26) называются формулами Крамера.
Примеры решения по формулам Крамера
ПРИМЕР 1. 1.13
1.13
Решить по формулам Крамера систему уравнений
Решение. Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель этой системы.
Так как ,то решение можно найти по формулам Крамера:
Тогда
Ответ: {1;2}.
ПРИМЕР 1.1.14
Решить матричным способом систему уравнений
Система содержит одинаковое число уравнений и неизвестных. Вычислим определитель этой системы:
Так как , то система может быть решена матричным способом.
Составим матрицы
Так как определитель системы , то матрица имеет обратную матрицу , где
Вычислим алгебраические дополнения всех элементов
Тогда
Так как решением является , то
Или Ответ: {1,1,1}
как методом крамера решить систему уравнений
Вы искали как методом крамера решить систему уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти дискриминант матрицы по методу крамера, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «как методом крамера решить систему уравнений».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти дискриминант матрицы по методу крамера, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «как методом крамера решить систему уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как методом крамера решить систему уравнений,как найти дискриминант матрицы по методу крамера,как решать линейные уравнения методом крамера,как решать матрицу методом крамера,как решать матрицы методом крамера,как решать метод крамера,как решать методом крамера,как решать методом крамера линейные уравнения,как решать методом крамера матрицы,как решать систему уравнений методом крамера,как решить матрицу методом крамера,как решить методом крамера систему,как решить методом крамера систему уравнений,как решить систему линейных уравнений методом крамера,как решить систему методом крамера,как решить систему уравнений методом крамера,крамер матрица,крамер метод,крамер формулы,крамера,крамера матрица,крамера метод пример,крамера метод это,линейные уравнения методом крамера,матрица крамер,матрица крамера,матрица метод крамера,матрица методом крамера,матрицу решить методом крамера,матрицы метод крамера,матрицы метод крамера примеры,матрицы примеры метод крамера,матрицы теорема крамера,метод гаусса и крамера,метод гаусса и метод крамера,метод гаусса крамера и,метод гаусса крамера и матричный метод,метод гаусса метод крамера матричный метод,метод крамер,метод крамера,метод крамера 4 на 4,метод крамера 4х4,метод крамера гаусса и,метод крамера для матрицы 4 порядка,метод крамера для решения систем линейных уравнений,метод крамера для чайников,метод крамера и гаусса,метод крамера и матричный метод,метод крамера и метод гаусса,метод крамера и метод гаусса решения систем линейных уравнений,метод крамера как решать,метод крамера матрица,метод крамера матрицы,метод крамера матрицы примеры,метод крамера метод гаусса,метод крамера метод гаусса и,метод крамера метод гаусса матричный метод,метод крамера пример,метод крамера примеры,метод крамера примеры с решением,метод крамера решение,метод крамера решение матриц,метод крамера решение систем линейных уравнений,метод крамера решения,метод крамера решения систем линейных уравнений,метод крамера система линейных уравнений,метод крамера системы линейных уравнений,метод крамера слау,метод крамера теория,метод крамера формула,метод крамера формулы,метод крамера это,метод обратной матрицы метод крамера,метод решение крамера,метод решения крамера,метод слау крамера,метода крамера,методом крамера,методом крамера как решать,методом крамера матрица,методом крамера решить,методом крамера решить матрицу,методом крамера решить системы уравнений,методом крамера решить уравнение,по крамеру решение,по формулам крамера,по формулам крамера решить систему,по формулам крамера решить систему линейных уравнений,по формулам крамера решить систему уравнений,по формуле крамера решить систему,по формуле крамера решить систему линейных уравнений,по формуле крамера решить систему уравнений,правила крамера,правило крамера,правило крамера решения систем,правило крамера решения систем линейных уравнений,пример метод крамера,примеры линейных уравнений решение методом крамера,примеры метод крамера,примеры решение линейных уравнений методом крамера,примеры формула крамера,решение линейных систем уравнений по формулам крамера,решение линейных уравнений методом крамера,решение линейных уравнений методом крамера примеры,решение матриц метод крамера,решение матриц методом крамера,решение матриц по методу крамера,решение матрицы методом крамера,решение метод крамера,решение методом крамера,решение по крамеру,решение по формуле крамера,решение систем линейных уравнений метод крамера,решение систем линейных уравнений методом крамера,решение систем линейных уравнений методом крамера методом гаусса,решение систем линейных уравнений по формулам крамера,решение систем методом крамера,решение систем по формулам крамера,решение систем уравнений методом крамера,решение систем уравнений методом крамера примеры с решением,решение систем уравнений по формулам крамера,решение системных уравнений методом крамера,решение системы линейных уравнений методом крамера,решение системы методом крамера,решение системы по формулам крамера,решение системы уравнений методом крамера,решение слау методом крамера,решение уравнений методом крамера,решение уравнений по формулам крамера,решение уравнения методом крамера,решения метод крамера,решите систему линейных уравнений методом крамера,решите систему уравнений методом крамера,решите систему уравнений по формулам крамера,решить матрицу методом крамера,решить методом крамера,решить методом крамера системы уравнений,решить методом крамера слау,решить методом крамера уравнение,решить по правилу крамера систему,решить по правилу крамера систему уравнений,решить по формулам крамера систему,решить по формулам крамера систему уравнений,решить по формуле крамера систему,решить по формуле крамера систему уравнений,решить систему алгебраических линейных уравнений методом крамера,решить систему линейных уравнений методом крамера,решить систему линейных уравнений по формулам крамера,решить систему линейных уравнений по формуле крамера,решить систему методом гаусса и методом крамера,решить систему методом крамера,решить систему методом крамера и методом гаусса,решить систему по правилу крамера,решить систему по формулам крамера,решить систему по формуле крамера,решить систему уравнений методом крамера,решить систему уравнений по правилу крамера,решить систему уравнений по формулам крамера,решить систему уравнений по формуле крамера,решить системы уравнений методом крамера,решить слау методом крамера,решить уравнение методом крамера,система крамера,система линейных уравнений метод крамера,система линейных уравнений методом крамера,система уравнений методом крамера,систему линейных уравнений решить по формулам крамера,систему уравнений решить по правилу крамера,системы линейных уравнений метод крамера,слау метод крамера,слау методом крамера,способ крамера,теорема крамера матрицы,теория крамера,теория метод крамера,уравнение крамера,уравнение методом крамера,формула крамера,формула крамера для решения,формула крамера для решения системы,формула крамера для решения системы линейных уравнений,формула крамера примеры,формула метод крамера,формулам крамера,формулы крамер,формулы крамера,формулы крамера для решения систем,формулы крамера для решения систем линейных уравнений,формулы метод крамера. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как методом крамера решить систему уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать линейные уравнения методом крамера).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как методом крамера решить систему уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать линейные уравнения методом крамера).
Где можно решить любую задачу по математике, а так же как методом крамера решить систему уравнений Онлайн?
Решить задачу как методом крамера решить систему уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Проект на тему “Метод Крамера, как способ решения практических задач”
Пятая лицейская научно-практическая конференция «Познание и творчество»
Физика-математика
Тема: «Метод Крамера, как способ решения практических задач»
Исследовательский проект
Автор: Кротова Анна
Ученица 10 «Б» класса МАОУ
« Лицей №21»
Руководитель:
Балашова Елена Ивановна,
учитель математики
Кротова Ирина Леонидовна,
учитель математики
Тема моего исследовательского проекта – «Метод Крамера, как способ решения практических задач».
В школьном курсе алгебры изучают методы решения систем линейных уравнений, такие как: метод подстановки, метод сложения, графический метод. Каждый из методов имеет свои достоинства и недостатки. Общее для них то, что большинство учащихся не могут их усвоить на необходимом уровне.
Я считаю, что тема моего проекта достаточно актуальна в первую очередь для меня, поскольку в математике есть такие задачи, которые нужно решать с помощью систем уравнений. Однако в школьном курсе изучаются системы уравнений, содержащие только две переменные. Мне бы хотелось познакомиться самой, а потом и научить других решать системы, содержащие большее количество неизвестных, что может помочь в решении более сложных задач не только в математике, но и в экономике. Но для того, чтобы познакомиться с самим методом, нужно знать что такое определитель второго порядка и научиться их вычислять.
Гипотеза: эффективность решения систем уравнений повышается, если использовать метод Крамера.
Задачи:
Рассмотреть метод Крамера.
Научить учащихся 8-10 класса пользоваться данным методом.
Предложить учащимся 8-10 класса, на выбор, решить несколько систем уравнений понравившимся способом.
Проанализировать полученный данные в ходе проведения самостоятельной работы, которую выполнят учащиеся.
Сделать выводы, на основе которых определить достоверность моей гипотезы.
Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария). Уже в детстве он опережал своих сверстников в интеллектуальном развитии и демонстрировал завидные способности в области математики.
В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы.
Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Понятие определителя вводится только для квадратной матрицы.
Определитель– это число, которое считается по определенным правилам. Порядок определителя– это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.
Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:
Обозначения:
Определителем второго порядка называется число, вычисляемое по правилу:
.
Пример . .
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.Решения систем методом Крамера
Метод Крамера – это метод решения систем линейных уравнений. Он применяется только к системам линейных уравнений, у которых число уравнений совпадает с числом неизвестных и определитель отличен от нуля.
Он применяется только к системам линейных уравнений, у которых число уравнений совпадает с числом неизвестных и определитель отличен от нуля.
Любая крамеровская система уравнений имеет единственное решение , которое определяется формулами , где – определитель матрицы, полученной из основной матрицы заменой -го столбца на столбец свободных членов системы, а – определитель основной матрицы. Эта формула называется формулой Крамера.
Пример 1:Задание: Решить систему методом Крамера.
Решение: Запишем основную матрицу системы
Найдем её определитель
Определитель , следовательно, заданная система может быть решена методом Крамера.
Вычислим определитель , для этого заменим первый столбец в основной матрице на столбец свободных членов , получим
Аналогично, заменяя второй столбец основной матрицы на , найдем :
Далее по формуле Крамера находим неизвестные переменные:
Ответ:
Пример 2:Задание: Решить систему методом Крамера.
Решение: В уравнениях системы перенесем свободный член вправо:
Тогда основная матрица , а столбец свободных членов .
Найдем определитель матрицы системы:
Определитель , следовательно, система имеет единственное решение и может быть решена методом Крамера. Заменяя первый столбец на столбец свободных членов, найдем, что
Заменяя второй столбец основной матрицы на столбец , получаем:
Тогда, по формуле Крамера, решением системы будет
Ответ:
Пример 3:Задание: Решить систему методом Крамера.
Решение: Найдем определитель основной матрицы системы:
Найдем определитель , для этого подставим в последний определитель вместо первого столбца столбец свободных членов :
Подставляя вместо второго столбца столбец свободных членов, найдем :
Аналогично найдем :
Далее по формуле Камера находим решение заданной системы
Ответ:
Пример 4:Задание: Решить систему методом Крамера.
Решение: Запишем основную матрицу системы:
и найдем её определитель по правилу треугольника:
Определитель основной матрицы равен нулю, следовательно, к данной системе нельзя применить метод Крамера.
Ответ: Данная система не может быть решена методом Крамера.
Конструкт урока для 7 классаКонструкт урока по теме «Метод Крамера как способ решения систем уравнений»
Учитель: Кротова Анна
Учебный предмет: математика
Класс: 7
Цель урока: показать применение метода Крамера, и закрепить умения и навыки при решении систем уравнений методом подстановки и методом алгебраического сложения. Продолжить отрабатывать вычислительные навыки при решении систем уравнений. Продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать.
Задачи:
– составлять системы уравнений и решать системы, используя алгоритмы;
– применять метод Крамера для решения систем уравнений, как один из рациональных методов решений.
Ход урока
Актуализация знанийУчитель предлагает учащимся задачу с двумя переменными: «на чашечных весах взвесили четырех кошек и трех котят, их вес оказался 15 кг. Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, если считать вес всех кошек одинаковым и вес всех котят также одинаковым.»
Ученики составляют систему и решают задачу вместе с учителем методом алгебраического сложения и подстановки.
Регулятивные: самостоятельно анализировать условия задачи.
Учитель предлагает решить задачу вторым способом, воспользовавшись методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Регулятивные: самостоятельно анализировать условия задачи.
Познавательные: ученики осваивают новый, ранее не изученный ими метод.
.
Постановка проблемы
Учитель предлагает решить самостоятельно систему методом алгебраического сложения и подстановки.
Сформулировать алгоритм решения данной системы.
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Учитель предлагает самостоятельно решить произвольную систему уравнений методом Крамера
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Рефлексия
Учитель предлагает задание для самостоятельного решения, проверяет самостоятельную работу и анализирует результаты.
Применение алгоритма при решении многошаговых уравнений.
Работают с заданием на анализ предъявляемой информации, формулируют свои оценочные суждения, аргументируют их примерами
Личностные: формулирование оценочных суждений, их аргументация;
Регулятивные: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.
Коммуникативные: умение вступать в диалог с учителем и со сверстниками.
Познавательные: оценка результатов деятельности.
Конструкт урока для 9 классаКонструкт урока по теме «Метод Крамера как способ решения систем уравнений»
Учитель: Кротова Анна
Учебный предмет: математика
Класс: 7
Цель урока: показать применение метода Крамера, и закрепить умения и навыки при решении систем уравнений методом подстановки и методом алгебраического сложения. Продолжить отрабатывать вычислительные навыки при решении систем уравнений. Продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать.
Задачи:
– составлять системы уравнений и решать системы, используя алгоритмы;
– применять метод Крамера для решения систем уравнений, как один из рациональных методов решений.
Ход урока
Актуализация знанийУчитель предлагает учащимся задачу с двумя переменными: «на чашечных весах взвесили четырех кошек и трех котят, их вес оказался 15 кг. Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, если считать вес всех кошек одинаковым и вес всех котят также одинаковым.»
Затем взвесили трех кошек и четырех котят, их вес составил 13 кг. Найти вес одной кошки и одного котенка, если считать вес всех кошек одинаковым и вес всех котят также одинаковым.»
Ученики составляют систему и решают задачу вместе с учителем методом алгебраического сложения и подстановки.
Регулятивные: самостоятельно анализировать условия задачи.
Учитель предлагает решить задачу вторым способом, воспользовавшись методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Регулятивные: самостоятельно анализировать условия задачи.
Познавательные: ученики осваивают новый, ранее не изученный ими метод.
.
Постановка проблемы
Учитель предлагает решить самостоятельно систему методом алгебраического сложения и подстановки.
Сформулировать алгоритм решения данной системы.
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Учитель предлагает решить систему из трех уравнений методом Крамера.
Ученики составляют систему и решают задачу вместе с учителем методом Крамера.
Учитель предлагает самостоятельно решить произвольную систему уравнений методом Крамера
Ученики самостоятельно решают систему уравнений
Регулятивные: самостоятельно анализировать условия задачи. Принимать решение в проблемной ситуации.
Принимать решение в проблемной ситуации.
Познавательные: ученики самостоятельно находят пути решения заданной системы.
Коммуникативные: аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом.
Познавательные: действовать по алгоритму.
Рефлексия
Учитель предлагает задание для самостоятельного решения, проверяет самостоятельную работу и анализирует результаты.
Применение алгоритма при решении многошаговых уравнений.
Работают с заданием на анализ предъявляемой информации, формулируют свои оценочные суждения, аргументируют их примерами
Личностные: формулирование оценочных суждений, их аргументация;
Регулятивные: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению.
Коммуникативные: умение вступать в диалог с учителем и со сверстниками.
Познавательные: оценка результатов деятельности.
В итоге работы над данным проектом я выполнила все поставленные перед собой задачи. С помощью дополнительной литературы я изучила метод Крамера, узнала, что такое определитель, как он находится и научилась применять данный метод на практике. Я провела уроки в 7 и в 9 классе. На уроке я предложила учащимся решить системы уравнений новым методом. Большинство учащихся, воспользовавшись методом Крамера, решили системы уравнений правильно.
Перед тем, как начать писать проект, я определила для себя такие риски и сложности как: исследуемая информация может быть сложна, в связи с тем, что изучаемый мною материал выходит за рамки школьной программы. Кроме того, может возникнуть трудность при передаче информации другим учащимся в связи с моей методической неграмотностью, т. е. незнание методов изложения материала. Но риск оказался не оправдан, т.к. тема не вызвала затруднений, и я смогла преподнести информацию так, что учащиеся смогли ее реализовать.
е. незнание методов изложения материала. Но риск оказался не оправдан, т.к. тема не вызвала затруднений, и я смогла преподнести информацию так, что учащиеся смогли ее реализовать.
В ходе работы над моим проектом я доказала справедливость моей гипотезы, что эффективность решения систем уравнения повышается, если использовать метод Крамера.
Результаты самостоятельной работы в 7 классеРезультаты самостоятельной работы в 9 классеМетодом Крамера шаг за шагом.
Данное решение сделано калькулятором, представленным на сайте.
Решим систему линейных уравнений, используя метод Крамера.
| – | 2 | x1 | + | x2 | + | x3 | = | -13 | |||
| – | x1 | + | x2 | + | 2 | x3 | = | -9 | |||
| 3 | x1 | + | x2 | + | x3 | = | 12 |
Запишем формулы Крамера:
x1 = det A1 / det A
x2 = det A2 / det A
x3 = det A3 / det A
На ноль делить нельзя. Поэтому если det A равен нулю, то использовать формулы Крамера невозможно.
Поэтому если det A равен нулю, то использовать формулы Крамера невозможно.
det A состоит из коэффициентов левой части системы уравнений.
| – | 2 | x1 | + | x2 | + | x3 | = | -13 | |||
| – | x1 | + | x2 | + | 2 | x3 | = | -9 | |||
| 3 | x1 | + | x2 | + | x3 | = | 12 |
| det A = | -2 | 1 | 1 | = | ||
| -1 | 1 | 2 | ||||
| 3 | 1 | 1 |
 подробнее
подробнее| -2 | 1 | 1 | ||
| -1 | 1 | 2 | ||
| 3 + ( -2) * ( -1) | 1 + 1 * ( -1) | 1 + 1 * ( -1) |
Данное элементарное преобразование не изменит значение определителя.
Разложим определитель по элементам строки 3. подробнее| Номер строки 3 Номер столбца 1 |
Элемент | Строку 3 и столбец 1 вычеркнули |
|||
| ( -1) 3 + 1 | * | 5 | * |
| Номер строки 3 Номер столбца 2 |
Элемент | Строку 3 и столбец 2 вычеркнули |
|||
| ( -1) 3 + 2 | * | 0 | * |
| Номер строки 3 Номер столбца 3 |
Элемент | Строку 3 и столбец 3 вычеркнули |
|||
| ( -1) 3 + 3 | * | 0 | * |
Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.
Если элемент равен нулю, то и произведение тоже равно нулю.
| = ( -1) 3 + 1 * 5 * | 1 | 1 | = | ||
| 1 | 2 |
= 5 * ( 1 * 2 – 1 * 1 ) =
= 5
det A не равен нулю. Использование формул Крамера возможно.
Вычислим det A1 подробнееНеобходимо заменить столбец 1 в det A на столбец свободных членов системы.
| Система | det A | det A1 | ||||||||||||||||||||||||||||||||||||
|
| det A1 = | -13 | 1 | 1 | = | ||
| -9 | 1 | 2 | ||||
| 12 | 1 | 1 |
 подробнее
подробнее| -13 | 1 | 1 | ||
| -9 | 1 | 2 | ||
| 12 + ( -13) * ( -1) | 1 + 1 * ( -1) | 1 + 1 * ( -1) |
Данное элементарное преобразование не изменит значение определителя.
| = | -13 | 1 | 1 | = | ||
| -9 | 1 | 2 | ||||
| 25 | 0 | 0 |
| Номер строки 3 Номер столбца 1 |
Элемент | Строку 3 и столбец 1 вычеркнули |
|||
| ( -1) 3 + 1 | * | 25 | * |
| Номер строки 3 Номер столбца 2 |
Элемент | Строку 3 и столбец 2 вычеркнули |
|||
| ( -1) 3 + 2 | * | 0 | * |
| Номер строки 3 Номер столбца 3 |
Элемент | Строку 3 и столбец 3 вычеркнули |
|||
| ( -1) 3 + 3 | * | 0 | * |
Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.
Если элемент равен нулю, то и произведение тоже равно нулю.
| = ( -1) 3 + 1 * 25 * | 1 | 1 | = | ||
| 1 | 2 |
= 25 * ( 1 * 2 – 1 * 1 ) =
= 25
Вычислим det A2 подробнееНеобходимо заменить столбец 2 в det A на столбец свободных членов системы.
| Система | det A | det A2 | ||||||||||||||||||||||||||||||||||||
|
| det A2 = | -2 | -13 | 1 | = | ||
| -1 | -9 | 2 | ||||
| 3 | 12 | 1 |
 подробнее
подробнее| -2 | -13 | 1 | ||
| -1 | -9 | 2 | ||
| 3 + ( -2) | 12 + ( -13) | 1 + 1 |
Данное элементарное преобразование не изменит значение определителя.
| = | -2 | -13 | 1 | = | ||
| -1 | -9 | 2 | ||||
| 1 | -1 | 2 |
| -2 + 1 * 2 | -13 + ( -1) * 2 | 1 + 2 * 2 | ||
| -1 | -9 | 2 | ||
| 1 | -1 | 2 |
Данное элементарное преобразование не изменит значение определителя.
| = | 0 | -15 | 5 | = | ||
| -1 | -9 | 2 | ||||
| 1 | -1 | 2 |
 подробнее
подробнее| 0 | -15 | 5 | ||
| -1 + 1 | -9 + ( -1) | 2 + 2 | ||
| 1 | -1 | 2 |
Данное элементарное преобразование не изменит значение определителя.
| = | 0 | -15 | 5 | = | ||
| 0 | -10 | 4 | ||||
| 1 | -1 | 2 |
| Номер строки 1 Номер столбца 1 |
Элемент | Строку 1 и столбец 1 вычеркнули |
|||
| ( -1) 1 + 1 | * | 0 | * |
| Номер строки 2 Номер столбца 1 |
Элемент | Строку 2 и столбец 1 вычеркнули |
|||
| ( -1) 2 + 1 | * | 0 | * |
| Номер строки 3 Номер столбца 1 |
Элемент | Строку 3 и столбец 1 вычеркнули |
|||
| ( -1) 3 + 1 | * | 1 | * |
Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.
Если элемент равен нулю, то и произведение тоже равно нулю.
| = ( -1) 3 + 1 * 1 * | -15 | 5 | = | ||
| -10 | 4 |
= -10
Вычислим det A3 подробнееНеобходимо заменить столбец 3 в det A на столбец свободных членов системы.
| Система | det A | det A3 | ||||||||||||||||||||||||||||||||||||
|
| det A3 = | -2 | 1 | -13 | = | ||
| -1 | 1 | -9 | ||||
| 3 | 1 | 12 |
 подробнее
подробнее| -2 + ( -1) * ( -1) | 1 + 1 * ( -1) | -13 + ( -9) * ( -1) | ||
| -1 | 1 | -9 | ||
| 3 | 1 | 12 |
Данное элементарное преобразование не изменит значение определителя.
| = | -1 | 0 | -4 | = | ||
| -1 | 1 | -9 | ||||
| 3 | 1 | 12 |
| -1 | 0 | -4 | ||
| -1 | 1 | -9 | ||
| 3 + ( -1) * ( -1) | 1 + 1 * ( -1) | 12 + ( -9) * ( -1) |
Данное элементарное преобразование не изменит значение определителя.
| = | -1 | 0 | -4 | = | ||
| -1 | 1 | -9 | ||||
| 4 | 0 | 21 |
| Номер строки 1 Номер столбца 2 |
Элемент | Строку 1 и столбец 2 вычеркнули |
|||
| ( -1) 1 + 2 | * | 0 | * |
| Номер строки 2 Номер столбца 2 |
Элемент | Строку 2 и столбец 2 вычеркнули |
|||
| ( -1) 2 + 2 | * | 1 | * |
| Номер строки 3 Номер столбца 2 |
Элемент | Строку 3 и столбец 2 вычеркнули |
|||
| ( -1) 3 + 2 | * | 0 | * |
Произведения суммируются. Если элемент равен нулю, то и произведение тоже равно нулю.
Если элемент равен нулю, то и произведение тоже равно нулю.
| = ( -1) 2 + 2 * 1 * | -1 | -4 | = | ||
| 4 | 21 |
= -5
Ответ:
x1 = det A1 / det A = 25/5 = 5
x2 = det A2 / det A = -10/5 = -2
x3 = det A3 / det A = -5/5 = -1
Правило Крамера с двумя переменными
Правило Крамера – еще один метод, позволяющий решать системы линейных уравнений с использованием определителей.
В терминах обозначений матрица – это массив чисел, заключенный в квадратные скобки, а определитель – это массив чисел, заключенный в две вертикальные черты.
Обозначения Формула для определения определителя матрицы 2 x 2 очень проста.
Давайте быстро рассмотрим:
Определитель матрицы 2 x 2
Быстрые примеры того, как найти детерминанты матрицы 2 x 2
Пример 1 : Найдите определитель матрицы A ниже.
Пример 2 : Найдите определитель матрицы B ниже.
Пример 3 : Найдите определитель матрицы C ниже.
Зная, как найти определитель матрицы 2 x 2, теперь вы готовы изучить процедуры или шаги по использованию правила Крамера.Вот так!
Правила Крамера для систем линейных уравнений с двумя переменными
- Назначьте имена для каждой матрицы
Матрица коэффициентов:
X – матрица:
Y – матрица:
Отдо найдите переменную x.
Отдо найдите переменную y.
Несколько моментов, которые следует учитывать при рассмотрении формулы:
1) Столбцы \ large {x}, \ large {y} и постоянные члены \ large {c} получаются следующим образом:
2) Оба знаменателя при решении \ large {x} и \ large {y} совпадают. Они происходят из столбцов \ large {x} и \ large {y}.
Они происходят из столбцов \ large {x} и \ large {y}.
3) Глядя на числитель при решении для \ large {x}, коэффициенты столбца \ large {x} заменяются постоянным столбцом (красным).
4) Таким же образом, чтобы найти \ large {y}, коэффициенты \ large {y} -столбца заменяются постоянным столбцом (красным).
Примеры решения систем линейных уравнений с двумя переменными с использованием правила Крамера
Пример 1 : Решите систему с двумя переменными по правилу Крамера
Начните с извлечения трех соответствующих матриц: коэффициент, \ large {x} и \ large {y}.Затем решите каждый соответствующий определитель.
После того, как все три детерминанты вычислены, пора найти значения \ large {x} и \ large {y}, используя приведенную выше формулу.
Я могу записать окончательный ответ как \ large {\ left ({x, y} \ right) = \ left ({2, – 1} \ right)}.
Пример 2 : Решите систему с двумя переменными по правилу Крамера
Задайте свои коэффициенты, матрицы \ large {x} и \ large {y} из данной системы линейных уравнений. Затем рассчитайте их детерминанты соответственно.
Затем рассчитайте их детерминанты соответственно.
Помните, что всегда вычитает произведений диагональных записей.
- Для матрицы коэффициентов (используйте коэффициенты обеих переменных x и y )
- Для X – матрица (заменить столбец x на столбец констант)
- Для Y – матрица (заменить y-столбец на постоянный)
Надеюсь, вам удобно вычислять определитель двумерной матрицы.Чтобы окончательно решить требуемые переменные, я получаю следующие результаты…
Записав окончательный ответ в точечной нотации, я получил \ large {\ left ({x, y} \ right) = \ left ({6, – 5} \ right)}.
Пример 3 : Решите систему с двумя переменными по правилу Крамера
Эту проблему на самом деле довольно легко решить методом исключения. Это связано с тем, что коэффициенты переменной x являются «одинаковыми», но только противоположными по знакам (+1 и -1). Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы, и переменная x исчезает, оставляя вам одношаговое уравнение в \ large {y}.Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать наиболее эффективную. Всегда уточняйте у своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.
Чтобы решить эту проблему с помощью метода исключения, вы добавляете соответствующие столбцы, и переменная x исчезает, оставляя вам одношаговое уравнение в \ large {y}.Я говорю об этом, потому что у каждой техники есть недостатки, и лучше выбрать наиболее эффективную. Всегда уточняйте у своего учителя, можно ли использовать другой подход, если метод не указан для данной проблемы.
В любом случае, поскольку мы учимся решать по правилу Крамера, давайте продолжим и разберемся с этим методом.
Я построю три матрицы (коэффициент, \ large {x} и \ large {y}) и оценю их соответствующие детерминанты.
- Для X – матрица (прописная D с нижним индексом x)
- Для Y – матрица (прописная D с индексом y)
После получения значений трех требуемых определителей я вычислю \ large {x} и \ large {y} следующим образом.
Окончательный ответ в виде баллов: \ large {\ left ({x, y} \ right) = \ left ({- 1,2} \ right)}.
Пример 4 : Решить по правилу Крамера систему с двумя переменными
Поскольку мы уже рассмотрели несколько примеров, я предлагаю вам попробовать решить эту проблему самостоятельно. Затем сравните свои ответы с решением ниже.
Если вы поймете все правильно с первого раза, это означает, что вы становитесь «профи» в отношении правила Крамера. Если вы этого не сделали, попытайтесь выяснить, что пошло не так, и научитесь не совершать ту же ошибку в следующий раз.Так вы станете лучше в математике. Изучите множество проблем и, что более важно, много практикуйтесь самостоятельно.
Вы должны получить ответ ниже…
Пример 5 : Решите систему с двумя переменными по правилу Крамера
В нашем последнем примере я включил ноль в столбец констант. Каждый раз, когда вы видите число ноль в столбце констант, я настоятельно рекомендую использовать правило Крамера для решения системы линейных уравнений. Почему? Потому что вычисление определителей для матриц \ large {x} и \ large {y} значительно упрощается. Убедитесь сами!
Почему? Потому что вычисление определителей для матриц \ large {x} и \ large {y} значительно упрощается. Убедитесь сами!
Окончательное решение этой проблемы –
Практика с рабочими листами
Возможно, вас заинтересует:
Правило Крамера 3 × 3
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.Один из способов – увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]
- Дополните [латекс] A [/ латекс] первыми двумя столбцами.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} | \ begin {array} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \ begin {array} {c } {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {array} | [/ latex]
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали.
 Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Рисунок 2
Алгебра выглядит следующим образом:
[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} – {a} _ {3} {b} _ {2} {c} _ {1} – {b} _ {3} {c} _ {2} {a} _ {1} – {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]
Пример 3: Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 при
[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} | \ begin {array} {c} 0 \\ 3 \\ 4 \ end {array} \ begin {array} {c} 2 \\ -1 \\ 0 \ end {array} | \ hfill \\ = 0 \ left (-1 \ right ) \ влево (1 \ вправо) +2 \ влево (1 \ вправо) \ влево (4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ left (1 \ right) -0 \ left (1 \ right) \ left (0 \ right) -1 \ left (3 \ right) \ left (2 \ right) \ hfill \\ = 0 + 8 + 0 + 4 – 0-6 \ hfill \\ = 6 \ hfill \ end {array} [/ latex]
Попробуйте 2
Найдите определитель матрицы 3 × 3.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]
Вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] \ text {3} \ text {} \ times \ text {} 3 [/ латексные] матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить Правило Крамера для решения системы трех уравнений с тремя переменными .Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
Рисунок 3
[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]
где
Рисунок 4
Если мы записываем определитель [latex] {D} _ {x} [/ latex], мы заменяем столбец [latex] x [/ latex] на столбец констант.Если мы пишем определитель [latex] {D} _ {y} [/ latex], мы заменяем столбец [latex] y [/ latex] постоянным столбцом. Если мы пишем определитель [latex] {D} _ {z} [/ latex], мы заменяем столбец [latex] z [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Пример 4: Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x – 2y + z = -5 \\ x + 3y – 2z = 14 \ end {array} [/ latex]
Решение
Используйте правило Крамера.
[латекс] D = | \ begin {array} {ccc} 1 & 1 & -1 \\ 3 & -2 & 1 \\ 1 & 3 & -2 \ end {array} |, {D} _ {x} = | \ begin { array} {ccc} 6 & 1 & -1 \\ -5 & -2 & 1 \\ 14 & 3 & -2 \ end {array} |, {D} _ {y} = | \ begin {array} {ccc} 1 & 6 & -1 \\ 3 & -5 & 1 \\ 1 & 14 & -2 \ end {array} |, {D} _ {z} = | \ begin {array} {ccc} 1 & 1 & 6 \\ 3 & -2 & -5 \\ 1 & 3 & 14 \ end {array} | [/ latex]
Затем,
[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = – 2 \ hfill \ end {array} [/ latex]
Решение [латекс] \ left (1,3, -2 \ right) [/ latex].
Попробовать 3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс] \ begin {array} {r} \ hfill x – 3y + 7z = 13 \\ \ hfill x + y + z = 1 \\ \ hfill x – 2y + 3z = 4 \ end {array} [/ латекс]
Пример 5: Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 3x – 2y = 4 \ text {} \ left (1 \ right) \\ 6x – 4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ латекс]
Решение
Начнем с нахождения определителей [латекс] D, {D} _ {x}, \ text {и} {D} _ {y} [/ latex].
[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель – исключить одну из переменных.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс].
- Добавьте результат к уравнению [латекс] \ left (2 \ right) [/ latex].
[латекс] \ begin {array} \ text {} \ hfill − 6x + 4y = −8 \\ \ hfill6x − 4y = 0 \\ \ hfill \ text {_____________} \\ \ hfill 0 = 8 \ end { array} [/ latex]
Получаем уравнение [латекс] 0 = -8 [/ латекс], которое неверно. Следовательно, у системы нет решения. График системы показывает две параллельные линии.
Следовательно, у системы нет решения. График системы показывает две параллельные линии.
Рисунок 5
Пример 6. Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
[латекс] \ begin {array} {rr} \ hfill x – 2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y – 2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x – 4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]
Решение
Давайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.
[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]
Затем,
[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) – \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ влево (3 \ вправо) \ влево (-2 \ вправо) = 0 [/ латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений. Чтобы выяснить это, нам нужно провести отбор.
Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс] и добавьте результат к уравнению (3):
[латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y – 6x = 0 \\ \ hfill 2x – 4y + 6z = 0 \ end {array}} {0 = 0} [/ latex ]
- Получение ответа [latex] 0 = 0 [/ latex], утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы видим, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Рисунок 6
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Вычисление определителя матрицы 2 × 2
Определитель – это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин. Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы , чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.
Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. В наших целях мы ориентируемся на определитель как на показатель обратимости матрицы. Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.
Общее примечание: Найдите определитель матрицы 2 × 2
Определитель матрицы [latex] 2 \ text {} \ times \ text {} 2 [/ latex], учитывая
[латекс] A = \ left [\ begin {array} {cc} a & b \\ c & d \ end {array} \ right] [/ latex]
определяется как
Рисунок 1
Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, включая [latex] \ mathrm {det} \ left (A \ right) [/ latex] и замену скобок в матрице прямыми линиями, [latex] | A | [/ latex] .
Пример 1: Нахождение определителя матрицы 2 × 2
Найдите определитель заданной матрицы.
[латекс] A = \ left [\ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} \ right] [/ latex]
Решение
[латекс] \ begin {array} {l} \ mathrm {det} \ left (A \ right) = | \ begin {array} {cc} 5 & 2 \\ -6 & 3 \ end {array} | \ hfill \ \ = 5 \ left (3 \ right) – \ left (-6 \ right) \ left (2 \ right) \ hfill \\ = 27 \ hfill \ end {array} [/ latex]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704–1752), который представил его в 1750 году во Введении к анализу линий Курб. algébriques. Правило Крамера – это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.
Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \ left (1 \ right) \\ {a} _ { 2} x + {b} _ {2} y = {c} _ {2} \ left (2 \ right) \ end {array} [/ latex]
Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажите, что мы хотим решить для [latex] x [/ latex]. Если уравнение (2) умножается на коэффициент, противоположный коэффициенту [латекс] y [/ латекс] в уравнении (1), уравнение (1) умножается на коэффициент [латекс] y [/ латекс] в уравнении (2) ), и мы добавляем два уравнения, переменная [latex] y [/ latex] будет удалена.
[латекс] \ begin {array} \ text {} b_ {2} a_ {1} x + b_ {2} b_ {1} y = b_ {2} c_ {1} \ hfill & \ text {Multiply} R_ { 1} \ text {by} b_ {2} \\ – b_ {1} a_ {2} x − b_ {1} b_ {2} y = −b_ {1} c_ {2} \ hfill & \ text {Умножить} R_ {2} \ text {by} −b_ {2} \\ \ text {______________________} \\ b_ {2} a_ {1} x − b_ {1} a_ {2} x = −b_ {2} c_ { 1} −b_ {1} c_ {2} \ end {array} [/ latex]
Теперь решите для [латекс] x [/ латекс].
[латекс] \ begin {array} {l} {b} _ {2} {a} _ {1} x- {b} _ {1} {a} _ {2} x = {b} _ {2 } {c} _ {1} – {b} _ {1} {c} _ {2} \ hfill \\ x \ left ({b} _ {2} {a} _ {1} – {b} _ {1} {a} _ {2} \ right) = {b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2} \ hfill \\ \ text { } x = \ frac {{b} _ {2} {c} _ {1} – {b} _ {1} {c} _ {2}} {{b} _ {2} {a} _ {1 } – {b} _ {1} {a} _ {2}} = \ frac {\ left [\ begin {array} {cc} {c} _ {1} & {b} _ {1} \\ { c} _ {2} & {b} _ {2} \ end {array} \ right]} {\ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} \ right]} \ hfill \ end {array} [/ latex]
Аналогичным образом, чтобы найти [latex] y [/ latex], мы исключим [latex] x [/ latex].
[латекс] \ begin {array} \ text {} a_ {2} a_ {1} x + a_ {2} b_ {1} y = a_ {2} c_ {1} \ hfill & \ text {Multiply} R_ { 1} \ text {by} a_ {2} \\ – a_ {1} a_ {2} x − a_ {1} b_ {2} y = −a_ {1} c_ {2} \ hfill & \ text {Умножить} R_ {2} \ text {by} −a_ {1} \\ \ text {______________________} \\ a_ {2} b_ {1} y − a_ {1} b_ {2} y = a_ {2} c_ {1 } −a_ {1} c_ {2} \ end {array} [/ latex]
Решение для [latex] y [/ latex] дает
[латекс] \ begin {array} {l} {a} _ {2} {b} _ {1} y- {a} _ {1} {b} _ {2} y = {a} _ {2 } {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ y \ left ({a} _ {2} {b} _ {1} – {a} _ {1} {b} _ {2} \ right) = {a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2} \ hfill \\ \ text { } y = \ frac {{a} _ {2} {c} _ {1} – {a} _ {1} {c} _ {2}} {{a} _ {2} {b} _ {1 } – {a} _ {1} {b} _ {2}} = \ frac {{a} _ {1} {c} _ {2} – {a} _ {2} {c} _ {1} } {{a} _ {1} {b} _ {2} – {a} _ {2} {b} _ {1}} = \ frac {| \ begin {array} {cc} {a} _ { 1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1 } & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |} \ hfill \ end {array} [/ latex]
Обратите внимание, что знаменатель для [latex] x [/ latex] и [latex] y [/ latex] является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения для [latex] x [/ latex] и [latex] y [/ latex], но правило Крамера также вводит новые обозначения:
Ключом к правилу Крамера является замена интересующего нас столбца переменных на столбец констант и вычисление детерминантов. Затем мы можем выразить [латекс] x [/ latex] и [latex] y [/ latex] как частное двух определителей.
Общее примечание: правило Крамера для систем 2 × 2
Правило Крамера – это метод, который использует детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.
Рассмотрим систему двух линейных уравнений с двумя переменными.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \ end {array} [/ latex]
Решение, использующее правило Крамера, дается как
[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {cc} {c} _ {1} & {b} _ {1} \\ {c} _ {2} & {b} _ {2} \ end {array} |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ { a} _ {2} & {b} _ {2} \ end {array} |}, D \ ne 0; \ text {} \ text {} y = \ frac {{D} _ {y}} {D } = \ frac {| \ begin {array} {cc} {a} _ {1} & {c} _ {1} \\ {a} _ {2} & {c} _ {2} \ end {array } |} {| \ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end {array} |}, D \ ne 0 [/ латекс].
Если мы решаем для [latex] x [/ latex], столбец [latex] x [/ latex] заменяется столбцом констант. Если мы решаем для [latex] y [/ latex], столбец [latex] y [/ latex] заменяется постоянным столбцом.
Пример 2: Использование правила Крамера для решения системы 2 × 2
Решите следующую систему [latex] 2 \ text {} \ times \ text {} 2 [/ latex], используя правило Крамера.
[латекс] \ begin {array} {c} 12x + 3y = 15 \\ \ text {} 2x – 3y = 13 \ end {array} [/ latex]
Решение
Решите для [латекс] x [/ латекс].
[латекс] x = \ frac {{D} _ {x}} {D} = \ frac {| \ begin {array} {rr} \ hfill 15 & \ hfill 3 \\ \ hfill 13 & \ hfill -3 \ end {array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {-45 – 39} {- 36 – 6} = \ frac {-84} {- 42} = 2 [/ latex]
Найдите [латекс] y [/ latex].
[латекс] y = \ frac {{D} _ {y}} {D} = \ frac {| \ begin {array} {rr} \ hfill 12 & \ hfill 15 \\ \ hfill 2 & \ hfill 13 \ end { array} |} {| \ begin {array} {rr} \ hfill 12 & \ hfill 3 \\ \ hfill 2 & \ hfill -3 \ end {array} |} = \ frac {156 – 30} {- 36 – 6} = – \ frac {126} {42} = – 3 [/ латекс]
Решение [латекс] \ left (2, -3 \ right) [/ latex].
Попробуйте 1
Используйте правило Крамера для решения системы уравнений 2 × 2.
[латекс] \ begin {массив} {l} \ text {} x + 2y = -11 \ hfill \\ -2x + y = -13 \ hfill \ end {array} [/ latex]
Cramér’s V – Учебное пособие для начинающих
Рубен Герт ван ден Берг в разделе Статистика A-Z и корреляцияV Крамера – это число от 0 до 1, которое указывает, насколько сильно связаны две категориальные переменные. Если мы хотим узнать, связаны ли 2 категориальные переменные, наш первый вариант – это проверка независимости хи-квадрат.2 \) – статистика хи-квадрат Пирсона из вышеупомянутого теста;
Cramér’s V – Примеры
Ученый хочет знать, связаны ли музыкальные предпочтения с учебной специальностью. Он спрашивает 200 студентов, в результате чего получается таблица непредвиденных обстоятельств, показанная ниже.
Эти необработанные частоты – именно то, что нам нужно для всех видов вычислений, но они не показывают большой закономерности.2 \) = 0. Согласно нашей формуле, хи-квадрат = 0 означает, что V Крамера = 0 . Это означает, что музыкальные предпочтения «ничего не говорят» об учебе. Соответствующая таблица и диаграмма поясняют это.
Обратите внимание, что частота распределения по специальности идентична в каждой группе музыкальных предпочтений. Если мы хотим спрогнозировать чью-либо специальность, знание его музыкальных предпочтений ничуть не поможет нам. Наше лучшее предположение – всегда закон или «другое».
Cramér’s V – умеренная ассоциация
Вторая выборка из 200 студентов показывает иную картину. Процентное соотношение строк показано ниже.
Эта таблица демонстрирует некоторую связь между музыкальными предпочтениями и специальностью: частотное распределение исследований различно для групп музыкальных предпочтений.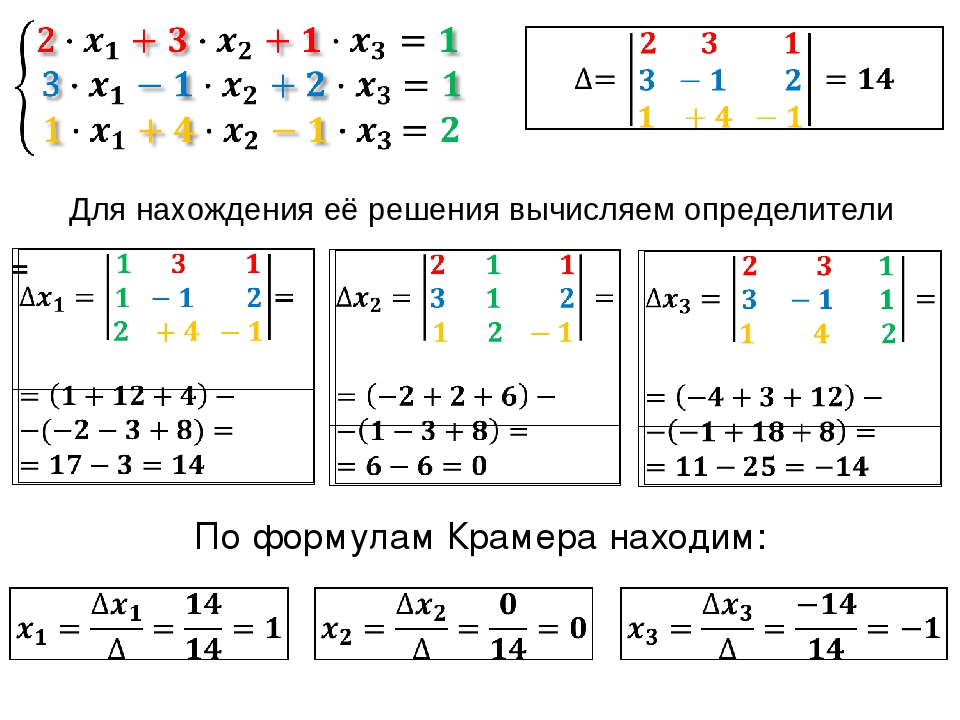 Например, 60% студентов, предпочитающих поп-музыку, изучают психологию. Те, кто предпочитает классическую музыку, в основном изучают право. На диаграмме ниже представлена наша таблица.2 \ приблизительно \) 113;
Например, 60% студентов, предпочитающих поп-музыку, изучают психологию. Те, кто предпочитает классическую музыку, в основном изучают право. На диаграмме ниже представлена наша таблица.2 \ приблизительно \) 113;
Отсюда следует, что
$$ \ phi_c = \ sqrt {\ frac {113} {200 (3)}} = 0,43. $$
, что является существенным, но не сверхвысоким, поскольку V Крамера имеет максимальное значение 1.
Cramér’s V – Perfect Association
В третьей и последней выборке студентов музыкальные предпочтения и предмет обучения полностью связаны. Таблица и диаграмма ниже показывают процентное соотношение строк.2 \) = 600, поэтому
$$ \ phi_c = \ sqrt {\ frac {600} {200 (3)}} = 1, $$
, что является максимально возможным значением для Cramér’s V.
.Альтернативные меры
Cramér’s V – SPSS
В SPSS, Cramér’s V доступен из
. Затем заполните диалоговое окно, как показано ниже.
Затем заполните диалоговое окно, как показано ниже.
Предупреждение: для таблиц размером более 2 на 2 SPSS возвращает бессмысленные значения для phi без выдачи предупреждений или ошибок. Часто они> 1, что невозможно даже для корреляций Пирсона.Как ни странно, вы не можете запросить V Крамера, не получив этих сумасшедших значений фи.
Заключительные ноты
Крамера V также известен как Крамеровский фи (коэффициент) 5 . Это расширение вышеупомянутого коэффициента phi для таблиц размером более 2 на 2, поэтому он обозначается как \ (\ phi_c \). Было предложено заменить его на «V», потому что старые компьютеры не могли печатать букву \ (\ phi \). 3
Спасибо за чтение.
Список литературы
- Ван ден Бринк, W.П. и Келе П. (2002). Statistiek, deel 3 [Статистика, часть 3]. Амстердам: Бум.
- Филд, А. (2013). Обнаружение статистики с помощью IBM SPSS Ньюбери Парк, Калифорния: Sage.

- Хауэлл, округ Колумбия (2002). Статистические методы психологии (5-е изд.). Пасифик Гроув Калифорния: Даксбери.
- Слотбум, А. (1987). Statistiek in woorden [Статистика прописью]. Гронинген: Вольтерс-Нордхофф.
- Шескин, Д. (2011). Справочник по параметрическим и непараметрическим статистическим процедурам .Бока-Ратон, Флорида: Chapman & Hall / CRC.
|
Правило Крамера
Рассмотрим общую линейную систему 2 на 2
Умножение первого уравнения на a 22 , второго на – a 12 и сложение результатов исключает y и позволяет оценить x :
при условии, что a 11 a 22 – a 12 a 21 ≠ 0.Точно так же умножение первого уравнения на – a 21 , второго на a 11 и сложение результатов исключает x и определяет y :
снова предполагая, что a 11 a 22 – a 12 a 21 ≠ 0. Эти выражения для x и y могут быть записаны в терминах определителей как следует:
Эти выражения для x и y могут быть записаны в терминах определителей как следует:
и
Если исходная система записана в матричной форме,
, то знаменатели в приведенных выше выражениях для неизвестных x и y оба равны определителю матрицы коэффициентов.Кроме того, числитель в выражении для первого неизвестного, x , равен определителю матрицы, которая получается, когда первый столбец матрицы коэффициентов заменяется столбцом констант, а числитель в выражении для вторая неизвестная, y , равна определителю матрицы, которая получается, когда второй столбец матрицы коэффициентов заменяется столбцом констант. Это Правило Крамера для линейной системы 2 на 2.
Расширение шаблона до линейной системы 3 на 3,
Правило Крамера гласит, что если определитель матрицы коэффициентов отличен от нуля, то выражения для неизвестных x, y и z принимают следующий вид:
Общая форма правила Крамера выглядит следующим образом: Система из n линейных уравнений в n неизвестных, записанных в матричной форме A x = b как
будет иметь уникальное решение, если det A ≠ 0, и в этом случае значение неизвестного x j дается выражением
, где A j – это матрица, которая получается, когда столбец j матрицы коэффициентов A заменяется матрицей столбцов b .
Два важных теоретических результата о квадратных системах вытекают из правила Крамера:
Теорема F . Квадратная система A x = b будет иметь уникальное решение для каждой матрицы столбцов b тогда и только тогда, когда det A ≠ 0.
Теорема G . Однородная квадратная система A x = 0 будет иметь только тривиальное решение x = 0 тогда и только тогда, когда det A ≠ 0.
Хотя правило Крамера имеет теоретическое значение, поскольку дает формулу для неизвестных, обычно это неэффективный метод решения, особенно для больших систем. Метод исключения Гаусса по-прежнему остается предпочтительным. Однако правило Крамера может быть полезно, когда, например, необходимо значение только одного неизвестного.
Пример 1 : Используйте правило Крамера, чтобы найти значение y , учитывая, что
Поскольку эта линейная система эквивалентна матричному уравнению
Правило Крамера подразумевает, что второе неизвестное, y , дается выражением
при условии, что знаменатель – определитель матрицы коэффициентов – не равен нулю. Сокращение строк с последующим расширением Лапласа по первому столбцу оценивает эти детерминанты:
Сокращение строк с последующим расширением Лапласа по первому столбцу оценивает эти детерминанты:
С этими расчетами (*) означает
Правило Крамера и обращение матрицы
1.3 Решение систем линейных уравнений: правило Крамера и обращение матрицы
Два уравнения с двумя переменными
Рассмотрим систему двух уравнений с двумя переменными x 1 и x 2 :
| a x 1 + b x 2 | = u |
| c x 1 + d x 2 | = v , |
Один из простых способов найти x 1 и x 2 – выделить одну из переменных в одном из уравнений и подставить результат в другое уравнение. Например, из второго уравнения имеем
Например, из второго уравнения имеем
x 2 = ( v – c x 1 ) / d .
Подставляя это выражение для x 2 в первое уравнение, получаемa x 1 + b ( v – c x 1 ) / d = u ,
который мы можем записать как( a – b c / d ) x 1 + b v / d = u .
Сначала предположим, что a ≠ b c / d . потом или же Чтобы найти x 2 , мы используем тот факт, что x 2 = ( v – c x 1 ) / d , чтобы получитьТеперь предположим, что a = b c / d . Тогда уравнения имеют вид
| a x 1 + b x 2 | = u |
| ( a d / b ) x 1 + d x 2 | = v |
| a d x 1 + b d x 2 | = u d |
| a d x 1 + b d x 2 | = v b . |
Таким образом, решения системы уравнений имеют три возможных вида.
- Если a d ≠ b c , то уравнения имеют уникальное решение,
( x 1 , x 2 ) = , . - Если a d = b c и u d = v b , то набором решений уравнений является набор пар
для любого числа x 1 .x 1 , 
- Если a d = b c и u d ≠ v b , то уравнения не имеют решения.
Этот метод выделения переменной в одном уравнении и подстановки ее в другое уравнение является громоздким, когда система состоит из более чем двух уравнений и двух переменных. Теперь я опишу более элегантный метод.
n уравнений в n переменныхМы можем записать систему двух уравнений с двумя переменными из предыдущего раздела в матричной форме, как
Общая система уравнений n в переменных n может быть записана какA x = b ,
где A – это матрица n × n , а x и b – это векторы-столбцы n × 1.Если A неособое число, то умножение каждой стороны на обратное значение A −1 от A дает
x = A -1 b ,
единственное решение в этом случае. Таким образом, решение системы уравнений в данном случае сводится к нахождению обратной матрицы A .
Таким образом, решение системы уравнений в данном случае сводится к нахождению обратной матрицы A .Если определитель A равен нулю, то будет ли система уравнений иметь много решений или ни одного, зависит от рангов A и расширенной матрицы, определенной следующим образом.
- Определение
- Пусть A – это матрица n × n , а b – вектор-столбец n × 1. Расширенная матрица ( A , b ) – это матрица с n строк и n + 1 столбцами, в которой A составляет первые n строк и столбцов, а b – последний столбец. .
- Источник предложения
- Пусть A будет матрицей n × n и пусть b будет вектором-столбцом n × 1. Если A невырожден, то система уравнений
A x = b
имеет уникальное решение: x = A −1 b . Если определитель A равен нулю, то система имеет бесконечно много решений, если ранг расширенной матрицы ( A , b ) равен рангу A , и в противном случае не имеет решения.
Если определитель A равен нулю, то система имеет бесконечно много решений, если ранг расширенной матрицы ( A , b ) равен рангу A , и в противном случае не имеет решения.
- Источник скрыть
- Для доказательства см. Hadley (1961), pp. 168–169.
Если n = 2 или n = 3, вычислить обратное к A относительно легко, так что, если система уравнений имеет решение, это решение может быть легко найдено, как показывают следующие примеры.
- Пример
- Рассмотрим систему уравнений
Запишите это в матричной форме. Если a d ≠ b c , тогда существует обратная матрица слева иa x 1 + b x 2 = u c x 1 + d x 2 = против .
так что у нас есть Таким образом а также как мы обнаружили раньше.д – б – в a 
- Пример
- Рассмотрим систему уравнений
При записи в матричной форме A x = b , матрица A будет2 x 1 + x 2 + 2 x 3 = 1 x 1 – x 2 + x 3 = 0 2 x 2 – x 3 = 3.
Определитель этой матрицы равен 3 ≠ 0, поэтому матрица невырожденная. Используя общую формулу для обратной матрицы, обратная матрица равна2 1 2 1 -1 1 0 2 -1 . 
Умножение этой матрицы на транспонирование (1, 0, 3) дает ( x 1 , x 2 , x 3 ) = (8/3, 1/3, −7 / 3), что, таким образом, является единственным решением системы уравнений. (Подставляя этот список значений в исходные уравнения, вы можете убедиться, что это действительно решение.)-1/3 5/3 1 1/3 -2/3 0 2/3 −4/3 -1 .
- Пример
- Рассмотрим систему уравнений
При записи в матричной форме матрица слева выглядит так:4 x 1 + 2 x 2 + x 3 = 1 2 x 1 – 2 x 2 + 2 x 3 = 0 4 x 2 – 2 x 3 = 3. 
Определитель этой матрицы равен 0; его ранг 2.Расширенная матрица4 2 1 2 −2 2 0 4 −2 .
Эта матрица имеет ранг 3 (определитель матрицы 3 × 3, состоящей из последних трех строк и столбцов, равен 14 ≠ 0), поэтому согласно предыдущему результату система уравнений не имеет решения.4 2 1 1 2 −2 2 0 0 4 −2 3 .  (Другой способ убедиться, что система не имеет решения, – это умножить второе уравнение на 2, а третье уравнение на 1,5 и прибавить
их вместе. Полученное уравнение несовместимо с первым уравнением.)
(Другой способ убедиться, что система не имеет решения, – это умножить второе уравнение на 2, а третье уравнение на 1,5 и прибавить
их вместе. Полученное уравнение несовместимо с первым уравнением.)
- Пример
- Рассмотрим систему уравнений
При записи в матричной форме матрица слева выглядит так:3 x 1 + 4 x 2 = 7 6 x 1 + 8 x 2 = 14.
Определитель этой матрицы равен 0; ее ранг равен 1. Расширенная матрица3 4 6 8 .
Эта матрица имеет ранг 1 (определитель каждой подматрицы 2 × 2 равен 0), поэтому согласно предыдущему результату система уравнений имеет бесконечно много решений.3 4 7 6 8 14 . 
Второе уравнение вдвое больше первого, поэтому любое ( x 1 , x 2 ), удовлетворяющее первому уравнению, удовлетворяет второму. Следовательно, ( x 1 , x 2 ) является решением системы уравнений тогда и только тогда, когда 3 x 1 + 4 x 2 = 7, или, если вы например, x 2 = (7 – 3 x 1 ) / 4.
Правило Крамера
Полезный вывод из того факта, что решение системы A x = b дается как x = A −1 b , если A неособое, следующий результат ( из-за Габриэля Крамера, 1704-1752), который дает явное выражение для значения каждой переменной в отдельности.
- Предложение (правило Крамера)
- Пусть A будет матрицей n × n , пусть b будет вектор-столбцом n × 1, и рассмотрим систему уравнений
A x = b
где x – вектор-столбец n × 1.Если A неособое, тогда (уникальное) значение x , которое удовлетворяет системе, определяется какx i = | A * ( b , i ) | / | A | для i = 1, …, n ,
где A * ( b , i ) – это матрица, полученная из A заменой i -го столбца на b .
- Доказательство
- У нас есть x = A −1 b , так что
x i = ∑ n
где v i j – ( i , j ) -й компонент A −1 .
j = 1 v i j b j ,Теперь, согласно предыдущему результату, ( i , j ) -й компонент A −1 равен (−1) i + j | A j i | / | A |. Таким образом
x i = ∑ n
Наконец, вычислите определитель A * ( b , i ) в выражении результата, развернув его по его i -му столбцу. Это столбец b , поэтому согласно второй части предыдущего результата мы имеем
j = 1 (−1) i + j | A j i | b j / | A |.| A * ( b , i ) | = ∑ n
установление результата.(Обратите внимание, что, поскольку i является индексом столбца , по которому мы расширяемся, роли i и j здесь поменялись местами относительно их ролей в формулировке результата, который мы используем.
j = 1 (−1) i + j b j | A j i |, )
)
- Пример
- Применение правила Крамера к системе
если a d ≠ b c получаемa x 1 + b x 2 = u c x 1 + d x 2 = v ,
а такжеx 1 = u б v д a d – b c
Вычисляя определители в числителях, имеем а такжеx 2 = a u c против a d – b c . .png)
- Пример
- Значение x 2 в решении системы уравнений
является, по правилу Крамера, определителем2 x 1 + x 2 + 2 x 3 = 1 x 1 – x 2 + x 3 = 0 2 x 2 – x 3 = 3
делится на определитель2 1 2 1 0 1 0 3 -1 2 1 2 1 -1 1 0 2 -1 . 

 Затем вы делите это на абсолютную сумму (200). Это (110×50) / 200 = 27,5
Затем вы делите это на абсолютную сумму (200). Это (110×50) / 200 = 27,5

