Примеры из жизни кинематика: приведите примеры кинематики – Школьные Знания.com

Кинематика

Кинематика — это раздел теоретической механики, в котором изучается движение механических систем с геометрической точки зрения, без учета причин (сил), вызывающих это движение и изменение движения.

Положение тела, его движение в пространстве может быть определено относительно другого неизменяемого тела. С ним связывают выбранную систему отсчёта — систему координат, в которой и определяют параметры движения.

Установление способов, с помощью которых может быть задано движение точек или тел по отношению к выбранной системе отсчёта, позволит определить кинематические характеристики движения (траектории точек, их скорости, ускорения, угловые параметры тел.)

Движение любой механической системы относительно выбранной системы отсчёта будет известно, если известно движение каждой точки этой системы. Поэтому изучение раздела «Кинематика» начинается с темы «Кинематика точки», далее рассматривается тема «Кинематика твёрдого тела».

Данное учебно-методическое пособие поможет студентам при выполнении контрольных работ по разделу «Кинематика».

В пособии кратко изложена теория, даны основные формулы, приведены примеры решения типовых задач.

Краткость изложения теории предполагает предварительное изучение курса по учебникам, в которых даны подробные обоснования определений, выводы, доказательства теорем.

Методическое пособие может быть рекомендовано и на практических занятиях и при выполнении расчётно-графических работ.

Содержание

1. Кинематика точки
1. Способы задания закона движения точки
1. Векторный
2. Координатный
3. Естественный
2. Кинематика твердого тела
1. Поступательное движение
2. Вращательное движение твердого тела
1. Вращение твердого тела вокруг неподвижной оси
2. Угловая скорость и угловое ускорение
3. Скорости и ускорения точек вращающегося твердого тела
4. Передаточные механизмы
3. Плоскопараллельное движение твердого тела
1. Определение скоростей точек в плоскопараллельном движении 
2. Теорема о скоростях точек в ППД
3. Следствие из теоремы о скоростях точек
4. Мгновенный центр скоростей
5. Определение МЦС
1. Ускорение точки в плоскопараллельном движении
2. Мгновенный центр ускорений
3. Частные случаи МЦУ
6. Сложное движение точки
1. Определение скоростей и ускорений точек в сложном движении
2. Ускорение Кориолиса
7. Сферическое движение
1. Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку
2. Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки
3. Скорости и ускорения точек при вращении тела вокруг неподвижной точки

Урок 36.

движение как перемещение – Естествознание – 10 класс

Естествознание, 10 класс

Урок 36. Движение как перемещение

Перечень вопросов, рассматриваемых в теме:

• Что называют механическим движением?
• Что понимают под относительностью механического движения?
• Какими характеристиками обладает механическое движение?
• Что является причиной механического движения?

Глоссарий по теме:

Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени.

Кинематика – раздел механики, изучающий характер движения.

Динамика – раздел механики, изучающий причины движения.

Материальная точка – тело, размерами которого можно пренебречь в данных условиях.

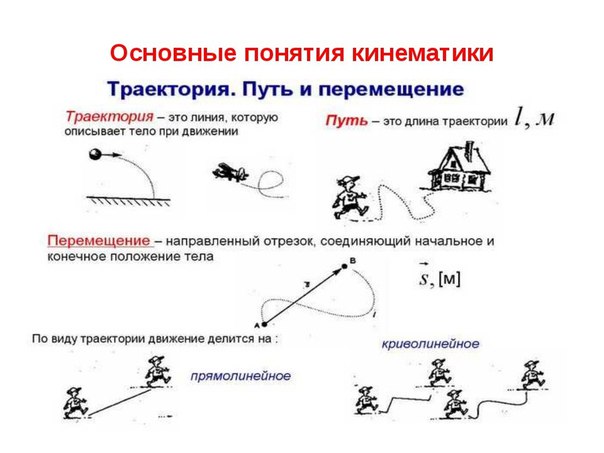
Траектория движения

– линия, вдоль которой движется тело.

Инерциальная система отсчета – система отсчета, в которой все тела в отсутствии внешних воздействий движутся прямолинейно и равномерно, либо покоятся.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

• Естествознание. 10 класс [Текст]: учебник для общеобразоват. организаций: базовый уровень / И.Ю. Алексашина, К.В. Галактионов, И.С. Дмитриев, А.В. Ляпцев и др. / под ред. И.Ю. Алексашиной. – 3-е изд., испр. – М.: Просвещение, 2017. – §55, стр. 166-168
• Физика. 10 класс [Текст]: учебник для общеобразоват. учреждений: базовый уровень; профильный уровень/А.В. Грачев, В.А. Погожев, А.М. Салецкий и др.- Вентана-Граф, 2011 стр. 6-224/

Теоретический материал для самостоятельного изучения

В жизни можно увидеть разные примеры механического движения: движение планет вокруг Солнца, полет птицы, скатывание шарика по жёлобу; во всех случаях изменяется положение тела, таким образом объект совершает перемещение. Изменение положения тела в пространстве с течением времени относительно других тел называется механическим движением. Говоря о механическом движении, необходимо выбрать тело отсчета. Тело, относительно которого происходит это движение, связанная с ним система координат и измеритель времени образуют систему отсчета.

Галилей установил характер относительности движения, поэтому ученые искали абсолютно покоящуюся систему отсчета.

Птолемей выдвинул предположение о том, что Земля – центр системы отсчета, а все планеты и Солнце вращаются вокруг неё. Такую систему отсчета называют геоцентрической.

Коперник же предлагал принять Солнце за неподвижный объект, а все планеты, соответственно, движущимися вокруг него. Эту систему отсчета называют гелиоцентрической, и она принята и по сей день.

Кроме качественного, есть и количественное описание движения. Например, описать характер движения каждой части тела бабочки в полете достаточно сложно. Крылья движутся вверх и вниз, а тельце остается практически на одной высоте. Поэтому если нас не интересуют отдельные детали, то можно представить всю бабочку как малый объект – материальную точку, то есть тело, размерами которого можно пренебречь в данных условиях.

Для точного описания движения материальной точки вводится система координат. При движении координаты точки изменяются.

Немаловажной характеристикой движения является траектория. Это воображаемая линия в пространстве, вдоль которой движется тело.

Иногда траекторию движения можно пронаблюдать и в жизни. Вспомните салют: когда в воздухе разрывается заряд, то видны дымовые и светящиеся следы от каждой искорки. Самолет оставляет белые полосы на небе.

Раздел физики, изучающий виды механического движения и его характеристики, называют кинематикой. Если же нас интересует не характер, а причины движения тел, то нужно обратиться к другому разделу механики – динамике.

На разных этапах развития науки представления ученых о причинах изменения характера движения менялись. Древнегреческий философ Аристотель считал, что для равномерного движения тела необходимо воздействие на него некоторой силы. Галилей, проделав ряд опытов, пришел к выводу, что тело движется равномерно, не взаимодействуя с другими телами.

Но оба вывода не совсем верны: рассмотрев движение мячика, лежащего на полу поезда, когда вагон трогается, можно заметить, что без сторонних сил мячик начнет двигаться с ускорением. Исаак Ньютон, изучив труды Галилея, уточняет закон инерции и вводит понятие инерциальных систем отсчета. Инерциальной системой отсчета называют такую систему, в которой тело покоится или движется равномерно, если на него не действуют другие тела (или действие тел скомпенсировано). В опыте с вагоном и мячиком вагон поезда выступает в роли неинерциальной системы отсчета. Неинерциальной системой отсчета является любая система отсчета, движущаяся в инерциальной системе отсчета с ускорением. На данный момент не обнаружено инерциальной системы отсчета.

Наш шарик движется в вагоне, вагон – с поездом, поезд – вместе с планетой вокруг своей оси и вокруг Солнца, Солнце – вокруг центра галактики, даже сама галактика не неподвижна.

Однако можно принимать некоторые неинерциальные системы отсчета за условно инерциальные при рассмотрении, например, школьных опытов и выполнении лабораторных работ.

Считать же парту, на которой проводится опыт, началом отсчета для описания движения планет нельзя.

Для описания движения планет инерциальной системой отсчета можно считать систему, центр которой находится в центре Солнца, а оси ориентированы по звездам, т.к. их положение относительно Земли постоянно.

Именно по этой причине движение тел лучше описывается в системе Коперника, чем Птолемея.

Так и был сформулирован первый закон Ньютона: в инерциальной системе отсчета тело, не взаимодействуя с другими телами, движется равномерно или покоится.

Подведем итог: изменение положения тела в пространстве с течением времени называется механическим движением. Само движение можно описать с точки зрения механики и с точки зрения динамики. При описании важно учитывать системы отсчета и помнить характеристики явления.

Примеры и разбор решения заданий тренировочного модуля:

Задание: Вставьте пропущенные слова.

В инерциальной системе отсчета тело, не взаимодействуя с другими телами, движется ____________или _________.

Пояснение: правильный ответ – равномерно; покоится. Речь идет о первом законе Ньютона и законе инерции Галилея.

Задание: Подчеркните правильный ответ на вопрос.

Что будет с мячиком массой 1 кг, который лежит на полу поезда с коэффициентом трения 0,3, когда вагон тронется влево?

Варианты ответов:

1. Мячик начнет двигаться с ускорением влево
2. Мячик начнет двигаться с ускорением вправо.
3. Мячик не будет двигаться.
4. Мячик начнет двигаться без ускорения вправо.

Правильный вариант: 2) Мячик начнет двигаться с ускорением вправо.

Пояснение: поезд, начиная движение влево, является неинерциальной системой отсчета. Мячик пытается сохранить свою скорость неизменной и по инерции движется вправо с ускорением.

Примеры лабораторных работ

Конспекты лекций

Конспект лекций 2020 (Лубенченко О.И.)

Лекционные демонстрации

Скачать (Яндекс Диск)

Программы курса

Программа подготовки к экзамену для 1го курса ЭТФ
Программа курса “Специальные вопросы физики”

Материалы по разделу “Механика и молекулярная физика” (1 семестр) для студентов 1 курса (1 семестр) АВТИ, ИРЭ, ИЭТ, ИЭЭ, ИнЭИ (ИБ)

Сборник задач “Механика и молекулярная физика”
Описания лабораторных работ

Материалы по разделу “Электричество и магнетизм” (2 семестр) для студентов 1 курса (2 семестр) АВТИ, ИРЭ, ИЭТ, ИЭЭ, ИнЭИ (ИБ)

Описания лабораторных работ (издание 2018 г. ) – для студентов очной формы обучения
Сборник задач “Электричество и магнетизм”
Описания лабораторных работ №№ 1 – 25, 30 (издание 2005 г.)
Описания лабораторных работ №№ 26 – 29, 31, 32 (издание 2013 г.)

Материалы по разделу “Оптика и атомная физика” (3 семестр) для студентов 2 курса (3 семестр) АВТИ, ИРЭ, ИЭТ, ИЭЭ и 3 курса (5 семестр) ИнЭИ (ИБ)

Программа курса общей физики ЭТФ III сем.
Сборник задач “Оптика и атомная физика”
Сборник задач по оптике с решениями
Описания лабораторных работ №№ 1 – 14
Описания лабораторных работ №№ 15 – 25
Приложение к лабораторным работам №№15-25

Материалы 4 семестр

Гармонический осциллятор

Перечень лабораторных работ по общему курсу физики
Механика и молекулярная физика
1. Погрешности при физических измерениях. Измерение объема цилиндра.
2. Определение плотности вещества и моментов инерции цилиндра и кольца.
3. Изучение законов сохранения при соударении шаров.
4. Изучение закона сохранения импульса.
5. Определение скорости пули методом физического маятника.
6. Определение средней силы сопротивления грунта и изучение неупругого соударения груза и сваи на модели копра.
7. Изучение динамики вращательного движения твердого тела и определение момента инерции маятника Обербека.
8. Изучение динамики плоского движения маятника Максвелла.
9. Определение момента инерции маховика.
10. Определение момента инерции трубы и изучение теоремы Штейнера.
11. Изучение динамики поступательного и вращательного движения с помощью прибора Атвуда.
12. Определение момента инерции плоского физического маятника.
13. Определение удельной теплоты кристаллизации и изменения энтропии при охлаждении сплава олова.
14. Определение молярной массы воздуха.
15. Определение отношения теплоемкостей Сp/Cv газов.
16. Определение средней длины свободного пробега и эффективного диаметра молекул воздуха.
17. Определение коэффициента внутреннего трения жидкости по методу Стокса.
Электричество и магнетизм
1. Исследование электрического поля с помощью электролитической ванны.
2. Определение электрической емкости конденсатора баллистическим гальванометром.
3. Весы напряжения.
4. Определение емкости коаксиального кабеля и плоского конденсатора.
5. Изучение диэлектрических свойств жидкостей.
6 Определение диэлектрической проницаемости жидкого диэлектрика.
7. Изучение электродвижущей силы методом компенсации.
8 Определение индукции магнитного поля измерительным генератором.
9. Измерение индуктивности системы катушек.
10. Изучение переходных процессов в цепи с индуктивностью.
11. Измерение взаимной индуктивности.
12. Изучение кривой намагничивания железа по методу Столетова.
13. Ознакомление с осциллографом и изучение петли гистерезиса.
14. Определение удельного заряда электрона методом магнетрона.
Волновая и квантовая оптика
1. Измерение длины световой волны с помощью бипризмы Френеля.
2. Определение длины волны света методом колец Ньютона.
3. Определение длины световой волны с помощью дифракционной решетки.
4. Изучение дифракции в параллельных лучах.
5. Изучение линейной дисперсии спектрального прибора.
6. Изучение дифракции Фраунгофера на одной и двух щелях.
7. Экспериментальная проверка закона Малю.
8. Исследование линейных спектров испускания.
9 Изучение свойств лазерного излучения.
10 Определение потенциала возбуждения атомов по методу Франка и Герца.
11. Определение ширины запрещенной зоны кремния по красной границе внутреннего фотоэффекта.
12 Определение красной границы фотоэффекта и работы выхода электрона из металла.
13. Измерение температуры спирали лампы с помощью оптического пирометра.


Урок 2. Законы развития систем

Одной из предпосылок ТРИЗ является то, что существуют объективные законы развития и функционирования систем, опираясь на которые можно строить изобретательские решения. Другими словами, многие технические, производственные, экономические и социальные системы развиваются по одним и тем же правилам и принципам.

Г. С. Альтшуллер обнаружил их, изучив патентный фонд и проанализировав пути развития и усовершенствования техники в течение долгого времени. Результаты, опубликованные в книгах «Линии жизни» технических систем» и «О законах развития технических систем», позже объединенные в работе «Творчество как точная наука», стали базисом для Теории развития технических систем (ТРТС).

В данном уроке мы предлагаем вам познакомиться с этими законами, подкрепленными примерами. В программе обучения ТРИЗ они занимают главное место, поскольку раскрываются и детализируются в правилах их применения, в стандартах, принципах разрешения противоречий, вепольном анализе и АРИЗе.

Содержание:

1. Терминология и краткое введение
2. Статика
3. Кинематика
4. Динамика
5. Проверочный тест

Терминология и краткое введение

Закон развития технической системы (ЗРТС) – это существенное, устойчивое, повторяющееся отношение между элементами внутри системы и с внешней средой в процессе прогрессивного развития, перехода системы от одного состояния к другому с целью увеличения ее полезной функциональности.

Г. С. Альтшуллер открытые законы разделил на три раздела «Статику», «Кинематику», «Динамику». Названия эти условны и не имеют прямого отношения к физике. Но можно проследить связь этих групп с моделью «начала жизни-развития-смерти» в соответствии с законом S-образного развития технических систем, который автор предложил для полной картины эволюции процессов в технике. Она изображается логистической кривой, которая показывает меняющиеся со временем темпы развития. Этапов три:

1	«Детство». Конкретно в технике это длительный процесс проектирования системы, ее доработки, изготовления опытного образца, подготовки к серийному выпуску. В глобальном понимании этап связан с законами «Статики» – группой, объединенной критериями жизнеспособности возникающих технических систем (ТС). Говоря простым языком, благодаря этим законам можно дать ответы на два вопроса: Будет ли жить и функционировать создаваемая система? Что нужно сделать для того, чтобы она жила и функционировала?
2	«Расцвет». Этап бурного совершенствования системы, ее становления в качестве мощной и производительной единицы. Он связан со следующей группой законов – «Кинематикой», которая описывает направления развития технических систем вне зависимости от конкретных технических и физических механизмов. В буквальном понимании это означает те изменения, которые должны произойти в системе, чтобы она отвечала возрастающим к ней требованиям.
3	«Старость». С какого-то момента развитие системы замедляется, а позже прекращается вовсе. Это обусловлено законами «Динамики», характеризующими развитие ТС в условиях действия конкретных технических и физических факторов. «Динамика» противоположна «Кинематике» – законы этой группы определяют лишь возможные изменения, которые могут быть совершены в данных условиях. Когда возможности совершенствования исчерпаны, на смену старой системе приходит новая, и весь цикл повторяется.

Законы первых двух групп – «Статики» и «Кинематики» – универсальны по своему характеру. Они действуют в любую эпоху и применимы не только к техническим системам, но и к биологическим, социальным и т. д. «Динамика» же, по словам Альтшуллера, говорит об основных тенденциях функционирования систем именно в наше время.

Как пример действия комплекса этих законов в технике можно вспомнить развитие такой технической системы, как весельный флот. Она прошла становление от маленьких лодок с парой весел до крупных боевых кораблей, где сотни весел располагались в несколько рядов, уступив в результате место парусникам. В социальном и историческом плане примером S-образной системы может служить зарождение, процветание и упадок афинской демократии.

Статика

Законы «Статики» в ТРИЗ определяют начальную стадию функционирования технической системы, начало ее «жизни», определяя необходимые для этого условия. Сама категория «система» говорит нам о целом, составленном из частей. Техническая система, как и любая другая, начинает свою жизнь в результате синтеза отдельных компонентов. Но не всякое такое объединение дает жизнеспособную ТС. Законы группы «Статика» как раз и показывают, какие обязательные условия должны выполняться для успешной работоспособности системы.

Закон 1. Закон полноты частей системы. Необходимым условием принципиальной жизнеспособности технической системы является наличие и минимальная работоспособность основных частей системы.

Основных частей четыре: двигатель, трансмиссия, рабочий орган и орган управления. Для обеспечения жизнеспособности системы нужны не только эти части, но и их пригодность к выполнению функций ТС. Другими словами, эти составляющие должны быть работоспособными не только по отдельности, но и в системе. Классический пример – двигатель внутреннего сгорания, который работает сам по себе, функционирует в такой ТС как легковой автомобиль, но не пригоден для применения в подводной лодке.

Из закона полноты частей системы следует вывод: чтобы система была управляемой, необходимо, чтобы хотя бы одна ее часть была управляемой. Управляемость означает способность менять свойства в зависимости от предполагаемых заданий. Это следствие хорошо иллюстрирует пример из книги Ю. П. Саламатова «Система законов развития техники»: воздушный шар, управлять которым можно с помощью клапана и балласта.

Похожий закон был сформулирован в 1840 г. Ю. фон Либихом и для биологических систем.

Закон 2. Закон «энергетической проводимости» системы. Необходимым условием принципиальной жизнеспособности технической системы является сквозной проход энергии по всем частям системы.

Любая техническая система является преобразователем энергии. Отсюда очевидная необходимость передачи энергии от двигателя через трансмиссию к рабочему органу. Если какая-то часть ТС не будет получать энергии, то и вся система не будет работать. Главным условием эффективности технической системы с точки зрения энергопроводимости является равенство способностей частей системы по принятию и передаче энергии.

Из закона «энергетической проводимости» следует вывод: чтобы часть технической системы была управляемой, необходимо обеспечить энергетическую проводимость между этой частью и органами управления. Этот закон статики также является основой определения трех правил энергопроводимости системы:

1. Если элементы при взаимодействии друг с другом образуют систему, проводящую энергию с полезной функцией, то для повышения ее работоспособности в местах контакта должны быть вещества с близкими или одинаковыми уровнями развития.
2. Если элементы системы при взаимодействии образуют энергопроводящую систему с вредной функцией, то для ее разрушения в местах контактирования элементов должны быть вещества с различными или противоположными уровнями развития.
3. Если элементы при взаимодействии друг с другом образуют энергопроводящую систему с вредной и полезной функцией, то в местах контактирования элементов должны быть вещества, уровень развития которых и физико-химические свойства изменяются под воздействием какого-либо управляемого вещества или поля.

Закон 3. Закон согласования ритмики частей системы. Необходимым условием принципиальной жизнеспособности технической системы является согласование ритмики (частоты колебаний, периодичности) всех частей системы.

Теоретик ТРИЗ А. В. Тригуб уверен, что для устранения вредных явлений или усиления полезных свойств технической системы, необходимо согласовать или рассогласовать частоты колебаний всех подсистем в технической системе и внешних системах. Попросту говоря, для жизнеспособности системы важно, чтобы отдельные части не только работали вместе, но и не мешали друг другу выполнять полезную функцию.

Этот закон прослеживается на примере истории создания установки для дробления камней в почках. Данный аппарат дробит камни целенаправленным лучом ультразвука, чтобы в дальнейшем они выводились натуральным путем. Но изначально для разрушения камня требовалась большая мощность ультразвука, что поражало не только их, но и окружающие ткани. Решение пришло после того, как была согласована частота ультразвука с частотой колебания камней. Это вызывало резонанс, который и разрушал камни, благодаря чему мощность луча удалось уменьшить.

Кинематика

Группа законов ТРИЗ «Кинематика» имеет дело с уже образованными системами, которые проходят этап своего становления. Условие, как было сказано выше, кроется в том, что эти законы определяют развитие ТС, независимо от конкретных технических и физических факторов, его обусловливающих.

Закон 4. Закон увеличения степени идеальности системы. Развитие всех систем идет в направлении увеличения степени идеальности.

В классическом понимании идеальная система – это система, вес, объем, площадь которой стремятся к нулю, хотя ее способность выполнять работу при этом не уменьшается. Иначе говоря – это когда системы нет, а функция ее сохраняется и выполняется. Все ТС стремятся к идеальности, но идеальных очень мало. Образцом может служить сплав леса плотами, когда корабль для транспортировки не требуется, а функция доставки выполняется.

На практике можно найти множество примеров подтверждения данного закона. Предельный случай идеализации техники заключается в ее уменьшении (вплоть до исчезновения) при одновременном увеличении количества выполняемых ею функций. Например, первые поезда были больше чем сейчас, а пассажиров и грузов перевозили меньше. В дальнейшем габариты уменьшились, усилилась мощность, благодаря чему стала возможной перевозка больших объемов грузов и увеличение пассажиропотока, что привело и к снижению стоимости самой транспортировки.

Закон 5. Закон неравномерности развития частей системы. Развитие частей системы идет неравномерно; чем сложнее система, тем неравномернее развитие ее частей.

Неравномерность развития частей системы является причиной возникновения технических и физических противоречий, и, следовательно, изобретательских задач. Следствием данного закона является то, что рано или поздно изменение одной составляющей ТС спровоцирует цепную реакцию технических решений, которые приведут к изменению и оставшихся частей. Закон находит свое подтверждение в термодинамике. Так, в соответствии с принципом Онсагера: движущая сила любого процесса – это появление неоднородности в системе. Значительно раньше, чем в ТРИЗ, этот закон был описан в биологии: «В ходе прогрессивной эволюции возрастает взаимное приспособление органов, происходит координация изменений частей организма и идет аккумуляция корреляций общего значения».

Отличной иллюстрацией справедливости закона служит развитие автомобильной техники. Первые двигатели обеспечивали относительно небольшую по сегодняшним меркам скорость в 15-20 км/час. Установка двигателей большей мощности увеличила скорость, что со временем стало причиной замены колес на более широкие, изготовления кузова из более прочных материалов и т.д.

Закон 6. Закон опережающего развития рабочего органа. Желательно, чтобы рабочий орган опережал в своем развитии остальные части системы, то есть обладал большей степенью динамизации по веществу, энергии или организации.

Некоторые исследователи выделяют этот закон как отдельный, но многие труды выводят его в комплексе с законом неравномерности развития частей системы. Такой подход нам кажется более органичным, и мы выносим индивидуальный блок для данного закона лишь для большей структурированности и понятности.

Значение этого закона в том, что он указывает на распространенную ошибку, когда с целью увеличения полезности изобретения развивается не рабочий орган, а любой другой, например, управленческий (трансмиссия). Конкретный случай – чтобы создать многофункциональный игровой смартфон, нужно не просто сделать его удобным для держания в руке и оснастить большим дисплеем, а, в первую очередь, позаботиться о мощном процессоре.

Закон 7. Закон динамизации. Жесткие системы для повышения эффективности должны становиться динамичными, то есть переходить к более гибкой, быстро меняющейся структуре и к режиму работы, подстраивающемуся под изменения внешней среды.

Данный закон является универсальным и находит свое отображение во многих сферах. Степенью динамизации – способностью системы приспосабливаться к внешней среде – обладают не только технические системы. Когда-то такую адаптацию прошли биологические виды, вышедшие из воды на сушу. Изменяются и социальные системы: все больше компаний практикуют вместо офисной работы удаленную, а многие работники отдают предпочтение фрилансу.

Примеров из техники, подтверждающих данный закон, также множество. Свой облик за пару десятилетий поменяли мобильные телефоны. Причем изменения были не только количественными (уменьшение в размерах), но и качественными (увеличение функиональности, вплоть до перехода в надсистему – планшетофоны). Первые бритвенные станки «Gilette» имели неподвижную головку, которая позже стала более удобной движущейся. Еще один пример: в 30-е гг. в СССР выпускались быстрые танки БТ-5, которые по бездорожью двигались на гусеницах, а выехав на дорогу, сбрасывали их и шли на колесах.

Закон 8. Закон перехода в надсистему. Развитие системы, достигшей своего предела, может быть продолжено на уровне надсистемы.

Когда динамизация системы невозможна, другими словами, когда ТС полностью исчерпала свои возможности и дальнейших путей ее развития нет, система переходит в надсистему (НС). В ней она работает в качестве одной из частей; при этом дальнейшее развитие идет уже на уровне надсистемы. Переход происходит не всегда и ТС может оказаться мертвой, как, например, произошло с каменными орудиями труда первых людей. Система может не переходить в НС, а оставаться в состоянии, когда не может быть существенно усовершенствована, но сохранять жизнеспособность в силу необходимости этого людям. Примером такой технической системы служит велосипед.

Вариантом перехода системы в надсистему может быть создание би- и полисистем. Его еще называют законом перехода «моно – би – поли». Такие системы более надежны и функциональны, благодаря приобретаемым в результате синтеза качествам. После прохождения этапов би- и поли- наступает свертывание – либо ликвидация системы (каменный топор), поскольку она свое уже отслужила, либо переход ее в надсистему. Классический пример проявления: карандаш (моносистема) – карандаш с ластиком на конце (бисистема) – разноцветные карандаши (полисистема) – карандаш с циркулем или ручка (свертывание). Или бритва: с одним лезвием – с двумя – с тремя и более – бритва с вибрацией.

Этот закон является не только общим законом развития систем, схемой, по которой развивается все, но и законом природы, ведь симбиоз живых организмов с целью выживания известен с незапамятных времен. Как подтверждение: лишайники (симбиоз гриба и водорослей), членистоногие (рак-отшельник и актинии), люди (бактерии в желудке).

Динамика

«Динамика» объединяет законы развития ТС характерные для нашего времени и определяет возможные изменения в них в научно-технических условиях современности.

Закон 9. Закон перехода с макроуровня на микроуровень. Развитие рабочих органов системы идет сначала на макро-, а затем на микроуровне.

Суть заключается в том, что любая ТС для развития своего полезного функционала стремится перейти с макроуровня на микроуровень. Другими словами, в системах соблюдается тенденция перехода функции рабочего органа от колес, шестерней, валов и т. д. к молекулам, атомам, ионам, которые легко управляются полями. Это одна из главных тенденций развития всех современных технических систем.

Понятия «макроуровень» и «микроуровень» являются в данном отношении скорее условными и призваны показать уровни мышления человека, где первый уровень – что-то физически соизмеримое, а второй – понимаемое. В жизни любой ТС наступает момент, когда дальнейшее экстенсивное (увеличение полезной функции за счет изменений на макроуровне) развитие невозможно. Дальше систему можно развивать только интенсивно, за счет повышения организованности все более низких системных уровней вещества.

В технике переход между макро- и микроуровнями хорошо демонстрирует эволюция строительного материала – кирпича. Сначала это была просто организация формы глины для удобства. Но однажды человек забыл кирпич на пару часов на солнце, а когда вспомнил о нем – тот затвердел, что сделало его более надежным и практичным. Но со временем было замечено, что такой материал плохо держит тепло. Было совершено новое изобретение – теперь в кирпиче оставляли большое количество воздушных капилляров – микропустот, что существенно понизило его теплопроводность.

Закон 10. Закон повышения степени вепольности. Развитие технических систем идет в направлении увеличения степени вепольности.

Г. С. Альтшуллер писал: «Смысл этого закона заключается в том, что невепольные системы стремятся стать вепольными, а в вепольных системах развитие идет в направлении перехода от механических полей к электромагнитным; увеличения степени дисперсности веществ, числа связей между элементами и отзывчивости системы».

Веполь – (вещество+поле) – модель взаимодействия в минимальной технической системе. Это понятие абстрактное, применяемое в ТРИЗ для описания некоторого вида отношений. Под вепольностью стоит понимать управляемость. Дословно закон описывает вепольность как последовательность изменения структуры и элементов веполей с целью получения более управляемых технических систем, т.е. систем более идеальных. При этом в процессе изменения необходимо осуществлять согласование веществ, полей и структуры. Примером может служить диффузионная сварка и лазер для резки различных материалов.

В заключение отметим, что здесь собраны лишь описанные в литературе законы, в то время как теоретики ТРИЗ говорят о существовании и других, открыть и сформулировать которые еще предстоит.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только один вариант. После выбора вами одного из вариантов система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Далее давайте познакомимся с АРИЗ.

Сергей КрутькоЕвгений Буянов

Дипломные работы выпускников

Здесь можно ознакомиться с дипломными работами, выполненными под руководством преподавателей и научных сотрудников кафедры. Замечания и пожелания просьба отправлять на эл. почту кафедры [email protected].

Дипломы под руководством проф. А.В.Ципенко: 


2012 г. Киреев Д.А. «Программный комплекс выбора оптимального сценария применения двух летательных аппаратов для обеспечения ресурсами наземных объектов». Презентация, текст диплома.

2013 г. Кузнецова К.Б. «Обтекание осесимметричного сегментально-конического тела невязким газом». Презентация, текст диплома.


2014 г. Олейник  В.И. “Определение эффективного модуля упругости углепластика при циклических нагрузках (эмпирическая модель) в условиях изменения температуры окружающей среды”. Презентация, текст диплома.

2015 г. Мошко К.С. “Программа расчета параметров критического газового эжектора с учетом конденсации”. Презентация, текст диплома.

Дипломы под руководством проф. С.О.Гладкова: 


2017 г. Молотков А.А. “Решение задачи Бернулли о брахистохроне с помощью динамических уравнений движения”. Презентация. Текст диплома.

2017 г. Михайлов Д.А. “Исследование движения шарика, подвешенного на резиновой нити”. Презентация. Текст диплома.


2017 г. Гурзо М.Д. “Решение задачи Бернулли о брахистохроне с учетом только одного сухого трения”. Презентация. Текст диплома.

2017 г. Алямов Р.Р. “Анализ движения системы, состоящей из двух отдельных математических маятников с учетом взаимодействия между ними”. Презентация не представлена в электронном виде. Текст диплома.

2016 г. Москаленко В.Е. “Электрический пробой водо–воздушного аэрозоля (цепочка капель)”. Презентация, текст диплома.

2016 г. Федотов Ф.И. “Аналитический и численный расчет оптимальной траектории ЛА при подходе к зоне аэропорта (расстояние и время фиксированы)”. Презентация, текст диплома.

2014 г. Семенов А.В. «Исследование процесса теплопроводности в сложном многокомпонентном композите».
Текст диплома. Презентация не представлена в электронном виде.

Дипломы под руководством проф. И.А.Знаменской:

2014 г. Малугин М.М. «Программный комплекс для кросс-корреляционного анализа данных газодинамического эксперимента». Презентация, текст диплома.
2014 г. Савенков М. “Анализ возможностей диагностического комплекса цифрового трассирования (PIV) для измерений в сверхзвуковом потоке”. Текст диплома. Презентация не представлена в электронном виде.

Дипломы под руководством проф. Г.Н.Измайлова:

2013 г. Чернова Н.Н. «Создание анимации для учебного курса физики по теме «Закон сохранения механической энергии». Презентация, текст диплома.
2014 г. Куликов К.А. «Анализ устойчивости квантового объекта в неоднородном гравитационном поле». Диплом и презентация не представлены в электронном виде.

Дипломы под руководством проф. Е.П.Скороход:

2013 г. Буньковский С.А. «Определение компонентного состава низкотемпературной плазмы аргона в рамках многоуровневой кинетики». Презентация, текст диплома.

Дипломы под руководством проф. Г.Г.Спирина: 

2013 г. Симахин Е.А. «Оценка вклада излучения при исследовании теплофизических свойств веществ в стадии иррегулярного теплового режима». Презентация, текст диплома.

2014 г. Михиенков Р.В. «Использование понятие “действие” при расчете коэффициента теплопроводности неоднородных материалов» 
Диплом и презентация не представлены в электронном виде. 

Дипломы под руководством проф. О.Н.Третьяковой:

2015 г. Мустафин А.Р. «Разработка моделирующей программы для управления машиной скоростной лазерной резки c дополнительными кинематическими осями». Презентация, текст диплома.

2014 г. Костин И.А. «Программа для тестирования устойчивости сетевой инфраструктуры к определенным типам атак». Текст диплома. Презентация. 

2014 г. Попова А.И. «Автоматизация расчета клапанов для систем автоматического регулирования давления в системах кондиционирования самолетов». Текст диплома. Презентация. 

2013 г. Иванов А.А. “Моделирование банковских процессов двудольными ориентированными графами». Презентация. Диплом не представлен в электронном виде.


2012 г. Комов В.Г. “Разработка управляющей программы для кинематической системы машины скоростной лазерной резки”. Презентация. Диплом не представлен в электронном виде.

2011 г. Кудимов Н.Ф. “Математическое моделирование сложного теплообмена в экспериментальных энергетических установках”. Презентация, текст диплома.

2011 г. Чупин А.В. “Разработка управляющей программы для установки лазерного управляемого термораскалывания диэлектрических материалов”. Презентация, текст диплома.


2011 г. Шевченко Г.Ю. “Разработка программного обеспечения для установки лазерного управляемого термораскалывания полупроводниковых материалов”. Презентация, текст диплома.


2011 г. Брижак Н.Е.”Разработка интернет-технологии для дистанционного обучения физике”. Презентация, текст диплома не представлен в электронном виде.


Дипломы под руководством научного сотрудника С.П.Перминова: 

2014 г. Давыдова А. «Численное исследование причин появления предвестника перед ударной волной, распространяющейся по слабоионизованному газу». Текст диплома. Презентация не представлена в электронном виде.

Дипломы под руководством В.А.Шахатова: 

2017 г. Старцева Н.Н. “Анализ спектров, создаваемых СВЧ генератором, в жидкостных углеводородах”. Презентация не представлена в электронном виде. Текст диплома.

Дипломы под руководством А.А.Федотова:

2017 г. Пищаев С.С. “Определение критериев развития повреждений слоистой пластины из полимерного композитного материала”. Презентация. Текст диплома.

2017 г. Батурина Е.И. “Определение критериев развития повреждений слоистой пластины из полимерного композитного материала”. Презентация не представлена в электронном виде. Текст диплома не представлен в электронном виде.

Дипломы под руководством В.В.Озолина:

2017 г. Борисова Ю.Г. “Определение поглощаемого теплового излучения падающего на произвольно ориентированную площадку в стратосфере Земли”. Презентация. Текст диплома.


Уравнения равноускоренного движения • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Галилео Галилей относится к числу людей, прославившихся совсем не тем, за что им следовало бы пользоваться заслуженной славой. Все помнят, как этого итальянского естествоиспытателя в конце жизни подвергли суду инквизиции по подозрению в ереси и заставили отречься от убеждения, что Земля вращается вокруг Солнца. На самом же деле, этот судебный процесс на развитие науки практически не повлиял — в отличие от ранее проделанных Галилеем опытов и сделанных им на основании этих опытов выводов, которые фактически предопределили дальнейшее развитие механики как раздела физической науки.

Движение физических тел изучалось с незапамятных времен, и основы кинематики были заложены задолго до рождения Галилея. Элементарные задачи описания движения сегодня изучают уже в начальной школе. Например, все знают, что если автомобиль равномерно движется со скоростью 20 км/ч, то за 1 час он проедет 20 км, за 2 часа — 40 км, за 3 часа — 60 км и т. д. И до тех пор, пока машина движется с постоянной скоростью (стрелка спидометра не отклоняется от заданного деления на его шкале), рассчитать пройденное расстояние труда не составляет — достаточно умножить скорость машины на время, которое она находится в пути. Этот факт известен настолько давно, что имя его первооткрывателя наглухо затерялось в тумане античных времен.

Сложности возникают, как только объект начинает двигаться с переменной скоростью. Трогаетесь вы, к примеру, от светофора — и стрелка спидометра ползет от нуля вверх, пока вы не отпустите педаль газа и не нажмете педаль тормоза. На самом деле стрелка спидометра на месте практически не стоит — она всё время движется вверх или вниз. В начале каждой отдельно взятой секунды реальная скорость машины одна, а в конце секунды — уже другая, и пройденный ею за секунду путь точно рассчитать не так-то просто. Эта проблема — описание движения с ускорением — волновала естествоиспытателей задолго до Галилея.

Сам же Галилео Галилей подошел к ней новаторски и, фактически, задал направление всего дальнейшего развития современной методологии естествознания. Вместо того чтобы сидеть и умозрительно решать вопрос о движении ускоряющихся тел, он придумал гениальные по своей простоте опыты, позволяющие экспериментально проследить, что в действительности происходит с ускоряющимися телами. Нам может показаться, что ничего особенно новаторского в таком подходе нет, однако до Галилея основным методом решения проблем «натурфилософии» — о чем говорит само название тогдашней естественной науки — было умозрительное осмысление происходящего, а не его экспериментальная проверка. Сама идея проведения физических экспериментов была в то время по-настоящему радикальной. Чтобы понять идею опытов Галилея, представьте себе тело, падающее под воздействием силы земного притяжения. Выпустите какой-нибудь предмет из рук — и он упадет на пол; при этом в первое мгновение скорость его движения будет равна нулю, но он тут же начнет ускоряться — и будет продолжать ускоряться, пока не упадет на землю. Если мы сможем описать падение предмета на землю, мы затем сможем распространить это описание и на общий случай равноускоренного движения.

Сегодня измерить динамику падения предмета не сложно — можно с большой точностью зафиксировать время от начала падения до любой промежуточной точки. Однако во времена Галилея точных секундомеров не было, да и любые механические часы по современным стандартам были весьма примитивны и неточны. Поэтому ученый первым делом разработал экспериментальный аппарат, позволяющий обойти эту проблему. Во-первых, он «разбавил» силу тяжести, замедлив время падения до разумных, с точки зрения имеющихся инструментов измерения, пределов, а именно — заставил тела скатываться по наклонной плоскости, а не просто падать отвесно. Затем он придумал, как обойти неточность современных ему механических часов, натянув на пути скатывающегося по наклонной поверхности шара ряд струн, чтобы он задевал их по дороге и можно было хронометрировать его движение по извлекаемым звукам. Раз за разом спуская шар по наклонной под рядом струн, Галилей перемещал струны, пока не добился, чтобы шар на всем своем пути, задевая натянутые струны, извлекал звуки через равные промежутки времени.

В конце концов Галилею удалось накопить достаточный объем экспериментальной информации о равноускоренном движении. Тело, стартующее из состояния покоя, далее движется так, как это описано в самом начале данной статьи. В переводе на язык математических символов равноускоренное движение описывается следующими уравнениями:

    

где a — ускорение, v — скорость, d — расстояние, пройденное телом за время t. Чтобы прочувствовать смысл этих уравнений, достаточно пристально пронаблюдать за падением предметов. Скорость падения зримо возрастает со временем, прошедшим с начала падения. Это следует из первого уравнения. Очевидно и то, что в процессе падения на прохождение первой части пути у тела уходит больше времени, чем на оставшуюся часть пути. Именно это и описывает вторая формула, поскольку из неё следует, что чем дольше тело ускоряется, тем больший отрезок пути оно преодолевает за одно и то же время.

Галилей сделал и еще одно важное наблюдение о теле, находящемся в состоянии свободного падения под воздействием силы гравитационного притяжения, хотя и не смог подтвердить его непосредственными измерениями. Экстраполировав результаты, полученные им при наблюдении скатывающихся по наклонной плоскости предметов, он сумел определить ускорение свободного падения тела на поверхность Земли. Ускорение свободного падения принято обозначать g, и оно равняется (приблизительно):

    g = 9,8 м/с²(метра в секунду за секунду)

То есть, если уронить предмет из состояния покоя, за каждую секунду падения его скорость будет возрастать на 9,8 метра в секунду. На исходе первой секунды падения тело будет двигаться со скоростью 9,8 м/с, на исходе второй — со скоростью 2 × 9,8 = 18,6 м/с и так далее. Величина g определяет коэффициент ускорения падения тела, находящегося в непосредственной близости от земной поверхности, в связи с чем g принято называть ускорением свободного падения, или гравитационным ускорением.

Здесь следует сделать два важных замечания относительно полученных Галилеем результатов. Во-первых, ученый получил чисто экспериментальное значение величины g, ни на каких теоретических прогнозах не основывающееся. Значительно позже Исаак Ньютон в своих знаменитых работах показал, что величину g можно рассчитать теоретически, исходя из сочетания сформулированных им законов механики Ньютона и закона всемирного тяготения Ньютона. Именно первопроходческий труд Галилея и проложил дорогу последующим триумфальным открытиям Ньютона и формированию классической механики в её общеизвестном виде.

Второй важнейший момент состоит в том, что ускорение свободного падения не зависит от массы падающего тела. По сути, сила притяжения пропорциональна массе тела, но это полностью компенсируется большей инерцией, присущей более массивному телу (его нежеланию двигаться, если хотите), а посему (если не учитывать сопротивление воздуха) все тела падают с одинаковым ускорением. Это практическое заключение вступало в полное противоречие с умозрительными предсказаниями древних и средневековых натурфилософов, которые были уверены, что всякой вещи свойственно стремиться к центру мироздания (коим им, естественно, представлялся центр Земли) и что чем массивнее предмет, тем с большей скоростью он к этому центру устремляется.

Свое видение Галилей, конечно же, подкрепил экспериментальными данными, но вот опыта, который ему традиционно приписывают, он, скорее всего, вовсе не проводил. Согласно околонаучному фольклору, он сбрасывал предметы различной массы с «падающей» Пизанской башни, чтобы продемонстрировать, что они достигают поверхности земли одновременно. В этом случае, однако, Галилея ждало бы разочарование, поскольку более тяжелые предметы неизбежно падали бы на землю раньше легких из-за разницы в удельном сопротивлении воздуха. Если бы сбрасываемые с башни предметы были одного размера, сила сопротивления воздуха, тормозящая их падение, была бы одинаковой для всех предметов. При этом из законов Ньютона следует, что более легкие предметы затормаживались бы воздухом интенсивнее тяжелых и падали на землю позднее тяжелых предметов. А это, естественно, противоречило бы предсказанию Галилея.

См. также:

Суд над Галилеем




Суд римско-католической инквизиции над Галилеем — такой же стойкий околонаучный миф, как и яблоко, якобы упавшее на голову Ньютону. И, как обычно и бывает в мифологии, к действительности эта история имеет мало отношения. Если верить этому мифу, Галилей привел суду неопровержимые доказательства правильности взглядов Николая Коперника на устройство Солнечной системы, согласно которым Земля вращается вокруг Солнца, а не наоборот, а затем был сломлен Церковью, желавшей подавить эту теорию, и принужден публично отречься от своих взглядов. На самом же деле Коперник, будучи весьма изощренным церковным политиком, представил свою гелиоцентрическую теорию в таком виде, что она вполне удовлетворяла богословские авторитеты того времени (в частности, называя её не иначе, чем «гипотезой»). Теория Коперника широко обсуждалась до Галилея и учеными, и даже самими ватиканскими богословами.

В 1616 году Галилей опубликовал книгу «Звездный вестник», в которой обобщил телескопические наблюдения и привел сильные доводы в пользу системы Коперника. Причем написана книга была на итальянском, а не на латыни, что сделало ее доступной не только ученым, но и широкому кругу образованных читателей. В ответ на упреки, что книга якобы противоречит церковным канонам, Коллегия кардиналов вызвала Галилея на свое заседание. Далее начинаются неясности, вызванные противоречивостью дошедших до нас свидетельств участников этого заседания. Согласно официальной версии, Галилею было указано на недопустимость дальнейших публичных обсуждений идей Коперника в иной форме, кроме как с указанием на то, что это всего лишь гипотеза, пока не будут представлены неопровержимые доказательства ее правильности. Галилей же стоит на том, что подобного предупреждения не получал.

Как бы то ни было, в 1632 году Галилей опубликовал работу «Диалог о двух главнейших системах мира», где привел развернутые аргументы в пользу гелиоцентрической системы Коперника, вложив при этом официальные возражения Папы в уста персонажа по имени Симпличо (по-итальянски «простак». — Прим. переводчика). Вот тогда-то против Галилея и было впервые выдвинуто обвинение в «подозрении на ересь»; при этом нужно понимать, что в устах инквизиции это обвинение соотносится с обвинением в собственно «ереси», примерно так же, как в современном гражданском судопроизводстве обвинение в непреднамеренном убийстве соотносится с обвинением в предумышленном убийстве при отягчающих обстоятельствах. От подозрения в ереси Галилей себя очистил, публично заявив, что сам не верит в то, что написал, после чего остаток жизни провел всего лишь под домашним арестом у себя во Флоренции. (В 1992 году Римско-католическая церковь официально пересмотрела приговор суда на том основании, что судьи не сумели отделить вопросов веры от научных фактов.)

Так что мы выносим из всей этой истории? По моему личному разумению, она описывает не более чем умышленное раскручивание маховика неповоротливой бюрократической машины человеком, намеренно стремящимся к конфронтации с ней. (Мне, например, представляется, что у Совета кардиналов имелись в то время дела и поважней, чем разбирательство с ученым по поводу абстрактной космологической теории.) Правда тут еще и в том, что доводы Галилея в пользу системы Коперника на поверку вовсе не являются такими уж убедительными. Более того, с точки зрения современной науки можно сказать, что Галилей пришел к верному заключению путем ошибочных рассуждений. Суда над ученым это, естественно, не оправдывает, однако всё действо, в этой связи, предстает в ином — куда менее мифологическом — свете.

Магнитные энкодеры RLS позволяют компании Marsi Bionics создавать экзоскелеты, существенно улучшающие качество жизни пациентов

Задача

Экзоскелет ATLAS 2030 имеет до шести степеней свободы движения для каждой конечности. Это устройство обеспечивает пациенту возможность садиться, вставать и ходить без посторонней помощи за счет собственных мышечных усилий. Полный экзоскелет включает в себя суставы и конечности с моторизованным приводом, электронную систему управления и систему электропитания.


Проектировщик должен найти компромисс между легкой и компактной конструкцией, с которой мог бы легко обращаться физически слабый пользователь, и роботизированной системой, которая реализована на основе физиологически полноценной биомеханической модели.


Чтобы обеспечить устойчивость при ходьбе, используется механизм поддержания устойчивого положения всей системы «экзоскелет-пользователь», что достигается путем отслеживания референсных значений точки нулевого момента (ТНМ), рассчитываемых на основании требуемого нормированного запаса динамической устойчивости (NDSM). Для поддержания устойчивости контроллер экзоскелета может затем адаптироваться под стиль ходьбы своего носителя, используя хранящиеся в памяти физиологические шаблоны походки.

Для успешной динамической ходьбы требуется точный контроль углов в суставах ног с учетом положения, скорости и ускорения, на основании обратных сигналов от углового энкодера. Это непростая задача, поскольку каждый механический сустав является податливым и включает в себя эластичные элементы, обеспечивающие имитацию и поддержку реальных суставов и мускулов использующего экзоскелет человека.


Альберто Плаза (Alberto Plaza), инженер-исследователь и руководитель проекта MAK в компании Marsi Bionics, так описывает жесткие требования, предъявляемые к используемым в ортопедических экзоскелетах энкодерам:

«Самая сложная задача при разработке экзоскелетов — это обеспечение надежности при получении точных референсных значений углового положения, поскольку они зависят от конкретной конструкции. Это усложняет стандартизацию и сборку устройств.Ранее мы использовали энкодеры PCB собственной разработки, которые были полностью связаны с кинематическими схемами экзоскелетов MAK и ATLAS. Но поскольку электроприводы суставов генерировали магнитные поля рассеяния, способные создавать помехи для работы энкодеров и приводить к неточным показаниям, у нас постоянно возникали проблемы.

кинематическая

кинематическая КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ

Цель этого веб-сайта, чтобы научить или помочь заинтересованным читателям лучше понять первые два кинематических уравнения физики. Надеюсь, вы поймете как использовать эти уравнения для решения проблем и применять их в реальной жизни Приложения. Приведу несколько примеров задач, поясняющих аналогичные уравнения. и предоставить ссылки на другие страницы с кинематикой.

Приложения в реальной жизни

– любой вид спорта, включает перемещение объекта
– движение автотранспорта


Уравнения

V = Vo + at – Первый Кинематическое уравнение
x = ½ (Vo + V) t – секунд Кинематика

V = финал скорость – метры в секунду (м / с)
Vo = начальное скорость -метры в секунду (м / с)
a = ускорение – метры на второй в квадрате (м / с²)
t = время – секунды x = расстояние – метры (м)


Эти два уравнения позволяют сканировать использоваться для определения конечной скорости, начальной скорости, ускорения, времени и расстояние до любого движущегося объекта.Все, что вам нужно знать, это какие числа и единиц для включения каждой переменной уравнения. Оттуда это просто алгебра для решения каждого уравнения. Самое сложное – это просто определить, какой уравнение для использования. Единственная разница в том, что первое уравнение имеет ускорение в нем, а второй – расстояние.

Примеры проблем
1. Джон ведет машину с начальным скорость 24 м / с, и он ударяется о кирпичную стену за 3 секунды.3с. Как далеко он проехал?

x = ½ (V + Vo) t
x = ½ (0 + 24 м / с) 3,3 с
x = 39,6 м

2. Келли запускает ракету в в воздухе, и требуется 2,3 секунды, чтобы вернуться на землю. Как далеко пролетела ракета путешествовать?

В = Vo + при
0 = Vo + (-9,8 м / с²) (2,3 с) -9,8 м / с = сила тяжести
Vo = 22,54 м / с

x = ½ (V + Vo) t
x = ½ (0 + 22.54 м / с) (2,3 с)
x = 25,921 м

3. Роб стреляет пулей со скоростью 112 м / с. конечная скорость 43 м / с. Если на то, чтобы добраться туда, потребовалось 6 секунд, каково было ускорение?

В = Vo + при
43 м / с = 112 м / с + a (6 с)
а = 43/6 – 112
a = – 104,833 м / с²

Родственные формулы
Вторые два кинематических уравнения:
x = Vot + ½at ²
В ² = Vo² + 2ax

V = финал скорость – метры в секунду (м / с)
Vo = начальное скорость -метры в секунду (м / с)
a = ускорение – метры на второй в квадрате (м / с²)
t = время – секунды x = расстояние – метры (м)

Второй два кинематических уравнения в основном представляют собой разные версии первых двух, но решают для ответов по-разному.Иногда вторые два более эффективны но обычно это не так. Эти четыре кинематических уравнения также помогают частично решить проблемы движения снаряда. Движение снаряда – запускаемый объект под некоторым углом и скоростью. К сожалению, это также связано с использованием нескольких больше несвязанных формул, чтобы решить одну из этих формул.

Ссылки
Нажмите здесь, чтобы моя другая физическая страница
Нажмите здесь, чтобы страница физики о других кинематических уравнениях
Нажмите здесь, чтобы страница физики по сторонам света



Авторские права Робби Уоррен 2001 г.
















Физико-кинематика: объекты в движении: 11 класс

Цель урока: Понимание значения кинематики, реальных примеров, элементов кинематики и введения в описание движения объектов с помощью чисел и уравнений.

Научный стандарт нового поколения: Используйте математические представления явлений для описания объяснений. (HS-PS2-2), (HS-PS2-4)

Материалы: Этот урок представляет собой вводный урок к более широкой концепции кинематики, больше похож на лекцию, чем на занятие. Заранее подготовьте проекции, в которых перечислены кинематические уравнения и пример. Вам также понадобится:

Стартер

Задайте вопрос: Кто-нибудь слышал раньше слово «кинематика»? (Позвольте студентам ответить.) Если да, то отлично. Вы можете мне сказать, что это значит? (Если кто-то ответит правильно, утвердите ответ и продолжайте.)

Say: Кинематика происходит от греческого слова Kinesis, что означает движение. Обычно это определяется как изучение движения точек, объектов или групп объектов. В физике он принадлежит к разделу Механика.

Кинематику не следует путать с кинетикой. Обе концепции являются ветвями движения и очень похожи.Однако кинетика – это изучение сил, которые влияют или вызывают движение (законы Ньютона), например, как трение влияет на ходьбу или бег или как фермент вызывает изменения в химической системе.

Сегодня мы обсуждаем кинематику, науку о движущемся объекте или веществе без учета сил, которые его стимулируют. Хорошая идея – думать об этом как о том, как и почему. Кинетика учитывает, почему происходит движение, а кинематика занимается тем, как это происходит.

Поскольку кинематика включает в себя значительный объем математики, мы должны сначала усвоить основные концепции и термины, чтобы лучше понять, почему мы выполняем математику, которая есть.

Основной

Say: Кинематика стреляет в баскетбольный мяч, вода стекает с водопада, движется поезд. Практически любой существующий объект имеет кинематику, пока он движется. Даже учебник на столе может быть примером кинематики, если учесть колебания атомов и молекул.

Это краткая и краткая теоретическая часть кинематики, и в основном все, что к ней нужно. Однако мы можем перевести эти слова в математические выражения, называемые кинематическими уравнениями.

Есть несколько элементов или величин, которые важны для математического расчета того, как происходит движение. Эти элементы являются векторными и скалярными величинами. Вы, наверное, уже слышали эти термины. Скалярные величины – это те, которые имеют только величину, то есть описываются только числовыми значениями.С другой стороны, векторные величины – это те, которые имеют как величину, так и направление.

Скаляры, которые мы рассмотрим сегодня: (напишите на доске) :

А векторов (напишите на доске):

• рабочий объем
• скорость
• ускорение

Позже вы увидите, что все вычисления будут сосредоточены на векторных величинах.

Как именно работают кинематические уравнения? Возьмем, к примеру, скорость.Скорость – это скорость и направление движения. Итак, представьте, что я бросаю мяч в мусорное ведро, и он движется со скоростью около 1 км / ч. С того места, где я стою, он будет двигаться на восток в контейнер.

Do : бросить мяч в пустой мусорный бак.

Спросите : Скажем, скорость просто 1 км / ч на восток, верно? (Позвольте студентам ответить).

Say: При расчете скорости движения кинематика учитывает расстояние, пройденное мячом, и время, необходимое для его остановки.Если бы мы могли это разбить, это означает, что мы рассматриваем начальную точку мяча (моя рука), конечную точку (мусорный бак) и его траекторию (путь, по которому он следует в пространстве). Вот почему физики часто называют кинематику «геометрией движения». По сути, кинематика изучает траектории точек, линий и других геометрических объектов при вычислении движения.

Однако кинематика

– это не только движение снаряда. Он также присутствует в вертикальном и горизонтальном движении.

Do: Подбросьте мяч прямо в воздух и дайте ему упасть на пол.

Say: Кинематика здесь включает скорость мяча, когда он поднимается, ускорение (изменение скорости), когда он возвращается вниз, и время, необходимое для остановки от начала до конца движения.

Сделайте: Толкните игрушечную машинку по столу.

Say: Здесь нас также интересует расстояние между точками A и B, скорость движения автомобиля и изменения скорости в пути.

Следующим шагом для нас является собственно выполнение вычислений. К счастью, для этого используется набор основных формул.

Do: Спроецируйте на экран следующую информацию. Дайте студентам время скопировать информацию.

• v = v0 + при
• d = ((v + v0) / 2) t
• d = v0t + 1 / 2at2
• v2 = v02 + 2ad

Ключи

• v0 = начальная скорость
• v = конечная скорость
• d = смещение
• a = ускорение
• t = временной интервал

Say: Эти формулы основаны на предположении, что ускорение является постоянным и что все параметры или величины относятся к одному и тому же направлению.

Do: Спроецируйте следующий пример.

Say: Теперь пример. Самолет движется по взлетно-посадочной полосе со скоростью 3,20 м / с2 в течение 32,8 с, пока наконец не оторвется от земли. Определите пройденное расстояние до взлета.

Do: Работайте над решением вместе с учащимися.

Параметры, которые у нас есть:

• a = 3,20 м / с2
• t = 32,8 с
• v = 0 м / с (самолет на старте неподвижен)
• d =?

По формуле:

Мы можем рассчитать расстояние (смещение) как:

• d = (0 м / с) * (32.8 с) + 1/2 (3,20 м / с2) * (32,8 с) 2
• d = 1721 м

Say: Продолжая этот раздел, вы начнете понимать, насколько просто применить кинематику к кинетическим ситуациям.

Обратная связь

Спросите: Как, по вашему мнению, инженеры применяют кинематику к чему-то вроде самолета, автомобиля или другого оборудования? Как бы они использовали эти разные уравнения? (Позвольте учащимся ответить.)

Say: Идите домой и бросьте какой-нибудь предмет через свою гостиную – только ничего не ломайте.Попросите кого-нибудь использовать таймер с точностью до миллисекунд. Они должны запускать таймер, когда вы отпускаете мяч, и останавливать его, когда он ударяется о землю. Прежде чем бросить мяч, отметьте свое место на полу.

После того, как объект приземлился, измерьте расстояние между местом, где вы бросили мяч, и тем местом, где он приземлился. По имеющейся у вас информации вычислите, как быстро мяч летел по воздуху. А теперь вычислите, как долго этот мяч должен лететь в воздухе, чтобы пролететь одну милю.

Мы обсудим ваши расчеты на следующем занятии.

Написано Анн Ифеани

Участник Education World

Авторские права © 2021 Education World

Насколько важна кинематика в повседневной жизни? – Mvorganizing.org

Насколько важна кинематика в повседневной жизни?

Во многих случаях важно только знать, как движется объект, без учета сил, вызывающих движение. Например, в компонентах машин обычно используется кинематический анализ для определения (неизвестной) скорости объекта, который связан с другим объектом, движущимся с известной скоростью.

Какие примеры кинетики?

Примеры кинетической энергии:

• Самолет обладает большим количеством кинетической энергии в полете из-за его большой массы и высокой скорости.
• Бейсбольный мяч, брошенный питчером, хотя и имеет небольшую массу, может иметь большое количество кинетической энергии из-за своей высокой скорости.

В чем разница между кинетикой и динамикой?

Кинематика – это исследование движения без учета причины.Динамика: С другой стороны, динамика – это изучение причин движения.

Какие два типа кинематики?

Кинематика траектории частицы в невращающейся системе отсчета

• Кинематические величины классической частицы: масса m, положение r, скорость v, ускорение a.
• Пройденное расстояние всегда больше или равно смещению.
• Относительные скорости между двумя частицами в классической механике.

Что означает кинематика?

Кинематика, раздел физики и подраздел классической механики, связанный с геометрически возможным движением тела или системы тел без учета задействованных сил (т.е., причины и следствия движений). …

Почему скорость – это векторная величина?

Скорость как векторная величина Поскольку человек всегда возвращается в исходное положение, движение никогда не приведет к изменению положения. Поскольку скорость определяется как скорость изменения положения, это движение приводит к нулевой скорости.

Скорость больше похожа на расстояние или смещение?

Направление средней скорости всегда совпадает с направлением смещения.В общем, средняя скорость и средняя скорость – это не одно и то же, потому что расстояние и перемещение – это не одно и то же.

Скорость – это расстояние?

Скорость – это мера расстояния, которое объект преодолевает за заданный промежуток времени. Вот словесное уравнение, которое выражает взаимосвязь между расстоянием, скоростью и временем: скорость равна пройденному расстоянию, деленному на время, необходимое, чтобы добраться туда.

Как сочетаются скорости?

Как можно комбинировать скорости? Скорость – это скорость и направление.Скорость может сочетаться с другой силой. Если лодка движется со скоростью 10 км / час, а против нее скорость течения 3 км / час, суммарные скорости составляют 7 км / час.

Кинематика – обзор | ScienceDirect Topics

Кинематика реконструированного коленного сустава передней крестообразной связки

Кинематические изменения коленного сустава также были зарегистрированы у пациентов, перенесших реконструкцию ПКС во время ходьбы и других динамических действий. ^42,52,53 В частности, большеберцовая кость имеет тенденцию быть более повернутой наружу в колене с реконструированной ACL, в отличие от сдвига в сторону внутренней ротации в колене с дефицитом ACL.В коленном суставе, реконструированном на ACL, большеберцовая кость сохраняет смещение внешней ротации (среднее значение, 2,3 градуса; 95% ДИ, 1,0–3,7 градуса) относительно нормы на протяжении фазы опоры цикла ходьбы (рис. 6-9). ⁴² Эти наблюдения дополнительно подтверждают утверждение о том, что ACL играет критическую роль в управлении вторичными движениями колена и что обычная реконструкция ACL неэффективна при воспроизведении сложной анатомии и функции нативной связки. Это согласуется с ранее опубликованными биомеханическими исследованиями in vitro, которые продемонстрировали, что традиционные методы реконструкции ACL часто размещают трансплантаты в неанатомической ориентации, которая не может воспроизвести стабильность вращения, обеспечиваемую нативной ACL. ^27,45

Интересно, что реконструкция ПКС не снижает повышенную частоту преждевременного ОА коленного сустава после травмы ПКС. ^29,33 Основываясь на кинематических данных и естественной истории коленного сустава с дефицитом ACL, многие исследователи также считают, что измененная кинематика большеберцовой кости является провоцирующим фактором дегенеративного процесса в коленном суставе, реконструированном ACL. ^6,7,20,42,43 Аналогичным образом смещение вращательного выравнивания колена с реконструированной ПКС во время ходьбы также смещает нагрузку на области тибиофеморального хряща, которые не могут адаптироваться к испытываемым высоким нагрузкам. во время ходьбы.Хотя сдвиг в контакте, вызванный изменением положения вращения, на первый взгляд может показаться относительно небольшим, он представляет собой довольно существенное изменение при рассмотрении общего диапазона вращательного движения, которое обычно происходит во время ходьбы (~ 10 градусов). ⁴² Предполагается, что в сочетании с хроническим повторяющимся характером ходьбы кумулятивный эффект даже незначительного кинематического изменения во времени может в конечном итоге сыграть важную роль в раннем начале ОА в этой популяции.Взятые вместе, эти исследования дополнительно подтверждают важность оценки успеха новых методов реконструкции ПКС на основе их способности воспроизводить нормальную трехмерную анатомию сустава, восстанавливать амбулаторную механику и предотвращать долгосрочные дегенеративные изменения.

10 примеров движения в реальной жизни – StudiousGuy

Если объект меняет свое положение относительно времени, говорят, что он движется. Известно, что движущийся объект движется.Движение – явление, очень распространенное в нашей повседневной жизни. Например, машина, в которой вы путешествуете, движется, воздух, которым мы дышим, находится в движении, кровь в наших жилах находится в движении, земля движется, вселенная движется и многое другое. Технически даже стационарные объекты на нашей планете находятся в движении, потому что сама Земля находится в постоянном движении, то есть вращении и вращении.

Указатель статей (Нажмите, чтобы перейти)

Типы движения

В повседневной жизни мы можем наблюдать множество действий, связанных с движением.Однако разные движущиеся объекты могут отличаться по манере движения. Например, качели при игре демонстрируют движение вперед-назад, а движение на батуте – вверх-вниз. Оба они двигаются, но по-разному. Исходя из этого, у нас есть разные типы движения. Движение можно условно разделить на четыре категории: линейное, вращательное, колебательное и возвратно-поступательное.

Ниже приведены различные типы движений:

1. Переводчик

Поступательное движение – это движение, при котором все частицы объекта перемещаются на одинаковое расстояние одновременно.Прямолинейные и криволинейные движения являются подкатегориями поступательного движения. Например, боулинг, вытаскивание ящика, стрельба и т. Д.

2. Прямолинейный

Считается, что прямолинейное движение, также известное как линейное движение, присутствует, если объект или частица движутся по прямой линии. Другими словами, прямолинейное движение также известно как прямолинейное движение. Например, дети скатываются с горки, яблоко падает с дерева и т. Д.

3.Криволинейный

Криволинейное движение возникает, когда объект движется по криволинейной траектории. Понятие криволинейного движения используется в приложениях, связанных с центростремительными и центробежными силами. Например, бумеранг, американские горки и т. Д.

4. Система кровообращения

Круговое движение или циркуляционное движение – это движение объектов по круговой траектории, то есть по траектории, каждая граничная точка которой равноудалена от фиксированной точки, т.е.е., центр. Например, движение планет вокруг Солнца, колеса гиганта и т. Д.

5. Поворотный

Считается, что вращательное движение существует, если объект вращается или вращается вокруг своей оси. Например, волчок, вращение Земли и других планет и т. Д.

6. Колебательный

При колебательном движении объект имеет тенденцию повторять определенные движения по одному и тому же шаблону снова и снова, пока на него не действует какая-то внешняя сила. В отсутствие трения колебательное движение может продолжаться вечно до вечности.Например, маятник, взмах крыльев птицы и т. Д.

7. Вибрационный

Некоторые объекты демонстрируют быстрое движение вперед и назад вокруг фиксированной точки, когда их состояние равновесия нарушено. Этот тип движения известен как вибрационное движение. Например, гитарные струны, голосовые связки и т. Д.

8. Периодический

Само название предполагает, что движение будет повторяться через определенный промежуток времени. Время, необходимое для завершения одного цикла движения, называется периодом.Например, движение стрелок часов, кресла-качалки и т. Д.

9. Поршневой

Возвратно-поступательное движение и колебательное движение очень тесно связаны друг с другом, но есть небольшое исключение: возвратно-поступательное движение обязательно включает в себя движение вверх-вниз или назад-вперед. Например, игла для швейных машин, поршневые насосы и т. Д.

10. Броуновский

Броуновское движение – это случайное движение взвешенных в среде частиц.Это также известно как педезис. Например, движение молекул воды, движение частиц пыли и т. Д.

11. Комбинация

Любое движение, которое является результатом комбинации любого из вышеупомянутых движений, может рассматриваться в категории комбинированных движений. Например, когда вы бежите с вертушкой в ​​руке, она делится с вами линейным движением и в то же время обладает вращательным движением, поскольку ветер толкает вентилятор, чтобы он вращался вокруг оси.Следовательно, из-за наличия двух разных типов движений тело может совершать множественные или комбинированные движения.

Законы движения

Три закона движения были обнаружены сэром Иссаком Ньютоном. Эти три фундаментальных закона заложили основу для других значительных открытий и достижений мира, в котором мы живем сегодня. Вы, должно быть, хорошо знакомы с анекдотом о Ньютоне и яблони, именно после этого инцидента мы смогли идентифицировать гравитацию как естественное явление.

1. Первый закон движения Ньютона

В нем говорится, что «объект стремится поддерживать свое состояние покоя или состояние движения, если на него не действует внешняя сила». Это также известно как закон инерции.

2. Второй закон движения Ньютона

В нем говорится, что «ускорение объекта прямо пропорционально действующей чистой силе и обратно пропорционально массе объекта». Математически F = m a; где F = сила, m = масса и a = ускорение.

3. Третий закон движения Ньютона

В нем говорится, что «на каждое действие есть равное и противоположное противодействие».

Примеры движения
1. Выдвижной

Это один из самых ярких примеров прямолинейного движения. Например, дети могут свободно скользить по различным горкам только потому, что в них присутствует сила тяжести; кроме того, во время скольжения дети также испытывают низкое трение; приводит к легкому и плавному скольжению.

2. Бумеранг

Бумеранги демонстрируют одно из самых захватывающих явлений. Слишком интересно видеть, как он возвращается к метающему после следования по изогнутой траектории. Это криволинейное движение выделяет его в категорию криволинейного движения.

3. Боулинг

Когда шар для боулинга находится в движении, между движением и временем устанавливается линейная зависимость. Следовательно, каждая его часть испытывает поступательное движение.Здесь также можно наблюдать применение первого закона движения Ньютона, поскольку мяч имеет тенденцию непрерывно перемещаться по дорожке, пока движение не будет прервано ударами кеглей.

4. Планеты вокруг Солнца

В Солнечной системе планеты вращаются вокруг Солнца по фиксированной орбите, такое движение можно назвать круговым движением.

5. Волчок

Все мы в детстве играли с прялкой, не зная, что за этим стоит наука.Волчок демонстрирует типичное вращательное движение, когда волчок продолжает вращаться вокруг своей оси.

6. Маятник

Когда свободно свисающий маятник слегка толкают, он меняет свое положение из положения равновесия на определенное расстояние с одной стороны, снова возвращается в состояние равновесия, затем перемещается на такое же расстояние с другой стороны и т. Д. Такой маятник называется колеблющимся, и такое движение называется колебательным движением. В этом случае можно соотнести второй закон движения Ньютона.Маятник с большей массой потребует большей силы, чтобы привести его в движение, тогда как маятник с меньшей массой потребует меньшей силы. Следовательно, сила пропорциональна массе. Точно так же, чем больше масса объекта, тем меньше будет его ускорение или наоборот. Следовательно, ускорение обратно пропорционально массе. Объединяя два наблюдения, мы получаем F = ma (второй закон движения).

7. Гитарные струны

Звук, который мы слышим от струнных инструментов, таких как гитара, ситар и т. Д.является результатом колебательного движения струн. Здесь кинетическая энергия, генерируемая вибрацией, преобразуется в звуковую энергию. Здесь можно четко наблюдать третий закон движения Ньютона, поскольку давление, оказываемое на струны, равно давлению, оказываемому струнами на пальцы игрока.

8. Тиканье часов

Движение стрелок часов повторяется через определенное время. Следовательно, он демонстрирует периодическое движение.Здесь важно отметить, что движение часов также является примером сложного движения, потому что, хотя стрелки часов демонстрируют периодическое движение, они также совершают вращательное движение.

9. Игла для швейных машин

Игла швейной машины движется вверх и вниз повторяющимся образом. Это движение вверх и вниз отвечает за то, чтобы поместить его в группу возвратно-поступательного движения.

10. Молекулы воды

Молекулы воды непредсказуемы, поскольку они не следуют никакому шаблону во время движения.Это случайное и случайное колебание молекул является примером педезиса или броуновского движения.

Кинематический анализ движения человека

Понимание кинематики движения человека имеет как фундаментальную, так и прикладную ценность в медицине и биологии. Измерение движения можно использовать для оценки функциональных характеристик конечностей в нормальных и аномальных условиях. Кинематические знания также необходимы для правильной диагностики и хирургического лечения заболеваний суставов, а также для создания протезов для восстановления их функций.В общем, кинематический анализ движения человека можно разделить на две основные области: 1) Грубое движение сегментов конечностей, соединенных суставами, где относительное трехмерное вращение суставов описывается с помощью системы углов Эйлера. При правильном выборе осей вращения между двумя сегментами кости связанное конечное вращение не зависит от последовательности. Эта концепция особенно полезна, поскольку точно соответствует клиническому определению движения суставов. 2) Подробный анализ движения шарнирно-сочлененной поверхности сустава, в котором описывается обобщенное трехмерное неограниченное вращение и поступательное движение с использованием концепции оси смещения винта.Зная геометрию поверхности и ограничения мягких тканей, можно проанализировать движение шарнирного сустава, чтобы получить основную информацию для исследований смазки и износа. Кроме того, при соответствующем численном дифференцировании скорость и ускорение могут быть получены из информации о смещении, описанной двумя вышеупомянутыми способами. Доступные в настоящее время методы измерения движения человека можно разделить на три категории: 1) методы электрического соединения; 2) стереометрические методы и методы бипланарной рентгенографии; 3) акселерометрические методы.Каждая система имеет свои уникальные преимущества и ограничения с точки зрения принципа работы, необходимых инструментов, обработки данных и типа производимой информации. Репрезентативный анализ движений верхних и нижних конечностей человека будет включен в качестве иллюстративных примеров.

приложений статики, включая стратегии решения проблем – College Physics

Цели обучения

• Обсудите применение статики в реальной жизни.
• Сформулируйте и обсудите различные стратегии решения задач в статике.

Statics может применяться в самых разных ситуациях, от подъема подъемного моста до неправильной осанки и напряжения спины. Мы начнем с обсуждения стратегий решения проблем, специально используемых для статики. Поскольку статика является частным случаем законов Ньютона, по-прежнему применимы как общие стратегии решения проблем, так и специальные стратегии для законов Ньютона, обсуждаемые в разделе «Стратегии решения проблем».

Стратегия решения проблем: ситуации статического равновесия

1. Первый шаг – определить, находится ли система в статическом равновесии.Это условие всегда имеет место, когда ускорение системы равно нулю и ускоренное вращение не происходит.
2. Особенно важно, чтобы нарисовал схему свободного тела для интересующей системы . Тщательно обозначьте все силы и отметьте их относительные величины, направления и точки приложения, когда они известны.
3. Решите проблему, применив одно или оба условия равновесия (представленные уравнениями и, в зависимости от списка известных и неизвестных факторов.Если задействовано второе условие, выбирает точку поворота, чтобы упростить решение . Можно выбрать любую точку поворота, но наиболее полезные из них приводят к тому, что крутящий момент неизвестных сил равен нулю. (Крутящий момент равен нулю, если сила приложена к оси поворота (тогда) или вдоль линии, проходящей через точку поворота (тогда)). Всегда выбирайте удобную систему координат для проецирования сил.
4. Проверьте решение, чтобы убедиться, ли оно разумно, проверив величину, направление и единицы ответа.Важность этого последнего шага никогда не уменьшается, хотя в незнакомых приложениях обычно труднее судить о разумности. Эти суждения становятся все легче с опытом.

Теперь применим эту стратегию решения проблем для прыгуна с шестом, показанную на трех рисунках ниже. Шест однородный и имеет массу 5,00 кг. На (Рисунок) центр тяжести шеста находится на полпути между руками прыгуна. Кажется разумным, что сила, прилагаемая каждой рукой, равна половине веса шеста, или 24.5 N. Очевидно, что это удовлетворяет первому условию равновесия. Второе условие также выполняется, как мы можем видеть, выбрав cg в качестве точки поворота. Груз не оказывает крутящего момента вокруг точки поворота, расположенной в точке cg, поскольку он приложен в этой точке, а его плечо рычага равно нулю. Равные силы, прикладываемые руками, равноудалены от выбранного шарнира, поэтому они создают равные и противоположные крутящие моменты. Аналогичные аргументы справедливы и для других систем, в которых опорные силы действуют симметрично относительно центра тяжести.Например, каждая из четырех ножек единого стола выдерживает четверть его веса.

На (Рис.) Показан прыгун с шестом, держащий шест, центр тяжести которого находится на полпути между руками. Каждая рука прикладывает силу, равную половине веса шеста. (b) Прыгун с шестом перемещает шест влево, и силы, прикладываемые руками, больше не равны. См. (Рисунок). Если шест держится так, чтобы его центр был слева от человека, то он должен толкать вниз правой рукой и вверх левой. Силы, которые он прилагает, здесь больше, потому что они направлены в противоположные стороны, а центр тяжести находится на большом расстоянии от обеих рук.

Аналогичные наблюдения можно провести с помощью измерительной линейки, удерживаемой в разных местах по ее длине.

Прыгун с шестом держит шест двумя руками горизонтально.

Прыгун с шестом держит шест обеими руками горизонтально. Центр тяжести рядом с его правой рукой.

Прыгун с шестом держит шест обеими руками горизонтально. Центр тяжести находится слева от прыгуна.

Если прыгун с шестом держит шест, как показано на (Рисунок), ситуация не так проста.Общая сила, которую он прилагает, по-прежнему равна весу шеста, но она неравномерно распределяется между его руками. (Если, то крутящие моменты вокруг cg не будут равны, поскольку рычаги разные.) По логике, правая рука должна выдерживать больший вес, так как она ближе к cg. Фактически, если правую руку перемещать прямо под ЦГ, она будет поддерживать весь вес. Эта ситуация в точности аналогична ситуации, когда два человека несут груз; тот, который ближе к центру тяжести, несет большую часть его веса.Как показывает следующий пример, найти силы и несложно.

Если прыгун с шестом держит шест около конца шеста ((Рисунок)), направление силы, прикладываемой правой рукой прыгуна, меняет свое направление на противоположное.

Какая сила необходима для поддержки веса, удерживаемого рядом с его ЦТ?

Для ситуации, показанной на (Рисунок), вычислите: (a) силу, действующую правой рукой, и (b), силу, прилагаемую левой рукой. Стрелки находятся на расстоянии 0,900 м друг от друга, а угол наклона шеста равен 0.600 м слева.

Стратегия

(рисунок) включает схему свободного тела для полюса, представляющей интерес. Недостаточно информации, чтобы использовать первое условие для равновесия), поскольку две из трех сил неизвестны, и в этом случае нельзя считать, что силы рук равны. Достаточно информации, чтобы использовать второе условие для равновесия, если точка поворота выбирается так, чтобы она находилась с любой стороны, тем самым делая крутящий момент от этой руки равным нулю. Мы решили расположить ось слева в этой части задачи, чтобы исключить крутящий момент с левой стороны.

Решение для (а)

Теперь есть только два ненулевых момента: от силы тяжести () и от толчка или тяги правой руки (). Формулируя второе условие с точки зрения крутящего момента по часовой стрелке и против часовой стрелки,

или алгебраическая сумма моментов равна нулю.

Вот это

, поскольку вес столба создает крутящий момент против часовой стрелки, а правый счетчик – с крутящим моментом по часовой стрелке. Воспользовавшись определением крутящего момента, отметив это, и подставив известные значения, получим

Таким образом,

Решение для (b)

Первое условие равновесия основано на диаграмме свободного тела на рисунке.Это означает, что по второму закону Ньютона:

Отсюда можно сделать вывод:

Решая, получаем

Обсуждение

оказывается ровно половиной от, как мы могли догадаться, поскольку применяется вдвое дальше от cg, чем.

Если прыгун с шестом держит шест, как в начале бега, как показано на (Рисунок), силы снова изменяются. Оба они значительно больше, и одна сила меняет направление.

Take-Home Experiment

Это эксперимент, который нужно провести, стоя в автобусе или поезде.Встаньте лицом боком. Как вы двигаете своим телом, чтобы скорректировать распределение вашей массы при ускорении и замедлении автобуса? Теперь встаньте лицом вперед. Как вы двигаете своим телом, чтобы скорректировать распределение вашей массы при ускорении и замедлении автобуса? Почему легче и безопаснее стоять лицом боком, а не вперед? Примечание. Для вашей безопасности (и для окружающих) убедитесь, что вы держитесь за что-нибудь, пока выполняете это действие!

Исследования PhET: Закон о балансе

Поиграйте с предметами на качелях, чтобы узнать о балансе.Проверьте, что вы узнали, попробовав игру Balance Challenge.


Сводка

• Статику можно применять в самых разных ситуациях, от подъема подъемного моста до неправильной осанки и напряжения спины. Мы обсудили стратегии решения проблем, особенно полезные для статики. Статика – это частный случай законов Ньютона, и общие стратегии решения проблем, и специальные стратегии для законов Ньютона, обсуждаемые в разделе «Стратегии решения проблем», по-прежнему применяются.

Концептуальные вопросы

При посещении некоторых стран можно увидеть человека, балансирующего нагрузку на голову. Объясните, почему центр тяжести груза должен находиться прямо над шейными позвонками человека.

Задачи и упражнения

Чтобы подняться на крышу, человек (массой 70,0 кг) ставит алюминиевую лестницу длиной 6,00 м (массой 10,0 кг) на бетонную площадку с основанием лестницы на расстоянии 2,00 м от дома. Лестница упирается в пластиковый водосточный желоб, который, как мы можем предположить, не имеет трения.Центр масс лестницы находится на расстоянии 2 м от низа. Человек стоит в 3 м от дна. Каковы значения сил на лестнице вверху и внизу?

В (рисунок) центр шеста, удерживаемый прыгуном с шестом, находится на расстоянии 2,00 м от левой руки, а руки на расстоянии 0,700 м друг от друга. Вычислите силу, прилагаемую (а) его правой рукой и (б) его левой рукой. (c) Если каждая рука поддерживает половину веса шеста (рисунок), покажите, что второе условие равновесия выполняется для оси, отличной от той, которая расположена в центре тяжести шеста.