Примеры как решать матрицы: определение, свойства и примеры решения задач

Приложение 1 – Примеры решения задач и комментарии

Пример 1. Даны два вектора {3, 1, –5} и {6, –3, 0}. Найти сумму и разность этих векторов

= + и = –.

Решение. Найдем координаты векторов и .

Xc = 3+6= 9; Yc = 1 – 3= – 2; Zc = – 5+0 = – 5;

Xd = 3 – 6 = – 3; Yd = 1 – (–3) = 4; Zd = –5 – 0 = –5.

Ответ: {9, –2, –5}, { –3, 4, –5}.

Пример 2. Даны два вектора {3, 1, –5} и {6, –3, 0}. Найти линейную комбинацию этих векторов = 2 +3 .

Решение. Найдем координаты вектора .

Xc = ; Yc =; Zc = ;

Ответ. {24, –7, –10}.

Пример 3. Даны три вектора {1, 1, –2}, {2, –1, 0} и . Найти тот вектор, модуль которого будет наибольшим.

Решение. найдем модули трех векторов: ;

; .

Ответ. Наибольший модуль у вектора .

Пример 4. Даны два вектора {1, 1, –2} и {2, –1, 0}.

Решение. Найдем координаты векторов и .

Xc = 2 ´ 1 – 2 = 0; Yc = 2 ´ 1 – (–1) = 3; Zc = 2 ´ (–2) – 0 = -4;

Xd = 1 + 2 = 3; Yd = 1 + (–1) = 0; Zd = –2 + 0 = –2.

Итак: {0, 3, –4}, {3, 0, –2}.

Вычислим модули этих векторов и их скалярное произведение:

Теперь можно вычислить косинус угла J между этими векторами:

.

Пример 5. При каком значении векторы – и a + ортогональны? (Координаты векторов и заданы в примере 4.)

Решение. Найдем координаты векторов – и a + :

;

.

Запишем условие ортогональности полученных векторов:

,

Или –a – 2 + 2a – 2 + 4a = 0.

После преобразования получим 5a – 4 = 0 ; откуда .

Пример 6. Вычислить определитель третьего порядка

.

Решение

Способ 1. Разложив определитель по первой строке, получим

Способ 2. Вычислим теперь тот же определитель, используя свойства определителя.

К элементам второй строки прибавим соответствующие элементы первой, умноженные на
(–2), а к элементам 3-й строки прибавим элементы первой строки, первую строку оставим без изменения (определитель не изменится):

.

Здесь произведены следующие действия: (1) – ко 2-й строке прибавили 3-ю; (2) – общий множитель второй строки вынесли за знак определителя; (3) – к 3-й строке прибавили 2-ю, умноженную на (–5). В результате получили определитель, под главной диагональю которого стоят нули (определитель верхней треугольной матрицы). Такой определитель равен произведению элементов главной диагонали (можно разложить по первому столбцу). Итак, мы вновь получили тот же ответ D = –2.

Этот способ выгодно использовать при вычислении определителей порядка N > 3.

Пример 7. Решить систему уравнений методом Крамера

.

Решение.

.

Вычислим теперь определители D, D1, D2, D3.

.

Поясним проделанные вычисления. Из второй строки определителя мы вычли первую строку, умноженную на 3. В результате получили вторую строку нового определителя. Затем из третьей строчки определителя вычли первую строку, умноженную на 2. В результате получили третью строку нового определителя. Полученный новый определитель разложен по первой строке.

, здесь определитель равен нулю, так как элементы первого столбца пропорциональны соответствующим элементам 3-го столбца.

, так как элементы второго столбца пропорциональны элементам третьего столбца.

.

Так как элементы третьего столбца являются четными числами, то мы вынесли число 2 за знак определителя. Далее из второй строки мы вычли элементы первой строки, умноженные на 3, а из элементов третьей строки вычли элементы первой строки, умноженные на 2. Величина определителя при этих преобразованиях не изменяется. В результате мы получили определитель, у которого в первом столбце стоят два нуля, и этот определитель можно вычислить путем разложения по первому столбцу.

Теперь, по правилу Крамера найдем решение системы:

Полезно сделать проверку, подставив решение в исходную систему. Проделав выкладки, легко убедиться, что решение найдено верно.

Пример 8. При каком значении С равен нулю определитель ?

Решение. Выпишем определитель . По условию задачи

. Отсюда следует, что .

Пример 9. Во сколько раз изменится определитель матрицы третьего порядка, если все его элементы увеличить в два раза?

Решение. Если все элементы матрицы увеличить в два раза, то из каждой строки матрицы можно за знак определителя вынести число 2. Так как таких строк три, то определитель исходной матрицы увеличится в раз.

Пример 10. Вычислить определитель матрицы А = .

Решение. Так как все элементы определителя, кроме элементов главной диагонали, равны нулю, то определитель равен произведению членов, стоящих на главной диагонали. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).

Ответ: .

Пример 11. Вычислить определитель матрицы А = .

Решение. Так как все элементы определителя, расположенные выше элементов побочной диагонали, равны нулю, то определитель равен произведению членов, стоящих на побочной диагонали, причем этот член будет входить в определитель со знаком минус. Это следует как из общего правила вычисления определителя, так и из разложения определителя по первой строке (или по первому столбцу).

Ответ: .

Пример 12. Вычислить определитель .

Решение. Так как все элементы определителя, расположенные в первой строке, пропорциональны элементам третьей строки, то определитель равен нулю.

Пример 13. Вычислить определитель .

Решение. Поскольку во второй строке определителя имеется только один ненулевой член, имеет смысл разложить определитель по элементам второй строки. В результате получим

.

На последнем шаге мы воспользовались основным тригонометрическим тождеством.

Пример 14. Матрица А равна А = . Написать матрицу, составленную из алгебраических дополнений ( i=1,2; j = 1,2) исходной матрицы.

Решение. Напомним, что алгебраическим дополнением элемента называется число , где – минор элемента , а минором элемента матрицы А называется определитель Mij, полученный из матрицы А путем вычеркивания из матрицы i-ой строки и j-го столбца. В нашем случае для элемента алгебраическим дополнением будет , для элемента алгебраическое дополнение равно , для алгебраическое дополнение равно (знак минус написан потому, что для этого элемента сумма номера строки и столбца – нечетное число), для алгебраическое дополнение .

Ответ: матрица алгебраических дополнений для исходной матрицы имеет вид .

Пример 15. Для матрицы А = написать матрицу, составленную из ее алгебраических дополнений.

Решение. Выпишем алгебраические дополнения для каждого элемента матрицы. В данном случае алгебраическими дополнениями будут определители второго порядка.

; ; .

; ; .

Знаки алгебраических дополнений определяются по правилу, описанному в предыдущем примере.

Ответ: матрица алгебраических дополнений имеет вид .

Пример 16. Вычислить определитель 4-го порядка .

Решение. При внимательном рассмотрении элементов определителя можно заметить, что каждый элементы третьей строки равен сумме соответствующих элементов первой и второй сроки. По разобранном в разделе 1.4 свойствам определителя это означает, что рассматриваемый определитель равен нулю.

Пример 17. Определить, при каких значения переменной верно следующее неравенство

<0 ?

Решение. Для решения задачи необходимо выразить определитель как функцию переменной и решить полученное неравенство. В данном случае удобно к первой строке определителя прибавить элементы третьей строки, после чего в первой строке останется только один ненулевой элемент.

Полученное неравенство справедливо при .

Ответ: .

Типовые примеры Действия над матрицами

Занятие № 1. Матрицы. Операции над матрицами.

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Что называется матрицей.

3. Какая матрица называется квадратной, диагональной, единичной.

4. Как выполнить операции сложения матриц и умножение матрицы на число.

5. Для каких матриц вводится операция умножения и правило ее выполнения.

6. Какие преобразования над матрицами являются элементарными.

7. Какую матрицу называют канонической.

Задача № 1. Даны матрицы

Найти матрицу D=(1)

Решение.По определению произведения матрица на число получаем:

Далее вычисляем выражение (1):

D=

Задача № 2. Найти произведение АВ двух квадратных матриц:

Решение.Обе матрицы являются квадратными матрицами 2-го порядка. Такие матрицы можно умножить, используя формулу

(2)

Формула (2) имеет следующий смысл: чтобы получить элемент матрицы С = АВ, стоящий на пересечении строки истолбца нужно взять сумму произведений элементов-ой строки матрицы А на соответствующие элементы-го столбца матрицы В.

В соответствии с формулой (2) найдем:

Следовательно, произведение С = АВ будет иметь вид:

Задача № 3.Найти произведение АВ и ВА матриц:

Решение.Согласно формуле (2),элементы матриц АВ и ВА будут иметь вид:

Вывод:Сравнивая матрицы АВ и ВА и пользуясь определением равенства матриц, делаем вывод, что АВВА, т. е. умножение матриц не подчиняется переместительному закону.

Задача № 4(устно). Даны матрицыСуществуют ли произведения (в скобках даны правильные ответы): АВ (да), ВА (нет), АС (да), СА (нет), АВС (нет), АСВ (да), СВА (нет).

Задача № 5.Найти произведение АВ и ВА двух матриц вида:

Решение.Приведенные матрицы видаследовательно, существуют произведения АВ и ВА данных матриц, которые будут иметь вид:

Задача № 6. Найти произведение АВ матриц:

Ответ:

_{Задачи для самостоятельного решения:}

1. Даны матрицы

Найти матрицу D=2А-4В+3С.

2. Найти произведения АВ и ВА квадратных матриц:

3. Найти произведение матриц:

3. Найти произведение матриц:

3. Найти произведение матриц:

3. Найти произведение матриц:

7. Найти произведение матриц:

8. Найти матрицу: В=6А²+8А, если.

9. Дана матрица .Найти все матрицы В, перестановочные с матрицей А.

10. Доказать, что если А – диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, тоже диагональная.

Занятие 2. Определители квадратных матриц и их вычисление. Обратная матрица.

Для усвоения практического материала нужно ответить на следующие теоретические вопросы:

1. Что называется определителем n-го порядка? Правила вычисления приn=1,2,3.

2. Свойства определителей.

3. Какая матрица называется невырожденной?

4. Какая матрица называется единичной?

5. Какая матрица называется обратной по отношению к данной?

6. Что является необходимым и достаточным условием для существования обратной матрицы?

7. Сформулировать правило нахождения обратной матрицы.

8. Ранг матрицы. Правила нахождения.

Задача № 1. Вычислить определитель:

а ) по правилу треугольника;

б) с помощью разложения по первой строке;

в) преобразованием, используя свойства определителей.

а)

б)

в)

Задача № 2. Найти минор и алгебраическое дополнение элементаa₂₃ определителяи вычислить его разложением по элементам строки или столбца.

Решение.

М₂₃; А₂₃

Задача № 3.Вычислить определитель с помощью разложения по 2 строке:

Ответ:

Задача № 4.Решить уравнение

Решение.

Задача № 5.Вычислить определитель 4-го порядка разложением по элементам строки или столбца:

Ответ: 63.

2.3: Матричные уравнения — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Дэн Маргалит и Джозеф Рабинофф
• Технологический институт Джорджии

Цели

1. Понять эквивалентность между системой линейных уравнений, расширенной матрицей, векторным уравнением и матричным уравнением.
2. Охарактеризуйте векторы \(b\) так, что \(Ax=b\) непротиворечиво, в терминах диапазона столбцов \(A\).
3. Охарактеризуйте матрицы \(A\) так, что \(Ax=b\) непротиворечиво для всех векторов \(b\).
4. Рецепт: умножить вектор на матрицу (два способа).
5. Picture: множество всех векторов \(b\) таких, что \(Ax=b\) непротиворечиво.
6. Словарь: матричное уравнение .

Матричное уравнение \(Ax=b\)

В этом разделе мы вводим очень краткий способ записи системы линейных уравнений: \(Ax=b\). Здесь \(A\) — матрица, а \(x,b\) — векторы (обычно разных размеров), поэтому сначала мы должны объяснить, как умножать матрицу на вектор.

Примечание \(\PageIndex{1}\)

Когда мы говорим, что \(A\) является матрицей \(m\×n\)”, мы имеем в виду, что \(A\) имеет \(m\) строк и \(n\) столбцов.

Примечание

В этой книге мы делаем , а не , резервируя буквы \(m\) и \(n\) для номеров строк и столбцов матрицы. Если мы напишем «\(A\) — матрица \(n\times m\)», то \(n\) — количество строк матрицы \(A\), а \(m\) — количество столбцов .

Определение \(\PageIndex{1}\): Продукт

Пусть \(A\) будет матрицей \(m\times n\) со столбцами \(v_1,v_2,\ldots,v_n\text{:} \) 9м\).

Пример \(\PageIndex{1}\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{ c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right) +2\left(\begin{ array}{c}5\\8\end{array}\right)+3\left(\begin{array}{c}6\\9\end{array}\right)=\left(\begin{array }{c}32\\50\end{массив}\right).\nonumber\]

Чтобы \(Ax\) имело смысл, число элементов \(x\) должно быть одинаковым в качестве количества столбцов \(A\text{:}\) мы используем записи \(x\) в качестве коэффициентов столбцов \(A\) в линейной комбинации. Результирующий вектор имеет то же количество элементов, что и число 9.m\text{,}\) и \(x\) — вектор, коэффициенты которого \(x_1,x_2,\ldots,x_n\) неизвестны. 2-1=0\) для \(x\). Второй вопрос, возможно, является новой концепцией для вас. Теорема 2.9м\). Рассмотрим векторное уравнение

\[ x_1v_1 + x_2v_2 + \cdots + x_nv_n = b. \nonumber \]

Это эквивалентно матричному уравнению \(Ax=b\text{,}\), где

\[A=\left(\begin{array}{cccc}|&|&\quad & | \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &|\end{массив}\right)\quad\text{and}\quad x=\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right).\nonumber \]

И наоборот, если \(A\) является любой матрицей \(m\times n\), то \(Ax= б\) эквивалентно векторному уравнению 93\).

Решение

Пусть \(A\) — матрица со столбцами \(v_1,v_2,v_3\text{,}\), а \(x\) — вектор с элементами \(2,3,-4 \). Затем

\[Ax=\left(\begin{array}{ccc}|&|&| \\ v_1 & v_2 & v_3 \\ |&|&|\end{array}\right)\:\left( \begin{array}{c}2\\3\\-4\end{array}\right) = 2v_1 +3v_2 -4v_3, \nonumber\]

, поэтому векторное уравнение эквивалентно матричному уравнению \(Ax =\left(\begin{массив}{c}7\\2\\1\end{массив}\right)\).

Примечание \(\PageIndex{4}\): четыре способа записи линейной системы

Теперь у нас есть четыре эквивалентных способа записи (и обдумывания) системы линейных уравнений:

1. В виде системы уравнений:
   \[\left\{\begin{array}{rrrrrrr} 2x_1 &+ & 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{массив}\right.\nonumber\]
2. В виде расширенной матрицы:
   \[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonnumber\]
3. В виде векторного уравнения (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
   \[x_{1}\left(\begin{array}{c}2\\1\end{array}\ вправо)+x_2\влево(\begin{массив}{c}3\\-1\конец{массив}\вправо)+x_3\влево(\begin{массив}{c}-2\\-3\конец{ array}\right)=\left(\begin{array}{c}7\\5\end{array}\right)\nonnumber\]
4. В виде матричного уравнения (\(Ax=b\)):
   \[\left(\begin{array}{ccc}2&3&-2 \\ 1&-1&-3\end{array}\right)\:\ влево(\begin{массив}{c}x_1 \\ x_2 \\ x_3\end{массив}\right)=\left(\begin{массив}{c}7\\5\end{массив}\right). \номер\]

В частности, все четыре имеют одинаковый набор решений .

Примечание \(\PageIndex{5}\)

Мы будем свободно перемещаться между четырьмя способами записи линейной системы снова и снова до конца книги.

Другой способ вычисления \(Ax\)

Приведенное выше определение продукта, определение \(\PageIndex{1}\), – полезный способ определения произведения матрицы на вектор, когда дело доходит до понимания связь между матричными уравнениями и векторными уравнениями. Здесь мы даем определение, которое лучше подходит для ручных вычислений.

Определение \(\PageIndex{3}\): вектор-строка

Вектор-строка представляет собой матрицу с одной строкой. Произведение вектора-строки длины \(n\) и вектора (столбца) длины \(n\) равно

\[\left(\begin{array}{cccc}a_1 &a_2 &\ cdots a_n \end{массив}\right)\:\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{массив}\right) =a_1 x_1 + a_2 x_2 +\ cdots + a_n x_n .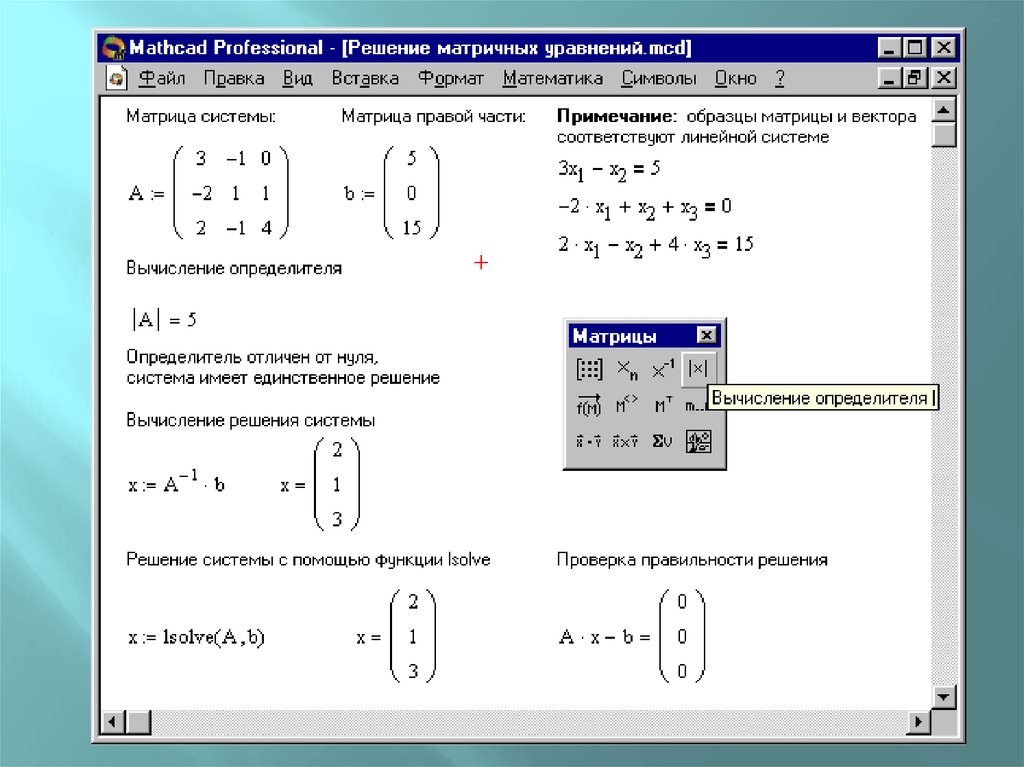 \nonumber\]

Это скаляр.

Рецепт: Правило строки-столбца для умножения матрицы на вектор 9n\text{,}\) then

\[Ax=\left(\begin{array}{c} — r_1 — \\ —r_2 — \\ \vdots \\ — r_m —\end{array}\right ) x=\left(\begin{массив}{c} r_1 x \\ r_2 x \\ \vdots \\ r_m x\end{массив}\right).\nonumber\]

Пример \(\PageIndex{3 }\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{array}{c}1\\2\\3 \end{массив}\right)=\left(\begin{array}{cc}{\left(\begin{array}{c}4&5&6\end{массив}\right)}&{\left(\begin{ array}{c}1\\2\\3\end{массив}\right)}\\{\left(\begin{array}{ccc}7&8&9\end{массив}\right)}&{\left(\begin{array}{c}1\\2\\3\end{массив}\right)}\end{массив}\right) =\left( \begin{array}{ccccccccccc} 4 & \cdot &1&+&5 &\cdot & 2&+& 6& \cdot & 3 \\ 7 &\cdot & 1&+&8 & \cdot & 2&+&9 & \cdot &3\end {array}\right)=\left(\begin{array}{c} 32\\50\end{array}\right).\nonumber\]

Это тот же ответ, что и раньше:

\[\ влево(\begin{массив}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{массив}{c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right)+2\left(\begin{массив}{c}5\\8\end{массив}\right) +3\влево(\begin{массив}{с}6\\9\end{массив}\right)=\left(\begin{array}{cccccccccc} 1 & \cdot & 4&+& 2& \cdot &5&+&3& \cdot &6 \\ 1 & \cdot &7&+& 2& \cdot &8& +&3& \cdot &9\end{массив}\right)=\left(\begin{array}{c}32\\50\end{массив}\right). \nonumber\]

Диапазоны и согласованность

Let \(A\) — матрица со столбцами \(v_1,v_2,\ldots,v_n\text{:}\)

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots & v_n \\ |&|&\quad &|\end{массив}\right).\nonumber\]

Тогда

\[ \begin{split} Ax=b&\text{ имеет решение} \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } A\left(\ begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) = b \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } x_1v_1 + x_2v_2 + \cdots + x_nv_n = b \\ &\iff \text{$b$ является линейной комбинацией } v_1,v_2,\ldots,v_n \\ &\iff \text{$b$ находится в диапазон столбцов $A$}. \end{split} \nonumber \]

Примечание \(\PageIndex{6}\): диапазоны и согласованность

Матричное уравнение \(Ax=b\) имеет решение тогда и только тогда, когда \(b\) находится в диапазоне столбцов \(A\).

Это дает эквивалентность между алгебраическим утверждением (\(Ax=b\) непротиворечиво) и геометрическим утверждением (\(b\) находится в диапазоне столбцов \(A\)) .

Пример \(\PageIndex{4}\): несогласованная система

Пусть \(A=\left(\begin{array}{cc}2&1\\ -1&0 \\ 1&-1\end{array}\ правильно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}0\\2\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1 =\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) }\color{black}{,}\nonumber\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{) c}0\\2\\2\конец{массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак рисуем картинку:

Рисунок \(\PageIndex{1}\)

 Похоже, что \(w\) не лежит в \(\text{Span}\{v_1,v_2\},\), поэтому уравнение несовместимо .

Давайте проверим наш геометрический ответ, решив матричное уравнение с помощью редукции строк. Помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c} 2&1&0 \\ -1&0&2 \\ 1&-1&2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left (\begin{array}{cc|c} 1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right).\nonumber\]

Последнее уравнение равно \(0=1\text{,}\), поэтому система действительно противоречива, и матричное уравнение

\[\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\right)x=\left(\begin {массив}{с}0\\2\\2\конец{массив}\справа)\номер\]

не имеет решения.

Пример \(\PageIndex{5}\): согласованная система

Пусть \(A=\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\ правильно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}1\\-1\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1=\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) },\номер\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{c}1\\-1\\2\end{ массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак, мы рисуем картинку:

Рисунок \(\PageIndex{3}\)

Похоже, что \(w\) действительно содержится в диапазоне столбцов \(A\text{;}\) на самом деле мы можем видеть

\[ w = v_1 – v_2 \ подразумевает x = \left(\begin{array}{c}1\\-1\end{array}\right). \номер\]

Давайте проверим наш геометрический ответ, решив матричное уравнение с помощью редукции строк. Мы помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c}2&1&1\\-1&0&-1\\1&-1&2\end{array}\right) \ quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&1 \\ 0&1&-1 \\ 0&0&0\end{массив}\right).\nonumber\]

Это дает нам \(x=1\) и \(y=-1\text{,}\), что соответствует картинке:

\[1\left(\begin{array}{c}2 \\-1\\1\конец{массив}\справа)-1\слева(\начало{массив}{с}1\\0\\-1\конец{массив}\справа)=\слева(\начало {массив} {c} 1\\-1\\2\end{массив}\right)\quad\text{or}\quad A\left(\begin{array}{c}1\\-1\end {array}\right)=\left(\begin{array}{c}1\\-1\\2\end{array}\right). \nonumber\]

Когда решения всегда существуют.

Опираясь на примечание \(\PageIndex{6}\): промежутки и согласованность, у нас есть следующий критерий, когда \(Ax=b\) непротиворечив для 9м\).

Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, отсюда следует, что 2 и 3 также эквивалентны.) Если \(A\) имеет точку опоры в каждой строке, то его сокращенная ступенчатая форма строки выглядит следующим образом:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&1&\star \end{array}\right),\nonumber\]

и, следовательно, \(\left(\begin{array}{c|c}A&b\end{array}\right)\) сводится к этому:

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &\star \\ 0&1&\star &0&\star &\star \\ 0&0&0&1&\star &\star\end{array}\ справа).\номер\]

Нет \(b\), который делал бы это несовместимым, поэтому всегда есть решение. Наоборот, если \(A\) не имеет стержня в каждой строке, то его уменьшенная ступенчатая форма строки выглядит так:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&0&0\end{array}\right),\nonumber\]

, что может привести к несогласованности системы после добавления \(b\text{:}\)

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &0 \\ 0&1&\star &0&\star &0 \\ 0&0&0&0&0&16\end{array}\right). \nonumber\]

Напомним, что эквивалентно означает, что для любой заданной матрицы \(A\text{,}\) либо все условий приведенной выше теоремы \(\PageIndex{1}\) выполняются , либо все они ложны.

Примечание \(\PageIndex{7}\)

Будьте внимательны при чтении формулировки приведенной выше теоремы \(\PageIndex{1}\). Первые два условия очень похожи на это примечание \(\PageIndex{6}\): диапазоны и согласованность, но логически они совершенно разные из-за квантификатора « для всех \(b\)».

Пример \(\PageIndex{6}\): Интерактивный режим: критерии теоремы выполнены 1}\) удовлетворены. Фиолетовая область — это диапазон столбцов \(v_1,v_2,v_3\) массива \(A\text{,}\), который совпадает с набором всех \(b\), таких что \(Ax=b \) имеет решение. Если вы перетащите \(b\text{,}\), демо решит за вас \(Ax=b\) и переместит \(x\).

Пример \(\PageIndex{7}\): Интерактивный: Критерии теоремы не выполняются 1}\) удовлетворяются , а не . m\), когда \(A\) имеет \ (м\) повороты.

---

Эта страница под названием 2.3: Матричные уравнения распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, переработана и/или курирована Дэном Маргалитом и Джозефом Рабинофф через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Дэн Маргалит и Джозеф Рабинофф

   Лицензия

   ГНУ ФДЛ

   Версия лицензии

   1,3

2. Теги

   1. источник@https://textbooks. math.gatech.edu/ila

Алгебраическое решение матричного уравнения

Переключить боковую панель оглавления

Используйте SymPy для решения матричного (линейного) уравнения. Например, решение \( \left[\begin{массив}{cc} c & d\\1 & -e\end{массив}\right] \left[\begin{массив}{cc} x\\y\end{массив}\right] = \left[\begin{array}{cc} 2\\0\end{массив}\right] \) дает \( \left[\begin{массив}{cc} x\\y\end{массив}\right] = \left[\begin{массив}{cc} \frac{2e}{ce+d}\\\frac{2}{ce+d}\end{массив}\right]\).

Альтернативы для рассмотрения

• Если ваша матрица и постоянный вектор содержат только числа, а не символы, для пример \(\left[\begin{массив}{cc} 1 и 2\\3 и 4\end{массив}\right] \left[\begin{массив}{cc} x\\y\end{массив}\right] = \left[\begin{массив}{cc} 2\\0\end{массив}\right]\), вы можете использовать один из этих других бесплатных и открытых пакеты вместо SymPy:

  • NumPy numpy. linalg.solve()

  • SciPy scipy.linalg.solve()

  • mpmath’s lu_solve()

• Решение матричного уравнения эквивалентно решению системы линейных уравнения, поэтому, если вы предпочитаете, вы можете Решите систему уравнений алгебраически

• Если вы сформулировали свою задачу как систему линейных уравнений и хотите преобразовать его в матричную форму, вы можете использовать linear_eq_to_matrix() , а затем следуйте процедурам, описанным в этом руководстве.

Решение матричного уравнения

Вот пример решения матричного уравнения с помощью SymPy sympy.matrices.matrices.MatrixBase.solve() . Используем стандартную матрицу формулировка уравнения \(Ax=b\), где

• \(A\) — матрица, представляющая коэффициенты в линейных уравнениях

• \(x\) — это вектор-столбец неизвестных, которые необходимо решить для

• \(b\) — вектор-столбец констант, где каждая строка — значение уравнение

 >>> из sympy import init_printing
>>> init_printing(use_unicode=Истина)
 

 >>> из символов импорта sympy
>>> из sympy. matrices импортировать матрицу
>>> c, d, e = символы ("c, d, e")
>>> A = Matrix([[c,d], [1, -e]])
>>> А
⎡к д ⎤
⎢ ⎥
⎣1 -е⎦
>>> b = Матрица ([2, 0])
>>> б
⎡2⎤
⎢ ⎥
⎣0⎦
>>> А.решить(б)
⎡ 2⋅е ⎤
⎢───────⎥
⎢с⋅е + г⎥
⎢ ⎥
⎢ 2 ⎥
⎢───────⎥
⎣с⋅е + г⎦
 

Руководство

Матрица обычно должна быть квадратной

Матрица \(A\) обычно должна быть квадратной, чтобы представить систему линейных уравнений с тем же числом неизвестных, что и уравнения. Если нет, SymPy выдаст ошибку ShapeError: `self` и `rhs` должны иметь одинаковое количество строк.

Исключение из требования, чтобы матрица была квадратной, связано с использованием SymPy псевдообратного Мура-Пенроуза .

Методы решения матричных уравнений

Метод решения матриц SymPy, sympy.matrices.matrices.MatrixBase.solve() , может использовать несколько различных методов, которые перечислены по этой справочной ссылке API. В зависимости от характера матрицы данный метод может быть более эффективным. От по умолчанию, Гаусс-Жордан будет использовано устранение.

Указание метода решения эквивалентно использованию специализированного метода решения. функция. Например, используя , решить с помощью method='LU' вызовов LUsolve() .

Решение нескольких матричных уравнений с одной и той же матрицей

Если вам нужно повторно решить матричные уравнения с одной и той же матрицей \(A\), но различных постоянных векторов \(b\), эффективнее использовать один из следующих методы.

Вы можете использовать разложение LU через LUsolve() :

 >>> из символов импорта sympy, матрица, глаз, упростить
>>> c, d, e = символы ("c, d, e")
>>> A = Matrix([[c,d], [1, -e]])
>>> А
⎡к д ⎤
⎢ ⎥
⎣1 -е⎦
>>> b = Матрица ([2, 0])
>>> б
 ⎡2⎤
 ⎢ ⎥
 ⎣0⎦
>>> решение = A.LUsolve(b)
>>> решение
 ⎡ 2⋅е ⎤
 ⎢───────⎥
 ⎢с⋅е + г⎥
 ⎢ ⎥
 ⎢ 2 ⎥
 ⎢───────⎥
 ⎣с⋅е + г⎦
>>> # Демонстрация правильного решения
>>> упростить (решение *)
 ⎡2⎤
 ⎢ ⎥
 ⎣0⎦
>>> b2 = Матрица ([4, 0])
>>> б2
 ⎡4⎤
 ⎢ ⎥
 ⎣0⎦
>>> решение2 = A. LUsolve(b2)
>>> решение2
 ⎡ 4⋅е ⎤
 ⎢───────⎥
 ⎢с⋅е + г⎥
 ⎢ ⎥
 ⎢ 4 ⎥
 ⎢───────⎥
 ⎣с⋅е + г⎦
>>> # Демонстрация правильности решения 2
>>> упростить(A * решение2)
 ⎡4⎤
 ⎢ ⎥
 ⎣0⎦
 905:00
 Другой подход заключается в вычислении обратной матрицы, но это почти всегда
медленнее и значительно медленнее для больших матриц. Если эффективное вычисление
не является приоритетом, вы можете использовать  inv()  :
 
 >>> из символов импорта sympy, Matrix, упростить
>>> c, d, e = символы ("c, d, e")
>>> A = Matrix([[c,d], [1, -e]])
>>> b = Матрица ([2, 0])
>>> б
 ⎡2⎤
 ⎢ ⎥
 ⎣0⎦
>>> b2 = Матрица ([4, 0])
>>> б2
 ⎡4⎤
 ⎢ ⎥
 ⎣0⎦
>>> инв = А.инв()
>>> инв
 ⎡ э д ⎤
 ⎢─────── ───────⎥
 ⎢c⋅e + d c⋅e + d⎥
 ⎢ ⎥
 ⎢ 1 -с ⎥
 ⎢─────── ───────⎥
 ⎣c⋅e + d c⋅e + d⎦
>>> # Решает Ax = b для x
>>> решение = инв * б
>>> решение
 ⎡ 2⋅е ⎤
 ⎢───────⎥
 ⎢с⋅е + г⎥
 ⎢ ⎥
 ⎢ 2 ⎥
 ⎢───────⎥
 ⎣с⋅е + г⎦
>>> # Демонстрация правильного решения
>>> упростить (решение *)
 ⎡2⎤
 ⎢ ⎥
 ⎣0⎦
>>> # Решает Ax = b2 для x
>>> решение2 = инв * b2
>>> решение2
 ⎡ 4⋅е ⎤
 ⎢───────⎥
 ⎢с⋅е + г⎥
 ⎢ ⎥
 ⎢ 4 ⎥
 ⎢───────⎥
 ⎣с⋅е + г⎦
>>> # Демонстрация правильности решения 2
>>> упростить(A * решение2)
 ⎡4⎤
 ⎢ ⎥
 ⎣0⎦
 905:00
 Определение обратной большой символьной матрицы не может быть вычислительно
сговорчивый.
 Работа с символьными матрицами 
 Вычислительная сложность манипулирования символьными матрицами может увеличиться
быстро с размером матрицы. Например, количество членов в определителе
символическая матрица увеличивается с факториалом размерности матрицы. Как
В результате максимальная размерность решаемых матриц больше
ограничено, чем для числовых матриц. Например, определитель этого 4x4
символьная матрица имеет 24 члена по четыре элемента в каждом члене:
 
 >>> из sympy импорта MatrixSymbol
>>> A = MatrixSymbol('A', 4, 4).as_explicit()
>>> А
⎡А₀₀ А₀₁ А₀₂ А₀₃⎤
⎢ ⎥
⎢А₁₀ А₁₁ А₁₂ А₁₃⎥
⎢ ⎥
⎢А₂₀ А₂₁ А₂₂ А₂₃⎥
⎢ ⎥
⎣А₃₀ А₃₁ А₃₂ А₃₃⎦
>>> А.дет()
 A₀₀> a₁₁g₂₂ age₃₃ - a₀₀> a₁₁g₁₁ a₂₃g₂₃ a₃₂ - a₀₀> a₁₂tairt
 ₃omA₂₁taira₃₂ - a₀₀> a₁₃g₂₂ he₂₂⋅a₃₁ - a₀₁> A₁₀ веза -a₃₃ + a₀₁> A₁₀ везете + A₀₁g₁₀ ag₁₀tet
 A₃₃ - a₀₁> A₁₂> A₂₃> A₀₁ - a₀₁g₁₃ ag₂₀test
 A₀₂> a₁₀g₂₃ age₃₁ - a₀₂> a₁₁g₁₁ a₂₀g₂₀ + a₀₂> a₁₁tairtairt
 ₃omA₂₁taira₃₀ - a₀₃> a₁₀g₂₁ he₂₁> a₀₃> a₁₀ везat
 А₃₀ - А₀₃⋅А₁₂⋅А₂₀⋅А₃₁ + А₀₃⋅А₁₂⋅А₂₁⋅А₃₀
 905:00
 и решение матричного уравнения из него занимает около минуты, тогда как аналогичное
Матрица 3x3 занимает менее одной секунды. Более несвязанные, символические записи в
матрица, тем более вероятно, что она будет медленной в управлении. Этот пример, нахождение
общее решение матрицы, где все элементы являются независимыми символами, есть
крайний случай и, следовательно, самый медленный для матрицы такого размера.
 Ускорение решения матричных уравнений 
 Вот несколько предложений:
 Если элементы матрицы равны нулю, убедитесь, что они распознаются как нулевые. Вы можете
сделать это, либо сделав их равными нулю, либо применив
предположения.
 Выбор метода решения, соответствующего свойствам матрицы, например
эрмитовым, симметричным или треугольным. Ссылаться на
Методы решения матричных уравнений.
 Используйте класс  DomainMatrix , который может работать быстрее
потому что это ограничивает область определения матричных элементов.
 Использовать результат решения 
 Использование решения в качестве вектора 
 Результат решения можно использовать как вектор. Например, чтобы доказать, что
решение \(x\) правильное, вы можете умножить его на матрицу \(A\) и убедиться, что оно
производит вектор констант \(b\):
 
 >>> из символов импорта sympy, упростить
>>> из sympy.matrices импортировать матрицу
>>> c, d, e = символы ("c, d, e")
>>> A = Matrix([[c,d], [1, -e]])
>>> b = Матрица ([2, 0])
>>> решение = A.solve(b)
>>> решение
 ⎡ 2⋅е ⎤
 ⎢───────⎥
 ⎢с⋅е + г⎥
 ⎢ ⎥
 ⎢ 2 ⎥
 ⎢───────⎥
 ⎣с⋅е + г⎦
>>> # Не сразу очевидно, является ли этот результат вектором нулей
>>> (А * решение) - б
 ⎡ 2⋅с⋅е 2⋅д ⎤
 ⎢─────── + ─────── - 2⎥
 ⎢c⋅e + d c⋅e + d ⎥
 ⎢ ⎥
 ⎣ 0 ⎦
>>> # упрощает показывает, что этот результат является вектором нулей
>>> упростить((A * решение) - б)
 ⎡0⎤
 ⎢ ⎥
 ⎣0⎦
 905:00
 Обратите внимание, что нам пришлось использовать  SimPy() , чтобы сделать SymPy
упростите выражение в матричном элементе, чтобы сразу стало очевидно, что
решение правильное.
 Извлечение элементов из раствора 
 Поскольку вы можете перебирать элементы в векторе-столбце, вы можете извлечь
его элементы с использованием стандартных методов Python.