Примеры на второй закон ньютона: Привести пример 2 закона ньютона

формулировка, область применения, формула, примеры задач

Содержание:

• Формулировка
• Область применения
• Формула
• Примеры задач

Содержание

• Формулировка
• Область применения
• Формула
• Примеры задач

Формулировка

Второй закон Ньютона представляет собой дифференциальную закономерность, характерную для механического перемещения, которая демонстрирует, как ускоряется некое тело под действием равнодействующей сил в зависимости от того, какова его масса.

Всего имеется три закона Ньютона. Рассматриваемый второй закон входит в их число. Это ключевая закономерность динамики. В качестве объекта принимают материальную точку в каком-то виде. Обязательным свойством материальной точки служит инерция.

Параметр инерции, в свою очередь, определяется массой. Исходя из традиционного принципа механики Ньютона, можно сделать вывод о том, что для материальной точки характерна какая-то масса, стабильная в процессе изменения времени, в условиях разных видов движения и контакте с прочими телами.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Наиболее распространена такое понимание второго закона Ньютона:  при скоростях, существенно ниже, если сравнить со световой скоростью, при рассмотрении в рамках инерциальных систем отсчета ускорение, развиваемое материальной точкой, зависит в прямой пропорции от формирующей это изменение скорости силы, не имеет связи с природным происхождением воздействующей силы, ориентировано соответственно вектору данной силы и находится в обратной пропорциональной зависимости от массы, характерной для рассматриваемой материальной точки.

Область применения

Понятие второго закона Ньютона в рамках поля действия и ключевых принципов традиционной механики распространяется на перемещение материальной точки. Подразумевается, что такая материальная точка характеризуется стабильной во времени массой. Формула, описывающая эту закономерность, является уравнением движения материальной точки и считается ключевым соотношением динамики материальной точки.

В определенных ситуациях в процессе изучения традиционной механики имели место попытки применения к телам с изменяющимися величинами массы рассматриваемого уравнения:

\(d{\vec {p}}/dt={\vec {F}}\)

Подобные манипуляции сопровождались рядом трудностей. Расширение области применения закономерности требовало модификации сформулированных ранее понятий и доработки фундаментальных законов. К примеру, возникала необходимость в пересмотре таких категорий, как точка, импульс, а также сила.

Нередко при поиске ответов к задачам и постановке экспериментальных опытов складывается ситуация, когда на материальную точку оказывают воздействие одновременно несколько разных сил.

В одно и то же время каждая из них придает объекту наблюдения какое-либо ускорение. Эту величину целесообразно вычислять с помощью второго закона Ньютона, руководствуясь принципом суперпозиции сил. По этой причине для расчета суммарного ускорения, которое приобретает материальная точка, достаточно путем подстановки добавить равнодействующую сил в соотношение для второго закона Ньютона.

В соотношении величин по второму закону Ньютона предусмотрена скалярная аддитивность масс:

\(\vec {F}=m{\vec {a}}\)

Математическую закономерность, описывающую движение материальной точки, допустимо использовать, чтобы описать механическое перемещение центра масс в рамках некой механической системы. Массовой центр меняет положение наподобие материальной точки с определенной массой, которая вычисляется, как общая масса системы. Рассматриваемая материальная точка испытывает на себе суммарное воздействие сил извне, которые направлены на точки системы. Таким образом, сформулирована теория о перемещении массового центра системы.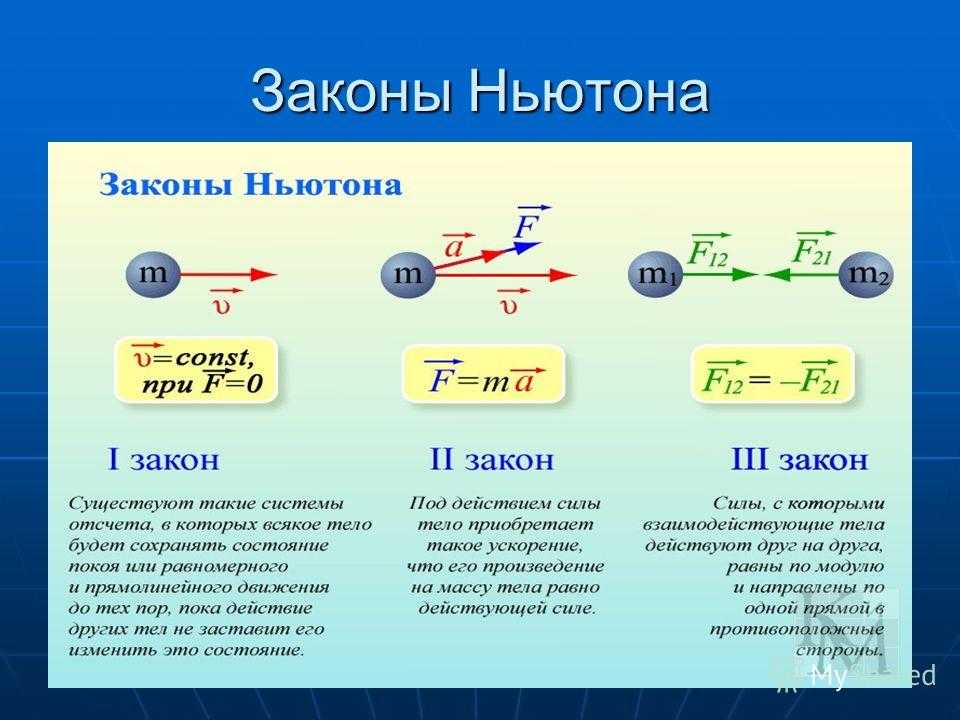

Закономерность, описывающая второй закон Ньютона, является справедливой лишь при рассмотрении движения в рамках инерциальных систем отсчета. Однако его смысл допустимо распространить и на не инерциальные системы отсчета. Это возможно при формировании таких условий, когда к силам извне прибавляют силы инерции. Формулировка записи при этом не меняется, как и понимание закона.

Формула

Уравнение второго закона Ньютона:

\(\vec {a}={\frac {{\vec {F}}}{m}}\)

Здесь \(\vec {a}\) обозначает ускорение тела, \(\vec{F}\) — силу, которая воздействует на рассматриваемое тело, m демонстрирует, чему равна масса рассматриваемого тела.

Имеет место и следующая справедливая форма записи: \(m{\vec {a}}={\vec {F}}\)

Интерпретировать второй закон Ньютона допустимо с применением определения импульса:

в инерциальных системах отсчета производная импульса материальной точки по времени вычисляется, как сила, действующая на эту материальную точку, то есть:

\(\frac {d{\vec {p}}{dt}}=\vec {F}\)

Здесь \({\vec p}=m{\vec v}\) обозначает импульс, то есть количество движения точки, \(\vec {v}\) характеризует скорость точки, t является временем. 2 \cdot 8 с = 6 м/с\)

Второй способ решения можно начать с записи соотношения для вычисления скорости:

\(v=v_0+at=v_0+\dfrac{F}{m} \cdot t\)

Если вписать в уравнение известные величины, то получим:

\(v=2 м/с + \dfrac{500 Н}{1000 кг} \cdot 8 c =6 м/с\)

Ответ: \(v= 6 м/с.\)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

3. Законы Ньютона. Примеры проявления законов Ньютона в природе и использование этих законов в технике

Первый закон Ньютона. Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела (или действия других тел компенсиру­ются). Этот закон часто называется законом инерции, поскольку движение с постоянной скоростью при компенсации внешних воздействий на тело называется инерцией. Второй закон Ньютона. Сила, действующая на тело, равна произведению массы тела на сооб­щаемое этой силой ускорение

. – ускорение прямо пропорционально действующей (или равнодействующей) силе и обратно пропорцио­нально массе тела. Третий закон Ньютона. Из опытов по взаимодействию тел следует , из второго закона Ньютона и , поэтому . Силы взаимодействия между телами: направлены по одной прямой, равны по величине, противоположны по направлению, приложены к разным телам (по­этому не могут уравновешивать друг друга), всегда действуют парами и имеют одну и ту же природу. Законы Ньютона выполняются одновременно, они позволяют объяснить закономерности движения планет, их естественных и искусственных спутников. Иначе, позволяют предвидеть траектории движения планет, рассчитывать траектории космических ко­раблей и их координаты в любые заданные моменты времени. В земных условиях они позволяют объяс­нить течение воды, движение многочисленных и раз­нообразных транспортных средств (движение автомо­билей, кораблей, самолетов, ракет). Для всех этих движений, тел и сил справедливы законы Ньютона.

9.

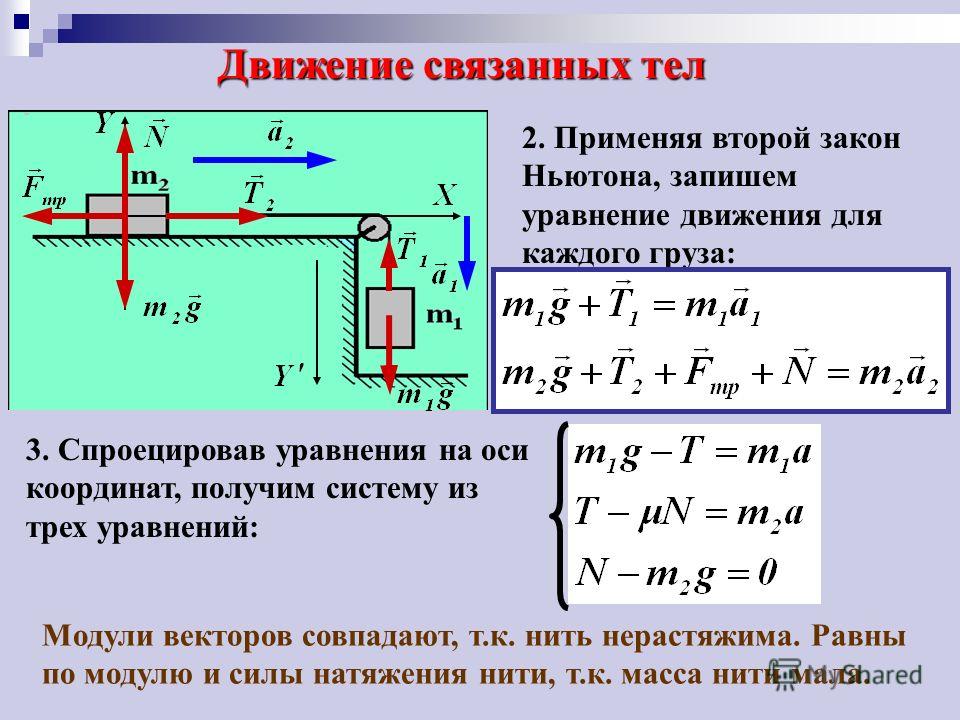
Потенциальная и кинетическая энергия. Примеры перехода энергии из одного вида в другой. Закон сохранения энергии

Энергия – характеристика состояния тела. Кинетическая энергия – энергия движуще­гося тела. Если на тело массой m действует постоян­ная сила P, совпадающая с направлением движения, то работа . Но , , тогда . Работа – мера изменения энергии. Кинетическая энергия . Работа дей­ствующих сил, приложенных к телу, равна изменению кинетической энергии . При , – кинетическая энергия равна работе, которую должна совершить сила, действующая на тело, чтобы сообщить данную скорость.

Потенциальная энергия – энергия взаимодействия. Работа – потенциальная энергия тела, поднятого на высоту h над нулевым уровнем (например, над уровнем Земли). Знак «-» означает, что, когда работа силы тяжести положи­тельна, потенциальная энергия тела уменьшается. Потенциальная энергия не зависит от скорости, а за­висит от координаты тела (от высоты). Потенциаль­ная энергия деформированной пружины . Сумму кинетической и потенциальной энергий тела называют его полной механической энергией. Полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или упругости, остается неизменной при любых движениях тел системы. Это утверждение является законом сохранения энергии в механических процессах. На примере свободно падающего тела можно пока­зать, что при его движении потенциальная энергия переходит в кинетическую. При этом потенциальная энергия уменьшается ровно на столько, на сколько увеличивается кинетическая энергия: или , т. е. пол­ная механическая энергия во все время падения остается неизменной, хотя потенциальная энергия превращается в кинетическую

Применение второго закона Ньютона: обзор

Возможно, вы уже знакомы со вторым законом Ньютона. Но что в этом хорошего? В этой статье мы убедим вас, что этот закон движения не является абстрактным математическим утверждением, оторванным от реальности. Вместо этого второй закон Ньютона правильно описывает многие явления, со многими из которых вы сталкиваетесь ежедневно.

Мы начнем с иллюстрации второго закона Ньютона, в которой мы рассмотрим значение символов в уравнении закона силы и обсудим, как связаны эти величины. Далее мы перечислим 10 приложений второго закона Ньютона к повседневным явлениям, прежде чем выбрать два примера для более глубокого полуколичественного анализа.

Иллюстрация второго закона движения Ньютона

динамическая величина – это величина, значение которой может меняться со временем

Если мы хотим описать движение физической системы, мы должны сначала знать ее динамические величины: смещение , скорость и ускорение . Для случая линейного движения , которое описывает движение объекта только в одном пространственном измерении вдоль прямой линии, применение второго закона Ньютона дает нам всю необходимую информацию об изменении движения объекта во времени. В этом случае мы напишем:

\[\vec{a} = \frac{\sum \vec{F}}{m}.\]

Напомним, что маленькие стрелки над ускорением \(\vec{a}\) и силой \ (\vec{F}\) обозначают векторных величин . Важно придерживаться векторной записи, потому что система может ускоряться в одном пространственном измерении, но не в другом. Например, яблоко, падающее с дерева, ускоряется только по вертикали.

Кроме того, поскольку ускорение и сила являются единственными векторными величинами во втором законе движения Ньютона (масса не имеет направления, так как это скаляр ), ускорение центра масс системы всегда будет в том же направлении , что и чистая сила, действующая на нее.

Символ перед \(\vec{F}\) — это греческая буква Sigma , которую мы используем для обозначения суммы в математике. То есть

\[\vec{F}_{\text{net}} = \sum \vec{F} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3 + \dots\]

Каждое из слагаемых в правой части представляет собой силу, действующую на центр масс системы.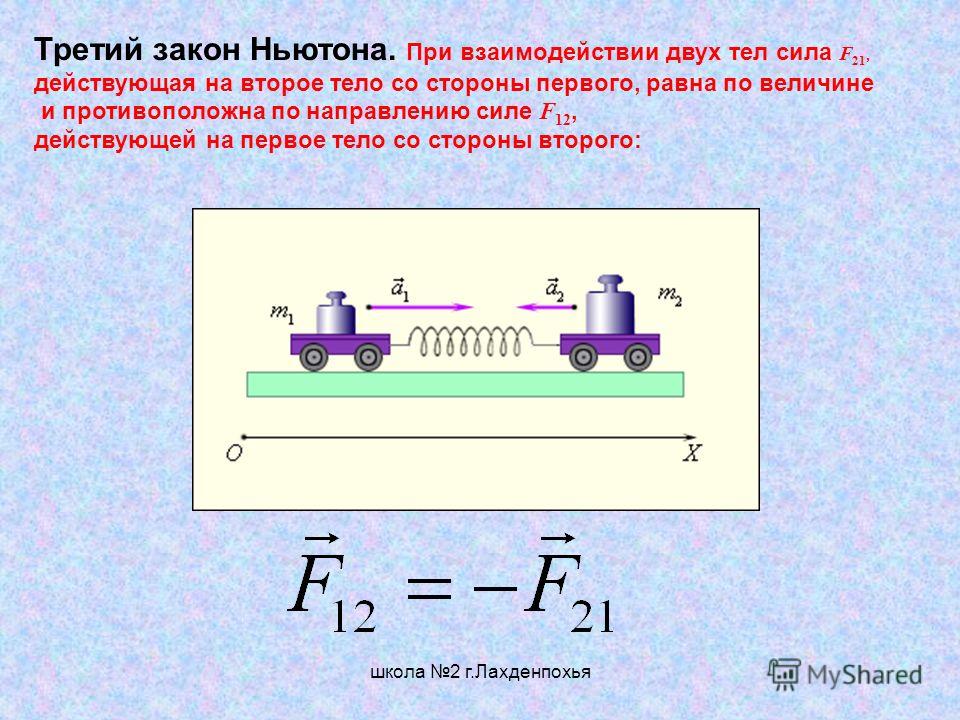 Поскольку все внешние силы, действующие на систему, могут исходить из разных направлений, очень важно не отбрасывать векторные обозначения, когда мы пишем результирующую силу! Если силы неуравновешены (что означает, что результирующие силы, действующие на объект, не равны нулю), то объект ускоряется.

Сравните это с массой, которая находится под разделительной линией с правой стороны. Если бы центр масс системы увеличился в десять раз, мы бы получили , разделив результирующей силы на значение в десять раз больше исходного значения. Следовательно, ускорение уменьшится в десять раз. Следовательно, ускорение центра масс системы равно и обратно пропорционально массе системы.

Рисунок ниже иллюстрирует то, что мы обсуждали выше. Убедитесь, что вы понимаете это, прежде чем читать дальше.

Предположим, мы знаем массу системы и вычислили ее ускорение по результирующей силе. Как это поможет нам найти другие динамические величины: скорость и перемещение ? Мы приходим к ответу из определения ускорения.

Ускорение — скорость изменения скорости во времени.

В виде уравнения имеем

\[\vec{a}_{\text{avg}}=\frac{\Delta \vec{v}}{\Delta t},\]

где \( \Delta \vec{v} = \vec{v} – \vec{v_0}\) обозначает разницу между конечной и начальной скоростью. Вы можете узнать из предыдущих математических занятий, что правая часть выглядит как наклон кривой. Именно это мы подразумеваем под фразой скорость изменения в приведенном выше определении. Но почему мы только что написали \(\vec{a}_{\text{avg}}\) вместо просто \(\vec{a}\)?

Мы делаем это, чтобы указать, что приведенная выше формула используется для расчета среднего ускорения объекта. Смысл среднего ускорения, в отличие от мгновенного ускорения , заключается в том, что мы вычисляем \(\Delta \vec{v}\) как разницу между конечной и начальной скоростью за фиксированный интервал времени \(\ Дельта т\). При этом, однако, мы пренебрегаем любыми промежуточными значениями, которые может принимать скорость. Следовательно, значение является только средним.

Скорость — скорость изменения смещения во времени.

Аналогично, средняя скорость на интервале времени удовлетворяет уравнению

\[\vec{v}_{\text{avg}}=\frac{\Delta \vec{x}}{\Delta t}.\ ]

где \(\Delta \vec{x} = \vec{x} – \vec{x_0}\) обозначает разницу между конечным и начальным перемещением. Работа со средними значениями ускорения и скорости достаточна для решения большинства задач, с которыми вы столкнетесь в курсах физики на основе алгебры. Но вам может быть интересно, как сделать среднее значение, которое является лишь приближением, более точным. При этом используется концепция мгновенное ускорение мы упоминали выше.

Чем меньше интервал времени, в течение которого изменяется скорость, тем точнее будет значение ускорения центра масс системы. Чтобы сделать знаменатель сколь угодно малым без того, чтобы выражение для ускорения стало неопределенным, мы должны позаимствовать идею из исчисления, которую мы называем пределом . В частности, мы говорим, что в пределе, когда временной интервал стремится к нулю, результирующее выражение, которое мы получаем, является выражением производная скорости по времени.

Просто для удовольствия, вот как выглядит ускорение как мгновенная скорость изменения из скорости по отношению к времени в курсе, основанном на исчислении, таком как AP Physics C:

\[\vec{a} = \frac{\mathrm{d}\vec{v}}{\mathrm{d}t}\]

Вам не нужно беспокоиться о том, чтобы выучить это уравнение. Когда вы будете изучать исчисление, вы поймете смысл замены \(\Delta \vec{v}\) и \(\Delta t\) на \(\mathrm{d}\vec{v}\) и \( \mathrm{d}t\).

10 приложений второго закона Ньютона

Ниже приведен список из 10 приложений второго закона Ньютона.

1. Игрок в гольф бьет по мячу клюшкой.
2. Мальчик отпускает веревочные качели, чтобы нырнуть в озеро.
3. Строительный кран поднимает стальную балку с земли.
4. Космический шаттл использует свои дроссели, чтобы скорректировать свой курс в космосе.
5. Скользящая хоккейная шайба останавливается.
6. Девочка бросает мяч своей матери.
7. Две собаки соревнуются в перетягивании каната за свою любимую игрушку для жевания.
8. Автомобиль врезается в припаркованную машину и тащит ее за собой.
9. Система Земля-Луна движется по фиксированной орбите вокруг Солнца.
10. Двое рабочих толкают ящик по пандусу.

Вот вам вопрос. Вы пассивно замечали, что описывала каждая ситуация, или пытались думать о динамических величинах, задействованных в каждом сценарии? Физика, как и математика, не зрелищный вид спорта. Вы должны активно думайте о том, что вы читаете, чтобы закрепить свое понимание. Задавать себе вопросы, подобные приведенным ниже, — отличный способ добиться этого.

• Какие системы взаимодействуют в этом сценарии?
• Каковы составные части каждой системы, если таковые имеются?
• Скорость какой системы меняется?
• Какие внешние силы действуют на движущуюся систему?
• Как будет выглядеть диаграмма свободного тела для этого сценария?

Приведенный ниже пример поможет вам эффективно ответить на эти вопросы.

Ответьте на вопросы по случаю подъема стальной балки строительным краном с земли.

• Какие системы взаимодействуют в этом сценарии?
  • Взаимодействующими системами являются строительный кран и стальная балка.
• Каковы составные части каждой системы, если таковые имеются?
  • Стальная балка представляет собой жесткий цельный объект без составных частей. С другой стороны, кран имеет множество составных частей: двигатель с противовесами, кабину оператора, рабочую стрелу, тележку с крюковым блоком и систему соединяющих все проводов. Тем не менее, Только компонент крана, который нам необходимо рассмотреть для анализа движения стальной балки, — это трос от рабочего рычага к крюковому блоку.
• Скорость какой системы меняется?
  • Скорость стальной балки изменяется от состояния покоя до ненулевого значения, направленного вверх, когда ее тянет кран.
• Какие внешние силы действуют на движущуюся систему?
  • Подвижная система представляет собой стальную балку, а внешние силы, действующие на нее, представляют собой силу тяжести и натяжение крюкового блока.
• Как будет выглядеть диаграмма свободного тела для этого сценария?
  • Диаграмма свободного тела для этого сценария приведена ниже. Обратите внимание, что мы опустили все детали, кроме двух сил, действующих на стальную балку: силы натяжения цепи крана, тянущей вверх, и силы тяжести, тянущей балку вниз. Поскольку луч имел положительную скорость, направленную вверх, приложенная сила по величине больше, чем противодействующая сила тяжести, как показано стрелками.

Прежде чем перейти к следующему разделу, попробуйте повторить это упражнение с другим из 10 приложений второго закона Ньютона, перечисленных выше.

Центр масс

Теперь, когда эти приложения второго закона Ньютона свежи в вашей памяти, у вас есть прекрасная возможность прояснить, почему мы продолжали использовать фразу центр масс в предыдущем разделе. Система может состоять из множества движущихся частей или иметь внутри себя объекты, взаимодействующие друг с другом. Однако, если взаимодействия между движущимися частями не влияют на внешнее движение системы в целом, ими можно пренебречь.

Например, астронавты могут перемещаться внутри шаттла, но, если смотреть снаружи, то, что они делают, не влияет на общее движение корабля. Таким образом, мы говорим, что переменные \(\vec{x}\), \(\vec{v}\) и \(\vec{a}\) всегда относятся к величинам центра масс, чтобы подчеркнуть, что мы только заботиться об общем движении системы.

2 примера второго закона движения Ньютона

Теперь, когда мы рассмотрели некоторые приложения второго закона движения Ньютона, пришло время более подробно проанализировать два примера. Давайте выберем два из списка выше: девочка, бросающая мяч своей матери, и система Земля-Луна. Мы выбрали эти два, потому что первый является примером движение снаряда , а второй пример круговое движение . Обе темы входят в экзамен AP Physics 1, поэтому вам необходимо ознакомиться с этими идеями!

Пример движения снаряда: подбрасывание мяча

Характерной чертой движения снаряда является то, что он описывает параболу. \circ\), какой максимальной высоты достигнет мяч на своем пути? Предположим, что девушка ростом \(1,40\,\mathrm{м}\). Не учитывать влияние сопротивления воздуха.

Решение

Прежде всего, обратите внимание, что единственная сила, действующая на мяч во время его полета, — это сила тяжести. Поскольку эта сила равномерно ускоряет все падающие объекты, мы находимся в ситуации постоянного ускорения. Это означает, что мы можем использовать кинематические уравнения. Более того, нас не интересует смещение мяча на по горизонтали на , поэтому нам нужно рассматривать только его движение по по вертикали на .

Приступаем к не зависящему от времени кинематическому уравнению: 92}}\right)} + 1,40 \, \mathrm{m},\\ &= 2,04 \, \mathrm{m}.\end{align}

Таким образом, мяч достигает максимальной высоты \(2,04 \ , \mathrm{m}\).

Приведенную выше задачу мы решили с помощью нестационарного кинематического уравнения. Однако это не единственный способ получить ответ. Можете ли вы придумать другой метод?

Подсказка : Используйте \(v_y = v_{0y} + a_yt\) для определения времени, необходимого мячу для достижения максимальной высоты, а затем подставьте этот результат в квадратное уравнение кинематики.

Примеры кругового движения: система Земля-Луна

На рисунке ниже показана диаграмма свободного тела объекта, вращающегося вокруг центрального силового поля. В центре диаграммы у нас есть гравитационный источник, а справа у нас есть объект на орбите. Поскольку Солнце удерживает систему Земля-Луна на орбите вокруг себя за счет гравитации, а гравитация — это сила, это пример второго закона Ньютона. Желтая точка — это Солнце, а синяя точка с серой точкой вокруг — система Земля-Луна.

Почему в этом примере мы игнорируем движение Луны? Хотя он чувствует гравитационное притяжение к Солнцу, его гравитационное взаимодействие с Землей намного сильнее. Действительно, неверно говорить, что Земля вращается вокруг Солнца. Скорее, это центр масс системы Земля-Луна, которая вращается вокруг Солнца. Иными словами, взаимодействие между Землей и Луной не способствует ускорению их центра масс из-за внешней силы, действующей со стороны Солнца.

Согласно законам Кеплера, планетарные орбиты на самом деле представляют собой эллипсов , что означает, что они не идеально круглые. Однако во многих случаях, таких как этот, движение системы Земля-Луна вокруг Солнца можно представить как круговое.

Применение второго закона. Ключевые выводы

• Смещение, скорость и ускорение центра масс системы описывают ее линейное движение.
• Ускорение центра масс системы всегда будет направлено в том же направлении, что и действующая на нее результирующая сила.
• Ускорение центра масс системы прямо пропорционально действующей на нее чистой силе и обратно пропорционально ее массе.
• Ускорение \(\vec{a}\) равно скорости изменения скорости во времени.
• Скорость \(\vec{v}\) равна скорости изменения положения во времени.
• Переменные \(\vec{x}\), \(\vec{v}\) и \(\vec{a}\) относятся к величинам центра масс.
• Если взаимодействующие объекты являются частями одной и той же системы, скорость центра масс этой системы не изменится.

---

Каталожные номера

1. Рис.1 – Ускорение падающего яблока, StudySmarter Originals
2. Рис.2 – Схема стальной балки со свободным телом, StudySmarter Originals
3. Рис.3 – Метание мяча по параболе, StudySmarter Originals
4. Рис. 4 — Система Земля-Луна, вращающаяся вокруг Солнца, StudySmarter Originals

13 Примеры второго закона Ньютона в повседневной жизни — наука

Видео: Второй закон Ньютона | Физика | Не запоминайте

Содержание

• Примеры второго закона Ньютона в реальной жизни
• 1- Kick A Ball
• 2- Поймайте мяч. Толкать две машины
• 5- Толкать одну и ту же полную или пустую тележку
• 6- Толкать машину
• 7- Управлять грузовиком или автомобилем
• 9 10 Два человека, идущих вместе 8-00117 9- Два человека, проталкивающие таблицу
• 10- Игра в гольф
• 11- Open A Дверь
• 12-педалирование велосипед
• Ссылки

Во втором законе Ньютона , известном как Основополагающий принцип динамики, ученый утверждает, что чем больше масса объекта, тем больше силы потребуется для его ускорения. То есть ускорение объекта прямо пропорционально действующей на него чистой силе и обратно пропорционально ускорению объекта.

Мы знаем, что объект может ускоряться, только если на этот объект действуют силы. Второй закон Ньютона точно говорит нам, насколько объект ускорится при заданной результирующей силе.

Другими словами, если результирующая сила удвоится, ускорение объекта будет вдвое больше. Точно так же, если бы масса объекта удвоилась, его ускорение уменьшилось бы вдвое.

Примеры второго закона Ньютона в реальной жизни

Этот закон Ньютона применим к реальной жизни, являясь одним из законов физики, который больше всего влияет на нашу повседневную жизнь:

1- удар по мячу

Когда мы ударяем по мячу, мы прикладываем силу в определенном направлении, в котором будет двигаться мяч.

Кроме того, чем сильнее бьют по мячу, тем большую силу мы прикладываем к нему и тем дальше он летит.

2- Поймать мяч рукой

Профессиональные спортсмены отводят руку назад после того, как поймают мяч, так как это дает мячу больше времени для замедления, при этом прилагая меньше усилий с их стороны.

3- Толкнуть автомобиль

Например, толкание продуктовой тележки с удвоенной силой приводит к удвоению ускорения.

4- Толкнуть две машины

С другой стороны, при толкании двух тележек из супермаркета с одинаковой силой ускорение будет вдвое меньше, поскольку оно изменяется обратно пропорционально.

5- Толкать одну и ту же полную или пустую тележку

Пустую тележку из супермаркета толкать легче, чем полную, поскольку полная тележка имеет большую массу, чем пустая, поэтому для толкания требуется больше силы полная тележка.

6- Толкнуть автомобиль

Чтобы рассчитать силу, необходимую для толкания автомобиля к ближайшей заправке, предполагая, что мы перемещаем однотонный автомобиль со скоростью около 0,05 метра в секунду, мы можем оценить силу, действующую на автомобиль. , что в данном случае составит около 100 ньютонов.

7- Вождение грузовика или легкового автомобиля

Масса грузовика намного больше, чем у легкового автомобиля, а это означает, что для такого же ускорения требуется больше усилий.

Когда, например, автомобиль проезжает 100 км по шоссе из 65 км, он, несомненно, израсходует гораздо меньше бензина, чем если бы ему пришлось проехать с той же скоростью такое же расстояние на грузовике.

8- Два человека, идущие вместе

Те же рассуждения, что и выше, можно применить к любому движущемуся объекту. Например, два человека, которые идут вместе, но один из них имеет меньший вес, чем другой, хотя они идут с одинаковой силой, тот, кто весит меньше, пойдет быстрее, потому что его ускорение, несомненно, больше.

9- Два человека толкают стол

Давайте представим двух людей, один с большей силой, чем другой, толкают стол в разные стороны.

Человек с наибольшей силой толкает на восток, а человек с наименьшей силой толкает на север.

Если мы сложим обе силы, то получим равнодействующую, равную движению и ускорению стола. Таким образом, стол будет двигаться в северо-восточном направлении, хотя и с большим наклоном к востоку, учитывая силу, прилагаемую более сильным человеком.

10- Игра в гольф

При игре в гольф ускорение мяча прямо пропорционально силе, действующей на клюшку, и обратно пропорционально ее массе. На путь влияет сила воздуха, которая может вызвать небольшое изменение его направления.

11- Открыть дверь

Когда мы открываем дверь, нам придется приложить различные усилия в зависимости от материала, из которого она сделана. Хотя она может иметь те же пропорции, на дверь из железного полотна придется прикладывать большее усилие по сравнению с деревянной дверью.

12- Велосипед

Согласно закону Ньютона ускорение велосипеда зависит от приложенной к нему силы. Чем больше сила, тем больше ускорение. По этой причине велосипедисты обычно довольно худые, а профессиональные велосипеды очень легкие.

13- Используйте бутылку с кетчупом

Чтобы извлечь кетчуп из горшка, мы должны нажать на него, чтобы он вышел через щель.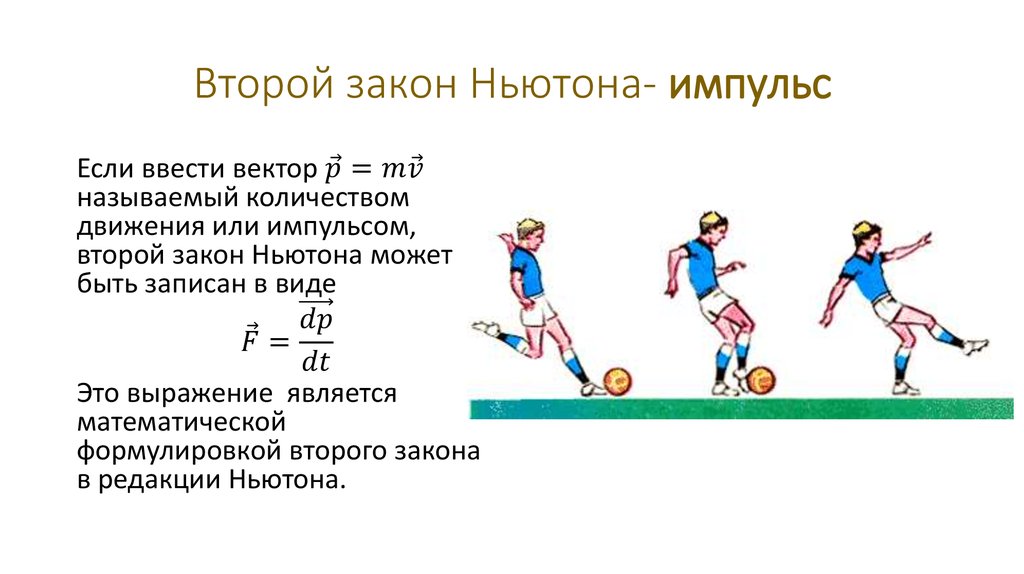 В зависимости от приложенной силы кетчуп может вытекать медленно и падать на бургер или вытекать с большой скоростью и рассыпаться по всей тарелке.

Законы Ньютона

Исаак Ньютон (4 января 1643 – 31 марта 1727), английский физик и математик, прославившийся своим законом всемирного тяготения, был ключевой фигурой в научной революции 17 века и разработал принципы современной физики.

Ньютон впервые представил свои три закона движения в « Principia Mathematica Philosophiae Naturalis » в 1686 году.

Эта работа предлагает точное количественное описание движущихся тел в трех основных законах:

1- Неподвижное тело останется неподвижным, если к нему не приложена внешняя сила;

2- Сила равна произведению массы на ускорение, а изменение движения пропорционально приложенной силе;

3- На каждое действие есть равное и противоположное противодействие.

Эти три закона помогли объяснить не только эллиптические орбиты планет, но и почти любое другое движение во Вселенной: как планеты удерживаются на орбите под действием притяжения Солнца, как Луна вращается вокруг Земли и как спутники Юпитера вращаются вокруг него и как кометы вращаются по эллиптическим орбитам вокруг солнца.

То, как движется почти все, что угодно, можно решить с помощью законов движения: какая сила потребуется, чтобы разогнать поезд, попадет ли пушечное ядро ​​в цель, как движутся воздушные и океанские течения, будет ли летать самолет. все применения второго закона Ньютона.

В заключение, этот второй закон Ньютона очень легко наблюдать на практике, если не в математике, поскольку все мы эмпирически убедились, что необходимо приложить больше силы (и, следовательно, больше энергии), чтобы сдвинуть тяжелый рояль. чем двигать маленький табурет по полу.

Или, как упоминалось выше, при ловле быстро движущегося мяча для крикета мы знаем, что он нанесет меньше урона, если рука будет отведена назад во время ловли мяча.

Вас могут заинтересовать 10 примеров применения первого закона Ньютона в реальной жизни.

Ссылки

1. Джа, А. “Что такое второй закон движения Ньютона?” (11 мая 2014 г.) в: The Guardian: Исаак Ньютон. Краткая история уравнений.