Примеры 2 и 3 закона ньютона. Примеры применения третьего закона ньютона
Три закона сэра Исаака Ньютона описывают движение массивных тел и как они взаимодействуют.
В то время как законы Ньютона могут показаться очевидными для нас сегодня, более трех веков назад они считались революционными.
Содержание:
Ньютон, пожалуй, наиболее известен своей работой по изучению гравитации и движения планет. Призванный астрономом Эдмондом Галлеем после признания того, что за несколько лет до этого он потерял доказательство эллиптических орбит, Ньютон опубликовал свои законы в 1687 году в своей оригинальной работе «Philosophiæ Naturalis Principia Mathematica» (Математические принципы естественной философии), в которой он формализовал описание того, как массивные тела движутся под воздействием внешних сил.
Формулируя свои три закона, Ньютон упростил обращение к массивным телам, считая их математическими точками без размера или вращения. Это позволило ему игнорировать такие факторы, как трение, сопротивление воздуха, температура, свойства материала и т.
Законы Ньютона
Законы Ньютона относятся к движению массивных тел в инерциальной системе отсчета, иногда называемой ньютоновской системой отсчета, хотя сам Ньютон никогда не описывал такую систему. Инерциальную систему отсчета можно описать как трехмерную систему координат, которая либо стационарна, либо равномерно линейна, т. е. Не ускоряется и не вращается. Он обнаружил, что движение в такой инерциальной системе отсчета может быть описано тремя простыми законами.
Первый закон движения Ньютона
Гласит: Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения. Это просто означает, что вещи не могут начинать, останавливать или изменять направление самостоятельно.
Требуется сила, действующая на них извне, чтобы вызвать такое изменение. Это свойство массивных тел сопротивляться изменениям в их движении иногда называют инерцией.
В современной физике первый закон Ньютона принято формулировать в следующем виде:
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.
Второй закон движения Ньютона
Описывает, что происходит с массивным телом, когда на него воздействует внешняя сила. В нем говорится: Сила, действующая на объект, равна массе этого объекта своего ускорения. Это написано в математической форме как F = ma, где F — сила, m — масса, a — ускорение. Жирные буквы указывают, что сила и ускорение являются векторными величинами, что означает, что они имеют как величину, так и направление. Сила может быть одной силой, или это может быть векторная сумма более чем одной силы, которая является чистой силой после объединения всех сил.
Когда постоянная сила действует на массивное тело, она заставляет ее ускоряться, т. е. Изменять свою скорость с постоянной скоростью. В простейшем случае сила, приложенная к неподвижному объекту, заставляет его ускоряться в направлении силы. Однако, если объект уже находится в движении или если эта ситуация просматривается из движущейся системы отсчета, это тело может показаться ускоряющимся, замедляющим или изменяющим направление в зависимости от направления силы и направлений, в которых объект и система отсчета перемещается относительно друг друга.
В современной физике второй закон Ньютона принято формулировать в следующем виде:
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
Третий закон движения Ньютона
Гласит: Для каждого действия существует равное противодействие.
Если один объект намного, гораздо более массивный, чем другой, особенно в случае привязки первого объекта к Земле, практически все ускорение передается второму объекту, и ускорение первого объекта можно безопасно игнорировать, Например, если вы бросили мяч на запад, вам не нужно было бы считать, что вы на самом деле заставили вращаться Землю быстрее, пока мяч находился в воздухе. Однако, если вы стоите на роликовых коньках, и вы бросили мяч для боулинга, вы начнете двигаться назад с заметной скоростью.
В современной физике третий закон Ньютона принято формулировать в следующем виде:
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Три закона были проверены бесчисленными экспериментами за последние три столетия, и до сих пор они широко используются для описания видов предметов и скоростей, с которыми мы сталкиваемся в повседневной жизни. Они составляют основу того, что сейчас известно как классическая механика, а именно изучение массивных объектов, которые больше, чем очень мелкие масштабы, рассматриваемые квантовой механикой, и которые движутся медленнее, чем очень высокие скорости, релятивистские механики.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F2, с какой лошадь тянет сани вперед (сила F1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
Сила F1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f1полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F2направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f2, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места.
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
ньютон третий движение отдача
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой
, с какой лошадь тянет сани вперед (сила
)? Почему эти силы не уравновешиваются? Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они, приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 72). Сила
со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения
полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней
, направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы
, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила
будет уравновешена силами
(первый закон Ньютона).
72). Сила
со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения
полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней
, направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы
, направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила
будет уравновешена силами
(первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон Ньютона позволяет рассчитатьявление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и снарядом, направлены противоположно, а по модулю обратно пропорциональны массам этих тел. В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через
, а скорость, полученную пушкой, через
, а массы этих тел обозначим через
и
соответственно. Тогда
В результате снаряд и пушка приобретут противоположно направленные скорости, находящиеся в том же отношении. Обозначим скорость, полученную снарядом, через
, а скорость, полученную пушкой, через
, а массы этих тел обозначим через
и
соответственно. Тогда
Примеров взаимодействия тел можно привести сколь угодно много. Когда вы, находясь в одной лодке, начнете за веревку подтягивать другую, то и ваша лодка обязательно продвинется вперед (рис. 1). Действуя на вторую лодку, вы заставляете ее действовать на вашу лодку.
Если вы ударите ногой по футбольному мячу, то немедленно ощутите об-ратное действие на ногу. При соударении двух бильярдных шаров изменяют свою скорость, т. е. получают ускорения, оба шара. Когда при формировании железнодорожного состава вагоны наталкиваются друг на друга, буферные пружины сжимаются у обоих вагонов. Все это проявления общего закона взаимодействия тел.
Действия тел друг на друга носят характер взаимодействия не только при непосредственном контакте тел. Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов.
Положите, например, на гладкий стол два сильных магнита разноименными полюсами навстречу друг другу, и вы тут же обнаружите, что магниты начнут двигаться навстречу друг другу. Земля притягивает Луну (сила всемирного тяготения) и заставляет ее двигаться по криволинейной траектории; в свою очередь Луна также притягивает Землю (тоже сила всемирного тяготения). Хотя, естественно, в системе отсчета, связанной с Землей, ускорение Земли, вызываемое этой силой, нельзя обнаружить непосредственно (непосредственно нельзя обнаружить даже значительно большее ускорение, вызываемое притяжением Земли Солнцем), оно проявляется в виде приливов.
Заметные изменения скоростей обоих взаимодействующих тел наблюдаются, однако, лишь в тех случаях, когда массы этих тел не сильно отличаются друг от друга. Если же взаимодействующие тела значительно различаются по массе, заметное ускорение получает только то из них, которое имеет меньшую массу. Так, при падении камня Земля заметно ускоряет движение камня, но ускорение Земли (а ведь камень тоже притягивает Землю) практически обнаружить нельзя, так как оно очень мало.
Силы взаимодействия двух тел
Выясним с помощью опыта, как связаны между собой силы взаимодействия двух тел. Грубые измерения сил взаимодействия можно произвести на следующих опытах.
1 опыт . Возьмем два динамометра, зацепим друг за друга их крючки и, взявшись за кольца, будем растягивать их, следя за показаниями, обоих динамометров (рис. 2).
Мы увидим, что при любых растяжениях показания обоих динамометров будут совпадать; значит, сила, с которой первый динамометр действует на второй, равна силе, с которой второй динамометр действует на первый.
2 опыт . Возьмем достаточно сильный магнит и железный брусок и положим их на катки, чтобы уменьшить трение о стол (рис. 3). К магниту и бруску прикрепим одинаковые мягкие пружины, зацепленные другими концами на столе. Магнит и брусок притянутся друг к другу и растянут пружины.
Опыт показывает, что к моменту прекращения движения пружины оказываются растянутыми совершенно одинаково. Это означает, что на оба тела со стороны пружин действуют одинаковые по модулю и противоположные по направлению силы:
\(\vec F_1 = -\vec F_2 \qquad (1)\)
Так как магнит покоится, то сила \(\vec F_2\) равна по модулю и противоположна по направлению силе \(\vec F_4\), с которой на него действует брусок:
\(\vec F_1 = \vec F_4 \qquad (2)\)
Точно так же равны по модулю и противоположны по направлению силы, действующие на брусок со стороны магнита и пружины:
\(\vec F_3 = -\vec F_1 \qquad (3)\)
Из равенств (1), (2), (3) следует, что силы, с которыми взаимодействуют магнит и брусок, равны по модулю и противоположны по направлению:
\(\vec F_3 = -\vec F_4 \qquad (1)\)
Опыт показывает, что силы взаимодействия между двумя телами равны по модулю и противоположны по направлению и в тех случаях когда тела движутся.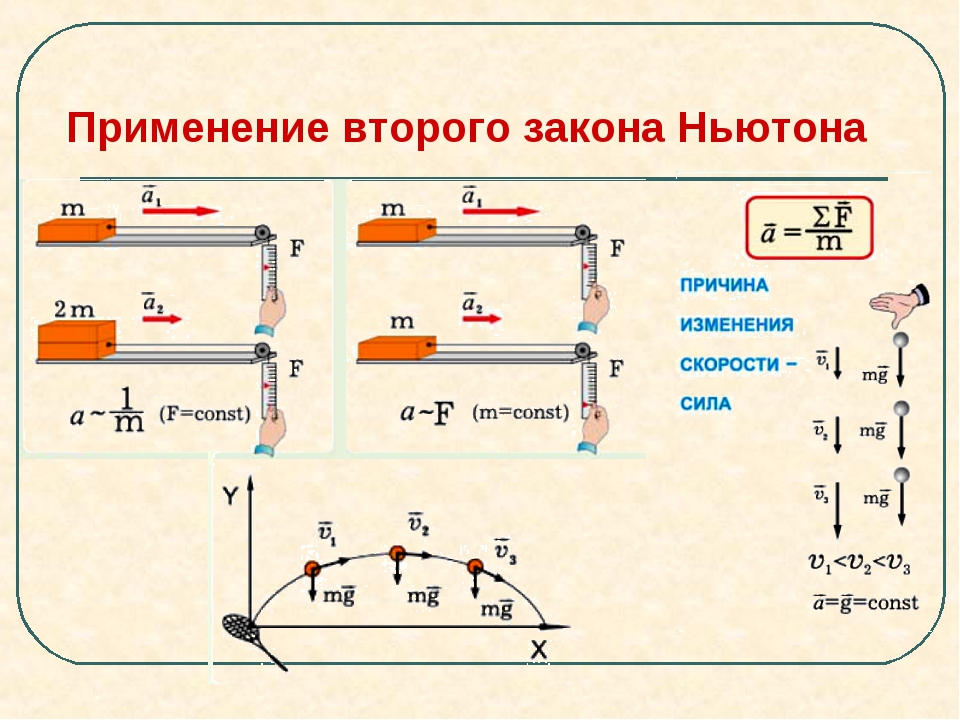
3 опыт . На двух тележках, которые могут катиться по рельсам, стоят два человека А и В (рис. 4). Они держат в руках концы веревки. Легко обнаружить, что независимо от того, кто натягивает («выбирает») веревку, А или В или оба вместе, тележки всегда приходят в движение одновременно и притом в противоположных направлениях. Измеряя ускорения тележек, можно убедиться, что ускорения обратно пропорциональны массам каждой из тележек (вместе с человеком). Отсюда следует, что силы, действующие на тележки, равны по модулю.
Третий закон Ньютона
На основе этих и подобных опытов можно сформулировать третий закон Ньютона.
Силы, с которыми тела действуют друг на друга, равны по модулю и на-правлены вдоль одной прямой в противоположные стороны.
Это означает, что если на тело А со стороны тела В действует сила \(\vec F_A\) (рис. 5), то одновременно на тело В со стороны тела А действует сила \(\vec F_B\), причем
\(\vec F_A = -\vec F_B \qquad (5)\)
Используя второй закон Ньютона, можно равенство (5) записать так:
\(m_1 \cdot \vec a_1 = -m_2 \cdot \vec a_2 \qquad (6)\)
Отсюда следует, что
\(\frac{a_1}{a_2} = \frac{m_2}{m_1}= \mbox{const} \qquad (7)\)
Отношение модулей а 1 и а 2 ускорений взаимодействующих тел определяется обратным отношением их масс и совершенно не зависит от природы действующих между ними сил.
(Здесь имеется в виду, что никакие другие силы, кроме сил взаимодействия, на эти тела не действуют.)
В этом можно убедиться на следующем простом опыте. Поставим на гладкие рельсы две тележки одинаковой массы и на одной из них закрепим небольшой электрический двигатель, на вал которого может наматываться нить, привязанная к другой тележке, а на другую поставим гирю, масса которой равна массе двигателя (рис. 6). При работающем двигателе обе тележки устремляются с одинаковыми ускорениями навстречу друг другу и проходят одинаковые пути. Если массу одной из тележек сделать вдвое большей, то ее ускорение окажется в два раза меньше, чем другой, и за то же время она пройдет вдвое меньший путь.
Связь ускорений взаимодействующих тел с их массами можно установить и на таком опыте (рис. 7). На горизонтальную платформу помещают два катка разной массы, соединенные нитью.
Опыт покажет, что можно найти такое положение катков, когда они при вращении платформы не перемещаются по ней.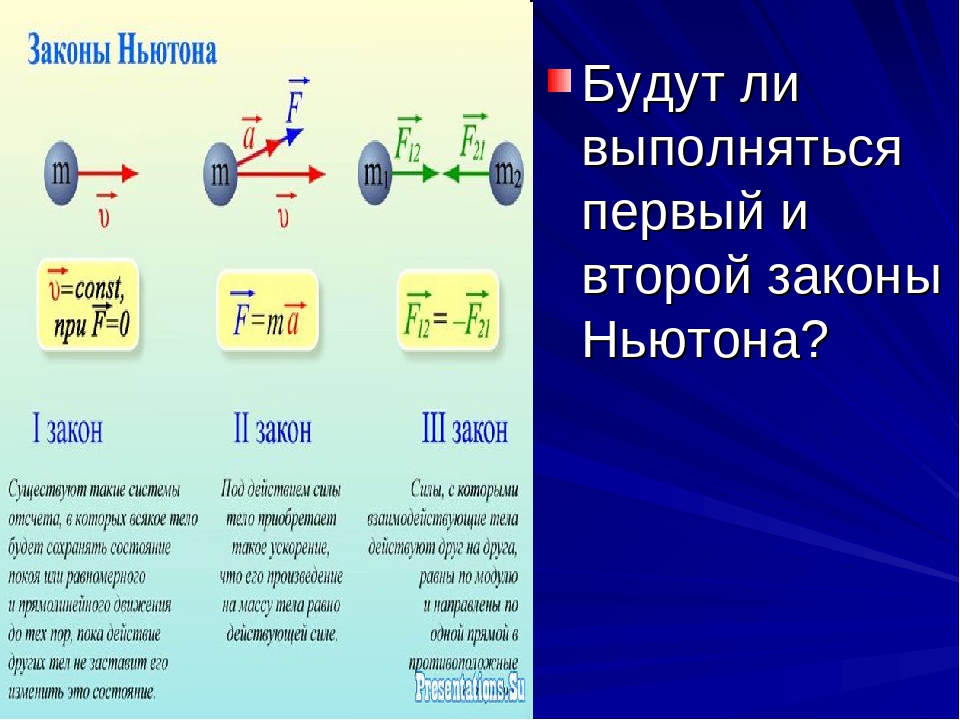 Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков:
Измерив радиусы обращения катков вокруг центра платформы, определим отношение центростремительных ускорений катков:
\(\frac{a_1}{a_2} = \frac{\omega \cdot R_1}{\omega \cdot R_2}\) или \(\frac{a_1}{a_2} = \frac{R_1}{R_2}\).
Сравнив это отношение с обратным отношением масс тел \(\frac{m_2}{m_1}\), убеждаемся, что \(\frac{a_1}{a_2} = \frac{m_2}{m_1}\) при любых скоростях вращения платформы.
Примечание
Надо помнить, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому не могут уравновешивать друг друга.
Непонимание этого часто приводит к недоразумениям. Так, иногда с помощью третьего закона Ньютона пытаются объяснить, почему то или иное тело находится в покое. Например, утверждают, что мел на столе покоится якобы потому, что сила тяжести \(\vec F_t\), действующая на тело, согласно третьему закону Ньютона, равна по модулю и противоположна по направлению силе упругости \(\vec N\) (силе реакции опоры), действующей на него со стороны стола. На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны.
На самом деле равенство \(\vec F_t + \vec N = 0\) является следствием второго закона Ньютона, а не третьего: ускорение равно нулю, поэтому и сумма сил, действующих на тело, равна нулю. Из третьего же закона Ньютона вытекает лишь, что сила реакции опоры \(\vec N\) равна по модулю силе \(\vec P\), с которой мел давит на стол (рис. 8). Эти силы приложены к разным телам и направлены в противоположные стороны.
Примеры применения третьего закона Ньютона.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Как объяснить, что лошадь везет сани, если, как это следует из закона действия и противодействия, сани тянут лошадь назад с такой же по модулю силой F 2 , с какой лошадь тянет сани вперед (сила F 1)? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и силы со стороны дороги (рис. 9).
9).
Сила F 1 со стороны лошади приложена к саням, испытывающим, кроме этой силы, лишь небольшую силу трения f 1 полозьев о снег; поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны саней F 2 направленной назад, приложены со стороны дороги, в которую она упирается ногами, силы f 2 , направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны скользкого льда будет недостаточна; и лошадь не сдвинет сани. То же будет и с очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь сдвинула сани и установилось равномерное движение саней, сила f 1 будет уравновешена силами f 2 (первый закон Ньютона).
Подобный же вопрос возникает и при разборе движения поезда под действием электровоза. И здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что, кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом» (сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Третий закон Ньютона позволяет объяснить явление отдачи при выстреле. Установим на тележку модель пушки, действующую при помощи пара (рис. 10) или при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд» (пробка) вылетает в одну сторону, а «пушка» откатывается в другую.
Откат пушки и есть результат отдачи. Отдача есть не что иное, как противодействие со стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку, выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и направлена противоположно ей.
О значении третьего закона Ньютона
Главное значение третьего закона Ньютона обнаруживается при исследовании движения системы материальных точек или системы тел. Этот закон позволяет доказать важные теоремы динамики и сильно упрощает изучение движения тел в тех случаях, когда их нельзя рассматривать как материальные точки.
Третий закон сформулирован для точечных тел (материальных точек). Его применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования. В данной формулировке нельзя применять этот закон и в неинерциальных системах отсчета.
Литература
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
- Элементарный учебник физики: Учебное пособие. В 3 т. / Под ред. Г.С. Ландсберга: Т. 1. Механика. Теплота. Молекулярная физика – М.: ФИЗМАТЛИТ, 2003. – 608с.
В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковыми силами, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет, а та, которая сильнее упирается в Землю.
Рис. 72. Лошадь сдвинет и повезет нагруженные сани, потому что со стороны дороги на ее копыта действуют большие силы трения, чем на скользкие полозья саней
Как объяснить,
что лошадь везет сани, если, как это следует из закона действия и
противодействия, сани тянут лошадь назад с такой же по модулю силой , с какой лошадь
тянет сани вперед (сила )? Почему эти силы не уравновешиваются?
Дело в том, что, во-первых, хотя эти силы равны и прямо противоположны, они,
приложены к разным телам, а во-вторых, и на сани и на лошадь действуют еще и
силы со стороны дороги (рис. 72). Сила со стороны лошади приложена к саням,
испытывающим, кроме этой силы, лишь небольшую силу трения полозьев о снег;
поэтому сани начинают двигаться вперед. К лошади же, помимо силы со стороны
саней ,
направленной назад, приложены со стороны дороги, в которую она упирается
ногами, силы ,
направленные вперед и большие, чем сила со стороны саней. Поэтому лошадь тоже
начинает двигаться вперед. Если поставить лошадь на лед, то сила со стороны
скользкого льда будет недостаточна, и лошадь не сдвинет сани. То же будет и с
очень тяжело нагруженным возом, когда лошадь, даже упираясь ногами, не сможет
создать достаточную силу, чтобы сдвинуть воз с места. После того как лошадь
сдвинула сани и установилось равномерное движение саней, сила будет
уравновешена силами (первый закон Ньютона).
Подобный же
вопрос возникает и при разборе движения поезда под действием электровоза. И
здесь, как и в предыдущем случае, движение возможно лишь благодаря тому, что,
кроме сил взаимодействия между тянущим телом (лошадь, электровоз) и «прицепом»
(сани, поезд), на тянущее тело действуют со стороны дороги или рельсов силы, направленные
вперед. На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни
сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
На идеально скользкой поверхности, от которой нельзя «оттолкнуться», ни
сани с лошадью, ни поезд, ни автомобиль не могли бы сдвинуться с места.
Рис. 73. При нагревании пробирки с водой пробка вылетает в одну сторону, а «пушка» катится в противоположную сторону
Третий закон
Ньютона позволяет рассчитать явление отдачи при выстреле.
Установим на тележку модель пушки, действующую при помощи пара (рис. 73) или
при помощи пружины. Пусть вначале тележка покоится. При выстреле «снаряд»
(пробка) вылетает в одну сторону, а «пушка» откатывается в другую. Откат пушки
и есть результат отдачи. Отдача есть не что иное, как противодействие со
стороны снаряда, действующее, согласно третьему закону Ньютона, на пушку,
выбрасывающую снаряд. Согласно этому закону сила, действующая со стороны пушки
на снаряд, все время равна силе, действующей со стороны снаряда на пушку, и
направлена противоположно ей. Таким образом, ускорения, получаемые пушкой и
снарядом, направлены противоположно, а по модулю обратно пропорциональны
массам этих тел. В результате снаряд и пушка приобретут противоположно
направленные скорости, находящиеся в том же отношении. Обозначим скорость,
полученную снарядом, через , а скорость, полученную пушкой,
через ,
а массы этих тел обозначим через и соответственно. Тогда
В результате снаряд и пушка приобретут противоположно
направленные скорости, находящиеся в том же отношении. Обозначим скорость,
полученную снарядом, через , а скорость, полученную пушкой,
через ,
а массы этих тел обозначим через и соответственно. Тогда
Здесь и – модули скоростей.
Выстрел из всякого оружия сопровождается отдачей. Старинные пушки после выстрела откатывались назад. В современных орудиях ствол укрепляется на лафете не жестко, а при помощи приспособлений, которые позволяют стволу отходить назад; затем пружины снова возвращают его на место. В автоматическом огнестрельном оружии явление отдачи используется для того, чтобы перезарядить орудие. При выстреле отходит только затвор. Он выбрасывает использованную гильзу, а затем пружины, возвращая его на место, вводят в ствол новый патрон. Этот принцип используется не только в пулеметах и автоматических пистолетах, но и в скорострельных пушках.
Рекомендуем также
10 примеров второго закона Ньютона в реальной жизни / наука | Thpanorama
В Второй закон Ньютона, ученый заявляет, что чем больше масса объекта, тем больше силы потребуется для его ускорения. .
.
То есть ускорение объекта прямо пропорционально действующей на него силе и обратно пропорционально ускорению объекта.
Мы знаем, что объект может ускоряться, только если на него действуют силы. Второй закон Ньютона говорит нам точно, насколько объект будет ускоряться для данной чистой силы.
Другими словами, если бы чистая сила была удвоена, ускорение объекта было бы в два раза больше. Точно так же, если бы масса объекта была удвоена, его ускорение уменьшилось бы вдвое..
Примеры второго закона Ньютона в повседневной жизниЭтот закон Ньютона применяется к реальной жизни, будучи одним из законов физики, который больше всего влияет на нашу повседневную жизнь:
1- пнуть мячКогда мы пинаем мяч, мы прикладываем силу в определенном направлении, то есть в каком направлении он будет двигаться.
Кроме того, чем сильнее удар по мячу, тем сильнее сила, которую мы на него надеваем, и тем дальше он пойдет.
2- Захватить мяч рукойПрофессиональные атлеты возвращают руки назад, как только они ловят мяч, так как это дает мячу больше времени, чтобы потерять скорость, и, в свою очередь, прикладывает меньше усилий с его стороны. .
.
Например, если толкнуть тележку супермаркета в два раза сильнее, она дает в два раза больше ускорения..
4- Нажмите две машиныС другой стороны, при нажатии на две тележки супермаркета с одинаковым усилием это приводит к половине ускорения, потому что оно изменяется обратно пропорционально.
5- Нажмите на ту же корзину, полную или пустуюПустую тележку супермаркета легче протолкнуть, чем полную, так как полная тележка имеет большую массу, чем вакуум, поэтому требуется больше силы, чтобы вытолкнуть тележку.
6- толкать машинуЧтобы рассчитать силу, необходимую для подталкивания автомобиля к ближайшей заправочной станции, предполагая, что мы перемещаем автомобиль со скоростью в одну тонну около 0,05 метра в секунду, мы можем оценить силу, действующую на автомобиль, которая в этом случае будет около 100 ньютон.
7- Вождение грузовика или автомобиляМасса грузовика намного больше, чем у автомобиля, а это значит, что для того, чтобы разогнаться до такой же степени, требуется больше силы.
Например, когда автомобиль проезжает 100 км по шоссе на протяжении 65 км, бензин будет использоваться гораздо меньше, чем если бы вам приходилось ехать с одинаковой скоростью на одном и том же расстоянии в грузовике..
8- Два человека, которые гуляют вместеТо же самое рассуждение выше может быть применено к любому движущемуся объекту. Например, два человека, которые ходят вместе, но один из них имеет меньший вес, чем другой, хотя они ходят, используя то же количество силы, кто меньше весит, пойдут быстрее, потому что их ускорение, несомненно, больше.
9- Два человека толкают столВообразите двух человек, один сильнее другого, толкающий стол в разные стороны.
Человек с наибольшей силой продвигается на восток, а человек с наименьшей силой направляется на север.
Если мы добавим обе силы, мы получим результат, равный движению и ускорению стола. Таким образом, стол будет двигаться в северо-восточном направлении, хотя и с большей склонностью к востоку, учитывая силу, оказываемую сильнейшим человеком. .
.
В игре в гольф ускорение мяча прямо пропорционально силе, приложенной к клюшке, и обратно пропорционально ее массе. Сила воздуха, способная вызвать небольшое изменение направления.
Законы НьютонаИсаак Ньютон (4 января 1643 года – 31 марта 1727 года), английский физик и математик, известный своим законом гравитации, был ключевой фигурой в научной революции семнадцатого века и разработал принципы современной физики.
Ньютон впервые представил свои три закона движения в Principia Mathematica Philosophiae Naturalis в 1686 году.
Считается самой влиятельной книгой по физике и, возможно, по всем наукам, она содержит информацию практически по всем основным понятиям физики..
Эта работа предлагает точное количественное описание движущихся тел в трех основных законах:
1- неподвижное тело будет оставаться неподвижным, если к нему не приложена внешняя сила;
2. Сила равна массе, умноженной на ускорение, а изменение движения пропорционально приложенной силе;
3- Для каждого действия есть равная и противоположная реакция.
Эти три закона помогли объяснить не только эллиптические орбиты планет, но и почти все другие движения вселенной: как планеты удерживаются на орбите благодаря притяжению гравитации Солнца, как Луна вращается вокруг Земли и спутников Луны. Юпитер вращается вокруг нее и как кометы вращаются по эллиптическим орбитам вокруг Солнца.
Путь, по которому движется почти все, может быть решен с помощью законов движения: сколько силы потребуется для ускорения поезда, достигнет ли пушечный ядр своей цели, как движутся воздушные и океанские течения или будет летать самолет все приложения второго закона Ньютона.
В заключение, очень легко наблюдать этот второй закон Ньютона на практике, если не в математике, поскольку все мы эмпирически убедились, что необходимо приложить больше силы (и, следовательно, больше энергии) для перемещения тяжелого рояля, чем для сдвиньте маленький табурет на полу.
Или, как уже упоминалось выше, когда вы ловите быстро движущийся крикетный мяч, мы знаем, что он будет наносить меньший урон, если вы будете двигать рукой назад, ловя мяч. .
.
Может быть, вы заинтересованы в 10 примерах первого закона Ньютона в реальной жизни.
ссылки- Jha, A. «Что такое второй закон движения Ньютона?» (11 мая 2014 г.) в: The Guardian: Исаак Ньютон. Краткая история уравнений. Получено: 9 мая 2017 г. от The Guardian. theguardian.com.
- Кейн и Штернхейм «Физика». Ред. Реверт. 1989.
- Агилар Перис и сенатор “Вопросы физики” Ed. Reverte, 1980.
- «Второй закон Ньютона» Получен: 9 мая 2017 года из Физического кабинета по адресу: physclassroom.com..
- “Исаак Ньютон. Biography “at: Biography.com Получено 9 мая 2017 г. из Biography / biography.com.
- «Что такое второй закон Ньютона?» В кн. Академия Хана Получена из Академии Хана по адресу: khanacademy.org.
- «Законы Ньютона» в SAEM Thales. Андалузское общество математического образования Фалеса. Получено: 9 мая 2017 г. от thales.cica.es.
Закон Ньютона, – Энциклопедия по машиностроению XXL
В механике ньютоновской несжимаемой жидкости закон Ньютона, определяющий вязкость ц, записывается в общем случае [c. 48]
48]III рода — поверхность тела обменивается теплотой со средой известной температуры по закону Ньютона (9.1) [c.112]
Составим уравнение баланса энергии для узла 2, одна из границ которого обменивается теплотой с окружающей средой по закону Ньютона (9.1) [c.116]
Физически продуваемый снизу плотный слой частиц теряет устойчивость потому, что сопротивление фильтрующемуся сквозь него газу становится равным весу столба материала на единицу площади поддерживающей решетки. Поскольку аэродинамическое сопротивление есть сила, с которой газ действует на частицы (и соответственно по третьему закону Ньютона —частицы на газ), то при равенстве сопротивления и веса слоя частицы (если рассматривать идеальный случай) опираются не на решетку, а на газ. [c.143]
Экспериментальные данные об энергии могут быть получены по испусканию или поглощению веществом излучения.
 Такие сведения о тепловом излучении и атомных спектрах накапливались в течение многих лет. Ранние попытки объяснить наблюдаемое тепловое излучение, применяя классические законы Ньютона к атомным системам, были только отчасти удовлетворительны. Например, в излучении абсолютно черного тела количество излученной энергии для коротких волн мало оно возрастает с увели-
[c.70]
Такие сведения о тепловом излучении и атомных спектрах накапливались в течение многих лет. Ранние попытки объяснить наблюдаемое тепловое излучение, применяя классические законы Ньютона к атомным системам, были только отчасти удовлетворительны. Например, в излучении абсолютно черного тела количество излученной энергии для коротких волн мало оно возрастает с увели-
[c.70]Здесь в соответствии с законом Ньютона для несжимаемой жидкости [c.37]
По закону Ньютона—Рихмана [c.44]
Для автомодельной области (закон Ньютона) при 10 [c.47]
Это же количество тепла подводится к шару через поверхность Рш согласно закону Ньютона — Рихмана [c.154]
Примеры математических моделей элементов систем неэлектрической природы, простыми элементами механических поступательных систем являются элементы массы п гибкости (жесткости). Математическая модель массы выражает закон Ньютона
[c. 172]
172]
Полученное выражение представляет собой обобщенный закон Ньютона в полярных координатах. [c.192]
Закон Ньютона — Рихмана. [c.357]
Однако вместо формул аналитической механики за исходное уравнение можно взять второй закон Ньютона. [c.414]
Силовая функция силы притяжения по закону Ньютона. [c.349]
Коэффициент к из закона Ньютона равен [c.547]
Это и есть закон Ньютона для касательных напряжений в жидкости. Для некоторых жидкостей линейной зависимости между тензорами напряжений и скоростей деформаций недостаточно. Такие жидкости называют неньютоновскими жидкостями. [c.573]
По закону Ньютона напряжение сдвига т в слое жидкости пропорционально градиенту скорости dv/dh v — скорость h — толщина слоя жидкости) т= [c.143]
Не подчиняются закону Ньютона только немногие так называемые неньютоновские жидкости, в частности загущенные масла. [c.143]
[c.143]
По закону Ньютона сдвигающая масляный слой сила или сила трения [c.390]
Согласно закону Ньютона, конвективный поток тепла ( 2 от частицы к жидкости определяется следующим образом [c.78]
Динамическими называются нагрузки, изменяющиеся во времени с большой скоростью (например, ударные нагрузки). Действие таких нагрузок сопровождается возникновением колебаний сооружений. При колебании же вследствие изменения скорости колеблющихся масс возникают силы инерции, пропорциональные (по второму закону Ньютона) колеблющимся мас-са.м п ускорениям. Эти силы инерции могут во много раз превосходить те же нагрузки, приложенные статически. [c.11]
В основе механики лежат законы, называемые законами классической механики (или законами Ньютона), которые установлены пу- [c.5]
Это положение выражает принцип Даламбера для материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом де/ю, второй закон Ньютона для рассматриваемой точки дает ma=f +jV. Перенося здесь величину та в правую часть равенства и учитывая обозначение (84), придем к соотношению (85). Наоборот, перенося в уравнении (85) величину f в другую часть равенства и учитывая обозначение (84), получим выражение второго закона Ньютона.
[c.345]
Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом де/ю, второй закон Ньютона для рассматриваемой точки дает ma=f +jV. Перенося здесь величину та в правую часть равенства и учитывая обозначение (84), придем к соотношению (85). Наоборот, перенося в уравнении (85) величину f в другую часть равенства и учитывая обозначение (84), получим выражение второго закона Ньютона.
[c.345]
Кроме уравнений (2.5) при составлении схемы учтено, что реакции в шарнире, согласно третьему закону Ньютона, с равным усилием действуют на тело и на неподвижную систему отсчета. [c.95]
Через источник Vs.t—Vi.x передается усилие Fx (таким включением автоматически выполняется третий закон Ньютона). [c.102]
Безразмерные комплексы обычно не являются точным отношением каких-то сил, а лишь качественно характеризуют их соотношение. В данном случае сила вязкого трения между соседними с.лоями движущейся в пограничном слое жидкости, действуюихая на единичную площадку, параллельную плоскости у —О, равна по закону Ньютона F = i (dw/dy). Заменяя производную отношением конечных разностей (dw/dy) получим цЯ р,Шж/бг, где 6г —толщина гидродинамического пограничного слоя. Принимая во внимание, что йг- /, получаем выражение
[c.82]
Заменяя производную отношением конечных разностей (dw/dy) получим цЯ р,Шж/бг, где 6г —толщина гидродинамического пограничного слоя. Принимая во внимание, что йг- /, получаем выражение
[c.82]
Согласно [Л. 310] поправка п области закона Стокса по Френсису равна (1—а в области закона Ньютона по Карману (1—dijDY . Влиянием стенок трубы можно пренебречь при, IQ, а при движении шара в восходящей суспензии — при Z>/rf 3,l [Л. ГЗ]. [c.57]
Реакции в кинематических парах обозначим двумя цифрами первая показывает номер звена, на которое действует сила, вторая — номер звена, со стороны которого действует сила. Наирнмер, реакция р2 — сн ча, действующая со стороны звена 1 иа звено 2. Причем по третьему закону Ньютона реакции / 21 и -F12 равны по значению, но противоположны по направлению [c.142]
Рассматриваемое плоское движение является криволинейным, поэтому выражение закона Ньютона (VIII—1) для жидкостного трения здесь неприменимо. [c.191]
[c.191]
Получим выражение закона Ньютона для этого случая движения. Выделим во вращающейся жидкости два слоя на радиусах гиг -fdr (рис. VIII—7) и определим скорость сдвига одного слоя относительно другого. За некоторый промежуток времени t точка А внутреннего слоя переместится в Ач, а точка В, которую шршйем для П ростоты рассуждений лежащей на продолжении радиуса точим А., переместится в [c.191]
Дифференциальное уравнение неустановпвшегося движения получим, применяя закон Ньютона (сила равн1 массе, умноженной па ускорение) к элементу массы жидкости с размерами с1Р У. 8 (рнс. XII—I). [c.335]
Законы конвективного теплообмена между поверхностью тела и окружающей средой отличаются большой сложностью и будут рассмотрены в специальном разделе курса. В основу изучения конвективного теплообмена положен закон Ньютона — Рнхмана [c.356]
Если вычислить силовую функцию, 10 на основании (82 ) будет известна и потенциальная энергия. Вычислим силовые функции однородного ноля силы тяжести, силового поля линейтюй силы упругости и силового гюля силы притяжения, действующей по закону Ньютона.
[c.348]
Вычислим силовые функции однородного ноля силы тяжести, силового поля линейтюй силы упругости и силового гюля силы притяжения, действующей по закону Ньютона.
[c.348]
В каждой точке пространства, занятого движущейся жидкостью, имеем тензор напряжений П и тензор скоростей деформаций S. Первоначально были сформулированы и экспериментально проверены простейшие частные случаи зависимости компонентов )тих двух гензоров, как, например, закон Ньютона для касательных напряжений. Эти зависимости оказались линейными. Это привело к предположению, что линейная зависимость соблюдается и в общем случае. Для жидкостей эта линейная зависимость тензора напряжений ог тензора скоростей деформаций носи название обобщенного закона Ньютона или закона Навье-Стокса. [c.571]
Т — окружная сила.по средней окружности, сотласно закону Ньютона [c.446]
Вследствие взаимного смещения слоев масла в ia iope в них возникают H itji вязкого сдвига, определяемые но закону Ньютона. Силы вязкого сдви1а, отнесенные к единице площади
[c.386]
Силы вязкого сдви1а, отнесенные к единице площади
[c.386]
Развитие динамики начинается значительно позже. В XV—XVI столетиях возникновение и рост в странах Западной и Центральной Европы буржуазных отношений послужили толчком к значительному подъему ремесел, торговли, мореплавания и военного дела (появление огнестрельного оружия), а также к важным астрономическим открытиям. Все это способствовало накоплению большого опытного материала, систематизация и обобщение которого привели в XVII столетии к открытию законов динамики. Главные заслуги в создании основ динамики принадлежат гениальным исследователям Галилео Галилею (1564—1642) и Исааку Ньютону (1643—1727). В сочинении Ньютона Математические начала натуральной философии , изданном в 1687 г., и были изложены в систематическом виде основные законы классической механики (законы Ньютона). [c.7]
Методы решения задач механики, которые до сих пор рассматривались, основываются на уравнениях, вытекающих или непосредственно и. з законов Ньютона, или же из общих теорем, являющихся следствием этих законов. Однако этот путь не является единственным. Оказывается, что уравнейия движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Да.шмбера.
[c.344]
з законов Ньютона, или же из общих теорем, являющихся следствием этих законов. Однако этот путь не является единственным. Оказывается, что уравнейия движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Да.шмбера.
[c.344]
Б. Уравнение массы (уравнение второго закона Ньютона) F = та = u(dVjdt), где а = dV/dt — ускорение Стл = т — аналог электрической емкости (масса элемента). [c.68]
Vlx = У гг. — Ш2Г21 Зт(ф30 + ф21)+ Mil ll 81п(ф10 + фи). Источник усилия f 1 равен Fx — усилию на источнике скорости. В этой схеме в явном виде учитывается третий закон Ньютона. [c.97]
„Границы применения законов Ньютона”, 10 класс
Додаток № 2
Открытый урок
по физике
на тему:
„Границы применения
законов Ньютона”
Цели урока:
образовательная: отработать обязательные результаты учения по теме «Законы Ньютона», систематизировать учебный материал путем использования структурной схемы динамики;
развиваюшая: совершенствовать навыки решения качественных и расчетных задач, умения проводить физический эксперимент;
воспитательная: расширить кругозор учащихся, развивать коммуникативные способности, развивать познавательный интерес к предмету.
Задачи: продолжить учиться работать в группах; развивать умения применять знания в нестандартных ситуациях; реализовать творческие способности учащихся.
Тип урока: обобщающий (с использованием ИКТ)
Оборудование: компьютер, проектор, экран, приборы для демонстрации опытов и экспериментальной работы учащихся, презентации учащихся :
„Биография И.Ньютона” , „Три закона Ньютона ”, “Законы Ньютона в природе и технике”, портрет Ньютона, плакаты с кроссвордом, таблицами
«Мыслящий ум не чувствует себя счастливым,
пока ему не удастся связать воедино разрозненные факты,
им наблюдаемые»
Д.Хевеши
Ход урока
I. Организационный момент. Вступительное слово учителя.
В истории есть немного имен и книг, пронизывающих века и даже тысячелетия и непрестанно влияющих на развитие культуры, техники и науки.
В архив науки сложены системы Птолемея, теплород и многое другое. Но есть научные открытия, которые оказываются пригодными для решения современных практических задач, и это означает, что они достоверны, ибо они прошли самое жесткое испытание – испытание временем. Именно таким великим законам физики посвящен наш урок. А о каких законах сегодня будем говорить, мы узнаем, отгадав кроссворд.
Капитаны групп получите оценочную ведомость и в течеении всего урока вы будете отмечать участие учащихся из вашей группы, а в конце урока выставите итоговую оценку. Ну что ж, начнем.
II. Отгадайте кроссворд.
( на доске плакат с кроссвордом)
1.Вектор, соединяющий начальное положение тела с его последующим положением. (Перемещение.)
2.Векторная величина, которая изменяется только в результате воздействия на тело силы. (Скорость.)
3.Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил. (Равнодействующая.)
(Равнодействующая.)
4. Длина траектории. (Путь.)
5. Прибор, измеряющий скорость движения. (Спидометр.)
6.Физическая величина, характеризующая быстроту изменения скорости движения. (Ускорение.)
7. Прибор для измерения силы. (Динамометр.)
Итак, сегодня наш урок посвящен “Законам Ньютона”. Ньютон – величайший ученый не только своего времени, но и истории. Он изучал природу света, построил зеркальный телескоп, но самая главная заслуга Ньютона в том, что он вывел три закона механики, которые управляют движением тел во Вселенной.
На уроке мы повторим законы движения, закрепим знания при решении задач, покажем связь законов с жизнью, закрепим навыки проведения физического эксперимента. Следующий этап нашего урока …
III Актуализация знаний
Законы Ньютона позволяют нам теперь ответить на многие вопросы «почему», которые я задаю вам:
1. Почему, при каких условиях тело совершает прямолинейное равномерное движение или находится в покое? Ответ дает 1-й закон Ньютона (первая группа дает формулировку закона)
2. Почему и при каких условиях тело движется равноускоренно? Ответ дает на этот вопрос 2-й закон Ньютона (вторая группа зачитывает формулировку закона)
Почему и при каких условиях тело движется равноускоренно? Ответ дает на этот вопрос 2-й закон Ньютона (вторая группа зачитывает формулировку закона)
3. Как вообще возникает сила? Ответ на этот вопрос дает 3-й закон Ньютона ( третья группа зачитывает формулировку закона)
IV. Особенности законов Ньютона.
Каждая группа получит сейчас конверт с утверждениями, которые имеют отношение к законам. Вам необходио выбрать те выражения, которые имеют отношение к закону. Первая группа – первый закон Ньютона, Вторая группа – второй закон Ньютона, третья группа – третьий закон Ньютона. У вас 3 минуты. (На доске висит плакат, учащиеся по-очереди выходят к доске и заполняют таблицу)
Справедлив для любых сил;Силы уравновешиваются, т.к. приложены к одному телу;
Если результирующая равна 0, то ускорение тоже равно 0
Верен для любых сил;
Сила – причина изменения скорости;
Вектор ускорения сонаправлен с вектором силы;
Силы возникают только парами и всегда при взаимодействии;
Силы не уравновешивают друг друга;
Силы одной природы;
Верен для всех сил в природе.
V. Работа с учебником
При изучении законов Ньютона с какими величинами вы встретились?
а) сила,
б) масса.
Первая группа, расскажите, что вы знаете о силе?
Ответы учащихся:
Сила-величина векторная
Сила F определяется:
1) модулем
2) направлением
3) точкой приложения
Сила – характеристика взаимодействия тел, количественная мера механического воздействия на тело со стороны других тел, в результате которого тело приобретает ускорение или изменяет форму и размеры.
Измерить силу – это значит сравнить её с другой, значение которой известно. На этом основан принцип действия динамометра.
Единица силы – Н . 1Н=1кг·1м/с2
Вторая группа, расскажите, что вы знаете о массе?
Величина скалярная, характеризующая инертность тела
Масса m мера количества вещества.
Способ получения:
1) По ускорению при взаимодействии с эталоном
2) Взвешиванием
Единица массы 1 кг
Третья группа напишите на доске формулы связанные с тремя законами Ньютона
Что мы можем найти, зная силу? Как запишется цепочка решения основной задачи механики в этом случае?
Сила ускорение скорость перемещение координата
VI. Решение задач
“Человек знает физику, если он умеет решать задачи” Энрико Ферми.
Законы Ньютона позволяют решить любую, без исключения, задачу механики. Докажем это, работая в группах над решением качественных, экспериментальных и расчетных задач. Каждой группе нужно выбрать по одному представителю на задачу (который защитит расчетную задачу, используя алгоритм решения задач на законы Ньютона)
Первая группа
Задача 1. (качественная).История о том, как «лебедь, рак да щука везти с поклажей воз взялись», известна всем. Рассматрите эту басню с точки зрения механики, и ответьте на воспрос почему воз и ныне там?
Рассматрите эту басню с точки зрения механики, и ответьте на воспрос почему воз и ныне там?
Напоминаем:
Лебедь рвется в облака,
Рак пятится назад,
А щука тянет в воду
Задача 2 (экспериментальная). Опытным путем доказать справедливость третьего закона Ньютона.
Задача 3. (расчетная). Масса скутера 300 кг, а гоночной машины 1т. Сравнить их ускорения, если сила тяги гоночной машины в 4 раза больше, чем скутера.
Вторая группа
Задача 1. (качественная).Если действие, как гласит закон, всегда равно и противоположно противодействию, то сила, с которой лошадь тянет телегу вперед, равна по модулю и противоположна по направлению силе, с которой телега «тянет» лошадь назад. Но телега движется вперед, а лошадь назад не движется. Почему и телега, и лошадь движутся вперед?
По третьему законуНьютона F1 =F2 . Равнодействующая сил, приложенная к лошади, и к телеге равна нулю. По превому закону Ньютона Лошадь с телегой либо движуться равновмерно и прямолинейно, либо покоятся. Следовательно, лошадь с телегой движутся в ту сторону, куда напрвлена начальная скорость , т.е. в сторону движения лошади.
Равнодействующая сил, приложенная к лошади, и к телеге равна нулю. По превому закону Ньютона Лошадь с телегой либо движуться равновмерно и прямолинейно, либо покоятся. Следовательно, лошадь с телегой движутся в ту сторону, куда напрвлена начальная скорость , т.е. в сторону движения лошади.
Задача 2 (экспериментальная). Проверить зависимость ускорения от движущей силы при постоянной массе.
Задача 3. (расчетная). Мяч массой 0,5кг после удара, длящегося 0,02с приобретает скорость 10м/с. Найти среднюю силу удара.
Третья группа
Задача 1. (качественная). Барон Мюнхгаузен утверждал, что вытащил себя из болота за волосы. Обоснуйте невозможность этого.
Невезможно. Так как сила действующая на голову вверх, равна силе, действующей вниз в плече.
Задача 2 (экспериментальная).Докажите экспериментально справедливость первого закона Ньютона.
Задача 3 (расчетная) Под действием некоторой силы тележка, двигаясь из состояния покоя, прошло путь 40см. Когда на тележку положили груз массой 200г, то под действием той же силы за это же время тележка прошла из состояния покоя путь 20 см. Какова масса тележки?
Когда на тележку положили груз массой 200г, то под действием той же силы за это же время тележка прошла из состояния покоя путь 20 см. Какова масса тележки?
VII. Составление обобщающей таблицы
Второй закон Ньютона
Третий закон Ньютона
Физическая система
Макроскопическое тело
Макроскопическое тело
Система двух тел
Модель
Материальная точка
Материальная точка
Система двух материальных точек
Описываемое явление
Состояние покоя или равномерного прямолинейного движения
Движение с ускорением
Взаимодействие тел
Суть закона
Существование инерциальной СО
Взаимодействие определяет изменение скорости, т.е. ускорение
Силы действия и противодействия равны по модулю и противоположны по направлению.
Примеры проявления
Движение космического корабля вдали от поверхности Земли.
Движение планет, падение тел; разгон и торможение автомобиля.
Взаимодействие тел:
Солнца и планет; автомобиля по поверхности земли
Границы применимости
ИСО. Макро – и мегамир. Движение со скоростями, много меньшими скорости света.
VIII. Творческие работы учащихся. (презентации)
а) “Биография И.Ньютона”,
б)“Три закона Ньютона”,
в)“Законы Ньютона в природе и технике”.
IX. Заключение.
Со времен установления Ньютоном основных законов движения прошло почти три столетия. За это время законы множество раз проверялись в различных условиях, и всякий раз полученные результаты подтверждали их истинность.
Х. Рефлексия.
Каждая группа записывает на трех полученных яблочках ответы на вопросы
на зеленом: Что нового вы узнали на уроке?
на красном: Что вызвало затруднения?
на желтом: Что заинтересовало?
Капитан каждой группы озвучивает ответы т и закрепляет яблоки на дереве.
ХI Подведение итогов.
Выставление оценок за работу на уроке и творческие работы учащихся.
ХII. Домашнее задание
Повторить 15-18,составить сенкан, это белый стих в котором синтезировани короткая информация из пяти рядков. Он помогает подитожить информацию, определить главные идеи , мысли.
Схема сенкана
Тема – одно сущемствительное
Описание – два прилагательных
Действие – три глагола.
Отношение к теме – фраза из четырех слов
Перефразирование содержания – одно слово.
Закон Ньютона
Фундаментальные, справедливые
Отображают, отвечают, объясняют
Дают описание движению тел
Механика
Сила
Векторная, скалярная
Изменяет, определяет, характеризует
Сообщает ускорение движению тел
Причина
Масса
Скалярная, количественная
Характеризует , обладает, изменяет
Является общим свойством теля
Инертность
План урока
Физика в картинках
Актуализация опорных знаний и умений
Отвечают на вопросы учителя
8
№ 3
5
Музей физики.
Верно ли высказывание.
Активные действия учащихся, формирование умения проводить опыты
Демонстрируют опыты, выполняют задание
8
№ 4
4
Проверь себя
Выявление пробелов в знаниях; воспитание адекватной самооценки учащихся
Выполняют тест самоконтроля
8
5
Решение задач
Умение применять знания при решении задач
Решают качественные и графические задачи
10
№ 5,6,7,8
6
Самостоятельная работа
Выявление качества и уровня овладения знаниями;
Решают расчетные задачи
10
7
Физкультминутка
3
8
Экспериментальная работа
Работая в парах, выполняют экспериментальную работу по проверке законов Ньютона
10
9
Творческие работы учащихся
Выступают с докладами и презентациями
10
10
Составление обобщающей таблицы
Формирование целостной системы основных знаний по теме
Заполняют обобщающую таблицу
5
№ 9
11
Подведение итогов.
Анализ и оценка успешности достижения целей и задач урока
Слушают учителя
3
№10
12
Рефлексия
Мобилизация учащихся на рефлексию своей деятельности на уроке
Заполняют концептуальную таблицу
4
итого
Законы Ньютона. Примеры проявления законов Ньютона в природе и их использование в технике. Билеты
Законы Ньютона. Примеры проявления законов Ньютона в природе и их использование в технике. БилетыВаш город: Екатеринбург
Регистрация
Вход
Название: Законы Ньютона.
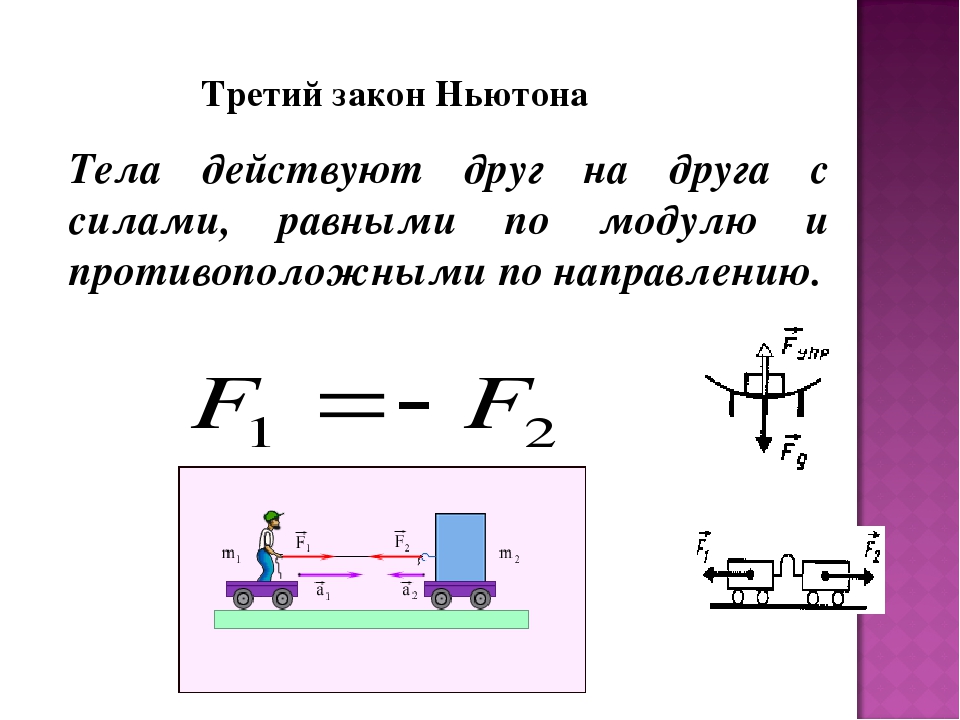 Примеры проявления законов Ньютона в природе и их использование в технике.
Примеры проявления законов Ньютона в природе и их использование в технике. Категория: Билеты
Предмет: Физика
Описание:
text_id = 69
К_2.02 Алгоритм применения второго закона Ньютона
1. Читаем ВНИМАТЕЛЬНО условие задачи.
Под действием двух ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ сил, по модулю равных 3 Н и 4 Н, тело из состояния ПОКОЯ за 2 с переместилось на 20 м по направлению равнодействующей силы. Определить массу тела.
Обратим внимание так же на то что НЕ ДАНО, а именно ни чего не известно о ориентации в пространстве (нет указаний на вертикали или горизонтали), ни чего не известно что за силы действуют (т. е. мы НЕ ЗНАЕМ что это за силы – это какие-то безымянные силы) т.о. перед нами число абстрактная задача без привязки к какой-либо реальной ситуации!
е. мы НЕ ЗНАЕМ что это за силы – это какие-то безымянные силы) т.о. перед нами число абстрактная задача без привязки к какой-либо реальной ситуации!
Проанализируем условие на предмет того какие “темы работают”. Так как речь о силовом воздействии то конечно – “Динамика” , так как известно время, начальная скорость и расстояние – работает так же “Кинематика”
Т.о. решение разбивается на два этапа
I) Работаем с динамикой;
II) Работаем с кинематикой;
ДИНАМИКА
I.1. Делаем рисунок и сразу показываем силы.
I.2. Определяемся с методом, который будем использовать.
В данном случае нам НЕ известно как направлено ускорение, и действует 2-е силы, следовательно будем использовать ГЕОМЕТРИЧЕСКИЙ МЕТОД.
I.3. Выполним построение – ГЕОМЕТРИЧЕСКИ сложим силы (например методом параллелограмма)
I.4. Записываем Второй закон Ньютона в векторной форме.
I.5. . Выразим численное значение равнодействующей.
Из рисунка понятно что
т. е. равнодействующую можно найти по теореме Пифагора.
е. равнодействующую можно найти по теореме Пифагора.
С учетом II закона Ньютона можем записать
(*)
Помним что нам нужно найти массу тела, следовательно нам не хватает ускорения тела. Найдем его из кинематики.
КИНЕМАТИКА
II.1. Известно расстояние пройденное телом (Δr = 20 м). Известна начальная скорость (V0 = 0), нужно найти ускорение – уравнение которое лучше всего “цепляет” имеющуюся информацию это уравнение перемещения
с учетом наших данных
Подставим это выражение в (*)
и выразим отсюда массу
Подставив численные значения, найдем что масса тела = 0.5 кг.
Первый закон ньютона закон инерции: формула и определение / Блог / Справочник :: Бингоскул — ЭкоДом: Дом своими руками
формула и определение / Блог / Справочник :: Бингоскул
Кратко о 1 законе Ньютона: формула, определение и формулировка
Помни!!!
- В основе динамики материальной точки лежат три закона Ньютона.
- Первый закон Ньютона — закон инерции
- Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.
1. Формулировка
«Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно».
2. Определение
Первый закон Ньютона — всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Первый закон Ньютона — закон инерции (Галилей вывел закон инерции)
Закон инерции: Если на тело нет внешних воздействий, то данное тело сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли.
Инерциальная система отсчёта (ИСО) – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Т.е. система отсчета, в которой выполняется 1-й закон Ньютона.
Т.е. система отсчета, в которой выполняется 1-й закон Ньютона.
- Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
- Сила – количественная мера взаимодействия тел. Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
3. Формула
Формулы нет. Формула первого закона Ньютона не существует.
Первый закон Ньютона содержится 2 важных утверждения:
- все тела обладают свойством инерции;
- инерциальные системы отсчета существуют.
Это интересно:
Первый закон Ньютона. Масса. Сила
Мы знаем, что тело может двигаться равномерно и прямолинейно. В таком случае его скорость постоянна и не меняется по величине и направлению. Если же скорость тела меняет величину или величину и направление, то тело движется с определенным ускорением a→.
С точки зрения кинематики нас не интересует, почему тело движется тем или иным образом. Динамика в физике, наоборот, рассматривает взаимодействие тел как причину, которая определяет характер движения.
Динамика
Взаимодействие тел определяет характер движения.
Динамика — раздел механики, в котором изучаются законы взаимодействия тел.
1 закон Ньютона
Законы динамики были сформулированы Исааком Ньютоном и опубликованы в 1687 году. Три закона Ньютона составляют основу классической механики, которая на протяжении нескольких столетий (вплоть до 20 века) главенствовала, как основная научная парадигма.
Классическая механика справедлива для тел, движущихся с малыми скоростями (скоростями, которые значительно меньше скорости света). Вообще законы Ньютона были выведены путем эмпирических наблюдений и обобщения опытных фактов.
Представим изолированное тело, на которое не действуют никакие другие тела. Это самая простая механическая система. Для описания движения тела необходима система отсчета.
Для описания движения тела необходима система отсчета.
Напомним, что система отсчета — это тело отсчета и связанные с ним системы координат и часов (отсчета времени). Причем в разных системах отсчета движение тела будет разным.
Сформулируем первый закон Ньютона. Он говорит о существовании так называемых инерциальных систем отсчета (ИСО) и называете также законом инерции. Существуют разные определения первого закона Ньютона.
Первый закон Ньютона
Существуют системы отсчета, называемые инерциальными. В таких системах отсчета тела движутся равномерно и прямолинейно или покоятся, если на них не действуют другие тела или если их действие скомпенсировано.
Инерция — это свойство тел сохранять свою скорость при отсутствии на него воздействий со стороны других тел. Именно поэтому второе название первого закона Ньютона — закон инерции.
Первая формулировка закона инерции была выведена еще Галилео Галилеем в 1632 году. Ньютон лишь обобщил его выводы.
Важно!
В классической механике законы движения формулируются для инерциальных систем отсчета.
При описании движения тел у поверхности Земли системы отсчета, связанные с Землей, можно приблизительно считать и инерциальными. Отклонения от закона инерции обнаруживаются при повышении точности экспериментов и обусловлены вращением Земли вокруг своей оси.
Приведем пример, иллюстрирующий неинерциальность системы отсчета, связанной с Землей. Рассмотрим колебания маятника Фуко. Это массивный шар, подвешенный на длинной нити и совершающий малые колебания относительно положения равновесия.
Плоскость колебаний маятника Фуко относительно Земли не остается неизменной вследствие вращения Земли. Проекция траектории маятника на поверхность Земли имеет вид розетки. Будь система инерциальной, плоскость качения маятника относительно Земли оставалась бы неизменной.
Еще одна система, которую можно приближенно принять за инерциальную — гелиоцентрическая система отсчета. Начало координат в ней помещено в центр Солнца, а оси направлены на отдаленные звезды. Эта система отсчета еще называется системой Коперника. Именно ее использовал Ньютон при выводе закона Всемирного тяготения (1682 г.).
Именно ее использовал Ньютон при выводе закона Всемирного тяготения (1682 г.).
Система отсчета, связанная с поездом, который с постоянной скоростью движется по прямым рельсам, также может считаться инерциальной. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно.
Что является причиной изменения скорости тела в инерциальной системе отсчета? Согласно первому закону Ньютона, это взаимодействие с другими телами. Чтобы количественно описать движение тела и взаимодействие его с другими телами, необходимо ввести понятия массы и силы.
Масса
Определение. Масса
Масса — физическая величина, мера инертности тела. Чем больше масса, тем больше инертность.
Единица измерения массы в международной системе СИ — килограмм (кг).
Масса в физике — скалярная и аддитивная величина.
Это значит, что если тело состоит из нескольких частей массами m1, т2, т3, .. , тn, то его общая масса будет равна сумме масс составных частей: m=m1+т2+т3+. .+тn.
.+тn.
Вы наверняка замечали, что разные тела по-разному меняют свою скорость. Тяжелый грузовик остановить гораздо сложнее, чем игрушечную машинку, так как он обладает большей массой и, соответственно, инертностью.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
В результате взаимодействия двух тел меняются их скорости. Это значит, что в процессе взаимодействия тела приобретают ускорения. При любых воздействиях отношение ускорений двух тел остается постоянным. При этом, массы тел обратно пропорциональны ускорениям, которые они приобретают.
m1m2=-a2a1
Здесь a1 и a2 — проекции векторов ускорений a1 →и a2 →на ось OX. Знак минус означает, что ускорения тел направлены в противоположные стороны.
Какие есть способы измерения массы тела? Самый простой и очевидный — сравнить массу тела с массой эталона. В системе СИ, как уже говорилось, mэт=1 кг.
Сила
Определение. Сила
Сила — векторная физическая величина, количественная мера взаимодействия тел.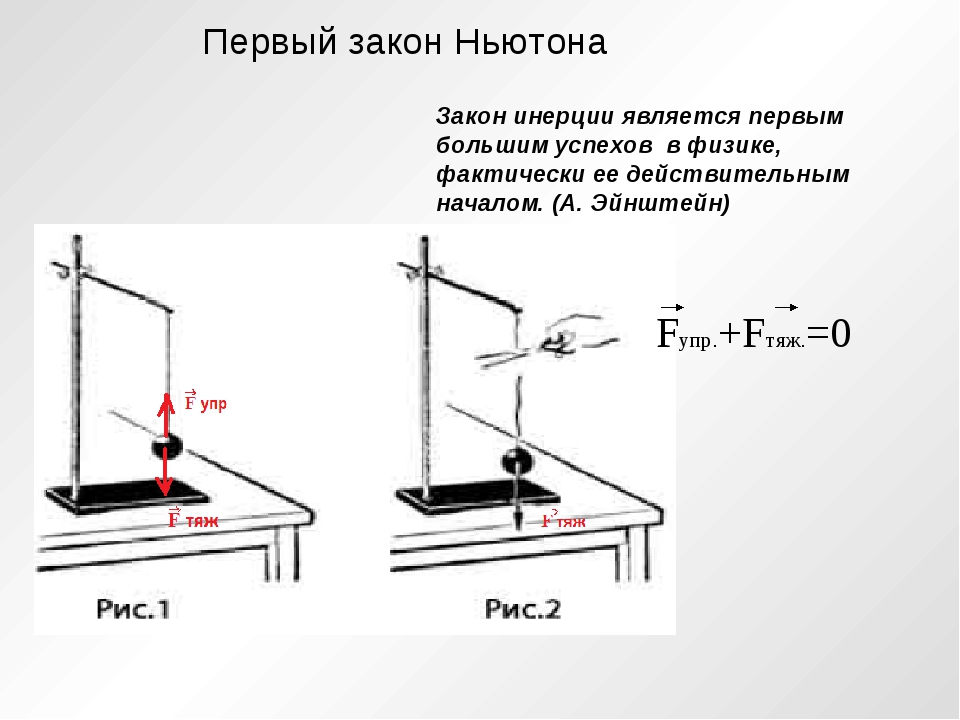
В системе СИ сила измеряется в Ньютонах (Н).
Именно сила — причина изменения движения тела. На тело может действовать несколько сил, которые имеют различную физическую природу. Например, сила тяжести, сила трения скольжения и сила трения качения, сила упругости и т.д.
Равнодействующая сила — векторная сумма всех сил, действующих на тело.
Как измерить силу? Необходимо установить эталон силы и найти способ сравнить другие силы с этим эталоном.
В качестве эталона можно использовать, например, силу, с которой растянутая до определенной величины пружина действует на прикрепленное к ней тело. Способ сравнения сил очень прост: если под действием двух сил (измеряемой F→ и эталонной F→0) тело движется равномерно или покоится, то эти силы равны по модулю.
F=F0.
Если измеряемая сила больше эталонной, то можно добавить еще одну эталонную пружину. При соблюдении условий, указанных выше, можно сказать, что в таком случае
F=2F0.
Для сравнения сил, меньших чем 2F0, можно использовать схему, приведенную ниже.
Эталон силы (единица измерения)
За эталон силы в международной системе СИ принята сила в 1 Ньютон. Это такая сила, которая сообщает телу массой 1 килограмм ускорение, равное 1 мс2.
Прибор для измерения силы — динамометр. По сути, это пружина, откалиброванная специальным образом. При растяжении пружины приложенная сила указывается на шкале динамометра.
Урок 7. законы динамики ньютона — Физика — 10 класс
Физика, 10 класс
Урок 7. Законы динамики Ньютона
Перечень вопросов, рассматриваемых на уроке: основные характеристики массы и силы; взаимодействие тел; законы динамики Ньютона и их особенности; экспериментальная проверка справедливости законов Ньютона.
Глоссарий по теме.
Масса – одна из основных характеристик материи, определяющая ее инерциальные и гравитационные свойства.
Сила – векторная физическая величина, являющаяся мерой взаимодействия тел.
Взаимодействие – одновременное влияние (действие) тел друг на друга.
Равнодействующая сила производит на тело такое же действие (вызывает такое же действие), как несколько сил, одновременно приложенных к телу.
Инерция – явление сохранения скорости тела при отсутствии (или компенсации) действия на него других тел.
Инерциальная система отсчета – система отсчета, в которой тело, не взаимодействующее с другими телами, сохраняет состояние равномерного прямолинейного движения или покоя.
Неинерциальные системы отсчета — система отсчета, которая двигается с ускорением относительно инерциальной системы отсчета.
Список литературы:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М. : Просвещение, 2017. – С. 64 – 87.
О. Ф. Кабардин, В. А. Орлов, А. В. Паномарева. Факультативный курс физики. М.: Просвещение, 1987. – С. 188 – 200.
Открытые электронные ресурсы:
http://kvant.mccme.ru/1971/05/zadachi_na_zakony_nyutona.htm
Основное содержание урока
Масса (лат. « massa» — ком, кусочек, глыба) — физическая величина, одна из основных характеристик материи, определяющая ее инерциальные и гравитационные свойства.
« massa» — ком, кусочек, глыба) — физическая величина, одна из основных характеристик материи, определяющая ее инерциальные и гравитационные свойства.
Способы измерения массы:1) сравнение с эталоном; 2) взвешивание на весах. В классической механике масса — аддитивная величина; не зависит от рода взаимодействия и скорости движения тела.
Сила — мера взаимодействия тел. Атрибуты силы: точка приложения силы, линия действия силы, модуль силы.
Первый закон Ньютона (закон инерции): если на тело не действуют другие тела, то тело движется прямолинейно и равномерно.
Особенности первого закона Ньютона: указывает на существование инерциальных систем отсчета; равнодействующая всех сил равна нулю: F = 0.
Если есть одна инерциальная система отсчета, то любая другая система, движущаяся относительно неё прямолинейно и равномерно, также является инерциальной.
Второй закон Ньютон: ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе: a =F/m.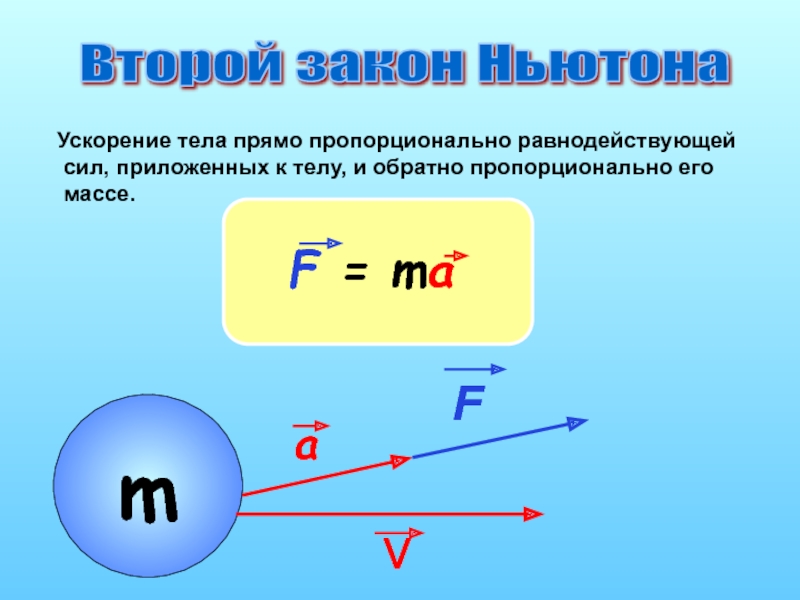
Другая запись формулы второго закона Ньютона (основное уравнение динамики): F =ma.
Формулировка второго закона Ньютона для системы тел: приращение импульса ∆Pсистемы тел равно по величине и по направлению импульсу внешних сил Fвн, действующих на тело, за то же время: ∆p =(F∆ Pсист).
Особенности второго закона Ньютона: выполняется в инерциальных системах отсчета; скорость тела мала по сравнению со скоростью света; макрообъекты; постоянная масса; справедлив для любых сил; сила — причина, ускорение – следствие; вектор ускорения а сонаправлен с вектором F.
Согласно третьему закону Ньютона тела действуют друг на друга с силами, равными по модулю и противоположными по направлению:
F12 =-F 21
Особенности третьего закона Ньютона: выполняется в инерциальных системах отсчета; силы всегда действуют парами; силы являются силами одной природы; силы не уравновешивают друг друга; выполняется для всех сил в природе
Разбор тренировочных заданий
1. Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание.
Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание.
Сила характеризует (_____________) одного тела на другое, в результате которого изменяется (___________) тела или происходит (______________) тел.
Правильный ответ: действие; скорость, деформация
2. Автомобиль массой 0,5 т. разгоняется с места равноускоренно и достигает скорости 40 м/с за 20 с. Равнодействующая всех сил, действующих на автомобиль равна __ кН.
Решение:
При V0=0 ускорение автомобиля равно:
a =v /∆t
Следовательно, равнодействующая сила по второму закону Ньютона равна:
F = ma = mv/∆t
Проверка размерностей: F = кг × м/с × с (-1)= [ Н ]
F= 500 кг × (40 м/с)/(20 с)= 1000 Н = 1 кН
Ответ: F= 1 кН.
Первый закон Ньютона, теория и онлайн калькуляторы
Задание. Небольшой камешек бросают в шахту, глубина которой равна $h$, выясняется, что падая, тело отклонилось от вертикали в восточном направлении.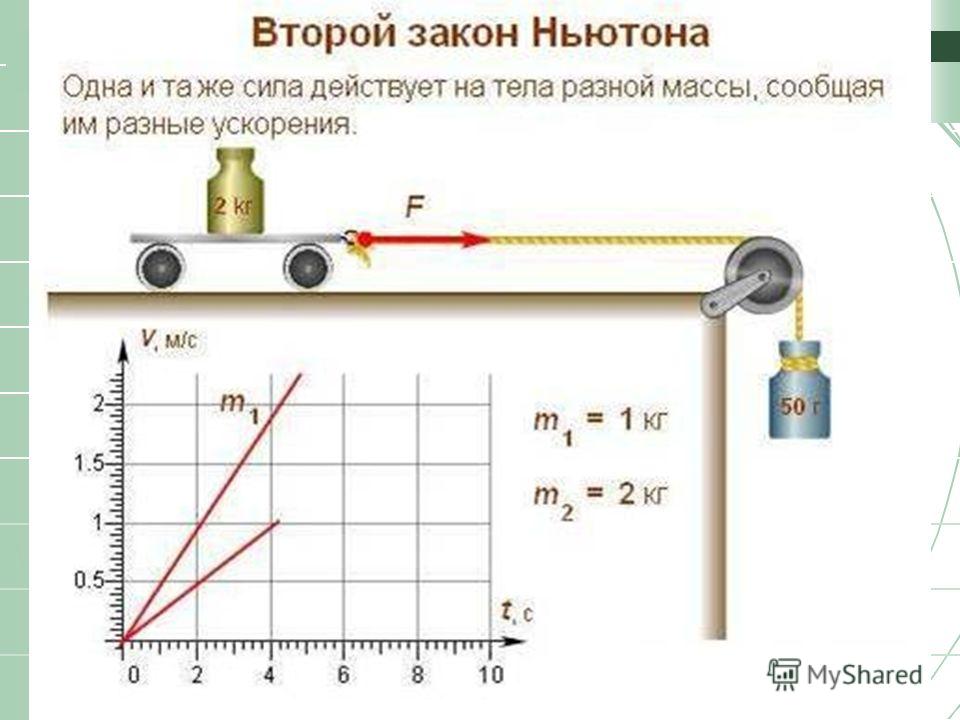 Каково это отклонение? Сопротивлением воздуха пренебречь. Что можно сказать, в связи с результатом данного опыта, об инерциальности системы отсчета, которую связывают с Землей?
Каково это отклонение? Сопротивлением воздуха пренебречь. Что можно сказать, в связи с результатом данного опыта, об инерциальности системы отсчета, которую связывают с Землей?
Решение. Сделаем рисунок.
Отклонение движения тела от вертикали происходит благодаря вращению Земли вокруг собственной оси. Обозначим скорость движения точек поверхности Земли как $v_1.$ Скорость движение точек дна шахты обозначим $v_2$, тогда разность этих скоростей равна:
\[\Delta v=v_2-v_1\left(2.1\right).\]
При своем падении камень отклонится от вертикали на расстояние:
\[x=\Delta vt\ \left(2.2\right),\]
где $t$ — время падения тела.
Величину $\Delta v$ найдем из периода обращения Земли вокруг своей оси (T):
\[T=\frac{2\pi R}{v}(2.3),\]
тогда
\[\Delta v=\frac{2\pi R}{T}-\frac{2\pi \left(R-h\right)}{T}=\frac{2\pi h}{T}\ \left(2.4\right),\]
где $R$ — Радиус Земли в районе экватора.
Если тело падает свободно в поле тяжести Земли, из кинематического уравнения движения имеем (движение по оси Y (рис. 2}{2}\left(2.5\right).\]
2}{2}\left(2.5\right).\]
Из формулы (2.5) выразим время, которое потратил камень на падение:
\[t=\sqrt{\frac{2h}{g}}\ \left(2.6\right).\]
Подставим в выражение (2.2) время ($t$) из (2.6) и изменение скорости ($\Delta v$) из (2.4) Найдем искомое отклонение от вертикали:
\[x=\frac{2\pi h}{T}\sqrt{\frac{2h}{g}}.\]
Ответ. $x=\frac{2\pi h}{T}\sqrt{\frac{2h}{g}}.\ $ В горизонтальном направлении на камень не действуют другие тела, тем не менее, $x\ne 0$ это означает, что система отсчета, связанная с Землей, строго говоря, не является инерциальной системой отсчета, так как в ней не выполняется первый закон Ньютона (или выполняется с некоторым допущением). Это понятно уже по тому, что если система отсчета вращается, как Земля, или просто движется по криволинейной траектории, относительно любой инерциальной системы, то она не может быть инерциальной. Однако, при решении большинства задач неинерциальностью системы отсчета, связанной с Землей пренебрегают.
Первый закон Ньютона
Пользователи также искали:
4 закон ньютона,
первый закон ньютона формула 9 класс,
первый закон ньютона формулировка,
первый закон ньютона кратко,
первый закон ньютона примеры,
сформулируйте первый закон ньютона,
законы,
закон,
Ньютона,
ньютона,
первый,
Первый,
Первый закон Ньютона,
формула,
законы ньютона формулы,
закон ньютона,
сформулируйте,
формулировка,
примеры,
кратко,
класс,
формулы,
первый закон ньютона примеры,
первый закон ньютона кратко,
первый закон ньютона формула 9 класс,
сформулируйте первый закон ньютона,
4 закон ньютона,
первый закон ньютона формулировка,
первый закон ньютона формула,
первый закон ньютона формула класс,
первый закон ньютона,
именные законы и правила. первый закон ньютона,
Физические основы механики
Г. Галилей (1564–1642) справедливо считается основателем физики как науки. Ему мы обязаны развитием современного метода исследований, кратко выражающегося в цепочке: эксперимент => модель (выделение в явлении главных особенностей, то есть применение абстракции) => математическое описание => следствия модели => новый эксперимент для их проверки.
Среди прочих научных достижений, в механике им были введены два основополагающих принципа: принцип инерции и принцип относительности. Принцип инерции Галилея был повторен И. Ньютоном (1643–1727) в качестве первого закона механики.
Первый закон Ньютона гласит:
Существуют такие системы отсчета, в которых всякая материальная точка находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока это состояние не будет изменено воздействием со стороны других тел. Такие системы отсчета принято называть инерциальными.
Ответ на вопрос: «Существуют ли инерциальные системы отсчета или нет?», как всегда, дает эксперимент. По результатам современных измерений гелиоцентрическая система отсчета, в которой неподвижен центр Солнца, и оси которой направлены на неподвижные звезды, является инерциальной. Это означает следующую простую вещь: существующие акселерометры (измерители ускорения) не обнаруживают отклонений от первого закона Ньютона в гелиоцентрической системе отсчета. Покой или равномерное прямолинейное движение — это состояние с равным нулю ускорением, следовательно, если тело, не подверженное воздействиям извне, приобретает ускорение, то это означает, что движение этого тела рассматривается в неинерциальной системе отсчета. Солнечная система совершает финитное движение в пределах нашей галактики (Млечный путь), любое финитное движение есть движение с ускорением, но солнечная система далека от центра галактики — мы периферийные жители — кривизна её траектории ничтожна, наши приборы не обнаруживают ускорений и мы утверждаем, что гелиоцентрическая система отсчета инерциальна. Инерциальная система отсчета — ещё одна идеализация: в точном смысле инерциальных систем отсчета не существует. Естественно предположить, что это обстоятельство было в ряду тех, что подвигли Эйнштейна на создание общей теории относительности, в которой утверждается физическое равноправие всех вообще, а не только инерциальных, систем отсчета, а поля сил инерции эквивалентны гравитационным полям (так называемый «принцип эквивалентности» подробнее речь об этом пойдет позже).
В дальнейшем будет видно, что любая система отсчета, движущаяся поступательно с постоянной по величине и направлению скоростью относительно некоторой инерциальной системы отсчета, также инерциальна. Другими словами, существование одной инерциальной системы отсчета означает существование бесконечно большого числа таких систем.
Свойство тела сохранять состояние покоя или прямолинейного равномерного движения называется инерцией. Сам этот принцип — принцип инерции Галилея (или первый закон Ньютона) — далеко не столь очевиден.
До Галилея думали, что для движения нужна какая-то причина, движущая сила. Даже великий Леонардо да Винчи писал: «Всякое движение стремится к своему сохранению, или же каждое движущееся тело движется постоянно, пока в нем сохраняется действие его двигателя». Удивительно, но туповатый полковник фон Циллергут из книги Я. Гашека «Похождения бравого солдата Швейка», мыслил похоже: нет бензина, не работает двигатель, автомобиль останавливается. После Галилея стала возможной чеканная латинская формулировка Р. Декарта (1596–1650): «Quod in vacuo movetur, semper moveri» (что движется в пустоте, будет двигаться всегда).
Дело в том, что в природе действительно никогда не наблюдаются тела, вечно сохраняющие состояние покоя или прямолинейного равномерного движения. Нужно было проявить ту самую способность строить модели, отбрасывать несущественное, абстрагироваться, чтобы открыть принцип инерции. Изучая основные законы механики, мы идеализируем систему: пренебрегаем силами трения, считаем, что поблизости нет других тел и т. д. И тогда принцип инерции проявляет себя во всей своей красе и силе:
Для равномерного прямолинейного движения не нужно двигателя, движущая сила нужна для изменения такого вида движения тела.
Видео 3.1. Стальной шарик в поле магнита. Эксперимент, показывающий, что для искривления траектории необходима соответствующая внешняя сила.
Дополнительная информация
http://www.plib.ru/library/book/14978.html – Д.В. Сивухин Общий курс физики, том 1, Механика Изд. Наука 1979 г. – стр. 91–97 (§16): обсуждается принцип относительности Галилея, приводится дословное рассуждение самого Галилея!
http://www.gaudeamus.omskcity.com/PDF_library_natural-science_2.html – Киттель Ч., Наит У., Рудерман М. Курс общей физики. Том 1. Механика. Изд. Наука, 1975 г. – стр. 79–88 – описание ультрацентрифуги и оценка ускорений реальных систем отсчета, применяемых в механике.
Три закона Ньютона | Физика
Раздел механики, в котором изучают, как взаимодействие тел влияет на их движение, называют динамикой.
Основные законы динамики открыли итальянский ученый Галилео Галилей и английский ученый Исаак Ньютон. Вы изучали эти законы в курсе физики основной школы. Напомним их.
1. Первый закон ньютона (закон инерции)
Повторим один из опытов, которые поставил итальянский ученый Галилео Галилей.
Поставим опыт
Будем скатывать шар по наклонной плоскости и наблюдать за его дальнейшим движением по горизонтальной поверхности.
Если она посыпана песком, шар остановится очень скоро (рис. 13.1, а).
Если она покрыта тканью, шар катится значительно дольше (рис. 13.1, б).
А вот по стеклу шар катится очень долго (рис. 13.1, в).
На основании этого и подобных опытов Галилей открыл закон инерции: если на тело не действуют другие тела или действия других тел скомпенсированы, то тлело движется равномерно и прямолинейно или покоится.
Сохранение скорости тела, когда на него не действуют другие тела или действия других тел скомпенсированы, называют явлением инерции.
? 1. Почему при встряхивании мокрого зонта с него слетают капли воды?
Особенно красиво смотрится явление инерции в фигурном катании (рис. 13.2).
Закон инерции называют также первым законом Ньютона, потому что Ньютон включил его в качестве первого закона в систему трех законов динамики, которые называют «тремя законами Ньютона».
Инерциальные системы отсчета
Закон инерции выполняется с хорошей точностью в системе отсчета, связанной с Землей. Но он не выполняется, например, в системе отсчета, связанной с тормозящим автобусом: при резком торможении пассажиры отклоняются вперед, хотя на них не действуют направленные вперед силы.
Системы отсчета, в которых выполняется закон инерции, называют инерциальными.
Инерциальных систем отсчета бесконечно много. Ведь если некоторая система отсчета является инерциальной, то инерциальной будет любая другая система отсчета, движущаяся относительно нее прямолинейно и равномерно.
Сформулируем теперь первый закон Ньютона с указанием систем отсчета, в которых он выполняется.
Существуют системы отсчета (называемые инерциальными), относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действия других тел скомпенсированы.
Изучать влияние взаимодействия тел на их движение удобнее всего именно в инерциальных системах отсчета, потому что в этих системах отсчета изменение скорости тела обусловлено только действием других тел на это тело.
Принцип относительности Галилея
Как показывает опыт, во всех инерциальных системах отсчета все механические явления протекают одинаково при одинаковых начальных условиях.
Это утверждение называют принципом относительности Галилея.
В справедливости принципа относительности Галилея легко убедиться, сидя в поезде, который плавно движется с постоянной скоростью. В таком случае все опыты с механическими явлениями, поставленные в вагоне, дадут одинаковые результаты независимо от того, едет поезд или стоит: например, лежащее на столе яблоко будет покоиться, а свободно падающие предметы будут падать вертикально вниз (относительно вагона!).
Поэтому пассажир может определить, едет поезд или стоит на станции, только посмотрев в окно (рис. 13.3).
2. Второй закон ньютона
Равнодействующая
Как вы уже знаете из курса физики основной школы, силы – векторные величины: каждая сила характеризуется числовым значением (модулем) и направлением. Силы измеряют с помощью динамометров. Единицей силы в СИ является 1 ньютон (Н). Определение ньютона мы дадим позже.
Если на тело, которое можно считать материальной точкой, действуют несколько сил, то их можно заменить одной силой, которая является векторной суммой этих сил. Ее называют равнодействующей.
На рисунке 13.4 показано, как найти равнодействующую двух сил: а
? 2. К телу приложены две силы, равные по модулю 1 Н и 2 Н. Отвечая на следующие вопросы, сделайте пояснительные чертежи.
а) Какое наименьшее значение может принимать равнодействующая этих сил? Как направлены силы в этом случае?
б) Какое наибольшее значение может быть у равнодействующей этих сил? Как направлены силы в атом случае?
в) Может ли равнодействующая этих сил быть равной 2 Н?
? 3. К телу приложены две силы, равные по модулю 3 Н и 4 Н. Может ли их равнодействующая быть равной 5 Н? Если да, то чему в этом случае равен угол между приложенными силами?
? 4. К телу приложены три равные по модулю силы по 1 Н каждая. Как они должны быть направлены, чтобы:
а) равнодействующая была равна 1 Н?
б) равнодействующая была равна нулю?
в) равнодействующая была равна 2 Н?
Масса тела
В курсе физики основной школы рассказывалось также об опытах, которые доказывают, что под действием постоянной силы тело движется с постоянным ускорением.
Коэффициент пропорциональности между силой и ускорением характеризует инертные свойства тела и называется массой тела. Чем больше масса тела, тем большую силу надо приложить к телу, чтобы сообщить ему то же ускорение.
Единицей массы в СИ является 1 килограмм (кг). Это масса эталона, хранящегося в Международном бюро мер и весов (Франция). Приближенно можно считать, что одному килограмму равна масса 1 л воды.
Обозначают массу буквой m.
Второй закон Ньютона
Соотношение между равнодействующей всех сил, приложенных к телу, массой тела и его ускорением Ньютон сформулировал как второй из трех основных законов механики.
Равнодействующая всех сил, приложенных к телу, равна произведению массы тела на его ускорение:
В инерциальной системе отсчета сила является причиной ускорения, поэтому второй закон Ньютона часто записывают так:
Итак, приобретаемое телом ускорение прямо пропорционально равнодействующей приложенных к телу сил, одинаково с ней направлено и обратно пропорционально массе тела.
Заметим, что второй закон Ньютона справедлив только в инерциальных системах отсчета. Напомним: в этих системах отсчета ускорение тела обусловлено только действием на него других тел.
Единицу силы в СИ определяют на основе второго закона Ньютона: сила в 1 ньютон сообщает телу массой 1 кг ускорение 1 м/с2. Поэтому 1 Н = 1 кг * м/с2.
Сила тяжести
Как вы уже знаете, под действием притяжения Земли все тела падают с одинаковым ускорением – ускорением свободного падения . Силу притяжения, действующую на тело со стороны Земли, называют силой тяжести и обозначают т.
Когда тело свободно падает, на него действует только сила тяжести, поэтому она и является равнодействующей всех приложенных к телу сил. При атом тело движется с ускорением , поэтому из второго закона Ньютона получаем:
? 5. С какой силой Земля притягивает:
а) килограммовую гирю?
б) человека массой 60 кг?
Сила, скорость и ускорение – кто «третий лишний»?
Неочевидное следствие второго закона Ньютона состоит в том, что он утверждает: направление ускорения тела совпадает с направлением равнодействующей приложенных телу сил. Скорость же вела может быть при этом направлена как угодно!
Поставим опыт
Бросим шарик вниз, затем – вверх, а потом – под углом к горизонту (рис. 13.5)
На шарик во время всего движения действует только направленная вниз сила тяжести. Однако в первом случае (а) скорость шарика совпадает по направлению с этой силой, во втором случае (б) – скорость вначале противоположна силе тяжести, а в третьем (в) – скорость направлена под углом к силе тяжести (например, в верхней точке траектории скорость перпендикулярна силе тяжести).
? 6. Тело равномерно движется по окружности. Чему равен угол между скоростью тела и равнодействующей?
? 7. Чему равен угол между скоростью автомобиля и равнодействующей приложенных к нему сил, когда автомобиль:
а) разгоняется на прямой дороге?
б) тормозит на прямой дороге?
в) движется равномерно по дуге окружности?
3. Третий закон ньютона
Поставим опыт
Предложим первокласснику и десятикласснику посоревноваться в перетягивании каната, стоя на скейтбордах: тогда трением между колесами и полом можно пренебречь (схема опыта показана на рисунке 13.6).
Мы увидим, что оба соперника движутся с ускорением. Значит, на каждого из них действу другого. Ускорения соперников направлено противоположно, причем ускорение первоклассника намного больше ускорения десятиклассника.
Точные опыты, подобные описанном выше, показывают, что модули ускорений обратно пропорциональны массам тел:
a1/a2 = m2/m1.
Поскольку ускорения направлены противоположно,
Согласно второму закону Ньютона m11 = 1 и m22 = 2, где 1 – сила, действующая на первое тело со стороны второго, а 2 – сила, действующая на второе тело со стороны первого.
Из соотношения (5) следует, что 1 = –2. Это и есть третий закон Ньютона.
Тела взаимодействуют друг с другом с силами, равными по модулю и противоположными по направлению.
Свойстве сил, с которыми тела взаимодействуют друг с другом:
– эти силы обусловлены одним и тем же взаимодействием и поэтому имеют одну и ту же физическую природу;
– эти силы направлены вдоль одной прямой;
– эти силы приложены к разным телам и поэтому не могут уравновешивать друг друга.
Примеры проявления третьего закона Ньютона
Когда камень падает на Землю, на него действует сила тяжести 1 со стороны Земли, а на Землю – сила 2 притяжения со стороны камня (рис. 13.7, для наглядности масштаб не соблюден). Обе эти силы относятся к силам всемирного тяготения.
? 8. Согласно третьему закону Ньютона F1 = F2. Почему же ускорение камня заметно, а ускорение Земли – нет?
Когда камень лежит на Земле, на него кроме силы тяжести, которую будем обозначать теперь т, действует еще направленная вверх сила давления со стороны опоры (рис. 13.8, а). Она направлена перпендикулярно поверхности опоры, поэтому ее называют силой нормальной реакции (перпендикуляр называют часто нормалью). (Когда тело можно считать материальной точкой, все действующие на него силы желательно изображать на чертежах приложенными в одной точке.)
Когда камень покоится, его ускорение равно нулю. Значит, согласно второму закону Ньютона равнодействующая приложенных к камню сил и т, равна нулю (будем говорить, что в таком случае силы уравновешивают друг друга):
Отсюда следует:
Опора давит на камень силой , направленной вверх, а камень, по третьему закону Ньютона, давит на опору силан , направленной вниз (рис. 13.8, 6). Обе эти силы – силы упругости.
Силу, с которой тело вследствие действия на него силы тяжести давит на горизонтальную опору или растягивает вертикальный поднес, называют весом тела.
Итак, – это вес камня. По третьему закону Ньютона
Из формул (8) и (9) следует:
Итак, вес покоящегося тела равен действующей на это тело силе тяжести. Однако несмотря на это вес и сила тяжести существенно отличаются друг от друга:
– эти силы приложены к разным телам: вес действует на опору или поднес, а сила тяжести – на само тело;
– эти силы имеют разную физическую природу: вес – это сила упругости, а сила тяжести – проявление сил всемирного тяготения.
Кроме того, как мы увидим несколько позже (§ 16), вес может быть не равен силе тяжести и даже быть равным нулю.
Дополнительные вопросы и задания
9. Ускорение тела в некоторой инерциальной системе отсчета равно 3 м/с2 и направлено вдоль оси x. Чему равно ускорение этого тела в инерциальной системе отсчета, движущейся относительно заданной со скоростью 4 м/с, направленной вдоль оси y? Есть ли здесь лишние данные?
10. Брусок массой 0,5 кг соскальзывает с наклонной плоскости с углом наклона 30º. Скорость бруска увеличивается. Ускорение бруска равно 2 м/с2. Изобразите на чертеже равнодействующую приложенных к бруску сил. Чему она равна? Есть ли в задаче лишние данные?
11. Зависимость координаты x автомобиля от времени выражается в единицах СИ формулой x = 20 – 10t + t2. Ось x направлена вдоль дороги, масса автомобиля 1 т.
а) Чему равна равнодействующая приложенных к автомобилю сил?
б) Как она направлена в начальный момент – в направлении скорости автомобиля или противоположно ей?
12. Автомобиль массой 1 т едет со скоростью 72 км/ч по выпуклому мосту, имеющему форму дуги окружности радиусом 50 м. Сделайте чертеж и ответьте на вопросы.
а) Чему равна и как направлена равнодействующая сил, приложенных к автомобилю в верхней точке моста?
б) Какие силы действуют на автомобиль в этой точке? Как они направлены и чему они равны?
в) Во сколько раз вес автомобиля в верхней точке моста меньше действующей на автомобиль силы тяжести?
закон инерции | Открытие, факты и история
Закон инерции , также называемый первым законом Ньютона , в физике постулирует, что если тело находится в состоянии покоя или движется с постоянной скоростью по прямой линии, оно будет оставаться в состоянии покоя или продолжайте двигаться по прямой с постоянной скоростью, если на него не действует сила. Закон инерции был впервые сформулирован Галилео Галилеем для горизонтального движения на Земле, а затем был обобщен Рене Декартом. До Галилея считалось, что любое горизонтальное движение требует прямой причины, но Галилей вывел из своих экспериментов, что движущееся тело будет оставаться в движении, если сила (например, трение) не заставит его остановиться.Этот закон также является первым из трех законов движения Исаака Ньютона.
Британская викторина
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Хотя принцип инерции является отправной точкой и фундаментальным предположением классической механики, он менее чем интуитивно очевиден для неподготовленного глаза. В механике Аристотеля и в обычном опыте объекты, которые не толкают, имеют тенденцию останавливаться. Закон инерции был выведен Галилеем из его экспериментов с шарами, катящимися по наклонным плоскостям.
Для Галилея принцип инерции был фундаментальным для его центральной научной задачи: он должен был объяснить, как это возможно, если Земля действительно вращается вокруг своей оси и вращается вокруг Солнца, мы не ощущаем этого движения. Принцип инерции помогает дать ответ: поскольку мы движемся вместе с Землей, и наша естественная тенденция состоит в том, чтобы сохранять это движение, Земля кажется нам покоящейся.Таким образом, принцип инерции далек от утверждения очевидного, а когда-то был центральным вопросом научных споров. К тому времени, когда Ньютон разобрался во всех деталях, стало возможно точно учесть небольшие отклонения от этой картины, вызванные тем фактом, что движение поверхности Земли не является равномерным движением по прямой линии. В ньютоновской формулировке обычное наблюдение, что тела, которые не толкают, имеют тенденцию приходить в состояние покоя, объясняется тем фактом, что на них действуют несбалансированные силы, такие как трение и сопротивление воздуха. В классической ньютоновской механике нет важного различия между покоем и равномерным движением по прямой: их можно рассматривать как одно и то же состояние движения, наблюдаемое разными наблюдателями: один движется с той же скоростью, что и частица, а другой движется с постоянной скоростью. скорость относительно частицы.
Первый закон движения Ньютона
В предыдущей главе исследования было описано множество способов, с помощью которых может быть описано движение (слова, графики, диаграммы, числа и т. Д.)) обсуждалось. В этом разделе («Законы движения Ньютона») будут обсуждаться способы объяснения движения. . Исаак Ньютон (ученый 17 века) выдвинул множество законов, объясняющих, почему объекты движутся (или не двигаются) именно так. Эти три закона стали известны как три закона движения Ньютона. В центре внимания Урока 1 находится первый закон движения Ньютона, который иногда называют законом инерции .
Первый закон движения Ньютона часто называют
.
Покоящийся объект остается неподвижным, а объект в движении остается в движении с той же скоростью и в том же направлении, если на него не действует неуравновешенная сила.
Два пункта и условие
В этом утверждении есть два пункта или части — один, который предсказывает поведение стационарных объектов, а другой, который предсказывает поведение движущихся объектов. Эти две части представлены на следующей диаграмме.
Поведение всех объектов можно описать, сказав, что объекты имеют тенденцию «продолжать делать то, что они делают» (если на них не действует неуравновешенная сила).Если они находятся в состоянии покоя, они будут продолжать в том же состоянии покоя. Если они движутся со скоростью 5 м / с на восток, они продолжат движение в том же состоянии (5 м / с, восток). Если они будут двигаться со скоростью 2 м / с влево, они продолжат движение в том же состоянии (2 м / с, слева). Состояние движения объекта поддерживается до тех пор, пока объект не подвергается воздействию несбалансированной силы. Все объекты сопротивляются изменениям в своем состоянии движения — они склонны «продолжать делать то, что делают».«
Существует важное условие, которое должно быть выполнено, чтобы первый закон был применим к любому данному ходатайству. Состояние описывается фразой «… если на него не действует неуравновешенная сила». Пока силы не разбалансированы, то есть пока силы уравновешены, применяется первый закон движения. Эта концепция сбалансированной и неуравновешенной силы будет обсуждаться более подробно позже в Уроке 1.
Предположим, вы наполнили форму для запекания водой до края и прошли по овальной дорожке, пытаясь пройти круг за наименьшее время.Вода имеет тенденцию выливаться из контейнера в определенных местах на трассе. В общем вода пролилась когда:
- контейнер был неподвижен, и вы пытались его переместить
- контейнер находился в движении, и вы пытались его остановить
- : контейнер двигался в одном направлении, и вы попытались изменить его направление.
Вода разливается при изменении состояния движения контейнера.Вода сопротивлялась этому изменению в своем собственном состоянии движения. Вода имела тенденцию «продолжать делать то, что делала». Контейнер был переведен из состояния покоя на высокую скорость на старте; вода осталась в покое и пролилась на стол. Контейнер был остановлен около финиша; вода продолжала двигаться и пролилась через передний край контейнера. Контейнер был вынужден двигаться в другом направлении, чтобы сделать изгиб; вода продолжала двигаться в том же направлении и пролилась через край.Поведение воды во время круга по трассе можно объяснить первым законом движения Ньютона.
Повседневное применение Первого закона Ньютона
Есть много применений первого закона движения Ньютона. Рассмотрим некоторые из ваших опытов в автомобиле. Вы когда-нибудь наблюдали поведение кофе в чашке, наполненной до краев, при запуске автомобиля из состояния покоя или при переводе автомобиля в состояние покоя из состояния движения? Кофе «продолжает делать то, что делает. «Когда вы разгоняете машину из состояния покоя, дорога создает неуравновешенную силу на вращающиеся колеса, чтобы толкать машину вперед; однако кофе (который был в состоянии покоя) хочет оставаться в состоянии покоя. Пока машина ускоряется вперед, кофе остается в в том же положении; впоследствии машина разгоняется из-под кофе, и кофе разливается вам на колени. С другой стороны, при торможении из состояния движения кофе продолжает двигаться вперед с той же скоростью и в том же направлении , в конечном итоге ударившись о лобовое стекло или приборную панель.Кофе в движении остается в движении.
Испытывали ли вы когда-нибудь инерцию (сопротивление изменениям в вашем состоянии движения) в автомобиле, когда он тормозит до полной остановки? Сила дороги на заблокированные колеса обеспечивает неуравновешенную силу для изменения состояния движения автомобиля, но нет неуравновешенной силы, чтобы изменить ваше собственное состояние движения. Таким образом, вы продолжаете движение, скользя по сиденью в поступательном движении. Человек в движении остается в движении с той же скоростью и в том же направлении… если на него не действует неуравновешенная сила ремня безопасности. Да! Ремни безопасности используются для обеспечения безопасности пассажиров, движение которых регулируется законами Ньютона. Ремень безопасности обеспечивает неуравновешенное усилие, которое переводит вас из состояния движения в состояние покоя. Возможно, вы могли бы предположить, что произойдет, если ремень безопасности не используется.
Есть еще много приложений первого закона движения Ньютона.Ниже перечислены несколько приложений. Возможно, вы могли бы подумать о законе инерции и дать объяснения для каждого приложения.
- Кровь приливает к ногам, быстро останавливаясь при езде на спускающемся лифте.
- Головку молотка можно закрепить на деревянной ручке, ударив нижней частью ручки о твердую поверхность.
- Кирпич безболезненно разбивают о руку учителя физики, ударив по нему молотком. (ВНИМАНИЕ: не пытайтесь сделать это дома!)
- Чтобы вытолкнуть кетчуп со дна бутылки с кетчупом, его часто переворачивают вверх дном и толкают вниз на высокой скорости, а затем резко останавливают.
- Подголовники устанавливаются в автомобилях для предотвращения хлыстовых травм при наезде сзади.
- Во время езды на скейтборде (тележке или велосипеде) вы летите вперед от доски при ударе о бордюр, камень или другой объект, который резко останавливает движение скейтборда.
Попробуйте дома |
|
Инерция и масса
Первый закон движения Ньютона гласит, что «объект в состоянии покоя остается в состоянии покоя, а объект в движении остается в движении с той же скоростью и в том же направлении, если только на него не действует неуравновешенная сила.«Объекты имеют тенденцию« продолжать делать то, что они делают ». Фактически, это естественная тенденция объектов сопротивляться изменениям в их состоянии движения. Эта тенденция сопротивляться изменениям в их состоянии движения описывается как инерция .
Инерция: сопротивление объекта изменению состояния движения.
Концепция инерции Ньютона прямо противоположна более популярным представлениям о движении. Доминирующей мыслью до дней Ньютона была естественная тенденция объектов приходить в положение покоя. Считалось, что движущиеся объекты в конечном итоге перестанут двигаться; сила была необходима, чтобы удерживать объект в движении. Но если его предоставить самому себе, движущийся объект в конце концов остановится, а покоящийся объект останется в покое; таким образом, идея, которая доминировала в мышлении людей почти за 2000 лет до Ньютона, заключалась в том, что это была естественная тенденция всех объектов принимать положение покоя.
Галилей и концепция инерции
Галилей, ведущий ученый семнадцатого века, разработал концепцию инерции. Галилей рассуждал, что движущиеся объекты в конечном итоге останавливаются из-за силы, называемой трением. В экспериментах с парой наклонных плоскостей, обращенных друг к другу, Галилей наблюдал, что шар катится по одной плоскости и поднимается по противоположной плоскости примерно на одинаковую высоту. Если бы использовались более гладкие плоскости, мяч катился бы по противоположной плоскости еще ближе к исходной высоте.Галилей рассуждал, что любая разница между начальной и конечной высотами связана с наличием трения. Галилей предположил, что если бы трение можно было полностью исключить, то мяч достиг бы точно такой же высоты.
Галилей далее заметил, что независимо от угла, под которым были ориентированы плоскости, конечная высота почти всегда была равна начальной высоте. Если бы наклон противоположного наклона был уменьшен, то мяч покатился бы на большее расстояние, чтобы достичь этой исходной высоты.
Рассуждения Галилея продолжались — если бы противоположный наклон был поднят почти на угол 0 градусов, то мяч катился бы почти бесконечно, пытаясь достичь исходной высоты. А если бы противоположный наклон вообще не был наклонен (то есть если бы он был ориентирован по горизонтали), то … движущийся объект продолжал бы движение ….
Смотрите!
Другой мысленный эксперимент Галилея объясняется в этом видео с использованием реального эксперимента, выполненного с использованием современного оборудования.
Силы не удерживают предметы в движении
Исаак Ньютон основывается на размышлениях Галилея о движении. Первый закон движения Ньютона гласит, что сила , а не , необходима для удержания объекта в движении. Переместите книгу по столу и посмотрите, как она переместится в исходное положение. Книга, движущаяся на столешнице, не приходит в положение покоя из-за отсутствия силы ; скорее это присутствие силы, которая является силой трения, которая приводит книгу в исходное положение.В отсутствие силы трения книга продолжала бы движение с той же скоростью и направлением — вечно! (Или, по крайней мере, до конца столешницы.) Для удержания движущейся книги в движении сила не требуется. На самом деле это сила, которая останавливает книгу.
Масса как мера инерции
Все объекты сопротивляются изменениям в своем состоянии движения.У всех объектов есть эта тенденция — у них есть инерция. Но имеют ли некоторые объекты большую тенденцию сопротивляться изменениям, чем другие? Абсолютно да! Тенденция объекта сопротивляться изменениям в его состоянии движения зависит от массы. Масса — это величина, равная исключительно , зависящая от инерции объекта. Чем больше инерция у объекта, тем больше у него масса. Более массивный объект имеет большую тенденцию сопротивляться изменениям в своем состоянии движения.
Предположим, что на лекционном столе по физике лежат два, казалось бы, одинаковых кубика.Однако один кирпич состоит из раствора, а другой — из пенополистирола. Не поднимая кирпичей, как вы могли определить, какой кирпич был из пенополистирола ? Вы можете дать кубикам такой же толчок, чтобы изменить их состояние движения. Кирпич с наименьшим сопротивлением — это кирпич с наименьшей инерцией — и, следовательно, кирпич с наименьшей массой (т. Е. Кирпич из пенополистирола ).
Обычная физическая демонстрация основана на том принципе, что чем массивнее объект, тем сильнее он сопротивляется изменениям в своем состоянии движения.Демонстрация выглядит следующим образом: на голову учителя кладут несколько массивных книг. Поверх книг кладут деревянную доску и молотком забивают в доску гвоздь. Из-за большой массы книг сила удара молотка имеет достаточное сопротивление (инерция). Об этом свидетельствует тот факт, что учитель не чувствует удара молотка. (Конечно, эта история может объяснить многие из наблюдений, которые вы ранее делали относительно своего «странного учителя физики».) Обычный вариант этой демонстрации включает в себя разбивание кирпича о руку учителя быстрым ударом молотка.Массивные кирпичи сопротивляются силе, и рука не болит. (ВНИМАНИЕ: не пробуйте эти демонстрации на hom
.
Смотрите!
Инструктор по физике объясняет свойство инерции с помощью демонстрации физики.
Проверьте свое понимание
1. Представьте себе место в космосе , вдали от всех гравитационных и фрикционных влияний. Предположим, вы посетили это место (представьте себе) и бросили камень. Скала будет
а. постепенно прекращать.
г. продолжать движение в том же направлении с постоянной скоростью.
2. Объект весом 2 кг движется по горизонтали со скоростью 4 м / с.Какая полезная сила требуется, чтобы удерживать объект в движении с этой скоростью и в этом направлении?
3. Мак и Тош спорят в кафетерии. Мак говорит, что если он бросит Jell-O с большей скоростью, у него будет большая инерция. Тош утверждает, что инерция зависит не от скорости, а, скорее, от массы. С кем ты согласен? Объяснить, почему.
4.Предположим, вы находитесь в космосе в невесомой среде , потребуется ли сила, чтобы привести объект в движение?
5. Фред большую часть воскресенья после обеда проводит на диване, наблюдая за профессиональными футбольными матчами и потребляя много еды. Какое влияние (если вообще есть) эта практика оказывает на его инерцию? Объяснять.
6.Бена Туклоуз преследует по лесу лось, которого он пытался сфотографировать. Огромная масса лосей-быков чрезвычайно устрашает. Тем не менее, если Бен сделает зигзагообразный узор в лесу, он сможет использовать большую массу лося в своих интересах. Объясните это с точки зрения инерции и первого закона движения Ньютона.
7. Два кирпича лежат на краю лабораторного стола.Ширли Шешорт встает на цыпочки и замечает два кирпича. У нее возникает сильное желание узнать, какой из двух кирпичей самый массивный. Поскольку Ширли препятствует вертикальному положению, она не может подняться достаточно высоко и поднять кирпичи; однако она может дотянуться достаточно высоко, чтобы толкнуть кирпичи. Обсудите, как процесс толкания кирпичей позволит Ширли определить, какой из двух кирпичей самый массивный. Какую разницу заметит Ширли и как это наблюдение может привести к необходимому выводу?
Видеоурок по физике — Первый закон Ньютона
Видеоурок по первому закону движения Ньютона
Видеоруководство по Первому закону Ньютона описывает два утверждения, связанных с Первым законом Ньютона, и одно условие, при котором эти утверждения верны.Вводится понятие инерции. Видеоурок отвечает на следующие вопросы:
- Какие два утверждения и одно условие сформулированы в первом законе Ньютона?
- Что означает первый закон Ньютона, когда дело доходит до предсказания движения объекта?
Чтобы повысить эффективность обучения, The Physics Classroom предоставил следующие инструменты:
Примечания к уроку
Заметки к уроку предназначены для распечатки и использования при просмотре видео.Они структурированы так, чтобы студенты могли следить за видео, записывать некоторые заметки и оставлять видео с документом, который можно назвать продолжением их обучения. Примечания к уроку доступны в формате PDF. Разрешается распечатать заметки или включить на них ссылку из системы управления обучением.
Просмотр заметок к уроку
Дополнительные и сопутствующие средства обучения
Обучение требует усилий. Просмотр видео — относительно пассивное занятие. Одно дело — послушать видео, представленное человеком, разбирающимся в материале.Но совсем другое дело — применить информацию из видео, чтобы лично понять материал. На этой странице перечислены различные инструменты, которые можно использовать для применения нового обучения. Инструменты включают те, которые могут использоваться учениками, и те, которые могут использоваться учителями со своими учениками в классе. Связанные ресурсы также включены в эти инструменты.
Просмотреть дополнительные средства обучения
Ресурсы для учителей
Так ты этому учишь? Может, мы сможем помочь… мы занимаемся этим некоторое время и у нас есть несколько ресурсов, которые могут вам пригодиться. Посетите страницу ресурсов для учителей и узнайте о некоторых инструментах, которые помогут вам преподавать и разрабатывать уроки по этой теме.
Просмотр ресурсов учителя
Слайды из видеоурока
Некоторым студентам полезно просматривать слайды презентации. Мы размещаем их здесь, на нашем сайте. Анимации, присутствующие в видео, преобразуются в одно статичное экранное изображение на слайдах.
Просмотреть слайды
Вы можете просмотреть это видео на YouTube или здесь, на нашем сайте:
Посмотреть видеоурок
Помогите нам Помогите вам
Это видео является частью нашей серии видеоуроков по законам Ньютона. Другие видеоуроки вы можете найти здесь, на нашем сайте. Чтобы получать самые свежие материалы из нашей серии видеоуроков по физике, мы предлагаем пользователям подписаться на канал The Physics Classroom на YouTube. Каждые лайков и каждые подписки помогает продвигать наше видео… так что спасибо за любую помощь, которую вы можете нам дать. Когда вы помогаете нам, мы можем помочь вам больше.
Первый закон движения Ньютона
| Эта страница предназначена для учащихся колледжей, старших и средних школ. Для младших школьников более простое объяснение информации на этой странице: доступно на Детская страница. |
Сэр Исаак Ньютон впервые представил свои три закона движения
в «Principia Mathematica Philosophiae Naturalis» 1686 г. Его первый закон
заявляет, что каждый объект будет оставаться в покое или в равномерном движении по прямой
линия, если она не вынуждена изменить свое состояние под действием внешней силы.
Обычно это определение инерции . Ключевой момент здесь
состоит в том, что при наличии нетто-силы в результате несбалансированной
силы, действующие на объект (если все внешние силы нейтрализуют друг друга),
тогда объект будет поддерживать постоянную скорость .Если эта скорость равна нулю,
тогда объект остается в покое. А если приложить дополнительную внешнюю силу,
скорость изменится из-за силы. Величина изменения скорости
определяется вторым законом движения Ньютона.
Есть много прекрасных примеров первого закона Ньютона, относящегося к аэродинамике.
Движение
самолет
Когда пилот меняет положение дроссельной заслонки двигателя, описывается первым законом.Движение
мяч
падая в атмосфере,
или
модель ракеты
выбросы в атмосферу — оба примера первого закона Ньютона.
Движение
летающий змей
при смене ветра также можно описать первым законом.
Мы создали отдельные страницы, которые более подробно описывают каждый из этих примеров.
чтобы помочь вам понять этот важный физический принцип.
Действия:
Экскурсии с гидом
Навигация..
- Руководство для начинающих Домашняя страница
Законы движения Ньютона
| Эта страница предназначена для учащихся колледжей, старших и средних школ. Для младших школьников более простое объяснение информации на этой странице: доступно на Детская страница. |
Движение самолета по воздуху можно объяснить и описать с помощью
физические принципы, открытые более 300 лет назад сэром Исааком Ньютоном. Ньютон работал
во многих областях математики и физики. Он разработал теории гравитации
в 1666 году, когда ему было всего 23 года. Примерно двадцать лет спустя, в 1686 году, он
представил свои три закона движения в «Principia Mathematica Philosophiae»
Naturalis.»Законы показаны выше, и применение этих законов
аэродинамике даны на отдельных слайдах.
Первый закон Ньютона гласит, что каждый
объект будет оставаться в покое или в равномерном движении по прямой линии
если не вынужден изменить свое состояние под действием внешнего
сила. Обычно это определение инерции .
Ключевым моментом здесь является то, что если нет действующей силы на
объект (если все внешние силы нейтрализуют друг друга), то
объект будет поддерживать постоянную скорость .Если эта скорость равна нулю,
тогда объект остается в покое. Если приложена внешняя сила,
скорость изменится из-за силы.
Второй закон объясняет, как скорость
объект меняется, когда на него действует внешняя сила.
Закон определяет, что сила равна изменению импульса (масса
умноженная на скорость) за изменение во времени. Ньютон также разработал математическое исчисление,
и «изменения», выраженные во втором законе, наиболее точно
определяется в дифференциале
формы.(Расчет также можно использовать для определения изменений скорости и местоположения
испытываемый объектом, подвергнутым внешней силе.) Для объекта с
постоянной массы м , второй закон гласит, что
force F это продукт
массы объекта и его ускорения a :
F = m * a
Для внешнего применения
силы, изменение скорости зависит от массы объекта.Сила будет
вызвать изменение скорости; и аналогично, изменение скорости приведет к
сила. Уравнение работает в обоих направлениях.
Третий закон гласит, что для каждого действия (силы)
в природе есть равная и противоположная реакция. Другими словами, если объект
A оказывает силу на объект B, затем объект B также оказывает такое же усилие на объект
A. Обратите внимание, что силы действуют на разные объекты. Третий закон может
использоваться для объяснения создания подъемной силы крылом
и создание тяги реактивным двигателем.
Вы можете просмотреть короткий
кино
из «Орвилла и Уилбура Райтов», объясняющих, как законы движения Ньютона
описал полет своего самолета. Файл фильма может
можно сохранить на свой компьютер и просмотреть как подкаст на проигрывателе подкастов.
Действия:
Экскурсии с гидом
Навигация..
- Руководство для начинающих Домашняя страница
Примеры инерции
Инерцию лучше всего объяснил сэр Исаак Ньютон в его первом законе движения. В основном, закон движения гласит, что неподвижный объект остается в покое, а объект в движении продолжает движение до тех пор, пока на него не действует внешняя сила. Рассмотрим несколько примеров инерции.
Закон инерции
Когда дело доходит до законов движения, инерция — одна из величайших составляющих.Инерция сопротивляется изменению движения. Объекты хотят оставаться в покое или движении, если только внешняя сила не вызовет изменения. Например, если вы катите мяч, он будет продолжать катиться, если трение или что-то еще не остановит его силой. Вы также можете подумать о том, как ваше тело продолжает двигаться вперед, когда вы нажимаете на тормоз на велосипеде. Инерция бывает разных типов, проверьте их.
Типы инерции
По инерции не бывает одного типа. Вместо этого вы найдете три разных типа инерции, включая:
- Инерция покоя — объект остается на месте, и он будет оставаться там, пока вы или кто-то другой не переместит его.(т.е. частицы пыли остаются в покое, пока вы не встряхнете ковер.)
- Инерция движения — Объект будет двигаться с той же скоростью, пока на него не подействует сила. (т.е. тело движется вперед, когда автомобиль останавливается.)
- Инерция направления — Объект будет продолжать двигаться в том же направлении, если на него не действует сила. (т. е. движение тела в сторону при резком повороте автомобиля.)
Читать об инерции — это здорово, но чтобы понять один из законов движения Ньютона, вам нужно взглянуть на примеры.
Примеры инерции покоя
Теперь, когда вы знаете, что такое инерция покоя, рассмотрим несколько примеров.
- Если быстро потянуть, скатерть можно вынуть из-под посуды. Посуда имеет тенденцию оставаться неподвижной до тех пор, пока трение от движения скатерти не слишком велико.
- Если в остановившуюся машину ударит движущийся автомобиль сзади, пассажиры внутри могут получить хлыстовые травмы в результате движения тела вперед и отставания головы.Голова испытывает инерцию.
- Воздушный шар в машине будет казаться движущимся, когда машина движется вперед, но на самом деле воздушный шар пытается остаться на том месте, где он был, это только машина, которая движется.
- Когда автомобиль резко ускоряется, водители и пассажиры могут чувствовать, как будто их тела движутся назад. На самом деле инерция заставляет тело оставаться на месте, пока машина движется вперед.
- Если учетная карточка помещена на стакан с пенни поверх нее, учетная карточка может быть быстро удалена, в то время как пенни падает прямо в стакан, поскольку пенни демонстрирует инерцию.
- Снимая пластырь, лучше потянуть его быстро. Ваша кожа будет оставаться в покое из-за инерции, и сила сдергивает пластырь.
Примеры инерции движения
Объекты в движении остаются в движении или хотят, как в этих примерах.
- Ремни безопасности затягиваются в автомобиле, когда он быстро останавливается.
- Людям в космосе труднее остановиться из-за отсутствия силы тяжести, действующей против них.
- Во время игры в футбол игрок захватили, и его голова ударилась о землю.Удар останавливает его череп, но его мозг продолжает двигаться и поражает внутреннюю часть черепа. Его мозг показывает инерцию.
- Если машину врезать прямо в кирпичную стену, она остановится из-за силы, приложенной к ней стеной. Однако водителю требуется сила, чтобы его тело не двигалось, например, ремень безопасности. В противном случае инерция заставит его тело продолжать двигаться с исходной скоростью, пока на его тело не воздействует какая-то сила.
- Когда бейсбольный мяч брошен, он продолжает двигаться вперед, пока на него не действует сила тяжести.Чем больше сила броска, тем тяжелее воздействовать на него гравитации.
- Хоккейная шайба будет продолжать скользить по льду, пока на нее не будет воздействовать внешняя сила.
- Если вы крутите педали на велосипеде, если вы перестаете крутить педали, велосипед продолжает движение, пока трение или гравитация не замедлит его.
- Автомобиль будет двигаться, даже если вы выключите двигатель.
- Если мяч упал на наклонную поверхность и вы отпустите его, сила тяжести заставит его скатиться по склону.Он инерционен, и если в нижней части склона есть ровная площадка, он продолжит движение.
- При входе в здание через вращающуюся дверь, инерция позволит двери ударить вас в спину, если вы не уйдете с дороги.
- Если вы катите тележку с чем-то сверху и ударите что-то, что заставляет тележку остановиться, то, что находится сверху, может упасть.
- Труднее остановить большое транспортное средство, например автобус, чем меньшее транспортное средство, например мотоцикл. У большего объекта больше инерции.
- Сотрясение мозга происходит из-за того, что ваш мозг все еще движется, а внешняя часть черепа остановлена. Это то, что вызывает травму.
- Если вы находитесь в поезде, а поезд движется с постоянной скоростью, подброшенная в воздух игрушка поднимется вверх, а затем опустится. Это потому, что у игрушки есть инерция, как у поезда и у вас.
- Если автомобиль движется вперед, он будет продолжать движение вперед, если только трение или тормоза не мешают его движению.
Инерция направления
Просмотрите, как объекты остаются в одном направлении, если не применяется другая сила.Изучите примеры инерции направления.
- Судно на воздушной подушке может быть проблемой для манипулирования, потому что, в отличие от автомобилей, у них нет такого же уровня трения, поэтому инерция заставляет судно на воздушной подушке продолжать движение в том же направлении, не останавливаясь и не поворачиваясь.
- Внезапная остановка тележки с предметом наверху приводит к его падению. Инерция вызывает это, заставляя объект продолжать движение в том направлении, в котором он был.
- Если вы прыгаете с движущегося автомобиля или автобуса, ваше тело все еще движется в направлении транспортного средства.Когда ваши ноги касаются земли, земля воздействует на ваши ноги, и они перестают двигаться. Вы упадете, потому что верхняя часть вашего тела не остановилась, и вы упадете в том направлении, в котором двигались.
- Когда вы перемешиваете кофе или чай и останавливаетесь, вихревое движение продолжается по инерции.
- Объекты, которые выходят на орбиту вокруг Земли, например спутники, продолжают двигаться по своей траектории за счет инерции.
- Если бросить камень прямо вверх, он не изменится со своего направления.
- Инерция позволяет фигуристам скользить по льду по прямой.
- Если дует ветер, ветки дерева двигаются. Кусок спелого плода, упавший с дерева, по инерции упадет в направлении ветра.
- Запущены космические зонды, чтобы миновать атмосферу Земли. Затем они движутся по инерции.
Понимание инерции
Посмотрите, сможете ли вы распознать инерцию, когда она возникает в течение дня.Вы можете быть удивлены тем, как часто вы замечаете моменты инерции в своей жизни.
5.4: Применение законов Ньютона – Physics LibreTexts
Применение второго закона Ньютона несложно, как только все силы, действующие на объект, были идентифицированы. Таким образом, перед тем, как продолжить, вам следует убедиться, что вы тратите большую часть своего времени на рисование хорошей и полной диаграммы свободного тела.
Второй закон Ньютона – это векторное уравнение, которое связывает векторную сумму всех сил, действующих на объект, и вектор ускорения объекта. Это соответствует одному скалярному уравнению на компонент вектора.
\ [\ begin {выровнено} \ sum \ vec F & = m \ vec a \\ \ sum F_x & = ma_x \\ \ sum F_y & = ma_y \\ \ sum F_z & = ma_z \ end {выровнено} \ ]
Чтобы использовать Второй закон Ньютона, нам необходимо ввести систему координат, чтобы мы могли работать с компонентами векторов (силы и ускорение) в этой системе координат. Обычно хорошим выбором является система координат, в которой ось \ (x \) (или \ (y \)) параллельна вектору ускорения. На рисунке \ (\ PageIndex {10} \) показана диаграмма свободного тела из блока \ (m_1 \) из предыдущего примера (, пример 5.4.4 ) наряду с хорошим выбором системы координат.
Чтобы применить Второй закон Ньютона с использованием диаграммы свободного тела и системы координат из рисунка \ (\ PageIndex {10} \), мы сначала выписываем весь вектор, а затем определяем их \ (x \) и \ (y \ ) компоненты. Векторы силы: \ [\ begin {выровнены} \ vec T & = T \ hat x + 0 \ hat y \\ \ vec f_ {k1} & = – f_ {k1} \ hat x + 0 \ hat y \ \ \ vec F_ {g1} & = m_1g (\ sin \ theta \ hat x- \ cos \ theta \ hat y) \\ \ vec N_1 & = 0 \ hat x + N_1 \ hat y \ end {выровнено} \] Мы теперь можно записать компонент \ (x \) Второго закона Ньютона: \ [\ begin {align} \ sum F_x = T-f_ {k1} -F_ {g1} \ sin \ theta & = m_1 a \\ \ поэтому T-f_ {k1} -F_ {g1} \ sin \ theta & = m_1 a \ end {align} \], где мы отмечаем, что нормальная сила не имеет компонента в направлении \ (x \).Компонент \ (y \) Второго закона Ньютона для массы \ (m_1 \) задается следующим образом: \ [\ begin {align} \ sum F_y = N_1-F_ {g1} & = 0 \\ \, следовательно, N_1-F_ { g1} & = 0 \ end {align} \], где отметим, что силы натяжения и трения не имеют компоненты \ (y \). Два уравнения, которые мы получили выше для \ (x \) и \ (y \), полностью определяют движение блока \ (m_1 \), если все величины известны 3 .
В следующем примере показано, как написать Второй закон Ньютона для системы из двух блоков.
Пример \ (\ PageIndex {5} \)
Рисунок \ (\ PageIndex {11} \): Два блока, соединенных безмассовой струной и безмассовым шкивом.Оба блока ускоряются.Блок массы \ (m_1 \) помещается на наклон, составляющий угол \ (\ theta \) с горизонтом. Блок массы \ (m_1 \) соединен безмассовой струной через безмассовый шкив со вторым блоком массы \ (m_2 \), который опирается на горизонтальную поверхность. Блоки ускоряются таким образом, что блок массы \ (m_1 \) ускоряется вниз по склону, как показано на рисунке \ (\ PageIndex {5} \). Коэффициент кинетического трения между любым блоком и поверхностью, на которой он опирается, равен \ (\ mu_k \).Напишите второй закон Ньютона для обоих блоков.
Решение :
Сначала мы определяем силы, действующие на каждую массу (каждый блок). По массе \ (m_1 \) силы:
- \ (\ vec F_ {g1} \), его вес.
- \ (\ vec N_1 \), нормальная сила, создаваемая наклонной плоскостью.
- \ (\ vec f_ {k1} \), сила кинетического трения, создаваемая наклонной плоскостью. Сила направлена в противоположном направлении движения, и ее величина определяется выражением \ (f_ {k1} = \ mu_kN_1 \).
- \ (\ vec T_1 \), сила натяжения струны.
По массе \ (m_2 \) силы:
- \ (\ vec F_ {g2} \), его вес.
- \ (\ vec N_2 \), нормальная сила от горизонтальной поверхности.
- \ (\ vec f_ {k2} \), сила кинетического трения, создаваемая горизонтальной поверхностью. Сила направлена в противоположном направлении движения, и ее величина определяется выражением \ (f_ {k2} = \ mu_kN_2 \).
- \ (\ vec T_2 \), сила натяжения струны.Эта сила имеет ту же величину, что и сила натяжения \ (\ vec T_1 \), действующая на массу \ (m_1 \), потому что шкив безмассовый.
Затем мы можем приступить к построению диаграммы свободного тела для каждой массы и использовать ее для записи Второго закона Ньютона. Для массы \ (m_1 \) диаграмма свободного тела показана на рисунке \ (\ PageIndex {12} \). Мы выбрали систему координат, в которой ось \ (x \) параллельна ускорению блока, а ось \ (y \) направлена вверх и перпендикулярна оси \ (x \), как показано.
Рисунок \ (\ PageIndex {12} \): диаграмма свободного тела для \ (m_ {1} \).Для \ (m_1 \) мы можем записать Второй закон Ньютона, начиная с компонентов \ (x \): \ [\ begin {align} \ sum F_x = F_ {g1} \ sin \ theta-f_ {k1} – T_1 & = m_1a_1 \\ \ поэтому m_1 g \ sin \ theta – \ mu_k N_1 – T_1 & = m_1 a_1 \ end {align} \], где во второй строке мы использовали величину веса (\ (F_ {g1 } = m_1g \)) и силы кинетического трения (\ (f_ {k1} = \ mu_kN_1 \)). Для компонента \ (y \) Второго закона Ньютона, в котором ускорение не имеет компонента, мы имеем: \ [\ begin {align} \ sum F_y = N_1 – F_ {g1} \ cos \ theta & = 0 \\ \ поэтому N_1 = m_1g \ cos \ theta \ end {align} \], что показывает нам, что величина нормальной силы может быть легко выражена через вес (\ (F_ {g1} = m_1g \)) и угол уклона.
Для \ (m_2 \) мы можем действовать примерно так же, выбирая другую систему координат, поскольку вектор ускорения для \ (m_2 \) указывает в другом направлении (нам не нужно выбирать другую систему координат , но мы можем, если обнаружим, что это упрощает задачу). Диаграмма свободного тела для \ (m_2 \) показана на рисунке \ (\ PageIndex {13} \) вместе с выбранной нами системой координат.
Рисунок \ (\ PageIndex {13} \): диаграмма свободного тела для \ (m_ {2} \).Начнем с того, что выпишем компонент \ (x \) Второго закона Ньютона для \ (m_2 \): \ [\ begin {align} \ sum F_x = T_2 – f_ {k2} & = m_2 a_2 \\ \, следовательно, T_2 – \ mu_k N_2 = m_2 a_2 \ end {align} \] где мы снова выразили кинетическую силу трения, используя нормальную силу и коэффициент кинетического трения.Компонент \ (y \) Второго закона Ньютона дает: \ [\ begin {align} \ sum F_y = F_ {g2} -N_2 & = 0 \\ \, следовательно, N_2 = m_2g \ end {align} \], где снова, мы выразили вес через массу и \ (g \) и обнаружили, что нормальная сила имеет ту же величину, что и вес.
Теперь, когда мы написали Второй закон Ньютона для каждой массы , мы можем написать все четыре уравнения, которые мы получили, чтобы описать систему двух масс . Следует также отметить, что величина сил натяжения одинакова для двух масс (\ (T_1 = T_2 = T \)), и что, поскольку массы связаны струной, величина их векторов ускорения одинакова. (\ (а_1 = а_2 = а \)).Используя это, мы можем описать всю систему следующими 4 уравнениями: \ [\ begin {align} m_1 g \ sin \ theta – \ mu_k N_1 – T & = m_1 a \\ N_1 = m_1g \ cos \ theta \\ T – \ mu_k N_2 = m_2 a \\ N_2 = m_2g \ end {выровнено} \] Из переменных выше (\ (m_1 \), \ (m_2 \), \ (\ mu_k \), \ (T \), \ (N_1 \), \ (N_2 \), \ (a \)), достаточно указать все, кроме четырех, чтобы полностью описать движение системы. Например, если указать две массы и коэффициент кинетического трения, можно определить все другие переменные.
Этот план урока особенно эффективен f
Законы НьютонаПОДГОТОВКА: Демонстрация Ньютона Три закона движения и закон тяготения
ЗАДАЧИ:
Студенты:
1) приведите примеры каждого из Три закона Ньютона в повседневной жизни2) визуализировать и различать разницу между прямой и обратной пропорцией по формуле F = ma
3) понять, как гравитационный закон влияет на приливы на земле
4) вычислить фактическую гравитационную сила между солнцем и землей и луной и землей, чтобы заключить, что имеет более сильное влияние
Справочная информация
Исаак Ньютон резюмировал движение тремя законами.Сегодня мы принимаем эти законы как должное, когда вырастаем, предполагая, что они верны. Мы не осознают, через какие трудности пришлось пройти ученым, пытаясь понять мир вокруг них. Следующие упражнения используют мозговой штурм, обсуждение, и простые лаборатории, чтобы проиллюстрировать законы.
Три закона Ньютона:
1) Объект, который движется с постоянной скорость или в состоянии покоя не изменяет свое состояние, если только сила действует на него.2) Ускорение объекта увеличивается по мере увеличения силы, вызывающей ускорение, увеличивается, когда масса постоянна.
3) Для каждой силы существует равная и противоположная сила.
ДЕЯТЕЛЬНОСТЬ № 1:
Первый закон Ньютона 20 мин.МАТЕРИАЛЫ: МЕЛ И ДСП
ПРОЦЕДУРА:
1) Мозговой штурм повседневных примеров первого закона.
2) Представьте студентам лекцию, включая следующие необходимая справочная информация:
Незадолго до времен Ньютона Галилей работал с идея ускорения.Галилей мог только догадываться о времени, поскольку точный часы не были изобретены. Вот почему он гладко катал металлические шары пандусы. Поскольку он заметил, как мяч замедляется, катясь по полу, он пришел к выводу, что причиной было трение. Таким образом, трение было ответственным за идею о том, что движущиеся объекты естественным образом останавливаются. Но “отдых” это всего лишь один из видов постоянной скорости. Понятие инерции и Ньютона Из этого понимания возник 1-й закон.
3) Используйте некоторые из следующих примеров, чтобы объяснить студенты, как первый закон Ньютона проявляется в повседневных событиях:
а) машина внезапно останавливается, и вы напрягаетесь ремень безопасностиб) при езде на лошади лошадь внезапно останавливается и вы летите над его головой
в) маг вытаскивает скатерть из-под стол, полный блюд
г) сложность толкания мертвой машины
e) боулинг на стриженной и свернутой лужайке стихи и необрезанный газон
е) автомобиль поворачивает налево, и кажется, что вы скользите направо
ДЕЯТЕЛЬНОСТЬ № 2:
Отношения в Ньютоне Второй закон 20 минутМАТЕРИАЛЫ: МЕТРОВЫЕ ПАЛКИ, УКАЗАТЕЛЬ КАРТЫ, ЛЕНТА, МАРКЕРЫ
ПРОЦЕДУРА:
1) Второй закон Ньютона имеет дело с F = MA.Когда написано A = F / M on видит, что ускорение будет напрямую зависеть от силы применяется и обратно пропорционально массе тела. Поскольку у студентов проблемы с этими терминами им может помочь простое наглядное пособие.
2) Возьмите три каталожные карточки и напишите A, F и M на них, а затем прикрепите карточку F к метке на отметке 50 см, чтобы что он свисает. Затем прикрепите карточку A на 0 см и карточку M к краю. Отметка 100 см.
3) Объясните ученикам, что если сила постоянна (либо переверните карту вверх, либо накройте ее рукой), при разгоне увеличивается (поднимите конец измерителя на 0 см под углом 30), масса должна снижаться.
4) Обратите внимание, что конец 100 см теперь наклонен вниз. Этот показывает обратную пропорциональную зависимость.
5) Теперь накройте рукой карту ускорения. Когда сила или масса увеличиваются или уменьшаются, другая переменная будет делать такой же. Это показывает прямую пропорциональную зависимость.
6) Наконец, проделайте то же самое с картой M.
7) Вставьте числа и проработайте несколько простых F = MA проблемы.
8) Используйте измерительную ручку, чтобы визуализировать, что ответ будет (больше или меньше).Наконец, проведите мозговой штурм по повседневным приложениям, некоторые примеры перечислены ниже.
а) при ударе по бейсбольному мячу удар сильнее, чем быстрее летит мячб) ускорение или замедление автомобиля
в) Позиционирование футболистов – массовых игроков на линии с более легкими (быстрее разгоняются) игроками на заднем поле
г) груженый по сравнению с незагруженным грузовиком
ДЕЯТЕЛЬНОСТЬ № 3:
Постоянное увеличение силы Скорость 25 минутМАТЕРИАЛЫ: СКЕЙТБОРД И ПРУЖИНА МАСШТАБ
ПРОЦЕДУРА:
1) Попросите ученика принести скейтборд.
2) Попросите одного ученика встать на скейтборд на перед классом и держитесь за один конец пружинной шкалы.
3) Другой ученик должен вывести первого ученика на постоянная сила 10 ньютонов.
4) Наблюдайте за скоростью учеников, пока они силовая постоянная.
5) Объясните, что это показывает прямую связь
между силой и ускорением.
ДЕЯТЕЛЬНОСТЬ № 4:
Третий закон Ньютона 10 минутМАТЕРИАЛЫ: МЕЛ И ДСП
ПРОЦЕДУРА:
1) Мозговой штурм повседневных примеров третьего закона с класс.Ниже приведены некоторые примеры:
а) ракеты покидают Землю – многие физики из девятнадцати сотен (время Годдарда) сказали, что ракеты никогда не могут покинуть землю. Обсудите, как космический корабль летает в космосе.б) стреляют из огнестрельного оружия – обсудите, почему они стреляют пропорционально к размеру пули. Почему приклад у карабина такой большой? Что произойдет ли, если ложа ружья вернется к остроконечной форме?
в) две машины ударились головой
г) космонавты в космосе
д) пул или бильярд
е) выпрыгивание из лодки на причал
г) оросители вращающиеся
ДЕЯТЕЛЬНОСТЬ № 5:
Полеты на воздушных шарах 50 минутМАТЕРИАЛЫ: 3 ДЛИННЫХ ШАРА, 1 ПЛАСТИКОВАЯ СОЛОМА, 60 СМ (ИЛИ БОЛЕЕ) ИЗ ТОНКОЙ ПРОВОЛОКИ ИЛИ ЛЕСКИ, ЛЕНТА, МОДЕЛЬ САМОЛЕТ (BALSA WOOD), МАРКЕР
ПРОЦЕДУРА:
1) Попросите учащихся следовать перечисленным процедурам ниже:
а) Воздушные шары надуть, закрепить резиной. полосы и обозначьте их A, B и C.2) Попросите учащихся ответить на следующие вопросы:b) Прикрепите соломинку продольно к баллону B и запустите проволока через соломинку.
c) Приклейте баллон C к верхней части фюзеляжа модель самолета, поместив отверстие воздушного шара в сторону хвостовой части самолета.
d) Очень медленно ослабьте резиновую ленту на баллоне A. и запишите скорость и направление движения.
e) Теперь, на воздушном шаре B, пусть партнер держится за каждый конец. протяните проволоку через соломинку и держите ее плотно.
Быстро разрежьте резиновую ленту и наблюдайте за воздушным шаром.Запишите наблюдения.
е) Нарисуйте эскиз, показывающий направление воздуха в воздушный шар переместился. Также на этом же эскизе нарисуйте схему того, как воздушный шар двигался по проволоке.
g) Чтобы проверить воздушный шар C, попросите партнера держать самолет. слабо. Обрежьте резиновую ленту, когда ваш партнер выпустит самолет. Записывать полет. Вы можете проводить соревнования олимпийского типа между лабораториями. партнеры.
Совет: попробуйте воздушные шары разной формы. Удлиненный должен работать лучше всех. Также могла быть спроектирована ракета туда и обратно.
а) Опишите реакцию резиновой ленты когда его разрезали.б) Опишите полет воздушного шара Б.
c) Какая сила двигала воздушный шар B?
d) Почему Воздушный шар B двигался иначе, чем Воздушный шар А?
e) Почему шары B и C двигались быстрее чем воздушный шар А?
е) Сформулируйте третий закон Ньютона и объясните, как это действие иллюстрирует это.
ДЕЯТЕЛЬНОСТЬ № 6:
Обратный мир 20-30 минутМАТЕРИАЛЫ: КАРАНДАШ И БУМАГА
ПРОЦЕДУРА:
1) Попросите учащихся написать статью на 2–3 страницы. художественный рассказ, описывающий, какие различия мы наблюдали бы, если бы из трех законов Ньютона были верны на Земле.Например, ружья не иметь отдачу, и масса пушки не должна быть больше пушки мяч. Вас также не оттолкнет на сиденье при ускорении. в машине.
2) В качестве альтернативы вы можете сделать устное
мозговой штурм о том, как все было бы на земле, если бы мы жили в
обратное законам Ньютона.
ДЕЯТЕЛЬНОСТЬ № 7:
Что действительно вызывает приливы 35 минутМАТЕРИАЛЫ: МЕЛ И ДСП
Справочная информация о мероприятииГравитационная сила Луны и Солнца важная роль в приливах.Когда солнце, земля и луна находятся на прямой линии, их совокупное гравитационное притяжение вызывает очень высокие и низкие приливы. известные как весенние приливы. Это происходит всякий раз, когда есть полнолуние или новолуние. Приливные приливы образуются, когда Солнце, Земля и Луна образуют прямую угол, вызывающий полумесяц. Вопрос в том, что, солнце или луна, имеет более сильное гравитационное притяжение?
ПРОЦЕДУРА:
1) Используя формулу тяготения Ньютона, получим студенты изучают (домашнее задание) необходимые данные и выполняют классный проект в доска делает расчеты.
2) В зависимости от способностей студентов каждый
студент может делать свои собственные расчеты.
Масса Земли 5,98 x 10 24 кг
Масса Солнца 1,98 x 10 30 кг2) Объясните студентам, что солнце, следовательно, должно имеют большую тяговую силу. Приливная выпуклость, создаваемая Солнцем, составляет 46%. из того, что произведено Луной. Приливы в первую очередь вызваны гравитационным притяжение луны. Помимо океанских приливов, Луна также вызывает приливы и отливы. твердое тело земли целых 25 см. Эти земные приливы очень трудно наблюдать или обнаруживать.Вода на краю земли рядом с Луна тянется к Луне с большей силой, чем средняя, вода на противоположной стороне тянется с силой меньше средней. Кроме того, вращение земли помогает поднять приливную выпуклость сбоку от Луна. Таким образом, в воде появляются две выпуклости по разные стороны от берега. земной шар. Приливные выпуклости возникают на 3 перед линией, проходящей между центрами. Земли и Луны.Масса Луны 7,36 x 10 22 кг
Расстояние от Земли до Солнца 1,50 x 10 11 м
Расстояние от Земли до Луны 3,84 x 10 8 м
F = G м 1 м 2 где G = 6,67 x 10 -11 м 3
d 2 кг сек 2
1) Солнце к Земле
F = 6.67 x 10 -11 м 3 x 1,98 x 10 30 кг x5,98 x 10 24 кг
кг · сек 2 (1,55 x 10 11 м) 2
F = 3,51 x 10 22 м / с 2
2) Луна к Земле
F = 6,67 x 10 -11 м 3 x 7,36 x 10 22 кг x 5,98 x 10 24 кг
кг / сек 2 (3.84 x 10 8 м) 2
F = 1,99 x 10 19 м / с 2
Тяга между Солнцем и Землей около 180. раз сильнее, чем притяжение между луной и землей.Итак, наши расчеты верны, но почему солнце не вызывает приливов в 180 раз больше? Так как на большом расстоянии солнца от земли, нет большой разницы на расстояниях от Солнца до ближней и дальней стороны Земли. Это означает что нет большой разницы в гравитационном притяжении солнца на ближайшем к нему океане и на самом дальнем от него. Относительно небольшая разница в тягах на противоположных сторонах земли незначительно удлиняет форму земли. Таким образом, Солнце производит приливные выпуклости меньше, чем те из луны.
Наклон земли также влияет на приливы и отливы. Наклон
приводит к тому, что 2 ежедневных прилива, наблюдаемых в большей части океана,
быть неравной по высоте.
ДЕЯТЕЛЬНОСТЬ № 8:
Дополнительный расчет силы тяжести для отличников 5 минутПРОЦЕДУРА:
1) Поскольку Юпитер находится на расстоянии 7,8 x 10 11 м от sun и имеет массу 1,8 x 10 27 кг. Попросите учащихся рассчитать Гравитационная сила Юпитера и определить, производит ли Солнце приливы. на Юпитере.
F = 6,67 x 10 -11 м 3 x 1,98 x 10 30 кг x 1,8 x 10 27 кгкг · сек 2 (7,8 x 10 11 м) 2
F = 3,9 x 10 23 м / с 2
ДЕЯТЕЛЬНОСТЬ № 9:
Форма Земли 15 минутМАТЕРИАЛЫ: ВОДА, МАЛЫЙ КРУГЛЫЙ ШАРЫ И СТРУНКА
ПРОЦЕДУРА:
1) Продемонстрируйте форму земли путем первого заполнения воздушный шар с водой.Возможно, лучше подумать о том, чтобы выполнить это на улице, в случае, если воздушный шар лопнет.
2) Затем завяжите его и надежно закрепите шнурком.
3) Покачивайте шар над головой и наблюдайте форма воздушного шара. Он должен выглядеть удлиненным.
4) Объясните, что это тот же процесс, который происходит на Земле, пока он вращается вокруг Солнца. Вода, покрывающая землю искажается и будет выпирать, как воздушный шар.
5) Прочтите о споре о форме Земли.
между последователями Ньютона и последователями Декарта в Томе Б.Джонс, Рисунок Земли , 1967 год.
ДЕЯТЕЛЬНОСТЬ № 10:
Почему Барби пристегивается ремнем безопасности 30 минутМАТЕРИАЛЫ: 2 ТЕЛЕЖКИ, 2 ШКИВА, 2 ДЕРЖАТЕЛЯ ДЛЯ КРЮЧКА, 2 БАРБИ, СТРУНКА, 2 ДЕРЕВЯННЫХ БЛОКА (2X4X8 “)
ПРОЦЕДУРА:
1) Поместите куклу Барби на каждую тележку. На одном из тележки используйте резинку, чтобы надежно закрепить Барби (ремень безопасности).
2) Прикрепите 2 метра веревки к каждой тележке.Прикреплять 200 г. к держателю крюковой массы. Присоедините шкивы к краю стола.
3) Поместите деревянный брусок перед шкивом и наденьте шнур на шкив.
4) Теперь прикрепите держатель массы к струне, пока кто-то держит тележку на месте.
5) Оттяните тележки назад и дайте весу ускориться.
тележки.
ДЕЯТЕЛЬНОСТЬ № 11:
Инерция – это гайки 30 минутМАТЕРИАЛЫ: КОЛБА 500 МЛ, 8 ДЮЙМОВ ПЯТЬ ДЛЯ ВЫШИВАНИЯ, ГАЙКИ 10-1 / 8ДЮЙМОВ
ПРОЦЕДУРА:
1) Поставьте пяльцы вертикально на колбу. рот.
2) Установите гайки на верхнюю часть пялец. Одной рукой быстро оторвите обруч, чтобы орехи упали в колбу.
3) Попросите учащихся выполнить задание и создать соревнование, чтобы увидеть, кто может положить больше орехов во фляжку.
4) Свяжите это с первым законом Ньютона и знаменитым
действие фокусника по вытаскиванию скатерти из-под посуды.
Библиография
Хьюитт, Пол Г. Концептуальная физика .
Джонс, Том Б. Фигура
Земля . 1967 г.
Джонс и Чайлдерс. Современный
Колледж физики .
Росс, Дэвид А. Введение в океанографию .
Как мы формулируем законы Ньютона? + Пример
Есть несколько способов сформулировать законы движения Ньютона. Вот к чему я пришел после многих лет обучения. Это самые ясные и простые для понимания учащиеся, которые с наименьшей вероятностью могут привести к неправильным представлениям (по крайней мере, на мой взгляд).
Первый закон Ньютона:
Объект остается в покое или движется с постоянной скоростью, если на него не действует неуравновешенная внешняя сила.
«Постоянная скорость» означает одну и ту же скорость в одном направлении и часто выражается как «равномерное движение по прямой линии».
Несбалансированная сила означает, что должна действовать результирующая сила.
Первый закон Ньютона описывает инерцию: свойство массы, которое означает, что для изменения скорости требуется сила.Это включает в себя изменение либо его направления, либо его скорости, либо и того, и другого.
Поскольку движение относительное, мы не можем сказать, находится ли что-то в покое или движется с постоянной скоростью. Это зависит от системы отсчета.
Второй закон Ньютона:
# “ускорение” = “сила” / “масса” #
# а = Ф / м #
Ускорение объекта, когда на него действует сила, прямо пропорционально силе (чем больше сила, тем больше ускорение), и обратно пропорционально массе (чем больше масса, тем меньше ускорение).
Иногда также выражается как # F = ma #, что одно и то же.
Третий закон Ньютона:
Для каждой силы существует другая сила такой же величины, действующая в противоположном направлении. Эти силы действуют на разные объекты.
Часто утверждается, что «для каждого действия существует равное и противоположное противодействие», но какая сила является действием и противодействием, зависит от нашего выбора, а понятие «силы действия» имеет тенденцию вызывать неправильные представления со стороны учащихся.
Третий Закон просто означает, что, например, если Земля оказывает на человека силу, человек оказывает на Землю силу такой же величины (размера). Второй Закон означает, что человек будет ускоряться намного, намного больше, чем Земля (мы не заметим ускорения Земли). Ракеты используют третий закон для ускорения вперед за счет ускорения топлива в обратном направлении. Если кто-то нырнет с лодки в одном направлении, лодка уйдет в обратном направлении.
Три закона движения работают вместе, и мы могли бы даже возразить, что если мы правильно понимаем Второй закон, первый закон не нужен, потому что это как раз тот случай, когда # F = 0 #.Понимание этих законов означает, что мы гораздо лучше понимаем силу, массу, ускорение и их действие.
10 реальных примеров законов Ньютона в повседневной жизни
Как мы все знаем, каждый закон, существующий в области изучения физики, основан на явлениях, которые происходят в нашей повседневной жизни. Итак, это нормально, что мы нашли некоторые реализации закона Ньютона в повседневной жизни.
Прежде чем мы обсудим этот закон о законе Ньютона в повседневной жизни, возможно, некоторые из вас забыли или даже не знают о законе, установленном английским ученым по имени Ньютон.Да, закон Ньютона или так называемый закон движения Ньютона – это основной закон классической механической физики, который описывает корреляцию между силой, действующей в объекте, и движением, которое оно вызывает.
Закон движения Ньютона настолько популярен в мире физики, что назван в честь его изобретателя, английского ученого по имени сэр Исаак Ньютон. В целом, закон Ньютона делится на три закона: первый закон Ньютона, второй закон Ньютона и третий закон Ньютона.
Каждое открытие Ньютона связано с законом физики.Его открытие позже было распространено в его работе под названием Philosophiae Naturalis Principia Mathematica , которая была опубликована 5 июля -го г. 1687 г. Работа Ньютона запомнилась и применяется до сих пор.
После понимания закона Ньютона вокруг нас есть какое-то явление, которое реализует все три закона движения Ньютона. Вот примеры законов Ньютона в повседневной жизни:
1. Первый закон Ньютона
Первый закон движения Ньютона также называется законом инерции.Этот закон гласит: «Если равнодействующая силы объекта равна нулю, то объект, который изначально был неподвижен, останется неподвижным. С другой стороны, объект, который изначально движется, будет продолжать двигаться с постоянной скоростью ». Уравнение первого закона движения Ньютона: F = 0.
В общем, первый закон Ньютона обсуждает инертную черту объекта, что означает, что каждый объект имеет тенденцию сохранять свое положение или место. В нашей повседневной жизни мы можем обнаружить это, когда человек останавливается или отдыхает на мотоцикле или байке.Импульс при внезапном перерыве и во время движения толкает всадника вперед. Другой пример: в то же время, когда человек наступает на педаль автомобиля, его тело внезапно тянет назад.
примеров законов Ньютона в повседневной жизни, основанных на применении первого закона:
- Качели маятниковые простые
- Монета, положенная поверх бумаги на столе, останется на месте, когда бумага будет вытягиваться
- Использование коробки передач на двигателе автомобиля
- Мяч, катящийся по поверхности, будет катиться с постоянной скоростью, потому что его результирующая сила равна нулю
2.Второй закон Ньютона
Второй закон движения Ньютона гласит: «Ускорение объекта прямо пропорционально суммарной силе, действующей на этот объект, и обратно пропорционально массе объекта». Формула второго закона движения Ньютона:
F = ma
Где:
F – чистая сила на объекте
м – масса объекта
а – ускорение
В отличие от первого закона Ньютона, второй закон Ньютона коррелирует с состоянием движущегося объекта.Затем будет подсчитана масса объекта и сила, приложенная к объекту. В повседневной жизни мы можем найти этот второй закон, когда человек толкает тележку с лапшой с определенной силой. Тогда эта тележка будет двигаться с определенным ускорением. У автомобиля массой 1 тонна этот автомобиль будет ускоряться с ускорением 1 м / с 2 .
Примеры закона Ньютона в повседневной жизни на основе второго закона движения:
- Грузовик с меньшей массой будет иметь большее ускорение, чем грузовик с большей массой
- Когда мы толкаем малый и большой стол, маленький стол будет иметь большее ускорение, так что меньший стол быстрее доберется до места назначения
- Взрослый, толкающий стол, будет иметь большее ускорение, чем ребенок, толкающий стол, с меньшей силой толкания
3.Третий закон Ньютона
Третий закон движения Ньютона гласит: «Если объект дает силу другому объекту, то объект, который получает силу, будет давать силу, равную силе, которую он получает от первого объекта в противоположном направлении». Некоторые реализации с использованием третьего закона движения Ньютона – это электрическая сила и магнитная сила. Формула третьего закона движения Ньютона:
F1 = -F2
Где:
F1 – сила, создаваемая первым объектом
F2 – сила, создаваемая вторым объектом
Третий закон Ньютона объясняет пару сил действие-противодействие.Объект, которому дана сила, вызовет реакцию на нас. В повседневной жизни мы можем найти применение третьему закону, когда человек пользуется весельной лодкой. Чтобы заставить лодку двигаться, человеку нужно какое-то действие, чтобы погрести лодку назад, чтобы создать реакцию от заданной силы, которая заставила гребную лодку двигаться вперед.
Другой пример третьего закона Ньютона можно найти в игрушке-водяной ракете. Если вы когда-либо играли с водяной ракетой, вы увидите давление воды, которое содержит моющее средство в высоком состоянии, а затем, когда крышка водяной ракеты открывается, происходит действие в виде струи воды, которая лопается вниз, чтобы вызвать реакцию. заставьте толкнуть ракету, чтобы запустить ее вверх.
Примеры законов Ньютона в повседневной жизни на основе третьего закона движения:
- Наша рука чувствует боль, когда мы ударяем по столу, потому что стол дает силу в ответ на нашу руку
- Когда кто-то плывет, сила, передаваемая его рукой в воду, вызывает силу реакции воды, общая сила которой равна силе его руки, но в противоположном направлении. Чтобы он двигался вперед, хотя и махнул рукой назад
Вы также можете прочитать о:
Это некоторые простые явления, которые иллюстрируют применение закона движения Ньютона в нашей повседневной жизни.Вы также можете найти другие примеры, которые обычно встречаются в повседневной жизни, которые коррелируют со всеми тремя законами движения Ньютона.
Урок для восьмого класса Первый закон Ньютона: Монетная активность (инерция)
Этот урок основан на интегрированной модели NGSS для средней школы Калифорнии.
MS-PS2 Движение и устойчивость: силы и взаимодействия
PE : MS-PS2-2 – Запланируйте расследование, чтобы предоставить доказательства того, что изменение движения объекта зависит от суммы сил, действующих на объект, и массы объекта.
DCI : PS2.A – Движение объекта определяется суммой действующих на него сил; Если общая сила объекта не равна нулю, его движение изменится (1-й закон Ньютона). Чем больше масса объекта, тем больше сила, необходимая для достижения того же изменения в движении. Для любого данного объекта большая сила вызывает большее изменение движения (2-й закон Ньютона).
Наука и инженерная практика 7 : Использование аргументов на основе доказательств
Концепция пересечения: Причина и следствие
Это задание можно использовать как самостоятельный урок или совместить с восемью другими уроками, разработанными как экспозиция, которую нужно пройти в течение трех дней.
Newton’s Laws Expo содержит:
- Монетная активность (1-й закон) (этот урок)
- Молоток / гвоздь (1-й закон)
- Греческий поднос официанта (1-й закон)
- Пенни на вешалке (1-й закон)
- Действия с мячом для пинг-понга (2-й закон)
- Гонщик на воздушном шаре (2-й закон)
- Гонщик скрепок (2-й закон)
- Скейтбординг (3-й закон)
- Колыбель Ньютона (3-й закон)
На этом уроке учащиеся выполнят короткое (восьмиминутное) задание, призванное продемонстрировать один из законов Ньютона.Студент должен будет использовать свидетельства, записанные во время упражнения, чтобы определить, какой из законов Ньютона выражается ( SP7 ). Каждое действие было тщательно отобрано для воспроизведения определенного эффекта ( CCC ).
Я также разработал три демонстрации законов Ньютона
Демонстрации
- Демонстрация первого закона Ньютона
- Демонстрация 2-го закона Ньютона
- Демонстрация 3-го закона Ньютона
Для упражнения с монетами ученики экспериментируют с Первым законом Ньютона, вытаскивая учетную карточку из-под набора сложенных монет.Монеты будут сопротивляться поступательному движению учетных карточек и упадут в чашку ниже ( MS-PS2-2 ). Монеты будут иметь инерцию (сопротивление изменению), и на монету не будет воздействовать сила ( PS2.A ). По мере того как учащиеся манипулируют этим упражнением в течение нескольких минут, они будут использовать собранные доказательства для доказательства Первого закона Ньютона ( SP7 ).
4.7 Дальнейшее применение законов движения Ньютона
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Применять методы решения проблем для определения величин в более сложных системах сил
- Интегрировать концепции кинематики для решения задач с использованием законов движения Ньютона
Информация, представленная в этом разделе, поддерживает следующие цели обучения AP® и научные практики:
- 3.A.2.1 Учащийся может представлять силы на диаграммах или математически, используя соответствующим образом обозначенные векторы с величиной, направлением и единицами измерения во время анализа ситуации. (С.П. 1.1)
- 3.A.3.1 Учащийся способен анализировать сценарий и делать утверждения – разрабатывать аргументы, обосновывать утверждения – о силах, действующих на объект другими объектами для различных типов сил или компонентов сил. (С.П. 6.4, 7.2)
- 3.A.3.3 Учащийся может описать силу как взаимодействие между двумя объектами и идентифицировать оба объекта для любой силы. (С.П. 1.4)
- 3.B.1.1 Учащийся может предсказать движение объекта, подверженного силам, действующим со стороны нескольких объектов, используя второй закон Ньютона в различных физических ситуациях с ускорением в одном измерении. (С.П. 6.4, 7.2)
- 3.B.1.3 Учащийся может повторно выразить представление диаграммы свободного тела в математическое представление и решить математическое представление для ускорения объекта. (С.П. 1.5, 2.2)
- 3.B.2.1 Учащийся может создавать и использовать диаграммы свободного тела для анализа физических ситуаций с целью качественного и количественного решения задач, связанных с движением. (С.П. 1.1, 1.4, 2.2)
Есть много интересных приложений законов движения Ньютона, некоторые из которых представлены в этом разделе. Они также служат для иллюстрации некоторых тонкостей физики и помогают развить навыки решения проблем.
Пример 4.7 Сила сопротивления на барже
Предположим, что два буксира толкают баржу под разными углами, как показано на рис. 4.23. Первый буксир имеет усилие 2,7 × 105 Н2,7 × 105 Н размером 12 {2 “”. 7 умноженных на “10” rSup {size 8 {5}} “N”} {} в направлении x , а второй буксир прикладывает силу 3,6 × 105 Н3,6 × 105 Н размером 12 {3 “. ” 6 раз по “10” rSup {size 8 {5}} “N”} {} в направлении y .
Рис. 4.23 (a) Вид сверху двух буксиров, толкающих баржу.(b) Схема свободного тела для корабля содержит только силы, действующие в плоскости воды. В нем не учитываются две вертикальные силы – вес баржи и выталкивающая сила поддерживающей ее воды, которые компенсируются и не показаны. Поскольку приложенные силы перпендикулярны, оси x и y имеют то же направление, что и FxFx размером 12 {F rSub {размер 8 {x}}} {} и FyFy размером 12 {F rSub {размер 8 {y}}} {}. Проблема быстро становится одномерной проблемой в направлении размера FappFapp 12 {F rSub {размер 8 {“app”}}} {}, поскольку трение происходит в направлении, противоположном FappFapp размера 12 {F rSub {размер 8 { “приложение”} } } {}.Если масса баржи составляет 5,0 × 106 кг, 5,0 × 106 кг размер 12 {5 раз “10” rSup {размер 8 {6}} “кг”} {} и ее ускорение составляет 7,5 × 10− 2 м / с 27,5 × 10–2 м / с2 размер 12 {7 “.” “52” умножить на “10” rSup {размер 8 {- 2}} “м / с” rSup {размер 8 {2}}} {} в указанном направлении. Какова сила сопротивления воды на барже, сопротивляющейся движение? Примечание. Сила сопротивления – это сила трения, создаваемая жидкостями, такими как воздух или вода. Сила сопротивления препятствует движению объекта.
Стратегия
Направления и значения ускорения и приложенных сил показаны на рисунке 4.23 (а) . Мы определим общую силу буксиров на барже как FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, так что
4.59 Fapp = Fx + Fy.Fapp = Fx + Fy. размер 12 {F rSub {размер 8 {ital “app”}} ital “= F” rSub {size 8 {x}} ital “+ F” rSub {size 8 {y}}} {}Поскольку баржа плоская снизу, сопротивление воды FDFD размером 12 {F rSub {размер 8 {D}}} {} будет в направлении, противоположном FappFapp размера 12 {F rSub {размер 8 {“app”}}} {}, поскольку показано на диаграмме свободного тела на рисунке 4.23 (б). Здесь представляет интерес система баржа, поскольку даны силы на , , и ее ускорение. Наша стратегия состоит в том, чтобы найти величину и направление чистой приложенной силы FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, а затем применить второй закон Ньютона для определения силы сопротивления FDFD размером 12 {F rSub {размер 8 {D}}} {}.
Решение
Поскольку размер FxFx 12 {F rSub {размер 8 {x}}} {} и размер FyFy 12 {F rSub {размер 8 {y}}} {} перпендикулярны, величина и направление размера FappFapp 12 {F rSub {size 8 {“app”}}} {} легко найти.Во-первых, результирующая величина дается теоремой Пифагора.
4,60 Fapp = Fx2 + Fy2Fapp = (2,7 × 105 Н) 2+ (3,6 × 105 Н) 2 = 4,5 × 105 NFapp = Fx2 + Fy2Fapp = (2,7 × 105 Н) 2+ (3,6 × 105 Н) 2 = 4,5 × 105 налиньл {stack { размер 12 {F rSub {размер 8 {ital “app”}} = \ (F rSub {размер 8 {x} rSup {размер 8 {2}}} + F rSub {размер 8 {y} rSup {размер 8 {2) }}} \) rSup {размер 8 {1/2}}} {} # F rSub {размер 8 {ital “app”}} = \ (\ (2 “.” 7 раз “10” rSup {размер 8 {5}} “N” \) rSup {размер 8 {2}} + \ ( 3 “.” 6 раз по “10” rSup {размер 8 {5}} “N” \) rSup {размер 8 {2}} \) rSup {размер 8 {1/2}} = 4 “.”” 50 “умножить на” 10 “rSup {размер 8 {5}}” N “”. “{} }} {}Угол равен
4,61 θ = tan − 1FyFxθ = tan − 13,6 × 105 N2,7 × 105 N = 53 °, θ = tan − 1FyFxθ = tan − 13,6 × 105 N2,7 × 105 N = 53 °, alignl {stack { размер 12 {θ = “tan” rSup {size 8 {- 1}} слева ({{F rSub {size 8 {y}}} больше {F rSub {size 8 {x}}}} справа)} {} # θ = “загар” rSup {размер 8 {- 1}} влево ({{\ (2 “.” 7 раз “10” rSup {размер 8 {5}} “N” \)} больше {\ (3 “. “6 раз” 10 “rSup {size 8 {5}}” N “\)}} вправо) =” 53 “”. ” 1 °, {} }} {}, которое мы знаем из-за первого закона Ньютона, совпадает с направлением ускорения.Размер FDFD 12 {F rSub {размер 8 {D}}} {} находится в направлении, противоположном направлению FappFapp размера 12 {F rSub {size 8 {“app”}}} {}, поскольку он замедляет ускорение. Следовательно, чистая внешняя сила имеет то же направление, что и FappFapp размером 12 {F rSub {size 8 {“app”}}} {}, но ее величина немного меньше, чем FappFapp размера 12 {F rSub {size 8 {“app “}}} {}. Проблема теперь одномерная. Из рисунка 4.23 (b) видно, что
4.62 Fnet = Fapp-FD.Fnet = Fapp-FD размер 12 {F rSub {size 8 {“net”}} = F rSub {size 8 {“app” }} – F rSub {размер 8 {D}}} {}.Но второй закон Ньютона гласит, что
4.63 Fnet = ma.Fnet = ma size 12 {F rSub {size 8 {“net”}} = ital “ma”} {}.Таким образом,
4.64 Fapp-FD = ma.Fapp-FD = ma size 12 {F rSub {size 8 {“app”}} – F rSub {size 8 {D}} = ital “ma”} {}.Это может быть решено для величины силы сопротивления водяного FDFD размером 12 {F rSub {size 8 {D}}} {} в терминах известных величин.
4,65 FD = Fapp − maFD = Fapp − ma размер 12 {F rSub {размер 8 {D}} = F rSub {размер 8 {“app”}} – ital “ma”} {}Подстановка известных значений дает
4.66 FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 N.FD = (4,5 × 105 Н) – (5,0 × 106 кг) (7,5 × 10–2 м / с2) = 7,5 × 104 N размер 12 {F rSub {size 8 {D}} = \ (4 “.” 50 “умножить на 10” rSup {size 8 {5}} “N” \ ) – \ (5 “.” “00” умножить на “10” rSup {размер 8 {6}} “кг” \) \ (7 “.” “50” умножить на “10” rSup {размер 8 {“- 2” }} “м / с” rSup {size 8 {2}} \) = 7 “.” “50” умножить на “10” rSup {размер 8 {4}} “N”} {}.Направление FDFD размера 12 {F rSub {размер 8 {D}}} {} уже было определено как направление, противоположное направлению FappFapp размера 12 {F rSub {size 8 {“app”}}} {}, или под углом 53º53º размером 12 {“53” “.”1 °} {} к югу от запада.
Обсуждение
Числа, использованные в этом примере, приемлемы для баржи среднего размера. Конечно, трудно добиться больших ускорений с буксирами, и желательна небольшая скорость, чтобы баржа не врезалась в доки. Сопротивление относительно мало для хорошо спроектированного корпуса на низких скоростях, что согласуется с ответом на этот пример, где размер FDFD 12 {F rSub {размер 8 {D}}} {} составляет менее 1/600 веса судно.
В предыдущем примере канатоходца мы отметили, что натяжение тросов, поддерживающих массу, было одинаковым только потому, что углы с обеих сторон были равны. Рассмотрим следующий пример, где углы не равны; требуется немного больше тригонометрии.
Пример 4.8. Различное натяжение под разными углами
Рассмотрим светофор (масса 15,0 кг), подвешенный на двух тросах, как показано на рисунке 4.24. Найдите натяжение в каждой проволоке, не обращая внимания на массу проволоки.
Рис. 4.24 Светофор подвешен на двух тросах. (б) Некоторые из задействованных сил. (c) Здесь показаны только силы, действующие на систему. Также показана схема свободного движения светофора. (d) Силы, проецируемые на вертикальную ( y ) и горизонтальную ( x ) оси. Горизонтальные составляющие натяжения должны нейтрализоваться, а сумма вертикальных составляющих натяжений должна равняться весу светофора. (e) Схема свободного тела показывает вертикальные и горизонтальные силы, действующие на светофор.
Стратегия
Рассматриваемая система – светофор, диаграмма свободного движения которого показана на рис. 4.24 (c). Эти три задействованные силы не параллельны, поэтому они должны быть спроецированы в систему координат. Наиболее удобная система координат имеет одну ось вертикальную и одну горизонтальную, и проекции вектора на нее показаны в части (d) рисунка. В этой задаче есть два неизвестных (размер 12 T1T1 {T rSub {размер 8 {1}}} {} и размер 12 T2T2 {T rSub {размер 8 {2}}} {}), поэтому для нахождения их.Эти два уравнения получены в результате применения второго закона Ньютона вдоль вертикальной и горизонтальной осей с учетом того, что чистая внешняя сила равна нулю вдоль каждой оси, потому что ускорение равно нулю.
Решение
Сначала рассмотрим горизонтальную ось или ось x .
4,67 Fnet x = T2x − T1x = 0. Fnet x = T2x − T1x = 0. размер 12 {F rSub {размер 8 {“net x”}} = T rSub {размер 8 {“2x”}} – T rSub {size 8 {“1x”}} = 0} {}Таким образом, как вы могли бы ожидать,
4.68 T1x = T2x.T1x = T2x размер 12 {T rSub {размер 8 {“1x”}} = T rSub {размер 8 {“2x”}}} {}.Это дает нам следующую взаимосвязь между размером 12 T1T1 {T rSub {размер 8 {1}}} {} и размером 12 T2T2 {T rSub {размер 8 {2}}} {}
4.69 T1cos (30º) = T2cos (45º) .T1cos (30º) = T2cos (45º) размер 12 {T rSub {размер 8 {1}} “cos” \ (“30” ° \) = T rSub {размер 8 { 2}} “cos” \ (“45” ° \)} {}.Таким образом,
4,70 T2 = (1,225) T1.T2 = (1,225) T1, размер 12 {T rSub {size 8 {2}} = \ (1 “.” “225” \) T rSub {size 8 {1}}} {} .Обратите внимание, что T1T1 размер 12 {T rSub {размер 8 {1}}} {} и T2T2 размер 12 {T rSub {размер 8 {2}}} {} в этом случае не равны, потому что углы с обеих сторон не равный. Разумно, что размер 12 T2T2 {T rSub {размер 8 {2}}} {} в конечном итоге больше, чем размер 12 T1T1 {T rSub {размер 8 {1}}} {}, потому что он действует более вертикально, чем T1T1 размер 12 {T rSub {размер 8 {1}}} {}.
Теперь рассмотрим компоненты силы по вертикали или оси y .
4,71 Fnet y = T1y + T2y − w = 0.Fnet y = T1y + T2y − w = 0. размер 12 {F rSub {размер 8 {“net y”}} = T rSub {size 8 {“1y”}} + T rSub {size 8 {“2y”}} – w = 0} {}Это означает
4.72 T1y + T2y = w.T1y + T2y = w размер 12 {T rSub {размер 8 {“1y”}} + T rSub {размер 8 {“2y”}} = w} {}.Подстановка выражений для вертикальных составляющих дает
4,73 T1sin (30º) + T2sin (45º) = w.T1sin (30º) + T2sin (45º) = размер 12 {T rSub {размер 8 {1}} “sin” \ (“30” ° \) + T rSub {размер 8 {2}} “sin” \ (“45” ° \) = w} {}.В этом уравнении есть два неизвестных, но замена выражения для T2T2 размера 12 {T rSub {size 8 {2}}} {} на T1T1 размера 12 {T rSub {size 8 {1}}} {} уменьшает это к одному уравнению с одним неизвестным.
4,74 T1 (0,500) + (1,225T1) (0,707) = w = мг, T1 (0,500) + (1,225T1) (0,707) = w = размер 12 мг {T rSub {размер 8 {1}} \ (0 ” . “” 500 “\) + \ (1”. “” 225 “T rSub {size 8 {1}} \) \ (0”. “” 707 “\) = w = ital” mg “} {},, что дает
4,75 1,366T1 = (15,0 кг) (9,80 м / с2) .1.366T1 = (15,0 кг) (9,80 м / с2) размер 12 {слева (1 дюйм. «366 дюймов справа) T rSub {размер 8 {1} } = \ (“15” “.” “0 кг” \) \ (9 “.” “80 м / с” rSup {size 8 {2}} \)} {}.Решение этого последнего уравнения дает величину T1T1 размера 12 {T rSub {size 8 {1}}} {} , равную
4.76 T1 = 108 N.T1 = 108 N размер 12 {T rSub {size 8 {1}} = “108” “N”} {}.Наконец, величина T2T2 размера 12 {T rSub {size 8 {2}}} {} определяется с использованием взаимосвязи между ними, размер T2T2 12 {T rSub {size 8 {1}}} {} = 1,225 T1T1 size 12 {T rSub {size 8 {2}}} {}, найдено выше. Таким образом, получаем
4,77 T2 = 132 N.T2 = 132 N, размер 12 {T rSub {size 8 {2}} = “132 N”} {}.Обсуждение
Оба натяжения были бы больше, если бы оба троса были более горизонтальными, и они были бы равны тогда и только тогда, когда углы с обеих сторон такие же, как в предыдущем примере канатоходца.
Весы для ванной – отличный пример нормальной силы, действующей на тело. Он обеспечивает количественное определение того, насколько он должен подтолкнуться вверх, чтобы выдержать вес объекта. Но можете ли вы предсказать, что бы вы увидели на шкале весов для ванной, если бы стояли на них во время поездки на лифте? Увидите ли вы значение, превышающее ваш вес, когда лифт пойдет? А как насчет того, когда лифт движется вверх с постоянной скоростью: будут ли весы показывать больше, чем ваш вес в состоянии покоя? Рассмотрим следующий пример.
Пример 4.9. Что показывают весы в лифте?
На рис. 4.25 показан мужчина весом 75,0 кг (около 165 фунтов), стоящий на весах в лифте. Рассчитайте показание шкалы: (а) если лифт ускоряется вверх со скоростью 1,20 м / с 21,20 м / с2 размер 12 {1 “.” “20 м / с” rSup {размер 8 {2}}} {}, и (b) если лифт движется вверх с постоянной скоростью 1 м / с.
Рис. 4.25 (a) Различные силы, действующие, когда человек стоит на весах в лифте.Стрелки приблизительно соответствуют тому, когда лифт ускоряется вверх – пунктирные стрелки обозначают силы, слишком большие для масштабирования. Размер TT 12 {T} – это натяжение поддерживающего троса, размер ww 12 {w} – вес человека, размер wsws 12 {w rSub {размер 8 {s}}} {} – вес весов, wewe size 12 {w rSub {size 8 {e}}} {} – это вес лифта, FsFs размер 12 {F rSub {size 8 {s}}} {} – это сила действия весов на человека, FpFp размер 12 {F rSub {размер 8 {p}}} {} – сила человека на весах, размер 12 FtFt {F rSub {размер 8 {t}}} {} – сила весов на полу лифта, а NN размер 12 {N} – сила пола, направленная вверх по шкале.(б) Диаграмма свободного тела показывает только внешние силы, действующие на обозначенную интересующую систему – человека.Стратегия
Если весы точные, их показание будет равно FpFp размеру 12 {F rSub {size 8 {p}}} {}, величине силы, которую человек прилагает к весу вниз. На рис. 4.25 (а) показаны многочисленные силы, действующие на лифт, весы и человека. Это заставляет эту одномерную проблему выглядеть гораздо более грозной, чем если бы человек был выбран в качестве представляющей интерес системы и была нарисована диаграмма свободного тела, как на рисунке 4.25 (б). Анализ диаграммы свободного тела с использованием законов Ньютона может дать ответы на обе части (а) и (b) этого примера, а также на некоторые другие вопросы, которые могут возникнуть. Единственными силами, действующими на человека, являются его вес ww размер 12 {w} {} и восходящая сила весов FsFs размера 12 {F rSub {размер 8 {s}}} {}. Согласно третьему закону Ньютона, размер FpFp 12 {F rSub {размер 8 {p}}} {} и размер FsFs 12 {F rSub {размер 8 {s}}} {} равны по величине и противоположны по направлению, так что мы нужно найти FsFs размером 12 {F rSub {size 8 {s}}} {}, чтобы найти то, что читает шкала.Мы можем сделать это, как обычно, применив второй закон Ньютона,
4.78 Fnet = ma.Fnet = ma size 12 {F rSub {size 8 {“net”}} = ital “ma”} {}.Из диаграммы свободного тела видно, что Fnet = Fs − wFnet = Fs − w размер 12 {F rSub {size 8 {“net”}} = F rSub {size 8 {s}} – w} {}, поэтому что
4.79 Fs − w = ma.Fs − w = ma size 12 {F rSub {size 8 {s}} – w = ital “ma”} {}.Решение для FsF размером 12 {F rSub {size 8 {s}}} {} дает уравнение только с одним неизвестным.
4.80 Fs = ma + w, Fs = ma + w size 12 {F rSub {size 8 {s}} = ital “ma” + w} {},или, поскольку w = mgw = mg, просто
4.81 Fs = ma + mg.Fs = ma + mg, размер 12 {F rSub {size 8 {s}} = ital «ma» + ital «mg»} {}.Никаких предположений об ускорении не делалось, поэтому это решение должно быть действительным для множества ускорений в дополнение к тем, что в этом упражнении.
Решение для (а)
В этой части задачи a = 1,20 м / с2a = 1,20 м / с2 размер 12 {a = 1 “.” “20” “м / с” rSup {размер 8 {2}}} {}, так что
4,82 Fs = (75,0 кг) (1,20 м / с2) + (75,0 кг) (9,80 м / с2), Fs = (75.0 кг) (1,20 м / с2) + (75,0 кг) (9,80 м / с2) размер 12 {F rSub {size 8 {s}} = \ (“75” “.” “0 кг” \) \ (1 “.” “20 м / с” rSup {размер 8 {2}} \) + \ (“75” “.” “0 кг” \) \ (9 “.” “80 м / с” rSup {размер 8 {2}} \)} {},дает
4.83 Fs = 825 N.Fs = 825 N размер 12 {F rSub {size 8 {s}} = 8 “25 N”} {}.Обсуждение для (а)
Это около 185 фунтов. Что бы показывали весы, если бы он был неподвижен? Поскольку его ускорение будет нулевым, сила весов будет равна его весу.
4.84 Fnet = ma = 0 = Fs − wFs = w = mgFs = (75,0 кг) (9,80 м / с2) Fs = 735 N.Fnet = ma = 0 = Fs − wFs = w = mgFs = (75,0 кг) (9,80 м / с2) Fs = 735 N.alignl {stack { размер 12 {F rSub {size 8 {“net”}} = ital “ma” = 0 = F rSub {size 8 {s}} – w} {} # F rSub {size 8 {s}} = w = ital “mg” {} # F rSub {size 8 {s}} = \ (“75” “.” 0 “кг” \) \ (9 “.” “80 м / с” rSup {size 8 {2}} \) {} # F rSub {size 8 {s}} = “735” “N” “.” {} }} {}Итак, показания весов в лифте больше, чем его вес 735-Н (165 фунтов). Это означает, что весы толкают человека вверх с силой, превышающей его вес, что необходимо для ускорения его движения вверх.Очевидно, что чем больше ускорение лифта, тем больше показание шкалы, соответствующее тому, что вы чувствуете при быстром ускорении по сравнению с медленно ускоряющимся лифтом.
Решение для (b)
Итак, что происходит, когда лифт достигает постоянной скорости вверх? Будут ли весы показывать больше, чем его вес? Для любой постоянной скорости – вверх, вниз или в неподвижном состоянии – ускорение равно нулю, потому что a = ΔvΔta = ΔvΔt размер 12 {a = {{Δv} по {Δt}}} {}, и Δv = 0Δv = 0 размер 12 {Δv = 0} {}.
Таким образом,
4.85 Fs = ma + mg = 0 + mg.Fs = ma + mg = 0 + mg, размер 12 {F rSub {size 8 {s}} = ital “ma” + ital “mg” = 0 + ital “mg”} {}.Сейчас
4,86 Fs = (75,0 кг) (9,80 м / с2), Fs = (75,0 кг) (9,80 м / с2) размер 12 {F rSub {size 8 {s}} = \ (“75” “.” “0 кг “\) \ (9”. “” 80 м / с “rSup {size 8 {2}} \)} {},, что дает
4.87 Fs = 735 N.Fs = 735 N размер 12 {F rSub {size 8 {s}} = 7 “35 N”} {}.Обсуждение для (б)
На весах 735 Н, что соответствует весу человека.Это будет иметь место, когда лифт имеет постоянную скорость – движется вверх, вниз или неподвижен.
Решение предыдущего примера также применимо к лифту, ускоряющемуся вниз, как уже упоминалось. Когда лифт ускоряется вниз, размер 12 {a} {} отрицательный, и показание весов на меньше, чем на вес человека, до тех пор, пока не будет достигнута постоянная скорость движения вниз, после чего показание весов снова станет равным вес человека. {- 10} \, \ mathrm { м}) \).{8} \, \ mathrm {m} / \ mathrm {s}) \).
Специальная теория относительности Эйнштейна заменяет ньютоновскую механику, когда скорость объекта приближается к скорости света. С другой стороны, квантовая механика заменяет механику Ньютона, когда размеры объекта близки к атомному масштабу.
3.2.1 Первый закон Ньютона
Давным-давно считалось, что для удержания объекта в движении необходима сила и что естественное состояние любого объекта должно быть в состоянии покоя. Позже эти утверждения оказались неверными.Чтобы понять это, предположим, что блок, лежащий на поверхности, получает толчок и отпускается. В результате блок какое-то время будет скользить, прежде чем остановиться. Время между толканием блока и его остановкой увеличивается по мере того, как поверхность становится более гладкой. Если поверхность станет настолько гладкой, что трение будет практически незначительным, блок продолжит движение по прямой с постоянной скоростью на большее расстояние, прежде чем остановится.
Примером движения без трения является движение шайбы по столу для аэрохоккея.Шайба плавает в тонком столбе воздуха, который используется в качестве смазки. В ситуациях, когда трение отсутствует совсем, объект будет продолжать двигаться по прямой с постоянной скоростью, не требуя никаких усилий для поддержания его движения. Однако для начала движения требуется сила. Эта концепция была сформулирована Ньютоном и стала его первым законом движения: Покоящийся объект остается в покое, а объект в движении будет продолжать движение с постоянной скоростью ( постоянная скорость по прямой ) , если на него не действует чистая внешняя сила .То есть, если$$ \ Sigma \ mathbf {F} = \ mathbf {0} $$
$$ \ mathbf {a} = \ mathbf {0} $$
Тенденция тела оставаться в покое или поддерживать форму движение по прямой называется инерцией. Таким образом, первый закон Ньютона часто называют законом инерции, где он определяет определенные виды систем отсчета, называемые инерциальными системами отсчета. Инерциальная система отсчета – это система отсчета, в которой действует первый закон Ньютона. То есть в инерциальной системе отсчета объект не имеет ускорения, если на него не действует действующая сила.Любая система отсчета, движущаяся с постоянной скоростью относительно инерциальной системы, также является инерциальной. Наблюдатели в разных инерциальных системах отсчета измеряют одинаковое ускорение движущегося объекта. Чтобы доказать это, рассмотрим две инерциальные системы отсчета \ (\ mathrm {S} \) и \ (\ mathrm {S} ‘\), упомянутые в разд. 2.5, где \ (\ mathrm {S} \) неподвижен, а \ (\ mathrm {S} ‘\) движется с постоянной скоростью относительно S. Дифференцируя уравнение. 2.20, у нас есть$$ \ frac {d \ mathbf {v} _ {PS}} {dt} = \ frac {d \ mathbf {v} _ {PS ‘}} {dt} + \ frac {d \ mathbf {v} _ {S’S}} {dt} $$
Поскольку \ (\ mathbf {v} _ {S’S} \) является константой, мы имеем$$ \ mathbf {a} _ {PS} = \ mathbf {a} _ {PS ‘} $$
То есть ускорение частицы \ (\ mathrm {P} \), измеренное в обеих инерциальных системах отсчета \ (\ mathrm {S} \) и \ (\ mathrm {S}’ \ ) то же самое.Чтобы показать, что первый закон Ньютона действителен только тогда, когда он применяется к инерциальной системе отсчета; представьте себе девушку по имени Миа, которая отдыхает, наблюдая, как ее подруга Леа ведет машину, движущуюся с постоянной скоростью. Ли пристегивает ремень безопасности и кладет чемодан на сиденье рядом с собой, не удерживая его. Теперь предположим, что Леа нажимает на тормоз, из-за чего ее автомобиль замедляется, и ее чемодан начинает двигаться вперед. По словам Ли, которая находится в ускоренном кадре, чемодан сдвинулся с места, несмотря на то, что на него не действовала видимая чистая внешняя сила.Следовательно, в рамках теории Ли первый закон Ньютона кажется неверным.Ситуация, однако, отличается от Миа, которая находится в инерциальной системе отсчета. С ее точки зрения, чемодан изначально двигался с постоянной скоростью, и результирующая сила на нем была равна нулю. Когда автомобиль начал замедляться, чистая сила, действующая на чемодан, по-прежнему равна нулю, и поэтому чемодан должен продолжать двигаться вперед с постоянной скоростью и останавливаться за счет трения или удара о внутреннюю часть автомобиля. Следовательно, для Миа очевидно, что действует первый закон Ньютона.Из предыдущего примера мы заключаем, что первый закон Ньютона (и в целом законы Ньютона) не действителен во всех видах систем отсчета; он действителен только тогда, когда применяется по отношению к инерциальным кадрам. То есть Ли не должна применять первый закон Ньютона в своей системе отсчета.
Та же ситуация наблюдалась бы у Ли, если бы она повернула свою машину во время движения. При повороте автомобиля чемодан начнет движение в направлении, противоположном повороту. И снова Ли замечает, что чемодан сдвинулся с места без какого-либо видимого воздействия на него силы, что, по ее мнению, противоречит первому закону Ньютона.Миа не видит противоречия с первым законом Ньютона, потому что, когда машина поворачивает, чемодан имеет тенденцию продолжать свое первоначальное равномерное прямолинейное движение, и поэтому он движется в направлении, противоположном повороту. Следовательно, при наблюдении из инерциальной системы отсчета объекты подчиняются законам Ньютона (см. Рис. 3.1).
Чтобы применить классическую (ньютоновскую) механику по отношению к неинерциальной системе отсчета, вводятся новые силы, названные псевдосилами. В этой книге используются только инерциальные системы отсчета, и все законы изложены применительно к этим системам.Одна удобная инерциальная система отсчета, используемая в этой книге, – это поверхность Земли. Землю можно рассматривать как инерциальную систему отсчета, поскольку ее движение вокруг своей оси и вокруг Солнца мало влияет на расчеты и, таким образом, им можно пренебречь. 3.1Мальчик выливает воду, бросая ведро вперед. Если он остановится, вода продолжит движение по прямой. Однако из-за силы тяжести он следует по параболическому пути
3.2.2 Принцип инвариантности
Некоторые величины, такие как масса, сила, время и ускорение, являются инвариантными, что означает, что они имеют одинаковые числовые значения при измерении в разных инерциальных системах отсчета. Другие величины, такие как скорость, кинетическая энергия и работа, имеют разные значения в разных инерциальных системах отсчета. Однако законы физики имеют одинаковую форму во всех инерциальных системах отсчета. Это называется принципом инвариантности.
3.2.3 Масса
Как упоминалось ранее, тенденция объекта сопротивляться любому изменению в своем движении (т.е.е., оставаться в состоянии покоя или поддерживать равномерное движение по прямой) называется инерцией. Эксперименты и повседневный опыт показывают, что определенная сила вызывает разное ускорение при приложении к разным телам. Это изменение произведенного ускорения зависит от количества вещества, содержащегося в теле. Такая величина известна как масса тела. Следовательно, масса является мерой инерции. Предметы с большими массами имеют меньшее ускорение при воздействии той же силы.Таким образом, масса – это величина, которая связывает ускорение тела с действующей на него силой. Единица массы в системе СИ – килограмм (кг). Экспериментально установлено, что отношение масс любых двух тел (скажем, \ (m_ {1} \) и \ (m_ {2} \)) равно обратному отношению величин их ускорений, если на обоих действует одна и та же сила. То есть, у нас есть$$ \ frac {m_1} {m_2} = \ frac {a_2} {a_1} $$
Массу любого тела можно определить, сравнив его ускорение с ускорением массы всего кг, когда оба тела действуют с той же силой.Это приводит к выводу, что масса не зависит от силы; это неотъемлемая характеристика материи. Кроме того, экспериментально доказано, что когда две массы \ (m_ {1} \) и \ (m_ {2} \) соединяются вместе, объединенное тело ведет себя как единое тело массы \ (m_ {1} + m_ {2} \). Таким образом, масса является скалярной величиной и подчиняется правилам обычной арифметики.3.2.4 Второй закон Ньютона
В отличие от первого закона Ньютона, второй закон Ньютона описывает ситуацию, в которой результирующая сила, действующая на объект, не равна нулю.Было обнаружено, что когда на объект действуют разные силы, объект испытывает разные ускорения. Величина ускорения прямо пропорциональна величине приложенной силы, и его направление совпадает с направлением этой силы. Кроме того, это ускорение обратно пропорционально массе объекта для определенной приложенной силы. {2} / R \) и \ (a_ {t} = dv / dt \).{4} \ mathbf {k} \ bigg) \, \ mathrm {m} $$Пример 3.5
Если человек взвешивает себя на лифте, который ускоряется вверх со скоростью на относительно наблюдателя за пределами в лифте (в инерциальной системе координат), как показано на рис. 3.3, какое значение он получит для нормальной силы, действующей на него со стороны этажа? какая сила, если лифт ускоряется вниз?
Решение 3.5
Нормальная сила равна \ (\ mathrm {n} = \ mathrm {m} (\ mathrm {a} + \ mathrm {g}) \) для восходящего ускорения и \ (\ mathrm {n} = \ mathrm {m} (\ mathrm {g} – \ mathrm {a}) \) для ускорения вниз.Поскольку весы измеряют нормальную силу и рассчитывают массу по ней, путешествие вниз может быть более приятным!
Рис. 3.3Человек, взвешивающийся в лифте
3.2.5 Третий закон Ньютона
Сила, действующая на объект, всегда возникает из-за другого объекта в окружающей среде. Третий закон Ньютона показывает, что: если тело 1 оказывает силу \ (\ mathbf {F} _ {21} \) на тело 2, то тело 2 будет оказывать равную и противоположную силу \ (\ mathbf {F} _ {12} \ ) на корпусе 1.Это$$ \ mathbf {F} _ {12} = – \ mathbf {F} _ {21} $$
Любую из этих сил можно назвать силой действия. Когда одна из этих сил называется силой действия, другая сила называется противодействием (см. Рис. 3.4). Этот закон иногда обозначается как « На каждое действие есть равная и противоположная реакция ». Обратите внимание, что силы действия и противодействия всегда действуют на разные объекты , то есть они не могут нейтрализовать друг друга. Этот закон также показывает, что силы действуют парами и что не существует единой изолированной силы.Рис. 3.4Гравитационная сила, прилагаемая Землей к яблоку, и сила, прилагаемая яблоком к Земле, образуют пару действие-реакция
Пример 3.6
Три блока масс \ (m_ {1}, m_ {2} \) и \ (m_ {3} \) помещаются на поверхность без трения и толкаются горизонтальной силой F , как показано на рис. 3.5. Определите (а) ускорение системы; (b) контактные силы между \ (m_ {1} \) и \ (m_ {2} \) и между \ (m_ {2} \) и \ (m_ {3}.
