Примеры программ маткад: Урок 12. Программирование в Mathcad — циклы

Урок 12. Программирование в Mathcad — циклы

Во втором уроке по программированию в Mathcad мы рассмотрим циклы – различные повторяющиеся вычисления. Помимо циклов мы рассмотрим, как можно находить ошибки в программах.

В этом уроке мы изучим три новые команды:

1. for – для циклов for.
2. while – для циклов while.
3. return – как команду для отслеживания ошибок.

Остановка вычислений

Операции Mathcad, которые мы рассматривали ранее, достаточно безвредны – они не заставят Ваш компьютер «зависнуть». Но с циклами это не так. Поэтому для начала следует изучить команды в меню Вычисления –> Элементы управления:

Здесь находятся четыре кнопки:

1. Автоматический расчет.
2. Остановить все расчеты.
3. Рассчитать.
4. Отключить область.

Кнопка «Автоматический расчет» обычно включена. Она отключается при нажатии на кнопку «Остановить все расчеты». Зеленый индикатор в левом нижнем углу становится серым.

«Остановить все расчеты» служит для прекращения всех расчетов в документе на случай, если что-то пошло не так. При автоматическом расчете вычисления производятся лишь в том случае, когда происходят какие-либо изменения. С помощью кнопки «Рассчитать» можно сделать пересчет всего документа. Кнопка «Отключить область» прекращает вычисления в тех математических областях, которые Вы выбрали.

На рисунке ниже видно, что область серая – значит, она отключена:

Нажмите на нее, затем на кнопку «Отключить область». Тем самым Вы запустите расчет в области. Вычисление займет некоторое время:

Его можно прекратить, нажав на кнопку «Остановить все расчеты», затем отключив область и снова включив автоматический расчет.

Циклы

for

Циклы forприменяются, когда заранее известно число повторений вычислений. Программа ниже формирует вектор из n+1 элементов. Значения начинаются с нуля и имеют шаг 1.

Цикл forначинается со второй строки. Он включает в себя счетчик (здесь – i), который является локальной переменной-диапазоном. Эту строку можно прочитать как: «Для диапазона целых чисел от 0 до nвключительно сделать: …». Затем следуют выполняемые действия – в нашем случае это простое присваивание. Когда цикл завершается, программа выполняет действия на следующей строке – здесь это оператор return.

Составим программу.

Задайте имя программы-функции, вставьте программную структуру (вертикальная линия) и определение цикла forиз меню Математика –> Операторы и символы –> Программирование или с помощью сочетания клавиш [Ctrl+Shift+”]:

Определите имя переменной-счетчика:

Определите диапазон счетчика:

Введите команды тела цикла и оператор return:

Проверим программу:

Как видно, использование дробных или отрицательных чисел – не лучшая идея. Вы можете изменить точку начала, но этого лучше избегать:

Видите нули, которые появились в начале вектора? Причиной появления этих нулей является то, что если не определить некоторые элементы вектора, то им автоматически присвоится значение 0:

Циклы

while

На рисунке ниже – простейший цикл while, который делает то же самое, что и предыдущий цикл for:

До цикла необходимо создать строку, содержащую определение начального значения счетчика. Следующую строку можно прочитать как «Выполнять цикл, пока соблюдается условие i?n». После определения элемента вектора нужно задать команду на увеличение переменной-счетчика, так как в цикле while это не происходит автоматически.

Другой, более «реалистичный», пример цикла while вычисляет экспоненту отрицательного числа, используя разложения в ряд:

Суммирование будем производить с помощью цикла while. Будем проверять, насколько изменяется общая сумма S при каждом увеличении k. Если абсолютное значение этого изменения достаточно мало, цикл завершится. Чтобы начать цикл, необходимо определить первые два элемента вектора:

Кроме того, мы определили начальное значение суммы S и счетчика k. Дальнейшие вычисления производятся в цикле:

Проверка:

С положительными числами программа работает хорошо, но для работы с отрицательными она не предназначена.

Отладка

Одна из простых технологий отладки программ – вывод промежуточных результатов вычислений и их сравнение с тем, какие значения должны быть. Пример на цикле while:

Число элементов вектора верное, но второй элемент неправильный. Похоже, что последние элементы нашего вектора получили правильный индекс, а второй элемент (с индексом 1) – нет. Мы можем проверить, какой индекс получил второй элемент, вставив «returni» в первую строку цикла while. Программа остановит вычисление и вернет значение i:

Вероятно, Вы уже поняли, что ошибка в первой строке. Замените 2 на 1, удалите дополнительную строку return, и Вы получите верный результат.

Можно получить выходное значение итерации цикла, отличной от первой. Для этого требуется применить оператор условия if. В программе ниже выводится элемент вектора после третьей итерации цикла:

После отладки всегда следует удалять дополнительные строки, которые Вы вводите, так как программа всегда прекращает работу после первого оператора return.

Подпрограммы

Примеры программ в этом уроке малы. Настоящие программы могут быть намного больше. В других языках программирования они обычно составляются как основная программа и следующие за ней подпрограммы и процедуры. Эти более малые программы можно составлять сами по себе и затем вызывать их в основной программе. Также могут быть подподпрограммы и так далее.

Ваша собственная программа

Когда Вы начинаете составлять свою собственную программу, может показаться, что Вы находитесь в замкнутом круге: чтобы начать, нужен опыт; чтобы получить опыт, нужно начать.

Начать необходимо, но не следует начинать с набора команд в Mathcad! Для начала следует подготовиться.

Прежде всего, нужно решить, что делает Ваша программа. Для больших, сложных программ это, как правило, нетривиальная задача. Какие выходные данные нужны, и какие входные для этого необходимы?

Возможно, самая сложная часть – это представление того, как будет получен желаемый результат. Будьте готовы потратить несколько листов бумаги. Нарисуйте различные структурные диаграммы и детализируйте их. Вы знаете следующие элементы:

1. Ввод (input)
2. Действие (или определение)
3. Вывод (output)
4. Одиночное ответвление (if..elseили if..if)
5. Многократное ответвление (if..if..if)
6. Цикл for
7. Цикл while

Решите, какие вспомогательные переменные (например, счетчики) необходимы, и какие имена Вы собираетесь им дать. Постарайтесь предусмотреть, где и что может пойти не так и как это можно проверить.

Только когда Вы поняли, что улучшить программу на бумаге больше нельзя, открывайте Mathcad. Остановите все вычисления, затем вводите код. Возможно, это самая простая часть написания программы.

После написания кода программы сохраните файл. Затем нажмите кнопку «Автоматический расчет», чтобы запустить вычисления. Будьте готовы увидеть неверный результат или ошибку – тогда программу придется отлаживать. Сохраняйте файл каждый раз, когда делаете большие изменения.

После запуска программы ее необходимо проверить. Попробуйте обычные входные значения, а также такие значения, с которыми могут возникнуть проблемы. Программа может дать сообщение об ошибке для неверного входного или выходного значения. В завершение подумайте, как можно улучшить программу.

Резюме

1. Отключайте вычисления при написании или редактировании программы (Вычисления –> Остановить все расчеты).
2. Цикл for – повторяет вычисления определенное количество раз. Цикл forобязательно включает в себя счетчик и число повторений.
3. Цикл while – выполняется, пока соблюдается определенное условие. Начальное значение счетчика следует задавать до цикла. В теле цикла изменение счетчика задается вручную.
4. Программы почти всегда требуют отладки. Полезная команда для этого – return, с помощью которой можно вывести промежуточное значение.
5. Важно подготовиться к написанию программы, например, составив структурную диаграмму до написания непосредственно кода.

Другие интересные материалы

1.

3.5. Программирование MathCAD 12 руководство

Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику (например, возвращение различных значений в зависимости от условий), в одну строку не удается. Назначение программных модулей как раз и заключается в определении выражений, переменных и функций в несколько строк, часто с применением специфических программных операторов.

Принцип программирования в Mathcad

При помощи элементов программирования можно определять переменные и функции (как показано в листинге 1.19).
Листинг 1.19. Функция условия, определенная с помощью программы

Традиционное программирование, упрощенный вариант которого применен в Mathcad и осуществляется при помощи панели инструментов Programming (Программирование), имеет ряд существенных преимуществ, которые в ряде случаев делают документ более простым и читаемым:

•  возможность применения циклов и условных операторов;
•  простота создания функций и переменных, требующих нескольких простых шагов;
•  возможность создания функций, содержащих закрытый для остального документа код, включая преимущества использования локальных переменных и обработку исключительных ситуаций.

Как видно из листинга 1.19, программный модуль обозначается в Mathcad вертикальной чертой, справа от которой последовательно записываются операторы языка программирования. Чтобы начать создание программного модуля, следует (в случае листинга 1.19 после символа присваивания) нажать на панели Programming (Программирование) кнопку Add One (Добавить линию). Затем, если приблизительно известно, сколько строк кода будет содержать программа, можно создать нужное количество линий повторными нажатиями кнопки Add Line (Добавить линию) (рис. 1.18).

Рис. 1.18. Начало создания программного модуля

В появившиеся местозаполнители введите желаемый программный код, используя программные операторы. В рассматриваемом примере в каждый местозаполнитель вводится строка, например, в средний — “positive” (рис. 1.19). Затем нажимается кнопка If (Если) на панели Programming (Программирование) и в возникший местозаполнитель вводится выражение х>0. После того как программный модуль полностью определен, и ни один местозаполнитель не остался пустым, функция может использоваться обычным образом, как в численных, так и в символьных расчетах.

ВНИМАНИЕ!

Не вводите с клавиатуры имена программных операторов. Для их вставки можно применять лишь сочетания клавиш, которые приведены в тексте всплывающей подсказки (рис. 1.18 и 1.19).

Рис. 1.19. Вставка программного оператора

Добавление строк программного кода

Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line (Добавить линию). Для этого следует предварительно поместить на нужное место внутри программного модуля линии ввода. Например, расположение линии ввода на строке, показанной на рис. 1.18, приведет к появлению новой линии с местозаполнителем перед этой строкой. Если передвинуть вертикальную линию ввода из начала строки (как это показано на рис. 1.20) в ее конец, то новая линия появится после строки. Если выделить строку не целиком, а лишь некоторую ее часть (рис. 1.20), то это повлияет на положение в программе новой строки кода (результат нажатия кнопки Add Line показан на рис. 1.21).

СОВЕТ

Не забывайте, что для желаемого размещения линий ввода внутри формулы можно использовать не только мышь и клавиши со стрелками, но и пробел. С помощью последовательных нажатий пробела линии ввода “захватывают” разные части формулы.

Рис. 1.20. Положение линий ввода влияет на положение создаваемой строки программы

Зачем может потребоваться вставка новой линии в положение, показанное на рис. 1.21? Новая вертикальная черта с двумя линиями выделяет фрагмент программы, который относится к условию х>0, находящемуся в его заголовке. Пример возможного дальнейшего программирования показан в листинге 1.20.

Рис. 1.21. Результат вставки новой линии в программу (из положения рис. 1.20)

Листинг 1.20. Пример усовершенствования программы

В режиме выполнения программы, а это происходит при любой попытке вычислить f (х), выполняется последовательно каждая строка кода. Например, в предпоследней строке листинга 1. 20 вычисляется f (1). Рассмотрим работу каждой строки кода этого листинга.

1. Поскольку х=1, то условие х<0 не выполнено, и в первой строке ничего не происходит.

2. Условие второй строки х>о выполнено, поэтому выполняются обе следующие строки, объединенные короткой вертикальной чертой в общий фрагмент.

3. Функции f(x) присваивается значение f (x)=”positive”.

4. Условие х>1000 не выполнено, поэтому значение “big positive” не присваивается f (х), она так и остается равной строке “positive”.

5. Последняя строка не выполняется, т. к. одно из условий (х>0) оказалось истинным, и оператор otherwise (т. е., “иначе”) не понадобился.

Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т. к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.

Локальное присваивание (<—)

Язык программирования Mathcad не был бы эффективным, если бы не позволял создавать внутри программных модулей локальные переменные, которые “не видны” извне, из других частей документа. Присваивание в пределах программ, в отличие от документов Mathcad, производится с помощью оператора Local Definition (Локальное присваивание), который вставляется нажатием кнопки с изображением стрелки (<-) на панели Programming (Программирование).

ВНИМАНИЕ!

Ни оператор присваивания :=, ни оператор вывода = в пределах программ применять не разрешается.

В Mathcad 12 переменным, которые впервые появляются в программных модулях, по умолчанию присваивается значение 0. В прежних версиях программы использование переменных в программах без предварительного присваивания им значений приводило к генерации ошибки (как в расчетах на рабочей области документов Mathcad).

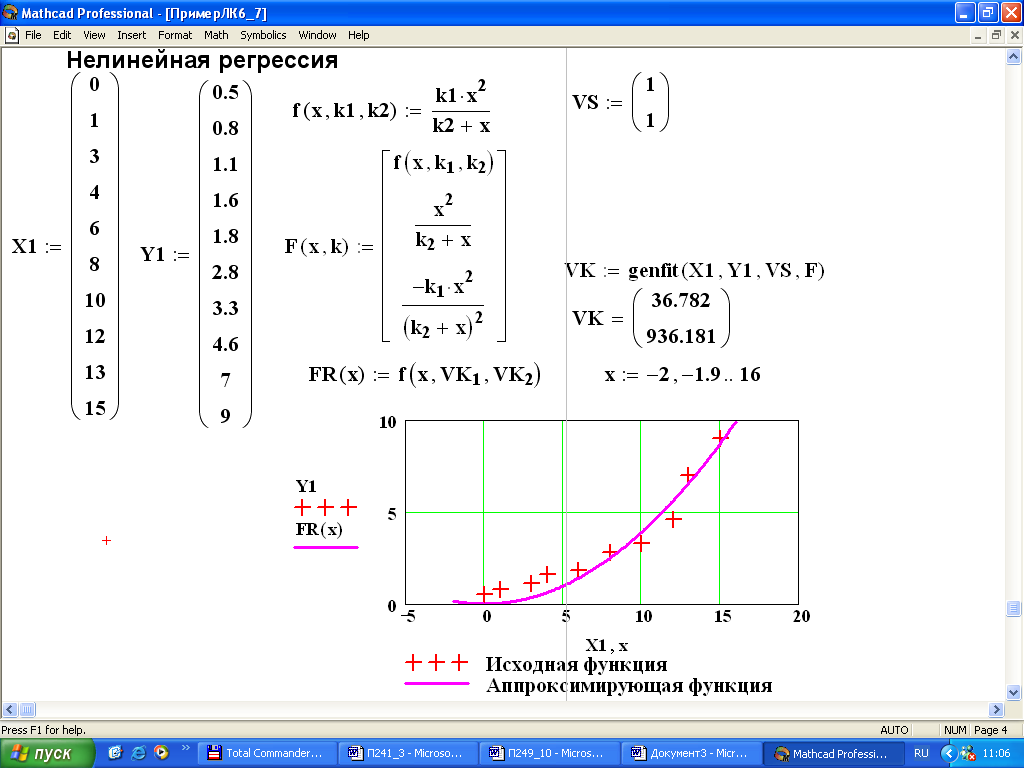
Локальное присваивание иллюстрируется листингом 1.21. Переменная z существует только внутри программы, выделенной вертикальной чертой. Из других мест документа получить ее значение невозможно. На этом же листинге вы видите пример применения оператора цикла for.

Листинг 1.21. Локальное присваивание в программе

Иллюстрированный самоучитель по MathCAD 11 › Программирование [страница – 93] | Самоучители по математическим пакетам

Программирование

• В ранних версиях Mathcad встроенного языка программирования не было. Чтобы применять привычные операции проверки условий и организовывать циклы, приходилось изобретать причудливую смесь из встроенных функций условия if (листинг 6 1) и until и комбинаций ранжированных переменных (листинг 6.2).

• Для вставки программного кода в документы в Mathcad имеется специальная панель инструментов Programming (Программирование), которую можно вызвать на экран нажатием кнопки Programming Toolbar на панели Math (Математика), как показано на рис. 6.1.

• Чтобы создать программный модуль (Add Line), например, представленный в предыдущем разделе (см. листинг 6.3): | Введите часть выражения, которая будет находиться слева от знака присваивания и сам знак присваивания. В нашем примере это имя функции f (х).

• Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line (Добавить линию). Для этого следует предварительно поместить на нужное место внутри программного модуля линии ввода.

• Язык программирования Mathcad не был бы эффективным, если бы не позволял создавать внутри программных модулей локальные переменные, которые “не видны” извне, из других частей документа.

• Рассмотрим операторы цикла – for, while, break, continue. | В языке программирования Mathcad имеются два оператора цикла: for и while. Первый из них дает возможность организовать цикл по некоторой переменной, заставляя ее пробегать некоторый диапазон значений.

• Если для определения переменной или функции применяется программный модуль, то его строки исполняются последовательно при вычислении в документе этой переменной или функции. Соответственно, по мере выполнения программы рассчитываемый результат претерпевает изменения.

• Программирование в Mathcad позволяет осуществлять дополнительную обработку ошибок (on error). Если пользователь предполагает, что выполнение кода в каком-либо месте программного модуля способно вызвать ошибку (например деление на ноль), то эту ошибку можно перехватить с помощью оператора on error.

• Рассмотрим два простых примера использования программных модулей в Mathcad для численных (листинг 6.16) и символьных (листинг 6.17) расчетов. В двух приведенных листингах используется большинство операторов, рассмотренных в данной главе.

Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.

В 11. системы математических вычислений mathcad, mathlab. назначение, возможности, примеры применения.

Системы математических вычислений — программы (или математические системы), которые можно использовать для различных вычислений и вычерчивания графиков (Mathematica, Derive, Statistica, MathCAD, MathLAB и др.). В этих системах процесс вычислений сильно автоматизирован, что позволяет экономить время и больше внимания уделять физическому смыслу получаемого результата. Выбор системы зависит от характера решаемых задач, от вкуса, от практики.

Система MathCAD -разработка фирмы MathSoft.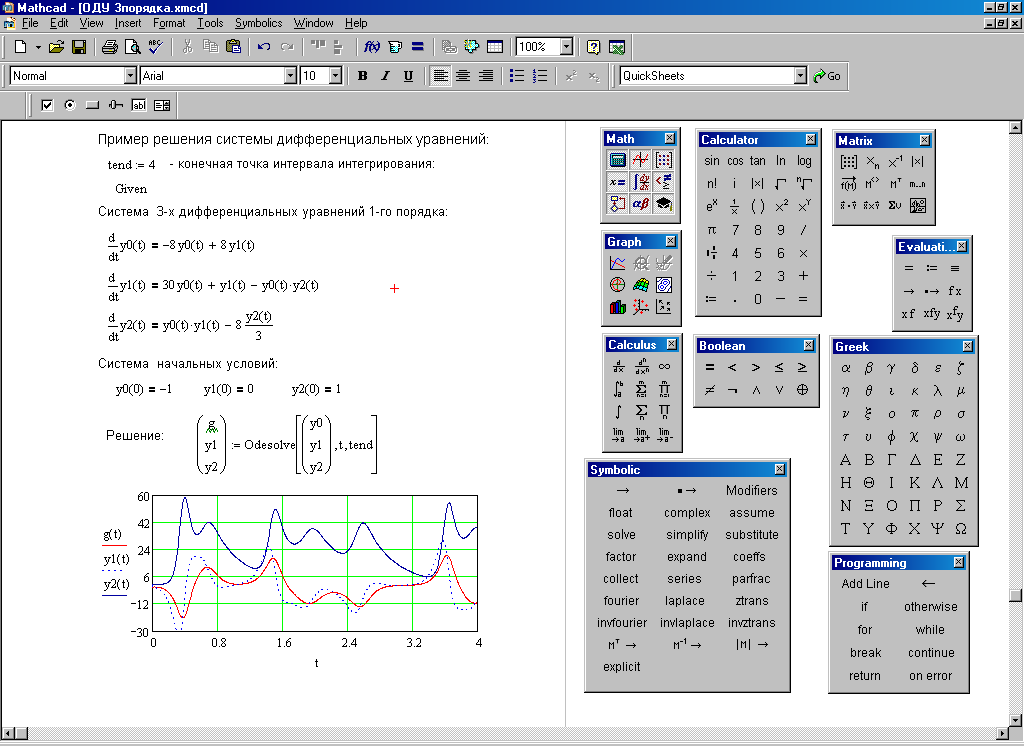 Примерно каждый год появляется новая версия этой системы. В настоящий момент известна версия Mathcad 12.

Назначение системы:MathCAD — это интегрированная система программирования, ориентированная на проведение математических и инженерно-технических расчетов. MathCAD содержит текстовый редактор, вычислитель, символьный процессор и графический процессор.

Фактически документы MathCadпредставляют собой программу, написанную на визуально-ориентированном языке программирования Язык программирования MathCad ориентирован на математические вычисления и потому практически не отличается от обычного языка математических статей, отчетов и книг.

Входной язык MathCad относится к интерпретируемому типу. Это значит, что, когда система опознает какой-либо объект, она немедленно исполняет указанные в блоке операции.

Визуально-ориентированный язык общения системы MathCad надо отличать от языка реализации системы, т.е. обычного языка программирования высокого уровня, на котором написана система. Языком реализации системы MathCad является один из самых мощных языков высокого уровня – С++.

По существу входной язык системы – промежуточное звено между скрытым от пользователя языком документа и языком реализации системы. По мере того как пользователь создает (средствами текстового, формульного, символьного и графического редакторов) в окне редактирования объекты (тексты, формулы, таблицы и графики), система сама составляет программу на некотором промежуточном языке связи. Эта программа хранится в оперативной памяти до тех пор, пока не будет записана на диск в виде файла с расширением .mcd. Однако от пользователя не требуется знание языков программирования (реализации и связи), достаточно освоить приближенный к естественному математическому языку входной язык системы.

К основным объектам входного языка системы MathCAD можно отнести: алфавит, константы, переменные, операторы, функции.

МАТЛАБ (MATLAB) – система компьютерной математики, которая в настоящее время широко применяется исследователями для решения прикладных и теоретических задач на ЭВМ. Название МАТЛАБ происходит от словосочетания “матричная лаборатория (matrixlaboratory), что первоначально соответствовало основному назначению системы – матричным вычислениям. Впоследствии, с развитием системы, в неё были добавлены функции и вычислительные алгоритмы из многих других областей математики. Но основной подход к элементарным операциям, когда число рассматривается как частный случай матрицы, сохранился. В настоящее время МАТЛАБ представляет собой развитую систему, включающую в себя в качестве составных частей инструменты для решения задач из разных областей математики, таких как линейная алгебра, численные методы, динамические системы и т. д.

Пользователю предлагается несколько вариантов использования системы. Основным режимом является режим командной строки, при котором команды, набираемые пользователем на клавиатуре в ответ на приглашение системы, выполняются в диалоговом режиме с немедленной выдачей результата. В этом режиме легко получить решение таких задач, как вычисление определителей, обращение и перемножение матриц, решение систем линейных алгебраических уравнений и др. Для выполнения этих и других операций необходимо вызвать соответствующую функцию системы, передав ей входные параметры и, возможно, сохранить результат для последующего использования.

Ядро МАТЛАБ содержит более тысячи функций. Помимо них доступно большое количество внешних функций, описанных в расширениях системы. В добавление к ним пользователь может создавать свои собственные функции, используя для этого специально предусмотренный язык программирования. Таким образом, МАТЛАБ является расширяемой системой, и это одно из важных её достоинств.

Помимо режима командной строки, являющегося основным режимом работы, некоторые расширения МАТЛАБ предлагают собственные диалоговые средства. Примером такого расширения является PDETool – графический интерфейс, предназначенный для решения дифференциальных уравнений в частных производных. Помимо функций, доступных из командной строки, он также предоставляет пользователю графическую среду, работающую в отдельном окне.

Выше упоминалось о том, что в МАТЛАБ имеется язык программирования. С его помощью можно создавать и реализовывать собственные алгоритмы, используя все доступные функции системы и все основные приёмы программирования, имеющиеся в других языках, такие как подпрограммы, циклы, ветвления, рекурсии и другие. Запись алгоритма на языке программирования МАТЛАБ сохраняется в файле в текстовом формате, либо в специальном внутреннем представлении.

Современные версии МАТЛАБ имеют развитые средства интеграции с другими языками программирования. Непосредственно из МАТЛАБ-программы можно создавать и использовать объекты Java; для написания S-функций (системных функций МАТЛАБ-Simulink) можно использовать языки высокого уровня C, C++, Ada, Fortran; кроме того функции системы МАТЛАБ можно экспортировать в dll и вызывать из других программ. Также можно использовать вычислительные возможности системы, передавая запросы удалённому компьютеру по сети.

На сегодняшний день система МАТЛАБ считается одной из наиболее мощных и развитых систем компьютерной математики.

Статьи к прочтению:

Introduction to MATLAB

Похожие статьи:

• Назначение системы smartmath

  Система SmartMath и ее возможности Назначение системы SmartMath Начиная с версии 4. 0 система MathCAD обзавелась новым средством оптимизации вычислений —…

• Вычисление значений математических выражений

  Для вычисления значений различных математических выражений в Pascal существуют различные арифметические функции: Функция Математическое обозначение…

Программирование В MathCad. Использование в программе функции циклических алгоритмов. Итерационные циклы и циклы с фиксированным числом повторений

Лабораторная работа № 5. Программирование В mathcad. Использование В программЕ-функциИ ЦИКЛИЧЕСКИХ алгоритмОВ. Итерационные циклы и циклы с фиксированным числом повторений.

цель работы: освоение основных приемов программирования РАЗЛИЧНЫХ циклических алгоритмов в пакете MathCad (4 часа)

Содержание

1. Программирование в программе-функции циклических алгоритмов.. 1

2. Арифметический цикл FOR (цикл с фиксированным числом повторений) 1

3. Итерационные циклы.. 2

4. Типовые алгоритмы обработки матриц. 4

4.1 Обращение к элементам главной диагонали. 5

4.2 Обращение к элементам побочной диагонали. 6

4. Дополнительные операторы программирования циклов в MathCad. 6

Порядок выполнения лабораторной работы.. 7

Задание 1. 7

Задание 2_1. 8

Задание 2_2. 9

Задание 3. 11

Задание 4. 12

Контрольные вопросы.. 13

1. Программирование в программе-функции циклических алгоритмов

Напомним, что циклические алгоритмы (или проще циклы) содержат повторяющиеся вычисления, зависящие от некоторой переменной. Такая переменная называется параметром цикла, а сами повторяющиеся вычисления составляют тело цикла.

Классификация циклов.   Циклы можно условно разделить на две группы:

·  ·  циклы с фиксированным количеством повторений, цикл типа арифметической прогрессии;

·  ·  итерационные циклы.

Характерной чертой первой группы циклов является то, что количество повторений тела цикла можно определить до начала выполнения программы, реализующей цикл.

Для итерационных циклов нельзя априори определить количество повторений тела цикла. Это обусловлено тем, что окончание таких циклов определяется не выходом параметра цикла за конечное значение, а и более сложными условиями.

2. Арифметический цикл FOR (цикл с фиксированным числом повторений)

Для программирования при помощи данного цикла, используется оператор FOR, вызов которого осуществляется одноименной кнопкой на панели Programming.

Структура оператора For:

 

  

где, в Поле 1 вводится имя параметра цикла;

в Поле 2 вводится диапазон значений параметра цикла в виде:                            1. нач_знач .. кон_знач                            2. нач_знач, нач_знач+шаг..кон_знач в Поле 3 вводятся операторы, составляющие тело цикла. По синтаксису оператора в цикле можно записать один оператор. Если операторов больше нужно создать дополнительные поля для ввода щелчком на кнопке “Add line” в панели программирования.

Пример 1: Вычислить значения функции .

Результат

Пояснение: результат расчета функции выводится в виде одномерного массива z. Для того, чтобы нумерация элементов массива начиналась с 1, установите значение функции ORIGIN=1 при помощи команды Options меню Math.

3. Итерационные циклы

Для программирования таких циклов используется оператор цикла WHILE, вызов которого осуществляется одноименной кнопкой на панели Programming.

Структура оператора While:

 

  

где, в Поле 1 вводится условие выполнение цикла;

в Поле 2 вводятся операторы, составляющие тело цикла. По синтаксису оператора в цикле можно записать один оператор. Если операторов больше нужно создать дополнительные поля для ввода щелчком на кнопке “Add line” в панели программирования.

Примечание: В теле цикла должна присутствовать переменная (параметр цикла), управляющая работой цикла и делающая, в итоге, условие цикла ложным для его завершения.

Принцип работы оператора WHILE:

1.  1.  Проверяется условие, записанное в Поле 1;

2.  2.  если результатом проверки условия является ответ “да”, то выполняются операторы, составляющие тело цикла;

3.  3.  если результатом проверки условия станет ответ “нет”, происходит выход из цикла.

Пример 2. Вычислить значения функции  в точках , шаг равен .

Пример 3. Найти сумму положительных элементов вектора V. Вектор задавать в отдельной программе.

Примечания:

1.  1.  Функция rnd(N) генерирует случайное вещественное число из диапазона [0; N-1];

2.  2.  В данной программе формируется вектор с числом элементов равных n.

Пример 4. Дан вектор V. Сформировать новый вектор V1 из элементов вектора V, значения которых больше числа d.

 

Примечание: переменная с именем nomer задает нумерацию элементов

примеров программирования »MathCadHelp.

com» Номер 1 в MathCad Assignments

• Facebook

• Твиттер

• Google+

• Реддит

• LinkedIn

Среда программирования Mathcad, имеющая всего десять кнопок на палитре программирования, проста в использовании. Тем не менее, за этой простотой скрываются удивительные возможности программирования.В сочетании с богатой числовой и символьной функциональностью Mathcad и вместе с абстрактными структурами данных, предоставляемыми вложенными массивами Mathcad, эти десять операторов позволяют писать сложные программы в Mathcad.

Следующие рисунки иллюстрируют лишь некоторые из возможностей. Поэкспериментируя с программированием в Mathcad, вы откроете для себя множество новых приложений. Дополнительные примеры программирования см. В разделе «Программирование» в QuickSheets Resource Center.А в Mathcad Professional Центр ресурсов включает специальный раздел «Казначейское руководство по программированию», который включает подробные примеры и приложения, чтобы показать вам, как получить больше от программ Mathcad.

Программа для поиска чисел, общих для двух векторов.

Использование сита Эратосфена для поиска простых чисел.

Степень случайной матрицы переходов.

Сглаживание матрицы

Связанные проекты MathCad

• Программирование
• Управление выполнением программы
• Программы в программах
• Условные операторы
• Ограничения символьной обработки
• Галерея анимаций
• Преимущества использования READPRN и WRITEPRN
• Поиск информации в электронной книге

Программирование с помощью PTC Mathcad Prime

Мы все понимаем, насколько важны расчеты и испытания для инженерных проектов. Иногда для получения правильных результатов требуется множество итераций. Однако выполнение этих тестов вручную требует множества проб и ошибок. Когда вы используете бумагу или программное обеспечение для элементарной математики, вы не можете запрограммировать свои вычисления так, чтобы они выполняли за вас нелинейные инструкции или регистрировали ошибки.

Все это и многое другое можно делать в PTC Mathcad. И вам не нужно знать Java, Python или какой-либо другой распространенный язык программирования. Фактически, вам совсем не нужен опыт написания кода. Твоих математических и инженерных знаний более чем достаточно.

Любой инженер с PTC Mathcad может включить логику программирования и:

• Условная оценка ветвей принятия решений
• Добавление контуров в инженерный анализ
• Добавьте точки останова или перехватите ошибки для устранения неполадок
• Экономия часов проб и ошибок по сравнению с традиционными методами

PTC Mathcad проведет вас через весь процесс создания программ. Пока вы знаете базовую логику проблемы, которую хотите решить, вы просто выбираете программные конструкции из меню и заполняете пустые поля.

Лучшая часть? Даже язык программирования в PTC Mathcad использует естественную математическую нотацию. Вот простой пример.

Начните с меню программирования в PTC Mathcad. Обратите внимание на простые варианты сборки с помощью мыши.

Используйте эти операторы для построения функции пузырьковой диаграммы. При программировании в PTC Mathcad можно пропустить матрицу и 18 команд построения графика. Просто настройте всю последовательность в несколько строк кода. В приведенном ниже примере устанавливается матрица, а затем методично строится каждое число, прежде чем вернуться назад, чтобы захватить и построить следующее число.После того, как последнее число в матрице нанесено на график, программа автоматически завершается.

Введите пример данных:

Создайте то, что нужно для участка:

Затем используйте первый столбец как значения x, а второй столбец как значения y на графиках XP:

Программирование в PTC Mathcad предназначено для инженеров. Он включает в себя естественную математическую нотацию, а код аккуратно вписывается во все ваши другие уравнения, таблицы, текст и графики.Вы можете скачать 30-дневную пробную версию сегодня и начать работу. Никаких книг, уроков или предыдущего опыта не требуется.

Совет: программирование также помещает больше ваших вычислений и тестового кода в меньшее количество областей, так что вам будет легче скрыть и защитить свою интеллектуальную собственность.

---

Mathcad Express против Mathcad Prime

PTC Mathcad – это программное обеспечение для инженерных расчетов, которое позволяет легко выполнять, анализировать, документировать и обмениваться расчетами.Проще говоря, Mathcad Express – это бесплатная версия Mathcad Prime с функциональными возможностями, ограниченными сроком действия.

При загрузке PTC Mathcad Express вы получаете доступ ко всем возможностям лицензионной версии PTC Mathcad Prime 6. 0 в течение первых 30 дней. По истечении 30 дней вы потеряете расширенные математические представления, но по-прежнему будете иметь пожизненный доступ к PTC Mathcad Express.

Возможности PTC Mathcad

* Доступно в течение первых 30 дней в Mathcad Express

9013 9013 9013 Стандартный процесс разработки с использованием стандартных шаблонов X Контур, 3D * Библиотеки –

	Express	Подписка
	PTC Mathcad Express	Индивидуальные / множественные лицензии
Новое в Prime 6.0
Проверка орфографии *	*	X
Гиперссылки в тексте *	*	X
Пользовательские поля, верхний колонтитул,			Размеры	X
Удобство использования
Запись уравнений с использованием натуральной математической нотации	X	X
Basic Math				9014 9013 Автоматическое обновление вычислений
Операторы и функции алгебры и тригонометрии	X	X
Документация
Комплексная документация	X	X			X	X
Защита содержимого * 9 0137	*	X
Обертка по уравнениям *	*	X
Построение графиков
XY Plots		*	X
Advanced Math
Программирование *	*	X
Решение систем линейных и нелинейных уравнений –	X
Вычислять выражения символически *	*	X
Встроить Excel прямо в свой рабочий лист *	*	X
Продвинутая инженерная математика: e. грамм. Планирование экспериментов, дифференциальные уравнения, решение регрессии *	*	X
Расширенные числовые функции: например, Преобразования Фурье, обработка сигналов, статистика и анализ данных *	*	X
Варианты лицензий
Централизованное ИТ-управление и администрирование	–	X
X

PTC Mathcad Express включает:

• Натуральное математическое представление
• Автоматическое обновление расчетов
• Операторы и функции алгебры и тригонометрии
• Исчерпывающая документация (объединяющая живую математику, текст, графики и изображения в одном месте)
• X-Y график
• Автоматическая проверка и преобразование единиц измерения
• Основные числовые функции и операторы

Mathcad Premium (лицензионная версия Mathcad) включает:

• Проверка орфографии, гиперссылки и настраиваемые поля, верхние и нижние колонтитулы
• Компонент Excel (интеграция с электронными таблицами Microsoft Excel)
• Защита контента (защита контента с помощью паролей, блокировки и степени доступа)
• Решение и оптимизация
• Программирование (настройка вашей среды в соответствии с вашими конкретными требованиями)
• Шаблоны (просто используйте шаблоны как основу для ваших новых рабочих листов)
• Расширенное черчение
• Symbolics Engine (аналитика / теоретический подход к математике)
• Экспорт в Microsoft Word (возможность сохранения в виде файла документа Word)
• Расширенные математические функции (выполнение линейной алгебры, нелинейной алгебры или манипуляции с матрицами)

Бесплатная пробная версия Mathcad

Загрузите PTC Mathcad Express, чтобы получить 30-дневную пробную версию всех возможностей полностью лицензированной версии PTC MC Prime 6. 0, и когда будете готовы приобрести лицензию, свяжитесь с нами.

FAQ

Можно ли открыть файл Mathcad Prime в Mathcad Express? Таблицы

Mathcad, созданные с помощью полностью лицензированной версии Mathcad Prime, можно открывать в Mathcad Express. В MC Express можно редактировать текст. В MC Express любые изменения, внесенные в математические расчеты, использующие премиум-функцию, выдадут пользователю сообщение о том, что для этой функции требуется лицензия.Математика, созданная с помощью дополнительных функций, не будет вычисляться в MC Express. Соответственно, математика, созданная с помощью функций Express / non-premium, фактически будет пересчитана в MC Express.

Нравится:

Нравится Загрузка …

Связанные

Mathcad – Mathcad_Examples of programming.pdf

Программирование и численные алгоритмы с помощью MathCAD – пример Чтобы показать, как мы можем выполнять элементарное программирование с помощью M

Просмотры 47 Загрузки 1 Размер файла 41KB

Отчет DMCA / Copyright

СКАЧАТЬ ФАЙЛ

Рекомендовать истории

---

Предварительный просмотр цитирования

---

Программирование и численные алгоритмы с помощью MathCAD – пример Чтобы показать, как можно выполнять элементарное программирование с помощью MathCAD, мы рассмотрим задачу расчета траектории полета снаряда. Это классическая физическая задача, имеющая отношение к задаче Lego Pentathlon “Свободный выстрел”. Как обычно, в задачах механики мы начинаем с Ньютона:   F = m a

(стрелки указывают векторные величины)

или   F a = m

Проще всего разбить траекторию на ее векторные компоненты: x-компонент (или диапазон) и y-компонент (или высоту). Обратитесь к примечаниям по проблеме траектории, чтобы увидеть подробности. Рассматривая силы трения, возникающие при столкновении с частицами воздуха аналитически как расширение Тейлора, мы можем записать в первом порядке: Ffriction = α v

, где  называется коэффициентом трения, а v

– скоростью. первый (линейный) член в разложении Тейлора.Это имеет смысл, потому что мы ожидаем, что силы трения увеличиваются по мере увеличения скорости (то есть больше столкновений в единицу времени) и исчезают, когда снаряд находится в состоянии покоя. Однако важно помнить, что могут быть и другие термины «высокого порядка», которыми мы пока пренебрегаем. Теперь давайте составим уравнения, которые необходимо решить. Мы сделаем это «численно», чтобы показать, как можно произвести расчет. Мы также сравним его с аналитическим решением, приведенным в дополнительных примечаниях к этому рабочему листу MathCAD.

В  10

м

«Начальная скорость пули» пусковой установки в м / с

с

θ π  Vx (θ)  V cos  180





Vy (θ)  V sin

θ π 

  180 

X-компонента скорости.  – угол места в градусах Y-компонента скорости.  – угол места в градусах

Напомним, что уравнения движения снаряда можно записать в виде: α d Vx = V mx dt

α d Vy = g   Vy m dt

где  – коэффициент трения (единицы кг / с) и m – масса снаряда (единицы кг).Чтобы решить подобные дифференциальные уравнения численно, мы можем преобразовать производные в «конечные разности». Напомним определение производной: f (x  Δx)  f (x) df (x) = lim Δx dx Δx  0

, если мы примем значение f в x + x равным fi + 1, а значение при x равным fi, тогда мы можем аппроксимировать эту производную с помощью выражения конечных разностей: ffi 1 idf (x) = x x dx i 1 i

Применяя эту формулу к нашим уравнениям движения выше, мы получаем

Vx  Vx i 1 it

i 1

t

=

i

α m

 Vx

Vy  Vy i 1 it

i

i

t

= g 

i

α m

 Vy

i

Их можно преобразовать в более удобную форму: α Vx = 1   t  t   Vx i i 1  imi1





α Vy = g  t  t  1   t  t  Vy i  1 ii  1 i i 1 i  m









Они известны как «конечная разность» уравнения, и они расскажут вам, как вычислить следующее значение Vx или Vy с учетом предыдущего значения. Дискретная разница во времени t

i 1

t

i

может быть записана как t, и мы должны сделать этот интервал

как можно меньшим, чтобы получить хорошее приближение к производной. Конечно, если он слишком мал, то на решение проблемы уйдет больше времени, и в MathCAD могут возникнуть проблемы конвергенции

проблемы конвергенции. Приступим к решению для скорости. Сначала задаем наш дискретный временной интервал и константы: α  1 

кг

Коэффициент трения

с

м  1  кг Δt  5  10

Масса снаряда в кг  2

s

Интервал времени в секундах Количество точек для оценки

n  500

Чтобы вычислить скорость, мы создадим небольшой цикл программирования в MathCAD:

Vx (θ) 

Здесь мы начали определять x-компонент скорости.Панель программирования добавляется щелчком на панели инструментов программирования и последующим щелчком по «Добавить строку» Vx (θ) 

Vx  V cos (θ) 0

Теперь мы присвоили начальное значение скорости как x-компонента начальной скорости. Нам потребуются дополнительные операторы в нашей программе, поэтому на красном квадрате мы еще раз нажимаем «Добавить строку»: Vx (θ) 

Vx  V cos (θ) 0 i1

Здесь мы определили наш “счетчик” целое число i и присвоил его начальное значение 1.Нет, мы снова расширяем нашу строку программирования с помощью «Добавить строку» и настраиваем цикл «for-next». Этот цикл выполняется для всех значений i, которые меньше максимального значения n. Внутри цикла увеличивается целое число счетчика и вычисляются последующие значения Vx:

Vx (θ) 

π  Vx  V cos θ  0180





i0 для i  0  n α  1   (Δt)   Vx Vx i 1  m  iii1 Vx

Этот последний шаг сообщает MathCAD, куда поместить данные из расчет.Мне это кажется немного избыточным, но так устроен синтаксис программы. Теперь проделаем то же самое для y-компоненты скорости:

Vy (θ) 

π  Vy  V sin θ  0180





i0 для i  0  n α Vy  g  (Δt)  1   (Δt)   Vy i 1  m  iii1 Vy

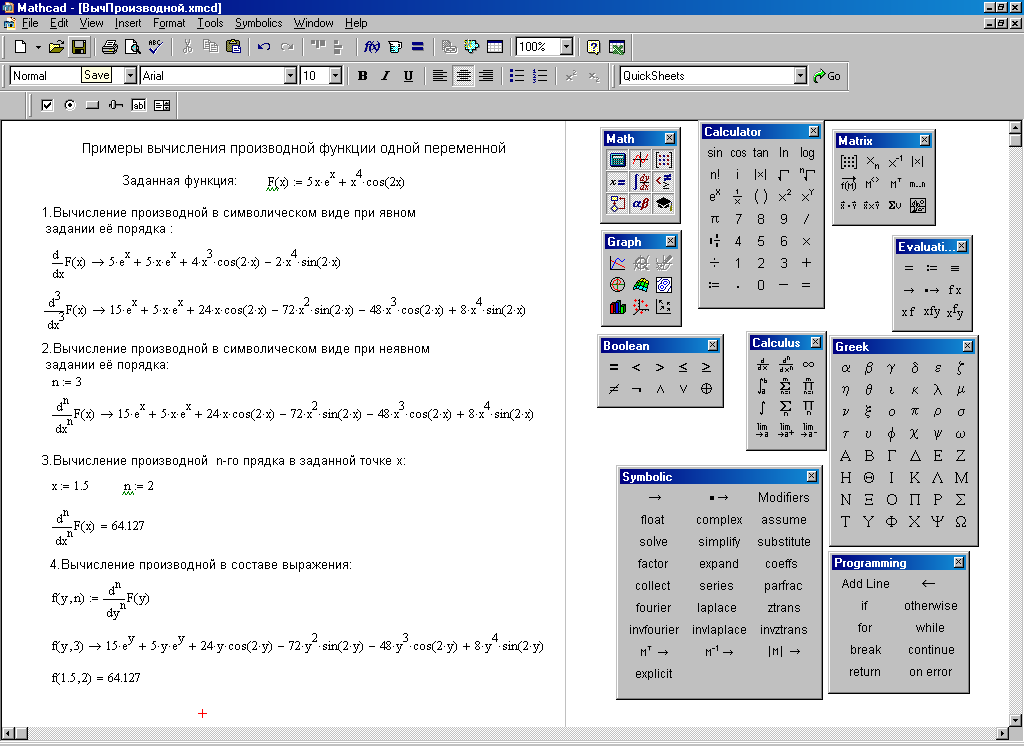
Мы можем перечислить значения Vx и Vy, просто используя знак «=»:

0

Vx (45) 

0

0

7. 071

0

7,071

1

6,718

1

6,227

2

6,382

2

5,425

3

5,425

3

4

3,94

5

5,471

5

3,253

6

5,198

6

2,6

7

4,938

7

98

8

4,691

8

1,39

9

4,457

9

0,831

10

4,234

10

0,2996

10

0,2996

9000 207

мс

Vy (45) 

мс

11

4,022

11

-0,207

12

3,821

12

-0,687

-0,687

3

13

-1,143

14

3,448

14

-1,576

15

…

15

…

Теперь, когда мы нашли компоненты x и y скорости, мы можем вычислить координаты положения, x и y. x

i 1

 x  Vx  Δt ii

y

i 1

 y Vy  Δt ii

Для оценки этих величин мы настроили петли, как и раньше: Xinitial  0  mx (θ) 

Yinitial  0  m

i0

y (θ) 

i0

x  Xinitial 0

y  Yinitial 0

для i  0  n

для i  0  n

x

i 1

 x  Vx (θ)  Δt ii

y

ii1

i 1

 y  Vy (θ)  Δt ii

ii1

x

y

Теперь построим траекторию для нескольких углов запуска.Мы также сравним численное решение с точным решением, полученным в сопроводительных примечаниях: χ (τ θ)  V cos θ

  m   1  exp α  τ       180  α   m 

 m   g m  V sin θ π     1  exp α  τ   g m  τ         α α  α  180     m  

ψ (τ θ) 

τ  0  s 1  10

π

3

 s  10 s

Задайте для параметра времени диапазон значений

3 y (60) ψ (t 60)

2. 7 2,4 2,1

y (45)

1,8 ψ (t 45) 1,5 y (30)

1,2

ψ (t 30) 0,9 0,6 0,3 0

0

0,6

1,2

1,8

2,4

3

3,6

4,2

4,8

x (60) χ (t 60) x (45) χ (t 45) x (30) χ (t 30)

5,4

6

e

Программы проектирования и анализа конструкций

Программы проектирования и анализа конструкций
Заявление об отказе от ответственности:	Несмотря на то, что эта программа прошла множество испытаний – все с удовлетворительными результатами – Департамент транспорта штата Нью-Йорк не дает никаких явных или подразумеваемых гарантий относительно точности и функционирования программы, а также факт распространения не является каким-либо такая гарантия, и Департамент транспорта штата Нью-Йорк не несет никакой ответственности в связи с этим.Загружая любые программы или рабочие листы, вы соглашаетесь с вышеуказанным отказом от ответственности.
Mathcad – Рабочие листы абатмента LRFD и стенки крыла
Содержимое:	Рабочие листы Mathcad Prime 7.0 были созданы для анализа и проектирования абатментов и стенок крыла в соответствии со Спецификациями проектирования мостовидного протеза AASHTO LRFD, 9-е издание, 2020 г. Рабочие листы не включают программу, посетите http: // www.ptc.com/products/mathcad/ для получения информации о получении программы Mathcad.
Статус:	Выпущено в июле 2009 г., последнее обновление – в августе 2021 г.
Контакты:	вопросов – Ратан М. Худа (518) 457-5877, электронная почта: [email protected]
Загрузить:	Mathcad Prime, рабочие листы для подпорных стенок и крыльев LRFD в единицах USC, последнее обновление – май 2021 г. (2.1 Мб) Таблицы абатментов Mathcad Prime 7. 0 LRFD в единицах USC, широта Обновлено в августе 2021 г. (1,0 МБ)
Mathcad – Таблицы подшипников LRFD
Содержимое:	Следующий заархивированный файл содержит рабочие таблицы Mathcad, в которых анализируются и проектируются эластомерные мостовые опоры в соответствии со спецификациями AASHTO LRFD 2012 с промежуточными редакциями 2013 года.Они доступны для загрузки только в единицах USC. Рабочие листы не включают программу, посетите http://www.ptc.com/products/mathcad/ для получения информации о получении программы Mathcad.
Статус:	Выпущено в июле 2009 г., последнее обновление – в июле 2021 г.
Контакты:	Вопросы – Трой Сока (518) 485-0138, электронная почта: Трой[email protected]
Загрузить:	Mathcad Prime 7.0 LRFD Таблицы эластомерных мостовых подшипников в единицах USC (1,0 МБ) Mathcad V15 LRFD Elastomeric Bridge Bearing Worksheets в единицах USC (2,0 Мб)
Таблица открывания швов без брони
Содержимое:	Следующий файл содержит электронную таблицу Excel, используемую для расчета размера проема для соединений без броневого моста штата Нью-Йорк.
Статус:	Выпущено в сентябре 2020 г., Последнее обновление – в сентябре 2020 г.
Контакты:	вопросов – Эрик Ланци (518) 485-5270, электронная почта: [email protected]
Загрузить:	Таблица открытия соединений без брони (35 кб)
Программа Scupper
Содержимое:	Следующий файл содержит электронную таблицу Excel, используемую для определения местоположения шпигатов на надстройке моста.
Статус:	Выпущено в марте 2021 г., последнее обновление – в марте 2021 г.
Контакты:	вопросов – Андреа Ридман (518) 485-7263, электронная почта: [email protected]
Загрузить:	Программа NYSDOT Scupper, v1.0 (1,37 Мб) NYSDOT Scupper Program User Manual, v1. 0 (1.0 Мб)

Mathcad

Mathcad

Mathcad

Mathcad будет использоваться на протяжении всего курса в качестве вспомогательного средства для решения уравнения, построение трендов и т. д. Студентам следует ознакомиться либо с Mathcad, либо с некоторыми аналогичная математическая программа. Обратите внимание, что профессор Цимбала использует только Mathcad, поэтому он не может помочь с Matlab, Mathematica, TKSolver и т. д., но если учащиеся хотят использовать одну из этих программ, они могут это сделать.

Все студенты, зарегистрированные на курс, могут использовать свои удостоверения личности для доступа в лабораторию ME PC 24 часа в сутки, 7 дней в неделю для использования Mathcad. Mathcad также доступен в большинстве компьютерных классов университета. Студентам следует ознакомиться с переплетенными копиями руководства Mathcad по резервному копированию. в инженерной библиотеке или на веб-сайте Mathcad, www. mathsoft.com для дополнительной информации.

Вот несколько примеров файлов Mathcad, которые вы можете скачать.Чтобы скачать и использовать:

1. Щелкните нужный файл.
2. В зависимости от вашего браузера, будь то ПК или Unix-машина, и как он настроен, он либо запустит Mathcad или подскажет, хотите ли вы открыть файл или сохранить его на диск.
3. Если на вашем компьютере есть Mathcad, выберите вариант открытия файла. (Возможно, вам придется просмотреть, чтобы найти правильное приложение.)
Примечание. На некоторых машинах Mathcad не может быть запущен, когда это файл запускается.
4. Вы также можете щелкнуть правой кнопкой мыши по желаемому файлу, чтобы увидеть другие параметры, такие как сохранение файла на диск.
5. Если Mathcad не существует на вашем компьютере, выберите вариант сохранения файла на диск. Затем вы можете отправить его по FTP в другое место, чтобы запустить файл.

Примеры общего назначения:

• Sample_simple_set_of_simpleous_equations. mcd – Простой пример того, как численно решить три одновременных уравнения.
• numeric_simterationous_equations.mcd – Более сложный пример численного решения двух одновременных уравнений.
• symbolic_simterationous_equations.mcd – Пример того, как решить два одновременных уравнения символически .
• одновременное_выражение_without_initial_guesses.mcd – Умный способ решения одновременных уравнений без необходимости исходных предположений .Решение представляет собой комбинацию символического и численного подходов.
• sample_read_data.mcd – Показывает, как читать данные из текстового файла в Mathcad, а затем сгенерируйте график данных.
  Примечание. Чтобы этот рабочий лист Mathcad работал правильно, также необходимо скачать текстовый файл:
  Чтобы загрузить этот текстовый файл, щелкните по нему. Если ваш браузер открывает его и его можно просмотреть, скопируйте все это и вставьте в файл, используя свой любимый редактор. Назовите файл my_data_points.txt и поместите его в тот же каталог. как рабочий лист mathcad. Если ваш браузер спросит, что делать с файлом, сохраните его как текстовый файл в каталоге рабочего листа mathcad.
  Вот текстовый файл:
  my_data_points.txt

Примеры из учебника МЭ 405:

• Example_1_9_Simple_intage_kutta_integration.mcd – Показывает, как использовать процедуру Рунге-Кутты Mathcad для решения простого ОДУ в стандартной форме (Пример 1.9 в тексте).
• example_2_1.mcd – Показывает, как составлять уравнения и как построить график для Пример задачи 2.1 в учебнике (влияние эмфиземы на поглощение газа).
• Runge_Kutta_body_burden_example.mcd – Использует программу Рунге-Кутты Mathcad для решения ODE для нагрузка на тело как функция времени (пример 2.4 в тексте).
• Example_5_5.mcd – Умный турист – Показывает, как составлять уравнения и строить график для Пример задачи 5. 5 в учебнике МЭ 405 (концентрация угарного газа в салоне с неисправным керосиновым обогревателем).
• Example_5_6.mcd – Отремонтированный конференц-зал – Показывает, как составлять уравнения и строить график для Пример задачи 5.6 в учебнике ME 405 (комната с новым ковром и непостоянным расходом воздуха).
• Terminal_velocity_calculation.mcd – Программа для расчета конечной скорости осаждения частицы, используя уравнения главы 8.Пример для воздуха в STP, но свойства (P и T) воздуха можно легко изменить.
• Particle_trajectory_at_STP.mcd – Программа Рунге-Кутта для расчета траектории частицы, используя уравнения главы 8. Пример для воздуха в STP, где U _x = 1 м / с и U _y = 0 (т.е. поток набегающего потока), но поле скорости воздуха можно легко изменить, чтобы оно зависело от x и y.

Mathcad Prime (Австралия)

Примечание. Для получения справки по установке Mathcad в первый раз щелкните ЗДЕСЬ. Однажды Mathcad запускается, появляется интерфейс холста рабочего листа как показано ниже. Различные регионы для этого интерфейса помечены для справки:

.

Mathcad Prime предлагает обновленный пользовательский интерфейс ленты на основе Microsoft ^® . Свободный пользовательский интерфейс. С помощью ленты пользователи получают быстрый доступ ко всем основным командам для математические, графические символьные параметры, а также различные функции редактирования и управление таблицами Mathcad. Открытие, сохранение, печать и Mathcad доступ к параметрам можно получить, щелкнув значок или выбрав значки в левый верхний угол.Все основные функции Mathcad разделены на категории, которые отображаются на вкладках в верхней части ленты.

Вставка текста, функций, значений и изменение системы единиц в Mathcad

В Mathcad положение в рабочей области показано синим перекрестием ( + ). Выбрав позицию на листе, вы сможете ввести значения, текст или уравнение в этом месте. Простая арифметика может быть вводится с помощью цифровой клавиатуры, расположенной с правой стороны клавиатуры.Введя знак равенства ( = ) после расчет, Mathcad предоставит решение. Добавляя разные единицы в предыдущее уравнение, просто повторно щелкнув область, в которой уравнение введено, позволит Mathcad пересчитать ответ в единицах измерения. Чтобы изменить единицы в окончательном ответе, просто удалите старую единицу и введите новые единицы, которые вы хотите отобразить.

В зависимости от регионального распределения Mathcad Prime, европейский версия будет иметь единицы измерения, основанные на системе СИ – однако вы можете изменить в британские / американские единицы, выбрав вкладку Математика> Единицы> Система единиц> Выберите либо SI / USCS / CGS.Единицы также можно вставить с помощью кнопки Единицы таб.

Пользователь также может перемещать одиночные или множественные вычисления в рабочей области. щелкнув левой кнопкой мыши по региону или выделив несколько регионов. Пользователь будет обратите внимание, что над выделенным полем появится значок белой оси, что позволит вам свободно перемещать вычисления в рабочем пространстве. Чтобы отменить выбор региона, просто щелкните другую часть рабочей области.

Ошибки и проверка решения для расчеты

Алгебраические выражения также можно вводить в Mathcad, а затем можно сгенерировать решение с заданными значениями.Для этого сначала нужно ввести выражение, а затем над ним введите значения различных терминов, отображаемых в уравнение. Обратите внимание, что если уравнение показывает некоторые выделенные части уравнение, это говорит пользователю, что он или она не вводили необходимые значения для выработки решения уравнения. Mathcad предоставляет ответ на выделенную ошибку в расчете нажатием на ошибку сам. Будет дано небольшое описание. Примечание: при вводе выражений используйте клавишу с двоеточием Shift + [:], так как это сообщает Mathcad, что вы присваиваете значение вместо того, чтобы оценивать это. Например, на изображении ниже вы можете увидеть, что Mathcad обнаружил проблему с моим вычислением здесь y. Она имеет выделил «b» красным, чтобы сказать мне, что я еще не определил его. Если я тогда продолжу для оценки “y” будет показано следующее сообщение:

Ввод символов и других функций с помощью ярлыков

Многие функции сгруппированы в сочетания клавиш. Примером этого являются греческие символы, которые чаще всего используются в инженерные уравнения и расчеты.Другие программы, такие как Excel, требуют вы должны перейти к картам персонажей и выбрать отдельный символ, а затем вставьте их в поле, затем вырежьте и вставьте выражение в желаемое уравнение. В Mathcad есть несколько сокращений. Например. символ пи. К создайте символ pi, вам просто нужно ввести букву p, а затем CTRL + G изменить его π. Дополнительные примеры других ярлыков можно найти, перейдя в вкладка «Приступая к работе»> «Сочетания клавиш». Это приведет вас к Mathcad ^® Prime ™ 3. 1 Сочетания клавиш pdf.

Графики

Графики различных точек могут выполняться по-разному в зависимости от на значениях, которые используются, а также на функции, которая используется для сгенерировать график. Теперь, создав таблицу значений (сделано по праву щелкнув в рабочей области> вставить таблицу или перейти к Матрицам / Таблицам tab> Insert Table ), вы можете использовать это для определения вашего графика. В первую очередь, вам нужно будет ввести значения в соответствующие поля, включая единицы.Пример показан ниже. Как только таблица определена, Наборы данных x и y можно использовать так же, как и векторы-столбцы. Чтобы оценить векторов введите x = и y = , и они будут автоматически созданный.

В качестве альтернативы вы можете создавать графики напрямую, определяя ваша матрица (x: =), а затем введите [Ctrl + M] , чтобы открыть матрицу или перейдя на вкладку Матрицы / Таблицы> Вставить матрицу . потом вы просто вводите свои значения.

После того, как значения осей x и y будут введены, перейдите на вкладку Графики> Вставить график> XY Plot . Это даст вам график который выглядит следующим образом:

Теперь вам нужно определить оси X и Y, введя наборы данных в заполнители . Как только вы это сделаете, нажмите вне поля графика, чтобы сгенерировать график. Вы можете отрегулировать верхнюю и нижние пределы значений осей x и y, нажав на первую и последнюю предельные значения на оси и их изменение.График также можно отформатировать основанный на предпочтении цвета, стиля, а также отображение линий сетки на графике. Все эти функции форматирования доступны на вкладке “Графики”, когда вы работаю на участке.

Множественные алгебраические выражения различных графов могут быть поместил все на особый график, чтобы сравнить различия между функциями составлен. Это делается с помощью функции Добавить трассировку один раз в участок. Цвет трассировки можно изменить с помощью функции цвета трассировки.

3D-графики могут быть созданы в Mathcad, перейдя в Plot Вкладка> Вставить график> 3D график. Ввод выражения, которое имеет более одного переменная сгенерирует трехмерный график. Интеграция нескольких выражений в один трехмерный график можно построить с помощью матричной функции, введя имя выражения с двумя переменными, создавая матрицу со строками и ввод значений в скобки матрицы. Изменение внешнего вида 3D-модель очень похожа на линейные 2D-графики.Это делается используя функции форматирования, доступные один раз в графиках. Примечание: помните, что не требуется вводить все выражение в график, так как вы может ссылаться на выражение через назначенную букву, как показано в этом примере.

Приложение: Интеграция Mathcad 15.0 с PTC Creo

Mathcad может быть интегрированным в различные программы продуктов PTC. В этом руководстве мы рассмотрим, как интегрироваться в Creo с помощью параметры, а также отношения внутри модели в Pro / Engineer.Во-первых, начните с создания детали, которую вы хотите использовать в профессиональном инженере. Здесь мы создали цилиндр для этого примера. После завершения мы переходим к вверху меню и перейдите в инструменты / параметры. Далее мы вводим новый параметр, переименуйте параметр в соответствующее имя и затем добавьте значение. Затем перейдите в правую часть меню и вставьте единицы измерения для рост.

Нажмите ОК для подтверждения. Затем перейдите в верхнее меню, чтобы анализ / внешний анализ, а затем в анализ Mathcad, это откроет новый диалог, как показано ниже.Вверху диалога вы можете загрузить ранее созданные рабочие листы Mathcad или создайте новый рабочий лист, который будет использоваться в Анализ. Нажмите «Создать», и откроется новый рабочий лист для Mathcad. Создать ссылка из Mathcad на Creo. Необходимо использовать нижний индекс здесь в выражениях, которые выписаны. Мы связали подписанные значение высоты обратно к высоте слова, чтобы убедиться, что Mathcad обрабатывает до правильного значения. А еще мы добавили сюда дополнительную строку с высотой [=], чтобы убедиться, что значение создано правильно.Далее нам нужно связать выражений в Pro / Engineer, перейдя в свойства к первому выражение, а затем перейдите в поле тега и введите proe2mc . Это сообщает разработчику программы, что нужно получить поле ввода из этого Mathcad. файл. Последнее выражение высоты, которое мы будем использовать, перейдем к свойствам, тегам и введите mc2proe. Это определяет поле вывода из Mathcad в Pro / Engineer. модель. После завершения нажмите «Сохранить» и присвойте файлу имя.

А теперь вернись в Creo в диалоговом окне Mathcad Analysis, нажмите кнопку загрузки и выберите Рабочий лист Mathcad, который вы создали.Затем перейдите в диалог, чтобы добавить параметр, выберите имя параметра, который был создан до и после щелкните поле ввода в Mathcad, которое было « Height_proe », и щелкните Ладно. Выйдите из дополнительного диалогового окна и перейдите к полю поля вывода в Диалоговое окно анализа Mathcad. Выберите поле вывода “ height_proe “. определены в Mathcad, и для тестирования мы будем использовать кнопку вычисления. Однажды это значение показывает, что он сработал, дав значение, которое мы определили в параметры в этом примере, мы нажимаем добавить функцию, называем анализ соответственно и затем сохраните.

Затем перейдите к отношениям, где нам нужно будет определить взаимосвязь значения высоты в модели с Mathcad рабочий лист. Для этого мы переходим в верхнее меню инструменты / отношения и вводим край для работы, выражение для использования, найденное в Mathcad, а затем где Анализ находится в дереве функций. Здесь показан пример цилиндра рост.

После завершения проверьте взаимосвязь, чтобы убедиться, что Creo, а затем щелкните “Восстановить”.Следует помнить, что если вы изменяете значения в параметрах после регенерации модели.