Пример: \(y = arccot( 2) => у’ = \frac{-1}{ 1+4} = \frac{-1}{ 5} \)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы “Альфа”. Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Вера Петровна Любчак
Репетитор по математике
Стаж (лет)
Образование:
Университет штата Аризона
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Владимир Николаевич Плехов
Репетитор по математике
Стаж (лет)
Образование:
Гомельский государственный университет им.
Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Мария Сергеевна Чуракова
Репетитор по математике
Стаж (лет)
Образование:
Московский государственный областной университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Физика
- Химия
- Русский язык
- Английский язык
- Обществознание
- История России
- Биология
- География
- Информатика
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Подготовка к ОГЭ по английскому языку
- Репетитор по английскому для взрослых
- Репетитор по истории для подготовки к ОГЭ
- ВПР по обществознанию
- Подготовка к ЕГЭ по биологии
- Подготовка к ОГЭ по биологии
- Подготовка к ОГЭ по литературе
Похожие статьи
- Пропорция в математике
- Свойства интегралов
- Биофак МГУ: что сдавать для поступления
- ЕГЭ по математике, профильный уровень.
Задачи по планиметрии - Нахождение нескольких частей числа
- Закаливание детей: мифы и реальность или почему нельзя сходу с головой в прорубь?
- Как вести себя со сложными подростками?
- Лучшие идеи декора на Хэллоуин своими руками
Задачи по планиметрииНажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Частные производные. Примеры решений
Частные производные. Примеры решений
На данном уроке мы познакомимся
с понятием функции двух переменных,
а также подробно рассмотрим наиболее
распространенное задание – нахождение частных производныхпервого
и второго порядка, полного дифференциала
функции.
Для эффективного изучения
нижеизложенного материала Вам
Начнем с самого понятия
функции двух переменных, я постараюсь
ограничиться минимумом теории, так
как сайт имеет практическую направленность.
Функция двух переменных обычно записывается
как
, при этом переменные
,
называются независимыми переменными или аргументами.
Пример: – функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Полезно знать геометрический смысл функций. Функции одной переменной соответствует определенная линия на плоскости, например, – всем знакомая школьная парабола. Любая функция двух переменных с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ, который никогда не давал списывать мой вузовский преподаватель является моим «коньком».
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных
справедливы все правила 
Есть только пара небольших
отличий, с которыми мы познакомимся прямо
сейчас.
Пример 1
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения:
или
– частная производная по «икс»
или
– частная производная по «игрек»
Начнем с . Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).
Решаем. На данном уроке я буду приводить полное решение сразу, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем
при нахождении частной
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу
решения. В данном случае, если Вы где-нибудь
нарисуете «штрих» без
, то преподаватель, как минимум, может
поставить рядом с заданием
(сразу откусить часть балла за невнимательность).
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».
(3) Используем табличные производные и .
(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.
Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).
(1) Используем те же
правила дифференцирования
,
. В первом слагаемом выносим константу
за знак производной, во втором слагаемом
ничего вынести нельзя поскольку
– уже константа.
(2) Используем таблицу
производным элементарных
Итак, частные производные первого порядка найдены
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:
1) Когда мы находим частную производную , переменная считается константой.
2) Когда мы находим частную производную , переменная считается константой.
3) Правила и
таблица производных
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
или
– вторая производная по «икс»
или
– вторая производная по «игрек»
или
– смешанная производная
«икс по игрек»
или
– смешанная производная
«игрек по икс»
В понятии второй производной
нет ничего сложного.
Говоря простым
языком, вторая производная
– это производная от первой производной.
Для наглядности я перепишу
уже найденные частные
Сначала найдем смешанные
производные:
Как видите, всё просто: берем частную производную и дифференцируем ее еще раз, но в данном случае – уже по «игрек».
Аналогично:
Для практических
примеров справедливо следующее
равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную
по «икс».
Никаких изобретений, берем
и дифференцируем её по «икс» еще раз:
Аналогично:
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для проверки не существует.
Пример 2
Найти частные производные первого и второго порядка функции
Это пример для самостоятельного
решения (ответ в конце урока).
Если возникли трудности с дифференцированием
корней, рекомендую ознакомиться уроком Как
найти производную?
При определенном опыте частные производные из примеров №№1,2 будут решаться Вами устно.
Переходим к более сложным примерам.
Пример 3
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Решение: Находим частные
производные первого порядка:
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
Дальнейшие комментарии:
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы
за знак производной, в данной
случае константой является
.
(2) Под штрихом у нас
осталось произведение двух
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .
Теперь находим смешанные производные второго порядка:
, значит, все вычисления выполнены верно.
Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого
порядка функции двух переменных
имеет вид:
В данном случае:
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:
Пример 4
Найти частные производные
первого порядка функции
.
Проверить, что
. Записать полный дифференциал первого
порядка
.
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5
Найти частные производные
первого порядка функции
.
Записать полный дифференциал
.
Решение:
(1) Применяем правило
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.
Аналогично:
Запишем полный дифференциал
первого порядка:
Пример 6
Найти частные производные
первого порядка функции
.
Записать полный дифференциал
.
Это пример для самостоятельного
решения (ответ в конце урока).
Полное решение не привожу, так как
оно достаточно простое
Довольно часто все
вышерассмотренные правила
Пример 7
Найти частные производные
первого порядка функции
.
(1) Используем правило дифференцирования суммы
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки». Знаете, всегда приятно, когда дробь удается превратить в ноль). Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в этом смысле ничего бы не изменилось, если бы вместо была дана функция – важно, что здесь произведение двух функций, КАЖДАЯ из которых зависит от «икс», а поэтому, нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
(1) В первом слагаемом
и в числителе и в знаменателе
содержится «игрек», 
Второе слагаемое зависит ТОЛЬКО от «икс»,
значит,
считается константой и превращается
в ноль. Для третьего слагаемого используем
правило дифференцирования сложной функции.
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:
Однажды в пространстве
функций появилась злобная
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Пример 8
Найти частные производные
первого порядка функции
.
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.
Пример 9
Дана функция двух переменных . Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Желаю успехов!
Ответы:
Пример 2: , , , ,
Пример 4: Ссылка для просмотра или скачивания ниже.
Пример 6: , ,
Примеры 8, 9:
Производные тригонометрических функций | Superprof
Нахождение производной функции является важным понятием исчисления.
Производная функции определяется следующим образом:
«Производная — это мгновенная скорость изменения функции в данной точке»
Процесс нахождения производных известен как дифференцирование . Обычно различают два типа функций: явные и неявные. В этой статье мы изучим, как дифференцировать явные тригонометрические функции. Мы используем правила дифференцирования, чтобы найти производные явных функций. Некоторые из общих правил дифференцирования – это правило констант, правило сумм, правило разности, правило степени, правило произведения, правило частного (используемое для дробей) и правило цепи.
Прежде чем перейти к соответствующим формулам и примерам, давайте сначала выясним, что такое тригонометрические функции.
Что такое тригонометрические функции?
Тригонометрия является важной отраслью математики, в которой мы изучаем отношения между сторонами и углами треугольника. Тригонометрические функции говорят нам, как углы треугольника связаны с его сторонами.
Другими названиями триггерных функций являются круговые функции, гониометрические и угловые функции. Однако слово «тригонометрические» широко используется для описания таких функций. Наиболее распространенными тригонометрическими функциями являются синус, косинус, тангенс, котангенс, косеканс и секанс. Обратные функции тригонометрических функций известны как обратные тригонометрические функции. Обратные тригонометрические функции также известны как функции дуги, циклометрические функции или антитригонометрические функции.
Прежде чем перейти к примерам, выясним производные обычных тригонометрических функций. Всегда лучше запомнить их, поскольку они используются для дифференциации функций, включающих тригонометрические функции.
Лучшие репетиторы по математике
Поехали
Производная синуса
Производная функция косинуса
Производная функция касательной
Производная функция котангента
.
Производная функции косеканса
Примеры производных тригонометрических функций
Пример 1
Вычислить производную от
Решение
Пусть
Мы знаем, что если , то . Это означает, что мы умножим производную внутренней функции u на производную внешней функции sin.
В этом примере . Следовательно, . Подставим его в приведенную выше формулу, чтобы получить окончательный ответ:
Так как , следовательно .
Пример 2
Дифференцировать
Раствор
Допустим .
Мы знаем, что если , то .
Здесь u = . Мы применим степенное правило, чтобы найти u ‘. Пример 3 Мы будем использовать цепное правило снова и снова, чтобы найти производную этой функции.
Помните об этом.
Пример 4
Дифференцировать
Решение
Эту функцию можно записать как
Мы знаем, что производная функции косинуса равна .
В приведенной выше функции , поэтому
Пример 5
Дифференцировать
Решение
Предположим .
Мы знаем, что если , то . Это означает, что производная внутренней функции будет умножена на косинус производной внешней функции.
Если , то .
Пример 6
Дифференцировать
Решение
Предположим .
Мы знаем, что если , то
Здесь, . Следовательно, .
Пример 7
Дифференцировать
Решение
Предположим .
Мы знаем, что если , то .
Пример 8
Дифференцировать
Решение
Предположим
Мы знаем, что если , то . Теперь подставим и, чтобы получить производную функции.
Пример 9
Дифференцировать
Решение
Предположим .
Мы знаем, что если , то
Замена и даст нам окончательный ответ на этот вопрос.
Пример 10
Дифференцировать .
Решение
Эта функция включает две тригонометрические функции, синус и косинус. Чтобы дифференцировать эту функцию, мы будем использовать правило разности производных и правило производной мощности.
Мы будем упростить и переписать его как:
Пример 11
Дифференциал
Решение
Мы будем использовать правило деривативного сумасшедшего, чтобы дифференцировать функцию выше.
После упрощения получим следующую производную функции.
5. Производная логарифмической функции
М. Борна
Далее На этой странице
Производная y = ln x
Производная логарифма функции
Производная логарифмов с основанием, отличным от e
Во-первых, давайте посмотрим на график логарифмической функции с основанием e , то есть:
f ( x ) = log e ( x ) (обычно пишется «ln x »).
Тангенс в точке x = 2 включено в график.
1234567-1123-1-2-3-4xy12slope = 1/2Открыть изображение на новой страницеГрафик `y=ln(x)`, показывающий касательную при `x=2`
Наклон касательной y = ln x при `x = 2` равен `1/2`. (Мы можем наблюдать это на графике, глядя на соотношение рост/рост).
Если y = ln x ,
| `х` | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| наклон графика | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
| `1/x` | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
Мы видим, что наклон графика для каждого значения x равен `1/x`.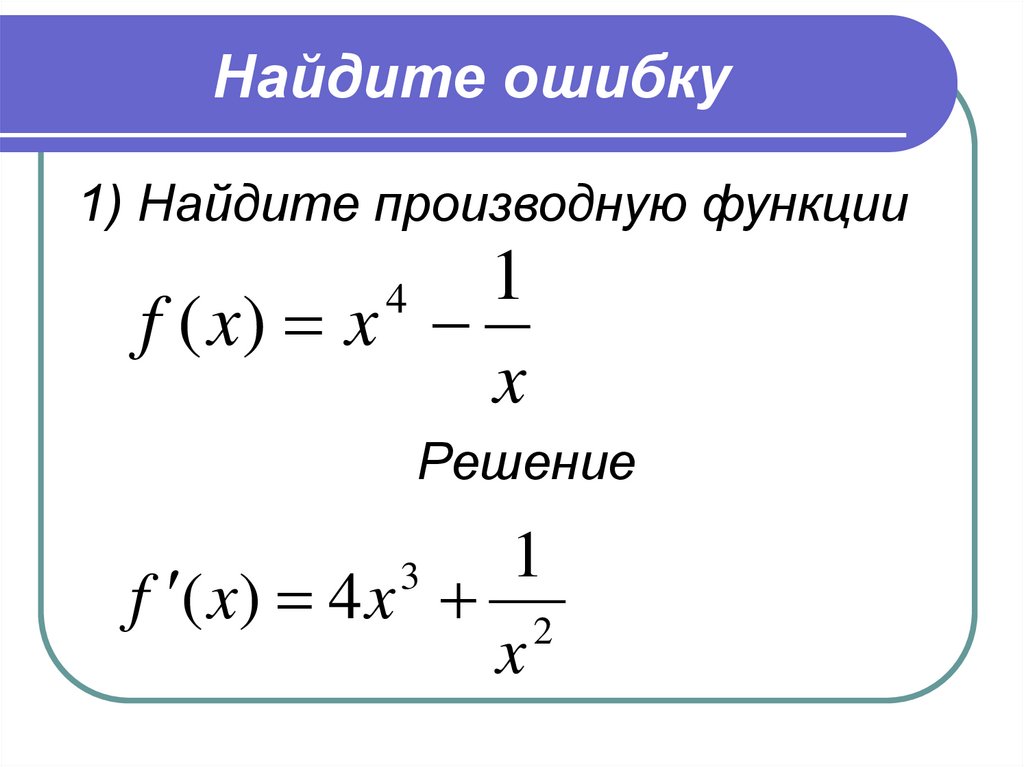
Это работает на любое положительное значение x (конечно, у нас не может быть логарифма отрицательного числа).
Если бы мы сделали еще много примеров, мы могли бы заключить, что производная логарифмической функции y = ln x равна
`dy/dx = 1/x`
Примечание 1: На самом деле этот результат исходит из первых принципов.
Примечание 2: Мы используем логарифмы с основанием e . Если вам нужно напоминание о функциях журнала, ознакомьтесь с Log base 9.0005 e от предыдущего.
Производная логарифмической функции
y = ln xПроизводная логарифмической функции y = ln x определяется как:
`d/(dx)(ln\ x)=1/x`
Вы увидите, что это написано и несколькими другими способами. Следующие эквивалентны:
`d/(dx)log_ex=1/x`
Если y = ln x , то `(dy)/(dx)=1/x`
Теперь мы покажем, откуда взялась формула для производной `log_e x`, используя первые принципы.
Доказательство формулы
Для этого доказательства нам понадобится следующая базовая математика.
Формула первых принципов для производной функции `f(x)`, то есть:
`(df)/(dx) = lim_{h->0}(f(x+h)-f(x))/h`
Законы логарифмирования
`журнал a – журнал b= журнал (a/b)`
и 9{1″/”t}` приближается к значению `e~~2.71828`.)
Я буду писать `log(x)` так, чтобы это означало `log_e(x) = ln(x)`, чтобы его было легче читать .
У нас есть `f(x) = log(x)`, поэтому производная будет равна:
`(df)/(dx) = lim_{h->0}(log(x+h)-log(x))/h `
Теперь вершина нашей дроби равна
.`log(x+h)-log(x)` `= log((x+h)/x)` `= log(1 + h/x)`.
Чтобы упростить алгебру, мы теперь заменим `t=h/x`, и это даст нам `h = xt`. Конечно 9{1″/”t})`
` = 1/x log(e)`
` = 1/x`
Совет
Для некоторых задач мы можем использовать законы логарифмирования, чтобы упростить наше логарифмическое выражение перед его дифференцированием.
Пример 1
Найдите производную числа
у = ln 2 х
Ответить
Используем логарифмический закон:
log ab = log a + log b
Мы можем написать наш вопрос как:
у = пер 2 х = пер 2 + пер х
Теперь производная константы равна 0, поэтому
`d/(dx)ln\ 2=0`
Итак, у нас осталось (из нашей формулы выше)
`d/(dx)(ln\ x)=1/x`
Окончательный ответ:
`(dy)/(dx)=1/x`
Из следующего графика видно, что наклон y = ln 2 x (кривая зеленого цвета, касательная пурпурного цвета) совпадает с наклоном y = ln x (кривая серого цвета, касательная серого штриха) в точке x = 2.
2=2 d/(dx)ln\ x=2/x` 92) на самом деле имеет 2 «руки», одну с отрицательной стороны и одну с положительной. На приведенном выше графике для простоты показано только положительное плечо.
Производная от
y = ln u (где u есть функция x )К сожалению, мы можем использовать законы логарифмирования только в ограниченном числе типов вопросов на дифференциацию логарифмов.
Чаще всего нам нужно найти производную логарифма некоторой функции х . Например, нам может понадобиться найти производную от y = 2 ln (3 x 2 – 1).
Для решения таких задач нам понадобится следующая формула.
Если
y = ln u
и u есть некоторая функция x , тогда:
`(dy)/(dx)=(u’)/u`
, где u’ является производным от u
Другой способ написать это
`(dy)/(dx)=1/u(du)/(dx)`
Вы также можете увидеть следующую форму.
Это означает то же самое.
Если
y = ln f ( x ),
, тогда производная от и будет равна:
`(dy)/(dx)=(f'(x))/(f(x)`
Пример 3
Найдите производную из
92-1)`Пример 4
Найдите производную из
y = ln(1 − 2 x ) 3 .
Ответить
Во-первых, мы упростим наше логарифмическое выражение, используя логарифмический закон:
log a n = n log a
Мы можем написать
y = ln(1 − 2 x ) 3 = 3 ln(1 − 92+1)`
Затем мы используем следующее правило (дважды), чтобы различать два термина журнала:
`(dy)/(dx)=(u’)/u`
На первый срок
u = sin 2 х
u ‘ = 2 cos 2 х
Для второго члена ставим
u = х 2 + 1,
дача
и ‘ = 2 92+1)`
Дифференцирование логарифмических функций с основанием, отличным от
eЕсли
u = f ( x ) является функцией x ,
и
y = log b u — логарифм с основанием b ,
, то мы можем получить производную логарифмической функции с основанием b , используя:
`(dy)/(dx)=(log_be)(u’)/u`
где
`u’` является производным от u
log b e — константа.
См. изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.) Примечание 1: Эта формула получена из первых принципов.
Примечание 2: Если мы выберем e в качестве базы, то производная ln u , где u является функцией x , просто дает нам нашу формулу выше:
`(dy)/(dx)=(u’)/u`
[Вспомним, что log e e = 1. ]
[См. главу об экспоненциальных и логарифмических функциях с основанием и , если вам нужно освежить в памяти все это.]
Пример 6
Найдите производную y = логарифм 2 6 x .
Ответ
Мы начнем с использования следующего правила журнала, чтобы упростить наш вопрос:
log ab = log a + log b
Мы можем написать наш вопрос как:
y = логарифм 2 6 x = логарифм 2 6 + логарифм 2 x
Первый член, log 2 6, является константой, поэтому его производная равна 0.
Производная второго члена, используя нашу формулу, выглядит следующим образом:
`(dy)/(dx)=(log_2e) (1/x)=(log_2e)/x`
Верхний член, log 2 e , является константой. Если нам нужно десятичное значение, мы можем вычислить его, используя изменение базы следующим образом:
`log_2e=(log_10e)/(log_10 2)=1.442695041`
Пример 7
Найдите производную y = 3 log 7 ( x 2 + 1).
Ответить
Ставим
93-х``х ≠ ±sqrt(0,5)`,
`х ≠ 0`
ПРИМЕЧАНИЕ: Нам нужно быть осторожными с доменом этого решения, так как оно правильно только для определенных значений х .
График y = ln(2 x 3 − x ) 2 (имеющий мощность 2 ) определен для всех x ` ± квадрат (0,5), 0` Его график выглядит следующим образом: График y = ln(2 x 3 − x ) 2 .3 , кроме
x8
