Метод Гаусса, СЛАУ — понятие, примеры задач
Иоганн Карл Фридрих Гаусс (1777-1855) немецкий математик, физик, механик, геодезист и астроном. Его называют «королём математиков». Гаусс внес величайший вклад в науку. Во всех областях математики он провёл фундаментальные исследования: в алгебре, в теории вероятностей, в теории чисел, в теории функций комплексного переменного, в дифференциальной и неевклидовой геометрии, в математическом анализе, в аналитической и небесной механике, в астрономии, в физике и в геодезии. Но метод Гаусса не был им открыт. Он был известен за долго до рождения математика. Впервые этот метод упоминается в китайском трактате «Математика в девяти книгах», возраст которого датируется примерно с ІІ в. до н. э.
Иоганн Карл Фридрих Гаусс (1777-1855)СЛАУ: определение, виды систем
Определение
Системой линейных алгебраических уравнений (СЛАУ), содержащей m линейных уравнений и n неизвестных, называется система вида
Число уравнений \[m\] не обязательно совпадает с числом неизвестных n. Особенности системы линейных алгебраических уравнений:
Особенности системы линейных алгебраических уравнений:
- Уравнение не обязательно заранее на совместность.
- Есть возможность при помощи метода Гаусса приводить к результату при сравнительно небольшом количестве вычисленных операций.
- Можно решать такие системы уравнений, у которых определитель основной матрицы равняется нулю или количество уравнений не совпадает с числом неизвестных переменных.
Система линейных алгебраических уравнений может иметь:
- Одно решение;
- Много решений;
- Не имеет решений.
Если решений нет тогда СЛАУ называется несовместима, если есть — совместимой. Если решение одно, тогда система линейных алгебраических уравнений называется определённой, если решений несколько – неопределённой.
Метод Гаусса и метод последовательного исключения неизвестных
Определения
Метод Гаусса – это метод решение квадратных систем линейных алгебраических уравнений (СЛАУ), суть которого заключается в последовательном исключение неизвестных переменных с помощью элементарных преобразований строк.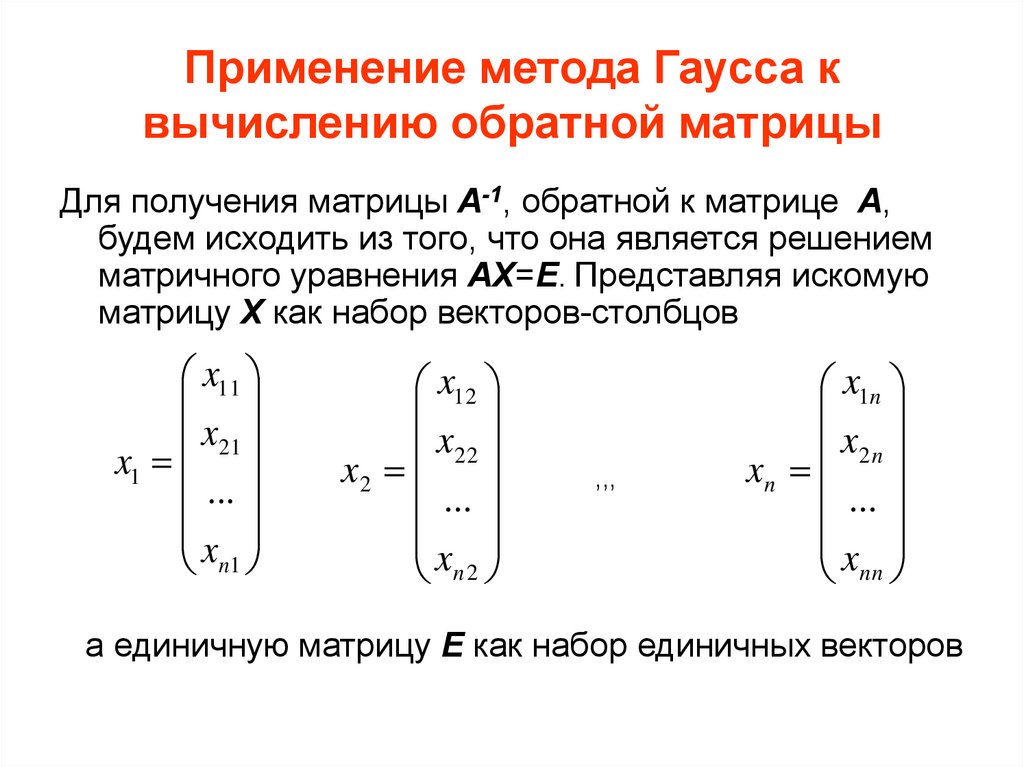
Прямой ход метода Гаусса – это поочерёдное преобразования уравнений системы для последующего избавления от переменных неизвестных.
Обратный ход метода Гаусса – это вычисление переменных неизвестных от последнего уравнения к первому.
Решение уравнений методом Гаусса
Пример №1 решение уравнений методом Гаусса:
С первой строки определяем х. Сначала -2у переносим на другую сторону уравнения, а затем обе стороны делим на 4.
Теперь во второе уравнение системы подставляем значение
Теперь когда у нас есть значение у, ми возвращаемся в первое уравнение и определяем х.
Ответ: \[x=-\frac{5}{4} ; \quad y=\frac{3}{2}\]
Пример №2.
Для упрощение перепишем уравнение так, чтобы на первом месте была строка с коэффициентом 1.
Теперь последовательно исключаем \[x_{1}\]с последующих строк. Для исключения с второго уравнения обе части первого уравнение надо умножаем на -3, а затем сложить с вторым.
Так же и с третьим уравнением, только умножение на -4.
Теперь приводим уравнение к ступенчатому виду. Нужно сделать так, чтобы во второй строке возле \[x_{2}\] стала 1. Значит нам надо обе части уравнения умножить \[-\frac{1}{4}\]
Для того чтобы избавится от \[x_{2}\] в третьим уравнении, мы множим вторую строку на 5 и слаживаем её с третьей.
Теперь с третьей строки находим \[x_{3}\].
Мы закончили прямой ход метода Гаусса. Теперь приступаем к обратному ходу. Подставляем значение х3 во вторую строку и вычисляем \[x_{2}\]
Подставляем значение \[x_{2} и x_{3}\] в первое уравнение и вычисляем \[x_{1}\].
\[\left\{\begin{array}{l} x_{1}=1 \\ x_{2}=2 \\ x_{3}=3 \end{array}\right.\]
Ответ: \[x_{1}=1, x_{2}=2, x_{3}=3\]
Рассмотрим решение систем уравнений методом Гаусса.
Определение
Матрица системы уравнений – это та матрица, которая создаётся только с коэффициентов при переменных неизвестных.
Матрицей данной системы линейных алгебраических уравнений есть:
Вектор неизвестных – это вектор \[\bar{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\], координатами которого являются неизвестные нашей системы.
Вектор \[\bar{b}=\left(b_{1}, b_{2}, \ldots, b_{m}\right)\] – это вектор-столбец из свободных членов правых частей уравнений.
Расширенная матрица – та, в которой ещё записаны и свободные члены.
Если хотя бы одно из чисел \[b_{1}, b_{2}, \ldots, b_{m}\] не равно нулю, то система называется неоднородной. Если в правой части стоят только нули \[\left(b_{1}=b_{2}=\ldots=b_{m}=0\right)\], то такая система однородная.
Решение системы уравнений – это набор чисел \[x_{1}, x_{2} \ldots, x_{n}\], то есть вектор \[\bar{x}\].
Эквивалентными системами называются, когда каждое решение одной системы является решением другой, и на оборот.
Элементарные преобразования матрицы
Если в матрице две строки становятся идентичными, оставляем одну, а другую убираем. Рассмотрим, например, матрицу
Рассмотрим, например, матрицу
В данной матрице второй и третий ряд одинаковые, а четвёртый (если разделить на 2) такой же, как и они. Значить нам достаточно оставить только одну строку. И теперь наша матрица будет выглядеть так:
Если в ходе работы с матрицей один из рядом имеет сплошные нули, его тоже нужно удалить.
В матрице строки и столбцы можно менять местами.
Матричную строку можно делить, умножать на любое число, не равное нулю.
В этом примере целесообразно первую строку разделить на 5, а вторую умножить на 2. И теперь матрица будет выглядеть так:
Данные преобразования не меняют совокупности решений системы линейных алгебраических уравнений, то есть новые системы эквивалентные прежней.
А теперь рассмотрим тот же пример системы линейных алгебраических уравнений, что рассматривали ранее, только теперь с помощью матрицы.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример №3:
Запишем матрицу.
Теперь так же само, как и в предыдущем варианте, надо 3 во втором ряду первом столбце превратить в 0. Каждое число первого ряда надо умножаем на -3, а затем сложить с числами второго.
Так же само 4 в третьем ряду первом столбце превращаем в 0. Каждое число первого ряда умножаем на -4, а затем сложить с числами третьего ряда.
Чтобы привести к ступенчатому виду, или как в научной и учебной литературе называется трапециевидный или треугольный вид. Нужно сделать так чтобы во второй строке во втором столбце место -4 стала 1. Умножаем на \[-\frac{1}{4}\]
В третьем ряду надо – 5 превратить в 0. Множим вторую строку на 5 и слаживаем её с третьей.
\[-\frac{7}{2}\] превращаем в 1. Третий ряд умножаем на \[-\frac{7}{2}\].
Теперь возвращаемся от матрицы к системе уравнений.
Конечный вариант выходит тот же.
\[ \left\{\begin{array}{l} x_{1}=1 \\ x_{2}=2 \\ x_{3}=3 \end{array}\right. \]
Ответ: \[x_{1}=1, x_{2}=2, x_{3}=3\].
Пример №4.
Записываем расширенную матрицу для данного СЛАУ.
\[ \left(\begin{array}{llrr} 3 & 2 & -5 \mid & -1 \\ 2 & -1 & 3 \mid & 13 \\ 1 & 2 & -1 & 9 \end{array}\right) \]
Переставляем третью строку на первое место.
\[ \left(\begin{array}{rrrr} 1 & 2 & -1 & 9 \\ 3 & 2 & -5 & -1 \\ 2 & -1 & 3 \mid & 13 \end{array}\right) \]
Убираем 3 с первого столбца второй строки. Первый ряд умножаем на -3 и складываем с вторым.
\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & -4 & -2 \mid & -28 \\ 2 & -1 & 3 \mid & 13 \end{array}\right) \]
Убираем 2 с первого столбца второй строки. Первый ряд умножаем на -2 и складываем с третьим.
\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & -4 & -2 \mid & -28 \\ 0 & -5 & 5 \mid & -5 \end{array}\right) \]
Превращаем -4 во втором столбце второй строки в 1. Умножаем второй ряд на -\[\frac{1}{4}\].
\[ \left(\begin{array}{cccc} 1 & 2 & -1 \mid & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & -5 & 5 \mid & -5 \end{array}\right) \]
Убираем -5 с второго столбца третьей строки. Второй ряд умножаем на 5 и складываем с третьим.
\[ \left(\begin{array}{cccc} 1 & 2 & -1 \mid & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & 0 & \frac{15}{2} \mid & 30 \end{array}\right) \]
Превращаем \[\frac{15}{2}\] с третьего столбце третьей строки в 1. Умножаем третий ряд на \[\frac{2}{15}\]
\[ \left(\begin{array}{cccc} 1 & 2 & -1 & 9 \\ 0 & 1 & \frac{1}{2} \mid & 7 \\ 0 & 0 & 1 \mid & 4 \end{array}\right) \]
А теперь возвращаемся к системе линейных алгебраических уравнений.
\[ \left\{\begin{array}{c} x+2 y-z=9 \\ y+\frac{1}{2} z=7 \\ z=4 \end{array}\right. \]
Приступаем к обратному ходу методу Гаусса.
\[
\left\{\begin{array}{c}
x+2 y-z=9 \\
y=5 \\
z=4
\end{array}\right.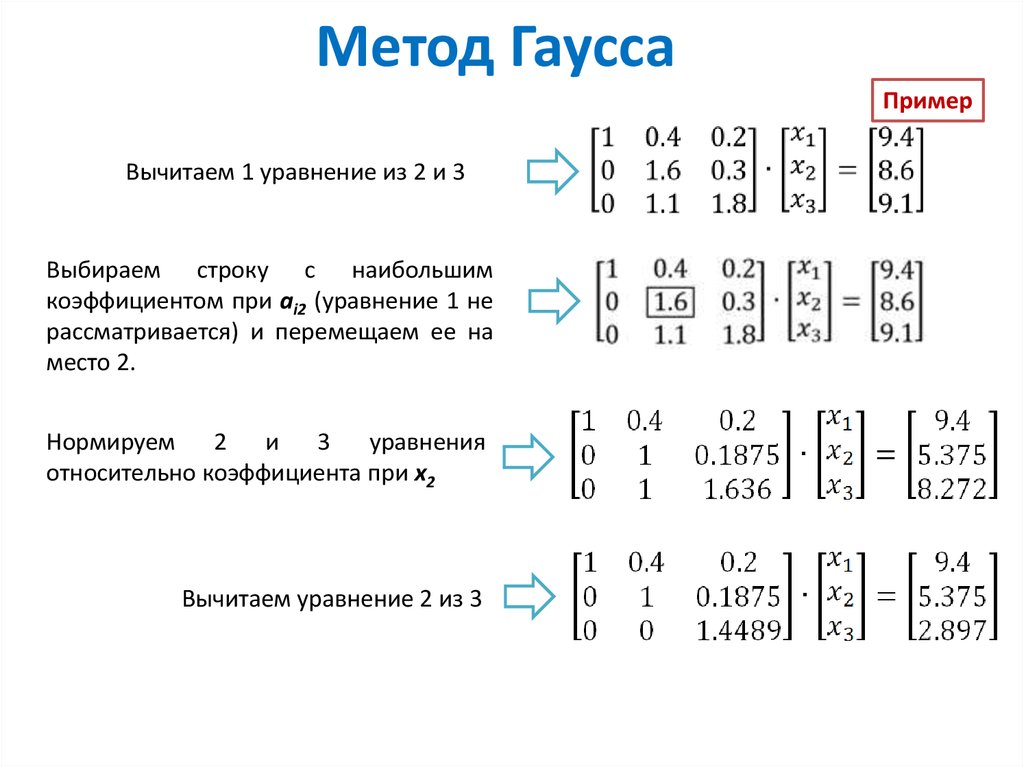 \]
\]
\[ \left\{\begin{array}{l} x=3 \\ y=5 \\ z=4 \end{array}\right. \]
Ответ: х=3, у=5, z=4.
Пример №5.
Переводим в матричную систему и проводим элементарные преобразование.
В конечном результате исходная система свелась к ступенчатой.
\[\left\{\begin{array}{c} x_{1}-x_{2}-5 x_{3}=2 \\ x_{2}+13 x_{3}-5 x_{4}=-3 \end{array}\right.\]
Ответ: \[x_{2}=5 x_{4}-13 x_{3}-3 ; \quad x_{1}=5 x_{4}-8 x_{3}-1\]<span tabindex=”0″ data-mathml=”x2=5×4−13×3−3;x1=5×4−8×3−1″ role=»presentation» style=»font-size: 109%; text-align: center; position: relative;»>x2=5×4−13×3−3;x1=5×4−8×3−1×2=5×4−13×3−3;x1=5×4−8×3−1×2=5×4−13×3−3;x1=5×4−8×3−1
Примеры решения задач – Информатика
Самоучитель > лекция 7 >
| |||||||||||||||||||||||||||||||||||
Решение
системы линейных алгебраических уравнений с n неизвестными. Систему уравнений можно записать в виде матричного уравнения: А × Х= В, где А — матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец (вектор) неизвестных В — матрица-столбец (вектор) свободных членов: Существует ряд методов решения системы, методы Крамера, Гаусса, обратной матрицы. С помощью MS Excel можно решить СЛАУ двумя методами: методом Крамера и обратной матрицы. Суть метода Крамера заключается в следующем: если определитель ∆ системы n линейных алгебраических уравнений отличен от нуля ∆≠ 0, то эта система имеет единственное решение, которое находится по формулам Крамера: – определители, образованные с заменой j-го столбца, столбцом свободных членов Задача. МТС оказывает услуги агротехсервиса: вспашку, культивацию, боронование и опрыскивание полей. Данные за 4 дня работы занесены в таблицу.
Определить стоимость каждого вида услуг (за 1 га). Пусть стоимость вспашки равна х1, стоимость культивации х2 , стоимость боронования х3 и стоимость опрыскивания х4. Тогда можно сформировать следующую систему уравнений: Систему можно представить как систему трех матриц: Решение задачи методом Крамера. Рассмотрим решение системы методом обратной матрицы. Будем считать, что квадратная матрица системы А является невырожденной, то есть ее определитель |А| ≠ 0. В этом случае существует обратная матрица А-1. Умножая слева обе части матричного равенства на обратную матрицу А получим: , отсюда решением системы методом обратной матрицы будет матрица-столбец X=A-1× B. Таким образом, для решения системы необходимо найти обратную матрицу коэффициентов и умножить ее справа на вектор свободных членов. Решение задачи методом обратной матрицы. | ||||||||||||||||||||||||||||||||||



