Метода Гаусса: примеры решения СЛАУ: понятия, определения, примеры задач
Найти решение этого же примера методом Гаусса в матричной форме записи:
3×1+2×2+x3+x4=-2×1-x2+4×3-x4=-1-2×1-2×2-3×3+x4=9×1+5×2-x3+2×4=4
Как решать?
Расширенная матрица системы представлена в виде:
x1 x2 x3 x432111-14-1-2-2-3115-12-2-194
Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.
Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на -a21a11=-13, -a31a11=–23=23 и на -а41а11=-13.
Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на -а32(1)а22(1)=-23-53=-25 и -а42(1)а22(1)=-133-53=135:
x1 x2 x3 x43211|-20-53113-43|-130-23-7353|2330133-4353|143~
x1 x2 x3 x4~3211|-20-53113-43|-130-23+(-25)(-53)-73+(-25)11353+(-25)(-43)|233+(-25)(-13)0133+135(-53)-43+135×11353+135(-43)|143+135(-13)~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415-95|195
Теперь исключаем переменную x3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а43(2)а33(2)=-415-195=4119.
x1 x2 x3 x43211|-20-53113-43|-1300-195115|39500415-95|195~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|39500415+4119(-195)-95+4119×115|195+4119×395~
x1 x2 x3 x4~3211|-20-53113-43|-1300-195115|3950005619|39219
Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:
В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:
x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219
стала диагональной, т.е. приняла следующий вид:
x1 x2 x3 x43000|а10-5300|а200-1950|а30005619|39219, где а1, а2, а3 – некоторые числа.
Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на
-1155619=-209280, на –435619=1942 и на -15619=1956.
x1 x2 x3 x43211|-20-53113-43|-1300-195115|3950005619|39219~
x1 x2 x3 x4~3211+(-1956)5619|-2+(-1956)392190-53113-43+1942×5619|-13+1942×3921900-195115+(-209280)5619|395+(-209280)392190005619|39219~
x1 x2 x3 x4~3210|-90-531130|900-1950|-3850005619|39219
Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на
-113-195=5557 и на -1-195=519.
x1 x2 x3 x43210|-90-531130|900-1950|-3850005619|39219~
x1 x2 x3 x4~321+519(-195)0|-9+519(-385)0-53113+5557(-195)0|9+5557(-385)00-1950|-3850005619|39219~
x1 x2 x3 x4~3210|-110-5300|5300-1950|-3850005619|39219
На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на -2-53=65.
x1 x2 x3 x43210|-110-5300|5300-1950|-3850005619|39219~
x1 x2 x3 x4~32+65(-53)00|-11+65×53)0-5300|5300-1950|-3850005619|39219~
x1 x2 x3 x4~3000|-90-5300|5300-1950|-3850005619|39219
Полученная матрица соответствует системе уравнений
3×1=-9-53×2=53-195×3=-3855619×4=39219, откуда находим неизвестные переменные.
Ответ: x1=-3, x2=-1,x3=2,x4=7.
Метод Гаусса. Примеры
Метод Гаусса заключается в последовательном исключении переменных и преобразовании системы линейных алгебраических уравнений
к треугольному виду
Предположим, что в системе коэффициент . Если это условие не выполняется, то на первое место переносим уравнение, которое ее удовлетворяет. С помощью первого уравнения исключим из остальных уравнений.
Для этого делят первую строчку на , обозначим
.
Дальше второй строки вычитаем первую строку, умноженную на ;от третьего первую строчку, умноженный на ; и так далее до последней строки. Получим таблицу коэффициентов:
Для неизвестных имеем систему уравнений. Выполняя, как и раньше, исключим из всех уравнений, начиная с третьего. Для этого сначала разделим вторую строчку на .
Если коэффициент , то переставим уравнения так, чтобы выполнялось условие .
Обозначив
,
от третьей строки вычтем вторую строчку, умноженный на ;
от четвертой строки вычтем вторую строчку, умноженный на и т.д. Получим таблицу коэффициентов:
Продолжая процесс исключения неизвестных получим таблицу:
Таблица коэффициентов при неизвестных сводится к треугольному виду. Все главной диагонали элементы . Запишем соответствующую систему уравнений:
Переход от первой системы уравнений до последней называется прямым ходом метода Гаусса. Обратный ход метода Гаусса начинается с последней системы уравнений. Ее решают с конца до начала. Из последнего уравнения находят . Подставив это значение в предпоследнее – находят и т.д. Из первого уравнения находят .
Если система уравнений с неизвестными имеет единственное решение, то эта система всегда может быть преобразована к треугольному виду. Для студентов не всегда требуют, чтобы диагональные элементы были равны единице. Достаточно просто свести систему линейных уравнений к верхней треугольной.
——————————————–
Пример 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Гаусса.
Решение.
Исключим неизвестную из второго и третьего уравнения. Для этого от них вычтем первое умноженное на
Видим, что наше уравнение в таком виде можно решать обратным ходом метода Гаусса. Для этого из последнего уравнения выразим
Подставим полученное значение в предыдущее уравнение и найдем
Из первого уравнения находим
Решение данной системы равен
—————————————–
В случаях систем больших размеров, а также для удобства, часто на практике используют другую схему решения. Вместо преобразований над системой выполняют соответствующие преобразования над матрицей, составленной из коэффициентов при неизвестных и столбца из свободных членов, который для удобства выделяют вертикальной линией. Такую матрицу называют расширенной матрицей системы.
—————————————–
Пример 2.
Решить систему четырех линейных алгебраических уравнений методом Гаусса.
Решение.
Выпишем расширенную матрицу для данной системы
Сведем ее к треугольному виду с помощью элементарных преобразований.
1.Поменяем местами первый и второй строки.
2. Добавим к элементам второго, третьего и четвертого строк элементы первой строки, умноженные соответственно на
3. Поменяем местами второй и третий строки. Добавим к элементам третьего и четвертого строк элементы второй строки, умноженные соответственно на
4. От четвертого уравнения умноженного на вычитаем третье уравнение умноженное на
Такой расширенной матрицы соответствует следующая система уравнений
С четвертого уравнения находим и подставляем в третье уравнение
Найденные значения подставляем во второе уравнение
Из первого уравнения находим первую неизвестную
Система полностью решена и – ее решение.
—————————————————–
Посмотреть материалы:
Метод Гаусса – определение с примерами решения
Содержание:
- Опишем метод Гаусса подробнее
- Примеры с решением
- Пример 4.4.
- Пример 4.5.
- Пример 1.18.
- Пример 1.7.
- Пример 1.8.
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений (4.3)
Процесс решения по методу Гаусса состоит из двух этапов. На нервом этапе (прямой ход) система приводится к i ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где
Коэффициенты называются главными элементами системы. На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Прямой ход. Будем считать, что элемент (если то первым в системе запишем уравнение, в котором коэффициент при отличен от нуля). Преобразуем систему (4.3), исключив неизвестное во всех уравнениях, кроме первого (используя элементарные преобразования системы).
Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы.
Затем умножим обе части первого уравнения на и сложим с третьим уравнением сиап стемы. Продолжая этот процесс, получим эквивалентную систему
Здесь
новые значения коэффициентов и правых частей, которые полу чаю юя после первого шага. Аналогичным образом, считая главным элементом исключим неизвестное из всех уравнений системы, кроме первого и второго, и так далее.
Продолжаем этот процесс, пока это возможно. Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы. Второй этап {обратный ход) заключается в решении ступенчатой системы.
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида их отбрасывают. Если же появится уравнение вида то это свидетельствует о несовместности системы. Второй этап {обратный ход) заключается в решении ступенчатой системы.
Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное через остальные неизвестные Затем подставляем значение в предпоследнее уравнение системы и выражаем затем находим Придавая свободным неизвестным произвольные значения, получим бесчисленное множество решений системы.
Возможно вам будут полезны данные страницы:
Замечания: 1. Если ступенчатая система оказывается треугольной, т. е. то исходная система имеет единственное решение. Из последнего уравнения находим хп, из предпоследнего уравнения далее поднимаясь по системе вверх, найдем все остальные неизвестные На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на ).
Примеры с решением
Пример 4.4.
Решить систему методом Гаусса:
Решение:
В результате элементарных преобразований над расширенной матрицей системы
исходная система свелась к ступенчатой:
Поэтому общее решение системы: Если положить, например, то найдем одно из частных решений этой системы
Пример 4.5.
Решить систему методом Гаусса:
Решение:
Произведем элементарные преобразования над строчками расширенной матрицы системы:
Полученная матрица соответствует системе
Осуществляя обратный ход, находим Рассмотрим решение системы (1.25) т линейных уравнений с п неизвестными. Заметим, что матрица коэффициентов системы не обязательно должна быть квадратной.
Предлагаемые методы решения систем линейных алгебраических уравнений сводятся к элементарным преобразованиям над уравнениями системы.
Преобразования Гаусса удобно проводить, осуществляя преобразования не самих уравнений, а строк матрицы их коэффициентов.
Рассмотрим матрицу
(1.33) называемую расширенной матрицей системы (1.25), так как в нее, кроме коэффициентов матрицы А системы (1.25), дополнительно включен столбец свободных членов В. Метод Гаусса (метод последовательного исключения неизвестных. Рассмотрим систему (1.25) в случае
Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы (1.33) приводится к равносильной матрице ступенчатого вида по алгоритму поиска ранга матрицы (см. пример 1.13). Это и есть прямой ход метода Гаусса.
На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.
Пример 1.18.
Решить систему уравнений методом Гаусса:
Решение:
Расширенная матрица системы имеет вид
Используя элементарные преобразования (см. пример 1.14), сведем эту матрицу к ступенчатой, не забывая при этом, что теперь в строке уже не три, а четыре элемента.
Вспомнив, что до черты стоят коэффициенты системы уравнений, а после нее — столбец свободных членов, выпишем получившуюся систему уравнений:
Теперь применим обратный ход метода Гаусса. Из последнего 4 2 тл уравнения полученной системы найдем
Из второго уравнения найдем Аналогично найдем из первого уравнения, подставив в него уже наиденные два неизвестных
Получим решение системы
Предлагаем читателю убедиться, что найденные числа образуют решение данной системы. Расширенная матрица системы. Ступенчатая матрица. Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:
Метод Гаусса. Коэффициенты системы (1.1) удобно объединить в прямоугольную таблицу, называемую матрицей системы. Для матрицы принято обозначение:
Матрица содержит т горизонтальных рядов, называемых строками, и вертикальных рядов, называемых столбцами, числа называются ее элементами. Таким образом, первый индекс элемента — это номер строки (номер уравнения системы (1.1)), а второй индекс — номер столбца (или номер неизвестного коэффициентом при котором является уравнении системы (1.1)).
Например, матрица
квадратная матрица 3-го — единичная матрица 2-го порядка. Если к матрице А добавить столбец из свободных членов, то получим так называемую расширенную матрицу А* системы, содержащую всю информацию о системе:
Для системы из примера 1.1 матрицей системы является а расширенной матрицей этой системы является матрица На практике элементарным преобразованиям подвергают не саму систему, а ее расширенную матрицу.
Преобразованиям двух типов над системой (1.1) соответствуют два типа элементарных преобразований над строками матрицы 1-й тип — перестановка местами двух любых ее строк; 2-й тип — сложение соответствующих элементов двух любых строк, все элементы одной из которых предварительно умножены на одно и то же число.
Целью элементарных преобразований является приведение расширенной матрицы системы (1.1) к так называемой ступенчатой форме.
Определение 1.6. Матрица называется ступенчатой, если для нее выполняются следующие условия: 1) если какая-либо строка данной матрицы состоит из нулей, то и все последующие строки также состоят из нулей; 2) если — первый ненулевой элемент строки, а — первый ненулевой элемент строки,то Так, например, матрица
является ступенчатой.
Матрица из одной строки считается ступенчатой по определению. Теорема 1.2. Любую матрицу Л конечным числом элементарных преобразований первого и второго типов можно преобразовать в ступенчатую матрицу.
Пример 1.7.
Привести к ступенчатому виду матрицу
Решение:
Выполним следующие элементарные преобразования над матрицей
1) к элементам второй строки прибавим элементы первой строки и из элементов третьей строки вычтем элементы первой строки, в результате преобразуется к виду: — расширенная матрица системы.
2) переставим вторую и третью строки:
3) из третьей строки полученной матрицы вычтем вторую строку, умноженную на 3, получим:
На приведении расширенной матрицы системы (1.1) к ступенчатой матрице основан метод Гаусса, или метод последовательного исключения неизвестных. Система линейных уравнений с расширенной ступенчатой матрицей называется ступенчатой системой, по теореме 1.1 она будет равносильна соответствующей системе в форме (1.1). Приведение системы (1.1) к ступенчатой форме называется прямым ходом метода Гаусса.
Решение полученной ступенчатой системы называется обратным ходом метода Гаусса. Он может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего уравнения ступенчатой системы, так и в форме преобразования матрицы к ступенчатой матрице специального вида.
Пример 1.8.
Решить методом Гаусса систему уравнений
Решение:
Прямой ход метода Гаусса. В примере 1.7 матрица при помощи элементарных преобразований приведена к ступенчатой матрице
Теперь матрице сопоставим систему, для которой она будет расширенной матрицей:
Обратный ход метода Гаусса. 1-й способ. Имеем: . 2-й способ.
Умножим последнюю строку матрицы на 1 /5, сложим со второй строкой, после чего к первой строке прибавим последнюю, умноженную на (-2), с целью получить нули в третьем столбце:
Напишем систему с расширенной матрицей
Ответ: система совместная и определенная, она имеет единственное решение:
Глава 11. Метод Гаусса | Контрольные работы по математике и другим пред
Метод Гаусса (или метод последовательного исключения неизвестных) состоит в том, что посредством последовательного исключения неизвестных данная система
(1. |
Превращается в ступенчатую (в частности, треугольную) систему
(1.11.2) |
Последняя система равносильна данной, но решать ее намного проще. Переход системы (1.11.1) к равносильной ей системе (1.11.2) называется Прямым ходом метода Гаусса, а нахождение переменных из системы (1.11.2) – Обратным ходом.
Рассмотрим этот метод на конкретных примерах.
Пример
Решить систему методом Гаусса:
Решение
Исключим x1 из 2–го т 3–го уравнений. Для этого 1–е уравнение умножим на (–2) и прибавим его ко 2–му, а затем 1–е уравнение умножим на (–3) и прибавим его к 3–му уравнению:
Новая система равносильна данной. Исключим из 3–го уравнения x2 для чего 2–е уравнение вычтем из 3–го:
Из последней системы находим x3 = –1, x2 = (56 + x3)/11 = (56 – 1)/11 = 55/11 = 5, x1 = –22 +4×2 – 3×3 = –22 + 4×5 – 3×(–1) = 1.
Пример
Решить систему методом Гаусса:
Решение
Умножим 2–е уравнение на (–2), а 1–е – на 3 и сложим, а затем 2–е уравнение умножим на (–5), а 3–е – на 3 и тоже сложим. Получим Исключим x2 из 3–го уравнения, умножив 2–е уравнение на (–2) и прибавив его к 3–му уравнению:
Последнее уравнение превратилось в неверное равенство. Это говорит о том, что система несовместна, т. е. решений не имеет.
Пример
Решить систему методом Гаусса:
Решение
Исключим x1 из 2–го и 3–го уравнений. Для этого умножим 1–е уравнение на (–1) и прибавляем его ко 2–му, далее умножим 1–е же на (–4) и прибавляем к 3–му уравнению:
Так 2–е и 3–е уравнения одинаковы, одно из них отбрасываем:
Число уравнений – два – меньше числа неизвестных – три. Такая система имеет бесчисленное множество решений. Пусть x3 = 13k, где k – произвольное число. Тогда x2 = (16/13)x3 = 16k, x1 = 3×2 – 5×3 = –17k.
Тогда x2 = (16/13)x3 = 16k, x1 = 3×2 – 5×3 = –17k.
Преобразования Гаусса удобно проводить не с самой системой уравнений, а с матрицей ее коэффициентов. Введем матрицу
(1.11.3) |
Называемую Расширенной матрицей системы (1.8.1) размера M´(N+1), так как матрица А дополнена столбцом свободных членов.
Пример
Найти решение системы уравнений методом Гаусса.
Решение
Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода Гаусса.
Шаг 1. Умножим первую строку матрицы AB на –2 и прибавим ее ко второй и третьей строке. Затем умножим первую строку матрицы AB на –3 и прибавим ее к четвертой строке. Получим
.
Поскольку две последние строки являются линейно зависимыми, то одну из них можно отбросить.
Шаг 2. Умножим вторую строку полученной матрицы на –7/5 и прибавим ее к третьей строке. Получим
.
Заключительный вид расширенной матрицы соответствует совместной системе трех уравнений с четырьмя неизвестными, ранг которой меньше числа неизвестных. Полагая X4 свободной переменной, получаем
Из этой системы получаем обратным ходом метода Гаусса
.
Данная система уравнений имеет бесчисленное множество решений, так как X4 может принимать любые значения.
Отметим Достоинства метода Гаусса по сравнению с методом обратной матрицы и методом Крамера:
– метод является значительно Менее трудоемким;
– метод дает возможность однозначно Установить, совместна система или нет, а в случае
Совместности, найти ее решения;
– метод дает возможность Найти максимальное число линейно независимых уравнений, т. е. определить ранг матрицы системы.
| < Предыдущая | Следующая > |
|---|
Решение систем линейных уравнений методом Гаусса
Содержание:
Решение систем линейных уравнений методом Гаусса
- Решение системы линейных уравнений Метод Гаусса (1) Одним из наиболее универсальных и эффективных методов решения систем линейной алгебры является метод Гаусса.
 i + ai2X2 H —— h alnxn = bi a22 x2 t ‘• * T a2n xn- » am2®2 + •• + GmUn = bn • Где (t, j = 2, m) — новое значение коэффициента, Правильная часть получена после первого шага. Аналогичным образом исключают неизвестные X2 из всех уравнений системы, учитывая основной элемент <4UФ0, исключая первое и второе.
i + ai2X2 H —— h alnxn = bi a22 x2 t ‘• * T a2n xn- » am2®2 + •• + GmUn = bn • Где (t, j = 2, m) — новое значение коэффициента, Правильная часть получена после первого шага. Аналогичным образом исключают неизвестные X2 из всех уравнений системы, учитывая основной элемент <4UФ0, исключая первое и второе.Примеры решения и задачи с методическими указаниями
Решение задач Лекции Сборник и задачник Учебник - Продолжайте этот процесс как можно больше. Если процесс приведения системы (1) к постепенной форме показывает нулевые уравнения, то есть уравнения вида 0 = 0, они отбрасываются. Если отображается уравнение вида 0 = aΦ0>, это указывает на несовместимость системы. Второй шаг (обратный) — это решение ступенчатой системы. В общем, существует множество решений системы градуированных уравнений. В последнем уравнении этой системы первое неизвестное xb представлено оставшимися неизвестными (£ fc + 1, …, xn). Затем подставьте значение Xk в предпоследнее уравнение системы и выразите Xk- \ через a: n).
Тогда найди Xk-2> … Примечания: 1. Если система ступеней представляет собой треугольник, то есть k = 7i, исходная система имеет единственное решение. Найти xn из последнего уравнения и из второго уравнения xn-1) из последнего далее в систему всех остальных неизвестных [xn — 2? ••• yXi). 2.
Прибавьте произвольные значения к свободным неизвестным …, xn), получите бесконечное число решений для системы. Людмила Фирмаль
На практике удобнее выполнять все базовые преобразования для строк, используя матрицу расширения, а не систему (1). Удобно, если коэффициент aj равен 1 (переместить уравнение на место или отделить обе стороны уравнения все ф 1). Пример: 1) Решить систему, используя метод Гаусса. 2x \ -x-2 + 3×3-5 # 4 = 1, X \ -X2-bx3 = 2 3xi-2×2-2hz-5×4 = 3, 7xi-5×2-9hz-10×4 = 8.
♦ В результате базового преобразования в расширенную матрицу системы / 2-1 3 «-5 1 \ 1-1-5 0 2 3 -2 -2 -5 3 \ 7-5-9-10 8 / 1 -1 -5 0 2 \ 0 1 13 -5 -3 0 1 13 -5 -3 х0 2 26-10-6 / ^ 1 -1 -5 0 2 \ 2-13 -5 1 3 -2 -2 -5 3 ^ 7-5-9-10 8J -1 О 1 Ах ах \ 0 O -5 0 ‘2 л 13-5-3 LLC O O O y Оригинальная система была уменьшена до ступенчатой системы.
 xi-x2-5xs = 2 x2 + 13 Гц + 5×4 = -3. Итак, общее решение системы: x2 = -5×4-13x-X \ = -5×4-8×3-1. 1, x2 = x3 = 0, x4 = 0. 2) Решить систему, используя метод Гаусса. — = О, -3, ♦ X1 + x2 + x3 = 3, 2xi + 3×2 + 3×3 = 7, 3X] + X2 + x3 = 5, 5xi-x2-. Xs = 3. ♦ Выполнять базовые преобразования в строках расширенной матрицы системы.
xi-x2-5xs = 2 x2 + 13 Гц + 5×4 = -3. Итак, общее решение системы: x2 = -5×4-13x-X \ = -5×4-8×3-1. 1, x2 = x3 = 0, x4 = 0. 2) Решить систему, используя метод Гаусса. — = О, -3, ♦ X1 + x2 + x3 = 3, 2xi + 3×2 + 3×3 = 7, 3X] + X2 + x3 = 5, 5xi-x2-. Xs = 3. ♦ Выполнять базовые преобразования в строках расширенной матрицы системы./ 11 1 3 \ / 11 1 3 \ / 1 1 1 3 \ / 1 1 1 3 \ 2337 010 1 0101 0101 31 15 ~ 0-2—2-4 ~ 0112 ~ 0011 \ 5 -1 -1 3 / \ 0 -b -6 -12 / \ 0 I 1 2 / \ 0 0 0 0 / Полученная матрица соответствует системе + X-2 + xs = 3, X-2 = 1 Xb = 1. Выполнение обратного хода приводит к £ 3 = 1, x2-1, Xj = 1.
Решение системы с исключением Гаусса
Результаты обучения
- Используйте метод исключения Гаусса для решения системы уравнений, представленной в виде расширенной матрицы.
- Интерпретировать решение системы уравнений, представленной в виде расширенной матрицы.
Мы видели, как написать систему уравнений с расширенной матрицей , а затем как использовать строковые операции и обратную подстановку для получения строковой формы .Теперь мы будем использовать метод исключения Гаусса как инструмент для решения системы, записанной в виде расширенной матрицы. В нашем первом примере мы покажем вам процесс использования исключения Гаусса в системе двух уравнений с двумя переменными.
Пример: решение системы 2 X 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {array} {l} 2x + 3y = 6 \ hfill \\ \ text {} x-y = \ frac {1} {2} \ hfill \ end {array} [/ latex]
Показать решениеСначала мы записываем это как расширенную матрицу.
[латекс] \ left [\ begin {array} {rr} \ hfill 2 & \ hfill 3 \\ \ hfill 1 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 6 \\ \ hfill \ frac {1} {2} \ end {array} \ right] [/ latex]
Нам нужна 1 в строке 1, столбце 1.
 Этого можно добиться, поменяв местами строку 1 и строку 2.
Этого можно добиться, поменяв местами строку 1 и строку 2.[латекс] {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 2 & \ hfill 3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 6 \ end {array} \ right] [/ latex]
Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на [latex] -2 [/ latex], а затем прибавив результат к строке 2.
[латекс] -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill 5 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill \ frac {1} {2} \\ \ hfill & \ hfill 5 \ end {массив } \ right] [/ latex]
У нас есть только один шаг, чтобы умножить строку 2 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ frac {1} {5} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill \ \ \ hfill 0 & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {cc} & \ frac {1} {2} \\ & 1 \ end {array} \ right] [/ latex]
Использовать обратную замену.Вторая строка матрицы представляет [латекс] y = 1 [/ латекс]. Подставьте обратно [latex] y = 1 [/ latex] в первое уравнение.
[латекс] \ begin {array} {l} x- \ left (1 \ right) = \ frac {1} {2} \ hfill \\ \ text {} x = \ frac {3} {2} \ hfill \ end {array} [/ latex]
Решение – точка [латекс] \ left (\ frac {3} {2}, 1 \ right) [/ latex].
Попробуйте
Решите данную систему методом исключения Гаусса.
[латекс] \ begin {массив} {l} 4x + 3y = 11 \ hfill \\ \ text {} \ text {} \ text {} x – 3y = -1 \ hfill \ end {array} [/ latex]
Показать решение[латекс] \ левый (2,1 \ правый) [/ латекс]
В нашем следующем примере мы решим систему двух уравнений с двумя зависимыми переменными.Напомним, что зависимая система имеет бесконечное количество решений, и результатом операций со строками в ее расширенной матрице будет уравнение, такое как [latex] 0 = 0 [/ latex].
 Мы также рассмотрим написание общего решения для зависимой системы.
Мы также рассмотрим написание общего решения для зависимой системы.Пример: решение зависимой системы
Решите систему уравнений.
[латекс] \ begin {array} {l} 3x + 4y = 12 \\ 6x + 8y = 24 \ end {array} [/ latex]
Показать решение Выполните строковых операций над расширенной матрицей, чтобы попытаться получить строковую форму .[латекс] A = \ left [\ begin {array} {llll} 3 \ hfill & \ hfill & 4 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 12 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] [/ latex]
[латекс] \ begin {array} {l} \ hfill \\ \ begin {array} {l} – \ frac {1} {2} {R} _ {2} + {R} _ {1} = { R} _ {1} \ to \ left [\ begin {array} {llll} 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \\ 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \ end { array} | \ begin {array} {ll} \ hfill & 0 \ hfill \\ \ hfill & 24 \ hfill \ end {array} \ right] \ hfill \\ {R} _ {1} \ leftrightarrow {R} _ {2} \ to \ left [\ begin {array} {llll} 6 \ hfill & \ hfill & 8 \ hfill & \ hfill \\ 0 \ hfill & \ hfill & 0 \ hfill & \ hfill \ end {array} | \ begin {array} {ll} \ hfill & 24 \ hfill \\ \ hfill & 0 \ hfill \ end {array} \ right] \ hfill \ end {array} \ hfill \ end {array} [/ latex]
Матрица заканчивается всеми нулями в последней строке: [latex] 0y = 0 [/ latex].Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите для [latex] y [/ latex].
[латекс] \ begin {array} {l} 3x + 4y = 12 \ hfill \\ \ text {} 4y = 12 – 3x \ hfill \\ \ text {} y = 3- \ frac {3} {4} x \ hfill \ end {array} [/ latex]
Итак, решение этой системы – [латекс] \ left (x, 3- \ frac {3} {4} x \ right) [/ latex].
Теперь мы перейдем на следующий шаг к решению системы линейных уравнений 3 на 3.Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.

Пример: решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
[латекс] \ begin {массив} {c} \ begin {array} {l} \ hfill \\ \ hfill \\ x-y + z = 8 \ hfill \ end {array} \\ 2x + 3y-z = -2 \\ 3x – 2y – 9z = 9 \ end {array} [/ latex]
Показать решениеСначала мы пишем расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill -1 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill -1 \\ \ hfill 3 & \ hfill -2 & \ hfill -9 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 8 \\ \ hfill -2 \\ \ hfill 9 \ end {array} \ right] [/ latex]
Затем мы выполняем операции со строками, чтобы получить форму «строка-эшелон».
[латекс] \ begin {array} {rrrrr} \ hfill -2 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} { rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 3 & \ hfill & \ hfill -2 & \ hfill & \ hfill -9 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill 9 \ end {массив} \ right] & \ hfill & \ hfill & \ hfill & \ hfill -3 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -18 \\ \ hfill & \ hfill -15 \ end {array} \ right] \ end {array} [/ latex]
Самый простой способ получить 1 в строке 2 столбца 1 – это поменять местами [латекс] {R} _ {2} [/ latex] и [latex] {R} _ {3} [/ latex].
[латекс] \ text {Interchange} {R} _ {2} \ text {и} {R} _ {3} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill – 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 8 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill & \ hfill -15 \\ \ hfill 0 & \ hfill & \ hfill 5 & \ hfill & \ hfill -3 & \ hfill & \ hfill -18 \ end {array} \ right] [/ latex]
Затем
[латекс] \ begin {array} {l} \\ \ begin {array} {rrrrr} \ hfill -5 {R} _ {2} + {R} _ {3} = {R} _ {3} \ в \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 57 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \\ \ hfill & \ hfill 57 \ end {array} \ right] & \ hfill & \ hfill & \ hfill & \ hfill – \ frac {1} {57} {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -12 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 8 \\ \ hfill & \ hfill -15 \ \ \ hfill & \ hfill 1 \ end {array} \ right] \ end {array} \ end {array} [/ latex]
Последняя матрица представляет собой эквивалентную систему.

[латекс] \ begin {массив} {l} \ text {} x-y + z = 8 \ hfill \\ \ text {} y – 12z = -15 \ hfill \\ \ text {} z = 1 \ hfill \ end {array} [/ latex]
Используя обратную подстановку, мы получаем решение как [latex] \ left (4, -3,1 \ right) [/ latex].
Напомним, что есть три возможных исхода решений для линейных систем. В предыдущем примере решение [латекс] \ left (4, -3,1 \ right) [/ latex] представляет точку в трехмерном пространстве. Эта точка представляет собой пересечение трех плоскостей.В следующем примере мы решаем систему, используя операции со строками, и обнаруживаем, что она представляет зависимую систему. Зависимая система в 3-х измерениях может быть представлена двумя идентичными плоскостями, как в 2-х измерениях, где зависимая система представляет две идентичные линии.
Пример: решение 3 x 3 зависимой системы
Решите следующую систему линейных уравнений, используя метод исключения Гаусса.
[латекс] \ begin {array} {r} \ hfill -x – 2y + z = -1 \\ \ hfill 2x + 3y = 2 \\ \ hfill y – 2z = 0 \ end {array} [/ latex]
Показать решениеНапишите расширенную матрицу.
[латекс] \ left [\ begin {array} {rrr} \ hfill -1 & \ hfill -2 & \ hfill 1 \\ \ hfill 2 & \ hfill 3 & \ hfill 0 \\ \ hfill 0 & \ hfill 1 & \ hfill -2 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill 2 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Сначала умножьте строку 1 на [latex] -1 [/ latex], чтобы получить 1 в строке 1, столбце 1. Затем выполните операции со строками , чтобы получить форму эшелона строки.
[латекс] – {R} _ {1} \ to \ left [\ begin {array} {rrrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill & \ hfill 1 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 & \ hfill & \ hfill 2 \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill & \ hfill 0 \ end {array} \ справа] [/ латекс]
[латекс] {R} _ {2} \ leftrightarrow {R} _ {3} \ to \ left [\ begin {array} {rrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 \ \ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 \\ \ hfill 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill 0 \ end {array} \ text {} | \ begin {array} { rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 2 \ end {array} \ right] [/ latex]
[латекс] -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -1 & \ hfill & \ hfill 2 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
[латекс] {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 2 & \ hfill & \ hfill -1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill -2 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill 0 & \ hfill \ end { array} | \ begin {array} {rr} \ hfill & \ hfill 2 \\ \ hfill & \ hfill 1 \\ \ hfill & \ hfill 0 \ end {array} \ right] [/ latex]
Последняя матрица представляет следующую систему.

[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y – 2z = 0 \ hfill \\ \ text {} 0 = 0 \ hfill \ конец {array} [/ latex]
По тождеству [latex] 0 = 0 [/ latex] мы видим, что это зависимая система с бесконечным числом решений. Затем мы находим общее решение. Решив второе уравнение для [латекс] y [/ латекс] и подставив его в первое уравнение, мы можем решить для [латекс] z [/ латекс] через [латекс] x [/ латекс].
[латекс] \ begin {array} {l} \ text {} x + 2y-z = 1 \ hfill \\ \ text {} y = 2z \ hfill \\ \ hfill \\ x + 2 \ left (2z \ справа) -z = 1 \ hfill \\ \ text {} x + 3z = 1 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \ end {array} [/ latex]
Теперь мы подставляем выражение для [латекс] z [/ латекс] во второе уравнение, чтобы найти [латекс] y [/ латекс] через [латекс] x [/ латекс].
[латекс] \ begin {массив} {l} \ text {} y – 2z = 0 \ hfill \\ \ text {} z = \ frac {1-x} {3} \ hfill \\ \ hfill \\ y – 2 \ left (\ frac {1-x} {3} \ right) = 0 \ hfill \\ \ text {} y = \ frac {2 – 2x} {3} \ hfill \ end {array} [/ latex ]
Общее решение: [latex] \ left (x, \ frac {2 – 2x} {3}, \ frac {1-x} {3} \ right) [/ latex].
Общее решение для зависимой системы 3 X 3
Напомним, что когда вы решаете зависимую систему линейных уравнений с двумя переменными с использованием исключения или подстановки, вы можете записать решение [latex] (x, y) [/ latex] через x, потому что существует бесконечно много (x, y) пары, которые будут удовлетворять зависимой системе уравнений, и все они попадают на линию [латекс] (x, mx + b) [/ latex].Теперь, когда вы работаете в трех измерениях, решение будет представлять собой плоскость, поэтому вы должны записать его в общей форме [латекс] (x, m_ {1} x + b_ {1}, m_ {2} x + b_ { 2}) [/ латекс].
Попробуйте
Решите систему, используя метод исключения Гаусса.
[латекс] \ begin {array} {c} x + 4y-z = 4 \\ 2x + 5y + 8z = 15 \ x + 3y – 3z = 1 \ end {array} [/ latex]
Показать решение[латекс] \ левый (1,1,1 \ правый) [/ латекс]
Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.

Как: решить систему уравнений с помощью матриц с помощью калькулятора
- Сохраните расширенную матрицу как матричную переменную [latex] \ left [A \ right], \ left [B \ right], \ left [C \ right] \ text {,} \ dots [/ latex].
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.
Пример: решение систем уравнений с помощью калькулятора
Решите систему уравнений.
[латекс] \ begin {array} {r} \ hfill 5x + 3y + 9z = -1 \\ \ hfill -2x + 3y-z = -2 \\ \ hfill -x – 4y + 5z = 1 \ end { array} [/ latex]
Показать решениеНапишите расширенную матрицу для системы уравнений.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 3 & \ hfill 9 \\ \ hfill -2 & \ hfill 3 & \ hfill -1 \\ \ hfill -1 & \ hfill -4 & \ hfill 5 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill -1 \\ \ hfill -2 \\ \ hfill 1 \ end {array} \ right] [/ latex]
На странице матриц калькулятора введите расширенную матрицу выше как матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ left [A \ right] = \ left [\ begin {array} {rrrrrrr} \ hfill 5 & \ hfill & \ hfill 3 & \ hfill & \ hfill 9 & \ hfill & \ hfill -1 \\ \ hfill – 2 & \ hfill & \ hfill 3 & \ hfill & \ hfill -1 & \ hfill & \ hfill -2 \\ \ hfill -1 & \ hfill & \ hfill -4 & \ hfill & \ hfill 5 & \ hfill & \ hfill 1 \ end {массив } \ right] [/ latex]
Используйте функцию ref ( в калькуляторе, вызывая матричную переменную [latex] \ left [A \ right] [/ latex].
[латекс] \ text {ref} \ left (\ left [A \ right] \ right) [/ latex]
Оценить.
[латекс] \ begin {массив} {l} \ hfill \\ \ left [\ begin {array} {rrrr} \ hfill 1 & \ hfill \ frac {3} {5} & \ hfill \ frac {9} {5 } & \ hfill \ frac {1} {5} \\ \ hfill 0 & \ hfill 1 & \ hfill \ frac {13} {21} & \ hfill – \ frac {4} {7} \\ \ hfill 0 & \ hfill 0 & \ hfill 1 & \ hfill – \ frac {24} {187} \ end {array} \ right] \ to \ begin {array} {l} x + \ frac {3} {5} y + \ frac {9} {5} z = – \ frac {1} {5} \ hfill \\ \ text {} y + \ frac {13} {21} z = – \ frac {4} {7} \ hfill \\ \ text {} z = – \ frac {24} {187} \ hfill \ end {array} \ hfill \ end {array} [/ latex]
При использовании обратной подстановки решение: [latex] \ left (\ frac {61} {187}, – \ frac {92} {187}, – \ frac {24} {187} \ right) [/ latex] .

Приложения систем уравнений
Теперь обратимся к приложениям, для которых используются системы уравнений. В следующем примере мы определяем, сколько денег было инвестировано по двум разным ставкам, учитывая сумму процентов, полученных на обоих счетах.
Пример: применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10,5% годовых, а другая – 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов.Сколько было вложено по каждой ставке?
Показать решениеУ нас есть система двух уравнений с двумя переменными. Пусть [latex] x = [/ latex] сумма, инвестированная под 10,5% годовых, а [latex] y = [/ latex] сумма, инвестированная под 12% годовых.
[латекс] \ begin {array} {l} \ text {} x + y = 12 000 \ hfill \\ 0.105x + 0.12y = 1335 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0.105 & \ hfill 0.12 \ end {array} \ text {} | \ text {} \ begin {array} { r} \ hfill 12 000 \\ \ hfill 1,335 \ end {array} \ right] [/ latex]
Умножить строку 1 на [латекс] -0.105 [/ latex] и добавьте результат в строку 2.
[латекс] \ left [\ begin {array} {rr} \ hfill 1 & \ hfill 1 \\ \ hfill 0 & \ hfill 0.015 \ end {array} \ text {} | \ text {} \ begin {array} {r } \ hfill 12,000 \\ \ hfill 75 \ end {array} \ right] [/ latex]
Затем,
[латекс] \ begin {array} {l} 0,015y = 75 \ hfill \\ \ text {} y = 5,000 \ hfill \ end {array} [/ latex]
Итак [латекс] 12 000 – 5 000 = 7 000 [/ латекс].
Таким образом, 5 000 долларов США были инвестированы под 12% годовых и 7 000 долларов США – под 10,5% годовых.
Пример: применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5%, другой – 8%, а третий – 9%.
Показать решение Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?У нас есть система трех уравнений с тремя переменными. Пусть [latex] x [/ latex] будет сумма, инвестированная под 5% годовых, пусть [latex] y [/ latex] будет суммой, инвестированной под 8%, и пусть [latex] z [/ latex] будет инвестированной суммой. под 9% годовых. Таким образом,
[латекс] \ begin {array} {l} \ text {} x + y + z = 10 000 \ hfill \\ 0.05x + 0,08y + 0,09z = 770 \ hfill \\ \ text {} 2x-z = 0 \ hfill \ end {array} [/ latex]
В качестве матрицы имеем
[латекс] \ left [\ begin {array} {rrr} \ hfill 1 & \ hfill 1 & \ hfill 1 \\ \ hfill 0,05 & \ hfill 0,08 & \ hfill 0,09 \\ \ hfill 2 & \ hfill 0 & \ hfill -1 \ end {array} \ text {} | \ text {} \ begin {array} {r} \ hfill 10,000 \\ \ hfill 770 \\ \ hfill 0 \ end {array} \ right] [/ latex]
Теперь мы выполняем исключение по Гауссу, чтобы получить форму строки-эшелон.
[латекс] \ begin {массив} {l} \ begin {array} {l} \ hfill \\ -0.05 {R} _ {1} + {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 2 & \ hfill & \ hfill 0 & \ hfill & \ hfill -1 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill 0 \ end {array} \ right] \ hfill \ end {array} \ hfill \\ -2 {R} _ {1} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0.03 & \ hfill & \ hfill 0.04 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 270 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ \ frac {1} {0.
 03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]Третья строка сообщает нам [латекс] – \ frac {1} {3} z = -2,000 [/ latex]; таким образом [латекс] z = 6,000 [/ латекс].
Вторая строка сообщает нам [латекс] y + \ frac {4} {3} z = 9000 [/ latex].
Подставляя [латекс] z = 6,000 [/ латекс], получаем
[латекс] \ begin {array} {r} \ hfill y + \ frac {4} {3} \ left (6000 \ right) = 9000 \\ \ hfill y + 8000 = 9000 \\ \ hfill y = 1000 \ end {array} [/ latex]
Первая строка сообщает нам [латекс] x + y + z = 10,000 [/ latex]. Подставив [latex] y = 1,000 [/ latex] и [latex] z = 6,000 [/ latex], мы получим
[latex] \ begin {array} {l} x + 1,000 + 6,000 = 10,000 \ hfill \\ \ text {} x = 3 000 \ text {} \ hfill \ end {array} [/ latex]Ответ: 3000 долларов вложены под 5%, 1000 долларов вложены под 8% и 6000 долларов вложены под 9%.
Попробуйте
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов.
Показать решение Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Используйте матрицы, чтобы найти сумму займа по каждой ставке.150 000 долларов США под 7%, 750 000 долларов США под 8%, 600 000 долларов США под 10%
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить страницуПодробнее
Алгебра – расширенные матрицы
Решите каждую из следующих систем уравнений.
a \ (\ begin {align *} 3x + y – 2z & = 2 \\ x – 2y + z & = 3 \\ 2x – y – 3z & = 3 \ end {align *} \) Показать решениеДавайте сначала запишем расширенную матрицу для этой системы.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \]Как и в предыдущих примерах, мы помечаем красным цветом числа, которые мы хотим изменить на данном шаге.Первый шаг здесь – получить 1 в верхнем левом углу, и, опять же, у нас есть много способов сделать это. В этом случае мы заметим, что если мы поменяем местами первую и вторую строки, мы сможем получить 1 в этом месте с относительно небольшой работой.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & 2 \\ 1 & {- 2} & 1 & 3 \\ 2 & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} \ leftrightarrow {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red} 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \]Следующим шагом будет получение двух чисел под этой единицей равными нулю.Также обратите внимание, что это почти всегда требует выполнения операции третьей строки. Кроме того, мы можем сделать и то, и другое за один шаг следующим образом.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ {\ color {Red} 3} & 1 & {- 2} & 2 \\ {\ color {Red } 2} & {- 1} & {- 3} & 3 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} – 3 {R_1} \ to {R_2 }} \\ {{R_3} – 2 {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \]Затем мы хотим превратить 7 в 1.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & {\ color {Red} 7} & {- 5} & {- 7} \\ 0 & 3 & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & {\ color {Красный} 3} & {- 5} & {- 3} \ end {array}} \ right] \] Мы можем сделать это, разделив вторую строку на 7.
Мы можем сделать это, разделив вторую строку на 7.Итак, у нас есть дробь.Такое случается время от времени, так что не стоит сильно волноваться по этому поводу. Следующий шаг – заменить 3 под этой новой единицей на 0. Обратите внимание, что мы пока не будем беспокоиться о -2 над ней. Иногда так же легко превратить это в 0 на том же этапе. Однако в этом случае это, вероятно, так же легко сделать позже, как мы увидим.
Итак, используя операцию третьей строки, мы получаем
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & { \ color {Red} 3} & {- 5} & {- 3} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} – 3 {R_2} \ в {R_3}} \\ \ в \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & { – 1} \\ 0 & 0 & {\ color {Red} – \ frac {{20}} {7}} & 0 \ end {array}} \ right] \]Далее нам нужно преобразовать число в правом нижнем углу в 1.Мы можем сделать это с помощью операции второй строки.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & 1 & 3 \\ 0 & 1 & {- \ frac {5} {7}} & {- 1} \\ 0 & 0 & { \ color {Red} – \ frac {{20}} {7}} & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {7} {{ 20}} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ цвет {Красный} – \ frac {5} {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]Теперь нам нужны нули над этой новой единицей.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 2} & {\ color {Red} 1} & 3 \\ 0 & 1 & {\ color {Red} – \ frac {5] } {7}} & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} + \ frac {5} {7} { R_3} \ to {R_2}} \\ {{R_1} – {R_3} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ цвет {Красный} – 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \] Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.
Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.Обратите внимание, что в этом случае последний столбец не изменился на этом этапе.Это произошло только потому, что последняя запись в этом столбце была нулевой. В общем, этого не произойдет.
Последний шаг – преобразовать -2 над 1 во втором столбце в ноль. Это легко сделать с помощью операции третьего ряда.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 2} & 0 & 3 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + 2 {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & {- 1} \\ 0 & 0 & 1 & 0 \ end {array}} \ right] \]Итак, у нас есть расширенная матрица в окончательном виде и решение будет
\ [x = 1, \, \, \, y = – 1, \, \, \, z = 0 \]Это можно проверить, подставив их во все три уравнения и убедившись, что все они удовлетворяются.
b \ (\ begin {align *} 3x + y – 2z & = – 7 \\ 2x + 2y + z & = 9 \\ – x – y + 3z & = 6 \ end {align *} \) Показать решениеОпять же, первый шаг – записать расширенную матрицу.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { – 1} & 3 и 6 \ end {array}} \ right] \]На этот раз мы не можем получить 1 в верхнем левом углу, просто поменяв местами строки.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} {\ color {Red} 3} & 1 & {- 2} & {- 7} \\ 2 & 2 & 1 & 9 \\ {- 1} & { – 1} & 3 и 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_1} – {R_2} \ to {R_1}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ {\ color {Red} – 1 } & {- 1} & 3 & 6 \ end {array}} \ right] \] Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.
Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.Теперь мы можем использовать операцию третьей строки, чтобы превратить два красных числа в нули.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ {\ color {Red} 2} & 2 & 1 & 9 \\ { \ color {Red} – 1} & {- 1} & 3 & 6 \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} – 2 {R_1} \ to {R_2 }} \\ {{R_3} + {R_1} \ to {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3 } & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41} \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \]Следующий шаг – получить 1 на месте, занимаемом красной 4.Мы могли бы сделать это, разделив всю строку на 4, но это добавило бы пару несколько неприятных дробей. Итак, вместо этого мы собираемся поменять местами вторую и третью строки. Причина этого станет очевидной достаточно скоро.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} 4} & 7 & {41 } \\ 0 & {- 2} & 0 & {- 10} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_2} \ leftrightarrow {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} – 2} & 0 & {- 10 } \\ 0 и 4 и 7 и {41} \ end {array}} \ right] \]Теперь, если мы разделим вторую строку на -2, мы получим 1 в том месте, которое нам нужно.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & {\ color {Red} – 2} & 0 & { – 10} \\ 0 & 4 & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {- \ frac {1} {2} {R_2}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & { 41} \ end {array}} \ right] \]
Прежде чем перейти к следующему шагу, давайте заметим здесь пару вещей.Во-первых, нам удалось избежать дробей, что всегда хорошо, а во-вторых, эта строка готова. В конечном итоге нам понадобился бы ноль в этом третьем месте, и мы получили его бесплатно. Более того, это не изменится ни в одной из последующих операций. Это происходит не всегда, но если это произойдет, наша жизнь станет легче.
Теперь давайте воспользуемся операцией третьей строки, чтобы заменить красную 4 на ноль.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & {\ color {Red} 4} & 7 & {41} \ end {array}} \ right] \ begin {array} {* {20} {c}} {{R_3} – 4 {R_2} \ to {R_3}} \\ \ to \ end {массив } \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {массив}} \ справа] \]Теперь мы можем разделить третью строку на 7, чтобы получить число в правом нижнем углу в единицу.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {- 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & {\ color {Red} 7} & {21} \ end {array}} \ right] \ begin {array} {* {20} {c}} {\ frac {1} {7} {R_3}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} – 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]Затем мы можем использовать операцию третьей строки, чтобы заменить -3 на ноль.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {- 1} & {\ color {Red} – 3} & {- 16} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end { array}} \ right] \ begin {array} {* {20} {c}} {{R_1} + 3 {R_3} \ to {R _ {\ kern 1pt}}}} \\ \ to \ end {array} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]
Последний шаг – затем снова превратить -1 в 0, используя операцию третьей строки.
\ [\ require {color} \ left [{\ begin {array} {rrr | r} 1 & {\ color {Red} – 1} & 0 & {- 7} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right ] \ begin {array} {* {20} {c}} {{R_1} + {R_2} \ to {R _ {\ kern 1pt}}} \\ \ to \ end {array} \ left [{\ begin { array} {rrr | r} 1 & 0 & 0 & {- 2} \\ 0 & 1 & 0 & 5 \\ 0 & 0 & 1 & 3 \ end {array}} \ right] \]Тогда решение этой системы:
\ [x = – 2, \, \, \, y = 5, \, \, \, z = 3 \]Исключение Гаусса-Иордана | Задачи по математике
Исключение Гаусса-Иордана
ОпределениеРассмотрим систему линейных уравнений $ m \ times n $:
\ begin {align *}
a_ {1 1} x_1 + a_ {1 2} x_2 + \ cdots + a_ {1 n} x_n & = b_1 \\
a_ {2 1} x_1 + a_ {2 2} x_2 + \ cdots + a_ {2 n} x_n & = b_2 \\
a_ {3 1} x_1 + a_ {3 2} x_2 + \ cdots + a_ {3 n} x_n & = b_3 \\
& \ vdots \\
a_ {m 1} x_1 + a_ {m 2} x_2 + \ cdots + a_ {mn} x_n & = b_m \\
\ end {align *}- Матрица коэффициентов системы:
\ [\ begin {bmatrix}
a_ {1 1} & a_ {1 2} & \ cdots & a_ {1 n} \\
a_ {2 1} & a_ {2 2} & \ cdots & a_ {2 n} \\
\ vdots & \ vdots & \ ddots & \ vdots \\
a_ {m 1} & a_ {m 2} & \ cdots & a_ {mn}
\ end {bmatrix} \] - Расширенная матрица системы:
\ [\ left [\ begin {array} {rrrr | r}
a_ {1 1} & a_ {1 2} & \ cdots & a_ {1 n} & b_1 \ \
a_ {2 1} & a_ {2 2} & \ cdots & a_ {2 n} & b_2 \\
\ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\
a_ {m 1} & a_ {m 2} & \ cdots & a_ {mn} & b_m
\ end {array} \ right] \] - [Исключение Гаусса-Джордана]
Для данной системы линейных уравнений мы можем найти решение следующим образом.

Эта процедура называется исключения Гаусса-Джордана .- Запишите расширенную матрицу системы линейных уравнений.
- Используйте элементарные операции со строками, чтобы преобразовать расширенную матрицу в (сокращенную) форму эшелона строк.
- Запишите систему линейных уравнений, соответствующую матрице, в виде ряда строк.
- Решите систему, используя обратную замену.
= раствор
Проблемы
- Решите следующую систему, преобразовав расширенную матрицу в уменьшенную форму эшелона.Укажите выполненные вами элементарные операции со строками.
\ begin {align *}
x_1 + x_2-x_5 & = 1 \\
x_2 + 2x_3 + x_4 + 3x_5 & = 1 \\
x_1-x_3 + x_4 + x_5 & = 0
\ end {align *} - Решите следующую систему линейных уравнений, используя метод исключения Гаусса.
\ begin {align *}
x + 2y + 3z & = 4 \\
5x + 6y + 7z & = 8 \\
9x + 10y + 11z & = 12
\ end {align *} - Решите следующую систему линейных уравнений методом исключения Гаусса-Жордана.
\ begin {align *}
6x + 8y + 6z + 3w & = – 3 \\
6x-8y + 6z-3w & = 3 \\
8y \, \, \, \, \, \, \, \, \, \, \, – 6w & = 6
\ end {align *} - Решите следующую систему линейных уравнений, преобразовав ее расширенную матрицу к приведенной эшелонированной форме (исключение Гаусса-Жордана).Найдите векторную форму для общего решения.
\ begin {align *}
x_1-x_3-3x_5 & = 1 \\
3x_1 + x_2-x_3 + x_4-9x_5 & = 3 \\
x_1-x_3 + x_4-2x_5 & = 1.
\ end {align *} - Данная матрица является расширенной матрицей для системы линейных уравнений. Приведите векторный вид общего решения.
\ [\ left [\ begin {array} {rrrrr | r}
1 & 0 & -1 & 0 & -2 & 0 \\
0 & 1 & 2 & 0 & -1 & 0 \\
0 & 0 & 0 & 1 & 1 & 0 \\
\ end {array} \ right].\] - Решите следующую систему линейных уравнений и задайте векторную форму для общего решения.

\ begin {align *}
x_1 -x_3 -2x_5 & = 1 \\
x_2 + 3x_3-x_5 & = 2 \\
2x_1 -2x_3 + x_4 -3x_5 & = 0
\ end {align *}
( The Государственный университет Огайо ) - Определите, находятся ли следующие расширенные матрицы в форме сокращенного ряда строк, и вычислите наборы решений связанных с ними систем линейных уравнений.
(a) $ \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -3 \\ 0 & 0 & 1 & 6 \ end {массив } \ right] $.{\ prime \ prime} (x) $ обозначают первую и вторую производные соответственно. - (a) Найдите функцию $ g (\ theta) = a \ cos (\ theta) + b \ cos (2 \ theta) + c \ cos (3 \ theta) $ такую, что $ g (0) = g (\ pi / 2) = g (\ pi) = 0 $, где $ a, b, c $ – константы.
(b) Найдите действительные числа $ a, b, c $ такие, что функция $ g (\ theta) = a \ cos (\ theta) + b \ cos (2 \ theta) + c \ cos (3 \ theta) $ удовлетворяет $ g (0) = 3 $, $ g (\ pi / 2) = 1 $ и $ g (\ pi) = -5 $. - У 2-значного числа есть два свойства: сумма цифр равна 11, и если число записано с перевернутыми цифрами и вычтено из исходного числа, результат будет 45.Найдите номер.
систем линейных уравнений: исключение Гаусса
систем линейных уравнений: исключение ГауссаРешать нелинейные системы уравнений довольно сложно, а линейные системы довольно легко изучать. Существуют численные методы, которые помогают аппроксимировать нелинейные системы линейными в надежде, что решения линейных систем достаточно близки к решениям нелинейных систем. Мы не будем здесь обсуждать это.Вместо этого мы сосредоточим наше внимание на линейных системах.
Для простоты мы ограничимся тремя, максимум четырьмя неизвестными. Читатель, интересующийся случаем большего количества неизвестных, может легко развить следующие идеи.
Определение. Уравнение
a x + b y + c z + d w = h
где a , b , c , d и h – известные числа, а x , y , z и w – неизвестные числа. называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений.
называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений.Например,
а также
линейные системы, а
является нелинейной системой (из-за y 2 ). Система
является однородной линейной системой.Матричное представление линейной системы
Матрицы помогают переписать линейную систему в очень простой форме.Затем для решения систем можно использовать алгебраические свойства матриц. Сначала рассмотрим линейную систему
Установите матрицы
Используя матричное умножение, мы можем переписать линейную систему выше как матричное уравнение
Как видите, это намного лучше, чем уравнения. Но иногда стоит решить систему напрямую, минуя матричную форму. Матрица A называется матричным коэффициентом линейной системы.Матрица C называется неоднородным термом . Когда , линейная система однородна. Матрица X – это неизвестная матрица. Его записи являются неизвестными линейной системы. Расширенная матрица , связанная с системой, является матрицей [ A | C ], гдеВ общем, если линейная система имеет n уравнений с m неизвестными, то матричный коэффициент будет матрицей nxm, а расширенная матрица – матрицей nx (m + 1).Теперь обратим внимание на решения системы.
Определение. Две линейные системы с n неизвестными считаются эквивалентами тогда и только тогда, когда они имеют одинаковый набор решений.
Это определение важно, поскольку идея решения системы состоит в том, чтобы найти эквивалентную систему, которую легко решить.
 Вы можете задаться вопросом, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями в системах. Посмотрим, как это работает в конкретном случае.
Вы можете задаться вопросом, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями в системах. Посмотрим, как это работает в конкретном случае.Пример. Рассмотрим линейную систему
Идея состоит в том, чтобы сохранить первое уравнение и поработать над двумя последними. При этом мы попытаемся убить одного из неизвестных и решить два других.Например, если мы сохраним первое и второе уравнение и вычтем первое из последнего, мы получим эквивалентную систему
Затем мы сохраняем первое и последнее уравнение и вычитаем первое из второго. Получаем эквивалентную систему
Теперь мы сосредоточимся на втором и третьем уравнениях. Повторяем ту же процедуру. Попробуйте убить одного из двух неизвестных ( y или z ). Действительно, мы сохраняем первое и второе уравнение и добавляем второе к третьему, умножив его на 3.Мы получили
Это, очевидно, означает z = -2. Из второго уравнения мы получаем y = -2, и, наконец, из первого уравнения мы получаем x = 4. Следовательно, линейная система имеет одно решение.
Переход от последнего уравнения к первому при решении для неизвестных называется обратным решением .Имейте в виду, что линейные системы, для которых матричный коэффициент является верхнетреугольным, легко решить. Это особенно верно, если матрица имеет эшелонированную форму.Таким образом, фокус состоит в том, чтобы выполнить элементарные операции по преобразованию исходной линейной системы в другую, для которой матрица коэффициентов имеет эшелонированную форму.

Используя наши знания о матрицах, можем ли мы в любом случае переписать то, что мы сделали выше, в матричной форме, которая упростит нашу нотацию (или представление)? Действительно, рассмотрим расширенную матрицу
Выполним над этой матрицей несколько элементарных операций со строками. Действительно, если мы сохраним первую и вторую строки и вычтем первую из последней, мы получим
Затем мы сохраняем первую и последнюю строки и вычитаем первую из второй.Мы получили
Затем мы сохраняем первую и вторую строки и добавляем вторую к третьей, умножив ее на 3, чтобы получить
Это треугольная матрица, не имеющая эшелонированной формы. Линейная система, для которой эта матрица является расширенной, есть
Как видите, мы получили ту же систему, что и раньше. Фактически мы следовали тем же элементарным операциям, что и выше. На каждом этапе новая матрица была в точности расширенной матрицей, связанной с новой системой.Это показывает, что вместо того, чтобы писать системы снова и снова, легко поиграться с элементарными операциями со строками, и как только мы получим треугольную матрицу, напишем связанную линейную систему, а затем решим ее. Это известно как Гауссово исключение . Подведем итоги процедуры:Исключение Гаусса. Рассмотрим линейную систему.
- 1.
- Построить расширенную матрицу для системы;
- 2.
- Используйте элементарные операции со строками, чтобы преобразовать расширенную матрицу в треугольную;
- 3.
- Запишите новую линейную систему, для которой треугольная матрица является связанной с ней расширенной матрицей;
- 4.
- Решите новую систему. Вам может потребоваться присвоить некоторые параметрические значения некоторым неизвестным, а затем применить метод обратной подстановки для решения новой системы.

Пример. Решите следующую систему методом исключения Гаусса
Расширенная матрица
Мы используем элементарные операции со строками, чтобы преобразовать эту матрицу в треугольную.Мы сохраняем первую строку и используем ее для получения всех нулей в любом месте первого столбца. У нас есть
Далее мы сохраняем первую и вторую строки и стараемся, чтобы во втором столбце были нули. Мы получили
Далее сохраняем первые три ряда. Добавляем последний к третьему, чтобы получить
Это треугольная матрица. Связанная с ним система
Очевидно, что v = 1. Установите z = s и w = t , тогда мы имеем
Из первого уравнения следует Используя алгебраические манипуляции, получаем
x = – – с – т .
Собрав все вместе, у нас естьПример. Используйте метод исключения Гаусса для решения линейной системы
Соответствующая расширенная матрица
Сохраняем первую строку и вычитаем первую строку, умноженную на 2, из второй строки. Мы получили
Это треугольная матрица. Связанная система
Ясно, что второе уравнение означает, что эта система не имеет решения. Следовательно, эта линейная система не имеет решения.Определение. Линейная система называется непоследовательной или переопределенной , если у нее нет решения. Другими словами, набор решений пуст. В противном случае линейная система называется согласованной .
Следуя приведенному выше примеру, мы видим, что если мы выполним элементарные операции со строками над расширенной матрицей системы и получим матрицу, одна из строк которой равна , где , тогда система несовместима.
[Назад] [Следующий] [Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]
С.O.S MATH: Домашняя страница
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор : М.А.Хамси
Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. – П.О. Box 12395 – El Paso TX 79913 – США
пользователей онлайн за последний часЧасть 6: Исключение по Гауссу. Исключение Гаусса – это алгоритм… | Авниш | Линейная алгебра
Метод исключения Гаусса – это алгоритм решения системы линейных уравнений.Он назван в честь немецкого математика Карла Фридриха Гаусса.
Карл Фридрих ГауссОн аналогичен методу исключения, описанному ранее.
Для выполнения исключения Гаусса:
- Создаем расширенную матрицу коэффициентов и констант данной системы линейных уравнений.
- Выбираем нашу pivot (это первый элемент по диагонали). Затем мы пытаемся уменьшить все элементы под ним (до «0»), используя pivot.
Мы делаем это, выполняя два вида операций:
a) Умножение сводной строки (строки сводного элемента) на скалярную величину и вычитание или добавление ее строк под ней.
b) Перестановка строк (например, строка 2 заменяется строкой 3)
Затем мы выбираем следующую точку поворота (следующий элемент по диагонали) и уменьшаем элементы под ней.
3. Разбиваем расширенную матрицу обратно на изображение строки и выполняем умножение с переменной матрицей. Получаем новые редуцированные уравнения.
Мы решаем эти уравнения, чтобы получить значения неизвестных (переменных).
Предположим, что нам нужно найти решение (я) следующей системы уравнений:
4x + y = 9 → (1)
2x-y = 3 → (2)
5x-3y = 7 → ( 3)
(пример «Одно уникальное решение» из Части 5)
Шаг 1 (Создание расширенной матрицы):
Для выполнения исключения Гаусса мы берем изображение строки (1), (2) и (3) .
 Это будет выглядеть следующим образом:
Это будет выглядеть следующим образом:Затем мы создаем расширенную матрицу для матрицы коэффициентов и постоянной матрицы.
Единая матрица со значениями коэффициентов и констант, разделенных пунктирной линиейШаг 2 (Исключение):
Шаг 2A:
Принимая элемент в верхнем левом углу (первый элемент по диагонали) в качестве стержня, мы стремимся исключить ( уменьшите до «0») все элементы под ним. Другими словами, мы должны преобразовать каждый элемент в столбце 1 в «0», кроме pivot.
Сводной элемент будет выделен красным, а элементы, которые нужно исключить, – синим.Итак, мы умножаем первую строку на скаляр 1/2 и вычитаем ее из второй строки.
Элемент в строке 2 и столбце 1 исключен.Затем мы умножаем первую строку на скаляр 5/4 и вычитаем из третьей строки.
Элемент в строке 3 и столбце 1 исключен.Теперь все элементы в первом столбце равны «0», кроме точки поворота.
Шаг 2B:
Теперь следующий элемент по диагонали (второй столбец второй строки) установлен как опорный, и мы стремимся удалить все элементы под ним.
Pivot выделен красным.Итак, мы умножаем вторую строку на скаляр 17/6 и вычитаем ее из третьей строки.
Элемент в строке 3 и столбце 2 исключен.Результат – верхняя треугольная матрица.
Текущее состояние расширенной матрицы называется эшелоном строк формы .
Шаг 3 (обратная подстановка):
Теперь мы конвертируем форму эшелона строки обратно в изображение строки.
У нас было аналогичное уравнение на этапе 1При умножении мы получаем:
Мы составляем уравнения из этих4x + y = 9 → (4)
-3y / 2 = -3/2 → (5)
Решая (5) относительно «y», получаем:
y = 1
Теперь подставляем y = 1 в (4):
4x + 1 = 9
4x = 8
x = 2
Итак, мы получаем x = 2 и y = 1, именно то, что мы получили, когда решали через изображение строки и изображение столбца в Части 5.

Теперь применим тот же алгоритм еще в двух случаях (бесконечно много решений и нет решения).
Бесконечно много решений
Возьмем тот же пример, что и в Части 5. То есть:
x + 2y = 4 → (6)
2x + 4y = 8 → (7)
Шаг 1 (Создание дополненного матрица):
Ая картина (6) и (7) дополненная матрица строки изображений вышеШаг 2 (ликвидация):
Принимая первого элемента является диагональной ( «1») в качестве опоры.
Pivot выделен красным, и мы должны удалить все элементы под ним (синим). Чтобы исключить «2», мы дважды вычитаем строку 1 из строки 2 Теперь последняя строка полностью заполнена 0Мы больше не делаем поворота так как исключать нечего.
Шаг 3 (обратная подстановка):
Мы конвертируем форму эшелона строк обратно в изображение строки:
После этого мы умножаем ее и получаем новые уравненияx + 2y = 4 → (8)
Уравнение (6) и уравнения (8) такие же, и у нас есть только одно уравнение после исключения, но два неизвестных («x» и «y»).
Существует множество значений, которыми можно заменить x и y, чтобы удовлетворить (8).
Нравится, x = 0 и y = 2. Подставляя в уравнение (8), получаем:
0 + 2 (2) = 4
4 = 4
Или x = 1 и y = 1.5. Подставляя в уравнение (8), получаем:
1 + 2 (1.5) = 4
1 + 3 = 4
4 = 4
Таким образом, система уравнений (6) и (7) имеет бесконечно много решений.
Нет решения
Рассмотрим систему линейных уравнений следующим образом:
x + y = 4 → (9)
x + y = 8 → (10)
xy = 0 → (11)
Применение гауссиана Устранение.
Шаг 1 (Создание расширенной матрицы):
Строковое изображение (9), (10) и (11) Расширенная матрица коэффициентов и константШаг 2 (Исключение):
Принятие первого элемента по диагонали в качестве точки поворотаМы выполняем следующие две операции:
и матрица, которую мы получаем:
У нас все еще нет формы эшелона строк (верхняя треугольная матрица).

Итак, мы выполняем обмен строк (который также является вариантом на этапе исключения метода исключения по Гауссу):
Замена строки 3 на строку 2 Форма эшелона строкиШаг 3 (обратная подстановка):
Форма эшелона строки преобразована обратно в изображение строкиУравнения, которые мы получаем после умножения матриц выше:
x + y = 4 → (12)
-2y = -4 → (13)
Решая уравнение (13) относительно «y», получаем:
y = 2
Подставляя y = 2 в уравнение (12), получаем:
x + 2 = 4
x = 2
Чтобы подтвердить, что x = 2 и y = 2 является решением, мы подставляем их в систему уравнений i.е. (9), (10) и (11).
Подставляя в (9), получаем:
2 + 2 = 4
4 = 4
x = 2 и y = 2, удовлетворяет (9).
Подставляя в (10), получаем:
2 + 2 = 8
4 ≠ 8, это не удовлетворяет (10).
Следовательно, x = 2 и y = 2 не являются решением (9), (10) и (11), и не существует решения этой системы линейных уравнений, как мы видели в прошлой статье.
Одно решение
Когда количество неизвестных (переменных) равно количеству уравнения в системе линейных уравнений.
На примере (1), (2) и (3):
4x + y = 9 → (1)
2x-y = 3 → (2)
5x-3y = 7 → (3)
Имеется 2 неизвестных («x» и «y») и 3 уравнения ((1), (2) и (3)).
Двух уравнений было бы достаточно для двух неизвестных.
Бесконечно много решений
Когда количество неизвестных превышает количество уравнений.
В примере (6) и (7):
x + 2y = 4 → (6)
2x + 4y = 8 → (7)
Есть 2 неизвестных («x» и «y») и 2 уравнения ((6) и (7)).
Но если мы посмотрим дальше, то заметим, что (7) просто (6) умножается на 2. Следовательно, (6) и (7) являются одними и теми же уравнениями. Таким образом, количество уравнений равно 1.
Нет решения
Обычно, когда количество уравнений превышает количество неизвестных.
 У него нет решения.
У него нет решения.Но также необходимо, чтобы никакое значение не могло быть заменено на неизвестные, если удовлетворяется система линейных уравнений. Для этого нужно дважды проверить, удовлетворяет ли полученное решение всем уравнениям в системе.
7.6 Решение систем с исключением Гаусса – Колледжская алгебра
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполнение операций со строками в матрице.
- Решите систему линейных уравнений с помощью матриц.
Рисунок 1 Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18 – начале 19 века, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика. Его открытия в области теории матриц изменили способ работы математиков за последние два столетия.
Мы впервые столкнулись с методом исключения Гаусса в «Системах линейных уравнений: две переменные».В этом разделе мы еще раз вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по сути заменяя знаки равенства.Когда система написана в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую систему уравнений 2 × 22 × 2.
3x + 4y = 74x − 2y = 53x + 4y = 74x − 2y = 5Мы можем записать эту систему в виде расширенной матрицы:
[344−2 | 75] [344−2 | 75]Мы также можем написать матрицу, содержащую только коэффициенты.
 Это называется матрицей коэффициентов.
Это называется матрицей коэффициентов.Система уравнений три на три, например
3x − y − z = 0 x + y = 5 2x − 3z = 23x − y − z = 0 x + y = 5 2x − 3z = 2имеет матрицу коэффициентов
[3−1−111020−3] [3−1−111020−3]и представлен расширенной матрицей
[3−1−111020−3 | 052] [3−1−111020−3 | 052]Обратите внимание, что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термов идут в первый столбец, – -термы во втором столбце и z -термы в третьем. столбец.Очень важно, чтобы каждое уравнение было записано в стандартной форме ax + by + cz = dax + by + cz = d, чтобы переменные совпадали. Если в уравнении отсутствует член переменной, коэффициент равен 0.
How To
Для данной системы уравнений напишите расширенную матрицу.
- Запишите коэффициенты членов x как числа в первом столбце.
- Запишите коэффициенты членов y как числа во втором столбце.
- Если имеется z -термин, запишите коэффициенты как числа в третьем столбце.
- Нарисуйте вертикальную линию и напишите константы справа от нее.
Пример 1
Запись расширенной матрицы для системы уравнений
Напишите расширенную матрицу для данной системы уравнений.
x + 2y − z = 32x − y + 2z = 6 x − 3y + 3z = 4 x + 2y − z = 32x − y + 2z = 6 x − 3y + 3z = 4Решение
Расширенная матрица отображает коэффициенты переменных и дополнительный столбец для констант.
[12−12−121−33 | 364] [12−12−121−33 | 364]Попробуй # 1
Запишите расширенную матрицу данной системы уравнений.
4x − 3y = 113x + 2y = 44x − 3y = 113x + 2y = 4Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы, чтобы помочь нам решать системы уравнений, потому что они упрощают операции, когда системы не перегружены переменными.
 Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.Пример 2
Написание системы уравнений из расширенной матричной формы
Найдите систему уравнений из расширенной матрицы.
[1−3−52−5−4−354 | −256] [1−3−52−5−4−354 | −256]Решение
Когда столбцы представляют переменные x, x, y, y и z, z,
[1−3−52−5−4−354 | −256] → x − 3y − 5z = −22x − 5y − 4z = 5−3x + 5y + 4z = 6 [1−3−52−5−4−354 | −256] → x − 3y − 5z = −22x − 5y − 4z = 5−3x + 5y + 4z = 6Попробуй # 2
Напишите систему уравнений из расширенной матрицы.
[1−112−13011 | 51−9] [1−112−13011 | 51−9]Выполнение операций со строками в матрице
Теперь, когда мы можем писать системы уравнений в форме расширенной матрицы, мы рассмотрим различные операции со строками, которые могут выполняться с матрицей, такие как сложение, умножение на константу и перестановка строк.
Выполнение операций со строками в матрице – это метод, который мы используем для решения системы уравнений. Чтобы решить систему уравнений, мы хотим преобразовать матрицу в форму строки-эшелона, в которой есть единицы вниз по главной диагонали от верхнего левого угла до нижнего правого угла и нули в каждой позиции ниже главной диагонали. как показано.
Форма “строка-эшелон” [1ab01d001] Форма “строка-эшелон” [1ab01d001]Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме. Вот рекомендации по получению формы рядного эшелона.
- В любой ненулевой строке первым ненулевым числом является 1. Оно называется ведущим 1.
- Любые нулевые строки помещаются внизу матрицы.

- Любая ведущая 1 находится ниже и правее предыдущей ведущей 1.
- Любой столбец, в котором в начале стоит 1, имеет нули во всех остальных позициях в столбце.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в форму ряда строк и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Замечание: Ri↔RjRi↔Rj)
- Умножьте строку на константу. (Замечание: cRicRi)
- Добавить произведение одной строки на константу к другой строке. (Замечание: Ri + cRj) Ri + cRj)
Каждая из строковых операций соответствует операциям, которые мы уже научились решать системы уравнений с тремя переменными.С помощью этих операций есть несколько ключевых ходов, которые быстро достигнут цели написания матрицы в виде эшелона строк. Чтобы получить матрицу в виде эшелона строк для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, так что строку 1 можно использовать для преобразования оставшихся строк.
Исключение по Гауссу
Метод исключения Гаусса относится к стратегии, используемой для получения матрицы в виде строки-эшелона. Цель состоит в том, чтобы записать матрицу AA с номером 1 в качестве записи вниз по главной диагонали и иметь все нули внизу.
A = [a11a12a13a21a22a23a31a32a33] → После исключения по Гауссу A = [1b12b1301b23001] A = [a11a12a13a21a22a23a31a32a33] → После исключения по Гауссу A = [1b12b1301b23001] чтобы изменить строки ниже.Как записаться
Учитывая расширенную матрицу, выполните операции со строками для получения формы «строка-эшелон».
- Первое уравнение должно иметь старший коэффициент 1.При необходимости поменяйте местами строки или умножьте на константу.

- Используйте операции со строками, чтобы получить нули в первом столбце под первой записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбец 2.
- Используйте операции со строками, чтобы получить нули в нижнем столбце 2, под записью 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбец 3.
- Продолжайте этот процесс для всех строк, пока в каждой записи по главной диагонали не будет 1, а внизу не останутся только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Пример 3
Решение системы 2 × 22 × 2 методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
2x + 3y = 6 x − y = 122x + 3y = 6 x − y = 12Решение
Сначала мы записываем это как расширенную матрицу.
[231−1 | 612] [231−1 | 612]Нам нужна 1 в строке 1, столбце 1. Этого можно добиться, поменяв местами строку 1 и строку 2.
R1↔R2 → [1−123 | 126] R1↔R2 → [1−123 | 126]Теперь у нас есть 1 как первая запись в строке 1, столбце 1.Теперь давайте получим 0 в строке 2, столбце 1. Это можно сделать, умножив строку 1 на −2, −2, а затем прибавив результат к строке 2.
−2R1 + R2 = R2 → [1−105 | 125 ] −2R1 + R2 = R2 → [1−105 | 125]У нас есть только один шаг, чтобы умножить строку 2 на 15,15.
15R2 = R2 → [1−101 | 121] 15R2 = R2 → [1−101 | 121]Использовать обратную замену. Вторая строка матрицы представляет y = 1. y = 1. Подставьте обратно y = 1y = 1 в первое уравнение.
x− (1) = 12 x = 32x− (1) = 12 x = 32Решением является точка (32,1).(32,1).
Попробуй # 3
Решите данную систему методом исключения Гаусса.
4x + 3y = 11 x − 3y = −14x + 3y = 11 x − 3y = −1Пример 4
Использование исключения Гаусса для решения системы уравнений
Используйте метод исключения Гаусса, чтобы решить данную 2 × 22 × 2 система уравнений.
2x + y = 14x + 2y = 6 2x + y = 14x + 2y = 6
Решение
Запишите систему как расширенную матрицу.
[2142 | 16] [2142 | 16]Получить 1 в строке 1, столбце 1.Этого можно добиться, умножив первую строку на 12,12.
12R1 = R1 → [11242 | 126] 12R1 = R1 → [11242 | 126] Далее нам нужен 0 в строке 2, столбце 1. Умножим строку 1 на −4−4 и прибавим строку 1 к строке 2.
−4R1 + R2 = R2 → [11200 | 124] −4R1 + R2 = R2 → [11200 | 124]Вторая строка представляет уравнение 0 = 4,0 = 4. Следовательно, система непоследовательна и не имеет решения.
Пример 5
Решение зависимой системы
Решите систему уравнений.
3x + 4y = 126x + 8y = 243x + 4y = 126x + 8y = 24Решение
Выполните операции со строками в расширенной матрице, чтобы попытаться получить форму строки-эшелона.
A = [3468 | 1224] A = [3468 | 1224] −12R2 + R1 = R1 → [0068 | 024] R1↔R2 → [6800 | 240] −12R2 + R1 = R1 → [0068 | 024] R1↔ R2 → [6800 | 240]Матрица заканчивается всеми нулями в последней строке: 0y = 0,0y = 0. Таким образом, существует бесконечное количество решений и система классифицируется как зависимая. Чтобы найти общее решение, вернитесь к одному из исходных уравнений и решите относительно y.y.
3x + 4y = 12 4y = 12−3x y = 3−34x3x + 4y = 12 4y = 12−3x y = 3−34xИтак, решение этой системы – (x, 3−34x).(x, 3−34x).
Пример 6
Выполнение операций со строками в расширенной матрице 3 × 3 для получения формы Row-Echelon
Выполнить операции со строками для данной матрицы, чтобы получить форму строки-эшелона.
[1−342−56−334 | 366] [1−342−56−334 | 366]Решение
В первой строке уже есть 1 в строке 1, столбце 1. Следующим шагом является умножение строки 1 на −2−2 и прибавление ее к строке 2.
−2R1 + R2 = R2 → [1−3401−2−334 | 306] −2R1 + R2 = R2 → [1−3401−2−334 | 306] Затем замените строку 2 результатом.
Затем замените строку 2 результатом.Затем получите ноль в строке 3, столбце 1.
3R1 + R3 = R3 → [1−3401−20−616 | 3015] 3R1 + R3 = R3 → [1−3401−20−616 | 3015]Затем получаем ноль в строке 3, столбце 2.
6R2 + R3 = R3 → [1−3401−2004 | 3015] 6R2 + R3 = R3 → [1−3401−2004 | 3015]Последний шаг – получить 1 в строке 3, столбце 3.
14R3 = R3 → [1−3401−2001 | 3−6154] 14R3 = R3 → [1−3401−2001 | 3−6154]Попробуй # 4
Запишите систему уравнений в виде строк.
x − 2y + 3z = 9 − x + 3y = −42x − 5y + 5z = 17 x − 2y + 3z = 9 − x + 3y = −42x − 5y + 5z = 17Решение системы линейных уравнений с использованием матриц
Мы видели, как написать систему уравнений с расширенной матрицей, а затем как использовать строковые операции и обратную подстановку для получения формы “строка-эшелон”.Теперь мы перейдем на шаг дальше от строковой формы, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для поиска других переменных.
Пример 7
Решение системы линейных уравнений с использованием матриц
Решите систему линейных уравнений с помощью матриц.
x − y + z = 82x + 3y − z = −23x − 2y − 9z = 9x − y + z = 82x + 3y − z = −23x − 2y − 9z = 9Решение
Сначала мы пишем расширенную матрицу.
[1−1123−13−2−9 | 8−29] [1−1123−13−2−9 | 8−29]Затем мы выполняем операции со строками для получения формы «строка-эшелон».
−2R1 + R2 = R2 → [1−1105−33−2−9 | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 | 8−18−15] −2R1 + R2 = R2 → [1−1105−33−2−9 | 8−189] −3R1 + R3 = R3 → [1−1105−301−12 | 8−18−15]Самый простой способ получить 1 в строке 2 столбец 1 предназначен для замены R2R2 и R3.R3.
Обмен R2 и R3 → [1−11801−12−1505−3−18] Обмен R2andR3 → [1−11801−12−1505−3−18]
Затем
−5R2 + R3 = R3 → [1−1101−120057 | 8−1557] −157R3 = R3 → [1−1101−12001 | 8−151] −5R2 + R3 = R3 → [1−1101−120057 | 8− 1557] −157R3 = R3 → [1−1101−12001 | 8−151]Последняя матрица представляет эквивалентную систему.
x − y + z = 8 y − 12z = −15 z = 1x − y + z = 8 y − 12z = −15 z = 1Используя обратную подстановку, мы получаем решение как (4, −3,1) . (4, −3,1).
Пример 8
Решение зависимой системы линейных уравнений с использованием матриц
Решите следующую систему линейных уравнений, используя матрицы.
−x − 2y + z = −1 2x + 3y = 2y − 2z = 0 − x − 2y + z = −1 2x + 3y = 2y − 2z = 0Решение
Напишите расширенную матрицу.
[−1−2123001−2 | −120] [- 1−2123001−2 | −120]Сначала умножьте строку 1 на −1−1, чтобы получить 1 в строке 1, столбце 1.Затем выполните операции со строками, чтобы получить форму эшелона строк.
−R1 → [12−123001−2 | 120] −R1 → [12−123001−2 | 120] R2↔R3 → [12−101−2230 | 102] R2↔R3 → [12−101−2230 | 102] −2R1 + R3 = R3 → [12−101−20−12 | 100] −2R1 + R3 = R3 → [12−101−20−12 | 100] R2 + R3 = R3 → [12−101−2000 | 210] R2 + R3 = R3 → [12−101−2000 | 210]Последняя матрица представляет следующая система.
x + 2y − z = 1 y − 2z = 0 0 = 0x + 2y − z = 1 y − 2z = 0 0 = 0Мы видим из тождества 0 = 00 = 0, что это зависимая система с бесконечным числом решений.Затем мы находим общее решение. Решив второе уравнение для yy и подставив его в первое уравнение, мы можем решить для zz через x.x.
x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3x + 2y − z = 1 y = 2zx + 2 (2z) −z = 1 x + 3z = 1 z = 1 − x3Теперь мы подставляем выражение для zz во второе уравнение, чтобы найти yy через xx
y − 2z = 0z = 1 − x3y − 2 (1 − x3) = 0y = 2−2x3y − 2z = 0z = 1 − x3y − 2 (1 − x3) = 0y = 2−2×3Общее решение: ( x, 2−2×3,1 − x3).
 (х, 2−2×3,1 − x3).
(х, 2−2×3,1 − x3).Попробуй # 5
Решите систему, используя матрицы.
x + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1x + 4y − z = 42x + 5y + 8z = 15x + 3y − 3z = 1Вопросы и ответы
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как записаться
Дана система уравнений, решите с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную [A], [B], [C],….[A], [B], [C],….
- Используйте в калькуляторе функцию ref (, вызывая каждую матричную переменную по мере необходимости.
Пример 9
Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1 5x + 3y + 9z = −1−2x + 3y − z = −2 − x − 4y + 5z = 1Решение
Напишите расширенную матрицу для системы уравнений.
[539−23−1−1−45 | −1−2−1] [539−23−1−1−45 | −1−2−1]На странице матриц калькулятора введите расширенную матрицу выше в качестве матричной переменной [A].[А].
[A] = [539−1−23−1−2−1−451] [A] = [539−1−23−1−2−1−451]Используйте ref (функция в калькуляторе, вызов матричной переменной [A]. [A].
Оценить.
[1359515011321−47001−24187] → x + 35y + 95z = −15y + 1321z = −47z = −24187 [1359515011321−47001−24187] → x + 35y + 95z = −15y + 1321z = −47z = −24187Использование обратная подстановка, решение будет (61187, −92187, −24187). (61187, −92187, −24187).
Пример 10
Применение матриц 2 × 2 к финансам
Кэролайн инвестирует в общей сложности 12 000 долларов в две муниципальные облигации, одна из которых выплачивает 10.
 5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?Решение
У нас есть система двух уравнений с двумя переменными. Пусть x = x = сумма, инвестированная под 10,5%, а y = y = сумма, инвестированная под 12%.
x + y = 12,0000,105x + 0,12y = 1,335 x + y = 12,0000,105x + 0,12y = 1,335В качестве матрицы мы имеем
[110.1050.12 | 12,0001,335] [110.1050.12 | 12,0001,335]Умножьте строку 1 на −0,105−0,105 и прибавьте результат к строке 2.
[1100.015 | 12,00075] [1100.015 | 12,00075]Тогда
0,015y = 75 y = 5,0000,015y = 75 y = 5,000Итак, 12,000-5,000 = 7,000. 12,000-5,000 = 7,000.
Таким образом, 5 000 долларов США были инвестированы под 12% годовых и 7 000 долларов США – под 10,5%.
Пример 11
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов в три счета, один из которых платит 5%, другой – 8%, а третий – 9%.Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Решение
У нас есть система трех уравнений с тремя переменными. Пусть xx будет суммой, инвестированной под 5%, пусть yy будет суммой, инвестированной под 8%, и пусть zz будет суммой, инвестированной под 9%. Таким образом,
x + y + z = 10,0000,05x + 0,08y + 0,09z = 770 2x − z = 0 x + y + z = 10,0000.05x + 0,08y + 0,09z = 770 2x − z = 0В качестве матрицы имеем
[1110.050.080.0920−1 | 10,0007700] [1110.050.080.0920−1 | 10,0007700]Теперь мы выполняем исключение по Гауссу, чтобы получить форму строки-эшелон.
−0.05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] −2R1 + R3 = R3 → [11100.030. 040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2 −3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] −0,05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] – 2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2−3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000]
040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2 −3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] −0,05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] – 2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2−3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000]Третья строка сообщает нам -13z = −2,000; −13z = −2,000; таким образом, z = 6000. z = 6000.
Вторая строка говорит нам, что y + 43z = 9000.y + 43z = 9000. Подставив z = 6000, z = 6000, мы получим
y + 43 (6000) = 9000y + 8000 = 9000y = 1000y + 43 (6000) = 9000y + 8000 = 9000y = 1000. х + у + г = 10,000. х + у + г = 10,000. Подставив y = 1,000y = 1,000 и z = 6,000, z = 6,000, мы получим
x + 1,000 + 6,000 = 10,000 x = 3,000x + 1,000 + 6,000 = 10,000 x = 3,000Ответ: 3,000 долларов вложены под 5% годовых, 1000 долларов инвестировано под 8%, а 6000 долларов – под 9%.
Попробуй # 6
Небольшая обувная компания взяла ссуду в размере 1 500 000 долларов на расширение своего ассортимента. Часть денег была взята под 7%, часть – под 8%, часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовая процентная ставка по всем трем займам составляла 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
7.6 Упражнения по разделам
Устные
1.Можно ли записать любую систему линейных уравнений в виде расширенной матрицы? Объясните, почему да или почему нет.Объясните, как написать эту расширенную матрицу.
2.Можно ли любую матрицу записать в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как написать эту систему уравнений.
3.Есть только один правильный метод использования операций со строками в матрице? Попытайтесь объяснить две различные операции со строками, которые можно использовать для решения расширенной матрицы [931−2 | 06].
4. [931−2 | 06].
[931−2 | 06].Можно ли решить матрицу с нулевым элементом на диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
5.Может ли матрица с 0 элементами для всей строки иметь одно решение? Объясните, почему да или почему нет.
Алгебраический
Для следующих упражнений напишите расширенную матрицу для линейной системы.
6.8x − 37y = 82x + 12y = 38x − 37y = 82x + 12y = 3
7.16y = 49x − y = 2 16y = 49x − y = 2
8.3x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 183x + 2y + 10z = 3−6x + 2y + 5z = 13 4x + z = 18
9.x + 5y + 8z = 1912x + 3y = 43x + 4y + 9z = −7 x + 5y + 8z = 1912x + 3y = 43x + 4y + 9z = −7
10.6x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −86x + 12y + 16z = 4 19x − 5y + 3z = −9 x + 2y = −8
Для следующих упражнений запишите линейную систему из расширенной матрицы.
11.[−256−18 | 526] [- 256−18 | 526]
12.[341017 | 10439] [341017 | 10439]
13.[320−1−94857 | 3−18] [320−1−94857 | 3−18]
14.[8291−175003 | 433810] [8291−175003 | 433810]
15.[45−2015887−3 | 122−5] [45−2015887−3 | 122−5]
Для следующих упражнений решите систему методом исключения Гаусса.
16.[1000 | 30] [1000 | 30]
17.[1010 | 12] [1010 | 12]
18.[1245 | 36] [1245 | 36]
19.[−124−5 | −36] [- 124−5 | −36]
20.[−2002 | 1−1] [- 2002 | 1−1]
21.2x − 3y = −95x + 4y = 58 2x − 3y = −95x + 4y = 58
22.6x + 2y = −43x + 4y = −176x + 2y = −43x + 4y = −17
23.2x + 3y = 12 4x + y = 142x + 3y = 12 4x + y = 14
24.−4x − 3y = −2 3x − 5y = −13−4x − 3y = −2 3x − 5y = −13
25.−5x + 8y = 310x + 6y = 5−5x + 8y = 310x + 6y = 5
26.3x + 4y = 12−6x − 8y = −24 3x + 4y = 12−6x − 8y = −24
27.−60x + 45y = 12 20x − 15y = −4−60x + 45y = 12 20x − 15y = −4
28.11x + 10y = 4315x + 20y = 6511x + 10y = 4315x + 20y = 65
29.
2x − y = 23x + 2y = 172x − y = 23x + 2y = 17
30.−1.06x − 2.25y = 5.51−5.03x − 1.08y = 5.40−1.06x − 2.25y = 5.51−5.03x − 1.08y = 5,40
31.34x − 35y = 414x + 23y = 134x − 35y = 414x + 23y = 1
32.14x − 23y = −112x + 13y = 314x − 23y = −112x + 13y = 3
33.[100011001 | 314587] [100011001 | 314587]
34.[101110011 | 5020−90] [101110011 | 5020−90]
35.[123056008 | 479] [123056008 | 479]
36.[−0.10.3−0.1−0.40.20.10.60.10.7 | 0.20.8−0.8] [- 0.10.3−0.1−0.40.20.10.60.10.7 | 0,20,8−0,8]
37.−2x + 3y − 2z = 3 4x + 2y − z = 94x − 8y + 2z = −6−2x + 3y − 2z = 3 4x + 2y − z = 94x − 8y + 2z = −6
38.x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30 x + y − 4z = −4 5x − 3y − 2z = 0 2x + 6y + 7z = 30
39.2x + 3y + 2z = 1 −4x − 6y − 4z = −210x + 15y + 10z = 5 2x + 3y + 2z = 1 −4x − 6y − 4z = −210x + 15y + 10z = 5
40.x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5 x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 5
41.x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 3 x + 2y − z = 1 − x − 2y + 2z = −23x + 6y − 3z = 3
42. 900 · 10 x + y = 2 x + z = 1 − y − z = −3 x + y = 2 x + z = 1 − y − z = −3 43. 900 · 10 x + y + z = 100 x + 2z = 125 − y + 2z = 25x + y + z = 100 x + 2z = 125 − y + 2z = 25. 44.14x − 23z = −1215x + 13y = 4715y − 13z = 2914x − 23z = −1215x + 13y = 4715y − 13z = 29
45.−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315−12x + 12y + 17z = −5314 12x − 12y + 14z = 3 14x + 15y + 13z = 2315
46.−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = −4945−12x − 13y + 14z = −296 15x + 16y − 17z = 431210−18x + 19y + 110z = – 4945
Расширения
Для следующих упражнений используйте метод исключения Гаусса для решения системы.
47.x − 17 + y − 28 + z − 34 = 0x + y + z = 6x + 23 + 2y + z − 33 = 5x − 17 + y − 28 + z − 34 = 0x + y + z = 6x + 23 + 2у + г – 33 = 5
48.
x − 14 − y + 14 + 3z = −1 x + 52 + y + 74 − z = 4 x + y − z − 22 = 1x − 14 − y + 14 + 3z = −1 x + 52 + y + 74-г = 4 х + у-г-22 = 1
49.x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8x + y + z = 1x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 8х + у + г = 1
50.x − 310 + y + 32−2z = 3x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32x − 310 + y + 32−2z = 3x + 54 − y − 18 + z = 32x − 14 + y + 42 + 3z = 32
51.x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7x + y + z = 1x − 34 − y − 13 + 2z = −1x + 52 + y + 52 + z + 52 = 7x + y + z = 1
Реальные приложения
Для следующих упражнений настройте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
52.Ежедневно в магазине кексов продается 5 000 кексов со вкусом шоколада и ванили. Если вкус шоколада в 3 раза популярнее, чем аромат ванили, сколько кексов продается в день?
53.В конкурирующем магазине кексов ежедневно продаются кексы на сумму 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы из красного бархата – 1,75 доллара. Если общее количество кексов, проданных в день, составляет 2200, сколько штук каждого вкуса продается каждый день?
54.Вы вложили 10 000 долларов в два счета: один с простой процентной ставкой 3%, а другой – с процентной ставкой 2,5%. Если ваша общая сумма процентов по истечении одного года составила 283,50 доллара, какая сумма была на каждом счете по истечении года?
55.Вы вложили 2300 долларов на счет 1 и 2700 долларов на счет 2.Если общая сумма процентов по истечении одного года составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза выше, чем на счете 1, каковы процентные ставки? Предположим простые процентные ставки.
56.Bikes’R’Us производит велосипеды по 250 долларов. Он стоит производителю 180 долларов за велосипед плюс стартовый взнос в размере 3500 долларов. Через сколько проданных велосипедов производитель выйдет на уровень безубыточности?
57.
Крупный магазин бытовой техники рассматривает возможность покупки пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по цене 86 долларов каждый, с оплатой доставки в размере 9 200 долларов, независимо от того, сколько пылесосов будет продано.Если магазин должен начать получать прибыль после продажи 230 единиц, сколько они должны взимать за пылесосы?
58.Три самых популярных вкуса мороженого – это шоколад, клубника и ваниль, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ваниль продается на 1% больше, чем в два раза больше клубники, а шоколад продается на 11% больше, чем ваниль, сколько в общем потреблении мороженого приходится на ароматы ванили, шоколада и клубники?
59.В магазине мороженого возрастает спрос на три вкуса.В прошлом году банановое, тыквенное и мороженое с каменистой дорогой составили 12% от общего объема продаж мороженого. В этом году на те же три вида мороженого пришлось 16,9% продаж мороженого. Продажи по каменистой дороге увеличились вдвое, продажи бананов увеличились на 50%, а продажи тыквы – на 20%. Если у мороженого по каменистой дороге было на один процент меньше продаж, чем у бананового мороженого, узнайте, какой процент продаж мороженого было произведено на каждое отдельное мороженое в прошлом году.
60.В пакете ореховой смеси кешью, фисташки и миндаль.Всего в сумке 1000 орехов, а миндаля на 100 меньше, чем фисташек. Кешью весит 3 г, фисташки – 4 г, миндаль – 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида в нем.
61.Пакет с ореховой смесью содержит кешью, фисташки и миндаль. Изначально в сумке было 900 орехов. Было съедено 30% миндаля, 20% кешью и 10% фисташек, и теперь в сумке осталось 770 орехов. Изначально кешью было на 100 штук больше, чем миндаля.Для начала выясните, сколько орехов каждого типа было в пакете.
Как использовать метод исключения Гаусса для решения системы уравнений?
ПРИМЕР:
Используйте метод исключения Гаусса для решения следующей системы уравнений.

# x + 2y + 3z = -7 #
# 2x-3y-5z = 9 #
# -6z-8y + z = -22 #Решение:
Настроить расширенную матрицу формы.
# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) #
Цель 1. Получите 1 в верхнем левом углу.
Уже сделано.
Цель 2a: Получите ноль под 1 в первом столбце.
Умножьте строку 1 на # -2 #, чтобы получить
# ((- 2, -4, -6, |, 14)) #
Добавьте результат в строку 2 и поместите результат в строку 2.
Обозначим операции как # -2R_2 + R_1 → R_2 #.
# ((1,2,3, |, -7), (2,3, -5, |, 9), (- 6, -8,1, |, 22)) stackrel (-2R_1 + R_2 → R_2) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) #
Цель 2b: Получите еще один ноль в первом столбце.
Для этого нам понадобится операция # 6R_1 + R_3 → R_3 #.
# ((1,2,3, |, -7), (0, -7, -11, |, 23), (- 6, -8,1, |, 22)) stackrel (6R_2 + R_3 → R_3) (→) ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) #
Цель 2c. Получить оставшийся ноль.
Умножить строку 2 на # -1 / 7 #.
# ((1,2,3, |, -7), (0, -7, -11, |, 23), (0,4,19, |, -64)) stackrel (- (1/7 ) R_2 → R_2) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,4,19, |, -64 )) #
Теперь используйте операцию # -4R_2 + R_3 → R_3 #.
# ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,4,19, |, -64)) stackrel (-4R_2 + R_3 → R_3) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,89 / 7, |, -356/7)) #
Умножьте третью строку на # 7/89 #.
# ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,89 / 7, |, -356 / 7)) stackrel (7 / 89R_3 → R_3) (→) ((1,2,3, |, -7), (0,1,11 / 7, |, -23 / 7), (0,0,1, | , -4)) #
Цель 3. Используйте обратную замену, чтобы получить значения # x #, # y # и # z #.

 11.1)
11.1) i + ai2X2 H —— h alnxn = bi a22 x2 t ‘• * T a2n xn- » am2®2 + •• + GmUn = bn • Где (t, j = 2, m) — новое значение коэффициента, Правильная часть получена после первого шага. Аналогичным образом исключают неизвестные X2 из всех уравнений системы, учитывая основной элемент <4UФ0, исключая первое и второе.
i + ai2X2 H —— h alnxn = bi a22 x2 t ‘• * T a2n xn- » am2®2 + •• + GmUn = bn • Где (t, j = 2, m) — новое значение коэффициента, Правильная часть получена после первого шага. Аналогичным образом исключают неизвестные X2 из всех уравнений системы, учитывая основной элемент <4UФ0, исключая первое и второе. xi-x2-5xs = 2 x2 + 13 Гц + 5×4 = -3. Итак, общее решение системы: x2 = -5×4-13x-X \ = -5×4-8×3-1. 1, x2 = x3 = 0, x4 = 0. 2) Решить систему, используя метод Гаусса. — = О, -3, ♦ X1 + x2 + x3 = 3, 2xi + 3×2 + 3×3 = 7, 3X] + X2 + x3 = 5, 5xi-x2-. Xs = 3. ♦ Выполнять базовые преобразования в строках расширенной матрицы системы.
xi-x2-5xs = 2 x2 + 13 Гц + 5×4 = -3. Итак, общее решение системы: x2 = -5×4-13x-X \ = -5×4-8×3-1. 1, x2 = x3 = 0, x4 = 0. 2) Решить систему, используя метод Гаусса. — = О, -3, ♦ X1 + x2 + x3 = 3, 2xi + 3×2 + 3×3 = 7, 3X] + X2 + x3 = 5, 5xi-x2-. Xs = 3. ♦ Выполнять базовые преобразования в строках расширенной матрицы системы.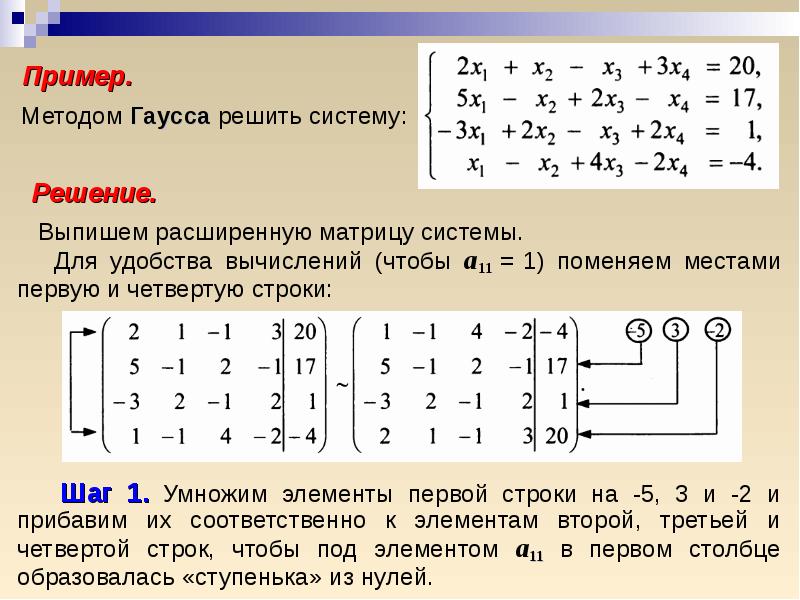 Этого можно добиться, поменяв местами строку 1 и строку 2.
Этого можно добиться, поменяв местами строку 1 и строку 2. Мы также рассмотрим написание общего решения для зависимой системы.
Мы также рассмотрим написание общего решения для зависимой системы.
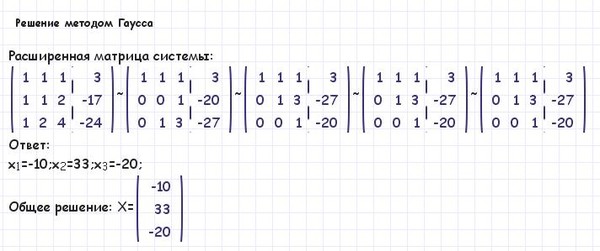



 Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке?
Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, была вдвое больше, чем сумма, вложенная под 5%. Сколько было вложено по каждой ставке? 03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex]
03} {R} _ {2} = {R} _ {2} \ to \ left [\ begin {array} {rrrrrr} \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill -2 & \ hfill & \ hfill -3 & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -20,000 \ end {array} \ right] \ hfill \\ 2 {R} _ {2} + {R} _ {3} = {R} _ {3} \ to \ left [\ begin {array} {rrrrrr} \ hfill 1 & \ hfill & \ hfill 1 & \ hfill & \ hfill 1 & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 1 & \ hfill & \ hfill \ frac {4} {3} & \ hfill \\ \ hfill 0 & \ hfill & \ hfill 0 & \ hfill & \ hfill – \ frac {1} {3} & \ hfill \ end {array} | \ begin {array} {rr} \ hfill & \ hfill 10,000 \\ \ hfill & \ hfill 9,000 \\ \ hfill & \ hfill -2,000 \ end {array} \ right] \ hfill \ end {array} [/ latex] Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Используйте матрицы, чтобы найти сумму займа по каждой ставке. Мы можем сделать это, разделив вторую строку на 7.
Мы можем сделать это, разделив вторую строку на 7. Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.
Итак, использование операции третьей строки дважды, как показано ниже, сделает то, что нам нужно.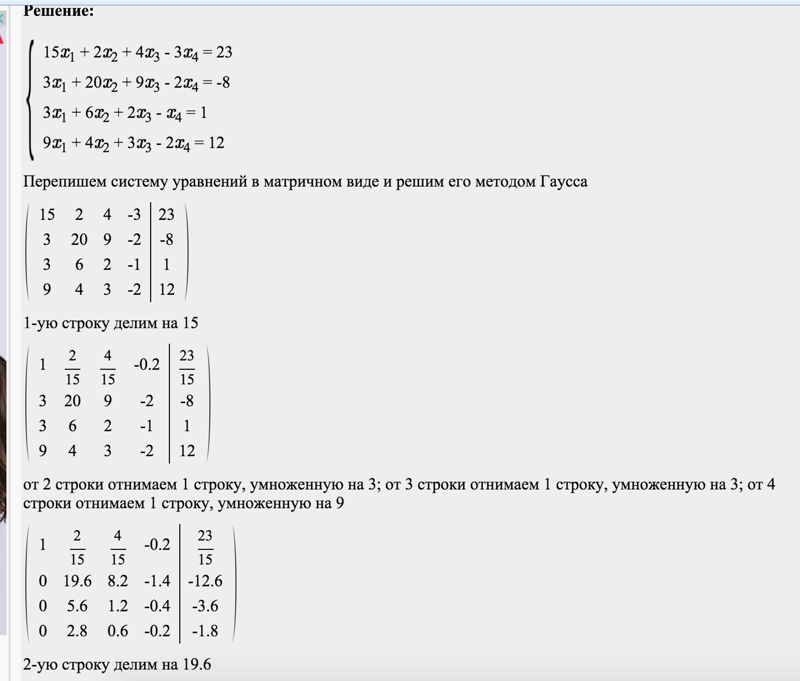 Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.
Мы могли бы поменять местами первую и последнюю строку, но это также потребовало бы другой операции, чтобы превратить -1 в 1. Хотя это несложно, это две операции. Обратите внимание, что мы можем использовать операцию третьей строки, чтобы получить 1 в этом месте следующим образом.



 называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений.
называется линейным уравнением .Если h = 0, линейное уравнение называется однородным . Линейная система представляет собой набор линейных уравнений, а однородная линейная система представляет собой набор однородных линейных уравнений. Вы можете задаться вопросом, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями в системах. Посмотрим, как это работает в конкретном случае.
Вы можете задаться вопросом, как мы придумаем такую систему? Легко, мы делаем это с помощью элементарных операций . Действительно, ясно, что если мы поменяем местами два уравнения, новая система все равно будет эквивалентна старой.Если мы умножим уравнение на ненулевое число, мы получим новую систему, по-прежнему эквивалентную старой. И, наконец, заменив одно уравнение суммой двух уравнений, мы снова получим эквивалентную систему. Эти операции называются элементарными операциями в системах. Посмотрим, как это работает в конкретном случае.


 Это будет выглядеть следующим образом:
Это будет выглядеть следующим образом:

 У него нет решения.
У него нет решения. Это называется матрицей коэффициентов.
Это называется матрицей коэффициентов. Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Однако важно понимать, как переключаться между форматами, чтобы поиск решений был более плавным и интуитивно понятным.Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.


 Затем замените строку 2 результатом.
Затем замените строку 2 результатом.
 (х, 2−2×3,1 − x3).
(х, 2−2×3,1 − x3). 5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
5% годовых, а другой – 12% годовых. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке? 040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2 −3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] −0,05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] – 2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2−3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000]
040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2 −3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] −0,05R1 + R2 = R2 → [11100.030.0420−1 | 10,0002700] – 2R1 + R3 = R3 → [11100.030.040−2−3 | 10,000270−20,000] 10.03R2 = R2 → [01101430−2−3 | 10,0009,000−20,000] 2R2 + R3 = R3 → [111014300−13 | 10,0009,000−2,000] [931−2 | 06].
[931−2 | 06].


