Примеры решения пределов со степенями: Как решать пределы со степенями, примеры

§ 8. Примеры вычисления пределов

Пример 1. Вычислить предел функции целочисленного

аргумента при

; .

Решение примера 1:

о

.

о

При вычислении предела в числителе и знаменателе пренебрегли постоянными слагаемыми по сравнению с бесконечно большой величиной ~ .

2. .

Здесь было использовано свойства бесконечности (бесконечно больших величин):

.

о о

2. .

о о

Здесь сначала пренебрегли постоянными в числителе и знаменателе по сравнению с бесконечно большими слагаемыми. Затем в числителе пренебрегли величиной по сравнению с бесконечно большой величиной высшего порядка .

В знаменателе также, величина , которой пренебрегаем, может рассматриваться как бесконечно малая по сравнению с величиной .

о о

2. .

о

Здесь опять постоянной величиной пренебрегали по сравнению с бесконечно большой величиной , которая сама является бесконечно малой по сравнению с , поскольку для степеней имеет место неравенство <  2/3.

В знаменателе по тем же причинам пренебрегли величиной по сравнению с ее квадратом . Последняя является бескончно большой величиной высшего порядка по сравнению с величиной .

Замечание: При сравнении порядков бесконечно больших степенных функций можно пользоваться шкалой бесконечно больших функций (см. §7 ).

2. .

Здесь учтено, что бесконечно большие величины в отрицательной степени становятся бесконечно малыми. Действительно, например,

.

о

2. .

о

Здесь пренебрегли постоянными величинами по сравнению с бесконечно большими, а также учтено, что бесконечно большая величина в отрицательной степени является бесконечно малой величиной.

Пример 2. Вычислить предел функции целочисленного аргумента при .

.

Решение примера 2.

.

При раскрытии неопределенности была использована формула разности кубов:

.

Ее использование приводит к уничтожению кубических корней. Формула срабатывает после умножения и деления заданного выражения на неполный квадрат суммы.

Приведем другой способ решения, с помощью различного представления функций, эквивалентных в нуле, см § 4.

.

.

В первом слагаемом под корнем единицей можно пренебречь по сравнению с бесконечно большой величиной . При сравнении двух бесконечно больших функций и первой из них можно пренебречь как бесконечно большой, низшего порядка, поскольку 1 / 7 < 1 / 2.

.

Здесь постоянными числами в числителе и знаменателе пренебрегаем по сравнению с бесконечно большой величиной .

.

Как и в предыдущем примере, постоянными числами пренебрегаем по сравнению с бесконечно большой величиной .

.

Для раскрытия неопределенности вида применяется стандартное преобразование с использованием основного логарифмического тождества в соответствии с формулой .

Для преобразования логарифмической функции использована формула эквивалентных в нуле функций (см. § 4):  ,

причем в качестве бесконечно малой величины здесь берется выражение

.

Пример 3. Вычислить предел функции целочисленного аргумента

при   

.

Замечание.  При вычислении пределов с использованием понятия факториала помимо определения факториала:

      или      

(например, 5 ! =  )

необходимо использовать свойства факториала, следующие из его определения:

1°  

2°  

3°

……………………………………………………………………….

!

Решение примера 3.

о

.

При решении было использовано второе свойство факториала, записанное в форме . Под знаком предела пренебрегли единицей по сравнению с бесконечно большой величиной .

.

Здесь было использовано первое свойство факториала, записанное в форме .

o

.

о

Здесь было использовано второе свойство факториала, записанное в форме .  Кроме того, под знаком предела пренебрегли единицей по сравнению с бесконечно большой величиной ~  .

о

.

о

Здесь в числителе и знаменателе пренебрегли постоянными величинами (не зависящими от ), затем было использовано первое свойство факториала, записанное в форме .

.

Здесь было использовано третье свойство факториала, записанное в форме , а также первое свойство факториала, записанное в форме .

.

Здесь было дважды использовано первое свойство факториала, записанное в формах  и   .

Пример 4. Вычислить пределы функций, если они существуют, при и при

.

Решение примера 4.

.

Ввиду того, что пределы слева и справа в точке х = 0 не совпадают, искомый предел не существует.

 о

.

Последний предел вычисляется аналогично предыдущему. В числителе дроби пренебрегли постоянным числом по сравнению с бесконечно большим слагаемым ~ .

.

Ввиду совпадения пределов слева и справа в нуле, искомый предел также равен бесконечности: .

  

В числителе пренебрегли единицей по сравнению с бесконечно большим слагаемым ~ .

о о

.

о

В числителе пренебрегли бесконечно малыми величинами по сравнению с конечным числом два.

В знаменателе пренебрегли вторым слагаемым как величиной бесконечно малой по сравнению с первым слагаемым ( известно, что при возведении числа , меньшего единицы в положительную степень, число становится тем меньше, чем больше степень).

Заметим здесь, что в этом конкретном примере пренебрегать вторым слагаемым в знаменателе было не обязательно, однако такое действие в некоторых случаях играет существенную роль.

Ввиду того, что оба вычисленных предела совпадают, искомый предел существует и равен тому же значению предела: .

о о о о

.

о о

Здесь в соответствии со шкалой бесконечно больших функций два первых слагаемых числителя и первое слагаемое знаменателя являются по сравнению с оставленными слагаемыми бесконечно малыми величинами, которыми можно пренебречь. Последнее можно объяснить и тем, что при возведении чисел, больших единицы в положительную степень, результат будет тем больше, чем больше величина степени, а в нашем случае в степень возводится сколь угодно большая величина.

.

.

Ввиду равенства обоих пределов искомый предел существует и равен вычисленному значению предела:  .

о

.

о

Здесь второе и третье слагаемые числителя взаимно уничтожаются (при любых положительных значениях ).

В знаменателе в соответствии со шкалой бесконечно больших функций слагаемым с меньшей степенью можно пренебречь. Единицей в числителе пренебрегаем по сравнению с бесконечно большим значением .

о о

.

о

Здесь второе и третье слагаемые числителя складываются (при любых отрицательных значениях ), образуя положительную величину .

Вторым слагаемое знаменателя пренебрегаем как величиной бесконечно большой низшего порядка, по сравнению с первым слагаемым (т.е. бесконечно малой по сравнению с первым слагаемым).

.

     .

Ввиду того, что вычисленные пределы не совпадают, искомый предел                              – не существует.

о о о

.         

                   о о

.

Оба последних предела вычисляются одинаково. Постоянными числами 1 и 4 пренебрегаем по сравнению с бесконечно большим значением .

Величиной также пренебрегаем, т. к. она является бесконечно малой:   при .

Пример 5. Вычислить пределы функций, если они существуют, при и при

.

Решение примера 5.

.

– не существует.

Последний предел не существует, т. к. под корнем в знаменателе стоит отрицательная величина. Это можно было сразу заметить, если бы мы рассмотрели область определения функции, стоящей под знаком предела.

Таким образом искомого предела функции при также не существует. Существует лишь предел слева в единице, который и был найден выше.

– предел не существует.

Последний предел не существует т. к. опять под корнем в знаменателе стоит отрицательная величина. Предела слева в точке x = 2 также не существует по тем же причинам.

.

Ввиду совпадения обоих пределов, в точке х =1,  искомый предел существует и равен значению вычисленного предела:

.

.

Здесь мы не стали вычислять отдельно левый и правый пределы в точке х=2, ввиду того, что скобка возводится в квадрат, и вычисления как левого, так и правого пределов не отличались бы друг от друга.

– не существует.

Здесь не существование предела связано с тем, окрестность точки х =1 не входит в область определения рассматриваемой функции, ввиду того, что аргумент логарифма должен быть только положительным: .

.

Предел слева в точке х = 2 не существует поскольку область определения рассматриваемой функции: . Таким образом, в точке х = 2 предел также не существует. (Существует лишь предел справа, который и был вычислен).

.

.

Поскольку в точке х = 1 пределы слева и справа не совпадают, искомый предел – не существует.

.

.

Ввиду того, что в точке х = 2 пределы справа и слева не совпадают, искомый   не существует.

При вычислении значения арксинуса в нуле можно использовать график функции

y=arcsin x

-1 0 1 x

Пример 6. Вычислить пределы функций при

Решение примера 6.

.

Здесь мы воспользовались формулами для функций, эквивалентных в нуле (см. § 4), причем для синуса и арктангенса ограничились лишь первым членом разложения в ряд Тейлора этих функций.

.

Здесь опять использованы различные формы функций, эквивалентных в нуле (см. § 4). Для синуса ограничились лишь первым членом разложения, а для показательной функции использованы ее два первых члена разложения в ряд Тейлора.

Необходимость учета именно двух членов разложения диктуется требованием, что в результате подстановки разложения под знак предела, после взаимного уничтожения слагаемых, какие то слагаемые должны оставаться. Здесь в знаменателе дроби осталось слагаемое ( ).

.

Здесь при использовании различных форм функций, эквивалентных в нуле (см. § 4), для логарифмической функции оставлен первый ее член разложения, а для косинуса оставлены два его первых члена разложения в ряд Тейлора.

Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали.

  

= .

Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали. Выражение, стоящее в знаменателе, преобразовывалось следующим образом:

.

Пример 7. Вычислить пределы функций, если они существуют, при

 Решение примера 7.

.

Здесь были использованы различные формы функций, эквивалентных в нуле (см. § 4), причем в качестве «нуля» выступала величина .

.

Здесь были опять использованы различные формы эквивалентных в нуле функций (см. § 4), где в качестве «нуля» выступала величина .

.

Здесь были опять использованы различные формы функций, эквивалентных в нуле, а в качестве «нуля» выступала величина .

.

Здесь было использовано свойство логарифма:  , где последнее равенство справедливо лишь при .

Рассмотрим теперь предел справа при :

       –предел не существует,

поскольку в знаменателе дроби имеется логарифм от отрицательной величины, в то время как действительная функция логарифм определена лишь для положительных значений аргумента. Таким образом, и искомый предел не существует.

Пример 8. Вычислить пределы функций, если они существуют, при и при

Решение примера 8.

о

.

о

Здесь пренебрегали бесконечно малой величиной в числителе по сравнению с единицей, а в знаменателе по сравнению с тройкой. Учтено также, что при возведении в бесконечно большую степень положительного числа, меньшего единицы, получается ноль.

о

.

о

Здесь в числителе и в знаменателе пренебрегли постоянными конечными числами по сравнению с бесконечно большим слагаемым ~ .

о

о

о о

о

Здесь в числителе и знаменателе, а также в показателе степени пренебрегли конечными величинами по сравнению с бесконечно большой величиной, ~ .

.

Для раскрытия неопределенности вида воспользовались основным логарифмическим тождеством: , а для освобождения от логарифма воспользовались различными формами функций, эквивалентных в нуле (см. § 4).

о

.

Для раскрытия неопределенности вида , опять воспользовались представлением

При раскрытии неопределенности вида использовали правило Лопиталя, при этом для упрощения под знаком логарифма пренебрегли единицей по сравнению с бесконечно большой величиной.

Аналогичного предела при не существует,  ввиду того, что при больших отрицательных значениях основание действительной степенно-показательной функции становится отрицательным , при этом мы выходим за рамки ее области определения.

        .

Здесь пренебрегалось бесконечно малыми величинами по сравнению с конечными – единицей, четверкой и двойкой.

о о

о о

.

Для раскрытия неопределенности вида воспользовались представлением: . Затем бесконечно малыми величинами (двойкой по сравнению с , четверкой по сравнению с , единицей по сравнению с и по сравнению с ) пренебрегли.

Аналогичный предел при не существует, поскольку основание действительной степенно-показательной функции при больших отрицательных значениях

становится отрицательным: , что не соответствует ее области определения: .

о

.

Здесь для раскрытия неопределенности вида воспользовались представлением . Далее пренебрегли единицей по сравнению с бесконечно большой величиной . При раскрытии неопределенности вида использовали правило Лопиталя.

.

Здесь при раскрытии неопределенности вида воспользовались представлением . Для разложении логарифма использовали формы функций, эквивалентных в нуле, см. § 4.

.

При раскрытии неопределенности вида воспользовались представлением .

Для раскрытия неопределенности вида использовали правило Лопиталя.

Искомый предел при не существует, ввиду отрицательности основания степени рассматриваемой функции .

Пример 9. Вычислить пределы функций при и при

Решение примера 9

о

.

Здесь для удобства введена новая переменная . Затем с помощью основного логарифмического тождества степенная функция выражена через показательную. Далее с учетом шкалы бесконечно больших функций пренебрегаем по сравнению с бесконечно большой величиной ~ . После раскрытия неопределенности вида по правилу Лопиталя, и представления предела как произведения пределов, вновь учитываем, что является величиной бесконечно малой по сравнению с .

.

Здесь после раскрытия неопределенности вида по правилу Лопиталя, в соответствии со шкалой бесконечно больших функций учтено, что является бесконечно малой величиной, по сравнению с .

о

.

о

Здесь неопределенности вида раскрывается по правилу Лопиталя.

о

.

о

Здесь в соответствии со шкалой бесконечно больших функций величиной пренебрегли как величиной бесконечно малой по сравнению с .

.

Здесь конечная величина обозначена как .

.

Здесь использовали различные формы функций, эквивалентных в нуле (см. § 4), в частности,  при  .

о

.

о

Здесь вводим новую переменную . Затем степенную функцию выражаем через показательную. Далее в соответствии со шкалой бесконечно больших функций, пренебрегаем бесконечно малой величиной по сравнению с величиной ~ . И наконец учитываем, что является бесконечно малой по сравнению и с показательной функцией .

о

.

Здесь в соответствии со шкалой бесконечно больших функций, пренебрегаем логарифмической функцией по сравнению со степенной .

о

.

Здесь бесконечно малой величиной пренебрегли по сравнению с бесконечно большой величиной .

о

.

Здесь неопределенность вида с помощью основного логарифмического тождества преобразовали в неопределенность вида , которую раскрывали с помощью правила Лопиталя. Далее в соответствии со шкалой бесконечно больших функций учтено, что является бесконечно малой величиной по сравнению со степенной функций , в результате чего, оказалось возможным пренебречь бесконечно малой величиной ~ по сравнению с единицей.

.

.

о

Здесь пренебрегли степенной функцией по сравнению с показательной , поскольку их отношение . (Соотношение легко проверяется, если к нему применить правило Лопиталя). Затем, неопределенность вида раскрывали с использованием правила Лопиталя.

Пример 10. Вычислить указанные пределы

.

Решение примера 10.

.

Ввиду того, что пределы слева и справа в точке не совпадают, искомого предела не существует.

.

Здесь учтено, что .

о

.

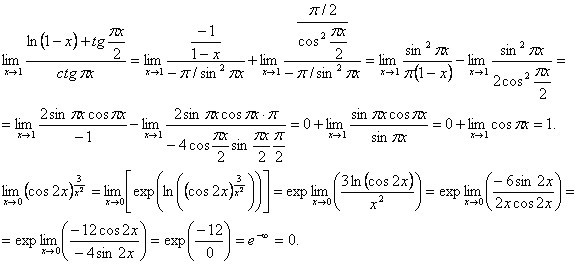
Здесь после освобождения от модуля для раскрытия неопределенности вида использовано правило Лопиталя. Затем, пренебрегая единицей по сравнению с бесконечно большой величиной, и желая применить шкалу бесконечно больших функций, вводим новую переменную .

В соответствии со шкалой бесконечно больших функций, учитываем, что является бесконечно малой по сравнению с функцией.

о

Здесь после выяснения вида неопределенности мы не стали применять правило Лопиталя, т. к. оно привело бы к усложнению функции, стоящей по знаком предела.

Вместо этого, используя основное логарифмическое тождество, прологарифмировали первоначально заданную функцию. Затем, пренебрегая конечной величиной по сравнению с бесконечно большой величиной , получаем конечный результат.

Пример 11. Найти поведение функции при

Решение примера 11.

.

.

Здесь после освобождения от модуля использована формула для эквивалентных в нуле функций: .

Поведение заданной функции определяется найденными пределами. Добавки (-0) означают, что график функции располагается ниже соответствующих значений пределов (см. Рис 1). Стрелки на графике означают исключение из области допустимых значений аргумента точки с абсциссой .

y y

1

o x

0 1 x

-1

Рис. 1 Рис. 2

.

.

Здесь неопределенность вида раскрывалась по правилу Лопиталя.

Поведение заданной функции определяется найденными значениями пределов. Схематический рисунок графика функции в окрестности точки см. на Рис. 2. Стрелка на графике означает, что точка с абсциссой исключена из области допустимых значений аргумента.

.

Здесь для раскрытия неопределенности вида было использовано правило Лопиталя.

Предела слева в точке рассматривать нет необходимости, т. к. заданная функция определена только для положительных значений аргумента .

Поведение функции справа от нуля изобразим на Рис. 3

y y

1

o x x

Рис. 3 Рис. 4

.

Здесь для раскрытия неопределенности вида использовали основное логарифмическое тождество. Затем использовали различные формы представления функций, эквивалентных в нуле. В частности, для логарифма использовали формулу , справедливую при . Далее, по шкале бесконечно больших функций определили, что логарифм является бесконечно малой величиной по сравнению со степенной функцией .

Поведение заданной функции при изображено на Рис. 4.

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.

Так, сумма a³ и b² есть a³ + b².
Сумма a³ – bⁿ и h⁵ -d⁴ есть a³ – bⁿ + h⁵ – d⁴.

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a² и 3a² равна 5a².

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.

Так, сумма a² и a³ есть сумма a² + a³.

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a³bⁿ и 3a⁵b⁶ есть a³bⁿ + 3a⁵b⁶.

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Из	2a4	3h2b6	5(a – h)6
Вычитаем	-6a4	4h2b6	2(a – h)6
Результат	8a4	-h2b6	3(a – h)6

Или:
2a⁴ – (-6a⁴) = 8a⁴
3h²b⁶ – 4h²b⁶ = -h²b⁶
5(a – h)⁶ – 2(a – h)⁶ = 3(a – h)⁶

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a³ на b² равен a³b² или aaabb.

Первый множитель	x-3	3a6y2	a2b3y2
Второй множитель	am	-2x	a3b2y
Результат	amx-3	-6a6xy2	a2b3y2a3b2y

Или:
x^-3 ⋅ a^m = a^mx^-3
3a⁶y² ⋅ (-2x) = -6a⁶xy²
a²b³y² ⋅ a³b²y = a²b³y²a³b²y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a⁵b⁵y³.

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат – это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a².a³ = aa.aaa = aaaaa = a⁵.

Здесь 5 – это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, aⁿ.a^m = a^m+n.

Для aⁿ, a берётся как множитель столько раз, сколько равна степень n;

И a^m, берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a².a⁶ = a²⁺⁶ = a⁸. И x³.x².x = x³⁺²⁺¹ = x⁶.

Первый множитель	4an	b2y3	(b + h – y)n
Второй множитель	2an	b4y	(b + h – y)
Результат	8a2n	b6y4	(b + h – y)n+1

Или:
4aⁿ ⋅ 2aⁿ = 8a²ⁿ
b²y³ ⋅ b⁴y = b⁶y⁴
(b + h – y)ⁿ ⋅ (b + h – y) = (b + h – y)ⁿ⁺¹

Умножьте (x³ + x²y + xy² + y³) ⋅ (x – y).
Ответ: x⁴ – y⁴.
Умножьте (x³ + x – 5) ⋅ (2x³ + x + 1).

Это правило справедливо и для чисел, показатели степени которых – отрицательные.

1. Так, a^-2.a^-3 = a^-5. Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y^-n.y^-m = y^-n-m.

3. a^-n.a^m = a^m-n.

Если a + b умножаются на a – b, результат будет равен a² – b²: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.

Так, (a – y).(a + y) = a² – y².
(a² – y²)⋅(a² + y²) = a⁴ – y⁴.
(a⁴ – y⁴)⋅(a⁴ + y⁴) = a⁸ – y⁸. 5}$. Ответ: $\frac{2x}{1}$ или 2x.

3. Уменьшите показатели степеней a²/a³ и a^-3/a^-4 и приведите к общему знаменателю.
a².a^-4 есть a^-2 первый числитель.
a³.a^-3 есть a⁰ = 1, второй числитель.
a³.a^-4 есть a^-1, общий числитель.
После упрощения: a^-2/a^-1 и 1/a^-1.

4. Уменьшите показатели степеней 2a⁴/5a³ и ²/a⁴ и приведите к общему знаменателю.
Ответ: 2a³/5a⁷ и 5a⁵/5a⁷ или 2a³/5a² и 5/5a².

5. Умножьте (a³ + b)/b⁴ на (a – b)/3.

6. Умножьте (a⁵ + 1)/x² на (b² – 1)/(x + a).

7. Умножьте b⁴/a^-2 на h^-3/x и aⁿ/y^-3.

8. Разделите a⁴/y³ на a³/y². Ответ: a/y.

9. Разделите (h³ – 1)/d⁴ на (dⁿ + 1)/h.

Math Tutor – Функции – Теория

Math Tutor – Функции – Теория – Ограничения

Здесь мы попытаемся угадать предел функции на бесконечности, конечно, мы также покажет, как подтвердить такую ​​догадку. Мы рассмотрим функции, которые включают все виды степеней (многочлены, экспоненты) и логарифмы, мы ниже будут показаны более точные характеристики.

Обратите внимание, что некоторые из этих соображений также применимы для предела при отрицательных значениях. бесконечность, но она может быть коварной и коварной. Есть маленькая хитрость, которая делает это безопасно для нас: учитывая предел на отрицательной бесконечности, используйте замена, чтобы превратить его в ограничение на бесконечность, и все приемы из этого раздела применимы.

Угадывание, которое мы рассмотрим здесь, очень полезно и обычно предлагает кратчайшее решение выражений, которые в противном случае пришлось бы решать в различными способами, часто с использованием правила Лопиталя, что приводит к сложным выражения. Он использует два основных ингредиента. Во-первых, хорошее знание предельная алгебра, особенно основных ограничений, вторым важным компонентом является понимание взаимодействие степеней и экспонент (и корней). Мы начнем с малого введение.

Во многих функциях встречаются суммы степеней и подобные выражения. Для Например, рассмотрим функцию x ³  + 5 x ^1/2  −  x ⁻² , нас интересует его предел на бесконечности. Первые две степени уходят в бесконечность (положительный показатель степени), третья мощность правильно записывается как 1/ x ² , что сходится к 0. Используя предельную алгебру, мы легко находим предел всей функции: ∞ + 5⋅∞ − 0 = ∞.

Теперь вот проблема: каков предел на бесконечности f ( x ) =  x ³  − 5 x ² ? Мы знаем, что ∞ − ∞ является неопределенным выражением. Существуют процедуры для нахождения результата, но соответствующие методы иногда приводят к сложным расчетам. В В этом разделе мы научимся угадывать правильный ответ и доказывать это легко (вроде).

Кстати, когда мы складываем и вычитаем какие-то объекты и даже умножая их на действительные числа, как мы делали в приведенном выше примере, мы называем это “линейная комбинация”. Таким образом, выражение в этом примере было «линейным сочетание полномочий». Мы будем использовать эту терминологию на протяжении всего этого раздела. Сначала мы определим, какие проблемы мы будем решать.

Многочлены и другие суммы (степеней)

Обратите внимание, что отрицательные степени не вызывают проблем в выражениях, подобных тому, что выше мы видели, что x ⁻² стремится к нулю на бесконечности и поэтому не вызывает проблем в предельной алгебре при добавлении к что-то другое. Поэтому мы будем рассматривать только положительные показатели в этом раздел. Если все показатели степени также являются целыми числами, мы на самом деле говоря полиномы здесь. Но мы будем работать в более общем плане, а также позволим для положительных показателей, которые не являются целыми числами (например, показатель степени 1/2, то есть квадратный корень).

Мы также будем учитывать «экспоненты», т. е. степени вида а ^х . Опять же, поскольку мы знаем что a ^x →0 на бесконечности, если a  < 1 и 0 не является проблемой в суммах, мы будет рассматривать только экспоненты a ^x с a  > 1.

Но это еще не все. В то время как «линейные комбинации» степеней и экспонент как указано выше (степени / экспоненты, умноженные на числа, а затем добавляются/вычитаются) встречаются довольно часто, мы включим еще больше выражений: логарифмы и даже степени вида х ^х . Сейчас мы готовы изложить проблему, которую мы пытаемся решить здесь:

Вопрос:
Имеем выражение вида α ⋅ A ( x ) +  β ⋅ B ( x ) +…, где функции A ( x ), B ( x ),… могут быть мощности x ^а с a  > 0, экспоненциальные a ^x с a  > 1, степени логарифмов [ln( x )] ^a с a  > 0 и общие полномочия, такие как х ^х . Что произойдет с этим выражением, если мы позволим х уходят в бесконечность?

Обратите внимание, что все перечисленные выше выражения стремятся к бесконечности, поскольку х →∞. Когда они объединены вместе в некоторой линейной комбинации, мы обычно получаем некоторое неопределенное выражение с участием бесконечностей, так как мы получаем результат сразу, только если все эти бесконечности складываются. А если их вычесть? мы скоро увидим что некоторые бесконечности «больше» или более важны, чем другие.

Решение проблемы:
Если мы допустим x →∞, то выражение, как указано выше будет вести себя точно так же, как его доминирующий термин. Чтобы доказать это математически, мы фактор доминирующий член из выражения, а затем применить предел. выражение, остающееся после факторизации, должно стремиться к ненулевому вещественному числу.

Под «преобладающим термином» мы подразумеваем термин, который для больших x преобладает над все остальные члены данной линейной комбинации, и поэтому другие члены могут игнорироваться, они не мешают тенденции, согласно которой господствующая сила имеет около бесконечности. Среди всех перечисленных выше типов существует иерархия (степени, экспоненты, логарифмы,…). Когда мы говорим, что «член А преобладает над термином B для больших значений x “, мы действительно имеем в виду что при исследовании предела выражения α ⋅ А  +  β ⋅ В для х стремясь к бесконечности, мы можем не принимать во внимание член B и просто беспокоиться о А . На самом деле, здесь мы намеренно немного расплывчаты и неточны, так как мы хотим показать практичный и простой подход; эту тему можно сделать правильно математически и связано с некоторыми другими понятиями, если вы заинтересованы, ознакомьтесь со следующим разделом, посвященным порядок функций.

Пример:
Вскоре мы увидим, что x ² преобладает над лн ( х ) на бесконечности. Теперь представьте, что нам нужно найти предел 23ln( x ) −  x ² на бесконечности. Когда х становится очень большим, второй член преобладает, мы можем игнорировать первый. Таким образом, это выражение будет вести себя (когда x увеличится до бесконечности) как выражение – x ² , которое как мы знаем стремится к минус бесконечности. Следовательно, и данное выражение уходит в отрицательную бесконечность при бесконечность.

Конечно, этот результат является лишь предположением. Мы писали выше (в Решении), что математически мы можем сделать это, выделив доминирующий член. Пробуем:

Обратите внимание, что член, оставшийся после вынесения за скобки доминирующей мощности действительно стремится к ненулевому вещественному числу, как указано выше. Факт то, что оно не равно нулю, становится важным для предельной алгебры, мы не можем получить ∞⋅0.

Есть способ правильно записать наши интуитивные рассуждения. Когда мы пишем A ( x ) ~ B ( x ), мы имеем в виду, что выражения A и B ведут себя одинаково, когда x →∞; для самых практичных целей выражения A ( x ) и B ( x ) являются то же самое, когда x действительно очень большое. Мы также говорим, что A и B “одного порядка”. Таким образом, приведенное выше интуитивное рассуждение можно записать следующим образом:

23ln( x ) −  x ²  ∼ − x ² →-∞.

Обратите внимание, что этот удобный способ записи не является общепринятым. Кроме того, это не является правильным решением – в конце концов, мы только догадывались там. Любой ответ, который мы получаем таким образом, должен быть подтвержден правильным математический расчет, например, процедура факторизации, которую мы показали выше.

Когда мы рассматриваем силы в виде линейной комбинации сил и других подобных терминах, мы на самом деле делаем две разные вещи. Во-первых, мы смотрим только на степени, экспоненты и т. д., то есть мы игнорируем мультипликативные константы до них. Таким образом мы определяем введите выражения. Для пример, выражение “13⋅[ln( x )] ³ ” имеет тип [ln( x )] ³ , а приведенный выше пример относится к типу x ² , потому что тип выражения задается типом своего доминирующего термина. Тип говорит нам примерно, как быстро данное выражение убегает, когда x действительно велико.

Этот тип используется при грубом сравнении поведения различных выражения, выясняя, какие можно игнорировать и т. д. Затем, когда мы действительно начнем угадывая предел в бесконечности, мы должны включить мультипликативное константы в наших рассуждениях. Таким образом, мы бы сказали, что 23ln( x ) −  x ² относится к типу x ² когда x уходит в бесконечность, но тогда мы бы имели сказать, что это порядок – x ² , когда мы пытаемся угадать лимит; то есть мы должны нести константы при использовании ∼ Процедура.

Как видите, интуитивная процедура может быть простой, если написать ее правильно. математически (по факторингу) может быть немного длиннее, но никогда не должно быть сложно, до тех пор, пока мы правильно определяем и исключаем доминирующий термин. Который подводит нас к основной части этого раздела:

Шкала сил

Вот список терминов, упомянутых выше, от самых доминирующих до наименее. То есть каждое перечисленное выражение превалирует над всеми перечисленными выражениями. позже:

(1) мощность x ^x ,
(2)   экспоненциальный a ^x для a  > 1,
(3)   мощность x ^a для a  > 0,
(4)   логарифм [ln( x )] ^a для a  > 0,

Для практического использования люди часто предпочитают более разговорный способ запоминания. эту иерархию, используя такие фразы, как «степени превосходят логарифмы на бесконечности» и «экспоненты бьют степени на бесконечности» и т. д. Показаны доказательства этой иерархии. для последовательностей в эту записку, для функций доказывается по существу таким же образом.

Исследуя линейную комбинацию таких членов, мы всегда сначала находим доминирующее выражение. Тем не менее, может быть больше терминов этой доминирующей категория. Таким образом, нам также необходимо знать взаимное доминирование внутри каждой категории. Там правило простое. В категориях (2), (3) и (4) всегда есть параметр (т.е. a ), а самый высокий из них является доминирующим.

По сути, вопрос о доминировании — это один из ответов на вопрос «какая бесконечность больше». На следующей картинке (не совсем в масштабе) мы попытаемся символически выразить отношения между различными видами выражения, получая шкалу степеней :

Пример:
Каков предел 13⋅2 ^x  +  x ²  – 5⋅3 ^x  – [ln( x )] ^1/2 на бесконечности?

Решение: Там есть три категории: экспоненты, степени и логарифмы. Экспоненты являются самыми высокими в списке, поэтому они будут обеспечивать доминирующее значение. срок. Есть два кандидата, 2 ^x и 3 ^х . Поскольку 3 > 2, последняя экспонента является доминирующей. терм, то есть данное выражение имеет вид 3 ^х . Таким образом, мы можем игнорировать все остальные термины и предположить, что

13=2 ^x + x ² – 5om3 ^x – [LN ( x )] ^1/2 ∼ – 5 % ^x З. 5⋅∞ = −∞.

Как мы можем подтвердить этот результат математически? Выбрасывая доминирующий термин.

С тремя дробями в скобках лучше работать отдельно. Первый один просто экспоненциальный, два других приведут к Правило Лопиталя:

Наконец мы получаем

Обратите внимание, что иногда мы можем применить это рассуждение даже к терминам, которые не выглядят точно так же, как приведенные выше, но могут быть преобразованы в них с помощью алгебры. Два наиболее типичных примера: (2 x ) ³  = 2 ³ ⋅ x ³  = 8⋅ x ³ и 3 ^{2 x +1}  = (3 ² ) ^x ⋅3 ¹  = 3⋅9 ^x .

Корни

Интуитивная процедура работает и в том случае, если в выражение; то есть, если некоторые части выражения закрыты под корнями. Затем мы следуем следующей процедуре. Сначала мы обрабатываем каждый корень индивидуально. Для каждого корня находим доминирующий член выражения внутри этого корня это определяет тип выражения под корнем. Когда мы применяем корень к этому выражению, мы получаем тип корня как целое. Мы можем подтвердить это, разложив его на множители, получившийся корень тогда должен иметь правильный ненулевой предел на бесконечности.

После обработки корней (если они есть) собираем вместе все типы (те, что были сами по себе и виды корней) и определяли доминирующий член все выражение. Эту процедуру можно повторить несколько раз, если есть корень, под которым есть выражение с другим корнем и так на. Наконец, определив доминирующий член всего данного выражение, мы можем обрабатывать его, как указано выше; то есть мы выносим за скобки доминанту выражение и проверьте предел.

Примечание. Выносить на множители обычно легче, если повторять угадывание. часть; то есть сначала выделяйте доминирующие термины из корней, а затем выход из положения.

Пример: Найти (если существует)

Сначала проверяем в корне. Под ним просто полномочия, поэтому они в та же категория, и побеждает тот, у кого более высокий показатель степени. В нашем случае выражение под корнем имеет тип x ⁶ . Когда корень применяется к этому, мы находим, что сам корень имеет тип x ^6/2  =  x ³ , точно так же, как вторая часть заданное выражение. Таким образом, мы получаем два термина одного типа, два доминирующих термина, и поэтому ни один из них не может быть проигнорирован. Мы пытаемся угадать сейчас, сначала игнорируя термин под корнем, который мы знаем, можно игнорировать.

Мы получили наше предположение (по пути мы увидели, что корень сам по себе ведет себя как 3 x ³ для больших x ) и сейчас мы это докажем. Мы начинаем с выдергивание доминирующего фактора из корня, как рекомендовано.

На самом деле, часть предположений выше могла быть неверной, и мы бы не знали. это, потому что мы еще не затронули важную тему. Нам тут повезло, но теперь пришло время для

Предупреждение: Что произойдет, если мы получим несколько доминирующих терминов? Если они добавлены, мы можем добавить их безопасно. Если их вычесть (т. е. если предел алгебра привела бы к неопределенной форме ∞ − ∞), тогда мы должны быть очень осторожный. Если применить обычную алгебру к доминирующим терминам в угадывании фаза сохранила бы этот доминирующий член, то мы можем сделать это как обычно. Если алгебра заставила бы этот термин исчезнуть, мы не можем использовать угадывание!

Например, если бы у нас было 4 x ⁶ вместо 9 х ⁶ в этом последнем примере корень будет вести себя как 2 x ³ , что отменит с другим термином. Затем шаг 2 x ³  − 2 x ³  = 0 не может быть сделано.

Почему это так? Потому что, когда мы угадываем, каждый термин на самом деле представляет не просто само по себе, но в нем могут быть спрятаны другие менее важные термины (например, “9 x ⁶ ” представляет также “+  x ⁴ ” часть в приведенный выше пример). Когда мы вычитаем доминирующие члены и некоторые остаются, то эти части, которые мы игнорировали раньше, все еще могут быть проигнорированы (доминирующий термин что затмевало их раньше, так и осталось) и угадывающий расчет есть правильный. Однако, если алгебра приведет к исчезновению доминирующего члена, то один из терминов, который мы ранее игнорировали, внезапно получил повышение до доминирование, поэтому этот новый доминирующий термин теперь будет определять исход от предела! В таких случаях мы должны использовать более точный, более осторожный метод оценки, метод, который не будет игнорировать термины, которые могут быть временно неважно.

Сравните следующие два примера; они могут выглядеть глупо, но они хорошо проиллюстрируйте суть. В каждом из них мы сначала угадываем (даже если это может быть неправильно), а затем сделать правильный расчет.

В первом примере догадка верна; обратите внимание, что в правильном расчет, после сложения условий мы все еще можем игнорировать “+ x “, так что это не играет роли в конечном результате. в второй расчет это х получает доминирование.

Правило для доминирующих терминов: Если мы оцениваем предел в бесконечности путем угадывания и в выражении есть более доминирующие термины, то мы можем сложить их вместе с помощью алгебры, только если они в результате не сокращаются.

Если они отменятся, нам придется отказаться от интуитивных расчетов и попробовать некоторые другой метод. Однако даже в этом случае эта угадывающая часть помогает в качестве подготовки, поскольку часто полезно знать типы терминов в выражении.

Реплика: Мы говорили о корнях, но это всего лишь особые способности (квадратный корень — это просто 1/2-я степень и т. д.). Конечно, процедура описанное выше работает для всех таких мощностей, поэтому мы не должны смущаться, если мы получаем выражение, включающее что-то вроде ( x ²  –  x  + 1) ¹³ . Тогда этот термин будет принадлежать среди тех, с которых мы начнем, мы найдем доминирующий термин x ² внутри, вся мощность тогда типа х ²⁶ .

Коэффициенты

Мы подошли к наиболее типичному выражению, которое можно обработать с помощью интуитивные вычисления: дробь, числитель и знаменатель которой тип, который мы описали выше. Как обращаться с такими дробями? Сначала мы по отдельности исследовать числитель и знаменатель: мы определяем доминирующий член каждого из них, а затем вынести их за скобки. Тогда у нас есть один доминирующий термин в числитель, единица в знаменателе, так что мы сокращаем их, если можем, и, наконец, мы найти предел полученного соотношения. Шкала полномочий снова может помочь здесь. Если член в числителе преобладает, мы получаем бесконечность как предел при бесконечность. Если член в знаменателе преобладает, мы получаем ноль в качестве предела на бесконечности.

Это вполне естественно. Обычно мы получаем бесконечность над бесконечностью, а преобладание означает, что одна бесконечность больше другой бесконечности, поэтому это побеждает. Например, когда бесконечность в знаменателе преобладает над бесконечность в числителе, значит, в знаменателе в итоге много намного больше, чем числитель, и полученное отношение, таким образом, очень маленькое, что говорит о том, что он стремится к нулю.

Мы упоминали, что иногда доминирующие члены знаменателя и числитель может быть отменен, когда они вынесены из отношения; мы тогда получить вид дроби в целом.

Иногда, сталкиваясь с отношением, люди предпочитают отмену, а не факторинг. сравнение. Это работает – но только иногда. Предлагаем подробно обсудить как обращаться с отношениями многочленов на бесконечности в этой заметке.

Пример: Найти (если существует)

Сначала будем интуитивно угадывать ответ, а потом делать это правильно. расчеты. Начать следует с обработки корней.

В кубическом корне доминирующим членом является куб, поэтому мы можем игнорировать другие термины для больших значений х . Из квадратного корня в знаменателя, экспонента преобладает над квадратом, поэтому мы можем игнорировать сила.

Теперь мы знаем типы бесконечно удаленных корней, поэтому можем сравнить их с остальные члены и найти доминанты, отдельно для числителя и знаменатель. Затем мы используем иерархию полномочий, чтобы угадать результат:

Какова была причина? В числителе степени превосходят логарифмы, а наибольшая мощность – квадрат. Кстати, это показывает, почему важно всегда сначала обрабатывайте корни. С первого взгляда можно было бы догадаться, что x ³ является доминирующим членом в числителе, но после того, как мы проанализировав корень, мы увидели, что на самом деле он ведет себя точно так же, как x .

В знаменателе доминирующим членом была экспоненциальная 2 ^x , поэтому мы проигнорировали остальные. Наконец, поскольку экспоненты степени биения на бесконечности, мы пришли к выводу, что это отношение стремится к нулю.

Теперь нам предстоит подтвердить нашу догадку расчетами, а именно факторингом. вне. Хотя опытный ученик сделал бы это в нескольких строчках, мы предпочитаем показать более подробно, а также добавить замечание относительно двух корней; поэтому мы предложить расчеты здесь.

Продукты

Хотя это случается не часто, иногда выражения вышеприведенного типа умножаются вместе. В таком случае применяется интуитивная процедура к каждому члену произведения, находя тип каждого. Тип целого продукт тогда является продуктом отдельных видов. Однако обычно делают не получить один из изученных выше типов (степени, экспоненты и т. д.), скорее продукт таких типов. Такие выражения не указаны в нашей шкале степеней, поэтому таким способом редко можно получить готовый ответ. Однако, часто можно использовать опыт работы с типами, чтобы узнать что-то полезное в любом случае.

Пример:

Заметим, что мы выяснили, что числитель имеет вид x 2 ^x и знаменатель имеет вид x ² 2 ^x ; к счастью, мы могли отменить два типа ловко и все же получили ответ, используя шкалу полномочий. Однако сейчас мы внесем небольшое изменение, и оно больше не будет работать:

Теперь мы сравниваем (после отмены) два типа, х 2 ^х в числителе и х ^х в знаменателе. Поскольку первое не входит в обычную шкалу силы, мы не знаем, что получится, когда эти два типа разделятся. Мы знаем что x ^x бьет 2 ^x , но очевидно x 2 ^x уходит в бесконечность гораздо быстрее, чем просто 2 ^x ; неужели это происходит настолько быстрее, что даже опережает х ^х , то есть возможно ли, что x 2 ^x ударов x ^x ?

Ответ – нет. На самом деле х 2 ^х это особый тип который превосходит 2 ^x и превосходит х ^х , так что он вписывается точно между этими двумя. Вышеупомянутая функция сходится к нулю при бесконечность; доказательство было бы модификацией доказательства того, что факториалы побеждают экспоненты, см. Приложение в это примечание.

---

Интуитивные рассуждения можно применить и к более сложным выражениям. Было бы трудно выразить точно, где мы можем применить этот вид рассуждений, но менее точно это звучит так: основной строительный блок линейная комбинация степеней, экспонент, степеней логарифмов и общие полномочия (их множители добавляются и/или вычитаются). Это основное комбинацию можно положить под какой-то корень/в силу, создав тем самым новую строительный блок, который может быть частью другой линейной комбинации. Эти линейные комбинации могут быть составлены с использованием соотношений/произведений и, таким образом, созданы новые члены дальнейших линейных комбинаций. Все эти процедуры можно повторить в любом порядке.

Предупреждение: Выше мы свободно игнорировали части линейных комбинаций и позже даже корни, когда они стали неважными по сравнению с некоторыми доминирующими условия. Тем не менее, есть две вещи, о которых следует быть осторожным. Сначала мы можно игнорировать только в линейных комбинациях; корни/силы и соотношения/продукты могут игнорироваться только тогда, когда они заменяются их доминирующими терминами и, таким образом, становятся приемлемыми частями линейных комбинаций. Во-вторых, что более важно, это игнорирование может быть сделано только в выражениях, как указано выше (линейные комбинации, корни/степени и отношения/произведения перепутаны). Это не допустимо делать игнорирование в выражениях, смешанных с другими функции. Например, мы можем заменить x  − ln( x ) всего с x , если он находится под корнем или частью дроби, но мы не может этого сделать, если это аргумент, скажем, экспоненциальный. Таким образом 2 ^{x -ln( x )} ∼ 2 ^x неправильно , sinh( x  − ln( x )) ∼ sin( x ) неправильно и т. д.

Для многих примеров мы ссылаемся на Решаемые проблемы – ограничения.

---

Порядок функций, асимптоты
Назад к теории – Пределы

Предел экспоненциальной функции

В этой статье мы обсудим, как решать экспоненциальные функции с ограничениями. Но прежде чем обсуждать это, сначала давайте посмотрим, что такое экспоненциальная функция.

Что такое показательная функция?

Показательная функция — это функция, в которой независимая переменная, т. е. x, является показателем степени или степенью основания. Он имеет вид:

Здесь:

• a — положительное действительное число, такое, что оно не равно единице
• Область определения экспоненциальной функции — все действительные числа
• Диапазон экспоненциальной функции — все положительные действительные числа 1), а горизонтальная асимптота y равна нулю

 

Лучшие репетиторы по математике

Поехали

Стандартные результаты пределов

Существует 5 стандартных результатов пределов, которые обсуждаются ниже. Эти стандартные результаты можно использовать в качестве формул при оценке пределов экспоненциальных функций.

Standard 1

   

Standard 2

   

Standard 3

   

Standard 4

   

Standard 5

   

In the next section, we will solve couple of examples in which we will be evaluating the пределы экспоненциальных функций

 

Пример 1

Оцените следующую экспоненциальную функцию:

   

Решение

Дано, что предел функции должен оцениваться по мере того, как x приближается к 0. Таким образом, когда мы прямо ставим 0 в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.

Итак, сначала продифференцируем числитель . Производная от первого члена равна . Аналогично, производная второго члена равна .

Теперь продифференцируем знаменатель. Производная x равна 1. Подставьте эти производные в приведенную выше функцию следующим образом:

   

Теперь примените ограничение к приведенному выше выражению, как показано ниже: Вычислите следующее выражение:

   

Решение

Известно, что предел функции должен оцениваться по мере того, как x приближается к 0. Таким образом, когда мы подставляем 0 непосредственно в приведенное выше выражение, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел. 9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна .

Теперь продифференцируем знаменатель. Производная от первого члена равна . Аналогично, производная второго члена равна .

Подставьте эти производные в приведенное выше выражение следующим образом:

   

Теперь примените ограничение к приведенному выше выражению, как показано ниже:0002 Оцените предел следующей экспоненциальной функции:

   

Решение

Дано, что предел функции должен оцениваться, когда x приближается к 0. Итак, когда мы подставляем 0 непосредственно в приведенное выше выражение, мы получаем неопределенная форма. Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.

Сначала найдем производную от числителя, которая равна . Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже:

Теперь мы возьмем предел выражения:

Пример 4

Оценить предел следующей экспоненциальной функции:

Решение

. Проще оценить выше. потому что после подстановки мы не получим неопределенную форму или . Таким образом, в этом примере нет необходимости применять правило Лопиталя.

   

Пример 5

Оцените следующее выражение:

   

Решение

В этом примере, если мы подставим x = 2 непосредственно в приведенное выше выражение, мы не получим неопределенный вид, поэтому правило Лопиталя неприменимо. здесь. Все, что нам нужно сделать, это заменить x = 2 в приведенном выше выражении:

     

 

Пример 6

Вычислить следующее выражение:

   

Решение

Основное понятие, которое будет использоваться при решении этой задачи, будет таким же, как и с рациональными выражениями. Сначала мы увидим наибольшую степень в числителе и знаменателе, а затем мы вынесем ее как из числителя, так и из знаменателя. Поскольку предел в этом примере равен плюс бесконечности, мы будем использовать только экспоненты с положительными показателями.