Примеры сложных функций: Примеры сложных функций | Математика

Примеры сложных функций | Математика

Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x),  а f — функция от u:  f=f(u), то функция y=f(u) — сложная.

А  u  в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:

y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.

y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.

y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u.

2) y=cos x — «простая» функция. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом:

y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u.

y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u.

3) y=tg x — «простая» функция. y = tg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — тангенс:

y=tg(17+5x²). Внутренняя функция u=17+5x², внешняя — y=tg u.

y=tg(9-x). Внутренняя u=9-x, внешняя — y=tg u.

4) y=ctg x — «простая» функция. y=ctg u — сложная функция, если u=u(x).

Примеры сложных функций для случаев, когда внешняя функция — котангенс:

y=ctg(2x+6). Внутренняя функция u=2x+6, внешняя — y=ctg u.

y=ctg(√x).  u=√x, f=ctg u.

5) y=√x — «простая» функция. y=√u — сложная, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — квадратный корень:

   

Здесь внутренняя функция y=sin x, а внешняя — f=√u.

   

Здесь u=9x³-12x+5, f=√u.

6) y=xⁿ — «простая» функция. y=uⁿ — сложная, если u=u(x). Примеры сложных функция для случая, когда внешняя функция — степенная.

y=sin³x. Внутренняя функция y=sin x (так как sin³x=(sin x)³), внешняя — у=u³.

   

7) y=arcsin x — «простая» функция. y=arcsin u — сложная, когда u=u(x).

Например, y=arcsin (3x-9) — сложная функция. Внутренняя функция u=3x-9,  внешняя — f=arcsin u.

y=arcsin (17-5x³).  u=17-5x³, f=arcsin u.

8) y=arccos x — «простая» функция. y=arccos u — сложная, при u=u(x).

Например, y=arccos (34x+5) — сложная функция. Внутренняя функция u=34x+5, внешняя — f=arccos u.

9) y=arctg x — «простая» функция. y=arctg u — сложная, при u=u(x).

Например, y= arctg (6x+2x³-7). Внутренняя функция u =6x+2x³-7, внешняя — f=arctg u.

10) y=arcctg x — «простая функция. При u=u(x) функция y=arcctg u — сложная.

Например, y= arcctg(2-11x+x²) — сложная функция. u=2-11x+x², f= arcctg u.

11) y=ln x — «простая» функция. y= ln u — сложная, при u=u(x).

Например, y=ln(4+32x-2x³). Внутренняя функция y=4+32x-2x³, внешняя — f=ln u.

   

Это — «простая» функция. А вот при u=u(x) получаем логарифм сложной функции:

   

Например,

   

   

Эта функция — «простая» (называется экспонента). А вот если в показателе стоит не x, а некоторая функция от икса: u=u(x), то это — уже экспонента сложной функции:

   

Например,

   

   

Эта функция — «простая». А вот если в показателе стоит не x, а некоторое выражение с x — функция u=u(x), то это уже степень сложной функции:

   

Например,

   

Эта функция — сложная. Внутренняя функция u=8x³+5x, а внешняя — степень сложной функции

   

Следует добавить, что внутренняя функция u, в свою очередь, может быть сложной функцией. И таких «вложенных» функций может быть несколько (теоретически — сколько угодно).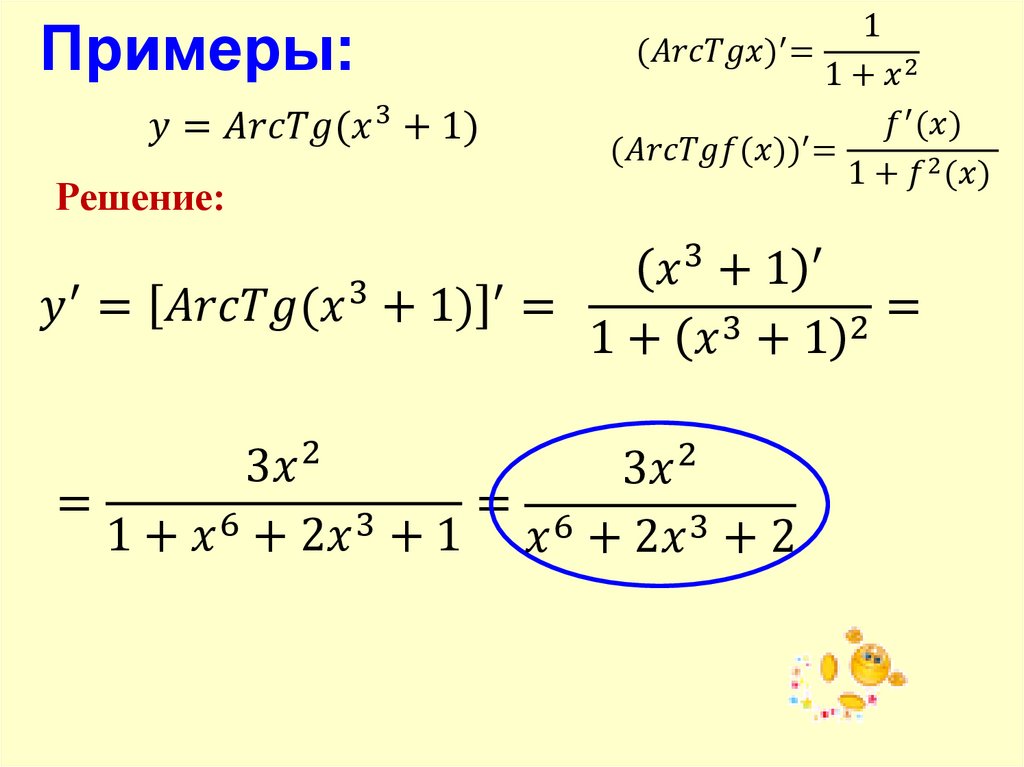 2\rightarrow \ln\boxdot \)

п.2. Теорема о производной сложной функции

Введем следующее обозначение производной (обозначение Лейбница):
\(f'(x)\overset{def}{=}\frac{df}{dx}\) – читается «де эф по де икс».
Это обозначение удобно, т.к. показывает и функцию и аргумент, по которому идет дифференцирование. Например:
\(z'(y)=\frac{dz}{dy},\ \ \varphi ‘(t)=\frac{d\varphi}{dt}\) и т.д.

Пусть внутренняя функция \(y=f(x)\), а внешняя \(z=g(y)=g(f(x))\).
При этом внутренняя функция дифференцируема в точке \(x_0\), а внешняя функция дифференцируема в точке \(y_0=f(x_0)\).
Справедлива следующая теорема:

Производная сложной функции равна произведению производной внешней функции на производную внутренней функции: $$ \begin{cases} y=f(x)\\ z=g(y)=g\circ f \end{cases} \Rightarrow \frac{dz}{dx}=\frac{dz}{dy}\cdot \frac{dy}{dx} $$

Доказательство:
По определению производная внешней функции в точке $y_0$ равна:
$$ g'(y_0)=\lim_{\triangle y\rightarrow 0}\frac{\triangle z}{\triangle y}=\frac{dz}{dy} $$ Перепишем это выражение в виде: \(\triangle z=g'(y_0)\triangle y+\varepsilon(\triangle y)\cdot\triangle y\),
где отклонение \(\varepsilon(\triangle y)\) зависит от величины приращения \(\triangle y\), причем: $$ \lim_{\triangle y\rightarrow 0}\varepsilon(\triangle y)=\varepsilon(0)=0 $$ Кроме того, т. к. внутренняя функция непрерывна: $$ \lim_{\triangle x\rightarrow 0}\varepsilon(\triangle y)=\varepsilon\left(\lim_{\triangle x\rightarrow 0}\triangle y\right)=\varepsilon(0)=0 $$ Также, поскольку внутренняя функция дифференцируема, существует предел: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\frac{dy}{dx} $$ Составим отношение: $$ \frac{\triangle z}{\triangle x}=g'(y_0)\frac{\triangle y}{\triangle x}+\varepsilon(\triangle y)\cdot\frac{\triangle y}{\triangle x} $$ Перейдем к пределу: \begin{gather*} z'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle z}{\triangle x}=\lim_{\triangle x\rightarrow 0}\left(g'(y_0)\frac{\triangle y}{\triangle x}+\varepsilon(\triangle y)\cdot\frac{\triangle y}{\triangle x}\right)=\\ =g'(y_0)\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}+\lim_{\triangle x\rightarrow 0}\varepsilon(\triangle y)\cdot \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=g'(y_0)\cdot f'(x_0)+0=g'(y_0)\cdot f'(x_0) \end{gather*} Или: $$ \frac{dz}{dx}=\frac{dz}{dy}\cdot\frac{dy}{dx} $$ Что и требовалось доказать.

2+2x-1)} \end{gather*}

в) \( y=\sqrt{cos(2x+1)} \) \begin{gather*} x\rightarrow (2x+1)\rightarrow cos\boxdot\rightarrow \sqrt{\boxdot} \end{gather*}

	Функция	Производная от функции	Аргумент в производной	Итоговый множитель
1	$$ \sqrt{\boxdot} $$	$$ \frac{1}{2\sqrt{\boxdot}} $$	$$ \boxdot=cos(2x+1) $$	$$ \frac{1}{2\sqrt{\boxdot}}=\frac{1}{2\sqrt{cos(2x+1)}} $$
2	$$ cos\boxdot $$	$$ -sin\boxdot $$	$$ \boxdot=2x+1 $$	$$ -sin\boxdot=-sin(2x+1) $$
3	$$ 2x+1 $$	$$ 2 $$	$$ – $$	$$ 2 $$

\begin{gather*} y'(x)=\frac{1}{2\sqrt{cos(2x+1)}}\cdot(-sin(2x+1))\cdot 2=-\frac{sin(2x+1)}{\sqrt{cos(2x+1)}} \end{gather*}

г) \( y=\frac{3}{\sqrt{cos(5x-3)}} \) \begin{gather*} x\rightarrow (5x-3)\rightarrow cos\boxdot\rightarrow \sqrt{\boxdot}\rightarrow\frac{3}{\boxdot} \end{gather*}

	Функция	Производная от функции	Аргумент в производной	Итоговый множитель
1	$$ \frac{3}{\boxdot} $$	$$ -\frac{3}{\boxdot^2} $$	$$ \boxdot=\sqrt{cos(5x-3)} $$	$$ -\frac{3}{\boxdot^2}=-\frac{3}{\left(\sqrt{cos(5x-3)}\right)^2} $$
2	$$ \sqrt{\boxdot} $$	$$ \frac{1}{2\sqrt{\boxdot}} $$	$$ \boxdot=cos(5x-3) $$	$$ \frac{1}{2\sqrt{\boxdot}}=\frac{1}{2\sqrt{cos(5x-3)}} $$
3	$$ cos\boxdot $$	$$ -sin\boxdot $$	$$ \boxdot=5x-3 $$	$$ -sin\boxdot=-\boxdot(5x-3) $$
4	$$ 5x-3 $$	$$ 5 $$	$$ – $$	$$ 5 $$

\begin{gather*} y'(x)=-\frac{3}{cos(5x-3)}\cdot\frac{1}{2\sqrt{cos(5x-3)}}\cdot(-sin(5x-3))\cdot 5=\frac{15tg(5x-3)}{2\sqrt{cos(5x-3)}} \end{gather*}

Пример 3*. 8\)

в) \( y=sin(sin(sinx)),\ \ x_0=\pi \) \begin{gather*} x\rightarrow sinx\rightarrow sin\boxdot\rightarrow sin\boxdot \end{gather*}

	Функция	Производная от функции	Аргумент в производной	Итоговый множитель
1	$$ sin\boxdot $$	$$ cos\boxdot $$	$$ sin(sinx) $$	$$ cos(sin(sinx)) $$
2	$$ sin\boxdot $$	$$ cos\boxdot $$	$$ sinx $$	$$ cos(sinx) $$
3	$$ sinx $$	$$ cosx $$	$$ – $$	$$ cosx $$

\begin{gather*} y'(x)=cos(sin(sinx))\cdot cos(sinx)\cdot cosx \end{gather*} Подставляем \(x_0=\pi\): \begin{gather*} y'(\pi)=cos(sin(sin\pi))\cdot cos(sin\pi)\cdot cos\pi=cos 0\cdot cos 0\cdot(-1)=1\cdot 1\cdot(-1)=-1 \end{gather*} Ответ: -1

г) \( y=\ln\sqrt{\frac{1-sinx}{1+sinx}},\ \ x_0=\frac\pi 6 \)
Преобразуем выражение под логарифмом: \begin{gather*} \ln\sqrt{\frac{1-sinx}{1+sinx}}=\frac12\ln\left(\frac{1-sinx}{1+sinx}\right)=\frac12(\ln(1-sinx)-\ln(1+sinx)) \end{gather*} Для первого слагаемого: \(x\rightarrow (1-sinx)\rightarrow\ln\boxdot\) \begin{gather*} (\ln(1-sinx))’=\frac{1}{1-sinx}\cdot(1-sinx)’=\frac{-cosx}{1-sinx} \end{gather*} Аналогично для второго слагаемого: \begin{gather*} (\ln(1+sinx))’=\frac{1}{1+sinx}\cdot(1+sinx)’=\frac{cosx}{1+sinx} \end{gather*} Получаем: \begin{gather*} y'(x)=\frac12\left(\frac{-cosx}{1-sinx}-\frac{cosx}{1+sinx}\right)=-\frac{cosx}{2}\cdot\frac{(1+sinx)+(1-sinx)}{(1-sinx)(1+sinx)}=\\ =-\frac{cosx}{2}\cdot\frac{2}{1-sin^2x}=-\frac{cosx}{cos^2x}=-\frac{1}{cosx} \end{gather*} Подставляем \(x_0=\frac\pi 6\): \begin{gather*} y’\left(\frac\pi 6\right)=-\frac{1}{cos\frac\pi 6}=-2 \end{gather*} Ответ: -2

Пример 4*. При каких значениях x производная функции \(f(x)\) равна нулю?
a) \( f(x)=sin3x-\sqrt{3}cos3x+3(cosx-\sqrt{3}sinx) \)
Берем производную: \begin{gather*} f'(x)=3cos3x+3\sqrt{3}sin3x+3(-sinx-\sqrt{3}cosx)=\\ =3(cos3x+\sqrt{3}sin3x)-3(sinx+\sqrt{3}cosx) \end{gather*} По условию: \begin{gather*} 3(cos3x+\sqrt{3}sin3x)-3(sinx+\sqrt{3}cosx)=0\\ cos3x+\sqrt{3}sin3x=sinx+\sqrt{3}cosx\ |\cdot\frac12\\ \frac12cos3x+\frac{\sqrt{3}}{2}sin3x=\frac12sinx+\frac{\sqrt{3}}{2}cosx\\ cos\frac\pi 3cos3x+sin\frac\pi 3sin3x=sin\frac\pi 6sinx+cos\frac\pi 6cosx\\ cos\left(3x-\frac\pi 3\right)=cos\left(x-\frac\pi 6\right)\\ cos\left(3x-\frac\pi 3\right)-cos\left(x-\frac\pi 6\right)=0\\ -2sin\frac{3x-\frac\pi 3+x\frac\pi 6}{2}sin\frac{3x-\frac\pi 3-x+\frac\pi 6}{2}=0\\ \left[ \begin{array}{l} sin\left(2x-\frac\pi 4\right)=0\\ sin\left(x-\frac{\pi}{12}\right)=0 \end{array} \right. \Rightarrow \left[ \begin{array}{l} 2x-\frac\pi 4=\pi k\\ x-\frac{\pi}{12}=\pi k \end{array} \right. \Rightarrow \left[ \begin{array}{l} 2x=\frac\pi 4+\pi k\\ x=\frac{\pi}{12}+\pi k \end{array} \right. \Rightarrow \left[ \begin{array}{l} x=\frac\pi 8+\frac{\pi k}{2}\\ x=\frac{\pi}{12}+\pi k \end{array} \right. \end{gather*}
Ответ: \(\left\{\frac\pi 8+\frac{\pi k}{2};\ \frac{\pi}{12}+\pi k\right\}\)

б) \( f(x)=20cos3x+12cos5x-15cos4x \)
Берем производную: \begin{gather*} f'(x)=-3\cdot 20sin3x-5\cdot 12sin5x+4\cdot 15sin4x=\\ =60(-sin3x-sin5x+sin4x) \end{gather*} По условию: \begin{gather*} 60(-sin3x-sin5x+sin4x)=0\\ (sin3x+sin5x)-sin4x=0\\ 2sin\frac{3x+5x}{2}cos\frac{3x-5x}{2}-sin4x=0\\ 2sin4xcosx-sin4x=0\\ sin4x(2cosx-1)=0\\ \left[ \begin{array}{l} sin4x=0\\ 2cosx-1=0 \end{array} \right. \Rightarrow \left[ \begin{array}{l} 4x=\pi k\\ cosx=\frac12 \end{array} \right. \Rightarrow \left[ \begin{array}{l} x=\frac{\pi k}{4}\\ x=\pm\frac{\pi}{3}+2\pi k \end{array} \right. \end{gather*}
Ответ: \(\left\{\frac{\pi k}{4};\ \pm\frac{\pi}{3}+2\pi k\right\}\)

Сложная функция

Ключевые слова: сложная функция, композиция функций, внешняя и внутренняя функция, график сложной функции, свойства функций

“Сложный, составной, сложенный или составленный из разных частей…”.
Толковый словарь В.И. Даля.

Мы часто в повседневной речи считаем слова “сложный” и “трудный” синонимами. Иногда можно услышать от тех учеников, которым нелегко дается математика, что сложная функция потому так называется, что она “трудная”. Но на самом деле “сложный” и “трудный” далеко не всегда означают одно и то же.

Понятие сложной функции встречается в курсе алгебры и начал математического анализа в 10 классе [3]. Для сложной функции выводится формула дифференцирования. Ученики без предварительной подготовки этот материал воспринимают с большим трудом. На чисто формальном уровне можно дать много примеров на нахождение внутренней и внешней функции для данных сложных функций. При определенной практике они начинают хорошо различаться и производную можно вычислять. Беда в том, что при этом учащиеся погружаются в технику дифференцирования, а само понятие сложной функции как композиции нескольких функций отходит на задний план.

Чтобы сложная функция предстала в более наглядном виде, и сделана данная презентация.

В зависимости от подготовленности класса этот материал может быть предложен и на факультативных занятиях, и на уроках, причем в некоторых случаях непосредственно в теме “Производная”, а в некоторых и раньше. Самое главное, чтобы основные свойства функций (в первую очередь – монотонность) к этому времени учащимися были хорошо усвоены и чтобы графики элементарных функций стали легко узнаваемы.

К этому времени учащимся будет и легче воспринимать само понятие функции как соответствие между множествами.

Несмотря на весь абстрактный характер понятия “функция” с ним нужно разобраться, постепенно вводя логические уточнения и учитывая возможности класса. А сложную функцию нужно изучать как композицию двух функций. Это понятие важно для определения взаимно обратных функций. В связи с этим в сильных классах данный материал целесообразно вводить до того, как изучаются обратные функции – например, обратные тригонометрические функции. Для классов со слабой подготовкой, где обратные тригонометрические функции вводятся на более простом уровне, разговор о сложной функции пойдет в теме “Производная”. Но и в этом случае должно быть подробное рассмотрение определения этой функции.

Поведение элементарных функций лучше всего иллюстрируется с помощью графика, поэтому и для исследования сложной функции наилучший, как мне кажется, подход – это дать представление о ее графике, построенном с использованием графиков внутренней и внешней функций.

При построении графиков сложных функций в презентации для большей наглядности используются анимационные эффекты, дающие представление о последовательных шагах, которыми характеризуется композиция нескольких соответствий.

Важно подчеркнуть, что при исследовании функций с помощью производной ученики получают более совершенный аппарат для построения графика, но и элементарные методы имеют свои преимущества: они позволяют учащимся на более простом материале воспринимать основные функциональные изменения и дают возможность “прочувствовать” поведение сложной функции. Построение графиков без производной может осуществляться с разных точек зрения. Примеры получения достаточно трудных графиков описаны, например, в [1]. Те приемы, которые предложены в данной презентации, с одной стороны, касаются именно сложных функций, но с другой демонстрируют достаточно наглядные рассуждения, которые могут помочь в исследовании функций при решении различных задач. Например, изученные приемы могут пригодиться в тех случаях, когда требуется узнать промежутки монотонности сложной функции, множество ее значений. Причем предложенный метод достаточно нагляден и не использует громоздких преобразований с формулами.

В предлагаемой презентации можно выделить три части:

1. Введение понятия сложной функции.
2. Построение графиков сложных функций.
3. Нахождение множества значений сложной функции.

1. Для того чтобы подробно описать, как “действует” сложная функция, сначала нужно повторить определение функции как соответствия между множествами, при котором каждому элементу первого множества соответствует не более одного элемента второго множества. То, что на слайде изображены круги Эйлера, не случайно: на них более ярко можно показать соответствие между элементами множеств.

Понятие функции к 10 классу должно быть сформировано, но ученикам с низкой мотивацией иногда трудно его запоминать, и в данном случае можно подробнее остановиться на контрольных вопросах, например, почему окружность или вертикальная прямая в системе координат не могут быть графиками функций (хотя их и можно задать уравнениями).

Сложную функцию рассматриваем как композицию двух функций, то есть как последовательное выполнение двух соответствий. По рисунку можно проследить, как некоторому элементу множества Х соответствует элемент множества Т, этот закон устанавливается внутренней функцией. А затем для элемента множества Т внешняя функция указывает соответствующее значение элемента из множества У. Таким образом, для первоначального х₀ мы находим t₀, а затем у₀. Устанавливается зависимость: x₀t₀у_0.

После того, как чертеж с тремя множествами и соответствиями подробно разобран, переходим к рассмотрению конкретных сложных функций. Рассматриваем примеры, где сложная функция задается формулой. Ученикам предлагается назвать внутреннюю и внешнюю функцию.

Аналогичные задания приводятся и в учебнике [3], но практика показывает, что если ограничиваться только рассмотрением формул, то от восприятия учеников ускользает структура самой композиции функций, последовательность в переходе от одного шага к другому, в итоге исчезает математическая суть сложной функции.

Восполнить этот пробел помогают графики.

2. Построим график функции (пример 1).

Укажем область определения: D(y) = (-∞; -2] U (2; +∞). Заметим, что это четная функция.

Внутренняя функция: g(x) = x² – 4, построим график в системе координат (х,t). Для простоты изложения мы строим всю параболу, но в дальнейшем рассматриваем только те х, которые входят в множество D(y).

Внешняя функция: f(t) =, построим график в системе координат (t,y).

График исходной сложной функции будем строить в системе координат (х,у).

Для наглядности на рисунке отмечено некоторое произвольное значение х₀, для него с помощью графика g(x) можно указать t₀=g(x₀), а для t₀ по графику внешней функции находим значение у₀=f(t₀), таким образом получаем цепочку соответствий: x₀t₀у₀, аналогичную той, которая была изображена на рисунке с кругами Эйлера.

После того, как два вспомогательных графика построены, переходим к главной задаче – построению графика сложной функции.

Пусть переменная х изменяется от 2 до бесконечности. По графику g(x) хорошо видно, что при этом переменная t изменяется от 0 до бесконечности. В силу возрастания квадратичной функции на данном участке об этом можно было догадаться и без графика, но график помогает в дальнейших рассуждениях.

Итак, переменная t изменяется от 0 до бесконечности. Переходим в систему координат с графиком внешней функции f(t). Значения функции, то есть у, меняются от 0 до бесконечности.

Все эти изменения приводятся в таблице на слайде.

Значит, для функции при увеличении аргумента от 2 до бесконечности получаем возрастание функции от 0 до бесконечности. И то, что мы выделили этот участок монотонности, уже очень важно! Можно хотя бы схематично изобразить график при х≥2.

Чтобы детям лучше был понятен этот переход, соответствующие участки на чертежах подчинены анимационным эффектам (слайд 10). Участки появляются по щелчку мыши последовательно, друг за другом, в определенном цвете. В результате в системе координат (х,у) выделяется промежуток [2; +∞) на оси абсцисс, а по оси ординат ему соответствует промежуток [0; +∞), функция возрастает. И появляется первый участок искомого графика.

В силу четности исходной функции получаем и второй участок графика, при х≤-2, отражая первый участок относительно оси ординат.

Но можно и другим способом получить ту же линию при х≤-2: рассмотреть изменение х от минус бесконечности до -2, тогда переменная t изменяется от +∞ до 0, а переменная у при этом изменяется от +∞ до 0. Значит, при изменении аргумента от -∞ до -2 значения сложной функции убывают – это мы и видим на графике. Данные рассуждения можно провести устно, но они хорошо иллюстрируются изображениями на слайдах.

Заметим, что в этих рассуждениях приходится намеренно отказываться от термина “промежутки” и от соответствующих скобок для их указания, потому что мы говорим именно об изменении величины, а не просто о множестве, на котором ее рассматриваем, то есть если переменная уменьшается, она изменяется, начиная с большего значения (а в промежутках на первом месте указывается меньшее значение).

Еще один вариант применения указанного способа построения графика – это подготовительный этап в изучении свойств растяжения и сжатия графиков. Например, чтобы ученик осмысленно и “своими руками” получил график у=sin2x, можно рассматривать данную функцию как сложную. Это построение разобрано в презентации (пример 2).

Не исключено, что гармонические колебания будут уже известны ученикам к моменту изучения сложной функции и, в частности, поведение графика у=sin2x. В этом случае можно предложить ученикам самостоятельно найти ответ на вопрос, как пользуясь свойствами внутренней и внешней функции, прийти к итоговому графику. Второй способ решения уже известной задачи ничуть не умаляет первый, а только лучше закрепляет полученную информацию.

В классах, где тригонометрические сведения усвоены не достаточно хорошо, весьма полезной будет повторение значений синуса для определенных углов и заполнение предложенной таблицы. В классах с высокой мотивацией в обучении эта работа достаточно легкая, таблицу можно заполнять устно, а в тетрадях только построить сам график, но действовать поэтапно.

Итак, рассматриваем функцию у=sin2x.

Замечаем, что она всюду определена, нечетная, периодична с наименьшим положительным периодом π.

Изображаем графики внутренней и внешней функции.

Начинаем с анализа изменения переменной х. Для каждого участка изменения указываем, как изменяется переменная t, а затем переменная у.

Рассматриваем участки изменения для переменной х: от 0 до π/4; от π/4 до π/2; от π/2 до 3π/4; от 3π/4 до π.

То, что нужны именно эти участки, можно объяснить поведением рассматриваемых функций. Мы должны указать такой участок для x, на котором характер изменения t не меняется – либо только увеличивается, либо только уменьшается, то есть важна монотонность внутренней функции, а при соответствующих t монотонность внешней функции тоже дает однозначный ответ, то есть можно определенно указать, что значения у либо увеличиваются, либо уменьшаются. Для простоты расчетов участки монотонности иногда дробятся на два – в данном случае учитываются нули – пересечение графика с осью абсцисс. Но характер монотонности на каждом отдельном участке постоянен.

Если у учеников появляются вопросы, то графические иллюстрации позволяют быстрее их разрешить, поэтому показ слайдов очень удобен – каждый участок можно проследить на подробном чертеже, выделение цветом помогает концентрировать внимание на обсуждаемом участке. Например, указывая изменение переменной х от 0 до π/4, мы видим, что t изменяется от 0 до π/2, а при этом изменении t значения синуса возрастают от 0 до 1 – соответствующий столбец таблицы приведен рядом с графиками на слайде.

Поскольку для большинства детей эта работа может оказаться непростой, в презентации сделаны отдельные слайды для каждого столбца с иллюстрациями на графиках. Таблица заполняется постепенно, один столбец следует за другим.

В итоге мы получаем заполненную таблицу (она приведена на отдельном слайде) и можем изобразить график у=sin2x сначала на участке от 0 до π, а затем, учитывая периодичность, и весь график.

С сильными учениками можно значительно сэкономить время, рассмотрев подробно один или два участка, а затем перейти к итоговому графику. Но в некоторых классах пригодится и более подробная работа. Учитель регулирует скорость изложения, учитывая состав и подготовленность учащихся.

В зависимости от того, какой материал по тригонометрии к этому моменту пройден в классе, можно подчеркнуть особенность сжатия графика, роль частоты и пр.

Общий вид графиков различных функций, в том числе и сложных, прекрасно можно получить, например, с помощью программы “АвтоГраф”. Они не требуют почти никаких затрат, если программа уже установлена. Когда ученики хорошо поймут сам принцип задания сложной функции и смогут хотя бы схематично указывать ее график, то для корректировки сделанного чертежа можно показать график, построенный более точно с помощью “АвтоГрафа”.

Такую работу я проводила уже на следующих уроках, когда проверяли домашнее задание и дети самостоятельно строили графики других сложных функций. Приятно было видеть, что они с большим азартом строили даже такие трудные графики, как .

Подчеркнем, что настоящая презентация ставит главную цель дать ученикам представление о самой сложной функции как композиции двух функций, о графике сложной функции, полученном с помощью внешней и внутренней функции. Эта работа требует осмысленного восприятия материала. “При осмысленном восприятии я вижу в предмете нечто большее, чем содержится в непосредственном зрительном акте, и восприятие предмета является уже в известной степени абстракцией, и в восприятии содержатся следы обобщения”, – эти слова Л.С. Выготского [2] характеризуют общие психологические особенности восприятия, но они, в частности, прекрасно иллюстрируют процесс изучения математики.

И сразу, без теоретической подготовки, предлагать ученикам только готовые графики преждевременно. С другой стороны, чисто формальные рассуждения, без графических иллюстраций затрудняют восприятие. Поэтому при изучении данного раздела нужно как можно больше наглядности и поэтапного погружения в материал.

После того, как в сознании учеников понятие сложной функции будет сформировано, можно проводить уроки по теме “Взаимно обратные функции” (в профильных классах), а также переходить к формуле производной сложной функции (если уже изучается тема “Производная”).

3. Как дополнительный вопрос в данной теме предлагается рассмотреть задачу о нахождении множества значений сложной функции. Эту задачу можно решить графически.

Например, требуется найти множество значений функции y=(3+sinx)^-1.

Выделяем внешнюю и внутреннюю функции. Замечаем, что внутренняя функция изменяется от 2 до 4 (так как -1≤sinx≤1). Значит, 2≤t≤4.

Отсюда следует важный факт: внешняя функция определена только для значений аргумента от 2 до 4.

Изображаем график внешней функции, выделяя соответствующий участок на гиперболе. И тогда легко видеть, что значения у находятся на промежутке [0,25; 0,5].

Значит, Е(у)= [0,25; 0,5].

Заметим, что в этой задаче участки монотонности не важны! Важно только множество значений внутренней функции для перехода к области определения внешней функции.

Итак, мы рассмотрели понятие сложной функции как композицию двух функций, внешней и внутренней. Научились выделять эти функции в конкретно заданной сложной функции. С помощью графиков внешней и внутренней функции строим график сложной функции. А также находим множество ее значений.

И в заключение отметим, что “сложный”, “сложенный” связаны с глаголами “сложить”, “складывать”. В словаре Даля читаем, что склад – это стройность, красота, порядок, устройство. “Складный ум – логичный, ясный и верный”. И я старалась, чтобы сложная функция для моих учеников оказалась в первую очередь не трудной, а интересно устроенной.

Работа учителя математики посвящена тому, чтобы не только облегчить ученикам восприятие трудного материала, но и дать им возможность почувствовать ту упорядоченность и красоту, которая всегда встречается в математике.

Литература.

1. Виленкин Н.Я.и др. Алгебра для 9 класса. – М.: Просвещение, 1996.
2. Выготский Л.С. Вопросы детской (возрастной) психологии // Собрание сочинений: в 6 т. – М.: Педагогика, 1984. – Т.4.
3. Колмогоров А.Н. и др. Алгебра и начала анализа. 10-11 класс. – М.: Просвещение, 2009.

Функция Python complex () с примерами

Функция Python complex () используется для преобразования чисел или строки в комплексное число. Этот метод принимает два необязательных параметра и возвращает комплексное число. Первый параметр называется действительной, а второй – мнимой.

Подпись

сложный ([реальный [, мнимый]])

Параметры

вещественный : необязательный числовой параметр.

мнимый : необязательный числовой параметр.

Возврат

Возвращает комплексное число.

Давайте посмотрим на несколько примеров функции complex (), чтобы понять ее функциональность.

Python complex () Пример функции 1

Это простой пример, показывающий использование функции complex (). Здесь мы передаем все аргументы целочисленного типа.

# Пример функции Python complex () # Вызов функции a = complex (1) # Передача одного параметра b = complex (1,2) # Передача обоих параметров # Отображение результата печать (а) печать (б)

Выход:

Python complex () Пример функции 2

Здесь мы передаем значения типа с плавающей запятой, и вывод, сгенерированный функцией, также имеет тип с плавающей запятой.

# Пример функции Python complex () # Вызов функции a = complex (1.5) # Передача одного параметра b = complex (1.5,2.2) # Передача обоих параметров # Отображение результата печать (а) печать (б)

Выход:

Python complex () Пример функции 3

Он также допускает строковые параметры, но должен быть целым числом.

# Пример функции Python complex () # Вызов функции a = complex (‘1’) # Передача одного параметра b = комплекс (‘1.5 ‘) # Отображение результата печать (а) печать (б)

Выход:

Python complex () Пример функции 4

Допускается только один строковый параметр. Если первый аргумент является строковым, он не позволяет передавать второй аргумент. При передаче второго параметра возникает ошибка.

# Пример функции Python complex () # Вызов функции a = complex (‘1’, ‘2’) # Передача двух параметров # Отображение результата печать (а)

Выход:

 TypeError: complex () не может принимать второй аргумент, если первый является строкой
 

Python complex () Пример функции 5

Он также позволяет передавать комплексное число в качестве параметра.См. Пример ниже.

# Пример функции Python complex () # Вызов функции a = complex (1 + 2j) # Передача одного параметра b = complex (1 + 2j, 2 + 3j) # Передача обоих параметров # Отображение результата печать (а) печать (б)

Выход:

Комплексные числа: абсолютное значение

Комплексные числа: абсолютное значение Важным понятием для чисел, действительных или комплексных, является абсолютное значение . Напомним, что абсолютное значение | x | действительного числа x само, если оно положительное или ноль, но если x отрицательное, то его абсолютное значение | x | это его отрицание – x, то есть соответствующее положительное значение. Например, | 3 | = 3, но | –4 | = 4. Функция абсолютного значения лишает знак действительного числа.

Для комплексного числа z = x + yi, определяем абсолютное значение | z | как расстояние от z до 0 в комплексной плоскости C .Это расширит определение абсолютного значения для действительных чисел, поскольку абсолютное значение | x | действительного числа x можно интерпретировать как расстояние от x до 0 на строке действительного числа. Мы можем найти расстояние | z | с помощью теоремы Пифагора. Рассмотрим прямоугольный треугольник с одной вершиной в 0, другой в z и третьим в x на действительной оси непосредственно под z (или выше z , если z оказывается ниже действительной оси). Горизонтальная сторона треугольника имеет длину | x |, вертикальная сторона имеет длину | y |, а диагональная сторона имеет длину | z |. Следовательно,

| z | ² = x ² + y ² .

(Обратите внимание, что для действительных чисел, таких как x, , мы можем опустить абсолютное значение при возведении в квадрат, поскольку | x | ² = x ² .) Это дает нам формулу для | z |, а именно,

Единичный круг.

Некоторые комплексные числа имеют абсолютное значение 1. Конечно, 1 – это абсолютное значение как 1, так и –1, но это также абсолютное значение как i , так и – i , поскольку они оба на одну единицу от 0 на мнимая ось. Единичный круг – это круг радиуса 1 с центром в 0. Он включает в себя все комплексные числа с абсолютным значением 1, поэтому он имеет уравнение | z | = 1.

Комплексное число z = x + yi будет лежать на единичной окружности, когда x ² + y ² = 1.Некоторые примеры, кроме 1, –1, i, и – 1 – это ± √2 / 2 ± i √2 / 2, где плюсы и минусы могут быть взяты в любом порядке. Это четыре точки на пересечении диагональных линий y = x и y = x с единичной окружностью. Позже мы увидим их как квадратные корни из i и – i.

Вы можете найти другие комплексные числа на единичной окружности из троек Пифагора. тройка Пифагора состоит из трех целых чисел a, b, и c , так что a ² + b ² = c ² Если разделить это уравнение на c ² , тогда вы обнаружите, что ( a / c ) ² + ( b / c ) ² = 1. Это означает, что a / c + i b / c – это комплексное число, которое лежит на блоке круг. Самая известная тройка Пифагора – 3: 4: 5. Эта тройка дает нам комплексное число 3/5 + i 4/5 на единичной окружности. Некоторые другие пифагорейские тройки: 5:12:13, 15: 8: 17, 7:24:25, 21:20:29, 9:40:41, 35:12:27 и 11:60:61. Как и следовало ожидать, их бесконечно много. (Для немного больше о троек Пифагора см. в конце страницы по адресу http://www.clarku.edu/~djoyce/trig/right.html.)

Неравенство треугольника.

Существует важное свойство комплексных чисел, относящееся к сумме абсолютного значения, называемое неравенством треугольника.Если z и w – любые два комплексных числа, то

Вы можете увидеть это из правила сложения параллелограмма. Рассмотрим треугольник с вершинами 0, z, и z + w. Одна сторона треугольника от 0 до z + w имеет длину | z + w |. Вторая сторона треугольника от 0 до z, имеет длину | z |.И третья сторона треугольника, от z до z + w, параллельна и равна прямой от 0 до w, и, следовательно, имеет длину | w |. Итак, в любом треугольнике любая сторона меньше или равна сумме двух других сторон, и, следовательно, мы имеем неравенство треугольника, показанное выше.

Примеры аналитических / голоморфных комплексных функций 1

Напомним со страницы аналитических / голоморфных комплексных функций, что если $ A \ substeq \ mathbb {C} $ открыто, $ z_0 \ in A $ и $ f: A \ to \ mathbb {C} $, то $ f $ является называется аналитическим в $ z_0 $, если $ f $ комплексно дифференцируем в окрестности $ z_0 $.2} {z – z_0} \\ & = \ lim_ {z \ to z_0} \ frac {z \ cdot \ overline {z} – z_0 \ cdot \ overline {z_0}} {z – z_0} \\ & = \ lim_ {z \ to z_0} \ frac {z \ cdot \ overline {z} – z \ cdot \ overline {z_0} + z \ cdot \ overline {z_0} – z_0 \ cdot \ overline {z_0}} {z – z_0 } \\ & = \ lim_ {z \ to z_0} \ frac {z (\ overline {z} – \ overline {z_0} + \ overline {z_0} (z – z_0)} {z – z_0} \\ & = \ lim_ {z \ to z_0} \ left (z \ cdot \ frac {\ overline {z} – \ overline {z_0}} {z – z_0} + z_0 \ right) \ end {align}

Предположим, что $ z_0 = 0 $. Тогда:

(3)

\ begin {align} \ quad f ‘(0) = \ lim_ {z \ to 0} z \ cdot \ frac {\ overline {z}} {z} = \ lim_ {z \ to 0} \ overline {z } = 0 \ end {align}

Итак, $ f $ комплексно дифференцируем в $ 0 $ и $ f ‘(0) = 0 $.

Теперь предположим, что $ z_0 \ neq 0 $. Покажем, что не существует следующего лимита:

(4)

\ begin {align} \ quad \ lim_ {z \ to z_0} \ frac {\ overline {z} – \ overline {z_0}} {z – z_0} \ end {align}

Посмотрим на предел по вертикальной и горизонтальной линиям, проходящим через эти точки. У нас это:

(5)

\ begin {align} \ quad \ lim_ {z \ to z_0, y = y_0} \ frac {\ overline {z} – \ overline {z_0}} {z – z_0} & = \ lim_ {x \ to x_0, y = y_0} \ frac {(x – yi) – (x_0 – y_0i)} {(x – x_0) + (y – y_0) i} \\ & = \ lim_ {x \ to x_0} \ frac {x – x_0} {x – x_0} \\ & = 1 \ end {align}

У нас также есть это:

(6)

\ begin {align} \ quad \ lim_ {z \ to z_0, x = x_0} \ frac {\ overline {z} – \ overline {z_0}} {z – z_0} & = \ lim_ {x = x_0, y \ to y_0} \ frac {(x – yi) – (x_0 – y_0i)} {(x – x_0) + (y – y_0) i} \\ & = \ lim_ {y \ to y_0} \ frac {- ( y – y_0) i} {(y – y_0) i} \\ & = -1 \ end {align}

Поскольку предел $ z \ to z_0 $ на $ f $ приближается к двум разным значениям по разным путям, мы должны иметь этот общий предел, $ \ displaystyle {\ lim_ {z \ to z_0} \ frac {\ overline {z} – \ overline {z_0}} {z – z_0}} $ не существует. Следовательно, $ f ‘(z_0) $ не существует всякий раз, когда $ z_0 \ neq 0 $.

Таким образом, единственная точка, для которой $ f $ является комплексно дифференцируемой, находится в точке $ z_0 = 0 $, и поэтому $ f $ не может быть аналитическим нигде, поскольку не существует окрестности точки $ 0 $, для которой $ f $ комплексно дифференцируем в этой окрестности.

Комплексное сопряжение: числа, функции и примеры – видео и стенограмма урока

Комплексное число

Комплексное число – это число, которое имеет действительную и мнимую части.Действительные числа содержат все рациональные числа (например, целые числа 0 и 7, целое число -5 и дробь 2/3) и все иррациональные числа (например, пи и квадратный корень из 3). Квадратный корень из отрицательного числа не существует в системе действительных чисел. Поэтому математики расширили систему чисел и создали мнимую единицу i , которая определяется как квадратный корень из -1. Это позволяет нам записывать квадратный корень из любого отрицательного числа и решать задачи, требующие извлечения квадратного корня из отрицательного числа.2 = -1.

Стандартная форма комплексного числа: a + bi , где a и b – действительные числа. Буква a представляет действительную часть комплексного числа, а член bi представляет мнимую часть комплексного числа. Вот пример комплексного числа: 8 + 3 i . 8 – действительная часть числа, а 3 i – мнимая часть.

Определение сложного конъюгата

Теперь давайте объединим приведенные выше определения.Комплексное сопряжение формируется путем изменения знака между двумя членами комплексного числа. Давайте посмотрим на пример: 4-7 i и 4 + 7 i . Эти комплексные числа представляют собой пару комплексно сопряженных чисел. Действительная часть (цифра 4) в каждом комплексном числе одинакова, но мнимые части (7 i ) имеют противоположные знаки. 2 заменяется на -1.Таким образом, мы удалили мнимые части исходной пары комплексно сопряженных чисел и остались с действительным числом; в данном случае целое число. Это всегда будет происходить, когда мы умножаем пару комплексных конъюгатов. Произведение пары комплексных сопряжений всегда является действительным числом.

Деление комплексных чисел

Комплексные сопряжения могут быть полезным инструментом при упрощении выражений с комплексными числами. Например, умножение комплексного числа на его сопряжение очень полезно при упрощении некоторых дробей.

Рассмотрим следующую дробь: (3 – 4 i ) / (1 + i )

Эта дробь не упрощается, потому что в знаменателе есть мнимая часть. Мнимая часть в числителе подходит, но не в знаменателе. Нам нужно избавиться от i в знаменателе. Одна из причин этого правила заключается в том, что дроби обычно легче складывать и вычитать, когда знаменатель не является комплексным числом.

Теперь мы знаем, что можно умножить знаменатель на его сопряжение, чтобы избавиться от i .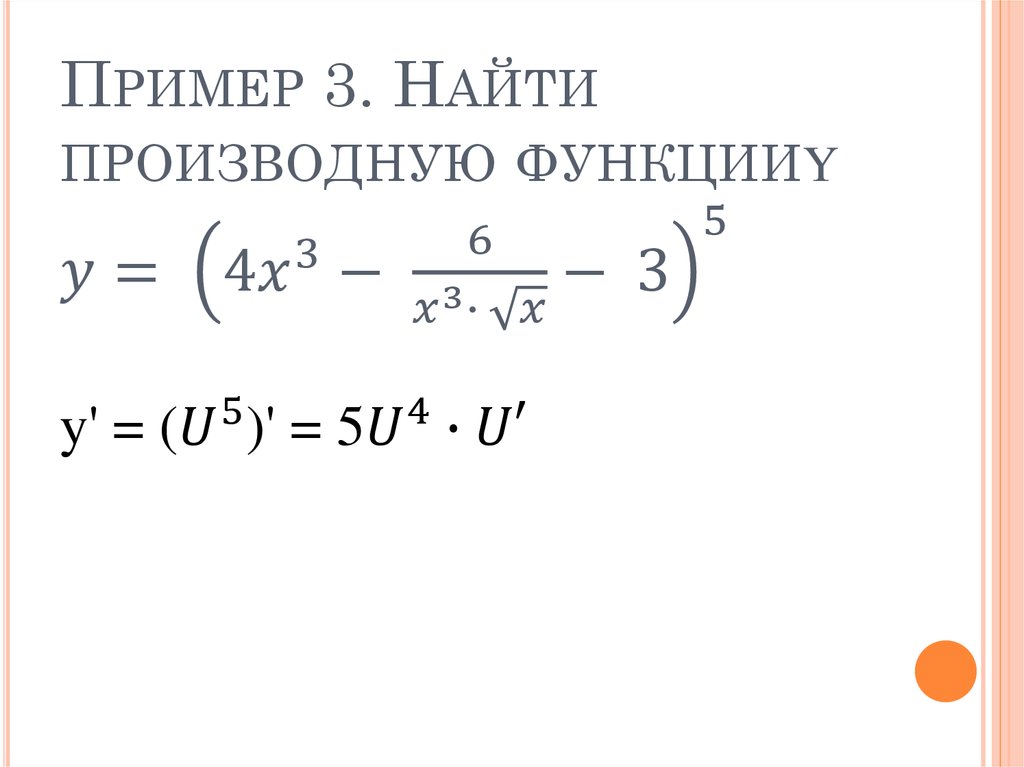 Однако это изменит значение дроби. Но мы также должны знать, что когда вы умножаете числитель и знаменатель дроби на то же число или выражение, мы получаем дробь, эквивалентную исходной дроби. Например, начнем с дроби 1/2. Затем умножьте числитель и знаменатель на 3: (1 x 3) / (2 x 3) = 3/6. В итоге получаем дробь, эквивалентную 1/2.

Следовательно, в нашей исходной задаче мы также должны умножить числитель на сопряжение знаменателя.2 на -1 и упростим:

(3-7 i + 4 (-1)) / (1 – (-1)) = (3-7 i -4) / (1 + 1) = (-1 – 7 i ) / 2

В знаменателе больше нет мнимых частей, и это то, что мы хотим. (Примечание: при упрощении не забывайте о двойных отрицаниях.)

Комплексные конъюгаты как решения квадратичных функций

Из ваших классов алгебры вы, возможно, помните, что квадратное уравнение иногда не пересекает ось x .Когда это происходит, решения квадратного уравнения являются комплексными числами. Обычно вы рассчитываете эти типы решений, используя формулу корней квадратного уравнения. Что ж, комплексные решения квадратичной функции с действительными числами в качестве коэффициентов всегда встречаются в комплексно сопряженных парах.

Например, если вам говорят, что квадратичная функция с вещественными числами в качестве коэффициентов имеет решение -2 + i , то -2 – i также должно быть решением. Давайте завершим пример: квадратное уравнение с действительными числами в качестве коэффициентов имеет решение 5-2 i .Запишите квадратное уравнение в стандартной форме.

Если 5 – 2 i – одно решение квадратного уравнения, то 5 + 2 i должно быть другим решением. Теперь мы можем записать уравнение в пересекаемой или факторизованной форме: y = ( x – (5-2 i )) ( x – (5 + 2 i ))

Нам нужно чтобы избавиться от внутренних скобок в каждом множителе и получить y = ( x – 5 + 2 i ) ( x – 5 – 2 i )

Если мы завершим умножение, мы получим следующие y = x ^ 2-5 x -2 xi -5 x + 25 + 10 i + 2 xi -10 i -4 i ^ 2

Затем измените i ^ 2 на -1 так, чтобы -4 i ^ 2 стало -4 (-1) и равнялось +4: y = x ^ 2-5 x -2 xi – 5 x + 25 + 10 i + 2 xi – 10 i + 4

Теперь мы можем комбинировать одинаковые члены (некоторые члены компенсируют друг друга) и получить следующее квадратное уравнение: л 9 0080 = x ^ 2-10 x + 29.

Резюме урока

Комплексные конъюгаты – это простая концепция, но они полезны при упрощении некоторых типов дробей. Пара комплексных конъюгатов образуется путем изменения знака между двумя членами комплексного числа. Чтобы создать сопряжение комплексного числа, просто перепишите его и измените знак мнимой части.

Еще кое-что, что нужно запомнить:

• Комплексное число – это число с мнимой частью.
• Произведение пары комплексных конъюгатов всегда является действительным числом.
• Мнимая часть числителя дроби допустима, но не знаменателя.
• Комплексные решения квадратичной функции с действительными числами в качестве коэффициентов всегда встречаются в комплексно сопряженных парах.

Примеры сложных функций c-2

Лейф Мейлбро получил образование математика в Копенгагенском университете , где он написал диссертацию на тему Линейные дифференциальные операторы с частными производными и распределения .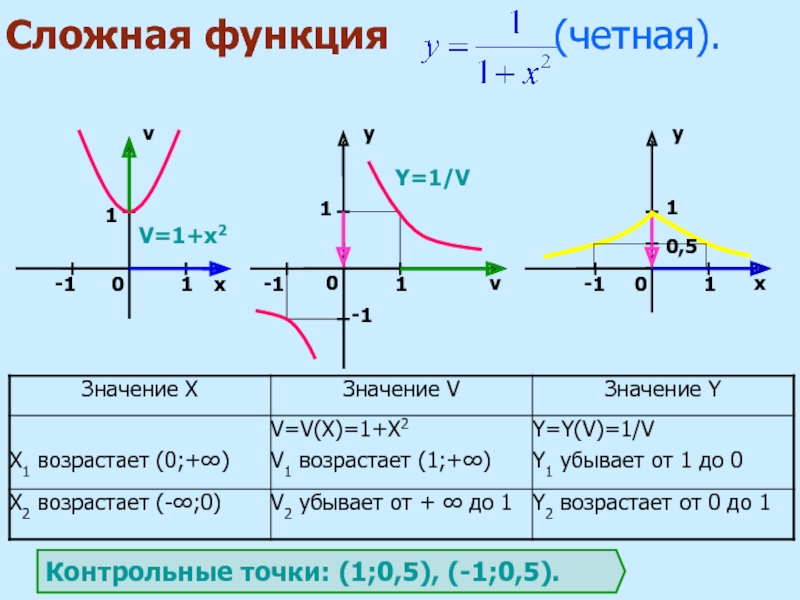 Вскоре после того, как он получил должность в Техническом университете Дании, , где он оставался до выхода на пенсию в 2003 году. Он дважды был в отпуске, первый раз в течение одного года в Шведской академии , Стокгольм, , и второй раз в . Копенгагенская телефонная компания , ныне часть Датской телекоммуникационной компании , в обоих местах проводит исследования.

В Техническом университете Дании он в течение более чем трех десятилетий читал лекции по таким различным математическим предметам, как элементарное исчисление , теория сложных функций, функциональный анализ, преобразование Лапласа, специальные функции, теория вероятностей и теория распределения , а также некоторые курсы, где Исчисление и различные Инженерные науки были объединены в более крупный курс, где преподаватели должны были сотрудничать, несмотря на их разное образование.Он написал учебники для многих из вышеперечисленных курсов.

Его исследования в Measure Theory и Complex Functions Theory слишком продвинуты, чтобы представлять интерес для большего, чем просто нескольких специалистов, поэтому здесь они не упоминаются. Однако следует признать, что философия теории меры глубоко вошла в повлиял на его мышление также во всех других математических вопросах, упомянутых выше.

После выхода на пенсию он работал консультантом в инжиниринговых компаниях {самое позднее для консорциума Femern Belt Consortium , настраивая некоторые модели для проникновения хлоридов в бетон и предлагая некоторые простые процедуры решения для этих моделей, которые можно применять без проблем. специалист по математике .Кроме того, он написал серию книг по некоторым из упомянутых выше тем для издателя Ventus / Bookboon .

Прекрасный мир сложных функций | Каспер Мюллер

Фракталы как результат рекурсивных сложных функций

Исследование скрытой структуры в более высоких измерениях

Это первая часть небольшой серии статей, предназначенных для понятного описания наиболее интересных результатов комплексного анализа. Даже если у вас не было курса по теории сложных функций, вы сможете получить некоторое ценное представление об этой фантастической области.Если вы изучаете математику или обновляете свои навыки, я считаю, что это тоже хорошее место, поскольку я представлю много отличных способов взглянуть на эту теорию.

Прежде чем приступить к изучению этой плодотворной и красивой темы, давайте начнем с некоторых основ.

При изучении действительных функций одной действительной переменной, непрерывность и дифференцируемость полагаются на некоторые условия, использующие пределы только с двух направлений. Направление слева направо и другое справа налево.Конечно, на реальной прямой нет других направлений, так как она одномерная.

Например, чтобы проверить непрерывность, один из способов – проверить, что предел значения функции, когда аргумент приближается к некоторому числу, скажем, a , слева, равен тому же значению, когда аргумент приближается к a справа, т.е.

В том же смысле дифференцируемость также имеет двустороннее условие, но это более сильное условие, чем непрерывность.

То, что предел может быть получен только с двух направлений, делает эти свойства довольно слабыми в том смысле, что в реальном анализе мы можем иметь много вредоносных функций, удовлетворяющих критерию дифференцируемости в некоторой точке вещественной прямой, но если функция удовлетворяет этому критерию, то ее производная не обязательно дифференцируем в этой точке.На самом деле, даже не гарантируется, что предел к этой точке существует!

Более того, слабые условия на самом деле делают нашу жизнь довольно сложной в том смысле, что мы плохо понимаем эти функции, и поэтому количество мощных инструментов для их выполнения не очень впечатляет.

Однако в мире комплексных чисел и их функций это совсем другая история, как вы сейчас увидите. Оказывается, условия намного сильнее, и поэтому в нашем распоряжении есть множество полезных инструментов и множество красивых теорем.

На самом деле, в реальном анализе есть много проблем, которые мы можем решить (на момент написания), только если мы будем использовать методы комплексного анализа.

Прежде чем мы углубимся в некоторые интересные факты, давайте договоримся о нескольких вещах. В реальном анализе мы обычно сопоставляем возможно бесконечный интервал (или их объединение) реальной линии с самим собой. В частности, области определения этих функций одномерны.

Прежде чем сосредоточиться на сложных функциях, я очень кратко напомню вам о некоторых свойствах комплексных чисел, их геометрии и топологии.

Начальной точкой является мнимая единица. Это число i , которое удовлетворяет тому, что i² = -1 .

Нет реального номера этой собственности!

Комплексные числа можно понимать как двумерное вещественное векторное пространство, натянутое на базис 1 и i. Другими словами. Комплексное число имеет форму a + bi и удовлетворяет обычным законам векторных пространств, например. закон распределения, закон коммутативности и т. д.

Следовательно, существует геометрия, связанная с комплексными числами.

У них есть величина и направление (потому что они векторы), и они должны визуализироваться лежащими на плоскости (называемой комплексной плоскостью), изоморфной (то есть той же алгебраической структуре) ℝ².

Так, например, комплексное число 3 + 4i является точкой (или вектором) (3, 4) в этой плоскости. В более общем смысле, комплексное число a + bi – это точка (a, b) на комплексной плоскости.

Приятно, что у нас есть это векторное представление комплексных чисел, которое очень похоже на ℝ², но на самом деле здесь больше структуры, чем эта, потому что мы, конечно, также можем умножать комплексные числа вместе.То есть это то, что математики называют кольцом , потому что векторные пространства – это абелевых групп по отношению к их операции сложения .

Оказывается, это даже больше, чем кольцо. Поскольку каждый ненулевой элемент (комплексное число) имеет инверсию, то есть вы также можете делить комплексные числа, это особый вид кольца, называемый полем .

Когда вы умножаете два комплексных числа, вы используете закон распределения и помните, что i² = -1 .

Отлично. Теперь у нас есть представление о комплексной плоскости.

В комплексном анализе мы обычно изучаем функции с подмножествами комплексной плоскости в качестве областей. В уме вы можете представить возможно деформированный диск с нулевым или большим количеством отверстий, который иногда представляет собой всю сложную плоскость.

В частности, области функций двумерны, и это, как выясняется, имеет некоторые интересные последствия.

Отправной точкой комплексного анализа является концепция сложных дифференцируемых функций, также называемых голоморфными функциями.

Как упоминалось во введении, дифференцируемость означает, что существует определенный предел, но когда функция определена в двумерной области, существует бесконечно много направлений, из которых можно приблизиться к числу. Это накладывает большие ограничения на набор голоморфных функций и придает этим функциям отличные свойства.

Прежде чем их изложить, давайте немного исследуем этот всенаправленный предел.

Поскольку сложная функция одной комплексной переменной отображает комплексное число в комплексное число, мы можем записать входные и выходные данные следующим образом:

Чтобы дать простой пример этого, рассмотрим

Что направление ограничения не материя подразумевает, что, в частности, если мы возьмем предел по действительной оси, мы получим тот же результат, что и если мы возьмем предел по мнимой оси.

Давайте посмотрим, что это значит.

где δ и η идут вдоль действительной оси. Эти два предела должны быть одинаковыми, давая

. Когда мы расширяем f в действительные функции u и v , как указано выше, так что f = u + iv, и подставляем это в дифференциальное уравнение, мы просто найдено, мы получаем систему дифференциальных уравнений в частных производных, известную как уравнения Коши-Римана .

Наш приведенный выше вывод показывает, что каждая голоморфная функция должна удовлетворять этим уравнениям, что накладывает на них строгое требование.Обратное почти верно. Но для того, чтобы это работало, нам нужны некоторые аргументы, связанные с преемственностью.

Также оказывается, что в точке, где производная данной голоморфной функции не равна нулю, функция сохраняет угол. Это называется конформным отображением и является важным и приятным обменом этих функций.

Первый признак того, что эти функции обладают некоторыми интересными свойствами, заключается в следующем. Оказывается, что если функция голоморфна, то есть комплексно дифференцируема в некоторой области, содержащей некоторую точку, скажем, p , то она комплексно дифференцируема бесконечно много раз в p .

Это можно сформулировать немного более компактно, а именно, что производная комплексной дифференцируемой функции является комплексно дифференцируемой.

Это, конечно, неверно для реальных функций в целом.

Аналитические функции

Это также означает, что голоморфные функции являются аналитическими , то есть они имеют сходящийся степенной ряд вокруг любой точки в своей области с некоторым радиусом сходимости. На самом деле верно и обратное.Любая аналитическая функция голоморфна. Поэтому мы иногда называем их аналитическими функциями вместо голоморфных функций. Эти два определения математически эквивалентны, хотя под двумя выражениями мы подразумеваем нечто иное. Мы сохраняем эти два определения, поскольку существует также понятие вещественных аналитических функций, которое, как определение, не эквивалентно реальной дифференцируемости.

Как упоминалось выше, голоморфная функция имеет расширение степенного ряда . У степенных рядов есть так называемый радиус сходимости.Вы должны попытаться представить себе диск в комплексной плоскости как область такого ряда, а радиус этого диска – это радиус его сходимости. Это означает, что на границе диска есть хотя бы одна точка, из-за которой ряды расходятся.

Как вы увидите в следующей части, есть способы обойти эти раздражающие точки, опять же из-за двумерности комплексной плоскости!

Прежде чем погрузиться в последствия голоморфности, я хочу поделиться с вами особенно приятным удовольствием, а именно геометрией укоренения.И я говорю не о корнях многочленов, а о квадратных корнях, кубических корнях и т. Д.

Мы все со школы знаем о квадратном корне. Что квадратный корень из, скажем, 4 равен 2. Но что это за операция на самом деле? Если ответить на вопрос, эквивалентный «», каков квадратный корень из 4? »равно« какое число в квадрате равно 4? », то, конечно, вопрос некорректно поставлен, потому что, конечно, есть два числа, удовлетворяющих этому.

По соглашению мы имеем в виду положительный квадратный корень из , но есть два квадратных корня из 4, а именно 2 и -2.

Как насчет кубического корня? Что ж, в какой-то момент мы все узнали, что существует ровно один кубический корень действительного числа. Но на самом деле это правда с доработками. Это правда, что существует только один действительный кубический корень действительного числа, но на самом деле есть два других корня, скрывающихся в другом измерении! Есть три различных кубических корня из любого числа , кроме 0 .

На самом деле, у любого комплексного (в том числе действительного, конечно) числа n различных корней n-й степени!

Как всегда, аддитивное тождество 0 – это особое число в мире мультипликативов.Если мы посчитаем так называемую множественность, то приведенное выше также верно для 0, , в противном случае мы должны исключить 0 из оператора.

Но что еще более удивительно, эти корни n комплексного числа z лежат симметрично на окружности окружности с радиусом, равным положительному корню n-й степени из длины z , с центром в 0.

Это объясняет, почему существует только один действительный кубический корень и два действительных квадратных корня действительного числа, потому что, если они должны быть размещены симметрично по окружности, то один корень определяет положение остальных.Например, один из квадратных корней из 1 равен 1, но тогда, поскольку есть ровно два квадратных корня, а другой корень должен быть размещен симметрично вокруг единичной окружности, он должен быть -1.

Таким же образом, один кубический корень из 1 равен 1, но тогда два других корня лежат в вершинах равностороннего треугольника, вписанного в единичный круг с одной вершиной в 1.

В общем случае n корни из 1 образуют вершины правильного n-угольника (многоугольника с n сторонами), и все они лежат на единичной окружности.Они называются корнями единства .

Корни 5-й степени из единицы

Корни n из единицы фактически образуют абелеву группу (относительно умножения) и в целом обладают многими интересными свойствами, но это уже для другой статьи.

Это уже показывает, что, расширив действительные числа на другое измерение, многие тайны, которые были скрыты в темноте, теперь становятся ясными, и это только начало нашего просветления.

Почти кажется (извините за мое философское мнение, которое я вам здесь навязываю), что воображаемое измерение необходимо для того, чтобы действительно понять многие из реальных концепций, таких как укоренение или умножение на -1 (вы можете взглянуть на в этой истории для обсуждения этого).

Как будто он был там все время, и мы изо всех сил пытались увидеть в темноте, в нижнем измерении – но мы видели только тени реальных вещей, что делало невозможным их правильное понимание. Однако дополнительное измерение дало нам свет, в котором мы так отчаянно нуждались.

Здесь все становится по-настоящему интересным.

Когда мы интегрируем действительные функции, мы делаем это на интервале (возможно, бесконечном интервале) реальной прямой, и здесь снова из-за одномерности, когда заданы конечные точки, у нас нет особого выбора в отношении интервала, кроме направления .

Это не относится к комплексным интегралам. Когда у нас есть две конечные точки на комплексной плоскости (которые могут быть одной и той же точкой), тогда у нас есть бесконечно много кривых (или объединение определенных связанных кривых, называемых контурами), по которым мы можем интегрировать, поскольку область является 2-мерной.

Это может показаться пугающим (и трудно вообразимым), но это не так плохо, как кажется. На самом деле для голоморфных функций верна следующая удивительная вещь.

Когда два контура (вы можете думать о контурах как кривые на комплексной плоскости) выбираются между одними и теми же двумя конечными точками, тогда, если мы можем непрерывно деформировать один контур в другой (т.е.е. если они гомотопны – см. ниже gif), то интегралы по ним равны.

Это интуитивно означает, что если в области между контурами нет отверстий, то не имеет значения, какой контур мы выберем.

Два гомотопически эквивалентных контура на комплексной плоскости

Это имеет некоторые интересные следствия по чисто топологическим причинам.

Это означает, например, что если две конечные точки контура совпадают (так что у нас есть замкнутый контур), то если пространство, которое вписывает контур, является сжимаемым i.е. гомотопен точке (постоянной кривой), то интеграл по этому контуру равен нулю. Это известно как теорема Коши после Огюстена-Луи Коши.

Итак, если функция голоморфна в этой области, то интеграл равен нулю.

для f голоморфная функция в области D, содержащей γ.

Напомним, что голоморфные функции не имеют полюсов в своей области определения, т.е. они не взрываются и не становятся бесконечными в любых точках. С ними очень приятно работать, но иногда вы хотите работать с функциями, которые голоморфны во всей своей области, за исключением счетного количества точек.

Эти функции называются мероморфными . Вы можете думать о них как об обобщении дробей многочленов. Самое замечательное в них то, что они обладают голоморфными свойствами, но также могут иметь полюса или особенности. Некоторые из наиболее важных функций в математике – это мероморфные функции, включая дзета-функцию Римана, , гамма-функцию, 1 / z и т.д. и оказывается, что контурный интеграл в сочетании с логарифмической производной дает нам инструмент для вычисления именно этого.

Если f – мероморфная функция внутри и на замкнутом контуре C, и f не имеет нулей или полюсов на C, тогда

Где Z – количество нулей, а P это количество полюсов в C.

Очень интересно видеть, что интеграл заботится только о топологии, а не о геометрии! Площадь и положение кривой не имеют значения, но важно то, что она замкнута и функция имеет полюсы и нули в подмножестве, вписанном в контур комплексной плоскости!

Этот результат связан с теорией, называемой исчислением остатков , которая тесно связана с расширением серии Тейлора под названием серии Лорана , но это уже для другой статьи.

Вы можете узнать больше о серии Тейлора здесь и вместе со мной изучить некоторые интересные свойства логарифмической производной здесь .

Прежде чем закончить эту часть, давайте подведем итоги того, что мы узнали.

Из-за разницы между геометрией и топологией в одном измерении и в двух измерениях, существуют более жесткие ограничения на сложные функции, чем на реальные функции, если они должны удовлетворять некоторым условиям, связанным с ограничениями.

Это, в свою очередь, приводит к сильным свойствам функций, удовлетворяющих этим условиям, что делает голоморфные функции чрезвычайно полезными при решении задач как комплексного, так и реального анализа.

Более того, оказывается, что область топологии становится полезной, потому что комплексные интегралы, известные как контурные интегралы, зависят только от классов гомотопической эквивалентности контуров, а не от самих путей.

Это привело к прекрасным открытиям Огюстена-Луи Коши и может быть использовано для вычисления нулей и полюсов мероморфных функций, которые мы вскоре исследуем.

В следующей части мы продолжим изучать красоту голоморфных и мероморфных функций, потому что, как вы увидите, у них есть некоторые свойства, которые имеют приложения к квантовой физике , еще не совсем понятны.Это связано с присвоением значений расходящимся рядам и извлечением глубокой информации из функций даже за пределами их области определения.

Многие, у кого была возможность узнать больше о математике, путают ее с арифметикой и считают ее пустой наукой. На самом деле, однако, это наука, требующая большого воображения.
~ Софья Ковалевская

Следующая часть этой серии вы найдете здесь.

Комплексные числа

A Комплексный номер

Комплексное число – это комбинация действительного числа
и мнимого числа

Реальные числа – это такие числа, как:

1

12.38

-0,8625

3/4

√2

1998

Практически любое число, которое вы можете придумать, является действительным числом!

Мнимые числа, когда возводят в квадрат , дают отрицательный результат .

Обычно этого не происходит, потому что:

Но только представьте, что такие числа существуют, потому что они нам нужны.

Давайте поговорим еще о мнимых числах…

«Единичное» мнимое число (например, 1 для действительных чисел) – это i, что является квадратным корнем из −1

Потому что, возводя i в квадрат, мы получаем −1

я ² = -1

Примеры мнимых чисел:

3i

1.04i

−2,8i

3i / 4

(√2) я

1998i

И мы оставляем там маленькое «i», чтобы напомнить нам, что нам нужно умножить на √ − 1

Комплексные числа

Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число :

Примеры:

1 + я

39 + 3i

0.8 – 2.2i

−2 + πi

√2 + я / 2

Может ли число быть комбинацией двух чисел?

Можем ли мы составить одно из двух других чисел? Мы можем точно!

Мы все время делаем это с дробями. Дробь ³ / ₈ – это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей».

Ну, комплексное число – это всего лишь , два числа, сложенные вместе (действительное и мнимое число).

Любая часть может быть нулевой

Итак, комплексное число имеет действительную и мнимую части.

Но любая часть может быть 0 , поэтому все действительные числа и мнимые числа также являются комплексными числами.

Комплексное число	Реальная часть	Воображаемая часть
3 + 2i	3	2
5	5	0	Чисто Настоящее
−6i	0	−6	Чисто воображаемое

Сложно?

Сложный не означает сложный.

Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , точно так же, как комплекс зданий (здания, соединенные вместе).

A Визуальное объяснение

Вы знаете, как идет числовая линия влево-вправо ?

Что ж, пусть воображаемые числа идут вверх-вниз :

И получаем сложный самолет

Теперь можно отображать комплексное число в виде точки:

Комплексный номер 3 + 4 и

Добавление

Чтобы сложить два комплексных числа, складываем каждую часть отдельно:

(a + b i ) + (c + d i ) = (a + c) + (b + d) i

Пример: сложите комплексные числа

3 + 2 i и 1 + 7 i

• сложите действительные числа и
• сложите мнимые числа:

(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7) i
= 4 + 9i

Попробуем еще:

Пример: сложите комплексные числа

3 + 5 i и 4 – 3 i

(3 + 5 i ) + (4 – 3 i )
= 3 + 4 + (5 – 3) i
= 7 + 2 i

На комплексной плоскости это:

Умножение

Для умножения комплексных чисел:

Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа

Просто используйте “FOIL”, что означает “ F irsts, O uters, I nners, L asts” (см. Биномиальное умножение для более подробной информации):

	Первые: a × c Внешний: a × d i Внутренние: b i × c Длина: b i × d i
(a + b i ) (c + d i ) = ac + ad i + bc i + bd i 2

Как это:

Пример: (3 + 2i) (1 + 7i)

(3 + 2i) (1 + 7i) = 3 × 1 + 3 × 7i + 2i × 1 + 2i × 7i

= 3 + 21i + 2i + 14i ²

= 3 + 21i + 2i – 14 (поскольку i ² = −1)

= −11 + 23i

А это:

Пример: (1 + i)

²

(1 + я) (1 + я) = 1 × 1 + 1 × я + 1 × я + я ²

= 1 + 2i – 1 (поскольку i ² = −1)

= 0 + 2i

Но есть более быстрый способ!

Используйте это правило:

(a + b i ) (c + d i ) = (ac − bd) + (ad + bc) i

Пример: (3 + 2i) (1 + 7i) = (3 × 1-2 × 7) + (3 × 7 + 2 × 1) i = −11 + 23i

Почему это правило работает?

Это просто метод “ФОЛЬГА” после небольшой работы:

(a + b i ) (c + d i ) = ac + ad i + bc i + bd i ² FOIL method

= ac + ad i + bc i – bd (потому что i ² = −1)

= (ac – bd) + (ad + bc) i (собирая похожие термины)

И вот у нас есть паттерн (ac – bd) + (ad + bc) i .

Это правило, безусловно, быстрее, но если вы его забудете, просто запомните метод FOIL.

Попробуем я

²

Ради интереса воспользуемся методом расчета i ²

Пример: i

²

Мы можем записать i с действительной и мнимой частью как 0 + i

я ² = (0 + я) ² = (0 + я) (0 + я)

= (0 × 0 – 1 × 1) + (0 × 1 + 1 × 0) i

= -1 + 0 я

= -1

И это хорошо согласуется с определением, что i ² = −1

Так что все работает замечательно!

Узнайте больше об умножении комплексных чисел.

Конъюгаты

Нам нужно будет узнать о конъюгатах через минуту!

Сопряжение – это где мы меняем знак в середине вот так:

Сопряжение часто пишется с чертой над ним:

Пример:

5–3 i = 5 + 3 i

Разделение

Конъюгат используется для облегчения сложного деления.

Уловка состоит в том, чтобы умножить верхний и нижний на конъюгат нижнего .

Пример: Сделайте это Подразделение:

2 + 3 i 4-5 i

Умножить верхнюю и нижнюю на конъюгат 4-5 i :

2 + 3 i 4-5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 i ² 16 + 20 i -20 i -25 i ²

Теперь запомните, что i ² = −1, поэтому:

= 8 + 10 i + 12 i -15 16 + 20 i -20 i + 25

Добавьте условия «Нравится» (и обратите внимание, как на нижних 20 i – 20 i отменяется!):

= −7 + 22 i 41

Наконец, мы должны вернуть ответ в форму a + b i :

= −7 41 + 22 41 i

СДЕЛАНО!

Да, нужно немного посчитать.Но это можно сделать .

Умножение на конъюгат

Но есть способ быстрее.

В предыдущем примере было интересно то, что произошло внизу:

(4-5 i ) (4 + 5 i ) = 16 + 20 i -20 i -25 i ²

Средние условия (20 i – 20 i ) аннулируются:

(4-5 i ) (4 + 5 i ) = 16-25 i ²

Также i ² = −1:

(4-5 i ) (4 + 5 i ) = 16 + 25

А 16 и 25 (магическим образом) являются квадратами 4 и 5:

(4-5 i ) (4 + 5 i ) = 4 ² + 5 ²

Это действительно довольно простой результат.Общее правило:

(a + b i ) (a – b i ) = a ² + b ²

Это может сэкономить нам время, когда мы делаем деление, например:

Пример: давайте попробуем еще раз

2 + 3 i 4-5 i

Умножить верхнюю и нижнюю на конъюгат 4-5 i :

2 + 3 i 4-5 i × 4 + 5 i 4 + 5 i = 8 + 10 i + 12 i + 15 я ² 16 + 25

= −7 + 22 i 41

А затем обратно в форму a + b i :

= −7 41 + 22 41 i

СДЕЛАНО!

Обозначение

Мы часто используем z для комплексного числа.И Re () для действительной части и Im () для мнимой части, например:

Что выглядит так на комплексной плоскости:

Набор Мандельброта

	Прекрасный набор Мандельброта (на фото) основан на комплексных числах. Это график того, что происходит, когда мы берем простое уравнение z 2 + c (оба комплексных числа) и снова и снова возвращаем результат в z . Цвет показывает, насколько быстро z 2 + c растет, а черный цвет означает, что он остается в определенном диапазоне.
Вот изображение, полученное путем увеличения набора Мандельброта
А вот центр предыдущего, увеличенный еще больше:

440, 1070, 273, 1071, 1072, 443, 3991, 271, 3992, 3993

.