Примеры сложных производных: Производная сложной функции. Примеры нахождения производных сложных функций.

Производная сложной функции – презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема урока: “Производная сложной функции”. Выполнила преподаватель математики ГАОУ СПО «АПТ»: К.Р. Абдуллина

Тема урока: “Производная
сложной функции”.
Выполнила преподаватель математики
ГАОУ СПО «АПТ»: К.Р. Абдуллина

2. Цели:

образовательная:
– знать понятие сложной функции;
– уметь находить по правилу производную сложной
функции;
– изучить алгоритм вычисления производной сложной
функции;
развивающая:
– развить умение обобщать, систематизировать на основе
сравнения,
делать вывод;
– развить наглядно-действенное творческое воображение;
– развить навыки самоконтроля, умение конспектировать,
переключаться с одного вида деятельности на другой.
2
воспитательная:
– воспитать чувство долга, ответственности, воли и
настойчивости для
достижения конечных результатов при нахождении
производных
сложных функций;
– формирование умения рационально, аккуратно оформить
задание на
доске и в тетради.
– воспитать умение слушать и уважать мнение других.
3

4. План урока:

1. Организационный момент. Рефлексия
настроения.
2. Обсуждение темы занятия, мотивация
обучения, целепологание.
3. Проверка домашнего задания.
4. Актуализация знаний, умений и навыков.
5. Усвоение новых знаний.
6. Закрепление изученного материала.
7. Формирование навыков.
8. Самостоятельная работа.
9. Домашнее задание.
10. Подведение итогов. Рефлексия.
4

5. Ответы

у
1 х 2 (2 х 7)
2
х
х
у 2 х 1
2
6
х
14 х
2
х
х2
х3 1
х4 2х
( х 3 1) 2
Слайд №
х 5
5х
6
5
3х 3
х
7
15
21х 4
х
6
5

6.

Лист контроляФ.И.О
студента
Группа
Домашнее
задание
Игра
«Лото»
Тест
Итоговая
оценка
6

7. Таблица производных.

Функция
Производная
С
Х
Хn
0
1
xn 1
n
1
Х
1
х2
х
sin x
cos x
tg x
ctg x
1
2 х
cos x
-sin x
1
cos 2 x
1
sin 2 x
Функция
arcsin x
arccos x
Производная
1
1 x2
1
1 x2
arctg x
1
1 x2
arcctg x
1
1 x2
a
x
e
x
a
xlna
ex
log a x
1
xlna
Ln x
1
x
Слайд №
7

8. Тест

6 5
1. Найдите производную функции:у 9 9 x x
1 6
5
9
1) у 9 х х х ; М
2
5
7
4
2) у 9 х 72 х 5х ; П
7
4
3) у 72 х 6 х ; Л
4) у 17 х 6 х ; К
7
4
8
2. Найдите производную функции: у 3х 2 сosx
1) у 6 х cos x; Е
2) у 6 х cos x 3x 2 sin x; А
3) у х3 cos x 3x 2 sin x; О
4) у 6 х cos x 3x 2 sin x;У
9
3. Найдите производную функции:
у ( х 1)( х 2) ( х 1)( х 3)
1) у 7; В
2) у 7; Г
3) у 1; Д
4) у 1; М
10
4. Найдите производную функции: у х 4 1
1
1) у 4 х х 2 ; Е
3
у
4
х
2)
х
1
;С
2
х
1
3) у 4 х х 2 ; Р
3
1
4) у 4 х х 2 ; А
11
5. Найдите производную функции у 2 х 1
4х 2
2
1) у (2 х 1) 2 ; В
2
;А
2) у
2
(2 х 1)
2
х
3) у
;Е
2
(2 х 1)
4)
у
2х
;У
2
(2 х 1)
12
6. Найти значение производной функции
2
у х sin x в х0
1) у 2 1;У
2) у 2 1; Н
3) у 2 1; П
4) у 2 ; Д
13
7. Найдите f (1) , если: f ( x) 5 4e x
х
1) 9;Т.
2) 5 4e; Ж
3) 5;Р
4) 5 4e; О
14

15. Ответы

Задание
1
2
3
4
5
6
7
Ответы
3
2
2
3
2
2
2
Л
А
Г
Р
А
Н
Ж
1
Жозе́ф Луи́ Лагра́нж-(1736-1813)-французский
математик , астроном и механик . Сначала Лагранж
заинтересовался филологией. Но в руки Лагранжа
случайно попал трактат по математической оптике,
и он почувствовал своё настоящее призвание.
В 1755 году Лагранж был назначен преподавателем
математики в Королевской артиллерийской школе в
Турине. В 1766 Лагранж переехал в Берлин . Здесь
он вначале руководил физико-математическим
отделением Академии наук, а позже стал
президентом Академии. агранж внёс существенный
вклад во многие области математики,
включая вариационное исчисление, теорию
дифференциальных уравнений, решение задач на
нахождение максимумов и минимумов, теорию
чисел (теорема Лагранжа), алгебру и теорию
вероятностей. Формула конечных приращений и
несколько других теорем названы его именем.
Слайд №
16

17. Производная сложной функции

Сложная функция: y g f x .
y f 5;
Примеры: 1) y 3 x 2 x .
2
2
5
f 3 x 2 x.
y f;
y cos f ;
3) y cos 2 x .
f sin x.
3
f 2x .
3
Правило нахождения производной сложной функции
/
/
/
g f x g f f x
2) y sin x .
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Слайд №
17

18. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
(производная сложной функции равна
/
/
/
g f x g f f x производной основной функции
Простая
функция
x
Производная
простой
функции
n
1
x
x
sin x
nx
n 1
1
2
x
1
2 x
cos x
на производную внутренней функции)
Сложная функция
Производная сложной
функции
f
n
x
1
f x
f x
sin f x
Слайд №
n f n 1 x f / x
f / x
2
f x
f / x
2 f x
cos f x f / x
18

19. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
g / f x g / f f / x
Простая
функция
Производная
простой
функции
(производная сложной функции равна
производной основной функции
на производную внутренней функции)
Сложная
функция
1
f x
1
x
1
2
x
1
1
Пример:
1) y
. y ;
f
sin x
f / sin x.
Производная сложной функции
/
f
x
1
/
2
f x 2
f x
f x
1
1
cos x
/
1
y
sin 2 x sin x sin 2 x cos x sin 2 x .
Слайд №
19
sin x
/

20. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
y
/
Производная сложной функции
f x
1
x
Пример:
Сложная
функция
2 x
1
2 f x
f / x
f / x
2 f x
1) y 2 x x . y f ;
f 2 x 3 x.
2x
3
3
x
4
/
1
2 2x x
3
2 x 1
3
Слайд №
/
6×2
2x 2x 1
2
3x
.
2 x 2 120

21. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Сложная функция: y g f x .
Правило нахождения производной сложной функции
сложной функции равна
g / f x g / f f / x (производная
производной основной функции
на производную внутренней функции)
Простая
функция
Производная
простой
функции
sin x
cos x
Пример:
Сложная
функция
1) y sin 2 x .
3
sin f x
Производная сложной
функции
cos f x f / x
y sin f ;
f 2x .
3 /
y sin 2 x cos 2 x 2 x 2 cos 2 x .
3
3
3
3
/
/
Слайд №
21

22. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Простая
функция
x
n
Производная
простой
функции
nx n 1
Сложная
функция
f n x
Производная сложной функции
n f n 1 x f / x
f / x
2
f x
f / x
1
x
1
2
x
1
f x
x
2 x
f x
cos x
sin f x
cos f x f / x
cos x
sin x
cos f x
sin f x f / x
tgx
1
2
cos x
sin x
1
tgf x
Слайд №
2 f x
/
f
x
1
/
f x
2
cos f x
cos 2 f 22x

23. Закрепление изученного материала.

Вычислите производные:
4
у
(
x
3
)
1)
2) у ( х3 х 2 11)3
3) у sin( 5 x 3)
4) у cos10 x
5) у tg 4 x
6)
Слайд №
у х2 1
23

24.

Домашнее задание. • Выучить алгоритм.
• Найти производную.
8
у
(
2
3
х
)
«3» 2
у
5
х
3
«4» –
«5» – у (2 х 3) 4
Слайд №
24
Подведение итогов урока, рефлексия:
– сдача листов контроля;
– рефлексия.
Вам предлагается каждому для себя ответить на
следующие вопросы:
-Что вы узнали нового?
-Смогли бы вы объяснить новый материал другу?
-Над чем вам надо еще поработать в данной теме?
-Какой вопрос сегодняшнего урока был самым трудным?
-Поставьте оценки по пятибалльной шкале за работу на
уроке
а) себе, оценив свою активность на уроке,
самостоятельность, правильность выполнения заданий.
б) классу,
в) учителю.
Слайд №
25
Спасибо за
урок.
Слайд №
26

English     Русский Правила

Видеоурок по математике “Производная сложной функции”

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Главная → Видеоуроки →  Алгебра. 10 класс. Производная. Описание видеоурока: Из видеоурока вы узнаете как находить производную сложной функции. Рассмотрены примеры нахождения производной сложной функции. Валерий Волков 6 13.02.2016 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования Материалов за текущий период нет.

ЕГЭ по математике Профильный уровень Задание 1     Задание 2 Задание 3     Задание 4 Задание 5     Задание 6 Задание 7     Задание 8 Задание 9     Задание 10 Задание 11     Задание 12 Задание 13     Задание 14 Задание 15     Задание 16 Задание 17     Задание 18 Задание 19     Задание 20 Задание 21 ГИА по математике Задача 1     Задача 2 Задача 3     Задача 4 Задача 5     Задача 6 Задача 7     Задача 8 Задача 9     Задача 10 Задача 11     Задача 12 Задача 13     Задача 14 Задача 15     Задача 16 Задача 17     Задача 18 Задача 19     Задача 20 Задача 21     Задача 22 Задача 23     Задача 24 Задача 25     Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс. Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 – 11 класс. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ

Блог

stephentu – Случайный ассортимент вещей

Я пришел к выводу, что у сложных аналитиков должны быть заголовки с лучшими каламбурами. из всех математиков.

В этом посте кратко обсуждаются некоторые вопросы окружающих сложную дифференциацию, и предоставить некоторые ссылки для более тщательного лечение.

Я не буду пытаться доказать какие-либо утверждения; ссылки внутри сделать работу намного лучше. $ \newcommand{\norm}[1]{\lVert #1 \rVert} \ новая команда {\ абс} [1] {| #1 |} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \ новая команда {\ ind} {\ mathbf {1}} \newcommand{\ip}[2]{\langle #1, #2 \rangle} $

Обзор действительного и комплексного дифференцирования

Для функции $f : \R \longrightarrow \R$ мы говорим, что $f$ дифференцируема в точке $x \in \R$, если существует следующий предел $$ \lim_{h \rightarrow 0} \frac{f(x + h) – f(x)}{h} \:. $$ Когда этот предел существует, этому числу присваивается имя $f'(x)$. Обратите внимание, что $f'(x)$ остается неизменным независимо от того, как $h$ стремится к нулю (иначе предела не существует). На реальная линия, $h$ может приближаться к нулю снизу ($h \nearrow 0$) или сверху ($h \searrow 0$). 92$ за секунду, видно, что есть еще степеней свободы для $h$, стремящихся к нулю. Например, написав $h = x + j y$, $h$ можно было бы стремиться к нулю, если сначала привести к нулю $x$, а затем $y$, или наоборот.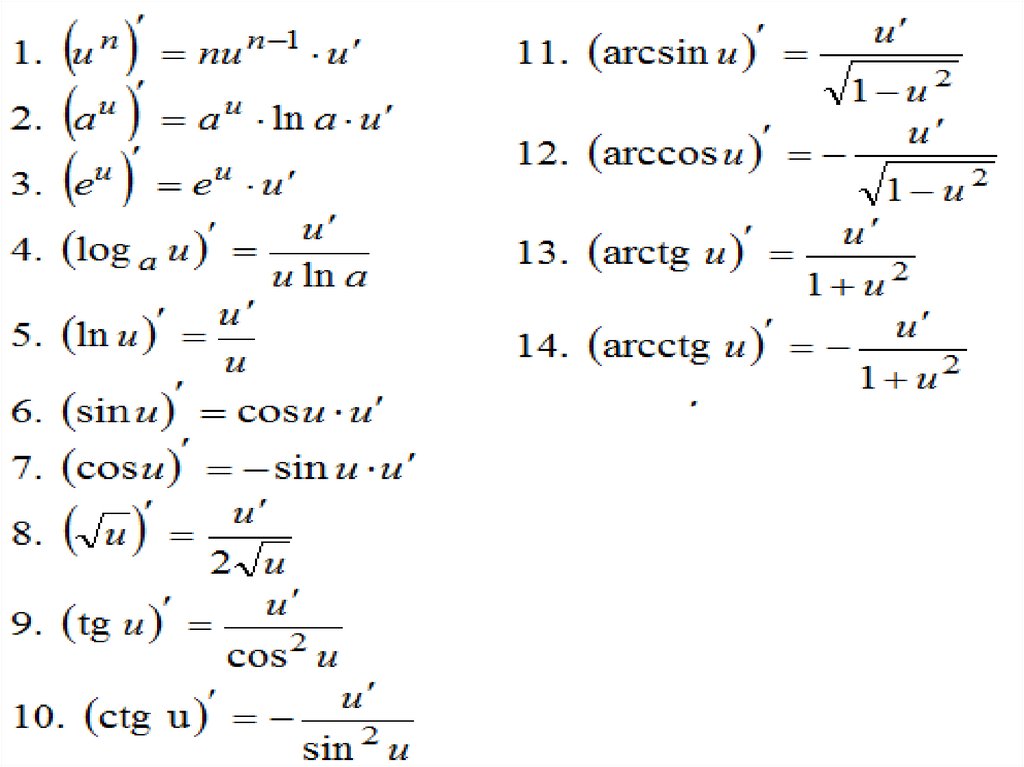

{-1}$ на $\C \setminus \{0\}$. С другой стороны, $f(z) = \mathrm{Re}(z)$ и $f(z) = \overline{z}$ нигде не встречаются. сложный дифференцируемый. 92 \длинная правая стрелка \R$. Уравнения Коши-Римана следующие уравнения в частных производных $$ \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \:\: \frac{\partial u}{\partial y} = -\frac{\partial v }{\partial x} \:. $$ Существует хорошая связь между уравнениями Коши-Римана и независимо от того, является ли функция комплексно дифференцируема. Записав $f(x, y) = u(x, y) + j v(x, y)$, необходимое условие комплексной дифференцируемости $f$ в $z \in \C$ состоит в том, что $f$ удовлетворяет уравнениям Коши-Римана в точке $z$. Это на самом деле не трудно увидеть, и исходит из установки двойных пределов равными $$ \lim_{\Delta x \rightarrow 0} \lim_{\Delta y \rightarrow 0} \frac{f(z + \Delta x + j \Delta y) – f(z)}{\Delta x + j\Delta у} = \lim_{\Delta y \rightarrow 0} \lim_{\Delta x \rightarrow 0} \frac{f(z + \Delta x + j \Delta y) – f(z)}{\Delta x + j\Delta у} \:.

2$ действительно дифференцируема в $z = (x, y)$, то если $f$ удовлетворяет условию уравнения Коши-Римана в $z$, то $f$ комплексно дифференцируема в $z$.

Голоморфные функции бесконечно непрерывно дифференцируемы

Утверждение состоит в том, что если $f$ голоморфна на $U$, то голоморфна $f’$. Затем прямой аргумент индукции восстанавливает это $f$ бесконечно комплексно дифференцируема на $U$. Это умопомрачительно заявление, и резко контрастирует с реальной дифференциацией, где она очень легко столкнуться со случаями, когда функция имеет только конечное число производных. Здесь находятся некоторые интуитивные объяснения того, почему это так.

Вещественнозначные функции с комплексными аргументами (почти) никогда не бывают голоморфными

Это очень интересно. Пусть $f : \C \longrightarrow \R$. Обратите внимание, что это происходит довольно часто в приложениях по обработке сигналов, когда $f$ представляет некоторую стоимость функция, а оптимизация $f$ по (некоторому подмножеству) $\C$ восстанавливает интересующий сигнал. Как правило, оптимизация выполняется с помощью итеративной процедуры, в которой используется информация о градиенте. спускаться к стационарным точкам. Однако оказывается, что $f$ нигде не голоморфна, если только $f$ не является постоянной функцией. Это прямое следствие уравнений Коши-Римана. (убедите себя, что это правда). 92 \longrightarrow \R$ и использовать действительные производные. Это работает, но дает довольно сумбурные выражения. Более элегантным решением является теория исчисления Виртингера. По существу заменой переменных можно определить два дифференциальных оператора $$ \frac{\partial f}{\partial z} = \frac{1}{2}\left( \frac{\partial f}{\partial x} – j \frac{\partial f}{\partial y} \правильно), \;\; \frac{\partial f}{\partial \overline{z}} = \frac{1}{2}\left( \frac{\partial f}{\partial x} + j \frac{\partial f}{ \partial y} \right) \:. $$ Оказывается, если $f$ дифференцируема в действительном смысле, то имеем следующая замена разложения Тейлора первого порядка в комплексном смысле $$ f(x + h) = f(x) + \begin{bmatrix} \frac{\partial f}{\partial \overline{z}}(x) \\ \frac{\partial f}{\partial z} (x) \end{bmatrix}^* \begin{bmatrix} h \\ \overline{h} \end{bmatrix} + o(\abs{h}) \:. $$ Это говорит о том, что мы можем рассматривать $\frac{\partial f}{\partial \overline{z}}(x)$ как направление наискорейшего подъема в точке $x$. Таким образом, естественным обобщением алгоритма градиентного спуска является $$ z_{k+1} = z_{k} – \mu \frac{\partial f}{\partial \overline{z}}(z_{k}) \:. $$ Чтобы оценить элегантность производной Виртингера, попробуйте дифференцировать функцию в обе стороны и посмотреть, какая формула чище

Дополнительная литература

Для более подробного ознакомления с этими темами я нашел несколько ресурсов в Интернете:

• Хосе Мигель Фигероа-О’Фаррил очень читабелен курсовые заметки по комплексному анализу.
• Превосходное изложение Пантелиса Бубулиса о производных Виртингера.

Что такое сложные производные? (с изображением)

`;

Разное

Факт проверен

Даниэль ДеЛи

Дата последнего изменения: 10 декабря 2022 г.

Сложные производные — это описания скорости изменения сложных функций, которые действуют в полях значений, содержащих мнимые числа. Они рассказывают математикам о поведении функций, которые трудно визуализировать. Производная сложной функции f at x ₀ , если он существует, определяется пределом при приближении x к x ₀ из ( f (x)- f (x ₀ ))/(x- x ₀ ).

Функции связывают значения в одном поле со значениями в другом поле, что называется сопоставлением. Когда одно или оба этих поля содержат числа, которые являются частью поля комплексных чисел, функция называется сложной функцией. Сложные производные получаются из сложных функций, но не каждая сложная функция имеет сложную производную.

Наборы значений, в которые и из которых сопоставляется сложная функция, должны включать комплексные числа. Это значения, которые могут быть представлены как a + b i , где a и b — действительные числа, а i — квадратный корень из отрицательной единицы, которая является мнимым числом. Значение b может быть равно нулю, поэтому все действительные числа также являются комплексными числами.

Производные – это скорости изменения функций. Как правило, производная является мерой единиц изменения по одной оси для каждой единицы другой оси. Например, горизонтальная линия на двумерном графике будет иметь производную, равную нулю, потому что для каждой единицы x значение y изменяется на ноль. Мгновенные производные, которые используются чаще всего, дают скорость изменения в одной точке кривой, а не в диапазоне. Эта производная представляет собой наклон прямой линии, касательной к кривой в нужной точке.

Однако производная существует не везде на каждой функции. Например, если в функции есть угол, производная не существует в углу. Это связано с тем, что производная определяется пределом, и если производная совершает скачок от одного значения к другому, то предела не существует. Функция, имеющая производные, называется дифференцируемой. Одним из условий дифференцируемости сложных функций является то, что частные производные или производные для каждой оси должны существовать и быть непрерывными в рассматриваемой точке.

Комплексные функции, имеющие комплексные производные, также должны удовлетворять условиям, называемым функциями Коши-Римана.