Примеры табличные интегралы: Найти неопределённый интеграл: начала начал, примеры решений

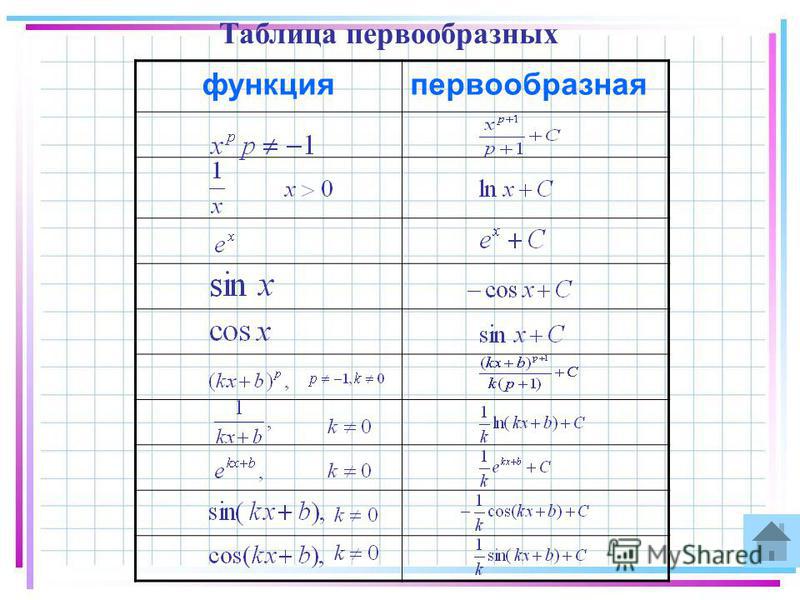
I. Табличное интегрирование

Неопределенный интеграл

Первообразная и неопределенный интеграл

Определение: Первообразной непрерывной функции f(x) на интервале (a; b) называется функция F(x), производная которой равна f(x) во всех точках данного интервала: F′(x) = f(x)

Теорема: Если есть две первообразные функции f(x), то они отличаются друг от друга только на постоянную величину.

Определение: Совокупность всех первообразных функции f(x) называется неопределенным интегралом.

где – знак интеграла,

f(x) – подынтегральная функция, dx – знак дифференциала, f(x) d x – подынтегральное выражение.

Теорема: Непрерывная на отрезке [a; b] функция интегрируема на интервале (a; b) (т.е. существует первообразная или неопределенный интеграл).

Свойства неопределенного интеграла:

Способы вычисления интегралов

Метод интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием.

Таблица интегралов (u=u(x)):

˜Пример I.1. Вычислить интеграл

Решение:

˜Пример I. 1а. Вычислить интеграл

II. Линейное преобразование выражения под знаком дифференциала

Если известен интеграл , то следующие интегралы могут быть вычислены с помощью линейного преобразования выражения под знаком дифференциала:

˜Пример II.1. Вычислить интеграл

Решение:

Вычислить интегралы:

III. Подведение (внесение) под знак дифференциала.

Один из множителей подынтегральной функции можно подвести под знак дифференциала. Для этого необходимо вычислить первообразную этого множителя и записать ее под знаком дифференциала. В дальнейшем все дополнительные вычисления и рассуждения будем записывать между двумя вертикальными чертами.

!Совет. Если после внесения одного из множителей под знак дифференциала возникли затруднения в дальнейших действиях, смело заменяйте полученное выражение под знаком дифференциала на новую переменную.

˜Пример III.1. Вычислить интеграл

Решение:

IV. Замена переменной под знаком интеграла (подстановка)

В неопределенном интеграле переменную интегрирования можно заменить на непрерывную и дифференцируемую функцию от другой переменной:

˜Пример IV.1. Вычислить интеграл

Решение:

Вычислить интегралы:

V. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе.

При интегрировании выражений, содержащих квадратный трехчлен в знаменателе:

необходимо использовать подстановку: .

˜Пример V.1. Вычислить интеграл

Решение:

Пример V.1а. Вычислить интеграл

Решение:

Вычислить интегралы:

VI.

Интегрирование по частям.

Формула интегрирования по частям

Случаи применения формулы интегрирования по частям:

Замечания:

1. Через Tr(x) обозначена тригонометрическая функция, P_n(x) означает многочлен степени n, а в квадратных скобках перечислены функции, к которым применима данная формула.

2. Во втором пункте вместо многочлена можно подставлять и степенную функцию.

˜Пример VI.1. Вычислить интеграл

Решение:

˜ Пример VI.2. Вычислить интеграл

Решение:

˜ Пример VI.3. Вычислить интеграл

Решение:

Вычислить интегралы:

VII.

Интегрирование рациональных дробей.

Определение. Рациональной дробью называется отношение двух многочленов: R(x) = , где P_m(x) – многочлен степени m, а Q_n(x) – многочлен степени n.

Определение. Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе

m < n, и неправильной, если m ≥ n.

Теорема. Неправильную дробь всегда можно представить в виде суммы многочлена (целая часть) и правильной дроби (дробная часть), если разделить числитель на знаменатель.

Например, дробь – неправильная. Разделим числитель на знаменатель:

Здесь целая часть равна (х – 1) , остаток деления равен (2х + 1) и, следовательно,

наша рациональная дробь представляется в следующем виде:

Определение. Правильные рациональные дроби вида

где A, B, C, E, L, K, a, p, q – действительные числа, называются простейшими рациональными дробями.

Теорема. Всякий многочлен с действительными коэффициентами Q_n(

x), степень которого выше двух (n > 2), можно разложить на линейные и квадратные множители с действительными коэффициентами, то есть многочлен можно представить в виде:

Здесь k₁+k₂+…+k_s +l_{1 +}l₂ +…+ l_r= n и все квадратные трёхчлены не имеют действительных корней, то есть их дискриминанты меньше нуля.

Теорема.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители :

можно представить единственным образом в виде суммы простейших дробей:

Алгоритм разложения:

1. Привести дробь к правильному виду (в дальнейшем будем рассматривать только правильную дробь).

2. Найти корни знаменателя правильной дроби и разложить его на линейные и квадратные множители.

3. Представить дробь в виде суммы всевозможных различных простейших дробей, в знаменателях которых стоят всевозможные множители знаменателя, а в числителях соответствующей степени многочлены с неопределенными коэффициентами.

! Контроль. Число неопределенных коэффициентов должно равняться степени многочлена в знаменателе исходной дроби.

4. Привести сумму простейших дробей к общему знаменателю. Общим знаменателем является знаменатель исходной дроби.

5. Приравнять числители получившейся и исходной дроби. Вычислить неопределённые коэффициенты. Для этого можно воспользоваться двумя способами: 1) приравнять коэффициенты при соответствующих степенях

   х в числителях многочленов в правой и левой частях равенства; 2) подставить вместо х конкретные числовые значения (в первую очередь – корни знаменателя). Лучше всего комбинировать эти два способа.

Общее правило интегрирования рациональных дробей:

1. Если под знаком интеграла стоит неправильная дробь, то путём деления числителя на знаменатель, её нужно представить в виде суммы многочлена и правильной дроби.

2. Разложив знаменатель правильной рациональной дроби на множители, представить её в виде суммы простейших рациональных дробей.

3. Вычислить интеграл от многочлена и каждой из простейших рациональных дробей.

˜ Пример VII.1. Вычислить интеграл

Решение:

Приравниваем числители:

.

Находим неопределённые коэффициенты: подставляя х = -1, получим 2 = D; сравнивая коэффициенты при х³, имеем А = 0. Выписываем коэффициенты при х²: 1 = 3A + B, следовательно, В = 1. При х = 0 имеем: 1 = A + B + C + D и С = 2.

Подставляем полученные коэффициенты в разложение:

;

Находим интегралы от простейших дробей

˜ Пример VII.2. Вычислить интеграл

Решение: Так как дробь является неправильной, разделим числитель на знаменатель:

Подынтегральная функция при этом представляется в следующем виде:

Разложим правильную дробь на сумму простейших:

Вычислить интегралы:

Краткий справочник для инженеров и студентов

Краткий справочник для инженеров и студентов

Краткий справочник для инженеров и студентов: Высшая математика. Физика. Теоретическая механика. Сопротивление материалов. / Полянин А. Д., Полянин В. Д., Попов В. А., Путятин Б. В., Сафрай В. М., Черноуцан А. И. — М.: Международная программа образования, 1996. — 432 с. Краткий многопрофильный справочник содержит основные понятия, законы, формулы, теоремы и методы высшей математики, физики, теоретической механики и сопротивления материалов. Предельно сжатое и ясное изложение позволяет читателю быстро найти (или восстановить в памяти) необходимую информацию. Во всех разделах разобраны примеры, поясняющие существо рассматриваемых вопросов и методов решения задач. Книга не имеет аналогов в справочной литературе и окажет неоценимую помощь широкому кругу инженеров и студентов (и будет полезна для преподавателей вузов и научных работников). Ее удобно использовать для систематизации знаний и при подготовке к экзаменам и зачетам. Оглавление ПРЕДИСЛОВИЕ 1. Аналитическая геометрия на плоскости 1. 1. Декартовы и полярные координаты. Расстояние между точками 1.2. Деление отрезка в данном отношении. Площадь многоугольника 1.3. Различные виды уравнения прямой 1.4. Угол между прямыми. Расстояние от точки до прямой 1.5. Окружность, эллипс, гипербола и парабола 1.6. Приведение общего уравнения кривой второго порядка к каноническому виду 2. Аналитическая геометрия в пространстве 2.2. Векторы 2.3. Действия над векторами. Скалярное произведение 2.4. Векторное и смешанное произведения 2.5. Плоскость в пространстве 2.6. Прямая в пространстве 2.7. Прямая и плоскость в пространстве 2.8. Поверхности второго порядка 3. Линейная алгебра 3.2. Матрицы 3.3. Системы линейных уравнений 3.4. Системы n-мерных векторов. Собственные значения и собственные векторы матрицы 4. Основные понятия математического анализа 4.2. Элементарные функции и их графики 4.3. Предел последовательности 4.4. Предел функции 4.5. Бесконечно малые и бесконечно большие функции 4. 6. Непрерывность 4.7. Асимптоты графика функции 5. Дифференциальное исчисление функций одной переменной 5.2. Таблица производных и правила дифференцирования 5.3. Теоремы о дифференцируемых функциях. Правило Лопиталя 5.4. Производные и дифференциалы высших порядков. Формула Тейлора 5.5. Экстремумы. Точки перегиба 5.6. Общая схема исследования функции и построение графика 6. Функции нескольких переменных 6.1. Точечные множества. Функции. Предел и непрерывность 6.2. Дифференцирование функций нескольких переменных 6.3. Производная по направлению. Геометрические приложения 6.4. Экстремумы функций нескольких переменных 7. Неопределенный интеграл 7.1. Первообразная. Неопределенный интеграл и его свойства 7.2. Таблица основных интегралов. Примеры интегрирования 7.3. Интегрирование по частям. Метод замены переменной 7.4. Интегрирование рациональных функций 7.5. Интегрирование иррациональных функций 7.6. Интегрирование показательных и тригонометрических функций 8. Определенный интеграл 8.1. Основные определения. Геометрический смысл определенного интеграла 8.2. Свойства определенного интеграла 8.3. Геометрические и физические приложения определенного интеграла 8.4. Несобственные интегралы 9. Двойные и тройные интегралы 9.1. Определение и свойства двойного интеграла 9.2. Вычисление двойного интеграла 9.3. Геометрические и физические приложения двойного интеграла 9.4. Определение и свойства тройного интеграла 9.5. Вычисление тройного интеграла. Некоторые приложения 10. Криволинейные и поверхностные интегралы 10.2. Криволинейный интеграл второго рода 10.3. Поверхностный интеграл первого рода 10.4. Поверхностный интеграл второго рода 10.5. Дифференциальные операции и интегральные формулы теории поля 11. Ряды 11.1. Числовые ряды 11.2. Функциональные ряды 11.3. Степенные ряды 11.4. Ряд Фурье 11.5. Интеграл Фурье. Преобразование Фурье 12. Обыкновенные дифференциальные уравнения 12. 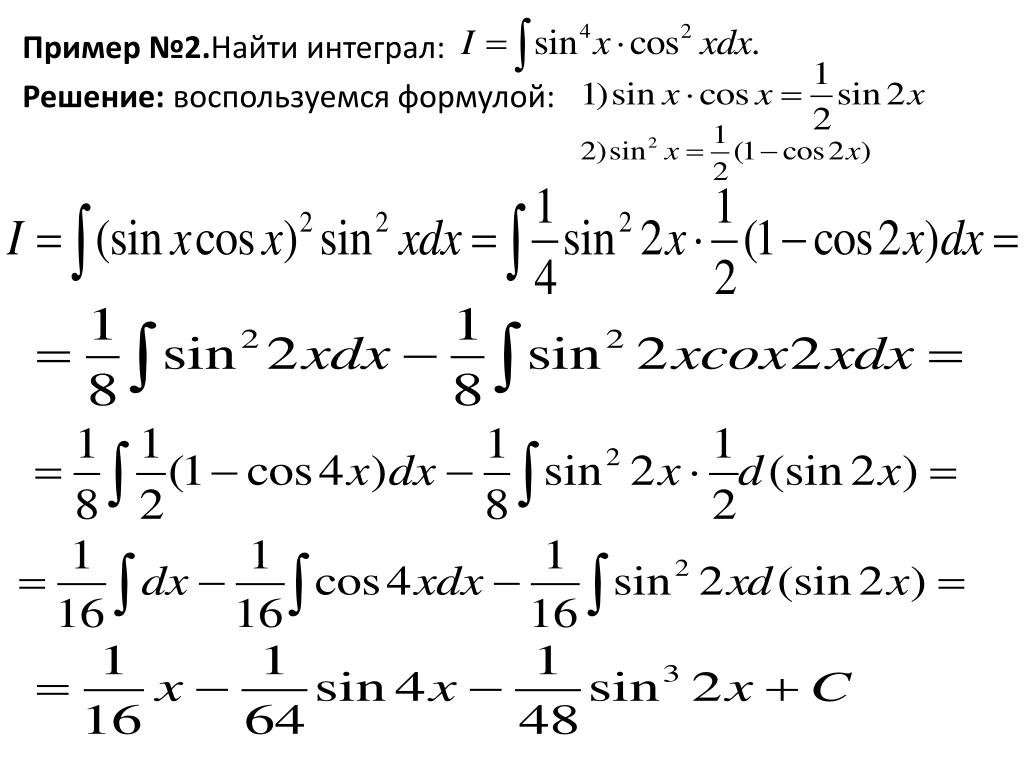2. Дифференциальные уравнения высших порядков 12.3. Линейные уравнения n-го порядка 12.4. Решение линейных однородных уравнений n-го порядка с постоянными коэффициентами 12.5. Линейные неоднородные уравнения n-го порядка 12.6. Системы обыкновенных дифференциальных уравнений 13. Приближенные вычисления 13.1. Метод наименьших квадратов 13.2. Приближенное решение алгебраических уравнений 13.3. Вычисление определенного интеграла 13.4. Численное интегрирование дифференциальных уравнений 14. Теория вероятностей 14.1. Правила и формулы комбинаторики 14.2. Основные понятия теории вероятностей 14.3. Условная вероятность. Теоремы и формулы теории вероятностей 14.4. Математическое ожидание и дисперсия 14.5. Закон больших чисел 1. Физические основы механики 1.1. Кинематика точки 1.2. Кинематика твердого тела 1.3. Динамика 1.4. Закон сохранения импульса 1.5. Закон сохранения энергии 1.6. Закон сохранения момента импульса 1. 7. Задана двух тел и движение в центральном поле 1.8. Поле тяготения 1.9. Неинерциальные системы отсчета 1.10. Динамика твердого тела 1.11. Специальная теория относительности 2. Молекулярная физика и термодинамика 2.2. Первое начало термодинамики 2.3. Второе начало термодинамики 2.4. Энтропия. Свободная энергия 2.5. Кинетическая теория идеального газа 2.6. Реальные газы. Уравнение Ван-дер-Ваальса 2.7. Равновесие фаз. Фазовые переходы 2.8. Поверхностное натяжение 2.9. Явления переноса в газах 3. Электродинамика 3.1. Электрический заряд. Закон Кулона 3.2. Электрическое поле. Напряженность поля 3.3. Электростатическое поле. Принцип суперпозиции для напряженности и потенциала 3.4. Теорема Гаусса 3.5. Электростатика проводников 3.6. Электростатика диэлектриков 3.7. Конденсаторы 3.8. Энергия электростатического поля 3.9. Постоянный ток 3.10. Магнитное поле. Сила Лоренца и закон Ампера 3.11. Вычисление магнитной индукции 3. 12. Циркуляция и поток вектора магнитной индукции 3.13. Магнитное поле в веществе 3.14. Электромагнитная индукция 3.15. Уравнения Максвелла 4. Колебания и волны 4.1. Гармонические колебания. Сложение колебаний 4.2. Свободные незатухающие колебания 4.3. Затухающие и вынужденные колебания 4.4. Упругие волны 4.5. Электромагнитные волны 5. Оптика 5.1. Геометрическая оптика. Фотометрия 5.2. Интерференция света 5.3. Дифракция 5.4. Поляризация света. Формулы Френеля 5.5. Дисперсия и поглощение света 5.6. Тепловое излучение 5.7. Световые кванты Список литературы 1. Кинематика 1.1. Кинематика точки 1.2. Кинематика твердого тела 1.3. Плоскопараллельное движение твердого тела 1.4. Произвольное движение твердого тела 1.5. Сложное движение точки 2. Основные понятия и аксиомы механики 2.2. Аксиомы механики 3. Статика 3.2. Условия уравновешенности систем сил, приложенных к твердому телу 3. 3. Решение задан статики 3.4. Центр параллельных сил. Центр тяжести твердого тела 3.5. Распределенные силы 3.6. Законы трения (законы Кулона) 4. Динамика материальной точки 4.2. Первая и вторая задачи динамики 5. Общие теоремы динамики механической системы 5.2. Теорема о движении центра масс 5.3. Теорема об изменении количества движения 5.4. Теорема об изменении кинетического момента 5.5. Теорема об изменении кинетической энергии 6. Принцип Даламбера. Элементы аналитической механики 6.2. Классификация механических связей. Обобщенные координаты 6.3. Принцип возможных перемещений 6.4. Общее уравнение динамики (принцип Даламбера — Лагранжа) 6.5. Уравнения Лагранжа второго рода 1. Основные понятия 1.1. Введение. Внешние и внутренние силы 1.2. Напряжения и деформации в точке 1.3. Основные понятия и допущения 2. Напряженно-деформированное состояние в точке 2.2. Одноосное растяжение и сжатие 2.3. Чистый сдвиг 3. Центральное растяжение и сжатие 3.2. Напряжения и деформации при растяжении или сжатии 3.3. Расчеты на прочность при растяжении и сжатии 4. Кручение 4.2. Напряжения и деформации при кручении 4.3. Расчеты на прочность при кручении 5. Прямой изгиб 5.2. Напряжения и деформации при прямом чистом изгибе 5.3. Напряжения и деформации при прямом поперечном изгибе 5.4. Расчет на прочность при прямом изгибе 6. Сложное сопротивление 6.2. Внецентренное растяжение или сжатие 6.3. Изгиб с кручением 7. Устойчивость сжатых стержней 7.2. Формула Эйлера 7.3. Влияние способов закрепления концов стержня на величину критической силы 7.4. Пределы применимости формулы Эйлера 7.5. Расчеты сжатых стержней на устойчивость ПРИЛОЖЕНИЯ 1. Элементарные функции и их свойства 2. Таблица неопределенных интегралов 3. Решения обыкновенных дифференциальных уравнений 4. Ортогональные криволинейные системы координат 5. Некоторые физические постоянные

Интеграционные таблицы: определения и экспоненциальные

Одним из величайших достижений человечества является письмо.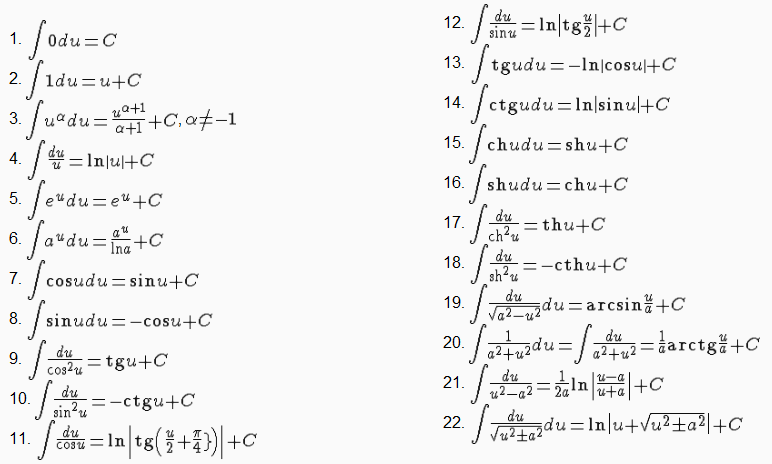 Благодаря этому наши знания сохраняются из поколения в поколение посредством книг, поэтому нам не нужно тратить время и силы на то, чтобы открывать все заново!

Одной из самых важных операций в исчислении является интегрирование, которое может занять много времени. К счастью, точно так же, как информация, полученная человечеством на протяжении веков, содержится в книгах, множество интегралов хранится в Интеграция T Способности.

Метод использования таблиц интеграции

Интеграция может быть трудоемкой операцией. Сначала нужно узнать, какой метод интегрирования больше подходит для данного интеграла. После этого идет сама операция. Кто знает, может быть, вам придется несколько раз делать интеграцию по частям! Это будет трудоемко и сложно.

Вместо прохождения этой пробной версии проще использовать таблицу интеграции .

Но как можно использовать таблицу для интеграции функции? Таблицы интегрирования содержат обобщенных формул для конкретных интегралов . Важно то, что вы определяете переменные и константы, присутствующие в каждой формуле.

Вот быстрый пример. Рассмотрим интеграл

\[ \int \sin{3x} \, \mathrm{d}x.\]

Чтобы решить этот интеграл, вам нужно выполнить интегрирование путем подстановки, положив

\[u=3x.\]

Вам также необходимо записать дифференциал \( \mathrm{d}x \) через \( u,\), что можно сделать сначала путем дифференцирования

\[ \frac{\mathrm{d}u}{\mathrm{d}x}=3,\]

умножив эту производную на \( \mathrm{d}x,\)

\[ \mathrm {d}u=3\,\mathrm{d}x,\]

и выделение \(\mathrm{d}x,\), поэтому

\[\mathrm{d}x=\frac{1}{ 3}\mathrm{d}u.\]

Теперь вы можете записать исходный интеграл в терминах \(u\), заменив каждый экземпляр \( x \) его эквивалентом в \( u,\) и каждый экземпляр \( \mathrm{d}x \) его эквивалентом в \( \mathrm{d}u,\), то есть

\[ \begin{align} \int \sin{3x} \, \mathrm{ d}x &= \int (\sin{u})\left(\frac{1}{3}\mathrm{d}u\right) \\ &= \frac{1}{3}\int \sin {u} \, \mathrm{d}u, \end{align}\]

, который является интегралом, имеющим общую формулу, которую вы можете проверить в нашей статье «Тригонометрические интегралы», то есть

\[\int \sin{u} \, \mathrm{d}u = -\cos{u} + C. \]

Зная это, можно записать интеграл

\[ \int \sin{3x}\,\mathrm{d}x = \frac{1}{3} \left( -\cos{u } + C \right),\]

и затем отменить замену. Обычно константа интегрирования добавляется в конце, поэтому

\[ \begin{align} \int \sin{3x}\,\mathrm{d}x &= \frac{1}{3} \left( – \cos{3x} \right) + C \\ &= -\frac{1}{3}\cos{3x}+C. \конец{выравнивание}\]

В приведенном выше примере, просмотрев таблицу интегрирования тригонометрических функций, вы, скорее всего, найдете формулу вида

\[ \int \sin{ax} \, \mathrm{d}x = -\frac{1} {a}\cos{ax}+C.\]

В этом случае вам не нужно делать какую-либо \(u-\)замену, но вы должны указать, что \(a=3.\)

\ [ \begin{align} \int \sin{ax}\,\mathrm{d}x &= \frac{1}{a} \left( -\cos{ax} \right) + C \\ \int \ sin{3x} \, \mathrm{d}x &= -\frac{1}{3}\cos{3x}+C. \конец{выравнивание}\]

Основная идея использования таблиц интеграции состоит в том, чтобы определить, какой интеграл из таблицы имеет тот же вид, что и тот, который вы пытаетесь решить. Интеграл, приведенный в таблице, уже решен, поэтому его можно использовать как формулу.

Вы можете различать переменные и константы, глядя на дифференциал интеграла. Переменная интегрирования – это та же самая переменная, которая присутствует в дифференциале, и обычно используются \(x\) или \(u\). Остальные буквы, которые вы найдете, скорее всего, являются константами, и обычно выбираются \(a,\) \(b,\) \(k,\) \(n,\) и \(m\).

Поскольку существует множество различных интегралов, таблицы интегрирования обычно разбиваются в зависимости от того, какие функции задействованы. Здесь мы рассмотрим некоторые примеры наиболее распространенных таблиц интеграции.

Таблицы интегрирования экспоненциальных функций

Интегрирование экспоненциальных функций обычно требует многократного интегрирования по частям. Вместо этого вы всегда можете посмотреть таблицы интеграции. Они могут содержать некоторые из следующих формул: 92}{5}-\frac{2x}{25}+\frac{2}{125}\right)+C. \end{align}\]

Довольно просто, правда?

Таблицы интегрирования для тригонометрических функций

Может быть трудно запомнить все первообразные основных тригонометрических функций, не говоря уже о некоторых особых случаях, когда задействованы и их степени. 2{ax}+C\end{align}\] 92}\,\mathrm{d}x\]

становится чрезвычайно актуальным. Поскольку вы не можете использовать основную теорему исчисления для вычисления вышеупомянутого интеграла, вместо этого он вычисляется численно, а его значения организованы в таблицы. Для получения дополнительной информации об этом ознакомьтесь с нашей статьей о нормальном распределении!

Таблицы интегрирования – ключевые выводы

• Таблицы интегрирования содержат обобщенные формулы для конкретных интегралов.
• Основная идея использования таблиц интеграции состоит в том, чтобы идентифицировать интеграл, который имеет ту же форму, что и интеграл из таблицы.
• Существуют таблицы интегрирования экспоненциальных функций, тригонометрических функций и многого другого! Вы должны найти таблицу, которая лучше всего соответствует интегралу, который вам нужно решить.

Таблица интегралов

Интегрирование — одна из основных математических операций. На этой странице таблицы содержат примеры наиболее распространенных интегралов.

В качестве произвольной постоянной интегрирования используется число C , которое можно определить, если в какой-то момент известно значение интеграла. Каждая функция имеет бесконечное число первообразных.

Основные формулы Общие правила интеграции функций Интегралы рациональных функций Интегралы трансцендентных функций Интегралы иррациональных функций Интегралы тригонометрических функций

Онлайн калькулятор: Решение интегралов

Основные формулы

1.	∫ 0·dx = C
2.	∫ a dx = ax + C      (a = const )
3.	∫ x n dx = x n+1 n + 1 + C      (n ≠ -1)
4.	∫ dxx = пер |х| + C
5.	∫ a x dx = a x ln a + C
6.	∫ e x dx = e x + C
7.	∫ sin x dx = -cos x + C
8.	∫ cos x dx = sin x + C
9.	∫ dxsin 2 x = -ctg x + C
10.	∫ dxcos 2 x = tg x + C
11.	∫ dxa 2 – x 2 = arcsin xa + C = -arccos xa + C      (x < a)
12.	∫ dxa 2 + x 2 = 1a arctg xa + C = -1a arctg xa + C
13.	∫ dxa 2 – x 2 = 12a ln x + ax – a + C      (|x| ≠ a)
14.	3

∫	дхх 2 ± а 2 = ln |x + x 2 ± а 2 |

Скачать интегральную таблицу:    

Общие правила интеграции функций

∫

с f(x) dx = с

∫

ф(х) дх

∫

[ f(x) + g(x)] dx =

∫

f(x)dx +

∫

г(х) дх

∫

[ f(x) – g(x)] dx =

∫

ф(х) дх –

∫

г(х) дх

∫

f(x)g(x) dx = f(x)

∫

г(х) дх –

∫∫

г(х) дх дф(х)

Интегралы рациональных функций

1.	∫ x n dx = x n+1 n + 1 + C      (n ≠ -1)
2.	∫ (ax + b) n dx = (ax + b) n+1 a(n + 1) + C      (n ≠ -1)
3.	∫ dxx = пер |х| + С
4.	∫ dxax + b = 1a ln |ax + b| + C
5.	∫ ax + bcx + d dx = acx + bc – adc 2 ln |cx + d| + К
6.	∫ дх(х + а)(х + б) = 1а – б пер |х + Ьх + а| + С
7.	∫ дхх 2 – а 2 = 12а пер |х – топор + а| + C
8.	∫ x dx(x + a)(x + b) = 1a – b (a ln |x + a| – b ln|x + b|) + C
9.	∫ x dxx 2 – a 2 = 12 ln |x 2 – а 2 | + C
10.	∫ dxx 2 + a 2 = 1a arctg (xa) + C
11.	∫ x dxx 2 + a 2 = 12 ln |x 2 + a 2 | + C
12.	∫ DX (x 2 + A 2 ) 2 = 12A 2 XX 2 + A 2 + 12A 3 (xa xa). ∫ x dx(x 2 + a 2 ) 2 = -121x 2 + a 2 + C 14.    ∫ x dx(x 2 + a 2 ) 3 = -141(x 2 + a 2 ) 2 + C 15.   ∫ dxax 2 + bx + c = 1б 2 – 4ас ln2ax + b – b 2 – 4ac2ax + b + b 2 – 4ac + C     (b 2 – 4ac &gt 0) 0222 00222 06,222 0 ∫ dxax 2 + bx + c = 14ас – б 2 arctg2ax + b4ac – b 2 + C     (b 2 – 4ac &lt 0) 17.   ∫ x dxax 2 + bx + c = 12a ln|ax 2 + bx + c| – б2а ∫ dxax 2 + bx + c 18.   ∫ х dxax + b = 1a 2 (ax + b – b ln |ax + b|) + C 19.    ∫ x 2 dxax + b = 1a 3 (12(ax + b) 2 -2b(ax + b) + b 2 ln |ax + b|) + C 20.   3 ∫ дхх(ах + б) = 1b пер. ось + bx + C 21.   ∫ дхх 2 (ах + б) = – 1bx + ab 2 ln ax + bx + C 22.   ∫ х dx(ax + b) 2 = 1a 2 (ln |ax + b | + bax + b) + C 23.   ∫ х 2 дх(ах + б) 2 = 1a 3 (ax + b – 2b ln |ax + b | – b 2 ax + b) + C Интегралы трансцендентных функций 1.   ∫ e x dx = e x + C 2.    ∫ а х дх = x ln a + C 3.   ∫ dxx ln x = ln |ln x| + C 4.   ∫ x n ln x dx = x n + 1 (ln xn + 1 – 1(n + 1) 2 ) + C 5.   ∫ e ax ln x dx = e ax ln xa – 1a ∫ e ax x dx 6.   ∫ x n ln m x dx = x n + 1 n + 1 ln m x – mn + 1 ∫ x n ln m – 1 x dx 7.   ∫ x н л м x dx = -x n + 1 (m – 1) ln m – 1 x + n + 1m – 1 ∫ x n ln m – 1 x dx 8.    ∫ ln x dx = x ln x – x + C 9.   ∫ arcsin x dx = x arcsin x + 1 – x 2 + C 10.   ∫ arctg x dx = x arctg x – ln 1 + x 2 + C 11.   ∫ e ax dx = e ax a + C 12.   ∫ x e ax dx = e ax a 2 (ax – 1) + C 13.   A 222222 ∫ A 22 ∫ A x x N DX = A x (N – 1) x N – 1 + LN AN – 1 2 ∫ A x 262222 – 2 A x 26222 ∫ A x 2222 ∫ 2 A 22222 ∫ 2 A 2222 ∫ 2 A 2222 ∫ 14.    ∫ sh(x) dx = ch(x) + C 15.   ∫ ch(x) dx = sh(x) + C Интегралы иррациональных функций 1.   ∫ dxax + b = 2aax + b + C 2.   ∫ ax + b dx = 23a(ax + b) 1,5 + C 3.   ∫ x dxax + b = 2(ax – 2b)3a 2 ax + b + C 4.   ∫ xax + b dx = 2(3ax – 2b)15a 2 (ax + b) 1,5 + C 5.   ∫ dx(x + c)ax + b = 1b – ac lnax + b – b – acax + b + b – ac + C     (b – ac > 0) 6.    ∫ dx(x + c)ax + b = 1ac – b arctgax + bac – b + C     (b – ac < 0) 7.   ∫ ax + bcx + d dx = 1c(ax + b)(cx + d) – ad – bccac arctg a(cx + d)c(ax + b) + C 8.   ∫ dxxax + b = 1b lnax + b – bax + b + b + C     (b > 0) 9.   ∫ dxxax + b = 1-b arctgax + b-b + C     (b < 0) 10.   ∫ dxx 2 ах + b = -ax + bbx – a2b ∫ dxxax + b 11.   ∫ топор + bx dx = 2ax + b + b ∫ dxxax + b 12.   ∫ а – хб + х dx = (а – х)(b + х) + (а + Ь)arcsinx + ба – х + С 13.    ∫ а + xb – x dx = -(a + x)(b – x) – (a + b)arcsinb – xa + x + C 14.   ∫ dxax 2 + bx + c = 1a ln|2ax + b + a(ax 2 + bx + c)| + С 15.   ∫ dxax 2 + bx + c = -1a arcsin2ax + bb 2 – 4ac + C 16.   ∫ ax 2 + bx + c dx = 2ax + b4aax 2 + bx + c + 4ac – b 2 8а ∫ dxax 2 + bx + c 17.   ∫ x 2 + a 2 dx = x2x 2 + a 2 + a 2 2 ln |x + x 2 + a 2 2 2 | + С 18.    ∫ х 2 – а 2 дх = х2х 2 – а 2 – а 2 2 ln |x + x 2 – а 2 | + С 19.   ∫ dxx 2 + a 2 = ln|x + x 2 + a 2 )| + С 20.   ∫ dxx 2 – a 2 = ln|x + x 2 – a 2 )| + С 21.   ∫ x dxx 2 + a 2 = x 2 + a 2 + C 22.   ∫ x 2 – a 2 x dx = x 2 – a 2 + a arcsin (xa) + C 23.   ∫ a 2 – x 2 dx = x2a 2 – x 2 + a 2 2 arcsin (xa) + C 24.    ∫ а 2 – х 2 х дх = а 2 – х 2 + а ln (ха + а 2 – х 2 ) + С 25.   ∫ dxa 2 – x 2 = arcsin (xa) + C 26.   ∫ x dxa 2 – x 2 = -a 2 – x 2 + C 27.   ∫ dxxa 2 – x 2 = 1a ln |xa + a 2 – x 2 | + С Интегралы тригонометрических функций 1.   ∫ sin (x) dx = -cos (x) + C 2.   ∫ cos (x) dx = sin (x) + C 3.    ∫ sin 2 (x) dx = x2 – 14 sin (2x) + C 4.   ∫ cos 2 (x) dx = x2 + 14 sin (2x) + C 5.   ∫ sin n (x) dx = -1n sin n – 1 (x) cos (x) + n – 1n ∫ sin n – 2 (x) dx 6.   ∫ cos n (x) dx = 1n cos n – 1 (x) sin (x) + n – 1n ∫ cos n – 2 (x) dx 7.   ∫ dxsin (x) = ln|tg(x2)| + С 8.   ∫ dxcos (x) = ln|ctg(x2)| + С 9.   ∫ dxsin 2 (х) = -ctg (х) + С 10.    ∫ dxcos 2 (х) = tg (х) + С 11.   ∫ sin (x) cos (x) dx = -14cos (2x) + C 12.   ∫ sin 2 (x) cos (x) dx = 13sin 3 (x) + C 13.   ∫ sin (x) cos 2 (x) dx = -13cos 3 (x) + C 14.   ∫ sin 2 (x) cos 2 (x) dx = -18x – 132sin (4x) + C 15.   ∫ tg (x) dx = -ln |cos (x)| + C 16.   ∫ ctg (x) dx = ln |sin (x)| + C 17.    ∫ sin (x) cos 2 (x) dx = 1cos (x) + C 18.   ∫ cos (x) sin 2 (x) dx = -1sin (x) + C 19.   ∫ sin 2 (x)cos 2 (x) dx = tg (x) – x + C 20.   ∫ cos 2 (x)sin 2 (x) dx = -ctg (x) – x + C 21.   ∫ sin 2 (x)cos (x) dx = ln|ctg(x2)| – грех (х) + С 22.   ∫ cos 2 (x)sin (x) dx = ln|tg(x2)| + cos (х) + С 23.   ∫ dxsin (x) cos (x) = ln|tg(x)| + С 24.    ∫ dxsin 2 (x) cos (x) = -1sin (x) + ln|ctg(x2)| + С 25.   ∫ dxsin (x) cos 2 (x) = 1cos (x) + ln|tg(x2)| + С 26.   ∫ dxsin 2 (x) cos 2 (х) = tg(x) – ctg(x) + C 27.   ∫ dxsin n (x) = -1n – 1cos (x)sin n – 1 (x) + n – 2n – 1 ∫ dxsin n – 2 (x) 28.   ∫ tg n (x) dx = tg n – 1 (x)n – 1 –  ∫ тг н – 2 (х)дх 29.   ∫ ctg n (x) dx = -ctg n – 1 (x)n – 1 –  ∫ ctg n – 2 (x) dx 30. Оставить комментарий Отменить ответ Для отправки комментария вам необходимо авторизоваться. Меню Поиск: