Примеры устного счета: 404 Страница не найдена - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Тренажёр устного счёта

Повышайте успеваемость в школе

Регулярные тренировки в тренажёре развивают навыки устного счёта и гарантируют рост успеваемости по математике в школе.

Задача математики в начальной школе — научить детей решать примеры на четыре арифметических действия: сложение, вычитание, умножение и деление. Школа учит детей считать письменно, но не менее важно развивать навыки устного счёта. В тренажёре удобно учить умножение и деление в пределах 100 и практиковаться в устном счёте в рамках программы математики начальной школы. Режимы повышенной трудности помогут старшеклассникам закрепить вычислительные навыки, необходимые при решении задач по геометрии и тригонометрии.

Развивайте память и концентрацию

В жизни мы ежедневно сталкиваемся с задачами, требующими быстрого решения. Продавец взвесил яблоки и назвал стоимость. Если он ошибся, у нас есть несколько секунд, чтобы его поправить, прежде чем оплатить покупку.

Онлайн-тренажёр устного счёта развивает скорость реакции, тренирует память и концентрацию, позволяет довести навыки устного счёта до автоматизма.

Тренируйте только нужное

Выбирайте в Тренажёре устного счёта нужные арифметические действия и один или несколько множителей, делителей, слагаемых или вычитаемых. Используйте настройки тренажёра для тренировки устного счёта с заданным числом, прохождения полного теста по таблице умножения, решения примеров повышенной сложности с отрицательными числами или устного счёта с большими числами.

Опирайтесь на подсказки

Тренажёр устного счёта не только удобный инструмент контроля знаний, но и надёжный помощник в освоении и развитии математических навыков. По ходу онлайн-теста тренажёр выводит для каждого примера подсказки: состав числа или конкретные математические выражения, дополняющие пример.

Регулируйте сложность примеров

Тренируйте сложение и вычитание в пределах двадцати или включите режим «Большие числа» и считайте в пределах ста с переходом через десятки. Регулируйте трудность примеров на умножение и деление: оставайтесь в рамках таблицы умножения или умножайте и делите в т.ч. и на двузначные числа. Используйте переключатель «Отрицательные числа» для добавления в примеры чисел меньше нуля.

Учитесь играючи!

Развивающие и образовательные игры — сила. Фокусировка внимания и позитивная мотивация в игре гарантируют крепкое усвоение материала.

Мы позаботились о простоте и удобстве тренажёра для детей и постарались оптимизировать его для мобильных устройств и планшетов. Для самых маленьких пользователей, которым сложно сохранять концентрацию, мы сделали возможность ограничить тест пятью вопросами и добавили в тренажёр космонавта, звёздочки, звуки, анимацию и конфетти.

Тренажер устного счета онлайн | Клуб любителей математики

Данный тренажер является одним из тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.

Принцип работы основан на генерации примеров по математике подходящего вам уровня сложности для всех классов, решение которых способствует развитию навыков устного счёта.

Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.

Разнообразие режимов

На странице настроек режима можно задавать необходимые параметры генерации примеров по математике для любого класса.

Тренажер устного счета позволяет отрабатывать 4 небезызвестных арифмитических действия на шести уровнях сложности.

Далее корректируете вид математического примера выбирая тип, устанавливая количество слагаемых, манипулируя числовыми множествами.

На данном этапе разработки были продуманы и реализованы режимы, позволяющие работать с двумя множествами чисел: Положительными и Отрицательными. В каждом из ним можно попрактиковаться в различных типах заданий:

«Пример», «Уравнение», «Сравнение».

– этот режим включает в себя обычные арифмитические примеры по математике состоящие из двух или трёх чисел.

– режим, искомое число в котором может находиться на любой позиции.

– режим, в котором необходимо правильно поставить знак сравнения между результатами двух примеров.

Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». А когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.

Бонусом является возможность загрузить и в дальнейшем распечатать «самостоятельную работу» в формате PDF, состоящую из 26 примеров соответствующего режима, кликнум по значку

Принтер.

Процесс счёта

Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звковые уведомления или перейти к Протоколу ошибок и подсказок.

Вы решаете заданый пример, вводите ответ с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки результат Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.

Если по какой-либо причине вы хотите обнулить свои результаты, нажмите на иконку «Сбросить результат» спарва.

Игровая форма

Приложение также предусматривает игровую анимацию «Сражение фехтовальщиков».

В зависимости от правильности введенного ответа, удар наносит тот или иной фехтовальщик, оттесняя своего оппонента. Однако стоит учитывать, что каждую секунду бездействия противник теснит вашего игрока, и при продолжительном ожидании выскакивает сообщение о проигрыше.

Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.

Если режим с анимацией вам мешает, его можно отключить на странице установок с помощью иконки

Протокол ошибок

В любой момент работы с тренажером вы можете перейти к разделу приложения «Протокол ошибок», кликнув на соответствующую иконку сверху, либо перелестнув страницу вниз.

Здесь вы сможете посмотреть свою статистику (количество примеров по категориям) за последние сутки и по последнему режиму.

А также увидеть список ошибок и подсказок (максимум 6 штук), либо перейти к подробной статистике.

Дополнительная информация

Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:

домен сайта + раздел приложения + кодировка данного режима

например:

matematika.club/app/#12301

Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.

😃 5 мощных ускорителей устного счета

В устном счете, как и везде, есть свои хитрости, и чтобы научиться быстрее считать нужно, знать эти хитрости и уметь применять на практике.

Сегодня мы этим и займемся!

1. Как быстро складывать и вычитать числа

Рассмотрим три случайных примера:

25 – 7 =
34 – 8 =
77 – 9 =

Если считать в уме обычным способом, то возникают затруднения, ведь вычитаемое число больше чем вторая цифра в первом числе и начинаются затруднения и торможения с запоминанием остатка.

Типа 25 – 7 = (20 + 5) – (5- 2) = 20 – 2 = (10 + 10) – 2 = 10 + 8 = 18

Согласитесь, что такие операции сложно проворачивать в голове.

Но есть более простой способ:

25 – 7 = 25 – 10 + 3, так как -7 = -10 + 3

Намного проще вычесть из числа 10 и прибавить 3, чем городить сложные вычисления.

Вернемся к нашим примерам:

25 – 7 =
34 – 8 =
77 – 9 =

Оптимизируем вычитаемые числа:

Вычесть 7 = вычесть 10 прибавить 3
Вычесть 8 = вычесть 10 прибавить 2
Вычесть 9 = вычесть 10 прибавить 1

Итого получим:

25 – 10 + 3 =
34 – 10 + 2 =
77 – 10 + 1 =

Вот теперь намного интересней и проще!

Посчитайте сейчас представленные ниже примеры этим способом:

91 – 7 =
23 – 6 =
24 – 5 =
46 – 8 =
13 – 7 =
64 – 6 =
72 – 19 =
83 – 56 =
47 – 29 =

2. Как быстро умножать на 4, 8 и 16

В случае умножения мы тоже разбиваем числа на более простые, например:

4 * 8 = ?

Если помните таблицу умножения, то все просто. А если нет?

Тогда нужно упростить операцию:

Наибольшее число ставим первым, а второе раскладываем на более простые:

8 * 4 = 8 * 2 * 2 = ?

Удваивать числа гораздо легче, нежели чем учетверять или увосьмирять их.

Получаем:

8 * 4 = 8 * 2 * 2 = 16 * 2 = 32

Примеры раскладывания чисел на более простые:

4 = 2*2
8 = 2*2 *2
16 = 22 * 22

Отработайте этот способ на следующих примерах:

3 * 8 =
6 * 4 =
5 * 16 =
7 * 8 =
9 * 4 =
8 * 16 =

3. Деление числа на 5

Возьмем следующие примеры:

780 / 5 = ?
565 / 5 = ?
235 / 5 = ?

Деление и умножение с числом 5 всегда очень простые и приятные, ведь пять это половина от десяти.

И как их быстро решить?

Легко!

780 / 10 * 2 = 78 * 2 = 156
565 /10 * 2 = 56,5 * 2 = 113
235 / 10 * 2 = 23,5 *2 = 47

Для того чтобы проработать этот способ решите следующие примеры:

300 / 5 =
120 / 5 =
495 / 5 =
145 / 5 =
990 / 5 =
555 / 5 =
350 / 5 =
760 / 5 =
865 / 5 =
1270 / 5 =
2425 / 5 =
9425 / 5 =

4.

Умножение на однозначные числа

С умножением немного сложнее, но не сильно, как бы Вы решили следующие примеры?

56 * 3 = ?
122 * 7 = ?
523 * 6 = ?

Без специальных фишек решать их не очень приятно, но благодаря методу «Разделяй и властвуй» мы можем сосчитать их гораздо быстрее:

56 * 3 = (50 + 6)3 = 503 + 6*3 = ?
122 * 7 = (100 + 20 + 2)7 = 1007 + 207 + 27 = ?
523 * 6 = (500 + 20 + 3)6 = 5006 + 206 + 36 =?

Нам остается только перемножить однозначные числа, некоторые из которых с нулями и сложить полученные результаты.

Для проработки этой техники решите следующие примеры:

123 * 4 =
236 * 3 =
154 * 4 =
490 * 2 =
145 * 5 =
990 * 3 =
555 * 5 =
433 * 7 =
132 * 9 =
766 * 2 =
865 * 5 =
1270 * 4 =
2425 * 3 =
9425 * 2 =
Делимость числа на 2, 3, 4, 5, 6 и 9

Проверьте числа: 523, 221, 232

Число делится на 3, если сумма его цифр делится на 3.

Например, возьмем число 732, представим его как 7 + 3 + 2 = 12. 12 делится на 3, а значит, число 372 делится на 3.

Проверьте, какие из следующих чисел делятся на 3:

12, 24, 71, 63, 234, 124, 123, 444, 2422, 4243, 53253, 4234, 657, 9754

Число делится на 4, если число, состоящее из последних двух его цифр, делится на 4.

Например, 1729. Последние две цифры образуют 20, которое делится на 4.

Проверьте, какие из следующих чисел делятся на 4:

20, 24, 16, 34, 54, 45, 64, 124, 2024, 3056, 5432, 6872, 9865, 1242, 2354

Число делится на 5, если его последняя цифра 0 или 5.

Проверьте, какие из следующих чисел делятся на 5 (самое легкое упражнение):

3, 5, 10, 15, 21, 23, 56, 25, 40, 655, 720, 4032, 14340, 42343, 2340, 243240

Число делится на 6, если оно делится и на 2 и на 3.

Проверьте, какие из следующих чисел делятся на 6:

22, 36, 72, 12, 34, 24, 16, 26, 122, 76, 86, 56, 46, 126, 124

Число делится на 9, если сумма его цифр, делится на 9.

Например, возьмем число 6732, представим его как 6 + 7 + 3 + 2 = 18. 18 делится на 9, а значит, число 6732 делится на 9.

Проверьте, какие из следующих чисел делятся на 9:

9, 16, 18, 21, 26, 29, 81, 63, 45, 27, 127, 99, 399, 699, 299, 49

Игра «Быстрое сложение»

Ускоряет устный счет
Тренирует внимание
Развивает творческое мышление

Отличный тренажер для развития быстрого счета. На экране дана таблица 4х4, а над ней показаны числа. Самое большое число нужно собрать в таблице. Для этого нажмите мышкой на два числа, сумма которых равна этому числу. Например, 15+10 = 25.

Играть сейчас

Игра “Быстрый счет”

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Играть сейчас

Игра “Угадай операцию”

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Игра “Упрощение”

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Играть сейчас

Задание на сегодня

Решить все примеры и тренироваться минимум 10 минут в игре Быстрое сложение.

Очень важно отработать все задания этого урока. Чем лучше Вы будете выполнять задания, тем больше будет пользы. Если Вы чувствуете, что Вам мало заданий – можете сами составлять себе примеры и решать их и тренироваться в математические развивающие игры.

Урок взят из курса “Устный счет за 30 дней”

Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. Научу использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Другие развивающие курсы

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

В 2-5 раз лучше запоминать тексты, лица, цифры, слова
Научится запоминать на более длительный срок
Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Как улучшить память и развить внимание

Бесплатное практическое занятие от advance.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Приемы устного счета

Сегодня перед поступлением в школу ребёнок должен знать буквы, цифры, уметь считать и читать простые выражения. Многие школы советуют мамам и папам научить ребёнка этому до прихода в 1 класс. На справедливый вопрос родителей: «Неужели детей не научат в школе вычитанию и сложению» можно дать такой ответ: «Конечно, научат. Но ребёнку будет гораздо сложнее запомнить материал под «давлением» школьной программы чем сверстникам, научившимся считать деревья и машины по дороге в садик».

Устный счёт развивает сообразительность, смекалку, тренирует память и мышление. Поэтому начинать учиться можно, когда ребёнок проявляет первый интерес к счёту: считает ступеньки, игрушки, делится вещами. Ненавязчиво, с помощью стишков, считалочек превратите игру в занятие. Не загружайте малыша больше 10-15 минут сразу. Если давить, ребёнок никогда не полюбит цифры и математику. Развивать устный счёт можно только после того, как ребёнок считает ступеньки в пределах 10, называет количество предметов на картинке, составляет по просьбе 5 игрушек, знает, что такое «больше» и «меньше».

Почему это важно? Счёт в уме – высший пилотаж для дошкольника. Малышу трудно считать без игрушек или палочек. Дошкольник еще не мыслит образами, а только конкретными предметами, которые можно потрогать. Воспользуйтесь этим, чтобы объяснить состав числа: 1 – один кубик, потрогай его; 2 – теперь 2 кубика, возьми их в ручки.

Главное: малыш должен понять, что за каждым числом стоят игрушки, яблочки и т.д., а не пустота. Тогда, считая в уме, ребёнок не запутается в абстрактных числах, а будет представлять их вес и состав.

Первый способ освоить устный счёт – выполнять упражнения с опорой на состав числа. Подходит для дошкольников.

1. Самое простое, не требующее никаких материалов, упражнение – «Покажи 6 пальцев разными способами». (Количество, которое нужно показать, конечно, может быть любым от 4 до 10).

2. Магазины игрушек предлагают весёлые и активные игры для тренировки устного счёта. Например: «Арбуз» (с 3 лет), «Турбосчёт», «Котосовы» (с 4 лет), «Фрукто 10» (с 5 лет), «10 Свинок» (с 6 лет) и др. По цене: 200-1300 р. Процесс игры захватывает детей. Они соревнуются и забывают, что игра в основе обучающая. Такая игра увлечёт даже взрослого, а заниматься нужно всего 15 минут в день.

4. Онлайн тренажёры. Сейчас существует большое количество онлайн тренажёров по устному счёту. Во многих из них можно выбрать уровень сложности. На сайте «Разумейкин» в разделах «Счёт и цифры», «Математика для 7-8 лет» и «Математика для 9-10 лет» представлены не только примеры и задачи для устного счета, но и короткие обучающие видео.

Второй и третий способы развития устного счёта сложнее, чем первый. Их можно использовать при обучении младших школьников.

Второй способ – заучивание таблиц.

Существуют таблицы на сложение и вычитание, умножение и деление. Главное — сначала прорешать с ребёнком несколько примеров, чтобы он понял, как работать с таблицей, а потом ребёнок сам будет представлять таблицу в уме при счёте. Сочетайте такой способ с напевками, считалками, типа: “Дважды два – четыре…”
Таблицы на сложение и деление подойдут для наглядного объяснения. Заучивать их не нужно. А вот без таблицы умножения никуда. Ее учим.

Третий способ – использование специальных приёмов устного счёта, например:

1. Если нужно прибавить 7, 8 или 9 — округлите до 10, а потом вычтите добавку. 46+8= 46+10-2= 54

2. При прибавлении двузначного числа: если последняя цифра больше 5, то округляем до 10, а потом вычитаем добавку; если последняя цифра меньше 5, то сначала складываем десятки, потом единицы. 34+29 = 34+30-1 = 64-1 = 63

3. При сложении трёхзначных чисел — разбиваем на сотни, десятки, единицы. 249+533 = (200+500)+(40+30)+(9+3) = 782

5. При умножении на 5 — сначала умножаем на 10, потом делим на 2. 12*5 = (12*10):2 = 120:2 = 60

6. При делении на 5 — сначала умножаем на 2, потом делим на 10. 125:5 = 125*2:10 = 250:10 = 25

7. При умножении на 9 — сначала умножаем на 10, потом вычитаем начальное число. 3*9 =3*10-3 = 30-3 = 27

Описанные способы — снова устного счёта. Вариантов их использования множество. Главное правило: не учите ребенка счёту по линеечке, прибавляя по единице. Так мышление не разовьётся, и ребенок будет считать медленно. Лучше считать группами чисел, чтобы запоминались результаты вычислений. Главное в устном счёте — это не столько решение примеров, сколько развитие смекалки, сообразительности, реакции, внимания и памяти. Эти навыки пригодятся в жизни ребенку больше, чем просто умение считать. Превратите обучение в игру, и тогда ребенок проявит инициативу.

Тренажер устного счета онлайн | Инструкция, нормы, разряды

ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ТРЕНАЖЕРА

Тренажер устного счета — легко и существенно повышает интеллектуальный потенциал человека.

Результатом приобретения навыков и здачи нормативной квалификации будет присвоение спортивного разряда (I разряд, II разряд, III разряд, кандидат в мастера спорта, мастер спорта и гроссмейстер).

Людей из группы выделяют как по умению красиво и правильно говорить, так и по умению быстро считать в уме, и относят их, как правило, к категории умных. Школьнику умение быстро считать в уме позволяет более успешно учиться, а инженеру и ученому сократить время получения результата их деятельности.
УС нужен не только школьникам, но и инженерам, учителям, медицинским работникам, ученым и руководителям разного уровня. Кто быстро считает, тому легче учиться и работать. УС – это не игрушка, хотя и развлекает. Он позволяет вернуться ученику на те “рельсы”, с которых он упал когда-то; повышает скорость и качество восприятия информации; дисциплинирует и производит точность во всем; приучает замечать детали и мелочи; приучает к экономии; создает образы предметов и явлений; позволяет предвидеть будущее и развивает интеллект человека.
«Евроремонт» в голове нужно начинать с простых арифметических действий, которые позволяют структурировать мозг.
Умение быстро считать в уме дает ученику уверенность в себе. Как правило, быстрее всех считают в уме те, кто хорошо учится в школе или в ВУЗе. Если отстающего ученика научить быстро считать в уме, то это обязательно благотворно повлияет на его успеваемость, и не только в естественных, но и во всех других предметах. Это доказано практикой.
Произвольное внимание и интерес во время устного счета меняет блуждающий взгляд отстающего ученика на фиксированный, а концентрация внимания достигает нескольких этажей глубины предмета или процесса, который изучается.
“Изучение математики дисциплинирует мышление, приучает к правильному словесному выражению мыслей, к точности, сжатости и ясности речи, воспитывает настойчивость, умение достигать намеченной цели, развивает работоспособность, способствует правильной самооценке владения предметом, который изучается”. (Кудрявцев Л.Д. – член-кор. РАН. 2006.).
Ученик, который научился быстро считать в уме, как правило, начинает и быстрее мыслить.
Тот, кто по своей природе хорошо считает, естественно обнаружит ум и в любой другой науке, а тот, кто считает медленно, учась этому искусству и овладевая им, сможет улучшить свой ум, сделать его острее (Платон).
Приобретенных навыков устного счета одним хватит на 5 — 10 лет, а другим на всю жизнь.
Нашим потомкам будет легче учиться и получать знания. Однако, культура устного счета всегда будет являться неотъемлемой частью общечеловеческой культуры.
Кто быстро считает в уме, тот, как правило, ясно мыслит, быстро воспринимает и глубже видит.
Освоение УС развивает образное, диаграммное и системное мышление, расширяет оперативную память, диапазон восприятия, приучает к мышлению на несколько ходов вперед, повышает качество мышления, оперируя количественными характеристиками объектов.
УС повышает ясность мышления, уверенность в себе, а также волевые качества (терпение, усидчивость, выносливость, трудолюбие). Приучает к глубокой и устойчивой концентрации внимания, домысливанию и договариванию начатых фраз (особенно у дошкольников и учеников начальных классов).

Простое в сложном. Устный счет

Игольченко Д.В. 1

1МОУ СШ №105 г.Волгограда

Уланкина Т.П. 1

1МОУ СШ №105 г.Волгограда

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Ученые обнаружили, что у современного поколения происходит снижение умственных способностей. «Если есть такая вещь, как калькулятор, который может посчитать все быстро и правильно, зачем себя утруждать?» – думают учащиеся. Вот и достаем мы при первой же необходимости калькуляторы и считаем. Мы рады, что не нужно утруждать себя подсчетами, родители наши рады, что все быстро сделано и правильно. А мозг при этом работает все хуже и медленнее.

В то же время, ученые доказывают, что активизирует мыслительную деятельность учащихся именно устный счет.

Устный счет – это математические вычисления, осуществляемые человеком без помощи дополнительных устройств (компьютер, калькулятор, счёты) и приспособлений (ручка, карандаш, бумага).

Оказывается: простое находится в сложном. При решении математических примеров активизируются и развиваются память, речь, внимание, способность воспринимать сказанное на слух, быстрота реакции, а значит, развиваются способности, необходимые для нашей учебной деятельности.

Актуальность: ученые бьют тревогу по поводу стремительного снижения умственной способности человечества и предлагают каждому человеку как можно чаще тренировать мозг. Способов развития интеллекта много, но самым простым и доступным является устный счет. В своей работе я хочу показать, как можно при помощи устного счета считать быстро и правильно, что процесс выполнения математических действий оказывается полезным и интересным занятием.

Цель: расширить знания о методах и приемах устного счета.

Задачи:

1. Систематизировать известные приемы устного счета;

2. Выбрать для себя самые интересные и использовать их на практике.

Объект: процесс вычисления.

Гипотеза: при использовании устного счета скорость вычислений увеличивается, вычисления упрощаются, количество ошибок уменьшается, повышается вычислительная культура учащихся.

Новизна: знакомство с нестандартными приемами вычислительных навыков устного счета, приёмами умножения.

Методика исследования. Сбор информации в сети Интернет. Систематизация и обобщение материала. Анкетирование. Анализ полученных в ходе исследования данных (Приложение 1).

Продукт: буклет «Устный счет. Различные приемы умножения» (Приложение 2)

Практическая значимость: выполнение вычислений с применением нестандартных алгоритмов устного счета на практике, данный материал можно использовать на уроках математики и для дополнительного образования. Любой ученик может развить в себе интерес к науке математике через данный материал.

. Из истории возникновения счета

Начало устного счета

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Возникала необходимость отвечать на жизненно важные вопросы: сколько человек в племени, по сколько плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас, сколько нужно сделать ножей и топоров. Таким образом, сам не замечая, человек начал считать и производить первые вычисления.

Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного крепкого птенца. Научившись выделять один предмет из множества других, говорили «один», а если их было больше – «много». Даже для названия числа «один» часто пользовались словом, которым обозначался единичный предмет, например «луна», «солнце». Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.

Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки) привели человека к представлению о числе два. До сих пор слово «два» на некоторых языках звучит так же, как «глаза» или «крылья».

Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трёх, затем до пяти и до десяти и так далее. Название каждого числа отдельным словом было великим шагом вперёд.

Для счёта люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах двадцати.

Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счёта.

Изменения устного счета

По мере развития речи люди начали использовать слова для обозначения чисел. Не возникала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы (Приложение 3). Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10.

При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

Древние торговцы для удобства счёта начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.

Особенно сложны и трудны были в старину действия умножения и деления, особенно последнее. «Умноженье – мое мученье, а с деленьем – беда» – говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приёма для каждого действия. В повседневной жизни использовали одновременно чуть ли не дюжину различных способов умножения и деления – приёмы один другого запутаннее. Запомнить такие приёмы не в силах был человек средних способностей. Каждый учитель счётного дела держался своего излюбленного приёма, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

Как постепенно дошли люди до настоящей арифметики

Так например в книге Всеволода Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1909) изложено 27 способов умножения. Автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом рукописных сборниках». Наш современный способ умножения описан там под названием «шахматного».

Был так же и очень интересный, точный, лёгкий, но громоздкий способ «галерой» или «лодкой», названный так в силу того, что при делении чисел этим способом получается фигура, похожая на лодку или галеру. У нас такой способ употреблялся до середины XVIII века. («Арифметика» – старинный русский учебник математики, которую Ломоносов назвал «вратами своей учености») пользуется исключительно способом «галеры»(Приложение 4), не употребляя, впрочем, этого названия.

Упоминаются такие способы, как «загибанием», «решеткой», «задом наперед», «ромбом», «треугольником» и многие другие. Многие такие приемы для умножения чисел долгие и требуют обязательной проверки.

Интересно, что и наш способ умножения не является совершенным, можно придумать еще более быстрые и еще более надежные.

Таблица умножения

Впервые, в привычном нам виде, таблица умножения появилась в сочинении Никомаха Геразского (I-II вв. н. э.) – «Введение в арифметику». Так кто придумал таблицу умножения? Принято считать, что первый, кто ее открыл, – это Пифагор, хотя прямых доказательств и подтверждений этому нет. Присутствуют только косвенные доказательства. Как, например, Никомах Геразский ссылается на Пифагора в своем сочинении.

При этом существует одна из старейших таблиц умножения, приведенная на глиняных табличках, возраст которой около 4-5 тысяч лет, и была она обнаружена в Древнем Вавилоне. В основе ее лежала шестидесятеричная система исчисления. Таблица же с десятичной системой исчисления была найдена в Китае, в 305 году до нашей эры. Поэтому четко ответить на вопрос: «Кто придумал таблицу умножения», – не получится (Приложение 5)

Таблица умножения – те необходимые в жизни каждого человека знания, которые требуется элементарно заучить, что на первых школьных порах даётся совсем не элементарно. Это потом уже с легкостью мага мы «щелкаем» примеры на умножение: 2·3, 3·5, 4·6 и т.д., но со временем все чаще забываемся на множителях ближе к 9, особенно если счетной практики давно не ведали, отчего отдаемся во власть калькулятора или надеемся на свежесть знаний друга.

Однако, овладев одной незамысловатой техникой «ручного» умножения, мы можем запросто отказаться от услуг калькулятора. Уточнение: речь идет о школьной таблице умножения для чисел от 2 до 9, умножаемых на числа от 1 до 10.

Умножение для числа 9 – 9·1, 9·2 … 9·10 – легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится» на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки.

Допустим, хотим умножить 9 на 7. Загибаем палец с номером, равным числу, на которое мы будем умножать 9. В нашем примере нужно загнуть палец с номером 7. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа – количество единиц. Слева у нас 6 пальцев не загнуто, справа – 3 пальца. Таким образом, 9·7=63. (Приложение 6).

Умножение для числа 8 – 8·1, 8·2 … 8·10 – действия здесь похожи на умножение для числа 9 за некоторыми изменениями. Во-первых, поскольку числу 8 не хватает уже двойки до круглого числа 10, нам необходимо каждый раз загибать сразу два пальца – с номером х и следующий палец с номером х+1. Во-вторых, тотчас же после загнутых пальцев мы должны загнуть еще столько пальцев, сколько осталось не загнутых пальцев слева.

В-третьих, это напрямую работает при умножении на число от 1 до 5, а при умножении на число от 6 до 10 нужно отнять от числа х пятерку и выполнить расчёт как для числа от 1 до 5. , а к ответу затем добавить число 40, потому что иначе придется выполнять переход через десяток, что не совсем удобно «на пальцах». Вообще надо заметить, что умножение для чисел ниже 9 тем неудобнее выполнять «на пальцах», чем ниже число расположено от 9.

Теперь рассмотрим пример умножения для числа 8. Допустим, хотим умножить 8 на 3. Загибаем палец с номером 3 и за ним палец с номером 4 (3+1). Слева у нас осталось 2 незагнутых пальца, значит нам необходимо загнуть еще 2 пальца после пальца с номером 4 (это будут пальцы с номерами 5, 6 и 7). Осталось 2 пальца не загнуто слева и 4 пальца – справа. Следовательно, 8·3=24.

Еще пример: вычислить 8·8=? Как было сказано выше, при умножении на число от 6 до 10 нужно отнять от числа х пятерку, выполнить расчет с новым число х-5, а затем добавить к ответу число 40. У нас х=8, значит загибаем палец с номером 3 (8-5=3) и следующий палец с номером 4 (3+1). Слева два пальца остались не загнуты, значит загибаем еще два пальца (с номером 5,6). Получаем: слева 2 пальца не загнуты и справа – 4 пальца, что обозначает число 24. Но к этому числу нужно еще добавить 40: 24+40=64. В итоге 8·8=64(Приложение 7).

Специалисты в устном счете

Уметь считать правильно и быстро – замечательная способность человеческого ума. Но далеко не все умеют ею пользоваться. Вместе с тем, счет в уме дает огромные преимущества. Это уверенность во многих житейских ситуациях, не только связанных непосредственно с вычислениями, что само по себе очень полезно, но и психологическая уверенность.

Быстрый счет часто означает не интеллектуальную способность мозга, а умение применять на практике методики счета в уме, разработанные и описанные учеными — математиками. Для их освоения вовсе необязательно иметь выдающиеся математические способности, достаточно изучить эти методики по их книгам и активно применить в жизни.

Особые способности в устном счёте встречаются с давних пор. Ими обладали многие ученые, в частности Андре Ампер и Карл Гаусс. Умение быстро считать было присуще и многим людям, чья профессия была далека от математики и науки в целом.

До второй половины XX века были популярны выступления специалистов в устном счёте. Иногда они устраивали показательные соревнования между собой. Известными российскими «суперсчетчиками» являются Арон Чиквашвили, Давид Гольдштейн, Юрий Горный, зарубежными – Борислав Гаджански, Вильям Клайн, Томас Фулер и другие (Приложение 8).

Хотя некоторые специалисты уверяли, что дело во врожденных способностях, другие аргументировано доказывали обратное: «дело не только и не столько в каких-то исключительных«феноменальных» способностях, а в знании некоторых математических законов, позволяющих быстро производить вычисления» и охотно раскрывали эти законы.

Истина как обычно, оказалась на некоей «золотой середине» сочетания природных способностей и грамотного, трудолюбивого их пробуждения, взращивания и использования. Те, кто следуя Трофиму Лысенко уповают исключительно на волю и напористость, со всеми уже хорошо известными способами и приемами устного счёта обычно при всех стараниях не поднимаются выше очень и очень средних достижений.

Более того, настойчивые попытки «хорошенько нагрузить» мозг такими занятиями как устный счёт, шахматы вслепую и т.п. легко могут привести к перенапряжению и заметному падению умственной работоспособности, памяти и самочувствия (а в наиболее тяжелых случаях – и к шизофрении). С другой стороны и одаренные люди при беспорядочном использовании своих талантов в такой области как устный счёт быстро «перегорают» и перестают быть в состоянии длительно и устойчиво показывать яркие достижения. Один из примеров удачного сочетания обоих условий (природной одаренности и большой грамотной работы над собой) показал наш соотечественник, уроженец Алтайского края Юрий Горный.

Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устного счёта создана была в годы второй мировой войны цюрихским профессором математики Я. Трахтенбергом. Она известна под названием «Система быстрого счёта». История ее создания необычная. В 1941г. гитлеровцы бросили Трахтенберга в концлагерь.

Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счёта. Уже с самого начала результаты были самые отрадные. Учащиеся радовались вновь приобретенным навыкам и с воодушевлением двигались вперед. Если раньше их отталкивала монотонность, то сейчас их привлекало разнообразие приёмов. Шаг за шагом, благодаря достигнутым ими успехам, рос интерес к занятиям. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.

Также разработкой приемов быстрого счета занимались другие ученые: Яков Исидорович Перельман, Георгий Берман и другие.

Устный счет – гимнастика ума. Различные приемы умножения

Умножение на 11 числа, сумма цифр которого не превышает 10

Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

Пример 1:

а) 17х11 = 1 (1+7) 7 = 187;

б) 32х11 = 3 (3+2) 2 = 352.

2.2. Умножение на 11 числа, сумма цифр которого больше 10

Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

Пример 2:

а) 86х11 = 8 (8+6) 6 = 8 (14) 6 = (8+1) 46 = 946;

б) 37х11 = 3 (3+7) 7 = 3 (10) 7 = (3+1) 07 = 407.

2.3. Умножение на одиннадцать (по Трахтенбергу)

Пример 3

533х11

Ответ пишется под 533 по одной цифре справа налево, как указано в правилах.

Первое правило. Напишите последнюю цифру числа 533 в качестве правой цифры результата

533х11

Второе правило. Каждая последующая цифра числа 533 складывается со своим правым соседом и записывается в результат.3+3 будет 6. Перед тройкой записываем результат 6.

533х11

Применим правило еще раз: 5+3 будет 8.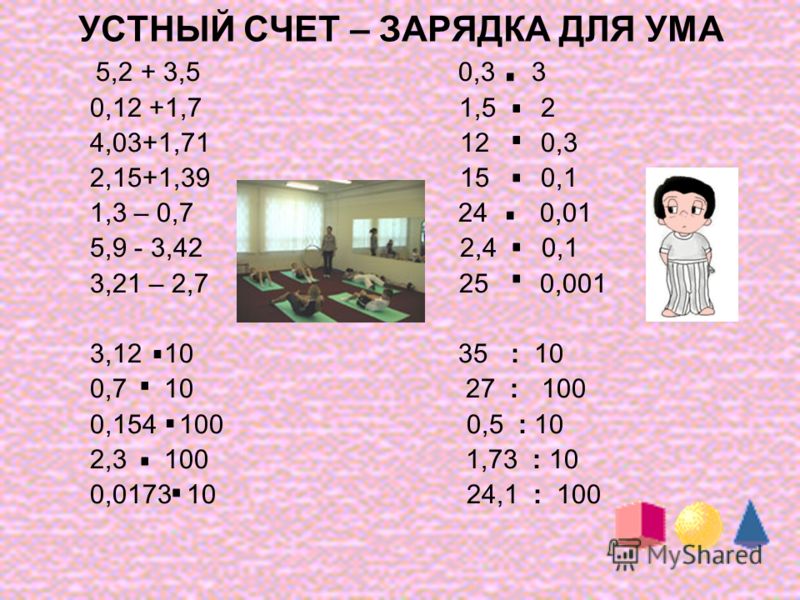 Записываем и эту цифру в результате:

533х11

863

Третье правило. Первая цифра числа 533, то есть 5, становится левой цифрой результата:

533х11

5863

Ответ: 5863.

2.4. Умножение на 22,33,44,55…,99

Чтобы двузначное число умножить на 22,33,…, 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 33 = 3х11; 44 = 4х11 и так далее. Затем произведение первых чисел умножить на 11.

Пример 4:

а) 52х22 = 52х2х11 = 104х11 = 1144;

б) 28х44 = 28х4х11 = 112х11 = 1232;

в) 73х55 = 73х5х11 = 365х11 = 4015;

г) 44х99 = 44х9х11 = 396х11 = 4356.

2.5. Умножение на число 111, 1111 и так далее, зная правила умножения двузначного числа на число 11

Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и так далее шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.

Пример 5:

а) 34х111 = 3 (3+4) (3+4) 4 = 3774 (количество шагов – 2)

б) 54х1111 = 5 (5+4) (5+4) (5+4) 4 = 59994 (количество шагов – 3)

Если сумма цифр первого множителя равна 10 или более 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и так далее шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. к первой цифре 7 прибавить 1, получим 8, далее 3+1 = 4; а последние цифры 3 и 6 оставляем без изменения. Получаем ответ 8436.

Количество шагов всегда меньше количества единиц на 1

Пример 6:

76х111 = 7 (7+6) (7+6) 6 = 7 (13) (13) 6 = (7+1) (3+1) 36 = 8436.

2.6. Умножение двузначного числа на 101, трёхзначного на 1001 и т.д.

Приписать число к самому себе. Умножение закончено.

Пример 7:

а) 52х101 = 5252;

б) 133х1001 = 133133;

в) 3438х10001 = 34383438;

г) 246932х1000001 = 246932246932.

2.7. Умножение на 37

Чтобы устно умножить число на 37, надо это число разделить на 3 и умножить на 111. Прежде чем научиться устно умножать на 37, надо хорошо знать признак делимости и таблицу умножения на 3.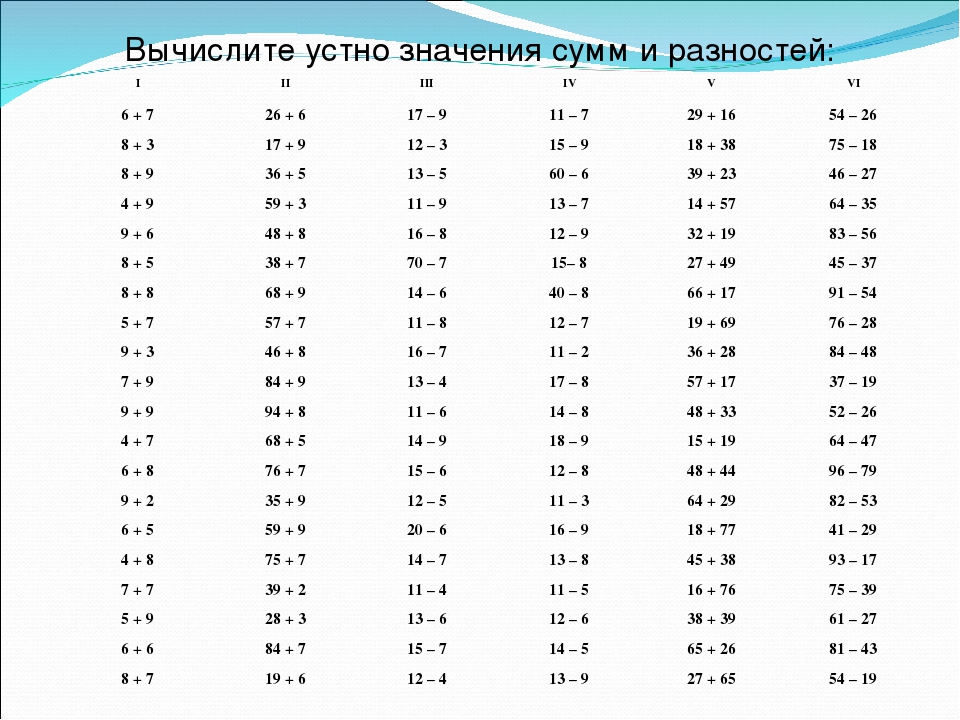

Пример 8:

а) 24х37 = (24:3)х37х3 = 8х111 = 888;

б) 54х37 = (54:3)х37х3 =18х111 = 1998.

2.8. Алгоритм перемножения двузначных чисел, близких к 100

Если нужно перемножить два двузначных числа, близких к 100, то необходимо:

1) найти недостатки сомножителей до сотни; 2 и 3

2) вычесть из одного сомножителя недостаток второго до сотни; 98-3=95

3) к результату приписать двумя цифрами произведение недостатков

сомножителей до сотни. 2х3 = 06

Пример 9

98х97

1) 2 и 3

2) 98-3 = 95

3) к результату приписать 2х3 = 06

98х97 = 9506.

2.9. Умножение трёхзначного числа на 999

При умножении трёхзначного числа на 999получается шестизначное число. Первые три цифры – есть умножаемое число, только уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

Пример 10:

а) 285х999 = 284715;

б) 943х999 = 942057;

в) 883х999 = 882117.

2.10. Умножение на шесть (по Трахтенбергу)

Нужно прибавить к каждой цифре половину «соседа».

Пример 11:

622084х6 = 37332504

622084х 6, 4 является правой цифрой этого числа и, так 4 как «соседа» у неё нет, прибавлять нечего.

6222084х6 Вторая цифра 8, «сосед» – 4. Мы берём 8 04 прибавляем половину 4 (2) и получаем 10, ноль пишем, 1 в перенос.

6222084х6 Следующая цифра ноль. Мы прибавляем к ней 504 половину «соседа» 8 (4), то есть 0 + 4 = 4 плюс перенос (1). Остальные цифры аналогичны.

37332504.

Правило умножения на 6: является «сосед» чётным или не чётным – никакой роли не играет. Мы смотрим только на саму цифру: если она чётная, прибавляем к ней её целую часть половины «соседа», если нечётная, то кроме половины «соседа» прибавляем еще 5.

Пример 12:

443052х6 = 2658312

443052х6, 2 – чётная и не имеет «соседа», напишем её снизу

443052х6, 5 – нечётная: 5+5 и плюс половина «соседа» 2 (1)

12 будет 11. Запишем 1 и в перенос 1

443052х6, половина от 5 будет 2, и прибавим перенос 1, то будет 3

312

443052х6, 3 – нечетная, 3 + 5 = 8

8312

443052х6, 4 + половина от 3 (1) будет 5

58312

443052х6, 4 + половина от 4 (2) будет 6

658312

443052х6, ноль + половина от 4 (2) будет 2

2658312 .

Заключение

Знание приемов устного счета позволяет упрощать вычисления, экономить время, развивает логическое мышление и гибкость ума. Процесс выполнения математических действий при этом оказывается полезным и интересным занятием.

Мы убедились, что устный счет это уже не тайна, а научно разработанная система. А если есть система, то значит, ее можно изучать, ей можно следовать, ею можно овладевать.

Рассмотренные методы устного счета иллюстрируют многолетний кропотливый труд ученых по выявлению простого в сложном, игры с цифрами.

Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов. При использовании устного счета вычисления упрощаются, количество ошибок уменьшается, повышается вычислительная культура учащихся.

Рассматривая старинные способы вычислений и современные приёмы быстрого устного счёта, мы видим, что как в прошлом, так и в будущем, без математики, науки созданной разумом человека, не обойтись.

При изучении старинных способов вычислений выяснили, что эти арифметические действия были трудными и сложными из-за многообразия способов и их громоздкости выполнения. А современные способы вычислений просты и доступны всем.

При знакомстве с научной литературой были обнаружены более быстрые и надежные способы вычислений.

Результаты работы оформлены в буклете «Устный счет. Различные приемы умножения», который может быть предложен одноклассникам. Возможно, что с первого раза не у всех получится быстро выполнять вычисления с применением этих приемов. Необходима постоянная вычислительная тренировка. Она и поможет приобрести полезные вычислительные навыки.

Библиографический список

Научная и учебная литература

1. Бикташева Л.В. Алгоритмы ускоренных вычислений, Журнал «Математика в школе», №11, 2001г.

2. Зайкин М.Н. Математический тренинг. – Москва, 1996г.

3. Зимовец К.А., Пащенко В.А. Интересные приемы устных вычислений. , Начальная школа, №6,1990г.

4. Зубелевич Г.И., Ефимов В.И. Мир чисел, М.: Просвещение,1980г.

4. Иванова Т. Устный счёт, Начальная школа, №7, 1999г.

5. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся, М.: Просвещение, 1986г.

6. Минских Е.М. От игры к знаниям, М.: Просвещение, 1982г.

7. Перельман Я.И. Живая математика. Екатеринбург: Тезис, 1994г.

8. Свечников А.А. Числа, фигуры, задачи. М.: Просвещение, 1977г.

9. Филиппов Г.А. Устный счёт – гимнастика ума, Волгоград: Перемена, 1995г

Электронные ресурсы удалённого доступа (INTERNET)

Дидактический материал для устного счета в 5-11 классах: https://nsportal.ru/shkola/raznoe/library;

Возможности человека: http://litresp. ru;

Системы устного счета и их создатели: https://4brain.ru;

Счетчики феноменальные: https://gufo.me//gufo.me;

Устный счет: https://ru.wikipedia.org;

Устный счет: http://fb.ru/article;

Устный счет: http://www.myshared.ru/slide/download;

Хитрые приемы быстрого счета: https://nsportal.ru;

Школьные секреты о пользе устного счета: http://chitalochka-ru.ru.

Приложение 1

Анализ анкетирования

Для того чтобы выяснить, знают ли современные школьники другие способы умножения кроме тех, которые производят в столбик было проведено анкетирование.

Я провел анкетирование среди учащихся 5, 7 и 11 классов. Всего было опрошено 43 ученика.

Вопросы анкеты:

1. Как часто ты пользуешься калькулятором?

2. Умеешь ли ты быстро и правильно считать?

3. Знаешь ли ты какие-либо приемы быстрого счета?

4. Хотел бы расширить свои познания в этой области?

5. Как ты думаешь, развивает ли устный счет память, внимание, способность сосредоточиться?

Результаты опроса:

Часто: 87%;

Иногда: 13%;

не пользуюсь: 0%.

Умею: 65%;

считаю медленно: 35%;

не умею: 0%.

Да: 80%;

Что-то слышал: 20%.

Да 96%;

нет 0%.

не знаю 4%

Да 100%;

нет 0%.

Проведя статистическую обработку данных, я сделал вывод, что далеко не все учащиеся знают приемы устного счета, поэтому целесообразно для учеников 5-11-х классов создать буклет с приемами быстрого счета, чтобы использовать их при выполнении умножений.

Приложение 2

Буклет

Приложение 3

Рисунки, чертежи, символы для изображения чисел.

Приложение 4

Способ «галеры»

Итальянцы так называли из-за того что после окончания вычислений цифры располагаются в виде фигуры, напоминающей это гребное судно. Англичане называли его – метод зачеркиваний, постоянно производится зачёркивание цифр.

Пример: 7968:24 Записываем делимое, а под ним делитель. Справа от делимого ставим скобку, за которой буду последовательно записывать цифры частного. Как и при обычном делении, подбором находится первая цифра частного, в данном случае 3. Записываю её. Теперь умножаю первую цифру делителя, 2, на 3 и результат вычитаю из первой цифры делимого. Разность 7 – 2·3=1 записываю сверху над цифрой 7, после чего зачёркиваю цифру 7 в делимом и цифру 2 в делителе – они уже «вышли» из игры. Перехожу ко второй цифре делителя – 4. И т.д. Выполняя деление по определенному алгоритму, запутанному и замысловатому, получаю в частом 332. И если запись повернуть на 90 градусов, то она будет напоминать галеру.

1740

7968 (332

2444

Приложение 5

Т аблица умножения

Вавилонская

Китайская

Японская

Индийская

Приложение 6

Умножение на пальцах на 9

Приложение 7

Умножения на пальцах на 8

Приложение 8

С пециалисты в устном счете

В начале века в России большую популярность приобрел «математик на эстраде» Р. Арраго.

«Один миллион пятьсот девяносто четыре тысячи триста двадцать три умножьте на три три тысячи четыреста пятьдесят шесть». Проходит несколько секунд, и все читают на доске результат – 5 509 980288.

Вот рассказ об эксперименте, проведенном одним из исследователей с мадемуазель Осака. Испытуемую просили возвести в квадрат 97, получить десятую степень того же числа. Она делала это моментально. Затем предлагали извлечь корень шестой степени из 40 242 074 782 776 576. Она отвечала тотчас и без ошибок.

В 1927 году доктор Ости и математик Сент-Лаге экзаменовали слепого счетчика Луи Флери. Среди поставленных задач была следующая: дается число, нужно разложить его на куб некоторого числа и четырехзначное число. Флери предложили число 707 353 209. Он размышлял 28 секунд и дал решение: 891 в кубе и 5238. Ему предложили 211 717 440. Ответ последовал через 25 секунд: 596 в кубе и 8704.

В Ванском районе Западной Грузии знаменит Арон Чиквашвили. Он свободно манипулирует в уме многозначными числами. “Счетный механизм” Чиквашвили не знает усталости и ошибок

Тбилисская студентка Лейла Джанджгава обладает удивительной способностью мгновенно подсчитывать количество букв в словах и предложениях
Какими же методами оперируют чудо счетчики? Приходит ли “дар” с детства, в юности или приобретается в течение жизни?
Пытались объяснить эту способность исключительной памятью, тем, что психологи называют “гипермнезией”. Конечно, до какой-то степени мы сталкиваемся здесь с проявлением поистине чудовищной памяти, но одной памятью не объяснить существа явления.

Рассказывают, что отец Гаусса обычно платил своим рабочим в конце недели, прибавляя к каждодневному заработку плату за сверхурочные часы. Однажды, после того как Гаусс-отец закончил расчеты, следивший за операциями отца ребенок, которому было едва три года, воскликнул:

– Папа, подсчет неверен! Вот какая должна быть сумма. Вычисления повторили и с удивлением убедились, что малыш указал правильную сумму. Несколько лет назад газеты сообщили о юном математическом феномене Бориславе Гаджански. – Можешь ли ты, Борислав, извлечь корень двадцать второй степени из числа 348 517 368 454 361 458 872? Мальчик на минуту задумывается: “Восемь”. – А теперь извлеки корень тридцать первой степени из числа 538 436 517 832 435 456 582. Еще минута на размышление: – Четыре. В свои одиннадцать лет Борислав Гаджански из югославского города Зренянине отлично знал высшую математику в объеме программы вуза и без помощи карандаша и бумаги производил сложнейшие математические расчеты.
Проявляется ли этот дар очень рано или очень поздно, его появление всегда стихийно. Происходит молниеносное превращение. Обладатель дара иногда бывает “отсталым ” во всех других областях, но среди цифр он чувствует себя как дома и быстро достигает фантастической виртуозности.

Теоретический отдел Европейского центра ядерных исследований помимо сложных ЭВМ пользуется также услугами Вильяма Клайна, человека-компьютера.

Что же происходит с чудо-счетчиками дальше? Обычно их умение бесконечно совершенствуется вплоть до глубокой старости. Но бывает и так, что мало-помалу оно исчезает, по мере того как его обладатель получает обычное для всех детей образование. Например, Ампер стал одним из крупнейших ученых, но он потерял способность к устному счету, по мере того как расширялись его познания в области классической математики. Наоборот, Гаусс и Эйлер соединяли вплоть до смерти обе стороны своей гениальности. Интересно, что многие люди-счетчики не имели вообще никакого понятия, как они считают: “Считаем, и все! А как считаем, бог его знает”. Такие ответы неудивительны. Некоторые из счетчиков были совсем необразованными людьми. Англичанин Бакстон, счетчик-виртуоз, так никогда и не научился читать, не знал цифр. Американский негр счетчик Томас Фаллер умер неграмотным в возрасте 80 лет. Такие люди всегда очень интересовали психологов и математиков, которые старались выяснить, в чем секрет их способностей. Но о бъяснения, которые чудо-счетчики давали, пытаясь раскрыть свое умение, на первый взгляд казались странными, и даже очень.

Феноменальный дар к счету проявился у француза Лидоро в три года, когда он не умел еще ни читать, ни писать (на фото справа) Например, Урания Диамонди говорила – владеть цифрами ей помогает их цвет: 0 – белый, 1 – черный, 2 – желтый, 3 – алый, 4 – коричневый,- синий, 6 – темно-желтый, 7 – ультрамарин, 8 – серо-голубой, 9 – темно-бурый. Процесс вычисления представлялся ей в виде бесконечных симфоний цвета.

Монде и Кальбюрн ясно видели, как перед их глазами выстраиваются ряды цифр, начертанные чьей-то невидимой рукой. Их “прием” заключался в том, чтобы прочесть эту “волшебную” запись. Брат Урании, Перриклес Диамонди, говорил: “Цифры как бы скапливаются у меня в черепной коробке”.

Очень “прост” метод Иноди. Ему казалось, будто вместо него считает чей-то голос, и, пока этот внутренний голос производит вычисления, сам он либо продолжает разговаривать, либо наигрывает на флейте. Морис Дагбер производит головокружительные вычисления, играя на скрипке. Несколько лет назад во Франции, в Лилле, в присутствии авторитетного жюри из физиков, инженеров, кибернетиков, математиков и психологов Морис Дагбер вступил в спор с электронной вычислительной машиной, производящей около миллиона операций в секунду. Дагбер заявил, что признает себя побежденным лишь в том случае, если машина решит семь задач раньше, чем он десять… Дагбер решил все десять задач за 3 минуты 43 секунды, а электронная машина только за 5 минут 18 секунд.

Подобные соревнования дело непростое. Я совсем недавно проводил их в Институте кибернетики Украинской академии наук. В состязании участвовали молодой счетчик-феномен Игорь Шелушков, аспирант Горьковского политехнического института (теперь он у же преподаватель этого института и готовится защищать диссертацию) и электронная вычислительная машина “Мир”

О машине стоит сказать несколько слов. Она может решать многие системы уравнений, задачи линейного программирования, рассчитывать сетевые графики – в общем, выполнять ряд сложных математических операций. Машину ее создатели прозвали “вычислителем с высшим образованием”. Не только за то, что она запоминает 12 тысяч символов (7страниц текста) и быстро считает. В нее “от рождения” заложены основные формулы, которым нас учили в школе и вузе. Как видите, партнер серьезный. Судили поединок люди авторитетные: руководитель отдела математического программирования – профессор и его сотрудники.

Не знаю, как на состязаниях во Франции, но здесь были созданы равные условия для человека и для машины. Дело в том, что многие задачи электронный вычислитель решает быстрее человека. А есть и такие, что человеку вообще не под силу. В Институте кибернетики подобрали соответствующие задачи, определили моменты их “ввода” для человека и для машины, необходимую точность решений – до какого знака и т.д. Надо отдать должное таланту Шелушкова. Он блестяще выиграл соревнование, как и Дагбер во Франции.
В последнее время чудо-счетчики хотя и соревнуются с машинами, но все меньше используют свои способности для демонстрации их публике. Их больше прельщают практическое использование таланта и научная работа. Дагбер, например, занимается математикой, а Шелушков преподает, готовит диссертацию.

В Сиднейском университете в Индии тоже проходили соревнования человека и машины. Шакунтала Деви тоже опередила несколько вычислительных машин. Ей тоже хочется приносить практическую пользу. Она помогла индийским банкам выверить и свести миллиардные балансы, провела огромные расчеты, которые помогут при решении сложной для Индии демографической проблемы.

Некоторые чудо-счетчики подвергались научному обследованию. Иноди однажды был приглашен на заседание Французской академии наук. Отчет о заседании был дан математиком Дарбу. Ученые пришли к выводу, что Иноли использует некоторые классические приемы, которые он сам “переоткрыл”. Одна из комиссий при академии, в которую, в частности, входили известные ученые Араго, Коши, исследовала Анри Монде. По свидетельству Коши, полуграмотный сын дровосека Моде применил бином Ньютона. К подобным выводам пришла академия и при эксперименте в 1948 году с Морисом Дагбером. Ученые считают, что дар феноменального счета в том виде, в каком он наблюдается у взрослых счетчиков, является в какой-то степени даром “воспитанным” (то есть приобретенным в результате систематических упражнений). Бродя по джунглям чисел, люди-счетчики зачастую находят приемы, которые дают им возможность сокращать вычисления.
Пожалуй, единственная научно обоснованная и достаточно подробно разработанная система резкого повышения быстроты устноного счета создана была в годы второй мировой войны цюрихским профессором математики Я.Трахтенбергом. Она известна под названием “Системы быстрого счета”. История ее создания необычная. В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета.
За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность. Система Трахтенберга позволяет резко ускорить процесс выполнения операций умножения, деления, сложения, возведения в степень и извлечение корня. Как мы видим, быстрый счет – это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит ее можно изучать, ей можно следовать, ею можно овладеть.

П рочитав как-то статью о математике-артисте Арраго, сотрудник отдела труда и зарплаты Мелекесского завода кузовной арматуры, карбюраторов и вкладышей Юзеф Приходько вдруг понял, что и он может проделывать подобные номера. “Первый, кому я раскрыл свои способности, – рассказывает Юзеф, – была моя жена. Ее реакция на мое сообщение была вполне естественной – выразительно покрутила указательным пальцем у виска”. Сейчас Приходько – известный в нашей стране математик-моменталист.

Надо отметить, что Яков Перельман (1882-1942) был выдающейся личностью. Наше поколение благодарно ему за то, что именно Перельман стал родоначальником жанра научно — занимательной литературы. Это сегодня принято обо всем рассказывать популярно, весело и доходчиво. А во времена Перельмана научная литература сильно отличалась от популярной.

Перельман написал более ста книг, которые и сегодня любимы взрослыми и детьми. Эти книги содержат по-настоящему ценные знания в разных областях, они способствуют развитию творческого подхода к точным наукам и раскрывают прекрасный мир математики, физики, астрономии. Это великолепные книги «Занимательная астрономия», «Занимательная алгебра», «Занимательная геометрия», «Занимательная физика» и другие.

К нига Я. Перельмана «Быстрый счет. Тридцать простых приемов устного счета» содержит полезные и эффективные способы быстрого счета в уме.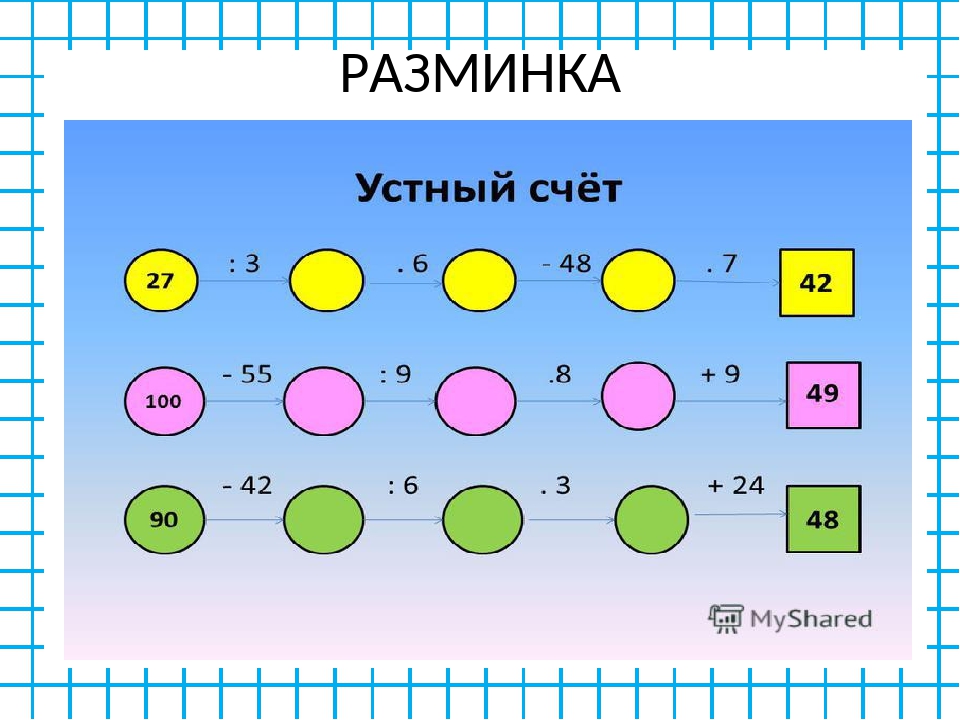 Они рассчитаны на способности обычного человека. Но если вы успешно освоите эти методы, вряд ли вас будут продолжать считать обычным человеком.

Профессор ботаники МГУ С.А. Рачинский (1833-1902) предпочел должность сельского учителя в Смоленской губернии. За время своей педагогической деятельности, Рачинский накопил огромный опыт, нашедший отражение в труде «1001 задача для умственных вычислений». Это задачник по математическим вычислениям, впервые увидевший свет в Санкт- Петербурге в 1891 году.

Просмотров работы: 1095

Приемы устного счета на уроках математики в 5

Департамент образования Администрации города Ноябрьск

муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа микрорайона Вынгапуровский»

муниципального образования город Ноябрьск

Приемы устного счета на уроках математики в 5 – 6 классах

Оденбах Е. С., учитель математики

Ноябрьск, 2018-2019 учебный год

Оглавление

Организация устного счета в 5 – 6 классах

Формы организации устного счета

Приемы устного счета

Устный счет на уроке

Карточки для устного счета

Заключение

Литература (интернет-источники)

АННОТАЦИЯ

Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день в своей жизни. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов.

Устные вычисления дают возможность не только быстро производить расчеты в уме, но и развивают память, культуру мысли, ее четкость, ясность и быстроту, сообразительность, умение отыскивать наиболее рациональные пути для решения поставленной цели, ясное понимание связи теории с практикой, уверенность в своих силах, помогает школьникам полноценно усваивать предметы физико-математического цикла.

Поэтому учителю математики надо обращать внимание на устный счет с того момента, когда учащиеся приходят к нему из начальной школы. Именно в среднем звене мы закладываем основы обучения математике наших воспитанников, раскрываем ее притягательные стороны. Хорошо развитые у учащихся навыки устного счета – одно из условий их успешного обучения в старших классах.

Умело поставленный и систематически проводимый устный счет развивает у учащихся способность быстро и безошибочно производить разнообразные устные вычисления. Нельзя не отметить, что отдельные приемы сокращенных вычислений, применяемые при устном счете, могут явиться дополнительным средством для закрепления математических знаний и алгебраических формул. Для того, чтобы учащиеся лучше осознали необходимость устных вычислений, их надо практиковать и при решении задач и примеров.

Цель данного пособия – практическая помощь учителю для организации устных упражнений, отвечающих современным требованиям.

ОРГАНИЗАЦИЯ УСТНОГО СЧЕТА В 5 – 6 КЛАССАХ

В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить в уме достаточно сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить в уме вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. Производя математические вычисления в уме, человек пользуется, по сути, теми же правилами, что и при письменных вычислениях.

Большинство учащихся испытывают затруднения при выполнении вычислений. Многие часто используют калькулятор, устно же в основном считают плохо. Приемов рациональных вычислений в учебниках очень мало, однако при сдаче ЕГЭ и ГИА использование калькулятора не разрешается, и на экзамене требуются умения и навыки хороших вычислений.

Одной из основных задач преподавания курса математики в основной школе является формирование у учащихся сознательных и прочных вычислительных навыков. О наличии у учащихся вычислительной культуры можно судить по их умению производить устные и письменные вычисления, рационально организовывать ход вычислений, убеждаться в правильности полученных результатов.

В зависимости от сложности задания на практике используются три вида вычисления: письменное, устное и письменное с промежуточными устными вычислениями. Успех в вычислениях во многом определяется степенью отработки у учащихся навыков устного счета. Устные упражнения используются как подготовительная ступень при объяснении нового материала, как иллюстрация изучаемых правил, законов, а также для закрепления и повторения изученного. В устном счете развивается память учащихся, быстрота реакции, воспитывается умение сосредоточиться, наблюдать, проявляется инициатива учащихся, потребность к самоконтролю, повышается культура вычислений.

Одним из важных этапов организации урока математики в 5-6 классах является устный счет.

Данный этап способствует развитию мыслительной деятельности учащихся. Выполнение устных упражнений развивает память, воображение, внимание, наблюдательность, умение сосредоточиться, способность воспринимать сказанное на слух, речь, точность, быстроту реакции учащихся.

Многие психологи отмечают, что устный счет способствует гармоничному развитию двух полушарий человека.

Использование устных упражнений на уроках математики в 5 – 6 классе преследует следующие цели, стоящие перед учителем при подготовке к уроку:

Повторение изученного материала; отработка умений и навыков применения знаний по определенной теме на практике.
Пропедевтика нового материала (т.е. система заданий и упражнений для подготовки к изучению нового материала).
Развитие вычислительных умений и навыков.

ФОРМЫ ОРГАНИЗАЦИИ УСТНОГО СЧЕТА

Понимая важность использования устных упражнений, учитель, работающий в 5 – 6 классе, должен не только грамотно спланировать содержание устной работы, но и форму ее проведения. Устная работа должна быть разнообразной, т.к. она направлена не только на активизацию мыслительной деятельности учащихся, на развитие интеллектуальных способностей учащихся, но и на развитие интереса к математике.

Существуют различные формы организации устной работы на уроках математики:

Беглый счет. При беглом счете преподаватель называет числа, говорит, какие действия надо над ними производить, а учащиеся говорят только ответ.
Беглый счет с последующей записью результата. Разница с предыдущим приемом заключается только в том, что если в первом случае учащиеся говорят ответ устно, то во втором они записывают его в тетрадях и показывают учителю.
Устный счет с предшествующей записью на классной доске чисел, даваемых для счета. Эта форма устных вычислений применяется как в том случае, когда числа, предложенные для счета, большие, так и в том случае, когда закрепляется какой-либо новый прием быстрых вычислений, при котором все внимание учащихся должно сосредоточиться не на числах, а на сущности самого приема.
Устный счет при решении задач. Учащиеся решают задачу либо устно, либо по написанным учителем на доске числовым данным задачи, либо для устного счета запоминают и содержание задачи, и числовые данные.

В 5, 6 классе на устные упражнения отводятся 5–7 минут урока. На уроке эти упражнения можно проводить для отработки навыков использования таблицы умножения, повторения ранее изученного материала, увеличения скорости вычислений, закрепления нового материала или для подготовки учащихся к его восприятию.

Чтобы заинтересовать учащихся, устное решение упражнений можно проводить с помощью таблиц или карточек с учетом индивидуальных особенностей школьников.

Устная работа должна быть разнообразной, т.к. она направлена не только на активизацию мыслительной деятельности учащихся, на развитие интеллектуальных способностей учащихся, но и на развитие интереса к математике.

Как организационные формы устного счета на уроках математики можно применять такие формы, как:

1. Математический диктант (5 класс).

Например:

I слагаемое 28, II слагаемое 57. Найдите сумму этих чисел.

Уменьшаемое 64, вычитаемое 46. Найдите разность этих чисел.

Число 75 увеличьте на 17.

Найдите разность 51 и 38.

Найдите сумму 43 и 49.

Число 81 уменьшите на 24.

I слагаемое 25, а второе на 14 больше. Найдите сумму этих чисел.

2. Цепочка.

Учитель просит учащихся записать число. Учитель просит изменить данное число при помощи определенного математического действия, запомнить промежуточный результат и выполнить следующее действие, предлагаемое учителем, снова запомнить результат и т.д.

На первых уроках можно разрешать учащимся писать промежуточные результаты, а в дальнейшем попробовать производить операции с промежуточными числами в уме и записать только конечный результат.

3. Круглые примеры.

Предлагается найти последний пример среди определенного числа примеров, записанных в разнобой. Учащиеся находят результат первого примера, далее им надо найти тот, который начинается с цифры, которая является результатом предыдущего примера и т.д. до тех пор, пока результат последнего примера не совпадет с начальной цифрой первого.

Данную работу можно организовать фронтально и индивидуально.

4. Ручеек.

На листочке даны примеры по количеству учащихся, сидящих на одном ряду. Решив первый пример, учащийся передает листочек сидящему за ним однокласснику. Тот должен найти ответ следующего по порядку примеру и передать листочек сидящему за ним однокласснику.

5. Лесенка.

На доске изображена лесенка примеров. Дается определенное время, за которое необходимо подняться на верхнюю ступеньку этой лесенки.

6. Расшифруй слово или фразу.

Таких заданий очень много в учебниках Л.Г. Петерсон и Г.В. Дорофеева.

Можно придумать и зашифровать тему урока или фамилию того или иного математика, ученого, которые внесли большой вклад в развитие математики.

7. Ромашка.

На доске изображены по кругу числа, а в середине или какое-то действие, или круг, разделенный на четыре или две части. В данных частях круга арифметические действия. Это задание направлено не только на отработку вычислительных навыков, но и на развитие внимания учащихся. Учитель поочередно связывает числа, расположенные по кругу, показывая на них указкой, определенными действиями из маленького круга.

8. Математический марафон.

На доске изображены примеры. Необходимо в уме быстро и правильно найти их результат и записать ответы в тетради.

Через определенное время проверить с классом данное задание и разобрать те задания, которые вызвали трудность.

9. Восстанови пример.

Учитель предлагает ученикам примеры, в которых пропущены или действия, или один из компонентов. Надо восстановить пропущенную запись.

10. Математическое лото.

Учащимся выдаются конверты с карточкой, на которой записаны примеры, расположенные в таблице, как в лото. Данные карточки можно предлагать или каждому ученику, или двум, сидящим на одной парте. Учащиеся решают примеры и закрывают ответы маленькими карточками, на которых изображены цифры, являющиеся ответами к примерам на карточке. По команде учителя ученики прекращают работу и переворачивают маленькие карточки. На большой карточке должен получиться рисунок, или какая-нибудь геометрическая фигура.

11. Найди ошибку.

Эту форму устной работы чаще всего использую при работе над единицами измерения. Предлагаем ученикам столбик равенств с метрическими величинами. Ученикам необходимо проверить правильно ли поставлены знаки равно и у себя в тетради отметить это в виде графической записи. Если ученик согласен с поставленным знаком равно, то он в тетради изображает дугу, размером в две клеточки, если же не согласен, то отрезок, длиной две клеточки.

Например:

Верно ли, что:

5 дм = 50 см 9 км 27 м = 927 м

6 мм = 60 см 65 см = 6 дм 5 см

8 км 78 м = 8780 м 369 мм = 3 см 69 мм

3 м 2 см = 302 см 973 см = 9 м 73 см

7 см 9 мм = 79 мм 5643 м = 5 км 643 м

1 дм 5 мм = 105 мм 730 дм = 73 м?

12. Оглянись назад.

Учитель предлагает ученикам определенное число и записывает его на доске, например 10,5. Далее учитель называет какое-то число меньшее или большее, чем данное. Учащиеся устно должны назвать число, которое поможет вернуться к данному числу.

13. Качели.

Это задание способствует развитию памяти учащихся. Учитель называет числа, например трехзначные. Учащиеся записывают данные числа наоборот, в обратном порядке, сначала пользуясь записями в тетради, а потом только по памяти.

14. «Числовые фокусы».

Можно в устные упражнения включать всевозможные числовые фокусы. Данные задания разнообразят урок и привнесут в него новизну. Например: «Проблема Гольдбаха». Живший в 18 веке в России математик Гольдбах открыл удивительную вещь: каждое четное число ему удавалось представить в виде суммы двух простых чисел (включая число «1»).

Задание: можно предложить 6-тиклассникам при изучении темы «Простые и составные числа» на одном уроке представить в виде суммы простых чисел первые 20 четных чисел; на втором уроке представить в виде суммы простых чисел числа от 20 до 50.

15. «Любопытные свойства натуральных чисел».

Возьмем любое число из 4-х цифр (например, 2365) и расставим их сначала в порядке возрастания (2356), затем убывания (6532). Из большего числа вычтем меньшее: 6532 – 2356 = 4176. С полученным числом проделаем то же самое: 7641 – 1467 = 6174. Интересно то, что к этому числу не более чем за 7 шагов мы приходим вышеуказанным способом от любого, взятого наугад четырехзначного числа.

3) 7641 – 1467 = 6174

Пример: 6598. Пример: 3582.

9865 – 5689 = 4176 1) 8532 – 2358 = 6174

7641 – 1467 = 6174.

Пример: 3198.

9831 – 1389 =8442

8442 – 2448 = 5994

9954 – 4599 = 5355

5553 – 3555 = 1998

9981 – 1899 = 8082

8820 – 288 = 8532

8532 – 2358 = 6174

ПРИЕМЫ УСТНОГО СЧЕТА

При устных вычислениях мысль учащихся все время работает над вопросом: « Какой прием лучше применить в том или другом случае, чтобы как можно быстрее производить требуемые вычисления? »

Существует определенный набор простейших арифметических правил и закономерностей, которые не только нужно знать для устного счета, но и постоянно держать в голове, чтобы в нужный момент оперативно применить самый эффективный алгоритм. Для этого необходимо довести их использование до автоматизма, закрепить в машинальной памяти, чтобы от решения самых простых примеров успешно перейти к более сложным арифметическим действиям. Вот основные алгоритмы, которые нужно знать, помнить и применять мгновенно, автоматически:

1. Вычитание 7, 8, 9.

Чтобы вычесть 9 из любого числа, нужно вычесть из него 10 и прибавить 1. Чтобы вычесть 8 из любого числа, нужно вычесть из него 10 и прибавить 2. Чтобы вычесть 7 из любого числа, нужно вычесть из него 10 и прибавить 3. Если обычно вы считаете по-другому, то для лучшего результата вам нужно привыкнуть к этому новому способу.

2. Умножение на 9

Быстро умножить любое число на 9 можно при помощи пальцев рук.

Хитрость приёма такова: Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе. Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке. Оставшееся количество пальцев слева будет соответствовать десяткам, справа – единицам. В нашем примере – 4 пальца слева и 5 справа. Ответ: 45.

3. Деление и умножение на 4 и 8.

Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно.

Например, 46*4=46*2*2 =92*2= 184.

4. Умножение на 5.

Умножать на 5 очень просто. Умножение на 5, и деление на 2 – это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте на 5, поделив число на 2 и умножив его на 10.

5. Умножение на 25.

Умножение на 25 соответствует делению на 4 (с последующим умножением на 100). Так 120*25 = 120/4*100=30*100=3000.

6. Умножение на однозначные числа.

Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать двух- или трехзначное число поразрядно.

Например, умножим 83*7. Для этого сначала умножим 8 на 7 (и допишем ноль, так как 8 – разряд десятков), и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7 +3*7= 560+21=581.

Возьмем более сложный пример: 236*3.

Итак, умножаем сложное число на 3 по разрядно: 200*3+30*3+6*3=600+90+18=708.

7. Раскладка на десятки и единицы.

Способ заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 +3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия:

1. Сначала умножаются десятки друг на друга.
2. Потом складываются 2 произведения единиц на десятки.
3. Затем прибавляется произведение единиц.

Схематично это можно описать так:

– Первое действие: 60*80 = 4800 – запоминаем
– Второе действие: 60*5+3*80 = 540 – запоминаем
– Третье действие: (4800+540)+3*5= 5355 – ответ.

8. Мысленная визуализация умножения в столбик.

56*67 – посчитаем в столбик. Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа.

Но его можно упростить:
Первое действие: 56*7 = 350+42=392
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752

9. Умножение на 11.

Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры.

Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.

Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10. Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа. Например: 324 * 11=3(3+2)(2+4)4=3564.

10. Опорное число.

Посмотрим на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8.

Для того, чтобы узнать их произведение, нужно совершить следующие операции:

15*18

1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.

11. Опорное число при умножении чисел до 100. Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. При умножении чисел до 100 опорными числами удобно использовать все числа кратные 10, а особенно 10, 20, 50 и 100.

Методика использования опорного числа зависит от того, являются ли множители больше или меньше опорного числа.

А) Оба числа меньше опорного (под опорным). Допустим, мы хотим умножить 48 на 47. Эти числа находятся достаточно близко к числу 50, а следовательно удобно использовать 50 в качестве опорного числа.
Чтобы умножить 48 на 47, используя опорное число 50, нужно:

47*48

1. Из 47 вычесть столько, сколько не хватает 48 до 50, то есть 2. Получается 45 (или из 48 вычесть 3 – это всегда одно и то же)
2. Дальше 45 умножаем на 50 = 2250
3. Затем прибавляем 2*3 к этому результату – 2 256

50 (опорное число)

47 48

3(50-47) 2(50-48)

(47-2)*50+2*3=2250+6=2256

Если числа меньше опорного, то из первого множителя вычитаем разность между опорным числом и вторым множителем.

Б) Если числа больше опорного, то к первому множителю прибавляем разность опорного числа и второго множителя .

50(опорное число)

51 63

1 13

(51+13)*50+(13*1)=3200+13=3213

В) Одно число под опорным, а другое над. Третий случай использования опорного числа – когда одно число больше опорного, а другое меньше. Такие примеры решаются не сложнее, чем предыдущие. Меньший множитель увеличиваем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей. Или больший множитель уменьшаем на разность между вторым множителем и опорным числом, результат умножаем на опорное число и вычитаем произведение разностей опорного числа и множителей.

50(опорное число)

45 52

5(50-45) 2(52-50)

(52-5)*50-5*2=47*50-10=2340 или (45+2)*50-5*2=47*50-10=2340

При умножении двузначных чисел из разных десятков в качестве опорного числа удобнее брать круглое число , которое больше большего множителя.

27*89

90(опорное число)

27 89

63 (90-27) 1 (90-89)

(89-63)*90+63*1=2340+63=2403

Таким образом, с помощью использования одного опорного числа можно умножать большую комбинацию двузначных чисел.

КАРТОЧКА ДЛЯ УЧАЩИХСЯ

Опорное число 100

Опорное число 100

Решить пример1: 96×97=

Посмотрим:

– сколько единиц не хватает до 100 у первого числа? 4 единицы,

– сколько единиц не хватает до 100 у второго числа? 3 единицы.

Запишем эти числа под соответствующими числами и вычитаем накрест:

96 × 97= 9312

96-3=93 или 97-4=93 это первая часть ответа
Перемножаем числа в кружках: 4×3=12 это вторая часть ответа (двузначное число)

Пример 2:

92×99=9108

92-1=91 и 8×1=8, но при умножении получается 8 поэтому записываем 08

Примеры для самостоятельного решения:

91×92=

91×93=

91×94=

91×95=

91×96=

91×97=

91×98=

91×99=

92×92=

92×93=

92×94=

92×95=

92×96=

92×97=

92×98=

92×99=

93×92=

93×94=

93×95=

93×96=

93×97=

93×98=

93×99=

94×94=

94×95=

94×96=

94×97=

94×98=

94×99=

95×95=

95×96=

95×97=

95×98=

95×99=

96×96=

96×98=

96×99=

96×97=

97×97=

97×98=

97×99=

98×98=

98×99=

99×99=

КАРТОЧКА ДЛЯ УЧАЩИХСЯ

Умножение чисел от 10 до 20

Опорное число 10

Решить пример1 13×14=

Посмотрим на сколько единиц первое число больше опорного числа? на 3 единицы,

на сколько единиц второе число больше опорного числа? на 4 единицы. Запишем эти числа над соответствующими числами со знаками «+» (так как больше) и складываем накрест накрест:

13 × 14= 182

13-+4=17 или 14+3=17
Умножаем полученное число на опорное число 10 17 × 10=170 (это промежуточный результат)
Перемножаем числа в кружках: 4×3=12 и прибавим к промежуточному результату

170+12=182 – это ответ

Примеры для самостоятельного решения:

12×18=

12×15=

14×14=

16×14=

15×15=

14×17=

18×13=

17×16=

13×19=

16×18=

19×16=

13×12=

УСТНЫЙ СЧЕТ НА УРОКЕ

Устный счет требует от учителя умелого подхода к индивидуальным особенностям каждого учащегося. Необходимо иметь ввиду, что одни учащиеся при устном счете считают правильно и довольно быстро; другие быстро, но часто ошибаются; третьи хотя и верно, но довольно медленно считают; четвертые считают совсем плохо и требуют от учителя индивидуальной помощи.

Устный счет может практиковаться почти на каждом уроке математики. В зависимости от темы и материалам урока, они могут ставиться учителем в начале урока, середине или в конце. В начале урока устный счет удобно применять тогда, когда нужно подготовить почву либо для изложения нового материала, либо для закрепления пройденных навыков. В середине урока устный счет лучше всего проводить тогда, когда он может быть связан с проходимым или пройденным на уроке материалом. В конце урока устный счет применяется обычно независимо от темы урока в специально оставленное для этой цели время (5-10 минут) как для упражнений

в применении различных приемов быстрых вычислений, которыми учащиеся уже владеют, так и для объяснения учителем новых приемов.

Скорость вычисления как при беглом счете, так при устном решении задач всецело зависит от степени трудности примеров, от степени подготовленности детей, от их умения пользоваться приемами быстрых вычислений, от умения преподавателя вести эту работу. Нельзя применять много различных видов упражнений на одном уроке, так как это утомляет учащихся и снижает их внимание. Практику устного счета надо развивать постоянно. Вообще надо сказать, что умело поставленный устный счет является для детей нередко чрезвычайно интересной работой, своего рода гимнастикой ума, игрой. Для развития у учащихся умения быстро производить устные вычисления учитель должен тщательно рассматривать с детьми некоторые свойства чисел, их сочетания, способы разложения и т. д. Это обеспечит всю последующую технику быстрых вычислений.

1. Необходимо, чтобы таблицы сложения , вычитания, умножения и деления были усвоены с детьми в совершенстве.

2. Надо, чтобы дети легко и быстро находили дополнения чисел до любого большего круглого числа (т. е. кратные 10)

3. Надо научить учащихся быстро делить и умножать на 2.

4. Учащиеся должны уметь разложить любые числа по разрядам, т.е. представить их в виде суммы.

5. Ученики обязаны хорошо знать основные законы четырех арифметических действий, зависимость между компонентами и результатами действий.

6. Представить число в виде разности двух чисел.

7. Использовать при вычислениях возможность замены одних действий другими действиями.

8. Знать значение квадратов чисел до 30.

Приступая к устным вычислениям, учитель должен начинать с более легких примеров и приемов, которые по мере их усвоения усложняются. Устный счет – очень нужный этап урока. Именно на этом этапе появляется настрой на весь урок. Устный опрос украшает урок, делает его логически стройным и интересным, способным лучшему усвоению программного материала. Вычислять быстро, подчас на ходу – это требование времени. Числа окружают нас повсюду, а выполнение арифметических действий над ними приводит к результату, на основании которого мы принимаем то или иное решение. Понятно, что без вычислений не обойтись как в повседневной жизни, так и во время учебы в школе. Этим, кстати, объясняется столь стремительное развитие удобных калькуляторов. Тем не менее, калькулятор не может обеспечить ответ на все возникающие вопросы. Он не всегда имеется под рукой и бывает достаточно определить лишь примерный результат.

Применение различных видов устной работы в основном зависит от творчества учителя.

Какой бы вид работы не выбрал учитель на уроке надо понимать, что устные упражнения способствуют не только развитию математических способностей учащихся, но и развитию вычислительных навыков. Как не странно, учащиеся, которые хорошо считают, порой лучше и быстрее справляются с заданиями по математике, чем даже те ученики, которые по природе своей имеют лучшие математические способности.

Применяя в организации устной работы в 5-6 классе задания вычислительного характера, учитель тем самым экономит время на вычисления при решении задач, уравнений, неравенств.

Помимо вышеперечисленных алгоритмов существует еще ряд приемов устного счета, которые полезно показать учащимся, и использовать их при решении заданий, требующих всевозможных арифметических вычислений.

1. «Промежуточное» приведение к «круглым» числам.

Пример: 187 + 198.

– одно из слагаемых необходимо привести к «круглому» числу десятков, сотен, тысяч и т.д.;

– выполнить действие сложения;

– учесть поправку.

187 + 198 = 200 + 187 -2 = 387 – 2=385.

2. Способ «корневых» чисел.

34 + 37 + 36 + 34 + 38 + 39 = 30*6 + (4 + 7 +6 +8 +9) = 180 + 34 = 214

34 + 33 + 35 +3 4 + 33 + 34 = 34*7 + (3 + 0 -1 + 1 – 1 +0 ) = 238 + 2 = 240

3. Использование изменения порядка счета.

При сложении чисел нередко бывает полезно складывать их, начиная со старшего разряда: 5879 + 654 = 9533

4. Использование дополнения числа для упрощения вычитания из числа.

700 – 238 = 700 – (300 – 2) = 400 + 2 = 402

5. Переход от вычитания к сложению.

3000 – 1264 = (3000 + 736) – 2000 = 1736

6. Приемы умножения чисел на 9, 99, 999.

А) 56 * 9 = 56 * 10 – 56 = 560 – 56 = 504

Б) 68 * 99 = 68 * 100 – 68 = 6800 – 68 = 6732

В) 73 * 999 = 73 * 1000 – 73 = 73000 – 73 = 72927

7. Приемы умножения на 111.

Пример: 359 * 111=…9

На последнем месте в результате пишем 9, т.к. 9 * 1 = 9.

Слева от 9 записываем цифру, которая получилась в результате сложения двух последних цифр в числе 359. Это 5 + 9 = 14, т.е. пишем цифру 4.

Затем находят суммы цифр, взятых по три и прибавляют 1 (если есть переход через разряд).

(3 + 5 + 9) + 1 = 18

Перед цифрой 4 пишем цифру 8.

Затем находим сумму двух последних цифр: (3 + 5) + 1 = 9.

Перед цифрой 8 пишем 9.

На первом месте запишем цифру 3, т.к. она первая цифра в данном множителе.

Итак, 359 * 11 = 39849.

Пример: 2356 * 111 = …6

5 + 6 = 11, тогда записываем …16

(3 + 5 + 6) + 1 = 15, тогда записываем …516

(2 + 3 + 5) + 1 = 11, тогда записываем …1516

(2 + 3) + 1 = 6, тогда записываем …61516

Итак, 2356 * 111 = 261516.

Пример: 895123 * 111 = …3

2 + 3 = 5 …53

1 + 2 + 3 = 6 …653

5 + 1 + 2 = 8 …8553

9 + 5 + 1 = 15 …58553

(8 + 9 + 5) + 1 = 23 ….358553

(8 + 9) + 2 = 19 …9358553

8 + 1 = 9

Итак, 895123 * 111 = 99358653

7. Умножение крестиком.

Данный прием применялся еще в древней Индии и назывался «молниеносным».

Пример: 54 * 26.

Умножаем 4 на 6, получаем 24, пишем на месте единиц 4, а 2 запоминаем.

5 умножаем на 6, получаем 30 и прибавляем цифру, которую запомнили, т.е. 2. Получаем 32. Запомним цифру 32.

2 умножаем на 4, получаем 8 и прибавляем 32,получаем 40. Цифру 0 пишем перед 4.

2 умножаем на 5 и прибавляем 4, получаем 14.

Пишем 14 перед всеми записанными цифрами.

Получили число 1404.

Пример: 67 * 39 .

7 * 9 = 63 …3

6 * 9 + 6 = 60

3 * 7 + 60 = 81 …1

3 * 6 + 8 = 26

Итак, 67 * 39 = 2613

Пример: 48 * 67.

8 * 7 = 56 …6

7 * 4 + 5 = 33

6 * 8 + 33 = 81 …16

6 * 4 + 8 = 32

Итак, 48 * 67 = 3216

8. Способ умножения путем изменения сомножителей.

Если один из сомножителей уменьшить в несколько раз, а другой увеличить во столько же раз, итог произведения не изменится, однако умножение может стать проще и быстрее.

Примеры: 24 * 25 = (24:4) * (25 * 4) = 6 * 100 = 600

17 * 12 = (17 * 4) * (12 : 4) = 68 * 3 = 204

28 * 55 = (28 : 2) * ( 55 * 2) = 14 * 110 = 1540

256 *5 = (256 : 2) * ( 5 * 2) = 128 * 10 = 1280

48 * 25 = (48 : 4) * (25 * 4) = 12 * 100 = 1200

64 * 125 = (64 : 8) * (125 * 8) = 8 * 1000 = 8000

9. Способ дополнения для умножения чисел, близких к .

94 * 97 = (100 – 6 – 3) * 100 + 6 *3 = 91 * 100 + 18 = 9118

98 * 96 = (100 – 2 – 4) * 100 + 2 * 4 = 94 * 100 + 8 = 9408

89 * 78 = (100 – 11 – 22) * 100 + 11 * 22 = 67 * 100 + 242 = 6942

113 * 108 = ( 100 + 13 + 8) * 100 + 13 * 8 = 121 * 100 + 104 = 12100 + 104 = 12204

106 * 98 = (100 + 6 -2) * 100 – 6 * 2 = 10400 – 12 = 10388

115 * 91 = (100 +15 – 9) * 100 – 15 * 9 = 10600 – 135 = 10465

108 * 112 = (100 + 8 + 12) * 100 + 8 * 12 = 12000 + 96 = 12096

1002 * 993 = (1000 + 2 – 7) * 1000 -2 * 7 = 995000 – 14 = 99 4986

1012 * 1005 = ( 1000 + 12 + 5) * 1000 + 12 * 5 = 1017000 + 60 = 107060

10. Способ вычитания дополнения при умножении чисел.

Пример: 196 * 198

Из какого-нибудь сомножителя вычитаем дополнение второго сомножителя.

198 – 4 = 194 или 196 – 2 = 194

Полученный результат умножаем на 2, т.к. оба числа дополняли до 200.

194 * 2 = 388

К полученному результату алгебраически (с учетом знака) и разрядности прибавляем произведение дополнений.

198 * 196 = 388 * 100 + 2 * 4 = 38800 + 8 = 38808

Пример: 65 * 78.

Округляем до 80.

78 – 15 = 63

63 * 8 = 504

65 * 78 = 504 * 10 + 15 * 2 = 5040 + 30 = 5070

Пример: 87 * 73.

Округляем до 80.

87 – 7 = 80

80 * 8 = 640

87 * 73 = 640 * 10 – 7 * 7 = 6400 – 49 = 6351

11. Признак делимости на 11.

Если сумма данного многозначного числа через одну равна сумме остальных цифр через одну или разность этих сумм делится на 11, то и данное число делится на 11.

Если суммы цифр через одну данного числа или их разность не делится на 11, то данное число не делится на 11.

Пример: Делится ли 390137 на 11?

Решение: 1) 3 + 0 + 3 = 6

2)9 + 1 + 7 = 17

3) 17 – 6 = 11

4) 11 : 11, значит и число 390137 делится на 11.

Пример: Делится ли 6880357 на 11?

Решение: 1) 6 + 8 + 3 + 7 = 24

2)8 + 0 + 5 = 13

3) 24 – 13 = 11

4) 11 : 11, значит данное число делится на 11.

Пример: Делится ли 985621 на 11?

Решение: 1) 9 + 5 + 2 = 16

2)8 + 6 + 1 = 15

3) 16 – 15 = 1

4) 1 не делится на 11, значит и число 985621 не делится на 11.

12. Возведение в квадрат чисел, оканчивающихся на 5.

Пример: 65 * 65 = 4225

6 дес. * 7 дес. = 42 с.

5 * 5 = 25

42 с. + 25 = 4225

Пример: 95 * 95 = 9025

9 дес. * 10 дес. = 90 с.

5 * 5 = 25

90 с. + 25 = 9025

Пример: 385 * 385 = 148225

38 дес. * 39 дес. = 1482 с.

5 * 5 = 25

1482 с. + 25 = 148225

Пример: 685 * 685 =469225

68 дес. * 69 дес. = 4692 с.

4692** + 25 = 469225

Пример: 7435 * 7435

743 дес. * 744 дес. = 552792 с.

552792 с. + 25 = 55279225

13. Умножение трехзначных чисел, оканчивающихся на 25.

Пример: 425 * 425.

В конце числа пишем 625.

Число сотен в числе (4) умножаем на 5. Получаем 20. Перед числом 625 пишем последнюю цифру числа 20, а цифру 2 запоминаем. (0625)

Число сотен данного числа возводим в квадрат, т.е. . Получаем 16. К 16 прибавляем ту цифру, которую мы запомнили, т.е. 2. Получаем 18.

Полученную цифру 18 припишем перед 0625.

Получили 180625.

Пример: 725 * 725.

В конце числа пишем 625.

7 * 5 = 35.

5625

49 + 3 = 52

Получили 525625

КАРТОЧКИ ДЛЯ УСТНОГО СЧЕТА

Развивая навыки устного счёта у учеников, можно использовать особые серии карточек. В каждой серии карточек есть разные упражнения с использованием нескольких приёмов устного счёта. В результате складывается некоторая система тренировочных упражнений для учеников 5-6 классов. Эта система даёт возможность повторить изученные раньше приёмы устного счёта и закрепление их. Эта система не забирает много времени на уроке, даёт возможность ученикам контролировать себя, вызывает интерес к математике, дисциплинирует учеников, развивает внимание и сосредоточенность.

В предложенной системе устных вычислений составляется замкнутый круг числовых вопросов и ответов: числовой ответ последней карточки даёт число, которое стоит на первой карточке. Можно брать любую карточку, начинать проводить вычисления – всё одно получим замкнутый круг числовых вопросов и ответов.

Если ученик выполнил вычисления неправильно, он не найдёт ответ ни на одной из этих карточек. Поэтому, система даёт ученикам возможность проводить самоконтроль. Принцип составления серии карточек заключается в следующем:

1) Учитель составляет примеры таким образом, что ответ первой карточки является компонентом второй; ответ второй – третьей и т. д.

2) Можно составлять самостоятельно серию из 6, 8, 10 и большего количества карточек, учитывая силы учеников и их знания.

3) Карточки нужно составлять равноценные по характеру примеров и сложности, чтобы дать ученикам возможность одновременно закончить работу по карточкам.

4) Для примеров на карточках можно использовать разные приёмы устного счёта или сосредоточить внимание учеников на одном – двух.

5) Важно не допускать одинаковых ответов, так как не будет замкнутого устного счёта, ученик не сможет проконтролировать себя – всегда всегда будут оставаться лишние карточки.

6) Кроме прямых действий, карточки для устного счёта могут быть усложнены обратными действиями, например, когда известно делимое и частное, нужно найти делитель. Принцип составления таких карточек аналогичный первому.

7) Для удобства карточки изготовляют небольших размеров и сохраняют в конвертах. Можно использовать компьютер с проектором или интерактивная доска. Серии карточек обязательно нужно номеровать. Это даёт возможность учителю следить за тем, чтобы ученик во время работы сразу получал карточки других номеров с соответствующими приёмами устного счёта.

8) Карточки можно использовать для индивидуальной и домашней работы.

9) На работу в классе можно использовать 3-5-7 минут, чтобы не перезагружать учеников.

Познакомить учеников с правилами устного счёта по карточкам необходимо провести по образцу одной серии. Ученики понимают и усваивают с первого разу.

Например, возьмём серию карточек на вычисление с десятичными дробями, которая состоит из 12 штук. Все карточки прикрепляются ( в любом порядке) на классной доске с обозначением мелом номер карточки.(можно использовать таблицу и т.п.)

Пусть карточки расположены на доске так:

3,7 + 1,4 =

III

5 – 3,7 =

2,1 + 1,4 =

13 ∙ 0,01 =

0,1 + 3,6 =

VII

5,1 : 0,3 =

VIII

3,5 : 0,7 =

1,5 + 2,4 =

1,3 : 13 =

17 – 15,5 =

XII

0,13 + 1,97 =

По желанию ученика берём любую карточку, например V. Эту карточку берём из ряда, прикрепляем на доске отдельно. Один из учеников читает пример 13 ∙ 0,01 = … .

Ответ ученики держат в уме (про это нужно детям говорить отдельно), ищут её в ряде карточек и находят её в карточке XII. Ответ (0,13) называется, карточка XII вынимается из ряда и прикрепляется выше карточки V, т.е. карточка V будет находиться при решении примеров внизу.

Далее появляется новый пример: 0,13 + 1,97 = … . Ученики читают его, ответ держат в голове, ищут её среди карточек, находят в карточке IV. Ответ (2,1) называется , карточка IV вынимается из ряда и прикрепляют выше V и XII.

Далее имеем новый пример: 2,1 + 1,4 = … . Ученики читают его, ответ держат в уме, находят её на карточке VIII. Ответ (3,5) называется, карточка вынимается из ряда, прикрепляется выше предыдущих. Так ведётся счёт до последней карточки:

III. 5 – 3,7 = ; X. 1,3 : 13 =; VI. 0,1 + 3,6 =; II. 3,7 + 1,4 =; VII. 5,1 : 0,3 =; XI. 17 – 15,5 =; IX. 1,5 + 2,4 =; I. 3,9 : 0,3 = . Все карточки взятые из рядов прикреплены в ряд, одна выше другой и образуют ряд. Читаем последний пример: 3,9 : 0,3 = . Ученик даёт ответ 13. Это т ответ – число13 – является ответом первой карточки внизу: 13 ∙ 0,01 =. Карточку берём снизу, показываем ученикам. Таким образом, получили замкнутый круговой устный счёт.

После того как ученики научились пользоваться карточками, можно их раздавать в конвертах с сериями примеров для самостоятельной работы.

А. Серия карточек на десятичные дроби.

3,35 + 0,65 =

4 – 1,45 =

2,55 : 0,5 =

5,1 ∙ 2 =

20.4 – 1,11 =

10,2 ∙ 2 =

№2

5 – 3,7 =

1,3 ∙ 5 =

14.4 : 9 =

1,6 ∙ 10 =

16 – 13,9 =

6,5 + 7,9 =

№3

15 – 12,5 =

2,5 ∙ 10 =

25 – 24,1 =

0,9 : 10 =

0,09 + 1,61 =

№4

0,04 + 0,68 =

0,72 : 0,3 =

2,4 + 15,6 =

№5

0,5 + 2,9 =

3,4 : 0.17 =

20 – 15,4 =

4,6 + 5,4 =

10 – 9,8 =

№6

4 ∙ 0,5 =

2 + 6,8 =

8,8 – 4,05 =

4,75 : 0,25 =

19 – 18,9 =

0,1 + 0.02 =

№7

3 – 2,25 =

0,75 : 0,5 =

1,5 ∙ 3 =

4,5 + 5,5 =

10 ∙ 1,8 =

18 – 15,65 =

2.35 + 1,25 =

№8

4 – 1,75 =

2,25 : 0,9 =

2,5 + 2,6 =

5,1 ∙ 0,1 =

0,51 + 0.09 =

0,6 ∙ 20 =

12 – 7,2 =

№9

0,8 : 0,4 =

2 – 0,6 =

1,4 ∙ 3 =

4,2 + 2,6 =

6,8 ∙ 0,1 =

0,68 – 0.41 =

№10

100 – 75,5 =

24,5 ∙ 0,1 =

2,45 + 5,65 =

8,1 : 0,9 =

9 – 7,5 =

№11

1,3 ∙ 0,2 =

0,26 + 0,64 =

0,9 : 0,15 =

6 ∙ 0,1 =

0,6 – 0,05 =

0,55 + 1,9 =

№12

2,1 – 0,5 =

1,6 ∙ 9 =

14,4 + 7,5 =

21,9 : 0,3 =

7,3 – 4,5 =

2,8 ∙ 0,1 =

0,28 + 14,42 =

№13

50 ∙ 0,24 =

12 + 5,1 =

17,1 ∙ 0,1=

1,71 : 0,9 =

1,9 – 0,02 =

1,88 – 0,19 =

№14

6 – 4,9 =

1,1 ∙ 0,1 =

0,11 + 1,9 =

2,01 : 0,3 =

6,7 ∙ 2 =

13,4 – 10,5 =

№15

1,2 ∙ 0,25 =

0,3 ∙ 3,15 =

0,945 : 0,9 =

1,05 + 0,85 =

1,9 : 0,1 =

19 – 16,82 =

№16

19,5 + 6,6 =

26,1 +0,5 =

29 – 11,5 =

№17

7 + 12,8 =

19,8 ∙ 0,1 =

1,98 + 4,42 =

6,4 ∙ 0,3 =

1,92 : 0,16 =

12 – 1,5 =

№18

6,5 ∙ 0,1 =

0,65 + 8,1 =

8,75 : 2,5 =

3,5 ∙ 0,3 =

1,05 – 0,9 =

0,15 + 19,45 =

№19

2 ∙ 0,15 =

0,3 + 0,8 =

1,1 : 0,1 =

11 – 5,45 =

5,55 + 1,06 =

6,61 – 6,47 =

№20

16 : 10 =

1,6 – 1,2 =

0,4 ∙ 0,7 =

0,28 + 9,82 =

10,1 – 4,7 =

5,4 ∙ 0,1 =

0,54 + 5,86 =

Б. Серия карточек на десятичные дроби на нахождение неизвестного компонента

? + 0,65 = 4

? – 1,45 = 2,25

? : 0,5 = 5,1

? ∙ 2 = 10,2

? – 11,1 = 9,3

? ∙ 2 = 20,4

№2

? : 3,7 = 1,3

? ∙ 5 = 6,5

? + 7,9 =14,4

? : 9 =1,6

? ∙ 10 =16

? – 13,9 = 2,1

№3

0,4 = 15

? – 12,5 = 2,5

?∙ 10 = 25

? – 24,1 = 0,9

?: 10 = 16

? -13,9 = 2,1

№4

? + 0,68 = 0,72

? : 0,3 = 2,4

? + 15,6 = 18

№5

?+ 2,9 = 3,4

? : 0,17 = 20

? – 15,4 = 4,6

? + 5,4 = 10

? – 9,8 0,2

№6

0,3 = 4

?∙0,5 = 2

? + 6,8 = 8,8

? – 4,05 = 4,75

?:0,25 = 19

? – 18,9 = 0,1

? + 0,02 = 0,12

№7

1,2 = 4

? – 1,75 = 2,25

? : 0,9 = 2,5

? + 2,6 = 5,1

? ∙ 0,1 = 0,51

? + 0,09 = 0,6

? ∙ 20 = 12

? – 7,2 = 4,8

№8

1,2 = 3

? – 2,25 = 0,75

? : 0,5 = 1,5

? ∙ 3 = 4,5

? + 5,5 = 10

?∙ 1,8 = 18

? – 15,65 = 2,35

? + 1,25 = 3,6

№9

? : 0,4 = 2

? – 0,6 = 1,4

? ∙ 3 = 4,2

? + 2,6 = 6,8

? ∙ 0,1 = 0,68

? – 0,41 = 0,27

№10

? – 75,5 = 24,5

? ∙ 0,1= 2,45

? + 5,65 = 8,1

? : 0,9 = 9

? – 7,5 = 1,5

№11

? ∙ 0,2 = 0,26

? + 0,64 = 0,9

? : 0,15 =6

? ∙ 0,1 = 0,6

? – 0,05 = 0,55

? + 1,9 = 2,45

№12

? – 0,5 = 1,6

? ∙ 9 = 1,6

? + 7.5 = 21,9

? : 3 = 7,3

? – 4,5 = 2,8

?∙ 0,1 = 0,28

?+ 14,42 = 14,7

№13

? ∙ 0,24 = 12

? + 5,1 = 17,1

? ∙ 0,1 = 1,71

? : 0,9 = 1,9

? – 0,02 = 1,88

? – 0,91 = 1,69

№14

? – 4,9 = 1,1

? ∙ 0,1 = 0,11

? + 1,9 = 2,01

? : 0,3 = 6,7

? ∙ 2 = 13,4

? – 10,5 = 2,9

№15

? ∙ 0,25 = 0,3

? + 9,15 = 9,45

? : 9 = 1,05

? + 0,85 = 1,9

? ∙ 10 = 19

? – 16,82 = 2,18

№16

? + 6,6 = 26,1

? : 0,9 = 29

? – 11,5 = 17,5

№17

? + 12,8 = 19,8

? ∙ 0,1 = 1,98

? + 4,42 = 6,4

? ∙ 0,3 = 1,92

? : 0,16 = 12

? – 1,5 = 10,5

№18

? ∙ 0,1 = 0,65

? + 8,1 = 8,75

? : 2,5 = 3,5

? ∙ 0,3 = 1,05

? – 0,9 = 0,15

? + 19,45 = 19,6

№19

? ∙ 0,15 = 0,3

? + 0,8 = 1,1

? : 0,1 = 11

? – 5,45 = 5,55

? + 1,06 = 6,61

? – 6,47 = 0,14

№20

? : 10 = 1,6

? – 1,2 = 0,4

? ∙ 0,7 = 0,28

? + 9,82 = 10

? – 4,7 = 5,4

? ∙ 0,1 = 0,54

? + 5, 86 = 6,4

В. Серия карточек на обыкновенные дроби.

№1

: =

+ =

№2

– =

: =

∙ 9 =

№3

1 : =

– =

Г. Серия карточек на нахождение неизвестного компонента с обыкновенными дробями

№1

? ∙ =

? : =

? + =

№2

? – =

? : =

? ∙ 9 = 1

№3

? ∙ =

? – =

Д.Серия карточек на проценты.

№1

ЗАКЛЮЧЕНИЕ

Чтобы научиться быстро считать в уме, нужна практика, нет волшебных методик, чтобы с первого раза начать быстро считать в голове, необходимо постоянно тренировать свой мозг и заставлять его быстро работать и считать.

Как и все способы вычислений, методы быстрого счета имеют свои достоинства и недостатки:

ПЛЮСЫ: С помощью различных методов быстрых вычислений даже самый малообразованный человек может считать. Способы быстрого счета могут помочь избавиться от сложного действия, путем замены его на несколько более простых.
Способы быстрого счета полезны в ситуациях, когда нельзя воспользоваться умножением в столбик. Способы быстрого счета позволяют сократить время вычислений. Устный счет развивает умственную деятельность, что помогает быстрее ориентироваться в сложных жизненных ситуациях. Техника устного счета делает процесс вычислений более увлекательным и интересным.

МИНУСЫ: Зачастую, решать пример, пользуясь способами быстрого счета, оказывается дольше, чем просто перемножать в столбик, так как приходится выполнять большее количество действий, каждое из которых проще первоначального.
Бывают ситуации, когда учащийся от волнения или еще чего-то забывает способы быстрого счета или вовсе – путается в них; в таких случаях ответ получается неправильным, а способы являются фактически бесполезными.
Не для всех случаев разработаны способы быстрого счета. Вычисляя с использованием техники быстрого счета, нужно держать множество ответов в голове, в чем можно запутаться и прийти к ошибочному результату.

Несомненно, практика играет важнейшую роль в развитии любых способностей. Но навык устного счета не опирается на один лишь опыт. Это доказывают люди, которые способны считать в уме сложные примеры. Например, такие люди могут умножать и делить трехзначные числа, совершать арифметические операции, которые не каждый человек и в столбик сможет посчитать. Что же необходимо знать и уметь обычному человеку, чтобы овладеть такой феноменальной способностью? На сегодняшний день существуют различные методики, помогающие научиться быстро считать в уме.

Изучив многие подходы к обучению навыку считать устно, можно выделить 3 основных составляющих данного навыка:

1. Способности. Способность концентрировать внимание и умение удерживать в краткосрочной памяти несколько вещей одновременно. Предрасположенность к математике и логическому мышлению.

2. Алгоритмы. Знание специальных алгоритмов и умение оперативно подобрать нужный, максимально эффективный алгоритм в каждой конкретной ситуации.

3. Тренировка и опыт, значение которых для любого навыка никто не отменял. Постоянные тренировки и постепенное усложнение решаемых задач и упражнения позволят вам улучшить скорость и качество устного счета. Нужно отметить, что третий фактор имеет ключевое значение. Не обладая необходимым опытом, вы не сможете удивить окружающих быстрым счетом, даже если вы знаете самый удобный алгоритм. Однако не стоит недооценивать важность первых двух составляющих, поскольку имея в своем арсенале способности и набор нужных алгоритмов, вы сможете удивить даже самого опытного «счетовода», при условии, что вы тренировались одинаковое время.

ЛИТЕРАТУРА

(ИНТЕРНЕТ-ИСТОЧНИКИ)

1. https://anisim.org/articles/priemy-bystrogo-scheta-bez-kalkulyatora/

2. https://1001sposob.ru/bystryy-schet-v-ume/.html

3. http://1obuchenie.com/kak-nauchitsya-bystro-schitat-v-ume.html

4.https://infourok.ru/priemi-ustnogo-scheta-na-urokah-matematiki-klassah-3730651.html

5. https://portalpedagoga.ru/servisy/publik/publ?id=37891

6.https://nsportal.ru/shkola/matematika/library/2018/11/08/nekotorye-priyomy-ustnogo-schyota-na-urokah-matematiki-v-5-6

17 фантастических идей для обучения механическому счету – раннее обучение

Один из основных навыков, лежащих в основе раннего математика, это способность механически считать. Механический подсчет – это просто произнесение чисел по порядку, обычно начиная с единицы, например 1,2,3,4,5 и т. Д. Это не значит подсчет предметов или подсчет действий, хотя это связано с этими навыки и умения. Это просто означает произнесение чисел по порядку, ни с чем не связанное.

Как научить механическому счету? Обучайте механическому счету с помощью простых песен, которые считают в возрастающем порядке.Подсчет простые действия и предметы, которые появляются в повседневной жизни, также рекомендуется, например, для подсчета лестниц. Позже такие игры, как счет во время хлопки в ладоши или марш помогают процессу.

Механический подсчет может быть забавным! Это просто и обычно требует очень мало подготовки или ресурсов для воплощения в жизнь.

Узнайте 16 лучших способов научить детей механическому счету и попробуйте сами! Если вы хотите узнать больше о том, что такое механический подсчет, ознакомьтесь с этим подробным руководством.

1. Счет с использованием разных голосов!

Дети любят брать на себя роли и смешные голоса персонажей. Это занятие подкрепляет этот энтузиазм и использует его для механического подсчета жизнь!

Когда я выполняю это задание, я всегда использую кости, которые у меня есть. сделано, на котором изображены разные персонажи. Эти кости начали свою жизнь как часть столба забора, и я просто распилил его на куб и нарисовал символы на нем с помощью перманентного маркера.

Нарисуйте на кубиках персонажей со смешными или отчетливыми голосами.На игральных костях я нарисовал принцессу, мышь, робота, инопланетянина, тигра и призрака. Призрак – мой самый любимый!

Игральные кости «Голоса персонажей» – фаворит в играх со счетом.

Идея состоит в том, что вы бросаете кости и смотрите, что вы получите, за пример робота. Затем вы просто считаете голосом робота – 1, 2, 3… Попробуйте и используйте роботизированное оружие и действительно воплотите его в жизнь. Считайте до тех пор, пока ребенок может управляйте и определенно переходите только после десяти, если можете.

Затем бросьте кости и попробуйте другой голос.

Если вам не нравится DIY, вы можете сделать простые игральные кости другим способом или просто попросите детей выбрать, какой голос они могут использовать. Это прекрасно работает, и механический подсчет определенно не то, для чего вам нужно много ресурсов.

Эта игра – одна из моих любимых 21 игр для дошкольников, на которую вы можете взглянуть здесь.

2. Подсчет с помощью марионетки

Дети очень любят кукол, и по непонятной причине часто слушают марионеток лучше, чем настоящих взрослых людей.

Окунитесь в эту странную магию, используя марионеток для механики. подсчет!

Если вы родитель, марионетка – отличная вещь, которую можно использовать с вашим ребенком, чтобы привлечь его внимание, и то же самое верно, если вы педагог.

Есть несколько способов сделать это. Самый простой – получить марионетка считать, а ребенок слушать.

Еще лучше заставить марионетку сосчитать, и ребенок присоединится дюйм

Вы можете расширить это занятие и усложнить его, если у детей это получается хорошо.Например, ребенок / дети и марионетка могут сказать альтернативные номера. Если марионетка говорит «один», ребенок / дети «два», марионетка «Три» и т. Д.

Марионетка может сидеть в кругу детей и заводить их. Марионетка говорит «один», затем следующие дети – «двое», затем следующие «трое» и т. Д. Марионетки хороши только для того, чтобы их сфокусировать и заинтересовать. Чтобы узнать больше о 14 кукольных математических играх, прочтите эту статью.

Марионетки отлично подходят для всех видов деятельности по счету

3.Подсчет песен, которые подсчитывают

Это может быть один из самых успешных способов начать дети уходят на путь механического счета.

Однако проблема с подсчетом песен заключается в том, что большинство они считают в обратном порядке. Это одна из странных загадок счета песен. Большинство из них придерживаются структуры «одним меньше». Есть такие песни, как Five Little Speckled Лягушки »или« Пять человечков в летающей тарелке », которые начинаются с пяти и затем получайте на один меньше с каждым стихом, который вы поете.

Это не та песня, которую нужно начинать детям механический подсчет. Им нужны песни, которые начинаются с единицы и идут вверх.

К счастью, они существуют!

Есть три хорошо известных примера этих типов песни.

Один – 1,2,3,4,5, «Однажды я поймал живую рыбу». Отлично для того, чтобы дети начали считать до десяти.

Два других примера: 1, 2, Buckle My Shoe и 1 Potato, 2 Potato, 3 Potato, 4. Список из десяти примеров таких песен, которые можно считать, можно найти в этой статье.

Спой много таких песен детям, и их способность механического подсчета должна улучшиться. Музыка – отличный инструмент для получения дети очень интересовались и увлекались математикой.

4. Подсчет действий в повседневной жизни

Это, строго говоря, не механический подсчет, как вы собственно подсчет того, что существует. Однако это один из лучших способов заставить детей заучивать счет, и это определенно то, что я не мог оставить в стороне.

Мы все сталкиваемся с последовательностями чисел на протяжении всей своей жизни.Некоторые классические примеры, которые часто будут видеть дети, – это скалолазание или скалолазание. лестница.

Если считать вместе с ребенком каждый раз, когда поднимаешься наверх лестницы, вы действительно закладываете отличный фундамент для механического счета.

Другими примерами являются такие вещи, как совместные прыжки и считать прыжки или хлопать и считать хлопки.

5. Подсчет предметов в повседневной жизни

Идея похожа на подсчет действий. На этот раз ты являются просто подсчетом предметов, часто опять же просто в повседневных жизненных ситуациях.

Прекрасным примером этого являются такие вещи, как подсчет блоков, когда вы кладете их обратно в коробку.

Подсчет количества имеющихся у вас кусочков еды, например количество моркови на вашей тарелке.

Или подсчитать, сколько у вас обуви.

Простое добавление счета в повседневную жизнь – отличная платформа для развития и консолидации механического счета. В моей статье о взаимном соответствии (и о лучших способах обучения этому) есть еще много примеров такого подсчета.

6. Счет по кругу

Это простая групповая игра, в которой участвуют все, и Надеюсь, это поможет очередности и сотрудничеству.

Один ребенок начинает, и они говорят «один». Затем следующий человек говорит “два”. Продолжайте так по кругу.

Чтобы лучше сфокусировать их внимание, вы можете использовать предмет. Например, попросите их передать игрушку или марионетку. Только ребенок, который держит марионетку может говорить!

Чтобы расширить эту игру, вы можете попробовать много разных вещей.Получать например, использовать другой голос! Тогда они все будут считать, как привидения или инопланетяне! Это действительно воодушевляет.

Вы также можете сказать, что есть один номер, который им не разрешено сказать. Или произнесите глупое слово вместо числа, например, вместо того, чтобы сказать “шесть” скажите “сосиски” вместо “колбасы”. Это развивает предвкушение, а также просто дает они смеются и наслаждаются этим.

7. Подсчет с партнером / взрослым

Эта игра похожа на прохождение по кругу. игра.Либо сядьте лицом к партнеру, либо к взрослому (в зависимости от того, как вы Это).

Один человек говорит «один», другой – «два», а затем вы просто продолжай так.

Когда вы посчитаете, насколько сможете, попробуйте начать заново. с другим человеком, говорящим одно. Таким образом, вы можете сказать цифры, которые никогда не сказал первый раз.

Эти игры, в которых вы по очереди заставляете их задуматься, смотрите на своего партнера, слушайте и сразу же по очереди.

Разбуди его голосами персонажей или заставь их пройти что-то между ними, когда они считают, например, плюшевый мишка или «счетный камень» (камень с нарисованными или нарисованными числами).

8. Подсчет в командах

Чтобы попробовать это, вам понадобится немало детей. Хватай их сидеть в двух «командах», одна команда смотрит на другую.

Хорошо работает, если есть что указать на команды когда настала их очередь говорить. Например, волшебная палочка подойдет для это.

Направьте волшебную палочку на первую команду, и они скажут «один».

Затем укажите на следующую команду, и они скажут «два». Возвращаться первые, которые говорят «три».

Продолжайте так. Это немного похоже на теннисный матч, с числа переходят от одной команды к другой. Продолжайте, насколько это возможно, помогая им, если требуется.

Чем больше вы будете выполнять все эти действия, тем дальше они будут уметь идти в долгосрочной перспективе.

9. Подсчет марта

Движение и математика идут рука об руку, и это занятие отлично подходит для этого. Движение помогает детям задействовать больше частей своего мозга, и обогащает любой учебный опыт.

Марширование – один из простейших способов заставить движение механический подсчет.

Достаточно просто заставить всех детей встать, а затем начать марш. При первом марше говорят «один», на втором – «два» и так на. Они могут маршировать по комнате или снаружи, или они могут просто маршировать по пятно, место.

Штамповка аналогична. Мне нравится, когда они топчутся, как гиганты с сердитыми лицами! Вы можете топать и считать, используя голос своего гиганта.

Это занятие также закладывает основу для понимания странного и даже числа позже.

Вы будете топать одной ногой для четных чисел, а другой – для четных. Дети не узнают, что это происходит, но почувствуют закономерность. Позже опыт приведет к большему пониманию.

Эти игры были бы великолепны на открытом воздухе. Чтобы узнать больше о других играх, не относящихся к математике, прочтите эту статью – Математические игры на открытом воздухе – 50 действительно работающих идей!

10. Счет танцев

Это аналогичная теория танцевального счета.Поднимите их и двигаться, и дети будут реагировать более позитивно и помнить навыки лучше.

Включите качающуюся музыку. Это может быть что угодно с хорошим яркий ритм.

Затем выберите два простых танцевальных движения, которые можно выполнять одно за другим. другой. Например, можно бросить руки влево, а затем бросить ваши руки вправо.

Тогда начни считать по мере того, как ты делаешь ходы! Бросьте руки к слева и скажите «один». Раскиньте руки вправо и скажите «два».Хранить собирается.

Когда они зайдут так далеко, как смогут, выберите еще два движется, и начните с одного.

11. Подсчет действий

Движение

также является ключевой частью этой идеи. Еще раз, как со многими из этих стратегий нет необходимости иметь какие-либо ресурсы или приготовить что угодно.

Вы просто выбираете действие, которое хотите попробовать, затем выполняете это действие и считать одновременно!

Например, действие может быть прыжком. Прыгай и считай!

Вы можете попробовать всевозможные движения, например подпрыгивание, кивание, прыжок, похлопывание по частям тела или мигание.

Это забавные вещи, и если детям нужно сосредоточиться на двух вещах сразу, кажется, это лучше работает в закреплении навыка механического счета.

12. Использование пальчиковых марионеток

Это хорошо работает, если у вас достаточно марионеток для всех детям, с которыми вы собираетесь заниматься этим занятием.

Попросите детей надеть марионетки на пальцы, а затем использовать их марионеточные голоса, чтобы считать в унисон. Если у вас много та же марионетка, тогда это будет звучать как припев этого голоса.Если у вас много мыши, например, все они будут озвучивать мышиные голоса.

Если у вас много разных персонажей для марионеток, вместо этого будет большая какофония голосов, объединенных воедино. Отлично подходит для весело считать!

13. Шепот как шпион

Дети любят шпионов и супергероев. а что может быть лучше супер-шпионского подсчета!

Для этого одному ребенку нужен партнер (или, если вы родитель, тогда только вы и ваш ребенок будете партнерами).

Вы собираетесь шептать числа друг другу, беря поворачивается, чтобы сказать число.

Например, один ребенок шепчет «один», а другой – «два». Продолжайте так! Не позволяйте никому вас слышать!

Шпионский шепот – отличный способ научить многим стратегиям. В моей статье упоминается о хитрых словах и о 12 лучших играх, чтобы их научить.

14. Zoom Zoom Zoom Game

Они отлично подходят для механического счета, а также для обратный отсчет, а также следующий шаг.

Это игра супер кругов. С детьми в кружке, встаньте в середину круга и затем укажите на одного ребенка. Идея состоит в том, чтобы медленно ходите по кругу с вытянутым пальцем так, чтобы вы медленно указывая на каждого ребенка по очереди. Пока вы это делаете, дети наизусть счет – 1, 2, 3 и т. д.

Когда вам стукнет 10, ребенок, на которого вы указываете, будет «космонавтом». Они должны встать и встать посреди круга – («ракеты»). Продолжать опять таки.

Когда вы выбрали 5 детей космонавтами, затем спойте песню Zoom Zoom Zoom:

Zoom Zoom Zoom

Мы на Луну!

Zoom Zoom Zoom

Мы будем там очень скоро!

5, 4, 3, 2, 1, 0 – Взлетать!

Затем все отправляются в космос с максимально возможными звуковыми эффектами. Повторите игру еще раз, пытаясь найти новых космонавтов, если сможете.

Это одна из моих любимых игр с парашютом. Чтобы ознакомиться с полным ассортиментом, взгляните на эти 40 величайших игр с парашютом для детей.

15. Змея, считающая и прыгающая

Это немного похоже на конгу, оживленную еще больше благодаря прыгать и считать!

Встаньте в большую линию конги. Тогда либо все вместе прыгают вперед и скажите «один», или все сделают шаг в сторону и скажут «один». Затем прыгните или сделайте шаг в сторону другую сторону и скажите «два». Продолжать!

Отлично на улице, где можно быть шумным и хриплым как вы, возможно, захотите.

Отличное занятие для совместной работы и помощи друзьям чтобы все работали вместе.

16. Splat The Playdoh

Математика для игр Playdoh – одна из лучших форм увлечения детей и их интереса к числам.

Эта игровая приставка – одна из самых лучших.

Вам понадобится туф или большой поднос, в который можно положить на столе. Затем попросите того, кто занимается этим делом, сделать жребий и много маленьких шариков playdoh.

Идея состоит в том, что ребенок шлепнет один мяч в пластилин и скажет «один». Затем следующий, введите «два» и продолжайте так. Они могут использовать что-нибудь для разбрызгивания, если хотите, например, мухобойку или небольшой удобный для детей молоток.

Продолжай шлепать и считать!

Одновременно могут заниматься несколько детей, или один ребенок может заниматься сначала, потом следующий и т. д.

17. Аплодисменты и счет

Хорошая простая отделка, но один из лучших способов Практика механического счета заключается в том, чтобы хлопать в ладоши одновременно со счетом.

Считай и хлопай! Это так просто.

Чтобы усложнить задачу, вы можете попробовать такие вещи, как счет в другой голос и хлопки одновременно. Или вы можете шептать, как шпион, и хлопать.

Все, что угодно, чтобы сделать его увлекательным и оживить счет!

Заключение

Удачи в этом механическом подсчете!

Механический счет – одна из основ математики, а важная основа для развития детей.Тем не менее, это определенно весело и простая вещь для обучения, на самом деле не требующая какой-либо работы или подготовки.

Маленькие и частые способы сделать это! Чем больше вы заставите их считать, тем лучше и увереннее они станут.

Если вы нашли эту статью полезной, то почему бы не взглянуть на одну из этих:

Мартин Уильямс

Привет, я Мартин Уильямс, создатель блога Early Impact Learning.Я дошкольный и младший педагог с десятилетним опытом, а также провожу практические курсы для детских садов и школ.

Недавние сообщения

ссылка на 15 лучших звуковых мероприятий фазы 1 (которые действительно работают!) ссылка на 45 примеров мелкой моторики

45 примеров мелкой моторики

Легко принять как должное, насколько нам необходимы мелкая моторика в повседневной жизни, поскольку многие из наших движений настолько хорошо отработаны, что мы используем их, даже не задумываясь! Пока мы склонны думать…

способов научить счету – PreKinders

Вот 15 способов обучения навыкам счета в Pre-K.

Наборы для изготовления

Используйте учетные карточки для небольших счетных циновок. Дети отсчитывают наборы на каждой карточке. (На этом фото дети считали наборы по 2 штуки)

Подсчет ящиков для мусора

Я использовала доски для сухого стирания в качестве счетного «коврика», на котором дети могли класть свои счетчики.Я написал цифру на доске для сухого стирания каждого ребенка, затем попросил их определить цифру и отсчитать это количество счетчиков на своей доске. После того, как я проверил их работу, они могли стереть номер, а я написал новый номер на их доске. Каждый ребенок мог работать в своем собственном темпе и на своем уровне способностей. Некоторые дети работали над числами 1-5, а другие считали больше 10.

Для математических счетчиков можно собрать множество интересных материалов. Некоторые идеи – пластиковые ящерицы или жуки из долларового магазина, пластмассовые драгоценности, маленькие пенистые фигурки, ключи, ракушки.

Пунктирные карты

Карточки с точками изготавливаются из учетных карточек и наклеек с цветными точками. Я сделал карточку для каждого числа 1-10, с цифрой, написанной рядом с точками. Дети считают вслух вслух, ставя каждый математический счетчик на каждую точку. Они используют их, когда начинают учиться счету, чтобы помочь им разместить правильное количество математических фишек на карточке. Загрузите точечные карточки для печати.

Подсчет фруктов

Я наклеил точки наклеек на одноразовые пластиковые тарелки и покрыл середину прозрачной контактной бумагой.На каждой пластине разное количество точек. Дети считают точки на тарелке, произносят число, затем считают количество фруктов и кладут на тарелку. Если счетчики для фруктов недоступны, можно использовать любой тип счетчика. Они похожи на карты с точками выше, за исключением того, что я не писал цифры рядом с точками, потому что в этой игре целью был подсчет и только однозначное соответствие, а не определение числа.

Путь Игры

Дети бросают игровой кубик и подсчитывают количество мест, на которые можно переместить свою игровую фишку.Игры с путями могут быть разработаны с учетом различных уровней навыков так же, как и игры с сеткой.

Игры на счет и совпадение

Я сделал этот набор из плаката, автомобильных наклеек и прозрачной контактной бумаги. Каждое число представляет собой две карточки. Дети считают машины на каждой карточке и сравнивают карточки с одинаковым количеством машин. Я позаботился о том, чтобы наклейки располагались по-разному, чтобы они не казались одинаковыми на первый взгляд (их действительно нужно пересчитывать).

Домино

Дети считают и сравнивают количество точек на домино.

Марки для лепки

Дети нажимают числовой штамп в пластилине и отсчитывают количество шариков, которое нужно вдавить в пластилин. (Эти марки для пластилина были доставлены из Лейкшор.)

Наборы нумерованных чертежей

Дети рисуют простые картинки (радуги, цветы, солнца, воздушные шары, человечки из палочек и т. Д.), Изображающие числа.Например, для числа 3 они могут нарисовать 3 солнца.

Рыбная ловля

Дети используют навыки числовой идентификации и счета, чтобы расположить числовую рыбку по порядку на синем фетре (пруд). Я сделал их, написав цифры на поролоновой рыбе из магазина для рукоделия (вы можете использовать любую форму поролона).

Игра божья коровка

В этой игре 2 уровня. На одной стороне палочек написано число, на котором выбито количество божьих коровок.Дети определяют число, затем кладут каждый жетон божьей коровки на божью коровку на палке, считая вслух. На оборотной стороне ручки есть цифра, написанная на ней, но не проштампованная. Более продвинутые дети могут использовать немаркированную сторону, а затем самостоятельно проверить свой ответ, проверив обратную сторону.

Счетные самолеты

Каждый месяц мы отслеживали, сколько самолетов пролетело над нашей игровой площадкой, пока мы были на улице. Когда дети видели на улице самолеты, мы в голове вели счет (обычно пролетало не более трех).Затем, когда мы заходили внутрь, мы добавляли столько самолетов к нашей карте. Детей часто видели на карте, считая, сколько мы уже видели.

Номерная книга

На фото сделанная нами книга для подсчета пауков. Дети определили число, а затем отметили это количество кругов на странице маркером бинго. Карандашом нарисовали ноги и глазки. Я всегда убеждаюсь, что детям комфортно считать с помощью манипуляторов, прежде чем делать книгу с числами, чтобы они не разочаровались, пытаясь сделать книгу без ошибок.

Носки Mystery

Дети вместе с партнером играют в эту игру. Им понадобится один носок и 5 плоских цветочных шариков (плоские шарики отлично подходят для математических манипуляций, потому что они не скатываются). Один ребенок кладет в носок несколько шариков. Другой ребенок, не выглядывая, тянется к носку, считает шарики на ощупь и называет число. Затем дети могут достать шарики из носка, чтобы проверить правильность ответа.

Ювелирные изделия

Струны драгоценных камней – это струны цветных пластиковых драгоценных камней, которые разрезаны на сегменты по 1 драгоценному камню на струну, 2 камня на струну, 3 камня на струну и так далее (до 10).Каждому ребенку нужен один набор цепочек с драгоценными камнями 1–10 и набор карточек с цифрами 1–10. Дети берут из контейнера по одной нитке драгоценных камней, подсчитывают количество драгоценных камней на веревке и сопоставляют ее с правильной цифровой карточкой.

Узнайте больше о способах обучения счету здесь.

Добро пожаловать!

Хотите подписаться на мою БЕСПЛАТНУЮ еженедельную рассылку обновлений? Присоединяйтесь к более чем 85 000 подписчиков!

Мы собираем, используем и обрабатываем ваши данные в соответствии с нашей Политикой конфиденциальности.
Не волнуйтесь – мы никогда не продаем и не передаем адреса электронной почты!

Почему важна индивидуальная переписка

Дети любят считать. Они считают все: от шагов, которые они делают, чтобы добраться из спальни до кухни, до количества друзей в школе каждый день. Подсчет помогает им понять мир и узнать, сколько чего-то. Со временем и с практикой дети развивают понимание «правил» или принципов счета.

Один из таких принципов известен как однозначное соответствие.Идея заключается в том, что числа соответствуют определенным количествам. Например, во время игры ребенок считает 1, 2, 3, 4, 5 точек на кубике и прыгает на 1, 2, 3, 4, 5 делений на доске, потому что 5 точек соответствуют 5 прыжкам. Число «пять» всегда соответствует точному количеству, независимо от того, что вы считаете.

Таким образом, отличительной чертой точного счета является то, что дошкольники начинают присваивать один номер и только один номер каждому объекту при подсчете. Мы видим это достижение, когда ребенок прикасается к каждому объекту или помечает его, произнося счетные слова.И это немалое достижение, так как требует точной синхронизации движений и речи.

В этом видео мы можем наблюдать за молодым математиком, который только начинает координировать свой устный счет с пометкой каждого блока по мере его подсчета. После нескольких попыток он показывает некоторую путаницу между тем, что он видит, и тем, что он говорит. Сроки еще не определены.

Чтобы полностью сфокусироваться на ребенке, щелкните здесь.

Но даже когда дети взаимно однозначно помечают каждый объект счетным словом, они могут еще не иметь полного представления о взаимно однозначном соответствии.Понимание соответствия между величиной и ее числовым названием (и цифрой) – это больше, чем просто пометка или отслеживание во время подсчета.

Дети часто сначала развивают чувство однозначного соответствия, играя с игрушками, которые требуют сопоставления одного объекта с одним пространством, например, складывание пластиковых яиц в коробку для яиц или подгонку фигур в головоломку. В конце концов, дети могут сами ставить предметы в соответствие друг с другом, например, накрыть на стол одну тарелку и одну салфетку на каждое сиденье.Но дети могут это делать, даже не понимая, что соответствующее количество тарелок, салфеток и сидений одинаково.

Важно обсуждать соответствия, которые возникают естественным образом и осмысленно в жизни маленьких детей. При надевании зимних перчаток каждый палец находит отверстие? На всех ли за столом хватит клея? Сколько гаражей нам нужно, чтобы припарковать все игрушечные грузовики?

У этого ученика совершенно другой вопрос.Ему нужно выяснить, как справедливо делиться куки-файлами между двумя друзьями.

Для демонстрации этого видео, используемого учителями, щелкните здесь.

Мы наблюдаем, как этот студент отсчитывает все печенье, раскладывая их по одному, туда и обратно, между двумя тарелками. Хотя он точно считает 10 файлов cookie, действие по раздаче файлов cookie – это не более чем сопоставление. Хотя он говорит, что эти две группы одинаковы, он не полностью понимает, что равным группам соответствует одно и то же число.Поэтому он считает 5 печений на одной тарелке, а затем ему нужно пересчитать печенья и на другой тарелке, вместо того, чтобы знать, что на ней тоже 5.

Углубляйте познания маленьких детей в числах посредством множества опытов и бесед о том, как индивидуальное сопоставление создает равные группы – если вы знаете число в одной из групп, то вы знаете число в другой. Это займет некоторое время. Понимание однозначного соответствия углубит у детей чувство числа и хорошо послужит им для счета и не только.

Просмотры сообщений: 28 563

Считайте до 100: стратегии и действия

Привет! Я вернулся, чтобы поделиться учебными стратегиями и упражнениями, чтобы научить учащихся начальных классов, как заучивать счет до 100. Как всегда, продолжайте читать, чтобы получить бесплатное задание для ваших математических центров или обучение в небольших группах!

Давай поговорим о счете!

Счетчик – один из самых важных или самых важных навыков, которым нужно заниматься с учениками начальной школы.Умение механически подсчитывать – это навык, который нужен учащимся, прежде чем они смогут развить мощность множества и прежде, чем они смогут освоить более сложные навыки, такие как составление и разложение чисел и… глоток… числовое значение.

Подсчет означает знать, какие числа идут следующими в последовательности. Это звучит просто, но механический счет может быть затруднен при первом изучении.

Некоторые препятствия, мешающие учащимся успешно считать:

1. Пропуск чисел или неправильное произнесение числа (особенно запутанные числа для подростков)
2.Невозможно сосчитать по десятилетиям (от 9 до 10, от 19 до 20, от 29 до 30 и т. Д.)
3. Невозможно рассчитывать от числа, отличного от 1 (начиная с 15, а затем повторяя 16, 17, 18 и т. Д.).

Хорошая новость: все эти препятствия на пути к механическому подсчету могут быть успешно устранены с помощью прямых, ясных инструкций и множества возможностей с использованием различных средств практики.

Простые математические процедуры, помогающие ученикам наизусть считать

Практикуйтесь в счете каждый день! Предложите ученикам считать, петь, танцевать и считать вместе с другом.На YouTube есть ТОННА бесплатных видео с подсчетом. Мои студенты любят Джека Хартмана, который считает видео. Щелкните здесь, чтобы посмотреть несколько его видео. Если ваш округ блокирует видео на YouTube, вы можете придумывать свои собственные танцевальные движения.
Научите студентов замечать закономерности – Используя таблицу 100, попросите студентов рассказать о том, что они замечают в расположении чисел. Они могут заметить, что он следует шаблону 0-9 или что каждый столбец имеет одинаковый номер. Попросите учащихся рассказать о закономерностях, которые они замечают, записать, что они говорят, и поделиться своими выводами с классом.
Сколько дней мы учимся в школе? – Это отличная практика для ежедневного счета до 100! Учащиеся каждый день добавляют соломинку (или то, что вы используете), чтобы обозначить, сколько дней они были в школе. Каждый раз, когда они набирают 10, они связывают соломинки. В 100-й день школы устройте вечеринку с математической тематикой!
Подсчет в календаре – Числа от 1 до 31 сложны! При обучении детей механическому счету я рекомендую в первую очередь сосредоточиться на числах от 1 до 31. Вы можете использовать календарь каждый день, чтобы практиковаться в написании чисел, говоря, какое число идет до и после, и подсчитывая, сколько дней осталось до особого события.Вы также можете перемещать числа в неправильном месте и просить учащихся найти число, которое находится в неправильном месте.
Считайте по кругу – Попросите учащихся сосчитать или сосчитать по кругу. Каждый ученик называет следующее число. Помните, не всегда начинайте с 1! Используйте карточки с цифрами, чтобы выбрать номер для начала. Если это начало года, я бы ограничил диапазон числами от 1 до 31.

Это действия, которые вы можете выполнять каждый день в рамках своей математической рутины.

Упражнения для обучения студентов счету

Вот некоторые упражнения, которые вы можете использовать, чтобы дать своим ученикам дополнительную практику, чтобы заучивать до 100!

Партнерские счетные карты

Лучший способ научиться механизировать счет – это счет! Это упражнение можно использовать в небольшой группе или целой группой. Вы выбираете карточку, или студент выбирает карточку, и они рассчитывают от этого числа, пока не достигнут целевого числа. Это отличный способ дифференциации и расширения диапазона чисел в зависимости от навыков вашего ученика.Например, если ученик работает над механическим счетом до 25, используйте счетные карточки до 25.

Карты с отсутствующими номерами

Ученики, которые пропускают числа при подсчете, выиграют от отсутствия карточек для подсчета чисел. Студенты считают и записывают недостающее число. Попросите их объяснить, откуда они знают, что номер отсутствует (т. Е. Они посмотрели на шаблон или знают, что идет до или после).

Чтение и запись

«Чтение и запись» – отличный способ научить учеников правильно считать и писать числа.Для учащихся этого возраста с точки зрения развития уместно иметь некоторые перевернутые буквы, но это не значит, что вы не можете дать им опыт, который поможет им правильно формировать числа. Для этого задания учащиеся выбирают, читают и записывают заданное число. Они могут использовать числовую полосу в верхней части страницы, чтобы помочь им правильно формировать буквы. Он начинается с 2, поскольку большинство студентов умеют писать 1.

Spin and Cover

Spin and Cover – отличный способ научить студентов читать числа до 100.Они крутят обе блесны, пишут число и закрывают число на 100-й диаграмме. Это интересный способ познакомиться с паттернами на графике 100.

Рассчитывай или вернись!

Что отличает ваши лучшие счетчики чисел от ваших развивающихся счетчиков чисел? Лучшие счетчики чисел знают, какое число стоит до и после целевого числа. У них сильные навыки владения числами. Студенты берут карточку и пишут, что стоит до и после этого числа.В зависимости от того, какую карточку вы выберете, студенты также могут отсчитывать от заданного числа.

Пазлов!

Кто не любит большие головоломки? Студенты сравнивают цифру с изображением. Это забавное занятие для тренировки счета на десятки.

Сколько пальцев?

Счетчик пальцев – очень важный навык в этом раннем возрасте. Почему? Ваши 10 пальцев – это, по сути, десять кадров! Вы можете использовать свои пальцы, чтобы складывать и вычитать, и рассчитывать на них! НО сейчас мы будем использовать пальцы, чтобы считать от десятков до 100.Учащиеся выбирают карточку с номером и используют карточки с пальцами, чтобы показать, сколько.

Путешествие к 100!

Это отличная партнерская игра! Учащимся нужен жетон, чтобы перемещаться по настольной игре. Студенты бросают кубик и перемещают столько мест на доске. Затем они говорят, какие числа идут до и какие после. Есть 2 дифференцированные настольные игры. Студентам, которым может потребоваться помощь со счетом, вы можете предоставить им таблицу 100.

Рулон и крышка

Я люблю игры с роликами и обложками! Их так просто объяснить, но они имеют большую обучающую ценность.Учащиеся бросают кубик, выбирают и читают число в столбце этого числа. После того, как они его прочитали, они закрывают его. Это может быть независимая или совместная игра.

Что будет дальше?

Это партнерская деятельность. Студент выбирает карточку, читает числа и говорит, что будет дальше. Если их ответ правильный, переместитесь на одну клетку. Затем наступает очередь другого игрока. Побеждает тот, кто первым придет к финишу.

Что между ними?

Это отличная партнерская игра для развития навыков владения числами.Студент берет карточку, читает числа и говорит, какое число находится посередине. Если они правы, они перемещаются на 1 деление. Затем наступает очередь другого игрока.

Что будет дальше?

Ученики вращают вертушку и записывают следующие 3 числа. Это отличное занятие для обучения студентов счету на десятилетия.

Что будет дальше?

Помните, когда я упоминал, что студентам сложно считать десятилетия? Вот ДРУГОЕ занятие, чтобы дать им возможность самостоятельно попрактиковаться.Студент бросает кости, читает числа в ряду и закрывает следующее число с помощью манипулятора. Это увлекательное занятие самостоятельно или с партнером. Есть и игра на счет десятками!

Что отсутствует? Игра №2

Это действие карточки задачи. Учащиеся выбирают карточку с заданием и записывают недостающее число, считая от заданного числа. Они записывают недостающий номер на регистрационном листе.

Запись и стирание

Учащиеся берут карточку и записывают недостающие числа на доске.

Выберите и запишите

Ученики берут карточку и записывают следующие несколько чисел в числовую строку. Они могут записать ответ на карточке или на доске.

Гигантские счетные карты

Ученики расставляют карточки с номерами в порядке от 1 до 100 или от 10 до 100. Это отличное упражнение для партнера, чтобы досчитать до 100 наизусть.

Задания

Студенты практикуются в написании и чтении чисел до 100.

Есть ли у вас какие-нибудь упражнения, которые вы используете, чтобы научить своих учеников механически считать до 100? Дайте мне знать в разделе комментариев ниже.

Загрузите бесплатные карты для подсчета пальцев, щелкнув ссылку ниже:

Вам нравится этот ресурс? Вы можете приобрести это здесь?

Счастливого обучения!
Тройник!

шаблонов подсчета | Группа развивающей математики

Предоставление детям младшего возраста (5-8 лет) соответствующих развивающих занятий заданий в области слова, количества, символов, отношений и операций – очень важный первый шаг в развитии чувства числа.Каждый месяц DMG будет фокусироваться на одной из важных концепций и давать идеи и задания, которые вы можете использовать со своим ребенком или учащимися в числовых концепциях и операциях.

Эти важные концепции закладывают основы математического мышления. «Чувство чисел иногда определяется как наличие хорошей интуиции в отношении чисел и их взаимосвязей. Он развивается постепенно в результате изучения чисел, их визуализации в различных контекстах и их соотнесения способами, которые не ограничиваются традиционными алгоритмами »(Howden 1989, p.11). Чувство чисел напрямую способствует способности решать проблемы и гибкому мышлению в числовых ситуациях. Уверенность в себе и позитивное отношение, проявляемые детьми с хорошими представлениями о числах, резко контрастируют с неуверенностью многих старшеклассников и взрослых, которые все еще полагаются на счет по пальцам (Van de Walle, 1990). Чувство чисел можно и нужно развивать с помощью инструкций, учебных программ и оценок.

СЛОВО КОЛИЧЕСТВО СИМВОЛОВ ВЗАИМООТНОШЕНИЯ ОПЕРАЦИИ

Август 2007 г.
В этом месяце мы фокусируемся на
WORD

Шаблоны устного счета
Гельман и Галлистель (1978) называют счет схемой в смысле Пиаже.То есть счет становится наизусть способом произносить числа, не обязательно развивая понимание количества.

Чтобы сосчитать до 100, ребенку необходимо знать:

однозначная последовательность от одного до девяти
переходы обозначаются девяткой (например, девятнадцать сигнализируют об окончании подросткового возраста и начале новой серии)
условия перехода для новой серии (например, двадцать следует за девятнадцатью)
правила создания новой серии (например,грамм. двадцатые и все последующие серии генерируются путем объединения члена перехода, в свою очередь, каждого члена в однозначной последовательности)
исключения из правил (11-15)

Дети, идущие в школу, обычно могут считать до девяти, если не до девятнадцати (Fuson 1988). Однако у многих воспитанников детского сада не будет второго компонента, указанного выше, и, как следствие, они будут чрезмерно расширять свои правила подсчета (т. Е. Допускать обусловленные правилами ошибки, такие как девятнадцать, десять, одиннадцать или двадцать девять, двадцать десять, двадцать одиннадцать “). .Большинство также не знают, через какое десятилетие начинается новый ряд (например, они считают до двадцати девяти и останавливаются, потому что не знают, что следующим будет тридцать). Действительно, только в первом классе многие дети осознают, что ряд декад параллелен однозначной последовательности (например, шесть + ти, семь + ти, восемь + ти), и осваивают декады (например, за двадцатью следует двадцать + одно, двадцать + два). Наконец, исключения из схем подсчета часто вызывают трудности. Например, пятнадцать лет – это подросток, которого чаще всего пропускают (Fuson 1988).

СЛОВА ДЕЯТЕЛЬНОСТЬ

Возраст и диапазон счета
2-3 года. 1-3
Подготовительный класс 1-10
Детский сад 1-20 Назад от 5
1 класс Диапазон счета 1-100 Назад от 10
Класс 2 Диапазон счета 1-1000 Назад из 20

Устный счет вперед
• Читайте счетные книжки, пойте песни, рассказывайте детские стишки
Примеры книг:

Оливия Графс, , Ян Фалконер,
, , Десять черных точек, , Дональд Крюс,
, , Очень голодная гусеница, , Эрик Карл. Книга подсчета Барбары МакГрат
Я могу сосчитать 100 кроликов и ты тоже Синди Секерес
Давайте посчитаем Тана Хобан

Пример песни:
«Пикник с божьей коровкой» – Улица Сезам

Примеры детских стишков:
“1-2 Buckle My Shoe”
“One Potato, Two Potato”

Устный счет назад
• Читайте счетные книжки, пойте песни, декламируйте детские стишки
Примеры книг:

Пять маленьких обезьянок, прыгающих на кровати Эйлин Кристелоу
10 резиновых утят Уильям Б.Winburn
Двадцать – это слишком много Кейт Дьюк

Пример песни:
«Пять крапчатых лягушек»

Примеры детских стишков:
«5 маленьких обезьянок прыгают на кровати»
«Десять в постели»

Дополнительные задания:
• Чтение числовых слов по порядку
Повторяйте за мной: «Один, два, три»
Добавляйте числовые слова по мере того, как они учат последовательность

• Начните с разных чисел
Скажите: «Я буду считать, и я хочу, чтобы вы сказали это за мной.
«Девять, десять. Давай сделаем это снова. Девять, десять».
Do для строк подсчета слов до 5. Измените последовательность в зависимости от возраста ребенка.

Измените последовательность в зависимости от возраста ребенка. По мере взросления ребенок должен уметь считать, начиная с разных цифр. Например: ребенок в детском саду должен уметь считать от 10 до 20. Следите за переходами для детей старшего возраста. Если вы слышите, как ребенок делает паузу при переходе с 9 на 10, с 19 на 20 или с 29 на 30, вы знаете, что они понимают, что необходимо изменение, но он / она еще не уверен в словах перехода.Помогите ребенку, научив его / ее наизусть считать от 10 до 100.

• Подготовьте числовой куб с числами от 0 до 5
Попросите ребенка катать кубик. Взрослый произносит числовое слово. Затем ребенок считает до этого числа. Вы также можете попросить ребенка прыгать, когда он произносит число, или хлопать в ладоши, когда он считает.

• Используйте ручную марионетку, чтобы делать ошибки при подсчете, и пусть ребенок прислушивается к ошибкам при подсчете. Убедитесь, что вы ведете счет вперед и назад в пределах правильного для ребенка диапазона.При подсчете начинайте с разных чисел.

• Поиграйте с ребенком в эхо-игру. Назовите три числа подряд и попросите ребенка повторить их эхо. Когда ребенок научится хорошо это делать, продолжайте считать. Назовите три числа, а затем ребенок продолжает еще три счета. Вы также можете чередовать подсчеты.

Что такое индивидуальная переписка? 9 занятий, чтобы научить его

Что такое индивидуальная переписка и почему она важна для развития ребенка?

Процесс познания чисел и развития чувства числа начинается у маленьких детей, прежде чем они научатся надежно считать.

Они могут сказать вам, сколько им лет, сколько пальцев у них на каждой руке или сколько свечей на их праздничном торте.

Подражая взрослым и детям старшего возраста, они начинают изучать названия чисел и символы, хотя на данном этапе они еще не имеют для них особого значения.

Вскоре они начинают считать.

Есть два этапа подсчета, которые проходят все дети – механический счет и рациональный счет (взаимно-однозначное соответствие).

Что такое механический подсчет?

Механический счет в основном означает счет, как у попугая. Это когда ребенок выучивает названия чисел и может дословно произносить их по порядку.

Механический счет важен, потому что детям необходимо запоминать названия чисел, чтобы они могли связать каждое имя с символом и выучить их в правильной последовательности.

В каком возрасте ребенок может считать до 10?

Ребенок в возрасте двух лет часто может наизусть считать до 10.К тому времени, когда она пойдет в школу, она может считать до 100 и более.

Дети начинают с изучения названий чисел и могут путать последовательность чисел, но со временем и практикой они могут перечислять числа в правильном порядке.

Я говорю, что перечисляет числа , а не счет , потому что счет – это на самом деле другой навык. Составление списка номеров зависит от способности запоминать названия номеров по порядку.

Ребенок, который умеет механически считать, не обязательно может считать каждый объект один раз или может пересчитывать один и тот же объект несколько раз.

Что такое рациональный счет?

Рациональный подсчет означает, что ребенок может присвоить правильное числовое имя каждому объекту по мере их последовательного подсчета.

Затем она может ответить на вопрос , сколько всего объектов составляет .

Разница между механическим счетом и рациональным счетом состоит в том, что первый – это процесс последовательного запоминания имен чисел , а второй – процесс развития понимания значения чисел .

Что такое

Индивидуальная переписка

Однозначное соответствие – это когда ребенок проходит мимо механического подсчета и может считать рационально – путем присвоения одного числа каждому элементу в правильной последовательности . Это означает надежный подсчет объектов, по одному, , и получение общего значения для ответа на вопрос «сколько?»

Ребенок, умеющий рационально считать, не просто составляет список чисел по порядку.Скорее, при подсчете она умеет использовать взаимно однозначную переписку.

Это означает, что она может сосчитать набор из 5 объектов, указав на каждый объект и присвоив каждому объекту следующее числовое имя, пока каждый объект не будет посчитан один раз.

Ребенок, у которого еще не сложилось взаимно-однозначное соответствие, может пропустить объект, посчитать объект более одного раза или еще не увидеть связи между именами чисел и объектами.

Ребенок, который понимает соответствие 1: 1, овладел четырьмя принципами счета :

Каждому объекту может быть присвоено только одно числовое имя .
Имена номеров должны использоваться в фиксированном порядке (один, два, три, четыре и т. Д.).
не имеет значения, в каком порядке подсчитываются объекты (начните с любого объекта и подсчитайте их в любом порядке, и общая сумма всегда будет одинаковой).
Последнее использованное числовое имя дает общее количество объектов (сколько). Это называется кардинальным числом.

Позже ребенок научится вести обратный счет , пропускать счет (т.е.грамм. сосчитать по двойкам, пятеркам и т. д.), и в конечном итоге распознать значение группы объектов на вид (например, набор из 5 объектов).

Поэтому важно, как только ваш ребенок научится считать до разумного числа, сместить акцент с увеличения и увеличения этого числа на обеспечение того, чтобы ваш ребенок мог надежно сосчитать небольшое количество предметов.

Индивидуальное соответствие намного лучше показывает понимание вашим ребенком чисел, чем длинный список запомненных чисел.

Как научить ребенка индивидуальной переписке

Так же, как вы научите своего малыша счету, вы можете ввести индивидуальную переписку с раннего возраста.

На самом деле есть два способа, которыми ваш ребенок научится этому навыку – случайно или через явное обучение,

Это означает, что ваш ребенок естественным образом выучит эту концепцию самостоятельно в процессе игры, но вы также можете предоставить возможность обучать этому во время игры.

Случайное обучение

детей естественным образом откроют возможности в своей повседневной жизни, которые помогут им узнать, что математика основана на реальных сценариях.

Дети будут общаться один на один во многих игровых и повседневных сценариях, например:

В песочнице (например, приготовление тортов и установка «свечей» на каждую из них)
Игра с чайным сервизом и подбор чашек к блюдцам
Надевание носков, обуви и перчаток (обучение стоимость пары)
Восхождение по ступенькам тренажерного зала в джунглях

Как родитель, вы можете смоделировать индивидуальную переписку в повседневном общении с ребенком, чтобы он учился, просто наблюдая за вами .

Например, при подсчете объектов касаются каждого из них и перемещают их по одному. Когда вы читаете, указывают на каждое слово по мере продвижения.

Явное обучение весёлый и содержательный (e.грамм. подсчитывая, сколько стаканов нам нужно на ужин), иначе ребенок потеряет интерес и не разовьет любовь к математике.

Когда вы считаете вместе, убедитесь, что вы всегда используете реальные, конкретные объекты . Позже вы сможете насчитать изображений объектов , когда будете читать («Сколько облаков вы видите на небе»). Дошкольники слишком молоды, чтобы считать абстрактные числа (например, 3 плюс 5).

Дети изучают математические концепции с помощью конкретного, графического и абстрактного подхода .Всегда начинайте с конкретного, вовремя вводите картинки и оставляйте абстрактное обучение формальному обучению, когда ваш ребенок будет к этому готов.

Не поддавайтесь соблазну обучать индивидуальной переписке с рабочими листами. Это не является осмысленным обучением и не подходит для детей младшего возраста с точки зрения развития. Рабочие листы могут быть опасны для развития вашего дошкольника.

Индивидуальные заочные занятия для дошкольников

Вот несколько замечательных занятий, которыми вы можете заниматься дома или в классе.

1.

Счетчик частей тела

Лучшее место для начала с малышами – это подсчет частей их тела, потому что детей воспринимают мир через свои тела.

Начните с подсчета одного носа, одного рта, затем перейдите к двум глазам и ушам. Попросите ребенка также посчитать ваши глаза и уши. Скоро она сможет пересчитывать пальцы на одной руке, потом на другой, потом на обоих вместе. Считайте также пальцы на ногах.

Попросите ее протянуть одну руку, и вы передадите ей одну чашку, или протяните две руки, и вы передадите ей две чашки.

Большая часть математического обучения основана на языке . Используйте любую возможность использовать язык при выполнении этих действий.

2.

Подсчет повседневных предметов

Возьмите за привычку считать вещи так, как вы встречаетесь с ними в повседневной жизни.

Считайте шаги , когда вы идете с ребенком, считайте ее носки , когда вы их надеваете, считайте синие машины , которые вы проезжаете по дороге, и т. Д.

Возможности повсюду – будьте готовы их найти!

3.Читай

Счетные рифмы

Счетные рифмы и игры пальцами отлично подходят для обучения вашего маленького ребенка счету. Возможно, у нее еще нет индивидуальной переписки, но это хорошее место для начала.

Сначала она будет запоминать только названия чисел, но с практикой она начнет соотносить правильное число с правильным пальцем или частью тела.

Вот пример простой пальцевой рифмы для обучения значению двойки:

Две птички-дикки
Две маленькие птички-дикки
Сидят на стене
Один по имени Питер
Тот по имени Пол
Улетай, Питер
Улетай, Пол
Вернись, Питер
Вернись, Пол

Вот пример стишка, который ваш ребенок может произносить, вытягивая по одному пальцу за раз, чтобы выучить значение десяти:

Один, два, три, четыре, пять
Один, два, три, четыре, пять,
Однажды я поймал рыбу живой,
Шесть, семь, восемь, девять, десять,
Потом я снова отпустил ее.
Почему ты это отпустил?
Потому что он так укусил меня за палец.
Какой палец укусил?
Этот мизинец справа от меня.

4. Играть

В ванне

Время купания – прекрасное время для обучения счету.

С маленьким ребенком предложите ей несколько игрушек, например, уток, сказав: «Я даю вам 2 утки», «Вот еще одна утка. А теперь посчитаем, сколько у вас их ». Прикасайтесь к каждой утке или поднимайте ее, медленно произнося имя каждого числа.

Когда она станет старше, предложите ей в ванне больше игрушек.Добавьте емкости и посчитайте, сколько чашек воды вам нужно, чтобы наполнить кувшин.

5. Играть

В песочнице

Песочница – еще одно место, где дети учатся математическим навыкам.

Сделайте пироги из грязи или кексы и попросите ребенка приготовить достаточно для каждого члена семьи. Составьте ряд получившихся фигур и сосчитайте их.

Обучайте ребенка математическому языку, попросив сделать еще один торт или на один меньше .

6. Проводите время

на кухне

Участвуйте в обучении вашего ребенка, пока вы вместе готовите.

Попросите ее принести вам 3 помидора для салата или посчитайте, сколько там рулетов.

Если ваш ребенок немного постарше, попросите его принести по одной картофелине на каждого члена семьи. Если она вырывается, сначала посчитайте на пальцах, сколько в семье членов семьи, а затем попросите ее принести это количество картошки.

Этот пост содержит партнерские ссылки на образовательные продукты, которые я лично рекомендую.Если вы совершаете покупку через один из них, я получаю комиссию без каких-либо дополнительных затрат для вас. Прочтите раскрытие для более подробной информации.

7. Играйте с

игрушками

Пусть ваши дети регулярно играют с кубиками (это хороший деревянный набор), конструкторами, конструктором Lego, шариками и т. Д.

Игра с такими игрушками дает ребенку возможность случайно учиться.

Узнайте больше о преимуществах блочной игры.

8. Сыграть

Число игр

Держите под рукой несколько игр с числами и играйте в них вместе со своим ребенком.Настольные игры также отлично подходят для развития чувства числа. Вот несколько идей игр:

9.

Play Hopscotch

Эта классная традиционная игра научит вашего ребенка цифрам, а также их возрастанию и убыванию. Дети могут использовать все свое тело во время этой игры, что делает их конкретным опытом обучения. Вот правила Hopscotch .

Надеюсь, вам понравилось читать о том, как ваш ребенок учится считать! Вот несколько забавных игр для распознавания n umber!

21 Задания по счету с пропуском и идеи для учеников начальной математики

Подсчет пропусков – важный навык, который естественным образом ведет детей к умножению.Дети могут научиться пропускать счет наизусть, но они получат больше пользы, увидев, как эта концепция соотносится с реальной математикой. Попробуйте эти действия и идеи, чтобы это произошло!

1. Спойте несколько песен с пропуском счета.

У Mr. R так много песен со счетом без промедления! Они намного веселее, чем просто повторять «пять, десять, пятнадцать, двадцать…». Найдите их всех здесь.

2. Прочтите книгу для подсчета пропусков.

Преподавайте в рамках учебной программы с помощью одной или нескольких милых книжек с картинками, в которых подсчет пропусков является частью истории.

3. Превратите полоски с предложениями в настенную таблицу.

Такой простой способ сделать красочную настенную диаграмму! (Нужны полоски с предложениями? Попробуйте этот проверенный набор от Amazon.)

Подробнее: This Reading Mama

4. Сгруппируйте объекты для ознакомления с концепцией.

Дошкольники и воспитанники начинают изучать этот навык с группировки предметов. Получите бесплатные страницы для печати для использования в этом упражнении по ссылке.

Подробнее: File Folder Fun

5.Пропустить счет с отпечатками ладоней.

Используйте отпечатки ладоней своих учеников, чтобы продемонстрировать счет по 5 и 10. Как мило!

Подробнее: Место для раннего обучения Лиз

6. Сыграйте в классики со счетом пропусков.

Это классический метод подсчета пропусков. Начните просто с маркировки блоков 2 или 5. Смешайте вещи, добавив несколько вариантов, которые нужно будет сделать по ходу дела.

Подробнее: Math Geek Mama

7.Кружевные тарелки, как считаешь.

Это задание легко настроить, и дети могут даже переворачивать тарелки, чтобы проверить свои ответы! Узнайте, как их сделать, по ссылке.

Подробнее: 123Homeschool4Me

8. Пройдите лабиринт со счетом пропусков.

Перейдите в лабиринт, чтобы попрактиковаться в подсчете пропусков. Получите бесплатные распечатки по ссылке ниже.

Подробнее: Признания ученика на дому

9. Подсчитайте и соедините точки.

Пропустить подсчет точек соединения очень популярны, и вы можете найти множество доступных в Интернете. Сначала попробуйте эти бесплатные примеры – вашему классу они обязательно понравятся!

Подробнее: Рабочие листы Сайт

10. Используйте скрепки на бумажной тарелке.

Спорим, у вас остались бумажные тарелки, оставшиеся после шнуровки, так что соедините их со скрепками для другой идеи, которая также обеспечивает тренировку мелкой моторики.

Подробнее: Creative Family Fun

11.Внесите некоторое движение.

Скорее просто называйте числа, заставляйте детей двигаться, пока они пропускают счет! (См. Более активные математические идеи здесь.)

Подробнее: Обучение с Terhune

12. Произвести подсчет пропусков арт.

Эта идея сочетает группировку с пуантилизмом, техникой создания искусства из крошечных точек. Все, что вам нужно, это ватные палочки и краска для плакатов.

Подробнее: Creative Family Fun

13.Возьмите пригоршню кубиков LEGO.

Кто не любит использовать LEGO в классе? Различные размеры кирпичей идеально подходят для разговора о подсчете пропусков.

Подробнее: Royal Baloo

14. Наполните стаканы кубиками.

Вы также можете использовать LEGO с этим или вытащить свои блоки Unifix. Дети собирают стопки и наполняют чашки.

Подробнее: Powerful Mothering

15. Приведите в порядок деревянные палочки для поделок.

Деревянные палочки для поделок находят очень широкое применение в классе. Отметьте их числами и используйте их для практики счета! Вы также можете попросить детей нарисовать одну палку и потренироваться считать вверх от этого числа. (Возьмите эти красочные палочки для поделок на Amazon здесь.)

Подробнее: Simply Kinder

16. Положите немного денег на кон.

центов и десятицентовиков – отличные инструменты для подсчета пропусков, и дети тоже получат денежную практику.

Подробнее: The OT Toolbox

17. Бросьте кубик для подсчета очков.

Попросите детей бросить кости, чтобы посмотреть, по каким числам они будут считать. Это дает возможность практиковаться вплоть до счета по 12 секунд.

Подробнее: 3 динозавра

18. Прикрепите прищепки к рулетке.

Настроить так просто – все, что вам нужно, это прищепки и измерительная лента!

Подробнее: Thriving STEM

19.Создание воздушных змеев для подсчета пропусков.

Эта бесплатная идея поделки для печати делает воздушных змеев со счетными хвостами. Когда закончите, повесьте их в классе!

Подробнее: Рабочие листы и игры для детского сада

20. Соберите головоломку с подсчетом пропусков.

Пазлы подсказывают детям, нужна ли им помощь, но они действительно тайно учатся считать.

Подробнее: Life Over CS

21.Сделайте плакаты с номерами.

Вы можете купить набор этих симпатичных цифр по ссылке ниже или разбить своих детей на группы и попросить их вырезать и обозначить свои собственные для демонстрации.

Подробнее: Блог From the Pond

Десять рамок – отличный инструмент для обучения счету пропусков. Найдите здесь 10 заданий и идей.

Добавьте больше математики во время чтения с этими 17 книжками с картинками по математике.

Этот пост содержит партнерские ссылки Amazon.WeAreTeachers может получать очень небольшую комиссию при совершении покупок по этим ссылкам.

Тренажёр устного счёта

Повышайте успеваемость в школе

Развивайте память и концентрацию

Тренируйте только нужное

(adsbygoogle=window.adsbygoogle||[]).push({}); Опирайтесь на подсказки

Регулируйте сложность примеров

Учитесь играючи!

Тренажер устного счета онлайн | Клуб любителей математики

Разнообразие режимов

Процесс счёта

Игровая форма

Протокол ошибок

Дополнительная информация

😃 5 мощных ускорителей устного счета

1. Как быстро складывать и вычитать числа

Рассмотрим три случайных примера:

Вернемся к нашим примерам:

Оптимизируем вычитаемые числа:

Итого получим:

Посчитайте сейчас представленные ниже примеры этим способом:

2. Как быстро умножать на 4, 8 и 16

Примеры раскладывания чисел на более простые:

Отработайте этот способ на следующих примерах:

3. Деление числа на 5

Возьмем следующие примеры:

Для того чтобы проработать этот способ решите следующие примеры:

4.

Игра «Быстрое сложение»

Игра “Быстрый счет”

Игра “Угадай операцию”

Игра “Упрощение”

Задание на сегодня

Урок взят из курса “Устный счет за 30 дней”

Другие развивающие курсы

Деньги и мышление миллионера

Скорочтение за 30 дней

Развитие памяти и внимания у ребенка 5-10 лет

Супер-память за 30 дней

Как улучшить память и развить внимание

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Приемы устного счета

Тренажер устного счета онлайн | Инструкция, нормы, разряды

ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ТРЕНАЖЕРА

Простое в сложном. Устный счет

Простое в сложном. Устный счет

2.5. Умножение на число 111, 1111 и так далее, зная правила умножения двузначного числа на число 11

Приемы устного счета на уроках математики в 5

17 фантастических идей для обучения механическому счету – раннее обучение

1. Счет с использованием разных голосов!

2. Подсчет с помощью марионетки

3.Подсчет песен, которые подсчитывают

4. Подсчет действий в повседневной жизни

5. Подсчет предметов в повседневной жизни

6. Счет по кругу

7. Подсчет с партнером / взрослым

8. Подсчет в командах

9. Подсчет марта

10. Счет танцев

11. Подсчет действий

12. Использование пальчиковых марионеток

13. Шепот как шпион

14. Zoom Zoom Zoom Game

15. Змея, считающая и прыгающая

16. Splat The Playdoh

17. Аплодисменты и счет

Заключение

Недавние сообщения

способов научить счету – PreKinders

Наборы для изготовления

Подсчет ящиков для мусора

Пунктирные карты

Подсчет фруктов

Путь Игры

Игры на счет и совпадение

Домино

Марки для лепки

Наборы нумерованных чертежей

Рыбная ловля

Игра божья коровка

Счетные самолеты

Опирайтесь на подсказки