Методы решения пределов. Неопределённости.Порядок роста функции
Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a .
Или другими словами, число A является пределом функции y = f (x) в точке x 0 , если для всякой последовательности точек из области определения функции , не равных x 0 , и которая сходится к точке x 0 (lim x n = x0) , последовательность соответствующих значений функции сходится к числу A .
График функции, предел которой при аргументе, который стремится к бесконечности, равен L :
Значение А является пределом (предельным значением) функции f (x) в точке x 0 в случае, если для всякой последовательности точек , которая сходится к x 0 , но которая не содержит x 0 как один из своих элементов (т.е. в проколотой окрестности x 0 ), последовательность значений функции сходится к A

Предел функции по Коши.
Значение A будет являться пределом функции f (x) в точке x 0 в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x , удовлетворяющего условию 0 , будет выполнено неравенство | f (x) A | .
Будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A , записывается таким образом:
Причем значение, к которому стремится переменная x , может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.
Чтоб понять, как находить пределы функции , лучше всего посмотреть примеры решения.
Необходимо найти пределы функции f (x) = 1/ x при:
x → 2, x → 0, x → ∞.
Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:
Найдем второй предел функции . Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции
Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x . Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/ x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю.
Необходимо вычислить предел функции
Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя – это x 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:
Ответ
Первым шагом в нахождении этого предела , подставим значение 1 вместо x , в результате чего имеем неопределенность . Для её решения разложим числитель на множители , сделаем это методом нахождения корней квадратного уравнения
D = 2 2 – 4*1*(-3) = 4 +12 = 16 → √ D = √16 = 4
x 1,2 = (-2 ± 4) / 2 → x 1 = -3; x 2 = 1.
Таким образом, числитель будет таким:
Ответ
Это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.
Чтобы решить пределы, следуйте правилам:
Разобравшись в сути и основных правилах решения предела , вы получите базовое понятие о том, как их решать.
Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.
Постоянное число а называется пределом последовательности {x n }, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству
Записывают это следующим образом: или x n → a.
Неравенство (6.1) равносильно двойному неравенству
a – ε x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .
Последовательность, имеющая предел, называется сходящейся , в противном случае – расходящейся .
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента
Пусть дана функция f(x) и пусть a – предельная точка области определения этой функции D(f), т. е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется предел функции f(x) при
Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.
Определение 2 . Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ
>0 (зависящее от ε), что для всех x , лежащих в ε-окрестности числа а , т.е. для x , удовлетворяющих неравенству
0
Это определение называют определением предел функции по Коши,
Определения 1 и 2 равносильны. Если функция f(x) при x →
a имеет предел , равный А, это записывается в виде
Если функция f(x) при x →
a имеет предел , равный А, это записывается в виде
В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.
Переменная величина, предел которой равен бесконечности, называется
Чтобы найти предел на практике пользуются следующими теоремами.
Теорема 1 . Если существует каждый предел
(6.4)
(6.5)
(6.6)
Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.
Теорема 2.
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,
Теорема 3.
(6.11)
где e » 2.7 – основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.
Используются на практике и следствия формулы (6.11):
(6.12)
(6.13)
(6.14)
в частности предел,
Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а . Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x 0 , если предел
(6.15)
Условие (6.15) можно переписать в виде:
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.
Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.
Функция f(x) называется непрерывной справа в точке x o , если предел
и непрерывной слева в точке x o, если предел
Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.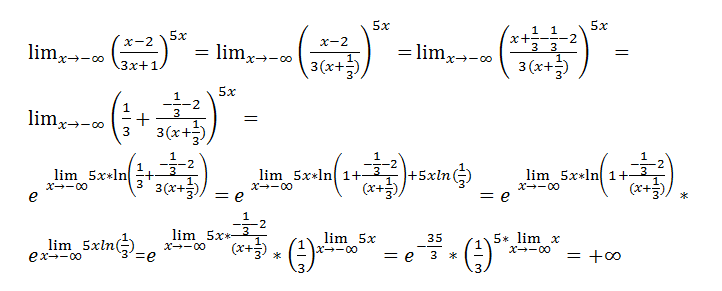
1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .
2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .
Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.
Рассмотрим пример Я. И. Перельмана , дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода – в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода – в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
100×(1 +1/10) 10 ≈ 259 (ден. ед.),
ед.),
100×(1+1/100) 100 ≈ 270 (ден. ед.),
100×(1+1/1000) 1000 ≈271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел
Пример 3.1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.
Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1|
Возьмем любое ε > 0. Так как
x n -1 =(n+1)/n – 1= 1/n, то для отыскания N достаточно решить неравенство 1/n1/ε и, следовательно, за N можно принять целую часть от 1/ε
N = E(1/ε). Мы тем самым доказали, что предел .
Пример 3.2. Найти предел последовательности, заданной общим членом .
Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:
Пример 3.3 . . Найти .
Решение.
Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.
Пример 3.4 . Найти ().
Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:
Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.
Решение. Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел Выберем теперь в качестве x n последовательность с общим членом x n = -1/n, также стремящуюся к нулю. Поэтому предел не существует.
Пример 3.6 . Доказать, что предел не существует.
Решение. Пусть x 1 , x 2 ,…, x n ,… – последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞
Если x n =
p
n, то sin x n = sin (p
n) = 0 при всех n и предел Если же
x n =2
p
n+
p
/2, то sin x n = sin(2
p
n+
p
/2) = sin
p
/2 = 1 для всех n и следовательно предел . Таким образом, не существует.
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная , поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна , значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
Решаем:
Разделим числитель и знаменатель на
Пример 15
Найти предел
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице . Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения , приходится использовать самые разные тригонометрические формулы , а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»Данную неопределённость «обслуживает» второй замечательный предел , и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой .
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы , которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. 2 стремится к нулю.
2 стремится к нулю.
Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их свойства перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются исключения из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1
В ряде задач встречаются функции, при вычислении пределов которых возникает неопределенность – ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится применение правила Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f”(x)/l”(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности.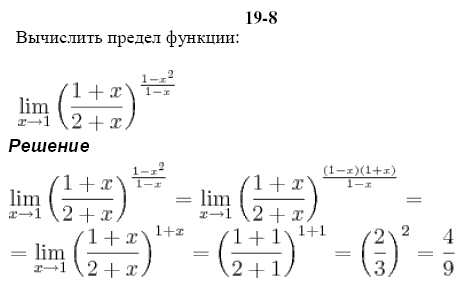 (n-1)
(n-1)
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Вычислить пример онлайн с решением
В Интернете столько различных программ, что возникает вопрос: можно ли вычислять примеры для их решения в режиме онлайн. Такие приложение уже существуют. Они самостоятельно ищут ответ на ваши задачи и показывают на экране ответ. Это очень удобно и практично. О них и пойдёт речь далее.
Содержание
- «Математический сканер по фото» — поможет вычислить любой пример
- Порядок действий для проведения вычислений онлайн:
- Решение задач онлайн через камеру телефона
- Mathway — онлайн-сервис для вычисления примеров
- «Контрольная работа» — быстрое решение сложных задач онлайн
- Pocket Teacher — поможет вычислить уравнения по математике
- Видео-инструкция
«Математический сканер по фото» — поможет вычислить любой пример
Задание по разным предметам иногда заставляет нас с любой успеваемости зайти в тупик. Пример может сильно отличаться от тех, которые были рассмотрены в школе. Чтобы решить его, придется искать решение в Интернете вручную. Или просить более опытных людей помочь с этим заданием. Есть ещё один вариант выхода с этого положения — воспользоваться онлайн сканером «Математический сканер по фото» на Андроид.
Или просить более опытных людей помочь с этим заданием. Есть ещё один вариант выхода с этого положения — воспользоваться онлайн сканером «Математический сканер по фото» на Андроид.
Он устанавливается на мобильный телефон в виде приложения и способен решать ваши задания при помощи фотографии.
Порядок действий для проведения вычислений онлайн:
- Работать сканер может в двух режимах: по фотографии и при вводе условий вручную;
- Чтобы сфотографировать пример, наведите камеру на условие и нажмите кнопку создания фото;
- На следующем экране появится решение этой задачи с несколькими действиями. Чтобы больше узнать о данном примере, просмотрите внимательно все его этапы решения. И попробуйте разобраться самостоятельно.
Если не выходит понять задачу, в меню приложение «Онлайн» сканер можно найти статьи по теме. В нём множество учебного материала на разные темы по математике и другим предметам. Для этой программы не требуется подключение к Интернету. Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню. Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню. Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Это может быть полезным: решение задач по физике по фото.
Решение задач онлайн через камеру телефона
С каждым учебным годом математика усложняет задачи для учащихся. Становится всё труднее решать примеры быстро и практически не задумываясь. Появляются новые темы, функции, уравнения и прочее. Чтобы со всем этим справиться при вычислении примеров с верным решением, используйте «Камеру Калькулятор» на Андроид.
Это один из лучших способов решать примеры автоматически, применяя лишь камеру мобильного телефона. Пользователю нужно сфотографировать пример, чтобы решить его.
Возможности приложения:
- В приложении есть умный и удобный калькулятор для решения любых задач по предмету;
- Встроен научный калькулятор со всеми инструментами, которые есть в классической версии;
- Отдельно реализован калькулятор уравнений.

Мобильное приложение «Камера Калькулятор» способно справляться с решением интегралов, интеграций, производных, дифференцирования, пределов и многое другое. Для тех пользователей, которым необходимы простые функции, он является таковым. Более сложные инструменты находятся в меню и могут быть запущены при необходимости. Поэтому вычислить любой пример онлайн и получить его подробное решение не составим труда. Программа будет полезна школьникам старших классов, которые сталкиваются со сложными заданиями на самостоятельных работах и контрольных.
Также «Камера Калькулятор» станет незаменимым помощником для студентов разных профессий. Приложение не займёт много памяти в мобильном телефоне и может работать беззвучно.
Читайте также: решение задач по геометрии по фото.
Mathway — онлайн-сервис для вычисления примеров
С вычислением сложных примеров и их вычислением в Интернете поможет онлайн-приложение Mathway. Без надобности устанавливать какие-либо программы на телефон. Откройте в браузере ссылку на сайт Mathway.com.
Без надобности устанавливать какие-либо программы на телефон. Откройте в браузере ссылку на сайт Mathway.com.
При нажатии на кнопку с фотоаппаратом на экране появится виртуальная клавиатура со всеми подходящими символами для решения математических уравнений. Если к вашему устройству подключена веб-камера или вы используете сайт с мобильного устройства, то появится возможность сфотографировать условия задачи.
Также его можно записать в пустой строке, которая выше виртуальной клавиатуры приглашает: «Введите задачу». Чтобы выбрать другой предмет в онлайн-сервисе, нажмите на кнопку меню вверху.
Среди них можно выбрать:
- Решение задач по элементарной математике;
- Тригонометрии;
- Статистике,
- Алгебре;
- Линейной алгебре;
- Химии;
- Создание графиков;
- Основа математического анализа.
В меню онлайн-программы доступны примеры по разным предметам. Чтобы их открыть, нажмите на кнопку с тремя точками вверху. И выберите пункт «Примеры». Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране. Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
И выберите пункт «Примеры». Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране. Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
«Контрольная работа» — быстрое решение сложных задач онлайн
Быстро и точно примеры может решать сервис «Контрольная работа» www.kontrolnaya-rabota.ru/s. Всё что нужно пользователю — это ввести условие в пустую строку. Сервис удобно использовать на мобильном телефоне через браузер или на компьютере во время выполнения задания. Чтобы получить большой список калькуляторов для разных условий, на главной странице необходимо выбрать кнопку «Начать сейчас».
Из перечня перед вами можно выбрать:
- Решение уравнений и упрощённых выражений онлайн с возможностью вводить условия;
- Калькулятор для решения неравенств с отображением графиков решения на экране;
- Поиск пределов в сервисе — найдите его для любой функции.
 Применяются решения по Лопиталю;
Применяются решения по Лопиталю; - На сайте есть производные функций, графики. Вы сможете построить свой график в пространстве;
- Калькулятор для решения неравенств;
- Доступны практически любые действия с неравенствами: умножение, возведение в степень, ранг матрицы, обратные матрицы и другое;
- На сайте есть возможность решить со своими условиями комплексные числа, геометрическую интерпретацию.
Кроме этого на сайте ещё множество возможностей, связанных с решением математических задач и условий по другим предметам. Можно найти таблицы интегралов, Брадиса, таблицы производных. Примеры из высшей математики и полезные и интересные калькуляторы. Если у вас возникнут трудности, в нижней части списка с возможностями находится подробная инструкция, как пользоваться тем или иным инструментом. Представлено множество текстов, описывающих не только работу калькуляторов и таблиц, но и с рассмотрением конкретных примеров.
Pocket Teacher — поможет вычислить уравнения по математике
Рассмотрим ещё один интересный онлайн-сервис с решениями для математики. Называется он Pocket Teacher.
Называется он Pocket Teacher.
Ссылка: https://www.pocketteacher.ru/solve-page. Сайт является большим и всесторонним инструментом, для решения практически любых математических условий заданий. На главной странице пользователю предлагается выбрать один из трёх основных разделов сайта: алгебра, геометрия, высшая математика и текстовая задача. На экране отображается клавиатура с математическими знаками.
- Начните вводить символы условия своей задачи;
- Возле примера находятся кнопки для управления вводом. Нажмите «Очистить» или «Удалить», если допустили ошибку при вводе;
- Чтобы пример решить, нажмите на соответствующую кнопку справа и выберите пункт «Решение».
Каждое решение на время сохраняется на сайте. Его можно вернуть при помощи кнопок на панели. Это приложение можно скачать на мобильный телефон с Android или с IOS. Ссылки расположены на главной странице сайта.
Видео-инструкция
Рассмотренные инструменты помогут вычислить любой сложный пример в режиме онлайн с подробным решением. Посмотрите о дополнительных приложениях в видео.
Посмотрите о дополнительных приложениях в видео.
Всегда есть предел. Пределы в математике для чайников: объяснение, теория, примеры решений
Хранил в себе один секрет и был в семье примерный муж.
Всё было, вроде, как всегда: жена готовила обед…
Но приключилась вдруг беда: он взял и вспомнил про секрет.
Под шум и кислый запах щей, ворчанье суженой с утра,
Он вспомнил всё до мелочей, как будто было то вчера…
…Она сидела у окна, и мягкий чудный лунный свет
Окрасил в бледные тона её прекрасный силуэт…
Струились пряди по плечам, скользили змейками на грудь…
И он подумал сгоряча: «Женюсь на ней когда – нибудь!»
Он вспомнил всё до мелочей: изгибы линий, мягкость губ…
И жар её простых речей, и за окном огромный дуб.

Сплетенье рук… Слиянье тел… Каскад каштановых волос…
И то, как он её хотел до исступления, до слёз!
Признаний трепетных поток, как он на ушко их шептал!
Смешной над ухом завиток, что от дыханья трепетал…
Она смотрела на него глазами влажными, как ночь.
Слова пьянили, как вино: «Люблю тебя… Роди мне дочь…»
С утра он потерял покой: то суетился, то скучал…
Потом, закрыв лицо рукой, сидел на стуле и молчал.
Жена ворчала, как всегда. Ругала убежавший суп…
И он отметил, что года ей, постаревшей, не к лицу.
Как не идёт ей белый цвет и пряди крашеных волос.
И целых двадцать восемь лет всё как – то было не всерьёз…
Вдруг он вскочил, схватил пальто, забыл про шапку и носки.
Все двадцать восемь лет – не то… Все двадцать восемь зим – тоски.
Нашёл тот дом. У дома – дуб. Взбежал по лестнице стрелой…
Унять бы дрожь с холодных губ, и трусость гадкую – долой!
Наверное, она сейчас пьет чай и кутается в шаль…
И из её прекрасных глаз струится тихая печаль…
А может, принялась вязать? А может кружево плести?
Так много надо ей сказать! А главное сказать – прости…
Открыла дверь… В глазах – вопрос.
 Ей было снова двадцать лет…
Ей было снова двадцать лет…Каскад каштановых волос… Знакомый сердцу силуэт…
Над ухом – лёгкий завиток… Как много лет назад – точь в точь…
” Вы не ошиблись?» – Нет, не мог… Вы Аня? ” Вера. Её дочь…»
” А Аня?”- ” Мамы больше нет… Кто Вы?» Он повернулся вспять:
«Я шёл к ней двадцать восемь лет…» – Она ждала Вас… Двадцать пять…
Как закружилась голова… Как сердце ухнуло в груди!
И вспомнил он её слова с мольбою: «Ты не уходи!»
Он сгорбился. Поплёлся прочь. Сплетенье рук… Слиянье тел…
Люблю тебя… Роди мне дочь… А он ведь вправду дочь хотел.
Как странно. Ани больше нет… Заплакал… Бросил в тишину:«Я буду много – много лет любить тебя… Тебя одну…»
P.S. БЕРЕГИТЕ ЛЮБОВЬ – она фундамент вашего счастья…
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Знай, у каждого разное «больно»,
Знай, у каждого разное «страшно».
Не суди со своей колокольни
Неизвестносколькоэтажной.
Не очерчивай взглядом границы,
Не придумывай мозгом пределы.
Что тебе в страшном сне не приснится,
Для кого-то – обычное дело.
Знай, у каждого разное «надо»,
Знай, у каждого разное «сложно».
Впрочем, и представление ада
Обобщить и сравнить невозможно.
Знай, что правда бывает другая,
А не та, что приносят на блюде.
Присмотрись к тем, чьи судьбы пугают,
Это – самые сильные люди.
Не говори, что я тебя не помню —
Я помню всё, и много раз на дню
Я повторяю номер телефонный,
Но никогда тебе не позвоню.
Вот-вот, казалось, сердце разорвется
И на пределе одиноких дней
За горизонт зашли в душе моей.
Была любовь, была любовь, была!
И к этой фразе нечего прибавить.
Сгорел волшебный замок наш дотла
И пепла не оставил нам на память.
Я помню всё, и сад цветущий помню,
И сквозь листву — лучи со всех сторон,
Как будто с белой-белой колокольни
В душе — ты слышишь — льётся тихий звон.
Любовь ушла и больше не вернётся,
И чтоб не вечно тосковать о ней,
Твои глаза, как два печальных солнца,
За горизонт зашли в душе моей.
За счастьем погоня опять неудачна…
И вечер дождливый, на улице мрачно…
А в детстве…намазала булку вареньем
И точно счастливая, до одуренья…
Гламур, этикет, бриллианты, джакузи…
Теперь, кроме счастья, в судьбе «All inclusive»,
А в детстве с подсолнуха семечки ела,
И счастью, казалось, не будет предела…
Мы стали похожи на клоунов очень…
У каждого грим, что снаружи хохочет…
А в детстве… лишь солнце с небес пробивалось
И сердце счастливое так улыбалось…
Людей отбираем, как в «Золушке» гречку…
Всех нужных – в контакты… Невыгодных в печку…
А в детстве в нас верило чистое небо…
Где радость от запаха свежего хлеба?
И дружба теперь покупается тоже…
Дожились… Живём в мире меха и кожи…
А в детстве дворнягу от ливня спасали…
И счастье давая, его получали.
Мы искренность, чуткость теряли с годами…
Границы и рамки придумали сами…
Есть булка и банка с вишнёвым вареньем?
Так будьте счастливыми, до одуренья!
Я смотрю на тебя и понимаю, что по-прежнему люблю тебя. Эта любовь – хроническая болезнь последних лет. Она приносит настолько нестерпимую боль, что я кидаюсь на совершенно посторонних людей, пытаясь обмануться ими, с ними вдруг в этих объятиях найду то самое обезболивающее, которое, по словам обладателей морщинистых сердец, вообще не существует. Я понимаю, что обманываюсь, но все равно продолжаю обниматься-убиваться не могу иначе, болит ведь, изводит, по ночам спать не дает, вот сижу на подоконнике и, еще минута, истошно закричу от пыток иллюзий. Обратиться к тебе за помощью? Бесполезно. Ты знаешь о моей любви, но тебе она ни к чему, «своих невысказанных чувств полный рот». Мы в одной паутине безответности, но не можем помочь друг другу. Ты обхватываешь руками тонкие белые нити-прутья и смотришь куда-то за пределы реальности, надеясь черт знает на чью помощь. И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то – подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то – подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
Ваша жизнь – сплошное вранье, порнуха, бытовуха, интернет-зависимость и сотово-мобильное рабство. Ну разве я не прав? Вот скажите мне, вы когда-нибудь совершали что-нибудь по настоящему из ряда вон? Никогда. И не сможете. Знаете почему? Потому что все это находится за пределами вашей зоны комфорта. Вы упакованы в нее. Как в полипропиленовый мешок. Вы куски мяса, зажатые рамками быта и работы. Или я не прав? Может, я ошибаюсь? Поправьте меня.
Например, можете подарить свой мобильник первому встречному? А? Вопрос на засыпку. Можете прямо сейчас отформатировать винт на вашем компьютере? Стремно? Обосрались? А знаете, почему вы этого не сделаете? Потому что это равноценно самоубийству. Вы без этого не существуете.
Вы без этого не существуете.
App Store: Mathway — решатель задач
Описание
Mathway — мировой лидер среди программ для решения задач, в арсенале которого миллиарды решенных задач и которому доверяют миллионы пользователей. От элементарной алгебры до комплексных расчетов, Mathway мгновенно решает самые сложные математические задачи — просто введите условия задачи (или наведите камеру и сделайте фото!) и вы немедленно получите бесплатный ответ. Необходимы подробные, пошаговые решения? Mathway — как карманный частный репетитор, который без промедления помогает в решении домашних заданий в любом месте и в любое время.
Mathway охватывает все уровни математики, в том числе:
Начальную математику (арифметика, целые числа, дроби, десятичные числа, корни, коэффициенты и многое другое)
Алгебру (линейные уравнения/неравенства, квадратные уравнения/неравенства, абсолютные уравнения/неравенства, системы уравнений, логарифмы, функции, матрицы, графики и многое другое)
Тригонометрию / начало анализа (тригонометрические функции, тождества, конические сечения, векторы, матрицы, комплексные числа, последовательности и ряды и многое другое)
Математический анализ (пределы, производные, интегралы и многое другое)
Статистику (вероятность, перестановки, комбинации и многое другое)
Есть математическая задача? Обратитесь к Mathway.
«Простая в использовании и эффективная программа Mathway понравится любому, кому приходится решать математические задачи, от учеников старших классов до студентов институтов», — Yahoo! News
«Если вам нужно решить математические задачи, обратитесь к Mathway. Это приложение продемонстрирует весь процесс решения, чтобы вы могли параллельно учиться сами», — CNET
«Mathway — незаменимый инструмент в тех случаях, когда нужно решить задачу. Это приложение помогает с домашними заданиями по математике. Оно не просто выполняет за вас задания, но и обучает правильному порядку решения. Все, что нужно сделать, — это ввести уравнение и нажать на кнопку Enter», — Lifehack
Mathway предоставляет ответы на задачи совершенно бесплатно. Для пошаговых решений доступна дополнительная ежемесячная или годовая подписка. Кроме того, Mathway предлагает дополнительную подписку на онлайн-обучение для связи с преподавателем в любое время, когда требуется дополнительная помощь. Если выбран вариант премиум-подписки:
Оплата будет списана с учетной записи iTunes при подтверждении покупки
Подписка автоматически продлевается, если автоматическое продление не будет отключено минимум за 24 часа до окончания текущего периода
С учетной записи будет снята плата за продление в течение 24 часов до окончания текущего периода подписки по тому же месячному или годовому тарифу, выбранному при ее оформлении
Подписками может управлять пользователь, а автоматическое продление можно отключить, перейдя в настройки учетной записи пользователя после покупки
Условия использования: https://www. mathway.com/terms
mathway.com/terms
Политика конфиденциальности: https://www.mathway.com/privacy
Версия 4.7.1
– исправление ошибок
Оценки и отзывы
Оценок: 3,2 тыс.
Супер!
Приложение лучшее из за объяснения решения! Максимум звёзд
Этот интерфейс…
Считает вроде бы правильно (лучше чем Photomath), но пользоваться приложением просто невозможно. Нет кнопок sin/cos, их надо набирать вручную «Очень удобно».
И да, если Photomath работает офлайн, то это бабуйня без интернета работать не будет
124
Пока что я смог это приложение запутать только при решении транцендентных уравнений, однако графики строит хорошо, в общем 5 звёзд просто потому что лучше я все оано ничего не нашёл))
Разработчик Mathway, LLC указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
- Контактные данные
- Идентификаторы
- Данные об использовании
Связанные с пользователем данные
Может вестись сбор следующих данных, которые связаны с личностью пользователя:
- Контактные данные
- Пользовательский контент
- Идентификаторы
- Данные об использовании
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
- Пользовательский контент
- Данные об использовании
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Подробнее
Информация
- Провайдер
- Mathway, LLC
- Размер
- 54,7 МБ
- Категория
- Образование
- Возраст
- 4+
- Copyright
- © 2022 Mathway
- Цена
- Бесплатно
- Сайт разработчика
- Поддержка приложения
- Политика конфиденциальности
Вам может понравиться
Примеры решения пределов с корнями с ответами
Основные свойства пределов с корнями
Теорема
Для нахождения предела функции необходимо подставить в предел вместо Х то значение переменной, к которому стремится Х.
Нужна помощь в написании работы?
Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений пределов с корнями
Пример №1
Задание
Найти предел
Решение
Мы имеем неопределенность вида
Первый шаг – разделить числитель и знаменатель на ”х” в высшей степени. Старшая степень для числителя в данном случае равна двум.
Со знаменателем немного сложнее. Так как у нас корень, обращаем внимание только на самое ”старшее” слагаемое –
Число (4) – это константа, его тоже отбрасываем. Находим корень
Так как числитель и знаменатель оказываются одного порядка роста, предел равен конечному числу, отличному от нуля.
Видим, что функции эквивалентны на бесконечности.
Оформляем решение:
Ответ: 1
Пример № 2
Задание
Найти предел с корнем
Решение
Подставляем
в подпредельную функцию:
Получаем неопределенность
Домножаем числитель и знаменатель на выражение, сопряженное к нему –
так как он содержит корень.
Далее, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел. Последний шаг – сокращение функции на
Ответ: -8
Пример №3
Задание
Решить предел с корнем
Решение
Подставляем
в предел и получаем неопределённость вида
Как и в предыдущих примерах, находим старшую степень для числителя и знаменателя, и выносим её за скобки.
И опять подставляем
в предел и решаем:
Ответ:
Пример №4
Задание
Вычислить предел корня:
Решение
Аналогично предыдущим примерам, подставляем
в предел и видим:
Находим сопряженное, в данном случае это
Как и в примере №2, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел:
Раскрываем скобки и упрощаем. Затем выносим х за скобки и сокращаем:
Как и в начале, подставляем в предел, получаем:
Ответ:
Пример №5
Задание
Вычислить предел функции
Решение
Если подставить х=1, видно, что и числитель, и знаменатель обращаются в ноль. Получаем неопределенность вида
Получаем неопределенность вида
Как и в предыдущих примерах, первым шагом находим сопряжённое –
и домножаем на него числитель и знаменатель.
Применяем правило разности квадратов
и преобразовываем предел:
Сокращаем числитель и знаменатель на (x-1) и приходим к конечному ответу:
Ответ: 6
Пример № 6 Задание Вычислить предел: Решение: Первый шаг – подставить в предел выражение и убедиться, что выходит неопределённость вида Шаг второй – раскрываем нашу неопределенность путём умножения числителя и знаменателя на сопряжённое выражение, в данном случае – Далее, пользуясь формулой разности квадратов раскладываем числитель: Подставляем х=3 в предел и вычисляем: Ответ:
Пример №7
Задание
Вычислить предел
Решение
Как и в предыдущих заданиях, подставляем
и убеждаемся, что имеем дело с неопределённостью вида
Порядок действий стандартный. Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Перемножаем знаменатель и сокращаем в числителе и знаменателе
Подставляем, как и ранее, х=3 и находим ответ:
Ответ: 17,8
Пример №8
Задание
Определить предел функции
Решение
Смотрим на функцию, подставляем
мы имеем дело с неопределённостью вида:
Начинаем работать с функциями, содержащими корень. Умножаем числитель и знаменатель на сопряжённое выражение и упрощаем предел:
После преобразований получаем ответ:
Ответ: -2
Пример №9
Задание
Решить предел
Решение:
Подставляя
в выражение лимита, подтверждаем догадки, что перед нами неопределённость вида
Как и раньше, первый шаг – избавиться от иррациональности с помощью домножения числителя и знаменателя на соответствующее сопряженное выражение.
Раскрываем скобки и сокращаем выражения на
Неопределённости
больше нет и ничего нам не мешает вычислить пример:
Ответ:
Пример №10
Задание
Вычислить предел
Решение
Оба лимита числителя и знаменателя равны нулю, значит опять неопределённость вида
Находим сопряжённое к числителю и знаменателю число:
Домножаем на полученное выражение числитель и знаменатель, раскрываем скобки и упрощаем:
Раскладываем числитель и знаменатель:
Вычисляем предел:
Ответ:
Средняя оценка 4 / 5. Количество оценок: 4
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
18700
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Оценка пределов – методы, объяснение и примеры
На уроках предварительного исчисления и исчисления вас попросят оценить пределы различных функций. В этой статье основное внимание будет уделено общим методам, которые нам понадобятся для оценки пределов различных функций.
В этой статье основное внимание будет уделено общим методам, которые нам понадобятся для оценки пределов различных функций.
При оценке пределов используются различные методы, которые потребуют от нас обновления наших знаний об оценке, факторинге и рационализации факторов. Эти методы ускорят оценку пределов.
Поиск пределов может быть как простым, как оценка значений функций, так и сложным, например, манипулирование функциями, чтобы мы могли найти его предел.
В этом разделе мы изучим различные методы, которые помогут нам оценить пределы простых и сложных функций.
Вот некоторые приемы, которые мы изучим в этой статье:
- Подстановка
- Факторинг
- Использование конъюгатов
- Алгебраические манипуляции
Пределами тригонометрических функций также можно манипулировать с помощью специальных свойств, но мы написали отдельную статью. В большинстве этих методов используются алгебраические концепции, поэтому этот раздел также является отличным способом освежить наши прошлые знания.
Оценка пределов путем подстановки
Существует большое количество функций, пределы которых можно вычислить путем подстановки. В общем случае $\lim_{x \rightarrow a} f(x)$ можно определить, найдя $f(a)$. Это означает, что предел функции при приближении $x$ к $a$ можно вычислить, подставив $a$ в выражение функции. 92 + 12x – 20$ равно $-60$. Предел полиномиальных функций, вообще говоря, можно вычислить с помощью этой техники.
Аналогичный процесс можно применить и для других функций! Это звучит просто, верно? Итак, почему бы нам не использовать эту технику для всех функций?
Бывают случаи, когда мы оцениваем $f(a)$ и получаем $\dfrac{0}{0}$ и $\dfrac{k}{0}$, где $k$ — константа. Когда это произойдет, нам придется применить другие методы, чтобы найти предел данной функции.
Оценка пределов с помощью факторинга
Один из методов, который может помочь нам, когда замена невозможна, — это факторизация функции. Обычно мы используем это при нахождении пределов рациональных функций, но подстановка возвращает либо $\dfrac{0}{0}$, либо $\dfrac{k}{0}$, где $k$ — константа. 2 + 4x + 4} = \dfrac{1}{2}$.
2 + 4x + 4} = \dfrac{1}{2}$.
Этот метод обычно применяется для $\lim_{x\rightarrow a} f(x)$, где $f(x)$ — рациональная функция, а $a$ — корень $f(x)$’ с знаменатель.
Оценка пределов с помощью сопряженных функций
Другой метод, помогающий нам при оценке пределов, — это использование сопряженных функций и обращение рационализации функции.
Этот метод обычно используется, когда мы хотим найти $\lim_{x\rightarrow a} f(x)$ и работаем с функцией, которая содержит подкоренные выражения, а $a$ является корнем знаменателя. Чтобы применить эту технику, мы применим следующие шаги:
- Найдите сопряженное число числителя.
- Умножьте числитель и знаменатель на сопряженное.
- Если новая функция не возвращает $\dfrac{0}{0}$, примените метод подстановки.
Давайте посмотрим на $\lim_{x \rightarrow 0} \dfrac{\sqrt{x + 4}-2}{x}$?
$ \begin{align} \lim_{x \rightarrow 0} \dfrac{\sqrt{x + 4}-2}{x} &= \dfrac{\sqrt{0 + 4}-2}{0} \\&=\dfrac{2 – 2}{0}\\&=\color{red} \dfrac{0}{0}\end{aligned}$ 92}{x(\sqrt{x + 4} + 2)}\\&=\lim_{x \rightarrow 0} \dfrac{x + 4 – 4}{x(\sqrt{x + 4} + 2) }\\&=\lim_{x \rightarrow 0} \dfrac{\cancel{x}}{\cancel{x}(\sqrt{x + 4} + 2)}\\&=\lim_{x \rightarrow 0} \dfrac{1}{\sqrt{x + 4} + 2}\end{aligned}$
После того, как мы переписали функцию, чтобы она не возвращала неопределенное значение, теперь мы можем заменить $x = 0$ в новое выражение.
$\begin{align} \lim_{x \rightarrow 0} \dfrac{1}{\sqrt{x + 4} + 2}&= \dfrac{1}{\sqrt{{\color{blue}0 } + 4} + 2}\\&= \dfrac{1}{\sqrt{4}+2}\\&=\dfrac{1}{2 + 2}\\&=\dfrac{1}{4 } \end{выровнено}$
Это означает, что $\lim_{x \rightarrow 0} \dfrac{\sqrt{x + 4}-2}{x} = \dfrac{1}{4}$, и мы смогли оценить предел, используя сопряжения числителя.
Оценка пределов с помощью алгебраических манипуляций
Бывают случаи, когда форма функции, представленная в задаче, должна быть изменена, прежде чем мы сможем найти предел функции. Если замена не применима к нашей задаче, мы можем сделать следующее:
- Проверить, можем ли мы еще больше упростить числитель или знаменатель. 9n}$, где $n$ — высшая найденная степень.
- Если числитель содержит дроби, умножьте и знаменатель, и знаменатель на наименьший общий знаменатель, общий для членов числителя.
В следующих примерах вы можете столкнуться с другими ситуациями, но вам не о чем беспокоиться. 2} – \ dfrac {1} {4}} {x – 2} $, когда $ x $ приближается к $ 2 $. 92 + 5х – 3 = 3$.
2} – \ dfrac {1} {4}} {x – 2} $, когда $ x $ приближается к $ 2 $. 92 + 5х – 3 = 3$.
Второе выражение показывает рациональную функцию. У вас может возникнуть соблазн исключить факторы, но всегда проверяйте, применяется ли сначала метод замещения.
$\begin{align} \lim_{x \rightarrow -2} \dfrac{x – 1}{3x} &=\dfrac{{\color{blue}-2} – 1}{3{\color{blue }(-2)}}\\&= \dfrac{-3}{-6}\\&= \dfrac{1}{2} \end{aligned}$
б. Это означает, что $\lim_{x \rightarrow -2} \dfrac{x – 1}{3x} = \dfrac{1}{2}$.
Используя тот же процесс, давайте посмотрим на оцениваемый предел для третьего выражения. 94 – 81}{х – 3} = 108$.
Пример 3
Оцените предел $f(x) = \dfrac{\sqrt{x + 8} – 4}{x – 8}$, когда $x$ приближается к $8$.
Решение
Давайте сначала перепроверим и посмотрим, можем ли мы напрямую подставить $x = 3$ в выражение.
$\begin{align} \lim_{x \rightarrow 8} \dfrac{\sqrt{x + 8} – 4}{x – 8} &= \dfrac{\sqrt{8 + 8} – 4}{ 8 – 8}\\&= \dfrac{4 – 4}{8 – 8}\\&=\color{red} \dfrac{0}{0}\end{aligned}$
Отсюда видно, что сначала нам нужно манипулировать $f(x)$. 2}{(x – 8)(\sqrt{x + 8} + 4)}\\&=\lim_{x \rightarrow 8}\dfrac{ x + 8 – 16}{(x – 8)(\ sqrt{x + 8} + 4)}\\&=\lim_{x \rightarrow 8}\dfrac{x -8}{(x – 8)( \sqrt{x + 8} + 4)} \end{aligned}$
2}{(x – 8)(\sqrt{x + 8} + 4)}\\&=\lim_{x \rightarrow 8}\dfrac{ x + 8 – 16}{(x – 8)(\ sqrt{x + 8} + 4)}\\&=\lim_{x \rightarrow 8}\dfrac{x -8}{(x – 8)( \sqrt{x + 8} + 4)} \end{aligned}$
Числитель был упрощен за счет использования разницы двух квадратов. Теперь, когда мы видим общий множитель $x – 8$, общий для числителя и знаменателя, мы можем сократить его, чтобы вычислить $\lim_{x \rightarrow 8} f(x)$ подстановкой.
$\begin{align} \lim_{x \rightarrow 8}\dfrac{\cancel{\color{blue}x-8}}{\cancel{\color{blue}(x-8)}(\sqrt {x + 8} + 4)}&= \lim_{x \rightarrow 8} \dfrac{1}{\sqrt{x + 8} + 4} \\\\ \lim_{x \rightarrow 8} \dfrac{ 1}{\sqrt{x + 8} + 4} &= \dfrac{1}{\sqrt{{\color{blue} 8} + 8} + 4}\\&=\dfrac{1}{\sqrt {16}+4}\\&=\dfrac{1}{8}\end{выровнено}$
Это означает, что $\lim_{x \rightarrow 8} \dfrac{\sqrt{x + 8} – 4}{x – 8} = \dfrac{1}{8} $, и мы смогли оценить это с помощью обратная рационализация выражения.
Пример 4
Оцените предел $f(x) = \dfrac{\dfrac{x}{2-x} + \dfrac{3}{4}}{x + 6}$ как $x$ приближается к $-6$.
Решение
Мы не можем вычислить $\lim_{x \rightarrow -6} f(x)$ подстановкой, что подтверждается вычислениями, показанными ниже.
$ \begin{align} \lim_{x \rightarrow -6} \dfrac{\dfrac{x}{2-x} + \dfrac{3}{4}}{x + 6}&= \dfrac{ \dfrac{\color{blue}-6}{2-\color{blue}(-6)} + \dfrac{3}{4}}{{\color{blue}(-6)} + 6}\ \&= \dfrac{-\dfrac{3}{4} + \dfrac{3}{4}}{-6 + 6}\\&=\color{red} \dfrac{0}{0}\end {aligned}$
Поскольку числитель состоит из двух дробей, мы можем сначала умножить числитель и знаменатель $f(x)$ на наименьший общий знаменатель $\dfrac{x}{2-x}$ и $\dfrac {3}{4}$, что равно $4(2 – x)$.
$\begin{align} \lim_{x \rightarrow -6} \dfrac{\dfrac{x}{2-x} + \dfrac{3}{4}}{x + 6} \cdot \dfrac{ \color{blue} 4(2 – x)}{\color{blue} 4(2 – x)}&= \lim_{x \rightarrow -6} \dfrac{\dfrac{x}{2-x} \ cdot {\ color {синий} 4 (2 – x)} + \ dfrac {3} {4} \ cdot {\ color {синий} 4 (2 – x)}} {(x + 6) [{\ color { blue} 4(2 – x)}]} \\&=\lim_{x \rightarrow -6} \dfrac{4x + 3(2 -x)}{4(x + 6)(2 – x)}\ end{aligned}$
Упростите новую форму числителя и посмотрите, содержит ли он общий делитель со знаменателем, чтобы исключить его.
$\begin{aligned} \lim_{x \rightarrow -6} \dfrac{4x + 3(2 -x)}{4(x + 6)(2 – x)}&= \lim_{x \rightarrow -6} \dfrac{4x + 6 – 3x}{4(x + 6)(2 – x)}\\&=\lim_{x \rightarrow -6} \dfrac{4x + 6}{4(x + 6)(2 – x)}\\&=\lim_{x \rightarrow -6} \dfrac{\cancel{\color{blue}4x + 6}}{4\cancel{\color{blue}(4x + 6)}(2 – x)}\\&=\lim_{x \rightarrow -6} \dfrac{1}{4(2 – x)}\end{aligned}$
С новым выражением для $f (x)$, теперь мы можем вычислить $\lim_{x \rightarrow -6} f(x)$, найдя $f(-6)$.
$\begin{align} \lim_{x \rightarrow -6} \dfrac{1}{4(2 – x)} &= \dfrac{1}{4[2 – {\color{blue}(- 6)}]}\\&= \dfrac{1}{4(8)}\\&= \dfrac{1}{32}\end{aligned}$
Отсюда имеем $\lim_{x \ стрелка вправо -6} \dfrac{\dfrac{x}{2-x} + \dfrac{3}{4}}{x + 6} = \dfrac{1}{32}$.
Этот конкретный пример показывает нам, насколько важно для нас применять алгебраические манипуляции для самых сложных функций, чтобы найти предел. Это означает, что нам нужно освоить все эти концепции, чтобы быстрее оценивать пределы.
Пример 5
Другим способом оценки пределов является использование таких технологий, как наши калькуляторы и графические утилиты. Постройте таблицу значений со значениями, близкими к $-6$, и сравните этот результат с нашим ответом в ответе 4. -6,01$
$x$
$-5,99$
$-5,9$
$ f (x) = \ dfrac {\ dfrac {x} {2-x} + \ dfrac {3} {4}} {x + 6} $
$ 0,03125 $
$ 0,03121 $
$? около $0,0313$. Это значение на самом деле имеет смысл, поскольку из примера 4 мы имеем $\lim_{x \rightarrow -6} f(x) = \dfrac{1}{32}$. Обратите внимание, что $\dfrac{1}{32} = 0,03125$, что близко к $0,0313$ (это также результат, когда мы оцениваем $\dfrac{1}{32}$ до трех знаков после запятой.
Это означает, что когда все остальное и методы неприменимы, мы также можем использовать технологию для оценки предела функции.
youtube.com/embed/klQ7xZ0PU5U?rel=0;controls=0;showinfo=0;theme=light” frameborder=”0″ allowfullscreen=”allowfullscreen”>Пределы — формула, значение, примеры
Пределы в математике определяются как значения, к которым функция приближается к выходным данным для заданных входных значений. Пределы играют жизненно важную роль в вычислениях и математическом анализе и используются для определения интегралов, производных и непрерывности. Он используется в процессе анализа и всегда касается поведения функции в конкретной точке. Предел последовательности далее обобщается в понятии предела топологической сети и связан с пределом и прямым пределом в категории теории. Обычно интегралы делятся на два типа, а именно: определенные и неопределенные интегралы. Для определенных интегралов правильно определены верхний и нижний пределы. Тогда как неопределенные интегралы выражаются без ограничений, и при интегрировании функции он будет иметь произвольную константу. Давайте подробно обсудим определение и представление пределов функции со свойствами и примерами.
Давайте подробно обсудим определение и представление пределов функции со свойствами и примерами.
| 1. | Что такое пределы? |
| 2. | Ограничения и функции |
| 3. | Свойства пределов |
| 4. | Предел функции двух переменных |
| 5. | Пределы сложных функций |
| 6. | Пределы экспоненциальных функций |
| 9. | Часто задаваемые вопросы о лимитах |
Что такое ограничения?
Пределы в математике — это уникальные действительные числа. Рассмотрим вещественную функцию «f» и действительное число «c», предел обычно определяется как \(\lim _{x \rightarrow c} f(x)=L\). Это читается как «предел f для x, когда x приближается к c, равному L». «lim» показывает предел, а тот факт, что функция f(x) приближается к пределу L, когда x приближается к c, показан правой стрелкой. 9{+}} \mathrm{f}(\mathrm{x})=\mathrm{L}\)
9{+}} \mathrm{f}(\mathrm{x})=\mathrm{L}\)
Примечание: Предел функции существует между любыми двумя последовательными целыми числами.
Свойства пределов
Вот некоторые свойства пределов функции: Если пределы \( \lim _{x \rightarrow a}\) f(x) и \(\lim _{x \rightarrow a}\ ) g(x) существует, а n является целым числом, тогда
- Закон сложения: \(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)\)
- Закон вычитания: \( \lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a } г(х)\)
- Закон умножения: \(\lim _{x \rightarrow a}[f(x) \cdot g(x)]=\lim _{x \rightarrow a} f(x) \cdot \lim _{x \ стрелка вправо а} g(x)\)
- Закон деления: \( \lim _{x \rightarrow a}\left[\frac{f(x)}{g(x)}\right]=\frac{\lim _{x \rightarrow a} f (x)}{\lim _{x \rightarrow a} g(x)}, \text { где } \lim _{x \rightarrow a} g(x) \neq 0\) 9{2}}\) < ∆ . Он определяется как \(\lim _{(x, y) \rightarrow(a, b)}\) f(x,y) = C.

Пределы функций и непрерывность
Пределы функции и непрерывность функции тесно связаны друг с другом. Функции могут быть непрерывными и прерывистыми. Чтобы функция была непрерывной, если есть небольшие изменения на входе функции, то должны быть небольшие изменения и на выходе.
В элементарном исчислении условие f(X) →λ при x → a означает, что число f(x) может лежать сколь угодно близко к числу λ, пока мы берем число, не равное числу а, но достаточно близко к а. Что показывает, что f(a) может быть очень далеко от λ и нет необходимости даже определять f(a). Очень важный результат, который мы используем для вывода функции, таков: f'(a) данной функции f при числе a можно рассматривать как
f'(a) =\(\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}\)Пределы сложных функций
Чтобы дифференцировать функции сложной переменной, следуйте следующей формуле:
9{х}=\infty\)
Функция \(f(z)\) называется дифференцируемой в \(z=z_{0}\), если
\(\lim _{\Delta z \rightarrow 0} \frac{f\left(z_{0}+\Delta z\right)-f\left(z_{0}\right)}{\Delta z}\ ) существуют. Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)
Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)
☛ Также проверьте:
- Исчисление
- Формула ограничения
- Интеграция
- Производная формула
- Формулы интегрирования
Часто задаваемые вопросы о лимитах
Что такое предельная формула?
Формула пределов: Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a.
Что такое ограничения в вычислениях?
Предел сообщает нам значение, к которому приближается функция по мере того, как входные данные этой функции становятся все ближе и ближе (приближаются) к некоторому числу. Идея предела лежит в основе всех дифференциалов и интегралов в исчислении.
Когда предел не может существовать?
Обычная ситуация, когда предел функции не существует, – это когда односторонние пределы существуют и не равны: функция “прыгает” в точке. Предела при x→0 не существует.
Почему мы используем ограничения в математике?
Предел, математическое понятие, основанное на идее близости, используется главным образом для присвоения значений определенным функциям в точках, где значения не определены, таким образом, чтобы они соответствовали ближайшим значениям.
Как узнать, является ли ограничение односторонним?
Односторонний предел — это значение, к которому функция приближается, когда значения x приближаются к пределу *только с одной стороны*. Например, f(x)=|x|/x возвращает -1 для отрицательных чисел, 1 для положительных чисел и не определено для 0. Односторонний *правый* предел f при x=0 равен 1, и односторонний *левый* предел при x=0 равен -1.
Как пределы вычислений используются в реальной жизни?
Пределы также используются в качестве реального приближения к расчету производных. Таким образом, для выполнения расчетов инженеры будут аппроксимировать функцию, используя небольшие различия в функции, а затем пытаться вычислить производную функции, используя все меньшие и меньшие интервалы в интервалах выборки функции.
Таким образом, для выполнения расчетов инженеры будут аппроксимировать функцию, используя небольшие различия в функции, а затем пытаться вычислить производную функции, используя все меньшие и меньшие интервалы в интервалах выборки функции.
Каков предел функции синуса?
Поскольку sin(x) всегда где-то в диапазоне от -1 до 1, мы можем установить g(x) равным -1/x и h(x) равным 1/x. Мы знаем, что предел как -1/x, так и 1/x при приближении x к положительной или отрицательной бесконечности равен нулю, поэтому предел sin(x)/x при приближении x к положительной или отрицательной бесконечности равен нулю.
Как найти предел функции алгебраически
Если вам нужно найти предел функции алгебраически, у вас есть четыре метода на выбор: подстановка значения x , разложение на множители, рационализация числителя и нахождение наименьшего общий знаменатель. Лучше всего начать с первой техники. Вы можете использовать этот метод только в том случае, если функция непрерывна при значении x , при котором вы берете предел. Если функция не определена в этом x , вы должны перейти к другим методам, чтобы упростить вашу функцию, чтобы вы могли подставить приближенное значение для x.
Если функция не определена в этом x , вы должны перейти к другим методам, чтобы упростить вашу функцию, чтобы вы могли подставить приближенное значение для x.
Найдите предел, подставив значение
x Первый метод алгебраического решения для предела состоит в том, чтобы подставить число, к которому приближается x , в функцию. Если вы получаете неопределенное значение (0 в знаменателе), вы должны перейти к другому методу. Но если ваша функция непрерывна в этом x , вы получите значение, и все готово; Вы нашли свой предел! Например, с помощью этого метода вы можете найти этот предел:Предел равен 3, потому что f (5) = 3, и эта функция непрерывна при x = 5.
Найдите предел, разложив на множители
Факторинг — это метод, который стоит попробовать, когда подключение не удается, особенно когда какая-либо часть данной функции является полиномиальным выражением.Скажем, вас попросили найти этот предел:
Сначала вы пытаетесь подставить 4 в функцию, и вы получаете 0 в числителе и знаменатель, который говорит вам перейти к следующей технике. Квадратное выражение в числителе требует, чтобы вы попытались его разложить на множители. Обратите внимание, что числитель предыдущей функции равен ( x – 4)( x – 2). x – 4 сокращения сверху и снизу дроби. На этом шаге у вас останется f ( x ) = x – 2. Вы можете подставить 4 в эту непрерывную функцию, чтобы получить 2.
Квадратное выражение в числителе требует, чтобы вы попытались его разложить на множители. Обратите внимание, что числитель предыдущей функции равен ( x – 4)( x – 2). x – 4 сокращения сверху и снизу дроби. На этом шаге у вас останется f ( x ) = x – 2. Вы можете подставить 4 в эту непрерывную функцию, чтобы получить 2.
Если построить график этой функции, она будет выглядеть как прямая линия 9.0006 f ( x ) = x – 2, но у него есть дыра, когда x = 4, потому что исходная функция все еще не определена (потому что она создает 0 в знаменателе). Рисунок иллюстрирует это.
Если после того, как вы разложили на множители верхнюю и нижнюю части дроби, член в знаменателе не сократился и искомое значение не определено, предел функции при этом значении составляет x не существует (что можно записать как DNE ).
Например, эта функция действует следующим образом:
( x – 7) вверху и внизу отменяется. Поэтому, если вас попросят найти предел функции, поскольку x приближается к 7, вы можете подставить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти
Поэтому, если вас попросят найти предел функции, поскольку x приближается к 7, вы можете подставить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти
предела DNE, потому что вы получите 0 в знаменателе. Таким образом, эта функция имеет предел везде, кроме случаев, когда x приближается к –1.
Найдите предел, рационализируя числитель
Третий метод, который вам нужно знать, чтобы найти пределы алгебраически, требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, вас попросили найти предел этой функции, поскольку x приближается к 13:Подстановка чисел завершается ошибкой, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет многочлена к фактору. В этой ситуации, если вы умножите числитель и знаменатель на сопряженное с числителем, член в знаменателе, который был проблемой, сократится, и вы сможете найти предел:
Умножьте верхнюю и нижнюю часть дроби на сопряженную.

Сопряженный числитель равен
.Умножив, вы получите такую настройку:
Умножьте члены, используя технику первый, внешний, внутренний, последний (FOIL) в числителе, чтобы получить
, что упрощается до x – 13 (два средних члена отменяются, и вы комбинируете аналогичные термины из ФОЛЬГИ).
Факторы отмены.
Отмена дает вам это выражение:
( x – 13) условия отменяются, оставляя вам этот результат:
Рассчитать пределы.
Когда вы подставляете 13 в функцию, вы получаете 1/6, что является пределом.
Найдите предел, найдя наименьший общий знаменатель
Когда вам дана сложная рациональная функция, вы используете четвертый и последний алгебраический метод нахождения предела. Техника вставки не работает, потому что вы получаете 0 в одном из знаменателей. Функция неразложима, и у вас нет квадратных корней, которые можно было бы рационализировать. Поэтому вы знаете, чтобы перейти к последней технике. С помощью этого метода вы объединяете функции, находя наименьший общий знаменатель (LCD). Условия отменяются, и в этот момент вы можете найти предел.
Поэтому вы знаете, чтобы перейти к последней технике. С помощью этого метода вы объединяете функции, находя наименьший общий знаменатель (LCD). Условия отменяются, и в этот момент вы можете найти предел.Например, выполните следующие действия, чтобы найти предел:
Найдите ЖК-дисплей фракций вверху.
Распределите числители сверху.
Сложите или вычтите числители, а затем сократите члены.
Вычитание числителей дает
, который затем упрощается до
.Используйте правила дробей для дальнейшего упрощения.
Подставьте предельное значение в эту функцию и упростите.
Вы хотите найти предел, поскольку x приближается к 0, поэтому предел здесь равен –1/36.
Об этой статье
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг. Изучала алгебру, деловое исчисление, геометрию и конечную математику в Университете Брэдли. в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг For Dummies, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Изучала алгебру, деловое исчисление, геометрию и конечную математику в Университете Брэдли. в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг For Dummies, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное вычисление,
Калькулятор пределов (решатель) – с шагами
Калькулятор пределов с шагами
Калькулятор пределов помогает найти предел функции с учетом к переменной. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению.
Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для вычисления точного значения.
С помощью этого калькулятора пределов вы можете оценить ограничения относительно \(\text{x , y, z , v, u, t}\) и \(w\) .
Это не так. Используя этот инструмент, вы также можете найти,
- Правый предел (+)
- Левосторонний предел (-)
- Двусторонний предел
Как работает калькулятор предела?
Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.
- Введите функцию в данное поле ввода.
- Выберите соответствующую переменную.
- Введите предельное значение.
- Выберите сторону ограничения. т. е. левое, правое или двустороннее.
- Нажмите кнопку Calculate для получения результата.
- Используйте кнопку Сброс для ввода новых значений и значок на клавиатуре для ввода дополнительных значений.
Вы найдете ответ под инструментом. Щелкните Show Steps , чтобы просмотреть пошаговое решение.
Что такое предел в исчислении?
Предел функции — это значение, к которому f(x) приближается по мере того, как x приближается к некоторому числу. Пределы можно использовать для определения производных, интегралов и непрерывности, находя предел данной функции. Пишется так:
\(\lim _{x\to a}\:f\left(x\right)=L\)
Если f – функция с действительным знаком, а a – действительное число, то Вышеприведенное выражение читается как
предел f x , поскольку x приближается к a равняется L.
Как найти предел? – С шагами
Пределы могут быть применены как числа, постоянные значения ( π, G, k ), бесконечность и т. д. Давайте рассмотрим несколько примеров, чтобы научиться вычислять пределы. 9x приближается к 0 равно 1.
Каков предел, когда x приближается к бесконечности ln(x)?
Предел при приближении x к бесконечности ln(x) равен + ∞ . Предел этого натурального логарифма может быть доказан доведением до абсурда.
Предел этого натурального логарифма может быть доказан доведением до абсурда.
- Если x >1ln(x) > 0 , предел должен быть положительным.
- Как ln(x 2 ) − ln(x 1 ) = ln(x 2 /x1) . Если x 2 >x 1 , разница положительна, поэтому ln(x) всегда возрастает.
- Если LIM x → ∞ ln (x) = M ∈ R , мы имеем LN (x) ⇒ x M , но x → ∞ SO M не может быть в R , а предел должен быть +∞ .
2.3 Ограничения
В предыдущих двух разделах мы вычислили некоторые интересующие величины.
(наклон, скорость), увидев, что некоторое выражение «идет в» или
«приближается» или «действительно приближается к» определенному значению. в
примеров, которые мы видели, эта идея могла быть достаточно ясной, но она слишком
нечетко полагаться в более сложных обстоятельствах. В этом разделе мы
увидим, как сделать идею более точной.
92\над \Дельта х}.
$$
Мы хотели знать, что происходит с этой дробью, когда «$\Delta x$
до нуля». Поскольку мы смогли упростить дробь, было легко
чтобы увидеть ответ, но это было не так просто, как «подставить
ноль для $\Delta x$,” так как это дало бы
$${-19,6\cdot 0 – 4,9\cdot 0\более 0},$$
что бессмысленно. Количество, которое нас действительно интересует,
не имеет смысла «в нуле», и поэтому ответ на исходный
проблема (нахождение скорости или наклона) не была сразу очевидной. В
Другими словами, мы, как правило, хотим выяснить, что
количество «приближается» в ситуациях, когда мы не можем просто подключить
ценность. Если вы хотите подумать о сложном примере (который мы
проанализировать позже) рассмотреть, что происходит с $(\sin x)/x$ при приближении $x$
нуль. Попробуйте вычислить это выражение на калькуляторе для меньшего и
меньшие значения $x$; они, кажется, приближаются к некоторому фиксированному значению?
В этом разделе мы
увидим, как сделать идею более точной.
92\над \Дельта х}.
$$
Мы хотели знать, что происходит с этой дробью, когда «$\Delta x$
до нуля». Поскольку мы смогли упростить дробь, было легко
чтобы увидеть ответ, но это было не так просто, как «подставить
ноль для $\Delta x$,” так как это дало бы
$${-19,6\cdot 0 – 4,9\cdot 0\более 0},$$
что бессмысленно. Количество, которое нас действительно интересует,
не имеет смысла «в нуле», и поэтому ответ на исходный
проблема (нахождение скорости или наклона) не была сразу очевидной. В
Другими словами, мы, как правило, хотим выяснить, что
количество «приближается» в ситуациях, когда мы не можем просто подключить
ценность. Если вы хотите подумать о сложном примере (который мы
проанализировать позже) рассмотреть, что происходит с $(\sin x)/x$ при приближении $x$
нуль. Попробуйте вычислить это выражение на калькуляторе для меньшего и
меньшие значения $x$; они, кажется, приближаются к некоторому фиксированному значению?
Пример 2. 3.1
Приближается ли $\ds \sqrt{x}$ к 1,41, когда $x$ приближается к 2? В этом случае
можно вычислить фактическое значение $\ds \sqrt{2}$ с высокой точностью
чтобы ответить на вопрос. Но так как вообще мы не сможем сделать
что, не будем. Мы могли бы начать с вычисления $\ds \sqrt{x}$ для значений
$x$ близко к 2, как мы делали в предыдущих разделах. Вот некоторые
значения: $\ds\sqrt{2.05} = 1.431782106$,
$\ds\sqrt{2,04} = 1,428285686$,
$\ds\sqrt{2,03} = 1,424780685$,
$\ds\sqrt{2.02} = 1.421267040$,
$\ds\sqrt{2,01} = 1,417744688$,
$\ds\sqrt{2,005} = 1,415980226$,
$\ds\sqrt{2,004} = 1,415627070$,
$\ds\sqrt{2,003} = 1,415273825$,
$\ds\sqrt{2,002} = 1,414920492$,
$\ds\sqrt{2,001} = 1,414567072$.
Так что представляется по крайней мере возможным, что эти значения действительно “приближаются” к
1.41 — уже $\ds \sqrt{2.001}$ довольно близко. Если мы продолжим это
процесс, однако, в какой-то момент может показаться, что мы «застопорились».
3.1
Приближается ли $\ds \sqrt{x}$ к 1,41, когда $x$ приближается к 2? В этом случае
можно вычислить фактическое значение $\ds \sqrt{2}$ с высокой точностью
чтобы ответить на вопрос. Но так как вообще мы не сможем сделать
что, не будем. Мы могли бы начать с вычисления $\ds \sqrt{x}$ для значений
$x$ близко к 2, как мы делали в предыдущих разделах. Вот некоторые
значения: $\ds\sqrt{2.05} = 1.431782106$,
$\ds\sqrt{2,04} = 1,428285686$,
$\ds\sqrt{2,03} = 1,424780685$,
$\ds\sqrt{2.02} = 1.421267040$,
$\ds\sqrt{2,01} = 1,417744688$,
$\ds\sqrt{2,005} = 1,415980226$,
$\ds\sqrt{2,004} = 1,415627070$,
$\ds\sqrt{2,003} = 1,415273825$,
$\ds\sqrt{2,002} = 1,414920492$,
$\ds\sqrt{2,001} = 1,414567072$.
Так что представляется по крайней мере возможным, что эти значения действительно “приближаются” к
1.41 — уже $\ds \sqrt{2.001}$ довольно близко. Если мы продолжим это
процесс, однако, в какой-то момент может показаться, что мы «застопорились». $\ds \sqrt{2}=1.414213562\ldots$, поэтому мы никогда не доберемся до
1,4142, сколько бы мы не продолжали последовательность.
$\квадрат$
92\над \Дельта х}=-19,6-4,9\Дельта х.
$$
Эти две величины равны, пока $\Delta x$ не равно нулю; если
$\Delta x$ равно нулю, левая величина не имеет смысла, а
правая рука стоит $-19,6$. Можем ли мы сказать больше, чем раньше, о
почему правая часть «приближается» к $-19,6$ в желаемом смысле?
Можем ли мы действительно приблизиться к $19,6 $? Давайте попробуем
прецедент. Можем ли мы сделать $-19,6-4,9\Delta x$ в пределах одной миллионной
($0,000001$) от -19,6$? Значения в пределах одной миллионной от $-19.6$ являются
в интервале $(-19.600001,-19.599999)$. Как $\Дельта х$
приближается к нулю, находится ли $-19.6-4.9\Delta x$ внутри
этот интервал? Если $\Delta x$ положителен, это потребует, чтобы
$-19,6-4,9\Дельта x> -19,600001$. Это то, чем мы можем манипулировать
с небольшой алгеброй:
$$\eqalign{-19,6-4,9\Дельта x&> -19,600001\cr
-4.9\Дельта x&>-0.000001\cr
\Дельта х& -19.
$\ds \sqrt{2}=1.414213562\ldots$, поэтому мы никогда не доберемся до
1,4142, сколько бы мы не продолжали последовательность.
$\квадрат$
92\над \Дельта х}=-19,6-4,9\Дельта х.
$$
Эти две величины равны, пока $\Delta x$ не равно нулю; если
$\Delta x$ равно нулю, левая величина не имеет смысла, а
правая рука стоит $-19,6$. Можем ли мы сказать больше, чем раньше, о
почему правая часть «приближается» к $-19,6$ в желаемом смысле?
Можем ли мы действительно приблизиться к $19,6 $? Давайте попробуем
прецедент. Можем ли мы сделать $-19,6-4,9\Delta x$ в пределах одной миллионной
($0,000001$) от -19,6$? Значения в пределах одной миллионной от $-19.6$ являются
в интервале $(-19.600001,-19.599999)$. Как $\Дельта х$
приближается к нулю, находится ли $-19.6-4.9\Delta x$ внутри
этот интервал? Если $\Delta x$ положителен, это потребует, чтобы
$-19,6-4,9\Дельта x> -19,600001$. Это то, чем мы можем манипулировать
с небольшой алгеброй:
$$\eqalign{-19,6-4,9\Дельта x&> -19,600001\cr
-4.9\Дельта x&>-0.000001\cr
\Дельта х& -19. 600001$. Мы могли бы сделать аналогичный расчет
если $\Delta x$ отрицательно.
600001$. Мы могли бы сделать аналогичный расчет
если $\Delta x$ отрицательно.
Итак, теперь мы знаем, что можем заработать -19 долларов.{-6}$, и я должны придумать число, показывающее, насколько близко $\Delta x$ должен быть равным нулю, чтобы гарантировать, что $-19,6-4,9\Delta x$ не меньше до $-19,6$, как вы просили.
Теперь, если мы на самом деле сыграем в эту игру, я мог бы повторить приведенный выше расчет.
за каждый новый номер, который вы предоставляете. Что я хотел бы сделать, так это как-то увидеть
что у меня всегда все получится, и даже больше, я хотел бы иметь простой
стратегию, чтобы мне не приходилось каждый раз заниматься всей этой алгеброй.
Стратегией в этом случае будет формула, дающая мне правильное
ответьте независимо от того, что вы указываете. Итак, предположим, что номер, который вы мне даете
равно $\эпсилон$. Насколько близко $\Delta x$ должно быть к нулю, чтобы
гарантия, что $-192\над \Дельта х}
= -19,6.
$$
Вот фактическое официальное определение «лимита».
Определение 2.3.2 (Предел) Предположим, что $f$ — функция. Мы говорим, что $\ds \lim_{x\to a}f(x)=L$, если для каждого $\epsilon>0$ существует $\delta > 0$, такое что всякий раз, когда $0
Здесь $\epsilon$ и $\delta$ играют ту же роль, что и в предшествующее обсуждение. В определении очень точно сказано, что $f(x)$ можно сделать сколь угодно близким к $L$ (это $|f(x)-L|
92\над \Дельта х}. $$ и переменная предела была не $x$, а $\Delta x$. $x$ было переменная исходной функции; когда мы пытались вычислить наклон или скорость, $x$ было, по существу, фиксированной величиной, говорящей нам в какой момент мы хотели склон. (В задаче о скорости это было буквально фиксированное количество, поскольку мы сосредоточились на времени 2.) Количество $a$ определения во всех примерах было равно нулю: мы всегда интересует, что произошло, когда $\Delta x$ стала очень близкой к нулю. Теперь, вооружившись точным определением, мы можем доказать, что некоторые
величины ведут себя определенным образом. Плохая новость в том, что даже
доказательства простых величин могут быть весьма утомительными и сложными; в
хорошая новость заключается в том, что нам редко приходится делать такие доказательства, потому что большинство
выражения действуют так, как вы ожидаете, и это можно доказать один раз
и для всех.
Плохая новость в том, что даже
доказательства простых величин могут быть весьма утомительными и сложными; в
хорошая новость заключается в том, что нам редко приходится делать такие доказательства, потому что большинство
выражения действуют так, как вы ожидаете, и это можно доказать один раз
и для всех.
Пример 2.3.3
Покажем аккуратно, что $\ds \lim_{x\to 2} x+4 = 6$. Это не
то, что нам «нужно» доказать, поскольку это «очевидно» истинно. Но если
мы не могли бы доказать это, используя наше официальное определение, было бы
что-то очень не так с определением.
92=х\cточка
x$, и спросите, что происходит, когда $x$ приближается к 2, мы могли бы сказать что-то
типа: «Ну, первый $x$ приближается к 2, а второй $x$
приближается к 2, поэтому произведение должно приближаться к $2\cdot2$.” На самом деле это
почти по деньгам, за исключением слова «должен».
действительно верно, что если $x$ приближается к $a$, а $y$ приближается к $b$, то
$xy$ приближается к $ab$? Да, но это не совсем очевидно, так как $x$
и $y$ может быть довольно сложным. Хорошая новость заключается в том, что мы можем видеть
что это правда раз и навсегда, и тогда нам не о чем беспокоиться
об этом когда-либо снова. Когда мы говорим, что $x$ может быть «сложным», мы
действительно означает, что на практике это может быть функция. Вот тогда что
мы хотим знать:
Хорошая новость заключается в том, что мы можем видеть
что это правда раз и навсегда, и тогда нам не о чем беспокоиться
об этом когда-либо снова. Когда мы говорим, что $x$ может быть «сложным», мы
действительно означает, что на практике это может быть функция. Вот тогда что
мы хотим знать:
Теорема 2.3.5. Предположим, что $\ds \lim_{x\to a} f(x)=L$ и $\ds \lim_{x\to a}g(x)=M$. затем
$\lim_{x\to a} f(x)g(x) = LM$.
Доказательство. Мы должны использовать официальное определение предела, чтобы иметь смысл этого. Итак, для любого $\epsilon$ нам нужно найти $\delta$ так, чтобы $0
Мы используем, как это часто бывает, немного алгебраич.
обманывать:
$$\eqalign{|f(x)g(x)-LM|&= |f(x)g(x)-f(x)M+f(x)M-LM|\cr
&=|f(x)(g(x)-M)+(f(x)-L)M|\cr
&\le |f(x)(g(x)-M)|+|(f(x)-L)M|\cr
&=|f(x)||g(x)-M|+|f(x)-L||M|.\cr}
$$
Все просто, за исключением, возможно, “$\le$”.
пример из неравенство треугольника ,
что говорит о том, что если $a$ и $b$ являются любыми действительными
числа, то $|a+b|\le |a|+|b|$. 2$. Мы можем найти $\delta_2$
так что $|x-a|
2$. Мы можем найти $\delta_2$
так что $|x-a|
Горстка таких теорем дает нам инструменты для вычисления многих пределов. без явной работы с определением предела.
Теорема 2.3.6. Предположим, что $\ds \lim_{x\to a}f(x)=L$ и $\ds \lim_{x\to a}g(x)=M$ и $k$ — некоторая константа. затем $$\выравнивание{ &\lim_{x\to a} kf(x) = k\lim_{x\to a}f(x)=kL\cr &\lim_{x\to a} (f(x)+g(x)) = \lim_{x\to a}f(x)+\lim_{x\to a}g(x)=L+M \кр &\lim_{x\to a} (f(x)-g(x)) = \lim_{x\to a}f(x)-\lim_{x\to a}g(x)=L-M\cr &\lim_{x\to} (f(x)g(x)) = \lim_{x\to}f(x)\cdot\lim_{x\to}g(x)=LM\cr &\lim_{x\to} {f(x)\over g(x)} = {\lim_{x\to a}f(x)\over\lim_{x\to a}g(x)}={L\over M},\hbox{, если $M$ не равно 0}\cr }$$ $\qed$ 92-3\cdot1+5\более 1-2}\кр &={1-3+5\более -1} = -3\кр }$$ $\квадрат$
Стоит прокомментировать тривиальный предел $\ds \lim_{x\to1}5$. От одного
точки зрения это может показаться бессмысленным, так как цифра 5 не может
“приближаться” к любому значению, так как это просто фиксированное число. 2 + 5 = х + 5 $. Вот компаньон для
теорема 2.3.6 для композиции:
2 + 5 = х + 5 $. Вот компаньон для
теорема 2.3.6 для композиции:
Теорема 2.3.9 Предположим, что $\ds \lim_{x\to a}g(x)=L$ и $\ds \lim_{x\to L}f(x)=f(L)$. затем $$\lim_{x\to a} f(g(x)) = f(L).$$ $\qed$
Обратите внимание на особую форму условия на $f$: недостаточно известно, что $\ds\lim_{x\to L}f(x) = M$, хотя это немного сложно увидеть Почему. Многие из наиболее известных функций обладают этим свойством, и поэтому эту теорему можно применить. Например:
Теорема 2.3.10. Предположим, что $n$ — натуральное число. затем $$\lim_{x\to}\root n\of{x} = \root n\of{a},$$ при условии, что $a$ положительно, если $n$ четно. $\qed$
Эту теорему нетрудно доказать, исходя из определения предела.
Еще один из самых распространенных алгебраических приемов использовался в раздел 2.1. Вот еще один пример:
Пример 2.3.11
Вычислите $\ds\lim_{x\to-1} {\sqrt{x+5}-2\over x+1}$.
$ $ \ eqalign {\ lim_ {x \ to-1} {\ sqrt {x + 5} -2 \ над x + 1} & =
\lim_{x\to-1} {\sqrt{x+5}-2\over x+1}{\sqrt{x+5}+2\over\sqrt{x+5}+2}\cr
&=\lim_{x\to-1} {x+5-4\over (x+1)(\sqrt{x+5}+2)}\cr
&=\lim_{x\to-1} {x+1\over (x+1)(\sqrt{x+5}+2)}\cr
&=\lim_{x\to-1} {1\over \sqrt{x+5}+2}={1\over4}\cr}
$$
На самом последнем шаге мы воспользовались теоремами 2. 3.9.2}$, верхняя половина
единичный круг. Что мы можем сказать о $\ds \lim_{x\to 1}f(x)$? это
видно из графика этой знакомой функции, что когда $x$ становится
близко к 1 слева, значение $f(x)$ приближается к нулю. Это
даже не имеет смысла спрашивать, что происходит, когда $x$ приближается к 1 из
справа, так как $f(x)$ там не определено. Определение
предел, однако, требует, чтобы $f(1+\Delta x)$ была близка к $f(1)$
является ли $\Delta x$ положительным или отрицательным. Иногда предел А.
функция существует с одной или другой стороны (или с обеих сторон), даже если
предела не существует. Поскольку полезно иметь возможность говорить об этом
ситуации, мы вводим понятие
93$
(отвечать)
3.9.2}$, верхняя половина
единичный круг. Что мы можем сказать о $\ds \lim_{x\to 1}f(x)$? это
видно из графика этой знакомой функции, что когда $x$ становится
близко к 1 слева, значение $f(x)$ приближается к нулю. Это
даже не имеет смысла спрашивать, что происходит, когда $x$ приближается к 1 из
справа, так как $f(x)$ там не определено. Определение
предел, однако, требует, чтобы $f(1+\Delta x)$ была близка к $f(1)$
является ли $\Delta x$ положительным или отрицательным. Иногда предел А.
функция существует с одной или другой стороны (или с обеих сторон), даже если
предела не существует. Поскольку полезно иметь возможность говорить об этом
ситуации, мы вводим понятие
93$
(отвечать)
Пример 2.3.15 $\ds\lim _{x\to 1} \cases{ x-5 & $x\neq 1$,\cr 7 & $x=1$.\cr}$ (отвечать)
Пример 2.3.16 $\ds\lim _{x\to 0} x\sin\left({1\over x}\right)$ (Подсказка: используйте тот факт, что $|\sin a |ответ)
Пример 2.3.17 Дайте доказательство $\epsilon$–$\delta$, подобное
пример 2. 3.3,
того факта, что
$\ds \lim_{x\to 4} (2x-5) = 3$.
3.3,
того факта, что
$\ds \lim_{x\to 4} (2x-5) = 3$.
Пример 2.3.18 Оцените выражения по этому графику: 9+} ф(х-2)$
(отвечать)
Пример 2.3.19 Используйте калькулятор для оценки $\ds\lim_{x\to 0} {\ грех х \ над х} $.
Пример 2.3.20 Используйте калькулятор для оценки $\ds\lim_{x\to 0} {\ загар (3x) \ над \ загар (5x)} $.
Объяснение урока: Число Эйлера (𝑒) как предел
В этом объяснении мы узнаем, как использовать определение 𝑒 (число Эйлера) для оценки некоторых специальные лимиты.
Число Эйлера (𝑒=2,71828…) очень полезно и возникает во многих различных областях науки. математика, включая расчет сложных процентов, задачи оптимизации, исчисление и определение функция, представляющая стандартное нормальное распределение вероятностей.
Число могло быть изначально найдено при поиске экспоненциальной функции, которая дифференцируется сама в себя. Однако мы также можем найти число Эйлера, используя пределы, и это то, что мы рассмотрим в этом объяснении.
Однако мы также можем найти число Эйлера, используя пределы, и это то, что мы рассмотрим в этом объяснении.
Мы можем определить число Эйлера, используя следующий предел: 𝑒=1+1𝑥.lim→∞
Используя таблицу значений, мы можем увидеть, как этот предел приближается к числу Эйлера по мере увеличения 𝑥.
| 𝑥 | 1+1 𝑥 |
|---|---|
| 1 | 1+11 = 2 |
| 10 | 1+110 = 2,59374… |
| 100 | |
| 100 | |
| 58 | |
| 58 | |
| 1 000 | 1+11000=2.71692… |
| 10 000 | 1+110000=2.71814… |
| 100 000 | 1+1100000=2,71826… |
Мы можем использовать этот предел, чтобы помочь оценить пределы и решить проблемы, связанные с пределами этой формы. Прежде чем мы посмотрим на любой
примеров, давайте рассмотрим другой предел, который также приводит к числу Эйлера.
Попробуем подставить 𝑥=1𝑦 в наш предыдущий предел. Поскольку мы рассматриваем предел как 𝑥→∞ и 𝑥=1𝑦, мы можем сказать, что при 𝑥→∞, 𝑦→0. Подставляя их в 𝑒=1+1𝑥lim→∞, мы получим 𝑒=(1+𝑦).lim→
Теперь мы знаем два предела, которые дают число Эйлера. Подведем итоги только что показанных результатов.
Определение: число Эйлера как предел оценить пределы, которые мы не могли раньше.
Пример 1: вычисление предела с использованием постоянной Эйлера
Определить lim→∞1+1𝑥.
Ответ
Мы могли бы сначала попытаться вычислить этот предел напрямую. В нашем пределе 𝑥 приближается к бесконечности, что означает, что знаменатель 1𝑥 неограниченно растет, а числитель остается постоянным, поэтому 1𝑥 приближается к 0. Это означает, что выражение в наших скобках приближается к 1. Однако наш показатель степени (4𝑥) равен приближается к бесконечности, когда 𝑥 приближается к бесконечности.
Итак, мы получаем lim→∞∞1+1𝑥=1, что является неопределенной формой. Это означает, что нам нужно будет попробовать какой-то другой метод для оценки нашего предела.
Это означает, что нам нужно будет попробовать какой-то другой метод для оценки нашего предела.
Заметим, что заданный нами предел очень похож на тот, который выражает значение числа Эйлера: 𝑒=1+1𝑥.lim→∞ нам дали показатель степени 4𝑥, а не 𝑥. Мы можем использовать законы экспонент, чтобы перевыразить это следующим образом:
Прежде чем мы сможем подставить число Эйлера в предельное выражение, нам нужно вывести показатель степени 4 за предел. При условии, что новый предел существует, мы можем использовать правило степени для пределов, чтобы добиться этого:
Предел внутри нашей экспоненты существует, потому что это просто наш предельный результат для числа Эйлера 𝑒. Итак, мы используем наш предельный результат и заменяем предел в скобках на 𝑒, что дает нам limlim→∞→∞1+1𝑥=1+1𝑥=𝑒.
Наш следующий пример показывает, как мы можем использовать наш другой предельный результат, чтобы помочь нам оценить предел.
Пример 2. Нахождение пределов путем их преобразования в формы пределов в натуральной степени
Определить lim→(𝑥+1).
Ответ
Поскольку нас просят оценить предел, мы могли бы начать с попытки сделать это напрямую. Когда 𝑥 приближается к 0, выражение в скобках приближается к 1, а величина нашего показателя степени неограниченно растет. Это неопределенная форма, а именно 1∞, поэтому нам нужно будет попробовать другой метод.
Мы видим, что наш предел аналогичен одному из наших предельных результатов, связанных с числом Эйлера, который равен lim→(1+𝑥)=𝑒.
Итак, мы можем попробовать использовать этот результат, чтобы оценить наш предел.
Для этого мы хотим, чтобы наш показатель степени 1110𝑥 был таким же, как у предельного результата, который равен 1𝑥. Чтобы сделать это, мы начнем с использования наших законов показателей степени, чтобы переписать наш предел: где мы переставляем члены в скобках и используем тот факт, что 1110𝑥=1𝑥⋅1110.
На этом этапе мы хотим использовать наш предельный результат, включающий число Эйлера; однако сначала нам нужно вывести нашу экспоненту за пределы нашего предела, а для этого нам нужно использовать правило степени для пределов.
Это говорит нам, что мы можем вывести экспоненту за пределы предела при условии, что наш новый предел существует.
В нашем случае имеем limlim→→(1+𝑥)=(1+𝑥), и мы знаем, что это верно потому что предел в наших скобках точно такой же, как предельный результат, включающий число Эйлера. Подставляя этот предел равным 𝑒, получаем (1+𝑥)=𝑒.lim→
Не всегда возможно напрямую использовать наши предельные результаты для числа Эйлера 𝑒. Возможно, нам придется использовать другие инструменты, такие как полиномиальное деление, факторинг или замену. Однако основная предпосылка та же самая: мы берем предел, который мы не можем оценить, и записываем его в форме для 𝑒, которую мы затем можем использовать для оценки наших предельных результатов.
Пример 3. Оценка предела путем преобразования его в форму предела в натуральной степени
Определить lim→∞1−7𝑥.
Ответ
Нас просят оценить предел, который мы могли бы попытаться оценить напрямую. Таким образом, когда 𝑥 приближается к ∞, выражение в скобках приближается к 1, а показатель степени неограниченно растет. Следовательно, имеем lim→∞∞1−7𝑥=1.
Таким образом, когда 𝑥 приближается к ∞, выражение в скобках приближается к 1, а показатель степени неограниченно растет. Следовательно, имеем lim→∞∞1−7𝑥=1.
Это неопределенная форма, поэтому нам нужно будет попробовать другой метод для оценки этого предела.
Этот предел аналогичен одному из предельных результатов, связанных с числом Эйлера, поэтому мы можем попробовать использовать этот результат, чтобы помочь нам оценить наш предел. У нас есть много вариантов, как это сделать.
Мы попытаемся записать этот предел в форме, где мы можем использовать 𝑒=(1+𝑛).lim→
Однако также можно использовать 𝑒=1+1𝑛. lim→∞
Обычно один из предельных результатов оказывается проще, чем другой, и может быть очень трудно сказать, какой предельный результат использовать, просто взглянув на вопрос, поэтому, если мы застряли, используя один результат, мы всегда можем попробовать использовать другой предел, который находится в форме с показателем степени 1𝑛.
Чтобы записать наш предел в этой форме, мы будем использовать замену. Мы хотели бы 1+𝑛 в наших скобках, поэтому мы используем замену 𝑛=−7𝑥.
Мы можем изменить эту замену, чтобы найти 𝑥 через 𝑛 так, чтобы 𝑥=−7𝑛.
Умножив это на 5, мы получим 5𝑥=−35𝑛.
Используя эту замену, мы можем переписать наш предел как limlim→∞→∞1−7𝑥=(1+𝑛).
и мы хотим знать, что происходит с точки зрения 𝑛, поэтому нам нужно посмотреть на нашу замену. Поскольку 𝑥 приближается к бесконечности, −7𝑥 приближается к 0, а поскольку 𝑛=−7𝑥, мы также должны иметь то, что 𝑛 приближается к 0,9.0003
Это дает нам limlim→∞→(1+𝑛)=(1+𝑛).
Теперь воспользуемся одним из законов экспонент: limlim→ →(1+𝑛)=(1+𝑛).
Наконец, применим степенное правило для пределов: limlim→→ (1+𝑛)=(1+𝑛),, что, как мы знаем, мы можем сделать в этом случае, потому что полученный предел является нашим предельным результатом, включающим число Эйлера.
Все, что нам нужно сделать сейчас, это заменить этот предел на 𝑒 и переставить, чтобы в итоге мы получили (1+𝑛)=𝑒=1𝑒.lim→
В нашем следующем примере мы рассмотрим предел рациональной функции, возведенной в линейный показатель.
Пример 4. Нахождение пределов путем преобразования их в формы пределов в натуральной степени
Определить lim→∞𝑥+4𝑥−4.
Ответ
Мы могли бы попробовать вычислить этот предел напрямую. В наших скобках у нас есть рациональная функция, и мы знаем, что по мере того, как 𝑥 приближается к ∞, мы можем увидеть, что происходит, посмотрев на частное старших членов в нашей рациональной функции. Поскольку это равно 1, предел нашей рациональной функции также равен 1. Однако наш показатель степени неограниченно растет, поэтому мы имеем lim→∞∞𝑥+4𝑥−4=1, что является неопределенная форма. Поэтому нам нужно будет попробовать другой метод для оценки этого предела.
Вместо этого попробуем оценить это, используя предельный результат, включающий число Эйлера: →∞→∞𝑥+4𝑥−4=𝑥−4+8𝑥−4=1+8𝑥−4.
Если мы сравним два предела, мы увидим, что нам нужно использовать замену. Мы хотим, чтобы в скобках было 1+1𝑛, поэтому мы используем замену 1𝑛=8𝑥−4.
Когда 𝑥 приближается к бесконечности, мы видим, что 8𝑥−4 приближается к 0, поэтому 𝑛 также должно стремиться к бесконечности.
Прежде чем использовать эту подстановку, нам также нужно перестроить, чтобы найти 𝑥 с точки зрения 𝑛, что мы можем сделать следующим образом.
Возьмем обратное значение обеих частей нашей замены, что даст нам 𝑛=𝑥−48.
Затем умножаем на 8 и прибавляем по 4 к обеим сторонам: 𝑥=8𝑛+4.
Теперь мы можем использовать эту замену, чтобы переписать наш предел: 1+1𝑛.
Мы хотим использовать наш предельный результат, но сначала нам нужно, чтобы показатель степени был равен 𝑛. Для этого нам сначала потребуется использовать законы экспонент в сочетании с правилом произведения для пределов, так что 1𝑛⋅1+1𝑛.
Чтобы использовать правило произведения для пределов, нам нужно, чтобы существовал предел обоих факторов. Мы покажем в нашей работе, что оба этих предела существуют.
Мы покажем в нашей работе, что оба этих предела существуют.
Мы можем вычислить один из этих пределов напрямую: lim→∞1+1𝑛=1.
Затем, чтобы вычислить наш другой предел, мы используем законы экспонент и правило степени для пределов, истинно при условии, что этот предел существует, а мы знаем, что он существует, потому что это наш предыдущий предельный результат. Это означает, что мы можем заменить этот предел константой Эйлера 𝑒: 1+1𝑛=𝑒.lim→∞
Следовательно, мы показали lim→∞𝑥+4𝑥−4=𝑒.
Мы также можем использовать эти результаты для решения пределов, включающих более сложные функции.
Пример 5. Оценка пределов путем преобразования их в формы пределов в натуральной степени
Определить limtan→−4𝑥+1cot.
Ответ
Мы могли бы попробовать вычислить этот предел напрямую. Внутри скобок у нас непрерывная функция, поэтому мы можем просто подставить 𝑥=0. Однако наш показатель степени неограниченно растет, поэтому мы имеем limtanlimtan→→∞∞−4𝑥+1=−40+1=1,cot, что является неопределенной формой, поэтому мы нужно будет попробовать другой метод, чтобы оценить этот предел.
Вместо этого попробуем оценить это, используя предельный результат, включающий число Эйлера, то есть 𝑒=(1+𝑛).lim→
Чтобы сравнить это с пределом, нам предлагается find нам нужно будет преобразовать выражение в скобках в форму 1+𝑛. Для этого мы начнем с подстановки 𝑛=−4𝑥.tan
. Мы знаем, что когда 𝑥 приближается к 0, −4𝑥tan будет приближаться к 0 путем прямой подстановки, поэтому 𝑛 также должно стремиться к 0. Кроме того, взяв обратную величину обоих стороны нашей замены и перестановки, мы имеем −4𝑛=1𝑥=𝑥.tancot
Используя все это, мы можем переписать наш предел следующим образом: законы показателей и правило степени для пределов для получения требуемого показателя степени 1𝑛: 𝑛).
Конечно, это при условии, что предел внутри скобок существует, что, как мы знаем, существует, поскольку lim→(1+𝑛)=𝑒.
Наконец, мы можем использовать наш предельный результат, чтобы вычислить предел в наших скобках как постоянную Эйлера:0003
Следовательно, мы смогли показать limtan→−4𝑥+1=1𝑒. cot
cot
До сих пор мы исследовали пределы, которые приводят к числу Эйлера. Рассмотрим теперь некоторые ограничения, приводящие к обратная функция 𝑓(𝑥)=𝑒. Когда мы рассматриваем любую экспоненциальную функцию, 𝑝(𝑥)=𝑎, мы знаем, что его обратная функция является логарифмической функцией с основанием 𝑎, 𝑞(𝑥)=𝑥log. Поэтому, когда мы рассматриваем обратную функцию 𝑓(𝑥)=𝑒, мы знаем, что это будет логарифмическая функция с основанием 𝑒, 𝑔(𝑥)=𝑥log, натуральный логарифм. Натуральный логарифм функция может быть записана как 𝑔(𝑥)=(𝑥)ln. Вот график, показывающий экспоненциальную функцию и функция натурального логарифма. Мы можем видеть, как они являются отражением друг друга в строке 𝑦=𝑥.
Прежде чем мы определим натуральный логарифм как предел, напомним некоторые полезные свойства:
- 𝑦=𝑥ln эквивалентно 𝑒=𝑥,
- 𝑒=𝑥ln, ln
- ln 00=1 =0,
- loglnln𝑥=𝑥𝑎.
Для каждого 𝑥, 𝑦∈ℝ и 𝑛∈ℝ, - lnlnln𝑥𝑦 = 𝑥+𝑦,
- lnlnln𝑥𝑦 = 𝑥 – 𝑦,
- lnln𝑥 = 𝑛𝑥,
- lnlog𝑥 × 𝑒 = 1.

Мы начнем с рассмотрения уравнения
| 𝑦=𝑎−1, | (1) |
где 𝑥 и 𝑦 — переменные, а 𝑎 — вещественная константа. Для этого уравнение, мы можем видеть, что когда 𝑥→0, 𝑎→1 и, следовательно, 𝑦→0 тоже. Мы можем переместить 1 в другую часть уравнения и взять натуральный логарифм обеих частей этого уравнения, чтобы получить lnln𝑎=(𝑦+1).
Используя свойства логарифмов, мы можем преобразовать это в
| 𝑥𝑎=(𝑦+1)𝑥=(𝑦+1)𝑎.lnlnlnln | (2) |
Рассмотрим теперь следующий предел: lim→𝑎−1𝑥.
Используя (1) и (2), мы можем переписать это как limlimlnln→→𝑎−1𝑥=𝑦𝑎(𝑦+1).
Обратите внимание, что, как упоминалось ранее, когда 𝑥→0, 𝑦→0 также. Мы можем изменить правую часть этого уравнения, используя свойства логарифмов и пределов, следующим образом:
limlimlnlnlimlnlnlimlnlnlnlimlnlnlnlim→→→→→→𝑎−1𝑥=𝑦𝑎(𝑦+1)=𝑎(𝑦+1)=𝑎(𝑎) +1)=𝑎(𝑦+1).
Теперь можно заметить, что предел в знаменателе дроби — это предел, равный числу Эйлера. Следовательно, мы можем сказать, что limlnlnln→𝑎−1𝑥=𝑎𝑒=𝑎.
Мы можем использовать это предельное определение натурального логарифма для решения задач. Еще пара определений пределов которые также могут помочь нам решить проблемы limloglogandlimln→→(𝑥+1)𝑥=𝑒(𝑥+1)𝑥=1.
Ниже мы можем обобщить пределы, полученные в виде логарифмов.
Определение: логарифмы как пределы
Давайте теперь рассмотрим несколько примеров того, как мы можем использовать эти ограничения для решения задач.
Пример 6: вычисление предела с помощью натурального логарифма
Определить lim→7−12𝑥.
Ответ
Здесь нам дали ограничение на оценку, поэтому мы можем сначала попытаться сделать это напрямую. Если мы подставим 0 в наш предел,
мы получим 00, который не определен. Следовательно, нам нужно будет использовать какой-то другой метод для определения
этот предел.
Когда мы смотрим на этот предел, мы можем заметить, что он очень похож на предел, вычисляемый с помощью натурального логарифма. Позволять сравним его с этим пределом: limln→𝑎−1𝑥=𝑎.
Мы заметили, что это очень похоже на предел, который нас попросили оценить. Константа 𝑎 равна до 7. У нас также есть небольшие различия в показателе степени и знаменателе дроби. Мощность 3𝑥 вместо 𝑥, а в знаменателе 2𝑥 вместо 𝑥. Чтобы оценить предел, нам нужно попытаться манипулировать им, чтобы он был более похож на предел, который нам дали.
Начнем с изменения показателя степени. Мы можем сделать это, используя замену. Мы хотим сделать так, чтобы экспонента была просто переменная, а не переменная, умноженная на константу. Мы можем использовать замену 3𝑥=𝑢, что эквивалентно к 𝑥=𝑢3.
Перед тем, как мы сделаем эту замену, мы должны рассмотреть, что произойдет с пределом. В пределе, указанном в вопросе, мы
рассматривают, когда 𝑥→0. Мы используем замену 𝑥=𝑢3, поэтому мы можем видеть
что когда 𝑥 стремится к 0, то же самое будет и 𝑢. Следовательно, когда 𝑥→0,
𝑢→0 также. Теперь мы можем выполнить нашу замену следующим образом:
limlim→→7−12𝑥=7−1.
Мы используем замену 𝑥=𝑢3, поэтому мы можем видеть
что когда 𝑥 стремится к 0, то же самое будет и 𝑢. Следовательно, когда 𝑥→0,
𝑢→0 также. Теперь мы можем выполнить нашу замену следующим образом:
limlim→→7−12𝑥=7−1.
Теперь мы можем видеть, что показатель степени равен просто 𝑢. Мы убрали коэффициент с помощью подстановки. Теперь это выглядит очень похоже на форму, которая нам нужна для ее оценки. Осталось разобраться с коэффициентом 𝑢 в знаменателе дроби. Мы можем начать с перемещения константы перед дробью: limlim→→7−1=327−1𝑢.
Теперь, используя предельные законы, мы можем переместить постоянный коэффициент перед пределом: limlim→→327−1𝑢=327−1𝑢.
Теперь мы можем видеть, что наш предел имеет форму limln→𝑎−1𝑥=𝑎, поэтому мы можем оценить чтобы получить наше решение: limlimln→→7−12𝑥=327−1𝑢=327.
Теперь мы рассмотрим последний пример в этом объяснении.
Пример 7. Вычисление предела с помощью натурального логарифма
Определить limln→(𝑥−1)𝑥−2.
Ответ
Мы могли бы попытаться решить этот вопрос с помощью прямой замены. Однако, если мы попытаемся подставить 𝑥=2 в пределе мы получим 00, что не определено. Нам нужно будет использовать другой метод в чтобы оценить этот предел. Заметим, что он похож на предел, который мы умеем вычислять, а именно limln→(𝑥+1)𝑥=1.
Мы заметили, что между этими двумя ограничениями есть несколько различий. Это значение, при котором лимит оценивается и с добавлением некоторых постоянных членов как в числителе, так и в знаменателе. Мы можем выполнить замену в нашем исходном пределе, чтобы попытаться заставить его выглядеть как предел, который мы знаем, как оценивать. мы заменим 𝑥−2=𝑢, что эквивалентно 𝑥=𝑢+2.
Прежде чем мы выполним эту замену, нам нужно рассмотреть, что произойдет с предельным значением 𝑥→2. Поскольку у нас есть 𝑢=𝑥−2, мы можем сказать, что при 𝑥→2, 𝑢→0. Мы
теперь готов заменить:
limlnlimln→→(𝑥−1)𝑥−2=(𝑢+1)𝑢.
Поскольку у нас есть 𝑢=𝑥−2, мы можем сказать, что при 𝑥→2, 𝑢→0. Мы
теперь готов заменить:
limlnlimln→→(𝑥−1)𝑥−2=(𝑢+1)𝑢.
После этой подстановки мы видим, что предел в точности имеет вид limln→(𝑥+1)𝑥=1. Следовательно, мы можем сказать, что limln→(𝑥−1)𝑥−2=1.
Давайте закончим повторением некоторых основных моментов этого объяснения.
Ключевые моменты
- Мы нашли и доказали два полезных предельных результата, связанных с числом Эйлера: 𝑒=(1+𝑥)𝑒=1+1𝑛.limandlim→→∞
- Мы нашли и доказали три полезных предельных результата, связанных с натуральным логарифмом: limlnlimlogloglimln→→→𝑎−1𝑥=𝑎,(𝑥+1)𝑥=𝑒,(𝑥+1)𝑥=1.
- Мы можем использовать эти результаты для оценки пределов, которые дают неопределенные формы путем прямой замены или оценки.
- Чтобы использовать эти результаты, иногда нам может понадобиться манипулировать нашим пределом, используя такие методы, как полиномиальное деление,
замещение или факторинг.




 Применяются решения по Лопиталю;
Применяются решения по Лопиталю;
 Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)
Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)