Приращение функции
Понятие приращения аргумента и приращения функции.
Пусть x – произвольная точка, ледащая в некоторой окрестности фиксированной точки x0. разность x – x0 называется приращение независимой переменной ( или приращением аргумента) в точке x0 и обозначается Δx. Таким образом,
Δx = x –x0,
откуда следует, что
x = x0 + Δx.
Говорят также, что первоначальное значение аргумента x0 получило приращение Δx. Вследствие этого значение функции f изменится на величину
f(x) – f(x0) = f (x0 +Δx) – f(x0).
Эта разность называется приращением функции f в точке x0, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф»), т.е. по определению
Δf = f (x0 + Δx) – f (x0),
откуда
При фиксированном x0 приращение Δf есть функция от Δx. Δf называют также приращение зависимой переменной и обозначают через Δy для функции y = f(x) .
Определение непрерывной в точке функции через приращение.
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
f(x) = f(x0), | (1) |
т.е.
” O( f(x0) ) $ O(x0)
: x О O(x0) Ю f(x) О O( f(x0)
) . |
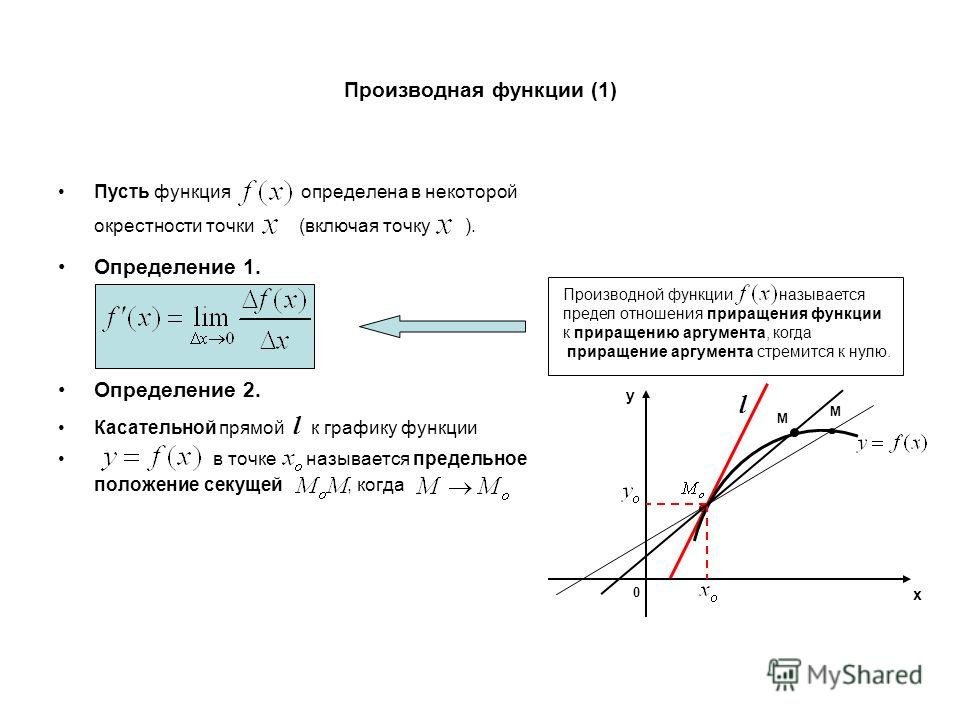
Определение производной функции в точке.
Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,
Геометрический смысл производной и дифференциала.
Если функция у = f(x) дифференцируема в точке x0, то ее производная в этой точке равна тангенсу угла наклона касательной к оси Ох, а дифференциал равен приращению ординаты касательной
f'(x0) = tg a.
Уравнения касательной и нормали к графику функции.
Уравнение
касательной имеет вид:
У
= f'(x0)
• (x – x0)
+ f(x
Если f'(x0)
0,
то уравнение нормали имеет вид:
Понятие дифференцируемости функции в точке.
Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δ
Теорема о необходимом и достаточном условии дифференцируемости .
Теорема Для
того, чтобы функция y=f(x) была дифференцируема в
точке x0,
необходимо и достаточно, чтобы она в
этой точке имела конечную
производную. Доказательство Необходимость.
Предположим: функция дифференцируема
в точке x0,
т.е. Δy=A·Δx+α(Δx)·Δx.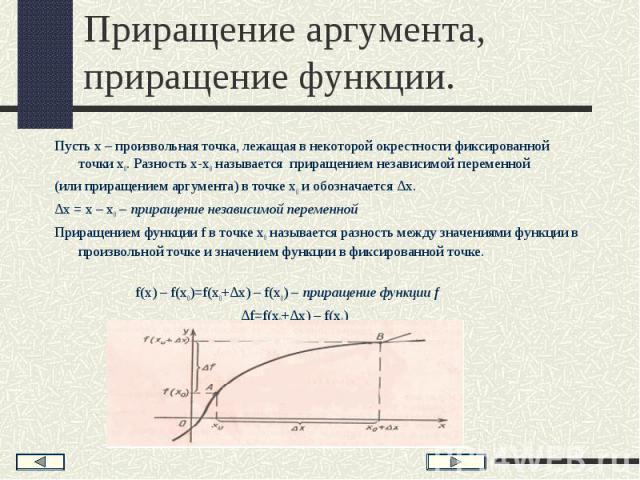
Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy.
Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: Δ
Связь
свойств дифференцируемости и непрерывности
.
Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке. Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции. Обратное утверждение не верно.
Например, функция y=∣x∣ непрерывна в точкеx=0, но не дифференцируема в этой точке. Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.
Дифференциал функции. Физический смысл производной.
Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x)
Производная функции пути по времени есть мгновенная скорость материальной точки в момент времени х:
v(x)
= f'(x).
Поскольку dy = f'(x)dx = v(x)dx, то дифференциал функции пути равен расстоянию, которое прошла бы точка за бесконечно малый промежуток времени dx, если бы она двигалась равномерно со скоростью, равной величине мгновенной скорости в момент времени х. Вторая производная функции пройденного пути также имеет простой смысл – это мгновенное ускорение точки в данный момент времени
a(x)=v'(x) = f”(x).
Производная суммы, разности, произведения и частного функций (все с доказательством кроме последнего).
Производная суммы (разности) функций
Производная алгебраической суммы функций выражается следующей теоремой.
Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:
Производная произведения функций.
Пусть u(x) и u(x) –
дифференцируемые функции.
Тогда
произведение функций u(x)v(x) также
дифференцируемо и
Производная произведения двух функций не равана произведению производных этих функций.
Пусть u(x) и u(x) – дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
Производная сложной функции .
“Двухслойная” сложная функция записывается в виде
где u = g(x) – внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g – дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна
Данная
формула показывает, что производная
сложной функции равна произведению
производной внешней функции на производную
от внутренней функции.
Определение логарифмической производной функции.
Логарифмической производной функции y=f(x) называется производная ее логарифма. тогда производная функции y=f(x) может быть найдена так:
1*. Понятие приращения функции и понятие производной. Геометрический и физический смысл производной.
Если y=f(x) опреелена на X, xo
∆у= ∆f(xo) = f(xo+∆x) – f(xo) – приращение функции
Производная функцией
f(x)
по независимой переменной x в точке xo–
предел отношения преращения ф-ии ∆f(xo)
к приращению аргумента ∆x
при ∆x→0,
если этот предел существует.
F’(xo) =
Геометрически производная = угловому коэффициенту ксательной к графику функции в точке xo: k= tg’α=f’(xo), α-угол наклона касательной.
Уравнение касательной в ее точке пересечения с кривой y(x) (в т.A(xo, yo)): y- yo= f’(xo)(x- xo)
Уравнение нормали: y- yo =
f’(xo) характеризует скорость изменения f(x) в точке xo – мгновенная скорость.
2. Определения касательной и нормали и их уравнения.
Касательная к кривой y(f) в точке M0(x0, f(x0)) – предельное положение секущей MN при неограниченном приближении N по кривой к M.
y-f(x0)= f’(x0)(x-x0) – ур-е касательной
Производная-
это tg угла наклона (угл.
коэфф) касательной
к кривой y= f(x)
в точке (x0;f(x0))
K=tgα= f’(x0), α-угол наклона касательной
Н ормаль к кривой y(f) в точке M0(x0, f(x0))- прямая, прохожящая через M и перпендикулярная касательной к кривой в этой точке.
k2=1/k1
y-f(x0)= -1/ f’(x0) * (x-x0)
f’(x0) характеризует скорость изменения ф-ии f(x) в точке x0– мгновенная скорость.
3*. Правила вычисления производных с демонстрацией на конкретных примерах.
№ | Y=f(x) | Y’=f’(x) |
1 | C | 0 |
2 | xm | mxm-1 |
3 | ax(0<a≠1) | axlna |
ex | ex | |
4 | logax (0<a≠1) | 1/x logae |
lnx | 1/x | |
5 | sinx | cosx |
6 | cosx | -sinx |
7 | tgx | 1/cos2x |
8 | ctgx | -1/sin2x |
9 | arcsinx | 1/√1-x2 |
10 | arccosx | -1/√1-x2 |
11 | arctgx | 1/1+x2 |
12 | arcctgx | -1/1+x2 |
12 | √x | 1/2√x |
1)(CU)’= C*U’
2)(U±V)’= U’±V’
3)(UV)’=U’V+UV’
4)(U/V)=U’V-UV’ / V2
4*.
Производная сложной функции с демонстрацией на конкретных примерах.Если функция u=f(x) имеет в некоторой точке x производную (∃u’x=u’(x))
Если y=f(u) имеет в соответствующей точке u производную (∃y’u= f’(u))
то y = f(u(x))в точке х также будет иметь производную, равную произведению производной u’(х) и y'(u) ф-й f(u) и u(x).
Y’x= y’u*u’x
5 . Производная обратной функции с демонстрацией на конкретных примерах.
Пусть
Ф-я f(x) в точке x= x0 имеет конечную и отличную от нуля производную ∃f'(x0)≠0
Для нее существует однозначная обратная ф-я ∃x=g(y), непрерывная в соответствующей точке y=y0, где y0=f(x0)
Тогда ∃ g'(y0) =
y’x= x’y= f’(x0)=tgα,
α-
угол наклона кас.
к ОХ;
g’(y0)=tgβ, β- угол наклона кас. к ОY
α +β=П/2, tgβ=1/ tgα
Пр. y=, y’x=?. ∃x=, x’y=, y’x=1/ x’y=1/ 1/x*.
Производная(метод приращения) — ежедневное руководство по математике
Главная » ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ , Производная с использованием метода приращения » Производная (метод приращения)
Производная с использованием метода приращения
Это основная концепция математических изменений. Говоря о производных, это просто говорит о том, что мы разбираем вещь, чтобы увидеть ее части. Обычно в качестве наглядного примера учителя приводят буханку хлеба, нарезанную только для того, чтобы посмотреть, что внутри. На самом деле их много. Все, что приближается к концу, является примером природы дифференциального исчисления. Обратите внимание, что даже при питье воды 100% приближаются к нулю, когда стакан пуст. Но самый яркий пример — это что-нибудь визуальное. Мы представляем метод приращения на этой странице. Это немного сложно, поэтому просто расслабьтесь.
Этот тип математики требует знакомства с алгеброй. Так как операции чисто алгебраические.
Мы подготовили основные математические примеры ниже. Мы постарались выделить части так, чтобы это не мешало вашему зрению. Есть три иллюстративных примера с подсказками и добавленными примерами задач с решениями для дальнейшей практики. Если вы заметили опечатку, сообщите нам об этом здесь. Давайте начнем!
Иллюстративные примеры
Найдите первую производную методом приращения.
1.)
, Отмените все темные зеленые
, . ,
, ответ
2.)
, помните y как заданное уравнение, n?
, компенсировать аналогичные условия
,
, ответ
3. )
, это y есть данное уравнение.
, подставив значение y
, Компенсация Darkgreen Color
, Cross Out
,
, Ответ
, Ответ
0404040402, .
Примеры задач с решениями:
Найдите первую производную методом приращения.
Эти задачи можно найти в учебнике «Дифференциальное и интегральное исчисление Лава и Рейнвилля»
, y из данного уравнения
, замените значение
y
, , удалив круглые скобки, и соберите/компенсируйте аналогичные термины.
, компенсировать все красным цветом
, зачеркнуть
,
, ответ
,
, answer
,
, ответ
,
, Ответ
,
,
, Ответ
Стоимость. 0006
Найдите первую производную методом приращения.
Нажмите, чтобы продолжить
Нажмите, чтобы продолжить
Нажмите, чтобы продолжить.0039
Простая викторина:
Найдите первую производную методом приращения.
Итак, какое самое сложное число вы думаете? Расскажите нам, разместив свой комментарий здесь!
Примечание: Если вы обнаружите ошибки, сообщите нам об этом в разделе «Оставить комментарий» ниже.
Свяжитесь с нами: Pinterest, Facebook, Twitter, Gmail, Instagram, Tumblr
Связанные ссылки: Деривативные алгебраические функции
Вторые производные
Алгебраический факторинг
Биномиальные операции
, как и в отличие от терминов
Посетите дно и кнопку Select, чтобы поделиться : «Для наших услуг!
Оставить комментарий
| |||||
| | |||||
ПРИРАЩИВАНИЯ И ДИФФЕРЕНЦИАЦИЯ В этом разделе мы расширим обсуждение пределов
и изучить идею производной, основу дифференциального исчисления.
Если x присвоено значение 10, соответствующее значение y будет (10) 2 или 100. Теперь, если мы увеличим значение x на 2, сделав это 12, мы можем назвать это увеличение на 2 приращением или Икс. Этот приводит к увеличению значения y, и мы можем назвать это увеличение приращение или у. От это мы пишем Когда x увеличивается с 10 до 12, y увеличивается со 100 до 144 так что и
Нас интересует соотношение поскольку предел этого отношения как Икс приближается к нулю является производной от у = f(X) Как вы помните из обсуждения лимитов, как
х это
сделал меньше,
ты получаешь
также меньше. Таблица 4-l.-Значения уклона Мы можем использовать гораздо более простой способ найти, что предел как x стремится к нулю, в данном случае равно 20. Мы иметь два уравнения и Расширив первое уравнение так, чтобы и вычитая из этого второе, получаем Разделив обе части уравнения на х дает Теперь, принимая предел как Икс приближается к нулю, дает Таким образом, ПРИМЕЧАНИЕ. Уравнение (1) является одним из способов выражения производной
у по отношению к х. | |||||