Проинтегрировать дифференциальное уравнение: Решение дифференциальных уравнений онлайн. Любые с подробным решением.

Решение дифференциальных уравнений | Онлайн калькулятор

Данный онлайн калькулятор позволяет вычислять дифференциальные уравнения практически любого типа и порядка: линейные дифференциальные уравнения, с разделяемыми или неразделяемыми переменными, уравнения Бернулли и т.д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям.

По умолчанию в уравнении функция y является функцией от переменной x. Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t. С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или не разделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание.

x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Смотрите также

Дифференциальные уравнения в полных дифференциалах

Введение

Дифференциальное уравнение первого порядка в полных дифференциалах

– это уравнение вида:
(1)   ,
где левая часть уравнения является полным дифференциалом некоторой функции U(x, y) от переменных x, y:
.
При этом   .

Если найдена такая функция U(x, y), то уравнение принимает вид:
dU(x, y) = 0.
Его общий интеграл:
U(x, y) = C,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx. Тогда   . В результате получаем уравнение, выраженное через дифференциалы:
(1)   .

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2)   .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y. Точка x₀, y₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U(x, y):
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что   . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2)   .
Покажем, что можно найти такую функцию U(x, y), что ее дифференциал:
.
Это означает, что существует такая функция U(x, y), которая удовлетворяет уравнениям:
(3)   ;
(4)   .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x₀ до x, считая что y – это постоянная:
;
;
(5)   .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y₀ до y:
;
;
.
Подставляем в (5):
(6)   .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U(x₀, y₀) является постоянной – значением функции U(x, y) в точке x₀, y₀. Ей можно присвоить любое значение.

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1)   .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2)   .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Решение

Здесь
,   .
Дифференцируем по y, считая x постоянной:


.
Дифференцируем по x, считая y постоянной:


.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d(u ± v);
v du + u dv = d(uv);
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Решить уравнение:
.

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1)   .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Ответ

.

Метод последовательного интегрирования

В этом методе мы ищем функцию U(x, y), удовлетворяющую уравнениям:
(3)   ;
(4)   .

Проинтегрируем уравнение (3) по x, считая y постоянной:
.
Здесь φ(y) – произвольная функция от y, которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ(y) и, тем самым, U(x, y).

Пример 2

Решить уравнение в полных дифференциалах:
.

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
,   .
Ищем Функцию U(x, y), дифференциал которой является левой частью уравнения:
.
Тогда:
(3)   ;
(4)   .
Проинтегрируем уравнение (3) по x, считая y постоянной:
(П2)  
.
Дифференцируем по y:

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U(x, y) = const.
Объединяем две постоянные в одну.

Ответ

.

Метод интегрирования вдоль кривой

Функцию U, определяемую соотношением:
dU = p(x, y) dx + q(x, y) dy,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x₀, y₀) и (x, y):
(7)   .
Поскольку
(8)   ,
то интеграл зависит только от координат начальной (x₀, y₀) и конечной (x, y) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9)   .
Здесь x₀ и y₀ – постоянные. Поэтому U(x₀, y₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6)   .
Здесь интегрирование производится сначала по отрезку, параллельному оси y, от точки (x₀ , y₀) до точки (x₀ , y) . Затем интегрирование производится по отрезку, параллельному оси x, от точки (x₀ , y) до точки (x, y) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки (x₀ , y₀) и (x, y) в параметрическом виде:
x₁ = s(t₁);   y₁ = r(t₁);
x₀ = s(t₀);   y₀ = r(t₀);
x = s(t);   y = r(t);
и интегрировать по t₁ от t₀ до t.

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x₀ , y₀) и (x, y). В этом случае:
x₁ = x₀ + (x – x₀) t₁; y₁ = y₀ + (y – y₀) t₁;
t₀ = 0;   t = 1;
dx₁ = (x – x₀) dt₁; dy₁ = (y – y₀) dt₁.
После подстановки, получается интеграл по t от 0 до 1.
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов.     Опубликовано: 10-08-2012   Изменено: 02-07-2015

примеры решения диффуров (ДУ) в математике

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой.

Ничего не понятно, что делать, как решать, с чего начать?

Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.

Основные понятия теории дифференциальных уравнений

Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.

Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных  уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также

ДУ находят широкое применение в биологии, химии, экономике и многих других науках.

Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.

Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.

Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.

Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.

Порядок дифференциального уравнения  определяется наивысшим порядком производных, входящих в него.

 

Решение уравнений

 

Обыкновенные дифференциальные уравнения

Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.

Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:

Решить такое уравнение можно, просто проинтегрировав его правую часть.

Примеры таких уравнений:

Уравнения с разделяющимися переменными

В общем виде этот тип уравнений выглядит так:

Приведем пример:

Решая такое уравнение, нужно разделить переменные, приведя его к виду:

После этого останется проинтегрировать обе части и получить решение.

 

Математика

 

Линейные дифференциальные уравнения первого порядка

Такие уравнения имеют вид:

Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:

Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).

Для решения таких уравнений необходима определенная подготовка и  взять их “с наскока” будет довольно сложно.

Пример решения ДУ с разделяющимися переменными

Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.

Сначала  перепишем производную в более привычном виде:

Затем разделим переменные, то есть в одной части уравнения соберем все “игреки”, а в другой – “иксы”:

Теперь осталось проинтегрировать обе части:

Интегрируем и получаем общее решение данного уравнения:

Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам.

В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему “Как решать дифференциальные уравнения”:

 

Локально различные решения количество дифференциальные уравнения. Дифференциальные уравнения

Или уже решены относительно производной , или их можно решить относительно производной .

Общее решение дифференциальных уравнений типа на интервале X , который задан, можно найти, взяв интеграл обоих частей этого равенства.

Получим .

Если посмотреть на свойства неопределенного интеграла, то найдем искомое общее решение:

y = F(x) + C ,

где F(x) – одна из первообразных функции f(x) на промежутке X , а С – произвольная постоянная.

Обратите внимание, что в большинстве задач интервал X не указывают. Это значит, что решение нужно находить для всех x , при которых и искомая функция y , и исходное уравнение имеют смысл.

Если нужно вычислить частное решение дифференциального уравнения , которое удовлетворяет начальному условию y(x 0) = y 0 , то после вычисления общего интеграла y = F(x) + C , еще необходимо определить значение постоянной C = C 0 , используя начальное условие. Т.е., константу C = C 0 определяют из уравнения F(x 0) + C = y 0 , и искомое частное решение дифференциального уравнения примет вид:

y = F(x) + C 0 .

Рассмотрим пример:

Найдем общее решение дифференциального уравнения , проверим правильность результата. Найдем частное решение этого уравнения, которое удовлетворяло бы начальному условию .

Решение:

После того, как мы проинтегрировали заданное дифференциальное уравнение, получаем:

.

Возьмем этот интеграл методом интегрирования по частям:

Т.о., является общим решением дифференциального уравнения.

Чтобы убедиться в правильности результата, сделаем проверку. Для этого подставляем решение, которое мы нашли, в заданное уравнение:

.

То есть, при исходное уравнение превращается в тождество:

поэтому общее решение дифференциального уравнения определили верно.

Решение, которое мы нашли, является общим решением дифференциального уравнения для каждого действительного значения аргумента x .

Осталось вычислить частное решение ОДУ, которое удовлетворяло бы начальному условию . Другими словами, необходимо вычислить значение константы С , при котором будет верно равенство:

.

.

Тогда, подставляя С = 2 в общее решение ОДУ, получаем частное решение дифференциального уравнения, которое удовлетворяет первоначальному условию:

.

Обыкновенное дифференциальное уравнение можно решить относительно производной, разделив 2 части равенства на f(x) . Это преобразование будет равнозначным, если f(x) не превращается в нуль ни при каких x из интервала интегрирования дифференциального уравнения X .

Вероятны ситуации, когда при некоторых значениях аргумента x ∈ X функции f(x) и g(x) одновременно превращаются в нуль. Для подобных значений x общим решением дифференциального уравнения будет всякая функция y , которая определена в них, т.к. .

Если для некоторых значений аргумента x ∈ X выполняется условие , значит, в этом случае у ОДУ решений нет.

Для всех других x из интервала X общее решение дифференциального уравнения определяется из преобразованного уравнения .

Разберем на примерах:

Пример 1.

Найдем общее решение ОДУ: .

Решение.

Из свойств основных элементарных функций ясно, что функция натурального логарифма определена для неотрицательных значений аргумента, поэтому областью определения выражения ln(x+3) есть интервал x > -3 . 2 + c.

К линейным уравнениям относите уравнения «первой ». Неизвестная функция с ее производными входит в подобное уравнение лишь в первой степени. Линейное имеет вид dy/dx + f(x) = j(x), где f(x) и g(x) – функции, зависящие от x. Решение записывается с помощью интегралов, взятых от известных функций.

Учтите, что многие дифференциальные уравнения – это уравнения второго порядка (содержащие вторые производные) Таким, например, является уравнение простого гармонического движения, записанное в виде общей : md 2x/dt 2 = –kx. Такие уравнения имеют, в , частные решения. Уравнение простого гармонического движения является примером достаточно важного : линейных дифференциальных уравнений, у которых имеется постоянный коэффициент.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.

Источники:

• как решить уравнение с одной переменной

Задачи на дифференциальное и интегральное исчисление являются важными элементами закрепления теории математического анализа, раздела высшей математики, изучаемой в вузах. Дифференциальное уравнение решается методом интегрирования.

Инструкция

Дифференциальное исчисление исследует свойства . И наоборот, интегрирование функции позволяет по данным свойствам, т.е. производным или дифференциалам функции найти ее саму. В этом и заключается решение дифференциального уравнения.

Любое является соотношением между неизвестной величиной и известными данными. В случае дифференциального уравнения роль неизвестного играет функция, а роль известных величин – ее производные. Кроме этого, соотношение может содержать независимую переменную:F(x, y(x), y’(x), y’’(x),…, y^n(x)) = 0, где x – неизвестная переменная, y(x) – функция, которую нужно определить, порядок уравнения – это максимальный порядок производной (n).

Такое уравнение называется обыкновенным дифференциальным уравнением. Если же в соотношении несколько независимых переменных и частные производные (дифференциалы) функции по этим переменным, то уравнение называется дифференциальным уравнением с частными производными и имеет вид:x∂z/∂y – ∂z/∂x = 0, где z(x, y) – искомая функция.

Итак, чтобы научиться решать дифференциальные уравнения, необходимо уметь находить первообразные, т.е. решать задачу, обратную дифференцированию. Например:Решите уравнение первого порядка y’ = -y/x.

РешениеЗамените y’ на dy/dx: dy/dx = -y/x.

Приведите уравнение к виду, удобному для интегрирования. Для этого умножьте обе части на dx и разделите на y:dy/y = -dx/x.

Проинтегрируйте:∫dy/y = – ∫dx/x + Сln |y| = – ln |x| + C.

Это решение называется общим дифференциального уравнения. С – это константа, множество значений которой определяет множество решений уравнения. При любом конкретном значении С решение будет единственным. Такое решение является частным решением дифференциального уравнения. 4 – 13·x² + 36 = 0

Теперь найдите корни исходного уравнения:x1 = √9 = ±3; x2 = √4 = ±2.

Химическая реакция – это процесс превращения веществ, протекающий с изменением их состава. Те вещества, которые вступают в реакцию, называются исходными, а те, которые образуются в результате этого процесса – продуктами. Бывает так, что в ходе химической реакции элементы, входящие в состав исходных веществ, изменяют свою степень окисления. То есть они могут принять чужие электроны и отдать свои. И в том, и в другом случае меняется их заряд. Такие реакции называются окислительно-восстановительными.

Рассмотрим линейное однородное уравнение второго порядка, т.е. уравнение

и установим некоторые свойства его решений.

Свойство 1
Если является решением линейного однородного уравнения, то C , где C – произвольная постоянная, является решением того же уравнения.
Доказательство.
Подставляя в левую часть рассматриваемого уравнения C , получим: ,
но , т. к. является решением исходного уравнения.
Следовательно,

и справедливость указанного свойства доказана.

Свойство 2
Сумма двух решений линейного однородного уравнения является решением того же уравнения.
Доказательство.
Пусть и являются решениями рассматриваемого уравнения, тогда
и .
Подставляя теперь + в рассматриваемое уравнение будем иметь:
, т.е. + есть решение исходного уравнения.
Из доказанных свойств следует, что, зная два частных решения и линейного однородного уравнения второго порядка, мы можем получить решение , зависящее от двух произвольных постоянных, т.е. от такого количества постоянных, какое должно содержать общее решение уравнение второго порядка. Но будет ли это решение общим, т.е. можно ли путем выбора произвольных постоянных и удовлетворить произвольно заданным начальным условиям?
При ответе на этот вопрос будет использовано понятие линейной независимости функций, которую можно определить следующим образом.

Две функции и называются линейно независимыми на некотором интервале, если их отношение на этом интервале не является постоянным, т.е. если
.
В противном случае функции называются линейно зависимыми .
Иными словами, две функции и называются линейно зависимыми на некотором интервале, если на всем интервале.

Примеры

1. Функции y 1 = e x и y 2 = e – x линейно независимы при всех значениях x , т.к.
.
2. Функции y 1 = e x и y 2 = 5 e x линейно зависимы, т.к.
.

Теорема 1.

Если функции и линейно зависимы на некотором интервале, то определитель , называемый определителем Вронского данных функций, тождественно равен нулю на этом интервале.

Доказательство.

Если
,
где , то и .
Следовательно,
.
Теорема доказана.

Замечание.
Определитель Вронского, фигурирующий в рассмотренной теореме, обычно обозначается буквой W или символами .
Если функции и являются решениями линейного однородного уравнения второго порядка, то для них справедлива следующая обратная и притом более сильная теорема.

Теорема 2.

Если определитель Вронского, составленный для решений и линейного однородного уравнения второго порядка, обращается в ноль хотя бы в одной точке, то эти решения линейно зависимы.

Доказательство.

Пусть определитель Вронского обращается в ноль в точке , т.е. =0,
и пусть и .
Рассмотрим линейную однородную систему

относительно неизвестных и .
Определитель этой системы совпадает со значением определителя Вронского при
x= , т.е. совпадает с , и, следовательно, равен нулю. Поэтому система имеет ненулевое решение и ( и не равны нулю). Используя эти значения и , рассмотрим функцию . Эта функция является решением того же уравнения, что и функции и . Кроме того, эта функция удовлетворяет нулевым начальным условиям: , т.к. и .
С другой стороны, очевидно, что решением уравнения , удовлетворяющим нулевым начальным условиям, является функция y =0.
В силу единственности решения, имеем: . Откуда следует, что
,
т.е. функции и линейно зависимы. Теорема доказана.

Следствия.

1. Если определитель Вронского, фигурирующий в теоремах, равен нулю при каком-нибудь значении x= , то он равен нулю при любом значении x из рассматриваемого интервала.

2. Если решения и линейно независимы, то определитель Вронского не обращается в ноль ни в одной точке рассматриваемого интервала.

3. Если определитель Вронского отличен от нуля хотя бы в одной точке, то решения и линейно независимы.

Теорема 3.

Если и – два линейно независимых решения однородного уравнения второго порядка , то функция , где и – произвольные постоянные, является общим решением этого уравнения.

Доказательство.

Как известно, функция является решением рассматриваемого уравнения при любых значениях и . Докажем теперь, что каковы бы ни были начальные условия
и ,
можно так подобрать значения произвольных постоянных и , чтобы соответствующее частное решение удовлетворяло заданным начальным условиям.
Подставляя начальные условия в равенства, получим систему уравнений
.
Из этой системы можно определить и , т.к. определитель этой системы

есть определитель Вронского при x= и, следовательно, не равен нулю (в силу линейной независимости решений и ).

; .

Частное решение при полученных значениях и удовлетворяет заданным начальным условиям. Таким образом, теорема доказана.

Примеры

Пример 1.

Общим решением уравнения является решение .
Действительно,
.

Следовательно, функции sinx и cosx линейно независимы. В этом можно убедиться, рассмотрев отношение этих функций:

.

Пример 2.

Решение y = C 1 e x + C 2 e – x уравнения является общим, т.к. .

Пример 3.

Уравнение , коэффициенты которого и
непрерывны на любом интервале, не содержащем точки x = 0, допускает частные решения

(легко проверить подстановкой). Следовательно, его общее решение имеет вид:
.

Замечание

Мы установили, что общее решение линейного однородного уравнения второго порядка можно получить зная два каких-либо линейно независимых частных решения этого уравнения. Однако, не существует общих методов для нахождения таких частных решений в конечном виде для уравнений с переменными коэффициентами. Для уравнений с постоянными коэффициентами такой метод существует и будет рассмотрен нами позднее.

Решение дифференциальных уравнений. Благодаря нашему онлайн сервису вам доступно решение дифференциальных уравнений любого вида и сложности: неоднородные, однородные, нелинейные, линейные, первого, второго порядка, с разделяющимися переменными или не разделяющимися и т.д. Вы получаете решение дифференциальных уравнений в аналитическом виде с подробным описанием. Многие интересуются: зачем необходимо решать дифференциальные уравнения онлайн? Данный вид уравнений очень распространён в математике и физике, где решить многие задачи без вычисления дифференциального уравнения будет невозможно. Также дифференциальные уравнения распространены в экономике, медицине, биологии, химии и других науках. Решение же такого уравнения в онлайн режиме значительно облегчает вам поставленные задачи, дает возможность лучше усвоить материал и проверить себя. Преимущества решения дифференциальных уравнений онлайн. Современный математический сервис сайт позволяет решать дифференциальные уравнения онлайн любой сложности. Как вы знаете, существует большое количество видов дифференциальных уравнений и для каждого из них предусмотрены свои способы решения. На нашем сервисе вы можете найти решение дифференциальных уравнений любого порядка и вида в онлайн режиме. Для получения решения мы предлагаем вам заполнить исходные данные и нажать кнопку «Решение». Ошибки в работе сервиса исключены, поэтому вы можете на 100% быть уверены, что получили верный ответ. Решайте дифференциальные уравнения вместе с нашим сервисом. Решить дифференциальные уравнения онлайн. По умолчанию в таком уравнении функция y – это функция от x переменной. Но вы можете задавать и свое обозначение переменной. Например, если вы укажете в дифференциальном уравнении y(t), то наш сервис автоматически определит, что у является функцией от t переменной. Порядок всего дифференциального уравнения будет зависеть от максимального порядка производной функции, присутствующей в уравнении. Решить такое уравнение – означает найти искомую функцию. Решить дифференциальные уравнения онлайн вам поможет наш сервис. Для решения уравнения от вас не потребуется много усилий. Необходимо лишь ввести в нужные поля левую и правую части вашего уравнения и нажать кнопку «Решение». При вводе производную от функции необходимо обозначать через апостроф. Через считанные секунды вы получите готовое подробное решение дифференциального уравнения. Наш сервис абсолютно бесплатный. Дифференциальные уравнения с разделяющимися переменными. Если в дифференциальном уравнении в левой части находится выражение, зависящее от y, а правой части – выражение, которое зависит от x, то такое дифференциальное уравнение называется с разделяющимися переменными. В левой части может быть производная от y, решение дифференциальных уравнений такого вида будет в виде функции y, выраженной через интеграл от правой части уравнения. Если же в левой части будет дифференциал функции от y, то в таком случае интегрируются обе части уравнения.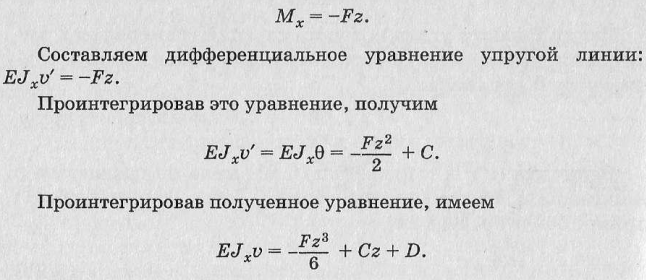 Когда переменные в дифференциальном уравнении не разделены, то их потребуется разделить, чтобы получить дифференциальное уравнение с разделенными переменными. Линейное дифференциальное уравнение. Линейным называется дифференциальное уравнение, у которого функция и все ее производные находятся в первой степени. Общий вид уравнения: y’+a1(x)y=f(x). f(x) и a1(x) – это непрерывные функции от x. Решение дифференциальных уравнений такого типа сводится к интегрированию двух дифференциальных уравнений с разделенными переменными. Порядок дифференциального уравнения. Дифференциальное уравнение может быть первого, второго, n-го порядка. Порядок дифференциального уравнения определяет порядок старшей производной, которая содержится в нем. В нашем сервисе вы можете решить дифференциальные уравнения онлайн первого, второго, третьего и т.д. порядка. Решением уравнения будет любая функция y=f(x), подставив которую в уравнение, вы получите тождество. Процесс поиска решения дифференциального уравнения называют интегрированием. Задача Коши. Если помимо самого дифференциального уравнения задается первоначальное условие y(x0)=y0, то это называется задачей Коши. В решение уравнения добавляются показатели y0 и x0 и определяют значение произвольной константы C, а потом частное решение уравнения при этом значении C. Это и является решением задачи Коши. Еще задачу Коши называют задачей с граничными условиями, что очень распространено в физике и механике. Также у вас есть возможность задать задачу Коши, то есть из всех возможных решений уравнения выбрать частное, которое отвечает заданным первоначальным условиям.

Учреждение образования «Белорусская государственная

сельскохозяйственная академия»

Кафедра высшей математики

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Конспект лекции для студентов бухгалтерского факультета

заочной формы получения образования (НИСПО)

Горки, 2013

Дифференциальные уравнения первого порядка

Понятие дифференциального уравнения. Общее и частное решения

При изучении различных явлений часто не удаётся найти закон, который непосредственно связывает независимую переменную и искомую функцию, но можно установить связь между искомой функцией и её производными.

Соотношение, связывающее независимую переменную, искомую функцию и её производные, называется дифференциальным уравнением :

Здесь x – независимая переменная, y – искомая функция,
– производные искомой функции. При этом в соотношении (1) обязательно наличие хотя бы одной производной.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Рассмотрим дифференциальное уравнение

. (2)

Так в это уравнение входит производная только первого порядка, то оно называется дифференциальным уравнением первого порядка.

Если уравнение (2) можно разрешить относительно производной и записать в виде

, (3)

то такое уравнение называется дифференциальным уравнением первого порядка в нормальной форме.

Во многих случаях целесообразно рассматривать уравнение вида

которое называется дифференциальным уравнением первого порядка, записанным в дифференциальной форме.

Так как
, то уравнение (3) можно записать в виде
или
, где можно считать
и
. Это означает, что уравнение (3) преобразовано в уравнение (4).

Запишем уравнение (4) в виде
. Тогда
,
,
, где можно считать
, т.е. получено уравнение вида (3). Таким образом, уравнения (3) и (4) равносильны.

Решением дифференциального уравнения (2) или (3) называется любая функция
, которая при подстановке её в уравнение (2) или (3) обращает его в тождество:

или
.

Процесс нахождения всех решений дифференциального уравнения называется его интегрированием , а график решения
дифференциального уравнения называетсяинтегральной кривой этого уравнения.

Если решение дифференциального уравнения получено в неявном виде
, то оно называетсяинтегралом данного дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка называется семейство функций вида
, зависящее от произвольной постояннойС , каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С . Таким образом, дифференциальное уравнение имеет бесчисленное множество решений.

Частным решением дифференциального уравнения называется решение, получаемое из формулы общего решения при конкретном значении произвольной постоянной С , включая
.

Задача Коши и её геометрическая интерпретация

Уравнение (2) имеет бесчисленное множество решений. Чтобы из этого множества выделить одно решение, которое называется частным, нужно задать некоторые дополнительные условия.

Задача отыскания частного решения уравнения (2) при заданных условиях называется задачей Коши . Эта задача является одной из важнейших в теории дифференциальных уравнений.

Формулируется задача Коши следующим образом: среди всех решений уравнения (2) найти такое решение
, в котором функция
принимает заданное числовое значение, если независимая переменная x принимает заданное числовое значение , т.е.

,
, (5)

где D – область определения функции
.

Значение называетсяначальным значением функции , а – начальным значением независимой переменной . Условие (5) называется начальным условием или условием Коши .

С геометрической точки зрения задачу Коши для дифференциального уравнения (2) можно сформулировать следующим образом: из множества интегральных кривых уравнения (2) выделить ту, которая проходит через заданную точку
.

Дифференциальные уравнения с разделяющимися переменными

Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции:

. (6)

Учитывая, что
, запишем уравнение в виде
или
. Интегрируя обе части последнего уравнения, получим:
или

. (7)

Таким образом, (7) является общим решением уравнения (6).

Пример 1 . Найти общее решение дифференциального уравнения
.

Решение . Запишем уравнение в виде
или
. Проинтегрируем обе части полученного уравнения:
,
. Окончательно запишем
.

Пример 2 . Найти решение уравнения
при условии
.

Решение . Найдём общее решение уравнения:
,
,
,
. По условию
,
. Подставим в общее решение:
или
. Найденное значение произвольной постоянной подставим в формулу общего решения:
. Это и есть частное решение дифференциального уравнения, удовлетворяющее заданному условию.

Уравнение

(8)

Называется дифференциальным уравнением первого порядка, не содержащим независимой переменной . Запишем его в виде
или
. Проинтегрируем обе части последнего уравнения:
или
– общее решение уравнения (8).

Пример . Найти общее решение уравнения
.

Решение . Запишем это уравнение в виде:
или
. Тогда
,
,
,
. Таким образом,
– общее решение данного уравнения.

Уравнение вида

(9)

интегрируется с помощью разделения переменных. Для этого уравнение запишем в виде
, а затем с помощью операций умножения и деления приводим его к такой форме, чтобы в одну часть входила только функция отх и дифференциал dx , а во вторую часть – функция от у и дифференциал dy . Для этого обе части уравнения нужно умножить на dx и разделить на
. В результате получим уравнение

, (10)

в котором переменные х и у разделены. Проинтегрируем обе части уравнения (10):
. Полученное соотношение является общим интегралом уравнения (9).

Пример 3 . Проинтегрировать уравнение
.

Решение . Преобразуем уравнение и разделим переменные:
,
. Проинтегрируем:
,
или – общий интеграл данного уравнения.
.

Пусть уравнение задано в виде

Такое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметрической форме.

Для разделения переменных нужно обе части уравнения разделить на
:

. (12)

Полученное уравнение называется дифференциальным уравнением с разделёнными переменными . Проинтегрируем уравнение (12):

.(13)

Соотношение (13) является общим интегралом дифференциального уравнения (11).

Пример 4 . Проинтегрировать дифференциальное уравнение .

Решение . Запишем уравнение в виде

и разделим обе его части на
,
. Полученное уравнение:
является уравнением с разделёнными переменными. Проинтегрируем его:

,
,

,
. Последнее равенство является общим интегралом данного дифференциального уравнения.

Пример 5 . Найти частное решение дифференциального уравнения
, удовлетворяющее условию
.

Решение . Учитывая, что
, запишем уравнение в виде
или
. Разделим переменные:
. Проинтегрируем это уравнение:
,
,
. Полученное соотношение является общим интегралом данного уравнения. По условию
. Подставим в общий интеграл и найдёмС :
,С =1. Тогда выражение
является частным решением данного дифференциального уравнения, записанным в виде частного интеграла.

Линейные дифференциальные уравнения первого порядка

Уравнение

(14)

называется линейным дифференциальным уравнением первого порядка . Неизвестная функция
и её производная входят в это уравнение линейно, а функции
и
непрерывны.

Если
, то уравнение

(15)

называется линейным однородным . Если
, то уравнение (14) называетсялинейным неоднородным .

Для нахождения решения уравнения (14) обычно используют метод подстановки (Бернулли) , суть которого в следующем.

Решение уравнения (14) будем искать в виде произведения двух функций

, (16)

где
и
– некоторые непрерывные функции. Подставим
и производную
в уравнение (14):

Функцию v будем подбирать таким образом, чтобы выполнялось условие
. Тогда
. Таким образом, для нахождения решения уравнения (14) нужно решить систему дифференциальных уравнений

Первое уравнение системы является линейным однородным уравнением и решить его можно методом разделения переменных:
,
,
,
,
. В качестве функции
можно взять одно из частных решений однородного уравнения, т.е. приС =1:
. Подставим во второе уравнение системы:
или
.Тогда
. Таким образом, общее решение линейного дифференциального уравнения первого порядка имеет вид
.

Пример 6 . Решить уравнение
.

Решение . Решение уравнения будем искать в виде
. Тогда
. Подставим в уравнение:

или
. Функциюv выберем таким образом, чтобы выполнялось равенство
. Тогда
. Решим первое из этих уравнений методом разделения переменных:
,
,
,
,. Функциюv подставим во второе уравнение:
,
,
,
. Общим решением данного уравнения является
.

Вопросы для самоконтроля знаний

Что называется дифференциальным уравнением?

Что называется порядком дифференциального уравнения?

Какое дифференциальное уравнение называется дифференциальным уравнением первого порядка?

Как записывается дифференциальное уравнение первого порядка в дифференциальной форме?

Что называется решением дифференциального уравнения?

Что называется интегральной кривой?

Что называется общим решением дифференциального уравнения первого порядка?

Что называется частным решением дифференциального уравнения?

Как формулируется задача Коши для дифференциального уравнения первого порядка?

Какова геометрическая интерпретация задачи Коши?

Как записывается дифференциальное уравнение с разделяющимися переменными в симметрической форме?

Какое уравнение называется линейным дифференциальным уравнением первого порядка?

Каким методом можно решить линейное дифференциальное уравнение первого порядка и в чём суть этого метода?

Задания для самостоятельной работы

Решить дифференциальные уравнения с разделяющимися переменными:

а)
; б)
;

в)
; г)
.

2. Решить линейные дифференциальные уравнения первого порядка:

а)
; б)
; в)
;

г)
; д)
.

Дифференциальные уравнения, общие понятия – Доктор Лом

В общем случае определение дифференциального уравнения может выглядеть так:

Дифференциальным уравнением называется равенство между функцией и ее производной или дифференциалом.

Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного аргумента. Например:

у’ = f(x) (539.1)

Напомню, функциональное уравнение может иметь следующий вид:

у = f(x) (538.1)

Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких аргументов. Например:

у’ = f(x₁,x₂) или у’ = f(x,u) (539.2)

где х₁, х₂ или х, u – возможные обозначения для различных аргументов функции.

Порядком дифференциального уравнения считается порядок наивысшей производной, входящей в уравнение. Например уравнение (539.1) является уравнением первого порядка. Уравнение второго порядка может иметь вид:

y” = f(x) (539.3)

Решением дифференциального уравнения является функция, подставление которой вместо неизвестной функции обращает уравнение в тождество. Другими словами уравнение становится равенством.

А теперь эти общие математические понятия (кстати тут приведены далеко не все основные понятия) попробуем описать простым человеческим языком, но начать придется издалека.

Производная функции

Мы живем в несовершенном, постоянно изменяющемся мире. Все течет, все изменяется, как подметил еще Гераклит. Однако в древности были и другие мыслители, которые в отличие от Гераклита пытались этот мир как-то понять и оценить. Так далеко в историю мы заглядывать не будем, хотя предпосылки к дифференциальному исчислению следует искать именно там, а ограничимся простыми и наглядными примерами:

Пример 1

Мы вышли из пункта А в пункт Б и находились в пути 4 часа, каждый час мы проходили по 2 километра. Вопрос: какое расстояние между пунктами А и Б?

Вообще это задачка для 3-4 класса начальной школы и решить ее вроде бы не сложно (потому я ее и выбрал): достаточно сложить все расстояния, пройденные за каждый час, а так как эти расстояния одинаковые, то можно еще больше упростить задачу, умножив на 4 расстояние, пройденное за один промежуток времени. Таким образом расстояние между пунктами А и Б составляет:

2 км · 4 = 8 км (539.4)

А между тем условия задачи можно рассматривать и по другому, т.е. как зависимость пройденного расстояния от времени. В этом случае у нас время -независимая переменная t или аргумент функции, а пройденное расстояние – значение функции в тот или иной момент времени или переменная s. Тогда условия задачи соответствуют следующему функциональному уравнению:

s = f(t) = 2t (539.5)

а также графику этой функции:

Рисунок 539. 1. График функции f(t) = 2t.

 

Так если по оси t откладывать промежутки времени Δt (ч), которое мы были в пути, а по оси s – преодоленное за эти промежутки времени расстояние Δs (км), то график указанной функции будет иметь такой вид, как показано на рисунке 539.1. В общем случае используются более привычные оси х и у, соответственно рассматриваются функции вида y = f(x), но сути дела это никак не меняет.

Решая уравнение (539.5) мы можем определить не только общее расстояние, преодоленное за 4 часа пути, но и в любой интересующий нас момент времени. Например, нас интересует, какое расстояние мы прошли за 1.5 часа. Согласно уравнению (539.5) это расстояние составит 2·1.5 = 3 километра.

А если нас интересует не расстояние, преодоленное к тому или иному моменту времени, а скорость движения? Можем ли мы определить эту скорость на основе имеющихся данных?

Оказывается можем, потому что скорость – это тоже функция, которая в свою очередь также зависит от времени.

Так как каждый час мы преодолевали по 2 км, то отсюда можно сделать вывод, что скорость нашего движения была постоянной, тогда по давно известному нам уравнению, описывающему движение с постоянной скоростью:

v = s/t = 8/4 = 2 км/ч (539.6)

В данном случае, так как скорость постоянная, не имеет значения, на каком временном промежутке мы эту скорость определяем. Тем не менее рассмотрим данную ситуацию с точки зрения математики.

Временные промежутки, когда засекалось пройденное расстояние, мы обозначим как Δt = 1, соответственно t = ΣΔt = 1 + 1 + 1 + 1 = 4. Расстояния, пройденные за эти промежутки времени обозначим как Δs = 2. На графике функции это будет выглядеть так:

Рисунок 539.2

С точки зрения математики временные промежутки Δt – это приращение аргумента функции:

Δt = t – t₀ (539.7)

Соответственно расстояния, пройденные за рассматриваемый промежуток времени – это приращение функции:

Δs = Δf(t) = f(t) – f(t₀) (539. 8)

А так как использовать греческую литеру Δ не всегда удобно (в частности мне для этого приходится заходить в отдельный редактор текста, а наборщикам в типографиях вставить эту литеру было еще сложнее), то часто приращение значения искомой функции и приращение аргумента функции обозначают как ds и dt.

Тогда формулу определения скорости можно записать так:

v = ds/dt (539.9)

Таким образом мы с одной стороны вроде бы просто разделили расстояние на время – задача для 3-4 класса, а с другой стороны мы определили производную функции s = f(t), соответствующим образом ее продифференцировав, а это уже задача курса алгебры, а то и высшей математики.

Возможно и не стоило это так подробно расписывать, но на мой взгляд это очень важно, чтобы показать, что в дифференциальном исчислении нет ничего трудного, если рассматривать его на соответствующих примерах.

Итак скорость v является производной функции s = f(t) = 2t. Дифференциальное уравнение в этом случае будет выглядеть так:

v = s’ = f'(t) (539.10.1)

v = (2t)’ = 2 (539.10.2)

Но и это еще не все, на основании имеющихся данных: времени в пути и расстояний, преодоленных за 1 час, мы можем определить ускорение нашего движения.

Так как скорость нашего движения оставалась постоянной, соответственно dv = 0, то само собой и ускорения никакого не было, ни положительного ни отрицательного. Другими словами ускорение нашего движения составляло а = 0 км/ч².

На языке математики это будет выглядеть так:

а = v’ = dv/dt = s” = d²s/dt² (539.11.1)

a = 0/1 = (2t)” = (2)’ = 0 (539.11.2)

Т.е. в данном случае для определения ускорения нужно определить первую производную функции скорости (уравнения, выражающего зависимость скорости от времени) или вторую производную функции расстояния (уравнения, выражающего зависимость пройденного расстояния от времени).

На основании вышеизложенного мы можем дать следующее предварительное определение производной:

Производная – это скорость изменения функции

В рассмотренном выше примере скорость движения – это скорость изменения функции расстояния, а ускорение – это скорость изменения функции скорости. Если бы мы все 4 часа сидели на месте, то и расстояние, пройденное нами, было бы равно нулю, и скорость и ускорение, но даже для такого случая можно записать соответствующие дифференциальные уравнения:

s = f(t) = 0

v = s’ = 0

a = v’ = s” = 0

Однако в жизни гораздо чаще встречаются функции, даже третьи производные которых не равны нулю.

Рассмотрим другой пример все с тем же движением, на этот раз чуть более сложный.

Пример 2

По ровной наклонной поверхности скатывается шар. Начальная скорость движения равна v_o = 0. Определить пройденное шаром за 4 секунды расстояние, скорость после 1, 2, 3 и 4 секунд движения и постоянное ускорение движения, если за первую секунду шар преодолел расстояние 3 м, за вторую – 9 м, за третью – 15 м, за четвертую – 21 м.

С определением пройденного расстояния по прежнему проблем нет: достаточно сложить расстояния, которые преодолел шар за каждую секунду s = ΣΔs = 3 + 9 + 15 + 21 = 48 метров. А вот скорость и ускорение в данном случае определить не так просто. Тем не менее попробуем.

Если воспользоваться полученными раннее знаниями, то вроде бы в первый промежуток времени скорость должна быть равна:

v₁ = ds₁/dt₁ = 3/1 = 3 м/с (539.12)

Вот только в данном случае у нас скорость – изменяющаяся величина, зависящая от времени, поэтому результат полученный при решении уравнения (539.12) можно рассматривать лишь как среднюю скорость движения на первом участке. Тогда более правильно уравнение скорости на первом участке записать так:

v_1ср = ds₁/dt₁ = 3/1 = 3 м/с (539.12.2)

Подобным образом мы достаточно легко можем определить среднюю скорость на всех участках пути, и она составит v_2ср = 9 м/с, v_3ср = 15 м/с, v_4ср = 21 м/с, но в данном случае нас интересует не среднее значение функции скорости на рассматриваемом участке, а значение функции скорости во вполне определенной точке, т. е. после 1, 2, 3 и 4 секунд движения. Как это сделать?

По условиям задачи ускорение – производная от скорости – является постоянной величиной, т.е. скорость изменения скорости будет постоянной. В этом случае значение средней скорости является средним арифметическим от начальной и конечной скорости на рассматриваемом участке:

v_1ср = (v_o + v₁)/2 = 3 м/с (539.13.1)

тогда при v_o = 0

v₁ = 3·2 = 6 м/с (539.13.2)

Соответствующим образом мы можем определить значения скорости и в остальных точках, например (6 + v₂)/2 = 9, v₂ = 9·2 – 6 = 12 м/с; (12 + v₃)/2 = 15, v₃ = 15·2 – 12 = 18 и так далее, а теперь переведем полученные данные на язык высшей математики. Мы видим, что v₁ = 6·1, v₂ = 6·2 = 12, v₃ = 6·3 = 18, т.е. значение скорости явно зависит от времени, соответственно уравнение скорости мы можем записать следующим образом:

v = s’ = 6t (539. 14)

Соответственно ускорение движения шара составит:

a = v’ = (6t)’ = 6 м/с² (539.15)

Между тем, если бы нам были заданы меньшие значения временных промежутков и соответственно меньшие значения пройденных расстояний за эти промежутки времени, например при dt₁ = 1 секунда, ds₁ = 3 м, dt₂ = 0.1 секунды и ds₂ = 0.63 м, то средняя скорость на рассматриваемом втором участке составила бы v_2ср = ds/dt = 0.63/0.1 = 6.3 м/с, а скорость в  в точке t₂: v_2сp = (6 + v₂)/2 = 6.3, v₂ = 12.6 – 6 = 6.6 м/с. Т.е. закономерность изменения значения скорости никуда не девается, тем не менее, чем меньше рассматриваемый временной промежуток dt, тем меньше разница между значением средней скорости изменения функции и скоростью изменения функции в рассматриваемой точке. Из этого можно сделать еще один очень важный вывод:

Скорость изменения функции может быть разная.

Чем меньше приращение аргумента функции dt, тем ближе значение среднего изменения скорости к изменению скорости функции в рассматриваемой точке.

На основании этого можно сформулировать более полное определение производной функции:

Производная функции в точке – это скорость изменения функции в рассматриваемой точке при стремлении приращения аргумента функции к нулю (Δt → 0)

Поэтому иногда производную называют мгновенной скоростью изменения функции. В нашем случае уравнение производной будет выглядеть так:

 (539.16)

На данном этапе вид формулы (539.16) нас уже не пугает (во всяком случае мне так кажется). Совсем другое дело, когда подобная формула приводится в начале темы, посвященной рассмотрению производных функции.

Дифференциал (первообразная) функции

С задачей определения скорости и ускорения в примере 2 мы вроде бы справились и даже составили соответствующие уравнения (539.14) и (539.15). Но иногда требуется решить и обратную задачу – например определить исходное уравнение, описывающее зависимость перемещения от времени.

Если скорость является производной функции расстояния v = s’, то расстояние при этом является первообразной (дифференциалом) функции скорости s = ∫v. Процесс нахождения первообразной функции называется интегрированием. Так, чтобы получить уравнение зависимости пройденного расстояния от времени, нам нужно проинтегрировать уравнение скорости. При этом уравнение расстояния более правильно записывать так

s = ∫vdt (539.17)

В общем случае интегрирование может быть более сложной задачей, чем дифференцирование, потому что функции бывают не только степенными, как в данном примере, но и тригонометрическими, обратными тригонометрическими  и т.п., но пока нас интересует, как проинтегрировать простую степенную функцию вида f(t) = 6t.

Вообще-то мы могли сразу построить график, отражающий зависимость пройденного расстояния от времени по данным примера 2, тем не менее сделаем это сейчас, а заодно построим график для уравнений скорости и ускорения и расположим их в такой последовательности:

Рисунок 539. 3. Графики степенных функции а) а= 6, б) v = at, в) s = at²/2.

Как видим, график, отражающий зависимость ускорения от времени, у нас самый простой. Ускорение постоянное, а = 6 м/с² и от времени никак не зависит. Тем не менее, зная ускорение, мы можем определить скорость движения в любой точке времени. Так из уравнений (539.14) и (539.15) следует, что:

v = 6t = at (539.14.2)

Соответственно решая это уравнение, мы можем определить скорость в любой момент времени.

Но если рассматривать это действие с точки зрения геометрии, то мы, умножая ускорение на время, определяем площадь прямоугольника со сторонами а = 6 и t. При t = 4 площадь прямоугольника составит 6·4 = 24, точнее 24 м/с так как мы все-таки определяем скорость.

Если мы построим график, отражающий зависимость изменения скорости от времени, то увидим, что на этом графике значения скорости в той или иной момент времени соответствуют площадям прямоугольника со сторонами а = 6 и t.

Получается, что если определить площадь треугольника со сторонами v и t, то это и будет расстояние, преодоленное к тому или иному промежутку времени:

s = vt/2 = at²/2 = 6t²/2 = 3t² (539.18)

Уравнение (539.18) можно записать как дифференциальное:

s = ∫6tdt = 3t² (539.18.2)

Если график, показанный на рисунке 539.3.в) также является графиком для производной некоторой функции, то для определения первообразной этой функции нам также следовало бы найти площадь фигуры, ограниченной квадратной параболой.

Сделать это в принципе не сложно, так как площадь фигуры, очерченной квадратной параболой таким образом, как показано на рисунке 539.3.в) в 3 раза меньше площади прямоугольника со сторонами s и t, соответственно S = st/3 = 3t²t/3 = t³ и эту процедуру можно повторять до бесконечности.

Почему площадь фигуры, ограниченной квадратной параболой именно в 3 раза меньше, чем площадь прямоугольника, а площадь фигуры ограниченной кубической параболой в 4 раза меньше площади прямоугольника, я здесь объяснять не буду, тем не менее такая закономерность существует и в математическом выражении выглядит так:

∫aхⁿdx = axⁿ⁺¹/n + C (539. 19)

В данном случае С – это некоторая постоянная величина. Как мы выяснили, при дифференцировании постоянные величины обращаются в нуль, как пример – уравнение (539.11.2), соответственно решая обратную задачу, т.е. интегрируя функцию, мы допускаем, что некая постоянная величина в первообразной функции была.

Например в общем случае уравнение скорости (539.14.2) должно выглядеть так:

v = v_o + at (539.14.3)

где v_o – это и есть некая постоянная величина. В нашем случае по условиям задачи v_o = 0, поэтому мы использовали сокращенную форму записи.

Определенный интеграл

В общем случае график функции может выглядеть как угодно, например так:

Рисунок 539.4

В этом случае сразу определить площадь фигуры, ограниченной графиком функции, не получится. Но мы можем разбить эту фигуру на участки шириной Δх и определить среднее значение у для каждого участка. Теперь определить площади трех прямоугольников большого труда не составит, вот только суммарная площадь прямоугольников не будет равна площади фигуры, ограниченной графиком функции:

S ≈ ∑y_iΔx (539.20)

Но чем больше будет у нас прямоугольников с шириной Δх, т.е, чем меньше будет значение Δх, тем точнее будет значение у, а значит и суммарная площадь прямоугольников будет ближе к площади фигуры, ограниченной графиком функции.

При интегрировании, как и при дифференцировании для получения более точного результата приращение аргумента функции должно стремиться к нулю (maxΔx → 0).

Из этого можно сделать следующий вывод:

Если существует предел суммы, определяемой по формуле (539.20) вне зависимости от количества прямоугольников и при стремлении ширины прямоугольников к нулю, то такой предел называется определенным интегралом, а суммы, определяемые по формуле (539.

20) – интегральными суммами.

Так как на рисунке 539.4 показан график непрерывной функции, то такая функция является интегрируемой и для определения дифференциала функции используется определенный интеграл. При этом 0 и 3 – это пределы интегрирования.

Дифференциальные уравнения с разделенными переменными

Многие студенты спрашивают “Как найти решение дифференциального уравнения?” Ответ возможно неординарен, но что Вы знаете о дифференциальных уравнениях (ДУ), их типах, какие распространенные схемы вычислений ДУ? С этого нужно начинать.
Сферы применения дифференциальных уравнений были в общем очерчены на предыдущем уроке. Здесь речь пойдет об одном из самых простых (в плане вычислений) типов ДУ первого порядка среди всех возможных уравнений что Вас ждут. Начнем с базовых понятий теории которые Вы должны знать и мы будем использовать в терминологии. Для одних это не нужно, потому что они ищут готовые ответы по дифференциальным уравнениям и думают, что таким образом решат все проблемы. Но это ошибка, потому что не знание элементарных понятий по теории ДУ сравнимо с тем, что Вы пытаетесь говорить, предварительно не изучив звуки и алфавит.
Дифференциальное уравнение первого порядка, которое можно записать формулой
N(х)dx+М(у)dy=0 (1)
называют уравнением с разделенными переменными.
Их не трудно обнаружить среди других уравнений, основной признак – множители при dx и dy являются функциями (константами), которые зависят только от х при множителе dx и у при dy.
Чтобы найти общее решение (общий интеграл) уравнения с разделенными переменными необходимо проинтегрировать уравнение (1)
Int(N(x), x) + Int(M(y),y) = С,

Для понимания дифференциальное уравнение (1) можно принимать, как условие равенства нулю полного дифференциала некоторой функции двух переменных U(x,y)

Отсюда следует что функция U(x,y)=С=const равна постоянной.
Дифференциальное уравнение вида
f₁(x)*g₁(y)dx+f₂(x)*g₂(y)dy=0 (2)
называют дифференциальным уравнением с разделяющимися переменными в симметричной форме.
В уравнении (2) коэффициенты при дифференциалах dx и dy является произведениями двух функций: одна зависит только от x, а вторая – от y. В области, где g1(y), f2(x) принимают отличные от нуля значения в уравнение с разделяющимися переменными (2) сводится к уравнению с разделенными переменными

Звучит как игра слов: разделенными, разделяющимися, однако между ними как видите есть маленькая разница, и теперь Вы ее знаете.
Рассмотрим типичные для практики задания на диф. уравнения первого порядка, которые в достаточно простой способ можно свести к уравнениям с разделенными переменными.

Пример 1 Решить дифференциальное уравнение
Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства

Далее выделим общие множители для каждой суммы и перепишем уравнение в дифференциалах в форме

После этого все, что содержит y переносим к dy, то же самое проделываем с множителями которые содержат переменную x.
В результате придем к дифференциальному уравнению с разделенными переменными

Теперь посмотрите почему данное уравнение называется уравнением с разделенными переменными? – Возле dx имеем функцию зависимую только от “икс”, у dy – только от y.
Проинтегрируем дифференциальное уравнение

Выносим множители, чтобы при переменной в знаменателе стояли единицы. Также, чтобы в числителе получить дифференциалы знаменателя умножаем обе части на 2

Это позволяет упростить вычисления интеграла ДУ (после интегрирования получить логарифмы)

Константу рекомендуем внести в логарифм, для этого записывайте всегда ее в виде C₁=ln(C)

Чтобы раскрыть логарифмическое уравнение экспонируем (находим экспоненту) правую и левую сторону зависимости
(3)
Также выделяем значение функции

Конечная запись имеет двойной корень и является общим решением уравнения с разделяющимися переменными. Это не совсем хороший тон подавать ответ, лучше решение оставить в виде формулы (3), только тройку перенести в правую сторону.

 

Пример 2 Найти общий интеграл дифференциального уравнения
Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства

С первых скобок выносим общий для двух слагаемых множитель y за скобки

Далее разделим множители так, чтобы при dy получить функцию только от y, а при dx – функцию аргумента x. В результате получим дифференциальное уравнение с разделенными переменными

После интегрирования

получим корневую зависимость для y и арктангенс в результате вычисления интеграла по аргументу (правая сторона).

Общий интеграл можем оставить в такой форме или перенести артангенс в левую часть зависимости.
Так же можем записать решение дифференциального уравнения в виде зависимости y(x) (явном виде). Для этого возведем обе части к квадрату

и перенеся сталую в правую сторону, вычислим корень квадратный

Это и есть искомое решение дифференциального уравнения.

 

Пример 3 Решить дифференциальное уравнение
Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства

и разделяем переменные

Проинтегрируем левую и правую сторону зависимости

В результате придем к логарифмическому уравнению вида

И снова обращаем Ваше внимание на то что в таком виде как правило не записывают.
Целесообразно, для компактности конечного решения, постоянную вносить под логарифм, то есть в форме

Взяв экспоненту от правой и левой части формулы придем к конечному виду решения дифференциального уравнения

Как Вы могли убедиться примеры достаточно просты, методика вычислений ДУ з разделенными переменными легкая для изучения.

Пример 4 Решить дифференциальное уравнениеРешение: Одно из слагаемых (не содержит производной) переносим за знак равенства

и записываем уравнение в дифференциалах. .

Следующим шагом сводим зависимость к дифференциальному уравнению с разделенными переменными.
Для заданного уравнения всего лишь перекрестным делением записываем корни в знаменатели

В таком виде можем интегрировать уравнения

Левая сторона содержит функцию которая при иртегрировании даст корневую зависимость, для правой стороны по формулам получим арксинус.

Выполняем манипуляции с корнем, чтобы получить зависимость вида y=y(x)

Решение дифференциального уравнения будет иметь вид

На этом вводный урок закончен и основные выводы Вы должны сделать самостоятельно.
Для закрепления темы рекомендуем самостоятельно решить несколько из следующих примеров.

Хотите верьте, а хотите – нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Схему вычислений должны заучить и знать на зубок – это один из основных методов решения сложных примеров на диф. уравнения.

Дифференциальные уравнения в полных дифференциалах

Краткая теория

---

Если для дифференциального уравнения

выполнено равенство

то уравнение (*) может быть записано в виде  и называется уравнением в полных дифференциалах. Общий интеграл уравнения есть .

Методы решения других видов дифференциальных уравнений:

Примеры решения задач

---

Задача 1

Решить дифуравнение.

Решение

Введем обозначения:

Частные производные:

Получаем:

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

Уравнение является уравнением в полных дифференциалах, а его левая часть есть полный дифференциал

Общий интеграл исходного дифуравнения имеет вид

 

Ответ:

---

Задача 2

Проинтегрировать дифференциальное уравнение. При заданном начальном условии найти соответствующий частный интеграл или частное решение.

Решение

Введем обозначения:

Частные производные:

Получаем:

Это уравнение в полных дифференциалах.

Дифференцируя  по , найдем:

Откуда  и

Окончательно получаем искомый общий интеграл данного уравнения:

 

Ответ:

Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .

На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете (срок решения 1,5 часа и меньше) осуществляется по предварительной записи.

Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.

Дифференциальные уравнения – линейные уравнения

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с “узкой” шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-1: Линейные дифференциальные уравнения

Первым частным случаем дифференциальных уравнений первого порядка, который мы рассмотрим, является линейное дифференциальное уравнение первого порядка.В этом случае, в отличие от большинства случаев первого порядка, которые мы рассмотрим, мы действительно можем вывести формулу для общего решения. Общее решение выводится ниже. Однако мы бы посоветовали вам не запоминать саму формулу. Вместо того, чтобы запоминать формулу, вы должны запомнить и понять процесс, который я собираюсь использовать для получения формулы. На самом деле с большинством проблем легче справиться, используя процесс, а не формулу.

Итак, давайте посмотрим, как решить линейное дифференциальное уравнение первого порядка.Помните, когда мы проходим этот процесс, цель состоит в том, чтобы прийти к решению в форме \ (y = y \ left (t \ right) \). Иногда легко упустить из виду цель, когда мы впервые проходим через этот процесс.

Чтобы решить линейное дифференциальное уравнение первого порядка, мы ДОЛЖНЫ начать с дифференциального уравнения в форме, показанной ниже. Если дифференциальное уравнение не в такой форме, то процесс, который мы собираемся использовать, не сработает.

\ [\ begin {уравнение} \ frac {{dy}} {{dt}} + p \ left (t \ right) y = g \ left (t \ right) \ label {eq: eq1} \ end {уравнение} \]

Где и \ (p (t) \), и \ (g (t) \) – непрерывные функции.Напомним, что быстрое и грязное определение непрерывной функции состоит в том, что функция будет непрерывной при условии, что вы можете рисовать график слева направо, даже не беря в руки карандаш / ручку. Другими словами, функция является непрерывной, если в ней нет дыр или разрывов.

Теперь мы собираемся предположить, что где-то в мире существует некоторая магическая функция, \ (\ mu \ left (t \ right) \), называемая интегрирующим коэффициентом . На этом этапе не беспокойтесь о том, что это за функция и откуда она взялась.Мы выясним, что такое \ (\ mu \ left (t \ right) \), когда у нас будет формула для общего решения.

Итак, теперь, когда мы предположили существование \ (\ mu \ left (t \ right) \), умножаем все в \ (\ eqref {eq: eq1} \) на \ (\ mu \ left (t \ right) \). Это даст.

\ [\ begin {уравнение} \ mu \ left (t \ right) \ frac {{dy}} {{dt}} + \ mu \ left (t \ right) p \ left (t \ right) y = \ mu \ left (t \ right) g \ left (t \ right) \ label {eq: eq2} \ end {уравнение} \]

Вот здесь-то и вступает в игру магия \ (\ mu \ left (t \ right) \).Мы собираемся предположить, что что бы ни было \ (\ mu \ left (t \ right) \), оно будет удовлетворять следующему.

\ [\ begin {уравнение} \ mu \ left (t \ right) p \ left (t \ right) = \ mu ‘\ left (t \ right) \ label {eq: eq3} \ end {уравнение} \]

Снова не беспокойтесь о том, как мы можем найти \ (\ mu \ left (t \ right) \), который будет удовлетворять \ (\ eqref {eq: eq3} \). Как мы увидим, при условии непрерывности \ (p (t) \) мы можем его найти. Итак, подставив \ (\ eqref {eq: eq3} \), мы приходим к.

\ [\ begin {уравнение} \ mu \ left (t \ right) \ frac {{dy}} {{dt}} + \ mu ‘\ left (t \ right) y = \ mu \ left (t \ right) g \ left (t \ right) \ label {eq: eq4} \ end {уравнение} \]

На этом этапе мы должны признать, что левая часть \ (\ eqref {eq: eq4} \) – не что иное, как следующее правило продукта.\ prime} \, dt}} = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} \] \ [\ begin {уравнение} \ mu \ left (t \ right) y \ left (t \ right) + c = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} \ label {eq: eq6} \ end {уравнение} \]

Обратите внимание, что здесь включена константа интегрирования \ (c \) из левой части интегрирования. Это жизненно важно. Если его не указывать, вы каждый раз будете получать неправильный ответ.

Последний шаг – это некоторая алгебра, которую нужно решить для решения, \ (y (t) \).

\ [\ begin {align *} \ mu \ left (t \ right) y \ left (t \ right) & = \ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} – c \\ y \ left (t \ right) & = \ frac {{\ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} – c} } {{\ mu \ left (t \ right)}} \ end {align *} \]

Теперь, с точки зрения обозначений, мы знаем, что постоянная интегрирования \ (c \) – это неизвестная константа, и поэтому, чтобы облегчить нашу жизнь, мы включим знак минус перед ней в константу и вместо этого будем использовать плюс. .Это НЕ повлияет на окончательный ответ решения. Итак, с этим изменением у нас есть.

\ [\ begin {уравнение} y \ left (t \ right) = \ frac {{\ int {{\ mu \ left (t \ right) g \ left (t \ right) \, dt}} + c}} {{\ mu \ left (t \ right)}} \ label {eq: eq7} \ end {уравнение} \]

Опять же, изменение знака константы не повлияет на наш ответ. Если вы решите сохранить знак минус, вы получите то же значение \ (c \), что и мы, за исключением того, что у него будет противоположный знак. Подключив \ (c \), мы получим точно такой же ответ.

С константами интеграции в этом разделе очень много шуток, так что вам нужно к этому привыкнуть. Когда мы делаем это, мы всегда будем стараться очень ясно дать понять, что происходит, и попытаться оправдать, почему мы сделали то, что мы сделали.

Итак, теперь, когда у нас есть общее решение \ (\ eqref {eq: eq1} \), нам нужно вернуться и определить, что это за магическая функция \ (\ mu \ left (t \ right) \). . На самом деле это более простой процесс, чем вы думаете.\ prime} = p \ left (t \ right) \]

Как и в случае с процессом, прежде всего, нам нужно объединить обе стороны, чтобы получить.

\ [\ begin {align *} \ ln \ mu \ left (t \ right) + k & = \ int {{p \ left (t \ right) \, dt}} \\ \ ln \ mu \ left (t \ right) & = \ int {{p \ left (t \ right) \, dt}} + k \ end {align *} \]

Вы заметите, что константа интегрирования с левой стороны, \ (k \), была перемещена в правую часть и снова поглощена знаком минус, как мы это делали ранее. {\ int {{p \ left (t \ right) \, dt}}}} \ label {eq: eq8} \ end {уравнение} \]

Итак, теперь у нас есть формула для общего решения \ (\ eqref {eq: eq7} \) и формула для интегрирующего множителя \ (\ eqref {eq: eq8} \). Однако у нас есть проблема. У нас есть две неизвестные константы, и чем больше у нас неизвестных констант, тем больше у нас проблем в дальнейшем. Поэтому было бы неплохо, если бы мы смогли найти способ устранить одну из них (мы не будем уметь устранить и то, и другое….).

На самом деле это довольно просто сделать.{\ int {{p \ left (t \ right) \, dt}}}}}} \ end {align *} \]

Итак, \ (\ eqref {eq: eq7} \) можно записать таким образом, что единственное место, где появляются две неизвестные константы, – это их соотношение. Тогда, поскольку и \ (c \), и \ (k \) – неизвестные константы, так же и отношение этих двух констант. Поэтому мы просто назовем соотношение \ (c \), а затем исключим \ (k \) из \ (\ eqref {eq: eq8} \), поскольку в конечном итоге оно просто поглотится в \ (c \). {\ int {{p \ left (t \ right) \, dt}}}} \ label {eq: eq10} \ end {формула} \]

Теперь реальность такова, что \ (\ eqref {eq: eq9} \) не так полезен, как может показаться.Часто проще просто выполнить процесс, который привел нас к \ (\ eqref {eq: eq9} \), чем использовать формулу. Мы не будем использовать эту формулу ни в одном из наших примеров. Нам нужно будет регулярно использовать \ (\ eqref {eq: eq10} \), поскольку эту формулу проще использовать, чем процесс ее получения.

Процесс решения

Процесс решения линейного дифференциального уравнения первого порядка выглядит следующим образом.

1. Приведите дифференциальное уравнение в правильную начальную форму, \ (\ eqref {eq: eq1} \).
2. Найдите интегрирующий коэффициент \ (\ mu \ left (t \ right) \), используя \ (\ eqref {eq: eq10} \).
3. Умножьте все в дифференциальном уравнении на \ (\ mu \ left (t \ right) \) и убедитесь, что левая часть становится правилом произведения \ (\ left ({\ mu \ left (t \ right) y \ left ( t \ right)} \ right) ‘\) и напишите это как таковое.
4. Объедините обе стороны, убедитесь, что вы правильно справились с постоянной интеграции.
5. Найдите решение \ (y (t) \).

Давайте поработаем пару примеров. Начнем с решения дифференциального уравнения, полученного нами в разделе «Поле направления».

Пример 1 Найдите решение следующего дифференциального уравнения. \ [\ frac {{dv}} {{dt}} = 9,8–0,196 об. \] Показать решение

Во-первых, нам нужно получить дифференциальное уравнение в правильной форме.

\ [\ frac {{dv}} {{dt}} + 0,196v = 9.{- 0,196т}} \]

Из решения этого примера мы теперь можем понять, почему постоянная интеграции так важна в этом процессе. Без него в этом случае мы получили бы одно постоянное решение \ (v (t) = 50 \). Используя постоянную интегрирования, мы получаем бесконечно много решений, по одному на каждое значение \ (c \).

Вернувшись в раздел поля направления, где мы впервые вывели дифференциальное уравнение, использованное в последнем примере, мы использовали поле направления, чтобы помочь нам наметить некоторые решения. Посмотрим, правильно ли мы их поняли. Чтобы набросать некоторые решения, все, что нам нужно сделать, это выбрать разные значения \ (c \), чтобы получить решение. Некоторые из них показаны на графике ниже.

Итак, похоже, мы неплохо сделали набросок графиков в секции поля направлений.

Теперь вспомните из раздела «Определения», что начальные условия позволят нам сосредоточиться на конкретном решении. В решениях дифференциальных уравнений первого порядка (не только линейных, как мы увидим) будет одна неизвестная константа, поэтому нам понадобится ровно одно начальное условие, чтобы найти значение этой константы и, следовательно, найти решение, к которому мы пришли.Начальное условие для дифференциальных уравнений первого порядка будет иметь вид

\ [y \ left ({{t_0}} \ right) = {y_0} \]

Напомним также, что дифференциальное уравнение с достаточным количеством начальных условий называется задачей начального значения (IVP). {- 0.{\ ln \, \, \ sec \ left (x \ right)}} = \ sec \ left (x \ right) \]

А интеграл сделать можно? Если нет, перепишите касательную обратно в синусы и косинусы, а затем используйте простую замену. Обратите внимание, что мы можем опустить столбцы абсолютного значения на секансе из-за ограничений на \ (x \). Фактически, это причина ограничений на \ (x \). Отметим также, что есть две формы ответа на этот интеграл. Они эквивалентны, как показано ниже. Что вы используете – это действительно вопрос предпочтений.{\ ln f \ left (x \ right)}} = f \ left (x \ right) \ label {eq: eq11} \ end {уравнение} \]

Это важный факт, о котором вы всегда должны помнить при возникновении подобных проблем. Мы захотим максимально упростить интегрирующий коэффициент во всех случаях, и этот факт поможет в этом упрощении.

Вернемся к примеру. Умножьте интегрирующий коэффициент на дифференциальное уравнение и убедитесь, что левая часть соответствует правилу произведения. Также обратите внимание, что мы умножаем интегрирующий коэффициент на переписанное дифференциальное уравнение, а НЕ на исходное дифференциальное уравнение.2} \ left (x \ right) \, dx}} \\ \ sec \ left (x \ right) y \ left (x \ right) & = – \ frac {1} {2} \ cos \ left ({ 2x} \ right) – \ tan \ left (x \ right) + c \ end {align *} \]

Обратите внимание на использование тригонометрической формулы \ (\ sin \ left ({2 \ theta} \ right) = 2 \ sin \ theta \ cos \ theta \), которая упростила интеграл. Затем найдите решение.

\ [\ begin {align *} y \ left (x \ right) & = – \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) – \ cos \ left (x \ right) \ tan \ left (x \ right) + c \ cos \ left (x \ right) \\ & = – \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) – \ sin \ left (x \ right) + c \ cos \ left (x \ right) \ end {align *} \]

Наконец, примените начальное условие, чтобы найти значение \ (c \).

\ [\ begin {align *} 3 \ sqrt 2 = y \ left ({\ frac {\ pi} {4}} \ right) & = – \ frac {1} {2} \ cos \ left ({\ frac {\ pi} {4}} \ right) \ cos \ left ({\ frac {\ pi} {2}} \ right) – \ sin \ left ({\ frac {\ pi} {4}} \ right) + c \ cos \ left ({\ frac {\ pi} {4}} \ right) \\ 3 \ sqrt 2 & = – \ frac {{\ sqrt 2}} {2} + c \ frac {{\ sqrt 2}} {2} \\ c & = 7 \ end {align *} \]

Тогда решение есть.

\ [y \ left (x \ right) = – \ frac {1} {2} \ cos \ left (x \ right) \ cos \ left ({2x} \ right) – \ sin \ left (x \ right) + 7 \ соз \ влево (х \ вправо) \]

Ниже представлен график решения.2} \]

Ниже представлен график решения.

Давайте рассмотрим последний пример, который больше рассматривает интерпретацию решения, а не поиск решения.

Пример 6 Найдите решение следующей IVP и определите все возможные варианты поведения решения как \ (t \ to \ infty \). {\ frac {t } {2}}} \]

Теперь, когда у нас есть решение, давайте посмотрим на долгосрочное поведение ( i.е. \ (t \ to \ infty \)) решения. Первые два члена решения останутся конечными при всех значениях \ (t \). Это последний член, который будет определять поведение решения. Экспонента всегда будет стремиться к бесконечности как \ (t \ to \ infty \), однако в зависимости от знака коэффициента \ (c \) (да, мы уже нашли его, но для простоты этого обсуждения мы продолжим называть это \ (c \)). В следующей таблице показано долгосрочное поведение решения для всех значений \ (c \).

Диапазон \ (c \)	Поведение решения при \ (t \ to \ infty \)
\ (с \) <0	\ (у \ влево (т \ вправо) \ к – \ infty \)
\ (с \) = 0	\ (y \ left (t \ right) \) остается конечным
\ (с \)> 0	\ (у \ влево (т \ вправо) \ в \ infty \)

Это поведение также можно увидеть на следующем графике некоторых решений.

Теперь, поскольку мы знаем, как \ (c \) относится к \ (y_ {0} \), мы можем связать поведение решения с \ (y_ {0} \). В следующей таблице показано поведение решения в терминах \ (y_ {0} \) вместо \ (c \).

Диапазон \ (y_ {0} \)	Поведение решения при \ (t \ to \ infty \)
\ ({y_0} <- \ frac {{24}} {{37}} \)	\ (у \ влево (т \ вправо) \ к – \ infty \)
\ ({y_0} = – \ frac {{24}} {{37}} \)	\ (y \ left (t \ right) \) остается конечным
\ ({y_0}> – \ frac {{24}} {{37}} \)	\ (у \ влево (т \ вправо) \ в \ infty \)

Обратите внимание, что для \ ({y_0} = – \ frac {{24}} {{37}} \) решение останется конечным.Так бывает не всегда.

Исследование долгосрочного поведения решений иногда бывает важнее, чем само решение. Предположим, что указанный выше раствор дает температуру в металлическом бруске. В этом случае нам нужно решение (я), которое останется конечным в долгосрочной перспективе. Благодаря этому исследованию у нас теперь будет значение начального условия, которое даст нам это решение, и, что более важно, значения начального условия, которых нам нужно избежать, чтобы мы не расплавили стержень.

1. Решение дифференциальных уравнений

Дифференциальное уравнение (или “DE”) содержит производные или дифференциалы .

Наша задача решить дифференциальное уравнение. В какой-то момент это потребует интеграции, и мы (в основном) получим выражение типа « y = …».

Вспомните из раздела «Дифференциал» в главе «Интеграция», что дифференциал можно рассматривать как производную , где dy / dx на самом деле не записывается в форме дроби. 2-3`

Как и раньше, интегрируем.3 / 3-3x + К`

Но откуда взялось это dy из `(dy) / (dx)`? Почему оно как будто исчезло?

В этом примере мы, кажется, интегрируем только часть x (справа), но на самом деле мы интегрировали также и относительно y (слева). DE похожи на это – вам нужно интегрировать по одной (иногда и больше) разных переменных, по одной за раз.

Мы могли бы написать наш вопрос, только используя дифференциалы :

dy = ( x ² -3) dx

(Все, что я сделал, это умножил обе стороны исходного dy / dx в вопросе на dx .3 / 3-3x + К`

С левой стороны мы интегрировали int dy = int 1 dy, чтобы получить y.

Примечание о константе: Мы интегрировали обе стороны, но есть константа интеграции только с правой стороны. 2 d \ theta = sin (t + 0.3} / 3 = -cos (t + 0,2) + K`

Мы проинтегрировали по θ слева и по t справа.

Вот график нашего решения, взяв K = 2:

Типичный график решения для примера 2 DE: `theta (t) = root (3) (- 3cos (t + 0.2) +6)`.

Решение дифференциального уравнения

Из приведенных выше примеров мы видим, что решение DE означает нахождение уравнение без производных, удовлетворяющее заданной DE.Решение дифференциального уравнения всегда требует одного или нескольких интеграции шагов.

Важно уметь идентифицировать тип DE , с которым мы имеем дело, прежде чем пытаться Найди решение.

Определения

Первый заказ DE: Содержит только первые производные

Второй порядок DE: Содержит вторые производные (и возможно также первые производные)

Степень: наивысшая степень из наивысшая производная , встречающаяся в DE. 7-5лет = 3`

Это DE имеет порядок 2 (самая высокая производная вторая производная ) и градусов 4 ( степень старшей производной 4.)

Общие и частные решения

Когда мы впервые выполнили интеграцию, мы получили общий раствор (с постоянной К ).

Мы получили частное решение заменой известных значения для x и y .Эти известные условия называется граничными условиями (или начальными условия ).

Это та же концепция, что и при решении дифференциальных уравнений – сначала найдите общее решение, а затем замените заданные числа, чтобы найти частные решения.

Рассмотрим несколько примеров ДУ первого порядка и первой степени.

Пример 4

а. Найдите общее решение для дифференциала уравнение

`dy + 7x dx = 0`

г.2 + К`

Ответ тот же – способ его написания и мышления немного отличается.

ПРИМЕЧАНИЕ 2: int dy означает int1 dy, что дает нам ответ y.

У нас также могло быть:

`intdt = t`

`intd тета = тета`

`int da = a`

и так далее. В этом разделе мы будем часто сталкиваться с такими интегралами.

(b) Теперь мы используем информацию y (0) = 3, чтобы найти K.2 + 3`.

Пример 5

Найдите частное решение

`y ‘= 5`

с учетом того, что когда `x = 0, y = 2`.

Ответ

Мы можем написать

год = 5

как дифференциальное уравнение:

dy = 5 dx

Объединение обеих сторон дает:

y = 5 x + K

Применяя граничные условия: x = 0, y = 2, получаем K = 2, поэтому:

y = 5 x + 2

Пример 6

Найдите частное решение

`у ” = 0`

при том, что:

у (0) = 3, у (1) = 4, у (2) = 6`

Ответ

Так как y ” ‘ = 0, когда мы интегрируем один раз, получаем:

y ” = A ( A – константа)

Повторное интегрирование дает:

y ‘ = Ax + B ( A, B – константы)

Еще раз:

`y = (Ax ^ 2) / 2 + Bx + C` ( A, B и C – константы)

Граничные условия:

y (0) = 3, y ‘ (1) = 4, y’ ‘ (2) = 6

Нам нужно подставить эти значения в наши выражения для y ‘ и y’ и наше общее решение, `y = (Ax ^ 2) / 2 + Bx + C` .

Сейчас

y (0) = 3 дает C = 3.

и

y ‘ (2) = 6 дает A = 6

(Фактически, y ” = 6 для любого значения x в этой задаче, поскольку нет члена x )

Наконец,

y ‘ (1) = 4 дает B = -2.

Итак, конкретное решение этого вопроса:

y = 3 x ² – 2 x + 3

Проверка решения путем дифференцирования и подстановки начальных условий:

y ‘= 6 x – 2

y ‘ (1) = 6 (1) – 2 = 4

у ” = 6

г ” = 0

Наше решение правильное.

Пример 7

После решения дифференциала уравнение,

`(dy) / (dx) ln x-y / x = 0`

(мы увидим, как решить эту DE в следующих раздел Разделение переменных), получаем результат

`y = c ln x`

Получили ли мы правильное общее решение?

Ответ

Теперь, если `y = c ln x`, то` (dy) / (dx) = c / x`

[См. Производную логарифмической функции, если вы не знаете этого.)

Так

`” LHS “= (dy) / (dx) ln x-y / x`

`= (c / x) ln x – ((c ln x)) / x`

`= 0`

`=” RHS “`

Делаем вывод, что у нас есть правильное решение.

DE второго порядка

Мы включили сюда еще два примера, чтобы дать вам представление о DE второго порядка. Позже в этой главе мы увидим, как решать такие линейные DE второго порядка.

Пример 8

Общее решение второго порядка DE

y ” + a ² y = 0

это

`y = A cos ax + B sin ax`

Пример 9

Общее решение второго порядка DE

л ‘- 3 л ‘ + 2 л = 0

это

y = Ae ^{2 x} + Be ^x

Если у нас есть следующие граничные условия:

y (0) = 4, y ‘ (0) = 5

, то конкретное решение дает:

y = e ^{2 x} + 3 e ^x

Теперь мы рассмотрим несколько примеров с использованием DE второго порядка, где нам дается окончательный ответ, и нам нужно проверить, является ли это правильным решением. (2x)`

Это очевидно.2) = 2 (dy) / (dx) `

Разделение переменных

Разделение переменных – это специальный метод решения некоторых дифференциальных уравнений

Когда я могу его использовать?

Разделение переменных может использоваться, когда:

Все члены y (включая dy) можно переместить в одну сторону уравнения, а

Все члены x (включая dx) на другую сторону.

Метод

Три ступени:

• Шаг 1 Переместите все члены y (включая dy) в одну сторону уравнения и все члены x (включая dx) в другую сторону.
• Шаг 2 Объедините одну сторону относительно x , а другую сторону относительно x . Не забудьте “+ C” (постоянная интегрирования).
• Шаг 3 Упростить

Пример: Решите это (k – константа):

dy dx = ky

Шаг 1 Разделите переменные, переместив все члены y в одну сторону уравнения и все члены x в другую сторону:

Умножаем обе стороны на dx: dy = ky dx

Разделите обе стороны на y: dy y = k dx

Шаг 2 Интегрируйте обе части уравнения отдельно:

Поставьте знак интеграла вперед: ∫ dy y = ∫ k dx

Интегрируйте левую часть: ln (y) + C = ∫ k dx

Интегрируйте правую часть: ln (y) + C = kx + D

C – постоянная интегрирования. И мы используем D для другого, поскольку это другая константа.

Шаг 3 Упростить:

Мы можем свести две константы в одну (a = D − C): ln (y) = kx + a

И e ^{kx + a} = e ^kx e ^a , поэтому получаем: y = e ^kx e ^a

e ^a – это просто константа, поэтому мы заменяем ее на c : y = ce ^kx

Мы решили:

y = ce ^kx

Это общий тип дифференциального уравнения первого порядка, который появляется во всевозможных неожиданных местах в реальных примерах.

Мы использовали y и x , но тот же метод работает для других имен переменных, например:

Пример: кролики!

Чем больше у вас будет кроликов, тем больше у вас будет кроликов. Потом кролики вырастают и тоже заводят детей! Население будет расти все быстрее и быстрее.

Важными частями этого являются:

• Население N ​​ в любое время т
• темп роста р
• Скорость изменения населения dN dt

Скорость изменения в любой момент равна скорости роста , умноженной на численность населения:

dN dt = rN

Но привет! Это то же самое, что и уравнение, которое мы только что решили! Просто у него разные буквы:

• N вместо y
• т вместо х
• r вместо
k

Итак, мы можем перейти к решению:

N = CE ^RT

А вот пример графика N = 0. 3e ^2t :

Экспоненциальный рост

Есть и другие уравнения, которые следуют этому шаблону, например, непрерывные сложные проценты.

Другие примеры

Хорошо, перейдем к различным примерам разделения переменных:

Пример: Решите это:

dy dx = 1 y

Шаг 1 Разделите переменные, переместив все члены y в одну сторону уравнения и все члены x в другую сторону:

Умножаем обе стороны на dx: dy = (1 / y) dx

Умножаем обе стороны на y: y dy = dx

Шаг 2 Интегрируйте обе части уравнения отдельно:

Поставьте знак интеграла впереди: ∫ y dy = ∫ dx

Интегрируйте каждую сторону: (y ² ) / 2 = x + C

Мы объединили обе стороны в одну линию.

Мы также использовали сокращение только одной константы интегрирования C. Это совершенно нормально, поскольку мы могли бы иметь + D на одном, + E на другом и просто сказать, что C = E − D.

Шаг 3 Упростить:

Умножаем обе стороны на 2: y ² = 2 (x + C)

Квадратный корень из обеих частей: y = ± √ (2 (x + C))

Примечание: это не то же самое, что y = √ (2x) + C, потому что C было добавлено до того, как мы взяли квадратный корень.Это часто случается с дифференциальными уравнениями. Мы не можем просто добавить C в конце процесса. Он добавляется при интеграции.

Мы решили:

у = ± √ (2 (х + С))

Более сложный пример:

Пример: Решите это:

dy dx = 2xy 1 + x ²

Шаг 1 Разделите переменные:

Умножьте обе стороны на dx, разделите обе стороны на y:

1 y dy = 2x 1 + x ² dx

Шаг 2 Интегрируйте обе части уравнения отдельно:

∫ 1 y dy = ∫ 2x 1 + x ² dx

Левая часть представляет собой простой логарифм, правая часть может быть интегрирована с помощью замены:

Пусть u = 1 + x ² , поэтому du = 2x dx : ∫ 1 y dy = ∫ 1 u du

Интегрировать: ln (y) = ln (u) + C

Тогда получаем C = ln (k) : ln (y) = ln (u) + ln (k)

Итак, мы можем получить это: y = uk

Теперь снова положим u = 1 + x ² : y = k (1 + x ² )

Шаг 3 Упростить:

Это уже настолько просто, насколько это возможно.Решили:

у = к (1 + х ² )

Еще более сложный пример: знаменитое уравнение Ферхульста

Пример: снова кролики!

Помните наше дифференциальное уравнение роста:

dN dt = rN

Что ж, этот рост не может продолжаться вечно, так как у них скоро закончится доступная еда.

Парень по имени Ферхульст включил тыс. (максимальное количество населения, которое может содержать еда), чтобы получить:

dN dt = rN (1 − N / k)

Уравнение Ферхюльста

Можно ли это решить?

Да, с помощью одной хитрости…

Шаг 1 Разделите переменные:

Умножаем обе части на dt: dN = rN (1 − N / k) dt

Разделите обе стороны на N (1-N / k): 1 N (1-N / k) dN = r dt

Шаг 2 Интегрировать:

1 N (1 − N / k) dN = ∫ r dt

Хммм … левую сторону сложно интегрировать. На самом деле это можно сделать с помощью небольшого трюка с частичными дробями… переставляем так:

Начнем с этого: 1 N (1 − N / k)

Умножить верх и низ на k: k N (k − N)

Теперь вот трюк, добавьте N ​​ и −N к вершине: N + k − N N (k − N)

и разделить его на две фракции: N N (k − N) + k − N N (k − N)

Упростите каждую дробь: 1 k − N + 1 N

Теперь решить намного проще.Мы можем интегрировать каждый член отдельно, например:

Наше полное уравнение теперь выглядит следующим образом: ∫ 1 k − N dN + ∫ 1 N dN = ∫ r dt

Интегрировать: −ln (k − N) + ln (N) = rt + C

(Почему это стало минус ln (k − N)? Потому что мы интегрируем по N.)

Шаг 3 Упростить:

Отрицательное из всех членов: ln (k − N) – ln (N) = −rt – C

Объединить ln (): ln ((k − N) / N) = −rt – C

Разделим степени e: (k − N) / N = e ^−rt e ^−C

e ^−C – постоянная, мы можем заменить ее на A: (k − N) / N = Ae ^−rt

Мы приближаемся! Еще немного алгебры, чтобы получить N само по себе:

Разделите члены дроби: (k / N) −1 = Ae ^−rt

Добавьте 1 к обеим сторонам: k / N = 1 + Ae ^−rt

Разделим оба значения на k: 1 / N = (1 + Ae ^−rt ) / k

Взаимное значение обеих сторон: N = k / (1 + Ae ^−rt )

И у нас есть решение:

N = к 1 + Ae ^−rt

Вот пример , график 40 1 + 5e ^−2t

Начинает расти экспоненциально,
затем выравнивается, достигая k = 40

Точные дифференциальные уравнения

Определение точного уравнения

Дифференциальное уравнение типа

\ [{P \ left ({x, y} \ right) dx + Q \ left ({x, y} \ right) dy} = {0} \]

называется точным дифференциальным уравнением, если существует функция двух переменных \ (u \ left ({x, y} \ right) \) с непрерывными частными производными такая, что

\ [{du \ left ({x, y} \ right) \ text {=}} \ kern0pt {P \ left ({x, y} \ right) dx + Q \ left ({x, y} \ right ) dy.} \]

Общее решение точного уравнения дается

\ [u \ left ({x, y} \ right) = C, \]

где \ (C \) – произвольная постоянная.

Тест на точность

Пусть функции \ (P \ left ({x, y} \ right) \) и \ (Q \ left ({x, y} \ right) \) имеют непрерывные частные производные в некоторой области \ (D. \) Дифференциальное уравнение \ (P \ left ({x, y} \ right) dx + \) \ (Q \ left ({x, y} \ right) dy \) \ (= 0 \) является точным уравнением, если и только если

\ [\ frac {{\ partial Q}} {{\ partial x}} = \ frac {{\ partial P}} {{\ partial y}}.\]

Алгоритм решения точного дифференциального уравнения

1. Сначала необходимо убедиться в точности дифференциального уравнения с помощью теста на точность:

   \ [\ frac {{\ partial Q}} {{\ partial x}} = \ frac {{\ partial P}} {{\ partial y}}. \]

2. Затем запишем систему двух дифференциальных уравнений, определяющих функцию \ (u \ left ({x, y} \ right): \)

   \ [\ left \ {\ begin {array} {l} \ frac {{\ partial u}} {{\ partial x}} = P \ left ({x, y} \ right) \\ \ frac {{\ partial u}} {{\ partial y}} = Q \ left ({x, y} \ right) \ end {array} \ right.. \]

3. Проинтегрируем первое уравнение по переменной \ (x. \) Вместо константы \ (C, \) запишем неизвестную функцию от \ (y: \)

   \ [{u \ left ({x, y} \ right) \ text {=}} \ kern0pt {\ int {P \ left ({x, y} \ right) dx} + \ varphi \ left (y \ right ).} \]

4. Дифференцируя по \ (y, \), подставляем функцию \ (u \ left ({x, y} \ right) \) во второе уравнение:

   \ [ {\ frac {{\ partial u}} {{\ partial y}} \ text {=}} \ kern0pt {\ frac {\ partial} {{\ partial y}} \ left [{\ int {P \ left ({x, y} \ right) dx} + \ varphi \ left (y \ right)} \ right]} = {Q \ left ({x, y} \ right).} \]

   Отсюда получаем выражение для производной неизвестной функции \ ({\ varphi \ left (y \ right)}: \)

   \ [ {\ varphi ’\ left (y \ right)} = {Q \ left ({x, y} \ right)} – ​​{\ frac {\ partial} {{\ partial y}} \ left ({\ int {P \ left ({x, y} \ right) dx } } \верно).} \]

5. Интегрируя последнее выражение, мы находим функцию \ ({\ varphi \ left (y \ right)} \) и, следовательно, функцию \ (u \ left ({x, y} \ right): \)

   \ [{u \ left ({x, y} \ right) \ text {=}} \ kern0pt {\ int {P \ left ({x, y} \ right) dx} + \ varphi \ left (y \ right ). 2}} \ right) dy \) \ (= 0.3} = C, \]

   где \ (C \) – произвольная постоянная.

   scipy.integrate.odeint – Справочное руководство SciPy v1.6.3

   Интегрируйте систему обыкновенных дифференциальных уравнений.

   Решите систему обыкновенных дифференциальных уравнений, используя lsoda из Библиотека FORTRAN odepack.

   Решает задачу начального значения для жестких или нежестких систем. од первого порядка:

    dy / dt = func (y, t, ...) [или func (t, y, ...)]
    

   , где y может быть вектором.

   Примечание

   По умолчанию требуемый порядок первых двух аргументов func находятся в порядке, обратном аргументам в системе функция определения, используемая классом scipy.integrate.ode и функция scipy.integrate.solve_ivp . Чтобы использовать функцию с подпись func (t, y, ...) , аргумент tfirst должен быть установлено значение True .

   Параметры

   func вызываемая (y, t,…) или вызываемая (t, y,…)

   Вычисляет производную y в точке t.Если подпись – callable (t, y, ...) , то аргумент tfirst должен быть установлен True .

   y0 массив

   Начальное условие для y (может быть вектором).

   t массив

   Последовательность моментов времени, для которых необходимо найти y. Начальный точка значения должна быть первым элементом этой последовательности. Эта последовательность должна быть монотонно возрастающей или монотонно возрастающей. уменьшение; допустимы повторяющиеся значения.

   args кортеж, необязательно

   Дополнительные аргументы для передачи функции.

   Dfun , вызываемая (y, t,…) или вызываемая (t, y,…)

   Градиент (якобиан) функции . Если подпись – callable (t, y, ...) , то аргумент tfirst должен быть установлен True .

   col_deriv bool, необязательно

   Истинно, если Dfun определяет производные по столбцам (быстрее), в противном случае Dfun должен определять производные по строкам.

   full_output bool, необязательно

   Истинно, если в качестве второго вывода нужно вернуть словарь дополнительных выходов

   printmessg bool, необязательно

   Следует ли печатать сообщение о конвергенции

   tfirst: bool, необязательно

   Если True, первые два аргумента func (и Dfun , если задано) должно быть t, y вместо значения по умолчанию y, t .

   Возвращает

   y массив, форма (len (t), len (y0))

   Массив, содержащий значение y для каждого желаемого времени в t, с начальным значением y0 в первой строке.

   infodict dict, возвращается, только если full_output == True

   Словарь, содержащий дополнительную информацию вывода

   ключ	означает
   ‘hu’	Вектор размеров шага успешно использован для каждого временного шага
   ‘tcur’	вектор со значением t, достигнутым для каждого временного шага (всегда будет не меньше времени ввода)
   «tolsf»	вектор масштабных коэффициентов допуска, больше 1.0, вычисляется, когда был обнаружен запрос на слишком большую точность
   ‘tsw’	значение t на момент последнего переключения метода (указывается для каждого временного шага)
   ‘nst’	совокупное количество временных шагов
   ‘nfe’	совокупное количество оценок функции для каждого временного шага
   ‘nje’	совокупное количество оценок якобиана для каждого временного шага
   ‘nqu’	вектор порядков методов для каждого успешного шага
   imxer	индекс компонента наибольшей магнитуды в взвешенный вектор локальной ошибки (e / ewt) при возврате ошибки, -1 в противном случае
   ‘lenrw’	требуемая длина двойного рабочего массива
   ‘leniw’	требуемая длина целочисленного рабочего массива
   «задумчивый»	вектор показателей метода для каждого успешного временного шага: 1: адамс (нетвердый), 2: bdf (жесткий)

   Другие параметры

   мл, mu int, необязательно

   Если любой из них не является None или неотрицательным, то Предполагается, что якобиан полосчатый.Это дает количество нижняя и верхняя ненулевые диагонали в этой ленточной матрице. Для случая с полосами Dfun должен вернуть матрицу, строки содержат ненулевые полосы (начиная с самой низкой диагонали). Таким образом, матрица возврата jac от Dfun должна иметь вид (ml + mu + 1, len (y0)) , когда ml> = 0 или mu> = 0 . Данные в jac должны храниться так, чтобы jac [i - j + mu, j] имеет производную i-го уравнения по j-му уравнению. переменная состояния.Если col_deriv имеет значение True, транспонирование этого jac необходимо вернуть.

   rtol, atol float, опционально

   Входные параметры rtol и atol определяют ошибку управление осуществляется решателем. Решатель будет управлять вектор, e, оцененных локальных ошибок в y, в соответствии с неравенство вида max-norm of (e / ewt) <= 1 , где ewt - вектор положительных весов ошибок, вычисленных как ewt = rtol * abs (y) + atol .rtol и atol могут быть векторами той же длины, что и y, или скалярами. По умолчанию 1.49012e-8.

   tcrit ndarray, необязательно

   Вектор критических точек (например, сингулярностей), по которым интегрировано следует проявлять осторожность.

   h0 float, (0: ​​определяется решателем), необязательно

   Размер шага, который будет выполняться на первом шаге.

   hmax float, (0: ​​определяется решателем), необязательно

   Максимально допустимый абсолютный размер шага.

   hmin float, (0: ​​определяется решателем), необязательно

   Минимальный допустимый абсолютный размер шага.

   ixpr bool, optional

   Следует ли генерировать дополнительную печать при переключателях метода.

   mxstep int, (0: ​​определяется решателем), необязательно

   Максимальное количество (определяемых внутри) шагов, разрешенных для каждого точка интеграции в т.

   mxhnil int, (0: ​​определяется решателем), необязательно

   Максимальное количество напечатанных сообщений.

   mxordn int, (0: ​​определяется решателем), необязательно

   Максимальный порядок, разрешенный для нежесткого (Адамса) метода.

   mxords int, (0: ​​определяется решателем), необязательно

   Максимальный допустимый порядок для жесткого метода (BDF).

   См. Также

   resolve_ivp

   решить задачу начального значения для системы ODE

   ode

   более объектно-ориентированный интегратор на основе VODE

   quad

   для определения площади под кривой

   Примеры

   Дифференциальное уравнение второго порядка для угла theta угла маятник под действием силы тяжести с трением можно записать:

    theta '' (t) + b * theta '(t) + c * sin (тета (t)) = 0
    

   , где b и c - положительные константы, а штрих (‘) означает производная.Чтобы решить это уравнение с на , мы должны сначала преобразовать это к системе уравнений первого порядка. Определив угловой скорость omega (t) = theta '(t) , получаем систему:

    тета '(т) = омега (т)
   омега '(т) = -b * омега (т) - с * грех (тета (т))
    

   Пусть y будет вектором [ theta , omega ]. Мы внедряем эту систему в Python как:

    >>> def pend (y, t, b, c):
   ... тета, омега = у
   ... dydt = [омега, -b * омега - с * нп.грех (тета)]
   ... вернуть дыдт
   ...
    

   Мы предполагаем, что константы равны b = 0,25 и c = 5,0:

   Для начальных условий мы предполагаем, что маятник почти вертикальный. с theta (0) = pi - 0,1, и изначально находится в состоянии покоя, поэтому омега (0) = 0. Тогда вектор начальных условий равен

   .

    >>> y0 = [np.pi - 0,1, 0,0]
    

   Мы сгенерируем решение из 101 равномерно распределенных отсчетов в интервале 0 <= т <= 10.Итак, наш массив значений времени:

    >>> t = np.linspace (0, 10, 101)
    

   Позвоните по номеру или , чтобы сгенерировать решение. Чтобы передать параметры b и c до до , мы передаем их odeint , используя args аргумент.

    >>> из scipy.integrate import odeint
   >>> sol = odeint (pend, y0, t, args = (b, c))
    

   Решение представляет собой массив формы (101, 2). Первый столбец это тета (т) , а второе - омега (т) .Следующий код графики обоих компонентов.

    >>> импортировать matplotlib.pyplot как plt
   >>> plt.plot (t, sol [:, 0], 'b', label = 'theta (t)')
   >>> plt.plot (t, sol [:, 1], 'g', label = 'omega (t)')
   >>> plt.legend (loc = 'лучший')
   >>> plt.xlabel ('т')
   >>> plt.grid ()
   >>> plt.show ()
    

   Интеграл дифференциального уравнения

   
   Решение дифференциального уравнения. Под интегралом дифференциального уравнения в первую очередь понимается соотношение вида $ \ Phi (x, y) = 0 $ определение решения $ y $ обыкновенного дифференциального уравнения

   $$ \ tag {1} F (x, y, y ^ \ prime \ dots y ^ {(} n)) = 0 $$

   как неявная функция независимой переменной $ x $.В этом случае решение также называется частным интегралом, в отличие от общего интеграла уравнения (1), то есть соотношением

   $$ \ tag {2} \ Phi (x, y, C _ {1} \ dots C _ {n}) = 0, $$

   , из которого можно получить подходящим выбором констант $ C _ {1} \ dots C _ {n} $ любая интегральная кривая уравнения (1), лежащая в некоторой заданной области $ G $ из $ (x, y) $ - самолет. Если произвольные константы $ C _ {1} \ dots C _ {n} $ исключаются из уравнения (2) и $ n $ соотношения, полученные из него повторным дифференцированием по $ x $ ( где $ y $ рассматривается как функция от $ x $), тогда получается уравнение (1).{(} k), \ C _ {1} \ dots C _ {n-} k) = 0, $$

   , содержащие производные до порядка $ k $, $ 1 \ leq k

   Если рассматривать систему обыкновенных дифференциальных уравнений первого порядка,

   $$ \ tag {4} \ frac {d x _ {i}} {dt} знак равно f _ {i} (t, x _ {1} \ dots x _ {n}), \ \ я = 1 \ точки п, $$

   , то под общим интегралом от него понимается совокупность соотношений

   $$ \ tag {5} \ Phi _ {i} (t, x _ {1} \ dots x _ {n}) = C _ {i}, \ \ я = 1 \ точки п, $$

   , где $ C _ {i} $ - произвольные постоянные, которые в неявной форме описывают все решения системы (4) в некоторой области $ G $ из $ (t, x _ {1} \ dots x _ {n}) $ - космос.Каждое из соотношений (5) само по себе называется первым интегралом системы (4). Чаще под первым интегралом системы (4) понимают функцию $ u (t, x _ {1} \ dots x _ {n}) $ со свойством постоянства вдоль любого решения системы (4) в области $ G $. В системе (4) ровно $ n $ независимые первые интегралы, знание которых позволяет найти общее решение без интегрирования системы; знание $ k $ независимых первых интегралов позволяет свести решение системы (4) порядка $ n $ решению системы порядка $ n - k $.{n} е _ {я} (т, х _ {1} \ точки х _ {п}) \ frac {\ partial u} {\ partial x _ {i}} = 0. $$

   Аналогичная терминология иногда используется в теории дифференциальных уравнений в частных производных первого порядка. Таким образом, интегралом дифференциального уравнения

   $$ \ tag {6} F \ left (x, y, z, \ \ frac {\ partial z} {\ partial x} , \ \ frac {\ partial z} {\ partial y} \ right) = 0, $$

   Под

   или его частным интегралом понимается решение этого уравнения (интегральная поверхность).Под полным интегралом уравнения (6) понимается семейство решений $ \ Phi (x, y, z, a, b) = 0 $ в зависимости от двух произвольных констант. Общий интеграл уравнения (6) - это отношение, содержащее одну произвольную функцию и дающее решение уравнения для каждого выбора этой функции.

   Ссылки

   [1]	W.W. [В.В. Степанов] Степанов, "Lehrbuch der Differentialgleichungen", Deutsch. Verlag Wissenschaft. (1956)

   Ссылки

   [a1]	K.Rektorys (ed.), Обзор прикладной математики , Iliffe (1969) pp. Sects. 17.2, 17.8, 17.18, 17.20
   [a2]	E.L. Инс, «Интегрирование обыкновенных дифференциальных уравнений», Оливер и Бойд (1956)

   Как процитировать эту запись:
   Интеграл дифференциального уравнения. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Integral_of_a_differential_equation&oldid=47377

   Эта статья была адаптирована из оригинальной статьи Н.Х. Розова (составитель), появившейся в Математической энциклопедии - ISBN 1402006098. См. Исходную статью

   PPLATO | Учебники | Дифференциальные уравнения

   d ² y dx ² + ( dy dx ) ³ = x ⁷

   является примером обыкновенного дифференциального уравнения (н.о.э.), поскольку оно содержит только обычные производные, такие как dy dx , а не частные производные, такие как ∂ y ∂ x .

   Зависимая переменная - это y, а независимая переменная - x. А. д. Е. имеет только одну независимую переменную, в то время как уравнение в частных производных имеет более одной независимой переменной.

   Приведенный выше пример представляет собой уравнение второго порядка, поскольку задействованная производная высшего порядка равна двум (член d ² y dx ² член).

   А. д. Е. является линейным, когда каждый член имеет y и его производные, появляющиеся только в степенной единице.Появление термина, включающего произведение y и dy dx , также будет означать o.d.e. нелинейный.

   В приведенном выше примере член ( dy dx ) ³ делает уравнение нелинейным .

   Общее решение ан ^-й заказать н.о.э. имеет n произвольных констант, которые могут принимать любые значения.

   В задаче начального значения решается порядок n ^th o.d.e. чтобы найти общее решение затем применяет n граничных решений («начальные значения / условия»), чтобы найти частное решение , которое не имеет произвольных констант.

   Обыкновенное дифференциальное уравнение следующего вида:

   dy / dx = ƒ ( x )

   может быть решена путем интегрирования обеих частей по x:

   y = ∫ ƒ ( x ) dx

   Этот метод, называемый прямым интегрированием , также может применяться, когда левая часть является производной более высокого порядка.

   В этом случае нужно интегрировать уравнение достаточное количество раз, пока не будет найдено y.

   Нажмите на вопросы, чтобы узнать их решение

   Упражнение 1:

   Покажите, что y = 2 e ^{2 x} является частным решением обыкновенного дифференциального уравнения:

   d ² y / dx ² - dy / dx - 2 y = 0

   Решение:

   Имеем: dy / dx	=	2⋅2 e 2 x = 4 e 2 x
   и: d 2 y / dx 2	=	2⋅4 e 2 x = 8 e 2 x
   ∴ d 2 y / dx 2 - dy / dx - 2 y	=	8 e 2 x - 4 e 2 x - 2⋅e 2 x
   	=	(8-8) e 2 x
   	=	0
   	=	RHS

   Упражнение 2:

   Покажите, что y = 7 cos (3 x ) - 2 sin (2 x ) является частным решением:

   d ² y / dx ² + 2 y = −49 cos (3 x ) + 4 sin (2 x )

   Решение:

   Имеем: dy / dx	=	−21 sin (3 x ) - 4 cos (2 x )
   и: d 2 y / dx 2	=	−63 cos (3 x ) + 8 sin (2 x )
   ∴ d 2 y / dx 2 + 2 y	=	−63 cos (3 x ) + 8 sin (2 x ) + 2 (7 cos (3 x ) - 2 sin (2 x ))
   	=	(−63 + 14) cos (3 x ) + (8-4) sin (2 x )
   	=	−49 cos (3 x ) + 4 sin (2 x )

   Примечание: уравнение второго порядка, поэтому общее решение будет иметь две произвольные (неопределенные) константы.

   Обратите внимание, насколько конкретное решение похоже на правую часть уравнения. Он включает в себя те же функции, но у них другой коэффициент, то есть: y имеет вид a cos (3 x ) + b sin (2 x ), где a = 7 и b = −2.

   Упражнение 3:

   Покажите, что y = A sin ( x ) + B cos ( x ), где A и B - произвольные константы, является общим решением:

   d ² y / dx ² + y = 0

   Решение:

   dy / dx	=	A cos ( x ) - B sin ( x )
   d 2 y / dx 2	=	- A sin ( x ) - B cos ( x )
   ∴ d 2 y / dx 2 + y	=	(- A sin ( x ) - B cos ( x )) + ( A sin ( x ) + B cos ( x ))
   	=	0

   Примечание: поскольку дифференциальное уравнение второго порядка и решение имеет две произвольные константы, это решение является общим решением.

   Упражнение 4:

   Выведите общее решение dy / dx = 2 x +3

   Решение:

   Это уравнение имеет вид dy / dx = ƒ ( x ), и его можно решить прямым интегрированием.

   Интегрируем обе стороны по x:

   ∫ dy / dx dx	=	∫ (2 x + 3) dx
   i.е. ∫ dy	=	∫ (2 x + 3) dx
   т.е. y	=	2⋅1 / 2 x 2 + 3 x + C
   т.е. y	=	x 2 + 3 x + C

   - где C - произвольная (комбинированная) константа, полученная в результате интегрирования обеих частей уравнения.Общее решение должно иметь одну произвольную константу, поскольку дифференциальное уравнение имеет первый порядок.

   Упражнение 5:

   Выведите общее решение d ² y / dx ² = - sin ( x )

   Решение:

   Это имеет вид d ² y / dx ² = ƒ ( x ), поэтому мы можем решить относительно y путем прямого интегрирования.

   Интегрируем обе стороны по x:

   dy / dx	=	- ∫ sin ( x ) dx
   	=	- (- cos x ) + A

   Снова интегрируйте:

   y

   =

   sin ( x ) + Ax + B

   - где A , B - две произвольные постоянные общего решения.Обратите внимание, что уравнение второго порядка.

   Упражнение 6:

   Получите общее решение d ² y / dt ² = a , где a = константа

   Решение:

   Интегрируем обе стороны относительно т :

   dy / dt	=	∫ и dt
   i.е. dy / dt	=	при + C

   Снова интегрируйте:

   y	=	∫ ( при + C ) dt
   y	=	1/2 при 2 + Ct + D

   - где C , D - две произвольные константы, необходимые для общего решения дифференциального уравнения второго порядка.

   Упражнение 7:

   Получите общее решение d ³ y / dt ² = 3 x ²

   Решение:

   Интегрируем обе стороны по x:

   d 2 y / dx 2	=	∫ 3 x 2 dx
   i.е. d 2 y / dx 2	=	3⋅1 / 3 x 3 + C
   т.е. d 2 y / dx 2	=	x 3 + C

   Снова интегрируйте:

   dy / dx	=	∫ ( x 3 + C ) dx
   i.е. dy / dx	=	x 4 /4 + Cx + D

   Снова интегрируйте:

   y	=	∫ ( x 4 /4 + Cx + D ) dx
   т.е. y	=	1/20 x 5 + C /2 x 2 + Dx + E
   i.е. л	=	1/20 x 5 + C ' x 2 + Dx + E

   где C ' (= C ⁄2), D и E - три требуемые произвольные постоянные для общего решения дифференциального уравнения третьего порядка.

   Упражнение 8:

   Получите общее решение e ^{- x} d ² y / dx ² = 3

   Решение:

   Умножение обеих частей уравнения на e ^x дает:

   e x ⋅e - x d 2 y / dx 2	=	e x ⋅3
   i.е. d 2 y / dx 2	=	3 e x

   Теперь это имеет вид d ² y / dx ² = ƒ ( x ), где ƒ ( x ) = 3 e ^x , а решение y находится прямым интегрированием.

   Интегрируем обе стороны по x:

   dy / dx	=	∫ (3e x ) dx
   т.е. dy / dx	=	3 e x + C

   Снова интегрируйте:

   y	=	∫ (3 e x + C ) dx
   i.е. л	=	3 e x + Cx + D

   - где C и D - две произвольные постоянные общего решения дифференциального уравнения второго порядка.

   ƒ ( x )	∫ ƒ ( x ) dx		ƒ ( x )	∫ ƒ ( x ) dx
   x n	x n +1 / n +1 ( n −1)		[ г ( x )] n г ' ( x )	[ г ( x )] n +1 / n + 1 ( n ≠ −1)
   1/ x	дюйм x		г ' ( x ) / г ( x )	дюйм г ( x )
   e x	e x		a x	a x / ln a ( a > 0)
   грех x	−cos x		sinh x	цвет x
   cos x	грех x		цвет x	sinh x
   желто-коричневый x	- ln cos x		танх x	ln cosh x
   кодексов x	желто-коричневый x /2		cosech x	ln tanh x /2
   сек x	ln sec x + tan x		сек x	2 желто-коричневый −1 e x
   сек 2 x	желто-коричневый x		сек 2 x	танх x
   детская кроватка x	лин x		детская кроватка x	лин x
   sin 2 x	x /2 - грех 2 x /4		sinh 2 x	sinh 2 x /4 - x /2
   cos 2 x	x /2 + грех 2 x /4		cosh 2 x	sinh 2 x /4 + x /2
   1/ a 2 + x 2	1/ a желто-коричневый −1 x / a ( a > 0)		√ a 2 + x 2	a 2 /2 [sinh −1 ( x / a ) + x √ a 2 - x 2 / a 2 9035]
   1/ a 2 - x 2	1/2 a ln a + x / a - x (0 < x < a )		√ a 2 - x 2	a 2 /2 [sin −1 ( x / a ) + x √ a 2 - x 2 / a ]
   1/ x 2 - a 2	1/2 a ln x - a / x + a ( x > a > 0)		√ x 2 - a 2	a 2 /2 [−cosh −1 ( x / a ) + x √ x 2 - a 2 / 2 ]
   1 / √ a 2 + x 2	ln x + √ a 2 + x 2 / a ( a > 0)
   1 / √ a 2 - x 2	sin −1 x / a (- a < x < a )		1 / √ x 2 - a 2	ln x + √ x 2 - a 2 / a ( x > a > 0)

   .