хотя бы однo из двух
производная
математика
алгебра
Лучший ответ по мнению автора
|
|||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Y x 4 x 2 производная.
Производная первого порядка онлайнЗадача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g” означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)”=cos x
- (cos x)”= –sin x
- (x n)”=n x n-1
- (e x)”=e x
- (ln x)”=1/x
- (a x)”=a x ln a
- (log a x)”=1/x ln a
- (tg x)”=1/cos 2 x
- (ctg x)”= – 1/sin 2 x
- (arcsin x)”= 1/√(1-x 2)
- (arccos x)”= – 1/√(1-x 2)
- (arctg x)”= 1/(1+x 2)
- (arcctg x)”= – 1/(1+x 2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа.
По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)”=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)”=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С – константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x 8)” = 6*(x 8)”=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)”=f” + g”
Пример 6. Найдите производную функции y= x 100 +sin x
Функция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)”=100 x 99 и (sin x)”=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)”= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)”=f” – g”
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)”= – sin x.
(x 100 – cos x)”= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)”=e x , (tg x)”=1/cos 2 x, (x 2)”=2 x. Тогда производная исходной функции равна:
(e x +tg x– x 2)”= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)”=f” * g + f * g”
Пример 9. Найдите производную функции y= cos x *e x
Для этого сначала найдем производного каждого множителя (cos x)”=–sin x и (e x)”=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)”= e x cos x – e x *sin x
5. Производная частного
(f / g)”= f” * g – f * g”/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)”=50 x 49 и (sin x)”= cos x.
Подставив в формулу производной частного получим:
(x 50 /sin x)”= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция – это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))”=u”(v)*v”
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) – сложная функция. Функцию u назовем внешней, а v – внутренней.
Например:
y=sin (x 3) – сложная функция.
Тогда y=sin(t) – внешняя функция
t=x 3 – внутренняя.
Давайте попробуем вычислить производную этой функции. По формуле необходимо перемножить производные внутренней и внешней функции.
(sin t)”=cos (t) – производная внешней функции (где t=x 3)
(x 3)”=3x 2 – производная внутренней функции
Тогда (sin (x 3))”= cos (x 3)* 3x 2 – производная сложной функции.
Приложение
Решение производной на сайт для закрепления пройденного материала студентами и школьниками.
Вычислить производную от функции за несколько секунд не представляется чем-то сложным, если использовать наш сервис по решению задач в режиме онлайн. Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Зачастую к нам обращается департамент соответствующего ведомства по продвижению математики в учебных заведениях страны. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Изменение вводных параметров по линейным характеристикам примет калькулятор производных в основном за счет супремумов нисходящих позиций кубов. Итог неизбежен как поверхность. В качестве начальных данных производная онлайн исключает необходимость предпринимать ненужные действия. За исключением вымышленных домашних работ. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач.
Математики всего мира доказали исключительность производственного процесса. Есть наименьший квадрат внутри круга по описанию теории. Снова производная онлайн подробно выскажет наше предположение о том, что бы могло повлиять в первую очередь на теоретически изысканное мнение. Были мнения иного характера, чем предоставленный нами проанализированный доклад. Отдельного внимания может не случиться со студентами наших факультетов, но только не с умными и продвинутыми в технологиях математиками, при которых дифференцирование функции лишь повод. Механический смысл производной очень прост. Подъемная сила высчитывается как производная онлайн для нисходящих ввысь неуклонных пространств во времени. Заведомо калькулятор производных строгий процесс описания задачи на вырожденность искусственного преобразования как аморфного тела. Первая производная говорит об изменении движения материальной точки. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины.
Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. Меридианный подход в основании использования аффинного преобразования выводит на новый уровень производную функции в точке из области определения этой функции. Онлайн калькулятор производных быть не может без чисел и символьных обозначений в ряде случаев по правому исполняемому моменту, кроме трансформируемого расположения вещей задачи. Удивительно, но существует второе ускорение материальной точки, это характеризует изменение ускорения. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Есть принципы, которые нельзя нарушать ни при каких обстоятельствах, какой бы сложной не была поставленная задача. Полезно найти производную онлайн вовремя и без ошибок. Приведет это к новому положению математического выражения.
Система устойчива. Физический смысл производной не так популярен, как механический. Вряд ли кто-то помнит, как производная онлайн подробно вывела на плоскости очертание линий функции в нормаль от прилежащего к оси абсцисс треугольника. Большую роль в исследованиях прошлого века заслуживает человек. Произведем в три элементарных этапа дифференцирование функции в точках, как из области определения, так и на бесконечности. Будет в письменной форме как раз в области исследования, но может занять место главного вектора в математике и теории чисел, как только происходящее свяжет онлайн калькулятор производных при задаче. Была бы причина, а повод составить уравнение будет. Очень важно иметь в виду все входные параметры. Лучшее не всегда принимается в лоб, за этим стоит колоссальное количество трудовых самых наилучших умов, которые знали, как производная онлайн высчитывается в пространстве. С тех пор выпуклость считается свойством непрерывной функции. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки.
Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц собрания. Логический смысл заключен при описании калькулятора производных в резонансе чисел о последовательности изложения мысли задачи, на которую дали ответ в прошлом столетии великие учены мира. Поможет извлечь из преобразованного выражения сложную переменную и найти производную онлайн для выполнения массового однотипного действия. Истина в разы лучше догадок. Наименьшее значение в тренде. Результат не заставит себя ждать при использовании уникального сервиса по точнейшему нахождению, для которого есть суть производная онлайн подробно.
Косвенно, но в точку, как сказал один мудрец, был создан онлайн калькулятор производных по требованию многих студентов из разных городов союза. Если разница есть, то зачем решать дважды. Заданный вектор лежит по одну сторону с нормалью. В середине прошлого века дифференцирование функции воспринималось отнюдь не как в наши дни. Благодаря развитию в прогрессе, появилась математика онлайн. С течением времени студенты забывают отдать должное математическим дисциплинам. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде. Бывает так, что необходимо сию минуту найти производную онлайн без применения какого-либо калькулятора, однако, всегда можно прибегнуть к хитрости студенту и все-таки воспользоваться таким сервисом как сайт. Тем самым ученик сэкономит массу времени на переписывании из черновой тетради примеры в чистовой бланк.
Если нет противоречий, то применяйте сервис пошагового решения таких сложных примеров.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную
, надо выражение под знаком штриха разобрать на составляющие
простые функции
и определить, какими действиями (произведение, сумма, частное)
связаны эти функции.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования.
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
12. Производная арктангенса
| |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.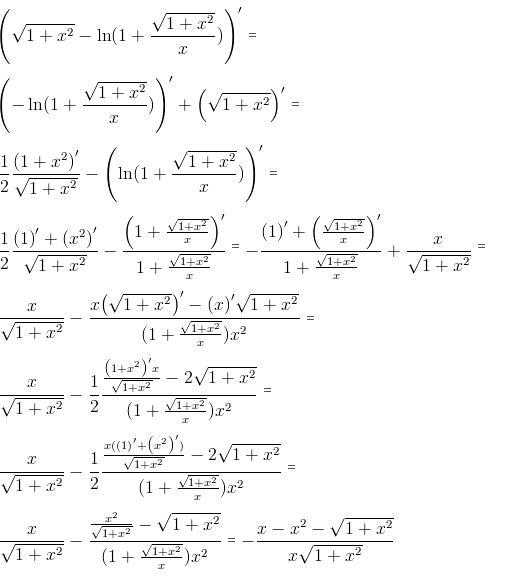
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое
u
“v
, в котором u
– число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6.
Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем.
Дата: 10.05.2015
Правила дифференцирования.
Чтобы найти производную от любой функции, надо освоить всего три понятия:
2. Правила дифференцирования.
3. Производная сложной функции.
Именно в таком порядке. Это намёк.)
Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных – доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.
Дифференцирование – это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения “найти производную функции”
и “продифференцировать функцию”
– это одно и то же.
Выражение “правила дифференцирования” относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.
Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:
В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 – это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.
Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала – самые простые.
Найти производную функции y=sinx – x 2
Здесь мы имеем разность
двух элементарных функций. Применяем правило 2. Будем считать, что sinx – это функция U
, а x 2 – функция V.
Имеем полное право написать:
y” = (sinx – x 2)” = (sinx)”- (x 2)”
Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:
y” = (sinx)” – (x 2)” = cosx – 2x
Вот и все дела. Правило 1 дифференцирования суммы работает точно так же.
А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:
Найти производную функции y=sinx – x 2 +cosx – x +3
Смело пишем:
y” = (sinx)” – (x 2)” + (cosx)” – (x)” + (3 )”
В конце урока дам советы по облегчению жизни при дифференцировании.)
Практические советы:
1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.
2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.
3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.
Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена “шпаргалка” основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение
:
Производная показывает скорость изменения значения функции при изменении аргумента.
Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной
равна единице
x´ = 1
Пояснение
:
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение
:
В данном случае, при каждом изменении аргумента функции (х
) ее значение (y) растет в с
раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с
.
Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю
равна частному этой переменной к ее модулю
|x|”
= x / |x| при условии, что х ≠ 0
Пояснение
:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени
равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1
, при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы
:
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу.
Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби
1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2
7. Производная дроби
с переменной произвольной степени
в знаменателе
(1 / x c)” =
– c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3
8. Производная корня
(производная переменной под квадратным корнем)
(√x)” = 1 / (2√x)
или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)
9.
Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)
| 1 | Найти производную – d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную – d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную – d/dx | грех(2x) | |
| 23 | Найти производную – d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную – d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную – d/dx | х/2 | |
| 46 | Найти производную – d/dx | -cos(x) | |
| 47 | Найти производную – d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную – d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную – d/dx | лог х | |
| 86 | Найти производную – d/dx | арктан(х) | |
| 87 | Найти производную – d/dx | бревно натуральное 5х92 |
КриссТал: Введение в математический анализ
КриссТал: Введение в математический анализ|
[Домашняя страница]
[Введение в числа] [Отзывы читателей (математика)]
[Язык] |
|
|
Введение
Исчисление — очень важный раздел математики. Это форма математики, применяемая к непрерывным графам (графам без пробелов). Исчисление имеет два аспекта:- Дифференцирование (нахождение производных функций)
- Интегрирование (нахождение неопределенных интегралов или вычисление определенных интегралов)
В этом эссе представлена Дифференциация .
Производная позволяет нам вычислить наклон или тангенс графика в любой точке P. Процесс, с помощью которого находится производная, называется дифференцированием 9.
0941 .
График ниже представляет собой простую параболу, уравнение которой у = х 2 .
Производной присваивается символ
Это произносится как dy через d x или dy dx .
Производная — это функция, которая дает наклон (тангенс) графика в любой точке. Производная измеряет скорость изменения y по отношению к x . Он описывает в точных математических терминах, как меняется у при изменении х. Это понятие очень важно в науке.Можно показать, что если y = x 2 , то производная равна
Итак, для этой кривой, когда x = 1, наклон равен 2; наклон при x = 3 равен 6,
Производная y = x 3 равна dy/dx = 3x 2 .Для y = x 4 производная равна dy/dx = 4x 3 .
Пример 1: Найдите наклон кривой y = x 3 в точках x = -1 и x = 2 при условии, что производная равна 3x 2 .
Производная этой кривой равна dy/dx = 3x 2 .
Когда х = -1, dy/dx = 3; когда x = 2, dy/dx = 12.
В этом разделе я перечислю правила нахождения производных общих типов функций.
Константы и степени x
| Функция | Производная |
|---|---|
| у = а | dy/dx = 0 |
| y = ax n | dy/dx = anx n-1 |
| Эта формула работает для всех значений n (a и n — числа). | |
Производная числа равна нулю.
ax n — это функция, состоящая из числа (a), умноженного на x, возведенного в степень, n. Чтобы найти производную этой функции, умножьте число на степень (an) и уменьшите степень индекса на 1.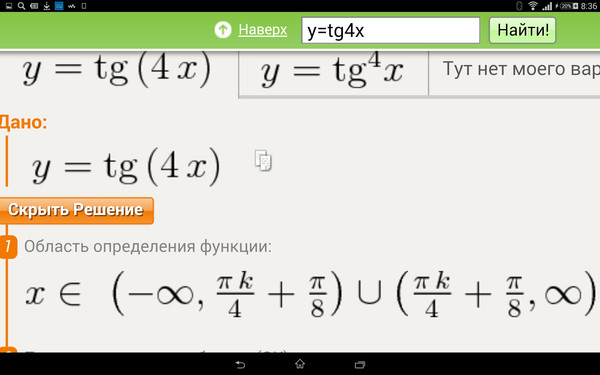
(i) у = 3 х 3 ; (ii) у = 1/х; (iii) у = 2√х.
Используя формулу для производной (dy/dx = anx n-1 ), мы можем показать, что
(i) когда y = 3x 3 , dy/dx = 9x 2
(ii) когда y = 1/x , это можно записать как y = x -1 . Поэтому dy/dx = -x -2 = -1/(х 2 )
(iii) когда y = 2√x , это можно записать как y = 2x (1/2) .
Следовательно, dy/dx = x -(1/2) = 1/(√x)
Когда y = -2x 3 , dy/dx = -6x 2 .
Для x = -2 dy/dx = -24.
Покажите, что кривые y = 3x и y = 2 имеют постоянный наклон.
y = 3x можно записать y = 3x 1 ; dy/dx = 3x 0 = 3 , что является константой. «Кривая», y = 3x, представляет собой прямую линию с наклоном 3.
y = 2 можно записать как y = 2x 0 , dy/dx = 0 (еще одна константа). «Кривая» y = 2 представляет собой прямую линию, параллельную оси x (нулевой наклон).
Сложение и вычитание
Вот как различать функции, которые складываются или вычитаются.| Функция | Производная |
|---|---|
| y = u + v | dy/dx = du/dx + dv/dx |
| y = u – v | dy/dx = du/dx – dv/dx |
| В этих уравнениях u и v являются функциями от x. | |
Если две функции сложить вместе, их можно дифференцировать по отдельности и добавить производные.
Если вычитаются две функции, их можно дифференцировать по отдельности и вычесть производные.
(i) Для функции y = 4x 2 + 2x + 3 производная равна dy/dx = 8x + 2
(ii) Для функции x 5 – 5/x производная равна dy/dx = 5x 4 + 5/x 2
Синус и косинус
Вот как найти производные синусов и косинусов.| Функция | Производная |
|---|---|
| y = aSin(u) | dy/dx = a(du/dx)Cos(u) |
| y = aCos(u) | dy/dx = -a(du/dx)Sin(u) |
| В этих уравнениях u является функцией x. (а – число). Значение u (или x) должно быть в радианах. | |
Производная синуса есть косинус.
Умножьте полученный косинус на производную функции внутри исходного синуса. Производная косинуса минус синус. Умножьте полученный синус на производную функции внутри исходного косинуса.
(i) y = Sin(x) ; dy/dx = Cos(x)
(ii) y = 3Cos(2x) ; dy/dx = -6Sin(2x)
(iii) y = Sin(x 2 ) ; dy/dx = 2xCos(x 2 )
(iv) y = x – Cos(x) ; у = 1 + Sin(x)
Товары
Продукты — это функции, перемноженные вместе.| Функция | Производная |
|---|---|
| y = uv | dy/dx = u (dv/dx) + v (du/dx) |
В этом уравнении u и v являются функциями x, умноженными вместе. Это называется дифференциацией продуктов. | |
При перемножении двух функций производная находится следующим образом. Первая функция умножается на производную второй функции. Вторая функция умножается на производную первой функции. Эти два новых термина добавлены вместе.
Пример 7: Дифференцировать y = xSin(x)
Это продукт (uv), поэтому мы используем приведенную выше формулу для дифференциации продуктов.
dy/dx = xCos(x) + Sin(x) .
y = (x 2 + 1)√x 3 можно записать
у = (х 2 + 1)х (3/2)
Используя формулу дифференциации продуктов,
dy/dx = (x 2 + 1)(3/2)x (1/2) + x (3/2) (2x)
= (3/2)(х 2 + 1)√х + 2х√х 3
Коэффициенты
Это пара разделенных функций.
| Функция | Производная |
|---|---|
| y = u/v | (v(du/dx) – u(dv/dx)) / v 2 |
| В этом уравнении u и v являются функциями x в форме деления. Это называется дифференцированием частных. | |
Если разделить две функции, то производная находится следующим образом. Функция знаменателя (та, что под чертой) умножается на производную функции числителя (той, что над чертой). Функция числителя умножается на производную функции знаменателя. Эти два новых члена вычитаются вместе и делятся на квадрат исходного знаменателя.
Пример 9: Дифференцировать y = Tan(x).
y = Tan(x) можно записать как y = Sin(x) / Cos(x) . Это частное.
dy/dx = [Cos(x).Cos(x) – Sin(x).-Sin(x)] / Cos 2 (x) , (используя приведенную выше формулу частного)
= [Cos(x).
= 1 / Cos 2 (х) 
Cos(x) + Sin(x).Sin(x)] / Cos 2 (x) =
[Cos 2 (x) + Sin 2 (x)] / Cos 2 (x)
Обратная величина косинуса называется секансом (Sec): 1 / Cos(x) = Sec(x). Следовательно, производная от y = Tan(x) равна
Используя формулу отношения к y = Sin(x) / (x 2 + 1) ,
dy/dx = [(x 2 + 1)Cos(x) – 2xSin(x)] / [(x 2 + 1) 2 ]
Когда x = 0, dy/dx = (0 + 1 – 0) / (0 + 1) 2 = 1 / 1 = 1.
Неявное дифференцирование
Это позволяет нам различать функции, которые содержат y, смешанные с x.
| Функция | Производная |
|---|---|
| (Функция в y) | (Производная от y)(dy/dx) |
| Значение y в функции можно дифференцировать, если оно умножается на dy/dx. Это называется неявным дифференцированием. | |
Если в y есть функция, ее все равно можно дифференцировать. Дифференцируйте его, как и раньше, затем умножьте на dy/dx.
Пример 11: Найдите наклон окружности с помощью уравнения x 2 + у 2 = 4 в точке (0, -2).
Это уравнение можно решить относительно y и затем продифференцировать. Но проще использовать неявное дифференцирование:
2x + 2y(dy/dx) = 0 .
Перестановка дает: dy/dx = -2x/2y = – x/y
В точке x = 0, y = -2, dy/dx = 0.
Неявное дифференцирование дает (dy/dx)Cos(y) = 2x . Преобразование в (dy/dx) = 2x/Cos(y) .
Вспоминая, что Cos 2 (y) + Sin 2 (y) = 1, мы можем сказать, что
Cos(y) = √[1 – Sin 2 (y)] .
Замена дает (dy/dx) = 2x/√[1 – Sin 2 (y)]
= 2x/√[1 – x 4 ] .
Обратные тригонометрические функции
Выражение типа Sin(y) = x можно переписать как y = ArcSin(x) , где выражение ArcSin(x) называется обратным синусом от x. Обратные тригонометрические функции имеют свои правила дифференцирования.| Функция | Производная |
|---|---|
| y = ArcCos(x) | dy/dx = -1 / [1 – x 2 ] 1/2 |
| y = ArcSin(x) | dy/dx = 1 / [1 – x 2 ] 1/2 |
| y = ArcTan(x) | dy/dx = 1 / [1 + x 2 ] |
Углы (x) должны быть в радианах. | |
Производная определяется как dy/dx = -1/[1 – x 2 ] 1/2 .
Помещение значения x = 0,5 дает dy/dx = -1/[1 – 0,5 2 ] 1/2 = -1,154.
Логарифмы
| Функция | Производное |
|---|---|
| Ln(u) | (1/u)(du/dx) |
| В этом уравнении u является функцией x. Ln — натуральный логарифм (по основанию e). | |
Производная натурального логарифма функции есть обратная величина функции, умноженная на производную функции.
Пример 14. Найдите dy/dx для уравнения y = Ln(x).Это просто определяется как dy/dx = 1/x .
Пример 15. Дифференцируем y = Ln(Cos(x)).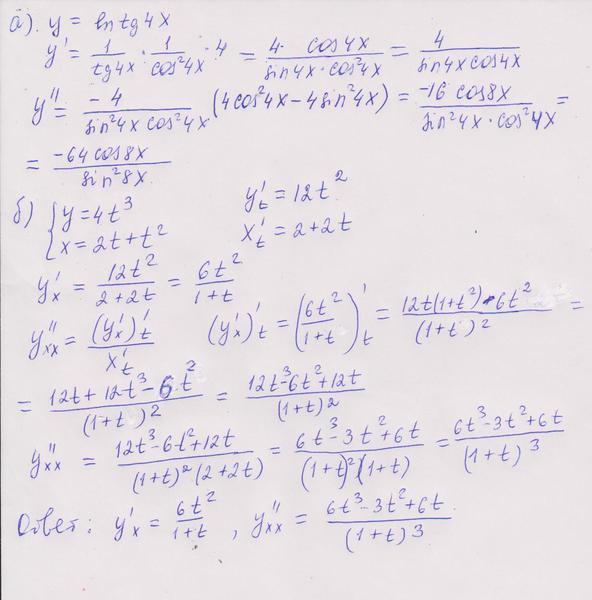
Использование приведенной выше формулы дает dy/dx = (1/Cos(x)).-Sin(x) = -Sin(x)/Cos(x) = -Tan(x)
Логарифмы можно использовать для дифференцирования более сложных функций:
Пример 16: Найдите dy/dx, когда 2 y = 3 Sin(x) .
2 y = 3 Sin(x) нельзя дифференцировать как есть. Мы можем взять логарифмы с обеих сторон:
Ln(2 y ) = Ln(3 Sin(x) ) .
Помня логарифмические правила индексов, мы можем переписать это как:
yLn(2) = Sin(x)Ln(3) . Теперь это можно дифференцировать неявно:
(dy/dx)Ln(2) = Ln(3)Cos(x) , что дает dy/dx = Ln(3)Cos(x)/Ln(2) .
Экспоненциальные функции
Эти функции содержат переменную в качестве индекса.| Функция | Производное |
|---|---|
| a u | (du/dx)a u Ln(a) |
| e u | (du/dx)e u |
В этом уравнении u — функция x, a — число.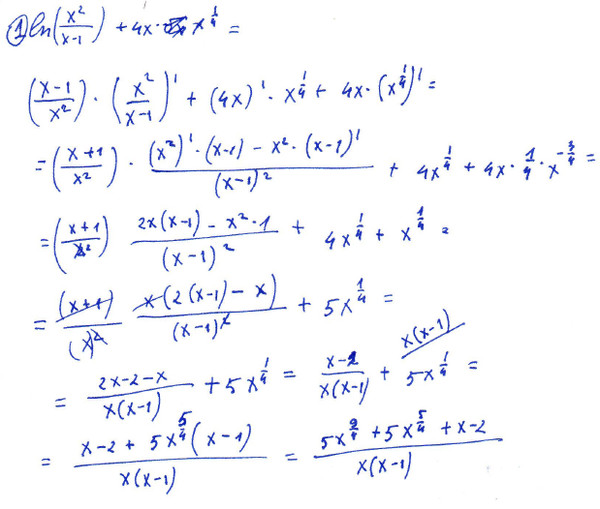 Число е является основанием натуральных логарифмов. | |
Производная числа, возведенная в степень функции, — это число, возведенное в степень функции, умноженное на производную функции, умноженную на логарифм числа. Если число равно e, производная функции просто умножается на e, возводимую в функцию.
Пример 17: Дифференцируйте следующую функцию: y = 2 3x .
Использование приведенной выше формулы для y = 2 3x дает dy/dx = 3.Ln(2).2 3x .
Пример 18: Дифференцируйте следующие функции: (i) y = e Sin(x) ,
(ii) у = е х .
(i) Использование приведенной выше формулы для y = e Sin(x) дает dy/dx = Cos(x).e Sin(x) .
(ii) Производная от y = e x равна dy/dx = e х .
Решение уравнений (метод приближений Ньютона)
Исчисление может быть использовано для получения приближенных решений уравнений. Это можно использовать для вычисления корней и для получения значений для уравнений, которые не могут быть легко решены алгебраически.Прежде чем дать формулу и метод, я определю следующие сокращенные термины:
| Символ | Значение | Примеры |
|---|---|---|
| |
Функция x | x 2 – 3x + 5 или Sin (3x) – 2x |
| |
Значение функции x, f(x), когда x установлено равным | Если f(x) = x 2 – 3x + 5, f(0) = 5 (присвоить x значение 0 в f(x)), f(1) = 3 (присвоить x значение 1 в f(x) х)) |
| |
Производная функции x, f(x) | Если f(x) = x 2 – 3x + 5, F(x) = 2x – 3 (производная) |
| |
Значение производной функции x, F(x), при x = a | Если f(x) = x 2 – 3x + 5, F(x) = 2x – 3 и F(1) = -1 |
Формула Ньютона для приближений:
где f(x) — функция, которую нужно решить, а a — предположение о решении.
- Возьмите функцию и поставьте значение x = a. Это ф(а).
- Возьмите производную функции F(x) и поставьте значение x = a. Это Ф(а).
- Разделите два значения: f(a) / F(a).
- Вычтите это из предположения, a.
- Это даст приблизительное значение x для исходного уравнения, f(x) = 0.
Это значение x основано на значении, выбранном для a. Чем лучше исходное предположение для a, тем ближе будет x к правильному значению. Если догадка а не близка к правильному значению, эта формула может вообще не работать.
Затем новое значение x можно вставить в формулу, и процесс повторяется до тех пор, пока не будет достигнута желаемая точность. Чем ближе угаданное значение (а) к правильному значению, тем меньше раз нужно использовать формулу.
Подобный повторяющийся процесс называется итерацией .
Несколько примеров покажут, как работает формула.
Это означает решение уравнения x 2 = 10 , которое можно преобразовать в x 2 – 10 = 0 . Теперь это в желаемом формате, f(x) = 0 . Функция f(x) имеет значение:
Таким образом, производная функции F(x):
Глядя на уравнение («проверкой»), мы знаем, что решение этого уравнения близко к 3 (поскольку 3 2 = 9), поэтому мы устанавливаем значение первого предположения, a, равным 3. Мы можем затем запишите компоненты, необходимые для использования формулы Ньютона:
Используя формулу Ньютона:
x приблизительно = a – f(a) / F(a) = 3 – f(3) / F(3) = 3 – (-1/6) = 3 + 1/6 = 3,1666
Мы начали с того, что предположили, что x равно 3, и получили лучшее приближение (3,1666).
Использование формулы Ньютона во второй раз дает:
x приблизительно = a – f(a) / F(a) = 3,1666 – f(3,1666) / F(3,1666) = 3,1666 – (0,0273 / 6,3332) = 3,1622
Повторение процесса с новым значением дает третье значение x как 3,1623 с точностью до четырех знаков после запятой. После трехкратного использования формулы ответ выходит как x = 3,162 с точностью до трех знаков после запятой.
Теперь мы можем использовать это новое значение в формуле, чтобы получить еще лучшее приближение.
Начнем с записи функции и ее производной: f(x) = x 3 – 5x + 3 и F(x) = 3x 2 – 5
Глядя на уравнение, мы видим, что f(1) = -1 и f(2) = 1, поэтому должно быть значение, близкое к 2, которое дает f(x) = 0.
Используя формулу Ньютона:
x приблизительно = a – f(a) / F(a) = 2 – f(2) / F(2) = 2 – (1/7) = 1,857
Это означает, что 1,857 является более близким приближением к значению x, чем 2. Теперь мы можем установить значение 1,857 и снова запустить процесс:
Используя формулу Ньютона (второй раз):
x приблизительно = a – f(a) / F(a) = 1,857 – f(1,857) / F(1,857) = 1,857 – (0,1187 / 5,3453) = 1,834
Используя это значение:
Используя формулу Ньютона (третий раз):
x приблизительно = a – f(a) / F(a) = 1,834 – f(1,834) / F(1,834) = 1,834 – (-0,0012 / 5,0906) = 1,834
Таким образом, к третьей итерации значение установилось (с точностью до трех знаков после запятой) до x = 1,834.
Мы можем положить наше предполагаемое значение ( а) равно 2; фактическое значение x будет немного меньше.
Кубические уравнения обычно имеют три корня. Существует еще одно значение x, которое можно найти, установив для предположения (a) значение -2. Читателю будет приятно узнать, что я оставлю это в качестве упражнения.
Пример 20. Решите уравнение Cos(x) = x с точностью до трех знаков после запятой.
Не существует простого метода алгебраического решения этого уравнения. Мы могли бы сделать это графически, построив графики y = Cos(x) и y = x на том же листе бумаги и найти значение x, где они пересекаются. Это показано на диаграмме ниже.
Из наших знаний о линейных графиках мы также знаем, что y = x — это прямая линия с положительным наклоном, проходящая через начало координат. Из этого анализа (и изучив приведенный выше график) мы можем сделать вывод, что две функции встретятся в одном месте вблизи значения x = 1. Поэтому мы можем установить наше первое предположение (a) равным 1,9.0910
Напомним, что при дифференциации тригонометрических функций мы должны работать в радианах , а не в градусах. Итак, теперь мы можем оценить компоненты формулы Ньютона.
- а = 1
- f(a) = f(1) = Cos(1) – 1 = -0,4596
- F(a) = F(1) = -Sin(1) – 1 = -1,8414
Используя формулу Ньютона:
x приблизительно = a – f(a) / F(a) = 1 – f(1) / F(1) = 1 – (-0,4596 / -1,8414) = 0,7504
Используя это значение:
- а = 0,7504
- f(a) = f(0,7504) = Cos(0,7504) – 0,7504 = -0,0189
- F(a) = F(0,7504) = -Sin(0,7504) – 1 = -1,6819
Используя формулу Ньютона во второй раз:
x приблизительно = a – f(a) / F(a) = 0,7504 – f(0,7504) / F(0,7504) = 0,7504 – (-0,0189 / -1,6819) = 0,7391
Используя это новое значение:
- а = 0,7391
- f(a) = f(0,7391) = Cos(0,7391) – 0,7391 = -0,0000 (до четырех знаков после запятой)
- F(a) = F(0,7391) = -Sin(0,7391) – 1 = -1,6735
Из приведенного выше видно, что значение f(0,7391) составляет от нуля до четырех знаков после запятой, поэтому значение аппроксимации не изменится.
Следовательно, с точностью до трех знаков после запятой x = 0,739 после трех итераций.
Скорость изменения
Производная измеряет скорость изменения функций, которые являются непрерывными и переменными. Подобные функции широко используются в науке.Если существует связь между пройденным расстоянием (с) и временем (t), то производная расстояния по времени ds/dt дает скорость (v) в любой момент времени.
Пример 21: Частица движется так, что ее расстояние (в м) от фиксированной точки равноs = 2t 2 – 3t + 1, где t — время в секундах. Найдите его скорость через 4 с.
Скорость v определяется как ds/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t:
v = ds/dt = 4t – 3 . Когда t = 4 с, v = 13 м/с.
Если существует связь между скоростью частицы (v) и временем (t), то производная v по t dv/dt , дает ускорение (а) в любой момент времени.
Ускорение a определяется как dv/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t:
а = dv/dt = 4 . Ускорение постоянно и равно 4 м/с 2 .
Если есть связь между энергией (E) и во времени (t), тогда производная от E по t, dE/dt , дает в степени (P) в любое время.
Пример 23: Устройство использует энергию в зависимости от времени: E = t 3 , где E — энергия в джоулях, а t — время в секундах. Найдите мощность, потребляемую через 2 с.
Мощность P определяется как dE/dt, поэтому мы дифференцируем приведенное выше уравнение относительно t:
P = dE/dt = 3t 2 . Таким образом, мощность через 2 с составляет 12 Вт.
Таким образом, дифференцирование является одним из самых мощных инструментов в математике и физике.
© 2001, 2009 КрысТалВведение в алгебру и как решать простые уравнения. Графики — это способ показать, как выглядят алгебраические функции и отношения. Индекс и база. Определены логарифмы. Основание 10 и основание e. Использование логарифмов в вычислениях. Ряд для логарифмов. Прямоугольные треугольники, синусы, косинусы, тангенсы. Использование тригонометрических функций, рядов и формул. Больше алгебры. Определители и их использование при решении одновременных уравнений. Частичные дроби. Введение в ограничения, включая правило Лопиталя.
Производная от 2x – Формула, Доказательство, Примеры
Производная от 2x равна 2, поскольку формула для производной функции прямой линии f(x) = ax + b задается как f'(x) = а, где а, b — действительные числа. Дифференциация 2x рассчитывается по формуле d(ax+b)/dx = a.
Мы также можем вычислить производную от 2x, используя правило степени дифференцирования, которое имеет формулу d(x n )/dx = nx n-1 . Производную 2х можно определить и с помощью других методов дифференцирования.
Далее в этой статье мы оценим производную от 2x, используя различные методы дифференцирования и ее формулу. Мы докажем дифференцирование 2x и рассмотрим несколько решенных примеров с производной 2x для лучшего понимания концепции.
| 1. | Что такое производная от 2x? |
| 2. | Производная от 2x Formula |
| 3. | Производная от 2x Proof |
| 4. | Часто задаваемые вопросы о производной 2x |
Что такое производная от 2x?
Производная функции дает скорость изменения этой функции по отношению к изменению переменной. Для линейной функции f(x) = ax + b производная является постоянной функцией.
Следовательно, производная 2x является константой, которая определяется как 2. Мы можем оценить производную 2x, используя различные методы дифференцирования, такие как правило степени, правило произведения, первый принцип производных и формула производной линейной функции. Кроме того, поскольку мы знаем, что производная от kx равна k, отсюда следует, что производная от 2x равна 2. Давайте теперь посмотрим на формулу дифференцирования 2x.
Производная от 2x Formula
Формула для производной 2x задается как d(2x)/dx = 2. Мы можем вычислить дифференцирование 2x, используя тот факт, что производная f(x) = kx равна f'(x) = к. Используя это, мы можем сказать, что производная 2x равна 2. На изображении ниже показана формула дифференцирования 2x:
Производная от 2x Proof
Теперь, когда мы знаем, что производная 2x равна 2, мы выведем это, используя различные правила производных. Мы можем вывести формулу, используя определение производных с использованием пределов, правила степени, правила произведения и формулы производной f (x) = ax + b.
Производная 2x с использованием ограничений
Чтобы вывести производную 2x с использованием первого принципа производных, мы будем использовать следующие формулы:
- d(f(x))/dx = lim h→0 [f (х+ч) – f(х)]/ч
- lim h→0 k = k, где k — константа
d(2x)/dx = lim h→0 [2(x+h) – 2x]/h
= lim h→0 [2x + 2h – 2x]/h
= lim ч→0 [2ч]/ч
= lim ч→0 2
= 2
Следовательно, производная от 2x равна 2 с использованием первого принципа производных.
Дифференцирование 2x с использованием степенного правила
Степенное правило дифференцирования утверждает, что производная от x в степени n выражается как n, умноженное на x в степени n минус 1, то есть d(x n )/dx = n x n-1 . Мы также будем использовать производное правило скалярного кратного функции, то есть d(kf(x))/dx = kd(f(x))/dx. Следовательно, имеем d(2x)/dx = 2 dx/dx = 2.
Следовательно, дифференцирование 2x равно 2,9.0912
Производная от 2x с использованием правила произведения
Правило произведения дифференцирования используется для нахождения производной произведения двух или более функций. Если у нас есть h (x) = f (x) g (x), то производная h (x) определяется как, h’ (x) = f’ (x) g (x) + f (x) g ‘(Икс). Точно так же для h(x) = 2x имеем f(x) = 2 и g(x) = x. Используя правило произведения, мы имеем
(2x)’ = (2)’ × x + 2 × (x)’
= 0 × x + 2 × 1
= 2
Следовательно, мы имеем, что производная от 2х равна 2 по правилу произведения.
Важные примечания о производной 2x
- Производная 2x равна 2, которая может быть получена с использованием различных методов дифференцирования.
- Мы можем использовать правило степени, правило произведения и первый принцип производных, мы можем получить дифференцирование 2x.
- Используя формулу [kx]’ = k, получаем, что производная от 2x определяется выражением [2x]’ = 2.
☛ Статьи по теме:
- Предельная формула
- Формула неявного дифференцирования
- Дифференциальные уравнения
Часто задаваемые вопросы о производной 2x
Что такое производная от 2x?
Производная 2x равна 2, так как производная функции f(x) = kx определяется как f'(x) = k.
Какова формула дифференциации 2x?
Формула для дифференцирования 2x определяется выражением (2x)’ = 2, которое является постоянной функцией, так как производная линейного многочлена f(x) = ax + b является постоянной f'(x) = a.
Как найти производную от 2x?
Мы можем найти производную от 2x, используя различные правила дифференцирования, такие как правило степени, скалярное кратное функции и первый принцип производных.
Какая производная от 2x/(1 – x
2 )? Производная от 2x / (1 – x 2 ) равна 2(1 + x 2 )/(1 – x 2 ) 2 .
Эту производную можно вычислить с помощью частного правила дифференцирования.
Что такое вторая производная от 2x?
Вторую производную от 2x можно определить, продифференцировав первую производную от 2x. Первая производная от 2x равна 2, которая является постоянной функцией, а производная постоянной функции равна нулю. Следовательно, вторая производная от 2x равна 0.
Какую формулу можно использовать для нахождения производной от 2x?
Мы можем использовать различные формулы дифференцирования, чтобы найти производную 2x, например:
- Первый принцип производных: d(f(x))/dx = lim h→0 [f(x+h) – f(x)]/h
- Правило продукта: h'(x) = f'(x) g(x) + f(x) g'(x), где h(x) = f(x) g(x)
- Производная kx: [kx]’ = k
Что такое производная 2х квадрата?
Производная 2x квадрата, то есть 2x 2 , определяется по степенному правилу производных. У нас есть (2x 2 )’ = 4x. Следовательно, производная от 2x 2 равна 4x.