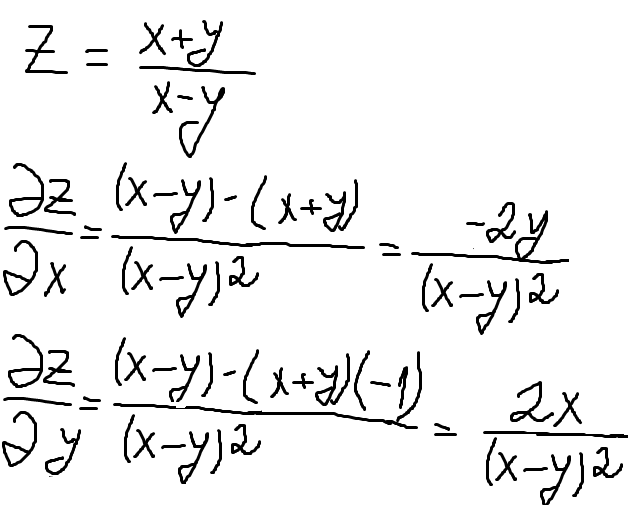Производная суммы дробей со степенями и корнями
При нахождении производной суммы дробей со степенями и корнями во избежание распространённых ошибок следует обращать внимание на следующие моменты:
- применяя формулу дифференцирования произведения и частного, чётко определять разницу между константой, производная которой равна нулю, и постоянным множителем, который просто выносится за знак производной;
- необходимо уверенно пользоваться знаниями из школьного курса по действиям со степенями и корнями, например, что происходит с показателями степени, когда умножаются степени с одинаковыми основаниями;
- что происходит со знаками, когда у производной слагаемого знак противоположен знаку самого слагаемого.
Пример 1. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Находим производную второго слагаемого:
.
Находим производную третьего слагаемого:
.
Здесь двойка перед иксом – постоянный множитель, поэтому его просто вынесли за знак производной.
Собираем всё вместе:
.
Если требуется в окончательном решении получить выражение с корнями, то преобразуем степени в корни и получаем искомую производную:
.
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 2. Найти производную функции
.
Решение. Находим производную первого слагаемого:
.
Здесь первая двойка в числителе промежуточного выражения была константой,
её производная равна нулю.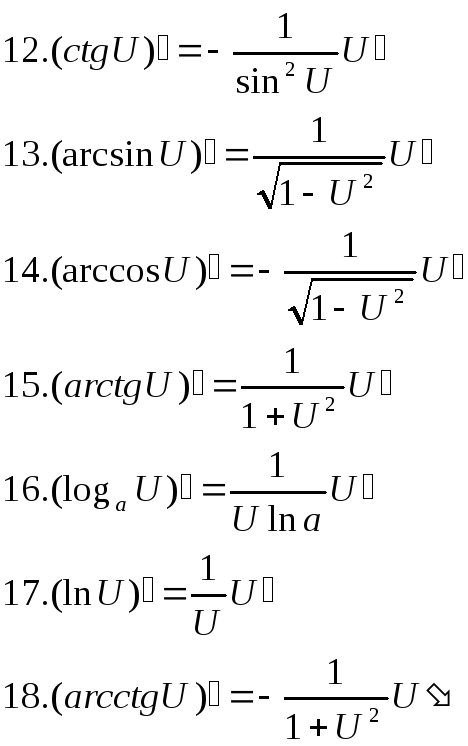
Находим производную второго слагаемого:
Находим производную третьего слагаемого:
Здесь применяли знания из школьного курса о действиях с дробями, их преобразовании и сокращении.
Собираем всё вместе, обращая внимание на то, что знаки производных первого и третьего слагаемых противоположны знакам слагаемых в исходном выражении:
.
Пример 3. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Здесь потребовались навыки в действиях с дробями.
Находим производную второго слагаемого:
Производная третьего слагаемого – константы 1/2 – равна нулю (бывает, что
студенты упорно пытаются найти отличную от нуля производную константы).
Собираем всё вместе, обращая внимание на то, что знак производной второго слагаемого противоположен знаку слагаемого в исходном выражении:
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 4. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Находим производную третьего слагаемого:
Собираем всё вместе, обращая внимание на то, что знаки производных второго и третьего слагаемых – минусы:
.
Пример 5. Найти производную функции
.
Решение. Находим производную первого слагаемого:
Находим производную второго слагаемого:
Находим производную третьего слагаемого:
Собираем всё вместе, обращая внимание на то, что знак производной второго слагаемого – минус:
.
2}.$
Напомним формулы производных элементарных функций:
Рисунок 1. Формулы производных элементарных функций. Автор24 — интернет-биржа студенческих работ
Примеры
Решим примеры. Преобразования, позволяющие применить другие свойства производной, мы применять не будем. В решениях будем использовать только формулу производной от дроби.
По условию даются функции. Нужно найти производные.
Пример 1
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 3. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 4. Пример. Автор24 — интернет-биржа студенческих работ
Пример 2
Рисунок 5. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 6. Пример. Автор24 — интернет-биржа студенческих работ
Пример 3
Рисунок 7.
Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 8. Пример. Автор24 — интернет-биржа студенческих работ
Пример 4
Рисунок 9. Пример. Автор24 — интернет-биржа студенческих работ
Рисунок 10. Пример. Автор24 — интернет-биржа студенческих работ
Пример 5
Рисунок 11.
Рисунок 12. Пример. Автор24 — интернет-биржа студенческих работ
определение, как найти, примеры решений
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной
как предела отношения приращения к приращению аргумента появились таблица производных и
точно определённые правила дифференцирования. Первыми на ниве нахождения производных
потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное)
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу.
Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.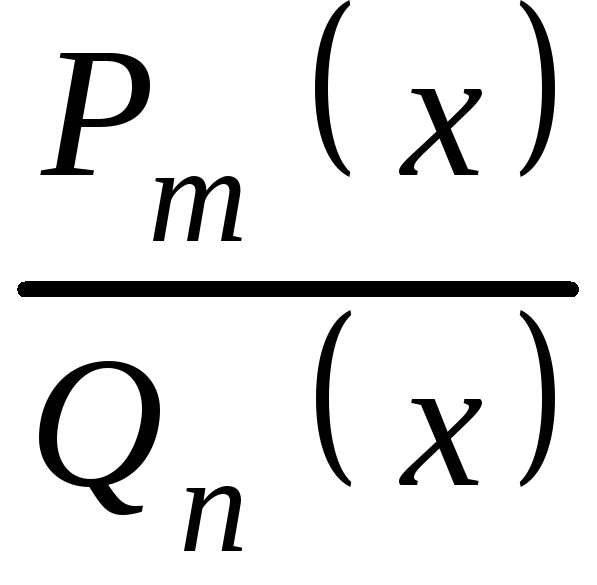
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6.
Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f”(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$
Для обозначения производной часто используют символ y”.
Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f”(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f”(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f”(x) \), т.е.
\(\Delta y \approx f”(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) – f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f”(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f”(0) \)
Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.
2} $$
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Происхождение дифференциального исчисления вызвано необходимостью решать определенные физические задачи. Предполагается, что человек, обладающий дифференциальным исчислением, может брать производные от разных функций. Умеете ли вы брать производную от функции, выраженной дробью?
Инструкция
1. Любая дробь имеет числитель и знаменатель. В процессе нахождения производной от дроби понадобится находить отдельно производную числителя и производную знаменателя.(-2) = -1 / x?.
Обратите внимание!
Дробь может содержать в своем составе еще несколько дробей. В таком случае комфортнее находить вначале отдельно производные «первичных» дробей.
Полезный совет
Когда вы ищите производные знаменателя и числителя, применяйте правила дифференцирования: суммы, произведения, трудных функций. Пригодно удерживать в голове производные простейших табличных функций: линейной, показательной, степенной, логарифмической, тригонометрических и т.д.
Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X .
По определению производной
Пример.
Выполнить дифференцирование функции .
Решение.
Исходная функция представляет собой отношение двух выражений sinx и 2x+1 . Применим правило дифференцирования дроби:
Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:
В заключении, давайте соберем все правила в одном примере.
Пример.
Найти производную функции , где a – положительное действительное число.
Решение.
А теперь по порядку.
Первое слагаемое .
Второе слагаемое
Третье слагаемое
Собираем все вместе:
4.Вопрос.Производные Основных элементарных функций.
Задание. Найти производную функции
Решение. Используем правила дифференцирования и таблицу производных:
Ответ.
5.Вопрос.Производная сложной функции примеры
Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x):
(f(φ(x)))′=f′u(φ(x0))⋅φ′(x0)
или, в более короткой записи: y′x=y′u⋅u′x.
В примерах этого раздела все функции имеют вид y=f(x) (т.е. рассматриваем лишь функции одной переменной x). Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.
В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.
Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.
Пример №1
Найти производную функции y=ecosx.
Решение
Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u:
y′=(ecosx)′=ecosx⋅(cosx)′(1.1)
Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом:
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2)
Так как x′=1, то продолжим равенство (1.2):
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3)
Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ.
Ответ : y′=−sinx⋅ecosx.
Пример №2
Найти производную функции y=9⋅arctg12(4⋅lnx).
Решение
Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т.е. число 9) можно вынести за знак производной:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.1)
Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12:
Дополняя равенство (2.1) полученным результатом, имеем:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2)
Примечание: показать\скрыть
Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx:
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′
Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x.
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′
Равенство (2.2) теперь станет таким:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.3)
Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно.
Ответ : y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Пример №3
Найти y′ функции y=sin3(5⋅9x)−−−−−−−−−√7.
Решение
Для начала немного преобразим функцию y, выразив радикал (корень) в виде степени: y=sin3(5⋅9x)−−−−−−−−−√7=(sin(5⋅9x))37. Теперь приступим к нахождению производной. Так как y=(sin(5⋅9x))37, то:
y′=((sin(5⋅9x))37)′(3.1)
Используем формулу №2 из таблицы производных, подставив в неё u=sin(5⋅9x) и α=37:
((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))37−1(sin(5⋅9x))′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′
Продолжим равенство (3.1), используя полученный результат:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′(3.2)
Теперь нужно найти (sin(5⋅9x))′. Используем для этого формулу №9 из таблицы производных, подставив в неё u=5⋅9x:
(sin(5⋅9x))′=cos(5⋅9x)⋅(5⋅9x)′
Дополнив равенство (3.2) полученным результатом, имеем:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′(3.3)
Осталось найти (5⋅9x)′. Для начала вынесем константу (число 5) за знак производной, т.е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9. Теперь можно продолжить равенство (3.3):
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′=37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅5⋅9x⋅ln9==15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x.
Можно вновь от степеней вернуться к радикалам (т.е. корням), записав (sin(5⋅9x))−47 в виде 1(sin(5⋅9x))47=1sin4(5⋅9x)−−−−−−−−−√7. Тогда производная будет записана в такой форме:
y′=15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Ответ : y′=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Пример №4
Показать, что формулы №3 и №4 таблицы производных есть частный случай формулы №2 этой таблицы.
Решение
В формуле №2 таблицы производных записана производная функции uα. Подставляя α=−1 в формулу №2, получим:
(u−1)′=−1⋅u−1−1⋅u′=−u−2⋅u′(4.1)
Так как u−1=1u и u−2=1u2, то равенство (4.1) можно переписать так: (1u)′=−1u2⋅u′. Это и есть формула №3 таблицы производных.
Вновь обратимся к формуле №2 таблицы производных. Подставим в неё α=12:
(u12)′=12⋅u12−1⋅u′=12u−12⋅u′(4.2)
Так как u12=u−−√ и u−12=1u12=1u−−√, то равенство (4.2) можно переписать в таком виде:
(u−−√)′=12⋅1u−−√⋅u′=12u−−√⋅u′
Полученное равенство (u−−√)′=12u−−√⋅u′ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения α.
Пример №5
Найти y′, если y=arcsin2x.
Решение
Нахождение производной сложной функции в данном примере запишем без подробных пояснений, которые были даны в предыдущих задачах.
Ответ : y′=2xln21−22x−−−−−−√.
Пример №6
Найти y′, если y=7⋅lnsin3x.
Решение
Как и в предыдущем примере, нахождение производной сложной функции укажем без подробностей. Желательно записать производную самостоятельно, лишь сверяясь с указанным ниже решением.
Ответ : y′=21⋅ctgx.
Пример №7
Найти y′, если y=9tg4(log5(2⋅cosx)).2}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=\frac\upsilon\nu. Все представленные переменные – это функции от х. Умножим их на \(\nu\). Получим \(y\times\nu=\upsilon\).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
\(\left(\upsilon\times\nu\right)’=\upsilon’\times\nu+\upsilon\times\nu’\)
Тогда выводим:
\(y’\times\nu+y\times\nu’=\upsilon’\)
Из этого вычисляем нужную нам производную:
\(y’\times\nu=\upsilon’-y\times\nu’=\upsilon’-\frac\upsilon\nu\times\nu’=\frac{\upsilon’v-\upsilon\nu’}\nu;\;y’=\frac{\upsilon’v-\upsilon\nu’}{\nu^2}\)
Что и требовалось доказать.3 + 1)
Там же вы можете получить подробное решение производной:
Применим правило производной частного:
и .
Чтобы найти :
В силу правила, применим: получим
Чтобы найти :
дифференцируем почленно:
Производная постоянной равна нулю.
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате:
Теперь применим правило производной деления:
Теперь упростим:
Ответ:
Общее правило
Производную от дроби очень просто посчитать (по-крайней мере от простых дробей)
Производная от дроби “единица, делённая на x” равна минус единице, делённой на x в квадрате.
Производная дроби примеры
Производная дроби примеры
Производная дроби примеры Область определения: Данная функция определена для: Решаем вспомогательное уравнение. Находим дискриминант. Дискриминант равен нулю, значит уравнение имеет один корень. Старший коэффициент положителен. Квадратичная функция принимает только неотрицательные значения. Следующее неравенство равносильно предыдущему. Ответ: Найдем первую производную Воспользуемся формулой производной частного. Вторая производная: Вторая производная это производная от первой производной. Воспользуемся формулой производной частного. Воспользуемся свойством степеней, а также воспользуемся правилом нахождения производной для сложной функции. Потом Выносим общий множитель. Воспользуемся свойством степеней. Изменим знаки выражений на противоположные. Точки пересечения с осью x: Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю. Дробь обращается в нуль тогда, когда числитель равен нулю. Находим дискриминант. Дискриминант равен нулю, значит уравнение имеет один корень. Воспользуемся формулой корней квадратного уравнения. Ответ: X=3 Точки пересечения с осью : Пусть x=0 Вертикальные асимптоты: Определим значения аргумента, при которых знаменатель функции обращается в ноль Находим дискриминант. Дискриминант равен нулю, значит уравнение имеет один корень. Воспользуемся формулой корней квадратного уравнения. Горизонтальные асимптоты: y=1 Наклонные асимптоты: нет. Для нахождения горизонтальных асимптот преобразуем исходное выражение. Предел данной функции на бесконечности равен числу 1 Критические точки: X=3 Для нахождения критических точек приравняем первую производную к нулю и решим полученное уравнение. Дробь обращается в нуль тогда, когда числитель равен нулю. Следующее уравнение равносильно предыдущему. Находим дискриминант. Дискриминант положителен, значит уравнение имеет два корня. Воспользуемся формулой корней квадратного уравнения. Корень 2 не входит в ОДЗ функции. Ответ: Таким образом, окончательный ответ X=3 Возможные точки перегиба: X=3.5 Для нахождения возможных точек перегиба приравняем вторую производную к нулю и решим полученное уравнение. Изменим знаки выражений на противоположные. Дробь обращается в нуль тогда, когда числитель равен нулю. Следующее уравнение равносильно предыдущему. Решаем уравнение методом разложения на множители. Разложим одночлены в сумму нескольких. Производим группировку. Выносим общий множитель. Выносим общий множитель. Теперь решение исходного уравнения разбивается на отдельные случаи. Случай 1 Перенесем известные величины в правую часть уравнения. Итак,ответ этого случая: . Случай 2 Находим дискриминант. Дискриминант положителен, значит, уравнение имеет два корня. Воспользуемся формулой корней квадратного уравнения. Итак,ответ 2 не входит в ОДЗ функции. Ответ: X=3.5 Точки разрыва: X=2 Симметрия относительно оси ординат: нет Функция f(x) называется четной, если f(-x)=f(x). Выносим знак минус из произведения. Приводим дроби к общему знаменателю. Производим сложение дробей с одинаковыми знаменателями. Приводим подобные члены. Выносим знак минус из произведения. Разложим числитель дроби на множители. Функция не может быть четной. Симметрия относительно начала координат: нет Функция f(x) называется нечетной, если f(-x)-f(x). Приводим дроби к общему знаменателю. Производим сложение дробей с одинаковыми знаменателями. Приводим подобные члены. Разложим числитель дроби на множители. Тестовые интервалы: Результаты исследования функции занесем в таблицу. Относительные экстремумы: Проходя через точку минимума, производная функции меняет знак с (-) на (+). Относительный минимум . Данные таблицы нанесем на координатную плоскость. Используя результаты исследования функции, построим ее график. Множество значений функции: Наименьшее значение: Наибольшее значение: нет
Производная частного двух функций (производная дроби).
⇐ ПредыдущаяСтр 5 из 89Следующая ⇒Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X.
По определению производной
Пример.
Выполнить дифференцирование функции .
Решение.
Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:
Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:
В заключении, давайте соберем все правила в одном примере.
Пример.
Найти производную функции , где a – положительное действительное число.
Решение.
А теперь по порядку.
Первое слагаемое .
Второе слагаемое
Третье слагаемое
Собираем все вместе:
4.Вопрос.Производные Основных элементарных функций.
Задание. Найти производную функции
Решение. Используем правила дифференцирования и таблицу производных:
Ответ.
5.Вопрос.Производная сложной функции примеры
Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x):
(f(φ(x)))′=f′u(φ(x0))⋅φ′(x0)
или, в более короткой записи: y′x=y′u⋅u′x.
В примерах этого раздела все функции имеют вид y=f(x) (т.е. рассматриваем лишь функции одной переменной x). Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.
В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.
Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.
Пример №1
Найти производную функции y=ecosx.
Решение
Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u:
Итак,
y′=(ecosx)′=ecosx⋅(cosx)′(1.1)
Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом:
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2)
Так как x′=1, то продолжим равенство (1.2):
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3)
Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ.
Ответ: y′=−sinx⋅ecosx.
Пример №2
Найти производную функции y=9⋅arctg12(4⋅lnx).
Решение
Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т.е. число 9) можно вынести за знак производной:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.1)
Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12:
Дополняя равенство (2.1) полученным результатом, имеем:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2)
Примечание: показать\скрыть
Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx:
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′
Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x.
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′
Равенство (2.2) теперь станет таким:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.3)
Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно.
Ответ: y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Пример №3
Найти y′ функции y=sin3(5⋅9x)−−−−−−−−−√7.
Решение
Для начала немного преобразим функцию y, выразив радикал (корень) в виде степени: y=sin3(5⋅9x)−−−−−−−−−√7=(sin(5⋅9x))37. Теперь приступим к нахождению производной. Так как y=(sin(5⋅9x))37, то:
y′=((sin(5⋅9x))37)′(3.1)
Используем формулу №2 из таблицы производных, подставив в неё u=sin(5⋅9x) и α=37:
((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))37−1(sin(5⋅9x))′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′
Продолжим равенство (3.1), используя полученный результат:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′(3.2)
Теперь нужно найти (sin(5⋅9x))′. Используем для этого формулу №9 из таблицы производных, подставив в неё u=5⋅9x:
(sin(5⋅9x))′=cos(5⋅9x)⋅(5⋅9x)′
Дополнив равенство (3.2) полученным результатом, имеем:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′(3.3)
Осталось найти (5⋅9x)′. Для начала вынесем константу (число 5) за знак производной, т.е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9. Теперь можно продолжить равенство (3.3):
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′=37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅5⋅9x⋅ln9==15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x.
Можно вновь от степеней вернуться к радикалам (т.е. корням), записав (sin(5⋅9x))−47 в виде 1(sin(5⋅9x))47=1sin4(5⋅9x)−−−−−−−−−√7. Тогда производная будет записана в такой форме:
y′=15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Ответ: y′=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Пример №4
Показать, что формулы №3 и №4 таблицы производных есть частный случай формулы №2 этой таблицы.
Решение
В формуле №2 таблицы производных записана производная функции uα. Подставляя α=−1 в формулу №2, получим:
(u−1)′=−1⋅u−1−1⋅u′=−u−2⋅u′(4.1)
Так как u−1=1u и u−2=1u2, то равенство (4.1) можно переписать так: (1u)′=−1u2⋅u′. Это и есть формула №3 таблицы производных.
Вновь обратимся к формуле №2 таблицы производных. Подставим в неё α=12:
(u12)′=12⋅u12−1⋅u′=12u−12⋅u′(4.2)
Так как u12=u−−√ и u−12=1u12=1u−−√, то равенство (4.2) можно переписать в таком виде:
(u−−√)′=12⋅1u−−√⋅u′=12u−−√⋅u′
Полученное равенство (u−−√)′=12u−−√⋅u′ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения α.
Пример №5
Найти y′, если y=arcsin2x.
Решение
Нахождение производной сложной функции в данном примере запишем без подробных пояснений, которые были даны в предыдущих задачах.
Ответ: y′=2xln21−22x−−−−−−√.
Пример №6
Найти y′, если y=7⋅lnsin3x.
Решение
Как и в предыдущем примере, нахождение производной сложной функции укажем без подробностей. Желательно записать производную самостоятельно, лишь сверяясь с указанным ниже решением.
Ответ: y′=21⋅ctgx.
Пример №7
Найти y′, если y=9tg4(log5(2⋅cosx)).
Решение
6 Вопрос. Производная обратной функции примеры.
Производная обратной функции
Формула
Известно свойство степеней, что
тогда
Используя производную степенной функции:
будем иметь:
Поиск по сайту:
Найдите производный инструмент, используя правило частного
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторинг триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Правило частного – DerivativeIt
В исчислении правило частного используется для нахождения производной функции, которая может быть выражена как отношение двух дифференцируемых функций.Другими словами, правило частного позволяет нам различать функции, представленные в виде дробей.
Скажем, у нас было две функции:
f (x) = x 2 и
g (x) = x
Теперь предположим, что мы хотели найти производную от
.Один из подходов к нахождению производной – это упростить функцию, а затем дифференцировать ее.
Таким образом, производная дроби f (x) / g (x) равна 1.
Теперь, ради интереса, давайте вычислим f ’(x) / g’ (x) (дифференцируя числитель, а затем знаменатель)
Итак, мы видим, что (f (x) / g (x)) ’= 1, и это не равно (f’ (x) / g ’(x)) = 2x
Производная частного не равна частному производных.
Чтобы дифференцировать частное, вы не можете просто взять производную числителя и разделить ее на производную знаменателя. Вместо этого нам нужно использовать правило частного , чтобы найти производную частного (аналогично тому, как правило продукта необходимо использовать для нахождения производной продукта).
Формула частного правила для дифференциации
Если две функции f (x) и g (x) дифференцируемы (т. Е. Существуют производные f (x) и g (x)), то их частное (f (x) / g (x)) дифференцируемо, и производная может быть найдена следующим образом:
Формула правила частного в словах
Правило частичного устанавливает, что производная частного равна знаменателю, умноженному на производную числителя, минус числитель, умноженный на производную знаменателя, и все делится на квадрат знаменателя.
Две уловки, чтобы запомнить правило частного
Подобно правилу произведения, вам нужно найти производную от f (x), затем умножить ее на g (x), а затем найти производную от g (x) и умножить ее на f (x). Однако, поскольку члены вычтены, порядок имеет значение, и есть также разделение, которое необходимо выполнить.
Это затрудняет запоминание правила частного по сравнению с правилом произведения.
Вот два метода, которые помогут вам запомнить правило частного:
1. Вы всегда начинаете с нижней функции (знаменатель) и заканчиваете квадратом нижней функции.
И если это не сработает…
2. Вот джингл, который можно использовать:
Lo d hi minus hi d low, по всей площади того, что внизу.
Здесь lo относится к знаменателю, hi относится к числителю, а d относится к «производной от». Это действительно глупо, но вот почему это работает!
Когда использовать правило частного
В исчислении правило частного может применяться, когда функция, которую вы хотите дифференцировать, состоит из частного (или дроби), а числитель и знаменатель частного являются самостоятельными дифференцируемыми функциями.
Например, функция f (x) = x / x 2 может быть дифференцирована с использованием правила частного для производных, потому что:
- Числитель (x) дифференцируемый – его производная 1
- Знаменатель (x 2 ) дифференцируема – его производная x
(Конечно, вы также можете сначала упростить функцию до 1 / x, а затем дифференцируйте его и получите тот же результат)
Примеры использования правила частичного
Лучший способ увидеть, как работает правило частного, – это посмотреть на несколько примеров.
Использование правила частного
В первом примере найдем производную от
. Назовем числитель f (x), поэтому f (x) = x 2 + 1
Назовем знаменатель g (x), так что g (x) = x 3
Это означает, что:
f ‘(x) = 2x
g’ (x) = 3x 2
Теперь мы можем применить правило частного, чтобы найти производную от f (x) / g (x). Формула для правила частного:
.Теперь мы можем подставить f (x), f ‘(x), g (x) и g’ (x) в формулу
А затем мы просто упрощаем использование факторизации и правил экспонент, чтобы найти окончательный ответ
Использование правила частного с триггерами
В качестве другого примера мы можем использовать правило частного, чтобы найти производную tan (x)
Прежде всего напомним, что tan (x) может быть выражено как sin (x), деленное на cos (x)
Назовем числитель f (x), поэтому f (x) = sin (x)
Назовем знаменатель g (x), так что g (x) = cos (x)
Это означает, что:
f ‘(x) = cos (x)
g’ (x) = -sin (x)
Теперь мы можем применить правило частного, чтобы найти производную от f (x) / g (x).Формула для правила частного:
.Теперь мы можем подставить f (x), f ‘(x), g (x) и g’ (x) в формулу:
Затем упростите запоминание триггерного тождества sin 2 (x) + cos 2 (x) = 1 и вспомните, что 1 / cos (x) равно sec (x).
Используя правило частного, производная tan (x) равна sec 2 (x)
Правило произведения и коэффициента
Доказательство частичного правила
Есть несколько способов доказать правило частного.Здесь мы рассмотрим доказательство правила частного с помощью:
- Первые принципы – определение производной и свойства пределов.
- Неявная дифференциация и правило произведения
- Правила продукта и цепочки
- Натуральные логарифмы и правило цепочки
Доказательство правила частного с использованием первых принципов
Пусть F (x) = f (x) / g (x)
Определение производной от F (x):
Затем мы помещаем F (x + h) и F (x) в
Это можно переписать, найдя в числителе наименьший общий знаменатель (g (x + h).g (x)) и снятие 1 / ч.
Следующий шаг необходим, чтобы немного позже облегчить жизнь. Что мы делаем, так это добавляем 0 в числитель, который вообще не меняет значение. Но вместо добавления прямого 0 мы добавляем его в виде -f (x) g (x) + f (x) g (x)
Теперь мы меняем местами два знаменателя – нам разрешено это делать, поскольку мы умножаем дроби.
Далее мы используем одно из свойств пределов, которое гласит, что предел произведения двух функций равен произведению их пределов.Затем мы также используем тот факт, что предел, когда h приближается к нулю для g (x + h), просто равен g (x)
Теперь мы разделим большую дробь на части и вычленим общий g (x) из первой части и общий -f (x) из второй части.
Еще одним свойством лимитов является то, что лимит суммы равен сумме лимитов. Таким образом, мы можем взять предел каждой дроби отдельно.
И тогда мы можем взять лимит каждой части продуктов
Теперь вы можете заметить, что два из приведенных выше пределов выглядят знакомыми – они являются точными определениями для f ‘(x) и g’ (x).
Наконец, предел, когда h приближается к 0 для g (x) и f (x), остается g (x) и f (x) (поскольку они не зависят от h). А дальше остается только переписать все в простейшем виде. И вот она – формула правила частного.Доказательство правила частного с использованием неявного дифференцирования и правила произведения
Пусть y = f (x) / g (x), тогда мы хотим найти y ’.
Сначала давайте изменим уравнение:
Теперь мы можем взять производную в левой и правой частях уравнения (используя правило произведения в правой части)
Затем подставьте y = f (x) / g (x) в приведенное выше уравнение
В конечном итоге мы хотим найти производную y (y ’), поэтому теперь мы решаем y’ и находим формулу для правила частного.
Доказательство правила частного с использованием правил продукта и цепочки
Пусть F (x) = f (x) / g (x).
Мы можем переписать это частное как произведение
Мы можем найти F ‘(x), используя правило произведения
Чтобы найти (g (x) -1 ) ’, мы можем применить цепное правило. Цепное правило гласит, что мы сначала берем производную от g (x) -1 через g (x) (= (-1) g (x) -2 ), а затем умножаем ее на производную от g ( x) через x (= g ‘(x)).
Затем мы приводим отрицательные показатели к знаменателю и затем упрощаем, находя наибольший общий знаменатель. У нас осталась формула правила частного.
Доказательство правила частного с использованием ln и цепного правила
Пусть y = f (x) / g (x)
Для начала возьмем натуральный логарифм (ln) с обеих сторон
Затем примените свойства журналов, чтобы разделить частное правой части на разницу бревен
Теперь возьмем производную с обеих сторон.Напомним, что производная ln (x) по x равна 1 / x. Аналогичным образом производная ln (y) по y равна 1 / y, производная ln (f (x)) по f (x) равна 1 / f (x), а производная ln (g (x)) относительно g (x) равно 1 / g (x).
Чтобы найти производные каждого члена по x, мы можем применить цепное правило, сначала дифференцируя по внутренней функции ln, а затем умножая это на производную внутренней функции.
Наконец, выделите y ’, подставьте y = f (x) / g (x) в, а затем упростите решение для y’
Правило частного по u и v
Что касается обозначений, правило частного иногда легче выразить, если вы используете u и v для обозначения числителя и знаменателя соответственно.Это может быть более компактным, чем использование обозначений функций f (x) и g (x).
Используя переменную u в числителе и v в качестве знаменателя, правило частного для нахождения производной функции u / v может быть выражено как:
Правило частного. Неявное дифференцирование
8
Правило частного
Доказательство правила частного
Неявное дифференцирование
Производная обратной функции
Правило частного
Следующее называется правилом частного:
“Производная частного двух функций равна
. знаменатель, умноженный на производную числителя
минус числитель, умноженный на производную знаменателя
, все делится на квадрат знаменателя.«
Например, если на момент принять, что производная sin x равна cos x (Урок 12):
| Задача 1. Вычислить производную от | x 2 sin x | . |
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| sin x · 2 x – x 2 cos x sin 2 x |
Проблема 2. Используйте цепное правило для вычисления производной
.| x 3 · 2 sin x cos x – sin 2 x · 3 x 2 x 6 | = | x 2 sin x (2 x cos x – 3 sin x ) x 6 |
| = | sin x (2 x cos x – 3 sin x ) x 4 | |
| Проблема 3.Вычислить производную от | x 2 -5 x -6 2 x + 1 | . |
| (2 x + 1) (2 x -5) – ( x 2 -5 x -6) · 2 (2 x + 1) 2 | = | 4 x 2 -8 x -5-2 x 2 + 10 x + 12 (2 x + 1) 2 |
| = | 2 x 2 + 2 x + 7 (2 x + 1) 2 | |
| Проблема 4.Вычислить производную от | 3 x 2 – x + 4 | . |
См. Пример, Урок 6 и Урок 22 по алгебре.
| = | ||
| = | ||
| = | ||
Доказательство правила частного
| ТЕОРЕМА. |
Доказательство. Так как г = г ( x ), то
| d dx | 1 г | = | d dg | 1 г | · | dg dx | = – | 1 г 2 | г ‘ |
согласно цепному правилу и задаче 4 урока 5.
Следовательно, согласно правилу продукта (Урок 6),
Это правило частного, которое мы хотели доказать.
Неявное дифференцирование
Рассмотрим следующее:
x 2 + y 2 = r 2
Это уравнение окружности с радиусом r . (Урок 17 Precalculus.)
Давайте посчитаем.
Для этого мы можем решить относительно y , а затем взять производную. Но вместо этого мы возьмем производную каждого члена. Что касается y 2 , мы считаем его неявно функцией x , и поэтому мы можем применить к нему цепное правило. Тогда будем решать за.
| d dx | x 2 | + | d dx | y 2 | = | d dx | r 2 |
| 2 x + 2 y | dy dx | = | 0 | |||
| dy dx | = | – | x y | . | ||
Это называется неявным дифференцированием. Мы рассматриваем y как функцию x и применяем цепное правило. Производная, которая получается в результате, обычно содержит и x , и y .
Задача 5. 15 л. + 5 л. 3 + 3 y 5 = 5 x 3 . Вычислите y ‘.
| 15 y ‘ + 15 y 2 y’ + 15 y 4 y ‘ | = | 15 x 2 |
| y ‘ (1 + y 2 + y 4 ) | = | x 2 |
| y ‘ | = | x 2 1 + y 2 + y 4 |
| Проблема 6. | Вычислить y ‘. |
Проблема 7.
а) В этом круге
x 2 + y 2 = 25,
а) какова координата y , когда x = −3?
y = 4 или −4. Для,
(−3) 2 + (± 4) 2 = 5 2
б) Каков наклон касательной к окружности в точке (−3, 4)?
c) Каков наклон касательной к окружности в точке (−3, −4)?
Проблема 8.В первом квадранте, каков наклон касательной к этой окружности,
( x – 1) 2 + ( y + 2) 2 = 169,
, когда x = 6?
[Подсказка: 5 2 + 12 2 = 13 2 – пифагорова тройка.]
В первом квадранте, когда x = 6, y = 10.
(6-1) 2 + (10 + 2) 2 = 13 2 .
| y ‘ = – | x – 1 y + 2 | . Следовательно, уклон – | 6 – 1 10 + 2 | = – | 5 12 |
Задача 9. Вычислите наклон касательной к этой кривой в точке (2, −1):
x 3 -3 x y 2 + y 3 = 1
| 3 x 2 – (3 x · 2 y y ‘ + y 2 · 3) + 3 y 2 y’ | = | 0 | ||
| в соответствии с правилом продукта. | ||||
| 3 x 2 -6 x y y ‘ – 3 y 2 + 3 y 2 y’ | = | 0 | ||
| x 2 -2 x y y ‘– y 2 + y 2 y’ | = | 0 | ||
| y ‘ ( y 2 -2 xy ) | = | y 2 – x 2 | ||
| г | = | y 2 – x 2 y 2 -2 xy | ||
| Следовательно, в (2, −1): | ||||
| г | = | (-1) 2 -2 2 (-1) 2 -2 · 2 · -1 | ||
| = | −3 5 | |||
| = | – | 3 5 | ||
Производная обратной функции
Когда у нас есть функция y = f ( x ) – например
y = x 2
– тогда мы часто можем решить для x .В данном случае
При обмене переменных получаем
| называется функцией, обратной y = x 2 . |
Напишем
| f ( x ) | = | x 2 |
| г ( x ) | = | |
И давайте назовем f прямой функцией и g обратной функцией .Формальная связь между f и g следующая:
f ( g ( x )) = g ( f ( x )) = x .
(Тема 19 Precalculus.)
Вот другие пары прямых и обратных функций:
| f ( x ) | = | грех x | г ( x ) | = | арксин x | |
| f ( x ) | = | a x | г ( x ) | = | журнал a x | |
| f ( x ) | = | x 3 | г ( x ) | = | ||
Теперь, когда мы знаем производную прямой функции f , то из нее мы можем определить производную g .
Таким образом, пусть g ( x ) будет инверсией f ( x ). Тогда
f ( g ( x )) = x .
Теперь возьмем производную по отношению к x :
Это означает следующее:
Теорема. Если g ( x ) является обратной величиной f ( x ), то
“Производная обратной функции равна
.величина, обратная производной прямой функции
, когда его аргумент – обратная функция.«
| Пример. Пусть f ( x ) = x 2 и | Тогда f ( g ) = g 2 . |
Следовательно,
Следующий урок: Мгновенная скорость и скорость изменения
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
World Web Math: дробные показатели
World Web Math: дробные показатели Предлагаемые пререквесты: Производные многочленов, Неявное дифференцирование, Цепное правилоМы знаем, что Правило мощности, расширение Правила продукта и Правило частного, выраженное как
действительно для любого целого показателя n .Какие о функциях с дробными показателями, таких как y = x 2/3 ? В этом случае, y может быть выражено как неявная функция x , y 3 = x 2 . Потом,
Это согласуется с Правилом мощности для n = 2/3.
Сделаем обобщение этого примера. Любой рациональное число n можно выразить как p / q для некоторых целых p и ненулевое q .Тогда для y = x n ,
Это именно то, что мы получили бы, если бы предположили то же правило власти справедливо для дробных показателей, как и для целых показателей. Примечание что нам не нужно было ничего предполагать о признаках p или q , кроме того, что q не может быть нулевым. Следовательно, теперь наше правило мощности можно безопасно применять к любые рациональные показатели.
Также можно использовать определение производной, но в качестве следующих двух примеры показывают, что прямое использование определения часто намного больше громоздко, чем улучшенное Правило Силы.
Рассмотрим довольно простой случай
Из определения производной
в соответствии с Правилом мощности для n = 1/2. Для n = –1/2 определение производной дает
и аналогичная алгебраическая манипуляция приводит к
опять же в соответствии с Правилом власти.
Чтобы увидеть, как можно обрабатывать более сложные дела, вспомните пример выше,
Из определения производной
еще раз в соответствии с Правилом власти.Этот пример должен ясно показывают, что для дробных показателей использование правила мощности гораздо удобнее, чем прибегать к определению производной.
Некоторые примеры:
Упражнения:
- Найдите производную по x каждого из
следующие функции.
-
-
-
Решения к упражнениям | Вернуться на страницу исчисления | Вернуться на главную страницу World Web Math
watko @ mit.edu Последнее изменение 16 февраля 2006 г.
математических образований. Насколько ошибочно считать $ \ frac {dy} {dx} $ дробью?
ОЧЕНЬ ошибочно рассматривать dy / dx как простую дробь, и я считаю, что это одна из основных ловушек системы обозначений Лейбница.
Что это такое: dy / dx – это дробь со встроенным условием !
Условие состоит в том, что dy – это изменение y (которое мы называем dy), ВЫЗВАННОЕ изменением x (dx). Dy зависит от от dx.Лучше думать о dy / dx как о функции, вместо этого вы должны подключить dx, получить промежуточный dy, а затем вернуть соотношение dy / dx.
Пример разрушения аналогии дроби:
a) Изобразите два базисных вектора, e1 и e2 , которые имеют одинаковую величину (но не обязательно единичную длину) и НЕ ортогональны (они наклонены друг к другу). Для наглядности представим, что угол между ними, тета, равен 60 градусам.
b) Поскольку векторы имеют одинаковую величину, мы можем сказать, что cos (theta) = cos ( e1 , e2 ) = dy / dx = dx / dy = 0,5 (cos (60))
… Верно! В этой ситуации (| e1 | = | e2 |): dy / dx = dx / dy, не обязательно равным 1. Если бы dy / dx было простой дробью, это было бы шоком.
Почему это правда: dy в числителе dy / dx – это , а не то же самое, что и в знаменателе dx / dy.Первое зависело от dx, но не второе.
в) В стороне, для общего случая, когда | e1 | ! = | e2 |,
cos (theta) = dSy / dSx = (| e2 | / | e1 |) * (dy / dx) = (| e1 | / | e2 |) * (dx / dy) = dSx / dSy
где dSx – длина дуги вдоль x, равная dx * | e1 | = dSx. Другими словами, dSx – это то, как длина в метрическом пространстве равна одному dx в том, что я называю «пространством компонентов» (при умножении на | e1 |).
, в то время как dSy в dSy / dSx – это то, насколько изменение Sy (метрическое или «длинное» скалярное поле, субтантированное осью y) мы получаем, когда делаем небольшое изменение в Sx (dSx) вдоль оси x.
Опять же, мы рискуем запутаться с нотацией Лейбница.
Пока мы можем вычислить dSx = dx * | e1 | и dSy = dy * | e2 | по отдельности их соотношение (dSy) / (dSx) не то же самое, что dSy / dSx = d / dSx (Sy). В dSy / dSx dSy зависит от dSx и, следовательно, от dx.
Как использовать правило частного для деривативов. Визуальное объяснение с цветными примерами
Краткий обзор
Примеры
Пример 1
Предположим, что $$ \ displaystyle f (x) = \ frac {2x + 3} {5x + 1} $$. Найдите $$ f ‘(x) $$.
Шаг 1Дифференцируйте, используя правило частного.2} $$.
Пример 3
Найдите $$ \ displaystyle \ frac d {dx} \ left (\ tan kx \ right) $$, где $$ k $$ – любая константа.
Шаг 1Выразите $$ \ tan kx $$ через синус и косинус.
$$ \ tan x = \ frac {\ sin kx} {\ cos kx} $$
Шаг 2Дифференцируйте с помощью правила частного.2 тыс. X $$
Продолжить практические задачиОшибка: Нажмите «Не робот», затем повторите попытку.
Правило частного – формула, доказательство, определение, примеры
Правило частных в исчислении – это метод нахождения производной или дифференцирования функции, заданной в форме отношения или деления двух дифференцируемых функций.Это означает, что мы можем применить правило частного, когда нам нужно найти производную функции вида: f (x) / g (x), такую, что и f (x), и g (x) дифференцируемы, а g (x) ≠ 0. Правило частного напрямую следует правилу произведения и концепции пределов дифференцирования. Давайте разберемся с формулой правила частного, ее доказательством с помощью решенных примеров подробно в следующих разделах.
Что такое правило частного?
Правило частных в исчислении – это метод, используемый для нахождения производной любой функции, заданной в форме частного, полученного в результате деления двух дифференцируемых функций.Правило частного в словах гласит, что производная частного равна отношению результата, полученного при вычитании числителя, умноженного на производную знаменателя от знаменателя, умноженную на производную числителя, к квадрату знаменателя. Это означает, что если нам дана функция вида: f (x) = u (x) / v (x), мы можем найти производную этой функции, используя производную правила частного как,
f ‘(x) = [u (x) / v (x)]’ = [v (x) × u '(x) – u (x) × v’ (x)] / [v (x)] 2
Формула правила частных
Мы можем вычислить производную или оценить дифференцирование частного двух функций, используя формулу производной правила частного.Формула производной правила частного имеет вид,
f ‘(x) = [u (x) / v (x)]’ = [v (x) × u '(x) – u (x) × v’ (x)] / [v (x)] 2
где,
- f (x) = Функция вида u (x) / v (x), для которой необходимо вычислить производную.
- u (x) = дифференцируемая функция, составляющая числитель функции f (x).
- u ‘(x) = Производная функции u (x).
- v (x) = дифференцируемая функция, которая составляет знаменатель данной функции f (x).
- v ‘(x) = производная функции v (x).
Выведение формулы правила частных
В предыдущем разделе мы узнали о формуле частного для нахождения производных частного двух дифференцируемых функций. Давайте посмотрим здесь на доказательство формулы правила частного. Существуют различные методы доказательства формулы правила частного, заданной как
.- Использование производных и предельных свойств
- Использование неявного дифференцирования
- Использование правила цепочки
Доказательство формулы правила частного с использованием производных и предельных свойств
Чтобы доказать формулу правила частного с использованием определения производной или пределов, пусть функция f (x) = u (x) / v (x).
⇒ f ‘(x) = \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) [f (x + h) – f (x)] / h
= \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) \ (\ frac {\ frac {u (x + h)} {v (x + h)} – \ frac {u (x )} {v (x)}} {h} \)
= \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) \ (\ frac {u (x + h) v (x) – u (x) v (x + h)} {h \ cdot v (x) \ cdot v (x + h)} \)
= \ (\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) – u (x) v (x + h)} {h} \ вправо) \ влево (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {1} {v (x) \ cdot v (x + h)} \ right) \)
= \ (\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) – u (x) v (x) + u (x) v ( x) – u (x) v (x + h)} {h} \ right) \) [1 / v (x) 2 ]
= \ (\ left [\! \ Left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) – u (x) v (x)} { h} \ right) \! \! \! – \! \! \ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x) v (x + h) – u (x ) v (x)} {h} \ right) \! \ right] \) [1 / v (x) 2 ]
= \ (\ Left [\! V (x) \! \ Left (\! \ Mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) – u (x)} {h } \ right) \! \! \! – \! \! u (x) \! \! \ left (\ mathop {\ lim} \ limits_ {h \ to 0} \! \! \ frac {v (x + h) – v (x)} {h} \ right) \! \! \ right] \) [1 / v (x) 2 ]
= \ (\ frac {v (x) u ‘(x) – u (x) v’ (x)} {[v (x)] ^ 2} \)
Доказательство формулы правила частного с использованием неявной дифференциации
Чтобы доказать формулу правила частного с использованием формулы неявного дифференцирования, возьмем дифференцируемую функцию f (x) = u (x) / v (x), так что u (x) = f (x) ⋅v (x).2} \)
Как применить правило частного при дифференциации?
Чтобы найти производную функции вида f (x) = u (x) / v (x), как u (x), так и v (x) должны быть дифференцируемыми функциями. Мы можем применить следующие шаги, чтобы найти вывод дифференцируемой функции f (x) = u (x) / v (x), используя правило частного.
- Шаг 1: Запишите значения u (x) и v (x).
- Шаг 2: Найдите значения u ‘(x) и v’ (x) и примените формулу правила частного, заданную как: f ‘(x) = [u (x) / v (x)]’ = [u ‘(x) × v (x) – u (x) × v’ (x)] / [v (x)] 2
Давайте посмотрим на следующий пример, приведенный ниже, чтобы лучше понять правило частного.
Пример: Найдите f ‘(x) для следующей функции f (x), используя правило частного: f (x) = x 2 / (x + 1).
Решение:
Здесь f (x) = x 2 / (x + 1)
и (х) = х 2
v (х) = (х + 1)
⇒u ‘(x) = 2x
⇒v ‘(х) = 1
⇒f ‘(x) = [v (x) u’ (x) – u (x) v ‘(x)] / [v (x)] 2
⇒f ‘(x) = [(x + 1) • 2x – x 2 • 1] / (x + 1) 2
⇒f ‘(x) = (2x 2 + 2x – x 2 ) / (x + 1) 2
⇒f ‘(x) = (x 2 + 2x) / (x + 1) 2
Ответ: Производная от x 2 / (x + 1) равна (x 2 + 2x) / (x + 1) 2 .
☛ Темы, связанные с правилом частного:
Часто задаваемые вопросы о правиле доли
Что такое частное правило дифференциации в исчислении?
Правило частного – это одно из правил производных, которое мы используем для нахождения производной функций вида P (x) = f (x) / g (x). Производная функции P (x) обозначается P ‘(x). Если производная функции P (x) существует, мы говорим, что P (x) дифференцируема. Итак, дифференцируемые функции – это те функции, у которых существуют производные.Функция P (x) дифференцируема в точке x = a, если существует следующий предел.
\ (P ‘(x) = \ mathop {\ lim} \ limits_ {h \ to 0} \ frac {P (a + h) -P (a)} {h} \)
Как найти производный финансовый инструмент с помощью правила частного?
Производные частного отношения двух дифференцируемых функций могут быть вычислены в исчислении с использованием правила частного. Нам нужно применить формулу правила частного для дифференцирования функции f (x) = u (x) / v (x). Формула правила частного имеет вид
.
f ‘(x) = [u (x) / v (x)]’ = [u ‘(x) × v (x) – u (x) × v’ (x)] / [v (x)] 2
где f ‘(x), u’ (x) и v ‘(x) – производные функций f (x), v (x) и u (x).
Что такое формула правила частного?
Формула производной правила частных – это правило дифференциального исчисления, которое мы используем для нахождения производной рациональных функций. Предположим, что две функции u (x) и v (x) дифференцируемы, тогда можно применить правило частного, чтобы найти (d / dx) [u (x) / v (x)] as,
f ‘(x) = [u (x) / v (x)]’ = [u ‘(x) × v (x) – u (x) × v’ (x)] / [v (x)] 2
Как вывести формулу для правила частных?
Формулу правила частных можно получить с помощью различных методов.2} \)
Как вывести правило частного, используя определение лимитов и производных финансовых инструментов?
Доказательство правила частного может быть дано с использованием определения и свойств пределов и производных. Для функции f (x) = u (x) / v (x) производная f ‘(x) может быть задана как,
⇒ f ‘(x) = \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) [f (x + h) – f (x)] / h
= \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) \ (\ frac {\ frac {u (x + h)} {v (x + h)} – \ frac {u (x) } {v (x)}} {h} \)
= \ (\ mathop {\ lim} \ limits_ {h \ to 0} \) \ (\ frac {u (x + h) v (x) \) – \ (u (x) v (x + h)} {h \ cdot v (x) \ cdot v (x + h)} \)
= \ (\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) \) – \ (u (x) v (x + h)} { h} \ right) \ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {1} {v (x) \ cdot v (x + h)} \ right) \)
= \ (\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) – u (x) v (x) + u (x) v (x) ) – u (x) v (x + h)} {h} \ right) \) [1 / v (x) 2 ]
= \ (\ left [\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) v (x) – u (x) v (x)} {h} \ справа) \) – \ (\ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x) v (x + h) – u (x) v (x)} {h}) \ right) \ right] \) [1 / v (x) 2 ]
= \ (\ left [v (x) \ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {u (x + h) – u (x)} {h} \ right) \) – \ (u (x) \ left (\ mathop {\ lim} \ limits_ {h \ to 0} \ frac {v (x + h) – v (x)} {h} \ right) \ right] \) [1 / v (x) 2 ]
Каковы приложения формулы производной по правилу частного? Приведите примеры.
Мы можем применить правило частного, чтобы найти дифференцирование функции вида u (x) / v (x). Например, для функции f (x) = sin x / x мы можем найти производную как, f ‘(x) = [x \ (\ frac {d} {dx} \) sin x – sin x \ ( \ frac {d} {dx} \) x] / x 2 , f ‘(x) = (x • cos x – sin x) / x 2 .
Как мы можем доказать правило частного с помощью неявной дифференциации?
Мы можем использовать метод неявного дифференцирования для вывода правила частного для дифференцируемой функции f (x) = u (x) / v (x), поэтому u (x) = f (x) ⋅v (x).2} \).
.