Производная функции в степени функции – Производная степенно-показательной функции, формулы и примеры

Производная степенной функции (степени и корни)

Производная от x в степени a равна a, умноженному на x в степени a минус один:
(1)   .

Производная от корня степени n из x в степени m равна:
(2)   .

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a:
(3)   .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Теперь находим производную, применяя правило дифференцирования сложной функции:
;
.
Здесь .

Формула (1) доказана.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4)   .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

По формуле (1) находим производную:
(1)   ;
;
(2)   .

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0. Найдем производную функции (3) при x = 0. Для этого воспользуемся определением производной:
.

Подставим x = 0:
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1)   .
Поэтому формула (1) справедлива и при x = 0.

Случай x < 0

Снова рассмотрим функцию (3):
(3)   .
При некоторых значениях постоянной a, она определена и при отрицательных значениях переменной x. А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.

Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x. Например, при n = 3 и m = 1 мы имеем кубический корень из x:
.
Он определен и при отрицательных значениях переменной x.

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a, для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1)   .

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3)   .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

.

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом, , то n-я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Примеры вычисления производных

Пример

Найдите производную функции:
.

Решение

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Применяем правило дифференцирования суммы и выносим постоянные за знак производной:

.

Применяем правило дифференцирования сложной функции:

.
Здесь .

Преобразуем степени в корни:
;
;
;
;
;
.

Ответ

Еще примеры

Найти производные следующих функций, зависящих от переменной x:
    Решение > > >           Решение > > >           Решение > > >           Решение > > >           Решение > > >      

Найти производную шестого порядка следующей функции:
.
Решение > > >

Все примеры > > >

Автор: Олег Одинцов.     Опубликовано: 09-04-2017

1cov-edu.ru

Производная степенно-показательной функции

Определение

Степенно-показательной функцией (или показательно-степенной, илифункцией в степени функция) называется функция вида 

Рассмотрим способы нахождения ее производной.

1-ый способ

Применяя формулу:

То есть вначале производная берется как от степенной функции, а потом как от показательной.

Замечание

Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:

2-ой способ

С помощью логарифмического дифференцирования:

3-ий способ

Представим функцию в следующем виде (используютсясвойства логарифмов):

Тогда

7. Дифференцирование неявной функции одной и двух переменных.

Если независимая переменная и функциясвязаны уравнением вида, которое не разрешено относительно, то функцияназываетсянеявной функцией переменной .

Всякую явно заданную функцию можно записать в неявном виде. Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно, оказывается возможным найти производную отпо. В этом случае необходимопродифференцировать обе части заданного уравнения, рассматривая функцию как функцию от, а затем из полученного уравнения найти производную.

7. Полное приращение и полный дифференциал функции двух переменных. Необходимое условие дифференцируемости.

7. Экстремум функции 2-х переменных. Необходимое условие. Достаточное условие.

8. Градиент скалярного поля. Свойства. Уравнение касательной плоскости и нормали к поверхности.

9. Производная по направлению и ее физический смысл. Формула для вычисления.

studfiles.net

63. Логарифмическое дифференцирование. Производная степенно-показательной функции.

Функция вида y = [u(x)]^v(x) называется степенно – показательной. Для вычисления ее производной (при условии, что у’ существует), нужно прологарифмировать функцию по любому основанию (обычно по основанию е). Затем нужно вычислить производную полученной неявной функции.

Пример. Найти производную функции y = (sinx)^x

Логарифмируем функцию по основанию е:lny = x lnsinx. Дифференцируем обе части равенства по х, получаем

,

отсюда или.

Рассмотренный прием называется логарифмическим дифференцированием. Он применяется не только для вычисления производных степенно-показательных функций, но и в случаях, когда аналитическое выражение функции содержит несколько множителей.

Пример. Найти производную функции . Логарифмируя, получаем. Дифференцируем обе части полученного равенства:

, отсюда или.

Если требуется найти производную функции, представляющей собой произведение нескольких сомножителей, или дробь, числитель и знаменатель которой содержат по несколько сомножителей, то представляется выгодным предварительно обе части данной функции прологарифмировать по основанию, а затем уже приступить к дифференцированию. Напомним основные правила логарифмирования:

1. . 2. .

3. . 4. , где n = const.

О п р е д е л е н и е. Логарифмической производной функции y = f (x) называется производная от логарифма этой функции

.

Пример 1. .

Решение. Прологарифмируем функцию

;

;

. Найдем :

.

Пример 2. .

Решение. Прологарифмируем функцию

;

;

;

.

5.4. Производная степенно-показательной функции

Будем называть функцию вида степенно-показательной. Производная от этой функции в общем виде имеет вид

,

т.е. производная степенно-показательной функции равна сумме производных этой функции как от степенной, а затем как от показательной.

Однако для нахождения производных степенно-показательной функции можно применить прием логарифмического дифференцирования, который позволяет легко и быстро найти производную.

Пусть . Прологарифмируем обе части:

.

Найдем производную обеих частей этого равенства:

.

Тогда

.              (5.11)

Пример 1. y = x^x, ( x > 0 ).

Решение. Прологарифмируем ln y = x ln x. Тогда

.

Пример 2. .

Решение:  ln y = cos x ln sin x;

;

.

Пример 3. .

Решение: ;

;

.

64. См. Отдельный файл.

65. Теоремы о среднем – Ферма, Ролля.

Теорема 17.1 (Теорема Ферма)

Если функция имеет производную и в точкеимеет экстремум, то значение производной в этой точке равно 0.

Доказательство

Пусть – точка минимума. Тогда при. Значение выражения. Значит,. Рассмотрим теперь, при этом также, и выражение. Значит, правая производная. По теореме

14.5 . Из ранее доказанного следует:. Теорема доказана.

 

2. Равность нулю производной – необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример: , но точка 0 – не экстремум.

 

Теорема 17.2 (Теорема Ролля)

Пусть:

1. Функция непрерывна на отрезке:;

2. Для любого x из интервала существует производная:;

3. Значения функции на концах отрезка равны: .

Тогда существует такое , что производная.

Доказательство

1. Функция непрерывна существуют.

2. Если , то функцияявляется константой, и ее производная в любой точке равна 0, т.е. теорема доказана.

3. Если же , то оба значенияне могут достигаться в концевых точках, т.к.и. Тогда хотя бы одно из них достигается во внутренней точкеc, и, по теореме Ферма 17.1 

Замечания:

1. Существует хотя бы одна точка, в которой касательная к графику функции параллельна оси Ox (см. рисунок к теореме Ферма).

2. Все условия теоремы Ролля существенны, т.е. нельзя отбростиь хотя бы одно из них.

Примеры:

1. Отбросим условие непрерывности. Рассмотрим функцию на отрезке. На интервалепроизводная всюду равна 1.

2. Отбросим условие дифференцируемости. Рассмотрим функцию . В точке, но 0 – точка минимума.

3. Отбросим условие равности функции на концах отрезка. Рассмотрим функцию на отрезке. При этом производная всюду на интервалеравна 1 .

 

Теорема 17.3 (Первое следствие теоремы Ролля)

Пусть:

1. Функция непрерывна на отрезке:;

2. Функция дифференцируема на интервале :;

3. Сужествуют такие, что.

Тогда такие, что

.

Доказательство

Рассмотрим отрезок . Данный отрезок удовлетворяет всем требованиям теоремы Ролля. Тогда.

Применив теорему Ролля k раз, доказываем данное следствие.

 

Теорема 17.4 (Второе следствие теоремы Ролля)

Пусть:

1. Существует функция, имеющая n производных, непрерывных на отрезке :;

2. Для любого x из интервала существует n+1 производная:;

3. Значения .

Тогда существует такая точка .

Доказательство

1. По теореме Ролля для на отрезке.

2. Рассмотрим отрезок , на которомнепрерывна. Тогда существует производнаяна интервале. Так как. Значит, существует точкатакая, что. Рассмотрим отрезок, на которомнепрерывна. Значит,. На

   n-ном шаге имеем: . Рассмотримна.

3. Функция непрерывна на , значит, она непрерывна и на:;

4. Для любого x из существуетn+1 производная: ;

5. Значения ее на концах равны: .

Данные 3 заключения удовлетворяют условию теоремы Ролля. Значит, .

studfiles.net

Производная степенной функции

3 февраля 2015

Этим видео я начинаю длинную серию уроков, посвященную производным. Этот урок состоит из нескольких частей.

В первую очередь, я расскажу вам, что вообще такое производные и как их считать, но не мудреным академическим языком, а так, как я сам это понимаю и как объясняю своим ученикам. Во-вторых, мы рассмотрим простейшее правило для решения задач, в которых будем искать производные суммы, производные разности и производные степенной функции.

Мы рассмотрим более сложные комбинированные примеры, из которых вы, в частности, узнаете, что подобные задачи, содержащие корни и даже дроби, могут быть решены при использовании формулы производной степенной функции. Кроме того, конечно, будет множество задач и примеров решений самого разного уровня сложности.

Вообще, изначально я собирался записать коротенький 5-минутный ролик, но сами видите, что из этого получилось. Поэтому хватит лирики — приступаем к делу.

Что такое производная?

Итак, начнем издалека. Много лет назад, когда деревья были зеленее, а жизнь была веселее, математики задумались вот над чем: рассмотрим простую функцию, заданную своим графиком, назовем ее $y=f\left( x \right)$. Разумеется, график существует не сам по себе, поэтому нужно провести оси $x$, а также ось $y$. А теперь давайте выберем любую точку на этом графике, абсолютно любую. Абсциссу назовем ${{x}_{1}}$, ордината, как не трудно догадаться, будет $f\left( {{x}_{1}} \right)$.

Рассмотрим на том же графике еще одну точку. Не важно, какую, главное, чтобы она отличалась от первоначальной. У нее, опять же, есть абсцисса, назовем ее ${{x}_{2}}$, а также ордината — $f\left( {{x}_{2}} \right)$.

Итак, мы получили две точки: у них разные абсциссы и, следовательно, разные значения функции, хотя последнее — необязательно. А вот что действительно важно, так это что, что из курса планиметрии нам известно: через две точки можно провести прямую и, причем, только одну. Вот давайте ее и проведем.

А теперь проведем через самую первую из них прямую, параллельную оси абсцисс. Получим прямоугольный треугольник. Давайте его обозначим $ABC$, прямой угол $C$. У этого треугольника возникает одно очень интересное свойство: дело в том, что угол$\alpha $, на самом деле, равен углу, под которым пересекается прямая $AB$ с продолжением оси абсцисс. Судите сами:

1. прямая $AC$параллельна оси $Ox$ по построению,
2. прямая $AB$ пересекает $AC$ под $\alpha $,
3. следовательно, $AB$ пересекает $Ox$под тем же самым $\alpha $.

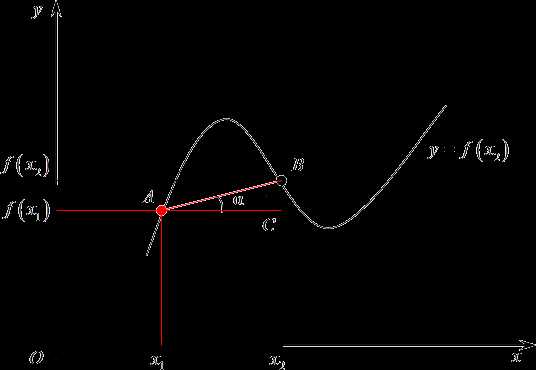
Что мы можем сказать об $\text{ }\!\!\alpha\!\!\text{ }$? Ничего конкретного, разве что в треугольнике $ABC$отношение катета $BC$ к катету $AC$ равно тангенсу этого самого угла. Так и запишем:

\[tg=\frac{BC}{AC}\]

Разумеется, $AC$ в данном случае легко считается:

\[AC={{x}_{2}}-{{x}_{1}}\]

Точно также и $BC$:

\[BC=f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)\]

Другими словами, мы можем записать следующее:

\[\operatorname{tg}\text{ }\!\!\alpha\!\!\text{ }=\frac{f\left( {{x}_{2}} \right)-f\left( {{x}_{1}} \right)}{{{x}_{2}}-{{x}_{1}}}\]

Теперь, когда мы все это выяснили, давайте вернемся к нашему графику и рассмотрим новую точку $B$. Сотрем старые значения и возьмем и возьмем $B$ где-нибудь поближе к ${{x}_{1}}$. Вновь обозначим ее абсциссу за ${{x}_{2}}$, а ординату — $f\left( {{x}_{2}} \right)$.

Вновь рассмотрим наш маленький треугольник $ABC$и $\text{ }\!\!\alpha\!\!\text{ }$ внутри него. Совершенно очевидно, что это будет уже совсем другой угол, тангенс будет также другим потому, что длины отрезков $AC$ и $BC$ существенно изменились, а формула для тангенса угла нисколько не поменялась — это по-прежнему соотношение между изменением функции и изменением аргумента.

Наконец, продолжаем двигать $B$ все ближе к изначальной точке $A$, в результате треугольник еще уменьшится, а прямая, содержащая отрезок $AB$, все больше будет походить на касательную к графику функции.

 

В итоге, если продолжать сближение точек, т. е., уменьшать расстояние до нуля, то прямая $AB$, действительно, превратится в касательную к графику в данной точке, а $\text{ }\!\!\alpha\!\!\text{ }$превратится из обычного элемента треугольника в угол между касательной к графику и положительным направлением оси $Ox$.

И вот тут мы плавно переходим к определению$f$, а именно, производной функции в точке ${{x}_{1}}$ называется тангенс угла $\alpha $ между касательной к графику в точке ${{x}_{1}}$ и положительным направлением оси $Ox$:

\[{f}’\left( {{x}_{1}} \right)=\operatorname{tg}\text{ }\!\!\alpha\!\!\text{ }\]

Возвращаясь к нашему графику, следует отметить, что в качестве ${{x}_{1}}$ можно выбрать любую точку на графике. Например, с тем же успехом мы могли снять штрих в точке, показанной на рисунке. 

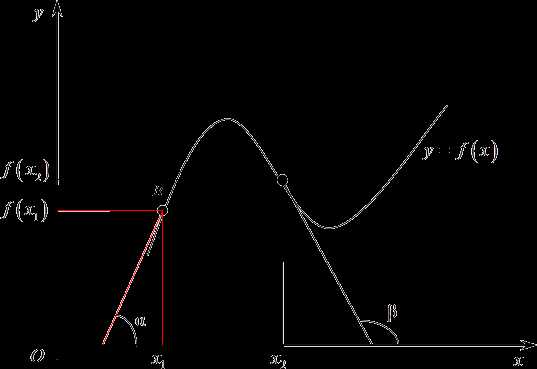
Угол между касательной и положительным направлением оси назовем $\beta $. Соответственно, $f$ в ${{x}_{2}}$ будет равна тангенсу этого угла $\beta $.

\[{f}’\left( {{x}_{2}} \right)=tg\text{ }\!\!\beta\!\!\text{ }\]

В каждой точке графика будет своя касательная, а, следовательно, свое значение функции. В каждом из этих случаев помимо точки, в которой мы ищем производную разности или суммы, или производную степенной функции, необходимо взять другую точку, находящуюся на некотором расстоянии от нее, а затем устремить эту точку к исходной и, разумеется, выяснить, как в процессе такого движения будет меняться тангенс угла наклона.

Производная степенной функции

К сожалению, подобное определение нас совершено не устраивает. Все эти формулы, картинки, углы не дают нам ни малейшего представления о том, как считать реальную производную в реальных задачах. Поэтому давайте немного отвлечемся от формального определения и рассмотрим более действенные формулы и приемы, с помощью которых уже можно решать настоящие задачи.

Начнем с самых простых конструкций, а именно, функций вида $y={{x}^{n}}$, т.е. степенных функций. В этом случае мы можем записать следующее: ${y}’=n\cdot {{x}^{n-1}}$. Другими словами, степень, которая стояла в показателе, показывается в множителе спереди, а сам показатель уменьшается на единицу. Например:

\[\begin{align}& y={{x}^{2}} \\& {y}’=2\cdot {{x}^{2-1}}=2x \\\end{align}\]

А вот другой вариант:

\[\begin{align}& y={{x}^{1}} \\& {y}’={{\left( x \right)}^{\prime }}=1\cdot {{x}^{0}}=1\cdot 1=1 \\& {{\left( x \right)}^{\prime }}=1 \\\end{align}\]

Пользуясь этими простыми правилами, давайте попробуем снять штрих следующих примеров:

\[f\left( x \right)={{x}^{6}}\]

Итак, мы получаем:

\[{{\left( {{x}^{6}} \right)}^{\prime }}=6\cdot {{x}^{5}}=6{{x}^{5}}\]

Теперь решим второе выражение:

\[\begin{align}& f\left( x \right)={{x}^{100}} \\& {{\left( {{x}^{100}} \right)}^{\prime }}=100\cdot {{x}^{99}}=100{{x}^{99}} \\\end{align}\]

Разумеется, это были очень простые задачи. Однако реальные задачи более сложные и они не ограничиваются одними лишь степенями функции.

Итак, правило № 1 – если функция представлена в виде других двух, то производная этой суммы равна сумме производных:

\[{{\left( f+g \right)}^{\prime }}={f}’+{g}’\]

Аналогично, производная разности двух функций равна разности производных:

\[{{\left( f-g \right)}^{\prime }}={f}’-{g}’\]

Пример:

\[{{\left( {{x}^{2}}+x \right)}^{\prime }}={{\left( {{x}^{2}} \right)}^{\prime }}+{{\left( x \right)}^{\prime }}=2x+1\]

Кроме того, есть еще одно важное правило: если перед некоторой $f$ стоит константа $c$, на которую эта функция умножается, то $f$ всей этой конструкции считается так:

\[{{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’\]

Пример:

\[{{\left( 3{{x}^{3}} \right)}^{\prime }}=3{{\left( {{x}^{3}} \right)}^{\prime }}=3\cdot 3{{x}^{2}}=9{{x}^{2}}\]

Наконец, еще одно очень важное правило: в задачах часто встречается отдельное слагаемое, которое вообще не содержит $x$. Например, мы можем наблюдать это в наших сегодняшних выражениях. Производная константы, т. е., числа, никак не зависящего от $x$, всегда равна нулю, причем совершенно неважно, чему равна константа $c$:

\[{{\left( c \right)}^{\prime }}=0\]

Пример решения:

\[{{\left( 1001 \right)}^{\prime }}={{\left( \frac{1}{1000} \right)}^{\prime }}=0\]

Еще раз ключевые моменты:

1. Производная суммы двух функций всегда равна сумме производных: ${{\left( f+g \right)}^{\prime }}={f}’+{g}’$;
2. По аналогичным причинам производная разности двух функций равна разности двух производных: ${{\left( f-g \right)}^{\prime }}={f}’-{g}’$;
3. Если у функции присутствует множитель константа, то эту константу можно выносить за знак производной: ${{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’$;
4. Если вся функция представляет собой константу, то ее производная всегда ноль: ${{\left( c \right)}^{\prime }}=0$.

Давайте посмотрим, как все это работает на реальных примерах. Итак:

\[y={{x}^{5}}-3{{x}^{2}}+7\]

Записываем:

\[\begin{align}& {{\left( {{x}^{5}}-3{{x}^{2}}+7 \right)}^{\prime }}={{\left( {{x}^{5}} \right)}^{\prime }}-{{\left( 3{{x}^{2}} \right)}^{\prime }}+{7}’= \\& =5{{x}^{4}}-3{{\left( {{x}^{2}} \right)}^{\prime }}+0=5{{x}^{4}}-6x \\\end{align}\]

В этом примере мы видим и производную суммы, и производную разности. Итого, производная равна $5{{x}^{4}}-6x$.

Переходим ко второй функции:

\[f\left( x \right)=3{{x}^{2}}-2x+2\]

Записываем решение:

\[\begin{align}& {{\left( 3{{x}^{2}}-2x+2 \right)}^{\prime }}={{\left( 3{{x}^{2}} \right)}^{\prime }}-{{\left( 2x \right)}^{\prime }}+{2}’= \\& =3{{\left( {{x}^{2}} \right)}^{\prime }}-2{x}’+0=3\cdot 2x-2\cdot 1=6x-2 \\\end{align}\]

Вот мы и нашли ответ.

Переходим к третьей функции — она уже посерьезней:

\[y=2{{x}^{3}}-3{{x}^{2}}+\frac{1}{2}x-5\]

Решаем:

\[\begin{align}& {{\left( 2{{x}^{3}}-3{{x}^{2}}+\frac{1}{2}x-5 \right)}^{\prime }}={{\left( 2{{x}^{3}} \right)}^{\prime }}-{{\left( 3{{x}^{2}} \right)}^{\prime }}+{{\left( \frac{1}{2}x \right)}^{\prime }}-{5}’= \\& =2{{\left( {{x}^{3}} \right)}^{\prime }}-3{{\left( {{x}^{2}} \right)}^{\prime }}+\frac{1}{2}\cdot {x}’=2\cdot 3{{x}^{2}}-3\cdot 2x+\frac{1}{2}\cdot 1=6{{x}^{2}}-6x+\frac{1}{2} \\\end{align}\]

Ответ мы нашли.

Переходим к последнему выражению — самому сложному и самому длинному:

\[y=6{{x}^{7}}-14{{x}^{3}}+4x+5,{{x}_{0}}=-1\]

Итак, считаем:

\[\begin{align}& {{\left( 6{{x}^{7}}-14{{x}^{3}}+4x+5 \right)}^{\prime }}={{\left( 6{{x}^{7}} \right)}^{\prime }}-{{\left( 14{{x}^{3}} \right)}^{\prime }}+{{\left( 4x \right)}^{\prime }}+{5}’= \\& =6\cdot 7\cdot {{x}^{6}}-14\cdot 3{{x}^{2}}+4\cdot 1+0=42{{x}^{6}}-42{{x}^{2}}+4 \\\end{align}\]

Но на этом решение не заканчивается, потому что нас просят не просто снять штрих, а посчитать ее значение в конкретной точке, поэтому подставляем в выражение −1 вместо $x$:

\[{y}’\left( -1 \right)=42\cdot 1-42\cdot 1+4=4\]

Идем далее и переходим к еще более сложным и интересным примерам. Дело в том, что формула решения степенной производной ${{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}$ имеет еще более широкую область применения, чем обычно принято считать. С ее помощью можно решать примеры с дробями, корнями и т. д. Именно этим мы сейчас и займемся.

Для начала еще раз запишем формулу, которая поможет нам найти производную степенной функции:

\[{{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}\]

А теперь внимание: до сих пор мы рассматривали в качестве $n$ лишь натуральные числа, однако ничего не мешаем рассмотреть дроби и даже отрицательные числа. Например, мы можем записать следующее:

\[\begin{align}& \sqrt{x}={{x}^{\frac{1}{2}}} \\& {{\left( \sqrt{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{2}}} \right)}^{\prime }}=\frac{1}{2}\cdot {{x}^{-\frac{1}{2}}}=\frac{1}{2}\cdot \frac{1}{\sqrt{x}}=\frac{1}{2\sqrt{x}} \\\end{align}\]

Ничего сложного, поэтому посмотрим, как эта формула поможет нам при решении более сложных задач. Итак, пример:

\[y=\sqrt{x}+\sqrt[3]{x}+\sqrt[4]{x}\]

Записываем решение:

\[\begin{align}& \left( \sqrt{x}+\sqrt[3]{x}+\sqrt[4]{x} \right)={{\left( \sqrt{x} \right)}^{\prime }}+{{\left( \sqrt[3]{x} \right)}^{\prime }}+{{\left( \sqrt[4]{x} \right)}^{\prime }} \\& {{\left( \sqrt{x} \right)}^{\prime }}=\frac{1}{2\sqrt{x}} \\& {{\left( \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{3}}} \right)}^{\prime }}=\frac{1}{3}\cdot {{x}^{-\frac{2}{3}}}=\frac{1}{3}\cdot \frac{1}{\sqrt[3]{{{x}^{2}}}} \\& {{\left( \sqrt[4]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{4}}} \right)}^{\prime }}=\frac{1}{4}{{x}^{-\frac{3}{4}}}=\frac{1}{4}\cdot \frac{1}{\sqrt[4]{{{x}^{3}}}} \\\end{align}\]

Возвращаемся к нашему примеру и записываем:

\[{y}’=\frac{1}{2\sqrt{x}}+\frac{1}{3\sqrt[3]{{{x}^{2}}}}+\frac{1}{4\sqrt[4]{{{x}^{3}}}}\]

Вот такое сложное решение.

Переходим ко второму примеру — здесь всего два слагаемых, но каждое из них содержит как классическую степень, так и корни.

\[y={{x}^{3}}\sqrt[3]{{{x}^{2}}}+{{x}^{7}}\sqrt[3]{x}\]

Сейчас мы узнаем, как найти производную степенной функции, которая, кроме того, содержит и корень:

\[\begin{align}& {{\left( {{x}^{3}}\sqrt[3]{{{x}^{2}}}+{{x}^{7}}\sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{3}}\cdot \sqrt[3]{{{x}^{2}}} \right)}^{\prime }}={{\left( {{x}^{3}}\cdot {{x}^{\frac{2}{3}}} \right)}^{\prime }}= \\& ={{\left( {{x}^{3+\frac{2}{3}}} \right)}^{\prime }}={{\left( {{x}^{\frac{11}{3}}} \right)}^{\prime }}=\frac{11}{3}\cdot {{x}^{\frac{8}{3}}}=\frac{11}{3}\cdot {{x}^{2\frac{2}{3}}}=\frac{11}{3}\cdot {{x}^{2}}\cdot \sqrt[3]{{{x}^{2}}} \\& {{\left( {{x}^{7}}\cdot \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{7}}\cdot {{x}^{\frac{1}{3}}} \right)}^{\prime }}={{\left( {{x}^{7\frac{1}{3}}} \right)}^{\prime }}=7\frac{1}{3}\cdot {{x}^{6\frac{1}{3}}}=\frac{22}{3}\cdot {{x}^{6}}\cdot \sqrt[3]{x} \\\end{align}\]

Оба слагаемых посчитаны, осталось записать окончательный ответ:

\[{y}’=\frac{11}{3}\cdot {{x}^{2}}\cdot \sqrt[3]{{{x}^{2}}}+\frac{22}{3}\cdot {{x}^{6}}\cdot \sqrt[3]{x}\]

Мы нашли ответ.

Производная дроби через степенную функцию

Но и на этом возможности формулы для решения производной степенной функции не заканчиваются. Дело в том, что с ее помощью можно считать не только примеры с корнями, но также и с дробями. Это как раз та редкая возможность, которая значительно упрощает решение таких примеров, но при этом зачастую игнорируется не только учениками, но и учителями.

Итак, сейчас мы попытаемся совместить сразу две формулы. С одной стороны, классическая производная степенной функции

\[{{\left( {{x}^{n}} \right)}^{\prime }}=n\cdot {{x}^{n-1}}\]

С другой стороны мы знаем, что выражение вида $\frac{1}{{{x}^{n}}}$ представимо в виде ${{x}^{-n}}$. Следовательно,

\[\left( \frac{1}{{{x}^{n}}} \right)’={{\left( {{x}^{-n}} \right)}^{\prime }}=-n\cdot {{x}^{-n-1}}=-\frac{n}{{{x}^{n+1}}}\]

Пример:

\[{{\left( \frac{1}{x} \right)}^{\prime }}=\left( {{x}^{-1}} \right)=-1\cdot {{x}^{-2}}=-\frac{1}{{{x}^{2}}}\]

Таким образом, производные простых дробей, где в числителе стоит константа, а в знаменателе — степень, также считаются с помощью классической формулы. Посмотрим, как это работает на практике.

Итак, первая функция:

\[f\left( x \right)=\frac{1}{{{x}^{2}}}\]

Считаем:

\[{{\left( \frac{1}{{{x}^{2}}} \right)}^{\prime }}={{\left( {{x}^{-2}} \right)}^{\prime }}=-2\cdot {{x}^{-3}}=-\frac{2}{{{x}^{3}}}\]

Первый пример решен, переходим ко второму:

\[y=\frac{7}{4{{x}^{4}}}-\frac{2}{3{{x}^{3}}}+\frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}}\]

Решаем:

\[\begin{align}& {{\left( \frac{7}{4{{x}^{4}}}-\frac{2}{3{{x}^{3}}}+\frac{5}{2}{{x}^{2}}+2{{x}^{3}}-3{{x}^{4}} \right)}^{\prime }}= \\& ={{\left( \frac{7}{4{{x}^{4}}} \right)}^{\prime }}-{{\left( \frac{2}{3{{x}^{3}}} \right)}^{\prime }}+{{\left( 2{{x}^{3}} \right)}^{\prime }}-{{\left( 3{{x}^{4}} \right)}^{\prime }} \\& {{\left( \frac{7}{4{{x}^{4}}} \right)}^{\prime }}=\frac{7}{4}{{\left( \frac{1}{{{x}^{4}}} \right)}^{\prime }}=\frac{7}{4}\cdot {{\left( {{x}^{-4}} \right)}^{\prime }}=\frac{7}{4}\cdot \left( -4 \right)\cdot {{x}^{-5}}=\frac{-7}{{{x}^{5}}} \\& {{\left( \frac{2}{3{{x}^{3}}} \right)}^{\prime }}=\frac{2}{3}\cdot {{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}=\frac{2}{3}\cdot {{\left( {{x}^{-3}} \right)}^{\prime }}=\frac{2}{3}\cdot \left( -3 \right)\cdot {{x}^{-4}}=\frac{-2}{{{x}^{4}}} \\& {{\left( \frac{5}{2}{{x}^{2}} \right)}^{\prime }}=\frac{5}{2}\cdot 2x=5x \\& {{\left( 2{{x}^{3}} \right)}^{\prime }}=2\cdot 3{{x}^{2}}=6{{x}^{2}} \\& {{\left( 3{{x}^{4}} \right)}^{\prime }}=3\cdot 4{{x}^{3}}=12{{x}^{3}} \\\end{align}\]…

Теперь собираем все эти слагаемые в единую формулу:

\[{y}’=-\frac{7}{{{x}^{5}}}+\frac{2}{{{x}^{4}}}+5x+6{{x}^{2}}-12{{x}^{3}}\]

Мы получили ответ.

Однако прежде чем двигаться дальше, хотел бы обратить ваше внимание на форму записи самих исходных выражений: в первом выражении мы записали $f\left( x \right)=…$, во втором: $y=…$ Многие ученики теряются, когда видят разные формы записи. Чем отличаются $f\left( x \right)$ и $y$? На самом деле, ничем. Это просто разные записи с одним и тем же смыслом. Просто когда мы говорим $f\left( x \right)$, то речь идет, прежде всего, о функции, а когда речь идет об $y$, то чаще всего подразумевается график функции. В остальном же это одно и то же, т. е., производная в обоих случаях считается одинаково.

Сложные задачи с производными

В заключение хотелось бы рассмотреть пару сложных комбинированных задач, в которых используется сразу все то, что мы сегодня рассмотрели. В них нас ждут и корни, и дроби, и суммы. Однако сложными эти примеры будут лишь в рамках сегодняшнего видеоурока, потому что по-настоящему сложные функции производных будут ждать вас впереди.

Итак, заключительная часть сегодняшнего видеоурока, состоящая из двух комбинированных задач. Начнем с первой из них:

\[y={{x}^{3}}-\frac{1}{{{x}^{3}}}+\sqrt[3]{x}\]

Считаем:

\[\begin{align}& {{\left( {{x}^{3}}-\frac{1}{{{x}^{3}}}+\sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{3}} \right)}^{\prime }}-{{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}+\left( \sqrt[3]{x} \right) \\& {{\left( {{x}^{3}} \right)}^{\prime }}=3{{x}^{2}} \\& {{\left( \frac{1}{{{x}^{3}}} \right)}^{\prime }}={{\left( {{x}^{-3}} \right)}^{\prime }}=-3\cdot {{x}^{-4}}=-\frac{3}{{{x}^{4}}} \\& {{\left( \sqrt[3]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{3}}} \right)}^{\prime }}=\frac{1}{3}\cdot \frac{1}{{{x}^{\frac{2}{3}}}}=\frac{1}{3\sqrt[3]{{{x}^{2}}}} \\\end{align}\]

Производная функции равна:

\[{y}’=3{{x}^{2}}-\frac{3}{{{x}^{4}}}+\frac{1}{3\sqrt[3]{{{x}^{2}}}}\]

Первый пример решен. Рассмотрим вторую задачу:

\[y=-\frac{2}{{{x}^{4}}}+\sqrt[4]{x}+\frac{4}{x\sqrt[4]{{{x}^{3}}}}\]

Во втором примере действуем аналогично:

\[{{\left( -\frac{2}{{{x}^{4}}}+\sqrt[4]{x}+\frac{4}{x\sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}={{\left( -\frac{2}{{{x}^{4}}} \right)}^{\prime }}+{{\left( \sqrt[4]{x} \right)}^{\prime }}+{{\left( \frac{4}{x\cdot \sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}\]

Посчитаем каждое слагаемое отдельно:

\[\begin{align}& {{\left( -\frac{2}{{{x}^{4}}} \right)}^{\prime }}=-2\cdot {{\left( {{x}^{-4}} \right)}^{\prime }}=-2\cdot \left( -4 \right)\cdot {{x}^{-5}}=\frac{8}{{{x}^{5}}} \\& {{\left( \sqrt[4]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{4}}} \right)}^{\prime }}=\frac{1}{4}\cdot {{x}^{-\frac{3}{4}}}=\frac{1}{4\cdot {{x}^{\frac{3}{4}}}}=\frac{1}{4\sqrt[4]{{{x}^{3}}}} \\& {{\left( \frac{4}{x\cdot \sqrt[4]{{{x}^{3}}}} \right)}^{\prime }}={{\left( \frac{4}{x\cdot {{x}^{\frac{3}{4}}}} \right)}^{\prime }}={{\left( \frac{4}{{{x}^{1\frac{3}{4}}}} \right)}^{\prime }}=4\cdot {{\left( {{x}^{-1\frac{3}{4}}} \right)}^{\prime }}= \\& =4\cdot \left( -1\frac{3}{4} \right)\cdot {{x}^{-2\frac{3}{4}}}=4\cdot \left( -\frac{7}{4} \right)\cdot \frac{1}{{{x}^{2\frac{3}{4}}}}=\frac{-7}{{{x}^{2}}\cdot {{x}^{\frac{3}{4}}}}=-\frac{7}{{{x}^{2}}\cdot \sqrt[4]{{{x}^{3}}}} \\\end{align}\]

Все слагаемые посчитаны. Теперь возвращаемся к исходной формуле и складываем вместе все три слагаемых. Получаем, что окончательный ответ будет таким:

\[{y}’=\frac{8}{{{x}^{5}}}+\frac{1}{4\sqrt[4]{{{x}^{3}}}}-\frac{7}{{{x}^{2}}\cdot \sqrt[4]{{{x}^{3}}}}\]

И на этом все. Это был первый наш урок. В следующих уроках мы рассмотрим более сложные конструкции, а также выясним, зачем вообще нужны производные. 

Смотрите также:

1. Производная произведения и частного
2. Правила вычисления производных
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Преобразование уравнений
5. Пробный ЕГЭ 2012 от 7 декабря. Вариант 5 (без производной)
6. Задача B2: лекарство и таблетки

www.berdov.com

Производная показательно-степенной функции | Математика

Мы рассмотрели общую схему нахождения производной показательно-степенной функции. Производная показательно-степенной функции вычисляется достаточно легко. Рассмотрим конкретные примеры.

Найти производную показательно-степенной функции:

 

   

Это показательно-степенная функция, поскольку и основание, и показатель степени содержат переменную x.

Действуем по схеме: сначала логарифмируем обе части по основанию e:

   

Показатель степени выносим за знак логарифма:

   

Теперь дифференцируем обе части равенства, с учетом того, что y=y(x), а значит, lny — сложная функция:

   

   

   

Обе части равенства умножаем на y:

   

Вспоминаем, что по условию y — это x  в степени sinx, и подставляем это выражение вместо y:

   

   

Действуем по схеме:

   

   

   

   

Здесь ln(2x+3) — сложная функция, внешняя функция f=lnu. внутренняя u=2x+3:

   

Умножаем обе части равенства на y:

   

Теперь подставляем в  вместо y его выражение из условия:

   

   

Логарифмируем обе части по основанию e:

   

Показатель степени выносим за знак логарифма:

   

Теперь дифференцируем обе части равенства:

   

   

√(7-x) сложная функция, внешняя функция f=√u, внутренняя u=7-x:

   

   

Теперь обе части умножаем на y:

   

И в заверщении, заменяем y на соответствующее выражение из условия: 

   

Примеры для самопроверки: найти производную показательно-степенной функции:

   

   

   

Показать решение

   

   

   

   

   

Здесь ln(sinx) — сложная функция. f=lnu — внешняя функция, u=sinx — внутренняя:

   

   

   

Умножаем обе части равенства на y:

   

и заменяем y выражением из условия: 

   

   

   

   

   

Здесь ln(arcsinx) — сложная функция. Внешняя функция f=lnu, внутренняя u=arcsinx: 

   

   

   

Теперь умножаем обе части равенства на y: 

   

И заменяем y на выражение из условия:

   

   

   

   

   

   

   

   

Теперь умножаем обе части равенства на y:

   

И заменяем y на его выражение из условия: 

   

www.matematika.uznateshe.ru

64. Вывод табличных производных. Производная постоянной.

При выводе самой первой формулы таблицы будем исходить из определения производнойфункции в точке. Возьмем , где x – любое действительное число, то есть, x – любое число из области определения функции . Запишем предел отношения приращения функции к приращению аргумента при :

Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.

Таким образом, производная постоянной функции равна нулю на всей области определения.

Производная степенной функции.

Формула производной степенной функции имеет вид , где показатель степени p – любое действительное число.

Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …

Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:

Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:

Следовательно,

Этим доказана формула производной степенной функции для натурального показателя.

Производная показательной функции.

Вывод формулы производной приведем на основе определения:

Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

Выполним подстановку в исходный предел:

Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

Производная логарифмической функции.

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.

Производные тригонометрических функций.

Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.

По определению производной для функции синуса имеем .

Воспользуемся формулой разности синусов:

Осталось обратиться к первому замечательному пределу:

Таким образом, производная функции sin x есть cos x.

Абсолютно аналогично доказывается формула производной косинуса.

Следовательно, производная функции cos x есть –sin x.

Вывод формул таблицы производных для тангенса и котангенса проведем с использованием доказанных правил дифференцирования (производная дроби).

Производные гиперболических функций.

Правила дифференцирования и формула производной показательной функции из таблицы производных позволяют вывести формулы производных гиперболического синуса, косинуса, тангенса и котангенса.

Производная обратной функции.

Перед началом изучения данной статьи рекомендуем вспомнить определение и свойства обратной функции.

Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, – это производная функции f(x) по x.

Теперь сформулируем правило нахождения производной обратной функции.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи .

Можно это правило переформулировать для любого x из промежутка , тогда получим .

Давайте проверим справедливость этих формул.

Найдем обратную функцию для натурального логарифма (здесь y – функция, а x– аргумент). Разрешив это уравнение относительно x, получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.

Из таблицы производных видим, что и .

Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:

Как видите, получили такие же результаты как и в таблице производных.

Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.

Начнем с производной арксинуса.

Для обратной функцией является . Тогда по формуле производной обратной функции получаем

Осталось провести преобразования.

Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.

Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1).

Для арккосинуса все делается абсолютно аналогично:

Найдем производную арктангенса.

Для обратной функцией является .

Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.

Пусть arctgx = z, тогда

Следовательно,

Схожим образом находится производная арккотангенса:

studfiles.net

Нахождение производных функций, содержащих степени — Мегаобучалка

Н.П. Зубарева

Математика

Методическое пособие по изучению темы

“Производная функции”

Калининград, 2015

Составитель: Н.П. Зубарева, канд. пед. наук, доцент.

Рецензент: Ю.Н. Антипов, доктор физмат. наук, профессор.

 

Методическое пособие предназначено студентам для изучения принципов дифференцирования функций. Подробно пояснено решение отдельных заданий. Для самостоятельного решения предложен ряд заданий, ответы на которые есть на с.20.

В пособии имеется справочный материал.

Печатается по решению

, протокол № от 20 г.

Содержание

 

1.Формулы дифференцирования. 4

2. Нахождение производных функций, содержащих степени. 6

3. Производная функций, содержащих логарифмы 11

4. Производная, содержащая тригонометрические функции 11.

5. Производная сложной функции 14

6. Производные высших порядков 16

7. Производная функции, заданной неявно. 17

8. Производная степенно-показательной функции

9. Производная функции, заданной параметрически

 

Ответы.. 20

 

 

Формулы дифференцирования

 

 

Производная постоянной величины равна нулю: C ‘ = 0.

Производная аргумента равна единице: x’ = 1.

Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же алгебраической сумме производных этих функций:

Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй сомножитель плюс произведение первого сомножителя на производную второго сомножителя:

.

Постоянный множитель можно вынести за знак производной:

, С – постоянная.

Производная частного двух функций может быть найдена по формуле:

.

 

Таблица производных

 

Задание 1.Найти производную функции .

Решение:

Функция равна произведению постоянной величины 5 и переменной х². По формуле выносим постоянную величину перед производной, затем по формуле находим производную х².

 

Задание 2. Найти производную функции .

Решение:

Использовали формулы , ,

 

Найти самостоятельно производную функции:

1а)

1б)

 

Нахождение производных функций, содержащих степени.

Для вычисления производных полезно сначала преобразовать выражение.

Напомним некоторые формулы действий со степенями из школьного курса.

 

А. .

При возведении степени в степень показатели степеней перемножаются.

Б. .

В. .

Если основания степеней одинаковы, то при умножении показатели степеней складываются, а при делении – показатели степеней вычитаются.

Г.

Д.

Е.

 

Например:

.

.

.

.

.

 

Задание 3.Найти производную функции .

Решение: Сначала преобразуем по формуле

.

Производную этой функции найдем по формуле

.

 

Задание 4.Найти производную функции .

Решение: Сначала преобразуем это выражение по формулам ,

.

Производную этой функции найдем по формулам ,

.

Производную этого выражения можно найти по формуле , а потом преобразовать:

 

Задание 5.Найти производную функции .

Решение:

 

Сначала преобразовали выражение по формулам , Производную вычисляли по формулам , , , затем преобразовали полученное выражение по формулам ,

Найти самостоятельно производную функции:

2а)

2б)

 

Задание 6.Найти производную функции .

Решение:

Применили формулу . Далее производные находим по формулам , , , затем упрощаем полученное выражение, перемножая выражение в скобках.

Найти самостоятельно производную функции:

3а)

3б)

 

Задание 7. Найти производную функции .

Решение:

 

Использовали формулу , затем формулы , , .

Найти самостоятельно производную функции:

4а) .

4а) .

 

Задание 8. Найти производную функции .

Подставим это выражение в виде степени:

.

Производную найдем сначала по формуле .

Затем производную находим по формулам , , .

Найти самостоятельно производную функции:

5а) .

5б) .

Задание 9.Найти производную функции .

Решение:

 

Сначала формула , затем формулы , , .

Найти самостоятельно производную функции:

6а) .

6б) .

 

Задание 10.Найти производную функции .

Решение:

Сначала формула , затем решаем по формулам , , , .

.

 

Найти самостоятельно производную функции:

7а) .

7б) .

 

megaobuchalka.ru