Там же вы можете получить подробное решение производной:
Применим правило производной частного:
и .
Чтобы найти :
В силу правила, применим: получим
Чтобы найти :
дифференцируем почленно:
Производная постоянной равна нулю.
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате:
Теперь применим правило производной деления:
Теперь упростим:
Ответ:
Общее правило
Производную от дроби очень просто посчитать (по-крайней мере от простых дробей)
Производная от дроби “единица, делённая на x” равна минус единице, делённой на x в квадрате.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.
Приведем доказательство данной формулы. Рассмотрим выражение y=\frac\upsilon\nu. Все представленные переменные – это функции от х. Умножим их на \(\nu\). Получим \(y\times\nu=\upsilon\).
Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:
\(\left(\upsilon\times\nu\right)’=\upsilon’\times\nu+\upsilon\times\nu’\)
Тогда выводим:
\(y’\times\nu+y\times\nu’=\upsilon’\)
Из этого вычисляем нужную нам производную:
\(y’\times\nu=\upsilon’-y\times\nu’=\upsilon’-\frac\upsilon\nu\times\nu’=\frac{\upsilon’v-\upsilon\nu’}\nu;\;y’=\frac{\upsilon’v-\upsilon\nu’}{\nu^2}\)
Что и требовалось доказать. 2}.\)
2}.\)
Логарифмическая производная. Дифференцирование показательно степенной функции.
Когда нам нужно выполнить дифференцирование показательно степенной функции вида y=(f(x))g(x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.
Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.
Как вывести формулу логарифмической производной
Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:
y=f(x)ln y=ln(f(x))(ln y)’=(ln(f(x)))’1y·y’=(ln(f(x)))’⇒y’=y·(ln(f(x)))’
Примеры использования формулы
Покажем на примере, как это делается.
Вычислить производную показательно степенной функции переменной x в степени x.
Решение
Проводим логарифмирование по указанному основанию и получаем ln y=ln xx. С учетом свойств логарифма это можно выразить как ln y=x·ln x. Теперь дифференцируем левую и правую части равенства и получаем результат:
ln y=x·ln xln y’=x·ln x’1y·y’=x’·ln x+·ln x’⇒y’=y·1·ln x+x·1x=y·(ln x+1)=xx·(ln x+1)
Ответ: xx’=xx·(ln x+1)
Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:
y=xx=eln xx=ex·ln x⇒y’=(ex·ln x)’=ex·ln x·x·ln x’=xx·x’·ln x+x·(ln x)’==xx·1·ln x+x·1x=xx·ln x+1
Рассмотрим еще одну задачу.
Пример 2Вычислите производную функции y=x2+13×3·sin x.
Решение
Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования.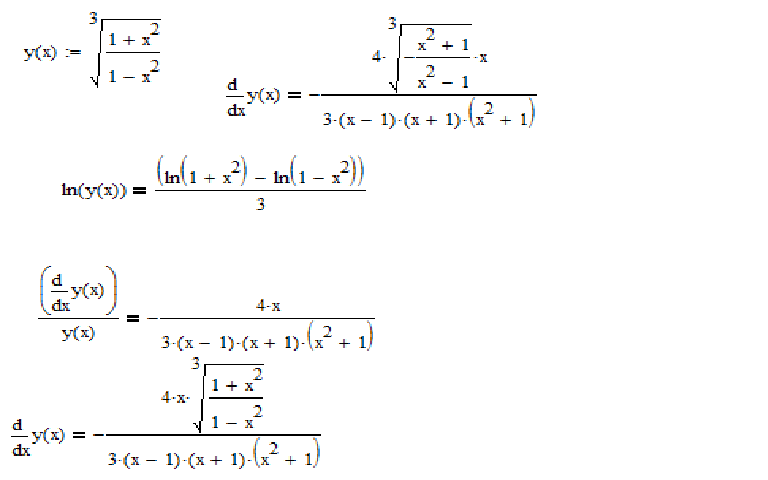 Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Начнем с нахождения ln(f(x)). Для дальнейшего преобразования нам потребуются следующие свойства логарифма:
- логарифм дроби можно представить в виде разности логарифмов;
- логарифм произведения можно представить в виде суммы;
- если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.
Преобразуем выражение:
В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:
(ln(f(x)))’=13ln(x2+1)-32ln x-12ln sin x’==13ln(x2+1)’-32ln x’-12ln sin x’==13(ln(x2+1))’-32(ln x)’-12(ln sin x)’==13·1×2+1·x2+1′-32·1x-12·1sin x·(sin x)’==13·2xx2+1-32x-cos x2 sin x
Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.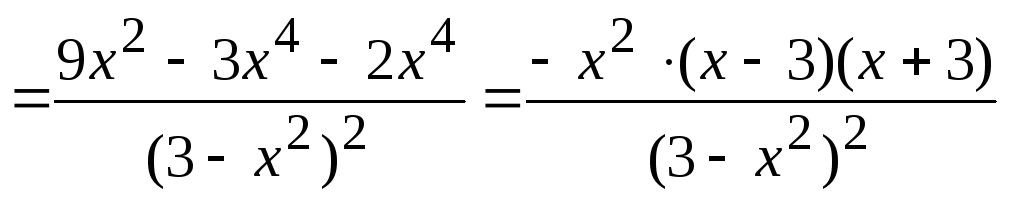
Ответ: y’=y·ln(f(x))’=x2+13×3·sin x·13·2xx2+1-32x-cos x2 sin x
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЧтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.
Пример 3Дана показательно степенная функция y=(x2+x+1)x3. Вычислите ее производную.
Решение:
y’=y·(ln(f(x)))’=(x2+x+1)x3·ln(x2+x+1)x3’==(x2+x+1)x3·x3·(x2+x+1)’==(x2+x+1)x3·x3’·ln(x2+x+1)+x3ln(x2+x+1)’==(x2+x+1)x3·3×2·ln(x2+x+1)+x3·1×2+x+1·x2+x+1’==(x2+x+1)x3·3×2·ln(x2+x+1)+x32x+1×2+x+1==(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Ответ: y’=y·(ln(f(x)))’=(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Вычислите производную выражения y=x2+13·x+1·x3+14×2+2x+2.
Решение
Применяем формулу логарифмической производной.
y’=y·lnx2+13·x+1·x3+14×2+2x+2’==y·lnx2+13+lnx+1+lnx3+14-lnx2+2x+2’==y·13ln(x2+1)+12lnx+1+14ln(x3+1)-12ln(x2+2x+2)’==y·(x2+1)’3(x2+1)+x+1’2(x+1)+(x3+1)’4×3+1-x2+2x+2’2×2+2x+2==x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2)
Ответ:
y’=x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2).
Логарифмическое дифференцирование функций
Метод логарифмического дифференцирования становится пригодным при дифференцировании произведения нескольких функций или их частки. Его удобно применять при дифференцировании выражений, содержащих корни из дробей (функций), а также когда показатель функции также представляет собой функцию
В таких случаях целесообразно обе части выражения сначала прологарифмировать по основанию , а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:
Суть метода с помощью формул можно описать следующим образом:
имеем сложную функцию вида
к обеим сторонам применяем логарифмирования
находим производные правой и левой части равенства
Приравниваем производные и выражаем
В этом суть метода, дальше все зависит от функции .
Если она представляет собой произведение функций
то по свойствам логарифма он будет равен сумме логарифмов
Если имеем дробь от функций
то применяя логарифмирования получим
Если имеем функцию в степени другой
то по свойствам логарифма получим
В случае корней дифференцировки значительно упрощается
Дальнейшее вычисление производных зависит от сложности самих функций. Рассмотрим конкретные примеры, чтобы данный материал стал для Вас более понятным и наглядным.
Задача.
Используя логарифмирования найти производную (Дубовик В.П., Юрик И.И. “Высшая математика. Сборник задач”)
1) (5. 2.178)
2.178)
2) (5.2.191)
3) (5.2.195)
4) (5.2.199)
Решение.
Примеры выбрано сложные для того, чтобы раскрыть всю силу метода логарифмического дифференцирования и рассмотреть типичные распространенные примеры.
1) Проведем логарифмирования левой и правой частей
Найдем производную правой части
Производная левой части показана при изложении теоретического материала. Записываем обе части
Далее переносим функцию из знаменателя в правую часть и не забываем поменять ее значение
Несмотря на сложный вид данный пример полностью решено.
2) Используем свойства логарифма к данному примеру
Проводим дифференцирования обеих частей равенства
Сведем к общему знаменателю правую сторону. В результате математических операций получим
Подставим в исходную равенство, перенеся функцию в правую часть
В результате ряда несложных математических манипуляций получили достаточно компактный конечный результат производной. При исчислении данного примера направления подобный результат пришлось бы искать очень долго.
При исчислении данного примера направления подобный результат пришлось бы искать очень долго.
3) Несмотря на сложный вид данное выражение, на основе свойств степеней, можно переписать в следующем виде
Применим к нему логарифмирования
Производная от правой части будет равна следующему выражению
Здесь для упрощения дальнейших выкладок введено обозначение .
Учитывая производную , окончательно получим
Можно оставлять в таком виде, поскольку суть данного урока научиться применять метод логарифмического дифференцирования. Но если Вы захотите для упрощения свести все к общему знаменателю, то получите следующее выражение
Поверьте это займет у Вас много времени.
4) Проводим логарифмирования функции
Дальше по методике находим производную правой части. Она будет равна выражению
Подставляя в формулу для производной от , получим
На этом решения примера завершен.
Практикуйте с подобными задачами и через некоторое время у Вас не будет никаких трудностей с такого сорта примерами.
III.3. Дифференцирование функции одной переменной
(схема 30)
Пусть явно задана функция y=f (x). Функция, зависящая непосредственно от переменной x, называется простой. Рассмотрим для простой функции точку x, принадлежащую ее области определения. Дадим приращение аргументу ∆x в точке x. Функция получит при этом соответствующее (3.9) приращение ∆y=f(x+∆x)–f(x).
Производной функции y=f (x) по переменной x в некоторой точке называется предел отношения приращения функции
 (3.15)
(3.15)Функция, имеющая в точке конечную производную, называется дифференцируемой в этой точке. Процесс нахождения производной называется дифференцированием и обозначается .
Производная характеризует скорость изменения функции в достаточно малой окрестности заданной точки.
Приведем таблицу производных основных элементарных функций (без доказательства), которые рассматриваются нами как функции простые и явно заданные.
Теорема 3.9. Если функция дифференцируема в некоторой точке, то она в этой точке непрерывна
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна,
но не дифференцируема. Так, функция y=|x| в точке x=0 непрерывна, но производной не имеет, так как в этой
точке к графику функции можно провести бесконечное множество
касательных (рис.
Среди явных функций особое место занимают обратные функции, производная которых находится с помощью следующей теоремы.
Теорема 3.10. Если строго монотонная функция y=f (x) дифференцируема на некотором интервале Х, причем ее производная не обращается в нуль на Х, то обратная к ней функция x=φ(y) также дифференцируема на этом интервале, при этом:
Доказательство. Дадим функции y=f (x) в точке x бесконечно малое приращение аргумента ∆x→0, функция при этом получит соответствующее приращение ∆y. Так как по условию теоремы функция
дифференцируема в каждой точке интервала Х, то в каждой точке этого
интервала функция непрерывна (по теореме 3.9). Следовательно, по определению
непрерывности функции выполняется: , это означает, что
при ∆x
Так как по условию теоремы функция
дифференцируема в каждой точке интервала Х, то в каждой точке этого
интервала функция непрерывна (по теореме 3.9). Следовательно, по определению
непрерывности функции выполняется: , это означает, что
при ∆x
По определению производной можно записать:
, теорема доказанаСреди явных функций выделяют класс сложных функций.
Функция называется сложной, если она представляет собой композицию нескольких функций: y=f (φ(x)). Функция f называется внешней, а φ – внутренней функцией, выступающей в качестве независимого переменного.
Теорема 3.11. Чтобы продифференцировать сложную функцию необходимо сначала продифференцировать внешнюю функцию по внутренней, считая внутреннюю функцию независимой переменной, затем продифференцировать внутреннюю функцию по независимому переменному и результаты дифференцирования перемножить, то есть
 31)
31)Пример 3.8. Найти производную функции .
Решение. Согласно формуле (3.31) и с учетом табличных формул (3.17), (3.19), (3.29) имеем:
.К явным функциям можно отнести функции, заданные параметрически, вида:,
где t – параметр. Производную такой функции несложно получить:
.
Пример 3.9. Найти производную функции .
Решение. Согласно формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Примечание. Функция, заданная в примере 3.9, представляет собой параметрическое уравнение окружности радиуса a. Действительно, возведем оба уравнения в квадрат и сложим их почленно, получим:Помимо таблицы производных имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме производных этих функций:
(3. 33)
33)
Данная теорема может быть обобщена для произвольного конечного числа функций-слагаемых.
Пример 3.10. Найти производную функции.
Решение. Согласно формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:
Теорема 3.13. Производная произведения двух дифференцируемых функций равна произведению производной первой функции-сомножителя на вторую функцию плюс произведение первой функции на производную второй функции–сомножителя, то есть
(3.34)
Пример 3.11. Найти производную функции .
Решение. Согласно формуле (3.34) и с учетом табличных формул (3.22), (3.24) имеем:
Теорема 3.14. Производная частного двух функций равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, то есть
(3. 35)
35)Пример 3.12. Найти производную функции.
Решение. Согласно формуле (3.35) и с учетом табличных формул (3.17), (3.29) имеем:
Все рассмотренные выше при дифференцировании функции были заданы в явном виде, то есть уравнением y=f (x), разрешенным относительно y.
Функция называется неявно заданной, если она
имеет вид F (x;y)=0.
Неявный способ задания к свойствам функции отношения не имеет. В этом случае
любое выражение, содержащее переменную y, нужно
рассматривать как функцию сложную. Следовательно, при нахождении производной неявных функций следует применять теорему о
дифференцировании сложной функции. В процессе отыскания все слагаемые,
содержащие , оставляют в левой части равенства и выносят из них за скобки как общий
множитель. Слагаемые, не содержащие , переносят в правую часть, и полученное уравнение разрешают
относительно искомой .
Пример 3.13. Найти производную неявной функции .
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.17) и (3.18) имеем:
Иногда для упрощения процесса дифференцирования
громоздких функций применяют их предварительное логарифмирование (логарифмическое
дифференцирование). Данный метод целесообразен в тех случаях, когда
функция представляет собой произведение и (или) частное различных функций,
таких как показательные и степенные выражения (особенно иррациональные).
Логарифмическое дифференцирование используется также для нахождения производных
показательно-степенных функций, которые без предварительного логарифмирования
вообще не дифференцируются. При использовании данного метода в левой части получают производную от натурального
логарифма y, которая равна . После этого обе части умножают на y, при этом в правой части заменяют y на заданную по
условию функцию.
Пример 3.14. Найти производную функции .
Решение. Прологарифмируем заданную функцию .
По свойству логарифма степени имеем:. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной произведения, с учетом табличных формул (3.19) и (3.29) можно записать
.После умножения обеих частей последнего равенства на y окончательно получим:. Заметим, что без предварительного логарифмирования производную заданной функции найти невозможно, так как нельзя обосновать использование формул дифференцирования (3.17) или (3.22)
Пусть функция y=f (x) дифференцируема в некоторой текущей точке x и при этом . Тогда по определению производной и формуле (3.15) можно записать: . Иначе: приращение функции имеет вид
. (3. 36)
36)
Дифференциалом функции y=f (x) в точке x называется главная часть приращения этой функции, равная произведению производной функции на приращение аргумента:
. (3.37)
Найдем дифференциал независимой переменной x, то есть дифференциал функции y=x. Так как , то по формуле (3.37) имеем dy=dx=∆x. Тогда формула (3.37) для вычисления дифференциала функции может быть записана в виде:
. (3.38)
Если в формуле
(3.36) отбросить бесконечно малую величину α∙∆x, то
получим приближенное равенство . Подставляя в него выражения для ∆y и dy из формул (3.9) и (3.37), получим или
Подставляя в него выражения для ∆y и dy из формул (3.9) и (3.37), получим или
Формула (3.39) применяется для вычисления приближенных значений функций.
Пример 3.15. Вычислить приближенно значение .
Решение. Рассмотрим функцию . По формуле (3.39) имеем:
.Так как x+∆x=0,95, то при x=1 и ∆x=-0,05 получаем:
Процесс дифференцирования может быть многократным. Производная от первой производной называется второй производной функции или производной 2-го порядка. Производная от последней, в свою очередь, является производной 3-го порядка и так далее. Производная функции n-го порядка – это производная от предыдущей производной (n-1)-го порядка заданной функции, то есть . (3.40)
(3.40)Сложные производные
, , ,
, , ,
, , Ответы в конце урока
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём:
берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1)Сначала нам нужно вычислить выражение , значит, сумма – самое глубокое вложение.
2)Затем необходимо вычислить логарифм:
3)Далее косинус:
4)Потом косинус возвести в куб:
5)На пятом шагу разность:
6)И, наконец, самая внешняя функция – это квадратный корень:
Формула дифференцирования сложной функции применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
Вроде без ошибок….
(1)Берем производную от квадратного корня.
(2)Берем производную от разности, используя правило
(3)Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
(4)Берем производную от косинуса.
(5)Берем производную от логарифма.
(6)И, наконец, берем производную от самого глубокого вложения
.
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень,
экспонента и логарифм.
В таких случаях необходимо последовательно применить правило дифференцирования произведения два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: , а за «вэ» – логарифм: .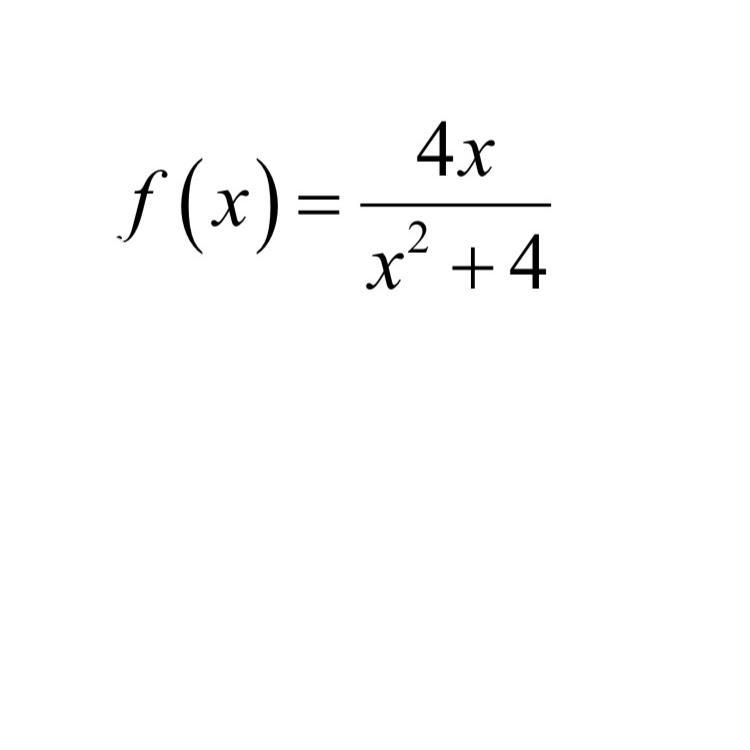 Почему так можно сделать? А разве – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Почему так можно сделать? А разве – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило к скобке :
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Готово.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны. Пример 5
Найти производную функции
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями. Пример 6
Найти производную функции Здесь можно пойти несколькими путями:
или так:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного , приняв за весь числитель:
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить? Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби:
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8
Найти производную функции
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени , а потом ещё и от
дроби .
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Само решение можно оформить примерно так:
Преобразуем функцию:
Находим производную:
Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения: Пример 9
Найти производную функции Пример 10
Найти производную функции
10.3.0. Вычисление производных.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 1.3k. Опубликовано
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x7+x5-x4+x3-x2+x-9. Применяем правило I, формулы 4, 2 и 1. Получаем:
Применяем правило I, формулы 4, 2 и 1. Получаем:
y’=7x6+5x4-4x3+3x2-2x+1.
2. y=3x6-2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x5-2=18x5-2.
Применяем правило I, формулы 3, 5 и 6 и 1.
Применяем правило IV, формулы 5 и 1.
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4. Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4. Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
2}. \ _ \ Квадрат \ end {align} dxd h (x) = (2x) 2 (2x) (9×2−1) – (3×3 − x − 2) (2) = 4x218x3−2x − 6×3 + 2x + 4 = x23x3 +1. □
Дифференцирование рационального члена довольно сложно и сбивает с толку, когда выражения очень сложные. В таких случаях вы можете принять числитель как одно выражение, а знаменатель как одно выражение и найти их отдельные производные. 2}.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (ax2 + bx + c) 2 (ax2 + bx + c) (0) – (2ax + b) (1) = (ax2 + bx + c) 2− (2ax + b) . □
2}.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (ax2 + bx + c) 2 (ax2 + bx + c) (0) – (2ax + b) (1) = (ax2 + bx + c) 2− (2ax + b) . □
Если y = ax + bcx + d (∣c∣ + ∣d∣ ≠ 0), y = \ frac {ax + b} {cx + d} \ \ big (| c | + | d | \ neq 0 \ big ), y = cx + dax + b (∣c∣ + ∣d∣ = 0), затем найдите dydx \ frac {dy} {dx} dxdy.
Запишите u (x) = ax + b ⟹ u ′ (x) = au (x) = ax + b \, значит u ‘(x) = au (x) = ax + b⟹u ′ (x) = a и v (x) = cx + d ⟹ v ′ (x) = cv (x) = cx + d \ влечет v ‘(x) = cv (x) = cx + d⟹v ′ (x) = c, так что y = u (x) v (x): y = \ frac {u (x)} {v (x)}: y = v (x) u (x):
dydx = ddx (u (x) v (x)) = v (x) u ′ (x) −v ′ (x) u (x) (v (x)) 2 = (cx + d) (a) – (c) (ax + b) (cx + d) 2 = ad − bc (cx + d) 2.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (cx + d) 2 (cx + d) (a) – (c) (ax + b) = (cx + d) 2ad − bc. □
ИсчислениеЕсли y = 1 − xx1 + xx (x> 0), y = \ frac {1 – x \ sqrt {x}} {1 + x \ sqrt {x}} \ (x> 0), y = 1 + xx 1 − xx (x> 0), затем найдите dydx \ frac {dy} {dx} dxdy.
Запишите u (x) = 1 − xx ⟹ u ′ (x) = 0 − x − x2x = −3x2u (x) = 1 – x \ sqrt {x} \, что подразумевает u ‘(x) = 0 – \ sqrt {x} – \ frac {x} {2 \ sqrt {x}} = – \ frac {3 \ sqrt {x}} {2} u (x) = 1 − xx ⟹u ′ (x) = 0− x −2x x = −23x и v (x) = 1 + xx ⟹ v ′ (x) = 0 + x + x2x = 3×2.2}. \ _ \ Квадрат \ конец {выровнено} y⇒dxdy = v (x) u (x) = (v (x)) 2v (x) u ′ (x) −v ′ (x) u (x) = (1 + xx) 2 (1 + xx) (- 23x) – (23x) (1 − xx) = 2 (1 + xx) 2−3x – 3×2− (3x −3×2) = 2 (1 + xx) 2−6x = – (1 + xx) 23x. □
– Нахождение производной рациональной функции с определением предела Исчисление
– Нахождение производной рациональной функции с определением предела – Mathematics Stack ExchangeСеть обмена стеками
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange – это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Создан 02 сен.
Джей Джей1,75311 золотых знаков1212 серебряных знаков1919 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Правило частного. Неявное дифференцирование
8
Правило частного
Доказательство правила частного
Неявное дифференцирование
Производная обратной функции
Правило частного
Следующее называется правилом частного:
“Производная частного двух функций равна
. знаменатель, умноженный на производную числителя
минус числитель, умноженный на производную знаменателя
, все делится на квадрат знаменателя.«
Например, если на момент принять, что производная sin x равна cos x (Урок 12):
Задача 1. Вычислить производную от Вычислить производную от | . x 2 sin x | . |
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| sin x · 2 x – x 2 cos x sin 2 x |
Проблема 2. Используйте цепное правило, чтобы вычислить производную
.| x 3 · 2 sin x cos x – sin 2 x · 3 x 2 x 6 = | x 2 sin x (2 x cos x – 3 sin x ) | x 6 |
| = | sin x (2 x cos x – 3 sin x ) x 4 | |
Проблема 3. Вычислить производную от Вычислить производную от | x 2 -5 x -6 2 x + 1 | . |
| (2 x + 1) (2 x -5) – ( x 2 -5 x -6) · 2 (2 x + 1) 2 | = | 4 x 2 -8 x -5-2 x 2 + 10 x + 12 (2 x + 1) 2 |
| = | 2 x 2 + 2 x + 7 (2 x + 1) 2 | |
| Проблема 4.Вычислить производную от | 3 x 2 – x + 4 | . |
См. Примеры, Урок 6 и Урок 22 по алгебре.
| = | ||
| = | ||
| = | ||
Доказательство правила частного
ТЕОРЕМА. |
Доказательство. Поскольку г = г ( x ), то
| d dx | 1 г | = | d dg | 1 г | · | dg dx | = – | 1 г 2 | г ‘ |
в соответствии с правилом цепочки и Задача 4 урока 5.
Следовательно, согласно правилу произведения (Урок 6),
Это правило частного, которое мы хотели доказать.
Неявное дифференцирование
Рассмотрим следующее:
x 2 + y 2 = r 2
Это уравнение окружности с радиусом r . (Урок 17 книги Precalculus.)
(Урок 17 книги Precalculus.)
Давайте посчитаем.
Для этого мы можем решить относительно y , а затем взять производную. Но вместо этого мы возьмем производную каждого члена. Что касается y 2 , мы считаем его неявно функцией x , и поэтому мы можем применить к нему цепное правило. Тогда будем решать за.
| d dx | x 2 | + | d dx | y 2 | = | d dx | r 2 |
| 2 x + 2 y | dy dx | = | 0 | |||
| dy dx | = | – | x y | . | ||
Это называется неявным дифференцированием. Мы рассматриваем y как функцию от x и применяем цепное правило. Производная, которая получается в результате, обычно содержит как x , так и y .
Задача 5. 15 y + 5 y 3 + 3 y 5 = 5 x 3 . Вычислите y ‘.
| 15 y ‘ + 15 y 2 y’ + 15 y 4 y ‘ | = | 15 x 2 |
| y ‘ (1 + y 2 + y 4 ) | = | x 2 |
| г | = | x 2 1 + y 2 + y 4 |
Проблема 6. | Вычислить y ‘. |
Проблема 7.
а) В этом круге
x 2 + y 2 = 25,
а) какова координата y , когда x = −3?
y = 4 или −4. Для,
(−3) 2 + (± 4) 2 = 5 2
б) Каков наклон касательной к окружности в точке (−3, 4)?
c) Каков наклон касательной к окружности в точке (−3, −4)?
Проблема 8.В первом квадранте, каков наклон касательной к этой окружности,
( x – 1) 2 + ( y + 2) 2 = 169,
, когда x = 6?
[Подсказка: 5 2 + 12 2 = 13 2 – тройка Пифагора.]
В первом квадранте, когда x = 6, y = 10.
(6-1) 2 + (10 + 2) 2 = 13 2 .
| y ‘ = – | x – 1 y + 2 | . Следовательно, наклон равен – | 6 – 1 10 + 2 | = – | 5 12 |
Задача 9. Вычислите наклон касательной к этой кривой в точке (2, −1):
x 3 – 3 x y 2 + y 3 = 1
| 3 x 2 – (3 x · 2 y y ‘ + y 2 · 3) + 3 y 2 y’ | = | 0 | ||
| согласно правилу продукта. | ||||
| 3 x 2 – 6 x y y ‘ – 3 y 2 + 3 y 2 y’ | = | 0 | ||
| x 2 -2 x y y ‘– y 2 + y 2 y’ | = | 0 | ||
| y ‘ ( y 2 -2 xy ) | = | y 2 – x 2 | ||
| г ‘ | = | y 2 – x 2 y 2 -2 xy | ||
| Следовательно, в (2, −1): | ||||
| г ‘ | = | (-1) 2 -2 2 (-1) 2 -2 · 2 · -1 | ||
| = | −3 5 | |||
| = | – | 3 5 | ||
Производная обратной функции
Когда у нас есть функция y = f ( x ) – например
y = x 2
– тогда мы часто можем решить для x . В данном случае
В данном случае
При обмене переменных получаем
| называется функцией, обратной y = x 2 . |
Напишем
| f ( x ) | = | x 2 |
| г ( x ) | = | |
И позвольте нам вызвать f прямую функцию и g обратную функцию .Формальная связь между f и g следующая:
f ( g ( x )) = g ( f ( x )) = x .
(Тема 19 Precalculus.)
Вот другие пары прямых и обратных функций:
| f ( x ) | = | грех x | г ( x ) | = | arcsin x | |
| f ( x ) | = | a x | г ( x ) | = | журнал a x | |
| f ( x ) | = | x 3 | г ( x ) | = | ||
Теперь, когда мы знаем производную прямой функции f , то из нее мы можем определить производную g .
Таким образом, пусть g ( x ) будет инверсией f ( x ). Тогда
f ( г ( x )) = x .
Теперь возьмем производную по x :
Это означает следующее:
Теорема. Если g ( x ) является обратной величиной f ( x ), то
“Производная обратной функции равна
.величина, обратная производной прямой функции
, если его аргумент – обратная функция.«
| Пример. Пусть f ( x ) = x 2 и | Тогда f ( г ) = г 2 . |
Следовательно,
Следующий урок: Мгновенная скорость и скорость изменения
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Правило частного – объяснение и примеры
Существует множество так называемых «сокращенных» правил для поиска производной функции. Правило частного – это правило, используемое для нахождения производной функции, которую можно записать как частное двух функций.Проще говоря, вы можете думать о правиле частного как о применении к функциям, которые записываются как дроби, где числитель и знаменатель сами являются функциями.
реклама
Содержание:
- Правило
- Запоминание правила частного
- Примеры использования правила частного
- Подсказки: экономия работы за счет упрощения в первую очередь
Формула правила частного
Для функций f и g с использованием простых чисел для производных формула:
Вспоминая правило частного
Вы, конечно, можете просто запомнить правило частного и настроиться на поиск производных, но вам может быть легче запомнить образец . Это показано ниже.
Это показано ниже.
Примеры
Естественно, лучший способ понять, как использовать правило частного, – это посмотреть на несколько примеров. Обратите внимание, что в каждом приведенном ниже примере этап вычисления выполняется намного быстрее, чем последующий этап алгебры. Это верно для большинства вопросов, где вы применяете правило частного. Вам часто придется немного упростить задачу, чтобы получить окончательный ответ.
Пример
Найти производную функции:
\ (f (x) = \ dfrac {x-1} {x + 2} \)
Решение
Это дробь, включающая две функции, поэтому сначала мы применяем правило частного.3}} \ end {align} \)
В приведенном выше примере помните, что производная константы равна нулю. Вот почему в ответе больше нет \ (\ dfrac {1} {5} \).
Неплохо, правда? Для практики вам следует попробовать применить правило частного и убедиться, что вы получили тот же ответ.
реклама
Продолжить изучение деривативов
Предыдущая: Правило произведения
Следующая: Правило цепочки
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеРазличение функций с помощью программы «Пошаговое решение математических задач»
Нахождение производной от
включает в себя вычисление следующих лимит:
Такой расчет, мягко говоря, неприятный. Мы хотели бы найти
способы вычисления производных без явного использования определения
производная как предел разностного частного.Полезный предварительный результат:
следующее:
Производная константы
lf c – любое действительное число, и если f (x) = c для всех x, то f ‘(x) = 0 для всех x.
То есть производная постоянной функции – это нулевая функция.
Это легко увидеть геометрически. Обращаясь к рисунку 1, мы видим, что
График постоянной функции f (x) = c представляет собой горизонтальную линию. Поскольку горизонтальный
линия имеет наклон 0, а линия является собственной касательной, отсюда следует, что наклон
касательная везде равна нулю.
Далее мы дадим правило дифференцирования f (x) = x n , где n – любое действительное число.
Некоторые из следующих результатов уже были проверены в предыдущем разделе, а остальные
можно проверить, используя определение производной.
Этот шаблон предлагает следующую общую формулу для степеней n, где n – это положительное число.
Правило питания
Фактически, правило мощности действительно для любого действительного числа n и, таким образом, может использоваться для дифференцировать множество неполиномиальных функций.Следующий пример иллюстрирует некоторые применения правила мощности.
Пример 1
Различайте каждую из следующих функций:
(a) Поскольку f (x) = 5, f – постоянная функция; следовательно, f ‘(x) = 0.
(b) При n = 15 в правиле мощности f ‘(x) = 15x 14
(c) Обратите внимание, что f (x) = x 1/2 . Следовательно, при n = 1/2 в правиле мощности
Следовательно, при n = 1/2 в правиле мощности
(d) Поскольку f (x) = x -1 , из правила мощности следует, что f
‘(x) = -x -2 = -1 / x 2
Правило дифференцирования постоянных функций и правило мощности явное правила дифференциации.Следующие правила говорят нам, как находить производные от комбинации функций в терминах производных составляющих их части. В каждом случае мы предполагаем, что f ‘(x) и g’ (x) существуют, а A и B суть константы.
Четыре перечисленных выше правила вместе с правилом дифференцирования константы функции и правило мощности, предоставляют нам техники для различения любых функция, которая выражается как степень или корень частного многочлена функции. Следующая серия примеров иллюстрирует это.Правило линейности и товарное правило будет обосновано в конце раздела; доказательство расширенное правило мощности появляется в разделе цепного правила.
Пример 2 Пусть
Найдите f ‘(x). 2 + 2bx + c
2 + 2bx + c
Пример 3 можно обобщить следующим образом:
A многочлен степени n всюду имеет производную, а производная есть многочлен степени (n – 1).
Пример 4 Пусть
Найдите f ‘(x).
Сначала мы используем правило произведения, поскольку f (x) задается как произведение x 2 и x 2 – х + 1:
Правило частного: формула и примеры – видео и стенограмма урока
Мнемоническое устройство
Формулу правила частного может быть трудно запомнить. Возможно, вам поможет небольшое пение в стиле йодлинг. Представьте себе лягушку, играющую йодль: «LO dHI меньше HI dLO над LO LO».’В этом мнемоническом устройстве LO относится к функции знаменателя, а HI относится к функции числителя.
Давайте снова переведем йодль лягушки в формулу для правила частного.
LO dHI означает знаменатель, умноженный на производную числителя: g ( x ) умноженный на df ( x ).
минус означает «минус».
HI dLO означает, что числитель умножен на производную знаменателя: f ( x ) умножить на dg ( x ).
больше означает «разделить на».
LO LO означает умножение на знаменатель: г ( x ) в квадрате.
Примеры
Давайте рассмотрим несколько примеров, в которых мы должны применить правило частного.
В первом примере возьмем производную от следующего частного:
Давайте определим функции для формулы правила частного и мнемонического устройства.2 – 1. dg ( x ) или dLO , это 2 x .
Теперь мы можем расположить эти части в формуле или мнемоническом устройстве, чтобы найти производную, которая, как вы можете видеть, выглядит так:
Затем вы можете умножить члены в числителе и объединить одинаковые члены, чтобы получить окончательную производную, которая, как вы можете видеть, составляет:
Рассмотрим другой пример. 3 в числителе, а затем уменьшите дробь, чтобы получить окончательную производную, которая, как вы можете видеть, равна:
3 в числителе, а затем уменьшите дробь, чтобы получить окончательную производную, которая, как вы можете видеть, равна:
Резюме урока
Давайте рассмотрим то, что мы только что узнали в этом уроке:
Правило частного – это формула для получения производной частного от двух функций. Формула:
Легкий способ запомнить формулу – использовать мнемоническое устройство: LO dHI меньше HI dLO над LO LO.И, наконец, после применения формулы вам все равно может потребоваться упростить получившееся выражение.
Как использовать правило частного для деривативов. Наглядное объяснение с цветными примерами
Краткий обзор
Примеры
Пример 1
Предположим, что $$ \ displaystyle f (x) = \ frac {2x + 3} {5x + 1} $$. 2} $$.
2} $$.
Пример 3
Найдите $$ \ displaystyle \ frac d {dx} \ left (\ tan kx \ right) $$, где $$ k $$ – любая константа.
Шаг 1Выразите $$ \ tan kx $$ через синус и косинус.
$$ \ tan x = \ frac {\ sin kx} {\ cos kx} $$
Шаг 2Дифференцируйте с помощью правила частного.2 тыс. X $$
Продолжить практические задачиОшибка: Нажмите «Не робот», затем повторите попытку.
.

