Производная функции в точке презентация, доклад
Презентация на тему Презентация на тему Производная функции в точке, предмет презентации: Математика. Этот материал содержит 27 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас – поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ
Лекция 1
Дифференциальное исчисление
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производная функции в точке
Пусть функция f (x) определена в некоторой окрестности точки х0.
Производной функции f (x) в точке x0 называется число, обозначаемое f ’(x0), равное пределу отношения
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
при
Дифференциальное исчисление
Определение 1:
если этот предел существует.
Определение 2:
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Производную функции y = f (x) принято обозначать так:
Дифференциальное исчисление
Производная функции в точке
Обозначения:
Производная функции f (x) в точке x0 есть предел отношения
её приращения
к соответствующему приращению
её аргумента
при
Односторонние производные функции в точке
Правая производная:
Если функция f (x) определена в некоторой правой полуокрестности точки x0 , то её правой производной называется предел
Автор: И. В. Дайняк, к.
т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Левая производная:
Если функция f (x) определена в некоторой левой полуокрестности точки x0 , то её левой производной называется предел
Пример 1:
Найти производную функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
в точке х0 = 0.
Дифференциальное исчисление
Производная функции в точке
Пример 2:
Найти производную функции
в точках х1 = 0 и х2 = 1.
Теорема:
Если функция f (x) имеет производную в точке x0, то она непрерывна в точке x0.
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Обратное утверждение неверно.
Дифференциальное исчисление
Производная функции в точке
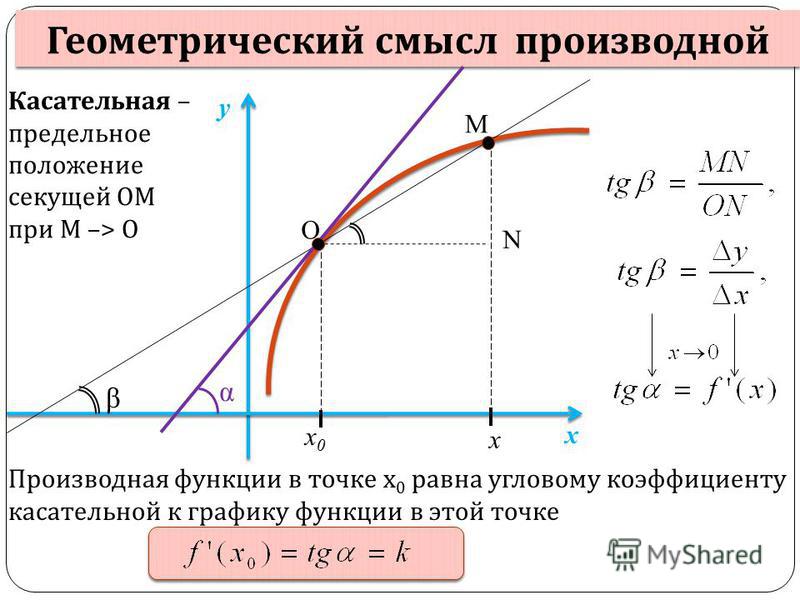
Геометрический смысл производной функции в точке
Автор: И.
В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Пусть f (x) – непрерывная функция, определённая в некоторой окрестности точки x0.
Дифференциальное исчисление
Рассмотрим две точки:
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Геометрический смысл производной функции в точке
Автор: И.
В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Приблизим точку В к точке А:
Дифференциальное исчисление
Геометрический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Геометрический смысл производной функции в точке: угловой коэффициент касательной к графику функции, проведенной в точке касания:
Дифференциальное исчисление
Уравнение касательной:
Уравнение нормали:
Физический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
1. Пусть материальная точка М движется прямолинейно,
и функция s(t) есть пройденный ею путь за время t.
Дифференциальное исчисление
Пусть t0 – момент начала движения.
Тогда отношение
– средняя скорость движения.
Предел
– мгновенная скорость
точки в момент t0.
Физический смысл производной функции в точке
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Пусть Δt – промежуток времени.
Тогда
– средняя сила тока за время Δt.
Предел
– мгновенный ток.
2. Пусть q (t0) – количество электричества, протекающего через
поперечное сечение проводника в момент времени t0.
Отношение
Теорема 1: Основные формулы дифференцирования
Пусть функции u = u(x) и v = v(x) имеют производную
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
тоже имеют производные в точке x = x0, вычисляемые по формулам:
Дифференциальное исчисление
Производная функции в точке
1)
константу можно выносить за знак производной
Теорема 1: Основные формулы дифференцирования
Автор: И.
В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производная функции в точке
2) формула производной суммы
3) формула производной произведения
4) формула производной частного
Теорема 2: Дифференцирование сложной функции
Пусть функция g(x) имеет производную в точке x0, а функция f (y) имеет производную в точке y0 = g(x0). Тогда сложная функция f (g(x)) имеет производную в точке x0, вычисляемую по формуле
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
или
Дифференциальное исчисление
Производная функции в точке
Если функция f (x) имеет производную в любой точке некоторого интервала [a, b], то её производная на этом интервале может быть выражена в виде некоторой функции g(x) = f ’(x), которая находится по основным формулам дифференцирования (теорема 1) и правилу нахождения производной сложной функции (теорема 2).
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производная функции на отрезке
1. Постоянная функция
f (x) = c, где с – константа.
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
2. Показательная функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Отсюда заключаем:
3. Степенная функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
При
имеем:
4.
Логарифмическая функция
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Отсюда следует, что
Кроме того,
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Синус: sin x
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Косинус: cos x
5. Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Тангенс:
Производная находится по формуле производной частного:
5.
Тригонометрические функции
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Дифференциальное исчисление
Производные элементарных функций
Тангенс:
Производная находится по формуле производной частного:
Высшая математика
Автор: И.В.Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
math.mmts-it.org
Скачать презентацию
Исчисление– Что описывает производная функции в точке?
спросил
Изменено 6 лет, 8 месяцев назад
Просмотрено 3к раз
$\begingroup$
Насколько я понимаю, производная функции $f$ в точке $x=x_{0}$ определяется как предел $$f'(x_{0})=\lim_{\Delta x\rightarrow 0} \frac{f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}$$, где $\Delta x$ – небольшое изменение аргумента $x$ при “движении ” из $x=x_{0}$ в соседнюю точку $x=x_{0}+\Delta x$.
Что меня смущает, так это то, как правильно интерпретировать его значение, то есть что на самом деле описывает производная $f'(x_{0})$?
В Википедии говорится, что « производная функции количественно определяет скорость, с которой значение функции изменяется при изменении входных данных » (или слова на этот счет). Однако функция имеет конкретное постоянное значение, $f(x_{0})$ в данной точке $x=x_{0}$, так как же можно осмысленно обсуждать скорость, с которой значение функции изменяется в таком случае?
Правильно ли интерпретировать производную функции в точке как описание того, как «быстро» изменяется ее значение по мере того, как мы движемся от этой точки к соседним (бесконечно близким) точкам? (Как и в приведенном выше примере, при перемещении из точки $x_{0}$ в точку $x_{0}+\Delta x$ значение функции $f$ изменяется на величину $f'(x_{0} )\Delta x$ для бесконечно малого изменения $\Delta x$). Значит ли это, что значение производной в этой точке просто равно наклону касательной к функции (кривой) в этой точке? (В общем случае производная функции сама по себе является функцией, значение которой в каждой точке равно наклону касательной к кривой в этой точке).
- исчисление
- производные
- интуиция
$\endgroup$
8
$\begingroup$
Я думаю, вы зациклились на идее, что скорость требует связанного временного интервала, к которому она применяется. Это неправда, я думаю, что большинство людей, вероятно, интуитивно думают об этом, но рассмотрим следующий сценарий.
Представьте себе мяч, брошенный из здания. В каждый возможный момент мяч движется с разной скоростью, потому что он постоянно ускоряется из-за силы тяжести. Скорость, конечно же, является скоростью, в частности скоростью, с которой меняется положение мяча. Итак, как бы вы ни искали, не существует интервала, каким бы малым он ни был, на котором скорость мяча является определенным числом. Он будет двигаться с определенной скоростью только в один момент времени. Итак, производная от положения шаров в некоторый момент времени t — это одна точная точка пространства, в которой мяч будет двигаться с этой скоростью.
Видеть? интервал не нужен.
Если это поможет вам думать о скорости как о разнице за некоторое бесконечно малое время, чем идти на это, определение предела выше говорит, что конкретный момент и эта бесконечно малая разница – одно и то же. Это одна из причин, почему результаты calc такие классные. Я думаю, как только вы почувствуете, что это одно и то же, вам не нужно будет связывать показатели с интервалом, к которому они относятся. Удачи.
$\endgroup$
7
$\begingroup$
Вы правильно понимаете производную. Единственное, что я бы немного переформулировал, так это то, что вместо
“при движении из точки $x_{0}$ в $x_{0}+\Delta x$ значение функции $f$ изменяется на величину $f ‘(x_{0})\Delta x$ для бесконечно малого изменения $\Delta x$”
Я бы написал
“при движении из точки $x_{0}$ в $x_{0}+\Delta x $, на сколько изменится значение функции $f$ приближается к $f'(x_{0})\Delta x$ , когда $\Delta x$ приближается к 0 ”
Я говорю это потому, что во многих случаях фактического значения $\Delta x нет.
$ таким образом, что изменение $f$ от $x_{0}$ до $x_{0}+\Delta x$ на самом деле равно $f'(x_{0})\Delta x$, поскольку не существует фактического числа, которое бесконечно мала
$\endgroup$
$\begingroup$
Ваше понимание интерпретации производной как скорости изменения верно, но есть одна тонкость. 92$, где $f:\mathbb R \to\mathbb R$.
$f'(x)=2x$, поэтому $f'(1)=2$.
Значит ли это, что производная $f'(1)$ является действительным числом $2$?
Нет. $2$ в данном случае — это функция, переводящая $x$ в $2x$. Только когда мы говорим о производной, мы обычно говорим, что она переводит $dx$ в $2dx$.
Фактически, $f'(x_0)$ сама по себе является линейной функцией, график которой является касательной к графику $f$ в точке $x_0$. Входные данные для этой функции называются касательным пространством, а $x_0$ является началом этого входного пространства.
$\endgroup$
до н.
э. Производная функции в точке
Мотивирующие вопросы
-
Как определяется средняя скорость изменения функции на заданном интервале и что измеряет эта величина?
-
Как определяется мгновенная скорость изменения функции в конкретной точке? Как мгновенная скорость изменения связана со средней скоростью изменения?
-
Что такое производная функции в данной точке? Что измеряет эта производная величина? Как мы интерпретируем значение производной графически?
-
Как формально используются ограничения при вычислении производных?
Мгновенная скорость изменения функции — это идея, которая лежит в основе исчисления. Это обобщение понятия мгновенной скорости и измеряет скорость изменения конкретной функции в данной точке. Если исходная функция представляет положение движущегося объекта, то эта мгновенная скорость изменения и есть скорость объекта. В других контекстах мгновенная скорость изменения может измерять количество клеток, добавляемых к бактериальной культуре в день, количество дополнительных галлонов бензина, потребляемых при увеличении скорости автомобиля на одну милю в час, или количество долларов, добавляемых к платежу по ипотеке.
на каждый процентный пункт увеличения процентной ставки. Мгновенная скорость изменения также может быть геометрически интерпретирована на графике функции, и эта связь является фундаментальной для многих основных идей исчисления.
Напомним, что для функции \(f(x)\) в области \([a,b]\text{,}\) средняя скорость изменения между \(a\) и \(b\) дается
\begin{уравнение*} AROC_{[a,b]} = \frac{f(b)-f(a)}{b-a}\text{.} \end{уравнение*}
Аналогично тому, как в подразделе 2.1.2, если мы запишем второе значение \(x\) \(b\) как \(a+h\) (где \(|h|\) можно рассматривать как расстояние \(b\) от \(a\)), мы получаем следующий вид средней скорости изменения функции между двумя точками:
Определение 2.2.1.
Для функции \(f\text{,}\) средняя скорость изменения \(f\) на интервале \([a,a+h]\) определяется значением
\begin{уравнение*} AROC_{[a,a+h]} = \frac{f(a+h)-f(a)}{h}\text{.} \end{уравнение*}
Эта форма средней скорости изменения функции называется разностным коэффициентом .
Преимущество использования коэффициента разности для записи средней скорости изменения заключается в том, что это позволяет нам сосредоточить внимание на одном \(x\) (значение \(x\) \(a\)) вместо двух \ (х\) значений. Наша конечная цель, как мы рассмотрим ниже, состоит в том, чтобы описать, как функция изменяется при одном значении \(x\).
Важно, чтобы вы понимали, как средняя скорость изменения \(f\) на интервале связана с его графиком.
Разминка 2.2.1.
Предположим, что \(f\) является функцией, представленной на графике ниже, и что \(a\) и \(a+h\) являются входными значениями, отмеченными на оси \(x\). Используйте график на рисунке 2.2.2, чтобы ответить на следующие вопросы.
Рисунок 2.2.2. График \(y = f(x)\) для разминки 2.2.1.-
Найдите и обозначьте точки \((a,f(a))\) и \((a+h, f(a+h))\) на графике.
-
Построить прямоугольный треугольник, гипотенузой которого является отрезок от \((a,f(a))\) до \((a+h,f(a+h))\text{.
}\) Какие длины соответствующих катетов этого треугольника? -
Каков наклон линии, соединяющей точки \((a,f(a))\) и \((a+h, f(a+h))\text{?}\)
-
Напишите осмысленное предложение, объясняющее, как связаны средняя скорость изменения функции на заданном интервале и наклон связанной прямой.
Подраздел 2.2.1 Производная функции в точке
Точно так же, как мы определяли мгновенную скорость через среднюю скорость в подразделе 2.1.2, теперь мы определяем мгновенную скорость изменения функции в точке через среднюю скорость изменения функции \(f\) по связанным интервалы. Эта мгновенная скорость изменения \(f\) в \(a\) называется “ производной от \(f\) в \(a\text{,}\)” и обозначается \(f’ (а)\текст{.}\)
Определение 2.2.3.
Пусть \(f\) функция и \(x = a\) значение в области определения функции. Определим производную от \(f\) по \(x\), оцененную при \(x = a\) , обозначаемую \(f'(a)\text{,}\) по формуле
\begin{уравнение*} f'(a) = \lim_{h \to 0} AROC_{[a,a+h]} = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h }\текст{,} \end{уравнение*}
при наличии этого ограничения.
Вслух мы читаем символ \(f'(a)\) либо как “\(f\)-простое число в \(a\)”, либо как “производная \(f\), оцененная в \(x = a\text{.}\)». Используя обозначения из подраздела 2.1.2, производная в точке \(a\) также может быть записана как \(IROC_{t=a}\text{.}\). Однако, продвигаясь вперед, мы по умолчанию будет использовать простую нотацию для производной.
Большая часть следующих нескольких глав будет посвящена пониманию, вычислению, применению и интерпретации производных. А пока отметим следующие важные вещи.
Сначала рассмотрим производную при заданном значении как наклон определенной линии.
Когда мы вычисляем мгновенную скорость изменения, мы допускаем сокращение интервала \([a,a+h]\) как \(h \to 0\text{.}\) Мы можем думать об одной конечной точке интервала как «скольжение» к другому. В частности, при условии, что \(f\) имеет производную в точке \((a,f(a))\text{,}\), точка \((a+h,f(a+h))\) будет подход \((a,f(a))\) как \(h \to 0\text{.}\) Поскольку процесс определения предела является динамическим, может быть полезно использовать вычислительные технологии для его визуализации.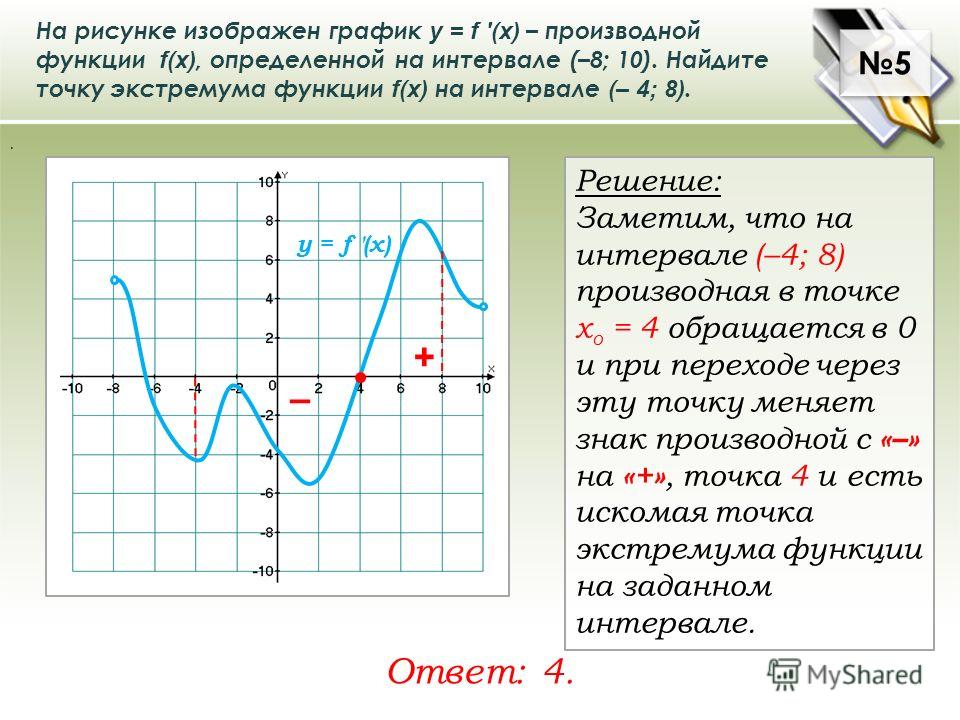
. Используйте интерактивное ниже, чтобы изменить расстояние \(h\) от значения \(x\) \(a=0\text{.}\) Попробуйте словесно описать, как линия, соединяющая две точки, начинает выглядеть как \( h\) становится очень близким (но не равным) \(0\)
На рис. 2.2.5 показана последовательность фигур с несколькими разными линиями, проведенными через точки \((a, f(a))\) и \((a+h,f(a+h))\text{,}\ ), порожденные различными значениями \(h\text{.}\) Эти линии (показаны на первых трех рисунках пурпурным цветом) часто называют секущими линиями к кривой \(y = f(x)\text{ .}\) Секущей к кривой называется просто линия, проходящая через две точки на кривой. Для каждой такой линии наклон секущей равен \(m = \frac{f(a+h) – f(a)}{h}\text{,}\), где значение \(h\) зависит от расположения точки, которую мы выбираем. На диаграмме видно, как по мере \(h \to 0\text{,}\) секущие линии начинают приближаться к единственной линии, проходящей через точку \((a,f(a))\text{. }\) Если существует предел наклона секущих, мы говорим, что полученное значение является наклоном касательная к кривой.
Эта касательная (показана на крайнем правом рисунке зеленым цветом) к графику \(y = f(x)\) в точке \((a,f(a))\) имеет наклон \(m = f ‘(а)\текст{.}\)
Если касательная в точке \(x = a\) существует, то граф \(f\) выглядит как прямая линия, если смотреть вблизи в точке \((a,f(a))\text{.}\). На рисунке 2.2.6 мы объединяем четыре графика на рисунке 2.2.5 в один один слева и увеличьте поле с центром в \((a,f(a))\) справа. Обратите внимание, как линия касательной расположена относительно кривой \(y = f(x)\) в точке \((a,f(a))\) и как она похожа на кривую рядом с \(x = a\text{. }\) 92}{ч}\текст{.} \end{equation*}
Затем мы удаляем общий множитель \(h\) как в числителе, так и в знаменателе и находим, что
\begin{equation*} f'(2) = \lim_{h \to 0} (-3-h)\text{.} \end{equation*}
Наконец, мы можем взять предел как \(h \to 0\text{,}\) и таким образом заключить, что \(f'(2) = -3\text{.
2\) в точке \((2,-2)\text{.}\) Рисунок 2.2.92\) в точке \((2,-2)\text{.}\)
Следующие упражнения помогут вам изучить множество ключевых идей, связанных с производными.
Мероприятие 2.2.2.
Рассмотрим функцию \(f\), формула которой имеет вид \(\displaystyle f(x) = 3 – 2x\text{.}\)
-
Какой знакомый тип функции \(f\text{?}\) Что вы можете сказать о наклоне \(f\) при каждом значении \(x\text{?}\)
-
Вычислить среднюю скорость изменения \(f\) на интервалах \([1,4]\text{,}\) \([3,7]\text{,}\) и \([5 ,5+h]\text{;}\) максимально упростить каждый результат. Что вы заметили в этих количествах?
-
Используйте предельное определение производной для вычисления точной мгновенной скорости изменения \(f\) по отношению к \(x\) при значении \(a = 1\text{.}\) То есть вычислите \(f'(1)\), используя определение предела. Показать свою работу. Ваш результат удивителен?
-
Каковы значения \(f'(2)\text{,}\) \(f'(\pi)\text{,}\) и \(f'(-\) без дополнительных вычислений? sqrt{2})\text{?}\) Почему?
Мероприятие 2.
2.3.
92 + 36\текст{.}
\конец{выравнивание*}
Используйте эту функцию, чтобы ответить на каждый из следующих вопросов.
-
Нарисуйте точный помеченный график \(s\) на осях, указанных на рисунке 2.2.10. Вы должны быть в состоянии сделать это без использования вычислительной техники.
Рисунок 2.2.10. Оси для построения \(y = s(t)\) в Упражнении 2.2.3. -
Вычислите среднюю скорость изменения \(s\) на интервале времени \([1,2]\text{.}\) Включите единицы измерения в свой ответ и напишите одно предложение, объясняющее значение найденного вами значения .
-
Используйте определение предела для вычисления мгновенной скорости изменения \(s\) по отношению ко времени, \(t\text{,}\) в момент времени \(a = 1\text{.}\) Показать свою работу, используя надлежащие обозначения, включите в свой ответ единицы и напишите одно предложение, объясняющее значение найденного вами значения.
-
На графике (а) нарисуйте две линии: одна, наклон которой представляет среднюю скорость изменения \(s\) на \([1,2]\text{,}\), другая, наклон которой представляет собой мгновенная скорость изменения \(s\) в момент \(a=1\text{.
}\) Четко обозначьте каждую строку. 9{t/5}\text{.}\) Используйте эту функцию, чтобы ответить на следующие вопросы. -
Нарисуйте грубый график \(P\) для \(t = 0\) до \(t = 5\) на осях, указанных на рисунке 2.2.11.
Рисунок 2.2.11. Оси для построения \(y = P(t)\) в Упражнении 2.2.4. -
Вычислите среднюю скорость изменения \(P\) между 2030 и 2050 годами. Включите единицы измерения в свой ответ и напишите одно предложение, объясняющее значение (на повседневном языке) значения, которое вы нашли.
-
Используйте определение предела, чтобы записать выражение для мгновенной скорости изменения \(P\) по времени, \(t\text{,}\) в момент времени \(a = 2\text{.}\ ) Объясните, почему этот предел трудно оценить точно.
-
Оцените предел в (c) для мгновенной скорости изменения \(P\) в момент \(a = 2\), используя несколько малых значений \(h\). Как только вы определили точную оценку \(P'(2)\text{,}\), включите единицы в свой ответ и напишите одно предложение (используя повседневный язык), чтобы объяснить значение найденного вами значения.
-
На приведенном выше графике нарисуйте две линии: одна, наклон которой представляет среднюю скорость изменения \(P\) на \([2,4]\text{,}\), другая, наклон которой представляет мгновенную скорость изменения изменение \(P\) в момент \(a=2\text{.}\)
-
Тщательно составленным предложением опишите поведение \(P'(a)\) по мере увеличения значения \(a\). Что это говорит о поведении данной функции \(P\text{?}\)
Подраздел 2.2.2 Резюме
-
Вопрос 2.2.12.
Как определяется средняя скорость изменения функции на заданном интервале и что измеряет эта величина? Ответ.Средняя скорость изменения функции \(f\) на интервале \([a,b]\) равна \(\frac{f(b)-f(a)}{b-a}\text{. }\) Единицами средней скорости изменения являются единицы \(f(x)\) на единицу \(x\text{,}\), а числовое значение средней скорости изменения представляет собой наклон кривой секущая линия между точками \((a,f(a))\) и \((b,f(b))\) на графике \(y = f(x)\text{.
}\) Если мы рассматриваем интервал как \([a,a+h]\) вместо \([a,b]\text{,}\) значение остается тем же, но средняя скорость изменения теперь вычисляется с использованием коэффициент разности, \(\frac{f(a+h)-f(a)}{h}\text{.}\) -
Вопрос 2.2.13.
Как определяется мгновенная скорость изменения функции в конкретной точке? Как мгновенная скорость изменения связана со средней скоростью изменения? Ответ.Мгновенная скорость изменения относительно \(x\) функции \(f\) при значении \(x = a\) обозначается \(f'(a)\) (читай “производная от \(f\) оценивается в \(a\)” или “\(f\)-простое в \(a\)”) и определяется по формуле
\begin{equation*} f'(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h}\text{,} \end{уравнение*}
при наличии ограничения. В частности, обратите внимание, что мгновенная скорость изменения при \(x = a\) является пределом средней скорости изменения при \([a,a+h]\) при \(h \to 0\text{.
}\ )
-
Вопрос 2.2.14.
Чему равна производная функции в данной точке? Что измеряет эта производная величина? Как мы интерпретируем значение производной графически? Ответ.Если производная \(f'(a)\) существует, ее значение говорит нам о мгновенной скорости изменения \(f\) по отношению к \(x\) в точке \(x = a\text{,} \), что геометрически представляет собой наклон касательной к кривой \(y = f(x)\) в точке \((a,f(a))\text{.}\) Мы даже говорим, что \( f'(a)\) — «наклон кривой» в точке \((a,f(a))\text{.}\)
-
Вопрос 2.2.15.
Как формально используются пределы при вычислении производных?Ответ.Ограничения позволяют нам перейти от скорости изменения за интервал к скорости изменения в одной точке.
Упражнения 2.2.3 Упражнения
1.
Рассмотрим график \(y = f(x)\), представленный на рисунке 2.2.16.
-
На графике \(y = f(x)\text{,}\) нарисуйте и обозначьте следующие величины:
-
секущую к \(y = f(x)\) на интервале \([-3,-1]\) и секущую к \(y = f(x)\) на интервале \ ([0,2]\текст{.
}\) -
касательная к \(y = f(x)\) в точке \(x = -3\) и касательная к \(y = f(x)\) в точке \(x = 0\text{. }\)
-
-
Каково приблизительное значение средней скорости изменения \(f\) на \([-3,-1]\text{?}\) на \([0,2]\text{?}\ ) Как эти ценности связаны с вашей работой в (а)?
-
Каково приблизительное значение мгновенной скорости изменения \(f\) при \(x = -3\text{?}\) при \(x = 0\text{?}\) Каковы эти значения связанные с вашей работой в (а)?
2.
Для каждой из следующих подсказок нарисуйте график функции с указанными свойствами по предоставленным осям на рисунке 2.2.17.
Рисунок 2.2.17. Оси для построения \(y = f(x)\) в (a) и \(y = g(x)\) в (b).-
\(y = f(x)\) такое, что
-
средняя скорость изменения \(f\) на \([-3,0]\) равна \(-2\), а средняя скорость изменения \(f\) на \([1, 3]\) равно 0,5, а
-
мгновенная скорость изменения \(f\) при \(x = -1\) равна \(-1\), а мгновенная скорость изменения \(f\) при \(x = 2\) равна 1.
t\), где \(t\) равно количество лет с начала 1993. -
Согласно модели, каково было общее изменение численности населения Китая с 1 января 1993 г. по 1 января 2000 г.? Какова будет средняя скорость изменения населения за этот период времени? Эта средняя скорость изменения больше или меньше мгновенной скорости изменения численности населения на 1 января 2000 г.? Объясните и обоснуйте, обязательно включив во все свои ответы правильные единицы измерения.
-
Согласно модели, какова средняя скорость изменения численности населения Китая за десятилетний период, начинающийся с 1 января 2012 г.?
-
Напишите выражение, включающее пределы, которые, если их вычислить, дадут точную мгновенную скорость изменения населения на сегодняшнюю дату. Затем оцените значение этого предела (обсудите, как вы это сделали) и объясните значение (включая единицы измерения) найденного вами значения.
-
Найдите уравнение касательной к функции \(y = P(t)\) в точке, где значение \(t\) равно сегодняшней дате.
-
-
-