Производная и ее функция – Производная функции — Википедия

Производная функции. Понятие производной. Геометрический смысл производной. Физический смысл производной. Правила дифференцирования. Производная сложной функции. Достаточное условие монотонности функции. Необходимое и достаточное условия экстремума.

Производная функции. Понятие производной, определение производной:
Производной (первой производной)  f ‘ (x) функции f  (x) в точке xo называется предел отношения приращения функции Δ f (x) = f (x0 + Δx) – f (x0) к приращению аргумента Δx при Δx→0, если этот предел существует: Второй производной  f ” (x) функции f  (x) в точке xo называется производная от производной f ‘ (x) в точке xo Дифференцирование – это операция нахождения производной f ‘ (x)
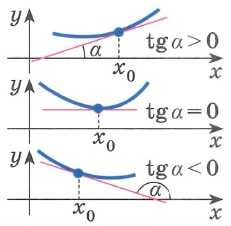
Производная функции. Геометрический смысл производной:
Производная функции f  (x) в точке xo равна угловому коэффициенту (тангенсу угла наклона) касательной прямой  к графику функции y = f  (x)  в точке M0(x0,y0), то есть: f ‘ (x0) = k, где k = tg α Уравнение касательной к кривой y = f (x) в точке x0 имеет вид: y = f ‘ (x)(x-x0) + f(x 0)
Производная функции. Физический смысл производной:
Если точка движется вдоль оси x и ее координата изменяется по закону x (t), то мгновенная скорость точки: а укорение (мгновенное ускорение):
Производная функции. Правила дифференцирования:

dpva.ru

22.Производная и ее свойства.

Определение: Пусть функция определена в точкеи в некоторой ее окрестности. Дадим аргументуприращение, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функциии составим отношение. Если существует предел этого отношения пристремящемся к нулю, то указанный предел называют производной функциив точкеи обозначают. Иначе говоря:

(— приращение функции,— приращение аргумента).

Если в каждой точке из множествау функциисуществует производная, то такая функция называется дифференцируемой на множестве.

Геометрический смысл производной: — угловой коэффициент касательной к графику функциив точкеуравнение касательной в этой точке .

Правила дифференцирования

Пусть функции иопределены и дифференцируемы на некотором множестве,и— любые действительные числа. Тогда на множествесправедливы соотношения:

Основные формулы дифференцирования.

23. Производная сложной и обратной функции.

Пусть у = f(и) и u = φ(х)– тогда у = f(φ{x)) — сложная функция с промежуточным аргументом и н независимым аргументом х.

По условию Отсюда, по теореме о связи функции, ее предела и бесконечно малой функции, имеем

 илигде. Функцияu = φ(х) имеет производную в точке х: , поэтомуПодставив значение Δи в равенство (20.6), получим т.е.Разделив полученное равенство на Δ

х и перейдя к пределу при Δх→0, получим Итак, для нахождения производной сложной функции надопроизводную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу. Это правило остается в силе, если промежуточных аргументов несколько. Так, если у = f(u), u = φ(v), v = g{х), то Пустьу = f(x) и х = φ(y)— взаимно обратные функции. Рассмотрим обратную функциюх = φ(y). Дадим аргументу у приращение Δу ≠ 0. Ему соответствует приращение Δх обратной функции, причем Δх ≠ 0 в силу строгой монотонности функции у = f(x). Поэтому можно записать   Если Δ y→0, то в силу непрерывности обратной функции приращение Δх→0. И так как , то из (20.7) следуют равенства

Таким образом, производная обратной функции равна обратной величине производной данной функции. Правило дифференцирования обратной функции записывают так: Пример 1. Найти производную функции Решение: Данная функция является сложной. Ее можно представить в виде цепочки «простых» функций: , где, гдеz = tg q, где q =.. По правилу дифференцирования сложной функции ()получаем:Пример 2. Пользуясь правилом дифференцирования обратной функции, найти производную для функцииРешение: Обратная функция имеет производную. Следовательно,

24.Геометрический смысл производной.

Геометрический смысл производной.

 Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y= f(x) в этой точке.

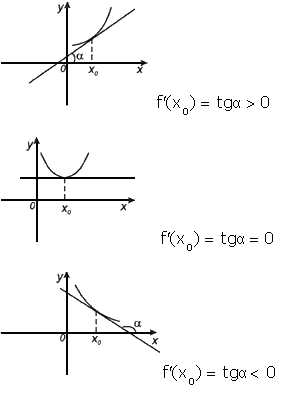
Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции: xf(x0+x)−f(x0)=tg, где – угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку 

B, то x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

studfiles.net

3. Производная функции в точке. Правила, дифференцирования.

Произво́дная (функции в точке) — основное понятие 

дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной.

4.Производная сложной и обратной функции.

Пусть теперь задана сложная функция , т.е. переменная  есть функция переменной , а переменная  есть, в свою очередь, функция от независимой переменной .

Теорема. Если  и   дифференцируемые функции своих аргументов, то сложная функция  является дифференцируемой функцией и ее производная равна произведению производной данной функции по промежуточному аргументу и производной промежуточного аргумента по независимой переменной:

.

Утверждение легко получается из очевидного равенства  (справедливого при  и ) предельным переходом при  (что в силу непрерывности дифференцируемой функции влечет ).

Перейдем к рассмотрению производной обратной функции.

Пусть на множестве  дифференцируемая функция   имеет множество значений  и на множестве  существует обратная функция .

Теорема. Если в точке  производная , то производная обратной функции  в точке  существует и равна обратной величине производной данной функции: , или

.

Эта формула легко получается из геометрических соображений.

Так как  есть тангенс угла наклона касательной линии  к оси , то  есть тангенс угла наклона той же касательной (той же линии ) в той же точке  к оси 

. 

Если  и  острые, то , а если тупые, то .

В обоих случаях . Этому равенству и равносильно равенство

.

 

5.Геометрический и физический смысл производной.

1) Физический смысл производной. 

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная– скорость изменения переменной y относительно переменной x в точке.  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная– скорость в момент времени.  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то– скорость изменения количества электричества в момент времени, т.е. сила тока в момент времени.

2) Геометрический смысл производной.

Пусть – некоторая кривая,– точка на кривой.

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точкеназывается предельное положение секущей,  если точкастремится к,  двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x)  (т.е. график функции  y = f(x)).  Пусть в точке он имеет невертикальную касательную.  Ее уравнение:(уравнение прямой, проходящей через точкуи имеющую угловой коэффициент  k).

По определению углового коэффициента , где– угол наклона прямойк оси.

Пусть– угол наклона секущейк оси,  где. Так как– касательная, то при

⇒⇒.

Следовательно,

.

Таким образом, получили, что– угловой коэффициент касательной к графику функции y = f(x) в точке(геометрический смысл производной функции в точке).  Поэтому уравнение касательной к кривой y = f(x) в точкеможно записать в виде

studfiles.net

10.3. Производная и ее геометрический смысл   математика-повторение

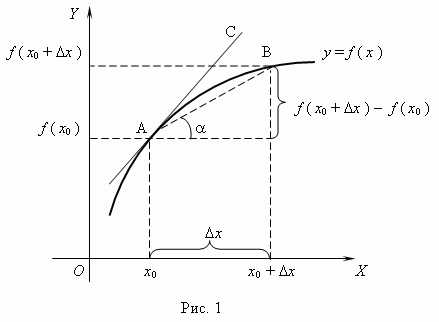
В координатной плоскости хОу рассмотрим график функции y=f (x). Зафиксируем точку М(х₀; f (x₀)). Придадим абсциссе х₀ приращение Δх. Мы получим новую абсциссу х₀+Δх. Это абсцисса точки N, а ордината будет равна f (х₀+Δх). Изменение абсциссы повлекло за собой изменение ординаты. Это изменение называют приращение функции и обозначают Δy.

Δy=f (х₀+Δх) — f (x₀).  Через точки M и N проведем секущую MN, которая образует угол φ с положительным направлением оси Ох. Определим тангенс угла φ из прямоугольного треугольника MPN.

Пусть Δх стремится к нулю. Тогда секущая MN будет стремиться занять положение касательной МТ, а угол φ станет углом α. Значит, тангенс угла α есть предельное значение тангенса угла φ:

Определение производной. Предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю, называют производной функции в данной точке:

Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох:

Смотрите видео 10.3. Определение производной. Геометрический смысл производной.

Примеры.

1. Найти приращение аргумента и приращение функции y=x², если начальное значение аргумента было равно 4, а новое  –4,01.

Решение.

Новое значение аргумента х=х₀+Δx. Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх=4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х₀+Δх) – f (x₀).  Так как у нас функция y=x²,  то Δу=(х₀+Δx)²— (х₀)²=(х₀)²+2x₀ · Δx+(Δx)²— (х₀)²=2x₀ · Δx+(Δx)²=

=2 · 4 · 0,01+(0,01)²=0,08+0,0001=0,0801.

Ответ: приращение аргумента Δх=0,01; приращение функции Δу=0,0801.

Можно было приращение функции найти по-другому: Δy=y (х₀+Δx) -y (х₀)=у(4,01) -у(4)=4,01²-4²=16,0801-16=0,0801.

2. Найти угол наклона касательной к графику функции y=f (x) в точке х₀, если f ‘(х₀) = 1.

Решение.

Значение производной в точке касания х₀ и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f ‘(х₀) = tgα = 1  → α = 45°,   так как  tg45°=1.

Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45°.

3. Вывести формулу производной функции y=xⁿ.

Смотрите видео: «10.3.0. Вывод формулы производной степени».

Дифференцирование — это действие нахождения производной функции.

При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же,  как мы вывели формулу производной степени: (xⁿ)’ = nx^n-1.

Вот эти формулы.     

Таблицу производных легче будет заучить, проговаривая словесные формулировки:

 

1. Производная постоянной величины равна нулю.

2. Икс штрих равен единице.

3. Постоянный множитель можно вынести за знак производной.

4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.

5. Производная корня равна единице, деленной на два таких же корня.

6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.

7. Производная синуса равна косинусу.

8. Производная косинуса равна минус синусу.

9. Производная тангенса равна единице, деленной на квадрат косинуса.

10. Производная котангенса равна минус единице, деленной на квадрат синуса.

Учим правила дифференцирования.

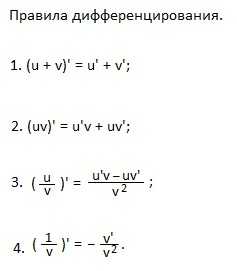1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.

2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.

3. Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».

4. Частный случай формулы 3.

Учим вместе!

 

 

www.mathematics-repetition.com

Дифференциальное исчисление функций

1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ В ТОЧКЕ

Пусть функция определена в точкеи некоторой ее окрестности. Придадим аргументуприращениетакое, что точкапопадает в область определения функции. Функция при этом получит приращение.

ОПРЕДЕЛЕНИЕ. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при(если этот предел существует и конечен), т.е.

.

Обозначают: ,,,.

Производной функции в точкесправа (слева) называется

(если этот предел существует и конечен).

Обозначают: ,– производнаяв точкесправа,

,– производнаяв точкеслева.

Очевидно, что справедлива следующая теорема.

ТЕОРЕМА. Функция имеет производную в точкетогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем

.

Следующая теорема устанавливает связь между существованием производной функции в точке и непрерывностью функции в этой точке.

ТЕОРЕМА (необходимое условие существования производной функции в точке). Если функция имеет производную в точке, то функцияв этой точке непрерывна.

ДОКАЗАТЕЛЬСТВО

Пусть существует . Тогда

,

где – бесконечно малая при.

⇒ ;

⇒

.

Но это означает, что непрерывна в точке(см. геометрическое определение непрерывности). ∎

Замечание. Непрерывность функции в точке не является достаточным условием существования производной этой функции в точке. Например, функциянепрерывна, но не имеет производной в точке. Действительно,

,

,

и, следовательно, не существует.

Очевидно, что соответствие является функцией, определенной на некотором множестве. Ее называютпроизводной функции и обозначают

, ,,.

Операцию нахождения для функции ее производной функции называютдифференцированием функции .

1) Физический смысл производной. Если функция и ее аргументявляются физическими величинами, то производная– скорость изменения переменнойотносительно переменнойв точке. Например, если– расстояние, проходимое точкой за время, то ее производная– скорость в момент времени. Если– количество электричества, протекающее через поперечное сечение проводника в момент времени, то– скорость изменения количества электричества в момент времени, т.е. сила тока в момент времени.

2) Геометрический смысл производной.

Пусть – некоторая кривая,– точка на кривой.

Любая прямая, пересекающая не менее чем в двух точках называетсясекущей.

Касательной к кривой в точке называется предельное положение секущей , если точкастремится к, двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую (т.е. график функции). Пусть в точкеон имеет невертикальную касательную. Ее уравнение:(уравнение прямой, проходящей через точкуи имеющую угловой коэффициент).

По определению углового коэффициента

,

где – угол наклона прямойк оси.

Пусть – угол наклона секущейк оси, где. Так как– касательная, то при

,

⇒ ,

⇒ .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции в точке (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой в точкеможно записать в виде

Замечание. Прямая, проходящая через точку перпендикулярно касательной, проведенной к кривой в точке, называетсянормалью к кривой в точке . Так как угловые коэффициенты перпендикулярных прямых связаны соотношением , то уравнение нормали к кривойв точкебудет иметь вид

, если .

Если же , то касательная к кривойв точкебудет иметь вид

,

а нормаль .

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x).

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0.

Уравнение нормали

Нормаль – это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали — это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

2. ТЕОРЕМА (необходимое условие существования производной функции в точке). Если функция имеет производную в точке, то функцияв этой точке непрерывна.

ДОКАЗАТЕЛЬСТВО

Пусть существует . Тогда

,

где – бесконечно малая при.

⇒ ;

⇒

.

Но это означает, что непрерывна в точке(см. геометрическое определение непрерывности). ∎

Замечание. Непрерывность функции в точке не является достаточным условием существования производной этой функции в точке. Например, функциянепрерывна, но не имеет производной в точке. Действительно,

,

,

и, следовательно, не существует.

Очевидно, что соответствие является функцией, определенной на некотором множестве. Ее называютпроизводной функции и обозначают

, ,,.

Операцию нахождения для функции ее производной функции называютдифференцированием функции .

3. Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

1. (f + g)’ = f ’ + g ’

2. (f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

studfiles.net

ПРОИЗВОДНАЯ | Энциклопедия Кругосвет

Содержание статьи

ПРОИЗВОДНАЯ – производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

.

Широко употребляются и другие обозначения:

Предел , где рассматривается только Dx > 0 или только Dx f в точке x. О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.

Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой, о вычислении скорости неравномерного движения, задачи о вычислении площади криволинейной фигуры. В работах Исаака Ньютона и Готфрида Вильгельма Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Однако современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. Современный математический анализ базируется на понятии предела, которое было дано (наряду с другими важнейшими понятиями – непрерывность, интеграл и т.д.) в работах французского математика Огюстена Луи Коши.

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M0 , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M0, а в некоторый следующий момент t + Dt оказалась в положении M1 – на расстоянии s + Ds от начального положения (см. рис.).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds. В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds.

Отношение представляет собой среднюю скорость движения точки за время Dt:

.

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

.

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt, когда приращение времени стремится к нулю. Так как

,

то.

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления.

Пусть кривая есть график функции y = f(x) в прямоугольной системе координат (см. рис.).

При некотором значении x функция имеет значение y = f(x). Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M1 перемещается вдоль кривой, приближаясь к точке M0, и угол j изменяется с изменением Dx. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

.

Следовательно, f´(x) = tga

т.е. значение производной f´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке M0(x,y) с положительным направлением оси Ox.

Дифференцируемость функций.

Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f(a) = f(b) = 0), то внутри отрезка [a,b] существует, по крайней мере одна, точка x = с, a c b, в которой производная fў(x) обращается в нуль, т.е. fў(c) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна точка с, a c b, что

f(b) – f(a) = f ў(c)(b – a).

Теорема об отношении приращений двух функций (теорема Коши). Если f(x) и g(x) – две функции, непрерывные на отрезке [a, b] и дифференцируемые во всех внутренних точках этого отрезка, причем gў(x) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a, b] найдется такая точка x = с, a c b, что

.

Производные различных порядков.

Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).

Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1–го и обозначается символом y(n) = (y(n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dx) = d2y = f ўў(x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1–го порядка:

dⁿy = d(dⁿ–1 y) = f(n)(x)dx(n).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x_i (i изменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… x_n), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x_i . Частная производная 1-ого порядка по x_i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x_i, сохраняют постоянные значения. Для частных производных вводятся обозначения

f_xn, или

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова

www.krugosvet.ru

Глава 5. Производная и ее применение

Глава 5. Производная и ее применение

Производная функции

Пусть функция определена на промежутке X. Возьмем точку хÎХ. Дадим значению х приращение , тогда функция получит приращение

.

Определение. Производной функции называется предел отношения приращения функции к приращению независимой пере­менной при стремлении последнего к нулю (если этот предел суще­ствует):

Производная функции имеет несколько обозначений: y’, , , .

Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, . Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функ­ция называетсядифференцируемой в этой точке.Функция, диф­ференцируемая во всех точках промежутка X, называетсядиффе­ренцируемой на этомпромежутке.

Геометрический смысл про­изводной: производная естьугловой коэффициент (тангенс угла наклона)касательной, проведенной к кривой в точке , т.е. k= .

Тогда уравнение касательной к кривой в точке при­мет вид

Механический смысл производной: производная пути по времени естьскорость точки в момент

Физический смысл производной: Если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

Зависимость между непрерывностью функции и дифференцируемостью.

Теорема. Если функция дифференцируема в точке x₀ , то она в этой точке непрерывна.

Правила дифференцирования.

1.Производная постоянной равна нулю, т.е. с’=0.

2. Производная аргумента равна 1, т.е. х¢=1.

В следующих правилах будем полагать, что и=и(х) и v=v(x) – дифф-ые функции.

3. Производная алгебраической суммы конечного числа дифферен­цируемых функций равна такой же сумме производных этих функ­ций, т.е. (u+v)¢=u¢+v¢.

4.Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. (uv)¢=u¢v+uv¢.

Следствие1. Постоянный множитель можно выносить за знак производной: (cu)¢=cu¢.

Следствие 2. Производная произведения нескольких дифференцируемх функций равна сумме произведений производной каждого из сомножителей на все остальные, например:

(uvw)¢=u¢vw+uv¢w+uvw¢.

5. Производная частного двух дифференцируемых функций равна

, при условии, что v¹0.

Производная сложной функций.

Пусть переменная у есть функция от переменной u (y=f(u)), a переменная u в свою очередь есть функция от независимой пере­менной х, т.е. задана сложная функция

.

Теорема. Если у=f(u) и — дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е.

Таблица производных.

Производная обратной функции.

Пусть – дифференцируемая и строго монотонная функция на некотором промежутке X. Если переменную у рас­сматривать как аргумент, а переменную х как функцию, то новая функция является обратной к данной и, как можно показать, непрерывной на соответствующем промежутке Y.

Теорема. Для дифференцируемой функции с производной, не рав­ной нулю, производная обратной функции равна обратной величине производной данной функции, т.е. .

Неявная функция и ее дифференцирование

Если функция задана уравнением , разрешенным относительно , то функция задана в явном виде. Под неявным заданием функции понимают задание функции в виде уравнения , не разрешенного относительно .

Если неявная функция задана уравнением , то для нахождения производной от по нет необходимости разрешать уравнение относительно : достаточно продифференцировать это уравнение по , рассматривая при этом как функцию , и полученное затем уравнение разрешить относительно .

Производная неявной функции выражается через аргумент и функцию .

Экстремум функции

Материал этого параграфа наиболее ва­жен для решения задач исследования функций и построения их графиков. Выделим наиболее важные, “узловые”, точки функ­ции, нахождение которых во многом определяет структуру графика. Это точки экстремума – максимума и минимума функции.

Определение 1. Точка называется точкой максимума функции , если в некоторой окрестности точки выполняется нера­венство £ .

Определение 2. Точка называется точкой минимума функции , если в некоторой окрестности точки выполняется неравен­ство ³ .

Значения функции в точках и называются соответст­венно максимумоми минимумомфункции. Максимум и минимум функции объединяются общим названием экстремума функции.

Экстремум функции часто на­зывают локальным экстремумом, подчеркивая тот факт, что понятие экстремума связано лишь с доста­точно малой окрестностью точки . Так что на одном промежутке функция может иметь несколько экстремумов, причем может слу­читься, что минимум в одной точке больше максимума в дру­гой, например, на рис. .

Наличие максимума (или минимума) в отдель­ной точке промежутка Х вовсе не означает, что в этой точке функ­ция ¦(x) принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)).

Необходимое условие экстремума. Если в точке дифферен­цируемая функция имеет экстремум, то в некоторой ок­рестности этой точки выполнены условия теоремы Ферма, и, следовательно, производная функции в этой точке равна нулю, т.е. . Но функция может иметь экстремум и в точках, в которых она не дифференцируема. Так, например, функция имеет экстремум (минимум) в точке x=0, но не дифференцируема в ней .

Поэтому необходимое условие экстремума может быть сфор­мулировано следующим образом.

Для того чтобы функция имела экстремум в точке , необходимо, чтобы ее производная в этой точке равнялась нулю или не существовала.

Точки, в которых выполнено необходимое условие экстрему­ма, т.е. производная равна нулю или не существует, называются критическими(или стационарными). Обращаем внимание на то, что эти точки должны входить в область определения функции.

Таким образом, если в какой–либо точке имеется экстремум, то эта точка критическая. Очень важно, однако, заметить, что обратное утверждение неверно. Критическая точка вовсе не обя­зательно является точкой экстремума.

Таким образом, для нахождения экстремумов функции требу­ется дополнительное исследование критических точек. Иными словами, требуется знать достаточное условие экстремума.

Асимптоты графика функции

В предыдущих параграфах мы изучали характерные точки функции. Теперь рассмотрим характерные линии. Важнейшими из них являются асимптоты.

Определение. Асимптотой графика функции у=¦(х) называется прямая, обладающая тем свойством, что расстояние от точки (x, ¦(х)) до этой прямой стремится к нулю при неограниченном удале­нии точки графика от начала координат.

На рис. а изображена вертикальнаяасимптота, на рис. 6 – горизонтальная асимптота, а на рис. в – наклонная. Этими тремя случаями исчерпываются все возможные расположения асимптот.

Нахождение асимптот графика основано на следующих утвер­ждениях.

Теорема 1. Пусть функция у =¦(х) определена в некоторой ок­рестности точки х₀ (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при (слева) или при (справа) – равен бесконечности, т.е. или . Тогда прямая х=x₀ является вертикальной асимптотой графика функции у =¦(х).

Очевидно, что прямая х=x₀ не может быть вертикальной асимптотой, если функция непрерывна в точке х₀, так как в этом случае . Следовательно, вертикальные асимптоты х=x₀ следует искать в точках разрыва функции у =¦(х) или на концах ее области определения (а, b), если а и b — конечные числа.

Теорема 2. Пусть функция у =¦(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у=b есть горизонтальная асимптота графика функции у =¦(х).

3 а м е ч а н и с. Если конечен только один из пределов или то функция имеет лишь левостороннюю y=b_л или правостороннюю y=b_п горизонтальную асимптоту.

В том случае, если , функция может иметь наклонную асимптоту.

Теорема 3. Пусть функция y=¦(x) определена при достаточно больших х и существуют конечные пределы и . Тогда прямая y=kx+b является наклонной асимптотой графика функции y=¦(x).

Наклонная асимптота, так же может быть правосторонней или левосторонней.

Глава 5. Производная и ее применение

Производная функции

Пусть функция определена на промежутке X. Возьмем точку хÎХ. Дадим значению х приращение , тогда функция получит приращение

.

Определение. Производной функции называется предел отношения приращения функции к приращению независимой пере­менной при стремлении последнего к нулю (если этот предел суще­ствует):

Производная функции имеет несколько обозначений: y’, , , .

Иногда в обозначении производной используется индекс, указывающий, по какой переменной взята производная, например, . Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функ­ция называетсядифференцируемой в этой точке.Функция, диф­ференцируемая во всех точках промежутка X, называетсядиффе­ренцируемой на этомпромежутке.

Геометрический смысл про­изводной: производная естьугловой коэффициент (тангенс угла наклона)касательной, проведенной к кривой в точке , т.е. k= .

Тогда уравнение касательной к кривой в точке при­мет вид

Механический смысл производной: производная пути по времени естьскорость точки в момент

Физический смысл производной: Если функция описывает какой-либо физический процесс, то производная есть скорость протекания этого процесса.

Зависимость между непрерывностью функции и дифференцируемостью.

Теорема. Если функция дифференцируема в точке x₀ , то она в этой точке непрерывна.

Правила дифференцирования.

1.Производная постоянной равна нулю, т.е. с’=0.

2. Производная аргумента равна 1, т.е. х¢=1.

В следующих правилах будем полагать, что и=и(х) и v=v(x) – дифф-ые функции.

3. Производная алгебраической суммы конечного числа дифферен­цируемых функций равна такой же сумме производных этих функ­ций, т.е. (u+v)¢=u¢+v¢.

4.Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. (uv)¢=u¢v+uv¢.

Следствие1. Постоянный множитель можно выносить за знак производной: (cu)¢=cu¢.

Следствие 2. Производная произведения нескольких дифференцируемх функций равна сумме произведений производной каждого из сомножителей на все остальные, например:

(uvw)¢=u¢vw+uv¢w+uvw¢.

5. Производная частного двух дифференцируемых функций равна

, при условии, что v¹0.

Рекомендуемые страницы:

lektsia.com