Производная интеграл и: Производная и интеграл — проще некуда / Хабр

Производная и интеграл — проще некуда / Хабр

19 декабря 2020 г. на Хабре вышла статья «Интуитивное объяснение интеграла».

В комментариях к ней некоторые пользователи указали, что объяснение получилось не очень интуитивным, например:

“Тема сама по себе интересная, недавно снова повторял курс, но должен сказать, что на мой взгляд, в материале нет изюминки. Автор прав, что в современных изданиях часто даются темы без описания их прикладного применения, из-за чего непонятен смысл их изучения.

Но конкретно интегралы это такая тема, которую надо описать или короче, чем у вас, или намного дольше.
Иначе и школьник не поймет, и те, кто знает, ничего нового не откроют.”

Я попробую изложить материал максимально коротко и просто. Так, чтобы школьники, наконец, поняли, пусть и с помощью родителей. Итак:

Я живу на плоскости, и мой мир выглядит так:

Все мои перемещения ограничиваются прямой линией, которую я называю «ось абсцисс» и обозначаю ее латинской буквой х. Таким образом, я могу гулять от точки, обозначенной цифрой ноль (там находится мой дом), вправо до бесконечности и назад, до нуля. Цифры на оси абсцисс позволяют мне понять, как далеко я от дома. Сейчас я нахожусь в 10 делениях от него.

Да, я слышал, что есть миры, в которых можно перемещаться и влево от нуля, и там расстояния обозначаются отрицательными числами: -1, -2 и т. д., до бесконечности. Кроме того, в тех мирах можно опуститься ниже оси абсцисс, но мой мир максимально прост.

Как-то раз, летящие птицы навели меня на мысль, что по нашему миру можно перемещаться не только влево или вправо, но и «вверх». Потом я узнал, что есть некие люди, умеющие строить дороги, ведущие в наши плоские небеса. Было бы неплохо бы с ними переговорить. И вот я общаюсь со специалистом (С), по строительству таких дорог:

Я: Здравствуйте, вы занимаетесь строительством дорог в небо?

С: Добрый день, да.

Я: А какие дороги вы умеете строить?

С: Самые простые варианты — прямые дороги различной крутизны.

Я: А что такое «крутизна»? Я всегда жил на горизонтальной прямой, и понятия не имею, что это слово может значить.

С: «Крутизна» показывает то, насколько трудно будет вам подниматься (или опускаться) по данной дороге. Чем круче дорога, тем тяжелее подъем или спуск. Давайте нарисуем на нашей плоскости еще одну ось — вертикальную. Мы назовем ее осью ординат, и обозначим латинской буквой у. На этой оси есть цифры, обозначающие «высоту» – расстояние до оси х.

Чтобы нам было проще ориентироваться в нашем двухмерном мире, нанесем на его плоскость линии, идущие от цифр, расположенных на осях х и у:

Теперь любое место (точку) на плоскости мы можем обозначить двумя цифрами. Первая цифра будет обозначать расстояние от нуля до проекции этой точки на ось х…

Я: Простите, а что такое «проекция»?

С: Видите внизу, на оси абсцисс, тень от летящей птицы? Она находится в точке, обозначенной цифрой 6 на оси х. Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.

Мы можем обозначить положение птицы двумя цифрами (6, 8). Первая цифра — проекция на ось х, вторая — проекция на ось у. Эти две цифры мы называем координатами птицы.

Вместо запятой между целой и дробной частями чисел, я буду ставить точку (т.е., не 13,5 а 13.5) для того, чтобы не путать с запятыми между соседними числами.

Я: Отлично, что дальше?

С: Дальше мы отгоним птицу и нарисуем дорогу:

Вы можете заметить, что эта дорога поднимается на одну клеточку вверх, при перемещении проекции на ось х на одну клеточку вправо.

Когда человек перемещается из точки с координатами (4, 4) в точку с координатами (10, 10), его проекция на ось х меняется на 6 цифр. То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.

Изменение какого-либо параметра (например, проекции на ось х или у), мы обозначаем буквой d (дельта). Изменение высоты мы запишем как dy, а изменение проекции на ось х — как dx. То есть, в данном случае, dу = 6, и dx также = 6.

Разделив изменение высоты на изменение положение тени человека при его перемещении (dy/dx), мы узнаём крутизну данного участка дороги: 6 / 6 = 1.

В нашей проектной документации мы используем очень краткое описание маршрута прокладываемой дороги. В данном случае оно будет выглядеть как математическая формула у = 1*х.

Это значит, что у всегда равен х, и это справедливо для любой точки дороги. Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.

Разумеется, можно было просто указать крутизну дороги одно цифрой, в данном случае, единицей, но проблема в том, что во-первых, дороги не всегда начинаются у вашего дома – в точке с координатами (0, 0). Во-вторых, существуют дороги, крутизна которых не постоянна. Но о них позже. А пока давайте нарисуем еще пару прямых дорог:

Мы видим, что верхняя дорога поднимается круче, чем та, которую мы рассмотрели ранее. А нижняя дорога – наоборот, более пологая. Высота (проекция на ось у), на которой находится человек, идущий по верхней дороге, равна 10. То есть, перемещаясь от начала координат до точки, в которой он находится сейчас, он изменил свою проекцию на ось у на 10 единиц. В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?

Я: Да, я понял это еще на первом примере. А если мы разделим проекцию перемещения человека, идущего по нижней дороге на ось у, на перемещение его тени по оси х, (5/10), мы получим цифру 0.5, или 1/2. Это и есть показатель крутизны нижней дороги?

С: Совершенно верно! Между каждой из дорог и осью х (горизонталью) есть некоторый угол. Чем больше этот угол, тем круче поднимается дорога. Соотношение координаты любой точки дороги (если дорога прямая) по оси у и координаты этой же точки по оси х, называют тангенсом этого угла. Для каждого угла — свой тангенс. Тангенс угла верхней дороги равен 2, тангенс угла нижней, более пологой дороги, равен 0. 5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.

Эти формулы мы называем функциями. Мы говорим, что у – функция от х, где х независимая переменная (мы ее задаём), а у – зависимая переменная, так как мы ее вычисляем, исходя из заданного значения х. И она жестко зависит от значения х. Например, задав х = 12 для дороги, описываемой формулой у = 0.5х, мы, подставляя цифру 12 вместо х, узнаём, что у в этой точке равен 6.

В математике функции обозначают, например, так: f(x) = x. Эта функция справедлива для дороги, рассмотренной нами в самом первом примере. Для второй и третьей дорог, функции будут выглядеть соответственно, как f(x) = 2x и f(x) = 0. 5x. Не очень сложно, да?

Я: Не очень. Что еще мне нужно знать о дорогах?

С: Мы делаем не только прямые дороги. Например, мы можем построить дорогу, которая описывается формулой (функцией) у = x², или f(x) = x². Крутизна этой дороги будет увеличиваться, по мере ее удаления от оси у.

Чтобы построить рисунок этой дороги, мы найдем (вычислим) координаты нескольких ее точек. Для этого мы подставим в формулу у = x² вместо х сначала 1, потом 2, затем 3 и т.д. И рассчитаем значение у для всех этих точек. Сначала подставим 1:

y = х² = 1² = 1.

Это значит, что для точки, с координатой по х равной 1, ее координата по у также равна 1. Нанесем эту точку на график:

Теперь рассчитаем координату по у для точки, с координатой по х равной 2:

y = x² = 2² = 4.

Таким образом, наша вторая точка будет иметь координаты (2, 4). Рассчитав у для точек с координатами по х 3 и 4, получим их полные координаты (3, 9) и (4, 16) соответственно. Нанесем эти точки на график:

Теперь соединим все точки линией, обозначающей дорогу:

Для любой точки этой дороги справедлива формула y = x². Например, для точки, с координатой по х = 1,5, мы получим ее координату по у, возведя 1,5 в квадрат. То есть, ее координаты (1.5, 2.25). Таким образом, мы можем узнать высоту любой точки дороги, задавая ее абсциссу (положение ее тени на оси х).

Но возникает проблема: мы не можем посчитать крутизну какой-либо точки дороги, так как она меняется постоянно. Не получится просто взять две точки дороги сверху и снизу от исследуемой и посмотреть, насколько изменится высота при прохождении пути между ними, разделив перемещение проекции на ось у на перемещение тени по оси х. Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:

Допустим, мы хотим узнать крутизну нашей кривой дороги на участке от начала координат (точки с координатами (0, 0)), до точки с координатами (3, 9). На этом участке дорога поднимается на 9 единиц, в то время, как удаление от начала координат по х составляет 3 единицы. Считаем крутизну так же, как мы считали ее для прямой дороги: 9 / 3 = 3. То есть, крутизна на этому участке, вроде бы, равна 3. Но если мы проведем прямую с крутизной, равной 3, то увидим, что на самом деле дорога в самом низу идет гораздо более полого, чем прямая, а в точке пересечения прямой и дороги, крутизна дороги уже больше крутизны прямой! Крутизна кривой в центре между этими точками также не совпадает с крутизной прямой. Засада. Что же делать? Как нам узнать крутизну каждой точки в ситуации, когда первая постоянно меняется, и нет ни единого прямого участка? Вот для таких случаев господин Ньютон и придумал дифференцирование.

Дифференцирование преобразует нашу функцию в другую функцию, которая как раз-таки позволяет точно вычислить крутизну дороги в данной точке. Мы не будем вдаваться в то, как он пришел к своему решению, а просто воспользуемся результатом его работы — таблицей дифференциалов. Я не буду ее приводить, в Сети такого добра навалом. Можно просто ввести в строку поиска формулу, которую нужно дифференцировать.

Для нашей функции f(x) = x² дифференцирование будет выглядеть таким образом: нам нужно перенести двойку из показателя степени влево, перед х, и уменьшить степень х на единицу. То есть, в данном случае степень х станет равна 1: f ‘(x) = 2x.

Обратите внимание на штрих после буквы f: f ‘(x) — так обозначается функция, которая произошла от нашей оригинальной функции. Поэтому ее называют производной функцией.

Но что нам теперь делать с этой производной? Как с ее помощью найти крутизну какой-либо точки оригинальной функции f(x) = x²? Очень просто. Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:

f ‘(x) = 2x = 2*1 = 2.

Эта двойка и показывает нам крутизну дороги над точкой 1 по оси х.

А какова крутизна дороги в точке с абсциссой 4 (проекцией на ось х = 4)? Подставляем эту четверку в производную функцию f ‘(x) = 2x = 2*4 и получаем цифру 8.

Эта восьмерка означает, что крутизна дороги в точке с абсциссой 4 равна 8. То есть, в этой точке дорога поднимается так же круто, как верхняя прямая на правом графике. Вот и весь смысл дифференцирования (нахождения производной).

Слева — график самой дороги, а справа — прямые, крутизна которых соответствует крутизне дороги в указанных точках. То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».

Давайте найдем производную нашей самой первой функции f (x) = x.

Мы проделаем такой же трюк: перенесем степень переменной вперед, перед х (это ничего не изменит, так как степень х была равна 1). Кроме того, мы уменьшим степень х на единицу. При этом степень станет равна нулю, и х превратится в единицу (потому, что любое число (кроме нуля) в нулевой степени равно 1).

Мы получили производную функции f(x) = x. Она выглядит так: f ‘(x) = 1. Что это значит? Это значит, что крутизна данной дороги на любом ее участке равна 1. То есть, при изменении абсциссы на dx, dy изменится ровно на такую же величину. В принципе, мы это знали и раньше, но теперь мы вычислили крутизну дороги через производную.

В учебниках пишут, что производная постоянной (некоторого числа) равна нулю. Почему это так?

Давайте построим дорогу, которая описывается функцией f(x) = 5. Это означает, что высота (проекция на ось у) любой точки данной дороги всегда равна 5, следовательно, dy (изменение высоты) равно нулю.

Поэтому эта дорога идет параллельно оси абсцисс, то есть, никакого изменения высоты не будет, на сколько бы мы не перемещались вправо. А раз крутизна дороги равна нулю, то и производная данной функции равна нулю (dy/dx = 0/dx = 0).

Повторим: производная отображает крутизну функции (графика, дороги), а в данном случае никакой крутизны нет. Что и имеется ввиду, когда говорят, что производная постоянной равна нулю.

Я: Хорошо, я все понял: по оригинальной функции я могу вычислить высоту дороги в любой ее точке, а по производной — крутизну в любой ее точке. Но дорога не может висеть в воздухе, она же должна опираться на ось х?

С: Совершенно правильный вопрос. Под дорогой нам придется сделать насыпь. И чем больше материала (клеточек) мы потратим на данный участок дороги, тем больше вам придется заплатить.

Я: А как вы посчитаете, сколько клеточек вам понадобится? Для участка прямой дороги, параллельной оси абсцисс f(x) = 5, все просто:

У нас получается прямоугольник, высота которого равна постоянной 5, а длину мы можем посчитать, вычитая координату по х левой стороны прямоугольника из координаты его правой стороны: 10 – 3 = 7. То есть, ширина прямоугольника равна 7, соответственно, его площадь равна 5 * 7 = 35 клеточек. Я буду вам должен за 35 клеточек.

Нет проблем и с дорогой, которая поднимается (или опускается) по прямой.

Как и в предыдущем случае, ширину основания мы узнаём, вычитая координаты границ по оси х друг из друга: 9 – 3 = 6.

Высоту найти немного сложнее: нам придется вычислить ее среднее значение. Для этого мы берем высоту (проекцию на ось у) левой верхней точки закрашенной фигуры, прибавляем к ней высоту правой верхней точки и делим пополам:

(1.5 + 4.5) : 2 = 3. Эта тройка — средняя высота фигуры. Мы умножаем ее на ширину фигуры и получаем цифру 18. То есть, на данный участок дороги потрачено 18 клеток, верно? Но как узнать, сколько клеток потребует участок дороги типа y = x²?

С протяженностью участка дороги слева направо разобраться легко, она равна 4 – 1 = 3 клетки, но как быть с высотой? Ведь мы не можем в данном случае сложить 1 и 16, затем разделить пополам и получить среднюю высоту фигуры? Как нам посчитать площадь этой насыпи?

С: Господин Ньютон предусмотрел и это. Метод подсчета площади криволинейных фигур называется «интегрирование». Нам придется вспомнить то, как мы находили производную функции f (x) = x²Она выглядит так: f ‘(x) = 2x.

Эту, как и многие другие математические операции, можно производить и в обратную сторону. Если нам известна производная функции, мы можем восстановить эту изначальную функцию, называемую первообразной. То есть, имея функцию, показывающую изменение крутизны дороги, мы можем восстановить функцию, показывающую саму дорогу — высоту любой ее точки.

Если для нахождения производной мы переносили вперед показатель степени переменной (двойку), и уменьшали степень переменной х на единицу

f(x) = x^{2=> f ‘(x) = 2x,}

то теперь нам следует поступить ровно наоборот: двойку, стоящую перед х следует перенести наверх, в степень: f ‘(x) = 2x => f(x) = x^{2.Так мы получаем первообразную функцию. То есть, ту функцию, от которой производная произошла.}

Но не все так просто, давайте рассмотрим дорогу, описываемую функцией

f (x) = x^{2+ 4:}

Она выглядит точно так же, как дорога f (x) = x^{2, но располагается выше. Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.}

Я: Почему?

С: Потому, что она не влияет на крутизну графика. Вы же помните, что производная описывает крутизну оригинального (первообразного) графика на каждом его участке? А теперь посмотрите на точки обоих графиков, расположенные, к примеру над цифрой 3 на оси х. Крутизна верхнего и нижнего графиков в этих точках одинакова! То же самое касается любых двух точек этих графиков, расположенных друг под другом. Эти две дороги идут параллельно друг другу, поэтому, их крутизна везде совпадает. Отличается только высота.

Но производная — это не про высоту, а про крутизну дороги. Потому и получается, что обе функции f (x) = x^{2и f (x) = x2+ 4 приводят к одной и той же производной f ‘(x) = 2x.}

Я: Погодите, но тогда получается, что функции, к примеру, f (x) = x² + 5 или f (x) = x² + 1.3 и даже f (x) = x^{2– 2 также приводят к одной и той же производной? Ведь они все параллельны друг другу, и их крутизна в точках, расположенных друг под другом, совпадает?}

С: Да, наша производная имеет бесконечный набор первообразных. Поэтому первообразную функции f (x) = 2x записывают как F (x) = x² + C, где буква С может быть любым числом. От этого числа зависит только высота, на которой проходит дорога. Точнее, разница высот между данной дорогой, и дорогой, у которой С = 0. Если Вы снова посмотрите на графики выше, то увидите, что любая точка верхнего графика ровно на 4 клетки выше аналогичной точки нижнего графика.

Обратите внимание также на то, что буква F в первообразной — заглавная (большая), Первообразная является «матерью» производной, поэтому мы относимся к ней с уважением, и пишем ее имя заглавной буквой.

Все множество функций, описываемых формулой F (x) = x² + C, называется неопределенным интегралом. Самая распространенная формула для нахождения неопределенного интеграла выглядит так:

По этой формуле мы можем найти неопределенный интеграл нашей функции f (x) = x². Для этого мы увеличиваем степень переменной на единицу, а в знаменатель просто ставим получившуюся степень переменной. Степень нашей переменной была 2, увеличив ее на единицу, получаем x³. Эту же тройку мы ставим в знаменатель (под дробную черту). Получается выражение F (x) = x³/3 + С.

Теперь вернемся к нашей криволинейной фигуре.

Чтобы узнать ее площадь, в полученный нами неопределенный интеграл нужно подставить абсциссу ее правой границы — цифру 4 (при этом постоянная С отбрасывается):

F (x) = x³/3 = 4³/3 = 21 1/3 (двадцать одна целая и одна треть)

То же самое проделаем с левой границей фигуры:

F (x) = x³/3 = 1³/3 = 1/3 (одна треть)

Теперь нам остается вычесть из первого числа второе: 21 1/3 – 1/3 = 21

Искомая площадь равна 21 клетке. Для проверки вы можете примерно посчитать закрашенные клетки на картинке.

Давайте подытожим все вышесказанное. Итак, у нас есть некоторая формула (функция) f(x), описывающая некую линию на графике.

Чтобы найти крутизну этой линии (функции) в какой-либо ее точке, мы находим производную данной функции f ‘(x), затем подставляем в полученную производную проекцию на ось х интересующей нас точки оригинальной функции, и вычисляем искомый параметр. Полученная цифра будет показывать тангенс угла наклона прямой, которая поднимается (или опускается) так же круто, как исходный график в исследуемой точке.

А чтобы найти площадь под участком графика исходной функции, следует найти ее первообразную F, затем, в эту первообразную по очереди подставить координаты по х правой и левой границы фигуры, площадь которой мы хотим найти, а затем вычесть два полученных числа друг из друга. Результат вычитания и есть искомая площадь.

Я: А почему вы отбросили постоянную С? Разве это не приведет к тому, что площадь под участками кривых f (x) = x^{2и f (x) = x2+ 4, находящимися друг под другом, будут одинаковыми?}

С: Не беспокойтесь, при нахождении интеграла второй функции, постоянная 4 в ее первообразной превратится в 4х, поэтому, к площади под ней добавится прямоугольник высотой 4 клеточки и ошибки не будет. Ну так что, какую дорогу Вы выбираете?

Понятие и свойства неопределённого интеграла, таблица интегралов

Неопределённый интеграл: 8 фактов, которые надо знать студенту

Факт 1. Интегрирование – действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F ‘(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x)..

Например, функция F(x) = sin x является первообразной для функции

f(x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x).

Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись

∫ 

f(x)dx

,

где знак ∫  называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.

Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то

∫ 

f(x)dx = F(x) +C

,                 (1)

где C – произвольная постоянная (константа).

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция – “быть дверью”. А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции “быть дверью”, то есть её неопределённым интегралом, является функция “быть деревом + С”, где С – константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции “сделана” из первообразной функции при помощи

формулы, которую мы узнали, изучая производную.

Тогда таблица функций распространённых предметов и соответствующих им первообразных (“быть дверью” – “быть деревом”, “быть ложкой” – “быть металлом” и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых “сделаны” эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой

C, например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна

f(x).

Пример 1.Найти множество первообразных функции

Решение. Для данной функции первообразной является функция

так как

Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.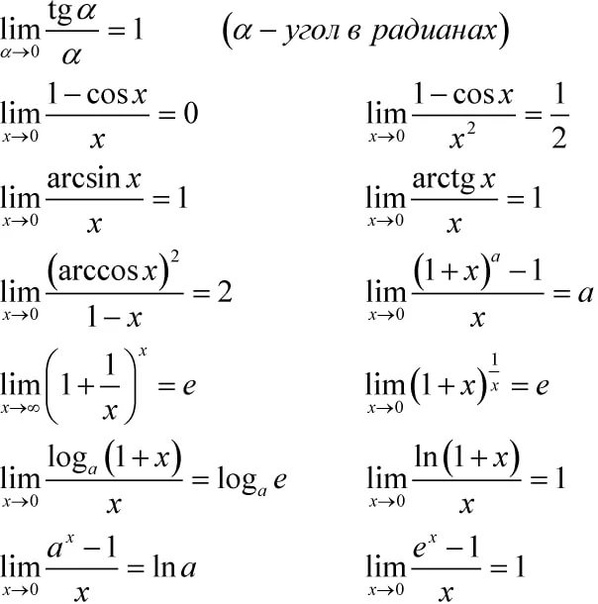 е.

или

                     (2)

Следовательно, функция – первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции

и вообще

где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.

---

Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.

---

В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.

Пример 2.  Найти множества первообразных функций:

1)   

2)

3)

Решение. Находим множества первообразных функций, из которых “сделаны” данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при n = 1/3,  имеем

3) Так как

то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной

x, а во втором – как функция от z.

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию

F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) – одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy.

Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.

Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.

Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

---

Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.

                  (3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

---

Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

  (4)

---

Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

  (5)

Факт 8. Пользусь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции.

Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

 

Продолжение темы “Интеграл”

Поделиться с друзьями

Урок 52.

производная и интеграл – Алгебра и начала математического анализа – 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №52. Производная и интеграл.

Перечень вопросов, рассматриваемых в теме:

• задачи, решаемые с применением производной
• задачи, решаемые с применением первообразной и интеграла

Глоссарий по теме

Производной функции в данной точке называется предел разностного отношения:

Уравнение касательной к графику данной функции в данной точке y=f(x)+f ‘(x₀)(x-x₀)

Функция у=f(x) возрастает на промежутке (a; b), если для любых х₁, х₂ из этого промежутка, таких, что х₁<х_2, выполняется неравенство у₁<у₂. Иными словами, меньшему значению аргумента соответствует меньшее значение функции.

Функция у=f(x) убывает на промежутке (a; b), если для любых х₁, х₂ из этого промежутка, таких что, х₁<х_2, выполняется неравенство у₁>у₂. Иными словами, меньшему значению аргумента соответствует большее значение функции.

Промежутки возрастания и убывания функции называют промежутками монотонности этой функции. Слова «функция монотонна на данном промежутке» означают, что функция на этом промежутке возрастает или убывает.

Точка х₁ называется точкой максимума функции f, если для всех х из окрестности точки х₁ выполняется неравенство f(x)<f(x₁).

Точка х₂ называется точкой минимума функции f, если для всех х из окрестности точки х₂ выполняется неравенство f(x)>f(x₂).

Для точек максимума и минимума принято общее название – точки экстремума.

Значения функции в этих точках называют соответственно максимумами и минимумами. Их общее название – экстремум функции.

Функция F(x) называется первообразной для функции f(x) на промежутке (a; b), если f(x)=F'(x) в каждой точке промежутка (a; b).

Дифференциальные уравнения связывают функцию и ее производные различных порядков. В дифференциальном уравнении в качестве неизвестной выступает не число, а функция.

Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество.

Фигура, ограниченная графиком неотрицательной функции f(x), заданной на отрезке [a; b], отрезком [a; b] и прямыми x=a и x=b, называется криволинейной трапецией.

Разность значений первообразной F для функции f точках b и a называется определенным интегралом этой функции от a до b.

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е.,   Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни– 2-е изд. – М.: Просвещение, 2010.

Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики – 4-е изд. – М.: Просвещение, 1995. – 288 с.: ил. – ISBN 5-09-0066565-9, сс. 7-50

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Федеральный центр информационно-образовательных ресурсов http://fcior.edu.ru/

Единая коллекция цифровых образовательных ресурсов http://school-collection.edu.ru/ 

Теоретический материал для самостоятельного изучения

1. Определение производной

Напомним, что производной функции в заданной точке называется предел разностного отношения:

Напомним правила вычисления производных:

Приведем пример:

Найти производную функции:

Решение:

Ответ: .

2. Решение задач с помощью производной.

Напомним, что геометрический смысл производной – это угловой коэффициент касательной. Те есть значение производной в данной точке равно угловому коэффициенту касательной к графику функции в заданной точке: f'(x₀)=k_кас.(x0)

Задача 1.

Найдем угол, под которым график функции пересекает ось абсцисс.

Найдем производную данной функции: .

Так как нам нужно узнать угол, под которым график функции пересекает ось абсцисс, нам нужно найти эти точки пересечения. Для этого решим уравнение: .

То есть график данной функции пересекает ось абсцисс в трех точках с найденными абсциссами.

Угол пересечения графика функции оси абсцисс – это угол, под которым касательная, проведенная к графику данной функции в точке с соответствующей абсциссой, пересекает ось абсцисс.

Угловой коэффициент касательной – это тангенс угла наклона касательной к оси абсцисс. Поэтому нужно найти значение производной данной функции в точках пересечения ее графика с осью абсцисс.

Найдем углы:

, , угол тупой, функция убывает

, , угол острый, функция возрастает

, угол острый, функция возрастает

Вспомним механический смысл производной.

Производная – это скорость материальной точки, положение которой изменяется по заданному закону.

Решим задачу 2.

Движение материальной точки описывается данным уравнением:

x(t) = 4+5t – 6t² + 2t³.

Найти скорость и ускорение точки в момент времени 3.

a(t)=-12+12·3=24.

Ответ: v=23; a=24.

Теперь напомним решение задачи на наибольшее и наименьшее значение, которая также решается с помощью производной.

Задача 3.

Найти прямоугольник наибольшей площади, вписанный в окружность радиуса R.

Решение:

Рисунок 1 – Иллюстрация к задаче 3

Исследуем функцию

При

Прямоугольником наибольшей площади, вписанным в круг радиуса R, является квадрат со стороной .

3. Теперь перейдем к повторению первообразной и интеграла.

Функция F(x) называется первообразной для функции f(x) на промежутке (a; b), если f(x)=F'(x) в каждой точке промежутка (a; b).

Все первообразные для данной функции отличаются друг от друга на константу

Пример.

Покажем, что функция является первообразной для функции .

Найдем производную: .

Преобразуем полученную функцию:

.

Получили функцию f(x).

4. Решение задач

Задача 4.

Найдите первообразную для функции , удовлетворяющую заданным условиям: F(1)=6.

Решение:

Для функции первообразными является функции вида

По условию: F(1)=6

С=5,4

Ответ:

Задача 5.

Точка движется прямолинейно с ускорением

Найдите закон движения точки, если в момент времени t=1с ее скорость равна 10м/с, а координата равна 12 (единица измерения ускорения 1м/с²)

Так как , то v(t) – первообразная для функции a(t).

Так как , то s(t) – первообразная для функции v(t).

,

,

Ответ:

Задача 6.

Вычислите объем тела, ограниченного плоскостями x=0, x=0,5 , площадь сечения которого плоскостью, параллельной плоскости yOz и отстоящей от нее на расстоянии х, меняется по закону:

Решение:

.

(куб.ед)

Задача 7.

Найдите площадь фигуры, ограниченной графиками следующих функций.

.

Решение:

Рисунок 2 – Иллюстрация к задаче 6.

Ответ: 7,5 кв.ед.

Примеры и разбор решения заданий тренировочного модуля

1. Найдите аргумент, при котором функция достигает наибольшего значения на отрезке [-3; -1].

Решение:

Найдем производную данной функции, сначала преобразуем функцию, выделив целую часть: .

Теперь найдем производную:

.

Полученная производная изменяет свой знак в точках 2 и -2, в точке 0 функция и производная не определены.

Так как задан отрезок [-3; -1], то рассмотрим поведение производной вокруг точки -2.

Так как на данном отрезке функция имеет единственную точку экстремума (максимум), то наибольшее значение она принимает в этой точке.

Ответ: -2

2. Вычислите массу участка стержня от x_1 до , если его линейная плотность задается формулой .

Решение:

Масса участка стержня на заданном участке выражается интегралом: .

Для того чтобы найти массу участка стержня от до x_2, если его линейная плотность задается формулой , вычислим интеграл:

.

Ответ: .

3. Найти путь, пройденный при свободном падении телом за первые 5 секунд (ускорение равно 9,8 м/с²)

Решение.

Скорость в момент времени t равна 9,8t.

Значит, путь, пройденный за промежуток времени [0; 5], выражается определенным интегралом:

м

Производная и интеграл. – Математика

Файл к занятию 29.

Производная. Применение производной. Первообразная.

Угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен производной функции в точке х_0..

Т.е. производная функции в точке х₀ равна тангенсу угла наклона касательной, проведенной к графику функции в точке (х₀; f(x₀)).

Задание 1. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

Ответ: 0,25

Задание 2. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀. Ответ: 0,6

Задание 3. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀. Ответ: -0,25

Задание 4. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀. Ответ: -0,2.

Механический смысл производной.

v ( t₀ ) = x’ ( t₀ )

 скорость – это производная координаты по времени.  Аналогично, ускорение – это производная скорости по времени: 

a = v’ ( t ).

Задание 5. Материальная точка движется прямолинейно по закону x(t)=12 t²+4 t+27, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=2 с. Ответ: 52

Задание 6. Материальная точка движется прямолинейно по закону x(t)=16 t³+t²−8 t+180, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 42 м/с? Ответ: 1

Достаточный признак возрастания (убывания) функции

1. Если f `(x)в каждой точке интервала (, то функция возрастает на (.

2. Если f `(x)в каждой точке интервала (, то функция убывает на (.

Необходимое условие экстремума

Если точка х₀ является точкой экстремума функции и в этой точке существует производная, то f `(x₀ )=0

Достаточное условие экстремума

Если f `(x₀) = 0 и при переходе через точку x₀ значение производной меняет знак с «+» на « – », то x₀ является точкой максимума функции.

Если f `(x₀) = 0 и при переходе через точку x₀ значение производной меняет знак с « – » на «+», то x₀ является точкой минимума функции.

Задание 7. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 10). Най­ди­те ко­ли­че­ство точек ми­ни­му­ма функ­ции f(x) на от­рез­ке [−3; 8].

Ре­ше­ние. Точки ми­ни­му­ма со­от­вет­ству­ют точ­кам смены знака про­из­вод­ной с ми­ну­са на плюс. На от­рез­ке [−3; 8] функ­ция имеет одну точку ми­ни­му­ма x = 4. Значит, такая точка 1. Ответ: 1.

Задание 8. На рисунке изображён график дифференцируемой функции y=f(x) и отмечены семь точек на оси абсцисс: x​1, x​2, x​3, x​4, x​5, x​6, x​7. В скольких из этих точек производная функции f(x) отрицательна? Ответ: 3

Задание 9. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11 ; − 1). Найдите точку из отрезка [− 7 ; − 2], в которой производная функции f(x) равна 0. Ответ: -4

Задание 10. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (2 ; 13). Найдите точку максимума функции f(x). Ответ: 9

Задание 11. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 3; 8). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение? Ответ: -2

Задание 12. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 2 ; 11). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси абсцисс или совпадает с ней. Ответ: 3

Задание 13. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4 ; 6). Найдите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна прямой y=3x или совпадает с ней. Ответ: 5

Задание 14. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 4 ; 13). Найдите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=− 2x−10 или совпадает с ней. Ответ: 5

 Задание 15. Прямая y=5x-8 является касательной к графику функции 4x²-15x+c. Найдите c. Oтвет: 17.

Первообразная

Первообразной функцией F(x) для функции f(x) называется функция, производная которой равна исходной функции. F‘ (x)= f(x).

Задание 16. На рисунке изображён график y=F (x) одной из первообразных некоторой функции f (x), определённой на интервале (1;13). Пользуясь рисунком, определите количество решений уравнения  f (x)=0 на отрезке  [2;11]. Ответ: 4

За­да­ние 17. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (− 7; 8). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [0; 5]. Ответ:1

Задание 18. На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x) и отмечены восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек функция f(x) отрицательна? Ответ: 3

Задание 19. На рисунке изображён график некоторой функции y=f(x). Функция F(x)=12x³−3x²+152x−92 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры. Ответ: 592

Алгоритм нахождения точек экстремума

1. Найти область определения функции.

2. Найти производную функции  f ‘(x)

3. Найти точки, в которых f ‘(x) = 0.

4. Отметить на числовой прямой область определения функции и все нули производной.

5. Определить знак производной для каждого промежутка. (Для этого подставляем “удобное” значение  x из этого промежутка в f ‘(x)).

6. Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере (max или min) в каждой из этих точек.

Задание 20. Найдите точку максимума функции y=(2x−1)cosx−2sinx+5, принадлежащую промежутку (0 ; π/2). Ответ: 0,5

Задание 21. Найдите точку максимума функции y=. Ответ: 6

Алгоритм нахождения наибольшего и наименьшего значение функции на отрезке

1. Найти производную функции f ‘(x).

2. Найти точки, в которых f ‘(x) = 0. Проверить принадлежность этих точек отрезку

3. Найти значение функции на концах отрезка и в данных точках.

4. Выбрать из полученных значений наибольшее или наименьшее.

Задание 22. Найдите наименьшее значение функции y=x−6x+1 на отрезке [2 ; 25]. Ответ: -31

Задание 23. Найдите наименьшее значение функции y=8cosx+30x/π+19 на отрезке [− 2π/3; 0]. Ответ: -5

Дополнительно. 1. Найдите точку максимума функции y=(x−11)^2​⋅e ^x − 7.

2. Найдите наибольшее значение функции y=х⁵-5х³-20х на отрезке [− 9 ; 1]. Ответ:48

08. ПРОИЗВОДНАЯ и ИНТЕГРАЛ – Физика это просто!!! 2016

Теперь пора познакомиться с математикой, которая поможет вам быстро и просто решать задачи механики.

И не только механики. Можно безо всякого преувеличения заметить, что производные и интегралы используются при описании физических моделей реального мира во всех разделах физики.

Итак, вернемся к рассмотренным в параграфах 3, 4, 5 понятиям пути, скорости и ускорения. Рассмотрим подробнее соотношения между координатами материальной точки, ее скоростью и ускорением в каждый момент времени.

            Ограничимся, для начала, случаем одномерного движения.

            Нарисуем произвольный график зависимости скорости V(t) материальной точки от времени t.

  Рисунок 6  

            В произвольный момент времени t₁ мгновенная скорость V₁ = V(t₁). 

            Запомним два утверждения:

1) Тангенс угла наклона касательной к графику V(t) в точке (в момент времени) t₁ равен по величине значению ускорения а(t₁) материальной точки в этот момент времени t₁.

2) Площадь под кривой V(t) от t₁ до t₂ равна по величине пути, пройденному материальной точкой за время от момента t₁ до момента   t₂ со скоростью, описываемой функцией V(t).

           

Строго математически это можно записать:

1.                   

– “ускорение” есть первая производная функции скорости по времени.

Просто запомните! Тангенс угла наклона касательной к функции f(t) в точке t есть значение первой производной этой функции в этой точке t !

Для нас с вами в данный момент, не вдаваясь в “глубины” дифференциального исчисления, важно следующее:

·        Для любой функции скорости материальной точки от времени V(t) существует функция a(t), которая определяет ускорение нашей материальной точки в любой момент времени t, в который определена функция скорости V(t). И, что самое приятное, мы можем в подавляющем большинстве случаев очень просто найти одну функцию из другой. И наоборот.

            Как мы помним, «вычисление производной» в математике называется операцией «дифференцирования», или «операцией взятия производной» (видимо, по аналогии «взятия крепости»). 

            Для некоторых функций эта операция по своей сложности, действительно, сравнима со взятием укрепленной крепости или покорением неприступной вершины. Но, к счастью, в курсе средней школы производные большинства функций можно просто брать из готовых таблиц. Либо, вообще, в интернет-сервисах.

Например, http://www.webmath.ru/web.php или http://www.wolframalpha.com/.

Просто задаете функцию – получаете производную!

Напомним основные правила дифференцирования:

•    производная суммы:

• производная произведения:

• производная частного:

•  производная сложной функции равна произведению производных:

Приведем таблицу производных простейших функций:

• Производная степенной функции: 

• Производная показательной функции:

• Поизводная экспонециальной функции: 

• Производная логарифмической функции:

• Производные тригонометрических функций:

• Производные обратных тригонометрических функций:

2.         Площадь под кривой, заданной функцией V(t) на отрезке от t₁ до t₂ есть значение “определенного интеграла” этой функции на отрезке [t₁;t₂].  Про первообразную функции мы уже  знаем. 

             Математически, определенный интеграл – это разность значения первообразной в конечной точке отрезка t₂ минус значение первообразной в начальной точке отрезка t₁. Он равен величине площади под кривой. На рисунке 2 эта площадь закрашена серым цветом.

где X_1,2(t₁,t₂) – перемещение, совершенное материальной точкой от момента времени t₁ до момента времени t₂.

!!!        Заметим, что формула (32) вычисляет именно «перемещение», потому что пройденный путь – это всегда положительная величина. Мы прошли километр в одну сторону, затем километр в обратную – в результате, пройденный путь равен двум километрам, а перемещение равно нулю. Мы никуда не переместились, вернувшись в исходную точку. Пройденный путь будет равен перемещению, только если мы движемся все время в одну сторону по прямой.

По формуле (32) мы вычисляем перемещение, как разность координат в конечный момент времени и в начальный момент времени.

            Для нас важно запомнить:

            Первое. Неопределенный интеграл (так называемая «первообразная») какой-либо функции f(t) – это такая функция, продифференцировав которую мы получим обратно саму функцию f(t). В математике первообразную функции часто обозначают заглавной буквой, например, для функции f(t)первообразную можно обозначить F(t). Определенный интеграл на каком-либо отрезке области определения функции f(t) – это, по сути, разница значений первообразной этой функции F(t) в конечной и начальной точках отрезка.

            Второе. Если мы интегрируем функцию скорости V(t) от точки t₁ до точки t₂, то интегралом будет перемещение X(t₂) – X(t₁).

            Резюме: 

·        Если мы знаем функцию зависимости координаты X(t) точки от времени t, то, найдя производную этой функции по времени t (обозначим эту производную V(t)), мы получим функцию зависимости мгновенной скорости точки от времени. 

·        Если мы далее продифференцируем полученную функцию скорости V(t) по времени t, то получим “первую производную” скорости по времени – функцию a(t) – функцию зависимости мгновенного ускорения от времени. 

            Причем, все это чистая математика. Более того, в большинстве случаев функции можно брать прямо из специальных таблиц производных.

            А что, если мы продифференцируем функцию a(t)?

            В результате (в общем случае) мы получим некую функцию зависимости мгновенного изменения ускорения от времени. Это будет функция, которая позволит нам видеть, как сильно в каждый момент времени меняется ускорение движения нашей точки. В принципе, можно долго продолжать эти операции последовательного дифференцирования. И, заметьте, все время мы будем получать функции, которые наделены физическим смыслом.

            К счастью, в рамках школьной программы мы ограничимся равноускоренным движением. Т.е. таким движением, при котором значение ускорения не изменяется. Оно равно некоторой “константе” (постоянной величине, не изменяющейся с течением времени).

A(t) = const.

            А производная от константы всегда равна нулю! И, соответственно, дальше, хоть задифференцируйся, будет 

A'(t) = … = A”^…‘(t) = 0.

            Все последующие производные будут равны нулю.

как понять и решать неопределенные и определенные интегралы, правила и примеры

 

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие «интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

«Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Производная – интеграл – Большая Энциклопедия Нефти и Газа, статья, страница 1

Производная – интеграл

Cтраница 1

Производная интеграла равна подынтегральной функции.  [1]

Производная интеграла с переменным верхним пределом равна значению подынтегральной функции при верхнем пределе.  [2]

Аналогичным образом производная интеграла по его нижнему пределу интегрирования равна отрицательному значению подынтегрального выражения в соответствующей точке.  [3]

Можно сказать и так: производная интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интеграции подставлен верхний предел.  [4]

Формулу (2.4) читают так: производная интеграла по параметру равна интегралу от производной подынтегральной функции по этому же параметру плюс производная верхнего предела ( по параметру), умноженная на значение подынтегральной функции при верхнем пределе, и минус производная нижнего предела, умноженная на значение подынтегральной функции при нижнем пределе.  [5]

Из теоретического курса известно, что производная интеграла с постоянным нижним пределом и переменным верхним пределом равна подынтегральной функции при значении ее аргумента, равном верхнему пределу.  [6]

К этому следует добавить, что производная интеграла Лебега по переменному верхнему пределу почтя всюду существует и равна подинтегральной функция.  [7]

При этом учтено соотношение (8.10), вследствие которого производная интеграла (10.6) по нижнему пределу обратится в нуль.  [8]

Если верхний предел определенного интеграла есть величина переменная, то производная интеграла по верхнему пределу равна значению подынтегральной функции при этом верхнем пределе.  [9]

Эту теорему коротко можно сформулировать следующим образом: для непрерывной функции производная интеграла по верхнему пределу равна самой функции.  [10]

Эту теорему коротко можно сформулировать следующим образом: для непрерывной функции производная интеграла по верхнему пределу равна самой функции.  [11]

Формула (10.5) называется формулой дифференцирования интеграла по параметру по правилу Лейбница: производная интеграла по параметру равна интегралу от производной подынтегральной функции по этому параметру.  [12]

Правило интегрирования функции с постоянным множителем и правило интегрирования алгебраической суммы функций доказываются одним и тем же методом, Этот метод основан на том, что производная интеграла равна подынтегральной функции и что два интеграла равны, если равны их производные.  [13]

Заметим, что к понятию сингулярного интеграла приходят, в частности, при рассмотрении вопроса о дифференцировании интегралов, зависящих от параметра. Известно, что производная интеграла по параметру совпадает с интегралом от производной по параметру подынтегрального выражения, если последний равномерно сходится по этому параметру.  [14]

Для определения оптимального норматива, соответствующего минимуму средних суммарных потерь, найдем производную этого выражения по Яд и приравняем ее к нулю. Как известно, производная интеграла по верхнему или нижнему пределу равна значению подинтегральной функции со знаком плюс или минус.  [15]

Страницы:      1    2

Производные и интегралы

Основные рабочие инструменты в исчислении, производные и интегральные пронизывают все аспекты моделирования природы в физических науках. Производная функции может быть геометрически интерпретирована как наклон кривой математической функции f (x), построенной как функция от x. Но его значение для моделирования природы намного глубже, чем может предполагать это простое геометрическое приложение. В конце концов, вы можете увидеть, как вы рисуете конечные треугольники, чтобы определить наклон, так почему же производная так важна? Его важность заключается в том, что многие физические объекты, такие как скорость, ускорение, сила и т. Д., Определяются как мгновенные скорости изменения некоторой другой величины.Производная может дать вам точное внутреннее значение для этой скорости изменения и привести к точному моделированию желаемой величины. Интеграл функции можно геометрически интерпретировать как площадь под кривой математической функции f (x), построенной как функция от x. Вы можете увидеть, как вы рисуете большое количество блоков, чтобы аппроксимировать область под сложной кривой, и получите лучший ответ, если вы используете больше блоков. Интеграл дает вам математический способ нарисовать бесконечное количество блоков и получить точное аналитическое выражение для площади.Это очень важно для геометрии – и чрезвычайно важно для физических наук, где определения многих физических объектов могут быть представлены в математической форме, такой как площадь под кривой. Площадь небольшого блока под кривой можно представить как ширину полосы, взвешенную на высоту полосы (т.е. умноженную на нее). Многие свойства непрерывных тел зависят от взвешенных сумм, которые, чтобы быть точными, должны быть бесконечными взвешенными суммами – задача, специально созданная для интеграла.Например, нахождение центра масс сплошного тела включает взвешивание каждого элемента массы по его расстоянию от оси вращения, процесс, для которого необходим интеграл, если вы собираетесь получить точное значение. Огромное количество физических проблем включает в себя такие бесконечные суммы в своих решениях, что делает интеграл важным инструментом для ученого-физика.

Указатель Производные концепции Интегральные концепции

исчисление – Интеграл от производной функции не равен исходной функции?

В дополнение к уже предоставленным отличным ответам, есть несколько субсидий, на которые следует прямо указать.

Существуют две основные концепции интеграции: первая – это неопределенное интегрирование , – поиск первообразной функции, а вторая – это определенное интегрирование , – определение меры (подписанной) области, заключенной в график функция и ось абсцисс. Существуют различные способы кодификации этих понятий на строгом математическом языке.

Например, если мы знаем, что $ f $ – вещественная функция над $ [a, b] $, $ a, b \ in \ mathbb {R} $, мы используем определение Римана для $$ \ int_ {a} ^ b f (x) \, \ operatorname {d} \! x \, $$ который можно найти в любом учебнике элементарного исчисления.При условии, что $ f $ удовлетворяет некоторым конкретным условиям, мы говорим, что $ f $ интегрируем по Риману над $ [a, b] $, и присваиваем вышеуказанному символическому выражению уникальное действительное значение. (Существует также теорема, согласно которой, если $ f $ интегрируем по Риману над $ [a, b] $, он также интегрируем по Риману над любым замкнутым подынтервалом в $ [a, b] $).

А как насчет неопределенной интеграции? Помните, что для действительной функции $ h $ на интервале $ I $ функция $ H: I \ to \ mathbb {R} $ называется первообразной $ h $ на всякий случай, если $ H ‘= h $.Вы должны заметить, что всякий раз, когда $ H $ является первообразной $ h $, $ H + c $ также является первообразной $ h $, и вы можете доказать, что любая первообразная $ h $ имеет вид $ H + c $ для некоторой константы c.

А теперь приготовьтесь к горькой правде …

Признавая, что существует бесконечное количество первообразных для $ h $ (все функции $ H + c $), математики сходят с ума, нарушают свои собственные правила и гордо заявляют: $$ \ int h (x) \, \ operatorname {d} \! x = H (x), $$ без малейшего стыда! Иногда мы даже доходим до утверждения, что « неопределенный интеграл от $ h (x) $ равен H (x) для всех $ x \ in I $»! На самом деле не существует такой вещи, как , неопределенный интеграл функции, поскольку не существует такой вещи, как , первообразная функции; их бесчисленное множество.x f ‘(t) \, \ operatorname {d} \! t, \ x \ in D, $$ где $ f ‘$ должно быть интегрируемым по Риману над $ D $ (напомним также, что $ a \ in D $, а $ D $ должен быть замкнутым и ограниченным интервалом). После всего этого вы можете использовать фундаментальную теорему исчисления и обнаружить, что $$ F (x) = f (x) – f (a), \ x \ in D, $$ как уже упоминалось другими.

Я знаю, что много писал, но думаю, что это помогает ОП разобраться с некоторыми обычными заблуждениями, которые лежат в основе ее / его вопроса. Любые комментарии / исправления приветствуются!

World Web Math: сводка расчетов

World Web Math: сводка расчетов Исчисление состоит из двух основных частей: дифференциального исчисления и интеграла. исчисление.Дифференциальное исчисление изучает производную и Интегральное исчисление изучает (сюрприз!) интеграл. Производная и интеграл связаны тем, что оба определены через понятие предела: это обратные операции друг друга (факт, который иногда называют фундаментальной теоремой исчисления): и они оба являются фундаментальными для большей части современной науки, поскольку мы знать это.

Деривативы

Предел функции f ( x ) как x приближается к , а равно b , если для каждой желаемой близости к b вы можете найти небольшой интервал вокруг (но не включая) a , который достигает этой близости, когда отображается на f .Пределы дают нам прочную математическую основу для изучения как бесконечное и бесконечное. С ними также легко обращаться алгебраически: где в последнем уравнении c – постоянная, а в первые два уравнения, если оба предела f и g существовать.

Следует помнить об одном важном факте:

совершенно не зависит от f (a) – по сути, f (a) часто не определяется. В счастливом случай, когда мы говорим, что f – это непрерывно на a .Это также иногда полезно говорить об одностороннем (левом или правом) пределы, где мы заботимся только о значениях x , которые меньше или больше a .

Производная от f ( x ) при x = a (или f´ ( a )) определяется как

везде, где существует предел. Производная имеет множество интерпретаций. и приложения, включая скорость (где f дает положение как функция времени), мгновенная скорость изменения или наклон касательной к графику f .С помощью алгебраические свойства пределов, вы можете доказать эти чрезвычайно важные алгебраические свойства производные: Эти правила, например, позволяют вычислить производную любого рациональная (= отношение двух многочленов) функция. В частности, цепное правило имеет много приложений. Во-первых, если у вас есть две обратные функции f и g , то есть если f ( g ( x )) & nbsp = & nbsp x , то цепное правило подразумевает, что f´ ( г ) = 1/ г´ ( x ).

Также, если у вас есть неявно определенная функция между x и y , например x ² – 2 x y + y ² = 1, то вы можете выполнять неявное дифференцирование (в основном, просто взяв производную от всего по отношению к x и y прихватывают dx s и dy s, чтобы указать какой), чтобы получить 2 x dx – 2 x dy -2 y dx + 2 лет = 0.Затем, если вы решите для dy / dx , это будет быть равным (по правилу цепочки) y ´, и если вы решите для dx / dy , это будет равно x с острым углом. Примечание что в этом случае любая производная будет в терминах обоих x и y .

Вам может быть интересно узнать о производных от вашего любимого тригонометрические функции. Хорошо,

Эти два факта в сочетании с приведенными выше правилами позволяют легко вычислить производные остальных тригонометрических функций и их обратное.Производные гиперболического функции аналогичны, за исключением того, что Многие физические приложения производных сводятся к поиску решений. к дифференциальным уравнениям: уравнения, связывающие функцию и ее производные. Например, и синус, и косинус удовлетворяют условию дифференциальное уравнение f ´´ ( x ) = – f ( x ), который моделирует идеальные маятники, пружины, и другие примеры простого гармонического движения. Уравнение f ´ ( x ) = k f ( x ) возникает при моделировании роста населения и радиоактивного распада, и решается функцией f ( x ) = e ^kx , где называется постоянной Эйлера и определяется как уникальное действительное число e , такое что ( e ^x ) ´ = e ^x .Обратное экспоненциальная функция e ^x – функция натурального логарифма журнал ( x ), обладающий множеством полезных и интересных свойств, в том числе:

• журнал ( ab ) = журнал a + журнал b
  [Таким образом логарифм превратить умножение в в дополнения было то, почему журнальные таблицы (и их аналоги, правила слайдов) использовались для долгого умножения до появления компьютеров.]
• журнал ( a / b ) = журнал a – журнал b
• e ^{(бревно x )} = x и лог e ^x = x
• бревно x ^a = a бревно x
• a ^x = e ^{( x лог a )}
• (лог ( x )) ´ = 1/ x
• журнал 1 = 0 Тесно связан с натуральным логарифмом логарифм по основанию b , (log _b x ), который может быть определен как журнал ( x ) / журнал ( b ).

  Наконец, для облегчения работы с графическими функциями можно использовать производные. Первый, они дают вам наклон графика в точке, что полезно. Во-вторых, точки, где наклон графика горизонтален ( f ´ ( x ) = 0) особенно важно, потому что это единственные точки, в которых родственник может иметь место минимум или максимум (в дифференцируемой функции). Эти точки, где f ´ ( x )) = 0, являются назвал критические точки . Чтобы определить, является ли критический точка – это минимум или максимум, или, в более общем смысле, для определения вогнутость функции, можно использовать вторые производные; f ´´ ( x ) f´´ ( x )> 0 означает относительный минимум / вогнутость вверх.Наконец, принимая предел как x переходит в положительную или отрицательную бесконечность дает информацию об асимпотитности функции. С этой целью деривативы могут помочь вам с некоторыми трудными ограничениями: Правило Лопиталя, если lim f ( x ) и lim g ( x ) оба равны нулю, тогда lim f ( x ) / lim g ( x ) знак равно lim f ´ ( x ) / lim g´ ( x ). Доказательство правила Л’Опиталя опирается на теорему о среднем значении: для любой функции f ( x ), различие между и и b , между a и b , так что производная от f при c такой же, как средний уклон между и и b :

  Интегралы

  Интеграл f ( x ) от до до b относительно x обозначается как и дает площадь под графиком f и выше интервал [ a , b ].Формально его можно определить как Риман сумма: предел площадей прямоугольных аппроксимаций площади по мере приближения все лучше и лучше.

  Как было сказано ранее, интегрирование и дифференцирование противоположны операции. Чтобы быть точным, основная теорема исчисления утверждает что

  В более общем плане, используя правило цепочки, Зная эти факты, мы теперь знаем огромное количество интегралов: просто переверните любую таблицу производных. Вот некоторые дополнительные факты об интегралах: Для c постоянная,
  Интеграл положительной непрерывной функции от до до b с b> a больше нуля.Интеграл от a до b f ( x ) – г ( x ), с f ( x )> г ( x ) в интервал [ a , b ] дает площадь от f ( x ) до g ( x ).

  Если этих свойств недостаточно для решения вашего интеграла, и если вы не может найти его ни в одной таблице, тогда вот еще несколько уловок обмен:

  • Замена (“ обратное ” цепному правилу):
  • Интеграция по частям (“ invserse ” Правила продукта):
  • Неполные дроби: каждая рациональная функция со знаменателем. который можно разбить в сумму дробей вида где A , B , C , D и E – константы (конечно, не те же константы в две формы) могут быть (более) легко интегрированы.
  • Численное приближение. Это может не дать вам точного ответ, но приблизительно область под f ( x ) с прямоугольниками, трапециями или даже более сложными формами может дать вы значение, близкое к интегралу, когда никакой другой метод не будет работать. Для краткое объяснение использования приложения, доступного MIT студенты, см. Определенный Интегралы на Maple, часть использования Maple для предметов ESG, используется как часть предмета MIT 18.01A в ESG.
  Интегралы определены для поиска областей, но их также можно использовать для вычислить другие свойства меры, такие как длина или объем.Для например, интеграл дает длина дуги графика f ( x ) между x = a и x = b . В интеграл дает объем, содержащийся, вращая график f ( x ) между x = a и x = b о x – ось. Интегральный дает объем, содержащийся, вращая график f ( x ) от x = до и x = b относительно оси y .Наконец, площадь поверхности, образованная вращением графика f ( x ) между x = a и x = б о ось x можно найти с помощью интеграла Иногда вы захотите взять интеграл по неограниченному интервалу. например, от 1 до бесконечности, или взять интеграл от функции, которая не определено в некоторых точках (например, 1/ x ^1/2 ). Это несобственные интегралы, и их можно найти, взяв предел интеграл по интервалу, который либо растет к бесконечности, либо к точкам, где функция не определена.

  ---

  Индексная страница исчисления | Вернуться на страницу категорий World Web Math

  ---

  [email protected]
  Последнее изменение 10 января 2000 г.

Введение в интеграцию

Интеграция – это способ добавления фрагментов для поиска целого.

Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но проще всего начать с поиска области между функцией и осью x следующим образом:

Что это за площадь?

Ломтики

Мы можем вычислить функцию в нескольких точках, и сложить срезы шириной Δx вот так (но ответ будет не очень точным):
Мы можем сделать Δx намного меньше, а сложить много маленьких кусочков (ответ становится все лучше):
И когда срезы приближаются к нулю по ширине , ответ приближается к истинному ответу . Теперь мы пишем dx , что означает, что срезы Δx приближаются к нулю по ширине.

Это много сложить!

Но складывать их не нужно, есть «ярлык», потому что …

… поиск интеграла – это , обратный нахождения производной.

(Так что вам действительно следует знать о производных финансовых инструментах, прежде чем читать больше!)

Как здесь:

Пример: 2x

Интеграл от 2x равен x ² …

… потому что производная x ² равна 2x

(Подробнее о “+ C” позже.)

Этот простой пример можно подтвердить вычислением площади:

Площадь треугольника = 1 2 (основание) (высота) = 1 2 (x) (2x) = x ²

Иногда интеграция может быть такой простой!

Обозначение

Символ «Интеграл» – стильная буква «S» (для «Сумма» – идея суммирования срезов):

После символа интеграла мы помещаем функцию, интеграл от которой мы хотим найти (называемую интегралом),

, а затем закончите с dx , что означает, что срезы идут в направлении x (и приближаются к нулю по ширине).

А вот как пишем ответ:

плюс C

Мы написали ответ как x ² , но почему + C?

Это «Константа интеграции». Это из-за всех функций, производная которых равна 2x :

• производная от x ² равно 2x ,
• и производная x ² +4 также 2x ,
• и производная x ² +99 также 2x ,
• и так далее!

Поскольку производная константы равна нулю.

Итак, когда мы перевернем операцию (чтобы найти интеграл), мы знаем только 2x , но могла быть константа любого значения .

Итак, мы завершаем идею, просто написав + C в конце.

Практический пример: кран и резервуар

Давайте воспользуемся краном, чтобы наполнить бак.

Вход (до интеграции) – расход от крана.

Мы можем интегрировать этот поток (сложить все маленькие кусочки воды), чтобы получить объема воды в резервуаре.

Представьте Постоянный расход 1:

При расходе 1 объем резервуара увеличивается на x . То есть Интеграция !

Интеграл от 1 равен x

При скорости потока 1 литр в секунду объем увеличивается на 1 литр каждую секунду, поэтому будет увеличиваться на 10 литров через 10 секунд, 60 литров через 60 секунд и т. Д.

Расход остается на уровне 1 , а объем увеличивается на x

И наоборот:

Если объем резервуара увеличивается на x , то расход должен быть 1.

Производная x равна 1

Это показывает, что интегралы и производные противоположны!

Теперь для увеличения скорости потока

Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, двигатель медленно открывает кран):

По мере увеличения расхода резервуар наполняется все быстрее и быстрее:

• Интеграция: при расходе 2x объем резервуара увеличивается на x ²
• Производная: если объем резервуара увеличивается на x ² , то расход должен быть 2x

Мы можем записать это так:

Интеграл расхода 2x сообщает нам объем воды:		∫2x dx = x 2 + C
Производная объема x 2 + C возвращает нам скорость потока:		d dx (x 2 + C) = 2x

И, привет, мы даже получили хорошее объяснение этого значения “C”… может быть, в баке уже есть вода!

• Поток по-прежнему увеличивает объем на ту же величину
• И увеличение объема может вернуть нам скорость потока.

Которая учит всегда помнить «+ C».

Прочие функции

Как интегрировать другие функции?

Если нам посчастливится найти функцию на стороне результата результат производной, тогда (зная, что производные и интегралы противоположны), у нас есть ответ.Но не забудьте добавить C.

Пример: что такое ∫cos (x) dx?

Из таблицы Rules of Derivatives мы видим, что производная sin (x) равна cos (x), поэтому:

∫cos (x) dx = sin (x) + C

Но многое из этого «обращения» уже сделано (см. Правила интеграции).

Пример: Что такое ∫x

³ dx?

В правилах интеграции есть «Правило власти», которое гласит:

∫x ⁿ dx = x ^{n + 1} n + 1 + C

Мы можем использовать это правило с n = 3:

∫x ³ dx = x ⁴ 4 + C

Знание того, как использовать эти правила, – ключ к успешной интеграции.

Так что выучите правила и получите много практики .

Изучите правила интеграции и практикуйтесь! Упражняться! Упражняться!
(для начала вам нужно задать несколько вопросов)

Определенные и неопределенные интегралы

До сих пор мы выполняли неопределенных интегралов .

A Определенный интеграл имеет фактические значения для вычисления между ними (они помещаются внизу и вверху буквы “S”):

Неопределенный Интегральный		Определенный Интегральный

Прочтите Определенные интегралы, чтобы узнать больше.{3} – 1} {\ ln t} \, dt.∫01 lntt3−1 dt.

---

Этот интеграл кажется устойчивым к стандартным методам интегрирования, таким как интегрирование по частям, u-подстановка и т. Д. Мы хотели бы использовать дифференцирование под знаком интеграла для его вычисления.

Как выбрать функцию для дифференцирования под знаком интеграла? Появление ln⁡t \ ln tlnt в знаменателе подынтегрального выражения весьма нежелательно, и мы хотели бы от него избавиться. x \ ln t, dxd tx = txlnt, поэтому дифференцирование числителя по показателю степени похоже на то, что мы ‘ хотел бы сделать.{1} = \ frac {1} {x + 1} .g ′ (x) = ∫01 ∂x∂ lnttx − 1 dt = ∫01 lnttxlnt dt = x + 1tx + 1 ∣∣∣ ∣∣ 01 = х + 11. Отсюда следует, что g (x) = ln⁡∣x + 1∣ + Cg (x) = \ ln | x + 1 | + Cg (x) = ln∣x + 1∣ + C для некоторой постоянной CCC.

Чтобы определить CCC, обратите внимание, что g (0) = 0g (0) = 0g (0) = 0, поэтому 0 = g (0) = ln⁡1 + C = C0 = g (0) = \ ln 1 + C = C0 = g (0) = ln1 + C = C. Следовательно, g (x) = ln⁡∣x + 1∣g (x) = \ ln | x + 1 | g (x) = ln∣x + 1∣ для всех xxx таких, что интеграл существует. В частности, g (3) = ln⁡4 = 2ln⁡2g (3) = \ ln 4 = 2 \ ln 2g (3) = ln4 = 2ln2. □ _ \ квадрат □

В этом примере часть подынтегрального выражения была заменена переменной, а результирующая функция исследовалась с помощью дифференцирования под знаком интеграла.{\ infty} \ cos tu \, du, 0 = g ′ (t) = ∫0∞ costudu, что абсурдно. Проблема в том, что функция f (x, t) = sin⁡tx / xf (x, t) = \ sin tx / xf (x, t) = sintx / x не является непрерывно дифференцируемой (рассмотрим ∂f / ∂t \ partial f / \ partial t∂f / ∂t при x = 0x = 0x = 0), что требовалось в предположениях, изложенных выше.

4π4 \ pi4π 2π2 \ pi2π π \ piπ 0

Вычислить определенный интеграл: ∫02πecos⁡θcos⁡ (sin⁡θ) dθ.{t \ cos \ theta} \ cos (t \ sin \ theta) \, d \ thetaf (t) = ∫02π etcosθcos (tsinθ) dθ

и используйте дифференцирование под знаком интеграла.

Модуль 16 – Основная теорема

Повторное изложение основной теоремы исчисления представлено в этом уроке вместе со следствием, которое используется для аналитического определения значения определенного интеграла.

---

Формулировка основной теоремы

Вы открыли фундаментальную теорему в контексте поиска площадей под кривой, но более общую версию этой теоремы можно доказать без обращения к площади.Ниже приводится повторение основной теоремы.

Если f является непрерывным на [ a , b ], то функция

имеет производную в каждой точке [ a , b ], а производная равна

То есть производная определенного интеграла от f , верхний предел которой – переменная x , а нижний предел – константа a , равна функции f , вычисленной как x .Это верно независимо от значения нижнего предела a . Функция с именем F такая же, как функция площади, которая была исследована ранее.

Использование переформулированной основной теоремы

• Установите угловой режим на радиан
• Выполните NewProb из меню Очистить

16.3.1 Используйте переформулировку основной теоремы для оценки следующих производных, а затем проверьте свои прогнозы с помощью TI-89.

Нажмите здесь, чтобы получить ответ.

16.3.2 Предскажите следующую производную. Проверьте свой ответ с помощью TI-89. Подсказка: вам нужно будет использовать цепное правило.

Щелкните здесь, чтобы получить ответ.

16.3.3 Оцените следующую производную и сверьте ее с вашим TI-89.

Щелкните здесь, чтобы получить ответ.

16.3.4 Найдите более общую версию основной теоремы, предсказав следующую производную. Проверьте свою работу с TI-89.

Щелкните здесь, чтобы получить ответ.

Использование следствия основной теоремы.

Следующее следствие основной теоремы дает метод вычисления определенного интеграла.

Следствие

Если f непрерывно на [ a , b ], то

, где .

Функция F называется первообразной функции f .

16.3.5 Используйте следствие, чтобы предсказать значение , затем проверьте свою работу с TI-89.

Щелкните здесь, чтобы получить ответ.

16.3.6 Используйте следствие из основной теоремы для вычисления затем проверьте свою работу с помощью калькулятора.

Щелкните здесь, чтобы получить ответ.

Методы интеграции | Безграничное исчисление

Основные принципы интеграции

Интегрирование – это процесс поиска области, ограниченной функцией; этот процесс использует несколько важных свойств.

Цели обучения

Применение основных принципов интеграции к интегральным задачам

Основные выводы

Ключевые моменты

• Термин интеграл может также относиться к понятию антипроизводной, функции [латекс] F [/ латекс], производной которой является заданная функция [латекс] f [/ латекс]. В этом случае он называется неопределенным интегралом и записывается как [латекс] \ int f (x) \, dx = F (x) + C [/ latex]. b \! f (x) \, dx [/ latex] неофициально определяется как область области на плоскости [latex] xy [/ latex], ограниченная графиком [latex] f [/ latex], [latex] ] x [/ latex] -ось, а вертикальные линии [latex] x = a [/ latex] и [latex] x = b [/ latex], так что область над [latex] x [/ latex] -осью прибавляет к общей сумме, а то, что ниже оси [latex] x [/ latex], вычитает из общей суммы.Термин интеграл может также относиться к понятию антипроизводной, функции [латекс] F [/ латекс], производной которой является заданная функция [латекс] f [/ латекс].

  Определенный интеграл : Определенный интеграл функции может быть представлен в виде области со знаком области, ограниченной ее графиком.

  Более строго, как только антипроизводная [латекс] F [/ латекс] [латекса] f [/ латекса] известна для непрерывной действительной функции [латекс] f [/ латекс], определенной на закрытом интервале [латекс] ] [a, b] [/ latex], определенный интеграл [latex] f [/ latex] по этому интервалу равен

  [латекс] \ displaystyle {\ int_a ^ b \! f (x) \, dx = F (b) – F (a)} [/ латекс]

  Если [latex] F [/ latex] является одним из антипроизводных [latex] f [/ latex], тогда все другие антипроизводные будут иметь форму [latex] F (x) + C [/ latex] для некоторых константа [латекс] C [/ латекс]. a f (x) \, dx} [/ latex]

  Интеграция заменой

  Обращая цепное правило, мы получаем метод, называемый интегрированием путем подстановки.Учитывая две функции [latex] f (x) [/ latex] и [latex] g (x) [/ latex], мы можем использовать следующую идентичность:

  [латекс] \ Displaystyle {\ int [е ‘(г (х)) \ cdot g’ (х)] \; \ mathrm d x = f (g (x)) + C} [/ латекс]

  или в терминах «фиктивной переменной» [latex] u = g (x) [/ latex]:

  [латекс] \ displaystyle {\ int f ‘(u) \; \ mathrm d u = f (u) + C} [/ латекс]

  Если мы собираемся использовать интегрирование подстановкой для вычисления определенного интеграла, мы должны соответственно изменить верхнюю и нижнюю границы интегрирования.

  Интеграция по частям

  Интеграция по частям – это способ интеграции сложных функций путем разделения их на отдельные части и их индивидуальной интеграции.

  Цели обучения

  Решите интегралы, используя интегрирование по частям

  Основные выводы

  Ключевые моменты

  • Интегрирование по частям – это теорема, которая связывает интеграл от произведения функций с интегралом от их производной и антипроизводной.
  • Теорема выражается как [латекс] \ int u (x) v ‘(x) \, dx = u (x) v (x) – \ int u’ (x) v (x) \, dx [/ latex ].
  • Интегрирование по частям можно интерпретировать не только математически, но и графически.

  Ключевые термины

  • интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются
  • производная : мера того, как функция изменяется при изменении ее входных данных

  Введение

  В исчислении интегрирование по частям – это теорема, которая связывает интеграл от произведения функций с интегралом от их производной и антипроизводной.Он часто используется для нахождения антипроизводной произведения функций в идеально более простую антипроизводную. Правило можно вывести в одну строку, просто интегрировав правило дифференциации продукта.

  Теорема интегрирования по частям

  Возьмем функции [латекс] u = u (x) [/ latex] и [latex] v = v (x) [/ latex]. Взяв их производные, мы останемся с [латексом] du = u ‘(x) [/ latex] и [latex] dxdv = v ‘(x) dx [/ latex]. Теперь давайте посмотрим на принцип интеграции по частям:

  [латекс] \ displaystyle {\ int u (x) v ‘(x) \, dx = u (x) v (x) – \ int u’ (x) v (x) \ dx} [/ латекс]

  или, более компактно,

  [латекс] \ displaystyle {\ int u \, dv = uv- \ int v \, du} [/ латекс]

  Проба

  Предположим, что [latex] u (x) [/ latex] и [latex] v (x) [/ latex] – две непрерывно дифференцируемые функции.{i = 2} [/ латекс]. Предполагая, что кривая гладкая в пределах окрестности, это обобщается до неопределенных интегралов [latex] \ int xdy + \ int y dx = xy [/ latex], которые можно преобразовать в форму теоремы: [latex] \ int xdy = xy – \ int y dx [/ латекс].

  Пример

  Чтобы вычислить [латекс] I = \ int x \ cos (x) \, dx [/ latex], пусть:

  [латекс] u = x \\ \ поэтому du = dx [/ latex]

  и

  [латекс] dv = \ cos (x) \, dx \\ \ поэтому v = \ int \ cos (x) \, dx = \ sin x [/ latex]

  , затем:

  [латекс] \ begin {align} \ int x \ cos (x) \, dx & = \ int u \, dv \\ & = uv – \ int v \, du \\ & = x \ sin (x) – \ int \ sin (x) \, dx \\ & = x \ sin (x) + \ cos (x) + C \ end {align} [/ latex]

  Тригонометрические интегралы

  Тригонометрические интегралы – это особый набор функций, используемых для упрощения сложных математических выражений с целью их вычисления.

  Цели обучения

  Решите основные тригонометрические интегралы

  Основные выводы

  Ключевые моменты

  • Некоторые выражения для тригонометрических интегралов находятся с использованием свойств тригонометрических функций.
  • Некоторые выражения были получены с использованием таких методов, как интегрирование по частям.
  • Нет гарантии, что тригонометрический интеграл имеет аналитическое выражение.

  Ключевые термины

  • тригонометрический : относящийся к функциям, используемым в тригонометрии: [latex] \ sin [/ latex], [latex] \ cos [/ latex], [latex] \ tan [/ latex], [latex] \ csc [ / латекс], [латекс] \ детская кроватка [/ латекс], [латекс] \ сек [/ латекс]
  • интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются

  Тригонометрические интегралы

  Тригонометрические интегралы – это семейство интегралов, которые включают тригонометрические функции ([latex] \ sin [/ latex], [latex] \ cos [/ latex], [latex] \ tan [/ latex], [latex] \ csc [ / латекс], [латекс] \ кроватка [/ латекс], [латекс] \ сек [/ латекс]).Ниже приводится список интегралов от тригонометрических функций. Некоторые из них были вычислены с использованием свойств тригонометрических функций, в то время как другие использовали такие методы, как интегрирование по частям.

  Обычно, если функция [latex] \ sin (x) [/ latex] является любой тригонометрической функцией, а [latex] \ cos (x) [/ latex] является ее производной, то

  [латекс] \ displaystyle {\ int a \ cos nx \; \ mathrm {d} x = \ frac {a} {n} \ sin nx + C} [/ latex]

  Во всех формулах предполагается, что константа [latex] a [/ latex] отлична от нуля, а [latex] C [/ latex] обозначает константу интегрирования.2 x = \ frac {1} {2} (1 – \ sin 2x) [/ latex] и [латекс] \ sin x \ cos x = \ frac {1} {2} \ sin 2x [/ latex].

Тригонометрическая замена

Тригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений и упростить интегрирование.

Цели обучения

Используйте тригонометрическую замену для решения интеграла

Основные выводы

Ключевые моменты

• Если подынтегральное выражение содержит [latex] a ^ 2 – x ^ 2 [/ latex], пусть [latex] x = a \ sin (\ theta) [/ latex].2 [/ latex], пусть [latex] x = a \ sec (\ theta) [/ latex].

Ключевые термины

• тригонометрический : относящийся к функциям, используемым в тригонометрии: [latex] \ sin [/ latex], [latex] \ cos [/ latex], [latex] \ tan [/ latex], [latex] \ csc [ / латекс], [латекс] \ детская кроватка [/ латекс], [латекс] \ сек [/ латекс]

Тригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений. Можно использовать тригонометрические тождества для упрощения некоторых интегралов, содержащих радикальные выражения (или выражения, содержащие корни [latex] n [/ latex] th).2 (\ theta)}} \\ & = \ int \ frac {d \ theta} {a} \\ & = \ frac {\ theta} {a} + C \\ & = \ frac {1} {a} \ arctan \ left (\ frac {x} {a} \ right) + C \ end {align} [/ latex]

Метод неполных дробей

Разложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции.

Цели обучения

Использовать частичное дробное разложение для интегрирования рациональных функций

Основные выводы

Ключевые моменты

• Любая рациональная функция действительной переменной может быть записана как сумма многочлена и конечного числа рациональных дробей, знаменателем которых является степень неприводимого многочлена, а числитель имеет степень ниже, чем степень этого неприводимого многочлена.2 + 1 [/ латекс]

Разложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции. Любую рациональную функцию действительной переменной можно записать как сумму многочлена и конечного числа рациональных дробей, знаменателем которых является степень неприводимого многочлена, а числитель имеет степень ниже, чем степень этого неприводимого многочлена. Вот несколько общих примеров.

Полином 1-й степени в знаменателе

Замена [latex] u = ax + b [/ latex], [latex] du = a \, dx [/ latex] уменьшает интеграл [latex] \ int {1 \ over ax + b} \, dx [/ латекс] к:

[латекс] \ begin {align} \ int {1 \ over u} \, {du \ over a} & = {1 \ over a} \ int {du \ over u} \\ & = {1 \ over a } \ ln \ left | u \ right | + C \\ & = {1 \ over a} \ ln \ left | ax + b \ right | + C \ end {align} [/ latex]

Повторяющийся многочлен 1-й степени в знаменателе

Та же самая замена уменьшает такие интегралы, как [latex] \ int {1 \ over (ax + b) ^ 8} \, dx [/ latex], до

[латекс] \ begin {align} \ int {1 \ over u ^ 8} \, {du \ over a} & = {1 \ over a} \ int u ^ {- 8} \, du \\ & = {1 \ over a} \ cdot {u ^ {- 7} \ over (-7)} + C \\ & = {-1 \ over 7au ^ 7} + C \\ & = {-1 \ over 7a ( ах + b) ^ 7} + C \ end {align} [/ latex]

Неприводимый многочлен 2-й степени в знаменателе

Далее мы рассматриваем такие интегралы, как

[латекс] \ displaystyle {\ int {x + 6 \ over x ^ 2-8x + 25} \, dx} [/ latex]

Самый быстрый способ увидеть, что знаменатель, [латекс] x ^ 2 – 8x + 25 [/ latex], несократим, – это заметить, что его дискриминант отрицательный.2-8x + 25) + {10 \ over 3} \ arctan \ left ({x-4 \ over 3} \ right) + C} [/ latex]

Интеграция с использованием таблиц и компьютеров

Для интегрирования обычно используются таблицы известных интегралов или компьютерных программ.

Цели обучения

Определить, какие интегралы следует решать с помощью таблиц или компьютеров в силу их сложности

Основные выводы

Ключевые моменты

• В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых составляющих функций, интегрирование – нет.
• В книгах с интегральными таблицами можно найти компиляцию списка интегралов и методов интегрального исчисления.
• Существует несколько коммерческих программ, таких как Mathematica или Matlab, которые могут выполнять символьную интеграцию.

Ключевые термины

• интегральный : также иногда называют первообразным; предел сумм, вычисленных в процессе, в котором область определения функции делится на небольшие подмножества, а возможное номинальное значение функции на каждом подмножестве умножается на меру этого подмножества, после чего все эти продукты суммируются

Интегрирование – основная операция в интегральном исчислении.В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых составляющих функций, интегрирование этого не делает, поэтому часто полезны таблицы известных интегралов. Нам также, возможно, придется прибегнуть к компьютерам для выполнения интеграла.

Интеграция с использованием таблиц

Сборник списка интегралов и методов интегрального исчисления был опубликован немецким математиком Мейером Хиршем еще в 1810 году. Более обширные таблицы были составлены в 1858 году голландским математиком Давидом де Биренс де Хааном.Новое издание вышло в 1862 году. Эти таблицы, содержащие в основном интегралы от элементарных функций, использовались до середины 20 века. Затем их заменили гораздо более обширные таблицы Градштейна и Рыжика. Вот несколько примеров интегралов в этих таблицах для логарифмических функций:

[латекс] \ int \ ln ax \; dx = x \ ln ax – x [/ латекс]

[латекс] \ displaystyle {\ int \ ln (ax + b) \; dx = \ frac {(ax + b) \ ln (ax + b) – ax} {a}} [/ латекс]

[латекс] \ int (\ ln x) ^ 2 \; dx = x (\ ln x) ^ 2 – 2x \ ln x + 2x [/ латекс]

[латекс] \ Displaystyle {\ int (\ пер х) ^ п \; dx = x \ sum ^ {n} _ {k = 0} (- 1) ^ {n-k} \ frac {n!} {k! } (\ ln x) ^ k} [/ латекс]

[латекс] \ Displaystyle {\ int \ frac {dx} {\ ln x} = \ ln \ left | \ ln x \ right | + \ ln x + \ sum ^ \ infty_ {k = 2} \ frac {(\ ln x) ^ k} {k \ cdot k! }} [/ latex]

[латекс] \ Displaystyle {\ int \ frac {dx} {(\ ln x) ^ n} = – \ frac {x} {(n-1) (\ ln x) ^ {n-1}} + \ frac {1} {n-1} \ int \ frac {dx} {(\ ln x) ^ {n-1}} \ qquad \ mbox {(для} n \ neq 1 \ mbox {)}} [/ латекс ]

Вы, конечно, видите, что эти интегралы сложно сделать просто «вручную».”

Интеграция с использованием компьютеров

Компьютеры могут использоваться для интеграции двумя основными способами. Во-первых, численные методы с использованием компьютеров могут быть полезны при вычислении определенного интеграла. Есть много методов и алгоритмов. Мы вкратце узнаем о численном интегрировании в другом атоме. Во-вторых, существует несколько коммерческих программ, таких как Mathematica или Matlab, которые могут выполнять символьную интеграцию.

Интеграция : Численное интегрирование заключается в нахождении численных приближений для значения [латекс] S [/ латекс].{b} f (x) \, dx = \ frac {ba} {2N} (f (x_1) + 2f (x_2) + 2f (x_3) + \ ldots + 2f (x_N) + f (x_ {N + 1) }))[/латекс].

В двух и более измерениях, где простые методы аппроксимации становятся непомерно дорогими с точки зрения вычислительных затрат, можно использовать другие методы, такие как метод Монте-Карло.

Ключевые термины

• трапеция : (выпуклый) четырехугольник с двумя (несмежными) параллельными сторонами

Численное интегрирование, в некоторых случаях также известное как числовая квадратура, требует значения определенного интеграла.Популярные методы используют одну из формул Ньютона – Котеса (например, правило средней точки или правило Симпсона) или квадратуру Гаусса. Эти методы основаны на стратегии «разделяй и властвуй», согласно которой интеграл на относительно большом множестве разбивается на интегралы на меньших множествах. В более высоких измерениях, где эти методы становятся непомерно дорогими с точки зрения вычислительных затрат, можно использовать другие методы, такие как метод Монте-Карло. Здесь мы изучим очень простой метод аппроксимации, называемый правилом трапеции.{b} f (x) \, dx \ приблизительно (b-a) \ frac {f (a) + f (b)} {2}} [/ latex]

Правило трапеции имеет тенденцию становиться чрезвычайно точным, когда периодические функции интегрированы по их периодам.

Аппроксимация линейными функциями : Функция [латекс] f (x) [/ latex] (синим цветом) аппроксимируется линейной функцией (красным цветом).

Численная реализация правила трапеции

Для домена, дискретизированного на [латекс] N [/ латекс] равномерно распределенные панели или [латекс] N + 1 [/ латекс] точки сетки [латекс] (1, 2, \ cdots, N + 1) [/ latex] , где шаг сетки равен [latex] h = \ frac {(ba)} {N} [/ latex], аппроксимация интеграла принимает следующий вид:

[латекс] \ begin {align} \ int_ {a} ^ {b} f (x) \, dx & \ приблизительно \ frac {h} {2} \ sum_ {k = 1} ^ {N} \ left ( f (x_ {k + 1}) + f (x_ {k}) \ right) {} \\ & = \ frac {ba} {2N} (f (x_1) + 2f (x_2) + \ cdots + 2f ( x_N) + f (x_ {N + 1})) \ end {align} [/ latex]

Хотя в этом методе также может использоваться неоднородная сетка, в этом примере для аппроксимации использовалась равномерная сетка. bf (x) \, \ mathrm {d} x [/ latex].bf (x) \, \ mathrm {d} x [/ latex], в котором берется ограничение в одной или другой (а иногда и в обеих) конечных точках.

Часто необходимо использовать несобственные интегралы, чтобы вычислить значение интегралов, которые могут не существовать в общепринятом смысле (например, интеграл Римана) из-за сингулярности функции или бесконечной конечной точки области определения интеграция.

Ключевые термины

• интегрируемое выражение : функция, которая должна быть интегрирована
• определенный интеграл : интеграл функции между верхней и нижней границей

Несоответствующий интеграл – это предел определенного интеграла, когда конечная точка интервала (ов) интегрирования приближается либо к заданному действительному числу, либо к [latex] \ infty [/ latex] или [latex] – \ infty [/ latex] или , в некоторых случаях, когда обе конечные точки приближаются к пределам.bf (x) \, \ mathrm {d} x [/ latex]

, в котором устанавливается ограничение на одной или другой конечной точке (а иногда и на обеих).

Несобственный интеграл второго рода : Несобственный интеграл Римана второго рода. Интеграл может не существовать из-за вертикальной асимптоты функции.

Интегралы также являются неправильными, если подынтегральное выражение не определено во внутренней точке области интегрирования или в нескольких таких точках. Часто необходимо использовать несобственные интегралы, чтобы вычислить значение интегралов, которые могут не существовать в обычном смысле (например, интеграл Римана) из-за сингулярности функции или бесконечной конечной точки области интегрирования. .2} \, \ mathrm {d} x \\ & = \ lim_ {b \ to \ infty} \ left (- \ frac {1} {b} + \ frac {1} {1} \ right) \\ & = 1 \ end {align} [/ latex]

Пример 2

Узкое определение интеграла Римана также не распространяется на функцию [latex] \ frac {1} {\ sqrt {x}} [/ latex] на интервале [latex] [0, 1] [/ latex]. +} (2 \ sqrt {1} -2 \ sqrt {a}) \\ & = 2 \ end {align} [/ latex]

Численное интегрирование

Численное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла.б \! f (x) \, dx [/ латекс].

Существует несколько причин для проведения численного интегрирования. Это может быть связано со специфическим характером функции (подлежащей интеграции) или ее первообразных.

Большой класс квадратурных правил может быть получен путем построения интерполирующих функций, которые легко интегрировать. Обычно эти интерполирующие функции являются полиномами. Простыми примерами являются метод средней точки и метод трапеции.

Ключевые термины

• трапециевидный : в форме трапеции или с несколькими гранями, имеющими одну пару параллельных сторон
• первообразная : неопределенный интеграл

Численное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла, и, в более широком смысле, этот термин также иногда используется для описания численного решения дифференциальных уравнений. 2) [/ latex], первообразная которого (функция ошибки, умноженная на константу) не может быть записана в элементарной форме.

Может быть возможно найти первообразную символически, но может быть проще вычислить численное приближение, чем вычислить первообразную. Это может иметь место, если первообразная дана как бесконечная серия или произведение, или если для ее оценки требуется специальная функция, которая недоступна.

Методы одномерных интегралов

Большой класс квадратурных правил может быть получен путем построения интерполирующих функций, которые легко интегрировать.b f (x) \, dx \ приблизительно (b-a) \, f \ left (\ frac {a + b} {2} \ right)} [/ латекс]

Правило прямоугольника : Иллюстрация правила прямоугольника.

Интерполирующая функция может быть аффинной функцией (полиномом степени 1), проходящей через точки [latex] (a, f (a)) [/ latex] и [latex] (b, f (b)) [/ латекс]. Это называется правилом трапеции.