Производная не существует если: Отыскание точек экстремума — урок. Алгебра, 11 класс.

№ 29.2 ГДЗ Алгебра 10-11 класс Мордкович. Помогите указать точки, в которых производная равна нулю – Рамблер/класс

№ 29.2 ГДЗ Алгебра 10-11 класс Мордкович. Помогите указать точки, в которых производная равна нулю – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

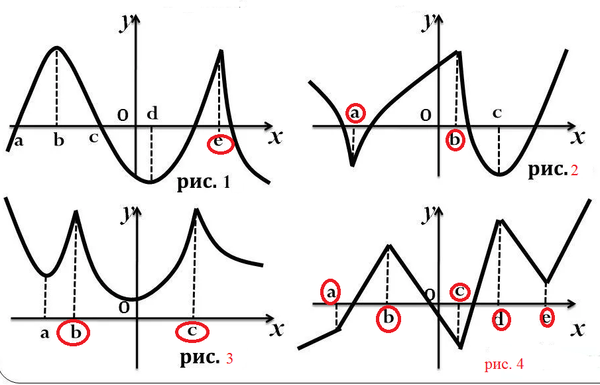
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания “Останкино”?

Укажите точки, в которых производная равна нулю, и точки, в которых производная не существует, если график функции изображен  на заданном рисунке:
а) рис. 43;     б) рис. 44;     в) рис. 45;     г) рис. 46.

ответы

Помогу тебе с точками

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х – 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

ГДЗ Тема 21 Физика 7-9 класс А. В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

Возрастание и убывание функции — как найти?

Поможем понять и полюбить математику

Начать учиться

108.4K

Сегодня мы поговорим о возрастании и убывании функции. Как вы знаете, эта тема достаточно важна, потому что встречается на ЕГЭ, во вступительных экзаменах. А еще ее подробно разбирают на уроках в школе. Сложная ли она? И да, и нет. Мы бы сказали, что она не трудная, а скорее комплексная — в теме много нюансов и моментов, которые тянутся к ней с начальной школы. Но не беспокойтесь, сегодня мы обязательно во всем разберемся!

Что такое функция

Как обычно, начнем мы с самого начала: с определения слова «функция».

Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Под функцией понимают правило, формулу, уравнение, которое описывает зависимость одной переменной от другой (например, у от х). Если изучить функцию, мы поймем:

• как изменится одна переменная, если другая увеличится;

• что произойдет с аргументом, если мы уменьшим функцию;

• что будет, если мы отобразим эту зависимость графически.

Спойлер: если изобразить зависимость в координатной системе, мы получим график! Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют.

Важное напоминание: функция — это зависимая переменная величина (чаще у), аргумент — независимая переменная (чаще х).

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Возрастание и убывание функции

В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными.

Монотонная функция — функция, которая возрастает или убывает на всем промежутке области определения.

Функцию считают немонотонной, если на промежутке области своего определения она чередует возрастание и убывание.

Постоянная функция, как ясно из названия, постоянна на всем промежутке и представляет собой прямую, параллельную оси x.

Теперь к теме раздела: приведем определение возрастающей и убывающей функции.

Функция называется возрастающей, когда при увеличении аргумента увеличивается и сама функция.

Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х, тем больше и значение у.

Функция считается убывающей, когда при увеличении аргумента функция уменьшается: чем больше х, тем меньше у.

Теперь вы знаете, как понять, что функция возрастает или убывает. Давайте решим пару задач, чтобы разобраться во всем наглядно.

Задача 1

Определите, возрастающая или убывающая функция y = 2x + 3.

1) Найдем область определения функции: х ∈ R.

2) Найдем координаты нескольких точек, которые ей принадлежат.

х	0	1	2	3
у	3	6	7	9

Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.

Задача 2

Определите, возрастающая или убывающая функция y = 1/2х.

1) Найдем область определения функции: х ≠ 0.

2) Найдем координаты нескольких точек, которые ей принадлежат.

х	1	2	3	4
у	½	¼	⅙	⅛

х	-1	-2	-3	-4
у	-½	-¼	-⅙	-⅛

Мы видим, что функция убывает при любом значении х ≠ 0.

Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.

Возрастание и убывание функции на интервале

Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:

• Как найти промежутки возрастания и убывания функции по графику?

• Что делать, если просят определить характер на числовом промежутке?

• Как определить поведение функции без построения?

Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:

• Подставим значение х из промежутка в функцию.

• Проанализируем полученные значения у.

• Если при увеличении х увеличивается и у — это промежуток возрастания функции.

• Если у уменьшается при увеличении х — это промежуток убывания функции.

Достаточно просто, правда? 🙂

Пример

Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:

у(0) = –6у(1) = -2у(2) = 2

Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.

Точки экстремума, экстремумы функции

Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.

Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве.

На графике выше y min — минимальное значение функции, точка минимума.

Точка минимума — это значение переменной х, при которой функция минимальна.

На том же графике y мах — максимальное значение функции, точка максимума.

Точка максимума — это значение переменной х, при которой функция максимальна.

Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.

В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.

Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет. Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.

Достаточные условия возрастания и убывания функции

У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.

Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.

Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.

К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!

Достаточные признаки возрастания и убывания функции на интервале:

• если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;

• если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.

Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:

1. Найдем область определения функции.

2. Найдем производную функции.

3. Решим неравенства ƒ`(x) > 0 и ƒ`(x) < 0 на области определения.

4. К полученным промежуткам добавим граничные точки, в которых функция определена и непрерывна.

5. Проверим достаточные признаки возрастания и убывания функции, подставив значения из промежутков.

Задача 3

Укажите промежутки возрастания и убывания функции у = х² + 5х + 6

Решение

1. Область определения функции: х ∈ R

2. Найдем производную функции: y’ = 2х + 5

3. Решим неравенство: 2х + 5 > 0

   2х+5 >02x>-5x> –2,5

4. Исследуем знаки производной с помощью числовой прямой.

Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)

Задача 4

Определите интервалы возрастания и убывания функции у = х³ – 18х.

Решение

1. Область определения функции: х ∈ R.

2. Найдем производную функции: y’ = 3x² + (–18).

3. Решим неравенство:

   3x² + (–18) > 03 (x²–9) > 03(x – 3)(x + 3) > 0

4. Исследуем знаки производной с помощью числовой прямой. Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.

Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).

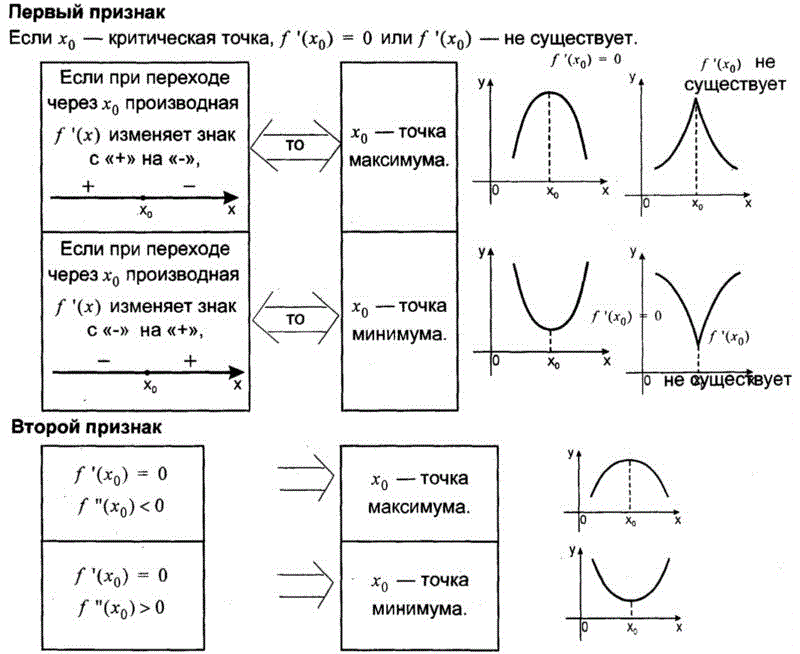
Первое достаточное условие экстремума

Пусть для функции у = f(x) определены следующие условия:

1. Функция непрерывна в окрестности точки x0 (нет разрыва).

2. ƒ′(x0) = 0 или ƒ′(x0) не существует;

3. Производная ƒ′(x) при переходе через точку x0 меняет свой знак.

Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.

Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.

Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.

Алгоритм для нахождения точек экстремума

Теперь разберемся, как найти точки экстремума функции. Для этого пройдем по этим шагам:

1. Найдем область определения функции.

2. Найдем производную функции на этой области.

3. Определим нули и точки, где функция не существует.

4. Определим знак производной на интервалах.

5. Выберем точки, где функция меняет знак.

6. Найдем точки минимума/максимума и экстремумы функции.

Задача 5

Найдите экстремумы функции у = –x² + 8x – 7.

Решение

1. Область определения функции: х ∈ R.

2. Производная функции: y’ = –2x + 8

3. Решим неравенство:

   –2x + 8 > 0–2x > –8x < 4

4. Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.

Ответ: у(4) = 9 — экстремум функции.

Задача 6

Найдите экстремумы функции у = ⅓ x³ + 2x² – 12x + 6.

Решение

1. Область определения функции: х ∈ R.

2. Производная функции: y’ = x² + 4x – 12.

3. Решим неравенство:

   x² + 4x – 12 > 0(x – 2)(x + 6) > 0

4. Определим знак производной на числовой прямой. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.

Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.

Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.

Как можно запомнить переход знаков для точек максимум или минимум:

• Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.

• Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.

Второе достаточное условие экстремума

x₀ — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f ”(x) ≠ 0). Причем, если вторая производная больше нуля (f ”(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f ”(x) < 0), то точкой максимума.

Рассмотрим это условие экстремума на примере из задачи 6 — функции у = ⅓ x³ + 2x² – 12x + 6:

1. Ее первая производная равна y’= x² + 4x – 12.

2. Определим нули производной — значение х, при котором производная обращается в ноль: x^{2 + 4x – 12 = 0 при х = 2 и х = –6.}

3. Возьмем вторую производную функции y’’= 2х + 4.

4. Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:

   y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума,y’’(–6) = –8, y’’ < 0, значит, х = –6 является точкой максимум.

В этом условии есть два важных замечания:

1. Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.

2. Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.

Третье достаточное условие экстремума

Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!

Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0. Пусть ƒ′(x₀) = ƒⁿ(x₀) = ƒ^m(x₀) = … = ƒ⁽ⁿ⁾(x₀) = 0 и ƒ⁽ⁿ⁺¹⁾(x₀) ≠ 0.

Тогда,

• если n – четное, то x₀ — точка перегиба;

• если n – нечетное, то x₀ — точка экстремума, причем

• если ƒ⁽ⁿ⁺¹⁾(x₀) > 0, то x₀ — точка минимума;

• если ƒ⁽ⁿ⁺¹⁾(x₀) < 0, то x₀ — точка максимума.

Думаем, вы убедились, что тема «Возрастание и убывание функции» достаточно интересна. В то же время, она требует умения исследовать графики, находить первую и вторую производную функции, определять знаки по числовым прямым. Получить практический опыт решения таких заданий можно на курсах по профильной математике в школе Skysmart! Там мы сможем закрепить полученные знания, подготовиться к контрольным работам и даже к ОГЭ! Заинтригованы? Тогда мы ждем вас на занятиях!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Разложение чисел на простые множители

К следующей статье

Плоскость

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Производные, когда касательные линии не существуют

• Главная /
• Вычисления /
• Производные /
• Упражнения /
• Когда касательные не существуют Упражнения

• Упражнения /
90 003 Когда касательных линий не существует Упражнения

Темы

• Введение
• Темы
• Производная как предел наклона
• Производная как мгновенная скорость изменения
• Касательные линии
• Как выглядят касательные линии
• Когда касательные линии не существуют
• Касательные линии и производная s
• Аппроксимация касательной
• Дифференцируемость и Непрерывность
• Производная функция
• Графики f ( x ) и f ‘ ( x )
• Теоремы
• В реальном мире
• Примеры
• Упражнения
• Викторины
• Условия
• Раздаточный материал
• Лучшее из Интернета
• Содержание

• НАЗАД
• СЛЕДУЮЩИЙ

Касательные линии не всегда существуют. Так как наклон касательной к f на a — это то же самое, что и производная от f по по , если f’  ( по ) не существует, то мы не можем провести касательную к f по точке по .

Пример задачи

Пусть f ( x ) = | х |. Ранее мы видели, что f ‘ (0) не существует из-за несоответствия между односторонними пределами. Если мы попытаемся провести касательную к f в точке 0, мы столкнемся с трудностями. Должно ли это выглядеть так?

Или это должно выглядеть так?

Поскольку невозможно решить, какой она должна быть, мы вообще не можем провести касательную к f в точке 0.

Пример задачи

Мы не можем провести касательную к f в точке a для функции f , показанной ниже: боковые пределы. Если мы подойдем к и справа, мы думаем, что касательная должна выглядеть так:

Но если мы подойдем к a слева, мы думаем, что касательная должна выглядеть так:

В общем, мы не можем рисовать касательные в частях графика, которые выглядят как «точки». или “углы”:

Мы также не можем рисовать касательные в местах, где функция не существует.

Это имеет смысл, если мы подумаем о предельном определении производной. Нам нужно использовать f ( a ) для вычисления f ‘  ( a ), поэтому, если f ( a ) не существует, нам не повезло.

• НАЗАД
• СЛЕДУЮЩИЙ

Процитировать эту страницу

---

Дифференцируемый

Дифференцируемость означает, что производная существует …

Пример: дифференцируемо ли x

² + 6x?

Производные правила сообщают нам производную x ² равно 2x, а производная x равна 1, поэтому:

Его производная равна 2x + 6

Итак, да! x ² + 6x дифференцируема.

… и он должен существовать для каждого значения в домене функции.

Домен В своей простейшей форме домен представляет собой все значения, которые входят в функцию

Пример (продолжение)

Если не указано иное, мы предполагаем, что это домен Real Numbers.

Для x ² + 6x производная от 2x + 6 существует для всех действительных чисел.

Итак, мы все еще в безопасности: x ² + 6x дифференцируемо.

А как насчет этого:

Пример: Функция f(x) = |x| (абсолютное значение):

|x| выглядит так:

При x=0 очень резкое изменение!

Существует ли производная при x=0?

Тестирование

Мы можем проверить любое значение “a”, установив, существует ли предел:

лим ч→0 е(а+ч) – е(а) ч

Пример (продолжение)

Вычислим предел для |x| при значении 0:

 

Начать с:lim ч→0 е(а+ч) – е(а) ч

f(x) = |x|:lim ч→0 |а+ч| − |а| ч

а=0:лим ч→0 |ч| − |0| h

Упростить:lim ч→0 |ч| h

На самом деле этого предела не существует! Чтобы понять, почему, давайте сравним левый и правый пределы:

С левой стороны:lim ч→0 ⁻ |ч| ч = −1

Справа: lim ч→0 ⁺ |ч| ч = +1

Пределы различны с обеих сторон, поэтому предел не существует при x=0

 

 f(x) = |x| не дифференцируем при x=0

Хороший способ представить себе это — подумать:

При увеличении масштаба функция становится прямой линией?

Функция абсолютного значения остается направленной на x=0 даже при увеличении.

Другие причины

Вот еще несколько примеров:

Функции пола и потолка не дифференцируемы при целых значениях, так как при каждом скачке есть разрыв. Но они дифференцируемы в другом месте.

Функция кубического корня x (1/3) Его производная равна (1/3)x -(2/3) (по степенному правилу) При x=0 производная не определена, поэтому x (1/3) не дифференцируемо, если мы не исключим x=0.

При x=0 функция не определена, поэтому нет смысла спрашивать, дифференцируемы ли они там. Чтобы быть дифференцируемой в определенной точке, функция должна быть прежде всего определена там!

По мере того, как мы приближаемся к x = 0, функция движется вверх и вниз все быстрее и быстрее, поэтому мы не можем найти значение, к которому она “направляется”. Так что там не дифференцируется.

 

Другой домен

Но мы можем изменить домен!

Пример: Функция g(x) = |x| с доменом (0, +∞)

Домен начинается с , но не включает 0 и далее (все положительные значения).

Который дифференцируем.

И я “абсолютно уверен” в этом 🙂

Итак, функция g(x) = |x| с областью определения (0, +∞) дифференцируема.

Мы также можем ограничить домен другими способами, чтобы избежать x=0 (например, все отрицательные действительные числа, все ненулевые действительные числа и т. д.).

 

Зачем беспокоиться?

Потому что, когда функция дифференцируема, мы можем использовать всю мощь исчисления при работе с ней.

Непрерывный

Когда функция дифференцируема, она также непрерывна.

Дифференцируемый ⇒ Непрерывный

Но функция может быть непрерывной, но не дифференцируемой .