Электронный учебник по математическому анализу
4.1 Производная
4.1.1 Определение производной
Понятие производной – одно из ключевых в математическом анализе. Пусть $f(x)$ задана на некотором интервале $(a,b) \subset\mathbb{R}$, точка $x_0 \in (a,b)$.
Рассмотрим отношение \[ A(x_0, \vartriangle x)=\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }. \]
Это функция двух переменных – $x_0$ и еще одной переменной, которую обозначают $ \Delta x$. Числитель этой дроби обозначают иногда как $\Delta f=f(x_0+\Delta x)-f(x_0)$ и называют приращением функции $f(x)$ в точке $x_0$, соответствующим приращению аргумента $\Delta x$, так что \[ A(x_0, \Delta x)=\frac{\Delta f}{\Delta x }. \]
Определение. Если существует конечный предел
\[
\lim _{\Delta \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x }=k,
\]
то говорят, что функция $f(x)$ дифференцируема в точке $x=x_0$, имеет там производную, равную $k$, которую обозначают $\frac{df}{dx}(x_0)$ или $f'(x_0)$.
Замечание. В точках разрыва функции $f(x)$ функция не имеет производной.
Контрольный вопрос.
Докажите последнее утверждение.
Первые физические приложения.
1. Путь $S(t)$ – путь, пройденный движущейся по прямой точкой. Тогда мгновенной скоростью точки будет \[ v(t)=\lim _{\Delta t \to 0} \frac{S(t+\Delta t)-S(t)}{\Delta t}= \frac {dS}{dt}(t). \]
2. Пусть через данное сечение провода к моменту $t$ протек заряд $Q(t)$, тогда электрический ток \[ I(t)=\lim _{\Delta t \to 0} \frac{Q(t+\Delta t)-Q(t)}{\Delta t}= \frac {dQ}{dt}(t). \]
Обсудим геометрический смысл производной. На рисунке изображен график функции $y=f(x)$, проходящий через (близкие друг другу) точки $A$ и $B$. Проведем через них хорду $AB$. Отношение $(f(x+\Delta x)-f(x))/\Delta x$ соответствует тангенсу угла наклона хорды $AB$. Когда $\Delta x \rightarrow 0$, точка $B$ стремится к точке $A$, при этом хорда превращается в касательную к графику функции, проходящую через точку $(x,f(x))$.
3. $f(x)=\sin x$, $f'(x)=\cos x$.
Вычисление. \[ A(x_0, \Delta x)=\frac{\sin (x_0+\Delta x)-\sin (x_0)}{\Delta x}. \]
Используя известное тригонометрическое тождество (разность синусов равна…), имеем: \[ A(x_0, \Delta x)=2\frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x}= \] \[ \frac{\sin (\Delta x/2)\cos (x_0+\Delta x/2)}{\Delta x /2}. \]
С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\cos (x_0). \]
4. $f(x)=\cos x$, $f'(x)=-\sin x$.
Вычисление. \[ A(x_0, \Delta x)=\frac{\cos (x_0+\Delta x)-\cos (x_0)}{\Delta x}. \]
Используя известное тригонометрическое тождество (разность косинусов равна…), имеем: \[ A(x_0, \Delta x)=-2\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x}= \] \[ -\frac{\sin (\Delta x/2)\sin (x_0+\Delta x/2)}{\Delta x /2} \]
С помощью тригонометрического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=-\sin (x_0) \]
5. $f(x)=\ln x$, $f'(x)=1/ x$.
$f(x)=\ln x$, $f'(x)=1/ x$.
Вычисление. \[ A(x_0, \Delta x)=\frac{\ln (x_0+\Delta x)-\ln (x_0)}{\Delta x}= \] \[ \frac{\ln ((x_0+\Delta x)/x_0)}{\Delta x}=\frac{1}{x_0}\frac{\ln (1+\Delta x/x_0)}{\Delta x/x_0} \]
С помощью логарифмического предельного соотношения при $\Delta x \rightarrow 0$ получаем: \[ \lim _{\Delta x\rightarrow 0}A(x_0, \Delta x)=\frac{1}{x_0} \]
4.1.3 Производная от суммы, произведения и частного функций
Производная возникает в результате предельного перехода. Поэтому свойства пределов приводят к соответствующим свойствам производных.
Теорема. Пусть функции $f(x)$, $g(x)$ дифференцируемы в точке $x$. Тогда
1. Функция $f(x)+g(x)$ также дифференцируема, причем $$(f(x)+g(x))’=f'(x)+g'(x),$$
2. Функция $f(x)\cdot g(x)$ дифференцируема, причем справедлива формула Лейбница $$(f(x)\cdot g(x))’=f'(x)\cdot g(x)+f(x)\cdot g'(x),$$
3. Если $g(x) \neq 0$, тогда $f(x)/g(x)$ дифференцируема в точке $x$, причем
$$ \left (\frac{f(x)}{g(x)}\right )’=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}.
Доказательство.
1. \[ A(x_0, \Delta x)=\frac{(\left ( f(x_0+\Delta x) +g(x_0+\Delta x)\right )-\left ( f(x_0) +g(x_0)\right )}{\Delta x}= \] \[ \frac{ f(x_0+\Delta x) – f(x_0) }{\Delta x}+\frac{ g(x_0+\Delta x) – g(x_0) }{\Delta x}. \]
Согласно условиям теоремы, обе дроби в последнем выражении имеют пределы при $\Delta x \rightarrow 0$, так что используя тот факт, что предел суммы равен сумме пределов (конечных!) получаем: \[ \lim _{\Delta x \rightarrow 0} A(x_0, \Delta x)=f'(x_0)+g'(x_0). \]
2.
\[
A(x_0, \Delta x)=
\]
\[
\frac{ f(x_0+\Delta x)\cdot g(x_0+\Delta x)- f(x_0) \cdot g(x_0)}{\Delta x}=
\]
\[
\frac{ f(x_0+\Delta x)\cdot g(x_0+\Delta x)- f(x_0+\Delta x)\cdot g(x_0)}{\Delta x}
\]
\[
{+f(x_0+\Delta x)\cdot g(x_0)- f(x_0) \cdot g(x_0)}{\Delta x}
\]
\[
=f(x_0+\Delta x)\frac{g(x_0+\Delta x)- g(x_0)}{\Delta x}+
\]
\[
g(x_0)\frac{f(x_0+\Delta x)- f(x_0)}{\Delta x}. \]
\]
Согласно условиям теоремы, при $\Delta x \rightarrow 0$ выражения $$ \frac{g(x_0+\Delta x)- g(x_0)}{\Delta x}, \quad \frac{f(x_0+\Delta x)- f(x_0)}{\Delta x}$$ имеют пределы, равные производным функций $g'(x_0), f'(x_0)$. Так как функция $f(x)$ дифференцируема в точке $x_0$, то она непрерывна в этой точке, значит $f(x_0+\Delta x) \rightarrow f(x_0) $ при $\Delta x \rightarrow 0$. В итоге получаем: \[ \lim _{\Delta x \rightarrow 0} A(x_0, \Delta x)=f'(x_0)\cdot g(x_0)+f(x_0)\cdot g'(x_0). \]
3.
\[
A(x_0, \Delta x)=\frac{\frac{f(x_0+\Delta x)}{g(x_0+\Delta x)}-\frac{f(x_0)}{g(x_0)}}{\Delta x}=
\]
\[
\frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0+\Delta x)}{g(x_0+\Delta x)g(x_0)\Delta x}=
\]
\[
\frac{1}{g(x_0+\Delta x)g(x_0)}\frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0)}{\Delta x}+
\]
\[
{f(x_0)g(x_0)-f(x_0)g(x_0+\Delta x)}{\Delta x}=
\]
\[
\frac{1}{g(x_0+\Delta x)g(x_0)}\frac{f(x_0+\Delta x)g(x_0)-f(x_0)g(x_0)}{\Delta x}-
\]
\[
\frac{f(x_0)g(x_0+\Delta x)-f(x_0)g(x_0)}{\Delta x} . 2)$.
2)$.
Предположим, что известны производные $dg/dx$, $dh/dy$. Возникает вопрос: как вычислить производную сложной функции $dz/dx$, где $z=h(g(x))$?
Теорема. Пусть $f(x)$ дифференцируема в точке $x=x_0$, $h(y)$ дифференцируема в точке $y_0=f(x_0)$. Тогда $z=h(g(x))$ дифференцируема в точке $x=x_0$, причем \begin{equation} \left. \frac{dz}{dx} \right|_{x=x_0}=\left. \frac{dh}{dy}\right|_{y=f(x_0)}\cdot \left.\frac{df}{dx}\right|_{x=x_0}. (8) \label{comp} \end{equation}
Доказательство.
Обозначим $y_0=f(x_0)$. В соответствии с нашими предположениями составим выражение \[ A(x_0, \Delta x)=\frac{h(f(x_0+\Delta x))-h(f(x_0))}{\Delta x}= \] \[ \frac{h(f(x_0+\Delta x))-h(f(x_0))}{f(x_0+\Delta x)-f(x_0)}\cdot \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}. \]
При $\Delta x \to 0$ в силу непрерывности $f(x)$ в точке $x_0$ имеем: $y_0+\Delta y=f(x_0+\Delta x) \to f(x_0)=y_0$. В силу условий теоремы первый множитель имеет пределом при $\Delta x \to 0$ величину $\left. h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\]
h'(y)\right|_{y=f(x_0)}$, второй множитель имеет пределом величину $f'(x_0)$. В итоге получаем:
\[
\lim _{\Delta x \to 0}A(x_0, \Delta x)=\left. h'(y)\right|_{y=f(x_0)}\cdot f'(x_0).
\]
Замечание. Соотношение (8) содержит в левой части 2 сомножителя – в соответствии с тем, что сложная функция образована композицией двух функций. Если сложная функция образована композицией 3 функций, в левой части имеется 3 сомножителя и т.д.
Напомним, что если задана функция $y=f(x)$, то обратной к ней функцией называется функция $x=h(y)$ со следующими свойствами: $h(f(x))=x$, $f(h(y))=y$. Разумеется, обратная функция существует не всегда.
Теорема. Пусть функция $y=f(x)$ имеет непрерывную производную в некоторой окрестности $V$ точки $x=x_0$, причем $f'(x_0) \neq 0$. Тогда в некоторой окрестности $U \subset V$, $x_0 \in U$, функция $f(x)$ имеет обратную, определенную в некоторой окрестности точки $y_0=f(x_0)$, причем выполняется равенство:
\begin{equation}
h'(y_0)=\left. 2}.
\]
2}.
\]
Далее, пусть для некоторых функций $a(t),b(t)$, заданных на интервале $\left[t_1,t_2\right]$, $x=a(t)$, $y=b(t)$ (в этом случае говорят, что переменные $ x $ и $ y $ заданы параметрически). Предположим, что для функции $x=a(t)$ существует обратная функция $t=\phi (x)$. Тогда $y=b(t)=b(\phi(x))$, так что появляется зависимость между $x$ и $y$. В этом случае говорят, что функция $y(x)$ задана параметрически (с помощью параметра $t$). Если известны производные функций $a(t)$, $b(t)$, то можно вычислить производную функции $y'(x)$.
Теорема. Предположим, что функции $a(t),b(t)$ дифференцируемы на интервале $\left[t_1,t_2\right]$, причем существует обратная функция $t=\phi (x)$, дифференцируемая при всех интересующих нас $x$. Тогда производная $y'(x)$ существует, причем \begin{equation} y'(x)=\left.\frac{b'(t)}{a'(t)}\right |_{t=\phi (x)}. (10) \label{par} \end{equation}
Доказательство.
Согласно условиям теоремы, функцию $y(x)$ можно представить как сложную функцию, $y(x)=b( \phi (x))$. 2}.$$
2}.$$
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34. biz
biz
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Определение, физический и геометрический смысл производной
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ \triangle x=x-x_0 $$ где \(x\) – произвольное число, которое мало отличается от начальной точки \(x_0\). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ \triangle y=f(x)-f(x_0 )=f(x_0+\triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
| \begin{gather*} y=2x-1\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. \begin{gather*} \triangle x= x-x_0=1,1-1=0,1\gt 0\\ \\ f(x)=f(1,1)=2\cdot 1,1-1=1,2\\ f(x_0 )=f(1)=2\cdot 1-1=1\\ \triangle y=f(x)-f(x_0 )=1,2-1=0,2\gt 0 \end{gather*} | |||||||||||||||||||||||||||||||||||||||||||||||
\begin{gather*} y=-x+2\\ x_0=1,\ x=1,1 \end{gather*} Найдем приращение аргумента и функции. 2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle y}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(6+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(6+\triangle x)=6+0=6 $$ 2=\triangle x(6+\triangle x) $$ Производная: $$ f'(x_0)=\lim_{\triangle x\rightarrow 0}\frac{\triangle x}{\triangle y}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(6+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(6+\triangle x)=6+0=6 $$ п.3. Физический смысл производнойРассмотрим прямолинейное движение. Мгновенная скорость это скорость тела в данный момент времени \(t_0\): $$ v(t_0)=\lim_{\triangle t\rightarrow 0}\frac{\triangle x}{\triangle t}=x'(t_0) $$ где \(\triangle x=x-x_0\) – путь тела за время \(\triangle t=t-t_0,\ x(t)\) – уравнение движения. Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной: Производная функции \(y=f(x)\) в точке \(x_0\) равна скорости изменения функции в этой точке. Или, ближе к физике/химии/биологии: Производная уравнения процесса \(s=f(t)\) в момент времени \(t_0\) равна скорости протекания процесса в этот момент. п.4. Геометрический смысл производной
Производная функции \(y=f(x)\) в точке \(x_0\) равна угловому коэффициенту касательной к графику этой функции в этой точке. п.5. Алгоритм поиска значения производной в заданной точкеНа входе: уравнение функции \(y=f(x)\), точка \(x_0\) Например: п.7. ПримерыПример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите: Ответ: а) 2; б) 18; в) 4; г) 12 Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции \(y=f(x)\): Производная постоянной равна нулю: \(C ‘=0\) б) \( f(x)=x\) Производная аргумента равна единице: \(x ‘=1\) в) \( f(x)=x^2\) e) \( f(x)=kx+b\) ж) \( f(x)=\sqrt{x}\) Дробная производная – это. .. Что такое Дробная производная? .. Что такое Дробная производная?Дробная производная (или производная дробного порядка) является обобщением математического понятия производной. Существует несколько разных способов обобщить это понятие, но все они совпадают с понятием обычной производной в случае натурального порядка. Когда рассматриваются не только дробные, но и отрицательные порядки производной, к такой производной обычно применяется термин дифферинтеграл. Дробные производные на отрезке вещественной осиДля функции , заданной на отрезке , каждое из выражений называется дробной производной порядка , , соответственно левосторонней и правосторонней. Дробные производные в приведенном виде называют обычно производными Римана — Лиувилля. Дробная производная порядка ( — действительное положительное число) определяется через интеграл Коши: , где интегрирование ведется по выбранному заранее контуру на комплексной плоскости. Непосредственное применение этой формулы затруднено из-за ветвления функции при дробном показателе степени в знаменателе. Основано на следующем свойстве интегрального преобразования Фурье Определение через общую формулуn-й производнойВ случае, если есть общее аналитическое выражение для производной n-го порядка, понятие дробной производной может быть введено естественным образом путём обобщения данного выражения (когда это возможно) на случай произвольного числа n. Пример 1: дифференцирование многочленовПусть есть моном вида Первая производная, как и обычно Повторение данной процедуры даёт более общий результат который после замены факториалов гамма-функциями приводит к Поэтому, например, половинная производная функции x есть Повторяя процедуру, будем иметь что представляет собой ожидаемый результат Таким образом можно ввести дробные производные произвольного положительного порядка от многочлена. на всех , таких что , и не являются целыми отрицательными числами. Следует заметить, что производная имеет место при целых отрицательных n, однако такая производная отличается от понятия первообразной n-го порядка, поскольку первообразная определена неоднозначно, в то время как производная в рассмотренном смысле совпадает лишь с одной из первообразных. Пример 2: дифференцирование тригонометрических функцийПусть Поскольку для любых a и b то, полагая , Действительно, В рассмотренном примере понятие производной обобщается на случай любого действительного и даже комплексного порядка. СвойстваОсновные свойства производной нецелого порядка:
в общем случае не выполняется [1]. Примечания
См. такжеЛитература
Ссылки
Понятие производной – презентация онлайнПроизводная Содержание 1. Понятие производной. 2. Алгоритм нахождения производной. 3. Примеры. 4. Таблица производных. 5. Физический смысл производной. 6. Правила нахождения производных. 7. Непрерывность функции. 8. Геометрический смысл производной. 3. Понятие производнойПроизводной функции у = f(x), заданной на некотороминтервале (a; b), в некоторой точке х этого интервала называют предел отношения приращения функции в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.  ∆f f ′(x) = lim ∆x→0 ∆x Нахождение производной называют дифференцированием 4. Понятие производнойу∆f f ′(x) = lim ∆x→0 ∆x f(x0) у = f(x) ∆f f(x0 + ∆х) ∆х 0 х0 х0+ ∆х х Алгоритм нахождения производной 1. Зафиксировать значение х0, найти f(x0). 2. Дать аргументу х0 приращение ∆х, перейти в новую точку х0 + ∆х, найти f(x0 + ∆х). 3. Найти приращение функции: ∆f = f(x0 + ∆х) – f(x0). ∆f 4. Составить отношение . ∆х ∆f 5. Вычислить lim . ∆x→0 ∆х 6. Этот предел и есть f ′(x0). 6. Примеры1. Найти производную функции y = kx + b в точке хo1. f x o kxo b 2. f xo Δx k xo Δx b 3. Δf f x o Δx f x o k x o Δx b kxo b kxo k Δx b kxo b k Δx Δf k Δx 4. k Δx Δx Δf 5. lim lim k k Δx 0 Δ x Δx 0 kx b k 7. Примеры2. Найти производную функции y = C (C – const) в точке хo1.  f xo С f xo С2. f xo Δx С 3. Δf f xo Δx f xo С С 0 Δf 0 4. 0 Δx Δx Δf 5. lim lim 0 0 Δx 0 Δ x Δx 0 С 0 8. Примеры3. Найти производную функции y = x2 в точке хo1. f xo xо 2 2. f xo Δx xo Δx 2 3. Δf f x o Δx f x o x o Δx x o 2 2 x о2 2 x o Δx Δx 2 x о2 2 x o Δx Δx 2 2x o Δx Δx 2 Δx 2 x o Δx Δf 4. 2 x o Δx Δx Δx Δx Δf 5. lim lim 2 x o Δx 2 x o Δx 0 Δx Δx 0 x 2х 2 9. Примеры4. Найти производную функции y = √x в точке хo1. f xo xo 2. f xo Δx x o Δx 3. Δf f xo Δx f xo xo Δx xo x o Δx x o x o Δx x o x o Δx x o x o Δx x o x o Δx x o Δf 4. Δx Δx x o Δx x 2 o x o Δx x o Δx x o Δx x o Δx x o Δx x o 2 1 x o Δx x o 10. Примеры4. Найти производную функции y = √x в точке хoΔf 4.  Δx Δx Δx x o Δx x o 1 x o Δx x o Δf 1 1 5. lim lim 2 x Δx 0 Δx Δx 0 x Δx x o o o x 1 2 х 11. Примеры5. Найти производную функции y = 1/x в точке хo1 1. f x o xо 1 2. f x o Δx x o Δx 1 1 3. Δf f x o Δx f x o x o Δx x o x o x o Δx Δx 2 x o x o Δx x о x o Δx Δf Δx 1 4. 2 2 Δx Δx x о x o Δx x о x o Δx 12. Примеры5. Найти производную функции y = 1/x в точке хoΔf Δx 1 4. 2 2 Δx Δx x о x o Δx x о x o Δx Δf 1 1 2 5. lim lim 2 Δx 0 Δx Δx 0 x x Δx xо o о 1 1 2 х х 13. Таблица производныхf (x)C f ′(x) 0 f ′(x) 1/(2√x) k f (x) √x ex kx + b x2 2x ax ax lna xn nxn–1 tg x 1/cos2x 1/x – 1/x2 ctg x – 1/sin2x sin x cos x ln x 1/x cos x – sin x loga x 1/(x lna) ex 14. Физический ( механический ) смысл производной Если при прямолинейном движении путь s, Физический ( механический ) смысл производной Если при прямолинейном движении путь s,пройденный точкой, есть функция от времени t, т.е. s = s(t), то скорость точки есть производная от пути по времени, т.е. v(t) = s′(t). Производная выражает мгновенную скорость в момент времени t. 15. Правила нахождения производной1. Если функции u(x) и v(x) имеют в точке хпроизводные, то их сумма u(x) + v(x) также имеет в этой точке производную, причем (u + v)′ = u′ + v′ 2. Если функция u(x) имеет в точке х производную и С – данное число, то функция С∙u(x) также имеет в этой точке производную, причем (Сu)′ = С∙u′ 16. Правила нахождения производной3. Если функции u(x) и v(x) имеют в точке хпроизводные, то их произведение u(x) ∙ v(x) также имеет в этой точке производную, причем (u ∙ v)′ = u′∙v + u∙v′ 4. Если функция v(x) имеет в точке х производную и 1 v(x) ≠ 0, то функция также имеет в этой точке v(x) производную, причем () v′ 1′ =– 2 v v 17. Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке х Правила нахождения производной 5. Если функции u(x) и v(x) имеют в точке хu(x) производные и v(x) ≠ 0, то функция также имеет v(x) в этой точке производную, причем ( ) u ′ u′v – uv′ v = v2 18. Производная сложной функции(f(g(x)))′ = f′(g(x))∙g′(x)Примеры: 1. ((5x – 3)3)′ = 3(5x – 3)2∙(5x – 3)′ = = 3(5x – 3)2 ∙ 5 = 15(5x – 3)2 2. (sin(4x + 8))′ = cos(4x + 8)∙(4x + 8)′ = = cos(4x + 8)∙4 = 4 cos(4x + 8) Если функция имеет производную (дифференцируема) в точке х, то она непрерывна в этой точке. Как репетитор по математике объясняет понятие — Колпаков Александр НиколаевичК концу 9 класса школьники, по сути, заканчивают изучать алгебру и знакомятся с еще одной (более сложной) дисциплиной — математическим анализом. Всякий репетитор по математике знает, как нелегко дается старшекласснику работа с бесконечно малыми величинами. Особенно тяжело идут первые уроки, когда вводятся такие понятия, как «производная» и «касательная». Темы тесно связаны друг с другом и довольно часто рассматриваются репетитором по математике одновременно. И не только потому, что они близки по смысловому наполнению и расположению в программе. Времени на их педантичное и подробное изучение всегда не хватает (обычно репетитор по математике занят устранением многочисленных пробелов в давно пройденном материале), да и способности большинства учеников не позволяют описывать поведение бесконечно малых величин с максимально возможной для подросткового восприятия математической строгостью. Как репетитору по математике объяснить производную? Как рассказать тему доступно и интересно? Долгое время я не рассматривал методики учебников как опорные, считая классические изложения темы «производная» неприемлемыми для большинства старшеклассников (если не считать одаренных детей). Техника моих объяснений принципиально отличалась от «официальной» до того момента, пока не был переиздан учебник Колмогорова. Каково же было мое изумление, когда в исправленном варианте я встретил ту же самую идею с представлением графика в виде бесконечного количества мелких отрезков, которую я старался вложить в сознание своих учеников на уроках по математическому анализу. Разные учебники в разное время по-своему подходили к адаптации курса высшей математики для школьного восприятия. И обычно сначала вводилось понятие «производная», а уже затем объяснялась касательная. Да, такой порядок подошел бы и репетитору по математике, будь его ученик «семи пядей во лбу», а обычная программа содержала главу «предел функции». К сожалению, из-за высокой сложности пределы практически полностью были исключены из базовых учебников, в связи с чем репетитор по математике оказался лишен точного инструмента для объяснений (если конечно не уходить в сторону от программы). Поэтому для средних и слабых детей приходилось искать какие-то обходные варианты подачи материала. Один из способов — замена слова «предел» на более понятную фразу «то, к чему стремится …» или на «то, к чему приближается». Однако, отсутствие смысловой привязки нового понятия к аналитическим формам позволяло репетитору по математике свободно изъясняться только до момента перехода к обоснованию правила вычисления производной. Я советую репетиторам по математике придерживаться следующего порядка изложения: В этой статье я опишу работу репетитора только со вторым и третьим пунктами. Как репетитор по математике вводит производную?Можно воспользоваться тем обстоятельством, что современные дети не могут и дня прожить без компьютера. Как правило, в старших классах многие из них уже умеют работать в сложных программах по обработке фотографий /музыки, загружают с сайтов различные электронные карты и, конечно же, умеют растягивать или сжимать изображения в своем планшете / смартфоне. Репетитор по математике, умеющий использовать интересы ребенка во благо обучения, получает очень хороший мотивационный плацдарм для объяснений понятия «касательная». Я говорю ученику: «Представь себе, что ты сфотографировал график функции или построил его в какой-нибудь программе. Компьютер не умеет рисовать окружности и показывает вместо них многоугольники с огромным количеством вершин. В масштабе 1:1 любой из них не отличишь от гладкой линии, но когда мы начинаем увеличивать размеры рисунка (во многих программах для этого предусмотрена соответствующая «лупа» или «зуммер»), то замечаем, как «окружность» превращается во множество крошечных отрезков. Нечто подобное происходит и с графиком функции». Репетитор по математике, знакомый с профессиональными чертежными программами, может загрузить ученику какую-нибудь из них, например AUTOCAD, и показать структуру объектов. На эти отрезки используются репетитором по математике для дальнейших объяснений: «Они оказываются настолько крошечными после сжатия, что мы не можем отличить из от точек. Можно считать, что каждая из них привязана к определенной прямой, проходящей через концы соответствующего точки отрезка. Эта прямая называется касательной к графику, а ее угловой коэффициент называется производной (будем считать, что репетитор по математике повторил тему «угловой коэффициент» на предыдущем уроке). Итак, определения введены!. Остается найти способ вычисления производной по ее аналитическому выражению. Практика показывает, что ученики лучше усваивают материал именно в такой обертке, так как наблюдения репетитора по математике имеет реальную визуальную основу (пусть даже не совсем точно отражающую понятие «график»). Если нет под рукой компьютера или ребенок не может представить себе, что линия — это множество крошечных отрезков размеров в точку, репетитор по математике раскрывает смысл касательной немного иначе: «Если увеличивать масштаб рисунка в районе некоторй точки(представим себе компьютер, позволяющий как угодно растягивать чертеж), то с определенного момента мы четко увидим, что график функции практически ничем не будет отличаться от некоторой прямой. Чем сильнее окажется увеличение отрезка MN, тем больше будет его длина (в новом масштабе). Но если касательную повернуть хотя бы на миллиардную долю градуса, то, как бы мы не увеличивали размеры чертежа, аналогичного слияния не произойдет. Все равно будет заметен угол между новым положением прямой и «отрезком» графика. Такой подход особенно полезен репетитору по математике для занятий с очень слабым учеником, на уроке с которым бесполезно вводить точное определение производной. Ему достаточно показать объект, о котором идет речь, и объяснить, как считаются его параметры (в нашем случае угловой коэффициент). Это лучше сделать сразу через табличные производные и правила вычисления (производную суммы, разности, произведения и частного) Если у Вас не безнадежный случай, то после «визуальных» определений репетитор может передать аналитическому закреплению. Переход репетитора по математике к аналитической формеВозникает вопрос: как можно вычислить производную (угловой коэффициент касательной) к в точке ? Преподаватель проводит произвольную секущую через точку касания А и получает классический рисунок для данной темы. Он показан выше. Положение точки B зависит от того, насколько ее абсцисса отклонена от абсциссы точки А. Величину этого отклонения репетитор обозначает привычным знаком . Далее записывается формула для поиска углового коэффициента этой прямой . Если уменьшать , то точка B будет двигаться в направлении точки A. С какого то момент В окажется в той области точек графика, которая сливается с касательной. И чем меньше ,чем сложнее нам будет развести точки (при увеличении) по разным линиям. Значит, все меньше и меньше будут отличаться угловые коэффициенты прямой АВ и касательной, а поэтому угловой коэффициент касательной и будет тем числом, к которому приближается значение углового коэффициента прямой АВ. Об использовании знака предела. Если бы впереди стоял знак предела, то он был равен . Вроде бы мелочь, но в совокупности эти «мелочи» сказываются не только на формировании определенной математической культуры ведения записей, но и на восприятие логики производимых преобразований и вычислений. Репетитор по математике, Колпаков А.Н. Москва. Строгино. Урок «Понятие производной»ПОНЯТИЕ ПРОИЗВОДНОЙ. МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Цель: ввести понятие производной, рассмотреть задачи, приводящие к понятию производной. Ход урока І. Анализ контрольной работы. 1. Итоги работы. 2. Характерные ошибки, допущенные при выполнении работы. 3. Решение упр. из КР. ІІ. Изучение нового материала Обратите внимание, что наш учебник называется «Алгебра и начала математического анализа». Историческая справка. Понятие «производная» возникло в XVII веке в связи с необходимостью решения ряда задач из физики, механики и математики. Великий французский математик Пьер Ферма в 1629 г. Научился находить касательные к алгебраическим прямым. В 1638г Ферма поделился этим открытием со своим земляком Рене Декартом, который тоже занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым. Ферма далеко продвинулся в применении дифференциальных методов. Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему. Тем не менее, выдвинутые идеи не пропали впустую. Многие из них легли в основу нового метода математического анализа – дифференциального исчисления. «Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники». Основоположниками этого метода считаются Вильгельм Лейбниц (1646 – 1716) и Исаак Ньютон (1642 – 1727). Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, а Г. С помощью дифференциального исчисления был решен целый ряд задач теоретической механики, физики и астрономии. В частности, ученые предсказали возвращение кометы Галлея, что было большим триумфом науки XVII века. Очень многие великие ученые внесли свой вклад в зарождение и развитие дифференциального исчисления. Среди них – Джеймс Грегори, Якоб Бернулли, Гийом Франсуа Лопиталь, Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, который в 1797 г. ввел термин «производная» и современные обозначения y´, f´. В настоящее время понятие производной находит большое применение в логистике и коммерческой деятельности. Умение применять производную к исследованию функции – важный элемент математической культуры. Продолжить свой урок мне хочется словами Бориса Пастернака
И сейчас мы постараемся дойти до самой сути определения производной и покажем ее применение в различных областях знаний. Сегодня у нас будет встречаться много новых терминов. «Производная» – это то, что «произведено» какой-то функцией. Простой пример: Яйцо – это производная курицы. Понятие производной довольно трудное, т.к. основано на абстрактном восприятии. Мы рассмотрим ситуацию, известную нам из повседневной жизни. Мы едем из Амвросиевки до Ростова (240 км). Рассмотрим график этого движения. На оси абсцисс – время t, по оси ординат – пройденный путь s(t). На весь путь ушло 4 часа. – Мы всё время ехали с такой скоростью? (Нет, в течение пути она менялась, могла быть и больше 60 и меньше). – Так какую скорость мы получим? (Среднюю). – Рассмотрим участок времени Δt (пусть с 10 до 11 часов). За это время мы проехали отрезок пути Δs (пусть 40 км). С какой скоростью мы проехали этот отрезок пути? (40 : 1 = 40 км/ч или Δs : Δt). – Какая скорость получится? (Средняя) Vср. = Δs : Δt – Если мы уменьшим отрезок времени до 0, что произойдет со скоростью? Представьте себе, на посту ГИБДД скорость отслеживается с помощью радара. В момент пересечения луча радара автомобилем на табло радара высвечивается цифры скорости. Будет ли она равна средней скорости (может да, а может, нет). Как можно назвать такую скорость (мгновенной), т.к. мы рассматриваем скорость в какое-то мгновение. Если отрезок времени стремится к 0, скорость из средней превращается в мгновенную: Вот мы подошли к понятию производной пути. Производная пути – это мгновенная скорость. Vмгнов. = S´(t) – Где мы можем увидеть значение мгновенной скорости? (Радар, спидометр). Перейдем от конкретной ситуации к любой математической функции f(x) по той же схеме. f´(x) = lim , где Δx – приращение аргумента, Δf – приращение функции. Определение производной. Производной функции y = f(x) в данной точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента, при условии, что приращение аргумента стремится к нулю. Обозначение производной: . – Где в жизни применяется понятие производной? В физике – это скорость, ускорение, работа; в математике – это исследование различных функций при практических расчетах в автомобилестроении, судостроении, электронике и т. Операция вычисления производной называется дифференцированием. III. Закрепление изученного материала. № 776 (2): S(t) = 1 + 3t, от t = 0,8 до t = 1. h = 1 – 0,8 = 0,2; vср. = = = 3. № 780 (2, 4), № 781 (2, 4), № 778 (самостоятельно) ІV. Итог урока. 1. Как называется раздел математики, который мы начали изучать? 2. Как найти скорость, зная расстояние и время? 3. Какую скорость мы получим? 4. Какую скорость мы видим на спидометре? 5. Где ещё можно увидеть значение мгновенной скорости? 6. Чем является мгновенная скорость для пути? 7. Как обозначается производная? 8. Что означает lim? 9. 10. Определение производной. 11. Как называется операция вычисления производной? 12. Где применяется понятие производной? Чтобы проконтролировать себя, запишите в тетради все опорные слова, старые и новые, которые использовались нами в течение урока. (4 минуты). Проверка в виде самоконтроля: – Я диктую термин, а вы ставите +, если он у вас записан.
Количество «+» разделите на 2 и поставьте себе отметку. VІ. Домашнее задание: §44, № 780 (1, 3), № 781 (1, 3), № 776(1). ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ Цель: формирование навыков решения задач на применение определения производной. Ход урока І. Актуализация знаний. 1. Как называется раздел математики, который мы начали изучать? 2. Как найти скорость, зная расстояние и время? 3. Какую скорость мы получим? 4. Какую скорость мы видим на спидометре? 5. Где ещё можно увидеть значение мгновенной скорости? 6. Чем является мгновенная скорость для пути? 7. Как обозначается производная? 8. Определение производной. 9. Где применяется понятие производной? 10. 11. Задания по карточкам.
II. 1. По определению найти производную функции: а) у = 3х2 – 4х + 5 в точке х0 = 2, в) у = х – 2х3, б) у = х3 + 3х2, г) у = 4х3 + 5х2 – 7х – 4. 2. № 782 (2), № 783 (2), № 785. 3. Тело, масса которого m = 5 кг, движется прямолинейно по закону s = l – t + t2. Найти кинетическую энергию тела через 10 с после начала движения. 4. Самостоятельно.
ІII. Итог урока.
ІV.
определение производной по The Free DictionaryОднако в некоторых случаях, поскольку рассматриваемое качество не имеет имени, невозможно, чтобы обладающие им имели производное имя. Например, имя, данное бегуну или боксеру, названному так в силу врожденных способностей, не происходит от имени какого-либо качества; для лоббирования эти способности не имеют присвоенного им названия. “Идиоты” – настолько очевидно производное произведение, что я не могу сказать что-либо об этом здесь.Но что касается вмешивающихся действий вышестоящей и подчиненной власти, изначальной и производной власти, природа и причина вещи указывают на обратное этому правилу, которое должно соблюдаться. дериватив может быть найден, принадлежит только людям, и что он не будет зависеть только от сравнительных амбиций или адреса различных правительств, сможет ли кто-либо из них или какое из них расширить сферу своей юрисдикции за счет другого. Следование по этому пути – это посвящение, благодаря которому они смогут отличать в искусстве, речи, чувствах, манерах, в людях и жизни в целом то, что является подлинным, одушевленным и выразительным, от того, что является лишь условным и производным, и, следовательно, невыразительно. – Я полагаю, он не читает это, если только он не улучшится с помощью этого, – думая, что жить каким-то производным старым способом в этой примитивной новой стране – ловить окуня с помощью фингалов. – Он гласит: – Vondervotteimittis – Vonder, lege Donder – Votteimittis, quasi und Bleitziz- Bleitziz obsol: – про Блитцен.”Эта производная, честно говоря, все еще поддерживается некоторыми следами электрического флюида, очевидными на вершине шпиля Дома городского совета. Движение, собственно говоря, является производным от нигилизма, хотя они известны только косвенно и понаслышке, поскольку они никогда не рекламируют свои действия в газетах. Мне кажется, что это производное и в значительной степени состоит из УБЕЖДЕНИЙ: убеждения, что то, что составляет мысль, связано с различными другими элементами, которые вместе составляют объект. Следование по этому пути – это посвящение, благодаря которому они смогут отличать в искусстве, речи, чувствах, манерах, в людях и жизни в целом то, что является подлинным, одушевленным и выразительным, от того, что является лишь условным и производным, и, следовательно, невыразительно. – Я полагаю, он не читает это, если только он не улучшится с помощью этого, – думая, что жить каким-то производным старым способом в этой примитивной новой стране – ловить окуня с помощью фингалов. – Он гласит: – Vondervotteimittis – Vonder, lege Donder – Votteimittis, quasi und Bleitziz- Bleitziz obsol: – про Блитцен.”Эта производная, честно говоря, все еще поддерживается некоторыми следами электрического флюида, очевидными на вершине шпиля Дома городского совета. Движение, собственно говоря, является производным от нигилизма, хотя они известны только косвенно и понаслышке, поскольку они никогда не рекламируют свои действия в газетах. Мне кажется, что это производное и в значительной степени состоит из УБЕЖДЕНИЙ: убеждения, что то, что составляет мысль, связано с различными другими элементами, которые вместе составляют объект. В последнее время даже простейшее производное от слова «наука» (термин сам по себе безобидный и неопределенный) обладал любопытной силой вызывать определенно оскорбительное ментальное видение господина Владимира в его теле, когда он жил, с почти сверхъестественной ясностью. начало и конец – это предупреждение тем, кто слишком легкомысленно относится к инстинктам и чрезмерно превозносит интеллект и его производные: разум и понимание. Нет; он никогда не путешествует с производными водорода. Обычно вы видите его наедине или с другим мужчиной.” В последнее время даже простейшее производное от слова «наука» (термин сам по себе безобидный и неопределенный) обладал любопытной силой вызывать определенно оскорбительное ментальное видение господина Владимира в его теле, когда он жил, с почти сверхъестественной ясностью. начало и конец – это предупреждение тем, кто слишком легкомысленно относится к инстинктам и чрезмерно превозносит интеллект и его производные: разум и понимание. Нет; он никогда не путешествует с производными водорода. Обычно вы видите его наедине или с другим мужчиной.”Определение производной – исчисление 2 Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org. Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Чтобы отправить уведомление, выполните следующие действия: Вы должны включить следующее: Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса – изображению, ссылке, тексту и т. Отправьте жалобу нашему уполномоченному агенту по адресу: Чарльз Кон
Varsity Tutors LLC Или заполните форму ниже: Что такое производный инструмент: определение, типы и примеры Если вы новичок в инвестировании или ищете способы управления своими активами, вы, возможно, слышали термин «производные финансовые инструменты». Объяснение производных финансовых инструментовПроизводные инструменты, используемые в финансах и инвестициях, относятся к типу контрактов. Вместо того, чтобы торговать физическим активом, производный инструмент просто получает свою стоимость от базового актива. Другими словами, он действует как обещание, что вы купите актив в какой-то момент в будущем. Конкретная дата и цена указаны в производном контракте. Итак, какие типы активов охватываются производным контрактом?
Производные инструменты часто используются для хеджирования позиций, увеличения кредитного плеча или спекулировать на движении актива. Первоначально они предназначались для балансировки обменных курсов, но теперь вы найдете их на основе любых данных, от данных о погоде до цен на виноград. В случае курсов обмена валют представьте следующий пример: Счета испанского инвестора в основном открыты в евро (EUR), но он хочет купить акции британской компании в фунтах стерлингов. Из-за колебаний цен на валюту существует риск того, что стоимость евро вырастет по сравнению с фунтом. Это означает, что акции станут менее ценными при обратном обмене с фунта стерлингов на евро. Чтобы помочь хеджировать риск с помощью деривативов, он мог купить дериватив на валюту, заблокированный по определенному обменному курсу. Понимание производных финансовых инструментов и торговля Как мы уже выяснили выше, производные финансовые инструменты используются для снижения риска, фиксируя определенные цены для защиты от колебаний курсов валют, цен на сырьевые товары или процентных ставок. Торговля производными финансовыми инструментами может сделать будущий денежный поток более предсказуемым, чтобы компании могли лучше прогнозировать свои доходы, что, в свою очередь, повысит цены на их акции. В финансовом мире большинство деривативов покупают и продают инвесторы и хедж-фонды.У них редко есть шанс прийти к соглашению до того, как они будут ликвидированы другим производным контрактом. Вот несколько способов торговли производными финансовыми инструментами:
Типы деривативов в финансахТак же, как существует множество вариантов использования деривативов, есть также несколько типов деривативов на выбор: Фьючерсы Фьючерсные контракты используются для таких сырьевых товаров, как нефть. ФорвардыЕще одним контрактом, используемым в торговле производными финансовыми инструментами, является форвард. В этих соглашениях также указывается конкретная цена и дата будущей продажи, но они продаются на внебиржевом рынке, а не на бирже. Это делает их более рискованными, чем фьючерсы, если одна из сторон не сможет выполнить свою часть сделки. СвопыВозможно, самый распространенный вид торговли производными финансовыми инструментами. Свопы обменивают один тип долга или актива на сопоставимый. Цель состоит в том, чтобы снизить риск для обеих сторон.В большинстве случаев свопы связаны с процентными ставками или валютами. Например, трейдер может обменять ссуду с переменной процентной ставкой на фиксированную процентную ставку. Опционы Наконец, опционы – это популярные типы производных инструментов, которые похожи на фьючерсные контракты. Каковы плюсы и минусы деривативов?Торговля производными финансовыми инструментами связана с преимуществами и рисками. Деривативы можно использовать для управления рисками и помощи компании в достижении финансовых целей, будь то хеджирование от колебаний цен на сырьевые товары или использование позиций. Вы можете зафиксировать цены и диверсифицировать свой портфель как инвестор. С другой стороны, торговля производными финансовыми инструментами также сопряжена с риском. Некоторые виды деривативов более рискованны, чем другие, особенно те, которые торгуются на внебиржевом рынке.Обязательно внимательно взвесьте все «за» и «против» перед покупкой. Мы можем помочь GoCardless поможет вам автоматизировать сбор платежей, сократив количество администраторов, с которыми ваша команда должна иметь дело при поиске счетов. GoCardless используется более чем 60 000 компаний по всему миру. Узнайте больше о том, как вы можете улучшить обработку платежей в своем бизнесе уже сегодня. Узнать большеЗарегистрироваться Производное определение | Банковская ставка.comЧто такое производная?Производный инструмент – это финансовый инструмент, стоимость которого определяется на основе базового актива , товара или индекса. Производный инструмент представляет собой контракт между двумя сторонами, которые соглашаются предпринять действия в будущем при соблюдении определенных условий, чаще всего для обмена ценного предмета. Фьючерсы, опционы и свопы являются обычными производными финансовыми инструментами. Более глубокое определение Инвесторы используют деривативы для управления рисками, спекуляций и получения кредитного плеча.Эти контракты «производятся» от базового актива, такого как акция, облигация, индекс или товар. Первоначально производные финансовые инструменты представляли собой фьючерсы на урожай, которые помогали фермерам хеджировать риски, связанные с колебаниями цен и спроса. Фермер подписывал контракт с посредником на продажу своего урожая в конце сезона по согласованной цене; если рыночная цена на урожай будет ниже, посредник понесет убытки, а фермер получит выгоду, но если рыночная цена будет выше, посредник получит выгоду, продав урожай по более высокой цене на рынке.В любом случае фермер мог планировать, основываясь на стабильной фиксированной цене на свой продукт. Фьючерсы и опционы остаются основным способом установления цен и торговли всеми видами товаров. Применительно к финансовым рынкам производные контракты позволяют участникам рынка оценивать риск и бесконечно спекулировать. Вместо товаров производные финансовые инструменты основаны на акциях, облигациях, валютах, процентных ставках и индексах.
Деривативы торгуются на внебиржевых или открытых биржах. Частные внебиржевые деривативы обычно более сложны и приспособлены к индивидуальным потребностям. Рынок внебиржевых деривативов может быть непрозрачным, а структура создаваемых и обмениваемых продуктов держится в секрете. Биржевые деривативы, как правило, представляют собой стандартизированные продукты, которые торгуются на специализированных биржах деривативов с гораздо большей открытостью, чем внебиржевой рынок. Ищете место, где можно припарковать деньги, не рискуя? Посмотрите на эти отличные ставки денежного рынка! Пример производного инструментаМногие аналитики и историки экономики утверждают, что производные финансовые инструменты, в частности обеспеченные долговые обязательства и свопы на дефолт по кредитам, были основной причиной финансового кризиса 2008 года. Деривативы в форме CDO и CDS были впервые созданы в 1970-х и 1980-х годах, чтобы помочь финансовым компаниям лучше понимать риски и управлять ими, но дерегулирование финансовых рынков в 1990-х годах открыло возможность использования таких производных инструментов в спекулятивных целях. До распространения недорогих компьютерных технологий было очень сложно создавать и оценивать сложные производные контракты, но эта проблема была более или менее решена к 1990-м годам, в том числе благодаря уравнению Блэка-Шоулза. Ценные бумаги, обеспеченные ипотекой, стали очень распространенными инвестиционными продуктами. : значение и определение | Capital.comЧто такое производные финансовые инструменты?Определение производного инструмента: Производные финансовые инструменты – это контракты, стоимость которых определяется рыночными характеристиками базового актива. Вместо фактического обмена актива заключаются соглашения, предусматривающие обмен денежных средств или других активов на базовый актив в течение определенного указанного периода времени. Эти базовые активы могут принимать различные формы, включая облигации, акции, валюты, товары, индексы и процентные ставки.Те, кто инвестирует в производные финансовые инструменты, фактически не владеют базовым предприятием, и инвестор, по сути, делает ставку относительно направления движения цены посредством соглашения с третьей стороной. Производные финансовые инструменты могут принимать различные формы, такие как фьючерсные контракты, опционные контракты, свопы, контракты на разницу (CFD), варранты или форвардные контракты, и они могут использоваться для различных целей, в том числе для хеджирования и спекуляций.
Где вы слышали о деривативах? Несмотря на то, что производные финансовые инструменты обычно считаются современным торговым инструментом, они, по сути, существуют уже очень давно.Сам термин, однако, появился в 1970-х годах, а деривативы были полурегулярным явлением в новостях и на финансовых страницах с 1980-х годов, иногда с большим количеством негативной прессы. Вы почти наверняка слышали этот термин после глобального экономического спада 2008 года, когда эти финансовые инструменты часто обвиняли в качестве одной из основных причин кризиса. Вы, наверное, слышали термин «деривативы», используемый в связи с хеджированием рисков.Фьючерсные контракты, CFD, опционные контракты и т. Д. – все это превосходные способы смягчения убытков, которые могут возникнуть в результате спадов на рынке или цены актива. Работая аналогично страховым полисам, деривативы являются важной частью портфелей многих инвесторов. Что нужно знать о производных финансовых инструментах.История деривативов Один из самых ранних примеров того, что мы сегодня считаем деривативами, был в Древней Греции и касался философа Фалеса, ученика Аристотеля.Фалес, который был опытным метеорологом, на основе своих наблюдений сделал прогноз, что в этом году будет рекордный урожай оливок. Он был настолько уверен в своих наблюдениях, что решил купить многие оливковые фермы в окрестностях Афин до сбора урожая того года. Оказалось, что предсказание Фалеса оказалось верным. Погодные условия того года уступили место рекордному урожаю оливок, и это принесло ему много денег в очень ранней версии того, что мы теперь называем форвардным контрактом. В XIX веке у фермеров США были проблемы с поиском покупателей для своих товаров. Чтобы решить эту проблему, в 1848 году был создан совместный рынок под названием Чикагская торговая палата (CBOT). Вскоре он превратился в первый в мире рынок деривативов, на котором вместо того, чтобы покупатели и продавцы заключали между собой собственные индивидуальные контракты, были введены и котируются на бирже Совета стандартизированные контракты, которые любой мог покупать и продавать. В 2007 году CBOT объединилась с Чикагской товарной биржей и превратилась в группу CME, которая по-прежнему остается одним из ведущих мировых рынков деривативов. Сегодня существует практически любой производный финансовый инструмент для всего, и многие современные инновации финансового рынка основаны на идеях производных финансовых инструментов. То, что начиналось как простая идея в далеком далеком прошлом, превратилось в стандартизированные контракты, а теперь превратилось в лабиринт сложных контрактов и финансовых инструментов. Виды производных финансовых инструментов.Наиболее распространенными формами производных финансовых инструментов являются:
Использование производных финансовых инструментов.Наиболее частые причины использования производных финансовых инструментов в ваших торговых стратегиях:
Ограничения использования производных финансовых инструментов. Производные инструменты часто критикуют по следующим причинам:
Узнайте больше о производных финансовых инструментах.MoneyWeek предлагает отличное руководство по инвестированию в дериваты и способы их использования в своих интересах. Смотрите здесь. Производная: определение, объяснение и типы
Когда вы думаете об инвестировании, вы можете быть более знакомы с акциями и облигациями.Другой тип инвестиционного инструмента, с которым вы, возможно, не так хорошо знакомы, – это деривативы. Хотя любое инвестирование в фондовый рынок сопряжено с неотъемлемым риском, некоторые виды инвестиций, как правило, более рискованные, чем другие. Деривативы попадают в этот лагерь. Что такое производная? Деривативы – это контракт, стоимость которого определяется базовым активом или индексом – отсюда и название «дериватив». Существует два типа деривативов: внебиржевые деривативы, переговоры по которым ведутся в частном порядке, а также стандартизированные деривативы, которыми можно торговать на стандартной бирже. Внебиржевые деривативы, также известные как внебиржевые деривативы, как известно, вызвали Великую рецессию, создав повышенный спрос на базовые активы, такие как ипотека. Начало рынка деривативов началось в 1865 году, когда фермеры и продавцы зерна объединились, чтобы застраховаться от рисков на рынке кукурузы.Эти деривативы использовались как часть хеджирования и спекуляций для снижения риска, что может привести к завышению цен, что может стать причиной манипуляций и мошенничества. Эти типы деривативов называются фьючерсными контрактами, о которых мы поговорим позже. «Деривативы отличаются от ценных бумаг тем, что они представляют собой скорее ставку, чем инвестицию. «Ценные бумаги, с другой стороны, могут быть бессрочными или погашаемыми, поэтому инвесторы могут просто держать их в долгосрочном периоде. Ключевым преимуществом деривативов по сравнению с ценными бумагами является кредитное плечо. Если трейдер убежден в изменении цены в пределах определенного В течение определенного периода времени они могут получить гораздо более высокую прибыль, торгуя деривативами вместо базовой ценной бумаги. Конечно, с этим более высоким потенциалом прибыли связан более высокий риск ». Типы контрактов с производными инструментами Производные инструменты могут быть сложными, поскольку существуют различные типы контрактов с производными инструментами.
Срочные контракты могут продаваться либо на внебиржевом рынке (OTC), либо на таких биржах, как Чикагская товарная биржа (CME Group) или Корейская биржа. Как работают деривативы?Деривативы могут использоваться различными способами для хеджирования рисков или использоваться в качестве спекулятивных инструментов.Как финансовый инструмент, стоимость операций с производными финансовыми инструментами зависит от рыночных условий, таких как кредит, собственный капитал и процентные ставки. По данным факультета экономики Государственного университета Сан-Хосе, деривативы и свопы играют важную роль в экономике, передавая риски. Риск передается другим сторонам, которые готовы взять его на себя за определенную плату. Таким образом, деривативы похожи на страховую отрасль, где вы хеджируете такие риски, как падение цены акций. Вы можете застраховаться от рисков с помощью производных контрактов, купив контракт, стоимость которого поможет компенсировать любые другие убытки, которые могут возникнуть у вас по другим позициям. Посредством хеджирования инвесторы стремятся снизить риск убытков, имея на рынке противоположные позиции, чтобы минимизировать риск. Деривативные контракты – это договоренности между двумя организациями, часто называемыми «контрагентами», которые работают вместе, чтобы снизить риск их общих инвестиций и базового актива. Деривативы также могут использоваться в качестве инструмента для увеличения доли заемных средств. При инвестировании кредитное плечо – это когда инвестор максимально использует заемные деньги, чтобы попытаться максимизировать прибыль. Хотя эта стратегия может увеличить прибыль, она также может увеличить риск. Спекуляция – это стратегия, при которой инвесторы покупают такие активы, как деривативы, и предполагают, что цена изменится в будущем. Подсказка: Перед тем, как начать инвестировать в производные финансовые инструменты, вы хотите оценить общий риск контрагента, который относится к вероятности того, что другая сторона не выполнит свою часть сделки. Плюсы и минусы деривативовЕсли вы думаете об инвестировании в деривативы, прежде чем приступить к работе, изучите плюсы и минусы. Этот тип инвестиций может иметь больше движущихся частей и соображений, поскольку есть контрагент и основан на базовых активах. Подсказка: Разберитесь, как деривативы работают с вашими общими финансовыми целями и как вы собираетесь их использовать для максимизации прибыли при минимизации убытков. Деривативы – это еще один инвестиционный инструмент, который используется для минимизации риска при максимизации прибыли. Это сложный финансовый инструмент, который имеет дело с активами, стоимость которых может меняться, но также предоставляет возможности для хеджирования рисков и использования кредитного плеча для получения прибыли.Важно отметить, что деривативы могут быть связаны с риском и возможностью мошенничества. «Деривативы не для начинающих или случайных инвесторов. Поскольку они, по сути, являются ставками, Уолл-Стрит очень хорошо проверяет их точные цены», – отмечает Рогови. «Поскольку деривативы имеют тенденцию к истечению срока, остается меньше права на ошибку. С ценными бумагами некоторые плохие сделки могут быть спасены путем удержания в течение длительного времени. Неопытные трейдеры печально известны тем, что теряют значительные суммы капитала из-за рискованных ставок на опционы на акции. Что означает производная?производное существительное Что-то производное. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное существительное Слово, производное от другого. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное существительное Финансовый инструмент, стоимость которого зависит от оценки базового актива; например, ордер, опцион и т. д. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное существительное Химическое вещество, производное от другого. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное существительное Производная функция функции. Производным от uE0006894uE001 является uE0006895uE001 Этимология: Среднеанглийский, от dérivatif и производного; см. производное существительное Значение этой функции для данного значения ее независимой переменной. Производная uE0006896uE001 при x = 3 – uE0006897uE001. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное прилагательное Подражает чужой работе. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное прилагательное Обращение к произведению, например, переводу или адаптации, основанному на другом произведении, которое может подпадать под ограничения авторского права. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. приятное. производное прилагательное Имея значение, которое зависит от базового актива переменной стоимости. Этимология: Среднеанглийский, от дериватифа и дериватуса; см. | |||||||||||||||||||||||||||||||||||||||||||||||


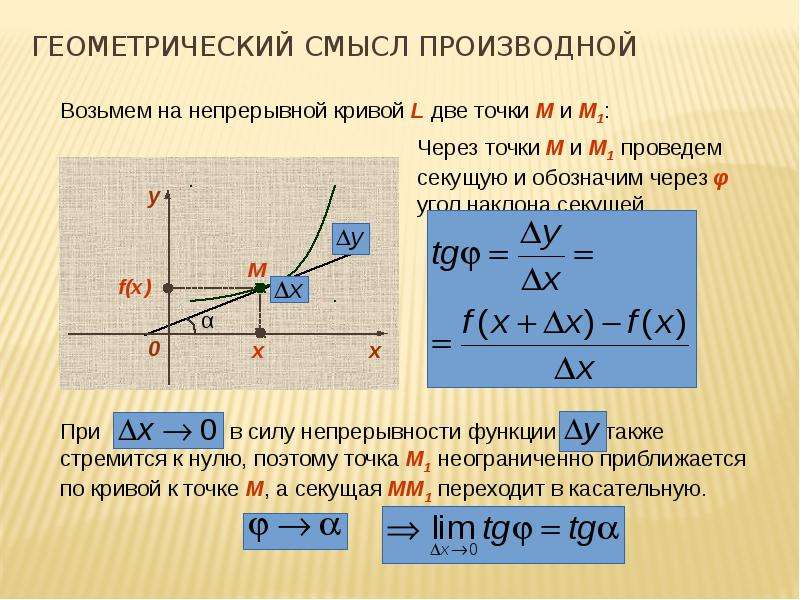
 В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=y'(x_0) $$
В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=\lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=y'(x_0) $$  2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2x+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2x+\triangle x)=2x+0=2x \end{gather*} Ответ: уравнение производной \(y\ ‘=2x\)
2=(x+\triangle x-x)(x+\triangle x+x)=\triangle x(2x+\triangle x) \end{gather*} Ищем предел: \begin{gather*} \lim_{\triangle x\rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow 0}\frac{\triangle x(2x+\triangle x)}{\triangle x}=\lim_{\triangle x\rightarrow 0}(2x+\triangle x)=2x+0=2x \end{gather*} Ответ: уравнение производной \(y\ ‘=2x\) 2)=12+0+0=12 \end{gather*} Искомая производная в заданной точке: \(f'(2)=12\)
2)=12+0+0=12 \end{gather*} Искомая производная в заданной точке: \(f'(2)=12\) 2}\)
2}\)
 Определение также естественно обобщается на аналитические функции. Рассматривая как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом
Определение также естественно обобщается на аналитические функции. Рассматривая как мероморфную функцию комплексного переменного, можно обобщить определение на случай произвольного порядка дифференцирования. При этом Так, при формула n-й производной даёт одну из первообразных функции .
Так, при формула n-й производной даёт одну из первообразных функции . — 272 с. — 5-9 221-0 440-3 экз.
— 272 с. — 5-9 221-0 440-3 экз.
 (англ.)
(англ.)
 Разница между моим приемом и тем, что предалгал Колмогоров была, но отправная точка совпадала. Обо всем по порядку.
Разница между моим приемом и тем, что предалгал Колмогоров была, но отправная точка совпадала. Обо всем по порядку.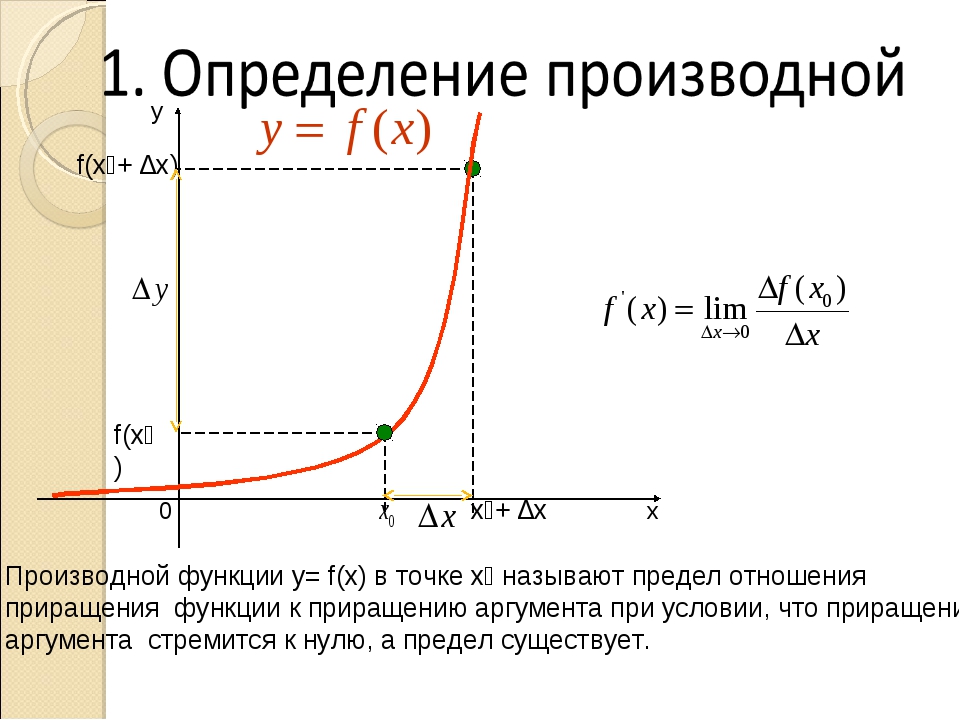 Учебники стремятся как можно быстрее выйти на классическое определение через предел отношения . К сожалению, большинство репетиторов по математике стараются еще больше ускорить переход к аналитике и дают его без какой-либо предварительной подготовки, порождая тем самым волну непонимания со стороны учеников. Ситуация осложняется тем, что при неудачной логике объяснений практически невозможно внятно объяснить взаимосвязь между «числом, к которому стремится» и касательной. Репетитору по математике придется увести ученика в строгие доказательства с бесконечно малыми, которые только еще больше его запутают. Какой выход можно найти из сложившейся ситуации и как донести тему слабому ученику?
Учебники стремятся как можно быстрее выйти на классическое определение через предел отношения . К сожалению, большинство репетиторов по математике стараются еще больше ускорить переход к аналитике и дают его без какой-либо предварительной подготовки, порождая тем самым волну непонимания со стороны учеников. Ситуация осложняется тем, что при неудачной логике объяснений практически невозможно внятно объяснить взаимосвязь между «числом, к которому стремится» и касательной. Репетитору по математике придется увести ученика в строгие доказательства с бесконечно малыми, которые только еще больше его запутают. Какой выход можно найти из сложившейся ситуации и как донести тему слабому ученику?
 Что собой представляет фотография / чертеж в любом цифровом формате? Набор точек определенной плотности и цвета, не более того. Если ты попытаешься увеличить картинку, то объекты станут более крупными, а изгибы линий уйдут за границы экрана, оставляя нам на обозрение только самые ровные кусочки. Можно представить себе результат увеличения, при котором эти кусочки выпрямятся практически до отрезков.
Что собой представляет фотография / чертеж в любом цифровом формате? Набор точек определенной плотности и цвета, не более того. Если ты попытаешься увеличить картинку, то объекты станут более крупными, а изгибы линий уйдут за границы экрана, оставляя нам на обозрение только самые ровные кусочки. Можно представить себе результат увеличения, при котором эти кусочки выпрямятся практически до отрезков.
 Это и есть касательная. На рисунке хорошо заметен отрезок MN — собирающий в себя все общие точки двух линий (хотя в
Это и есть касательная. На рисунке хорошо заметен отрезок MN — собирающий в себя все общие точки двух линий (хотя в Введенного понятия.
Введенного понятия. Эти рассуждения позволяют репетитору по математике подвести ученика к той мысли, что значение производной – это предел отношения при
Эти рассуждения позволяют репетитору по математике подвести ученика к той мысли, что значение производной – это предел отношения при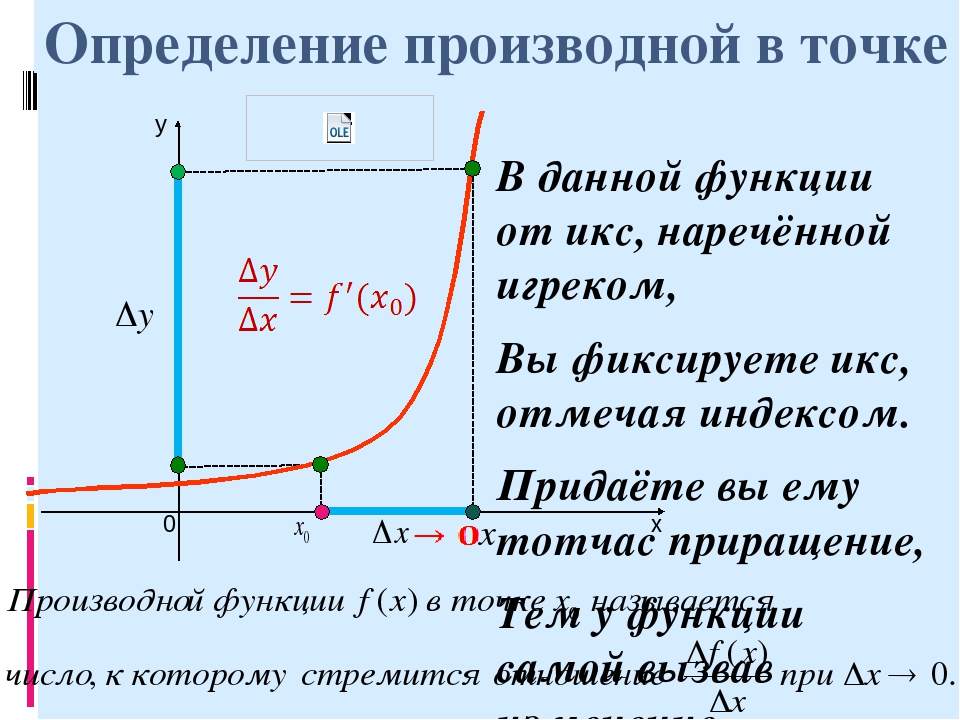
 Мы начинаем изучать новый раздел математики «Математический анализ». В нашей учебной программе мы будем изучать только основы – «начала» анализа. Одна из тем этого раздела – «Понятие производной». Математика в школе – это достаточно сложный предмет и самое главное для учащихся – понять, зачем она нужна. Мы изучаем производную. А так ли это важно в жизни? Давайте попробуем вместе в этом разобраться.
Мы начинаем изучать новый раздел математики «Математический анализ». В нашей учебной программе мы будем изучать только основы – «начала» анализа. Одна из тем этого раздела – «Понятие производной». Математика в школе – это достаточно сложный предмет и самое главное для учащихся – понять, зачем она нужна. Мы изучаем производную. А так ли это важно в жизни? Давайте попробуем вместе в этом разобраться. Он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей.
Он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей. Лейбниц использовал понятие бесконечно малой.
Лейбниц использовал понятие бесконечно малой.
 Как узнать, с какой скоростью мы ехали. (Пройденный путь разделить на время 240 : 4 = 60 км/ч)
Как узнать, с какой скоростью мы ехали. (Пройденный путь разделить на время 240 : 4 = 60 км/ч)
 д.
д. Что означает Δx; Δf?
Что означает Δx; Δf?
 Как называется операция вычисления производной?
Как называется операция вычисления производной? Решение упражнений.
Решение упражнений.
 Домашнее задание: §44, № 782 (1), № 783 (1), № 784.
Домашнее задание: §44, № 782 (1), № 783 (1), № 784.
 д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. – относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Деривативы – это тип контрактов, используемых в торговле, но они не лишены риска. Вот что вам нужно знать.
Деривативы – это тип контрактов, используемых в торговле, но они не лишены риска. Вот что вам нужно знать.

 Покупка и доставка актива оговариваются по конкретной цене и в будущем. Фьючерсные деривативы торгуются на бирже со стандартными контрактами.
Покупка и доставка актива оговариваются по конкретной цене и в будущем. Фьючерсные деривативы торгуются на бирже со стандартными контрактами. Однако главное отличие состоит в том, что покупатели не обязаны заключать договор купли-продажи. Могут, если хотят, но это скорее возможность, чем обязанность. Применительно к фондовому рынку возможность покупки называется «колл-опцион», а возможность продать – «пут-опционом».
Однако главное отличие состоит в том, что покупатели не обязаны заключать договор купли-продажи. Могут, если хотят, но это скорее возможность, чем обязанность. Применительно к фондовому рынку возможность покупки называется «колл-опцион», а возможность продать – «пут-опционом». Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами.
Узнайте, как GoCardless может помочь вам со специальными или регулярными платежами. Проще говоря, производный контракт – это сделка между двумя сторонами по обмену базового актива, если цена актива достигнет согласованного уровня в какой-то момент в будущем.
Проще говоря, производный контракт – это сделка между двумя сторонами по обмену базового актива, если цена актива достигнет согласованного уровня в какой-то момент в будущем. Рассмотрим рынок опционов: трейдеры пишут контракт, в котором указывается, что держатель будет иметь опцион, но не обязан покупать определенное количество акций в будущем, если акция достигнет указанной цены, а продавец опциона будет обязан продать акции держателю.После создания контракта он может быть продан другой стороне. Стоимость контракта определяется доходностью данной акции.
Рассмотрим рынок опционов: трейдеры пишут контракт, в котором указывается, что держатель будет иметь опцион, но не обязан покупать определенное количество акций в будущем, если акция достигнет указанной цены, а продавец опциона будет обязан продать акции держателю.После создания контракта он может быть продан другой стороне. Стоимость контракта определяется доходностью данной акции. Фьючерсы – это стандартизированные контракты, торгуемые на биржах, в то время как форварды очень индивидуализированы и торгуются на внебиржевом рынке (OTC).
Фьючерсы – это стандартизированные контракты, торгуемые на биржах, в то время как форварды очень индивидуализированы и торгуются на внебиржевом рынке (OTC).
 Вместо того, чтобы использовать деривативы для эффективного уравновешивания рисков, институциональные трейдеры начали их скупать, чтобы создать кредитное плечо и взять на себя гораздо больший риск. Когда в 2006 и 2007 годах рынок жилья в США начал рушиться, инвестиции MBS, распространившиеся по всей банковской системе, начали быстро терять ценность, что спровоцировало кризис.
Вместо того, чтобы использовать деривативы для эффективного уравновешивания рисков, институциональные трейдеры начали их скупать, чтобы создать кредитное плечо и взять на себя гораздо больший риск. Когда в 2006 и 2007 годах рынок жилья в США начал рушиться, инвестиции MBS, распространившиеся по всей банковской системе, начали быстро терять ценность, что спровоцировало кризис.


 Есть деривативы на сырьевые товары, акции, недвижимость и индексы. Есть даже производные на основе других производных. Причина этого в том, что деривативы очень хорошо удовлетворяют потребности множества различных предприятий и частных лиц по всему миру.
Есть деривативы на сырьевые товары, акции, недвижимость и индексы. Есть даже производные на основе других производных. Причина этого в том, что деривативы очень хорошо удовлетворяют потребности множества различных предприятий и частных лиц по всему миру. Форвардный контракт заключается между двумя сторонами и представляет собой соглашение о покупке или продаже актива или товара по заданной цене в заданную дату. Основное различие между форвардными и фьючерсными контрактами заключается в том, что форвардные контракты нестандартизированы и торгуются на внебиржевом рынке, а не на формальном организованном рынке.
Форвардный контракт заключается между двумя сторонами и представляет собой соглашение о покупке или продаже актива или товара по заданной цене в заданную дату. Основное различие между форвардными и фьючерсными контрактами заключается в том, что форвардные контракты нестандартизированы и торгуются на внебиржевом рынке, а не на формальном организованном рынке. Своп – это контракт, по которому две стороны буквально обмениваются или обмениваются денежными потоками финансового инструмента в течение ограниченного периода времени.Выгода от этого сильно варьируется и во многом зависит от характера обмениваемого финансового инструмента. В отличие от фьючерсных и опционных контрактов, свопы торгуются на внебиржевой основе между вовлеченными сторонами, и на рынке свопов доминируют финансовые учреждения и корпорации, в которых участвует несколько частных лиц.
Своп – это контракт, по которому две стороны буквально обмениваются или обмениваются денежными потоками финансового инструмента в течение ограниченного периода времени.Выгода от этого сильно варьируется и во многом зависит от характера обмениваемого финансового инструмента. В отличие от фьючерсных и опционных контрактов, свопы торгуются на внебиржевой основе между вовлеченными сторонами, и на рынке свопов доминируют финансовые учреждения и корпорации, в которых участвует несколько частных лиц. Необеспеченный кредитный производный инструмент – это двустороннее соглашение между двумя сторонами, и каждая из сторон несет ответственность за выполнение своих платежей. Финансируемый кредитный производный инструмент – это когда продавец защиты (сторона, которая принимает на себя кредитный риск) производит платеж, который позже используется для урегулирования любых кредитных событий, которые могут произойти.
Необеспеченный кредитный производный инструмент – это двустороннее соглашение между двумя сторонами, и каждая из сторон несет ответственность за выполнение своих платежей. Финансируемый кредитный производный инструмент – это когда продавец защиты (сторона, которая принимает на себя кредитный риск) производит платеж, который позже используется для урегулирования любых кредитных событий, которые могут произойти. Например, те, кто хочет защитить себя в случае падения цен на свои акции, могут купить опцион пут. Это означает, что независимо от того, вырастет или упадет цена акций, владелец получит прибыль, потому что любой потенциальный убыток будет хеджирован.
Например, те, кто хочет защитить себя в случае падения цен на свои акции, могут купить опцион пут. Это означает, что независимо от того, вырастет или упадет цена акций, владелец получит прибыль, потому что любой потенциальный убыток будет хеджирован. Это, в свою очередь, может привести к цепной реакции, которая приведет к финансовому кризису.
Это, в свою очередь, может привести к цепной реакции, которая приведет к финансовому кризису.
 Одним из примеров производных финансовых инструментов являются опционы, поскольку их стоимость изменяется в зависимости от движения цены базовых акций.
Одним из примеров производных финансовых инструментов являются опционы, поскольку их стоимость изменяется в зависимости от движения цены базовых акций. Большинство распространенных контрактов с производными финансовыми инструментами имеют дату истечения срока, что означает ограниченное время для получения прибыли», – объясняет Ашер Рогови, консультант по инвестициям, зарегистрированный в SEC. и главный инвестиционный директор Magnifina.
Большинство распространенных контрактов с производными финансовыми инструментами имеют дату истечения срока, что означает ограниченное время для получения прибыли», – объясняет Ашер Рогови, консультант по инвестициям, зарегистрированный в SEC. и главный инвестиционный директор Magnifina. Некоторые распространенные типы деривативов включают:
Некоторые распространенные типы деривативов включают: Но важно отметить, что форвардные контракты не торгуются на бирже.
Но важно отметить, что форвардные контракты не торгуются на бирже. Но вместо того, чтобы называть «страхование», это называется хеджированием.
Но вместо того, чтобы называть «страхование», это называется хеджированием. Учитывая его название, это больше предположение, чем достоверные данные. Инвестор, использующий эту стратегию, надеется получить максимальную прибыль, но, как предполагает термин, все это спекулятивно, и может быть очень рискованным.
Учитывая его название, это больше предположение, чем достоверные данные. Инвестор, использующий эту стратегию, надеется получить максимальную прибыль, но, как предполагает термин, все это спекулятивно, и может быть очень рискованным.
 «
« приятное.
приятное.