Производная по времени от пути: «Когда говорят: “производная по времени – скорость. Производная по скорости

Блог Олега Кривошеина: Физический смысл производной.

Ещё часть задач из раздела В8 ЕГЭ по математике связана с физическим смыслом производной. Напомним его.  

Если положение точки при её движении задаётся функцией S = f(t), где t – время движения, то производная функции S  есть мгновенная скорость движения в момент времени t, v(t) = S‘(t).

Скорость – есть производная от пути по времени.

Уместно заметить, что ускорение – это скорость изменения скорости тела, значит а(t) = v‘(t)= S”(t).

Ускорение – есть производная от скорости по времени, или вторая производная от пути по времени.

Кстати, по аналогии вообще говорят о том, что производная функции у = f(x) – скорость изменения функции в точке х.

Решим несколько задач уровня В8 из Открытого банка задач для подготовки к ЕГЭ по математике на использование физического смысла производной.

Пример 1. Решим задание В8 (№ 119975). 

Материальная точка движется прямолинейно по закону x(t) = 6t² – 48t + 17  , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9c.

Решение.

1. Найдем производную функции x(t) = 6t² – 48t + 17 :

 x‘(t) = 12t – 48  

2. Найдем значение производной в точке t = 9:

 x‘(9) = 12×9 – 48

 x‘(9) = 60.

Ответ: 60 м/с.

Пример 2. Решим задание В8 (№ 122875). 

Материальная точка движется прямолинейно по закону x(t) = – t⁴

+6t³ + 2t²+ 9t – 22 , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.

Решение.

1. Найдем производную функции x(t) = – t⁴ +6t³ + 2t²+ 9t – 22:

 x‘(t) = -4t³ + 18t²+ 4t + 9

2. Найдем значение производной в точке t = 3:

 x‘(3) = -4×3³ + 18×3²+ 4×3 + 9

 x‘(3) = 75.

Ответ: 75 м/с.

Пример 3. Решим задание В8 (№ 119978)

Материальная точка движется прямолинейно по закону x(t) = t²

– 13t + 23 , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?

Решение.

Найдем производную функции x(t) = 6t² – 48t + 17

 x‘(t) = 2t – 13

По условию, скорость точки равна 3 м/с.

Получаем уравнение:

 x‘(t) = 2t – 13= 3, 2t

= 16

Отсюда  t = 8 с.

Ответ: 8

Пример 4. Аналогичное задание.  Задание В8 (№123871)

Материальная точка движется прямолинейно по закону x(t) = t³ – 6t²– 8t + 4, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 88 м/с?

Решение.

Найдем производную функции

x(t) = t³ – 6t²– 8t + 4:

 x‘(t) = 3t²– 12t – 8

По условию, скорость точки равна 88 м/с.

Получаем уравнение:

 x‘(t) = 3t²– 12t – 8 =88

Решим его:

3t²– 12t – 8 =88

3t²– 12t – 96 =0, разделим обе части уравнения на 3,

t²– 4t – 32 =0

t₁ = 8,

t₂ = – 4 – не соответствует условию задачи: время не может быть отрицательным.

Ответ: 8

Потренируйтесь сами.

Задание B8 (№ 121761)

Материальная точка движется прямолинейно по закону x(t) = t² + 7t – 3 , где x  — расстояние от точки отсчета в метрах, t  — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 10c.

Ответ: 27 м/с.

Задание B8 (№ 121763)

Материальная точка движется прямолинейно по закону x(t) = t² + 2t – 14  , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.

Ответ: 14 м/с.

Задание B8 (№ 121765)

Материальная точка движется прямолинейно по закону x(t

) = t² + 6t + 16, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.

Ответ: 18 м/с.

Задание B8 (№ 121769)

Материальная точка движется прямолинейно по закону x(t) = 0,25t² + 6t + 25, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 10с.

Ответ: 11 м/с.

Задание B8 (№ 121771)

Материальная точка движется прямолинейно по закону

x(t) = t² + 4t – 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6с.

Ответ: 16 м/с.

Задание B8 (№ 122877)

Материальная точка движется прямолинейно по закону x(t) = 0,5t⁴ +t³ + 6t²– 5t – 30 , где x — расстояние от точки отсчета в метрах,

t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 2c.

Ответ: 47 м/с.

Задание B8 (№ 122879)

Материальная точка движется прямолинейно по закону x(t) = – t⁴ +9t²+ 4t – 7 , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 2c.

Ответ: 8 м/с.

Задание B8 (№ 123879)

Материальная точка движется прямолинейно по закону x(

t) = t³ – 3t²– 7t – 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?

Ответ: 3 м/с.

Некоторые пути изучения понятия производной в школьном курсе математики



В данной статье дается один из путей изучения понятия «Производной», на доступном для учащихся языке составляется математическая модель физического процесса, представление этой модели в виде математического понятия и интерпретация этого понятия. Подробно рассматривается применение нового понятия для вывода формул.

Ключевые слова: методика, пути изучения, понятие производной, приращение аргумента, приращение функции, геометрический смысл, физический смысл, алгоритм.

Одной из важных побудительных сил учения является мотив достижения успеха. По словам Сухомлинского «интерес к учению есть только там, где есть вдохновение, рождающееся от успеха».

Нужно на каждом уроке, для каждого ученика создавать ситуацию успеха, сущность которой заключается в том, что каждый ученик работает на уровне своих возможностей, позволяющих ему справляться с предъявленными к нему требованиями.

Посильные трудности вырабатывают у учащихся положительную мотивацию учения, позволяют превратить учение из принудительного в добровольное.

Для достижения желаемого результата учитель должен создать на уроке такую ситуацию, использовать такие методы и средства обучения, которые были бы интересны ученику, располагали бы его к совместной деятельности, активизировали бы его учение.

Только там, где царят творческий труд, взаимное доверие, учителю легко работать, а ученику радостно жить.

В своей работе показан методический подход к процессу обучения именно с этой позиции.

При переходе из среднего звена обучения в старшее, когда начинается изучение «алгебры и начала анализа» в 10 классе, учащиеся испытывают достаточно большие трудности. Этой касается и основной темы данного курса — «Производная».

Целью данной методической разработки является оказание помощи учащимся в преодолении этих трудностей. Особенностью учебного материала это наглядное, доступное и достаточно научное изложение понятия «производной».

Опыт показывает, что относительно нетрудно научить учащихся формулировать определение производной, вычислять производную, находить производную функции в точке, пользуясь основными правилами дифференцирования. Не вызывает особых затруднений и применение производной к исследованию функции. А для этого в самом начале изучения темы следует найти правильный путь введения производной, ввести на доступном уровне учебный материал. Если учащийся сумеет применить определение производной для ее нахождения, показать геометрический и физический смыслы, то можем сказать, что он сможет и в дальнейшем видеть ее в различных приложениях, в физике, химии, биологии и т. д.

Вводная часть

Представим себе, что мы отправляемся в автомобильную поездку. Садясь в машину, посмотрим на счётчик километража. Теперь в любой момент времени мы сможем определить путь, пройденный машиной. Скорость движения мы узнаем по спидометру. Таким образом, с движением автомобиля, как и с движением любой материальной точки, связаны величины — путь S и скорость V, которые являются функциями времени t.

Ясно, что путь и скорость связаны между собой количественными характеристиками.

В конце XVII века английский учёный Исаак Ньютон открыл общий способ описания этой связи. Это открытие стало поворотным пунктом в истории естествознания. Оказалось, что связь между количественными характеристиками многих процессов, исследуемых физикой, химией, биологией, техническими науками, аналогична связи между путём и скоростью.

Основными математическими понятиями, выражающими эту связь, являются производная и интеграл.

Построенная Ньютоном модель механического движения остаётся самым важным и простым источником математического анализа, изучающего производную и её свойства. Вот почему на вопрос, что такое производная, короче всего ответить так:

Производная — это скорость, это скорость изменения функции.

В учебнике производная функции в точке х определяется как предел разностного отношения

=f'(х)

Также определён предел функции при х→0 т. е.

y=

Поэтому необходимо ввести понятие предела на нескольких простых задачах.

Пример 1:

Дан квадрат со стороной 1. Разделим его пополам, затем половину пополам, затем четверть пополам, и т. д., получим последовательность чисел ; ; ; ; и т. д. Вычислить предел, к которому стремится сумма всех членов этой последовательности.

Данная последовательность сходящаяся, её члены составляют бесконечно убывающую геометрическую прогрессию. Эти понятия и сумму бесконечно убывающей геометрической прогрессии изучаем в 9 классе. По чертежу легко видеть, что сумма чисел + + + + … в целом даёт 1, т. к. если заштриховать все получившиеся прямоугольники, то получится весь квадрат, площадь которого равна 1. Значит предел, к которому стремится сумма всех данных дробей, при неограниченном увеличении знаменателя есть число 1.

Подобного рода примеры поясняют учащимся предел числовой последовательности.

Вернёмся к движению. Представим себе любой движущийся предмет материальной точкой. Пусть данная материальная точка движется по прямой по определённому закону, выражающему зависимость S как функцию от времени. Рассмотрим отрезок времени []. Определим среднюю скорость движения материальной точки на данном отрезке как отношение пройденного пути к продолжительности движения:

Для определения скорости движения точки в момент времени t (её в механике часто называют мгновенной скоростью) поступим так: возьмём отрезок времени [t; ], вычислим среднюю скорость на этом отрезке и начнём уменьшать отрезок [t; ] приближая t. Значение средней скорости будет стремиться к некоторому числу, т. е. к пределу, который называется мгновенной скоростью в момент времени t. =

Наряду с И. Ньютоном основные законы математического анализа открыл немецкий математик Г.Лейбниц, решая задачу проведения касательной к произвольной кривой.

Пусть дана некоторая кривая и точка P на ней. Возьмём на этой кривой другую точку , и проведём прямую PР₁, которую называют секущей.

Заставим стремиться точку Р₁ к_{точке Р по данной кривой. Тогда положение секущей будет меняться. Как только точка Р1 займёт положение точки Р, секущая займёт положение касательной к данной прямой в точке Р.}

Т.о. предельное положение секущей при стремлении точки Р₁ к точке Р будет касательная к кривой в точке Р.

Переведём описанное построение на язык формул. Пусть данная кривая является графиком некоторой функции y=f(x). Точка Р имеет координаты (а; f(а)). Точка Р₁ имеет координаты (х₁;f(x₁)). РР₁ — секущая. РК – касательная к графику функции в точке Р.

Угол φ– угол наклона секущей к положительному направлению оси ОХ.

Угол α — угол наклона касательной к положительному направлению оси ОХ.

И секущая, и касательная являются прямыми линиями, уравнение которых в общем виде записывается как у = kх + b, где k — угловой коэффициент к прямой равный тангенсу угла наклона прямой к положительному направлению оси ОХ. Из Δ РМР, имеем

k=tgφ=

Т. к. касательная – это предельное положение секущей, то =tgα==

Итак, == ;=lim tgφ=

Мы видим, что две различные задачи привели в процессе решения к одному и тому же результату или, как чаще говорят в математике, к одной и той же математической модели — пределу разностного отношения функции и аргумента при условии, что разность аргументов стремится к нулю.

Решение многих задач сводится к необходимости осуществления предельного перехода в выражении вида при стремлении к x. Этот предельный переход носит название дифференцирования функции, а сам предел отношения — производной функции.

Дифференцирование, или нахождение производной функции — это новая математическая операция, имеющая тот же смысл, что в механике нахождение скорости, в геометрии — вычисление углового коэффициента касательной.

Для нахождения значения производной в данной точке надо рассмотреть маленький участок изменения аргумента вблизи этой точки. Производная приближённо будет равна средней скорости на этом участке (на языке механики) или угловому коэффициенту секущей (на языке геометрии).

Для точного вычисления производной надо совершить предельный переход — стянуть отрезок изменения аргумента в точку. Тогда средняя скорость превратится в мгновенную, а секущая — в касательную, и мы вычислим производную.

Итак, при вычислении производной функции мы совершаем предельный переход. В чём его суть?

При определении функции мы имеем дело с переменными величинами. Пусть y = f(x) — функция от аргумента х. Рассмотрим, как ведёт себя функция f(x) при приближении х к некоторому числу a.

При х→а, f(x)→f(a). Иными словами =f(a).

Пусть заданы функции (¹) f(x)=3+ и f(x)= (²)

Предельный переход для (¹) и (²) функций при х→1 определим следующим образом:

==3+=4

===

Если при х→, f(x)→f() т. е. =f(), то говорят, что функция непрерывна в точке , а значит в этой точке она имеет производную. График этой функции плавная, непрерывная кривая линия.

Определение производной функции.

Перейдём непосредственно к определению производной функции.

Пусть задана функция у = f(x). При сравнении значения этой функции в некоторой фиксированной точке со значениями функции в различных точках х, лежащих в окрестности , удобно выражать разность f(x)-f() через разность х-.

Разность х- называется приращением независимой переменной или приращением аргумента в точке х₀ и обозначается Δх. Т.о. Δх=х-х₀ (1). Из (1) следует, что х=х₀+Δх (2).

Говорят также, что первоначальное значение аргумента х₀ получило приращение Δх. Вследствие этого значение функции f тоже изменилось.

f(x)=f(x₀+Δx), тогда Δf=f(x)-f(x₀)=f(x₀+Δx)-f(x₀) (3)

Δf называется приращением функции в точке х₀.

Из (³) следует, что f(x)=f(x₀+Δx)=f(x₀)+Δf (4)

Δf называют также приращением зависимой переменной и обозначают через Δу.

Механический смысл производной — скорость изменения функции в точке.

Геометрический смысл производной заключается в следующем: существование производной непрерывной функции в некоторой точке х₀, равносильно существованию касательной, проведённой к графику данной функции в точке с абсциссой х₀. Угловой коэффициент этой касательной равен тангенсу угла её наклона к положительному направлению оси ОХ и равно значению производной функции в точке х₀.

k=tgα=f ‘(х₀) (5)

Алгоритм нахождения производной

1. Зафиксировав значение х, находим f(x).
2. Придав аргументу х приращение Δх так, чтобы не выйти из области определения функции f(x), найти f(x+Δx).
3. Вычислить приращение функции

Δf=f(x+Δx)-f(x)

4. Составить отношение
5. Найти предел отношения при Δх→0.

Теперь рассмотрим примеры нахождения некоторых функций на основе определения производной, применяя алгоритм ее нахождения.

Найти: 1) у=х, 2)у=Сх, 3)у=kx+b, 4)у=х²,у=, 5)у=х³, 6)у= ,7)у=хⁿ, 8)у=.

1. Найти у’, если у=x.2. Найти у’, если у=Сx.

1) х – фиксированное; f(x)=x 1) х – фиксированное; f(x)=Сx

2) Δx; x+Δx; f(x+Δx)=x+Δx2) Δx; x+Δx; f(x+Δx)=С(x+Δx)

3) Δf=f(x+Δx)–f(x)= 3)Δf=f(x+Δx)–f(x)=

=(x+Δx)–x=x+Δx–x= Δx =С(x+Δx)–Сx=Сx+СΔx–Сx= СΔx

4) ==14) ==С

5) ==15) ==С

Итак, x’=1.Итак, (Сx)’=С.

3. Найти у’, если у=kx+b.4. Найти у’, если у=х²

1) х – фиксированное;f(x)=kx+b1) х – фиксированное, f(x)=x²

2) Δx; x+Δx; f(x+Δx)=k(x+Δx)+b2) Δх; х+Δх; f(x+Δx)=(x+Δx)²

3)Δf=f(x+Δx)–f(x)=(k(x+Δx)+b)–(kx+b))=3) Δf=(x+Δx)²–x²= x²+2xΔx+()²–x²=

=kx+kΔx+b- kx-b= kΔx=2xΔx+()²

4) ==k4) ==2x+Δx

5) ==k5) ==2x

Итак, (kx+b)’=kИтак, (х²)’=2х.

5. Найти у’, если у=х³ 6. Найти у’, если у=

1) х – фиксированное, f(x)=x³1) х – фиксированное, х≠0; f(x)=

2) Δх; х+Δх; f(x+Δx)=(x+Δx)³2) Δх; х+Δх; f(x+Δx)=

3) Δf=(x+Δx)³–x³= 3) Δf=– = –

=x³+3x²Δx+3x ()² +()³– x³= 4) = –= –

=3x²Δx+3x ()² +()³ 5) = –= –

Итак, ()’= –

4) ==

=

5) ==

Итак, (х³) ‘=.

Зная производные у=х, у=х²,у=х³, можно методом частичной индукции записать производную для у=хⁿ, т. е. (хⁿ)’=. Доказательство этой формулы можно и не приводить. В нашей работе обычно формула доказывается. Приведем ее.

7. Найти у’, если у=хⁿ

1) х — фиксированное, f(x)=xⁿ

2) Δх; х+Δх; f(x+Δx)=(x+Δx)ⁿ

Применим бином Ньютона для раскрытия скобок

(x + a)n = xn + axn-1 + a²xn-2 +.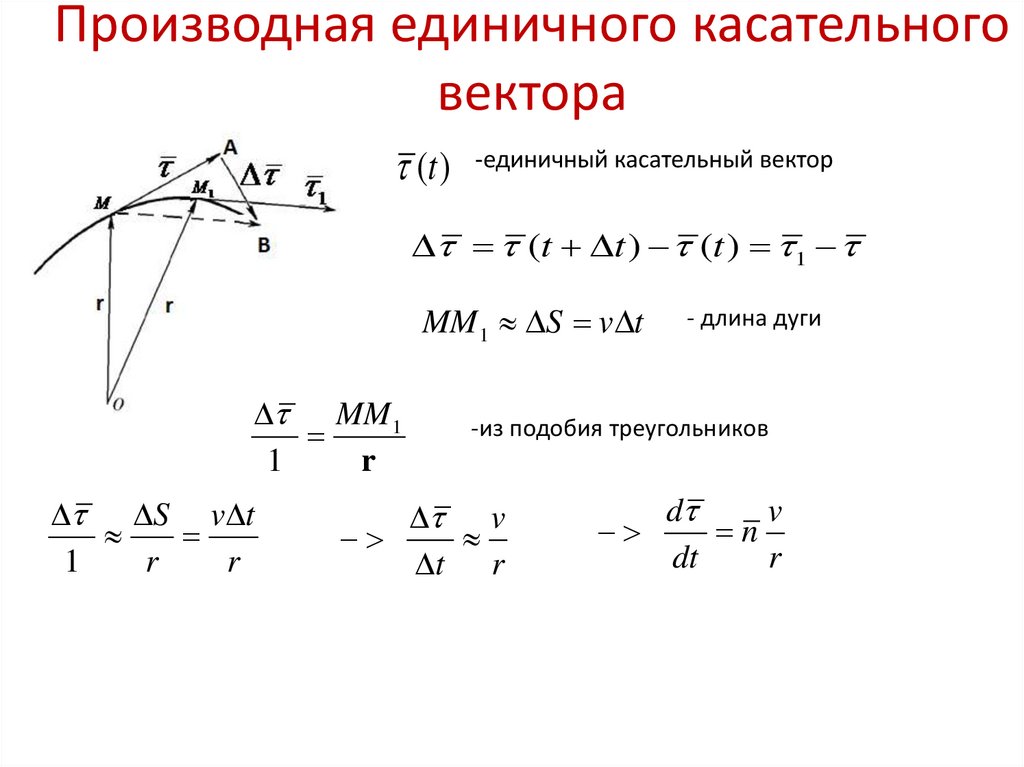 .. +an-1xn + an,

где k — порядковый номер слагаемого в многочлене, тогда

3) Δf=(x+Δx)ⁿ–xⁿ= xn + Δxxn-1 + (Δx)²xn-2 — +… + (Δx)^n-1 xn + (Δx)^{n— – xn= Δx xn-1 + (Δx)2xn-2 +… + (Δx)n-1 xn + (Δx)n}

4) =

=

=

5) ==, где =

Итак, (хⁿ)’==.

8. Найти у’, если у=

Преобразуем =. Так как, (хⁿ)’=, тогда ) ‘== .

Следовательно, ) ‘= .

С помощью приведённого алгоритма выводятся все формулы и правила дифференцирования. Таким образом, заполняется таблица производных. Самое главное все формулы выводятся, а не даются в готовом виде.

Литература:

1. Рогановский Н. М. Методика преподавания в средней школе. Мн., «Высшая школа», 1990.
2. Фройденталь Г. Математика как педагогическая задача. М., «Просвещение», 1998.
3. Н.Н. Математическая лаборатория. М., «Просвещение», 1997.
4. Колягин Ю. М. Методика преподавания математики в средней школе. М., «Просвещение», 1999.
5. Столяр А. А. Логические проблемы преподавания математики. Мн., «Высшая школа», 2000.
6. Далингер В. А. Начала математического анализа. — Омск: ООО «Издательство Полиграфист», 2002. – 158 с.

Основные термины (генерируются автоматически): производная функция, предельный переход, производная, функция, положительное направление оси ОХ, момент времени, приращение функции, скорость, скорость движения, эта.

Производная 1 порядка определение. Что такое производная?Определение и смысл производной функции

Производная – главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x

Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Наиболее употребительны следующие обозначения производной :

Пример 1. Пользуясь определением производной , найти производную функции

Решение. Из определения производной вытекает следующая схема её вычисления.

Дадим аргументу приращение (дельта) и найдём приращение функции:

Найдём отношение приращения функции к приращению аргумента:

Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:

Физический смысл производной

К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле – задачи о мгновенной скорости неравномерного прямолинейного движения точки.

Пусть камешек поднят и затем из состояния покоя отпущен. Путь s , проходимый за время t , является функцией времени, то есть. s = s (t ). Если задан закон движения точки, то можно определить среднюю скорость за любой промежуток времени. Пусть в момент времени камешек находился в положении A , а в момент – в положении B . За промежуток времени (от t до ) точка прошла путь . Поэтому средняя скорость движения за этот промежуток времени, которую обзначим через , составляет

.

Однако движение свободно падающего тела явно неравномерное. Скорость v падения постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути. Такая характеристика тем точнее, чем меньше промежуток времени . Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени t ) называется предел средней скорости при :

(при условии, что этот предел существует и конечен).

Так выясняется, что мгновенная скорость есть предел отношения приращения функции s (t ) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.

.

Решение обозначенной задачи представляет собой физический смысл производной . Итак, производной функции y=f (x ) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

Пример 2. Найти производную функции

Решение. Из определения производной вытекает следующая схема для её вычисления.

Шаг 1. Дадим аргументу приращение и найдём

Шаг 2. Найдём приращение функции:

Шаг 3. Найдём отношение приращения функции к приращению аргумента:

Шаг 4. Вычислим предел этого отношения при , то есть производную:

Геометрический смысл производной

Пусть функция определена на интервале и пусть точка М на графике функции соответствует значению аргумента , а точка Р – значению . Проведём через точки М и Р прямую и назовём её секущей . Обозначим через угол между секущей и осью . Очевидно, что этот угол зависит от .

Если существует

проходящую через точку , называют предельным положением секущей МР при (или при ).

Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .

Из определения следует, что для существования касательной достаточно, чтобы существовал предел

,

причём предел равен углу наклона касательной к оси .

Теперь дадим точное определение касательной.

Касательной к графику функции в точке называется прямая, проходящая через точку и имеющая угловой коэффициент , т.е. прямая, уравнение которой

Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x . В этом состоит геометрический смысл производной.

Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.

Правила дифференцирования

1. (k⋅ f(x))′=k⋅ f ′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
5. Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
6. Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
7. Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
8. Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.

Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.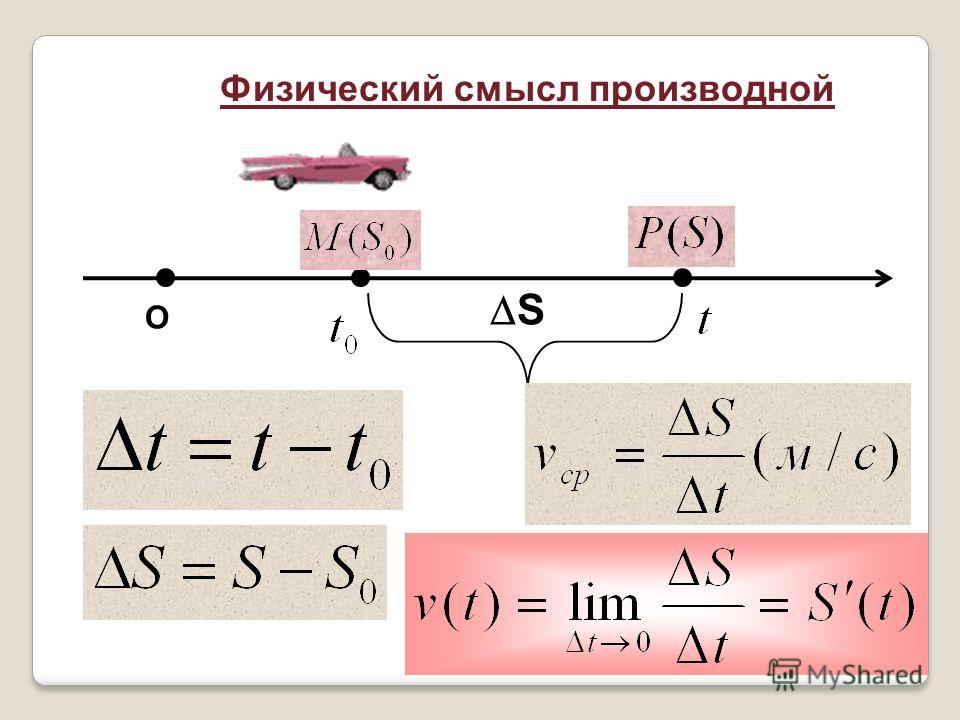

Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f”(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$

Для обозначения производной часто используют символ y”. Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .

Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f”(a) \)

Поскольку \(k = tg(a) \), то верно равенство \(f”(a) = tg(a) \) . 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) – f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f”(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f”(0) \)

Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. 2} $$

Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке х o называется предел

= .

Если этот предел конечный, то функция f(x) называется дифференцируемой в точке x o ; при этом она оказывается обязательно и непрерывной в этой точке.

Если же рассматриваемый предел равен  (или – ), то при условии, что функция в точке х o непрерывна, будем говорить, что функция f(x) имеет в точке х o бесконечную производную .

Производная обозначается символами

y , f (x o), , .

Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том,что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке х o ; физический смысл – в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t o .

Если с – постоянное число, и u = u(x), v = v(x) – некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ” = 0, (cu) ” = cu”;

2) (u+v)” = u”+v”;

3) (uv)” = u”v+v”u;

4) (u/v)” = (u”v-v”u)/v 2;

5) если y = f(u), u = (x), т.е. y = f((x)) – сложная функция, или суперпозиция , составленная из дифференцируемых функций  и f, то , или

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем  0, то .

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u )” =  u  1 u” (  R ).

2. (a u)” = a u lna u”.

3. (e u)” = e u u”.

4. (log a u)” = u”/(u ln a).

5. (ln u)” = u”/u.

6. (sin u)” = cos u u”.

7. (cos u)” = – sin u u”.

8. (tg u)” = 1/ cos 2 u u”.

9. (ctg u)” = – u” / sin 2 u.

10. (arcsin u)” = u” / .

11. (arccos u)” = – u” / .

12. (arctg u)” = u”/(1 + u 2).

13. (arcctg u)” = – u”/(1 + u 2).

Вычислим производную степенно-показательного выражения y=u v , (u>0), где u и v суть функции от х , имеющие в данной точке производные u” , v” .

Прологарифмировав равенство y=u v , получим ln y = v ln u.

Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:

y”/y = vu”/u +v” ln u, откуда y” = y (vu”/u +v” ln u).

(u v)”=u v (vu”/u+v” ln u), u > 0.

Например, если y = x sin x , то y” = x sin x (sin x/x + cos x ln x).

Если функция y = f(x) дифференцируема в точке x , т.е. имеет в этой точке конечную производную y” , то = y”+, где 0 при х 0; отсюда  y = y” х +  x.

Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y” х. Если положить в этой формуле y=x, то получим dx = x”х = 1х =х, поэтому dy=y”dx, т. е. символ для обозначения производной можно рассматривать как дробь.

Приращение функции  y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.

Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .

Аналогично определяются и обозначаются:

производная третьего порядка – ,

производная четвертого порядка –

и вообще производная n-го порядка – .

Пример 3 .15. Вычислить производную функции y=(3x 3 -2x+1)sin x.

Решение. По правилу 3, y”=(3x 3 -2x+1)”sin x + (3x 3 -2x+1)(sin x)” = = (9x 2 -2)sin x + (3x 3 -2x+1)cos x.

Пример 3.16 . Найти y”, y = tg x + .

Решение. Используя правила дифференцирования суммы и частного, получим: y”=(tgx + )” = (tgx)” + ()” = + = .

Пример 3 .17. Найти производную сложной функции y= , u=x 4 +1.

Решение. По правилу дифференцирования сложной функции, получим: y” x =y ” u u” x =()” u (x 4 +1)” x =(2u + . Так как u=x 4 +1,то (2 x 4 +2+ .

В задаче B9 дается график функции или производной, по которому требуется определить одну из следующих величин:

1. Значение производной в некоторой точке x 0 ,
2. Точки максимума или минимума (точки экстремума),
3. Интервалы возрастания и убывания функции (интервалы монотонности).

Функции и производные, представленные в этой задаче, всегда непрерывны, что значительно упрощает решение. Не смотря на то, что задача относится к разделу математического анализа, она вполне по силам даже самым слабым ученикам, поскольку никаких глубоких теоретических познаний здесь не требуется.

Для нахождения значения производной, точек экстремума и интервалов монотонности существуют простые и универсальные алгоритмы — все они будут рассмотрены ниже.

Внимательно читайте условие задачи B9, чтобы не допускать глупых ошибок: иногда попадаются довольно объемные тексты, но важных условий, которые влияют на ход решения, там немного.

Вычисление значения производной. Метод двух точек

Если в задаче дан график функции f(x), касательная к этому графику в некоторой точке x 0 , и требуется найти значение производной в этой точке, применяется следующий алгоритм:

1. Найти на графике касательной две «адекватные» точки: их координаты должны быть целочисленными. Обозначим эти точки A (x 1 ; y 1) и B (x 2 ; y 2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.
2. Зная координаты, легко вычислить приращение аргумента Δx = x 2 − x 1 и приращение функции Δy = y 2 − y 1 .
3. Наконец, находим значение производной D = Δy/Δx. Иными словами, надо разделить приращение функции на приращение аргумента — и это будет ответ.

Еще раз отметим: точки A и B надо искать именно на касательной, а не на графике функции f(x), как это часто случается. Касательная обязательно будет содержать хотя бы две таких точки — иначе задача составлена некорректно.

Рассмотрим точки A (−3; 2) и B (−1; 6) и найдем приращения:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Найдем значение производной: D = Δy/Δx = 4/2 = 2.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 3) и B (3; 0), найдем приращения:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Теперь находим значение производной: D = Δy/Δx = −3/3 = −1.

Задача. На рисунке изображен график функции y = f(x) и касательная к нему в точке с абсциссой x 0 . Найдите значение производной функции f(x) в точке x 0 .

Рассмотрим точки A (0; 2) и B (5; 2) и найдем приращения:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Осталось найти значение производной: D = Δy/Δx = 0/5 = 0.

Из последнего примера можно сформулировать правило: если касательная параллельна оси OX, производная функции в точке касания равна нулю. В этом случае даже не надо ничего считать — достаточно взглянуть на график.

Вычисление точек максимума и минимума

Иногда вместо графика функции в задаче B9 дается график производной и требуется найти точку максимума или минимума функции. При таком раскладе метод двух точек бесполезен, но существует другой, еще более простой алгоритм. Для начала определимся с терминологией:

1. Точка x 0 называется точкой максимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≥ f(x).
2. Точка x 0 называется точкой минимума функции f(x), если в некоторой окрестности этой точки выполняется неравенство: f(x 0) ≤ f(x).

Для того чтобы найти точки максимума и минимума по графику производной, достаточно выполнить следующие шаги:

1. Перечертить график производной, убрав всю лишнюю информацию. Как показывает практика, лишние данные только мешают решению. Поэтому отмечаем на координатной оси нули производной — и все.
2. Выяснить знаки производной на промежутках между нулями. Если для некоторой точки x 0 известно, что f’(x 0) ≠ 0, то возможны лишь два варианта: f’(x 0) ≥ 0 или f’(x 0) ≤ 0. Знак производной легко определить по исходному чертежу: если график производной лежит выше оси OX, значит f’(x) ≥ 0. И наоборот, если график производной проходит под осью OX, то f’(x) ≤ 0.
3. Снова проверяем нули и знаки производной. Там, где знак меняется с минуса на плюс, находится точка минимума. И наоборот, если знак производной меняется с плюса на минус, это точка максимума. Отсчет всегда ведется слева направо.

Эта схема работает только для непрерывных функций — других в задаче B9 не встречается.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−5; 5]. Найдите точку минимума функции f(x) на этом отрезке.

Избавимся от лишней информации — оставим только границы [−5; 5] и нули производной x = −3 и x = 2,5. Также отметим знаки:

Очевидно, в точке x = −3 знак производной меняется с минуса на плюс. Это и есть точка минимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7]. Найдите точку максимума функции f(x) на этом отрезке.

Перечертим график, оставив на координатной оси только границы [−3; 7] и нули производной x = −1,7 и x = 5. Отметим на полученном графике знаки производной. Имеем:

Очевидно, в точке x = 5 знак производной меняется с плюса на минус — это точка максимума.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−6; 4]. Найдите количество точек максимума функции f(x), принадлежащих отрезку [−4; 3].

Из условия задачи следует, что достаточно рассмотреть только часть графика, ограниченную отрезком [−4; 3]. Поэтому строим новый график, на котором отмечаем только границы [−4; 3] и нули производной внутри него. А именно, точки x = −3,5 и x = 2. Получаем:

На этом графике есть лишь одна точка максимума x = 2. Именно в ней знак производной меняется с плюса на минус.

Небольшое замечание по поводу точек с нецелочисленными координатами. Например, в последней задаче была рассмотрена точка x = −3,5, но с тем же успехом можно взять x = −3,4. Если задача составлена корректно, такие изменения не должны влиять на ответ, поскольку точки «без определенного места жительства» не принимают непосредственного участия в решении задачи. Разумеется, с целочисленными точками такой фокус не пройдет.

Нахождение интервалов возрастания и убывания функции

В такой задаче, подобно точкам максимума и минимума, предлагается по графику производной отыскать области, в которых сама функция возрастает или убывает. Для начала определим, что такое возрастание и убывание:

1. Функция f(x) называется возрастающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). Другими словами, чем больше значение аргумента, тем больше значение функции.
2. Функция f(x) называется убывающей на отрезке если для любых двух точек x 1 и x 2 из этого отрезка верно утверждение: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Т.е. большему значению аргумента соответствует меньшее значение функции.

Сформулируем достаточные условия возрастания и убывания:

1. Для того чтобы непрерывная функция f(x) возрастала на отрезке , достаточно, чтобы ее производная внутри отрезка была положительна, т.е. f’(x) ≥ 0.
2. Для того чтобы непрерывная функция f(x) убывала на отрезке , достаточно, чтобы ее производная внутри отрезка была отрицательна, т.е. f’(x) ≤ 0.

Примем эти утверждения без доказательств. Таким образом, получаем схему для нахождения интервалов возрастания и убывания, которая во многом похожа на алгоритм вычисления точек экстремума:

1. Убрать всю лишнюю информацию. На исходном графике производной нас интересуют в первую очередь нули функции, поэтому оставим только их.
2. Отметить знаки производной на интервалах между нулями. Там, где f’(x) ≥ 0, функция возрастает, а где f’(x) ≤ 0 — убывает. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.
3. Теперь, когда нам известно поведение функции и ограничения, остается вычислить требуемую в задаче величину.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−3; 7,5]. Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки.

Как обычно, перечертим график и отметим границы [−3; 7,5], а также нули производной x = −1,5 и x = 5,3. Затем отметим знаки производной. Имеем:

Поскольку на интервале (− 1,5) производная отрицательна, это и есть интервал убывания функции. Осталось просуммировать все целые числа, которые находятся внутри этого интервала:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Задача. На рисунке изображен график производной функции f(x), определенной на отрезке [−10; 4]. Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Избавимся от лишней информации. Оставим только границы [−10; 4] и нули производной, которых в этот раз оказалось четыре: x = −8, x = −6, x = −3 и x = 2. Отметим знаки производной и получим следующую картинку:

Нас интересуют промежутки возрастания функции, т.е. такие, где f’(x) ≥ 0. На графике таких промежутков два: (−8; −6) и (−3; 2). Вычислим их длины:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Поскольку требуется найти длину наибольшего из интервалов, в ответ записываем значение l 2 = 5.

Квантовая теория поля – Порядок времени и производная по времени в формализме интегралов по траекториям и операторном формализме

В операторном формализме, например, двухточечная упорядоченная по времени функция Грина определяется как

$$\langle\mathcal{T}\phi (x_1)\phi(x_2)\rangle_{op}=\theta(x_1-x_2)\phi(x_1)\phi(x_2)+\theta(x_2-x_1)\phi(x_2)\phi(x_1), $$

, где индексы “op” и “pi” относятся к формализму оператора и интеграла по траекториям соответственно. Теперь, если взять производную от него по времени, результат будет 9*}$ product”, а регистр оператора просто “$\mathcal{T}$ product”.

Меня не очень интересует, в чем причина разницы (все же пояснения по этому поводу приветствуются), потому что я уже смутно вижу, что это должно к какой-то двусмысленности в определении произведения полей в одинаковое время. Меня интересует вопрос, что правильно использовать при расчете диаграмм Фейнмана?

Я нашел случай, когда оба дают одинаковый результат, т.е. QED (см. Itzykson & Zuber, раздел 6-1-4 и этот пост), но всегда ли это так? Если эти две формулировки не эквивалентны эффективно, то кажется, что каждый раз, когда мы записываем что-то вроде $\langle\partial_0\ phi\cdots\rangle$, мы должны указать, является ли это определением интеграла по путям или определением оператора.{iS} = \ frac {1} {a} \ langle T \ {A (t + a) B (t) \} \ rangle- \ frac {1} {a} \ langle A (t) B (t) \rangle,$$

обратите внимание, что второй член имеет неоднозначность порядка из интеграла по путям (скажем, $A=\dot{\phi},B=\phi$), и мы можем сделать его в любом порядке, который мы хотим, выбрав соответствующая временная дискретизация, ср. Пост Рона Маймона, цитируемый Дрейком. Имея это в виду, мы продолжаем:

$$\frac{1}{a}\langle T\{A(t+a)B(t)\}\rangle-\frac{1}{a}\langle A (t) B (t) \ rangle \\ = \ frac {1} {a} \ theta (a) \ langle A (t + a) B (t) \ rangle + \ frac {1} {a} \ theta ( -a)\langle B(t)A(t+a)\rangle-\frac{1}{a}\langle A(t)B(t)\rangle\\=\frac{1}{a}\ тета (а) \ langle A (t + a) B (t) \ rangle + \ frac {1} {a} [1- \ theta (a)] \ langle B (t) A (t + a) \ rangle- \ frac {1} {a} \ langle A (t) B (t) \ rangle \\ = \ frac {\ theta (a)} {a} \ langle [A (t + a), B (t)] \rangle+\frac{1}{a}[\langle B(t)A(t+a)\rangle-\langle A(t)B(t)\rangle].$$ 9+)=\theta(0)=\frac{1}{2}$, но на самом деле это неверно, потому что $\theta$ разрывна.)

Однако, с другой стороны, поскольку $a$ было определено как положительная бесконечно малая, в самом начале мы могли бы написать

$$\frac{1}{a}\langle T\{A(t+a)B(t)\}\rangle-\frac{1} {a}\langle A(t)B(t)\rangle=\frac{1}{a}\langle A(t+a)B(t)\rangle-\frac{1}{a}\langle A (t)B(t)\rangle,$$

, то весь приведенный выше вывод не работает. Я уверен, что парадоксов будет больше, если мы продолжим эти манипуляции.

ИНТЕГРАЛЫ ПУТЕЙ В ФАЗОВОМ ПРОСТРАНСТВЕ | Интегралы по траекториям в квантовой механике

Фильтр поиска панели навигации Oxford AcademicPath Integrals in Quantum MechanicsAstronomy and AstrophysicsMathematical and Statistical PhysicsBooksJournals Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicPath Integrals in Quantum MechanicsAstronomy and AstrophysicsMathematical and Statistical PhysicsBooksJournals Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Еще

Cite

Zinn-Justin, Jean,

‘PATH INTEGRALS IN PHASE SPACE’

,

Path Integrals in Quantum Mechanics

, Oxford Graduate Texts

(

Oxford,

2004;

online edn,

Oxford Academic

, 1 января 2010 г.

), https://doi.org/10.1093/acprof:oso/9780198566748.003.0010,

, по состоянию на 9 октября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicPath Integrals in Quantum MechanicsAstronomy and AstrophysicsMathematical and Statistical PhysicsBooksJournals Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicPath Integrals in Quantum MechanicsAstronomy and AstrophysicsMathematical and Statistical PhysicsBooksJournals Термин поиска на микросайте

Advanced Search

Abstract

Эта глава содержит несколько дополнительных результатов, таких как определение интегралов по путям по траекториям в фазовом пространстве и проблемы, возникающие при квантовании лагранжианов с потенциалами, квадратичными по скоростям. Сначала рассматривается важный пример гамильтонианов, квадратичных по импульсным переменным. В простейших ситуациях, рассмотренных в предыдущих главах, после явного интегрирования по импульсам p(t) восстанавливается обычный интеграл по путям. Более общие гамильтонианы часто встречаются, например, при квантовании движения на римановых многообразиях. Анализ иллюстрируется квантованием свободного движения на сфере (или гиперсфере) S   _N-1 . Сначала рассматриваются несколько важных элементов классической механики.

Ключевые слова: интегралы по траекториям, фазовое пространство, классическая механика, квантование, свободное движение, сфера, лагранжианы, гамильтонианы, импульсные переменные

Предмет

Астрономия и астрофизика Математическая и статистическая физика

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
• Просмотр институциональных учетных записей, предоставляющих доступ.

Выполнен вход, но нет доступа к содержимому

Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.

Ведение счетов организаций

Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.

Покупка

Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.

Информация о покупке

Как анализировать положение, скорость и ускорение с помощью дифференциации

Каждый раз, когда вы садитесь в машину, вы воочию наблюдаете дифференциацию. Ваша скорость есть первая производная от вашего положения. И когда вы нажимаете на педаль акселератора или на тормоз — ускоряетесь или замедляетесь — вы испытываете вторую производную.

Если функция дает положение чего-либо как функцию времени, первая производная дает его скорость, а вторая производная дает его ускорение. Итак, вы различаете положение, чтобы получить скорость, и вы различаете скорость, чтобы получить ускорение.

Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей как функция времени определяется функцией, где t в секундах, а H ( t ) в дюймах. При t = 0 он находится на высоте 30 дюймов над землей, а через 4 секунды — на высоте 18 дюймов.

Рисунок 1

Высота йо-йо, от 0 до 4 секунд

Скорость , V ( t ) — производная положения (высоты в этой задаче) и ускорения, A ( t ), является производной скорости. Таким образом

Рисунок 2

На графиках показаны функции высоты, скорости и ускорения йо-йо от 0 до 4 секунд.

Скорость против скорости

Ваши друзья не будут жаловаться или даже не заметят, если вы будете использовать слова «скорость» и «скорость» взаимозаменяемо, но ваш дружелюбный математик будет жаловаться. Вот разница.

Для функции скорости на рисунке 2 движение вверх определяется как положительная скорость и нисходящая скорость определяются как отрицательная скорость — это стандартный способ обработки скорости в большинстве математических и физических задач. (Если движение горизонтальное, движение вправо имеет положительную скорость, а движение влево — отрицательную скорость.)

Скорость , с другой стороны, всегда положительна (или равна нулю). Если автомобиль движется со скоростью 50 миль в час , например, вы говорите, что его скорость равна 50, и вы имеете в виду положительное 50, независимо от того, движется ли он вправо или влево.

Для скорости важно направление; для скорости это не так. В повседневной жизни скорость — более простая идея, чем скорость, потому что она согласуется со здравым смыслом. Но в исчислении скорость на самом деле является более сложной идеей, потому что она плохо вписывается в трехфункциональную схему, показанную на рис. 2.

При анализе скорости и ускорения необходимо помнить о разнице между скоростью и скоростью. Например, если объект движется вниз (или влево) все быстрее и быстрее, его скорость увеличивается, но его скорость равна уменьшает , потому что его скорость становится больше отрицательной (а большие отрицательные числа — это меньшие числа). Это кажется странным, но так оно и работает.

И вот еще одна странность: ускорение определяется как скорость изменения скорости, а не скорости. Таким образом, если объект замедляется, двигаясь в направлении вниз, и, таким образом, имеет увеличивающуюся скорость — потому что скорость становится меньше отрицательной — объект имеет положительное ускорение . На повседневном английском вы бы сказали, что объект замедляется (замедляется), но на уроках математики вы говорите, что объект имеет отрицательную скорость и положительное ускорение.

Кстати, «замедление» — не совсем технический термин, так что вам, вероятно, следует избегать его на уроках математики. Лучше всего использовать следующую лексику: «положительное ускорение», «отрицательное ускорение», «ускорение» и «замедление».

Максимальная и минимальная высота

Максимальная и минимальная высота H ( t ) приходятся на локальные экстремумы, которые вы видите на рисунке 1. Чтобы найти их, установите производную H ( t ) — это0139 t ) — приравнять к нулю и решить.

Эти два числа являются нулями V ( t ) и t -координаты – это время -координаты – максимума и минимума H ( t ), которые вы можете видеть на рисунке 2. Другими словами, это моменты, когда йо-йо достигает максимальной и минимальной высоты. Подставьте эти числа в H ( t ), чтобы получить высоты:

H (0,47) ≈ 31,1

H (3,53) ≈ 16,9

Таким образом, йо-йо поднимается на высоту около 31,1 дюйма над землей при t ≈ 0,47 секунды и опускается на высоту около 16,9 дюйма при t ≈ 3,53 секунды.

Полный водоизмещение

определяется как конечное положение минус начальное положение. Итак, поскольку йо-йо начинается на высоте 30 и заканчивается на высоте 18,

T общее смещение = 18 – 30 = –12.

Это отрицательное значение, поскольку чистое движение равно вниз .

Средняя скорость равна общему перемещению, деленному на прошедшее время. Таким образом,

Этот отрицательный ответ говорит вам, что йо-йо в среднем движется на вниз 3 дюймов в секунду .

Максимальная и минимальная скорость

Максимальная и минимальная скорость йо-йо в интервале от 0 до 4 секунд определяются производной от V ( t ): Установите производную от V ( t ) — это A ( t ) — равно нулю и решить:

Теперь оцените V ( t ) в критическом числе 2 и в конечных точках интервала 0 и 4:

Итак, йо-йо имеет максимальную скорость 5 дюймов в секунду дважды — и в начале, и в конце интервала. Он достигает минимальной скорости — 7 дюймов в секунду при т = 2 секунды.

Общее пройденное расстояние

Общее пройденное расстояние определяется путем сложения расстояний, пройденных на каждом этапе пути йо-йо: подъеме, опускании и втором подъеме.

Во-первых, йо-йо поднимается с высоты 30 дюймов примерно до 31,1 дюйма (где находится первая точка разворота). Это расстояние около 1,1 дюйма. Затем она снижается примерно с 31,1 до примерно 16,9 (высота второй точки разворота). Это расстояние 31,1 минус 16,9 или около 14,2 дюйма. Наконец, йо-йо снова поднимается примерно с 16,9 дюймов до своей окончательной высоты 18 дюймов. Это еще 1,1 дюйма. Сложите эти три расстояния, чтобы получить общее пройденное расстояние: ~1,1 + ~14,2 + ~1,1 ≈ 16,4 дюйма.

Средняя скорость равна общему пройденному расстоянию, деленному на затраченное время. Таким образом,

Максимальная и минимальная скорость

Ранее вы определили максимальную скорость йо-йо (5 дюймов в секунду ) и его минимальную скорость (-7 дюймов в секунду ). Скорость -7 соответствует скорости 7, так что это максимальная скорость йо-йо. Его минимальная нулевая скорость возникает в двух точках разворота.

Для непрерывной функции скорости минимум скорость равна нулю, если максимальная и минимальная скорости имеют противоположные знаки или когда одна из них равна нулю. Когда максимальная и минимальная скорости положительны или обе отрицательны, тогда минимальная скорость является меньшим из абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость равна большему абсолютных значений максимальной и минимальной скоростей. Это глоток или что?

Максимальное и минимальное ускорение

Максимальное и минимальное ускорение могут показаться бессмысленными, когда вы можете просто посмотреть на график A ( t ) и увидеть, что минимальное ускорение –12 происходит в крайнем левом углу, когда t = 0, и что ускорение затем идет до максимума в 12 в крайнем правом углу, когда t = 4. Но не исключено, что вы получите одного из тех невероятно требовательных учителей исчисления, которые имеют наглость требовать, чтобы вы действительно занимались математикой и показывали свою работу — так что кусай пулю и делай это.

Чтобы найти минимальное и максимальное ускорение от t = 0 до t = 4, приравняем производную A ( t ) к нулю и решим:

Это уравнение, конечно, не имеет решений , так что критических чисел нет, и поэтому абсолютные экстремумы должны приходиться на конечные точки интервала, 0 и 4.

Вы пришли к уже известным вам ответам.

Обратите внимание, что когда ускорение отрицательное — на интервале [0, 2) — это означает, что скорость равна уменьшение . При ускорении положительном — на интервале (2, 4] — скорость увеличивается на .

Ускорение и замедление

Выяснение того, когда йо-йо ускоряется и замедляется, вероятно, более интересно и описывает его движение, чем информация выше. Объект ускоряется (то, что мы называем «ускорением» в повседневной речи) всякий раз, когда скорость и расчетное ускорение оба положительны или оба отрицательны. И объект замедляется (то, что мы называем «замедлением»), когда скорость и расчетное ускорение имеют противоположные знаки.

Посмотрите еще раз на все три графика на рисунке 2. От t = 0 до приблизительно t = 0,47 (когда скорость равна нулю) скорость положительна, а ускорение отрицательно, поэтому йо-йо замедляет город (пока не достигнет максимальной высоты).

Когда t = 0, замедление максимальное (12 дюймов в секунду за секунду ; на графике показано ускорение отрицательное 12, но здесь мы называем это замедлением, поэтому 12 положительное). Примерно с 9От 0139 t = 0,47 до t = 2, и скорость, и ускорение отрицательны, поэтому йо-йо снова замедляется (пока не достигнет дна на самой низкой высоте).

Наконец, примерно с t = 3,53 до t = 4 и скорость, и ускорение положительны, поэтому йо-йо снова ускоряется.