Чему равна производная дроби. Как найти производную от дроби
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x_0) $$
Для обозначения производной часто используют символ y”. Отметим, что y” = f(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x)
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f”(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f”(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f”(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f”(x) \), т.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) – f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f”(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f”(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f”(0) \)
Итак, мы познакомились с новым свойством функции – дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.
2} $$ Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена “шпаргалка” основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|” = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы :
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х.
То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)” = – c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)” = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 10Следующая ⇒ При нахождении производных функций руководствуются следующими основными правилами дифференцирования. Правило 1. Производная постоянной величины равна нулю. , где Правило 2. Постоянный множитель можно выносить за знак производной. , где Правило 3. Производная алгебраической суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций. . Обращаем внимание на то, что некоторые слагаемые могут быть отрицательными. Перед ними сохраняется знак минус. Правило 4. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую функцию и первой функции на производную второй функции. Правило 5. Правило 6. Производная сложной функции. Если и – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу, умноженной на производную самого промежуточного аргумента по независимой переменной. или в другой форме записи . Как определить, что имеем дело со сложной функцией? Если в выражении, от которого ищем производную, независимая переменная встречается только один раз, то функция сложная. Если же независимая переменная встречается более одного раза, то функций несколько, и при нахождении производной сначала следует воспользоваться правилами 3–5. При нахождении производных функций следует помнить о порядке выполнения арифметических действий: приоритет перед остальными действиями имеют возведение в степень и извлечение корня (помним, что корни можно заменять степенями), далее рассматривают умножение и деление и в последнюю очередь сложение и вычитание. Исходя из определения производной, вычислены производные элементарных функций. 1) , где Отметим, что: а) б) при нахождении производных от корней корень заменяют соответствующей степенью и определяют производную от степенной функции
Рассмотрим примеры нахождения производных функций. Пример 1. . В этом случае удобно представить дробь в виде суммы дробей, почленно поделив числитель на знаменатель, а затем искать производные от полученных слагаемых. Пример 2. Распишем выражение по правилу для нахождения производной от произведения функций, далее найдем производные от элементарных функций Пример 3. Сначала запишем правило для нахождения производной частного, а затем найдем производные элементарных функций. Пример 4. Здесь мы имеем дело со сложной функцией (независимая переменная встречается в выражении один раз). Если ввести обозначения вложенных функций, то получим следующее: Тогда производную этой сложной функции с учетом приоритета действий можно записать так: В результате имеем: Иногда бывает проще понять процесс нахождения производной сложной функции, ассоциируя его с раскрыванием матрешки.
Результат получили такой же. Пример 5. В этом случае найти производную сразу не удастся. Сначала прологарифмируем выражение, получим: . По правилам логарифмирования степень подлогарифмического выражения можно поставить перед логарифмом, тогда: . Теперь можно искать производную. В ходе решения учтем, что : Рассмотрим примеры нахождения дифференциалов функций. Пример 1. Дифференциал функции находим по формуле Пример 2. Умение находить дифференциал функции потребуется при решении интегралов и дифференциальных уравнений. Рассмотрим пример приблизительного вычисления значений функции. Пример 1. Пусть дана функция , где . Получить формулу для приблизительных вычислений значений данной функции и вычислить по ней значения и . Общая формула для приближенных вычислений значений функции имеет вид . Определим эту вид формулы для нашей функции. Для этого найдем производную функции . Преобразуем в исходной формуле корень в степень и воспользуемся формулой для нахождения производной степенной функции: ; , где . Для всех достаточно малых приращение функции в точке будет равно: . Тогда значение функции в точке будет приблизительно равно: . По полученной формуле произведем приблизительные вычисления. Найдем . Представим подкоренное выражение в виде суммы и : . Тогда: Найдем .
Производные высших порядков Пусть функция определена на некотором интервале (a,b), и пусть в каждой точке этого интервала она имеет производную . Эту производную называют первой производной или производной первого порядка для данной функции. Эта производная сама может являться функцией , определенной на интервале (a,b). Если функция имеет на этом интервале производную в точке , то эту производную называют второй производной или производной второго порядка для функции и обозначают . Аналогично эта производная может являться функцией , определенной на интервале (a,b). Если и она имеет на интервале (a,b) в точке производную, то эту производную называют третьей производной или производной третьего порядка для функции и обозначают . Такие же рассуждения можно провести для производной любого порядка. В общем случае n-ой производной функции или производной n-го порядка в точке называют производную от производной (n-1)-го порядка в этой точке: . Производные порядков выше первого называют производными высших порядков. Порядок таких производных указывают в круглых скобках, чтобы не путать их со степенями функций. Производные высших порядков можно обозначать и через дифференциалы. Например, или – производная второго порядка функции ; или – третья производная функции . Рассмотрим примеры нахождения производных высших порядков. Пример 1. . Найдем все возможные производные высших порядков для этой функции. Видим, что эта функция имеет ненулевые производные для первых трех порядков, а производные 4-го и более высоких порядков будут равны нулю. Пример 2. . Найдем 100-ю производную этой функции. Заметим, что выражения найденных производных имеют схожие элементы, и можно записать общую формулу для определения производной n-го порядка: . Тогда сотая производная исходной функции будет равна: . Но так красиво бывает далеко не всегда. Довольно часто функция, являющаяся производной очередного порядка, становится более сложной чем та, от которой эту производную нашли. Пример 3. . Найдем несколько первых производных этой функции. Как видим, производные более высоких порядков этой функции становятся все более сложными.
1.5. Задания для самостоятельного решения I. Найдите производные функции одной переменной
II.
III. Найдите приближенное значение функции в точке , если известно, что:
IV. Найдите приближенно числовое значение функции при заданном аргументе , если известно, что:
V. Найдите производные указанных порядков для приведенных функций:
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 256; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Определение реакций опор и моментов защемления
Производная частного двух дифференцируемых функций (при условии, что знаменатель не обращается в ноль) равна дроби, числитель которой представляет собой разность между произведением производной первой функции на вторую функцию и произведением первой функции на производную второй функции, а знаменатель равен квадрату знаменателя данной дроби.
Например, функция является сложной, независимая переменная в ней встречается один раз. А функция представляет собой сумму двух слагаемых.
Раскрывая внешнюю матрешку, мы оставляем нетронутым все, что у нее внутри. Так же и с отысканием производной сложной функции: сперва найдем производную от внешней функции, опираясь на приоритет арифметических действий, оставив внутренние функции нетронутыми, затем следующую и так до тех пор, пока не дойдем до независимой переменной. При этом все найденные производные перемножаются. В рассмотренном примере это выглядит так:
Представим подкоренное выражение в виде суммы и : . Тогда:
Найдите дифференциалы функций одной переменной
2
Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю. 
Например, для x2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x2 . Немного “не научно”, но очень просто запомнить. 
Производная переменной под корнем произвольной степени 
Уже в Средневековье было установлено, что пределом этого выражения является число е.
Она вычисляется несколько иначе.
Применяя правило о том, что постоянный множитель можно выносить за знак производной, а затем формулу (2) при
И как всегда соединяем две производные знаком произведения. Результат:
Снова воспользуемся правилом дифференцирования сложной функции:
2+2x}
В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
— возведение в степень.
Например, оно входит в уравнение цепной линии, которое описывает провис каната под действием собственного веса, когда его концы закреплены на опорах.
Найти производную функции
Он описывает:Производная от корня из x. Производная степенной функции (степени и корни)
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 .
Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое –4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) – f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f “(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f “(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)” = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.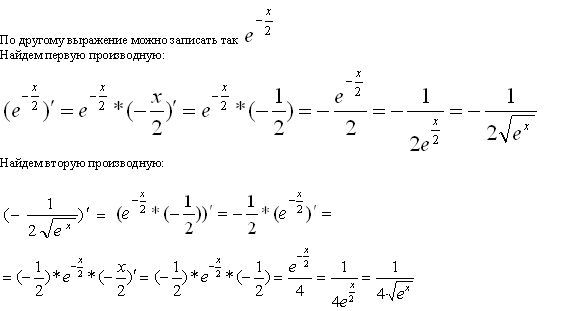
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
На котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся.
Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией , а функцию – внутренней (или вложенной) функцией .
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.
Первый шаг , который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней .
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .
Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением , в данном случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем .
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Постоянный множитель обычно выносят в начало выражения:
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя.
Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения . Таким образом, результат применения правила дифференцирования сложной функции следующий:
Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью.
Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение необычно. Вот характерный пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово.
В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного – в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего “икса”. Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11.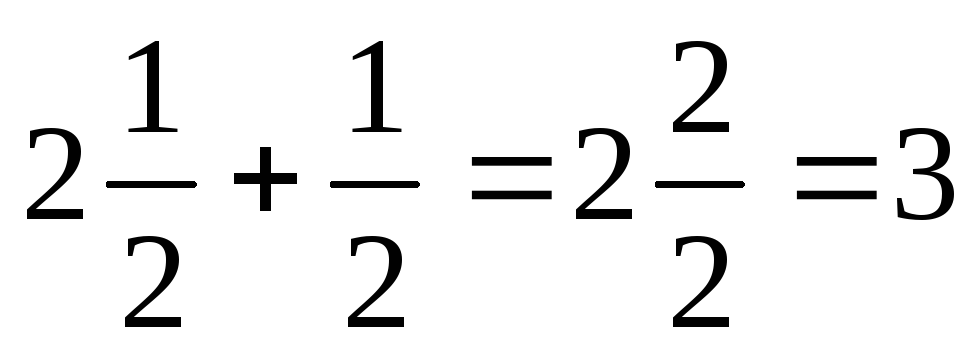 Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель.
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль. Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6.
Найти производную функции
Решение. В данной функции видим частное, делимое которого – квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу.
При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной.
Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Здравствуйте, уважаемые читатели.
После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант . Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение ) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции – запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где – время, – начальная скорость, – ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть – им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка – ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли – мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями.
Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Примеры решения задач к разделу пределы и…
Привет, мой друг, тебе интересно узнать все про ы решения задач к разделу пределы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое ы решения задач к разделу пределы, производная дифференциальое исчисление , настоятельно рекомендую прочитать все из категории Математический анализ. Дифференциальное исчисление.
Пример N 1
Вычислить: .
Решение.
Числитель и знаменатель дроби неограниченно возрастают при .
В этом случае говорят, что имеет место неопределенность типа . Разделим числитель и знаменатель дроби на старшую степень переменной x , в нашем случае – на x2 :
.
Так как при каждая из дробей .
Ответ: 3
Пример N 2
Вычислить: .
Решение.
Числитель и знаменатель дроби при также стремятся к нулю. В этом случае имеет место неопределенность типа . Умножим числитель и знаменатель дроби на :
Знаменатель дроби при , следовательно .
Ответ: .
Пример N 3
Вычислить: .
Решение.
Воспользуемся тригонометрической формулой и заменим числитель и знаменатель дроби эквивалентными бесконечно малыми и :
Ответ: 0.
Пример N 4
Вычислить: .
Решение.
При выражение , а (x +7) неограниченно возрастает.
В этом случае имеет место неопределенность типа . Об этом говорит сайт https://intellect.icu .
Рекомендуется использовать второй замечательный предел или следствие из него:
Так как при , то . Учитывая, что (см. пример N1), окончательно получаем
Ответ: .
Пример N 5
Вычислить: .
Решение.
Так как при выражение , имеет место неопределенность типа . Преобразуем функцию так, чтобы использовать второй замечательный предел. Выделим целую часть из дроби (для этого к числителю дроби прибавим и отнимем 3): , тогда
Так как при , то .
Учитывая, что окончательно получим:
Ответ: .
Пример N 6
Исследовать функцию на непрерывность и построить схематически ее график.
Решение.
Данная функция терпит разрыв в точках и , так как при этих значениях знаменатель дроби обращается в нуль. Исследуем характер разрыва в каждой из этих точек.
Для этого найдем
Для точки :
Так как
и , то в точке функция имеет разрыв первого рода или скачок.
Для точки :
Таким образом, для точки и , значит, и при функция также терпит разрыв первого рода или скачок. Для схематического построения графика исследуем поведение функции при
Следовательно, при график функции находится около прямой y = 1 . Найдем точку пересечения графика с осью ОУ:
.
Ответ: Схематический график функции (рис. 8):
Рис. 8
Пример N 7
Найти производную функции .
Решение.
Преобразуем квадратный корень в степень: .
Данная функция – сложная, используем последовательно формулы: производная степенной функции, производная дроби, производная логарифма.
Ответ: .
Пример N 8
Вычислить производную функции .
Решение.
Данная функция относится к виду показательно – степенной функции . Для нахождения ее производной прологарифмируем данную функцию: .
Дифференцируя левую и правую часть этого равенства, получаем
Ответ: .
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про ы решения задач к разделу пределы Надеюсь, что теперь ты понял что такое ы решения задач к разделу пределы, производная дифференциальое исчисление
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математический анализ. Дифференциальное исчисление
Из статьи мы узнали кратко, но емко про ы решения задач к разделу пределы
Частное правило. Неявное дифференцирование
Подход
к
C A L C U L U S
Содержание | Дом
8
Правило частных
Доказательство правила отношения
Неявное дифференцирование
Производная обратной функции
Частное правило
Следующее правило называется частным правилом:
“Производная от частного двух функций равна
знаменатель умножить на производную от числителя
минус числитель умножить на производную от знаменателя
все разделить на квадрат знаменателя.”
Например, если принять на данный момент, что производная sin x равна cos x (Урок 12):
Задача 1. Вычислить производную от | x 2 sin x | . |
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите “Обновить” (“Reload”).
Сначала решай задачу сам!
| грех x · 2 x − x 2 cos x sin 5 |
Задача 2. Используйте цепное правило для вычисления производной числа
.| sin 2 x x 3 | . |
| х 3 · 2 sin x cos x − sin 2 x · 3 x 2 x 6 | = | x 2 SIN x (2 x COS x – 3 SIN x ) x 6 |
| = | sin x (2 x cos x − 3 sin x ) x 4 | 11|
Задача 3. Вычислить производную от | x 2 − 5 x − 6 2 x + 1 | . |
| (2 x + 1) (2 x – 5) – ( x 2 – 5 x – 6) · 2 (2 – 6) · 2 (2 – 6) · 2 (2 – 6) · 2 (2 – 6) · 2 (2 – 6) · 2 (2 – 6) · 2 (2 – 6). ) 2 | = | 4 x 2 – 8 x – 5 – 2 x 2 + 10 x + 12 (2 x + 1) 241451 (2 x + 1) |
| = | 2 x 2 + 2 x + 7 (2 x + 1) 2 | |
Задача 4. Вычислить производную от | 3 x 2 − x + 4 | . |
См. пример, урок 6 и урок 22 по алгебре.
| = | ||
| = | ||
| = | ||
Доказательство правила отношения
| ТЕОРЕМА. |
Доказательство. Поскольку г = г ( x ), то
| d 1 5 9004 3 dx 9 | 1 г | = | д дг | 1 г | · | дг дх | = − | 1 г 2 | г’ |
по цепному правилу и задаче 4 урока 5.
Следовательно, по правилу произведения (урок 6)
Это правило частных, которое мы хотели доказать.
Неявное дифференцирование
Рассмотрим следующее:
x 2 + у 2 = r 2
Это уравнение окружности с радиусом r . (Урок 17 Предварительного исчисления.)
Подсчитаем .
Для этого мы могли бы найти и , а затем взять производную. Но вместо этого мы возьмем производную от каждого члена. Что касается y 2 , мы неявно считаем его функцией x , и поэтому мы можем применить к нему цепное правило. Затем мы решим для .
| д дх | х 2 | + | д дх | г 2 | = | г дх | р 2 |
| 2 х + 2 у | дх дх | = | 0 | |||
| dy dx | = | — | х у | . | ||
Это называется неявным дифференцированием. Мы рассматриваем х как функцию х и применяем цепное правило. Полученная производная обычно содержит как x , так и y .
Задача 5. 15 y + 5 y 3 + 3 y 5 = 5 x 3 . Вычислить и .
| 15 г + 15 г 2 г + 15 г 4 36 | = | 15 x 2 |
| у’ (1 + у 2 + у 4 ) | = | х 2 |
| у’ | = | x 2 1 + y 2 + y 4 |
Задача 6. | Рассчитать и . |
| = | 0 | |
| = | ||
| у’ | = | |
Задача 7.
а) В этом круге
х 2 + у 2 = 25,
а) что такое y -координата, когда x = −3?
у = 4 или -4. Для,
(−3) 2 + (±4) 2 = 5 2
b) Каков наклон касательной к окружности в точке (−3, 4)?
| 3 4 | . Для производная – | х у | . |
c) Каков наклон касательной к окружности в точке (−3, −4)?
Задача 8.
В первом квадранте, каков наклон касательной к этой окружности,
( х − 1) 2 + ( у + 2) 2 = 169,
, когда х = 6?
[Подсказка: 5 2 + 12 2 = 13 2 — пифагорейская тройка.]
В первом квадранте, когда х = 6, y = 10,
(6 − 1) 2 + (10 + 2) 2 = 13 2 .
| г’ = – | х − 1 у + 2 | . Следовательно, наклон – 90 045 | 6 − 1 10 + 2 | = − | 5 12 |
Задача 9. Вычислить наклон касательной к этой кривой в точке (2, −1):
х 3 − 3 x у 2 + у 3 = 1
3 x 2 – (3 x · 2 y y ‘ + Y 2 · 3) + 3 Y · 3) + 3 Y · 3) + 3 Y · 3) + 3 Y · 3) + 3 Y · 3) + 3 Y · 3) + 3 Y · 3). | = | 0 | |||||||||||||||||||||||||||||||||||||
| по правилу продукта. | |||||||||||||||||||||||||||||||||||||||
| 3 x 2 – 6 x Y Y ‘ – 3 Y 2 + 3 Y 2 Y’ | = | 0 | |||||||||||||||||||||||||||||||||||||
| x 2 − 2 x у у’ − г 2 + г 2 г’ | = | 0 | |||||||||||||||||||||||||||||||||||||
| у’ ( у 2 − 2 ху ) | = | г 2 − x 2 | |||||||||||||||||||||||||||||||||||||
| у’ | = | y 2 − x 2 y 2 − 2 xy | Следовательно, в (2, −1): | | у’ | = | (-1) 2 − 2 2 | (-1) 2 − 2 · 2 · 5-1 9004 | | | = | −3 | 5 | | | = | — | 3 | 5 | ||||||||||||||||||||
Производная обратной функции
Когда у нас есть функция y = f ( x ) – например,
у = х 2
— тогда мы часто можем найти x .
В данном случае
При обмене переменными имеем
| называется обратной функцией y = x 2 . |
Напишем
| f ( x ) | = | х 2 |
| г ( x ) | = | |
И назовем f прямой функцией и g обратной функцией . Формальная связь между f и g следующая:
f ( г ( x )) = г ( f ( x )) = x .
(Тема 19 Предварительного исчисления.)
Вот другие пары прямых и обратных функций:
| f ( x ) | = | грех х | г ( x ) | = | угловых синусов x | |
| f ( x ) | = | а х | г ( x ) | = | бревно a x | |
| f ( x ) | = | х 3 | г ( x ) | = | ||
Теперь, когда мы знаем производную прямой функции f , то по ней мы можем определить производную g .
Таким образом, пусть г ( x ) будет обратным f ( x ). Затем
ф ( г ( х )) = х .
Теперь возьмем производную по x :
Это подразумевает следующее:
Теорема. Если г ( x ) обратно f ( x ), то
“Производная обратной функции равна
обратная производная прямой функции
, когда ее аргументом является обратная функция.”
| Пример. Пусть f ( x ) = x 2 и | Тогда f ( г ) = г 2 . |
Следовательно,
Следующий урок: Мгновенная скорость и скорость изменения
Содержание | Главная
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Вычисление производных: проблемы и решения – Matheno.com
Вычисление производных: проблемы и решения
Вы работаете над вычислением производных в исчислении? Давайте шаг за шагом решим некоторые распространенные проблемы, чтобы вы могли научиться решать их самостоятельно. 92\right) + \dfrac{d}{dx}(\cos x) = \, …$
Правило произведения для производных
\begin{align*}
\dfrac{d}{dx}(fg)& = \left(\dfrac{d}{dx}f \right)g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= \Big[\text{ (производное 1-го) } \times \text{ (2-е) }\Big] + \Big[\text{ (1-е) } \times \text{ (производное 2-го )}\Большой]
\end{выравнивание*}
IV. Частное правило для производных
\begin{align*}
\dfrac{d}{dx}\left(\dfrac{f}{g} \right) &= \dfrac{\left(\dfrac{d}{dx }f \right)g – f\left(\dfrac{d}{dx}g \right)}{g^2} \\[8px]
&=\dfrac{{\Big[\text{(производная числителя) } \times \text{ (знаменатель)}\Big] – \Big[\text{ (числитель) } \times \text{ (производная знаменателя )}}\Big]}{\text{все разделить на [знаменатель в квадрате]}} 9{46}.
$
Два конкретных случая, которые вы быстро запомните:
$$\dfrac{d}{dx}\text{(константа)} = 0$$
$$\dfrac{d}{dx}( x) = 1$$
Задача дифференцирования по степенному правилу #1
Дифференцировать $f(x) = 2\pi$.
Нажмите, чтобы просмотреть решение исчисления
$2\pi$ — это просто число: это константа. И производная любой константы равна 0:
\[ \begin{align*}
\dfrac{d}{dx}(2\pi) &= \dfrac{d}{dx}(\text{constant}) \ \[8px]
&= 0 \quad \cmark 9{x+1} \quad \cmark
\end{align*} \]
Обратите внимание, что последние две строки полностью эквивалентны. Любой правильный ответ.
[свернуть]
III. Производные триггерной функции
\[ \bbox[yellow,5px]{
\begin{align*}
\frac{d}{dx}\left(\sin x\right) &= \cos x &&& \frac{d }{dx}\left(\csc x\right) &= -\csc x \cot x \\ \\
\dfrac{d}{dx}\left(\cos x\right) &= -\sin x &&& \frac{d}{dx}\left(\sec x\right) &= \sec x \tan x \\ \\ 92 x
\end{align*}} \]
Обратите внимание, что перед производными кофункций: косинуса, косеканса и котангенса стоит знак минус.
Запустить задачу дифференцирования #1
Дифференцировать $f(x) = \sin x – \cos x$.
Нажмите, чтобы просмотреть расчетное решение
Напомним из таблицы, что $\dfrac{d}{dx}(\sin x) = \cos x,$ и $\dfrac{d}{dx}(\cos x) = -\sin x.$
\[ \begin{align*}
\dfrac{d}{dx} \left(\sin x – \cos x \right) &= \dfrac{d}{dx}(\sin х) – \dfrac{d}{dx}(\cos x) \\[8px]
&= \cos x – (-\sin x) \\[8px]
&= \cos x + \sin x \quad \cmark 92 x \quad \cmark
\end{align*} \]
[свернуть]
IV. Правило продукта
\[\bbox[yellow,5px]{
\begin{align*}
\dfrac{d}{dx}(fg)&= \left(\dfrac{d}{dx}f \right) g + f\left(\dfrac{d}{dx}g \right)\\[8px]
&= [{\small\text{(производное 1-го)} \times\text{(2-е)}}]\, + \,[{\small\text{(1-е)} \times\text{ (производное 2-го)}}]
\end{align*}}\]
Задача дифференциации правил произведения №1
Дифференцировать $f(x) = x\sin x.
$
Нажмите, чтобы просмотреть решение исчисления
Поскольку функция является произведением двух отдельных функций, $x$ и $\sin x$, мы должны использовать правило произведения. Напомним, что $\dfrac{d}{dx}x = 1,$ и что $\dfrac{d}{dx}\sin x = \cos x.$
\[ \begin{align*}
\dfrac{d }{dx} \left( x\sin x\right)&= \left(\dfrac{d}{dx}x\right)\sin x + x \left( \dfrac{d}{dx}\sin x \справа) \\[8px]
&= (1)\sin x + x \,(\cos x) \\[8px]
&= \sin x + x\cos x \quad \cmark
\end{align*} \]
\end{align*}}\] Многие учащиеся запоминают правило частных, представляя числитель как «привет», демонинатор как «ло», производную как «д», а затем напевая
«ло д-при минус привет д-ло над ло-ло».
2 x$$ 92} \quad \cmark
\end{align*} \]
[свернуть]
VI. Цепное правило
Цепное правило — большая тема, поэтому у нас есть отдельная страница для задач, требующих цепного правила.
Нужно использовать производную, чтобы найти уравнение касательной (или уравнение нормальной линии)? У нас есть отдельная страница на эту тему здесь.
У вас есть вопрос, предложение или пункт, который вы хотели бы, чтобы мы включили? Пожалуйста, дайте нам знать на нашем форуме!
Хотите получить доступ к всем нашим задачам и решениям по исчислению? Войдите бесплатно с помощью своей учетной записи Google, Facebook или Apple или с помощью специальной учетной записи Matheno (которую вы можете создать за 60 секунд). Затем посетите наш главный экран исчисления.
И если у вас есть вопрос по математическому анализу, с которым вам может понадобиться помощь, зайдите на наш форум и опубликуйте его.
Будем рады помочь!
По состоянию на сентябрь 2022 года мы используем наш форум для комментариев и обсуждения этой темы, а также для любых математических вопросов. Будем рады вас видеть и помочь! Нажмите, чтобы посетить наш форум: community.matheno.com.
Латексная частная производная — Javatpoint
следующий → ← предыдущая ПроизводнаяПроизводная в математике означает скорость изменения. Частная производная определяется как метод сохранения постоянных переменных. Команда \partial используется для записи частной производной в любом уравнении. Существуют разные порядки производных. Запишем порядок производных, используя код Latex. Мы можем рассмотреть выходное изображение для лучшего понимания. Код приведен ниже: \documentclass[12pt]{статья} \usepackage{mathtools} \usepackage{xfrac} \начать{документ} \[ Первый \; заказ \; производная = f'(x) % \; команда используется для пробела \] \[ Второй \; заказ \; производная = f”(x) % здесь мы использовали отдельные среды для отображения текста в разных строках \] \[ В третьих \; заказ \; производная = f”'(x) \] \[ \vточки \] \[ К\; заказ \; производная = f ^ {k} (x) \] \конец{документ} Вывод: Давайте воспользуемся приведенными выше производными, чтобы написать уравнение. Вывод: Мы можем изменить уравнение и параметры в соответствии с требованиями. ДифференциацияКоманда \diff используется для отображения символа дифференцирования. Чтобы реализовать дифференцирование, нам нужно использовать пакет diffcoeff . Пакет записывается как: \usepackage{diffcoeff} Рассмотрим несколько примеров дифференцирования. Первый пример — отображение дифференциального уравнения первого порядка. Код указан ниже \documentclass[12pt]{статья} \usepackage{mathtools} \usepackage{diffcoeff} \начать{документ} \[ \diff[1]yx 3x = 3 \] \[ \ разность {у} {х} 2х = 2 \] % мы можем использовать любой из двух методов, чтобы написать дифференциальное уравнение первого порядка \конец{документ} 92 + 4х + 3) = 4х + 4 \] \конец{документ} Вывод: Дифференцирование с частными производными Команда \diffp используется для отображения символа дифференцирования с частными производными. Рассмотрим несколько примеров дифференцирования с частными производными. В первом примере показано дифференциальное уравнение в частных производных первого порядка. Код приведен ниже: \documentclass[12pt]{статья} \usepackage{mathtools} \usepackage{diffcoeff} \начать{документ} \[ \diffp{u}{t} = \diffp{u}{x} + \diffp{u}{y} \] \конец{документ} Вывод: Второй пример — отображение дифференциального уравнения в частных производных второго порядка. Код приведен ниже: \documentclass[12pt]{статья} \usepackage{mathtools} \usepackage{diffcoeff} \начать{документ} \[ \diffp[2]ut = \diffp[2]ux + \diffp[2]uy \] \конец{документ} Вывод: В третьем примере будет показана частная производная, содержащая постоянное значение. Он также будет включать другие примеры, поясняющие концепцию. Код для такого примера приведен ниже: \documentclass[12pt]{статья}
\usepackage{mathtools}
\usepackage{diffcoeff}
\начать{документ} \[
\ diffp {G (х, у)} х [(1,1)]
\]
\[
\diffp ST[D]
\]
\[
\разн[]
\]
\[
\diffp[1,3]F{х,у,г}
\]
\[
\diffp[2,3,2]F{x,y,z} % степень числителя равна сумме степеней переменных знаменателя. Вывод: Следующая темаLatex Online Editors ← предыдущая следующий → |
k}
\] \конец{документ}
93 F{\ парциальное х \ парциальное у \ парциальное г}
\] \конец{документ}
\]
\конец{документ}Первый тест производной: интуиция и примеры
Первый тест производной — это инструмент для определения того, является ли критическая точка функции максимумом, минимумом или ни тем, ни другим. Этот тест может сбивать с толку, если вы не понимаете лежащую в его основе интуитивную идею.
На этой странице мы углубимся в интуицию и увидим, как легко ее применять, когда у нас есть это понимание.
О чем первый производный тест
На странице о критических точках мы видели, что крайние точки, то есть точки максимума или минимума, должны быть критическими точками. Мы научились находить критические точки. Следующий шаг — определить, какие из этих критических точек являются крайними, а какие — нет. Именно тогда мы применяем тест первой производной.
Этот тест состоит в анализе производной функции слева и справа от критической точки.
Давайте посмотрим, как это работает.
Предположим, что x 0 является критической точкой функции f(x). Допустим также, что производная слева от критической точки положительна, а справа от нее производная отрицательна.
Используя эту информацию, мы можем построить график критической точки и касательных линий к функции вблизи критической точки. В критической точке касательная горизонтальна, потому что производная равна нулю. Слева от критической точки касательные имеют положительный наклон, а справа от нее отрицательный наклон.
Это показано на следующем рисунке.
Используя касательные линии, мы можем получить представление о том, как выглядит график функции вблизи критической точки
Мы видели на странице о линейных приближениях, что касательная является хорошим приближением графика функции вблизи точка касания. Таким образом, мы можем рассматривать фигуру на рисунке выше как приближение к реальному графику функции.
Что говорит нам картинка? Что критическая точка, вероятно, является точкой максимума. На самом деле, это говорит нам о том, что это точка максимума, потому что касательные линии точно говорят, как изменяется функция.
И правило, которое мы только что вывели, является первой частью первого теста производной. Мы показали, что , если производная слева от критической точки положительна, а справа отрицательна, то это точка максимума.
Другой способ выразить это так: если происходит изменение знака производной с положительного на отрицательный, то критическая точка является максимальной.
Мы можем провести тот же анализ с обратным знаком. Если в критической точке знак производной изменится с отрицательного на положительный, график будет выглядеть примерно так:
Если производная меняется с отрицательной на положительную, критической точкой является точка минимума
В этом случае у нас есть минимум, как показано на рисунке.
Эти правила очень легко запомнить. Вам просто нужно подумать о наклонах касательных линий и рассмотреть различные возможные знаки, которые они могут иметь.
Есть третий случай, который мы не рассмотрели. Это когда знак производной не меняется в критической точке. Например, производная может быть положительной как слева, так и справа от критической точки. В этом случае график выглядит следующим образом:
Если производная не меняет знак, критическая точка не является экстремумом
В этом случае мы видим, что точка не является ни максимумом, ни минимумом, потому что функция продолжает расти с увеличением x. То же самое верно, если производная отрицательна в обе стороны, точка не находится в крайней точке.
И это все, что нужно для этого теста. Это действительно интуитивная идея, помните, что вам просто нужно подумать о наклонах касательных линий и знаках, которые они могут иметь. Теперь мы готовы узнать, как это работает на практике.
Основные примеры
Пример 1: f(x) = x 2Найдем крайние точки функции
Сначала найдем критические точки. Для этого нам нужно знать производную
Теперь решим уравнение f'(x) = 0,
Единственная критическая точка x = 0. Чтобы определить, экстремум это или нет, нужно проверить знак производной слева и справа от критической точки. Слева имеем x<0,
Производная отрицательна слева от критической точки. Теперь вправо: x>0,
Производная положительна справа от критической точки. Производная меняет знак с отрицательного на положительный. Это означает, что x=0 является точкой минимума.
Пример 2: f(x) = x 3Посмотрим, имеет ли следующая функция какие-либо экстремальные точки
Теперь найдем критические точки, вычислим производную и решим уравнение f'(x)= 0.
Эта функция имеет единственную критическую точку при x=0. Теперь посмотрим на выражение производной.
Производная положительна для любого ненулевого значения x. Это потому, что квадрат ненулевого числа всегда положителен. Следовательно, производная не может менять знак с отрицательного на положительный. Делаем вывод, что x=0 не является экстремумом.
Дополнительные примеры
В предыдущих примерах было легко определить знак производной, потому что у нас была только одна критическая точка, равная x = 0. Теперь для большинства функций это не так. В общем случае мы получаем набор критических точек.
Что мы делаем в таких случаях? Нам нужно только проверить знак производной в одной точке слева и в одной точке справа от каждой критической точки. Между двумя критическими точками знак производной будет постоянным (положительным или отрицательным).
Это может показаться сложным, но это не так. Это просто. Это можно лучше понять на примерах. Если f(x) имеет три критические точки, график ее производной f'(x) может выглядеть следующим образом:
Это график f'(x) для функции с тремя критическими точками
Знак f'(x) не может менять знак между двумя критическими точками.
Геометрически, если f'(x) меняет знак, это означает, что ее график пересекает ось x. Но пересечение оси x означает, что f'(x) становится равным нулю, и тогда у нас будет еще одна критическая точка. Но у нас всего три критических точки! Поэтому он не может менять знак между двумя критическими точками.
Мы можем разделить приведенный выше график на четыре подинтервала. Один из них представляет собой интервал, состоящий из чисел xb.
Знак производной постоянен на каждом из этих интервалов из-за того, что мы только что сказали. Итак, чтобы определить знак производной в каждом из этих интервалов, нам просто нужно оценить производную в одной точке. Знак во всех остальных точках отрезка будет таким же, как и в этой точке.
Хватит болтать. Если это вас смутило, вы почувствуете это, увидев и решив несколько примеров. Давайте посмотрим, как это делается.
Пример 3: многочлен с несколькими критическими точкамиНайдем крайние точки функции
Производная равна
Теперь решим уравнение f'(x).
Мы можем сделать это, разложив на множители
Эти две точки являются критическими. Эти две точки делят ось x на три сегмента. Один состоит из чисел x<1, другой представляет собой интервал (1,3), а третий представляет собой интервал, состоящий из чисел x>1. Знак на каждом из этих интервалов постоянный, положительный или отрицательный.
Чтобы определить знак производной каждого интервала, нам просто нужно вычислить f'(x), где x — любое число на нем. Для первого интервала нам нужно взять x<1. Мы можем выбрать х=0. Это кажется мудрым выбором, поскольку может упростить расчеты.
Итак, мы оцениваем производную в этой точке,
Она положительна. Теперь определим знак второго интервала. Нам нужно число от 1 до 3. Мы можем выбрать x=2. Оценим производную в этой точке,
Она отрицательна. Это означает, что в первой критической точке x=1 производная изменилась с положительной на отрицательную. Это означает, что x=1 является точкой максимума.
Теперь проведем тот же анализ с x=3.
Мы только что показали, что производная на интервале (1,3) отрицательна. Нам нужно знать знак последнего интервала, где x>3. Мы можем выбрать x=4,
Положительный. Это показывает, что при x=3 производная меняется с отрицательной на положительную. Делаем вывод, что x=3 является точкой минимума.
График полиномиальной функции f(x) показан ниже.
График полиномиальной функции f(x)
Пример 4: Рациональная функцияНайдем критические точки функции
Нам нужно вычислить производную этой штуки. Мы можем применить правило частного, но, как вы знаете, я предпочитаю применять правило произведения. Мы можем записать f(x) как
Теперь мы применяем правило произведения и правило цепочки для вычисления производной,
Теперь мы выполняем алгебру, чтобы получить более простое выражение,
Теперь f'(x)=0, только если числитель выше равен нулю. То есть критическими точками являются решения
У нас есть две критические точки, поэтому нам нужно проанализировать знак производной на трех интервалах.
Сначала нам нужно число x
Знаменатель положительный, потому что это квадрат ненулевого числа. Итак, производная имеет знак числителя, который равен
Производная положительна. Теперь нам нужно число от -√2 до √2. Можно взять х=0.
Это отрицательно. При x=-√2 производная изменилась с положительной на отрицательную. Это означает, что x=-√2 является максимальным. Теперь возьмем число x>√2. Мы можем взять х=2. Нам нужно только вычислить числитель f'(2), потому что знаменатель всегда положителен.
Это положительно. Что касается f'(0), я думаю, что этих примеров достаточно, чтобы дать вам представление о том, как применять критерий первой производной. Чтобы освоить эту тему, вам нужно решить несколько задач самостоятельно. Если у вас есть сомнения или проблема, которую вы хотите обсудить, вы можете оставить комментарий ниже.
3.7: Производные обратных функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2496
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Вычисление производной обратной функции.
- Распознавать производные стандартных обратных тригонометрических функций.
В этом разделе мы исследуем взаимосвязь между производной функции и производной обратной функции. Для функций, производные которых мы уже знаем, мы можем использовать это соотношение, чтобы найти производные обратных функций, не прибегая к предельному определению производной. В частности, мы будем применять формулы производных обратных функций к тригонометрическим функциям. Эта формула также может быть использована для распространения правила степени на рациональные показатели. 9{−1}(x)\big)}.\label{inverse1} \]
Альтернативно, если \(y=g(x)\) является инверсией \(f(x)\), то
\[g'(x)=\dfrac{1}{f’\big(g(x)\big)}. \label{inverse2} \]
Пример \(\PageIndex{1}\): Применение теоремы об обратной функции
Используйте теорему об обратной функции, чтобы найти производную \(g(x)=\dfrac{x+2 }{Икс}\). Сравните полученную производную с производной, полученной прямым дифференцированием функции.
Решение
Обратное выражение \(g(x)=\dfrac{x+2}{x}\) равно \(f(x)=\dfrac{2}{x−1}\). 9{−1/3} \nonumber \]
и
\[\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber \]
наклон касательной к графику в точке \(x=8\) равен \(\frac{1}{3}\).
Подставив \(x=8\) в исходную функцию, получим \(y=4\). Таким образом, касательная проходит через точку \((8,4)\). Подставляя в формулу точки-наклона прямой, получаем касательную
\[y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber \]
Упражнение \(\PageIndex{3}\) 9{−1/2}\)
Производные обратных тригонометрических функций
Обратимся теперь к нахождению производных обратных тригонометрических функций. Эти производные окажутся бесценными при изучении интегрирования далее в этом тексте. Производные обратных тригонометрических функций довольно удивительны тем, что их производные на самом деле являются алгебраическими функциями. Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций являются тригонометрическими функциями.
Здесь мы впервые видим, что производная функции не обязательно должна быть того же типа, что и исходная функция. 9{−1}x\) в \(x=0.\)
- Подсказка
\(f′(0)\) — наклон касательной.
- Ответить
\(у=х\)
Основные понятия
- Теорема об обратной функции позволяет вычислять производные от обратных функций без использования предельного определения производной.
- Мы можем использовать теорему об обратной функции, чтобы вывести формулы дифференцирования для обратных тригонометрических функций. 92−1}}\)
Авторы и авторство
Эта страница под названием 3.7: Производные обратных функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу Оглавление
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- Производная функции арккосеканса
- Производная функции арккосинуса
- Производная функции арккотангенса
- Производная функции арксеканса
- Производная функции арктангенса
- Теорема об обратной функции
- Степенное правило с рациональными показателями
- источник@https://openstax. org/details/books/calculus-volume-1
Правила мощности, произведения и частного
By Stefania Cristina on 9 июля 2021 г. в исчислении
Последнее обновление: 9 июля 2021 г.
Оптимизация, как один из основных процессов во многих алгоритмах машинного обучения, основана на использовании производных, чтобы решить, каким образом обновить значения параметров модели, чтобы максимизировать или минимизировать целевую функцию.
В этом руководстве мы продолжим изучение различных методов, с помощью которых мы можем находить производные функций. В частности, мы будем изучать правила степени, произведения и отношения, которые мы можем использовать для получения производных функций быстрее, чем если бы нам пришлось находить каждую производную из первых принципов. Следовательно, для функций, которые особенно сложны, хранение таких правил под рукой для нахождения их производных будет становиться все более важным.
В этом уроке вы познакомитесь с правилами степени, произведения и частного для нахождения производной функции.
После прохождения этого урока вы будете знать:
- Степенное правило, которому следует следовать при нахождении производной переменного основания, возведенной в фиксированную степень.
- Как правило произведения позволяет нам найти производную функции, которая определяется как произведение двух других (или более) функций.
- Как правило частных позволяет нам найти производную функции, являющейся отношением двух дифференцируемых функций.
Начнем.
Правила мощности, произведения и частного
Обзор учебника
Фотография Андреаса М., некоторые права защищены.Это руководство разделено на три части; они:
- Правило силы
- Правило продукта
- Частное правило
Если у нас есть переменное основание, возведенное в фиксированную степень, правило, которому нужно следовать, чтобы найти его производную, состоит в том, чтобы уменьшить степень перед переменным основанием, а затем вычесть степень на 1.
Например, если у нас есть функция f ( x ) = x 2 , производную которой мы хотели бы найти, мы сначала приносим 2 перед x и затем уменьшите мощность на 1:
ф ( х ) = х 2
f ’( х ) = 2 х
Чтобы лучше понять, откуда взялось это правило, давайте пойдем более длинным путем и найдем производную от 9.0035 f ( x ), начиная с определения производной:
Здесь мы подставляем вместо f ( x ) = x 2 и затем приступаем к упрощению выражения:
Когда ч приближается к значению 0, этот предел приближается к 2 x , что согласуется с результатом, который мы получили ранее, используя правило степени.
Применительно к f ( x ) = x , правило степени дает нам значение 1. Это потому, что, когда мы ставим значение 1 перед x , а затем вычитаем степень на 1, то, что у нас остается является значением 0 в показателе степени.
Так как х 0 = 1, то f ’ ( х ) = (1) ( х 0 ) = 1.Лучший способ понять эту производную — понять, что f(x) = x — это линия, соответствующая форме y = mx + b, поскольку f(x) = x совпадает с f(x) = 1x + 0 (или у = 1х + 0). Наклон (m) этой линии равен 1, поэтому производная равна 1. Или вы можете просто запомнить, что производная x равна 1. Но если вы забудете обе эти идеи, вы всегда можете использовать правило степени.
Страница 131, Исчисление для чайников, 2016.
Правило степени можно применять к любой степени, будь то положительная, отрицательная или дробная. Мы также можем применить его к радикальным функциям, сначала представив их показатель степени (или степень) в виде дроби:
f ( х ) = √ х = х 1/2
f’ ( x ) = (1 / 2) x -1/2
Правило продукта г.Предположим, что теперь у нас есть функция f ( x ), для которой мы хотели бы найти производную, являющуюся произведением двух других функций, u ( x ) = 2 x 2 и v ( х ) = х 3 :
F ( x ) = U ( x ) V ( x ) = (2 x 2 ) ( x 3 ) ) ( x 3 )0003
Чтобы узнать, как найти производную от f ( x ), давайте сначала начнем с нахождения производной произведения u ( x ) и v ( x ). напрямую:
( U ( x ) V ( x )) )’ = 10 х 4
Теперь давайте посмотрим, что произойдет, если в противном случае нам придется сначала вычислять производные функций по отдельности, а затем перемножать их:
U ‘ ( x ) V’ ( x ) = (2 x 2 ) ‘( x 3 )’ = (4 x ) (3 3 ) 2 ) = 12 х 3
Понятно, что второй результат не совпадает с первым, и это потому, что мы не применили правило произведения .
Правило произведения говорит нам, что производная произведения двух функций может быть найдена как:
f’ ( x ) = u’ ( x ) v ( x ) + u ( x ) v’ ( x )
Мы можем прийти к правилу произведения, если проделаем весь путь, применяя свойства пределов, снова начав с определения производной:
Мы знаем, что f ( x ) = u ( x ) v ( x ) и, следовательно, мы можем заменить f ( x ) и f ( x + ч ):
На данном этапе наша цель состоит в том, чтобы разложить числитель на несколько пределов, которые затем можно оценивать по отдельности. Для этого вводится вычитание слагаемых u ( x ) v ( x + h ) – u ( x ) v ( x 6 + h 9 ). в числитель. Его введение не меняет определения f ’( x ), которое мы только что получили, но оно поможет нам разложить числитель на множители:
Полученное выражение кажется сложным, однако, если мы присмотримся повнимательнее, то поймем, что у нас есть общие термины, которые можно вынести за скобки:
Выражение можно еще больше упростить, применив предельные законы, которые позволяют разделить суммы и произведения на отдельные пределы:
Теперь решение нашей проблемы стало яснее.
Мы видим, что первый и последний члены в упрощенном выражении соответствуют определению производной от u ( x ) и v ( x ), которые мы можем обозначить как u ( x )’ и v ( x )’, соответственно. Второй член приближается к непрерывной и дифференцируемой функции, v ( x ), поскольку h приближается к 0, тогда как третий член равен u ( x ).Следовательно, мы снова приходим к правилу произведения:
f’ ( x ) = u’ ( x ) v ( x ) + u ( x ) v’ ( x )
With this new tool in hand, let’s reconsider finding f ‘( x ) when u ( x ) = 2 x 2 and v ( x ) = x 3 :
f’ ( x ) = u’ ( x ) v ( x ) + u ( x 9)0036) v’ ( x )
F ‘ ( x ) = (4 x ) ( x 3 ) + (2 x 2 ) (3 x 2 ) = 4 x 505050505050505555050505050505050505050555.
4 + 6 х 4 = 10 х 4 Полученная производная теперь правильно соответствует производной произведения ( u ( x ) v ( x ))’, которое мы получили ранее.
Это был довольно простой пример, который мы могли бы вычислить напрямую. Однако у нас могут быть более сложные задачи, связанные с функциями, которые нельзя умножать напрямую, и к которым мы можем легко применить правило произведения. Например:
f ( х ) = х 2 sin х
f’ ( x ) = ( x 2 )’ (sin x ) + ( x 2 ) (sin x )’ = 2 x sin x + x 2 cos x
Мы можем даже распространить правило произведения на более чем две функции. Например, скажем, f ( x ) теперь определяется как произведение трех функций: u ( x ), v ( x ) и w (3 x 9):
f ( x ) = u ( x ) v ( x ) ш ( x )
Мы можем применить правило произведения следующим образом:
F ‘( x ) = U ‘ ( x ) V ( x ) W ( x ) + U ( x ) ).
x ) w ( x ) + u ( x ) v ( x ) w ‘( 3) Частное правило г.Точно так же правило частных говорит нам, как найти производную функции, f ( x ), то есть отношение двух дифференцируемых функций, x ( x ) и v ( x ):
Мы можем вывести правило частных из первых принципов, как мы сделали для правила произведения, то есть, начав с определения производной и применяя свойства пределов. Или мы можем пойти по более короткому пути и вывести правило частного, используя само правило произведения. Давайте на этот раз пойдем по этому маршруту:
Мы можем применить правило произведения к u ( x ), чтобы получить:
U ’( x ) = F ’ ( x ) V ( x ) + F ( x ) V ’( x ) ) V ’ ( x ) ) V ’( x ) ) V ’ ( x ) ) V ’( X 9000) )
Обратное решение для f ’( x ) дает нам:
Один последний шаг заменяет f ( x ), чтобы получить правило частных:
Мы видели, как найти производную функций синуса и косинуса.
Используя правило частных, теперь мы можем найти и производную функции тангенса:f ( x ) = tan x = sin x / cos x
Применение правила отношения и упрощение полученного выражения:
Из тождества Пифагора в тригонометрии мы знаем, что cos 2 x + sin 2 х = 1, следовательно:
Таким образом, используя правило отношения, мы легко нашли, что производная тангенса есть функция квадрата секущей.
Дополнительная литератураВ этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.
Книги- Исчисление для чайников, 2016.
- Силовое правило, Википедия.
- Правило продукта, Википедия.
- Частное правило, Википедия.
В этом руководстве вы узнали, как применять правила степени, произведения и частного для нахождения производной функции.
В частности, вы узнали:
- Степенное правило, которому следует следовать при нахождении производной переменного основания, возведенной в фиксированную степень.
- Как правило произведения позволяет нам найти производную функции, которая определяется как произведение двух других (или более) функций.
- Как правило частных позволяет нам найти производную функции, являющейся отношением двух дифференцируемых функций.
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.Познакомьтесь с вычислениями для машинного обучения!
Почувствуйте себя умнее с концепциями исчисления
…чтобы лучше понять символы и термины исчисления
Узнайте, как в моей новой электронной книге:
Исчисление для машинного обученияОн содержит учебных пособий для самостоятельного изучения с полным рабочим кодом по:
дифференциация , градиент , Лагранжев множитель , Матрица Якоби , и многое другое.
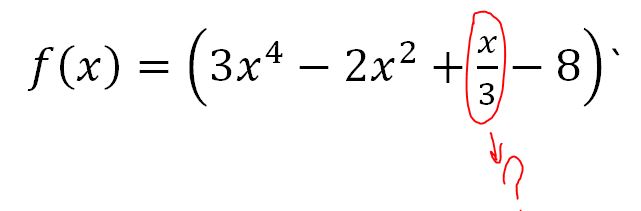org/details/books/calculus-volume-1
Так как х 0 = 1, то f ’ ( х ) = (1) ( х 0 ) = 1.
Мы видим, что первый и последний члены в упрощенном выражении соответствуют определению производной от u ( x ) и v ( x ), которые мы можем обозначить как u ( x )’ и v ( x )’, соответственно. Второй член приближается к непрерывной и дифференцируемой функции, v ( x ), поскольку h приближается к 0, тогда как третий член равен u ( x ).
4 + 6 х 4 = 10 х 4 
x ) w ( x ) + u ( x ) v ( x ) w ‘( 3) Частное правило г.
Используя правило частных, теперь мы можем найти и производную функции тангенса:
