Производная Произведения
Производная ПроизведенияA-Z Keywords
Keyword Suggestions
Images for Производная Произведения
1 страница. Определение 1. Производной функции f(x) в …
helpiks.org
Производная произведения и частного функции
function-x.ru
Производная первого порядка, все формулы и примеры
solverbook.com
Производная произведения и частного – YouTube
ytimg.com
Формулы. Производная произведения. Производная частного …
dpva.ru
Производная произведения и частного функции
function-x.ru
Правила нахождения производной – Помощь в обучении
poreshaem.com
Формулы. Производная произведения. Производная частного .
dpva.ru
Правила дифференцирования. Доказательство и примеры …
cleverstudents.ru
Презентация на тему: “ЛЕКЦИЯ 2 по дисциплине «Математика …
myshared.ru
Презентация на тему: “П РОИЗВОДНАЯ И ЕЁ ГЕОМЕТРИЧЕСКИЙ …
myshared.ru
Производные – Помощь первокурсникам
google.com
Производная произведения .Сложная функция. Урок 5 – YouTube
ytimg.com
Тема 8. Производная и первообразная функции – Материалы …
pinimg.com
Презентация на тему: “Первообразная. Работа над ошибками …
Производная суммы, разности, произведения и частного функций
9219603113.com
Реферат: Формулы по математике (11 кл.) – Xreferat.com …
xreferat.com
Производная суммы, разности, произведения и частного функций
9219603113.
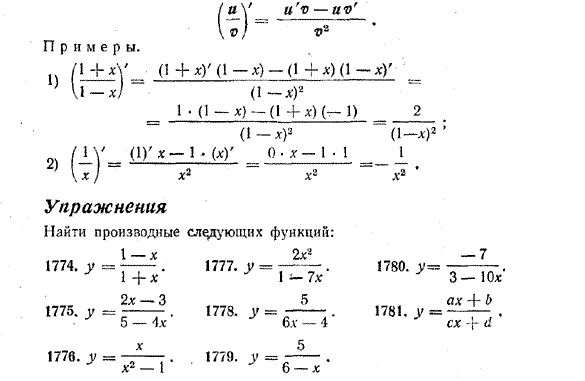com Производная произведения и частного
multiurok.ru
Производная 4. Произведения, дроби и сложной функции …
ytimg.com
Презентация на тему: “Теорема 1 Производная суммы …
Производная произведения функций – доказательство – примеры
1cov-edu.ru
Геометрический смысл производной
studfiles.net
Таблица первообразных и производных
studfile.net
Геометрический смысл производной
studfile.net
Тема: Производная сложной функции
infourok.ru
Формулы производных., калькулятор онлайн, конвертер
calc.ru
Презентация по математике “Дифференциал и интеграл …
Презентация на тему “Производная”
infourok.
ru Формулы нахождения производной – Производная функции …
csri.ru
Производная произведения и частного
multiurok.ru
Тема: Производная сложной функции
infourok.ru
Формулы нахождения производной – Производная функции …
csri.ru
Тема: Производная сложной функции
infourok.ru
Правила дифференцирования 1) производная суммы (разности …
Презентация по математике “Производная суммы, разности …
ppt4web.ru
Реферат: Формулы по математике (11 кл.) – Xreferat.com …
xreferat.ru
2.3. Производная функции двух переменных
studfile.net
Производная произведения и частного
multiurok.ru
Производная произведения и частного
multiurok.
ru Самостоятельные, контрольные, СРС – Производная
sobol2016.at.ua
Правила дифференцирования. Доказательство и примеры …
Все о вычислении производной в школе +примеры из ЕГЭ – YouTube
ytimg.com
Презентация по физике “Применение производной в физике …
ppt4web.ru Tags: Таблица первообразных, таблица производных математикаповторение, 1 страница Определение 1 Производной функции fx в, Производная произведения и частного функции, Производная первого порядка все формулы и примеры, Производная произведения и частного YouTube, Формулы Производная произведения Производная частного, Производная произведения и частного функции, Правила нахождения производной Помощь в обучении, Формулы Производная произведения Производная частного, Правила дифференцирования Доказательство и примеры,
Дробные производные формулы.
Правила вычисления производных Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции.
Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного – в правилах
дифференцирования.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная “икса” равна единице, а производная синуса – косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные – в статье “Производная произведения и частного функций ” .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u “v , в котором u – число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка – механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений.
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие “Производная суммы дробей со степенями и корнями “.
Если же перед Вами задача вроде , то Вам на занятие “Производные простых тригонометрических функций”.
Пошаговые примеры – как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители – суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, “икс” у нас превращается в единицу, а минус 5 – в ноль.
Во втором выражении “икс” умножен на 2, так что двойку умножаем на ту же единицу как
производную “икса”. Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2.
Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие “Производная суммы дробей со степенями и корнями” .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок “Производные простых тригонометрических функций” .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых – квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение.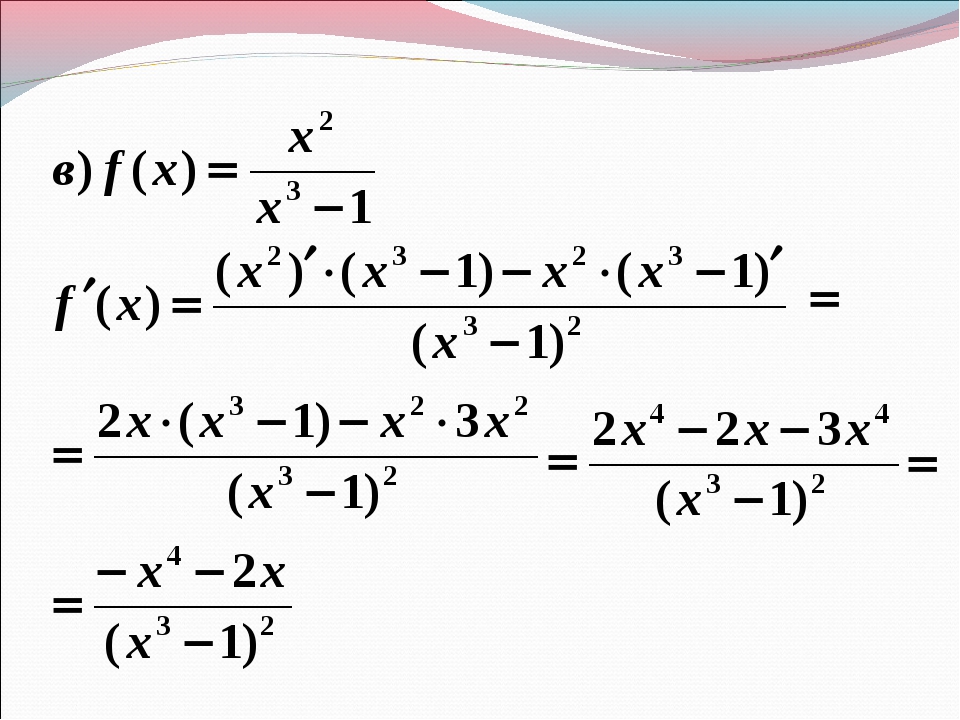
В данной функции видим частное, делимое которого – квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Докажем правило дифференцирования частного двух функций (дроби) . Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X .
По определению производной
Пример.
Выполнить дифференцирование функции .
Решение.
Исходная функция представляет собой отношение двух выражений sinx и 2x+1 . Применим правило дифференцирования дроби:
Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:
В заключении, давайте соберем все правила в одном примере.
Пример.
Найти производную функции , где a – положительное действительное число.
Решение.
А теперь по порядку.
Первое слагаемое .
Второе слагаемое
Третье слагаемое
Собираем все вместе:
4.Вопрос.Производные Основных элементарных функций.
Задание. Найти производную функции
Решение. Используем правила дифференцирования и таблицу производных:
Ответ.
5.Вопрос.Производная сложной функции примеры
Все примеры этого раздела опираются на таблицу производных и теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция u=φ(x) имеет в некоторой точке x0 производную u′x=φ′(x0), 2) функция y=f(u) имеет в соответствующей точке u0=φ(x0) производную y′u=f′(u). Тогда сложная функция y=f(φ(x)) в упомянутой точке также будет иметь производную, равную произведению производных функций f(u) и φ(x):
(f(φ(x)))′=f′u(φ(x0))⋅φ′(x0)
или, в более короткой записи: y′x=y′u⋅u′x.
В примерах этого раздела все функции имеют вид y=f(x) (т.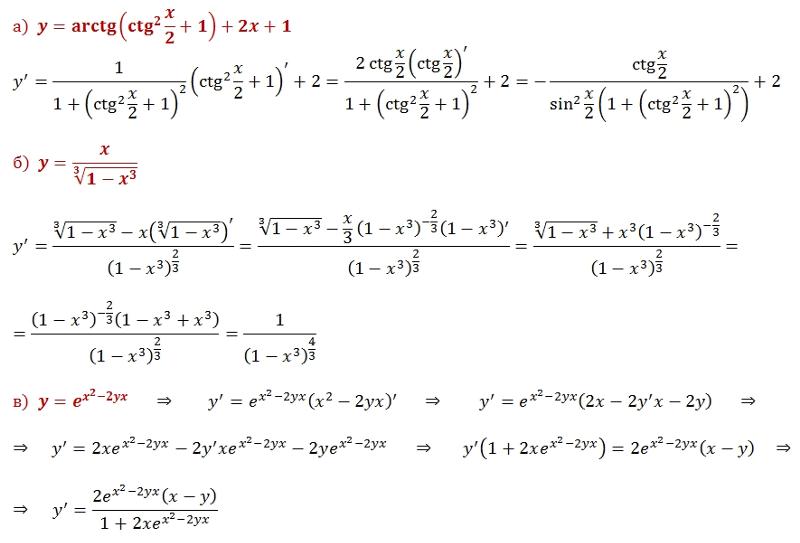
е. рассматриваем лишь функции одной переменной x). Соответственно, во всех примерах производная y′ берётся по переменной x. Чтобы подчеркнуть то, что производная берётся по переменной x, часто вместо y′ пишут y′x.
В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.
Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.
Пример №1
Найти производную функции y=ecosx.
Решение
Нам нужно найти производную сложной функции y′. Так как y=ecosx, то y′=(ecosx)′. Чтобы найти производную (ecosx)′ используем формулу №6 из таблицы производных. Дабы использовать формулу №6 нужно учесть, что в нашем случае u=cosx. Дальнейшее решение состоит в банальной подстановке в формулу №6 выражения cosx вместо u:
y′=(ecosx)′=ecosx⋅(cosx)′(1.
1)
Теперь нужно найти значение выражения (cosx)′. Вновь обращаемся к таблице производных, выбирая из неё формулу №10. Подставляя u=x в формулу №10, имеем: (cosx)′=−sinx⋅x′. Теперь продолжим равенство (1.1), дополнив его найденным результатом:
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)(1.2)
Так как x′=1, то продолжим равенство (1.2):
y′=(ecosx)′=ecosx⋅(cosx)′=ecosx⋅(−sinx⋅x′)=ecosx⋅(−sinx⋅1)=−sinx⋅ecosx(1.3)
Итак, из равенства (1.3) имеем: y′=−sinx⋅ecosx. Естественно, что пояснения и промежуточные равенства обычно пропускают, записывая нахождение производной в одну строку, – как в равенстве (1.3). Итак, производная сложной функции найдена, осталось лишь записать ответ.
Ответ : y′=−sinx⋅ecosx.
Пример №2
Найти производную функции y=9⋅arctg12(4⋅lnx).
Решение
Нам необходимо вычислить производную y′=(9⋅arctg12(4⋅lnx))′. Для начала отметим, что константу (т.е. число 9) можно вынести за знак производной:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′(2.
1)
Теперь обратимся к выражению (arctg12(4⋅lnx))′. Чтобы выбрать нужную формулу из таблицы производных было легче, я представлю рассматриваемое выражение в таком виде: ((arctg(4⋅lnx))12)′. Теперь видно, что необходимо использовать формулу №2, т.е. (uα)′=α⋅uα−1⋅u′. В эту формулу подставим u=arctg(4⋅lnx) и α=12:
Дополняя равенство (2.1) полученным результатом, имеем:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′(2.2)
Примечание: показать\скрыть
Теперь нужно найти (arctg(4⋅lnx))′. Используем формулу №19 таблицы производных, подставив в неё u=4⋅lnx:
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′
Немного упростим полученное выражение, учитывая (4⋅lnx)2=42⋅(lnx)2=16⋅ln2x.
(arctg(4⋅lnx))′=11+(4⋅lnx)2⋅(4⋅lnx)′=11+16⋅ln2x⋅(4⋅lnx)′
Равенство (2.2) теперь станет таким:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′(2.
3)
Осталось найти (4⋅lnx)′. Вынесем константу (т.е. 4) за знак производной: (4⋅lnx)′=4⋅(lnx)′. Для того, чтобы найти (lnx)′ используем формулу №8, подставив в нее u=x: (lnx)′=1x⋅x′. Так как x′=1, то (lnx)′=1x⋅x′=1x⋅1=1x. Подставив полученный результат в формулу (2.3), получим:
y′=(9⋅arctg12(4⋅lnx))′=9⋅(arctg12(4⋅lnx))′==108⋅(arctg(4⋅lnx))11⋅(arctg(4⋅lnx))′=108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅(4⋅lnx)′==108⋅(arctg(4⋅lnx))11⋅11+16⋅ln2x⋅4⋅1x=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Напомню, что производная сложной функции чаще всего находится в одну строку, – как записано в последнем равенстве. Поэтому при оформлении типовых расчетов или контрольных работ вовсе не обязательно расписывать решение столь же подробно.
Ответ : y′=432⋅arctg11(4⋅lnx)x⋅(1+16⋅ln2x).
Пример №3
Найти y′ функции y=sin3(5⋅9x)−−−−−−−−−√7.
Решение
Для начала немного преобразим функцию y, выразив радикал (корень) в виде степени: y=sin3(5⋅9x)−−−−−−−−−√7=(sin(5⋅9x))37.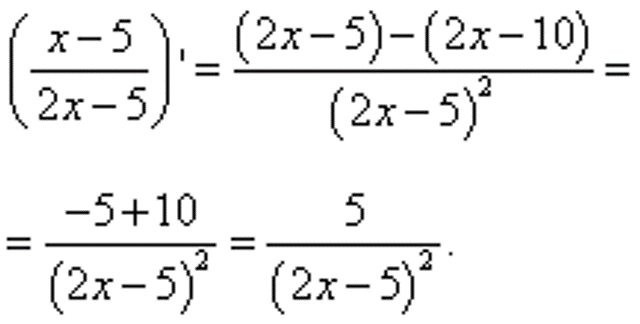
Теперь приступим к нахождению производной. Так как y=(sin(5⋅9x))37, то:
y′=((sin(5⋅9x))37)′(3.1)
Используем формулу №2 из таблицы производных, подставив в неё u=sin(5⋅9x) и α=37:
((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))37−1(sin(5⋅9x))′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′
Продолжим равенство (3.1), используя полученный результат:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′(3.2)
Теперь нужно найти (sin(5⋅9x))′. Используем для этого формулу №9 из таблицы производных, подставив в неё u=5⋅9x:
(sin(5⋅9x))′=cos(5⋅9x)⋅(5⋅9x)′
Дополнив равенство (3.2) полученным результатом, имеем:
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′(3.3)
Осталось найти (5⋅9x)′. Для начала вынесем константу (число 5) за знак производной, т.е. (5⋅9x)′=5⋅(9x)′. Для нахождения производной (9x)′ применим формулу №5 таблицы производных, подставив в неё a=9 и u=x: (9x)′=9x⋅ln9⋅x′. Так как x′=1, то (9x)′=9x⋅ln9⋅x′=9x⋅ln9.
Теперь можно продолжить равенство (3.3):
y′=((sin(5⋅9x))37)′=37⋅(sin(5⋅9x))−47(sin(5⋅9x))′==37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅(5⋅9x)′=37⋅(sin(5⋅9x))−47cos(5⋅9x)⋅5⋅9x⋅ln9==15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x.
Можно вновь от степеней вернуться к радикалам (т.е. корням), записав (sin(5⋅9x))−47 в виде 1(sin(5⋅9x))47=1sin4(5⋅9x)−−−−−−−−−√7. Тогда производная будет записана в такой форме:
y′=15⋅ln97⋅(sin(5⋅9x))−47⋅cos(5⋅9x)⋅9x=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Ответ : y′=15⋅ln97⋅cos(5⋅9x)⋅9xsin4(5⋅9x)−−−−−−−−−√7.
Пример №4
Показать, что формулы №3 и №4 таблицы производных есть частный случай формулы №2 этой таблицы.
Решение
В формуле №2 таблицы производных записана производная функции uα. Подставляя α=−1 в формулу №2, получим:
(u−1)′=−1⋅u−1−1⋅u′=−u−2⋅u′(4.1)
Так как u−1=1u и u−2=1u2, то равенство (4.1) можно переписать так: (1u)′=−1u2⋅u′. Это и есть формула №3 таблицы производных.
Вновь обратимся к формуле №2 таблицы производных.
Подставим в неё α=12:
(u12)′=12⋅u12−1⋅u′=12u−12⋅u′(4.2)
Так как u12=u−−√ и u−12=1u12=1u−−√, то равенство (4.2) можно переписать в таком виде:
(u−−√)′=12⋅1u−−√⋅u′=12u−−√⋅u′
Полученное равенство (u−−√)′=12u−−√⋅u′ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения α.
Пример №5
Найти y′, если y=arcsin2x.
Решение
Нахождение производной сложной функции в данном примере запишем без подробных пояснений, которые были даны в предыдущих задачах.
Ответ : y′=2xln21−22x−−−−−−√.
Пример №6
Найти y′, если y=7⋅lnsin3x.
Решение
Как и в предыдущем примере, нахождение производной сложной функции укажем без подробностей. Желательно записать производную самостоятельно, лишь сверяясь с указанным ниже решением.
Ответ : y′=21⋅ctgx.
Пример №7
Найти y′, если y=9tg4(log5(2⋅cosx)).
Решение
6 Вопрос. Производная обратной функции примеры.
Производная обратной функции
Формула
Известно свойство степеней, что
Используя производную степенной функции:
Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:- Таблица производных экспоненциальных и логарифмических функций
Производные простых функций
1. Производная от числа равна нулюс´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента.
Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|” = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы :
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу.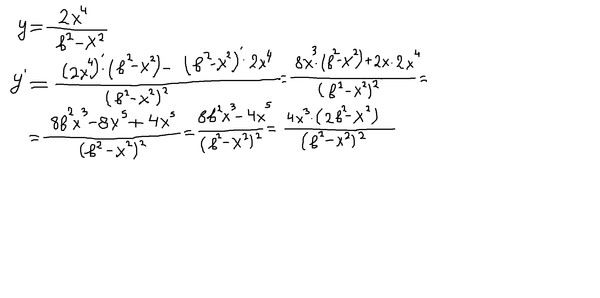
Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)” = – c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)” = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)
9.
Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках.
Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .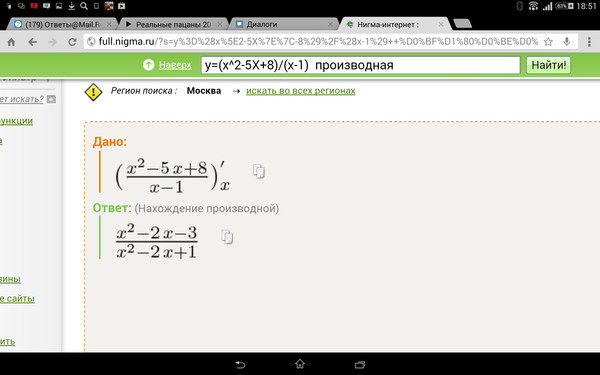
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
| 1 | Trovare la Derivata – d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata – d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata – d/dx | 1/x | |
| 6 | Trovare la Derivata – d/dx | x^2 | |
| 7 | Trovare la Derivata – d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata – d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata – d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata – d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata – d/dx | x^3 | |
| 17 | Trovare la Derivata – d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata – d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata – d/dx | sin(2x) | |
| 23 | Trovare la Derivata – d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata – d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata – d/dx | cos(2x) | |
| 28 | Trovare la Derivata – d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata – d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata – d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata – d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata – d/dx | 2e^x | |
| 35 | Trovare la Derivata – d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata – d/dx | -sin(x) | |
| 37 | Trovare la Derivata – d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata – d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata – d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata – d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata – d/dx | x/2 | |
| 46 | Trovare la Derivata – d/dx | -cos(x) | |
| 47 | Trovare la Derivata – d/dx | sin(3x) | |
| 48 | Trovare la Derivata – d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata – d/dx | x^x | |
| 52 | Trovare la Derivata – d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata – d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata – d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata – d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata – d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata – d/dx | y=x^2 | |
| 62 | Trovare la Derivata – d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata – d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata – d/dx | e^2 | |
| 67 | Trovare la Derivata – d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata – d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata – d/dx | x^5 | |
| 73 | Trovare la Derivata – d/dx | 2/x | |
| 74 | Trovare la Derivata – d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata – d/dx | x^(1/2) | |
| 76 | Trovare la Derivata – d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata – d/dx | cos(x^2) | |
| 78 | Trovare la Derivata – d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata – d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata – d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata – d/dx | логарифм x | |
| 86 | Trovare la Derivata – d/dx | arctan(x) | |
| 87 | Trovare la Derivata – d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata – d/dx | 5e^x | |
| 89 | Trovare la Derivata – d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata – d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata – d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata – d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata – d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata – d/dx | натуральный логарифм x^2 |
Математика Подготовительные курсы
Тема 1.
Структура и содержание контрольно-измерительных материалов Единого государственного экзамена по математике. Демонстрационный вариант КИМ ЕГЭ 2014 г. Система оценивания. Примеры заданий с кратким ответом (задания В1-В14). Примеры заданий с развернутым ответом (задания С1-С6). Тренировочные варианты ЕГЭ 2014 г. Входное тестирование в форме ЕГЭ.Тема 2. Числа, корни и степени. Дроби и проценты. Целые числа Степень с натуральным показателем. Дроби, проценты, рациональные числа. Степень с целым показателем. Корень степени п > 1 и его свойства Степень с рациональным показателем и ее свойства. Свойства степени с действительным показателем. Задачи практического содержания (дроби, проценты, смеси и сплавы, движение, работа).
Тема 3. Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов.
Синус и косинус двойного угла.
Тема 4. Логарифмы. Логарифм числа. Логарифм произведения, частного, степени. Десятичный и натуральный логарифмы, число е
Тема 5. Преобразования выражений. Преобразования выражений, включающих арифметические операции. Преобразования выражений, включающих операцию возведения в степень. Преобразования выражений, включающих корни натуральной степени. Преобразования тригонометрических выражений. Преобразование выражений, включающих операцию логарифмирования. Модуль (абсолютная величина) числа.
Тема 6. Функции. Определение и график функции. Функция, область определения функции. Множество значений функции. График функции. Примеры функциональных зависимостей в реальных процессах и явлениях. Обратная функция. График обратной функции. Преобразования графиков: параллельный перенос, симметрия относительно осей координат. Элементарное исследование функций. Монотонность функции.
Промежутки возрастания и убывания. Четность и нечетность функции. Периодичность функции. Ограниченность функции. Точки экстремума (локального максимума и минимума) функции. Наибольшее и наименьшее значения функции. Основные элементарные функции. Линейная функция, ее график. Функция, описывающая обратную пропорциональную зависимость, ее график. Квадратичная функция, ее график. Степенная функция с натуральным показателем, ее график. Тригонометрические функции, их графики. Показательная функция, ее график. Логарифмическая функция, ее график.
Тема 7. Уравнения и неравенства. Уравнения. Квадратные уравнения. Рациональные уравнения. Иррациональные уравнения. Тригонометрические уравнения. Показательные уравнения. Логарифмические уравнения. Равносильность уравнений, систем уравнений. Простейшие системы уравнений с двумя неизвестными. Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Использование свойств и графиков функций при решении уравнений.
Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. Неравенства. Квадратные неравенства. Рациональные неравенства. Показательные неравенства. Логарифмические неравенства. Системы линейных неравенств. Системы неравенств с одной переменной. Равносильность неравенств, систем неравенств. Использование свойств и графиков функций при решении неравенств. Метод интервалов. Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем.
Тема 8. Начала математического анализа. Производная. Понятие о производной функции, геометрический смысл производной. Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного.
Производные основных элементарных функций. Вторая производная и ее физический смысл Исследование функций. Применение производной к исследованию функций и построению графиков. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах Первообразная и интеграл. Первообразные элементарных функций. Примеры применения интеграла в физике и геометрии.
Тема 9. Планиметрия. Треугольник. Параллелограмм, прямоугольник, ромб, квадрат. Трапеция. Окружность и круг. Окружность, вписанная в треугольник, и окружность, описанная около треугольника Многоугольник. Сумма углов выпуклого многоугольника. Правильные многоугольники. Вписанная окружность и описанная окружность правильного многоугольника
Тема 10. Прямые в пространстве. Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых. Параллельность прямой и плоскости, признаки и свойства Параллельность плоскостей, признаки и свойства Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трех перпендикулярах.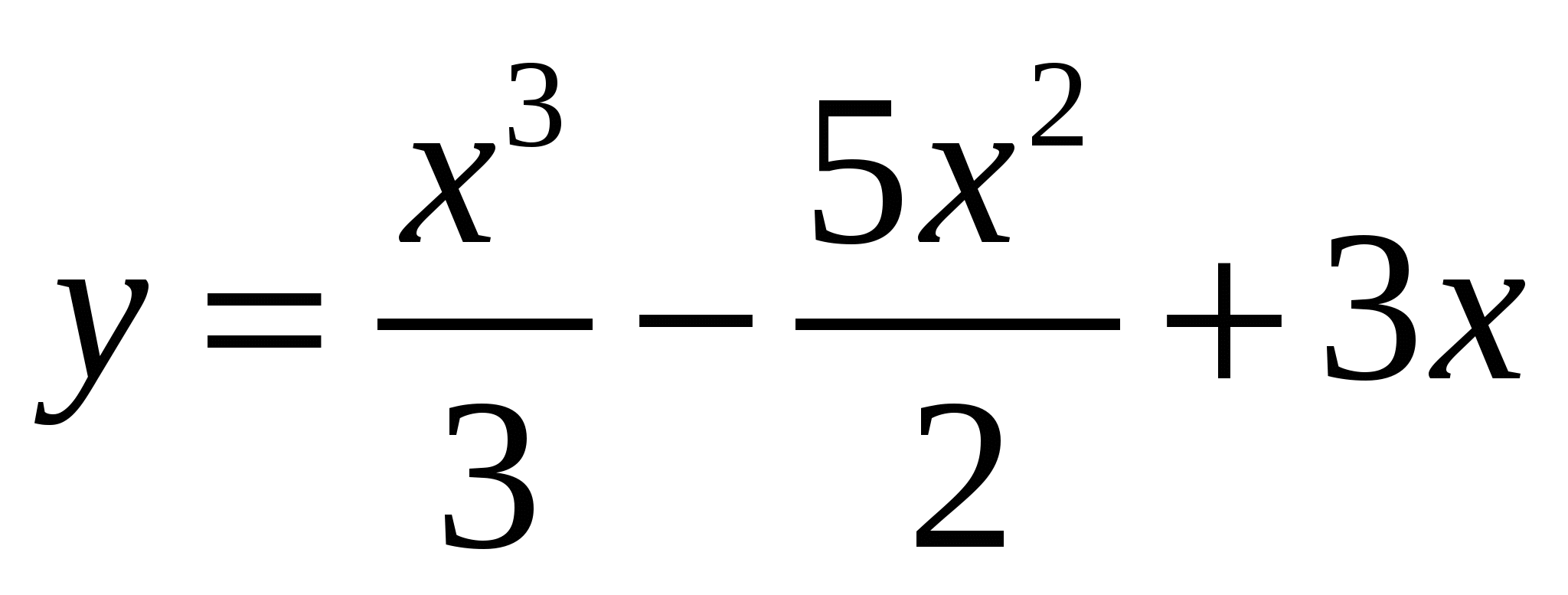
Перпендикулярность плоскостей, признаки и свойства Параллельное проектирование. Изображение пространственных фигур
Тема 11. Многогранники. Призма, ее основания, боковые ребра, высота, боковая поверхность; прямая призма; правильная призма. Параллелепипед; куб; симметрии в кубе, в параллелепипеде. Пирамида, ее основание, боковые ребра, высота, боковая поверхность; треугольная пирамида; правильная пирамида. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
Тема 12. Тела и поверхности вращения. Цилиндр. Основание, высота, боковая поверхность, образующая, развертка. Конус. Основание, высота, боковая поверхность, образующая, развертка. Шар и сфера, их сечения Измерение геометрических величин. Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности. Угол между прямыми в пространстве; угол между прямой и плоскостью, угол между плоскостями.
Длина отрезка, ломаной, окружности, периметр многоугольника. Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными и скрещивающимися прямыми, расстояние между параллельными плоскостями. Площадь треугольника, параллелограмма, трапеции, круга, сектора. Площадь поверхности конуса, цилиндра, сферы. Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара.
Тема 13. Координаты и векторы. Декартовы координаты на плоскости и в пространстве. Формула расстояния между двумя точками; уравнение Сферы векторов и умножение вектора на число. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение по трем некомпланарным векторам. Координаты вектора; скалярное произведение векторов; угол между векторами
Тема 14. Элементы комбинаторики, статистики и теории вероятностей. Элементы комбинаторики. Поочередный и одновременный выбор. Формулы числа сочетаний и перестановок.
Бином Ньютона. Элементы статистики. Табличное и графическое представление данных. Числовые характеристики рядов данных. Элементы теории вероятностей. Вероятности событий. Примеры использования вероятностей и статистики при решении прикладных задач.
Решение задач по всем темам. Промежуточное и итоговое тестирование.
Логарифмическое дифференцирование функций
Метод логарифмического дифференцирования становится пригодным при дифференцировании произведения нескольких функций или их частки. Его удобно применять при дифференцировании выражений, содержащих корни из дробей (функций), а также когда показатель функции также представляет собой функцию
В таких случаях целесообразно обе части выражения сначала прологарифмировать по основанию , а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:
имеем сложную функцию вида
к обеим сторонам применяем логарифмирования
находим производные правой и левой части равенства
Приравниваем производные и выражаем
В этом суть метода, дальше все зависит от функции .
Если она представляет собой произведение функций
то по свойствам логарифма он будет равен сумме логарифмов
Если имеем дробь от функций
то применяя логарифмирования получим
Если имеем функцию в степени другой
то по свойствам логарифма получим
В случае корней дифференцировки значительно упрощается
Дальнейшее вычисление производных зависит от сложности самих функций. Рассмотрим конкретные примеры, чтобы данный материал стал для Вас более понятным и наглядным.
Задача.
Используя логарифмирования найти производную (Дубовик В.П., Юрик И.И. “Высшая математика. Сборник задач”)
1) (5.2.178)
2) (5.2.191)
3) (5.2.195)
4) (5.2.199)
Решение.
Примеры выбрано сложные для того, чтобы раскрыть всю силу метода логарифмического дифференцирования и рассмотреть типичные распространенные примеры.
1) Проведем логарифмирования левой и правой частей
Найдем производную правой части
Производная левой части показана при изложении теоретического материала.
Записываем обе части
Далее переносим функцию из знаменателя в правую часть и не забываем поменять ее значение
Несмотря на сложный вид данный пример полностью решено.
2) Используем свойства логарифма к данному примеру
Проводим дифференцирования обеих частей равенства
Сведем к общему знаменателю правую сторону. В результате математических операций получим
Подставим в исходную равенство, перенеся функцию в правую часть
В результате ряда несложных математических манипуляций получили достаточно компактный конечный результат производной. При исчислении данного примера направления подобный результат пришлось бы искать очень долго.
3) Несмотря на сложный вид данное выражение, на основе свойств степеней, можно переписать в следующем виде
Применим к нему логарифмирования
Производная от правой части будет равна следующему выражению
Здесь для упрощения дальнейших выкладок введено обозначение .
Учитывая производную , окончательно получим
Можно оставлять в таком виде, поскольку суть данного урока научиться применять метод логарифмического дифференцирования. Но если Вы захотите для упрощения свести все к общему знаменателю, то получите следующее выражение
Поверьте это займет у Вас много времени.
4) Проводим логарифмирования функции
Дальше по методике находим производную правой части. Она будет равна выражению
Подставляя в формулу для производной от , получим
На этом решения примера завершен.
Практикуйте с подобными задачами и через некоторое время у Вас не будет никаких трудностей с такого сорта примерами.
определение, как найти, примеры решений
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
2 – 4x + 7 $$
{\large\bf Производная функции}
Рассмотрим функцию y=f(x) , заданную на интервале (a, b) . Пусть x – любое фиксированная точка интервала (a, b) , а Δx – произвольное число, такое, что значение x+Δx также принадлежит интервалу (a, b) . Это число Δx называют приращением аргумента.
Определение . Приращением функции y=f(x) в точке x , соответствующим приращению аргумента Δx , назовем число
Δy = f(x+Δx) – f(x) .
Считаем, что Δx ≠ 0 . Рассмотрим в данной фиксированной точке x отношение приращения функции в этой точке к соответствующему приращению аргумента Δx
Это отношение будем называть разностным отношением. Так как значение x мы считаем фиксированным, разностное отношение представляет собой функцию аргумента Δx . Эта функция определена для всех значений аргумента Δx , принадлежащих некоторой достаточно малой окрестности точки Δx=0 , за исключением самой точки Δx=0 .
Таким образом, мы имеем право рассматривать вопрос о существовании предела указанной функции при Δx → 0 .
Определение . Производной функции y=f(x) в данной фиксированной точке x называется предел при Δx → 0 разностного отношения, то есть
При условии, что этот предел существует.
Обозначение . y′(x) или f′(x) .
Геометрический смысл производной : Производная от функции f(x) в данной точке x равна тангенсу угла между осью Ox и касательной к графику этой функции в соответствующей точке:
f′(x 0) = \tgα .
Механический смысл производной : Производная от пути по времени равна скорости прямолинейного движения точки:
Уравнение касательной к линии y=f(x) в точке M 0 (x 0 ,y 0) принимает вид
y-y 0 = f′(x 0) (x-x 0) .
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f′(x 0)≠ 0 , то уравнение нормали к линии y=f(x) в точке M 0 (x 0 ,y 0) записывается так:
Понятие дифференцируемости функции
Пусть функция y=f(x) определена на некотором интервале (a, b) , x – некоторое фиксированное значение аргумента из этого интервала, Δx – любое приращение аргумента, такое, что значение аргумента x+Δx ∈ (a, b) .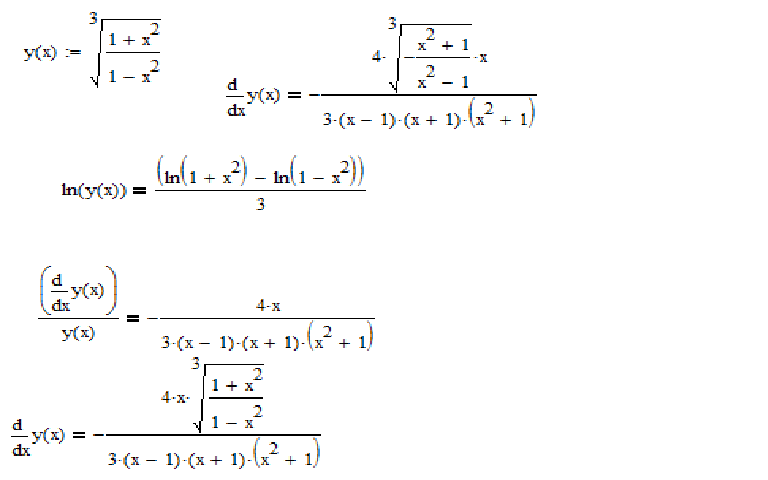
Определение . Функция y=f(x) называется дифференцируемой в данной точке x , если приращение Δy этой функции в точке x , соответствующее приращению аргумента Δx , может быть представимо в виде
Δy = A Δx +αΔx ,
где A – некоторое число, не зависящее от Δx , а α – функция аргумента Δx , являющая бесконечно малой при Δx→ 0 .
Так как произведение двух бесконечно малых функций αΔx является бесконечно малой более высокого порядка, чем Δx (свойство 3 бесконечно малых функций), то можем записать:
Δy = A Δx +o(Δx) .
Теорема . Для того, чтобы функция y=f(x) являлась дифференцируемой в данной точке x , необходимо и достаточно, чтобы она имела в этой точке конечную производную. При этом A=f′(x) , то есть
Δy = f′(x) Δx +o(Δx) .
Операцию нахождения производной обычно называют дифференцированием.
Теорема .
Если функция y=f(x) x , то она непрерывна в этой точке.
Замечание . Из непрерывности функции y=f(x) в данной точке x , вообще говоря, не вытекает дифференцируемость функции f(x) в этой точке. Например, функция y=|x| – непрерывна в точке x=0 , но не имеет производной.
Понятие дифференциала функции
Определение . Дифференциалом функции y=f(x) называется произведение производной этой функции на приращение независимой переменной x :
dy = y′ Δx, df(x) = f′(x) Δx .
Для функции y=x получаем dy=dx=x′Δx = 1· Δx= Δx , то есть dx=Δx – дифференциал независимой переменной равен приращению этой переменной.
Таким образом, можем записать
dy = y′ dx, df(x) = f′(x) dx
Дифференциал dy и приращение Δy функции y=f(x) в данной точке x , оба отвечающие одному и тому же приращению аргумента Δx , вообще говоря, не равны друг другу.
Геометрический смысл дифференциала : Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение Δx .
Правила дифференцирования
Теорема . Если каждая из функций u(x) и v(x) дифференцируема в данной точке x , то сумма, разность, произведение и частное этих функций (частное при условии, что v(x)≠ 0 ) также дифференцируемы в этой точке, причем имеют место формулы:
Рассмотрим сложную функцию y=f(φ(x))≡ F(x) , где y=f(u) , u=φ(x) . В этом случае u называют промежуточным аргументом , x – независимой переменной .
Теорема . Если y=f(u) и u=φ(x) – дифференцируемые функции своих аргументов, то производная сложной функции y=f(φ(x)) существует и равна произведению этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т.
е.
Замечание . Для сложной функции, являющейся суперпозицией трех функций y=F(f(φ(x))) , правило дифференцирования имеет вид
y′ x = y′ u u′ v v′ x ,
где функции v=φ(x) , u=f(v) и y=F(u) – дифференцируемые функции своих аргументов.
Теорема . Пусть функция y=f(x) возрастает (или убывает) и непрерывна в некоторой окрестности точки x 0 . Пусть, кроме того, эта функция дифференцируема в указанной точке x 0 и ее производная в этой точке f′(x 0) ≠ 0 . Тогда в некоторой окрестности соответствующей точки y 0 =f(x 0) определена обратная для y=f(x) функция x=f -1 (y) , причем указанная обратная функция дифференцируема в соответствующей точке y 0 =f(x 0) и для ее производной в этой точке y справедлива формула
Таблица производных
Инвариантность формы первого дифференциала
Рассмотрим дифференциал сложной функции. Если y=f(x) , x=φ(t) – дифференцируемы функции своих аргументов, то производная функции y=f(φ(t)) выражается формулой
y′ t = y′ x x′ t .
По определению dy=y′ t dt , тогда получим
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx ,
dy = y′ x dx .
Итак, доказали,
Свойство инвариантности формы первого дифференциала функции : как в случае, когда аргумент x является независимой переменной, так и в случае, когда аргумент x сам является дифференцируемой функцией новой переменной, дифференциал dy функции y=f(x) равен производной этой функции, умноженной на дифференциал аргумента dx .
Применение дифференциала в приближенных вычислениях
Мы показали, что дифференциал dy функции y=f(x) , вообще говоря, не равен приращению Δy этой функции. Тем не менее с точностью до бесконечно малой функции более высокого порядка малости, чем Δx , справедливо приближенное равенство
Δy ≈ dy .
Отношение называют относительной погрешностью равенства этого равенства. Так как Δy-dy=o(Δx) , то относительная погрешность данного равенства становится как угодно малой при уменьшении |Δх| .
Учитывая, что Δy=f(x+δ x)-f(x) , dy=f′(x)Δx , получим f(x+δ x)-f(x) ≈ f′(x)Δx или
f(x+δ x) ≈ f(x) + f′(x)Δx .
Это приближенное равенство позволяет с ошибкой o(Δx) заменить функцию f(x) в малой окрестности точки x (т.е. для малых значений Δx ) линейной функцией аргумента Δx , стоящей в правой части.
Производные высших порядков
Определение . Второй производной (или производной второго порядка) функции y=f(x) называется производная от ее первой производной.
Обозначение второй производной функции y=f(x) :
Механический смысл второй производной . Если функция y=f(x) описывает закон движения материальной точки по прямой линии, то вторая производная f″(x) равна ускорению движущейся точки в момент времени x .
Аналогично определяется третья, четвертая производная.
Определение . n -й производной (или производной n -го порядка) функции y=f(x) называется производная от ее n-1 -й производной:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′ .
Обозначения: y″′ , y IV , y V и т.д.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 .
Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое –4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) – f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f “(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f “(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)” = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой “у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Вычисление производной – одна из самых важных операций в дифференциальном исчислении. Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:- Таблица производных экспоненциальных и логарифмических функций
Производные простых функций
1. Производная от числа равна нулюс´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента.
Поскольку число никак не меняется ни при каких условиях – скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)” = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4.
Производная переменной по модулю равна частному этой переменной к ее модулю |x|” = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 – единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных – наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)”= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)” = 2x
(x 3)” = 3x 2
Для запоминания формулы :
Снесите степень переменной “вниз” как множитель, а потом уменьшите саму степень на единицу.
Например, для x 2 – двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 – тройку “спускаем вниз”, уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного “не научно”, но очень просто запомнить.
6. Производная дроби 1/х
(1/х)” = – 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)” = (x -1)” , тогда можно применить формулу из правила 5 таблицы производных
(x -1)” = -1x -2 = – 1 / х 2
7. Производная дроби с переменной произвольной степени в знаменателе
(1 / x c)” = – c / x c+1
Пример:
(1 / x 2)” = – 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)” = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)” = (х 1/2)” значит можно применить формулу из правила 5
(х 1/2)” = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)” = 1 / (n n √x n-1)
Разумеется, в этих расчетах ничего не используется.
новым, и, в частности, производная от $f(g(x))$ была несколько
утомительно вычислять по определению.
$\квадрат$ Предположим, нам нужна производная от $f(g(x))$.
Опять же, давайте настроим производную и поиграем с некоторыми алгебраическими трюками:
$$\выравнивание{
{d \ над дх} е (г (х))
&=\lim_{\Delta x\to0} {f(g(x+\Delta x))-f(g(x))\over\Delta x}\cr
&=\lim_{\Delta x\to0} {f(g(x+\Delta x))-f(g(x))\over g(x+\Delta
x)-g(x)} {g(x+\Delta x)-g(x)\over\Delta x}\cr
}$$
Теперь мы сразу видим, что вторая дробь превращается в $g'(x)$
когда мы берем предел.Первая фракция сложнее, но она
тоже выглядит как производная. Знаменатель $g(x+\Delta
x)-g(x)$, является изменением значения $g$, поэтому будем сокращать
как $\Delta g=g(x+\Delta
x)-g(x)$, что также означает $g(x+\Delta x)=g(x)+\Delta g$. Это дает
нас
$$\lim_{\Delta x\to0} {f(g(x)+\Delta g)-f(g(x))\over \Deltag}.$$
Поскольку $\Delta x$ стремится к 0, также верно, что $\Delta g$ стремится к 0,
потому что $g(x+\Delta x)$ переходит в $g(x)$.
Таким образом, мы можем переписать этот предел
в виде
$$\lim_{\Deltag\to0} {f(g(x)+\Deltag)-f(g(x))\over\Deltag}.$$
Теперь это выглядит точно так же, как производная, а именно $f'(g(x))$, то есть
функция $f'(x)$ с заменой $x$ на $g(x)$. Если это все
выдерживает проверку, то мы получаем
$${d\over dx}f(g(x))=f'(g(x))g'(x).$$
К сожалению, в рассуждениях есть небольшой изъян. Напомним, что
под $\lim_{\Delta x\to0}$ подразумевается, что происходит, когда $\Delta x$
близко к 0 , но не равно 0. Квалификация очень
важно, так как мы должны уметь делить на $\Delta x$.
Но когда $\Delta x$ близко к 0, но не равно 0,
$\Дельта г=г(х+\Дельта
x))-g(x)$ близко к 0 и, возможно, равно 0. Это значит, что
нет смысла делить на $\Delta g$.
К счастью, можно изменить аргумент, чтобы избежать этого.
сложность, но это немного сложно; мы не будем включать детали,
которые можно найти во многих книгах по математическому анализу. Обратите внимание, что многие функции
$g$ обладают тем свойством, что $g(x+\Delta x)-g(x)\not=0$, когда $\Delta
x$ мало, и для этих функций приведенный выше аргумент подходит.
Цепное правило имеет особенно простое выражение, если мы используем Обозначение Лейбница для производной.Величина $f'(g(x))$ есть производная от $f$ с заменой $x$ на $g$; это можно написать $дф/дг$. Как обычно, $g'(x)=dg/dx$. Тогда цепное правило становится $${df\over dx} = {df\over dg}{dg\over dx}.$$ Это выглядит как тривиальная арифметика, но это не так: $dg/dx$ не является дробь, то есть не буквальное деление, а единичный символ, который означает $g'(x)$. Тем не менее оказывается, что то, что выглядит тривиально арифметика, и поэтому легко запоминается, действительно верно.
Потребуется немного практики, чтобы привыкнуть к цепному правилу. естественно — это сложнее, чем предыдущая дифференциация правила, которые мы видели.2+1)}.\кр }$$ Конечно, это можно упростить, но мы сделали все расчеты, так что осталась только алгебра. $\квадрат$
Пример 3.5.5
Вычислите производную $\ds \sqrt{1+\sqrt{1+\sqrt{x}}}$. Здесь у нас есть
более сложная цепочка композиций, поэтому используем цепное правило
дважды.
{-1/2}{d\over dx}
\left(1+\sqrt{1+\sqrt{x}}\right).2}}$
в $\ds (1,\sqrt{4+\sqrt{5}})$.
(отвечать)
Частное правило. Неявное дифференцирование
8
Правило частных
Доказательство правила отношения
Неявное дифференцирование
Производная обратной функции
Правило частных
Следующее правило называется частным правилом:
“Производная от частного двух функций равна
знаменатель умножить на производную от числителя
минус числитель умножить на производную от знаменателя
все разделить на квадрат знаменателя.”
Например, примем на данный момент, что производная sin x равна cos x (Урок 12):
| Задача 1. Вычислить производную от | x 2 sin x | . |
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите “Обновить” (“Reload”).
Сначала решай задачу сам!
| SIN x 2 2 2 Cos x 2 COS x |
Задача 2. Используйте цепное правило для вычисления производной числа
.| x | = | x |
| = | sin x (2 x cos x − 3 sin x ) x 4 | |
| Проблема 3.Вычислите производную от | x 2 − 5 x − 6 2 x + 1 | . |
| (2 x + 1) (2 x – 5) – ( x 2 – 5 x – 6) · 2 (2 x + 1) 2 | = | 4 x – 8 x – 5 – 2 x + 12 2 1 x + 12 2 |
| = | 2 x 2 + 2 x + 7 (2 x + 1) 2 | |
Проблема 4. Вычислите производную от | 3 x 2 − x + 4 | . |
См. пример, урок 6 и урок 22 по алгебре.
| = | ||
| = | ||
| = | ||
Доказательство правила отношения
| ТЕОРЕМА. |
Доказательство. Поскольку г = г ( x ), то
| г дх | 1 г | = | д дг | 1 г | · | дг дх | = − | 1 г 2 | г’ |
по цепному правилу и задача 4 урока 5.
Следовательно, согласно правилу произведения (Урок 6),
Это правило частных, которое мы хотели доказать.
Неявное дифференцирование
Рассмотрим следующее:
x 2 + у 2 = r 2
Это уравнение окружности с радиусом r . (Урок 17 Предварительного исчисления.)
Подсчитаем .
Чтобы сделать это, мы могли бы найти и , а затем взять производную. Но вместо этого мы возьмем производную от каждого члена. Что касается y 2 , мы неявно считаем его функцией x , и поэтому мы можем применить к нему цепное правило. Затем мы решим для .
| д дх | х 2 | + | г дх | г 2 | = | г дх | р 2 |
| 2 х + 2 у | дх дх | = | 0 | |||
| dy dx | = | — | х у | . | ||
Это называется неявным дифференцированием. Мы рассматриваем х как функцию х и применяем цепное правило. Полученная производная обычно содержит как x , так и y .
Задача 5. 15 y + 5 y 3 + 3 y 5 = 5 x 3 . Вычислите и .
| 15 у’ + 15 у 2 у’ + 15 у 4 у’ 6 | = | 15 x 2 |
| у’ (1 + у 2 + у 4 ) | = | х 2 |
| у’ | = | x 2 1 + y 2 + y 4 |
Проблема 6.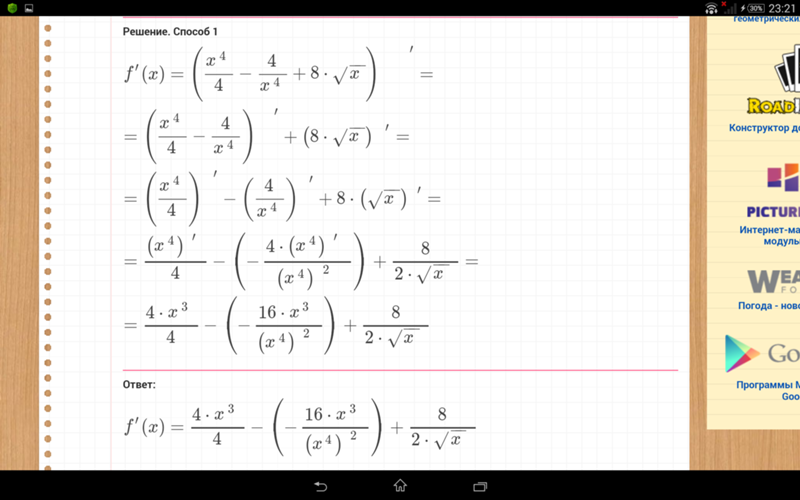 | Рассчитать и . |
Задача 7.
а) В этом круге
х 2 + у 2 = 25,
а) что такое y -координата, когда x = −3?
у = 4 или -4. Для,
(−3) 2 + (±4) 2 = 5 2
b) Каков наклон касательной к окружности в точке (−3, 4)?
c) Каков наклон касательной к окружности в точке (−3, −4)?
Проблема 8.В первом квадранте, каков наклон касательной к этой окружности,
( х – 1) 2 + ( у + 2) 2 = 169,
, когда х = 6?
[Подсказка: 5 2 + 12 2 = 13 2 — пифагорейская тройка.]
В первом квадранте, когда x = 6, y = 10,
(6 − 1) 2 + (10 + 2) 2 = 13 2 .
| у’ = – | х − 1 у + 2 | . Следовательно, наклон – 90 235 | 6 − 1 10 + 2 | = − | 5 12 |
Задача 9. Вычислить наклон касательной к этой кривой в точке (2, −1):
x 3 − 3 x y 2 + y 3 = 1
| 3 x 2 – (3 x · 2 y y ‘ + y + y 2 · 3) + 3 y 2 y’ | = | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| в соответствии с правилом произведения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 x y y y y y y + 3 y + 3 y 2 y ‘ | = | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x 2 − 2 x y y’ − y 2 + y 2 2 90 = | 0 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| у’ ( у 2 − 2 ху ) | = | г 2 − x 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| у’ | = | y 2 − x 2 y 2 − 2 xy
Производная обратной функции Когда у нас есть функция y = f ( x ) – например, у = х 2 — тогда мы часто можем найти x . При обмене переменными имеем
Напишем
И назовем f прямой функцией и g обратной функцией .Формальная связь между f и g следующая: f ( г ( x )) = г ( f ( x )) = x . (Тема 19 Предварительного исчисления.) Вот другие пары прямых и обратных функций:
Теперь, когда мы знаем производную прямой функции f , то по ней мы можем определить производную g . Таким образом, пусть г ( x ) будет обратным f ( x ). Затем ж ( г ( х )) = х . Теперь возьмем производную относительно x : Это подразумевает следующее: Теорема. Если г ( x ) обратно f ( x ), то “Производная обратной функции равна обратная производная прямой функции , когда его аргументом является обратная функция.”
Следовательно, Следующий урок: Мгновенная скорость и скорость изменения Содержание | Дом Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] Найдите производную дроби Производные. Если вы в настоящее время принимаете Calc 1 (что, вероятно, и происходит, если вы оказались здесь), вы, вероятно, по уши в проблемах с производными. Один тип — это производная дроби, или, лучше сказать, частное .2} Честно говоря, я не нахожу это очень полезным, так как я путаю «Lo» и «Hi». Я просто помню, что знаменатель стоит первым сверху. Вы просто находите способ, который работает для вас, и идете по нему. Теперь несколько примеров: Пример 1Найдите производную: \begin{equation*} Если вы беспокоитесь о том, чтобы расставить все по местам в формуле, может помочь выписать \(f(x)\) и \(g(x)\) по отдельности, а также их производные: \begin{array}{cc} Теперь просто подключите все: \begin{equation*} Ура! (Примечание. Теперь найдем производную от \(h(x)\).2 \sqrt{\ln x}} Весело, да? Когда вы решаете такие задачи, просто помните: это делает вас умнее. Надеюсь, эти примеры дадут вам некоторое представление о том, как найти производную дроби. Если у вас есть какие-либо комментарии или вопросы, пожалуйста, оставьте их ниже! Как найти производную дроби 11 класс математики CBSEПодсказка:Для нахождения производной дроби мы будем использовать правило частного, чтобы дифференцировать дробь или любую другую дробь, которая записывается как частное или дробь двух функций или выражений.2}}}$ Таким образом, мы можем найти производную для дробей. Примечание: Степени дифференциальных уравненийПоказатель старшей производной функции в нерадикальном и не дробном дифференциальном уравнении называется степенью дифференциального уравнения.1-у+9 = 0$ Следовательно, степень этого дифференциального уравнения равна единице и оно называется дифференциальным уравнением первой степени. В некоторых случаях дифференциальные уравнения могут содержать дроби и радикалы. Таким образом, радикалы и дроби должны быть исключены из дифференциальных уравнений в первую очередь для оценки степени любого дифференциального уравнения. В этом примере вторая производная является старшей производной, а ее показатель степени равен $5$.4}-2\dfrac{dz}{dy}-11$ $\,=\,$ $0$ В этом случае девятая производная является старшей производной, а ее показатель степени равен $1$. Поэтому степень этого уравнения равна единице и оно называется дифференциальным уравнением первой степени. Видео с вопросами: Нахождение производной рациональной функции с использованием предельного определения производныхСтенограмма видеоИспользуя определение производной, оцените 𝑑 на 𝑑𝑥 единицы на 𝑥 плюс один. По определению, производная от 𝑓 от 𝑥 — 𝑑 по 𝑑𝑥 от 𝑓 от 𝑥 — это предел 𝑓 от 𝑥 плюс ℎ минус 𝑓 от 𝑥 по ℎ, когда ℎ приближается к нулю. Это также пишется как 𝑓 тире от 𝑥 или 𝑓 штрих от 𝑥, чтобы подчеркнуть, что это функция от 𝑥. Применим это определение к нашей задаче. Знаменатель ℎ копируем из определения. Теперь мы готовы найти этот предел. Важно отметить, что это предел, поскольку ℎ приближается к нулю. Это не предел, так как 𝑥 приближается к некоторому значению. И наш окончательный ответ будет в терминах 𝑥. Если мы попытаемся прямо заменить здесь ℎ равным нулю, мы получим неопределенную форму ноль над нулем. Если не верите мне, можете проверить. Нам придется упростить дробь в пределе и, надеюсь, найти множитель ℎ в числителе, который нужно сократить с ℎ в знаменателе, прежде чем мы сможем вычислить предел.В настоящее время у нас есть дроби в нашей фракции. В числителе две дроби. Если мы умножим и числитель, и знаменатель на 𝑥 плюс ℎ плюс один, мы избавимся от одной из этих дробей. Здесь мы распределили 𝑥 плюс ℎ плюс один по двум слагаемым в числителе. Для начала можно избавиться от ненужных скобок вокруг 𝑥 плюс ℎ. И мы замечаем, что два 𝑥 сокращаются. У нас есть 𝑥, из которого мы затем вычитаем 𝑥. И что-то подобное происходит с теми. Так что у нас просто остался минус ℎ в числителе. И в знаменателе тоже есть множитель ℎ. Отменив эти множители, числитель станет отрицательным, а знаменатель будет равен 𝑥 плюс ℎ плюс один, умноженный на 𝑥 плюс один. И, сократив этот множитель ℎ в числителе и знаменателе, мы теперь можем напрямую подставить.Подставив ноль вместо ℎ, мы получим минус один на 𝑥 плюс ноль плюс один, умноженный на 𝑥 плюс один. И, конечно же, нам не нужно писать это плюс ноль явно. Мы получаем минус один на 𝑥 плюс один, умноженный на 𝑥 плюс один, следовательно, или минус один на 𝑥 плюс один в квадрате. Используя определение производной, мы показали, что 𝑑 на 𝑑𝑥 единицы больше 𝑥 плюс единица минус единица больше 𝑥 плюс единица в квадрате. Как и было обещано, эта производная является функцией 𝑥. Правило взаимности: определение, примеры – Исчисление КакПроизводные > В исчислении правило взаимности может означать одно из двух:
В базовой математике также существует обратное правило для деления , основная идея которого заключается в инвертировании делителя и умножении. Хотя это и не одно и то же, это похожая идея (на одном этапе процесса вы инвертируете знаменатель). Существуют взаимные правила в различных других областях , таких как фотография и теория следов, но они не имеют отношения к математическим правилам, изложенным здесь. Это правило нахождения производной обратной функции почти такое же, как и правило отношения.Однако вы можете использовать правило взаимности только в том случае, если ваш числитель является константой. Предполагая, что функция дифференцируема, вы можете найти производную по следующей формуле (Stewart, 2009): Основные шаги:
Это очень полезное правило для нахождения производных функций, имеющих дробный формат. Однако вам придется найти производную от знаменателя, поэтому вам, возможно, придется использовать другие правила для производных (например, правило степени или правило цепочки). Примечание : Убедитесь, что ваш знаменатель не равен нулю, иначе это правило не будет работать. Пример правила взаимности (производные)Примечание : В этом примере для работы с формулой используется правило степени.Если вы не знакомы с этим правилом, посмотрите короткое видео под ответом, чтобы узнать, как оно работает. Пример вопроса: Найдите производную следующей функции, используя правило взаимности:
Правило взаимности для пределов гласит, что предел обратной функции равен обратной величине предела функции, когда x приближается к a . Если это выглядит (и звучит) сложно, на самом деле это не так. Он использует тот же здравый смысл, что и фраза «99,9999 близко к 100». Тем не менее, доказательство «утомительно» (Taalman, 2013), поэтому вы обычно не встретите его в большинстве популярных учебников, кроме краткого упоминания. обратная функция является мультипликативной инверсией «обычной» функции: функции, которая при умножении на исходную функцию дает константу 1. Если f(x) ваша функция, — обратная функция. Путаница в терминологииХотя обратная величина является мультипликативной обратной функцией, важно понимать, что она может не совпадать с «обратной» этой функции. В то время как обратная функция — это функция, которая при умножении на оригинал равняется 1, обратное функции — это функция, которая, взятая как составная часть с исходной функцией, становится x. Инверсию обычно обозначают f -1 (x). Для инверсии f -1 (x), f( f -1 (x)) = x и f -1 ( f(x) ) = x. Для мультипликативного обратного (обратного) g(x), f(x) · g(x) = 1, Примеры обратных функций Обратная функция f(x) = x равна g(x)= 1/x. На изображении ниже показаны обе функции, изображенные на одном графике. Исходная функция выделена синим цветом, а обратная — красным. Обратите внимание, что в этом случае обратная или мультипликативная обратная функция такая же, как обратная функция f -1 (x). Обратная функция f(x) = x + 5 равна g(x) = 1/(x + 5). Обратите внимание, что в этом случае обратное (мультипликативное обратное) отличается от обратного f -1 (x). Для этой функции f -1 (x) = x – 5. Ниже представлены графики всех трех функций; оригинал – красным, обратный – синим, а обратный – зеленым. Каталожные номера Математический словарь Блэки. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
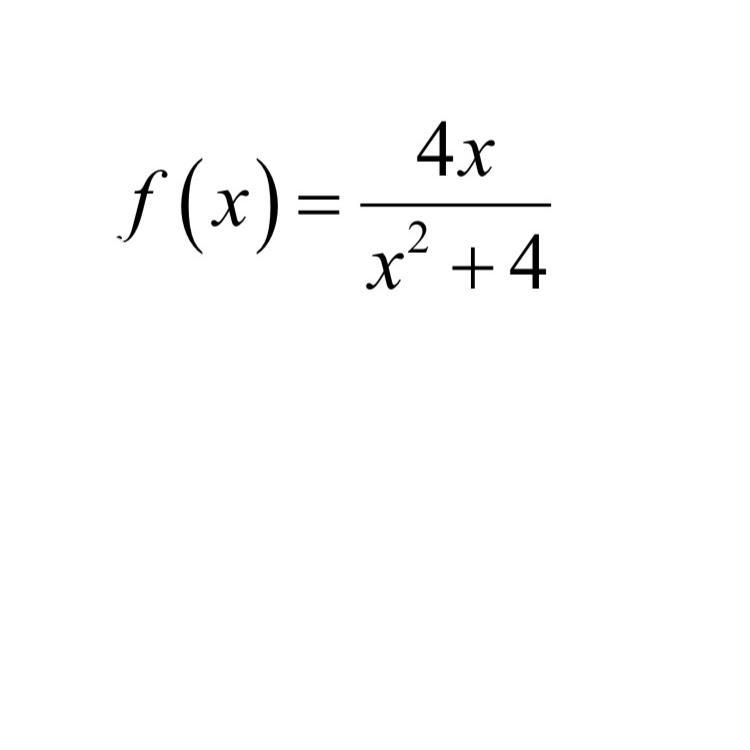
В данном случае
{-1/2}\frac{1}{x} = \frac{1}{2x \sqrt{\ln x}} 
2$ $- $ $144\dfrac{dl}{dx}$ $-$ $81$ $\,=\,$ $0$
Также, надеюсь, ясно, что 𝑓 из 𝑥 должно быть на один больше 𝑥 плюс один для нашего вопроса. Конечно, это в левой части уравнения. Возможно, немного сложнее понять, что такое 𝑓 из 𝑥 плюс ℎ.Ну, если 𝑓 из 𝑥 на один больше 𝑥 плюс один, то 𝑓 из 𝑥 плюс ℎ будет один больше 𝑥 плюс ℎ плюс один.
Итак, мы можем распознать первую дробь как единицу. Чтобы избавиться от другой дроби в числителе, мы умножаем на 𝑥 плюс один на 𝑥 плюс один. И снова упрощаем. Так что теперь наши знаменатели становятся намного сложнее, но наш числитель намного проще.А на самом деле его можно еще упростить.
Итак, это наш ответ.
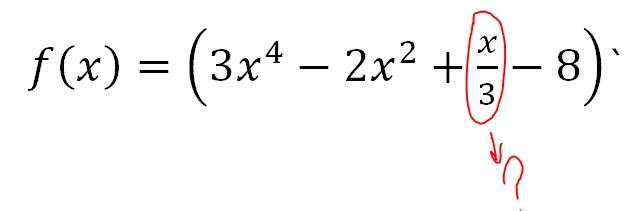
В виде формулы это: 
Мультипликативная обратная может быть обозначена как [f(x)] -1 .