ОглавлениеПредисловие ко второму русскому изданиюЧто такое математика? Глава I.  Натуральные числа Натуральные числа§ 1. Операции над целыми числами 2. Представление целых чисел с помощью письменных знаков (нумерация). 3. Арифметические действия в недесятичных системах счисления. § 2. Бесконечность системы натуральных чисел. Математическая индукция 2. Арифметическая прогрессия. 3. Геометрическая прогрессия. 4. Сумма n первых квадратов. 5. Одно важное неравенство. 6. Биномиальная теорема. 7. Дальнейшие замечания по поводу метода математической индукции. Дополнение к главе I Теория чисел 2. Распределение простых чисел. § 2. Сравнения 2. Теорема Ферма. 3. Квадратические вычеты. § 4. Алгоритм Евклида 2. Применение к основной теореме арифметики 3. Функция Эйлера. Еще раз о теореме Ферма. 4. Непрерывные дроби. Диофантовы уравнения Глава II. Математическая числовая система § 1. Рациональные числа 2. Возникновение надобности в рациональных числах внутри самой математики.  Принцип обобщения. Принцип обобщения.3. Геометрическое представление рациональных чисел. § 2. Несоизмеримые отрезки. Иррациональные числа, пределы 2. Десятичные дроби: конечные и бесконечные. 3. Пределы. Бесконечные геометрические прогрессии. 5. Общее определение иррациональных чисел посредством стягивающихся отрезков. 6. Иные методы определения иррациональных чисел.Декиндовы сечения. § 3. Замечания из области аналитической геометрии 2. Уравнения прямых и кривых линий. § 4. Математический анализ бесконечного 2. Счетность множества рациональных чисел и несчетность континуума. 3. «Кардинальные числа» Кантора. 4. Косвенный метод доказательства. 5. Парадоксы бесконечного. 6. Основания математики. § 5. Комплексные числа 2. Геометрическое представление комплексных чисел. 3. Формула Муавра и корни из единицы. § 6. Алгебраические и трансцендентные числа 2.  Теорема Лиувилля и конструирование трансцендентных чисел. Теорема Лиувилля и конструирование трансцендентных чисел.Дополнение к главе II. Алгебра множеств 2. Применение к математической логике. 3. Одно из применений к теории вероятностей. Глава III. Геометрические построения. Алгебра числовых полей Часть 1. Доказательства невозможности и алгебра 1. Построение полей и извлечение квадратных корней. 2. Правильные многоугольники. 3. Проблема Аполлония. § 2. Числа, допускающие построение, и числовые поля 2. Все числа, допускающие построение, — алгебраические. 2. Одна теорема о кубических уравнениях. 3. Трисекция угла. 4. Правильный семиугольник. 5. Замечания по поводу квадратуры круга. Часть 2. Различные методы выполнения построений § 4. Геометрические преобразования. Инверсия 2. Свойства инверсии. 3. Геометрическое построение обратных точек. 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.  § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля 1. Классическая конструкция, служащая для удвоения куба. 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды. 4. Шарнирные механизмы. Инверсоры Поселье и Гарта. § 6. Еще об одной инверсии и ее применениях 1. Инвариантность углов. Семейства окружностей. 2. Применение к проблеме Аполлония. 3. Повторные отражения. Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии 1. Классификация геометрических свойств. Инвариантность при преобразованиях. 2. Проективные преобразования. § 2. Основные понятия 1. Группа проективных преобразований. 2. Теорема Дезарга. § 3. Двойное отношение § 4. Параллельность и бесконечность 3. Двойное отношение с бесконечно удаленными элементами. § 5. Применения 2. Двумерное доказательство теоремы Дезарга.  3. Теорема Паскаля. 4. Теорема Брианшона. 5. Замечание по поводу двойственности. § 6. Аналитическое представление 2. Однородные координаты. Алгебраические основы двойственности. § 7. Задачи на построения с помощью одной линейки § 8. Конические сечения и квадрики 2. Проективные свойства конических сечений. 3. Конические сечения как «линейчатые кривые». 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений. § 9. Аксиоматика и неевклидова геометрия 2. Гиперболическая неевклидова геометрия. 3. Геометрия и реальность. 4. Модель Пуанкаре. 5. Эллиптическая, или риманова, геометрия. Приложение. Геометрия в пространствах более чем трех измерений Глава V. Топология § 1. Формула Эйлера для многогранников § 2. Топологические свойства фигур 2. Свойства связности. § 3. Другие примеры топологических теорем 2. Проблема четырех красок. 3. Понятие размерности. 4.  Теорема о неподвижной точке. Теорема о неподвижной точке.§ 4. Топологическая классификация поверхностей 2. Эйлерова характеристика поверхности. 3. Односторонние поверхности. Приложение 2. Теорема Жордана для случая многоугольников. 3. Основная теорема алгебры. Глава VI. Функции и пределы § 1. Независимое переменное и функция 2. Радианная мера углов. 3. График функции. Обратные функции. 4. Сложные функции. 5. Непрерывность. 6. Функции нескольких переменных. 7. Функции и преобразования. § 2. Пределы 2. Монотонные последовательности. 3. Число Эйлера e. 4. Число «пи» 5. Непрерывные дроби. § 3. Пределы при непрерывном приближении 2. Замечания по поводу понятия предела 4. Пределы при х -> оо. § 4. Точное определение непрерывности § 5. Две основные теоремы о непрерывных функциях 2. Доказательство теоремы Больцано. 3. Теорема Вейерштрасса об экстремальных значениях. 4. Теорема о последовательностях.  Компактные множества. Компактные множества.§ 6. Некоторые применения теоремы Больцано 2. Применение к одной механической проблеме. Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность 4. Разрывные функции как предел непрерывных. 5. Пределы при итерации. § 2. Пример, относящийся к непрерывности Глава VII. Максимумы и минимумы 2. Теорема Герона. Экстремальное свойство световых лучей. 3. Применения к задачам о треугольниках. 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства. 5. Экстремальные расстояния точки от данной кривой. § 2. Общий принцип, которому подчинены экстремальные задачи § 3. Стационарные точки и дифференциальное исчисление 2. Максимумы и минимумы функций нескольких переменных. Седловые точки. 3. Точки минимакса и топология. 4. Расстояние точки от поверхности. § 4. Треугольник Шварца 4. Треугольники, образованные световыми лучами.  5. Замечания, касающиеся задач на отражение и эргодическое движение. § 5. Проблема Штейнера 2. Анализ возникающих альтернатив. 3. Дополнительная проблема. 4. Замечания и упражнения. 5. Обобщение: проблема уличной сети. § 6. Экстремумы и неравенства 1. Средние арифметическое и геометрическое двух положительных величин. 2. Обобщение на случай n переменных. 3. Метод наименьших квадратов. § 7. Существование экстремума. Принцип Дирихле 3. Экстремальные проблемы элементарного содержания. 4. Трудности, возникающие в более сложных случаях. § 8. Изопериметрическая проблема § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой 2. Вариационное исчисление. Принцип Ферма в оптике. 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли. 4. Геодезические линии на сфере. Минимаксы. § 11. Экспериментальные решения минимальных проблем.  x и функций lnx в виде пределов. x и функций lnx в виде пределов.5. Бесконечный ряд для логарифма. Вычисление логарифмов. § 7. Дифференциальные уравнения 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты. 3. Другие примеры. Простейшие колебания. 4. Закон движения Ньютона. Дополнение к главе VIII § 1. Вопросы принципиального порядка 3. Другие приложения понятия интеграла. Работа. Длина кривой. § 2. Порядки возрастания 2. Порядок возрастания ln(n!) § 3. Бесконечные ряды и бесконечные произведения 2. Формула Эйлера cos x + i sin x = exp(ix). 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения. § 4. Доказательство теоремы о простых числах на основе статистического метода Приложение. Дополнительные замечания, задачи и упражнения Аналитическая геометрия Геометрические построения Проективная и неевклидова геометрия Топология Функции, пределы, непрерывность Максимумы и минимумы Дифференциальное и интегральное исчисления Техника интегрирования Рекомендуемая литература |
Скорость как производная.
 Производная от координаты по времени есть скорость. x'(t)=v(t) Физический смысл производной. Некоторые применения производной в физике
Производная от координаты по времени есть скорость. x'(t)=v(t) Физический смысл производной. Некоторые применения производной в физикеПроцедура, которую мы только что выполнили, настолько часто встречается в математике, что для величин ε и х было придумано специальное обозначение: ε обозначается как ∆t, а х – как ∆s. Величина ∆t означает «небольшой добавок к t», причем подразумевается, что этот добавок можно делать меньше. Значок ∆ ни в коем случае не означает умножение на какую-то величину, точно так же как sin θ не означает s·i·n·0. Это просто некоторый добавок ко времени, причем значок ∆ напоминает нам о его особом характере. Ну, а если ∆ не множитель, то его нельзя сократить в отношении ∆s/∆t. Это все равно, что в выражении sin θ/sin 2θ сократить все буквы и получить 1/2. В этих новых обозначениях скорость равна пределу отношения ∆s/∆t при ∆t, стремящемся к нулю, т. е.
Это по существу формула (8.3), но теперь яснее видно, что здесь все изменяется, а, кроме того, она напоминает, какие именно величины изменяются.
Существует еще один закон, который выполняется с хорошей точностью. Он гласит: изменение расстояния равно скорости, умноженной на интервал времени, за которое это изменение произошло, т. е. ∆s = υ∆t. Это правило строго справедливо только тогда, когда скорость не изменяется в течение интервала ∆t, а это, вообще говоря, происходит, только когда ∆t достаточно мало. В таких случаях обычно пишут ds = υdt, где под dt подразумевают интервал времени ∆t при условии, что он сколь угодно мал. Если интервал ∆t достаточно велик, то скорость за это время может измениться и выражение ∆s = υ∆t будет уже приближенным. Однако если мы пишем dt, то при этом подразумевается, что интервал времени неограниченно мал и в этом смысле выражение ds = υdt точное. В новых обозначениях выражение (8.5) имеет вид
Величина ds/dt называется «производной s по t» (такое название напоминает о том, что изменяется), а сложный процесс нахождения производной называется, кроме того; дифференцированием. Если же ds и dt появляются отдельно, а не в виде отношения ds/dt, то они носят названия дифференциалов. Чтобы получше познакомить вас с новой терминологией, скажу еще, что в предыдущем параграфе мы нашли производную от функции 5t 2 , или просто производную от 5t 2 . Она оказалась равной 10t. Когда вы больше привыкнете к новым словам, вам станет более понятна сама мысль. Для тренировки давайте найдем производную более сложной функции. Рассмотрим выражение s = At 3 + Bt + С, которое может описывать движение точки. Буквы А, В, С, так же как и в обычном квадратном уравнении, обозначают постоянные числа. Нам нужно найти скорость движения, описываемого этой формулой в любой момент времени t. Рассмотрим для этого момент t + ∆t, причем к s прибавится некоторая добавка ∆s, и найдем, как выражается ∆s через ∆t. Поскольку
Чтобы получше познакомить вас с новой терминологией, скажу еще, что в предыдущем параграфе мы нашли производную от функции 5t 2 , или просто производную от 5t 2 . Она оказалась равной 10t. Когда вы больше привыкнете к новым словам, вам станет более понятна сама мысль. Для тренировки давайте найдем производную более сложной функции. Рассмотрим выражение s = At 3 + Bt + С, которое может описывать движение точки. Буквы А, В, С, так же как и в обычном квадратном уравнении, обозначают постоянные числа. Нам нужно найти скорость движения, описываемого этой формулой в любой момент времени t. Рассмотрим для этого момент t + ∆t, причем к s прибавится некоторая добавка ∆s, и найдем, как выражается ∆s через ∆t. Поскольку
Но нам нужна не сама величина ∆s, а отношение ∆s/∆t. После деления на ∆t получим выражение
которое после устремления ∆t к нулю превратится в
В этом состоит процесс взятия производной, или дифференцирования функций. На самом деле он несколько легче, чем это кажется на первый взгляд. Заметьте, что если в разложениях, подобных предыдущим, встречаются члены, пропорциональные (∆t) 2 или (∆t) 3 или еще более высоким степеням, то их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в конце мы будем ∆t устремлять к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять, а что сразу отбрасывать. Существует много правил и формул для дифференцирования различных видов функций. Их можно либо запомнить, либо пользоваться специальными таблицами. Небольшой список таких правил приводится в табл. 8.3.
Заметьте, что если в разложениях, подобных предыдущим, встречаются члены, пропорциональные (∆t) 2 или (∆t) 3 или еще более высоким степеням, то их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в конце мы будем ∆t устремлять к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять, а что сразу отбрасывать. Существует много правил и формул для дифференцирования различных видов функций. Их можно либо запомнить, либо пользоваться специальными таблицами. Небольшой список таких правил приводится в табл. 8.3.
Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.
Во-первых, меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами вроде таких:
Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:
производная функции x(t) обозначается | ||
(читается ¾дэ икс по дэ тэ¿).
Остановимся подробнее на смысле обозначения (29 ). Математик понимает его двояко либо как предел:
либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.
Физик, не скованный требованиями математической строгости, понимает обозначение (29 ) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (30 ) с устраивающей нас точностью.
И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло. Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.
Давайте вернёмся к исходному примеру (26 ) и посчитаем производную координаты, а заодно посмотрим на совместное использование обозначений (28 ) и (29 ):
x(t) = 1 + 12t 3t2 ) x(t) =dt d (1 + 12t 3t2 ) = 12 6t:
(Символ дифференцирования dt d перед скобкой это всё равно что штрих сверху за скобкой в прежних обозначениях.)
Обратите внимание, что вычисленная производная координаты оказалась равна скорости тела (27 ). Это не случайное совпадение, и нам нужно обсудить его более подробно.
2.1 Производная координаты
Прежде всего заметим, что скорость в (27 ) может быть как положительной, так и отрицательной. А именно, скорость положительна при t 2.
Как это понимать? Очень просто: мы имеем дело не с абсолютной величиной скорости, а с проекцией vx вектора скорости на ось X. Поэтому вместо (27 ) правильнее было бы написать:
vx = 12 6t: |
Если вы забыли, что такое проекция вектора на ось, то прочитайте соответствующий раздел статьи ¾Векторы в физике
¿. Здесь мы напомним лишь, что знак проекции vx
отражает связь направления скорости и направления оси X:
Здесь мы напомним лишь, что знак проекции vx
отражает связь направления скорости и направления оси X:
vx > 0 , тело движется в направлении оси X ; vx
(Например, если vx = 3 м/с, то это означает, что тело движется со скоростью 3 м/с в сторону, противоположную оси X.)
Поэтому в нашем примере (31 ) мы имеем следующую картину движения: при t 2 тело, разгоняясь, движется в отрицательном направлении оси X.
Допустим, что скорость тела по абсолютной величине равна v. Возможны два случая направления движения.
1. Если тело движется в положительном направлении оси X, то малое изменение координаты dx положительно и равно пути, проходимому телом за время dt. Поэтому
x = dx dt = v:
2. Если тело движется в отрицательном направлении оси X, то dx
x = dx dt = v:
Заметим теперь, что в первом случае vx = v, а во втором случае vx = v. Тем самым оба случая объединяются в одну формулу:
x = vx ; |
и мы приходим к важнейшему факту: производная координаты тела равна проекции скорости тела на данную ось.
Легко видеть, что работает признак возрастания (убывания) функции. А именно:
x > 0) vx > 0) тело двигается в направлении оси X) координата x увеличивается; x
2.2 Ускорение
Скорость тела характеризует быстроту изменения его координаты. Но скорость также может меняться медленнее или быстрее. Характеристикой быстроты изменения скорости служит физическая величина, называемая ускорением.
Пусть, например, скорость автомобиля при равномерном разгоне увеличилась с v0 = 2 м/с до v = 14 м/с за время t = 3 с. Ускорение автомобиля вычисляется по формуле:
v v0 | ||||||||
и в данном случае оказывается равно: | ||||||||
Таким образом, за одну секунду скорость автомобиля увеличивается на 4 м/с.
А чему равно ускорение, если скорость, наоборот, уменьшилась с v0 = 14 м/с до v = 2 м/с за то же время t = 3 c? Тогда по формуле (33 ) получаем:
За одну секунду, как видим, скорость уменьшается на 4 м/с.
Можно ли говорить об ускорении, если скорость меняется неравномерно? Конечно, можно, но только это будет мгновенное ускорение, которое также зависит от времени. Схема рассуждений вам уже хорошо знакома: в формуле (33 ) вместо промежутка времени t берём малый промежуток dt, вместо разности v v0 берём приращение dv скорости за время dt, и в результате получаем:
Таким образом, получается, что ускорение это производная скорости.
Формула (34
), однако, не описывает все ситуации, которые возникают в механике. Например, при равномерном движении по окружности скорость тела не меняется по модулю, и в соответствии с (34
) мы должны были бы получить a = v = 0. Но вы прекрасно знаете, что ускорение у тела имеется, оно направлено к центру окружности и называется центростремительным. Поэтому формула (34
) нуждается в некоторой модификации.
Поэтому формула (34
) нуждается в некоторой модификации.
Cвязана эта модификация с тем, что ускорение на самом деле является вектором. Оказывается, вектор ускорения показывает направление изменения скорости тела. Что это означает, мы сейчас выясним на простых примерах.
Пусть тело движется вдоль оси X. Давайте рассмотрим два случая направления ускорения: по оси X и против оси X соответственно.
1. Вектор ускорения ~a сонаправлен с осью X (рис. 18 ). Проекция ускорения на ось X положительна: ax > 0.
Рис. 18. ax > 0
В данном случае скорость изменяется в положительном направлении оси X. А именно:
Если тело движется вправо (vx > 0), то оно разгоняется: скорость тела по модулю увеличивается. Проекция скорости vx при этом также увеличивается.
Если тело движется влево (vx
Таким образом, если ax > 0, то проекция скорости vx возрастает вне зависимости от того,
в каком направлении движется тело.
2.
Вектор ускорения ~a направлен противоположно оси X (рис. 19
). Проекция ускорения на ось X отрицательна: ax
19
). Проекция ускорения на ось X отрицательна: ax
Рис. 19. ax
В данном случае скорость изменяется в отрицательном направлении оси X. А именно:
Если тело движется вправо (vx > 0), то оно тормозит: скорость тела по модулю уменьшается. Проекция скорости vx при этом также уменьшается.
Если тело движется влево (vx
Таким образом, если ax
Обнаруженная в этих примерах связь знака проекции ускорения ax с возрастанием (убыванием) проекции скорости vx приводит нас к нужной модификации формулы (34 ):
Пример. Ещё раз вернёмся к примеру (26 ):
x = 1 + 12t 3t2
(координата измеряется в метрах, время в секундах). Последовательно дифференцируя два раза, получаем:
vx = x = 12 6t;
ax = vx = 6:
Как видим, ускорение постоянно по модулю и равно 6 м/с2 . Направлено ускорение в сторону, противоположную оси X.
Приведённый пример есть случай равноускоренного движения, при котором модуль и направление ускорения неизменны (или, короче говоря, ~a = const).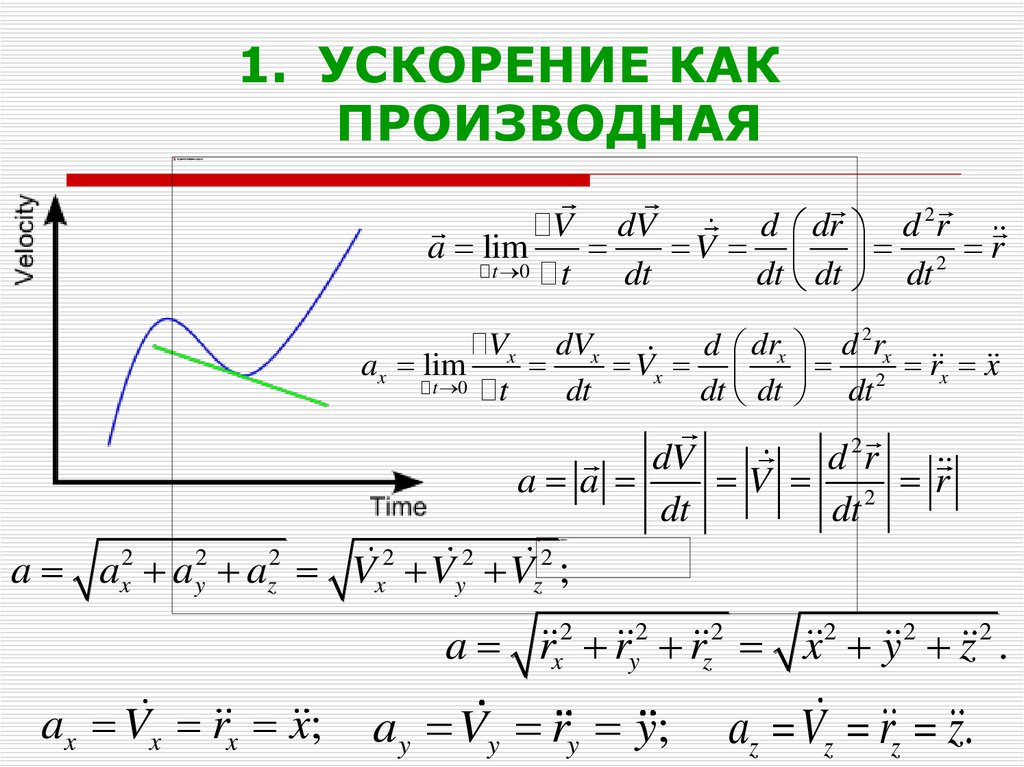 Равноускоренное движение один из важнейших и часто встречающихся видов движения в механике.
Равноускоренное движение один из важнейших и часто встречающихся видов движения в механике.
Из данного примера нетрудно понять, что при равноускоренном движении проекция скорости является линейной функцией времени, а координата квадратичной функцией.
Пример. Рассмотрим более экзотический случай:
x = 2 + 3t 4t2 + 5t3 .
Производная от координаты по времени есть скорость. x”(t)=v(t) Физический смысл производной
Производная от скорости по времени или вторая производная от координаты по времени есть ускорение. a(t)=v “(t)=x””(t)
Точка движется по координатной прямой согласно закону x(t)= t²+t+2, где x(t) – координата точки в момент времени t (время измеряется в секундах, расстояние в метрах). В какой момент времени скорость точки будет равна 5 м/с? Решение: Скорость точки в момент времени t есть производная от координаты по времени. Т. к. v(t) = x”(t) = 2t+1 и v = 5 м / с, то 2t +1= 5 t=2 Ответ: 2.
При торможении маховик за t секунд поворачивается на угол φ (t)= 6 t- t² радиан. Найдите угловую скорость ω вращения маховика в момент времени t=1с. (φ (t)- угол в радианах, ω(t)- скорость в рад/с, t- время в секундах). Решение: ω (t) = φ “(t) ω (t) = 6 – 2t t = 1 c. ω (1) = 6 – 2 × 1 = 4 рад/с Ответ:4.
Найдите угловую скорость ω вращения маховика в момент времени t=1с. (φ (t)- угол в радианах, ω(t)- скорость в рад/с, t- время в секундах). Решение: ω (t) = φ “(t) ω (t) = 6 – 2t t = 1 c. ω (1) = 6 – 2 × 1 = 4 рад/с Ответ:4.
При движении тела по прямой его скорость v(t) по закону v(t)=15+8 t -3t² (t – время движения тела в секундах).Каким будет ускорение тела (в м/с²) через секунду после начала движения? Решение: v(t)=15+8t-3t² a(t)=v”(t) a(t)=8-6t t=1 a(1)=2 м / с ² Ответ: 2.
Применение производной в физических задачах. Заряд, проходящий через поперечное сечение проводника, вычисляется по формуле q(t)=2t 2 -5t. Найти силу тока при t=5c. Решение: i(t)=q”(t) i(t)=4t-5 t=5 i(5)=15 А. Ответ:15.
При движении тела по прямой расстояние s(t) от начальной точки М изменяется по закону s(t)=t 4 -4t 3 -12t +8 (t- время в секундах). Каким будет ускорение тела (в м/с 2) через 3 секунды? Решение. a(t)=v “(t)=s””(t). Найдем v(t)=s”(t)=(t 4 -4t 3 -12t +8)” =4t 3 -12t a(t)=v “(t)= s””(t)= (4t 3 -12t 2 -12)” =12t 2 -24t, a(3)=12× ×3=108-72=36м/с 2. Ответ. 36.
Ответ. 36.
Иногда в задаче B9 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» B9.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=x\left(t \right)$, то $v$ мы можем посчитать следующим образом:
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. {2}}=0\]
{2}}=0\]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
кинематика – Терминология для производной скорости по времени (не скорости)
Существует ли какая-либо стандартная терминология для производной величины скорости по времени (пригодная для использования в исчислении первого года обучения)? Слово «ускорение» в его техническом смысле — это именно то, что я ищу , а не ; это производная от самой скорости, но мне нужна производная от ее величины, скорости.
Это полезная концепция, потому что она соответствует разговорный смысл слова «ускорение»; если эта величина положительна, то объект ускоряется (ускоряется), если отрицательна, то замедляется (тормозит), а если равна нулю, то ничего не делает (хотя может менять направление). Как $ v $ иногда используется для величины вектора скорости $ \boldsymbol v $, так $ a $ иногда используется для величины, которую я ищу, но обратите внимание, что $ a = \mathrm d v / \mathrm d t $ равно , а не величине вектора ускорения $ \boldsymbol a = \mathrm d \boldsymbol v / \mathrm d t $. (В конце концов, $ a $ может быть отрицательным.) 92 \boldsymbol N = a \boldsymbol T + \omega v \boldsymbol N $, где $ \boldsymbol T = \boldsymbol v / v $ — единичный вектор в направлении движения (поэтому член $ a \boldsymbol T $ равен аналогично размерности $\pm a$ в $1$), $\boldsymbol N$ — единичный вектор в направлении кривизны, $\kappa$ — величина кривизны, $\omega = \kappa v$ — угловой скорость. (В размерностях $3$ угловая скорость относительно центра соприкасающейся окружности равна $ \boldsymbol \omega = \omega \boldsymbol B $, где $ \boldsymbol B = \boldsymbol T \times \boldsymbol N $ — единичный бинормальный вектор , но угловая скорость имеет смысл в любом количестве измерений.
Как $ v $ иногда используется для величины вектора скорости $ \boldsymbol v $, так $ a $ иногда используется для величины, которую я ищу, но обратите внимание, что $ a = \mathrm d v / \mathrm d t $ равно , а не величине вектора ускорения $ \boldsymbol a = \mathrm d \boldsymbol v / \mathrm d t $. (В конце концов, $ a $ может быть отрицательным.) 92 \boldsymbol N = a \boldsymbol T + \omega v \boldsymbol N $, где $ \boldsymbol T = \boldsymbol v / v $ — единичный вектор в направлении движения (поэтому член $ a \boldsymbol T $ равен аналогично размерности $\pm a$ в $1$), $\boldsymbol N$ — единичный вектор в направлении кривизны, $\kappa$ — величина кривизны, $\omega = \kappa v$ — угловой скорость. (В размерностях $3$ угловая скорость относительно центра соприкасающейся окружности равна $ \boldsymbol \omega = \omega \boldsymbol B $, где $ \boldsymbol B = \boldsymbol T \times \boldsymbol N $ — единичный бинормальный вектор , но угловая скорость имеет смысл в любом количестве измерений. ) Так что это, безусловно, полезная концепция для анализа ускорения, в частности, разбивая ускорение на изменение скорости и изменение направления. 92 = \omega v $), что является не столько термином, сколько его определением, но оно также не очень хорошо работает в измерении $1$.
) Так что это, безусловно, полезная концепция для анализа ускорения, в частности, разбивая ускорение на изменение скорости и изменение направления. 92 = \omega v $), что является не столько термином, сколько его определением, но оно также не очень хорошо работает в измерении $1$.
Итак, есть ли для этого стандартный термин? Если люди думают, что какой-либо из терминов, связанных с векторами, является достаточно стандартным, чтобы я мог с невозмутимым видом сказать своим студентам, изучающим исчисление с одной переменной: «Термин для производной скорости по времени — это «скалярное ускорение»; в следующем году вы узнаете, что означает «скаляр», а пока это просто технический жаргон.›, тогда я буду использовать его. Или, если для этого есть другой стандартный термин, о котором я не слышал, я буду использовать его. Если нет, то я буду придерживаться «разговорного ускорения», хотя это явно 9xf(x)dx$ — плохая запись, которая может привести к ошибкам и путаница.)
Важное применение этого принципа происходит, когда мы
интересует положение объекта в момент времени $t$ (скажем, на
$x$-ось) и мы знаем ее положение в момент времени $\ds t_0$. ta(u)du.
$$
92.$$
$\квадрат$
ta(u)du.
$$
92.$$
$\квадрат$
Напомним, что интеграл функции скорости дает чистого расстояния пройдено, то есть водоизмещение. Если вы хотите узнать всего пройденное расстояние, вы должны найти, где функция скорости пересекает ось $t$, интегрируем отдельно по интервалам времени, когда $v(t)$ положительна, а когда $v(t)$ отрицательна, складываем абсолютную значения различных интегралов. Например, если предмет брошен прямо вверх на 19{3/2} {1\over \pi}\left({1\over2}+\sin(\pi t)\right)\,dt\Bigr|\cr &={1\over \pi}\left( {7\over 12}+{1\over \pi}\cos(7\pi/6)+{1\over \пи}\справа)+ {1\более \pi}\Bigl|{3\более 4}-{7\более 12} +{1\over\pi}\cos(7\pi/6)\Bigr|\cr &={1\over \pi}\left( {7\over 12}+{1\over \pi}{\sqrt3\over2}+{1\over \пи}\справа)+ {1\более \pi}\Bigl|{3\более 4}-{7\более 12} +{1\over \pi}{\sqrt3\over2}.\Bigr| \приблизительно 0,409 \hbox{метров}\cr }$$ $\квадрат$
Для каждой функции скорости найти как чистое расстояние, так и полное расстояние, пройденное за указанный интервал времени (график $v(t)$ до определить, когда он положительный, а когда отрицательный):
Пример 8. 2.1 $v=\cos(\pi t)$, $0\le t\le 2.5$
(отвечать)
2.1 $v=\cos(\pi t)$, $0\le t\le 2.5$
(отвечать)
Пример 8.2.2 $v=-9.8t+49$, $0\le t\le 10$ (отвечать)
Пример 8.2.3 $v=3(t-3)(t-1)$, $0\le t\le 5$ (отвечать)
Пример 8.2.4 $v=\sin(\pi t/3)-t$, $0\le t\le 1$ (отвечать)
Пример 8.2.5 Объект выстреливается вверх с уровня земли с начальным скорость 2 метра в секунду; подчиняется только силе сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на что он падает на землю. (отвечать)
Пример 8.2.6 Объект выстреливается вверх с уровня земли с начальным скорость 3 метра в секунду; подчиняется только силе сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на что он падает на землю. (отвечать)
Пример 8.2.7 Объект выстреливается вверх с уровня земли с начальным
скорость 100 метров в секунду; подчиняется только силе
сила тяжести (отсутствие сопротивления воздуха). Найдите его максимальную высоту и время на
что он падает на землю.
