Производная сложная формулы: Производные сложных функций, основные формулы и примеры решений

2

формулы, значение, как писать функции

Производная функции – одно из фундаментальных понятий в математике, без понимания которого становится невозможным решение большинства математических и физических задач. Что же это такое?

Производная функции — краткое описание, суть

Если совсем просто, то:

Производная – это скорость изменения функции в данной точке.

Выражаясь математическим языком, это предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Формула:

 

Она понимается в двух смыслах: геометрическом и физическом.

Геометрический смысл: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

 

Физический смысл: производная пути по времени равна скорости прямолинейного движения.

Таким образом, значение скорости в определённый момент времени t₀ определяется по формуле:

 

Вычисление производной называется дифференцированием. Обратный процесс – интегрированием.

Основные правила нахождения производных

Дифференцирование строится на следующих правилах.

Правило №1: производная от произведения числа на функцию равна

(c * f (x))’ = c * f’ (x),

где с – любое число.

Правило №2: производная от суммы функций равна

(f (x) + g (x))’ = f ‘ (x) + g’ (x).

Правило №3: производная от разности функций равна

(f (x) – g (x))’ = f ‘ (x) – g’ (x).

Правило №4: производная от произведения двух функций равна

(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x).

Правило №5: производная от дроби равна

 

Существует и так называемая сложная функция (композиция функции) вида f (g(x)). В данном случае f (x) считается внешней функцией, g (x) – внутренней.

Правило дифференцирования сложной функции

Производная сложной функции вычисляется по формуле:

[ f (g (x))]’ = f ‘ (g (x)) g’ (x).

Пример нахождения

Задача: продифференцировать (x+2)¹⁰. Обозначим её как u=x+2.

Решение: так как (x¹⁰)’=10x⁹,

то ((x+2) ¹⁰)’=(u¹⁰)’=10u⁹⋅u’=10(x+2) ⁹⋅1=10(x+2) ⁹.

Ответ: 10(x+2) ⁹.

Логарифмическая производная

Логарифмическая производная — это производная от натурального логарифма функции.

Вычисляется по формуле:

 

Часто применяется для упрощения дифференцирования некоторых функций.

Пример поиска производной

Пусть y = y(x).

Для удобства прологарифмируем данную функцию:

ln y = ln y(x).

Теперь вычислим производную по правилу дифференцирования сложной функции:

 

Из этого следует, что

 

Тогда ответ:

 

Производная обратной функции

Теорема: для дифференцируемой функции с производной, не равной нулю, производная обратной функции равная обратной величине производной данной функции.

Общая формула:

 

Формулы и пример решения

Производные обратных тригонометрических функций:

 

Задача: продифференцировать y=x²-7lnx.

Решение: находим по формуле

 

отсюда

 

Производная функции, заданной параметрически

Пусть функция задана параметрическим уравнением:

 

Тогда производная равна:

 

Формулировка, решение примеров

Задача: продифференцировать функцию.

 

Решение: (при записи производной всегда необходимо писать t в нижнем индексе)

 

Подставляем в формулу:

 

Ответ:

 

В ответе составляется система, в которой кроме полученной производной необходимо писать х = t – 4.

Производная неявной функции

Если функция у = у(х) задана уравнением F (x; y(x)) = 0 то говорят, что она задана неявно.

Теоретическое обоснование

Для нахождения производной неявной функции нужно:

1. Продифференцировать обе части уравнения по независимой переменной х предполагая, что у – это дифференцируемая по х функция.
2. Решить полученное уравнение относительно производной у’ (х).

Решение в примерах

Задача: решить функцию , заданную неявно:

 

Решение:

1) перенесём 3у -1 в левую часть и дифференцируем обе части равенства

 

Получим

 

Считая, что у – это функция от х, находим производную как от сложной функции:

 

Тогда

 

Для заданной функции имеем:

 

2) Решаем полученное уравнение относительно у’:

 

Ответ:

 

Полная таблица производных

Приводим табличную форму, которая существенно облегчает вычисления:

 

Формул из этого списка достаточно для дифференцирования любой элементарной функции. 2}\] \(\bullet\) Производная сложной функции: \[\big(h(f(x))\big)’=h’_f(f)\cdot f’_x(x)\]

 

Факт 3.
\(\bullet\) Если \(y=f(x)\) – некоторая функция, то касательная к ней в точке с абсциссой \(x_0\) имеет вид: \[y=f(x_0)+f'(x_0)\cdot (x-x_0)\] \(\bullet\) Следовательно, \(k=f'(x_0)=\mathrm{tg}\,\alpha\) – тангенс угла наклона касательной к положительному направлению оси \(Ox\), он же угловой коэффициент касательной, если ее уравнение записать как \(y=kx+b\).

 

Факт 4.
\(\bullet\) Если \(f'(x)>0\) на \((a;b)\), то \(f(x)\) возрастает на \((a;b)\).
\(\bullet\) Если \(f'(x)<0\) на \((a;b)\), то \(f(x)\) убывает на \((a;b)\).
\(\bullet\) Если \(f'(x_0)=0\) и в точке \(x_0\) производная меняет свой знак, то \(x_0\) — функции \(f(x)\):

— если производная меняет знак с “\(-\)” на “\(+\)” (считая слева направо), то \(x_0\) — ;
— если производная меняет знак с “\(+\)” на “\(-\)” (считая слева направо), то \(x_0\) — . b f(x)\,dx=F(b)-F(a)\] \(\bullet\) Тогда \(F(b)-F(a)\) равно площади закрашенной фигуры \(ABCD\), называемой криволинейной трапецией:

 

Производная сложной функции

Содержание:

Производная сложной функции

Производная сложной функции. Теперь вы можете установить очень важное правило в практическом открытии производных. Это позволяет вычислить производную комплексной функции, если известна производная компонентной функции. V. предположим: 1) функция u = cp (q) является производной в некоторой точке x0, где u’x-y ’(x0), 2) Функция y = f (u) является соответствующей точкой a,, = p(x; 0) производной uy = f ’(u). в свою очередь, комплексная функция y = f (y (x)) в ранее упомянутой точке x9 также имеет производную, равную произведению производной функции f (u) и p (*). ??( * )) Г=Л (?) (

))•? ’（•）*） Или, короче говоря、 Ух = ух * » х.

Он вычисляется по аргументу (а не по x) со значением u = y (0) для этого аргумента. Людмила Фирмаль

• Чтобы доказать, дайте x произвольное приращение Ax; пусть Di-соответствующее приращение функции u =(p (x), и, наконец, пусть Au-приращение функции y = f (x), вызванное приращением Di. Использование соотношения (2а) включение X и перепишем его в виде Дю = г а-о-| А * Д» А то. Да. Это хорошая вещь.* (Зависит от DS и стремится к нулю).Разделите его на D *для каждого члена、 Если Ax стремится к нулю, то Dee также стремится к нулю[88, 2°], и, как известно, величина a в зависимости от Di также стремится к нулю. Поэтому существуют ограничения НШ а * о А то. д * Ди•Я Ву-у-у *и» А * * 0 ЛДГ Это и есть искомая производная Замечания. Полезность аннотации N°82 здесь влияет на значение a at Ddr = 0.

As пока Ax является независимой переменной приращения, вы можете предположить, что это * ) Символ / U (y (d0)) подчеркивает, что он означает дифференциальную функцию f (u) Ненулевое, но когда bx заменяется приращением функции q = cp (x), даже Dogφ0 больше не квалифицируется как diφ0.

-; год= ; 1 + P 6)г = 8Вт топор; ых = АУ-ах•(а) ’ = а•уд Ач (V; 12, 3). Один 1 + х * 8) затем Один Ух = Один ’Т’ * Один 。 Один $ ЕКА-гггг： («И (В; 3） * ЕС, Т * ’(5-Х), (У:8） Вот несколько примеров применения всех правил. 11) в форме упражнений рассмотрим также задачу о производной закона*экспоненциального выражения y = u *(w> 0).

Для сложных функций, полученных в результате некоторой суперпозиции, они исчерпываются последовательным применением правила V. Людмила Фирмаль

• Где u и V-функции x с производной от V ’в данной точке. Если мы получим логарифм y = a’ °、 1p. u=: 1 / * 1pi. (4 )） Таким образом, выражение для y можно переписать в виде y = e * ’} pa, и уже ясно, что производная от y существует. Сам расчет легче выполнить, уравнивая производные по отношению к x с обеих сторон уравнения (4).при этом используйте правила V и III(напомним, что u, y и y являются функциями x).Возьми./ = y ’* 1n и 4-V -• Y «и Откуда Г = г(^ Или замените выражение вместо y на、 (5） ？ =И 1зи). Эта формула основана на Лейбница и И. Она была учреждена Бернулли. Например для y = d: 5SH * к y’X = x81n x + cos x * 1n.

Смотрите также:

Решение задач по математическому анализу

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

Методическая разработка по Математике на тему “Понятие производной, правила и формулы нахождения производной”

МИНИСТЕРСТВО ТРАНСПОРТА РФ

Федеральное агентство морского и речного транспорта

ИНСТИТУТ ВОДНОГО ТРАНСПОРТА ИМЕНИ Г.Я. СЕДОВА

– филиал Федерального государственного бюджетного образовательного учреждения высшего образования

«Государственный морской университет имени адмирала Ф.Ф. Ушакова»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ПО ДИСЦИПЛИНЕ

«Математика»

Тема «Понятие производной, правила и формулы нахождения производной»

Выполнила:

преподаватель Колледжа

ИВТ им. Г.Я. Седова

Люшнина И.И.

г.Ростов-на-Дону

2018 год

ВВЕДЕНИЕ

Методическая разработка предназначена для изучения математики алгоритмическими методами.

В данной методичке систематизируются понятия предела и непрерывности функций в точке. Повторяются и углубляются знания по данной теме.

Теоретический материал разработки изложен в доступной форме, приводится достаточное количество примеров, что способствует лучшему усвоению учебного материала.

Методическая разработка предназначена для курсантов колледжа Института водного транспорта имени Г.Я. Седова.

1. Непрерывность основных элементарных функций

Функция y = f(x) называется непрерывной при данном значении х, если бесконечно малому приращению х соответствует бесконечно малое приращение y, то есть если (рис. 1).

Рис.1

2. Производная функции, её геометрический и механический смысл

Производной функции f(x) называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.

(1)

1) Геометрический смысл производной

Пусть функция y = f(x), x  [c; d] дифференцируема в точке x = a  ]c; d[ (рис.2)

Рис.2

Производная функции y = f(x) в точке x = a равна угловому коэффициенту касательной, проведенной к графику данной функции в его точке с абсциссой x = a.

(2)

2) Механический смысл производной

Пусть материальная точка движется прямолинейно по закону S = f (t).

Мгновенная скорость прямолинейного движения материальной точки в момент времени t есть производная пути по времени.

V(t) = S(t) (3)

3. Формулы дифференцирования основных элементарных функций

Заданы функции u=f(x), v=(x), c = const.

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

Пример 1. Найти производную функции

Решение:

Пример 2. Найти производную функции

Решение:

Пример 3. Найти производную функции y = x²(4x – 1)

Решение:

y = 4x³ – x²,

y = 12x² – 2x

Пример 4. Найти производную функции

Решение:

Пример 5. Найти производную функции

Решение:

Пример 6. Написать уравнение касательной к кривой y = 1 – 2x² в точке ее А с абсциссой, равной 2.

Решение:

Найдем ординату точки А:

y = 1 – 22² = 1 – 8 = – 7

Искомая касательная находится среди прямых, определяемых уравнением y – y₁ = k(x – x₁).

Определим угловой коэффициент касательной по формуле k = y

k = (1 – 2x²) = -4x

k = -42 = -8

Искомое уравнение примет вид:

y + 7 = -8(x-2)

y + 7 = -8x + 16

8x + y – 9 = 0

4. Сложная функция. Производная сложной функции

Сложной функцией называется функция вида y = F(f(x)). Её можно записать: y = F(u), где u = f(x).

Пример 1. Функция y = sin5x есть сложная, составленная из функций y=sin u, где u = 5x.

Пример 2. Функция – сложная; , где u = 1 – x³.

Пример 3. Функция – сложная; y=ln u, где u = cos x

Производная сложной функции находится по формуле:

(2)

Производная сложной функции равна произведению производных функций, её составляющих.

Например:

Пример 4. Найти производную функции y = sin 5x

Решение:

Обозначим u = 5x. Получим y = sin u

По формуле (2) имеем

Пример 5. Найти производную функции

Решение:

Обозначим . Получим y = sin u.

По формуле (2) находим

Пример 6. Найти производную функции .

Решение:

5. Производные высших порядков. Механический смысл второй производной

Производные высших порядков

Задана функция y = f(x), которая определена на интервале ]a;b[. Пусть в каждой точке этого интервала она имеет производную .

Производной второго порядка функции y = f(x) называется производная от её первой производной: .

Производной третьего порядка функции y= f(x) называется производная от её второй производной: .

Производной n-го порядка функции y = f(x) называется производная от её (n-1)-й производной: .

Пример 1. Найти производную третьего порядка функции y=4x³ – 3x² + 1.

Решение:

Механический смысл второй производной

Материальная точка движется прямолинейно по закону S=f(t), тогда скорость движения равна (формула (3)). Если движение неравномерное, то скорость v(t) также есть функция времени. Поэтому можно рассмотреть скорость изменения скорости движения, т.е. ускорение

Ускорение прямолинейно движущейся материальной точки равно производной скорости во времени или второй производной пути по времени.

Пример 2. Точка движется неравномерно прямолинейно по закону

S = 2t³ – 4t + 1. Найти величину ускорения в конце третьей секунды.

Решение:

Поставим в значение t = 3:

м/с².

6. Производные обратных тригонометрических функций

Функции y=f(x) и x=F(y) называются взаимно обратными, если:

1. D(f) = E(F)

2. E(f) = D(F)

3. y₀ = f(x₀) x₀ = F(y₀),

где D – область определения;

E – область значений функции.

Теорема.

Если производная заданной монотонной функции существует и не равна нулю, то производная обратной функции x(y) определяется по формуле:

Доказательство.

Составим отношение . Так как функции y=f(x) и x=F(y) непрерывны, то при x0; y0. Поэтому ;

, (1)

что и требовалось доказать.

Пример 1. Найти производную функции

Решение:

; x = sin y – взаимно обратные функции

Итак, (2)

Пример 2. Найти производную функции y = arccos x.

Решение:

и x=cos y – взаимно обратные функции.

(3)

Пример 3. Найти производную функции y = arctg x.

Решение:

;

(4)

Пример 4. Найти производную функции y = arcctg x.

Решение:

;

(5)

ЛИТЕРАТУРА

Основная

1. Башмаков М.И. Математика. – М.: Издательский центр «Академия», 2014.

2. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов (на базе средней школы). – М.: Наука, 1980.

3. Выгодский М.Я. Справочник по элементарной мате­матике. – М.: АСТ, 2006.

4. Алгебра и начало анализа, I и П ч. /Под редакцией Г.Н.Яковлева. – М.: Наука, 1978.

5. Геометрия, ч. I. /Под редакцией Г.Н.Яковлева. – М.: Наука, 1977.

6. Яремчук Ф.П., Руденко П.А. Алгебра и элементарные функции (справочник). – Киев: Наукова думка, 1976.

Дополнительная

1. Курс математики для техникумов, ч. I и П. /Под ред. Н.М.Матвеева. – М.: Наука, 1977.

2. Зайцев И.Л. Элементы высшей математики для техникумов.- М.: Наука, 1972.

3. Калкин Р.А. Алгебра и элементарные функции. – М.: Наука, 1969.

Дифференцирование. Основные правила дифференцирования. Формулы производных основных элементарных функций

Часть 2. Дифференцирование.

Контрольная работа №2. Цель данной контрольной работы помочь студентам в овладении навыками нахождения производных функций одной переменной. Операция нахождения производной называется дифференцированием функции. Производная функции y=f(x) обозначается либо , либо .

Сформулируем основные правила дифференцирования и приведем формулы производных основных элементарных функций:

1.                                                           10.

2.                                        11.

3.                                         12. 

4.                                                   13. 

5.                                                   14. 

6.                                                 15.

7.                                               16.

8.                                                 17. 

9.  

Отметим, что полезно запомнить частный случай формулы 5

.

Большое  значение для вычисления производных различных функций имеет следующая теорема:

Теорема о производной сложной функции. Пусть  где , тогда

или эта формула записывается в виде

Так, например, если , то формулы  5, 6, 10, 13 принимают вид:

5а.  

6а. 

10а.

13а.

Задача 1a.

Основная цель данной задачи проверить навыки дифференцирования сложной функции. Рассмотрим примеры.

Найти , где  .

Приведем подробное решение этой задачи. (Мы предполагаем, что студенты к моменту выполнения контрольной работы изучили таблицу производных основных элементарных функций.)

Функция имеет вид , где .

Воспользуемся формулой производной сложной функции. Тогда

, где . Функция u(x) имеет вид , где . Получаем  .  Функция  имеет вид , где  . Получаем ==

=.

Теперь можем записать окончательный ответ

Ответ: =.

Отметим, что нет необходимости (если вы уверенно владеете техникой дифференцирования) при выполнении контрольной работы столь подробно проводить все выкладки.

Задача. Найти , где .

Используя последовательно формулы 10, 5, 6, 4 и 5, а также правило дифференцирования сложной функции, получим:

=

=.

Отметим, что все производные по промежуточным аргументам можно выполнять в уме и непосредственно давать готовый ответ.

Задача. Найти , где .

Ответ: .

Задача 1б.

Целью данной задачи является закрепления навыков нахождения производной произведения функций.

Задача. Найти , если .

Используя формулу производной произведения, получаем

.

Далее воспользуемся формулой производной сложной функции. Получаем

.

Вычисляя табличные производные, получаем ответ.

Ответ:

.

Как мы уже упоминали ранее, при уверенном владении техникой дифференцирования в контрольной работе нет необходимости приводить столь подробное описание.

Рассмотрим еще один пример.

Задача. Найти , если

Сначала воспользуемся формулой производной произведения, а затем формулой дифференцирования сложной функции:

==

=

=.

Приведем решение еще одного примера, где все промежуточные рассуждения проведены в уме.

Задача. Найти , если .

=

Задача 1в.

Целью данной задачи является закрепления навыков нахождения производной частного.

Задача. Найти , если .

Вычисление сложных процентов

Показывает, как составляются формулы, с примерами!

С помощью сложных процентов мы вычисляем проценты за первый период, добавляем их к общей сумме, и , затем вычисляем проценты за следующий период и так далее …, например:

Создайте формулу

Давайте для начала посмотрим на первый год:

1000 долларов США + (1000 долларов США × 10%) = 1100 долларов США

Переставить можно так:

Итак, прибавление 10% процентов равносильно умножению на 1.10

(Примечание: процентная ставка была преобразована в десятичную дробь путем деления на 100: 10% = 10/100 = 0,10 , прочтите Проценты, чтобы узнать больше.)

И эта формула работает для любого года:

• В следующем году мы могли бы сделать так: 1100 долларов × 1,10 = 1210 долларов
• А затем перейдите к следующему году: 1210 долларов × 1,10 = 1331 доллар
• и т. д …

Так работает:

Фактически, мы могли бы сразу перейти к 5-му году обучения, если мы умножим

5 на :

1000 $ × 1.10 × 1,10 × 1,10 × 1,10 × 1,10 = 1 610,51 долл. США

Но проще записать серию умножений, используя экспоненты (или степени), например:

Формула

Мы использовали реальный пример, но давайте сделаем его более общим к , используя буквы вместо чисел , например:

(Сравните это с расчетом выше: PV = 1000 долларов США, r = 0,10, n = 5 и FV = 1610,51 доллара США)

• Если процентная ставка годовая, тогда n – это количество лет
• При ежемесячной процентной ставке n – количество месяцев
• и так далее

Примеры

Как насчет примеров…
… что, если бы заем пошел на 15 лет ? … просто измените значение “n”:

. .. а если бы ссуда была на 5 лет, а процентная ставка всего 6%? Здесь:

(обратите внимание, что это 1,06 , а не 1,6)

Четыре формулы

Итак, основная формула для сложного процента:

FV = PV (1 + r) ⁿ

• FV = будущая стоимость,
• PV = текущая стоимость,
• r = процентная ставка (в виде десятичного числа) и
• n = количество периодов

С этим мы можем рассчитать будущую стоимость FV , когда мы знаем текущую стоимость PV , процентную ставку r и количество периодов n

И мы можем переставить эту формулу, чтобы найти FV, процентную ставку или количество периодов, когда мы знаем три других.

Вот все четыре фурмулы:

FV = PV (1 + r) n		Найдите будущую стоимость , когда мы знаем текущую стоимость, процентную ставку и количество периодов.
PV = FV / (1 + r) n		Найдите текущую стоимость , когда мы знаем будущую стоимость, процентную ставку и количество периодов.
r = (FV / PV) 1 / n – 1		Найдите процентную ставку , когда мы знаем текущую стоимость, будущую стоимость и количество периодов.
п = лн (FV / PV) пер. (1 + р)		Найдите количество периодов , когда мы знаем текущую стоимость, будущую стоимость и процентную ставку

Как мы получили эти три формулы? Читать дальше!

Расчет текущей стоимости

Пример: Сэм хочет достичь 2000 долларов через 5 лет под 10% годовых.

С чего Сэму следует начать?

Другими словами, мы знаем будущую стоимость, а хотим знать текущую стоимость .

Мы можем просто изменить формулу так, чтобы она подходила … разделив обе стороны на (1 + r) ⁿ , мы получим:

Начать с: FV = PV (1 + r) ⁿ

Поменять местами стороны: PV (1 + r) ⁿ = FV

Разделите обе стороны на (1 + r) ⁿ : PV = FV (1 + р) ⁿ

Итак, теперь мы можем вычислить ответ:

Пример (продолжение):

ЛС = 2000 долл. США / (1 + 0.10) ⁵ = 2000 долларов / 1,6 1051 = 1241,84 доллара

Итак, Сэм должен начать с 1241,84 доллара

Работает так:

Другой пример: Сколько вам нужно инвестировать сейчас, чтобы получить 10 000 долларов через 10 лет под 8% процентной ставки?

PV = 10000 долларов США / (1 + 0,08) ¹⁰ = 10000 долларов США / 2,1589 = 4631,93 долларов США

Итак, 4631,93 долларов США , инвестированные под 8% в течение 10 лет, вырастают до 10 000 долларов США

Расчет процентной ставки

Пример: у Сэма всего 1000 долларов, и он хочет, чтобы через 5 лет они выросли до 2000 долларов.

Какую процентную ставку следует искать Сэму?

Нам нужна перестановка первой формулы, чтобы вычислить это:

Начать с: FV = PV (1 + r) ⁿ

Поменять местами стороны: PV (1 + r) ⁿ = FV

Разделим обе стороны на PV: (1 + r) ⁿ = FV PV

Извлечь корень n-й степени из обеих частей: 1 + r = ( FV PV ) ^{1 / п}

Вычтем 1 с обеих сторон: r = ( FV PV ) ^{1 / п} – 1

(Примечание: чтобы понять шаг «извлечения корня n-й степени», прочтите «Дробные экспоненты»)

Результат:

r = (FV / PV) ^{1 / n} – 1

Теперь у нас есть формула, достаточно “вставить” значения, чтобы получить результат:

Пример (продолжение):

r = (2000 долл. США / 1000 долл. США) ^1/5 – 1
= (2) ^0.2 – 1
= 1,1487 – 1
= 0,1487

И 0,1487 в процентах составляет 14,87%

Итак, Сэму нужно 14,87% , чтобы превратить 1000 долларов в 2000 долларов за 5 лет.

Другой пример: Какая процентная ставка нужна, чтобы превратить 1000 долларов в 5000 долларов через 20 лет?

r = (5000 долларов / 1000 долларов) ^1/20 – 1 = (5) ^0,05 – 1 = 1,0838 – 1 = 0,0838

И 0.0838 в процентах составляет 8,38% . Таким образом, через 20 лет 8,38% превратят 1000 долларов в 5000 долларов.

Определение количества периодов

Пример: Сэм может получить процентную ставку только 10%. Сколько лет понадобится Сэму, чтобы получить 2000 долларов?

Когда мы хотим знать, сколько периодов потребуется, чтобы превратить 1000 долларов в 2000 долларов при 10% -ной процентной ставке, мы можем изменить основную формулу.

Но для этого нам нужно использовать функцию натурального логарифма ln () .

Начать с: FV = PV (1 + r) ⁿ

Поменять местами стороны: PV (1 + r) ⁿ = FV

Разделите обе стороны на PV: (1 + r) ⁿ = FV / PV

Разделим обе части на ln (1 + r): n = лн ( FV / PV) пер. (1 + р)

(Примечание: чтобы понять шаг «использовать логарифмы», прочтите «Работа с экспонентами и логарифмами»).

Теперь давайте “подставим” значения:

Пример (продолжение):

n = ln (2000 долларов / 1000 долларов) / ln (1 + 0.10) = ln (2) / ln (1,10) = 0,69315 / 0,09531 = 7,27

Magic! Потребуется 7,27 года , чтобы превратить 1000 долларов в 2000 долларов под 10% годовых.

Бедному Сэму придется ждать больше 7 лет.

Другой пример: Сколько лет, чтобы превратить 1000 долларов в 10 000 долларов при 5% -ной процентной ставке?

n = ln (10 000 долл. США / 1000 долл. США) / ln (1 + 0,05) = ln (10) / ln (1,05) = 2,3026 / 0,04879 = 47,19

47 лет! Но речь идет о 10-кратном увеличении, всего под 5% годовых.

Заключение

Знание того, как выводятся и используются формулы, облегчает их запоминание и использование в различных ситуациях.

Сложные проценты | Формулы, вывод и решенные примеры

Сложные проценты – это проценты, накопленные на основную сумму долга и проценты вместе за определенный период времени. Проценты, накопленные по основной сумме долга за определенный период времени, также учитываются по основной сумме долга.Кроме того, начисление процентов за следующий период времени производится по накопленной основной стоимости. Сложные проценты – это новый метод начисления процентов, используемый для всех финансовых и деловых операций по всему миру. Сила начисления сложных процентов можно легко понять, если мы наблюдаем за значениями сложных процентов, накопленных за последовательные периоды времени.

Сумма денег в 100 долларов, вложенная в течение определенного периода времени по ставке 10%, даст простой процент в размере 10, 10, 10 долларов …за последовательные периоды времени в 1 год, но даст сложные проценты в размере 10, 11, 12,1, 13,31 доллара … Давайте разберемся с этим и расчетами сложных процентов в нижеследующем содержании.

Что подразумевается под сложным процентом?

Сложные проценты – это проценты, выплачиваемые как на основную сумму долга, так и на проценты, начисляемые через определенные промежутки времени. Через регулярные промежутки времени накопленные проценты объединяются с существующей основной суммой, а затем проценты рассчитываются для новой основной суммы.Новая основная сумма равна сумме Первоначальной основной суммы и накопленных к настоящему времени процентов.

Сложные проценты = Проценты на основную сумму + Сложные проценты с регулярными интервалами

Сложный процент рассчитывается через определенные промежутки времени, например, ежегодно (ежегодно), раз в полгода, ежеквартально, ежемесячно и т. Д .; Это похоже на то, что повторное инвестирование процентного дохода от инвестиций заставляет деньги со временем расти быстрее! Это именно то, что сложные проценты делают с деньгами. Банки или любая финансовая организация рассчитывают сумму только на основе сложных процентов.

Формула сложных процентов

Сложные проценты рассчитываются после расчета общей суммы за период времени на основе процентной ставки и первоначальной основной суммы. Для начального основного долга P, годовой процентной ставки r, периода времени t в годах, частоты начисления процентов ежегодно n формула расчета суммы выглядит следующим образом.

Вышеупомянутая формула представляет общую сумму на конец периода времени и включает начисленные проценты и основную сумму.Кроме того, мы можем рассчитать сложные проценты, вычтя основную сумму из этой суммы. Формула расчета сложных процентов следующая

В приведенном выше выражении

• P – основная сумма
• r – процентная ставка (десятичная)
• n – частота или нет. раз в год начисляются проценты
• т – общий срок владения.

Следует отметить, что приведенная выше формула является общей формулой, когда основная сумма начисляется n раз в год. Если данная основная сумма начисляется ежегодно, сумма после периода времени по процентной ставке, r, определяется как:

A = P (1 + r / 100) ^t , и C.I. будет: P (1 + r / 100) ^t – P.

Выведение формулы сложного процента

Формула сложных процентов может быть получена из формулы простых процентов. Формула для простого процента представляет собой произведение основной суммы, периода времени и процентной ставки (SI = ptr / 100).Прежде чем приступить к выводу формулы сложного процента, давайте поймем основное различие между простым процентом и вычислением сложного процента. Основная сумма долга остается неизменной в течение определенного периода времени для простых вычислений через Интернет, но для расчета сложных процентов проценты добавляются к основной сумме для расчета сложных процентов.

Деривация:

Пусть основная сумма – P, а процентная ставка – r. В конце первого периода начисления сложных процентов простой процент по основной сумме составляет P × r / 100. Следовательно, сумма равна P + P × r / 100 = P (1 + r / 100). Сумма принимается в качестве основной на второй расчетный период.

В конце второго периода начисления сложных процентов простой процент по основной сумме составляет: P (1 + r / 100) × r / 100, и, следовательно, сумма составляет: P (1 + r / 100) × r / 100 + П (1 + r / 100) × r / 100 = P (1 + r / 100) ² .

Продолжая таким же образом для n периодов начисления сложных процентов, сумма в конце n ^{-го периода начисления процентов} будет A = P (1 + r / 100) ⁿ .

Из приведенных выше формул и вычислений можно заметить, что сложный процент совпадает с простым процентом для первого интервала. Но с течением времени наблюдается заметная разница в доходности.

Стоимость простых процентов для каждого года одинакова, поскольку основная сумма, на которую они рассчитываются, является постоянной. Но сложный процент меняется и увеличивается с годами. Потому что основная сумма, по которой рассчитывается сложный процент, увеличивается. Основная сумма за конкретный год равна сумме первоначальной основной стоимости и накопленных процентов за прошлые годы.

Например, сумма в размере 10 000 долларов США вносится по ставке 10%. В приведенной ниже таблице объясняется разница между расчетом простых процентов и сложных процентов по этой основной сумме:

Расчет простых процентов (r = 10%)	Расчет сложных процентов (r = 10%)
Для 1 st год: P = 10 000 Время = 1 год Проценты = 1000	Для 1 st год: P = 10 000 Время = 1 год Проценты = 1000
Для 2 nd год: P = 10 000 Время = 1 год Проценты = 1000	Для 2 nd год: P = 11000 Время = 1 год Проценты = 1100
Для 3 ряд год: P = 10 000 Время = 1 год Проценты = 1000	Для 3 ряд год: п = 12100 Время = 1 год Проценты = 1210
Для 4 -го год: P = 10 000 Время = 1 год Проценты = 1000	Для 4 -го год: п = 13310 Время = 1 год Проценты = 1331
Для 5 -го год: P = 10 000 Время = 1 год Проценты = 1000	Для 5 -го год: п = 14641 Время = 1 год Проценты = 1464. 1
Всего простой процент = 5000	Общая сумма процентов = 6105,1
Общая сумма = 1000 + 5000 = 6000	Общая сумма = 1000 + 6105,1 = 7105,1

Формула сложных процентов для разных периодов времени

Сложные проценты для данной основной суммы могут быть рассчитаны для разных периодов времени с использованием разных формул.

Формула сложных процентов – полугодие

Проценты в случае сложных процентов варьируются в зависимости от периода начисления.Если период времени для начисления процентов составляет полугодие, проценты рассчитываются каждые шесть месяцев, а сумма начисляется дважды в год.

Формула для расчета сложных процентов при начислении основной суммы раз в полгода или раз в полгода имеет следующий вид:

Здесь сложный процент рассчитывается за полугодовой период, и, следовательно, ставка процента r делится на 2, а период времени удваивается. Формула для расчета суммы при начислении основной суммы раз в полгода или раз в полгода имеет следующий вид:

В приведенном выше выражении

• A – сумма на конец периода
• P – начальная основная стоимость, r – годовая процентная ставка
• t – период времени
• С.I. – это сложные проценты.

Формула сложных процентов – ежеквартально

Если период времени для начисления процентов – ежеквартальный, проценты начисляются за каждые три месяца, а сумма начисляется 4 раза в год. Формула для расчета сложных процентов при ежеквартальном начислении основной суммы имеет следующий вид:

Здесь сложный процент рассчитывается за квартальный период времени, и, следовательно, ставка процента r делится на 4, и период времени увеличивается в четыре раза.Формула для расчета суммы при ежеквартальном начислении основной суммы имеет следующий вид:

В приведенном выше выражении

• A – сумма на конец периода
• P – начальная основная стоимость, r – годовая процентная ставка
• t – период времени
• C. I. это сложные проценты.

Формула ежемесячных сложных процентов

Формула ежемесячных сложных процентов также известна как ежемесячные проценты i.е., n = 12. Общая сумма сложных процентов – это окончательная сумма без учета основной суммы. Формула ежемесячных сложных процентов выражается как:
CI = P (1 + r / 12) ^12t – P

Формула суточных сложных процентов

Если количество увеличивается ежедневно, это означает, что количество увеличивается 365 раз в год. т.е. n = 365. Формула суточных сложных процентов выражается как:
CI = P (1 + r / 365) ^365t – P

Важные примечания

1. Сложные проценты зависят от суммы, накопленной в конце предыдущего срока пребывания в должности, но не от первоначальной основной суммы.{4 n} \ end {формула}
2. При расчете сложных процентов процентная ставка и каждый временной период должны иметь одинаковую продолжительность.

Советы и хитрости

• Правило 72: Это быстрый способ узнать, сколько времени потребуется, чтобы ваши деньги удвоились. Время удвоения = 72 / процентная ставка
  Используя правило 72, мы можем найти количество лет, за которое ваши деньги удвоятся, просто разделив 72 на процентную ставку.Например, при комбинированной процентной ставке 8% ваши деньги удвоятся через 72 ÷ 8 = 9
.
• Срок действия процентной ставки определяется множеством различных терминов. Иногда его называют «за год», «за год» или «за год». Все это означает, что вы получите заданную процентную ставку в течение 1 года. Полугодовой – 6 месяцев. А ежеквартально – продолжительностью 3 месяца.

---

Часто задаваемые вопросы о сложных процентах

Как рассчитать сложный процент?

Формула, используемая для расчета сложных процентов: CI = P (1 + r / 100) ⁿ – P.Здесь в этой формуле рассчитывается сумма, а затем из нее вычитается основная сумма, чтобы получить значение сложных процентов.

В чем разница между простым и сложным процентом?

Простые проценты – это проценты, выплачиваемые только на основную сумму долга, тогда как сложные проценты – это проценты, выплачиваемые как на основную сумму долга, так и на проценты, начисляемые через регулярные промежутки времени.

Как рассчитать сумму с использованием сложных процентов?

Существует прямая формула расчета сложных процентов.А = P (1 + r / 100) ⁿ . Здесь нам нужно определить процентную ставку и временной интервал, за который рассчитывается сложный процент.

Как рассчитать сумму с использованием формулы сложного процента?

Существует общая формула сложных процентов для расчета сложных процентов, т. Е.
CI = Сумма – Основная сумма
где Amount = P (1 + r / 100) ^t . Подставляя заданные параметры, такие как P (основная сумма), r (процентная ставка) и t (время), можно легко вычислить.

Что такое формула ежемесячного сложного процента?

Формула ежемесячных сложных процентов составляет
CI = P (1 + (r / 12)) ^12t – P.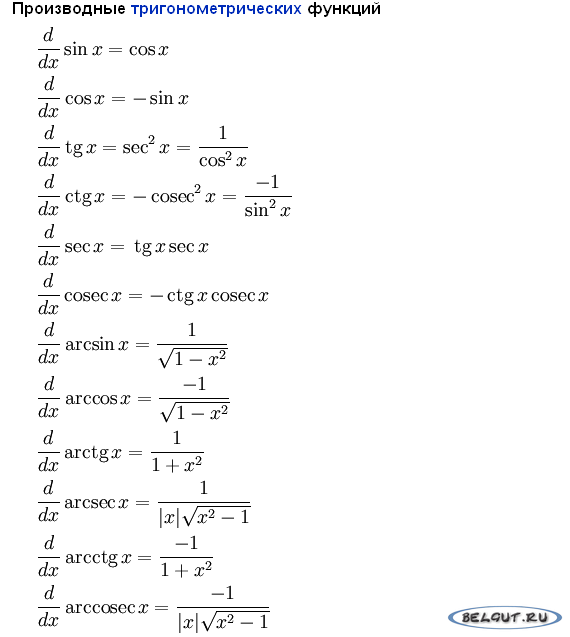 Где, P – основная сумма, r – процентная ставка в десятичной форме, n = 12 (это означает, что сумма, составляющая 12 раз в год ), t – время.

Что такое формула ежедневного сложного процента?

Формула суточных сложных процентов составляет
A = P (1 + r / 365) ^{365 t} , где P – основная сумма, r – процентная ставка в десятичной форме, n = 365 (это означает, что сумма начисляется 365 раз в год), а t – время.

Что такое формула сложных процентов на будущую стоимость?

Формула сложных процентов будущей стоимости выражается как FV = PV (1 + r / n) ^{n t} . Здесь PV = текущая стоимость (начальные инвестиции), r = процентная ставка, n = количество раз, когда сумма увеличивается, и t = время в годах.

Ежедневное начисление процентов лучше, чем ежемесячное?

Ежедневно начисляемые проценты имеют 365 циклов начисления сложных процентов в год. Он будет приносить больше денег по сравнению с ежемесячным начислением сложных процентов, которое имеет только 12 циклов начисления сложных процентов в год.

Каковы основные недостатки сложных процентов?

Если мы также пропустим оплату на день, к концу срока пребывания в должности это может привести к огромным убыткам. Расчет процентов предназначен для следующего цикла и для более высокого значения. Сложные проценты на самом деле предназначены для помощи кредиторам, но не заемщикам.

Как сложный процент зависит от периода времени?

Сложный процент зависит от временного интервала начисления процентов. Временной интервал для начисления процентов может быть днем, неделей, месяцем, кварталом, полугодием.Для более короткого периода расчета чистые накопленные сложные проценты выше.

Насколько сложный процент больше, чем простой процент?

Сложные проценты могут превышать простые проценты. Величина сложных процентов меняется и увеличивается в течение последовательных периодов времени. Первоначальный основной капитал в размере 100 долларов, вложенный в течение определенного периода времени, даст простые проценты в размере 10 долларов, 10 долларов, 10% . .. за последовательные периоды времени в 1 год, но даст сложные проценты в размере 10, 11, 12 долларов.1, $ 13.31 ….. Таким образом, сложные проценты больше, чем простые проценты. Только для первого года или для первого цикла расчета значения сложных и простых процентов равны.

Может ли сложный процент быть больше основного долга?

Сложный процент может превышать основную сумму долга. Величина сложных процентов меняется и увеличивается в течение последовательных периодов времени. Первоначальный основной капитал в размере 100 долларов, вложенный в течение определенного периода времени, даст сложные проценты в размере 10, 11, 12 долларов.1, 13,31 доллара …. за последовательные периоды времени продолжительностью 1 год каждый. Таким образом, сложный процент увеличивается с течением времени и может превышать первоначальную основную стоимость.

Как рассчитать сложный процент за полгода?

Формула расчета сложных процентов за полгода: CI = p (1 + {r / 2} / 100) ^2t . – p. Здесь в этой формуле «A» – окончательная сумма, «p» – основная сумма, а «t» – время в годах. В формуле мы видим, что процентная ставка уменьшается вдвое, а время удваивается, чтобы учесть расчет сложных процентов за полгода.

Какая информация требуется для расчета сложных процентов?

Для расчета сложных процентов нам необходимо знать основную сумму, процентную ставку и период времени. Также нам необходимо знать временной интервал, за который будет рассчитываться процент.

Что такое сложные проценты?

Единицы сложных процентов – это денежная единица, которая совпадает с единицей, используемой для определения основной суммы долга. Если основная сумма выражена в долларах или иенах, сложные проценты также будут в долларах или иенах.

---

рабочих примеров

рабочих примеров

15.2.2 Рабочие примеры

Пример 15.4. Формулы сложных процентов
Предположим, мы должны были инвестировать основную сумму P в счет, на котором начисляется процентная ставка r каждый год (это годовая процентная ставка). Это означает, что в конце первого год, вы заработаете дополнительные деньги RP. Таким образом, через год на вашей учетной записи A появится ценить

Если бы вы оставили деньги на счете на второй год, вы бы заработали проценты, а не только на основную сумму долга, но также и на проценты, заработанные вами в первый год:

Что, если вы позволите деньгам приносить проценты в течение третьего года? У вас будет всего

Немного поработав, мы можем показать, что, как правило, через n лет при годовой процентной ставке r ваш принципал P будет заработать в общей сложности

Теперь предположим, что наши проценты рассчитываются не ежегодно, а вычисляются ежемесячно, на основе АПР.Это означает, что фактическая ежемесячная процентная ставка составляет r ∕ 12 и что в течение одного года у нас есть 12 периодов начисления сложных процентов. Логика аналогична предыдущему случаю сообщит нам, что после t лет начисления сложных процентов ежемесячно по этой ставке мы будем имеют

На счету

долларов. Точно так же, если мы позволяем суммировать деньги n раз в год, мы будем иметь процентную ставку r ∕ n за каждый период и в общей сложности nt периодов начисления сложных процентов через t лет. Этот дает нам количество

Это, очевидно, экспоненциальная функция, но с основанием (1 + r ∕ n), а не естественная база эл.Однако они связаны. Подумайте, что произойдет, если мы вложим 1 доллар в 100% годовых за один год при разных периодах начисления сложных процентов, как показано в таблице ниже.

---

График	Количество периодов	14 Всего
1	2
Ежемесячно	12	2.61303529
Еженедельно	52	2.692596954
Ежедневно	365	2.714567482
Почасовая	8760	2.718126692
Каждую минуту	525600	2.718279243
Каждую секунду	31536000	2.718281781
Каждую десятую долю секунды	315360000	2.71828187
Каждую сотую долю секунды	3153600000	2.718281661

Обратите внимание, что количество денег продолжает расти, но не с той же скоростью. Фактически, это Кажется, что сумма, которую мы зарабатываем, приближается к фиксированной сумме.Математически это Было доказано, что это так, и что число, к которому оно приближается, является числом е:

Число e – это сумма денег, заработанная на счете после вложения 1 доллара. на один год под 100% процентную ставку, непрерывно начисляются.

Математики записывают этот факт в предельных обозначениях:

Теперь мы можем использовать этот факт для создания формулы для непрерывно начисленных процентов. Сначала мы введем новую переменную m так, чтобы n = r ⋅ m.Тогда у нас есть эквивалентное выражение для интерес, предоставленный

Таким образом, наша формула для суммы на счете с n периодами начисления сложных процентов изменится на по следующей формуле, если мы постоянно ее составляем:

Пример 15.5. Производные от экспоненциальных функций
Теперь, когда мы знаем о производных от логарифмических функций, мы можем легко использовать идею логарифмическая производная для определения производной экспоненциальной функции.Один из самых общие экспоненциальные функции, возникающие в деловом мире, связаны с будущей стоимостью инвестиции. Однако, чтобы добраться до этого, нам нужно развить идею составного интерес.

Итак, хотя нам потребовалось некоторое время, чтобы добраться туда, и мы пропустили несколько шагов, мы видим, что экспоненциальная функция тесно связана с идеей сложных процентов. Теперь мы можем спросить следующее. Предположим, вы вложили фиксированную сумму денег P под фиксированную процентную ставку r.Как быстро (в время) ваши деньги растут в цене?

Вопрос «насколько быстро» сразу напоминает нам об идее скорости изменения, Итак, мы знаем, что на самом деле говорим о производной от суммы денег в учетная запись. Итак, какова производная от суммы? Мы будем использовать наши знания логарифмической производные в помощь.Мы действительно хотим знать производную от A (t), но мы не знаем производная от экспоненты. Однако экспоненциальная функция и логарифмический функции являются обратными друг другу, поэтому формулу суммы можно переписать в качестве

, где мы использовали правила манипулирования логарифмами и тот факт, что ln (e) = 1. Теперь мы можно взять производную от каждой стороны этого уравнения, используя цепное правило:

Теперь произвести производную правой части несложно, поскольку это действительно линейная функция (обратите внимание, что ln (P) – постоянная; он не зависит от переменной t, относительно которой мы берем производная):

Теперь мы можем собрать все это вместе, поскольку мы сделали то же самое с обеими сторонами уравнение (а именно возьмем производную по t), так что они все равно равны каждому Другие.

Итак, истинная скорость увеличения стоимости вашего счета – это сумма r * exp (rt) долларов в год. Если вы оставите его на t = 10 лет со скоростью 2,5%, ваши деньги будут увеличиваться со скоростью A ′ (10) = 0,025 ⋅ P ⋅ exp (0,025 * 10) = 0,025 ⋅ P ⋅ exp (0,25) = 0,032P доллара в год. Если если вы изначально вложили 1000 долларов, это приведет к темпам роста около 32 долларов в год.

Пример 15.6. Производная экспоненциальной функции
Найти относительную скорость изменения функции g (r, t, P) = Pe ^rt относительно переменная r.Относительная скорость изменения – это просто скорость изменения, деленная на функцию сам, поэтому у нас есть относительная скорость изменения как (1 ∕ g) ⋅ (производная g по р).

= (Pe rt )		Определение относительной скорости изменения с использованием обозначение частной производной, поскольку есть несколько переменных в функции
= ⋅ P ⋅ (rt)		Производная от постоянной, умноженной на функцию
= ⋅ P ⋅ e rt ⋅ r		Производная экспоненциального правила И цепочки
= ⋅ r ⋅ g		Производная линейной функции
= r		Упрощение

Это означает, что относительная скорость изменения формулы для непрерывно процент просто равен самой процентной ставке.Чтобы понять, что это значит, подумайте о единицы скорости изменения относительно r: единицы доллара, разделенные на единицы процента. Когда мы разделите это на сумму (в долларах), и мы получим относительную скорость изменения, которая измеряется в 1 / (процентная ставка). Это относительная сумма, поэтому она похожа на процент. Таким образом, каждый фактический прирост на 1% в процентной ставке (с 1% до 2% или с 5,25% до 6,25%) увеличит значение на нашем счету фиксированная сумма основного долга, вложенная на фиксированный период времени в размере r%.

Пример 15.7. Применение маржинального анализа к бизнес-решениям
Группа аналитиков Koduck определила следующую информацию о вашем текущем уровень производства:

Предельные затраты (MC) = 2,25 доллара США за единицу
Предельный доход (MR) = – 1,15 долл. США / единица

Что это значит для Koduck?

Для начала отметим, что отрицательное значение маржинального дохода означает, что если вы увеличите производство на 1 единицу, ваш общий доход (цена * количество проданных) фактически снизится.(Это должно быть потому что вы уже наводнили рынок; в конце концов, сколько картинок водоплавающих птиц ты можешь продать в данном городе?) Тот факт, что предельная стоимость положительная, означает, что это будет стоить вам дороже сделать еще одну единицу товара. Таким образом, кажется, что увеличение текущего уровня производства не Будьте мудры: общая стоимость вырастет, а выручка упадет, что приведет к снижению прибыли. Нет один хочет этого. Фактически, нам, вероятно, следует сократить производство, чтобы увеличить прибыль! Если мы уменьшим производство, скажем, на 5 единиц, то можно ожидать, что выручка составит увеличивать:

Изменение выручки = MR * изменение производства = (- $ 1.15 / шт.) * (- 5 шт.) = 5,75 $.

В то же время это приведет к снижению стоимости:

Изменение затрат = MC * изменение производства = (2,25 доллара за единицу) * (- 5 единиц) = – 11,25 доллара.

Это приводит к общему изменению прибыли на 17 долларов! Это факт (который мы рассмотрим позже), что максимально возможная прибыль (= выручка – затраты) должна произойти, когда предельные затраты и предельный доход равны. Поскольку мы можем увеличить прибыль за счет снижения производства, мы должны производство большего количества единиц, чем необходимо для достижения максимальной прибыли.

Шпаргалка по производным

: Химия 130 Архив документов курса: Архив проектов и размещенных сайтов: Swain Library

Химия 130 архив документов курса

Руководство по созданию производных инструментов

Проконсультироваться Руководство по созданию производных финансовых инструментов чтобы помочь решить, какую производную делать.

Инструкции доступны в Интернете и в вашем курсе читатель. Для синтеза производных доступны как печатные, так и электронные ресурсы.Видеть Страница с библиографией по производным инструментам Свейна для списка ресурсов.

Ниже приведены методы поиска, которые можно использовать для поиска информации о физических свойствах и их обобщения. информация для вашей производной в CCD и в Beilstein Crossfire. Обратите внимание, что тип информация, собранная для соединений, значительно различается, поэтому вам может потребоваться несколько ресурсы и / или несколько различных стратегий поиска. Увидеть Лекция по поиску деривативов для обзора процесса и графического руководства по использованию CCD и Beilstein Crossfire для поиска производных.Ниже приводится краткое описание обычного поиска. методы, которые могут вам понадобиться в ПЗС-матрицах или в Beilstein Crossfire:

Сначала выполните поиск в комбинированном химическом словаре (CCD)

• Выполните поиск по номеру реестра CAS или химическому названию.
• Просмотр информации о деривативах в результатах поиска. Обратитесь к первоисточникам для получения обобщающей информации.
• Если производное, которое вы хотите создать, отсутствует в списке или если ваше родительское соединение указано как производное в CCD, выполните поиск по Байльштейну.

Выполните поиск в Beilstein, если вы не нашли нужную информацию в CCD

• Выполнить поиск по номеру реестра CAS и просмотреть производное поле в записи родительского соединения.
• Если вашего производного нет в списке, выполните поиск по химической реакции, указав вашего родителя. соединение в качестве реагента и ваше производное в качестве продукта.
• Если вы получили нулевой результат, пропустите реагент и повторите поиск.
• Если вы по-прежнему получаете нулевой результат, выполните поиск химического вещества в продукте или производном вы хотите сделать.Проконсультируйтесь с администраторами библиотеки или библиотекарями за помощью.

Подробные инструкции по поисковой стратегии для поиска деривативов

Сначала выполните поиск в комбинированном химическом словаре (CCD)

Поскольку CCD включает производные, содержащие общие функциональные группы, сначала проконсультируйтесь с CCD.

Найдите регистрационный номер CAS или химическое название вашего родительского соединения.

Если ваше родительское соединение указано в качестве основной записи в CCD (первое соединение занесено в протокол)

Определите, указана ли производная, которую вы хотите создать, в CCD.Если он указан, обратите внимание на физические свойства. Прочтите библиографию в конце записи. Ссылки могут быть аннотированы либо «производный», либо «синтезаторный». Возможно, вам придется обратиться к первоисточникам, чтобы узнать, какие производные перечисленные в определенном источнике.

Если ваше исходное соединение указано как производное в CCD

Выполните поиск по Байльштейну, если ваше исходное соединение указано как производное в CCD или найти дополнительную информацию о своем производном.

Выполните поиск в Beilstein, если вы не нашли нужную информацию в CCD

Beilstein содержит 8 миллионов соединений и 5 миллионов реакций и является наиболее полным источником для получения информации о производных финансовых инструментах. Однако, поскольку Байльштейн определяет химические производные более узко чем это сделано в Chem 130/132, необходимая вам информация может содержаться в записи о веществе производного вы хотите синтезировать.

Найдите номер в реестре CAS для неизвестного родительского соединения

Выполните поиск по номеру реестра CAS в Байльштейне. Поместите курсор в нижнем левом окне и введите RN = , за которым следует регистрационный номер CAS, сохраняя дефисы (например, RN = 50-00-0). Затем нажмите кнопку Начать поиск .

Просмотрите результаты , чтобы узнать, собрана ли / какая информация производные: перейдите в строку меню Просмотр . Если результаты включают более одного элемента, выберите Короткий дисплей для просмотра результатов. Дважды щелкните поле, содержащее интересующее вас соединение.Перейти к Просмотрите строку меню и выберите Все поля . Вернитесь в строку меню «Просмотр» и выберите FieldAvailability . Откроется небольшое окно со списком всех типов данных, собранных в этой записи. Щелкните один раз в По алфавиту по имени , а затем прокрутите список, чтобы увидеть, есть ли в нем производные инструменты. Если В списке производных финансовых инструментов дважды щелкните слово Производные инструменты , чтобы просмотреть информацию о производных финансовых инструментах. составлен.

Производные записи в производном поле : Химическое название, плавка точка или точка кипения, и ссылка на то, как синтезировать производное, обычно включается в каждый Производная запись.Одна и та же производная может быть указана более одного раза, если экспериментальные условия отличаются. Обратитесь к исходной ссылке для получения информации о том, как синтезировать производную. Проконсультируйтесь с библиотечным TA или Swain персонал, если вам нужна помощь в переводе литературных ссылок.

Запись о веществе в Байльштейне может быть очень длинной (например, 1000 страниц)! Так что вы необходимо определить формат отображения, чтобы он содержал только те поля, которые вы хотите распечатать. Кому создайте определяемый пользователем формат отображения, перейдите в строку меню Options и выберите Define Просмотр пользователя .Щелкните New , чтобы определить новое отображение. Затем нажмите Удалить все кнопку, если в окне с правой стороны есть что-либо в списке. Выделите и скопируйте Substance . и Библиографическая информация в окно с правой стороны экрана. Они содержат информация об идентификации вещества и ссылки на литературу для данных, представленных в других полях записи. Используйте кнопку Найти , чтобы найти папки, содержащие другие данные, которые вы хотите отобразить.Скопируйте выделенное поле в окно в правой части экрана. После определения всех полей, которые вы хотите для включения в формат отображения нажмите OK и затем сохраните формат отображения. Закройте Просмотры пользователей экрана. После того, как ваше пользовательское представление определено, следующим шагом будет выбор вашего пользовательского представления. Перейдите в строку меню View , прокрутите вниз до User View и выберите своего названного пользователя. Посмотреть. После загрузки пользовательского представления нажмите кнопку печати.

Если ваше производное не включено в запись родительского соединения, выполните поиск по химической реакции. путем извлечения как реагента (вашего родительского соединения), так и продукта (производного, который вы хотите получить)

В Beilstein Commander (начальный вид) дважды щелкните большое окно, чтобы перейти в структуру. Редактор. Перейдите в строку меню Options , выберите Molecule View , а для Atom View выберите C в качестве точки , чтобы случайно не наложить атомы на одну. Другая.Теперь используйте варианты кольца, атома и связи, чтобы нарисовать структуру. Удерживайте нажатой клавишу Shift при изменении атома или связи ценить. Если не указано иное, предполагается, что все открытые позиции насыщены водородом. (Если вы хотите разрешить дальнейшая замена в определенной позиции в структуре, щелкните атом в этой позиции и установите Стоимость бесплатных сайтов.)

Чтобы использовать предварительно нарисованные шаблоны, перейдите к команде Файл , выберите Шаблоны , выберите интересующий файл шаблона (например,грамм. Остатки для ярлыков), а затем щелкните значок шаблона то есть непосредственно слева от значков кольца (выглядит как небольшая сетка). Дважды щелкните элемент по выбору, чтобы использовать в структуре. Если вам нужно переориентировать структурный фрагмент, используйте Highlighter и Rotator (выглядит как круг) инструменты. Обратите внимание, что функциональные группы нарисованы в нейтральном состоянии (или без заряда) в Beilstein (например, NO ₂ – обе связи с кислородом являются двойными связями).

После того, как вы закончили рисовать свою структуру, перейдите в режим редактирования в строке меню и выберите Reaction .Используйте инструмент Highlighter Tool (инструмент под карандашом), чтобы нарисуйте рамку вокруг конструкции. Затем нажмите кнопку Продукт , чтобы обозначить структуру. как реагент или продукт реакции. Нажмите -> BC и нажмите Start кнопка.

Просмотр результатов в кратком формате. Дважды щелкните запись интерес. Прокрутите список реакций. Дважды щелкните гипертекстовые ссылки идентификатора реакции, чтобы увидеть реакцию детали, эл.грамм. реакция с использованием разных растворителей.

Если вы не получили результатов поиска по реакции, запустите его еще раз, но укажите только продукт.

Зайдите в Редактор структуры, выделите реагент и затем выберите Вырезать из Редактировать барное меню. Щелкните -> BC и нажмите кнопку Start , чтобы повторно запустить поиск. Другой поиск варианты поиска деривативов включают в себя поиск по структуре продукта, который вы хотите создать. Под Посмотреть в строке меню выберите Reaction View , а затем Substance as a Product .

Если вы проводите много времени в поисках производной или если все вышеперечисленные методы не работают, обратитесь за помощью.

Что такое производное в науке? – Mvorganizing.org

Что такое производное в науке?

В химии производное – это соединение, полученное из аналогичного соединения в результате химической реакции. Термин «структурный аналог» широко используется в органической химии. В биохимии это слово используется для обозначения соединений, которые, по крайней мере, теоретически могут быть образованы из соединения-предшественника.

Какая производная равна скорости?

Сводка

производная	терминология	означает
0	положение (смещение)	позиция
1	скорость	скорость изменения позиции
2	ускорение	скорость изменения скорости
3	рывок	скорость изменения ускорения

Что такое Gago по-английски?

Гаго.Гаго является потомком испанского слова gago, что означает «глупый», «глупый» или «невежественный». Он взаимозаменяем со связанными словами танга, (б) угок, «ботлог», (б) улол и бобо. По-испански gago означает «заика», но на тагальском оно полностью изменило свое значение.

Что такое формула дифференциации?

Некоторые из общих формул дифференцирования: Правило мощности: (d / dx) (xn) = nx. п-1. Производная константы a: (d / dx) (a) = 0. Производная константы, умноженная на функцию f: (d / dx) (a.

Что такое УФ-формула?

Правило произведения Это еще одна очень полезная формула: d (uv) = vdu + udv. dx dx dx. Это используется при различении продукта двух функций.

Что такое производная первого принципа?

Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная – это мера мгновенной скорости изменения, которая равна. f ′ (x) = lim ⁡ h → 0 f (x + h) – f (x) h.

Как отличить продвинутых учеников?

Определите их сильные стороны, а также те области, которые вам, возможно, придется решить, прежде чем ученики уйдут. Рассмотрите возможность группирования одаренных учеников хотя бы на часть школьного дня. План дифференциации. Подумайте о предварительных оценках, дополнительных мероприятиях и сжатии учебной программы.

Как вы различаете уроки?

Учителя, практикующие дифференциацию в классе, могут:

1. Уроки дизайна, основанные на стилях обучения учащихся.
2. Группируйте учащихся по общим интересам, теме или способностям для выполнения заданий.
3. Оцените успеваемость учащихся с помощью формирующего оценивания.
4. Управляйте классом, чтобы создать безопасную и благоприятную среду.

Что такое многоуровневые уроки?

Многоуровневые уроки – это уроки, которые имеют разные уровни деятельности, основанные на базе знаний учащегося. После определения уровня базовых навыков учащегося посредством предварительной оценки, учащимся даются задания (направленные на достижение той же цели или стандарта), требующие разного уровня глубины.

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

---

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

---

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

---

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Формула сложных процентов – определение, вывод формулы, приложения и проблемы с решениями

• Давайте узнаем, что такое сложные проценты. Сложные проценты определяются как проценты, начисленные на основную сумму долга и проценты, накопленные за предыдущий период времени.

• Сложные проценты отличаются от простых процентов.

• В простых процентах проценты не прибавляются к основной сумме при расчете процентов в течение следующего периода, в то время как в сложных процентах проценты добавляются к основной сумме для расчета процентов.

Сложные проценты (CI) = основная сумма (1 + ставка / 100) n – основная сумма

где P равно основной сумме, R равно процентной ставке, T равно времени (период)

[Изображение будет загружено в ближайшее время]

Еще немного о сложных процентах

Сначала мы поймем концепцию и что такое сложные проценты, а затем перейдем к формуле сложных процентов.Теперь проценты можно определить как сумму, которую мы рассчитываем на предоставленную нам основную сумму. Но в сложных процентах мы рассчитываем проценты на основную сумму и проценты, накопленные за предыдущий период.

По сути, сложные проценты – это проценты на проценты! Таким образом, в этом методе, вместо выплаты процентов, они реинвестируются и становятся частью основной суммы долга.

Как вы могли заметить в простых процентах, сумма процентов остается неизменной для каждого периода.В случае сложных процентов дело обстоит иначе. Поскольку предыдущая сумма процентов реинвестируется, размер процентов каждый год незначительно увеличивается. Вот почему у нас есть целая отдельная формула сложных процентов, чтобы помочь нам рассчитать сложные проценты за любой конкретный год.

Формула сложных процентов в математике:

Сумма = основная сумма (1 + ставка / 100) n

где P равно основной сумме, ставка равна ставке Проценты, n равно времени (Период)

Вывод формулы сложного процента

Чтобы лучше понять концепцию, давайте взглянем на вывод формулы сложного процента.В данном случае мы возьмем нашу основную сумму в рупии 1 / – и постепенно будем приближаться к годовой процентной ставке.

Год 1

• Процентная ставка по 1 рупии за 1 год равна r / 100 = i (предполагается)

• Процентная ставка после 1 года равна Pi

• FV (Окончательное значение) после года 1 равно P + Pi = P (1 + i)

год 2

год t

• Окончательное значение (сумма) после года «t» равно P (1 + i ) t

• Теперь подставляя фактические значения, мы получаем Окончательное значение равно (1 + R / 100) t

• CI = FV – P равно P (1 + R / 100) t – P

Это вывод по формуле сложного процента

Заявки на сложный процент

Вот некоторые из приложений, представляющих сложный процент:

1. Увеличение или уменьшение населения.

2. Рост бактерий.

3. Повышение стоимости предмета.

4. Амортизация стоимости объекта.

Теперь, когда у нас есть некоторая ясность в отношении концепции и значения сложных процентов и формулы сложных процентов в математике, давайте попробуем решить некоторые задачи сложных процентов с решениями, чтобы углубить наше понимание предмета.

Проблемы со сложными процентами с решениями

Вопрос 1) Было обнаружено, что количество бактерий определенного вида увеличивается со скоростью 5% в час.Каков будет рост бактерий через 3 часа, если изначально было 6000?

Решение) Поскольку популяция бактерий увеличивается со скоростью 5% в час,

Мы знаем формулу для расчета суммы, формулу сложных процентов в математике

Сумма = Основная сумма (1 + R / 100) n

Таким образом, население в конце 3 часов = 6000 (1 + 3/100) 3

= 6000 (1 + 0,03) 3 = 6000 (1,03) 3 = 6556,36 рупий

Вопрос 2) Г-н А решил открыть банковский счет и выбрал вариант сложного процента по ставке 10%.