Производная сложная онлайн: Дифференцирование функции, заданной неявно

Производная сложной функции – презентация онлайн

Похожие презентации:

Производная сложной функции

Производная сложной функции

Производная функции

Сложная функция. 10 класс

Производная сложной функции

Производная сложной функции

Производная сложной функции

Производная функции

Сложная функция

Обратная функция

1. Производная сложной функции

2. Функция h есть сложная функция, составленная из функций g и f, если h(x)=g(f(x))

f(x) – «внутренняя функция»
g(f) – «внешняя функция»

3. Определим внутреннюю(f) и внешнюю(g) элементарные функции, из которых составлена сложная функция h(x)=g(f(x))

1) h(x) = cos3x
f(x) = 3x
g(f) = cosf
2) h(x) = tg(2x- /4)
f(x)= 2x- /4
g(f) = tgf
3) h(x)=(3-5x)5
f(x) = 3-5x
g(f) = f 5
4) h(x) = sin x
f(x) = sin x
g(f) = f
Определите внутреннюю(f) и внешнюю(g)
элементарные функции, из которых составлена
сложная функция y=g(f(x))
1) y = 9-x2
2) y = sin
x
3
3) y = 2(3×3-6x)7
f(x)= 9-x2,
f(x)=
x
3
,
f(x)= 3×3-6x,
g(f)= f
g(f)=sin f
g(f)=2f 7
Формула производной сложной
функции
.
h΄(x) = g´(f) f ´(x)
h΄(x) = g´(f) • f ´(x)
Алгоритм нахождения производной
сложной функции
1)
Определи внутреннюю и внешнюю элементарные
функции f(x) и g(f)
2)
Найди производную внутренней функции f
3)
Найди производную внешней функции g´(f)
4)
´(x)
Перемножь производные внутренней и внешней
функции и получишь производную сложной
функции
h΄(x) = f ´(x) • g´(f)
Задание 1. Найдите производную функции
h(x) = (2x+3)100
1. Определим внутреннюю(f)и внешнюю(g) функции
f(x)=2x+3
g(f)=f 100
2. Найдем производную внутренней функции
f ´(x)=(2x+3)´=2
3. Найдем производную внешней функции
g´(f)=(f 100)´=100 f 99
4. Перемножим производные внутренней и внешней
функций
h´ (x) = 2 . 100 f 99= 200 f 99 = 200(2x+3) 99

Задание 2. Найдите производную функции
y(x) =4cos 3x
1. Определим внутреннюю(f)и внешнюю(g) функции
f(x)=3x
g(f)=4cosf
2. Найдем производную внутренней функции
f ´(x)=(3x)´=3
3. Найдем производную внешней функции
g´(f)=(4cosf)´= – 4sin f
4. Перемножим производные внутренней и внешней
функций
y´ (x) = 3 .( – 4sin f) = – 12sin f = – 12sin3x
Задание 3. Найдите производную функции
a) y= 9 х
2
a) f(x)=9-x2, g(f)= f
f ´(x)=(9-x2)´= -2x
g´ (f)=( f )´=
1
х
б) у= 6sin 3
х
б) f(x)=
, g(f)= 6sin f
3
f ´(x)=( х ) ´= 1
3
3
2 f
g´ (f)=(6sin f)´=6cos f
2x
y ´ = -2x
==
2 f
2 f
1
y´ = .6cos f = 2cos f=
3
x
=f
х
= 2cos
3
1
=
x
9 x2
Тест
1 вариант
А
В
С
1.
2.
3
4.
5.
2 вариант
1
2
3
4
5
А
В
С

English     Русский Правила

Найти производную методом логарифмического дифференцирования онлайн. Сложные производные

Пусть
(1)
есть дифференцируемая функция от переменной x . В начале мы рассмотрим ее на множестве значений x , для которых y принимает положительные значения: .

В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .

В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции ,
.
Отсюда
(2) .

Производная от логарифма функции называется логарифмической производной:
.

Логарифмическая производная функции y = f(x) – это производная натурального логарифма этой функции: (ln f(x))′ .

Случай отрицательных значений y

Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:

.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .

Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .

Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x , отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:

.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.

Свойство логарифмической производной

Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма , формулы производной суммы и производной постоянной , имеем:

.

Применение логарифмической производной

Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.

Пример 1

Найти производную функции:
.

Решение

Логарифмируем исходную функцию:
.

Дифференцируем по переменной x .
В таблице производных находим:
.

Применяем правило дифференцирования сложной функции .
;
;
;
;
(П1.1) .
Умножим на :

.

Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.

Примечание

Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.

Ответ

Пример 2

С помощью логарифмической производной, найдите производную функции
.

Решение

Логарифмируем:
(П2.1) .
Дифференцируем по переменной x :
;
;

;
;
;
.

Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.

Производная исходной функции:
.

Примечание

Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку

и
,
то это не повлияет на окончательный результат.

Ответ

Пример 3

Найдите производную
.

Решение

Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .

Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .

Поскольку , то

.

Примечание

Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3. 1) имеем:
;

.
Сравнивая с (П3.2) мы видим, что результат не изменился.

Вам кажется, что до экзамена еще много времени? Это месяц? Два? Год? Практика показывает, что ученик лучше всего справляется с экзаменом в том случае, если начал готовиться к нему заблаговременно. В ЕГЭ немало сложных заданий, который стоят на пути школьника и будущего абитуриента к высшим баллам. Эти преграды нужно научиться преодолевать, к тому же, делать это несложно. Вам необходимо понять принцип работы с различными заданиями из билетов. Тогда и с новыми не возникнет проблем.

Логарифмы на первый взгляд кажутся невероятно сложными, но при детальном разборе ситуация значительно упрощается. Если вы хотите сдать ЕГЭ на высший балл, вам стоит разобраться в рассматриваемом понятии, что мы и предлагаем сделать в этой статье.

Для начала разделим эти определения. Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.

В этом случае основание, стоящее внизу, необходимо возвести во вторую степень, чтобы получить число 4.

Теперь разберемся со вторым понятием. Производная функции в любом виде называется понятие, характеризующее изменение функции в приведенной точке. Впрочем, это школьная программа, и если вы испытываете проблемы с данными понятиями по отдельности, стоит повторить тему.

Производная логарифма

В задания ЕГЭ по этой теме можно привести несколько задач в качестве примера. Для начала самая простая логарифмическая производная. Необходимо найти производную следующей функции.

Нам нужно найти следующую производную

Существует специальная формула.

В этом случае x=u, log3x=v. Подставляем значения из нашей функции в формулу.

Производная x будет равняться единице. С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).

Теперь просто подставьте полученные значения в формулу. Попробуйте сами, далее сверим ответ.

В чем здесь может быть проблема для некоторых? Мы ввели понятие натурального логарифма. Расскажем о нем, а заодно разберемся, как решать задачи с ним. Ничего сложного вы не увидите, особенно, когда поймете принцип его работы. К нему вам стоит привыкнуть, так как он нередко используется в математике (в высших учебных заведениях тем более).

Производная натурального логарифма

По своей сути, это производная логарифма по основанию e (это иррациональное число, которое равняется примерно 2,7). На деле ln очень прост, поэтому часто используется в математике в целом. Собственно, решение задачи с ним тоже не станет проблемой. Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.

Представим ее как сложную функцию, состоящую из двух простых.

Достаточно преобразовать

Ищем производную от u по x

Когда нам нужно выполнить дифференцирование показательно степенной функции вида y = (f (x)) g (x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.

Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.

Как вывести формулу логарифмической производной

Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:

y = f (x) ln y = ln (f (x)) (ln y) ” = (ln (f (x))) ” 1 y · y ” = (ln (f (x))) ” ⇒ y ” = y · (ln (f (x))) “

Примеры использования формулы

Покажем на примере, как это делается.

Пример 1

Вычислить производную показательно степенной функции переменной x в степени x .

Решение

Проводим логарифмирование по указанному основанию и получаем ln y = ln x x . С учетом свойств логарифма это можно выразить как ln y = x · ln x . Теперь дифференцируем левую и правую части равенства и получаем результат:

ln y = x · ln x ln y ” = x · ln x ” 1 y · y ” = x ” · ln x + · ln x ” ⇒ y ” = y · 1 · ln x + x · 1 x = y · (ln x + 1) = x x · (ln x + 1)

Ответ: x x ” = x x · (ln x + 1)

Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:

y = x x = e ln x x = e x · ln x ⇒ y ” = (e x · ln x) ” = e x · ln x · x · ln x ” = x x · x ” · ln x + x · (ln x) ” = = x x · 1 · ln x + x · 1 x = x x · ln x + 1

Рассмотрим еще одну задачу.

Пример 2

Вычислите производную функции y = x 2 + 1 3 x 3 · sin x .

Решение

Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования. Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y ” = y · ln (f (x)) ” . Поясним, почему такое вычисление удобнее.

Начнем с нахождения ln (f (x)) . Для дальнейшего преобразования нам потребуются следующие свойства логарифма:

• логарифм дроби можно представить в виде разности логарифмов;
• логарифм произведения можно представить в виде суммы;
• если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.

Преобразуем выражение:

ln (f (x)) = ln (x 2 + 1) 1 3 x 3 · sin x 1 2 = ln (x 2 + 1) 1 3 – ln (x 3 · sin x) 1 2 = = 1 3 ln (x 2 + 1) – 3 2 ln x – 1 2 ln sin x

В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:

(ln (f (x))) ” = 1 3 ln (x 2 + 1) – 3 2 ln x – 1 2 ln sin x ” = = 1 3 ln (x 2 + 1) ” – 3 2 ln x ” – 1 2 ln sin x ” = = 1 3 (ln (x 2 + 1)) ” – 3 2 (ln x) ” – 1 2 (ln sin x) ” = = 1 3 · 1 x 2 + 1 · x 2 + 1 ” – 3 2 · 1 x – 1 2 · 1 sin x · (sin x) ” = = 1 3 · 2 x x 2 + 1 – 3 2 x – cos x 2 sin x

Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.

Ответ: y ” = y · ln (f (x)) ” = x 2 + 1 3 x 3 · sin x · 1 3 · 2 x x 2 + 1 – 3 2 x – cos x 2 sin x

Чтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.

Пример 3

Дана показательно степенная функция y = (x 2 + x + 1) x 3 . Вычислите ее производную.

Решение:

y ” = y · (ln (f (x))) ” = (x 2 + x + 1) x 3 · ln (x 2 + x + 1) x 3 ” = = (x 2 + x + 1) x 3 · x 3 · (x 2 + x + 1) ” = = (x 2 + x + 1) x 3 · x 3 ” · ln (x 2 + x + 1) + x 3 ln (x 2 + x + 1) ” = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + x 3 · 1 x 2 + x + 1 · x 2 + x + 1 ” = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + x 3 2 x + 1 x 2 + x + 1 = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + 2 x 4 + x 3 x 2 + x + 1

Ответ: y ” = y · (ln (f (x))) ” = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + 2 x 4 + x 3 x 2 + x + 1

Пример 4

Вычислите производную выражения y = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 .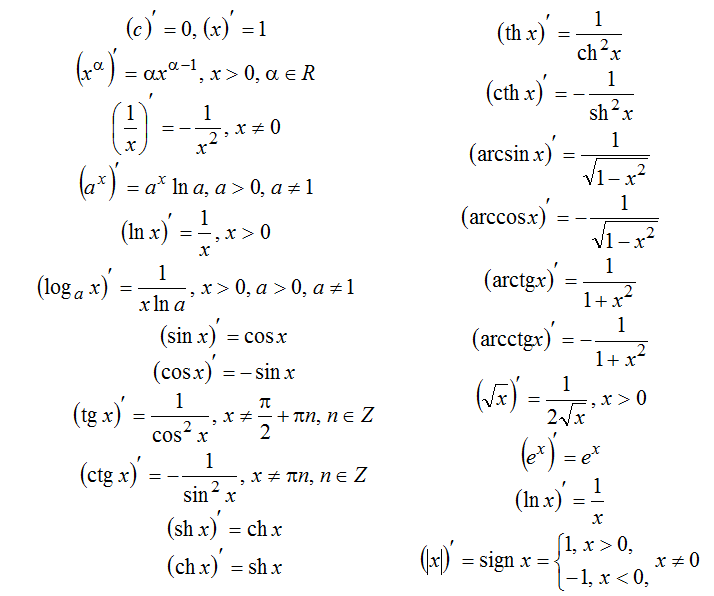

Решение

Применяем формулу логарифмической производной.

y ” = y · ln x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 ” = = y · ln x 2 + 1 3 + ln x + 1 + ln x 3 + 1 4 – ln x 2 + 2 x + 2 ” = = y · 1 3 ln (x 2 + 1) + 1 2 ln x + 1 + 1 4 ln (x 3 + 1) – 1 2 ln (x 2 + 2 x + 2) ” = = y · (x 2 + 1) ” 3 (x 2 + 1) + x + 1 ” 2 (x + 1) + (x 3 + 1) ” 4 x 3 + 1 – x 2 + 2 x + 2 ” 2 x 2 + 2 x + 2 = = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 · 2 x 3 (x 2 + 1) + 1 2 (x + 1) + 3 x 2 4 (x 3 + 1) – 2 x + 2 2 (x 2 + 2 x + 2)

Ответ:

y ” = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 · 2 x 3 (x 2 + 1) + 1 2 (x + 1) + 3 x 2 4 (x 3 + 1) – 2 x + 2 2 (x 2 + 2 x + 2) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно. Пройдите курсы по математике, естественным наукам и бизнесу

Подготовка к экзаменам по математике и естественным наукам, домашнее задание.

Проверьте свою работу.

— Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.—

95% купили больше ПРИЛОЖЕНИЙ.	97% сообщили об улучшении показателей.	Рейтинг: 4,89 из 5 звезд.	Доступно 46 ПРИЛОЖЕНИЙ.

КОВИД СПЕЦИАЛЬНЫЙ

Купите 3 приложения Made Easy по цене 2 приложений.

Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenie ur Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyPhysik Leicht EasyPhysik Research Made EasyPhysik Research Made Easy GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometr ia de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysics Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics with de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysics Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtTransforms Made EasyTrigonometry Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht

Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.

Находится в разделе 5:Настройки → 4:Статус → О программе

ID может выглядеть так: 1008000007206E210B0 BD92F455 . ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.

или на международном уровне:

В конце оплаты PayPal вам будет отправлено электронное письмо, содержащее ваш ключ и программное обеспечение.

---

Хотите купить TI-калькулятор?

Получите самые низкие цены на TI-Calculators
(со сравнением цен)

СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.

Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Установите оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, восстановленные, подержанные калькуляторы.
Посмотрите обучающие видео и прочитайте руководства по калькуляторам.
Прочтите последние новости о калькуляторах в Интернете.

БЕСПЛАТНАЯ загрузка:
Решатель квадратных уравнений (шаг за шагом)

Загрузите пошаговый решатель квадратных уравнений

. Этот решатель является частью приложения Algebra Made Easy.

– Загрузите бесплатные пробные версии здесь.

– Срок действия пробных и платных приложений неограничен.

– Будущие обновления бесплатны – навсегда!

---

Онлайн-репетиторство по математике

Получите онлайн-репетиторство.

Репетиторы с отличными оценками по математике будут рады помочь вам.

Получите индивидуальную помощь по математике.

Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.

Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, исчисление AP и BC, статистику AP, тригонометрию, дискретную математику.

Репетиторы работали более 10 лет в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).

Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.

Наши преподаватели имеют более 20 лет опыта преподавания.

1. урок стоит 50$, после этого 100$ в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.

Забронируйте сеанс репетиторства по электронной почте: [email protected]

Для вопросов, заказов и т. д.: ОБЩАЙТЕСЬ С НАМИ.

Первый урок (50 долларов США)	Один урок (100 долларов США)	Несколько уроков

Онлайн-калькулятор производных | Калькулятор дифференциации

Калькулятор производных онлайн

Производные — одна из причин, по которой учащиеся не любят исчисление. Производные не сложны, но сложны. Требуется МНОГО времени и усилий, чтобы понять хитрости и применить правильные принципы для решения производных.

Вы, вероятно, уже знаете это, учитывая, что вы ищете онлайн-калькулятор деривативов.

Вы не единственный, кто борется с деривативами. Множество студентов ежедневно пользуются нашим онлайн-калькулятором производных. Почему бы вам тоже не попробовать наш калькулятор производных и не увидеть результаты своими глазами?

Лучшие университеты, студенты которых предпочитают нас для калькулятора производных

Получите мгновенных экспертов

Наш калькулятор производных поможет вам избавиться от стресса

Мы разработали лучший калькулятор производных, чтобы облегчить вам вычисление производных функций. Если вы не можете решить вопросы в математическом задании или вам нужно попрактиковаться, наш калькулятор производных в вашем распоряжении. Наш калькулятор производных поддерживает все типы производных, такие как:

• Первая производная
• Вторая производная
• Третьи производные
• Производная в точке
• Частная производная
• Неявная производная
• Вторая неявная производная
• Производная с использованием определения

Возможно, вам придется вычислять первую, вторую или третью производную или дифференцировать функции в задании. Без проблем; наш калькулятор дифференциации поможет вам.

Выберите тип производной, которую вы хотите решить, и следуйте инструкциям нашего калькулятора дифференцирования. Калькулятор дифференциации применяет адекватные принципы и теории для получения точных результатов. Независимо от того, насколько сложна тема, наш калькулятор производных всегда к вашим услугам.

Заказать сейчас

Как работает калькулятор дифференциации?

Калькулятор дифференцирования основан на передовых технологиях, благодаря чему вы получаете только точные результаты. Хотите знать, как работает наш калькулятор дифференцирования? Вот подробный обзор того, как работает наш калькулятор производных:

Вот как работает наш онлайн-калькулятор производных (простая версия)

• Калькулятор дифференцирования использует таблицу тождеств, которая больше, чем те, которые вы найдете в стандартном исчислении. учебник.
• Идентифицирует тип производной.
• Затем решатель производных применяет соответствующие правила, такие как правило произведения, правило цепочки и т. д., в зависимости от типа производных.

Вы получите результаты после того, как калькулятор дифференцирования выполнит все шаги, упомянутые выше.

Так работает наш онлайн-калькулятор производных (Техническая версия)

• Парсер преобразует математическую функцию в понятную компьютеру форму.
• После запуска производного инструмента он отправляет математические функции и настройки на сервер. Калькулятор производной снова анализирует функцию.
• На этот раз инструмент конвертирует его в понятную форму для системы компьютерной алгебры Maxima.
• Теперь Maxima применяет соответствующие принципы и правила для точного расчета производных.
• Результаты конвертируются в LaTex и представляются пользователю.

У вас остались вопросы о нашем калькуляторе дифференцирования? Наша команда по работе с клиентами работает круглосуточно и без выходных. Свяжитесь с нами сегодня.

Как пользоваться калькулятором дифференциации?

Использование нашего калькулятора дифференциалов проще и быстрее, чем их решение вручную. Вот три простых шага для использования нашего дифференциального калькулятора.

• Введите функцию в соответствующее поле калькулятора дифференциации.
• Следуйте инструкциям на инструменте.
• Нажмите «Рассчитать».

Калькулятор дифференциации мгновенно выдает точные результаты. Наш дифференциальный калькулятор совместим со всеми типами функций. Посетите наш веб-сайт, даже если вы ищете калькулятор частных производных.

Как пользоваться пошаговым онлайн-калькулятором производных?

Наш онлайн-калькулятор производных показывает шаги, необходимые для решения вопросов. С помощью этих шагов вы можете научиться решать проблемы самостоятельно. Вы даже можете включить шаги в свое задание и получить более высокие оценки по математике. Доверьтесь нашему онлайн-калькулятору производных для более высоких оценок.

Вот краткий обзор шагов, которые показывает онлайн-калькулятор производных:

Предположим, вы использовали онлайн-калькулятор производных для решения dxd​(xsin(x)) .

Таким образом, шаги будут такими:

• Применяя правило произведения, мы получаем:

(dxd​(xsin(x))=(dxd​(x)sin(x)+xdxd​(sin(x)))

Производная синуса = dxd​(sin(x))=cos (x)

Итак,

x(dxd​(sin(x)))+sin(x)dxd​(x)=x(cos(x))+sin(x)dxd​(x)

• Применяя силовое правило получаем:

xcos(x)+sin(x)(dxd​(x)) = xcos(x)+sin(x)(1)

d/dx​(xsin(x)) = xcos(x)+sin (Икс).

Ищите дальше, чем MyAssignmenthelp.com, если вы ищете надежный калькулятор дифференцирования с шагами. Попробуйте лучший онлайн-калькулятор производных с мгновенным решением прямо здесь.

Заказать сейчас

Зачем студентам нужен калькулятор производных с решением?

Разные учащиеся решают вопросы с помощью калькулятора производных по разным причинам. Независимо от того, какова ваша причина, наш производный решатель прикроет вашу спину. Вот обычные причины, по которым студенты доверяют нашему производному решателю.

• Отсутствие интереса

Попробуйте наш решатель производных, если математические вычисления вас не интересуют. Сосредоточьтесь на том, что вам нравится, в то время как наш производный калькулятор решит проблемы для вас автоматически.

• Сложные вопросы

Дифференциальный онлайн-калькулятор отлично разбирается в решении любого типа вопросов, какими бы сложными они ни были.

• Нехватка времени

Нехватка времени свойственна всем учащимся, будь то школа или колледж. Воспользуйтесь нашим онлайн-калькулятором дифференциала, если у вас нет времени на решение задач.

Используйте лучший калькулятор частных производных на MyAsignmenthelp.com и получайте точные результаты в кратчайшие сроки. Делитесь вопросами и получайте ответы почти мгновенно.

Почему стоит выбрать калькулятор частных производных от MyAssignmenthelp.Com?

Если вы ищете эффективный онлайн-калькулятор для задач дифференцирования, вы обратились по адресу. Наш решатель производных онлайн фиксирует уровень удовлетворенности клиентов почти 99,8% благодаря своим удивительным функциям. Итак, давайте посмотрим, почему студенты выбирают наш решатель производных:

• Это бесплатно
• Инструмент дает точные результаты.
• Вы получаете результаты мгновенно вместе с шагами.
• Для загрузки результатов с шагами не требуется регистрация.

Чего ты ждешь? Попробуйте наш калькулятор дифференциации, не задумываясь.

 Самые популярные часто задаваемые вопросы, которые искали студенты:

Q1. Что такое производная?

Ответ. Производные все о наклонах. Это наклон линии, касательной к кривой в определенной точке. Скорее всего, вы найдете производную функции y = f(x). Вы также можете вычислять производные других функций, таких как косинус, синус, логарифмы и многое другое.

Q2. Как рассчитать производные?

Ответ. Допустим, вам нужно найти производную функции y = f(x). Итак, вам нужно использовать формулу наклона:

(Изменение Y)/(Изменение X) = Δy/ Δx

Δy/ Δx  = { f(x+Δx) − f(x) }/ Δx

Упрощая формулу, мы уменьшаем Δx до нуля.

Q3. Как найти калькулятор производной?

Ответ. Онлайн-калькулятор деривативов находится всего в нескольких щелчках мыши на MyAssignmenthelp.com. У нас самый продвинутый калькулятор, построенный на основе искусственного интеллекта, машинного обучения и обработки естественного языка. Эти технологии гарантируют, что инструмент будет давать точные результаты.

Q4. Какие существуют методы нахождения производных?

Ответ. Существуют различные методы нахождения производных:

• Правило произведения
• Правило частных
• Цепная линейка

Требуется время, чтобы освоить эти приемы. Таким образом, если у вас мало времени, наш онлайн-калькулятор доступен бесплатно.