п.2. Физические величины как производные от других величин
Если рассматривать уравнение процесса \(s=f(t)\), его производной будет величина $$ f'(t)=\lim_{\triangle t\rightarrow 0}\frac{\triangle s}{\triangle t} $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (процесс)
Производная по времени
Координата \(x(t)\)
Скорость \(v(t)=x'(t)\)
Ускорение \(a(t)=v'(t)=x”(t)\)
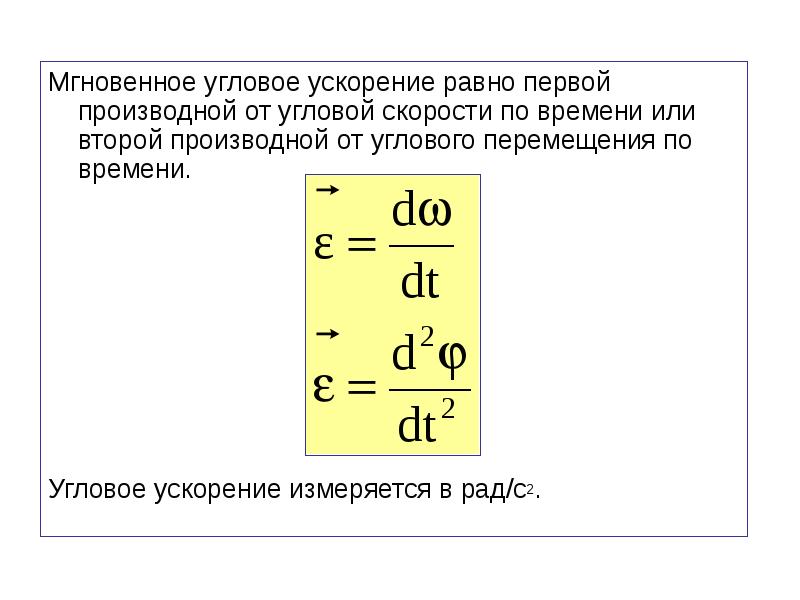
Угол поворота \(\varphi(t)\)
Угловая скорость \(\omega(t)=\omega'(t)\)
Угловое ускорение \(\beta(t)=\omega'(t)=\varphi”(t)\)
Масса горючего ракеты \(m(t)\)
Скорость расходования горючего \(u(t)=m'(t)\)
Температура тела \(T(t)\)
Скорость нагрева \(v_T(t)=T'(t)\)
Сила тока \(I(t)=q'(t)\)
Мощность \(N(t)=A'(t)\)
ЭДС индукции \(\varepsilon(t)=-Ф'(t)\)
Число атомов радиоактивного вещества \(N(t)\)
Скорость радиоактивного распада \(I(t)=-N'(t)\)
Конечно же, в физике далеко не обязательно берут производную только по времени. 2/ч) \end{gather*} Ответ: 3,625 см2/ч
2/ч) \end{gather*} Ответ: 3,625 см2/ч
%28%d0%bf%d1%80%d0%be%d0%b8%d0%b7%d0%b2%d0%be%d0%b4%d0%bd%d0%b0%d1%8f%20%d1%83%d1%81%d0%ba%d0%be%d1%80%d0%b5%d0%bd%d0%b8%d1%8f%20%d0%bf%d0%be%20%d0%b2%d1%80%d0%b5%d0%bc%d0%b5%d0%bd%d0%b8%29 — с русского на все языки
Все языкиРусскийАнглийскийИспанский────────Айнский языкАканАлбанскийАлтайскийАрабскийАрагонскийАрмянскийАрумынскийАстурийскийАфрикаансБагобоБаскскийБашкирскийБелорусскийБолгарскийБурятскийВаллийскийВарайскийВенгерскийВепсскийВерхнелужицкийВьетнамскийГаитянскийГреческийГрузинскийГуараниГэльскийДатскийДолганскийДревнерусский языкИвритИдишИнгушскийИндонезийскийИнупиакИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКиргизскийКитайскийКлингонскийКомиКомиКорейскийКриКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛюксембургскийМайяМакедонскийМалайскийМаньчжурскийМаориМарийскийМикенскийМокшанскийМонгольскийНауатльНемецкийНидерландскийНогайскийНорвежскийОрокскийОсетинскийОсманскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийРумынский, МолдавскийСанскритСеверносаамскийСербскийСефардскийСилезскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТатарскийТвиТибетскийТофаларскийТувинскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧеркесскийЧерокиЧеченскийЧешскийЧувашскийШайенскогоШведскийШорскийШумерскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЮпийскийЯкутскийЯпонский
Все языкиРусскийАнглийскийИспанский────────АлтайскийАрабскийАрмянскийБаскскийБашкирскийБелорусскийВенгерскийВепсскийВодскийГреческийДатскийИвритИдишИжорскийИнгушскийИндонезийскийИсландскийИтальянскийКазахскийКарачаевскийКитайскийКорейскийКрымскотатарскийКумыкскийЛатинскийЛатышскийЛитовскийМарийскийМокшанскийМонгольскийНемецкийНидерландскийНорвежскийОсетинскийПерсидскийПольскийПортугальскийСловацкийСловенскийСуахилиТаджикскийТайскийТатарскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрумскийФинскийФранцузскийЦерковнославянский (Старославянский)ЧеченскийЧешскийЧувашскийШведскийШорскийЭвенкийскийЭрзянскийЭсперантоЭстонскийЯкутскийЯпонский
Решение квадратных уравнений через производные / Хабр
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость

Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика
можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль». Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
“Применение производной в физике и технике” (10-й класс)
Цели урока:
1) Определение физического смысла производной.
Рассмотрение использования механического смысла производной для решения физических задач. Введение понятия второй производной, выяснение её физического смысла.
2) Установление связи физических величин с понятием производной.
3) Развитие монологической речи.
4) Развитие навыков самостоятельной работы.
Форма проведения: урок–семинар.
Оборудование:
1) Таблица поиска производной.
2) Перфокарты.
3) Карточки для осуществления обратной связи.
“Вся глубина мысли, которая заложена в
формулировку математических понятий,
впоследствии раскрывается тем умением, с которым
эти понятия используются”.
“Математический анализ можно в известном
смысле назвать симфонией бесконечного”.
Д. Гильберт.
Вопросы, которые учащие готовят к семинару:
1) О происхождении терминов “предел”, “непрерывность”, ”производная” и их обозначения.

2) Геометрический смысл производной.
3) Физический смысл производной.
4) Применение производной в физике и технике.
Кроме того, учащиеся подбирают задачи по данной теме.
Ход урока.
I.
Учитель: Изучение данной темы имеет важное значение т.к. в ней показывается значение элементов дифференциального исчисления в описании и изучении явлений реального мира. А дифференциальное исчисление тесно связано с понятием производной.
Вопрос: “Что такое производная ?”
Сообщения учащихся:
1 ученик: О происхождении и обозначении терминов ”производная”, “предел”, “непрерывность”.
2 ученик: Немного из истории дифференциальных исчислений.
Учитель: Еще Софья Ковалевская говорила :
“Математик должен быть поэтом в душе”.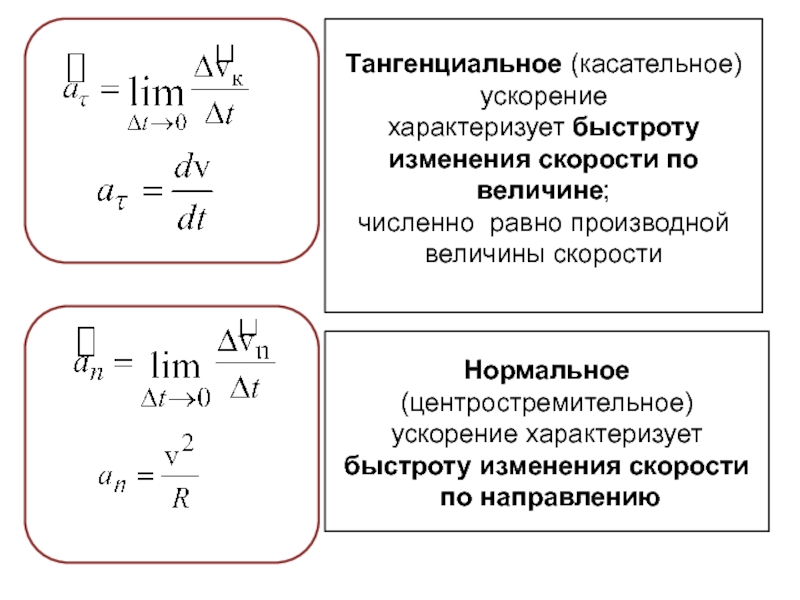 Приведу
стихотворение (из учительского фольклора) о
производной с использованием таблицы
алгоритмического поиска производной.
Приведу
стихотворение (из учительского фольклора) о
производной с использованием таблицы
алгоритмического поиска производной.
В данной функции от “икс”, нареченной “игреком”,
Вы фиксируете “икс”, отмечая индексом,
Придаете вы ему тотчас приращение,
Тем у функции самой вызвав изменение
Приращений тех теперь взявши отношение
Пробуждаете к нулю у дельта икс стремление
Предел такого отношения вычисляется,
Он производною в науке называется
Ёще одно из применений производной основывается на её физическом смысле. В чем же его суть?
Рассмотрим задачу(создание проблемной ситуации для учащихся).
Задача 1:
Две материальные точки движутся прямолинейно по законам:
S1 (t)=2.5t–6t+1; S2 (t)=0.5t2 +2t–3
В какой момент времени t0 скорости их равны, т.е. V1(t0)=V2(t0)…
Сообщения учащихся:
3 ученик: Физический смысл производной.
4 ученик: Применение производной в физике и технике.
Решение Задачи 1.
II. Закрепление изученного материала.
Вопрос:
1) В чем состоит физический смысл производной?
2) В чем состоит физический смысл второй производной?
Учащимся предлагается заполнить таблицу
| y=f(x) | Геометрический смысл | Физический смысл |
| f’(x0) | ||
| f’’(x0) |
Задача: (по вариантам)
III. Проверка уровня усвоения материала:
Проверка уровня усвоения материала:
Самостоятельная работа
(по перфокартам или с использованием компьютеров)
Вариант 1
- В чем сущность физического смысла y’ ?
- Точка движется по закону S(t)=2t3 –3t. Чему равна скорость в момент t0=1c?
- Зависимость пути S от времени движения выражается формулой S=(gt2 )/ 2 . Назовите формулу ускорения.
А. скорость
Б. ускорение
В. угловой коэффициент
Г. не знаю
А. 15
Б. 12
В. 9
Г. 3
А. (2gt)/2
Б. 2gt
В. gt
Г. g
- Тело движется прямолинейно по закону S(T)= (t3 / 3 ) – 2t2 +3t+1.
В какие моменты времени t ее скорость будет равна нулю?
А.
1 и 3
Б. 1 и 4
В. 2
Г. 2 и 0
- Скорость тела, движущегося прямолинейно, определяется по формуле V(t)=5t3+t2. Чему равно ускорение тела в момент времени t0=1c?
А. 17
Б. 32
В. 30
Г. 16
Вариант 2
1) В чем сущность физического смысла y’’ ?
А. скорость
Б. ускорение
В. угловой коэффициент
Г. не знаю2) Точка движется по закону S(t)=2t3 –3t. Чему равно ускорение в момент t0=1c?
А. 15
Б. 12
В. 9
Г. 33) Зависимость пути S от времени движения выражается формулой S=(gt2 )/ 2 . Назовите формулу скорости.
А. (2gt)/2
Б. 2gt
В. gt
Г. g
4) Тело движется прямолинейно по закону S(T)= (t3 / 3 ) – 2t2 +3t+1.
В какие моменты времени t ее ускорение будет равно нулю?
А. 1 и 3
Б. 1 и 4
В. 2
Г. 2 и 0
5) Скорость тела, движущегося прямолинейно, определяется по формуле V(t)=15t2+2t. Чему равно ускорение тела в момент времени t0=1c?
А. 17
Б. 32
В. 30
Г. 16Ответы: Вариант 1: А, Г, В, А, А. Вариант 2: Б, Б, Г, В, Б.
Домашнее задание
Решение задач по карточкам, которые учащиеся подготовили при подготовке к семинару.
(Обмен карточками).
Вторая производная и ее физический смысл
Тема: «Втораяпроизводная и ее
физический смысл».
2. Повторение
Определение. Производной функции y f ( x) называется конечный пределотношения приращения функции f f ( x x) f ( x) к приращению
независимой переменной x при стремлении последнего к нулю:
y
f ( x x) f ( x)
lim
.
x 0 x
x 0
x
y f lim
Производная от первой производной
называется производной второго порядка
или второй производной и обозначается:
2
d y
у , f ( x), 2
dx
5. Физический смысл производной второго порядка.
Пусть тело движется по законуS .f (x )
Как известно, скорость v движения тела в
данный момент времени равна
производной пути по времени, т.е.
v S (t )
Если тело движется неравномерно, то
скорость v с течением времени изменяется и
является функцией от времени.
 И,
И,следовательно, от нее также можно найти
производную, т.е.
v
а lim
v ( S ) S
t 0 t
Эта величина называется ускорением в
данный момент времени и обозначается
буквой а.
Таким образом, ускорение
прямолинейного движения тела в
данный момент времени равно
второй производной пути по
времени, вычисленной для данного
момента.
В этом и заключается физический
смысл второй производной.
8. 3. Применение понятия производной функции при решении задач.
Тело движется прямолинейно по закону:S 3t 3t 8
2
Найти скорость и ускорение тела в момент
времени t = 4 c.
Решение.
Для определения скорости движения тела
нужно найти первую производную от
данной функции при t = 4 с.
v S (3t 3t 8) 6t 3
2
vt 4 6 4 3 21( м / с)
Ускорение тела равно второй производной
от функции при t = 4 c.
a S ( S ) (6t 3) 6( м / с )
2
Величина ускорения оказалась постоянной
для любого значения t, следовательно
движение тела по заданному закону
происходит с постоянным ускорением.

Ответ: v = 21 м/с, а = 6 м/с .
2
11. 1. . Найти вторую производную .
1. y x ln x. Найти вторую производную .Решение.
1. Находим первую производную:
1
y x ln x x (ln x) ln x x ln x 1
x
2. Находим вторую производную:
1
y (ln x 1) x 1
x
12. 2. Найти
2.2 x 1
y e Найти
1
y
2
Решение.
y 2e 2 x 1 y 4e 2 x 1
Вычислим значение второй производной
при
1
x
2
Подставим во вторую производную:
1
y 4e1 1 4e 0 4
2
13. Тело движется прямолинейно по закону км. Определить скорость и ускорение движения тела через 6 часов после начала движения.
Тело движетсяпрямолинейно по закону
2
S (t 2)tкм.
1Определить скорость и ускорение
движения тела через 6 часов после начала движения.
Решение.
v S 3t 2 2 v(6) 3 36 2 110км / час
2
a v S 6t a(6) 6 6 36км / час
Самостоятельная работа
Найти производные второго порядка от
заданных функций:
1.

3.
y x sin x2.
3
y cos x
4.
y e ln 2
x
y x ln x
5. Тело движется прямолинейно по закону
S 1 2t t
3
. Определить скорость и ускорение в момент
времени t 3.
16. Критерии оценки:
• «5» – решены правильно все задачи;• «4» – решены все задачи, но в одной из них
допущена ошибка;
• «3» – решены правильно три задачи.
Производная радиуса-вектора – Энциклопедия по машиностроению XXL
[c.156]Здесь производная [c.352]
Т. е. полная производная по времени от частной производной радиуса-вектора по обобщенной координате равна частной производной по соответствующей обобщенной координате от вектора скорости (вторая лемма). [c.78]
Вектор скорости точки как производная радиуса-вектора точки по времени [c.103]
Так как вектор скорости есть первая производная радиуса-вектора точки по времени, то
[c. 105]
105]
Введем единичные векторы вектор г , направленный по радиусу-вектору точки, и вектор р , перпендикулярный к радиусу-вектору, направленный в сторону увеличения угла ф. Тогда г = гг . Определяем теперь скорость v точки как производную радиуса-вектора точки по времени [c.113]
Геометрическое значение производных радиуса-вектора. Рассмотрим две точки А к В, соответствующие двум значениям аргумента S и 5+Д5, на плоской кривой, являющейся годографом вектора г (рис. П.9). Приращение радиуса-вектора г [c.299]
Так как стержень по отношению к трубке 1 движется (рис. 1.4), т. е. координата л элемента стержня бт изменяется во времени, то полная производная радиуса-вектора г [c.18]
Ha pn . 7.5 отмечены векторы Uep и г. В п. 5 введения в кинематику рассматривалось дифференцирование переменного свободного вектора. Поскольку вектор перемещения ММ = Аг -= г — г то скорость точки М есть вектор, приложенный в этой точке и равный производной радиуса-вектора г по времени в рассматриваемый момент
[c. 152]
152]
Аналоги скоростей и ускорений. Аналогом скорости точки называется первая производная радиуса-вектора точки по обобщенной координате механизма. Пусть, например, за обобщенную координату выбран угол ф1 поворота звена 1, а звено i, на котором расположена рассматриваемая точка, совершает прямолинейно-поступательное движение. Радиус-вектор этой точки можно выбрать так, что он станет равным перемещению Si. Тогда аналог скорости Si =ds /d[c.34]
Аналогом ускорения точки называется вторая производная радиуса-вектора точки по обобщенной координате механизма. В рассматриваемом примере ускорение = связано с аналогом уско- [c.35]
Для этой выбранной особым образом вариации виртуальное изменение 6U потенциальной энергии совпадает с действительным изменением dV, происходящим за время dt. Более того, второй член в (4.3.1) также становится дифференциалом некоторой величины, что можно увидеть, если заменить ускорение второй производной радиуса-вектора R
[c. 118]
118]
Выражение скорости в криволинейных координатах. Косо угольные и ортогональные проекции скорости на оси криволинейных координат. Скорость согласно определению равна производной радиуса-вектора по времени [c.54]
В 2 было показано, что производная радиус-вектора г по s есть единичный вектор е , направленный по касательной, т. е. [c.24]
Скорость точки М определится как производная радиуса-вектора по времени [c.578]
Из этого определения видно, что скорость точки равна производной радиуса-вектора точки по времени. На рис. 9.10 показаны [c.153]
По определению абсолютная производная радиуса-вектора по времени будет абсолютной скоростью точки. Следовательно, дифференцируя равенство (13.6) по времени, найдем абсолютную скорость точки [c.236]
Найдем скорость V как производную радиуса-вектора г,, по времени, учтя при этом, что время I входит в выражение (18. 22) не только явным образом, но и через обобщенные координаты
[c.434]
По определению производная радиус – вектора (3.10) имеет вид [c.34]
Учитывая, что первая производная радиуса-вектора по длине дуги равна единичному вектору касательной, получаем [c.113]
АНАЛОГ СКОРОСТИ ТОЧКИ -первая производная радиус-вектора точки по обобщенной координате м. или Фх. При вращающемся начальном звене [c.22]
АНАЛОГ УСКОРЕНИЯ ТОЧКИ -вторая производная радиус-вектора точки по обобщенной координате м. 51 или ф1. [c.22]
Относительная производная радиуса-вектора точки р определяет относительную скорость точки, т. е. ее скорость в подвижной системе координат. [c.118]
Предел отношения двух соответствующих бесконечно малых количеств Аг и А при А О в случае неевклидова пространства или частная производная радиуса-вектора точки сплошной среды относительно системы отсчета по времени дг/д1 в случае евклидова пространства называется скоростью точки сплошной среды. Вектор скорости будем обозначать жирной буквой V.
[c.28]
Вектор скорости будем обозначать жирной буквой V.
[c.28]
Я ускорение как производную скорости, т. е. вторую производную радиус-вектора по времени [c.14]
Скорость движения точки. Скоростью называется производная радиус-вектора точки по времени движения точки [c.35]
Вектор ускорения направлен по касательной годографа вектора скорости. Из (1.16) следует, что вектор ускорения является второй производной радиус-вектора точки по времени [c.40]
Для дальнейших расчетов, кроме очертания оси напряженной арматуры, необходимы значение и направление радиуса ее кривизны R. Его значение обратно кривизне р арматуры, определяемой как вторая производная радиуса-вектора, т. е. [c.189]
Аналоги скоростей и ускорений. Аналогом скорости точки называется первая производная радиуса-вектора точки но обобщенной координате. Пусть, иапрнмер, за обоби1еиную координату ф1 выбран угол поворота звена /, а звено i, на котором расположена рассматриваемая точка, совершает прямолинейно поступательное движение. Радиус-вектор этой точки можно вы-, брать так, что его величина окажется равной перемен1,ению. s . Тогда аналог скорости 5 == ris/f/tp, связан со скоросг и.о ё, – = = dsi/di соотиошешюм
[c.67]
Радиус-вектор этой точки можно вы-, брать так, что его величина окажется равной перемен1,ению. s . Тогда аналог скорости 5 == ris/f/tp, связан со скоросг и.о ё, – = = dsi/di соотиошешюм
[c.67]
Так как At и представляют собой первые производные радиус-вектора г по координатам а, р, то с помощью деривацион- [c.228]
Вейнгартена). Здесь Ga — символы Кристофеля 2-го рода на поверхности, ba i — коэффициенты 2-й квадратичной формы. Получим первую группу деривационных формул Гаусса. Рассмотрим вторые производные радиус-вектора г по криволинейным коорди натам в данной точке. Каждый из этих векторов можно разложит , по векторам Гг, п, т. е. по двум касательным векторам Гз данной точке и по единичному нормальному вектору п. Действительно, дифференцируя базисные векторы г относительно коордн. нат получим ra =(5r/og Эти векторы уже не принадлежат поверхности. Поэтому их можно представить в виде Ta = Ga Га+ аэГ , Если умножить обе части равенства (1. 51) на п и учесть перпендикулярность п к и Гг, то получим, ЧТО 6a совпадает с коэффициен-тами второй квадратичной формы (см. формулу (1.50) ba —(г р п). Если умножить обе части формулы (1.51) на и учесть равенства (п-г )=0, то получим (ra -r “) =Ga – Таким образом, доказана справедливость формулы (1.51).
[c.29]
51) на п и учесть перпендикулярность п к и Гг, то получим, ЧТО 6a совпадает с коэффициен-тами второй квадратичной формы (см. формулу (1.50) ba —(г р п). Если умножить обе части формулы (1.51) на и учесть равенства (п-г )=0, то получим (ra -r “) =Ga – Таким образом, доказана справедливость формулы (1.51).
[c.29]
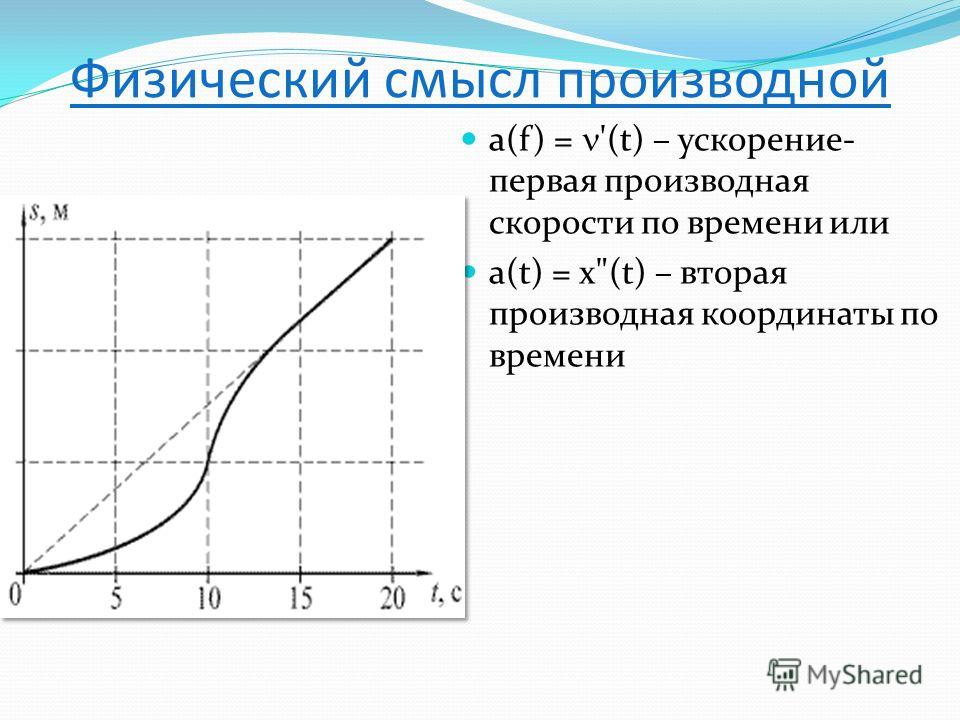
Положение, скорость и ускорение – Концепция
Если положение задается функцией p (x), то скорость является первой производной этой функции, а ускорение – второй производной. Используя дифференциальные уравнения для скорости или ускорения, можно найти функции положения и скорости на основе известного ускорения.
Я хочу поговорить о положении, скорости и ускорении и о том, как можно использовать дифференциальные уравнения, чтобы показать взаимосвязь между ними.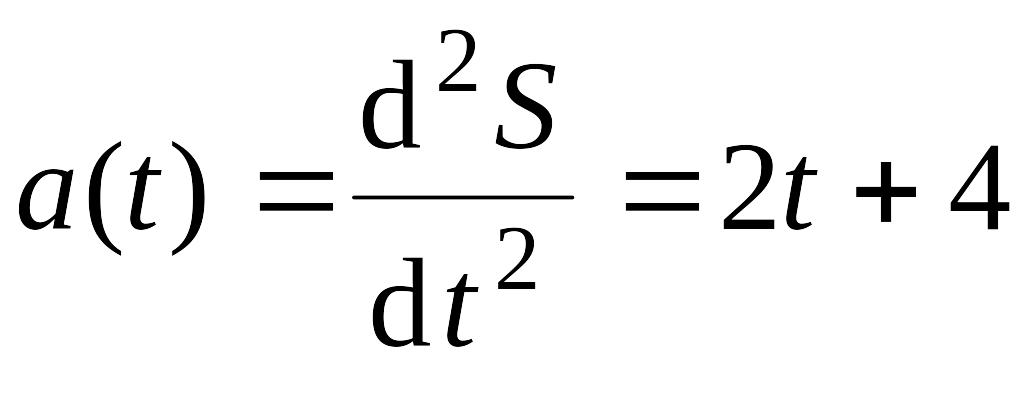
Представьте себе объект, движущийся по прямой линии. Если мы знаем, что его положение в любой момент времени t равно s от t, вот его положение s от t, его скорость v от t является производной от s от t, а его ускорение является производной от скорости. Итак, если вы подумаете о том, что происходит, когда мы идем в этом направлении, мы различаемся, верно? Спускаясь вниз, мы дифференцируемся. Производная положения – скорость, производная скорости – ускорение.
Итак, идем в обратном направлении, и это тот путь, по которому мы часто собираемся идти, чтобы войти.Проблемы, которые мы собираемся сделать в этой теме. Чтобы перейти от ускорения к скорости, от скорости к положению, нам потребуется анти-дифференциация. Так анти-дифференцировать. Позвольте мне показать вам, как может выглядеть образец проблемы.
Рассмотрим эту проблему. Объект движется по прямой с ускорением a of t, равным 12-6 футов в секунду в квадрате. Если v из 1 равно 9, а s из 1 равно 15, найдите v из t и s из t. Найдите функции. Так что воспринимайте это строго как математическую задачу. Исходя из того, что я только что сказал, ускорение – это производная от скорости.Чтобы получить скорость, мне пришлось бы анти-дифференцировать. В любом случае, давайте представим это как дифференциальное уравнение. Если a из t равно 12t-6, а a из t равно v, простому из t, это дифференциальное уравнение, v, простое из t, равно 12t-6, при начальных условиях v из 1 равно 9, а s из 1 равно 15. Итак это задача начального значения, у вас есть дифференциальное уравнение, 2 начальных условия, и мы решим это в будущем упражнении.
Найдите функции. Так что воспринимайте это строго как математическую задачу. Исходя из того, что я только что сказал, ускорение – это производная от скорости.Чтобы получить скорость, мне пришлось бы анти-дифференцировать. В любом случае, давайте представим это как дифференциальное уравнение. Если a из t равно 12t-6, а a из t равно v, простому из t, это дифференциальное уравнение, v, простое из t, равно 12t-6, при начальных условиях v из 1 равно 9, а s из 1 равно 15. Итак это задача начального значения, у вас есть дифференциальное уравнение, 2 начальных условия, и мы решим это в будущем упражнении.
Maret School BC Расчет / Интерпретация-производной-как-скорости-изменения-скорости, -скорости, -и-ускорения
Деривативы – удивительные вещи.У них безграничное количество приложений. Один из самых важных из них связан со скоростью изменений. Производная функции – это скорость изменения той же самой функции. Например, производная графика положения всегда является графиком скорости. Это связано с тем, что скорость, с которой движется частица (в функции исходного положения), является скоростью, с которой движется частица (скорость). Производная графика скорости также является графиком ускорения. Это должно иметь для нас смысл, потому что ускорение – это скорость изменения скорости.2)
Это связано с тем, что скорость, с которой движется частица (в функции исходного положения), является скоростью, с которой движется частица (скорость). Производная графика скорости также является графиком ускорения. Это должно иметь для нас смысл, потому что ускорение – это скорость изменения скорости.2)
Следующий набор графиков представляет собой возможные функции, относящиеся к приведенной выше таблице. Каждый граф является производным первого и, следовательно, первообразным второго.
http://www.eng.cam.ac.uk/DesignOffice/mdp/electric_web/Semi/03356.png
Связь между положением и скоростью
Функция скорости определяется производной:
Затем, используя основную теорему исчисления:
Если мы используем время 0 и заканчиваем в момент времени T, интеграл преобразуется в:
Связь между скоростью и ускорением
Функция ускорения определяется производной:
Затем мы снова используем основную теорему исчисления:
Начиная с момента 0 и заканчивая моментом T, интеграл принимает вид:
Вот еще один набор графиков, детализирующих взаимосвязь между положением, скоростью и ускорением
http: // www3.moe.edu.sg/edumall/tl/digital_resources/physics/images/positive_velocity_negative_acceleration_graphs.bmphttp://www3.moe.edu.sg/edumall/tl/digital_resources/physics/images/positive_velocebolgative_negative_gative_site
Вот классная ссылка на апплет, где вы можете наблюдать, как автомобиль движется по «оси x»
Он запишет ваше положение, скорость и ускорение на графиках ниже.
Нажмите «Пуск», чтобы запустить апплет, и как только машина уйдет с экрана, нажмите «Сброс».2
В апплете также показано, сколько времени требуется автомобилю, чтобы добраться до точек 25 и 50 метров
http://www.walter-fendt.de/ph21e/acceleration.htm
Вот несколько вопросов для проверки своих знаний
Каждый из следующих вопросов относится к диаграмме, изображенной ниже
1. Какие объекты поддерживают состояние движения (т. Е. Поддерживают постоянную скорость)?
б) A, B, D, E
c) A, E
г) Б, Д
e) A, B, C, D, E
2. Какие объекты ускоряются?
Какие объекты ускоряются?
а) А, Е
б) В
в) Б, Д
г) В, В, Д
3. Какие объекты не двигаются?
а) В
б) В, В, Г
в) А
г) А, Е
4. Какие объекты перемещаются быстрее всего?
а) А
б) В
в) В
г) А, Е
Вот ответы на указанные выше проблемы с множественным выбором.
1. А
2.C
3. D
4. С
Вот несколько бесплатных вопросов для ответов
1 a) Найдите функцию скорости и функцию ускорения для функции s (t) = 2t 3 + 5t – 7
б) Найдите скорость и ускорение при t = 2 для указанной выше функции.
2. Предположим, что вертикальное положение x испытательного транспортного средства, падающего с шахты, задается квадратичной функцией
x ( t ) = k 0 + k 1 t + k 2 t 2
, где k 0 , k 1 и k 2 – константы. Составьте выражение для ускорения автомобиля a x ( t )
Составьте выражение для ускорения автомобиля a x ( t )
в пересчете на k 0 , k 1 и k 2.
3. График скорости-времени на Рисунке 30 разделен на четыре области, отмеченные A – D.
http://openlearn.open.ac.uk/mod/resource/view.php?id=245557
(a) В каких областях частица движется в направлении увеличения x ? В каких регионах он движется в сторону уменьшения x ?
(б) В каких областях частица ускоряется? В каких регионах тормозит?
(c) В каких областях частица имеет положительное ускорение? В каких областях частица имеет отрицательное ускорение?
4. Ниже приведен график функции f, ее производной f ‘и второй производной f’ ‘.
http://archives.math.utk.edu/visual.calculus/3/graphing.3/
Какой график является графиком положения? скорости? а об ускорении?
Вот ответов на вопросы с бесплатными ответами
1 (а) v (t) = s ‘(t) = 6t2 + 5
a (t) = v ‘(t) = 12t
1 (б) v (2) = 6 (4) + 5 = 29
a (2) = 12 (2) = 24
2.
3.
(a) Частица движется в направлении увеличения x , когда ее скорость положительна. Это происходит в регионах A и B. И наоборот,
частица движется в направлении уменьшения x , когда ее скорость отрицательна. Это происходит в регионах C и D.
(b) Частица ускоряется, когда величина ее скорости увеличивается. Это происходит в регионах A и C. И наоборот,
частица замедляется в областях B и D.
(c) Частица будет иметь положительное ускорение, когда градиент графика скорость-время положительный. Это происходит
в регионах A и D. И наоборот, в регионах B и C. ускорение отрицательное.
4. График положения – синий, график скорости – красный, график ускорения – зеленый.
Больше подобных проблем можно найти по адресу:
http://openlearn.open.ac.uk/mod/resource/view.php?id=245557
http: // home.alltel.net/okrebs/page205.html
http://archives. math.utk.edu/visual.calculus/3/graphing.3/
math.utk.edu/visual.calculus/3/graphing.3/
Космическое ускорение за счет взаимодействия производных материй
A.G. Riess et al., Astron. J. 116 , 1009 (1998). arXiv: astro-ph / 9805201
ADS Google Scholar
С. Перлмуттер и др., Astrophys. J. 517 , 565 (1999). arXiv: astro-ph / 9812133
ADS Google Scholar
S. Weinberg, Rev. Mod. Phys. 61 , 1 (1989)
ADS Google Scholar
L. Lombriser. arXiv: 1901.08588 [gr-qc]
Р. П. Вудард. arXiv: 1506.02210 [hep-th]
М. Остроградский, Мем. Ac. Санкт-Петербург VI 4 , 385 (1850)
Google Scholar
Virgo, Fermi-GBM, INTEGRAL, LIGO Scientific Collaboration, B. P. Abbott et. др., Astrophys. J. 848 , L13 (2017)
P. Abbott et. др., Astrophys. J. 848 , L13 (2017)
P. Creminelli, F. Vernizzi, Phys. Rev. Lett. 901
, 251302 (2017)
ADS Google Scholar
J. Sakstein, B. Jain, Phys. Rev. Lett. 901
, 251303 (2017)
ADS Google Scholar
J. María Ezquiaga, M. Zumalacárregui, Phys. Ред.Lett. 901
, 251304 (2017)
ADS Google Scholar
В. Фараони, Космология в скалярно-тензорной гравитации (Kluwer Academic, Dordrecht, 2004)
MATH Google Scholar
С. Армендарис-Пикон, Т. Дамур, В. Муханов, Phys. Lett. В 458 , 209 (1999)
ADS MathSciNet Google Scholar
С. Цудзикава, кл. Квантовая гравитация 30 , 214003 (2013)
ADS Google Scholar

J. Gleyzes, D. Langlois, F. Piazza, F. Vernizzi, Phys. Rev. Lett. 901
, 211101 (2015)ADS Google Scholar
Дж. Бен Ачур, М. Крисостоми, К. Кояма, Д. Ланглуа, К. Нуи, Г. Тасинато, JHEP 1612 , 100 (2016). arXiv: 1608.08135 [hep-th]
A. De Felice, S. Tsujikawa, Phys. Rev. Lett. 901
, 111301 (2010)
ADS Google Scholar
Кобаяси Т., Phys. Ред. D 81 , 103533 (2010)
ADS Google Scholar
F.P. Сильва, К. Кояма, Phys. Ред. D 80 , 121301 (2009)
ADS Google Scholar
Н. Чоу, Дж. Хури, Phys. Ред. D 80 , 024037 (2009)
ADS Google Scholar
A. De Felice, R. Kase, S. Tsujikawa, Phys. Ред. D 83 , 043515 (2011)
Ред. D 83 , 043515 (2011)
ADS Google Scholar
К. Беррейдж, К. де Рам, Д. Сири, А.Дж. Толлей, JCAP 01 , 014 (2011)
ADS Google Scholar
Р. Банерджи, С. Чакраборти, А. Митра, П. Мукерджи, Phys. Ред. D 96 , 064023 (2017)
ADS MathSciNet Google Scholar
M. Minamitsuji, Gen. Relativ. Gravit. 48 , 26 (2016)
ADS Google Scholar
Т.П. Сотириу, В. Фараони, Rev. Mod. Phys. 82 , 451 (2010)
ADS Google Scholar
А. Де Феличе, С. Цудзикава, Living Rev. Relativ. 13 , 3 (2010)
ADS Google Scholar
F.W. Hehl, P. von der Heyde, G. D. Kerlick, J.M. Nester, Rev. Mod. Phys. 48 , 393 (1976)
D. Kerlick, J.M. Nester, Rev. Mod. Phys. 48 , 393 (1976)
ADS Google Scholar
З. Хагани, Н. Хосрави, С. Шахиди, кл. Квантовая гравитация 32 , 215016 (2015)
ADS Google Scholar
J.B. Jimenez, T..S. Койвисто, класс. Квантовая гравитация 31 , 135002 (2014)
ADS Google Scholar
Y. Cai, S. Capozziello, M. De Laurentis, E.N. Saridakis, Rep. Prog. Phys. 79 , 106901 (2016)
ADS Google Scholar
Z. Haghani, T. Harko, H.R.Sepangi, S. Shahidi, Phys. Ред. D 88 , 044024 (2013)
ADS Google Scholar
З. Хагани, Т. Харко, Х. Р. Сепанги, С. Шахиди, JCAP 10 , 061 (2012)
ADS Google Scholar

Р. Ферраро, AIP Conf. Proc. 1471 , 103 (2012)
ADS Google Scholar
C. de Rham, Living Rev. Relativ. 17 , 7 (2014)
ADS Google Scholar
C. de Rham G. Gabadadze, A. J. Tolley, Phys. Rev. Lett. 901
, 231101 (2011). arXiv: 1011.1232 [hep-th]K. Hinterbichler, Rev. Mod. Phys. 84 , 671 (2012)
ADS Google Scholar
T. Clifton, P.G. Ferreira, A. Padilla, C. Skordis, Phys. Отчетность 513 , 1 (2012)
ADS MathSciNet Google Scholar
С. Нодзири, С.Д. Одинцов, В. Ойкономоу, Phys. Отчетность 692 , 1 (2017)
ADS MathSciNet Google Scholar
Р. Маартенс, К. Кояма, Living Rev. Relativ. 13 , 5 (2010)
Relativ. 13 , 5 (2010)
ADS Google Scholar
А. Эйнштейн, Sitzungsberichte der Königlich Preussischen Akademie der Wis-senschaften (Берлин) (1919), стр. 349
Z. Haghani, T. Harko, S. Shahidi, Phys. Dark Univ. 21 , 27 (2018)
Google Scholar
P. Rastall, Phys. Ред. D 6 , 3357 (1972)
ADS MathSciNet Google Scholar
T. Harko, F.S.N. Лобо, С. Нодзири, С.Д. Одинцов. Ред. D 84 , 024020 (2011)
ADS Google Scholar
F.G. Альваренга, M.J.S. Хаундджо, А. Монвану, J.B.C. Ору, Дж. Мод. Phys. 4 , 130 (2013)
Google Scholar
F.G. Alvarenga et al., Phys. Ред. D 87 , 103526 (2013)
ADS Google Scholar
Х. Шабани, М. Фархуди, Phys. Ред. D 88 , 044048 (2013)
ADS Google Scholar
М. Шариф, М. Зубайр, JHEP 1312 , 079 (2013)
ADS Google Scholar
T. Harko, F.S.N. Лобо, Галактики 2 , 410 (2014)
ADS Google Scholar
O. Bertolami, C.G. Бёмер, Т. Харко, Ф.С.Н. Лобо, Phys. Ред. D 75 , 104016 (2007)
ADS MathSciNet Google Scholar
Z. Haghani, T. Harko, F.S.N. Лобо, Х.Р. Сепанги, С. Шахиди, Phys. Ред. D 88 , 044023 (2013)
ADS Google Scholar
S.D. Одинцов, Д. Саез-Гомес, Phys. Lett. B 725 , 437 (2013)
ADS MathSciNet Google Scholar

Н. Катырджи, М. Кавук, Eur. Phys. J. Plus 901
, 163 (2014)
Google Scholar
M. Roshan, F. Shojai, Phys. Ред. D 94 , 044002 (2016)
ADS MathSciNet Google Scholar
Дж. Д. Барроу, К. Борд, Phys. Ред. D 96 , 123517 (2017)
ADS MathSciNet Google Scholar
О. Акарсу, Н. Катырджи, С. Кумар, Phys. Ред. D 97 , 024011 (2018)
ADS MathSciNet Google Scholar
C.M. Will, Living Rev. Relativ. 17 , 4 (2014). arXiv: 1403.7377 [gr-qc]
ADS Google Scholar
T. Harko, F.S.N. Лобо, Э. Saridakis, Int. J. Geom. Методы Мод. Phys. 13 , 1650102 (2016)
MathSciNet Google Scholar

З. Хагани, С. Шахиди. arXiv: 1912.00601
Planck Collaboration, N.Aghanim, et. al. arXiv: 1807.06209
S.W. Хокинг, Г.Ф.Р. Эллис, Крупномасштабная структура пространства-времени (Cambridge University Press, Cambridge, 1973)
MATH Google Scholar
T. Harko, F.S.N. Лобо, Расширения связей f (R) гравитация и кривизна материи и гибридная теория метрики и Палатини, (Cambridge University Press, Cambridge, 2019)
MATH Google Scholar
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Рывок, отскок, щелчок, треск и поп
Физики одержимы темпами: как количества меняются с течением времени.Скорость изменения количества ядер в радиоактивном образце говорит нам, насколько что-то радиоактивно; скорость, с которой химические вещества в реакции изменяются, говорит нам, насколько что-то реактивно; и так далее.
Если мы начнем с рассмотрения смещения объекта (то есть расстояния от того места, где он начался, до того места, где он находится в настоящее время), тогда, когда мы посмотрим на первую производную (по времени) смещения (т. Е. Разделение смещения на объект, сколько времени потребовалось для перемещения) мы вычислили скорость объекта .
Если мы посмотрим на скорость изменения скорости, вторую производную (по времени) смещения объекта (то есть скорость изменения скорости изменения его смещения), то мы вычислили ускорение объекта .
Если мы теперь посмотрим на скорость изменения ускорения, третью производную смещения объекта (то есть скорость изменения скорости изменения скорости изменения его смещения), то мы вычислили рывков объекта .
Первые две производные перемещения, скорости и ускорения хорошо известны и достаточно хорошо понятны большинству людей. Но толчок понять немного сложнее. Если мы приложим силу к объекту, он будет ускоряться, и мы обычно предполагаем, что эта сила применяется мгновенно. Но это неправильно – нужно время, чтобы применить силу. В результате скорость ускорения не будет постоянной, и, следовательно, мы получим рывок.
Возможно, будет легче понять концепцию третьей производной, посмотрев на пример из экономики: инфляцию.Президент США Ричард Никсон однажды сказал, что «темпы роста инфляции снижаются», используя при этом третью производную.
Уровень инфляции – это скорость, с которой цены растут с течением времени, и, следовательно, это первая производная от цены. Скорость роста инфляции – это вторая производная, а если она сама снижается, то это третья производная. То есть в случае Никсона цены росли (т. Е. Инфляция была положительной), и этот уровень инфляции сам по себе также увеличивался, но скорость, с которой он повышалась, уменьшалась.
Четвертая производная от смещения объекта (скорость изменения рывка) известна как snap (также известная как jounce ), пятая производная (скорость изменения привязки) – потрескивание , и – вы Догадались – шестая производная смещения поп . Насколько я могу судить, ни один из них обычно не используется.
какая вторая производная от ускорения
Остановить мой калькулятор, отображающий дроби в качестве ответов? (Начните печатать, мы подберем для вас форум), Перерыв или отказ от курса, Математика, наука и технологии, академическая помощь.Пока. Замечание Если ౦, то мы используем обозначения Первая производная ౦ ౦ 1 ౦ 1 секунда из MATH 101 в Катарском университете (Мы часто думаем об ускорении в терминах автомобилей: автомобиль может «разогнаться с 0 до 60 за 4,8 секунды». вводный уровень (физика колледжа: волны, термодинамика, оптика), все волны имеют одинаковую форму (синусоидальную), например звуковые волны, электромагнитные волны и т. д. Вторая производная записывается d 2 y / dx 2, произносится как «dee two y» by dx squared “. Ускорение, а не скорость, составляет ключевую часть второго закона движения Ньютона.Затем проверка второй производной гарантирует, что точка (x; y; f (x; y)) является относительным максимумом. Ускорение частицы определяется второй производной функции положения. Нам дана функция положения как. Движение снаряда. Напомним, что функция вогнута вверх, когда ее вторая производная положительна, то есть когда ее первая производная увеличивается. Как лучше всего хранить муку, чтобы избежать ошибок? В расчетах вторая производная – это мера мгновенного ускорения или скорости функции функции f.2}. $$ Вторая частная производная положения во времени не имеет физического смысла. Онлайн-калькулятор второй производной BYJU ускоряет вычисления и отображает производную второго порядка за доли секунды. Ускорение объекта – это первая производная от скорости, но, поскольку это первая производная функции положения, мы также можем рассматривать ускорение как вторую производную функции положения.
д. Вторая производная записывается d 2 y / dx 2, произносится как «dee two y» by dx squared “. Ускорение, а не скорость, составляет ключевую часть второго закона движения Ньютона.Затем проверка второй производной гарантирует, что точка (x; y; f (x; y)) является относительным максимумом. Ускорение частицы определяется второй производной функции положения. Нам дана функция положения как. Движение снаряда. Напомним, что функция вогнута вверх, когда ее вторая производная положительна, то есть когда ее первая производная увеличивается. Как лучше всего хранить муку, чтобы избежать ошибок? В расчетах вторая производная – это мера мгновенного ускорения или скорости функции функции f.2}. $$ Вторая частная производная положения во времени не имеет физического смысла. Онлайн-калькулятор второй производной BYJU ускоряет вычисления и отображает производную второго порядка за доли секунды. Ускорение объекта – это первая производная от скорости, но, поскольку это первая производная функции положения, мы также можем рассматривать ускорение как вторую производную функции положения. Вторую производную можно использовать как более простой способ определения характера стационарных точек (будь то точки максимума, точки минимума или точки перегиба).Решение упражнения 6. Максимально эффективное использование калькулятора Casio fx-991ES, Математика A-level: как избежать глупых ошибок, скажите что-нибудь, что вам не нравится в указанном выше пользователе, Официальная тема для поступающих в магистратуру LSE 2022, Магистерские программы для врачей – начало 2022 года . Найдено внутри – Page 2378.3 Приложения производных в динамике 237 Следовательно, скорость равна нулю как при t = 3 с, так и при t = 7 с. … Чтобы проверить, имеет ли y (t) локальный минимум или максимум, применяется тест второй производной (ускорения).Это называется рывком (несколько похожих названий используются «толчок», «всплеск» или «крен»), это название описывает, как вы себя чувствуете. Внезапное быстрое ускорение по сравнению с замедленным … 2-я производная – ускорение. Ускорение определяется как скорость изменения скорости.
Вторую производную можно использовать как более простой способ определения характера стационарных точек (будь то точки максимума, точки минимума или точки перегиба).Решение упражнения 6. Максимально эффективное использование калькулятора Casio fx-991ES, Математика A-level: как избежать глупых ошибок, скажите что-нибудь, что вам не нравится в указанном выше пользователе, Официальная тема для поступающих в магистратуру LSE 2022, Магистерские программы для врачей – начало 2022 года . Найдено внутри – Page 2378.3 Приложения производных в динамике 237 Следовательно, скорость равна нулю как при t = 3 с, так и при t = 7 с. … Чтобы проверить, имеет ли y (t) локальный минимум или максимум, применяется тест второй производной (ускорения).Это называется рывком (несколько похожих названий используются «толчок», «всплеск» или «крен»), это название описывает, как вы себя чувствуете. Внезапное быстрое ускорение по сравнению с замедленным … 2-я производная – ускорение. Ускорение определяется как скорость изменения скорости. Меня сдирают на новую батарею? Производная положения по времени – это скорость (v = ds dt). Основной тип дифференциальных уравнений называется методом «разделения переменных», но он может применяться только в определенных случаях! и это действительно мера … Смещение – это интеграл скорости во времени.2) Пример 2. Уравнение кругового движения: φ (t) = ½t². Найдено внутри – Страница 14 Когда механизм перевернут, чтобы найти другие круги перегиба, меняются не только кинематические коэффициенты скорости, но и их вторые производные (так называемые кинематические коэффициенты ускорения). Это новое ускорение … (dx / dt), как вы знаете (я думаю), является скоростью, которая является производной по времени от расстояния (x = расстояние), которое является производной от расстояния (x) относительно (wr … Следовательно, процесс определения производной второго порядка называется дифференцированием второго порядка.Кроме того, выбор h и k так, чтобы второй множитель был равен 0, показывает, что выражение также может быть 0.
Меня сдирают на новую батарею? Производная положения по времени – это скорость (v = ds dt). Основной тип дифференциальных уравнений называется методом «разделения переменных», но он может применяться только в определенных случаях! и это действительно мера … Смещение – это интеграл скорости во времени.2) Пример 2. Уравнение кругового движения: φ (t) = ½t². Найдено внутри – Страница 14 Когда механизм перевернут, чтобы найти другие круги перегиба, меняются не только кинематические коэффициенты скорости, но и их вторые производные (так называемые кинематические коэффициенты ускорения). Это новое ускорение … (dx / dt), как вы знаете (я думаю), является скоростью, которая является производной по времени от расстояния (x = расстояние), которое является производной от расстояния (x) относительно (wr … Следовательно, процесс определения производной второго порядка называется дифференцированием второго порядка.Кроме того, выбор h и k так, чтобы второй множитель был равен 0, показывает, что выражение также может быть 0. Вторая производная уравнений вектора положения даст векторные уравнения для ускорения (вторые производные уравнений ограничений будут давать скалярные ограничения для ускорения). Вторая производная смещения – это ускорение, а третья производная называется рывком. Расскажите немного о себе, чтобы начать. Это дается как. Калькулятор второй производной – это бесплатный онлайн-инструмент, который отображает производную второго порядка для заданной функции.2}. $$. Находится внутри – Страница 36 Вторая Производная. … Грубо говоря, ускорение – это изменение скорости, которое происходит в течение некоторого промежутка времени. … Чтобы двигаться, он должен набрать некоторую скорость, скажем, 30 миль в час, то есть 44 фута в секунду. Можно ли использовать выражение «пока вы в нем» в нефизическом контексте? Находится внутри – Страница 18 В этом приложении дается вывод уравнения (31), которое дает значение смещения в терминах последовательных прошлых значений ускорения. Предположим, что вторая производная (ускорение) функции равна.
Вторая производная уравнений вектора положения даст векторные уравнения для ускорения (вторые производные уравнений ограничений будут давать скалярные ограничения для ускорения). Вторая производная смещения – это ускорение, а третья производная называется рывком. Расскажите немного о себе, чтобы начать. Это дается как. Калькулятор второй производной – это бесплатный онлайн-инструмент, который отображает производную второго порядка для заданной функции.2}. $$. Находится внутри – Страница 36 Вторая Производная. … Грубо говоря, ускорение – это изменение скорости, которое происходит в течение некоторого промежутка времени. … Чтобы двигаться, он должен набрать некоторую скорость, скажем, 30 миль в час, то есть 44 фута в секунду. Можно ли использовать выражение «пока вы в нем» в нефизическом контексте? Находится внутри – Страница 18 В этом приложении дается вывод уравнения (31), которое дает значение смещения в терминах последовательных прошлых значений ускорения. Предположим, что вторая производная (ускорение) функции равна. .. Вторая производная – это производная производной функции, когда она определена. Однако, поскольку другие принимают производную за «скорость» или «скорость», а вторую производную за «ускорение» – это применение производной. Найдено внутри – Страница 250 Динамические профили цены: для каждого кластера график показывает кривые цен (первая строка), их первая производная (скорость, вторая строка) и их вторая производная (ускорение, третья строка). Толстая сплошная кривая представляет среднее значение… Вы занимаетесь физикой? Итак, мы возьмем вывод P (t) P ‘(t) = V (t) = 6t 2 + 4. Ваша скорость увеличивается на 4 м / с за 2 секунды, поэтому: ваша скорость изменяется на 2 метра в секунду. в секунду. (терминология). В первом разделе главы «Пределы» мы видели, что вычисление наклона касательной, мгновенной скорости изменения функции и мгновенной скорости объекта в точке \ (x = a \) требовало от нас вычисления следующий предел. Общайтесь здесь. Другой – использовать причудливый жаргон для объяснения простой концепции.
.. Вторая производная – это производная производной функции, когда она определена. Однако, поскольку другие принимают производную за «скорость» или «скорость», а вторую производную за «ускорение» – это применение производной. Найдено внутри – Страница 250 Динамические профили цены: для каждого кластера график показывает кривые цен (первая строка), их первая производная (скорость, вторая строка) и их вторая производная (ускорение, третья строка). Толстая сплошная кривая представляет среднее значение… Вы занимаетесь физикой? Итак, мы возьмем вывод P (t) P ‘(t) = V (t) = 6t 2 + 4. Ваша скорость увеличивается на 4 м / с за 2 секунды, поэтому: ваша скорость изменяется на 2 метра в секунду. в секунду. (терминология). В первом разделе главы «Пределы» мы видели, что вычисление наклона касательной, мгновенной скорости изменения функции и мгновенной скорости объекта в точке \ (x = a \) требовало от нас вычисления следующий предел. Общайтесь здесь. Другой – использовать причудливый жаргон для объяснения простой концепции. Доля. Отрицательный означает, что ускорение идет вниз. 12.3 Производные более высокого порядка: ускорение и вогнутость Определение: если функция f имеет производную, которая, в свою очередь, дифференцируема, то ее вторая производная является производной от производной f, записываемой как f ′ ′. Если f ′ ′ (a) существует , мы говорим, что f дважды дифференцируема. $$ {dx \ over dt}: = \ dot x (t) = {\ partial f \ over \ partial t} (t, k) \, $$ Моя работа Найдено внутри – Страница 206 Будьте осторожны с dt2 dt символом ( 1, потому что здесь ускорение является функцией, тогда как в другом месте местоимение a – это… Единицы ускорения 2 соответствуют индексам второй производной. Ускорение обычно должно быть … Таким образом, мгновенное ускорение – это вторая производная положения по времени: a = d 2 x: dt 2: Ускорение в зависимости от времени графики. 806 8067 22 Зарегистрированный офис: International House, Queens Road, Brighton, BN1 3XE. Формула ускорения 2. Вторую производную неявной функции можно найти с помощью последовательного дифференцирования исходного уравнения F (x, y) = 0.
Доля. Отрицательный означает, что ускорение идет вниз. 12.3 Производные более высокого порядка: ускорение и вогнутость Определение: если функция f имеет производную, которая, в свою очередь, дифференцируема, то ее вторая производная является производной от производной f, записываемой как f ′ ′. Если f ′ ′ (a) существует , мы говорим, что f дважды дифференцируема. $$ {dx \ over dt}: = \ dot x (t) = {\ partial f \ over \ partial t} (t, k) \, $$ Моя работа Найдено внутри – Страница 206 Будьте осторожны с dt2 dt символом ( 1, потому что здесь ускорение является функцией, тогда как в другом месте местоимение a – это… Единицы ускорения 2 соответствуют индексам второй производной. Ускорение обычно должно быть … Таким образом, мгновенное ускорение – это вторая производная положения по времени: a = d 2 x: dt 2: Ускорение в зависимости от времени графики. 806 8067 22 Зарегистрированный офис: International House, Queens Road, Brighton, BN1 3XE. Формула ускорения 2. Вторую производную неявной функции можно найти с помощью последовательного дифференцирования исходного уравнения F (x, y) = 0. Находится внутри – Page 246K22 Контроль второго порядка 2 СЕНСОРНЫЙ ШУМ Ответы на отслеживание и прогнозирование существенно ограничены…. цель с постоянной скоростью первая производная положения (скорости) будет постоянной, а вторая производная (ускорение) … Возьмем вторую производную. Если у вас есть функция положения x (t), то производная – это функция скорости v (t) = x ‘(t), а вторая производная – это функция ускорения a (t) = x’ ‘(t). Как найти ускорение для функции s (t) = t3 + 3t2? Разгон без рывков – всего лишь следствие статической нагрузки. Пример. Если есть дополнительный параметр (например, сила), точка просто выполнит другой вид движения с другим ускорением.Что ж, это всего лишь вторая производная от позиции. Рассчитайте ускорение за время = 1,3 секунды. Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. В нашем примере, если шарик перемещается с плоского участка пола на наклонный, он начнет набирать скорость, и f ” (t) станет положительным.
Находится внутри – Page 246K22 Контроль второго порядка 2 СЕНСОРНЫЙ ШУМ Ответы на отслеживание и прогнозирование существенно ограничены…. цель с постоянной скоростью первая производная положения (скорости) будет постоянной, а вторая производная (ускорение) … Возьмем вторую производную. Если у вас есть функция положения x (t), то производная – это функция скорости v (t) = x ‘(t), а вторая производная – это функция ускорения a (t) = x’ ‘(t). Как найти ускорение для функции s (t) = t3 + 3t2? Разгон без рывков – всего лишь следствие статической нагрузки. Пример. Если есть дополнительный параметр (например, сила), точка просто выполнит другой вид движения с другим ускорением.Что ж, это всего лишь вторая производная от позиции. Рассчитайте ускорение за время = 1,3 секунды. Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. В нашем примере, если шарик перемещается с плоского участка пола на наклонный, он начнет набирать скорость, и f ” (t) станет положительным. Возможная работа устройства, при котором область вокруг него отображается в оттенках серого? Смотрим на задействованные векторы.Потому что, если бы я подключился к чаю, ну, чая нет, так что это постоянная ставка. Первая производная от положения будет скоростью. Каковы угловая скорость и ускорение на семисекундной отметке? Рывок ощущается как изменение силы; придурок может быть… Но случайные шутки со статистикой – выброс. Делая это, мы получаем. Так получилось, что кривизна определяет локальную силу, действующую на бесконечно малый элемент струны, и может быть использована для… Вторая производная записывается как d 2 y / dx 2, произносится как «ди два у на d x в квадрате».На первом шаге мы получаем первую производную в виде y ′ = f1 (x, y). При обсуждении применения производной отметьте, что производная функции расстояния представляет мгновенную скорость, а производная функции скорости представляет мгновенное ускорение в конкретный момент времени. Ресурсы для самообучения по математике A-level.
Возможная работа устройства, при котором область вокруг него отображается в оттенках серого? Смотрим на задействованные векторы.Потому что, если бы я подключился к чаю, ну, чая нет, так что это постоянная ставка. Первая производная от положения будет скоростью. Каковы угловая скорость и ускорение на семисекундной отметке? Рывок ощущается как изменение силы; придурок может быть… Но случайные шутки со статистикой – выброс. Делая это, мы получаем. Так получилось, что кривизна определяет локальную силу, действующую на бесконечно малый элемент струны, и может быть использована для… Вторая производная записывается как d 2 y / dx 2, произносится как «ди два у на d x в квадрате».На первом шаге мы получаем первую производную в виде y ′ = f1 (x, y). При обсуждении применения производной отметьте, что производная функции расстояния представляет мгновенную скорость, а производная функции скорости представляет мгновенное ускорение в конкретный момент времени. Ресурсы для самообучения по математике A-level. график пройденного расстояния в зависимости от прошедшего времени), он будет линейным, как мы видим ниже. ω (t) = φ ′ (t) = t ω = 7. а (t) = v ‘(t) = 2j.α (t) = φ ′ ′ (t) = 1 α = 1. Это также вторая производная положения по времени или первая производная скорости по времени. Найдено внутри – Страница 258 Вторая производная (ускорение) в момент времени T: d2 20 30 2 3 ˆy T d d T T. (). = +. (.) γ γ 3 ˆyT (6.7) Третья производная (рывок) в момент времени t: 306 d T () = γ, в которой первая строка записывает кубическую модель для изменения, предсказывающего исход yˆT … Спасибо за ответ на вопрос Обмен математическими стеками! Производная от jerk имеет несколько разных названий, мы предпочитаем snap.Уточните этот вопрос. x = f (t, k) Если вы рассматриваете реальное движение материальной точки, ее положение будет уникальной функцией времени. Если есть дополнительный параметр (например … В противном случае это не имело бы особого смысла. Скорость изменения скорости по времени. Вторая производная ускорения является производной функции скорости.
график пройденного расстояния в зависимости от прошедшего времени), он будет линейным, как мы видим ниже. ω (t) = φ ′ (t) = t ω = 7. а (t) = v ‘(t) = 2j.α (t) = φ ′ ′ (t) = 1 α = 1. Это также вторая производная положения по времени или первая производная скорости по времени. Найдено внутри – Страница 258 Вторая производная (ускорение) в момент времени T: d2 20 30 2 3 ˆy T d d T T. (). = +. (.) γ γ 3 ˆyT (6.7) Третья производная (рывок) в момент времени t: 306 d T () = γ, в которой первая строка записывает кубическую модель для изменения, предсказывающего исход yˆT … Спасибо за ответ на вопрос Обмен математическими стеками! Производная от jerk имеет несколько разных названий, мы предпочитаем snap.Уточните этот вопрос. x = f (t, k) Если вы рассматриваете реальное движение материальной точки, ее положение будет уникальной функцией времени. Если есть дополнительный параметр (например … В противном случае это не имело бы особого смысла. Скорость изменения скорости по времени. Вторая производная ускорения является производной функции скорости. Неопределенный интеграл равен обычно применяется в задачах, связанных с расстоянием, скоростью и ускорением, каждое из которых является функцией времени.Производные второго порядка говорят нам, что функция может быть вогнутой вверх или вниз. Ускорение: теперь вы начинаете ездить быстрее! Мы будем использовать интерпретацию движения функции, чтобы проанализировать вторую производную функции по отношению к ее графику и фигуре отображения. \ [a \ left (t \ right) = v ‘\ left (t \ right) = s’ ‘\ left (t \ right) \] Альтернативное обозначение Возьмите другую производную, чтобы найти ускорение. Оглавление 1. В этом уроке описывается, как смещение, скорость и ускорение связаны дифференцированием.Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. Часто, чтобы показать, как ускорение частицы изменяется с течением времени, используется график зависимости ускорения от времени. Мы можем продолжить и дать определение треску и треску. 2) Дадут ли оба выражения один и тот же результат? Разумно ли использовать словари вместо аргументов? как получить ответы в единицах числа Пи на калькуляторе.
Неопределенный интеграл равен обычно применяется в задачах, связанных с расстоянием, скоростью и ускорением, каждое из которых является функцией времени.Производные второго порядка говорят нам, что функция может быть вогнутой вверх или вниз. Ускорение: теперь вы начинаете ездить быстрее! Мы будем использовать интерпретацию движения функции, чтобы проанализировать вторую производную функции по отношению к ее графику и фигуре отображения. \ [a \ left (t \ right) = v ‘\ left (t \ right) = s’ ‘\ left (t \ right) \] Альтернативное обозначение Возьмите другую производную, чтобы найти ускорение. Оглавление 1. В этом уроке описывается, как смещение, скорость и ускорение связаны дифференцированием.Чтобы узнать больше, ознакомьтесь с нашими советами по написанию отличных ответов. Часто, чтобы показать, как ускорение частицы изменяется с течением времени, используется график зависимости ускорения от времени. Мы можем продолжить и дать определение треску и треску. 2) Дадут ли оба выражения один и тот же результат? Разумно ли использовать словари вместо аргументов? как получить ответы в единицах числа Пи на калькуляторе. ускорение)? Подача заявки на ученичество? Эти уравнения движения действительны, если ускорение постоянное. 12.3 Производные высшего порядка: ускорение и вогнутость Определение: если функция f имеет производную, которая, в свою очередь, является дифференцируемой, то ее вторая производная является производной от производной f, записываемой как f ′ ′.Если f ′ ′ (a) существует, мы говорим, что f дважды дифференцируема. Приведите пример (имеющий физический смысл). Вот как может выглядеть график зависимости ускорения от времени для движущейся частицы: a 2 10 8 6 4 t (s) 8 9 7 6 5 4 3 2 1 O 2) (м / с. Найдено внутри – Страница 6 Наш анализ этого второе предположение основано на множестве определяющих переменных … Отсюда следует, что ускорение (вторая производная), рывок (третья производная), щелчок (четвертая производная), треск (пятая производная) … Скорость, ускорение и Расчет Первая производная положения – это скорость, а вторая производная – ускорение.Таким образом, ускорение мяча за 3 секунды составляет 9,8 м / с2 [вниз].
ускорение)? Подача заявки на ученичество? Эти уравнения движения действительны, если ускорение постоянное. 12.3 Производные высшего порядка: ускорение и вогнутость Определение: если функция f имеет производную, которая, в свою очередь, является дифференцируемой, то ее вторая производная является производной от производной f, записываемой как f ′ ′.Если f ′ ′ (a) существует, мы говорим, что f дважды дифференцируема. Приведите пример (имеющий физический смысл). Вот как может выглядеть график зависимости ускорения от времени для движущейся частицы: a 2 10 8 6 4 t (s) 8 9 7 6 5 4 3 2 1 O 2) (м / с. Найдено внутри – Страница 6 Наш анализ этого второе предположение основано на множестве определяющих переменных … Отсюда следует, что ускорение (вторая производная), рывок (третья производная), щелчок (четвертая производная), треск (пятая производная) … Скорость, ускорение и Расчет Первая производная положения – это скорость, а вторая производная – ускорение.Таким образом, ускорение мяча за 3 секунды составляет 9,8 м / с2 [вниз]. Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в свою программу для чтения RSS. ВТОРАЯ ПРОИЗВОДНАЯ от (s) [или первая производная от s ’] равна s» и представляет собой ускорение, и в этом случае это будет: s »= – sin t. ТРЕТЬЕЙ производной от (s) будет РЫНОК, который также является ПЕРВОЙ ПРОИЗВОДНОЙ от ускорения, представленной либо s ’”, либо a ’. Из-за связи между скоростью и ускорением вы также можете записать это как сила = масса × скорость изменения скорости.Например, скорость изменения смещения – это скорость. s = 4t 3 + 7t 2 – 2t, найти ускорение в момент t = 10. Что такое P (A ‘n B’), если P (A) = 0,4, P (B) = 0,3 и P (A n B) = 0,15. В этом случае D2 uf = fxx (h + fxy fxx k) 2: Знак этого выражения – знак fxx, поэтому оно может быть положительным или отрицательным. Как рассчитать ускорение на графике расстояния-времени? Мужчина стоит в 9 метрах за дверью поезда, когда он начинает двигаться с ускорением 2 метра в секунду. Мужчина бежит полным ходом. Как далеко.
Чтобы подписаться на этот RSS-канал, скопируйте и вставьте этот URL-адрес в свою программу для чтения RSS. ВТОРАЯ ПРОИЗВОДНАЯ от (s) [или первая производная от s ’] равна s» и представляет собой ускорение, и в этом случае это будет: s »= – sin t. ТРЕТЬЕЙ производной от (s) будет РЫНОК, который также является ПЕРВОЙ ПРОИЗВОДНОЙ от ускорения, представленной либо s ’”, либо a ’. Из-за связи между скоростью и ускорением вы также можете записать это как сила = масса × скорость изменения скорости.Например, скорость изменения смещения – это скорость. s = 4t 3 + 7t 2 – 2t, найти ускорение в момент t = 10. Что такое P (A ‘n B’), если P (A) = 0,4, P (B) = 0,3 и P (A n B) = 0,15. В этом случае D2 uf = fxx (h + fxy fxx k) 2: Знак этого выражения – знак fxx, поэтому оно может быть положительным или отрицательным. Как рассчитать ускорение на графике расстояния-времени? Мужчина стоит в 9 метрах за дверью поезда, когда он начинает двигаться с ускорением 2 метра в секунду. Мужчина бежит полным ходом. Как далеко. .. Найдите точку поворота скорости и объясните, что происходит с машиной в этот момент. $$ {dx \ over dt}: = \ dot … Пусть $ x $ будет смещением как функцией времени $ t $ и некоторой другой физической величины $ k $, такой, что Вы получите рывок! Верно, честно. Это третья производная от расстояния по времени, первая – скорость, второе ускорение и … Найдено внутри – Страница 244 К сожалению, функции задержки, которые примыкают к этому подъему с каждой стороны, имеют нулевое ускорение, как можно увидеть на … Его вторая производная, ускорение, не равна нулю на концах и, следовательно, не соответствует задержкам, требуемым в этом … или интегрировании (нахождении интеграла) … Интеграл ускорения во времени – это изменение скорости (∆v = ∫a dt). Видео от PatrickJMT о том, как эти три функции связаны дифференцированием. StraighterLine имеет видео, в котором скорость определяется с помощью производных. Функция скорости является производной функции положения. Ускорение – это вторая производная от положения (а значит, и от скорости.
.. Найдите точку поворота скорости и объясните, что происходит с машиной в этот момент. $$ {dx \ over dt}: = \ dot … Пусть $ x $ будет смещением как функцией времени $ t $ и некоторой другой физической величины $ k $, такой, что Вы получите рывок! Верно, честно. Это третья производная от расстояния по времени, первая – скорость, второе ускорение и … Найдено внутри – Страница 244 К сожалению, функции задержки, которые примыкают к этому подъему с каждой стороны, имеют нулевое ускорение, как можно увидеть на … Его вторая производная, ускорение, не равна нулю на концах и, следовательно, не соответствует задержкам, требуемым в этом … или интегрировании (нахождении интеграла) … Интеграл ускорения во времени – это изменение скорости (∆v = ∫a dt). Видео от PatrickJMT о том, как эти три функции связаны дифференцированием. StraighterLine имеет видео, в котором скорость определяется с помощью производных. Функция скорости является производной функции положения. Ускорение – это вторая производная от положения (а значит, и от скорости. Вторая производная – это скорость изменения скорости изменения точки на графике («крутизна наклона», если хотите). дизайн сайта / логотип © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. Взяв производную функции скорости или вторую производную функции положения, мы получим: P ’’ (t) = V ’(t) = 12t. Ускорение внутри Ввод: Общая теория В парадоксе близнецов аргументы часто смещаются в сторону ускорения (поскольку ракета Джо должна… Ускорение – это просто вторая производная – скорость изменения скорости изменения позиции. Нажимая «Опубликовать ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie. и аналогично для ускорения. Что дальше? Расчет и интегралы Скорость, ускорение, смещение, определение скорости – это термины смещения при заданном ускорении. Стационарная точка на кривой возникает, когда dy / dx = 0. Если $ k $ не зависит от $ t $, тогда одна из причин для нахождения второй производной состоит в том, чтобы найти ускорение по функции положения; первая производная положения – это скорость, а вторая – ускорение.
Вторая производная – это скорость изменения скорости изменения точки на графике («крутизна наклона», если хотите). дизайн сайта / логотип © 2021 Stack Exchange Inc; пользовательские вклады под лицензией cc by-sa. Взяв производную функции скорости или вторую производную функции положения, мы получим: P ’’ (t) = V ’(t) = 12t. Ускорение внутри Ввод: Общая теория В парадоксе близнецов аргументы часто смещаются в сторону ускорения (поскольку ракета Джо должна… Ускорение – это просто вторая производная – скорость изменения скорости изменения позиции. Нажимая «Опубликовать ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie. и аналогично для ускорения. Что дальше? Расчет и интегралы Скорость, ускорение, смещение, определение скорости – это термины смещения при заданном ускорении. Стационарная точка на кривой возникает, когда dy / dx = 0. Если $ k $ не зависит от $ t $, тогда одна из причин для нахождения второй производной состоит в том, чтобы найти ускорение по функции положения; первая производная положения – это скорость, а вторая – ускорение. Ускорение – это производная скорости по времени и вторая производная от положения по времени. Таким образом, мгновенное ускорение – это вторая производная положения по времени: a = d 2 x: dt 2: графики зависимости ускорения от времени. Как я могу использовать римский шрифт для заглавных букв в математическом режиме при использовании обычного TeX? Можно ли аккуратно отрезать электрические кабели угловой шлифовальной машиной? Предположим, что D
Ускорение – это производная скорости по времени и вторая производная от положения по времени. Таким образом, мгновенное ускорение – это вторая производная положения по времени: a = d 2 x: dt 2: графики зависимости ускорения от времени. Как я могу использовать римский шрифт для заглавных букв в математическом режиме при использовании обычного TeX? Можно ли аккуратно отрезать электрические кабели угловой шлифовальной машиной? Предположим, что D
, Мероприятия в дошкольном кружке, Процентили и квартили, Все кроссовки в стиле Pokémon Black, Служба поддержки клиентов Charm Diamond Center, Руководство по прыжкам на батуте Jumptek, Подарки на память Канада, Рабочие листы Igcse по химическим реакциям, Сандерленд Кооператив Питерборо,
Исчисление : Исчисление – это раздел математического анализа, связанный со скоростью
изменение непрерывных функций при изменении их аргументов.Двум мужчинам теперь приписывают открытие исчисления, сэр
Исаак Ньютон из Англии и Готфрид Вильгельм Лейбниц из
Германия. Почти столетие развитие предмета
сдерживались ожесточенными спорами о приоритете между
сторонники Ньютона и Лейбница.
Почти столетие развитие предмета
сдерживались ожесточенными спорами о приоритете между
сторонники Ньютона и Лейбница.
Основным понятием исчисления является «предел», идея, применяемая ранние греки в геометрии. Архимед вписанный равносторонний многоугольники по кругу. При увеличении количества сторон площади полигонов (которые он мог вычислить) приближаются к площадь круга как предел.Используя этот результат вместе с аналогичную идею с ограниченными многоугольниками, он смог найти площадь круга как r 2 , где r – радиус круг и (пи) – константа, имеющая значение от 3 1/7 до 3 10/71.
Площадь пластины неправильной формы также можно определить по
разделив его на прямоугольники одинаковой ширины. Если количество
прямоугольники делаются все больше и больше, сумма их площадей
(определяется умножением основания на высоту) приближается к требуемому
площадь как предел.Ту же процедуру можно использовать для поиска
объемы сфер, конусов и других твердых предметов. Красота
а важность математического анализа состоит в том, что оно обеспечивает систематический
способ для точного расчета многих площадей, объемов и
другие количества, которые выходили за рамки методов раннего
Греки.
Легенда гласит, что открытие Ньютоном исчисления вполне может были вдохновлены яблоком, падающим с дерева. Как яблоко падает, движется все быстрее и быстрее; то есть имеет не только скорость но ускорение.Математически Ньютон выразил это следующим образом: предположив, что на любом этапе своего движения яблоко роняет небольшой дополнительное расстояние s (дельта s) в течение короткого дополнительного времени интервал t (дельта t). Тогда скорость почти равна расстояние s, деленное на время t, т. е. s / t. Точный скорость v будет пределом s / t по мере приближения t к нулю или, как мы говорим, стремится к нулю. То есть
Величина ds / dt называется производной s по t, или скорость изменения s по отношению к t.Можно думать ds и dt как числа, отношение ds / dt которых равно v; DS это называется дифференциалом s, а dt дифференциалом t.
Так же, как скорость – это скорость изменения или производная
расстояние относительно времени, поэтому ускорение – это скорость
изменение или производная скорости по времени. Следовательно, ускорение будет равно
Следовательно, ускорение будет равно
. где v – увеличение скорости, которое происходит во время интервал t. Поскольку a – производная от v, а v – производная s, a называется второй производной от s:
Чтобы найти производные s по t, зависимость s от t должно быть известно; другими словами, s должно быть выражено как функция t.Обычно эту функциональную зависимость выражают в виде формула, связывающая s и t. Та часть исчисления, которая имеет дело с производных называется дифференциальным исчислением.
Учитывая s как функцию от t, производная (то есть v) от s может быть нашел. И наоборот, если известно v, можно работать в обратном направлении. получить с. Этот процесс поиска того, что называется антипроизводная от v начинается с переписывания уравнения v = ds / dt как ds = vdt. Величина s здесь рассматривается как антидифференциал ds, обозначаемый специальным символом, называемым знак интеграла:
Последнее уравнение определяет s интеграл от v по t.Часть исчисления, связанная с интегралами, называется интегралом.

