ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23.  Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 2. 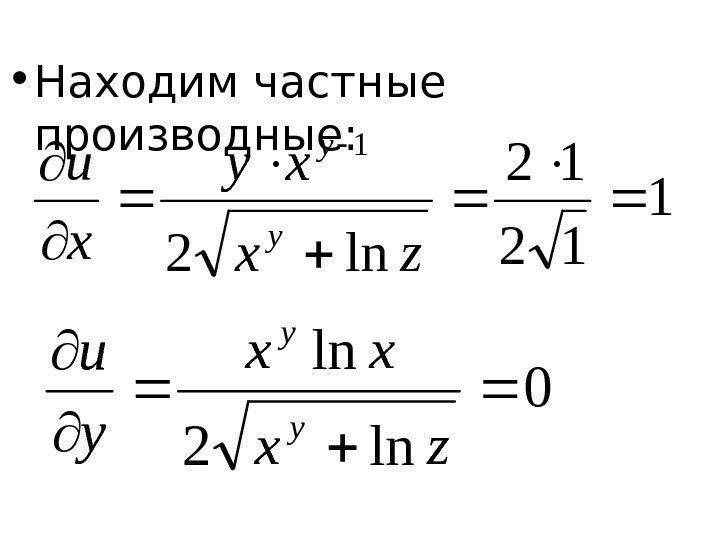 Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла |
6.3. Частные производные.
Пусть функция определена на множестве , точки , , , .
Определение. Частной производной функции
по переменной x в точке
называется предел отношения частного
приращения функции z по переменной x в точке
к приращению аргумента
,
когда
.
.
Определение. Частной производной функции по переменной y в точке называется предел отношения частного приращения функции z по переменной y в точке к приращению аргумента y, когда .
.
Замечание: 1) все правила дифференцирования функции одной переменной справедливы для функций многих переменных; 2) при нахождении частной производной функции по одной переменной все остальные переменные считают постоянными, то есть для функции при вычислении , при вычислении ; для функции при вычисления , при вычислении , при вычислении
Пример.
Лекция 7. Дифференцируемость функции двух переменных.
7.1. Определение дифференцируемости функции двух переменных.
Определение
полного дифференциала. Приближенные
вычисления с помощью полного дифференциала.
Дифференциалы высших порядков.
7.2. Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных частных производных.
7.3. Производная функции по направлению.
7.4. Градиент функции
7.5. Экстремумы функции двух переменных. Необходимое и достаточное условия существования экстремумов.
7.1. Определение дифференцируемости функции двух переменных. Определение полного дифференциала. Приближенные вычисления с помощью полного дифференциала.
Пусть функция определена в области , точка .
Определение. Функция называется дифференцируемой в точке , если ее полное приращение в точке представимо в виде где числа A и B не зависят от и , , при , и , .
Определение. Главная линейная по
и
часть полного приращения функции
в точке
называется полным дифференциалом
функции z в
точке
и обозначается .
Для независимых переменных x и y их приращения совпадает с дифференциалами, то есть , , поэтому
. В приближённых вычислениях при малых приращениях и или
.
Для вычисления приближённого значения функции используют формулу .
7.2. Частные производные и дифференциалы высших порядков. Теорема о равенстве смешанных частных производных.
Пусть функция дифференцируема в области и ее частные производные первого порядка сами являются функциями двух переменных.
Определение. Частная производная от частной производной первого порядка называется частной производной второго порядка.
Определение. Частными производными порядка называются частные производные от частных производных порядка.
Определение. Частные производные по различным
переменным называется смешанными.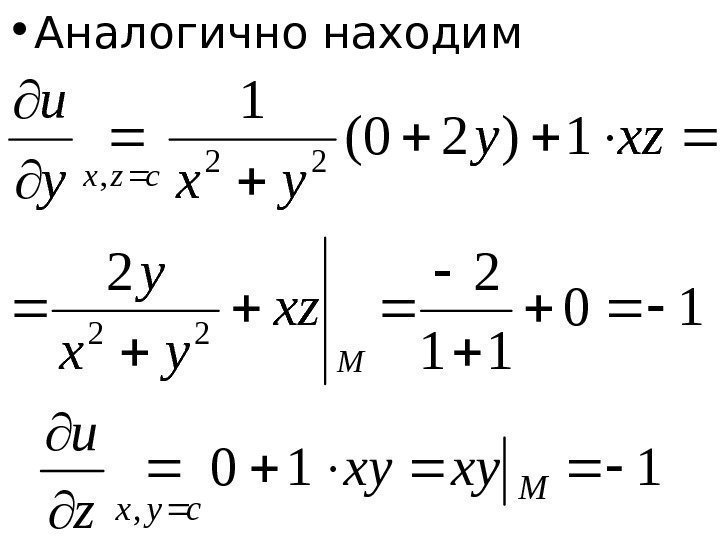
Их
обозначают , …
Теорема. Если смешанные производные существуют и непрерывны, то они равны между собой, то есть .
Пример.
Определение. Полным дифференциалом второго порядка функции называется ее полный дифференциал от полного дифференциала первого порядка.
Определение. Полным дифференциалом порядка функции двух переменных называется ее полный дифференциал от полного дифференциала порядка и
7.3. Производная функции по направлению.
П усть функция определена в области , и функция z дифференцируема в точке , тогда .
Определение. Производной функции в точке в направлении вектора называется предел отношения приращения функции z в направлении вектора в точке к
величине , когда .
где – направляющие косинусы вектора
(они же координаты единичного вектора ).
Производная функции по направлению характеризует скорость изменения функции в точке в направлении вектора .
Пример. Найти производные функции в точке в направлении вектора где .
1)
2)
3) В точке М функции возрастает в направлении вектора .
Правило частного – Концепция
Правило частного полезно при попытке найти производную функции, которая делится на другую функцию. Пока обе функции имеют производные, правило частных говорит нам, что окончательная производная представляет собой определенную комбинацию как исходных функций, так и их производных.
дифференциация частное правило правило произведения производные
Я хочу поговорить о другом очень важном правиле дифференцирования, называемом правилом частного.
Правило частного предназначено для дифференциации функций, таких как q от x, которые могут быть представлены как частное двух других функций f от x по g от x, поэтому наша цель на сегодня – найти q, простое от x.
Итак, давайте начнем с представления этой связи между q, f и g в виде произведения, поэтому, когда я умножаю обе части этого уравнения на g от x и получаю q от x, умноженное на g от x, равно f от x, вот что я’ будем работать с здесь. Поскольку я уже знаю правило произведения, и поэтому я могу дифференцировать обе его части, используя правило произведения, теперь дифференцирование левой части дает мне первый куб, умноженный на производную второго простого числа g, плюс второе число g, умноженное на производную от x. сначала q простое число, а дифференцирование в правой части просто дает мне f простое число x, поэтому в этом уравнении, поскольку я ищу q простое число, мне нужно решить для этого парня, поэтому я собираюсь вычесть этот член, я получаю g x, умноженное на q, простое число x равно f, простое число x минус этот термин минус q числа x oops q числа x g, простое число x, и тогда я должен разделить g числа x.
Теперь я решил для простого q здесь, но я еще не совсем я еще не совсем закончил, потому что я хотел бы, чтобы мой ответ был только с точки зрения f и g я не хочу я не хочу q в моем ответ, так что я собираюсь заменить q x на f и g через мгновение, но прежде чем я это сделаю, я собираюсь умножить верх и низ этого уравнения на g x, g x на g x теперь внизу это даст мне г х количества в квадрате. В верхней части у меня будет f простых чисел, умноженных на g из x, или g от x, умноженных на f простых чисел, а затем у меня будет минус q из x, умноженных на g из x, умноженных на g простых чисел. Теперь q от x, умноженное на g от x, давайте вспомним, что это f от x, и поэтому мы сделаем замену, когда я умножу, поэтому давайте снова возьмем это здесь слева, у нас есть q простое число от x и умножение g g от x на f простое число я получаю g от x f простого числа, и у меня есть знак минус g от x, умноженное на q от x, как я уже говорил, это f от x, умноженное на g, простое число и так далее, посмотрите, что у нас внизу, g от x, умноженное на g от x у нас есть количество g x в квадрате.
Это правило частных, и будет еще лучше, если я запишу его в терминах f и g, это q x равно f и g, поэтому на самом деле мы рассматриваем здесь производную f x по g x. напишу так. Производная f от x по g от x равна g от x, умноженному на f простое от x минус f от x g простое от x по g от x в квадрате. Это частное правило.
Сейчас я обрамлю его большой рамкой, это важное правило, и я также хочу дать вам, ребята, способ запомнить это правило. И хотите верьте, хотите нет, это пришло от студента, которого я никогда не учил этому, студент сказал мне это, поэтому, когда вы берете производную функции, которая является частным от других функций, давайте назовем эту функцию низкой, а эту – высокой. функция. Это лоу-де-хай минус хай-де-лоу над квадратом того, что ниже. Когда я говорю low de high, я имею в виду производную от функции high so low de high минус high de low по квадрату того, что ниже. Я буду говорить это в будущих уроках просто для того, чтобы напомнить вам, что такое правило частного.
исчисление – Почему необходимо правило частного при дифференцировании?
спросил
Изменено 7 месяцев назад
Просмотрено 985 раз
$\begingroup$
- Исчисление — производные — правило частных 92$. Но большинство студентов изучают правило частных и не испытывают проблем после его применения (а затем им приходится учиться не путать его с отношением производных в правиле Лопиталя позже).
Однажды я встретил очень известного математика, который , а не знает правило отношения: он изучал математику в Европе, где университетские курсы часто начинаются с анализа, а не элементарного исчисления, и он никогда не преподает математику первокурсникам, поэтому у него нет причин контакт с частным правилом.
Я что-то обсуждал с ним, и когда понадобилась производная от отношения, он нашел ее с помощью правила произведения и сказал мне, что не знает другого способа и ему все равно, есть ли другой способ.
$\endgroup$
2
$\begingroup$
Мне нравится использовать $(\ln(f))’ =\dfrac{f’}{f} $ для общего произведения и частное.
Если $f = \dfrac{\prod u_k}{\prod v_k} $ затем $\ln(f) = \сумма\ln(u_k)-\сумма\ln(v_k) $ так $(\ln(f))’ = \сумма \dfrac{u_k’}{u_k}-\сумма \dfrac{v_k’}{v_k} =\dfrac{f’}{f} $ так $f’ = f\left(\sum\dfrac{u_k’}{u_k}-\sum\dfrac{v_k’}{v_k}\right) $.
9{-1}$ относительно $x$. Можно заметить, что с тем же успехом мы могли бы сказать, что все правила избыточны, если у вас есть определение производной. Однако есть то, что называется формальной производной, которая определяется алгебраически, а не через определение, основанное на пределе (потому что в этом контексте это не имеет смысла).