Таблица производных. Доказательство формул
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y=C (C)’=0 Степенная функция y=xp (xp)’=p·xp-1 | Показательная функция y=ax (ax)’=ax·ln a В частности, при a=e имеем y=ex (ex)’=ex |
Логарифмическая функция (logax)’=1x·ln a В частности, при a=e имеем y=ln x (ln x)’=1x | Тригонометрические функции (sin x)’=cos x(cos x)’=-sin x(tgx)’=1cos2x(ctgx)’=-1sin2x |
Обратные тригонометрические функции (arcsin x)’=11-x2(arccos x)’=-11-x2(arctg x)’=11+x2(arcctg x)’=-11+x2 | Гиперболические функции (shx)’=chx(chx)’=shx(thx)’=1ch3x(cthx)’=-1sh3x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x0=x, где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f(x)=C. Составим запись предела отношения приращения функции к приращению аргумента при ∆x→0:
lim∆x→0∆f(x)∆x=lim∆x→0C-C∆x=lim∆x→00∆x=0
Обратите внимание, что под знак предела попадает выражение 0∆x. Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f(x)=C равна нулю на всей области определения.
Пример 1Даны постоянные функции:
f1(x)=3,f2(x)=a, a∈R,f3(x)=4.13722,f4(x)=0,f5(x)=-87
Необходимо найти их производные.
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от
В первой функции мы видим производную натурального числа 3. В следующем примере необходимо брать производную от
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f1′(x)=(3)’=0,f2′(x)=(a)’=0, a∈R,f3′(x)=4.13722’=0,f4′(x)=0’=0,f5′(x)=-87’=0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (xp)’=p·xp-1, где показатель степени p является любым действительным числом.
Приведем доказательство формулы, когда показатель степени – натуральное число: p=1, 2, 3, …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
(xp)’=lim∆x→0=∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x+∆x)p-xp=Cp0+xp+Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+. ..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
..++Cpp-1·x·(∆x)p-1+Cpp·(∆x)p-xp==Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p
Таким образом:
(xp)’=lim∆x→0∆(xp)∆x=lim∆x→0(x+∆x)p-xp∆x==lim∆x→0(Cp1·xp-1·∆x+Cp2·xp-2·(∆x)2+…+Cpp-1·x·(∆x)p-1+Cpp·(∆x)p)∆x==lim∆x→0(Cp1·xp-1+Cp2·xp-2·∆x+…+Cpp-1·x·(∆x)p-2+Cpp·(∆x)p-1)==Cp1·xp-1+0+0+…+0=p!1!·(p-1)!·xp-1=p·xp-1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3Чтобы привести доказательство для случая, когда p – любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x>0. Тогда: xp>0. Логарифмируем равенство y=xp по основанию e и применим свойство логарифма:
y=xpln y=ln xpln y=p·ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
Определим ее производную:
(ln y)’=(p·ln x)1y·y’=p·1x⇒y’=p·yx=p·xpx=p·xp-1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x<0, причем является четной: y(x)=-y((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Тогда xp<0 и возможно составить доказательство, используя логарифмическую производную.
Если p есть нечетное число, тогда степенная функция определена и при x<0, причем является нечетной: y(x)=-y(-x)=-(-x)p. Тогда xp<0, а значит логарифмическую производную задействовать нельзя. В такой ситуации возможно взять за основу доказательства правила дифференцирования и правило нахождения производной сложной функции:
y'(x)=(-(-x)p)’=-((-x)p)’=-p·(-x)p-1·(-x)’==p·(-x)p-1=p·xp-1
Последний переход возможен в силу того, что если p – нечетное число, то p-1 либо четное число, либо нуль (при p=1), поэтому, при отрицательных x верно равенство (-x)p-1=xp-1.
Итак, мы доказали формулу производной степенной функции при любом действительном p.
Пример 2Даны функции:
f1(x)=1×23,f2(x)=x2-14,f3(x)=1xlog712
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y=xp, опираясь на свойства степени, а затем используем формулу:
f1(x)=1×23=x-23⇒f1′(x)=-23·x-23-1=-23·x-53f2′(x)=x2-14=2-14·x2-14-1=2-14·x2-54f3(x)=1xlog712=x-log712⇒f3′(x)=-log712·x-log712-1=-log712·x-log712-log77=-log712·x-log784
Производная показательной функции
Доказательство 4(ax)’=lim∆x→0ax+∆x-ax∆x=lim∆x→0ax(a∆x-1)∆x=ax·lim∆x→0a∆x-1∆x=00
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z=a∆x-1 (z→0 при ∆x→0). В таком случае a∆x=z+1⇒∆x=loga(z+1)=ln(z+1)ln a. Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(ax)’=ax·lim∆x→0a∆x-1∆x=ax·ln a·lim∆x→011z·ln(z+1)==ax·ln a·lim∆x→01ln(z+1)1z=ax·ln a·1lnlim∆x→0(z+1)1z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(ax)’=ax·ln a·1lnlimz→0(z+1)1z=ax·ln a·1ln e=ax·ln a
Пример 3Даны показательные функции:
f1(x)=23x,f2(x)=53x,f3(x)=1(e)x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f1′(x)=23x’=23x·ln23=23x·(ln 2-ln 3)f2′(x)=53x’=53x·ln 513=13·53x·ln 5f3′(x)=1(e)x’=1ex’=1ex·ln1e=1ex·ln e-1=-1ex
Производная логарифмической функции
Доказательство 5Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
(logax)’=lim∆x→0loga(x+∆x)-logax∆x=lim∆x→0logax+∆xx∆x==lim∆x→01∆x·loga1+∆xx=lim∆x→0loga1+∆xx1∆x==lim∆x→0loga1+∆xx1∆x·xx=lim∆x→01x·loga1+∆xxx∆x==1x·logalim∆x→01+∆xxx∆x=1x·logae=1x·ln eln a=1x·ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim∆x→01+∆xxx∆x=e является верным в соответствии со вторым замечательным пределом.
Пример 4Заданы логарифмические функции:
f1(x)=logln3 x,f2(x)=ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f1′(x)=(logln3 x)’=1x·ln(ln 3);f2′(x)=(ln x)’=1x·ln e=1x
Итак, производная натурального логарифма есть единица, деленная на
Производные тригонометрических функций
Доказательство 6Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x
Формула разности синусов позволит нам произвести следующие действия:
(sin x)’=lim∆x→0sin (x+∆x)-sin x∆x==lim∆x→02·sin x+∆x-x2·cosx+∆x+x2∆x==lim∆x→0sin ∆x2·cosx+∆x2∆x2==cosx+02·lim∆x→0sin ∆x2∆x2
Наконец, используем первый замечательный предел:
sin’ x=cos x+02·lim∆x→0sin∆x2∆x2=cos x
Итак, производной функции sin x будет cos x.
Совершенно также докажем формулу производной косинуса:
cos’ x=lim∆x→0cos (x+∆x)-cos x∆x==lim∆x→0-2·sin x+∆x-x2·sinx+∆x+x2∆x==-lim∆x→0sin∆x2·sinx+∆x2∆x2==-sinx+02·lim∆x→0sin∆x2∆x2=-sin x
Т. е. производной функции cos x будет –sin x.
е. производной функции cos x будет –sin x.
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
tg’x=sin xcos x’=sin’ x·cos x-sin x·cos’ xcos2 x==cos x·cos x-sin x·(-sin x)cos2 x=sin2 x+cos2 xcos2 x=1cos2 xctg’x=cos xsin x’=cos’x·sin x-cos x·sin’xsin2 x==-sin x·sin x-cos x·cos xsin2 x=-sin2 x+cos2 xsin2 x=-1sin2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
sh’x=ex-e-x2’=12ex’-e-x’==12ex–e-x=ex+e-x2=chxch’x=ex+e-x2’=12ex’+e-x’==12ex+-e-x=ex-e-x2=shxth’x=shxchx’=sh’x·chx-shx·ch’xch3x=ch3x-sh3xch3x=1ch3xcth’x=chxshx’=ch’x·shx-chx·sh’xsh3x=sh3x-ch3xsh3x=-1sh3x
Рекомендуется выучить формулы из таблицы производных: они не столь сложны для запоминания, но экономят много времени, когда необходимо решать задачи дифференцирования.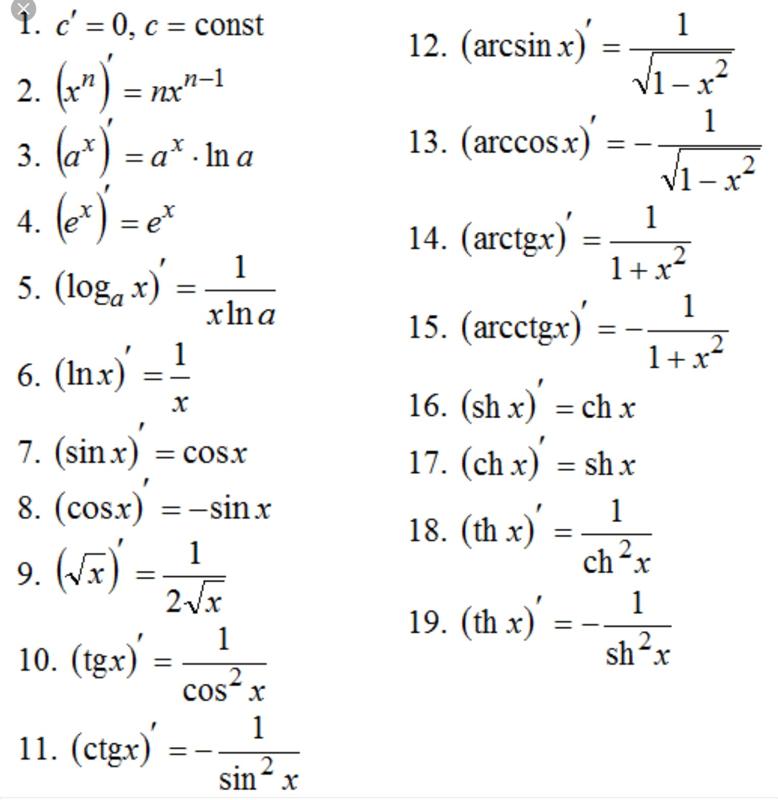
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Производные структуры NET_BUFFER_LIST – Windows drivers
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
NDIS предоставляет функции, которые могут использоваться драйверами для управления структурами NET_BUFFER_LIST , которые являются производными от других структур NET_BUFFER_LIST. Эти функции обычно используются промежуточными драйверами.
Эти функции обычно используются промежуточными драйверами.
Следующие функции NDIS могут создавать производные структуры NET_BUFFER_LIST из существующей структуры NET_BUFFER_LIST:
ндисаллокатеклоненетбуфферлист
ндисаллокатефрагментнетбуфферлист
ндисаллокатереассембледнетбуфферлист
Эти функции улучшают производительность системы, так как NDIS создает производные структуры без копирования сетевых данных. Существует три типа структур NET_BUFFER_LIST , которые могут быть производными от существующей структуры NET_BUFFER_LIST:
Клонировать
Клонированная структура NET_BUFFER_LIST является дубликатом, который ссылается на исходные данные. Драйверы могут использовать этот тип структуры для эффективного перемещения одних и тех же данных в несколько путей.
Fragment
Структура фрагмента NET_BUFFER_LIST содержит набор структур NET_BUFFER , которые ссылаются на исходные данные. Однако данные делятся на единицы, размер которых не превышает максимальный. Драйверы могут использовать этот тип структуры для эффективного разбиения больших буферов на меньшие буферы.
Однако данные делятся на единицы, размер которых не превышает максимальный. Драйверы могут использовать этот тип структуры для эффективного разбиения больших буферов на меньшие буферы.
Соединителем
Собранная структура NET_BUFFER_LIST содержит структуру NET_BUFFER, которая ссылается на исходные данные из нескольких структур NET_BUFFER источника. Драйверы могут использовать этот тип структуры для эффективного объединения большого числа буферов меньшего размера в один большой буфер.
Следующие разделы содержат дополнительные сведения о производных структурах NET_BUFFER_LIST.
- Отношения между поколениями NET_BUFFER_LIST
- Клонированные структуры NET_BUFFER_LIST
- Фрагментированные NET_BUFFER_LIST структуры
- Собранные структуры NET_BUFFER_LIST
реальный анализ – Что такое определение производного числа? (в обшивке Виталий)
спросил
Изменено 4 года, 6 месяцев назад
Просмотрено 2к раз
$\begingroup$
В определении охвата Виталия я вижу слово “производное число”, но не знаю, что оно означает.
Пример покрытия vitali: Если $f$ строго возрастает и
$$E=\{x: \text{ существует производное число } Df(x)
затем
$$\mathcal V=\{V \in I: \lambda(f(V)) образует покрытие Витали для E $\endgroup$ 3 $\begingroup$ Расширенное действительное число N является производным числом в точке $x\in [0,1]$ действительной функции f на [0,1], если существует последовательность $x_n \to x$, $x_n \in [0 ,1]\setminus \{х\}$
такой, что
$$
\frac{ f(x_n) – f(x) }{ x_n – x } \to N
.
$$ [Так что это что-то вроде производной, но вы допускаете многие из них, поскольку для каждой из них у вас есть указанное выше требование только для одной последовательности $x_n$.] Частный случай
$$
\liminf_{y\to x+} \frac{f(y)-f(x)}{y-x}
$$
которое можно было бы назвать правым нижним производным числом $f$ в $x$. Это должно быть определено, например. в:
В. Ярник: Über die Differenzierbarkeit stetiger Funktionen, Fund. Мат. 21 (1933), 48-58. Имеющаяся у меня современная англоязычная литература, к сожалению, определяет только более продвинутые, сильные варианты, такие как существенное производное число (начиная с французского V. Jarník: Sur les nombres dérivés apximatifs, Fund. Math. 22 (1934), 4—16). $\endgroup$ 2 Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но никогда не отображается Электронная почта Требуется, но не отображается [ Действительно, вы можете найти последовательность $x_n$, реализующую это число. ]
Остаются еще три частных случая и/или верхние варианты этого (то есть с «-» вместо «+» и/или с $\limsup$ вместо $\liminf$.
[ Действительно, вы можете найти последовательность $x_n$, реализующую это число. ]
Остаются еще три частных случая и/или верхние варианты этого (то есть с «-» вместо «+» и/или с $\limsup$ вместо $\liminf$. Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Суммирование
Суммирование– Как получаются решения для конечных сумм натуральных чисел?
спросил
Изменено 4 года, 8 месяцев назад
Просмотрено 2к раз
$\begingroup$
Итак, я изучал теорию множеств самостоятельно (Lin, Shwu-Yeng T., and You-Feng Lin. Set Theory: An Intuitive Approach. Houghton Mifflin Co., 1974.) и столкнулся с бесконечными суммами. натуральных чисел. С тех пор, как я много лет назад взялся за алгебру II, я знаю результаты этих сумм для решения суммирования. (Я также знаю формулу (и ее недостатки), которая утверждает, что сумма множества натуральных чисел равна $-1/12$). Просто для справки, ниже я перечислил шесть бесконечных рядов натуральных чисел (это те шесть, которые перечислены в учебнике 44-летней давности, которым я пользуюсь): 9{n}\frac{1}{k(k+1)}=\frac{n}{n+1}$$
Теперь, когда я начал изучать теорию множеств, я теперь знаю, как доказать эти результаты, используя математическая индукция (что, надо признать, доставило мне массу удовольствия). Тем не менее, у меня все еще есть несколько вопросов по этому поводу. Во-первых, путем собственных исследований я нашел список математических серий в Википедии, но в этом списке нет всех серий, перечисленных в учебнике. Итак, есть ли где-нибудь список всех рядов натуральных чисел, и если да, то где? (Теперь, когда я думаю об этом, что, если существует бесконечное количество бесконечных рядов; хотя это может быть так, очевидно, что не все из них будут практичными, поскольку многие, возможно, могут быть упрощены до общих случаев). Во-вторых (и самое главное), хотя я знаю, как доказать эти результаты с помощью математической индукции, я не знаю, как их вывести. Как можно на самом деле получить такой результат для бесконечного ряда? Метод не может быть методом проб и ошибок с использованием математической индукции по случайным выражениям. Я сам не могу придумать метод в настоящее время, но я знаю, что должен быть какой-то способ сделать это. И, наконец, если вы можете придумать лучшее название для вопроса, пожалуйста, дайте мне знать, поскольку у меня возникли проблемы с придумыванием подходящего названия.
Тем не менее, у меня все еще есть несколько вопросов по этому поводу. Во-первых, путем собственных исследований я нашел список математических серий в Википедии, но в этом списке нет всех серий, перечисленных в учебнике. Итак, есть ли где-нибудь список всех рядов натуральных чисел, и если да, то где? (Теперь, когда я думаю об этом, что, если существует бесконечное количество бесконечных рядов; хотя это может быть так, очевидно, что не все из них будут практичными, поскольку многие, возможно, могут быть упрощены до общих случаев). Во-вторых (и самое главное), хотя я знаю, как доказать эти результаты с помощью математической индукции, я не знаю, как их вывести. Как можно на самом деле получить такой результат для бесконечного ряда? Метод не может быть методом проб и ошибок с использованием математической индукции по случайным выражениям. Я сам не могу придумать метод в настоящее время, но я знаю, что должен быть какой-то способ сделать это. И, наконец, если вы можете придумать лучшее название для вопроса, пожалуйста, дайте мне знать, поскольку у меня возникли проблемы с придумыванием подходящего названия. N Df(k) = f(N+1) – f(0).
$$
(Вы можете легко доказать этот факт.)
Этот факт дает метод вычисления конечных сумм, аналогичный методу вычисления интегралов в исчислении. 9х$? Для каких значений $x$ действителен ряд? (Попробуйте принять $x$ за положительное целое число, чтобы восстановить стандартную комбинаторную идентичность.)
N Df(k) = f(N+1) – f(0).
$$
(Вы можете легко доказать этот факт.)
Этот факт дает метод вычисления конечных сумм, аналогичный методу вычисления интегралов в исчислении. 9х$? Для каких значений $x$ действителен ряд? (Попробуйте принять $x$ за положительное целое число, чтобы восстановить стандартную комбинаторную идентичность.)
$\endgroup$
1
$\begingroup$
Судя по вашим примерам, я интерпретирую ваш “бесконечный ряд” как “последовательность частичных сумм, связанных с некоторой последовательностью”. Я буду называть это «выражениями частичной суммы».
9{\mathbb{N}}$ из некоторого набора индексов натуральных чисел $I\subset \mathbb{N}$ (по сути, “перечисление”). Но если в $R$ есть хотя бы два элемента, такой сюръекции не существует!С другой стороны, мы можем перечислить выражения частичной суммы, соответствующие вычислимым последовательностям.
Я буду называть это «вычислимыми выражениями частичной суммы».
Второе (и самое главное), хотя я знаю, как доказать эти результаты с помощью математической индукции…
Даже если рассматривать только вычислимые выражения частичной суммы, не существует алгоритмической процедуры для определения, когда они равны заданной последовательности. Это потому, что такая процедура могла бы сказать нам, когда вычислимая последовательность тождественно равна нулю, но такой процедуры не существует!
Для меня значение этих результатов состоит в том, что исследование общих методов получения закрытых форм для выражений частичной суммы является безнадежным делом, и что вместо этого у человека нет иного выбора, кроме как принять специальный подход.
$\endgroup$
$\begingroup$
Все первые пять ваших уравнений приводят к тому, что сумма многочлена степени $n$ имеет степень $n+1$.

