Производная: определение и основные формулы. 11 класс
Похожие презентации:
Неопределенный интеграл. Основные понятия и определения
Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций
Производная. Основные теоремы о производных. Формулы дифференцирования функций. (Лекция 5)
Производные элементарных функций. 11 класс
Устные упражнения. Определение производной. (10 класс)
Определение производной
Производная показательной функции. 11 класс
Определение производной
Непосредственное вычисление производных. Табличное дифференцирование. Общее определение производной. (Семинар 7)
Определение производной
1. Дистанционный урок «Производная: определение и основные формулы »
алгебра и начала анализа11 класс
2. Содержание:
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

13.
Цели и задачи
Определение производной
Физический смысл производной
Правила дифференцирования
Основные формулы производных
Примеры взятия производных
Производные элементарных функций
Производная сложной функции
Задания для закрепления материала
Задания для самоанализа
Ответы
Домашнее задание
Основная литература
3. Цели и задачи
Цель: познакомиться с одним из важных элементовматематического анализа – производной: ее
определением, физическим смыслом, а также
освоить аппарат нахождения производной различных
функций.
Задачи:
1.
2.
3.
Знать определение производной;
Знать и уметь применять правила
дифференцирования;
Знать и уметь применять формулы для
вычисления производных элементарных
функций.
Определение производной
y
x = x – x0
x = x0 + x
y=f(x)
В
f(x)
приращение аргумента
f
f(x0)
А
f = f(x) – f(x0)
f(x) = f(x0) + f
приращение функции
x
O
x0
x
f f(x0 + x) – f(x0)
— = ———————
x
x
x
разностное
отношение
Производной функции f в точке x0
называется число, к которому
стремится разностное отношение
при x 0.

f f(x0 + x) – f(x0)
f´(x0)= lim — = ———————
при x 0 x
x
Физический смысл производной
x
Если тело движется по прямой и за время t
его координата изменяется на x, то
t t(x0 + x) – t(x0) – средняя скорость
Vср( t) = — = ——————— движения тела за t
x
x
Таким образом, физический смысл
производной – это мгновенная скорость
Правила дифференцирования
Если функция y = f(x) имеет производную, то она называется
дифференцируемой; операция нахождения производной
функции называется дифференцированием.
Пусть f(x) , g(x) – дифференцируемые функции, С – постоянная.
(c f ( x)) c f ( x)
( f ( x) g ( x)) f ( x) g ( x)
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
f ( x) f ( x) g ( x) f ( x) g ( x)
2
g ( x)
g ( x)
Основные формулы производных
x 1
c 0
n 1
x n x
n
x 2
kx b n kx b
n
n 1
1
k
x
Примеры взятия производной
8 0
0
5x 5
5
x 6x
x
8
x 7 x
x
6
7
x5
100
3, 4 x 3, 4
100 x99
100
100 x 101
52 5 32 5 x 3
x x
2
2
1
5
3 4
3
3
4
4 3x 4 x 4 5
x
4 x
Производные элементарных функций
1
ln x
x
log a x
1
x ln a
sin
x
cos x
cos
x
sin x
tgx
1
2
cos x
1
ctgx 2
sin x
x
e e
x
x
a a ln a
x
Производная сложной функции
Пусть f(x) , g(x) – дифференцируемые функции.
 Тогда:
Тогда:f g x
f g x g x
Пример:
sin 4x
5
cos 4 x
3x
2
5
2
5
2
sin 4 x 3x 4 x 3x
5
3x 20 x 6 x
2
4
Задания для закрепления материала
Найдите производные, используя образцы.
5
4
4
Образец:(2 x) 2; (5 x 1) 5; (3x ) 3 5 x 15 x
(4 x) ….
(6 x 2) …..
(3 2 x) …..
(2 x 4 ) ……….
(3×6 ) ………..
Образец:y 3e x ; y 3e x
f ( x) e3 x 1; f ( x) e3 x 1 (3x 1) 3e3 x 1
y 5e x ; y ……..
y e2 x ; y ……….
y 3e4 x ; y 3(e4 x ) …………… …………
y 0,5e6 x 2 ; y 0,5 (e6 x 2 ) 0,5 e………… (…………) ……………….. ……………….
Образец: y 52 x 1;
y 52 x 1 ln 5 (2 x 1) 2ln 5 52 x 1
y 63 2 x ; y ……… ln… (………..) …………………..
y 5 23 x ; y …………………………………………………….
Образец:f ( x)
x2 2x ;
f ( x) ( x 2 ) (2 x ) 2 x 2 x ln 2
f ( x) 2 x4 4x ; f ( x) (.
 …..) (…..) …………………………………………………………
…..) (…..) …………………………………………………………y 3×6 52 x 1; y ……………………………………………………………..
y 4 x5 2 63 2 x ; y ……………………………………………………………..
14. Для каждой из функций, графики которых изображены в верхнем ряду, найдите график ее производной.
Задания для самоанализаЗадание 1. Найдите производные функций:
1. f x 3 x 5
2. f x 4 x 5 x 9 x
2
3
3 x
3. f x
x 3
2
5 7
4. f x 2 3
x
x x
5. f x x 4
1
1
6. f x
2 4x
3x 2 x
Задание 2. Найдите производные функций:
2. f x x 5 x x x
2
3 x
3. f x 3
x
2
2 x 5
4. f x
x 1
5. f x
x 4
3
2
x 2
1 1 2
6. f x 4 x
2 x
English Русский Правила
Производная функции. Формулы и правила дифференцирования .
Тема урока : Производная функции. Формулы и правила дифференцирования .
Формулы и правила дифференцирования .
Конспект урока
Производные – это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным отношением называется отношение разности значения функции к разности значений переменной.
После закрепления знаний по таблице производной, приступаем к изучению теорем дифференцирования.
Теорема 1. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:
Теорема 2. Производная произведения двух функций равна:
Теорема 3. Производная частного двух функций равна:
Приложение 1
Ранее мы рассматривали производные отдельных функций. Здесь мы рассмотрим правила дифференцирования, то есть правила дифференцирования суммы, разности, произведения и частного отдельных функций. Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Производная суммы
Дано: ; .
Существует ; .
Доказать, что существует производная от суммы заданных функций и она вычисляется по следующему правилу:
Доказательство
Пусть задана функция , требуется найти .
По стандартному алгоритму требуется найти отношение :
При получаем:
Что и требовалось доказать.Так, производная от суммы функций равна сумме производных этих функций.Аналогично производная разности функций равна разности производных:
Пример
1. .
2. Найти значение производной функции в точке :
;
Производная произведения
Дано: ; .
Существует ; .
Доказать, что существует производная от произведения и вычисляется она по правилу:
Доказательство .Нужно использовать разностное отношение по стандартному алгоритму нахождения производной. Это разностное отношение можно проиллюстрировать. Пусть есть прямоугольник со сторонами ; . Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
Пусть первая сторона получает приращение , вторая, соответственно, . Приращение может быть любого знака. Получили новый прямоугольник, см. рис. 1.
Рис. 1. Разностное соотношениеПлощадь любого прямоугольника (старого, нового, их разности) мы можем посчитать.Составим разностное соотношение. Пусть , ищем :
При :
А первое слагаемое стремится к нулю, так как стремится к нулю.
Так, производная произведения функций:
Что и требовалось доказать.Рассмотрим важное следствие. Пусть , константа. Согласно правилу:
Так, постоянный множитель можно вынести за знак производной.
Производная степенной функции
Производная степенной функции:
Рассмотрим частные случаи:
;
Найдем эту производную по правилу произведения:
С другой стороны:
И так далее. Поэтому угадывается формула:
– мы принимаем ее без доказательства.
Производная частного
Дано: ; .
Существуют ; .
При этом , а значит, существует дробь .
Доказать, что существует производная частного и вычисляется по формуле:
Доказательство
Представим .
Тогда по формуле производной произведения:
С другой стороны:
Из этих двух выражений получаем уравнение:
Умножим все уравнение на :
Что и требовалось доказать.
Решение примеров
Пример
.
.
Домашнее задание: Итоговые тесты по теме «Производная функции»
1. Найдите производную функции y(х) = x4+ 3x3 + 4.
1) 4x3 + 9x2 + 4
2) 4x3 + 9x2 + 4x
3) 4x2 + 3x2 + 4
4) 4x3 + 9x2
2. Производная функции F(x) = cos(4x) равна:
1) -4sin(4x)
2) 4cos(- 4x)
3) 4xsin(4x)
4) 4xcos(- 4x)
3. Найдите значение производной функции
при х=1
Найдите значение производной функции
при х=1
1) 0,5
2) -1
3) -0,5
4) 1
4. Вычислите значение производной функции в точке .
1) | 16 | 2) | 64 | 3) | – 16 | 4) | – 64 |
5. Найдите производную функции .
1) | 3) | ||
2) | 4) |
6. Найдите производную функции
1) | 3) | ||
2) | 4) |
Просмотр содержимого документа
«Тема урока : Производная функции.
 Формулы и правила дифференцирования .»
Формулы и правила дифференцирования .»Тема урока : Производная функции. Формулы и правила дифференцирования .
Конспект урока
Производные – это такие функции, которые получаются из заданных функций путем вычисления предела разностного отношения. Разностным отношением называется отношение разности значения функции к разности значений переменной.
После закрепления знаний по таблице производной, приступаем к изучению теорем дифференцирования.
Теорема 1. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:
Теорема 2. Производная произведения двух функций равна:
Теорема 3. Производная частного двух функций равна:
Приложение 1
Ранее мы рассматривали производные отдельных функций. Здесь мы рассмотрим правила дифференцирования, то есть правила дифференцирования суммы, разности, произведения и частного отдельных функций. Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Мы выведем соответствующие формулы, обоснуем их и решим типовые примеры.
Производная суммы
Дано: ; .
Существует ; .
Доказать, что существует производная от суммы заданных функций и она вычисляется по следующему правилу:
Доказательство
Пусть задана функция , требуется найти .
По стандартному алгоритму требуется найти отношение :
При получаем:
Что и требовалось доказать.Так, производная от суммы функций равна сумме производных этих функций.Аналогично производная разности функций равна разности производных:
Пример
1. .
2. Найти значение производной функции в точке :
;
Производная произведения
Дано: ; .
Существует ; .
Доказать, что существует производная от произведения и вычисляется она по правилу:
Доказательство .Нужно использовать разностное отношение по стандартному алгоритму нахождения производной.
Рис. 1. Разностное соотношениеПлощадь любого прямоугольника (старого, нового, их разности) мы можем посчитать.Составим разностное соотношение. Пусть , ищем :
При :
А первое слагаемое стремится к нулю, так как стремится к нулю.
Так, производная произведения функций:
Что и требовалось доказать.Рассмотрим важное следствие. Пусть , константа. Согласно правилу:
Так, постоянный множитель можно вынести за знак производной.
Производная степенной функции
Производная степенной функции:
Рассмотрим частные случаи:
;
Найдем эту производную по правилу произведения:
С другой стороны:
И так далее. Поэтому угадывается формула:
Поэтому угадывается формула:
– мы принимаем ее без доказательства.
Производная частного
Дано: ; .
Существуют ; .
При этом , а значит, существует дробь .
Доказать, что существует производная частного и вычисляется по формуле:
Доказательство
Представим .
Тогда по формуле производной произведения:
С другой стороны:
Из этих двух выражений получаем уравнение:
Умножим все уравнение на :
Что и требовалось доказать.
Решение примеров
Пример
.
.
Домашнее задание: Итоговые тесты по теме «Производная функции»
1. Найдите производную функции y(х) = x4+ 3x3 + 4.
1) 4x3 + 9x2 + 4
2) 4x3 + 9x2 + 4x
3) 4x2 + 3x2 + 4
4) 4x3 + 9x2
2.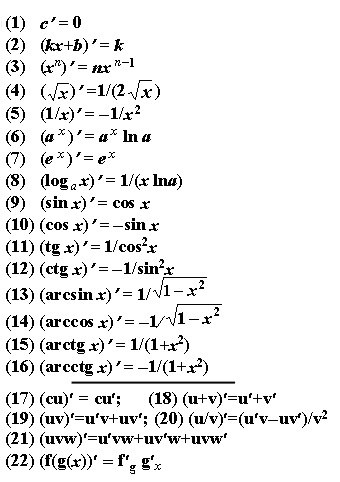 Производная функции F(x) = cos(4x) равна:
Производная функции F(x) = cos(4x) равна:
1) -4sin(4x)
2) 4cos(- 4x)
3) 4xsin(4x)
4) 4xcos(- 4x)
3. Найдите значение производной функции
при х=1
1) 0,5
2) -1
3) -0,5
4) 1
4. Вычислите значение производной функции в точке .
1) | 16 | 2) | 64 | 3) | – 16 | 4) | – 64 |
5. Найдите производную функции .
1) | 3) | ||
2) | 4) |
6. Найдите производную функции
1) | 3) | ||
2) | 4) |
3: Производные – Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2489
- Гилберт Стрэнг и Эдвин «Джед» Герман
- OpenStax
Вычисление скорости и изменения скорости — важное применение исчисления, но оно гораздо более распространено. Исчисление важно во всех областях математики, науки и техники, а также для анализа в бизнесе и здравоохранении. В этой главе мы исследуем один из основных инструментов исчисления — производную — и покажем удобные способы вычисления производной. В этой главе мы применяем эти правила к различным функциям, чтобы затем исследовать применение этих методов.
Исчисление важно во всех областях математики, науки и техники, а также для анализа в бизнесе и здравоохранении. В этой главе мы исследуем один из основных инструментов исчисления — производную — и покажем удобные способы вычисления производной. В этой главе мы применяем эти правила к различным функциям, чтобы затем исследовать применение этих методов.
- 3.0: Prelude to Derivatives
- Вычисление скорости и изменения скорости — важное применение исчисления, но оно гораздо более распространено. Исчисление важно во всех областях математики, науки и техники, а также для анализа в бизнесе и здравоохранении. В этой главе мы исследуем один из основных инструментов исчисления — производную — и покажем удобные способы вычисления производной. В этой главе мы применяем эти правила к различным функциям, чтобы затем изучить их применение.0008
- 3.1: Определение производной
- Наклон касательной к кривой измеряет мгновенную скорость изменения кривой.
 Мы можем вычислить его, найдя предел разностного отношения или разностного отношения с приращением h. Производная функции f(x) при значении a находится с использованием любого из определений наклона касательной. Скорость – это скорость изменения положения. Таким образом, скорость v(t) в момент времени t является производной положения s(t) в момент времени t.
Мы можем вычислить его, найдя предел разностного отношения или разностного отношения с приращением h. Производная функции f(x) при значении a находится с использованием любого из определений наклона касательной. Скорость – это скорость изменения положения. Таким образом, скорость v(t) в момент времени t является производной положения s(t) в момент времени t. - 3.1E: Упражнения к разделу 3.1
- 3.2: Производная как функция
- . График производной функции f(x) связан с графиком f(x). Где (f(x) имеет касательную с положительным наклоном, f′(x)>0. Где (x) имеет касательную с отрицательным наклоном, f′(x)<0. Где f(x) имеет горизонтальную касательной, f′(x)=0. Если функция дифференцируема в точке, то она непрерывна в этой точке.
- 3.2E: Упражнения к разделу 3.2
- 3.3: Правила дифференцирования
- Производная постоянной функции равна нулю.
 Производная степенной функции — это функция, в которой степень x становится коэффициентом при члене, а степень x в производной уменьшается на 1. Производная константы c, умноженная на функцию f, равна константе умножить на производную. Производная суммы функции f и функции g равна сумме производной функции f и производной функции g.
Производная степенной функции — это функция, в которой степень x становится коэффициентом при члене, а степень x в производной уменьшается на 1. Производная константы c, умноженная на функцию f, равна константе умножить на производную. Производная суммы функции f и функции g равна сумме производной функции f и производной функции g. - 3.3E: Упражнения к разделу 3.3
- 3.4: Производные как скорости изменения
- В этом разделе мы рассмотрим некоторые приложения производной как скорости изменения, сосредоточившись на интерпретации скорости производной изменения функции. Эти приложения включают ускорение и скорость в физике, темпы роста населения в биологии и предельные функции в экономике.
- 3.4E: Упражнения к разделу 3.4
- 3.5: Производные тригонометрических функций
- Мы можем найти производные sin x и cos x, используя определение производной и предельные формулы, найденные ранее.
 {n−1}g′(x)\).
{n−1}g′(x)\). - 3.6E: Упражнения к разделу 3.6
- 3.7: Производные обратных функций
- Теорема об обратных функциях позволяет вычислять производные обратных функций без использования предельного определения производных обратных функций. Мы можем использовать теорему об обратной функции для разработки формул дифференцирования для обратных тригонометрических функций.
- 3.7E: Упражнения для раздела 3.7
- 3.8: Неявное дифференцирование
- Мы используем неявное дифференцирование для нахождения производных неявно определенных функций (функций, определяемых уравнениями). Используя неявное дифференцирование, мы можем найти уравнение касательной к графику кривой.
- 3.8E: Упражнения к разделу 3.8
- 3.
 9: Производные экспоненциальных и логарифмических функций
9: Производные экспоненциальных и логарифмических функций - В этом разделе мы исследуем экспоненциальные и логарифмические производные экспоненциальных функций. Как мы обсуждали во Введении в функции и графики, экспоненциальные функции играют важную роль в моделировании роста населения и распада радиоактивных материалов. Логарифмические функции могут помочь изменить масштаб больших величин и особенно полезны для перезаписи сложных выражений.
- 3.9E: Упражнения для раздела 3.9
- 3.
- 3.10: Упражнения на обзор главы 3
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Глава
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
- 10 видео | 1ч 9м 27с
- Включает оценку
- Получает значок
откройте для себя ключевые понятия, изучаемые в этом курсе
получить базовое представление об исчислении и описать дифференцирование и производные
узнать, как рассчитывается уклон между двумя точками
описание того, как вычислить наклон в точке, исследуя геометрическое определение производных
использовать производные в реальных сценариях
схема дифференциальных уравнений и типов разностей
вычисление производных от постоянных функций
вычислить производные линейных и постоянных функций
использовать встроенные функции для вычисления производных
обобщить ключевые понятия, изучаемые в этом курсе
1 м 58 с
БЕСПЛАТНЫЙ ДОСТУП5 м 22 с
БЕСПЛАТНЫЙ ДОСТУП- Заблокировано
3.
 Расчет уклона между двумя точками
Расчет уклона между двумя точками5 м 1 с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
4. Расчет уклона в точке
7м 5с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
5. Применение производных
13м 23с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
6.
 Понимание дифференциальных уравнений и различий
Понимание дифференциальных уравнений и различий8м 19с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
7. Вычисление производных постоянных функций
6 м 52 с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
8. Вычисление производных линейных функций
7 м 52 с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
9.
 Вычисление производных с помощью встроенных функций
Вычисление производных с помощью встроенных функций11м 31с
БЕСПЛАТНЫЙ ДОСТУП - Заблокировано
10. Резюме курса
2м 5с
БЕСПЛАТНЫЙ ДОСТУП
0 Производная BY; OpenStax)
Эта страница под названием 3: Деривативы распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
Исчисление: начало работы с производными — математика — СРЕДНИЙ
Математика | Средний
Исчисление — это раздел математики, который занимается непрерывными изменениями и тем, как изменяется результат функции, когда входные данные этой функции изменяются на исчезающе малые величины. Исчисление имеет широкое применение — в оптимизации, машинном обучении, экономике и медицине. Вы начнете этот курс с определения производной с точки зрения ее математической формулы и интерпретации этой производной функции в точке двумя способами: как наклон касательной к функции в этой точке или как мгновенная скорость изменения эта функция в этот момент. Вы также примените эти концепции к постоянной функции, убедитесь, что ее производная равна нулю, и поймете причину этого. К тому времени, когда вы закончите этот курс, у вас будет хорошая основа в основах дифференциального исчисления.
Вы также примените эти концепции к постоянной функции, убедитесь, что ее производная равна нулю, и поймете причину этого. К тому времени, когда вы закончите этот курс, у вас будет хорошая основа в основах дифференциального исчисления.
Skillsoft предоставляет вам возможность заработать цифровой значок после успешного завершения некоторых из наших курсов, которым можно поделиться в любой социальной сети или бизнес-платформе.

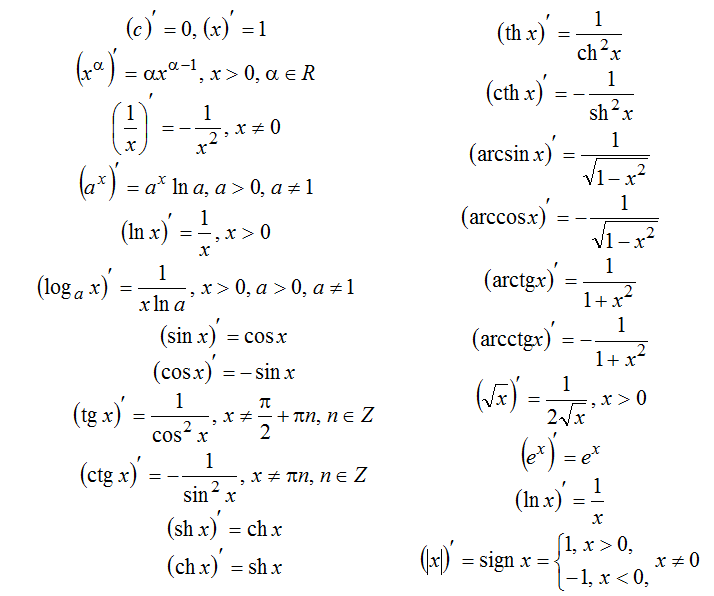 Мы можем вычислить его, найдя предел разностного отношения или разностного отношения с приращением h. Производная функции f(x) при значении a находится с использованием любого из определений наклона касательной. Скорость – это скорость изменения положения. Таким образом, скорость v(t) в момент времени t является производной положения s(t) в момент времени t.
Мы можем вычислить его, найдя предел разностного отношения или разностного отношения с приращением h. Производная функции f(x) при значении a находится с использованием любого из определений наклона касательной. Скорость – это скорость изменения положения. Таким образом, скорость v(t) в момент времени t является производной положения s(t) в момент времени t. Производная степенной функции — это функция, в которой степень x становится коэффициентом при члене, а степень x в производной уменьшается на 1. Производная константы c, умноженная на функцию f, равна константе умножить на производную. Производная суммы функции f и функции g равна сумме производной функции f и производной функции g.
Производная степенной функции — это функция, в которой степень x становится коэффициентом при члене, а степень x в производной уменьшается на 1. Производная константы c, умноженная на функцию f, равна константе умножить на производную. Производная суммы функции f и функции g равна сумме производной функции f и производной функции g. {n−1}g′(x)\).
{n−1}g′(x)\). 9: Производные экспоненциальных и логарифмических функций
9: Производные экспоненциальных и логарифмических функций org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 Расчет уклона между двумя точками
Расчет уклона между двумя точками Понимание дифференциальных уравнений и различий
Понимание дифференциальных уравнений и различий Вычисление производных с помощью встроенных функций
Вычисление производных с помощью встроенных функций