Производные и интегралы: Урок 2 Интеграл и производная : Русский как неродной - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Типы задач, поддерживаемые помощником по преобразованию в математические выражения

При использовании помощника по математическим формулам в OneNoteвы заметите, что в зависимости от выбранного уравнения изменяется в dropdown Select an action (Выбрать действие) под формулой. Вот некоторые из типов проблем, которые поддерживаются в зависимости от формулы, которая вы пытаетесь решить.

Массивы	Для списка реальных чисел поддерживаются все ниже. Оценить Сортировка Среднее Медиана Мода Сумма Продукт Наибольший распространенный фактор Наименьшее общее кратное Дисперсия Стандартное отклонение Минимумы Максимум Для полиномиалов поддерживаются действия Наибольший общий фактор и Наименьший распространенный кратное. Чтобы просмотреть графики всех функций, можно также выбрать вариант График в двухдд.
Выражения	Для любого выражения доступны такие действия: Оценить Проверяем подлинность Развернуть (если применимо) Фактор (если применимо) Двухявная диаграмма (доступна только при наличии переменной) Дифференцировать (доступно только при наличии переменной) Интеграция (доступна только при наличии переменной)
Уравнения и уравнения	Для уравнений и уравнений доступны следующие действия: Решение для {переменной} Двухуголовые диаграммы. Каждая сторона равенства или разноявной разлияется в виде отдельной функции. Двухуголовые диаграммы — график уравнений или разнонавязных решений Graph Graph — пометка области решения на графике
Системы	Важно иметь одинаковое количество формул и переменных, чтобы обеспечить доступ к правильным функциям. Системы можно писать двумя способами: Одна под другой, с большой скобки или без нее перед ними В одной строке, разделенной запятой
Производные и интегралы	Производные могут быть записаны перед функцией с помощью d/dx или с помощью первой метки. Действия, доступные для производных продуктов и интегралов: Оценить Двухуголовые графики Дифференцировать Интеграция (только для производных
Матриц	Матрицы можно в квадратных или круглых скобках. Для матриц поддерживаются следующие действия: Оценить Вычислять определители Инвертировать матрицу Вычисления трассировки Транспонная матрица Размер матрицы Уменьшение матрицы Матричные уравнения в настоящее время не поддерживаются.
График в координатах	Для графизации функции в координатах координаты r должны быть выражены как функцияta.
Сложный режим	Примечание. Выберите Параметры, чтобы переключаться между реальными и комплексными числами. Для сложных выражений и чисел, содержащих мнимую единицу i, доступны следующие действия: Оценить Real Part Мнимая часть Конъюгированная Модуль Аргумент Дифференцировать (только если имеется переменная) Интеграция (только если имеется переменная)

См.

также

Создание математических формул с помощью рукописного ввода или текста в OneNote с использованием помощника по преобразованию в математические выражения

Решение уравнений с помощью помощника по математике в OneNote

Построение графиков математических функций в OneNote с использованием помощника по преобразованию в математические выражения

Производные и интегралы от стационарных функций

Интегралы такого вида характерны для различных задач дифракции. Рассмотрим один из часто используемых методов их приближенного вычисления — метод стационарной фазы. Сущность его состоит в том, что в мнимый показатель экспоненты, стоящей под интегралом, входит безразмерный большой параметр рг > I. Поэтому с изменением переменной г подынтегральная функция быстро осциллирует, так что существенный вклад в интеграл вносит лишь малый учя юк оси г.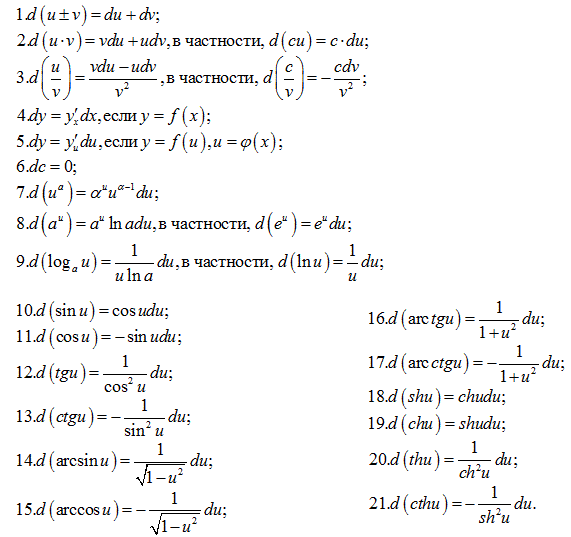

включающий точку, где производная от подынтегральной функции по г обращается в нуль (отсюда название метода). [c.175]
Мы заменяем первоначальный интеграл суммой (2.7.13) и ищем стационарное значение этой суммы. Это уже задача обычного типа задана функция S п переменных yi,. .., г/ (вместо фигурировавших раньше переменных Ui,. .., u ). Мы знаем, что задача решается приравниванием нулю частных производных S по у . В заключение придется лишь исследовать переход /S.x 0. [c.75]

Обращение в нуль G происходит тогда, когда существует интеграл Якоби или вообще какой-нибудь однозначный пространственный интеграл. Пусть / (xi, Х2, Хп, fi) есть такой интеграл. Частную производную df/dXr обозначим через /г- Предположим, что ас = а не является стационарной точкой функции / (зс 0), т. е. не все производные (а 0) равны нулю. Тогда в силу (21.1.9) и (30.7.13) т — i первых производных /г (а 0) не могут все равняться нулю, и, расположив переменные в определенном порядке, мы всегда мон[c. 615]

Аналогично формулируется условие максимума функционала. Из условия стационарности (9) может быть получено дифференциальное уравнение, которому должна удовлетворять искомая функция, доставляющая стационарное значение функционалу, а также те граничные условия, которым она может быть подчинена. Для этого, последовательно интегрируя выражение для первой вариации функционала (7) по частям, избавимся от вариаций производных искомой функции под знаком интеграла ь [c.383]

Поскольку коэффициенты в уравнении (4.3.24) зависят от времени через одночастичную функцию распределения, найти точное решение этого уравнения не удается. Однако его можно решить в марковском приближении, т. е. в случае достаточно медленных процессов, когда можно пренебречь производной по времени в левой части. Простейшее стационарное решение, которое соответствует борновскому приближению для интеграла столкновений, легко найти, если пренебречь двумя последними членами в уравнении (4. 3.24). Подставляя результат в (4.3.21), получим интеграл столкновений [c.287]

Пользуясь каноническими уравнениями Гамильтона, легко получить интеграл энергии для случая стационарных связей. Докажем сначала, что полная производная по времени от функции Гамильтона Я равна частной производной от той же функции по времени. [c.514]

Л. А. Галин [102] рассмотрел задачу о круговом штампе с помощью функции Грина для пространства с плоским круговым разрезом. Он получил выражение для давления под основанием штампа в виде производной от некоторого несобственного интеграла и простую формулу для величины прижимающей силы. В случае, когда задача является осесимметричной и поверхность штампа гладкая, Л. А. Галин получил простую формулу для определения давления под основанием штампа, осадки штампа, Л. А. Галин рассмотрел также задачу о влиянии нагрузки, действующей вне штампа, на распределение давления под основанием штампа в частности, им получена простая формула для давления под основанием плоского штампа, находящегося под действием центральной силы, при наличии сосредоточенной нормальной силы вне штампа.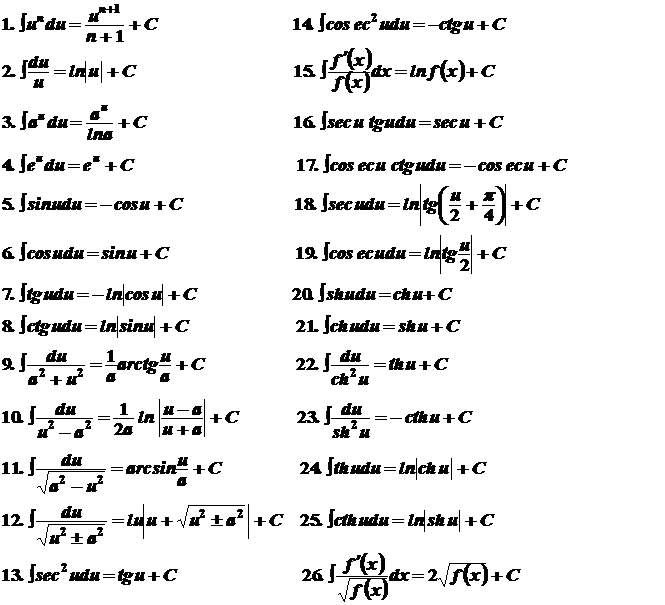 Кроме того, Л. А. Галин рассмотрел задачу об учете сил трения при стационарном вращении штампа в предположении, что задача является осесимметричной и силы трения, действующие по всей площадке контакта, зависят только от скорости вращения. В этом случае Л. А. Галин доказал, что силы трения ие влияют на распределение давления под штампом, и получил ряд формул для величины. момента, [c.197]

Что метод перевала не может дать, так это учет сближения критических точек. Пусть, например, простая перевальная точка у , расположена вблизи концевой точки а контура у. Асимптотика, полученная методом перевала, равна сумме вкладов (11.9) стационарной точки и (11.15) точки и = = а. Если р фиксировано, а – а, то f a) -> О, и соотношение (11.15) Теряет смысл. Однако при совпадении особенностей метод перевала пригоден. В нашем примере при а асимптотика интеграла дается формулой (11. 16). Когда Ф ан + , всегда найдется достаточно большое значение р, при котором можно пользоваться формулами (11.

9) и (11.15). Только при =а нужно использовать другую формулу – (11.16). Большим параметром в методе перевала, в сущности, является не р, а величина, характеризующая медленность изменения функций / и в существенной при интегрировании окрестности критической точки. Напри мер, в (11.15) истинным большим параметром будет pf a) p a w ), если / ” и производные Р порядка единицы. При сближении двух стационарных точек большой параметр — зто р х (см, (11.26)). [c.225]

Чтобы найти полную свободную энергию макроскопического образца, проинтегрируем выражение (5.195) по всему объему. Получающийся интеграл будет функционалом неизвестной функции распределения порядка г (г), по которой и следует производить варьирование, чтобы найти стационарное значение F. Вычисление функциональной производной (5.191) приводит к дифференциальному уравнению в частных производных [c.235]

Если Ш (х) — четная функция, то производная IV (х) — нечетная функция, уравнение (11. 21) имеет один корень к при ж > О и этот корень положителен. Поэтому первый интеграл в формуле (11.16) дает только один вклад. Однако для второго интеграла в решении (11.16) стационарные точки удовлетворяют уравнению [c.359]

Из последних выражений следует, что интеграл от стационарной случайной функции на интервале [О, Л не будет стационарной функцией. Действительно, интегрирование сигнала, в частности, приводит к перераспределению энергии сигнала в область низких частот и к появлению низкочастотного тренда, что обусловливает возможную пестационарность процесса после интегрирования. Таким образом, если измеряемый процесс (виброперемещение) является стационарным, то его производные (виброскорость или виброускорение) могут приниматься также стационарными без дополнительных проверок. Чтобы судить о стационарности интегрально преобразованного сигнала, необходимо располагать его значениями на интервале [О, Г], причем Т t. [c.57]

Уравнение (4. 3) называют уравнением Лапласа. Как видно, нестационарные процессы распространения тепла описываются уравнением теплопроводности, стационарные — уравнением Лапласа или Пуассона. Огметим, что уравнения (4.1). .. (4.3) описывают и многие другие физические процессы, а не только связанные с переносом тепла (например, диффузию). Любые функции класса т. е. непрерывные вместе с производными до второго порядка включительно, удовлетворяющие уравнению Лапласа, называются гармоническими функциями. Задачи, связанные с отысканием решений уравнения Лапласа, называют гармоническими задачами. При постановке и решении гармонических задач важное значение имеет следующее свойство гармонических функций интеграл по замкнутой поверхности от нормальной производной гармонической функции равен нулю. Пусть функция и (М) (D). Воспользуемся формулой Остроградского—Гаусса применительно к вектору grad и [c.120]

Интерактивное пособие по алгебре для 10-11 классов

Описание Электронное пособие «Производные и интегралы» посвящено одной из самых трудных для понимания школьником тем курса математики.

Пособие поможет ребёнку быстро разобраться с принципами выполнения заданий, в которых встречаются интегралы и производные, и освоить тему в рамках школьной программы.
Программа разработана с учётом возрастных особенностей школьников, соблюдением санитарных требований при работе на компьютере и снабжена интуитивно понятным интерфейсом.

Тренажёр пособия имеет три режима работы
• Режим обучения предназначен для использования учеником во время учебного процесса. Он выбирает тему, а тренажер генерирует задание. Каждое последующее задание по теме отличается от предыдущего параметрами, условием и формулировкой вопроса.
• В режиме самостоятельной работы формируется группа из нескольких заданий, выполнение которых учеником обязательно (ученик не может перейти к следующему заданию, не решив правильно предыдущего).
• В режиме контроля формируется группа из нескольких заданий, решение которых позволяет объективно оценить знания ученика по выбранной теме (оценка выставляется компьютером).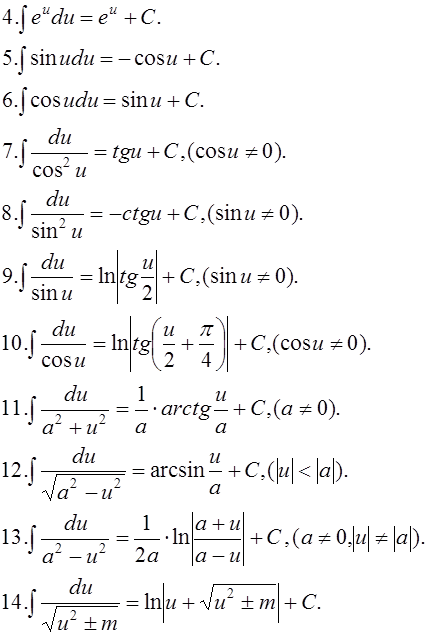

Наличие плакатов по каждой изучаемой теме и возможность изменения размеров рабочего поля позволяет применять пособие как на обычном компьютере при индивидуальном обучении, так и в классе при использовании электронной интерактивной доски. Пособие предназначено для учителей и учеников 10–11-х классов.

Скачать демоверсию

Скачать бесплатную демоверсию электронного пособия “Производные и интегралы”
Объем программы – 1,3 Мб.
Демоверсия расположена на ресурсе Яндекс. Диск.
Проверено антивирусной программой.
Примечание: если у вас демонстрационная версия программы не запускается, попробуйте отключить антивирусную программу и скачать программу ещё раз.

Технические характеристики

Язык интерфейса программы – русский.
Операционная система – Windows 2000/XP/Vista/7/8/10.
Примечание: приложение НЕ работает на платформах Linux, Mac и Android.

Оплата и доставка

– Методы оплаты
Вы можете выбрать наиболее удобный для Вас способ оплаты.

Интернет-магазин “Интеграл” предлагает Вам следующие варианты оплаты:

Банковские карты.
Интернет-банкинг – онлайн платежи.
Терминалы оплаты.
Банковские переводы.
Электронные деньги.

Более подробнее о методах оплаты.
– Доставка
Электронная доставка бесплатная. Электронный ключ или ключ активации высылается на e-mail заказчика после оплаты. При необходимости также высылается ссылка на скачивание.
На текущий момент мы не пересылаем покупателям коробочные версии или программы, записанные на CD или DVD носителях.
По всем вопросам обращайтесь на наш контактный e-mail: [email protected].

Отзывы покупателей о программе

Отзывов пока нет!

13.2: Производные и интегралы векторных функций

Чтобы изучить исчисление векторных функций, мы идем по тому же пути, что и при изучении действительных функций. Сначала мы определяем производную, затем исследуем приложения производной, а затем переходим к определению интегралов. Однако по пути мы найдем некоторые интересные новые идеи в результате векторной природы этих функций и свойств пространственных кривых.

Производные векторных функций

Теперь, когда мы увидели, что такое вектор-функция и как выйти за ее пределы, следующий шаг – научиться дифференцировать вектор-функцию.Определение производной векторной функции почти идентично определению вещественной функции одной переменной. Однако, поскольку диапазон векторной функции состоит из векторов, то же самое верно и для диапазона производной векторной функции.

Определение: производная векторных функций

Производная векторной функции \ (\ vecs {r} (t) \) равна

\ [\ vecs {r} ′ (t) = \ lim \ limits _ {\ Delta t \ to 0} \ dfrac {\ vecs {r} (t + \ Delta t) – \ vecs {r} (t)} { \ Delta t} \ label {eq1} \]

при наличии ограничения.-} \ dfrac {\ vecs {r} (b + \ Delta t) – \ vecs {r} (b)} {\ Delta t} \]

Многие правила вычисления производных от действительных функций могут быть применены также к вычислению производных от векторных функций. Напомним, что производную функции с действительным знаком можно интерпретировать как наклон касательной или мгновенную скорость изменения функции. Производная векторной функции также может пониматься как мгновенная скорость изменения; например, когда функция представляет положение объекта в данный момент времени, производная представляет его скорость в тот же момент времени.2 + 3) \, \ mathbf {\ hat {i}} + (5t − 6) \, \ mathbf {\ hat {j}} \).

Подсказка: Используйте уравнение \ ref {eq1}.

Ответ: \ [\ vecs {r} ′ (t) = 4t \, \ mathbf {\ hat {i}} + 5 \, \ mathbf {\ hat {j}} \ nonumber \]

Обратите внимание, что в вычислениях в примере \ (\ PageIndex {1} \) мы также могли получить ответ, сначала вычислив производную каждой компонентной функции, а затем поместив эти производные обратно в векторнозначную функцию.Это всегда верно для вычисления производной векторнозначной функции, будь то в двух или трех измерениях. Сформулируем это в следующей теореме. Доказательство этой теоремы следует непосредственно из определений предела векторной функции и производной векторной функции.

Теорема \ (\ PageIndex {1} \): Дифференцирование векторных функций

Пусть \ (f \), \ (g \) и \ (h \) – дифференцируемые функции от \ (t \).

Если \ (\ vecs {r} (t) = f (t) \, \ mathbf {\ hat {i}} + g (t) \, \ mathbf {\ hat {j}} \), то \ [ \ vecs {r} ′ (t) = f ′ (t) \, \ mathbf {\ hat {i}} + g ′ (t) \, \ mathbf {\ hat {j}}.t \, \ mathbf {\ hat {j}} – (\ sin t + \ cos t) \, \ mathbf {\ hat {k}} \ nonumber \]
Мы можем распространить на вектор-функции свойства производной, которые мы представили ранее. В частности, правило множественных констант, правила суммы и разности, правило произведения и правило цепочки распространяются на векторнозначные функции. Однако в случае правила продукта на самом деле есть три расширения:
1. для действительной функции, умноженной на векторную функцию,
2. для скалярного произведения двух векторных функций и
3. для векторного произведения двух векторных функций.
Теорема: свойства производной векторных функций
Пусть \ (\ vecs {r} \) и \ (\ vecs {u} \) – дифференцируемые вектор-функции от \ (t \), пусть \ (f \) – дифференцируемая вещественнозначная функция от \ ( t \), и пусть \ (c \) – скаляр.
\ [\ begin {array} {lrcll} \ mathrm {i.} & \ Dfrac {d} {\, dt} [c \ vecs r (t)] & = & c \ vecs r ‘(t) & \ text {Скалярное кратное} \ nonumber \\ \ mathrm {ii.} & \ dfrac {d} {\, dt} [\ vecs r (t) ± \ vecs u (t)] & = & \ vecs r ‘(t ) ± \ vecs u ′ (t) & \ text {Сумма и разность} \ nonumber \\ \ mathrm {iii.} & \ dfrac {d} {\, dt} [f (t) \ vecs u (t)] & = & f ′ (t) \ vecs u (t) + f (t) \ vecs u ′ (t) & \ text {Скалярное произведение} \ nonumber \\ \ mathrm {iv.} & \ dfrac {d} {\, dt} [\ vecs r (t) ⋅ \ vecs u (t)] & = & \ vecs r ′ (t) ⋅ \ vecs u (t) + \ vecs r (t) ⋅ \ vecs u ′ (t) & \ text {Точечный продукт} \ nonumber \\ \ mathrm {v.} & \ dfrac {d} {\ , dt} [\ vecs r (t) × \ vecs u (t)] & = & \ vecs r ′ (t) × \ vecs u (t) + \ vecs r (t) × \ vecs u ′ (t) & \ text {Перекрестное произведение} \ nonumber \\ \ mathrm {vi. 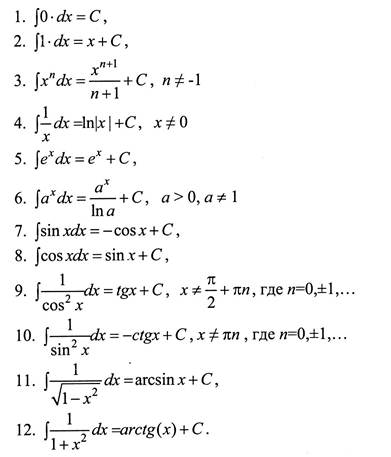} & \ dfrac {d} {\, dt} [\ vecs r (f (t))] & = & \ vecs r ′ (f (t )) ⋅f ′ (t) & \ text {Цепное правило} \ nonumber \\ \ mathrm {vii.} & \ text {Если} \; \ vecs r (t) · \ vecs r (t) & = & c, \ text {then} \; \ vecs r (t) ⋅ \ vecs r ′ (t) \; = 0 \; . & \ mathrm {} \ nonumber \ end {array} \ nonumber \]
Проба
Доказательства первых двух свойств следуют непосредственно из определения производной векторнозначной функции. Третье свойство может быть получено из первых двух свойств вместе с правилом продукта. Пусть \ (\ vecs u (t) = g (t) \, \ mathbf {\ hat {i}} + h (t) \, \ mathbf {\ hat {j}} \). Тогда
\ [\ begin {align *} \ dfrac {d} {\, dt} [f (t) \ vecs u (t)] & = \ dfrac {d} {\, dt} [f (t) (g (t) \, \ mathbf {\ hat {i}} + h (t) \, \ mathbf {\ hat {j}})] \\ [4pt]
& = \ dfrac {d} {\, dt} [f (t) g (t) \, \ mathbf {\ hat {i}} + f (t) h (t) \, \ mathbf {\ hat {j}}] \\ [4pt]
& = \ dfrac {d} {\, dt} [f (t) g (t)] \, \ mathbf {\ hat {i}} + \ dfrac {d} {\, dt} [f (t) h (t) ] \, \ mathbf {\ hat {j}} \\ [4pt]
& = (f ′ (t) g (t) + f (t) g ′ (t)) \, \ mathbf {\ hat {i }} + (f ′ (t) h (t) + f (t) h ′ (t)) \, \ mathbf {\ hat {j}} \\ [4pt]
& = f ′ (t) \ vecs u (t) + f (t) \ vecs u ′ (t). \ end {align *} \]
Для подтверждения собственности iv. пусть \ (\ vecs r (t) = f_1 (t) \, \ mathbf {\ hat {i}} + g_1 (t) \, \ mathbf {\ hat {j}} \) и \ (\ vecs u ( t) = f_2 (t) \, \ mathbf {\ hat {i}} + g_2 (t) \, \ mathbf {\ hat {j}} \). Тогда
\ [\ begin {align *} \ dfrac {d} {\, dt} [\ vecs r (t) ⋅ \ vecs u (t)] & = \ dfrac {d} {\, dt} [f_1 (t ) f_2 (t) + g_1 (t) g_2 (t)] \\ [4pt]
& = f_1 ′ (t) f_2 (t) + f_1 (t) f_2 ′ (t) + g_1 ′ (t) g_2 ( t) + g_1 (t) g_2 ′ (t) = f_1 ′ (t) f_2 (t) + g_1 ′ (t) g_2 (t) + f_1 (t) f_2 ′ (t) + g_1 (t) g_2 ′ ( t) \\ [4pt]
& = (f_1 ′ \, \ mathbf {\ hat {i}} + g_1 ′ \, \ mathbf {\ hat {j}}) ⋅ (f_2 \, \ mathbf {\ hat { i}} + g_2 \, \ mathbf {\ hat {j}}) + (f_1 \, \ mathbf {\ hat {i}} + g_1 \, \ mathbf {\ hat {j}}) ⋅ (f_2 ′ \ , \ mathbf {\ hat {i}} + g_2 ′ \, \ mathbf {\ hat {j}}) \\ [4pt]
& = \ vecs r ′ (t) ⋅ \ vecs u (t) + \ vecs r (t) ⋅ \ vecs u ′ (t).\ end {align *} \]
Доказательство свойства v. Аналогично доказательству свойства iv. Свойство vi. можно доказать с помощью цепного правила. Наконец, свойство vii. следует из свойства iv:
\ [\ begin {align *} \ dfrac {d} {\, dt} [\ vecs r (t) · \ vecs r (t)] & = \ dfrac {d} {\, dt} [c] \ \ [4pt]
\ vecs r ′ (t) · \ vecs r (t) + \ vecs r (t) · \ vecs r ′ (t) & = 0 \\ [4pt]
2 \ vecs r (t) · \ Vecs r ′ (t) & = 0 \\ [4pt]
\ vecs r (t) · \ vecs r ′ (t) & = 0 \ end {align *} \]
Теперь несколько примеров использования этих свойств.3−3t) \, \ mathbf {\ hat {k}}, \ nonumber \]
вычисляет каждую из следующих производных, используя свойства производной векторнозначных функций.
1. \ (\ dfrac {d} {\, dt} [\ vecs {r} (t) ⋅ \ vecs {u} (t)] \)
2. \ (\ dfrac {d} {\, dt} [\ vecs {u} (t) \ times \ vecs {u} ′ (t)] \)
Решение
У нас есть \ (\ vecs {r} ′ (t) = 6 \, \ mathbf {\ hat {i}} + (8t + 2) \, \ mathbf {\ hat {j}} + 5 \, \ mathbf {\ hat {k}} \) и \ (\ vecs {u} ′ (t) = 2t \, \ mathbf {\ hat {i}} + 2 \, \ mathbf {\ hat {j}} + (3t ^ 2−3) \, \ mathbf {\ hat {k}} \). 2−3) \, \ mathbf {\ hat {k}}] = 2 \, \ mathbf {\ hat {i} } + 6t \, \ mathbf {\ hat {k}}.{2t} (2t + 1) – \ sin 2t) \, \ mathbf {\ hat {j}} + (t \ cos t + \ sin t− \ cos 2t) \, \ mathbf {\ hat {k}} \ )
Касательные векторы и единичные касательные векторы
Напомним, что производную в точке можно интерпретировать как наклон касательной к графику в этой точке. В случае векторной функции производная представляет собой касательный вектор к кривой, представленной функцией. Рассмотрим вектор-функцию
\ [\ vecs {r} (t) = \ cos t \, \ mathbf {\ hat {i}} + \ sin t \, \ mathbf {\ hat {j}} \ label {eq10} \]
Производная этой функции равна
.
\ [\ vecs {r} ′ (t) = – \ sin t \, \ mathbf {\ hat {i}} + \ cos t \, \ mathbf {\ hat {j}} \ nonumber \]
Если мы подставим значение \ (t = π / 6 \) в обе функции, мы получим
\ [\ vecs {r} \ left (\ dfrac {π} {6} \ right) = \ dfrac {\ sqrt {3}} {2} \, \ mathbf {\ hat {i}} + \ dfrac { 1} {2} \, \ mathbf {\ hat {j}} \ nonumber \]
и
\ [\ vecs {r} ′ \ left (\ dfrac {π} {6} \ right) = – \ dfrac {1} {2} \, \ mathbf {\ hat {i}} + \ dfrac {\ sqrt {3}} {2} \, \ mathbf {\ hat {j}}.\ nonumber \]
График этой функции показан на рисунке \ (\ PageIndex {1} \) вместе с векторами \ (\ vecs {r} \ left (\ dfrac {π} {6} \ right) \) и \ (\ vecs {r} ‘\ left (\ dfrac {π} {6} \ right) \).
Рисунок \ (\ PageIndex {1} \): касательная в точке вычисляется по производной векторнозначной функции \ (\ vecs {r} (t) \).
Обратите внимание, что вектор \ (\ vecs {r} ′ \ left (\ dfrac {π} {6} \ right) \) касается окружности в точке, соответствующей \ (t = \ dfrac {π} {6 } \). Это пример касательного вектора к плоской кривой, определяемой уравнением \ ref {eq10}.
Определение: касательный вектор главной единицы
Пусть \ (C \) кривая, заданная векторнозначной функцией \ (\ vecs {r} \), и предположим, что \ (\ vecs {r} ′ (t) \) существует, когда \ (\ mathrm { t = t_0} \) Касательный вектор \ (\ vecs {r} \) в \ (t = t_0 \) – это любой вектор, такой, что, когда хвост вектора помещен в точку \ (\ vecs r (t_0) \) на графике вектор \ (\ vecs {r} \) касается кривой \ (C \). 2−3) \, \ mathbf {\ hat {i}} + (2t + 1) \, \ mathbf {\ hat {j}} + (t − 2 ) \, \ mathbf {\ hat {k}}.2 + 5}} \, \ mathbf {\ hat {k}} \ nonumber \]
Интегралы от векторных функций
Мы ввели первообразные вещественнозначных функций в первообразных и определенные интегралы вещественнозначных функций в Определенном интеграле. Каждое из этих понятий может быть расширено до векторных функций. Кроме того, точно так же, как мы можем вычислить производную векторнозначной функции, дифференцируя составляющие функции по отдельности, мы можем вычислить первообразную таким же образом.Кроме того, основная теорема исчисления применима также к векторным функциям.
Первообразная векторной функции появляется в приложениях. Например, если векторная функция представляет скорость объекта в момент времени t , то ее первообразная представляет положение. Или, если функция представляет ускорение объекта в данный момент времени, тогда первообразная представляет его скорость. bh (t) \, dt \ right] \, \ hat {\ mathbf {k}}.\]

Поскольку неопределенный интеграл векторной функции включает неопределенные интегралы компонентных функций, каждый из этих компонентных интегралов содержит константу интегрирования. Все они могут быть разными. Например, в двумерном случае мы можем иметь

\ [\ int f (t) \, dt = F (t) + C_1 \; а также \; \ int g (t) \, dt = G (t) + C_2, \ nonumber \]

, где \ (F \) и \ (G \) – первообразные от \ (f \) и \ (g \) соответственно. Тогда

\ [\ begin {align *} \ int [f (t) \, \ hat {\ mathbf {i}} + g (t) \, \ hat {\ mathbf {j}}] \, dt & = \ left [\ int f (t) \, dt \ right] \, \ hat {\ mathbf {i}} + \ left [\ int g (t) \, dt \ right] \, \ hat {\ mathbf {j }} \\ [4pt]
& = (F (t) + C_1) \, \ hat {\ mathbf {i}} + (G (t) + C_2) \, \ hat {\ mathbf {j}} \ \ [4pt]
& = F (t) \, \ hat {\ mathbf {i}} + G (t) \, \ hat {\ mathbf {j}} + C_1 \, \ hat {\ mathbf {i} } + C_2 \, \ hat {\ mathbf {j}} \\ [4pt]
& = F (t) \, \ hat {\ mathbf {i}} + G (t) \, \ hat {\ mathbf { j}} + \ vecs {C} \ end {align *} \]

, где \ (\ vecs {C} = C_1 \, \ hat {\ mathbf {i}} + C_2 \, \ hat {\ mathbf {j}} \).2−4t) \, \ mathbf {\ hat {j}}] \, dt = 16 \, \ mathbf {\ hat {i}} + 10 \, \ mathbf {\ hat {j}} \ nonumber \]

Исчисление: дифференциалы и интегралы

Дифференциация: Насколько быстро что-то меняется?

Скорость – это скорость изменения смещения. Рассмотрим очень простой случай. Странный человек в этой анимации движется по прямой с постоянной скоростью один метр в секунду. Это означает, что за каждую секунду его перемещения его смещение от исходного положения увеличивается на 1 м.

(Помимо физиков: скорость – это вектор, что означает, что у него есть направление, а также величина. Итак, здесь мы могли бы сказать, что его скорость составляет 1 м / с, а его скорость – 1 м / с вправо. В этих примерах , мы будем рассматривать только движение по прямой, поэтому мы можем указать направление просто так: положительная скорость означает движение вправо, отрицательная скорость означает движение влево. Между прочим, величина скорости называется скоростью, которая мы могли бы написать как | v |.Скорость – это скаляр, скорость – вектор. Просмотреть векторы для исправления.)

Когда часы показывают ноль, он находится в точке x = 3 м. Назовем это его начальным смещением и запишем x ₀ = 3 м.

Когда часы показывают t = 2 с, он находится на x = 5 м. Так что же такое v? Водоизмещение увеличилось на 2 м, время увеличилось на 2 с, поэтому v равно

Обратите внимание на геометрическое значение получения производной: если посмотреть на треугольник, нарисованный на этом графике, высота равна 2 м, а основание – 2 с, поэтому производная представляет собой наклон графика . Часто говорят, что это рост (здесь Δx) по сравнению с пробегом (здесь Δt). Также обратите внимание, что в этом случае не имеет значения, насколько большой или где мы рисуем треугольник.Если бы мы сделали пробег 0,3 с, то подъем был бы 0,3 м и т. Д. Это, однако, только для этого особого случая, когда v является постоянным, а значит, v и одинаковыми. Производная x в этом случае постоянна, как показано на графике v (t) выше.

Различные производные

Что, если v не постоянна? Вот простой случай, когда тот же парень ускоряется вперед, поэтому его скорость увеличивается. Давайте рассчитаем его скорость в любой конкретный момент времени t, просто используя график x (t).Мы хотим найти наклон этой кривой при различных значениях t, как показано на анимации. Как мы можем сделать это? Что ж, в большинстве случаев, и особенно в случае экспериментального измерения, мы делаем то же самое, что и в простом случае: мы рисуем треугольник и помещаем изменение смещения Δx по сравнению с изменением во времени Δt. Опять же, это числовое дифференцирование.

Если нам нужен наклон при t = 0 с, мы могли бы взять t = 0 с и t + Δt = 2 с.Таким образом, Δt равно двум секундам, используя введенные выше обозначения. Но проблема в том, что это дает нам треугольник, наклон которого (черная линия) несколько больше, чем наклон при t = 0 s (красная линия). Фактически, наклон черной линии дает нам среднюю скорость от 0 до 2 секунд, но это не то, что нам нужно. Мы можем добиться большего, по крайней мере, в этом случае, нарисовав наш треугольник по обе стороны от t = 0 s. Попробуйте, но вы обнаружите, что это тоже дает завышенную оценку.

Мы можем добиться большего, взяв меньшее значение Δt.Сначала мы ожидаем улучшения оценки по мере того, как мы будем брать все меньше и меньше Δt. Здесь возникает практическая проблема: если мы измеряем значения, неизбежно существует предел точности каждого измерения, и по мере того, как Δt и Δx становятся меньше, эта ошибка становится пропорционально более важной. Если мы вычисляем x и t численно, мы сталкиваемся с той же проблемой. Таким образом, на практике мы идем на компромисс в отношении размера Δt: достаточно маленького, чтобы дать локальную форму кривой, но достаточно большого, чтобы ошибки измерения или расчета были небольшими.Есть и другие приемы, которые мы увидим ниже.

Аналитические производные

₀

Степенные члены и многочлены

₀

Но как насчет такого термина, как x = Ct ²? (В нашем примере C = a / 2, но оставим это в общих чертах.) Давайте сделаем «пробег» для нашего расчета наклона от t до (t + Δt). Тогда «подъем» на треугольнике будет от Ct ² до C (t + Δt) ². Итак, наклон

На этом этапе, если вы делали это в математической школе, вы могли бы начать беспокоиться о бесконечно малых и принимать предел, когда Δt стремится к нулю. У меня могут возникнуть проблемы из-за того, что я укажу на это, но во Вселенной нет бесконечно малых величин, и количества не стремятся к нулю в физике. Бесконечно малые, как и многие вещи в математике, являются человеческими изобретениями. Таким образом, для большинства целей в физике принятый предел – это просто размер, необходимый для обеспечения математической точности выше, чем у наших измерений, или больше, чем у наших численных расчетов.(Вам действительно стоит пройти этот курс математики, но я не думаю, что вам понадобятся бесконечно малые числа в физике.)

На всех графиках на этой странице красная кривая является производной фиолетовой. Это хорошее упражнение для сравнения этих двух и проверки того, что во всех случаях и по всей кривой красная линия представляет наклон фиолетовой. Здесь, например, наклон y = 1 равен нулю. Наклон прямой y = t, очевидно, постоянный. На третьей кривой вы можете видеть, что наклон сначала отрицательный, нулевой при t = 0, а затем становится все более положительным.

Возможно, вы видите здесь закономерность? Взяв положительное целое число n и расширив (t + Δt) ⁿ, вы увидите, что если y = Ct ⁿ, производная y равна nCt ^{n − 1}.Часто это пишут так:

Сумма сроков

Скорость изменения суммы функций равна сумме их индивидуальных скоростей изменения. (Производная суммы – это сумма производных.) Благодаря этому неудивительному результату мы теперь можем дифференцировать многочлены, например: Если

Тригонометрические функции

В определении синуса угла используется прямоугольный треугольник. Это отношение стороны, противоположной углу, к гипотенузе треугольника. Определение косинуса – это другая сторона (которая примыкает к углу), разделенная гипотенузой.

На этой диаграмме сначала посмотрите на треугольник с синими сторонами.Радиус нарисован под углом θ. Вертикальная сторона – это, по определению, sin θ, а горизонтальная сторона – cos θ.

Теперь давайте изменим θ на величину Δθ: мы получим еще один радиус и еще один треугольник, две стороны которого показаны зеленым. Насколько мы изменили sin θ? Другими словами, что такое Δ (sin θ)?

По определению Δ (sin θ) – это величина, которая увеличивается в θ, когда θ увеличивается на Δθ). Так должно быть (sin (θ + Δθ) – sin θ). На этой диаграмме Δ (sin θ) показано как подъем маленького треугольника, показанного красным.(Для наглядности этот треугольник повторяется за пределами основной диаграммы.) Длина этого треугольника равна −Δ (cos θ). В этом случае пробег идет влево, поэтому он имеет отрицательный знак. Этот отрицательный знак возникает из-за того, что по мере увеличения θ в этом квадранте cos θ уменьшается.

Теперь посмотрите на маленький прямоугольный треугольник красного цвета. Мы называем его гипотенузой h. Применяя определение синуса и cos и помня, что cos θ уменьшается, мы имеем

Δ (sin θ) = h cos φ и Δ (cos θ) = – h sin φ.

Опять же, мы используем соглашение, согласно которому dx означает значение Δx, достаточно маленькое, чтобы сделать приближения лучше, чем наши измерения. Итак, в этом пределе и с использованием результатов предыдущего абзаца (θ = φ и h = dθ для достаточно малых значений Δθ) приведенные выше уравнения становятся

d (sin θ) = dθ cos θ и d (cos θ) = – dθ sin θ

* Обратите внимание на использование определения: угол в радианах = дуга / радиус.Следовательно, dθ в этих уравнениях необходимо выражать в радианах. Чтобы преобразовать градусы в радианы, умножьте на π и разделите на 180.

Цепная линейка

Круговое и простое гармоническое движение

y = A.sin θ = A.sin (ωt + φ),

Интеграция

: как складываются результаты переменной ставки?

Допустим, в ведре уже есть объем воды V ₀, и что мы ставим ведро под кран (мы начинаем интегрирование) в момент времени t = 0. Кран уже открыт, с расходом f ₀, называемый начальным расходом. Рассмотрим первый короткий интервал Δt. Скорость потока по определению является объемом в секунду, поэтому в первый раз Δt в ведро наливается объем приблизительно f ₀ .Δt.f ₀ .Δt показано первым красным прямоугольником на верхнем графике. «Приблизительно» присутствует, потому что во время Δt расход не постоянный, а меняется – в нашем примере он увеличивается.

Точно так же в любое время позже объем, попадающий в ковш в коротком интервале Δt, составляет приблизительно f.Δt. Итак, для каждого Δt мы добавляем шаг f.Δt к высоте фиолетовой кривой, представляющей объем в ведре, как показано на нижней кривой. Обратите внимание, что при высоком потоке область f.Δt велико, поэтому объем в ковше быстро увеличивается. Обратите внимание, что когда поток падает до нуля (отводной кран), объем больше не увеличивается. И, конечно, падение кривой V (t) будет означать, что вода будет вытекать из ведра, что мы должны назвать отрицательным потоком в ведро. (Например, в ведре может быть течь.)

Какой объем V _f в ковше в последний момент времени t _f? (Индекс f здесь означает «окончательный», а не «поток».) Мы можем найти приблизительный объем как

₀

₁

₂

«Примерно» появляется потому, что расход меняется во времени Δt. Однако, если мы сделаем Δt достаточно малым, это изменение станет меньше, чем предел нашей точности *. Как и выше, когда Δt достаточно мало, мы называем это dt. Таким образом, приведенное выше уравнение становится:

₀

₁

₂

Эта сумма называется интегралом от f относительно t

В способе, который я представил в этом примере, V ₀ – это константа интеграции . Интеграция не дает вам полного ответа, она только говорит вам, насколько что-то изменилось в процессе. В этом случае, чтобы узнать окончательный объем в ковше, нам нужно знать не только интеграл потока, но также, сколько было в ковше до того, как он начал интегрировать поток. В большинстве случаев вам нужно будет найти константу интегрирования – очень часто, используя начальные условия , как мы это делали здесь.

Возможно, сейчас самое время вернуться к приведенным выше анимациям и проверить, что интегрирование скорости (поиск области под кривой) дает смещение.

Численное интегрирование

Очень важный практический момент: когда мы сделали Δt малым при дифференцировании, мы столкнулись с проблемой, что отношение Δx / Δt стало чувствительным к экспериментальной или расчетной ошибке, когда Δt стало малым. Эта проблема не возникает при умножении. Более того, ошибки вычислений, иногда положительные, а иногда отрицательные, имеют тенденцию устраняться.Таким образом, численное интегрирование намного проще и безопаснее, чем численное дифференцирование. Последнее требует особой осторожности (и именно поэтому на моем калькуляторе нет кнопки «дифференцировать»).

Аналитическая интеграция

противоположна дифференциации

При дифференцировании мы вычитаем V (t) из V (t + dt) и делим на dt
. При интегрировании мы умножаем f (t) на dt и добавляем его к V (t), где f – производная V по t.

ⁿ

^n-1

ⁿ

при условии, что n не равно нулю

Разделив последнее уравнение на n и подставив m = n − 1, получим

Интеграл от t ^m равен t ^{m + 1} / (m + 1)

Показательная функция

Выбрана функция e ^x и значение e определено так, чтобы производная от e ^x была e ^x.Другими словами, e ^x – это кривая, наклон которой равен ее значению во всех точках. Так что это тоже ее собственный составной элемент.

На графике кривая (фиолетовая) показывает e ^x vs x. В этом случае производная не отображается красным цветом, потому что функция и ее производная равны. Прямая линия (зеленая) y = e x. При x = 1 наклон кривой равен e ¹ = e . Это также значение y при x = 1.Обратите внимание, что при x = 0 наклон кривой равен единице. При x = −1 наклон равен 1/ e и т. Д.

Использование цепного правила говорит нам, что

Производная от e ^ax равна. e ^ax, где a – постоянная, и
Интеграл e ^ax равен e ^ax / a.

₀

Этот пример предлагает интересную проблему: какова связь между силой и скоростью для частицы массы m, скорость которой определяется выражением

₀

квадрату

1 / x и функция журнала

Выше было исключение, и есть одно здесь. Очевидно, это не может работать для m = −1, потому что это дало бы интеграл, не зависящий от t. Интеграл от 1 / x равен ln (x).Посмотрим почему. (Если вам нужно, см. Что такое логарифм? Краткое введение ниже.)

Запомните этот – вы будете его часто использовать.

Итак, на графике справа фиолетовая кривая y = ln x. Его наклон (скорость, с которой он увеличивается) показан красной кривой (dy / dx = 1 / x). В качестве альтернативы мы могли бы сказать, что пурпурная кривая растет со скоростью, заданной красной кривой (интегрирование функции означает последовательное добавление ее значения).

В этом и последующих разделах вы заметите, что в примерах используются числа x и y, а не смещения как функция времени.Величины с размерами добавляют дополнительные константы, как мы видим ниже, и легче начать без них.

Интеграл синуса и cos

Интеграл от cos θ равен sin θ, и
интеграл sin θ равен – cos θ.

Способы интеграции

Измените переменные, чтобы они больше походили на интеграл, который я знаю. Вот пара примеров:
- для интегрирования dx / (1 + x) попробуйте заменить y = 1 + x. Здесь dy равно dx, поэтому получается интеграл, который мы видели выше: dy / y = d ln y.
- , чтобы интегрировать x.dx (1 – x ²) ^−1/2, который возникает в различных областях физики, попробуйте заменить x = sin θ.Теперь мы можем записать (1 – x ²) = cos θ и dx = cos θ.dθ. Вау, теперь это выглядит намного проще! (Это всего лишь одна из целого семейства тригонометрических замен.)
Интегрировать по частям. Этот метод исходит из производной произведения двух функций. (Это выходит за рамки того, что нам нужно для материала, поэтому см. Книгу по исчислению для получения более подробной информации.)
Посмотрите таблицу интегралов! У них есть страницы и страницы интегралов, которые предположительно собраны «наоборот» – i.е. авторы, вероятно, составляют таблицу производных, а затем индексируют ее с помощью интегралов. Вот один в Википедии.
Попробуйте алгебраико-математический пакет. (Там, где это полезно, вы часто чувствуете себя укропом из-за того, что не видели этого сами.)
Интегрировать численно – для многих проблем это единственный способ.

Вернуться к Physclips: механика с анимацией и видеоклипами

* Вы можете спросить, что бы произошло, если бы количество изменялось бесконечно быстро.Однако физических величин нет, так что это еще одна вещь, которую мы оставим математикам.

Частные производные

В двух измерениях, когда у нас есть функция y (x), мы можем легко определить dy / dx как наклон кривой y (x). Здесь мы будем использовать два конкретных примера, чтобы проиллюстрировать частные производные: сначала мы рассмотрим кривую y (x), которая также является функцией времени, то есть y (x, t). Затем мы рассмотрим поверхность в трех пространственных измерениях, f (x, y).

Сначала рассмотрим y (x, t). В качестве конкретного примера, пусть это будет смещение y точки на строке как функция положения на строке x и времени t. Итак, теперь мы можем думать о двух разных производных. Мы пишем их по-разному.

∂y / ∂x. Думайте об этом как dy / dx в заданное постоянное время t. Представьте, что вы делаете снимок (время постоянно: оно имеет одинаковое значение для всех точек изображения): на фотографическом изображении, сделанном в момент времени t, ∂y / ∂x – наклон формы y (x) в момент фотографии.

∂y / ∂t. Думайте об этом как dy / dt в данной позиции x. Si ∂y / ∂t – это просто наклон y (t), то есть скорость, с которой y изменяется на в определенной точке x на струне. (Кстати, это не скорость волны).

y = A sin (kx – ωt).

Давайте явно покажем зависимость от x и t, построив y (x, t) = A sin (kx – ωt), где t – отдельная ось, перпендикулярная x и y.

На приведенном выше графике фиолетовая кривая вдоль оси x представляет собой «снимок» волны в момент t = 0: это уравнение y _{t = 0} = A sin kx. Последовательные снимки в более позднее время (y _{t> 0} = A sin (kx – ωt)) показаны черным цветом.Красный график по оси t показывает простое гармоническое движение при x = 0: это уравнение y _{x = 0} = – A sin ωt. Конечно, аналогичные графики можно было бы нарисовать при любом значении x. В качестве примера мы используем функцию y = A sin (kx – ωt), поэтому

В этом случае, если мы возьмем вторые производные по тем же переменным, мы получим

На рисунке ниже мы снова записываем эти уравнения в стандартных обозначениях и задаем их с производными по времени слева и производными по пространству справа.

Причина использования вторых производных в этом случае – показать решение волнового уравнения для струны. Если струна имеет натяжение T и массу на единицу длины μ, то мы покажем в другом месте, что волновое уравнение имеет вид:

Вы можете подробно увидеть этот вывод и решение в по этой ссылке , из которой мы позаимствовали анимацию выше.

Теперь рассмотрим поверхность в трех измерениях f = f (x, y). В качестве конкретного примера мы можем представить, что f – это высота или высота земли как функция положения в восточном (x) и северном (y) направлениях, поэтому f (x, y) – это форма ландшафта. Вот набросок. Над большим квадратом на плоскости x, y я нарисовал очертания изогнутого участка f (x, y), ограниченного четырьмя изогнутыми линиями.В одном углу в точке (x, y) я нарисовал небольшой участок шириной dx и глубиной dy.

Насколько крутой этот пейзаж? Если бы я был ограничен плоскостью f (x) (т.е. если бы я мог идти только на восток и запад, поднимаясь или опускаясь вместе с ландшафтом), то мой наклон был бы задан как df / dx, как указано выше. Но в трех измерениях наклон зависит от моего направления. Чтобы оценить это количественно, давайте посмотрим на небольшую область в нижнем углу. Я предполагаю, что функция f является непрерывной и хорошо себя ведет, поэтому, когда я делаю dx и dy достаточно маленькими, этот маленький синий квадрат будет плоским – с любой точностью, которая мне нужна.

Приближение того, что f (x, y является локально плоским, позволяет записать простое уравнение для изменения высоты df. Предположим, я иду в x (восточном) направлении от (x, y), то есть вдоль фронта лицо в блоке на скетче выше. Наклон моего пути был бы написан dy / dx, если бы у нас было только два измерения. Однако в трех (или более) измерениях возможны разные пути, поэтому у нас есть другой символ, здесь Я пишу частную производную, произносится как «duh f duh x», где новый символ ∂ напоминает мне, что f изменяется по более чем одной переменной.Итак, если я перемещаюсь на расстояние dx в направлении x, моя высота f увеличивается на. Точно так же, если бы я шел в направлении y (север), у меня был бы другой наклон, и мой рост увеличился бы на.

Давайте теперь представим, что я иду в произвольном направлении, так что мое смещение в плоскости x, y равно dx i + dy j . (При необходимости измените векторы.) (На скетче выше это смещение находится в квадранте NE, но, меняя знак и величину dx и dy, я мог выбрать любое направление.) Если мои dx и dy достаточно малы, чтобы синяя область выше была приблизительно плоской, то я могу написать уравнение для изменения f из-за произвольных (небольших) изменений dx и dy:

Что такое логарифм? Краткое введение.

на

⁻²

⁶

Но что, если n не целое число? Поскольку правила, которые мы использовали до сих пор, не говорят нам, что это будет значить, мы можем определить это так, чтобы оно означало то, что нам нравится, но мы должны выбрать наше определение так, чтобы оно было согласованным.Определение логарифма числа a (с основанием 10) таково: Другими словами, , логарифм числа a – это степень, в которую вы должны возвести 10, чтобы получить число a . В качестве примера числа, логарифм которого не является целым числом, давайте рассмотрим квадратный корень из 10, который равен 3,1623 …, другими словами 3,1623 ² = 10. Используя наше определение выше, мы можем записать это как

^{лог 3,1623}

Однако, используя наше правило, что (10 ⁿ) ^m = 10 ^нм, мы видим, что в этом случае log 3,1623 * 2 = 1, поэтому логарифм 3,1623 … равен 1/2. Квадратный корень из 10 равен 10 ^0,5. Теперь есть пара вопросов: как считать логи? и можем ли мы быть уверены, что все действительные числа больше нуля имеют действительные журналы? Мы оставляем это математикам (которые, кстати, были бы счастливы дать вам более строгую трактовку показателей, чем это поверхностное описание).

Стоит отметить еще несколько важных примеров. 10 ⁰ будет обладать тем свойством, что независимо от того, сколько раз вы умножали его на себя, оно никогда не достигло бы 10. Кроме того, независимо от того, сколько раз вы делили его на 1, вы никогда не получите меньше, чем 1/10. Используя наше правило (10 ⁿ) ^m = 10 ^nm, вы увидите, что 10 ⁰ = 1 удовлетворяет этому правилу, поэтому логарифм единицы равен нулю.

В физике мы обычно используем натуральных логарифмов .Рассмотрим функцию y = a ^x, где a> 0. Чем больше величина a, тем круче увеличивается эта величина. Число e = 2,718 … обладает тем свойством, что производная от e ^x равна e ^x. Эта функция изображена выше. Журналы для базы e обычно записываются как ln , поэтому, например, мы можем написать:

пер. (2.718) = 1.000.

Вернуться к началу страницы.

журнал ₁₀ x против x.

операторов порядка матриц как расширение дробного исчисления

с ,  и . В экв. В уравнениях (1.1) и (1.2) ядра  и  изменяются

в зависимости от варианта интегрирования дроби.Функции  и  также могут

принимать любую форму в зависимости от  и -производных от , . В таблице 1

показаны различные формы этих операторов для разных ядер и формы интегрируемых функций

с некоторыми соответствующими ссылками.

Таблица 1 – Различные версии дробно-дифференциальных интегральных операторов (: a)

Риман: [1] Миллер и Росс, 1993; б) Лиувилль: [1] Миллер и Росс, 1993, [2] Oliveira e

Machado, 2014; c) Риман-Лиувилль, уравнение Абеля: [1] Миллер и Росс, 1993, [3] Трухильо

и др., 2006, [3] [4] Самко, Килбас и Маричев; г) Вейл: [5] Рудольф Хильфер, 1993, [6] Фаусто

Феррари; д) Капуто: [2] Трухильо и др., 2006, [7] Капуто, 1966, [8] Капуто, 1967, [9] Кумар

и др., 2019.

Начиная с версии Римана-Лиувилля, принимая, , с нижним пределом интегрирования

, дробная производная становится:



 

 





 (1,3)

 

 

















 

 









 









 





; 







;

; 













;



 

















 





;

; 





 



;

; 









исчисление: интегралы

Теперь мы начинаем обсуждение интегралов, которое является второй темой в исчислении.Интегралы – это интересный способ сложить значение функции, чтобы получить «целое». или сумма его значений за некоторый интервал. Обычно интегральное исчисление преподается как отдельный курс после дифференциального исчисления. но это разделение не обязательно и может даже привести к обратным результатам.

Производная $ f ‘(x) $ измеряет изменение в $ f (x) $, т. Е. производная измеряет различия в $ f $ для небольшого изменения $ \ epsilon $ входная переменная $ x $: \ [ \ text {производная} \ \ propto \ \ f (x + \ epsilon) -f (x).\] С другой стороны, интегралы измеряют сумму значений $ f $ между $ a $ и $ b $ с регулярными интервалами $ \ epsilon $: \ [ \ текст {интеграл} \ propto \ \ \ f (a) + f (a + \ epsilon) + f (a + 2 \ epsilon) + \ ldots + f (b-2 \ epsilon) + f (b- \ epsilon). \] Лучший способ понять интеграцию – представить ее как обратная операция дифференцирования: сложение всех изменений в функции дает вам значение функции.

В исчислении I мы узнали, как взять функцию $ f (x) $ и найти ее производную $ f ‘(x) $.В интегральном исчислении нам будет дана функция $ f (x) $, и мы будем попросить найти его интеграл на различных интервалах.

Определения

Вот некоторые концепции, с которыми вы уже должны быть знакомы:

\ [ f: \ mathbb {R} \ to \ mathbb {R}, \]

, что означает, что $ f $ принимает в качестве входных данных некоторое число (обычно мы называем это число $ x $)
  и он производит в качестве вывода другое число $ f (x) $ (иногда мы также указываем псевдоним для вывода $ y = f (x) $).* $ \ lim _ {\ epsilon \ to 0} $: пределы являются математически строгими
  так сказать об очень малых числах.
* $ f '(x) $: производная от $ f (x) $ - это скорость изменения $ f $ при $ x $:
  \ [
f '(x) = \ lim _ {\ epsilon \ to 0} \ frac {f (x + \ epsilon) \ - \ f (x)} {\ epsilon}.
  \]
  Производная также является функцией вида
  \ [
     f ': \ mathbb {R} \ to \ mathbb {R}.
  \]
  Функция $ f '(x) $ представляет // наклон //
  функция $ f (x) $ в точке $ (x, f (x)) $. x \! f '(t) \ dt = F (x).x f (t) dt \ right]
   = \ frac {d} {dx} \ left [F (x) - F (0) \ right]
   = f (x).
  \]

Формулы

Сумма Римана

Сумма Римана – хороший способ определить интеграл из первых принципов. Мы разделим область под кривой на множество маленьких полосок, высота которых меняется в зависимости от $ f (x) $. Чтобы получить общую площадь, мы суммируем – все площади прямоугольников. Суммы Римана мы обсудим в следующем разделе, но сначала мы смотрим на свойства интегралов.б е (х) \; dx. \]

Для некоторых функций можно найти антипроизводную функцию $ F (\ tau) $, который описывает «текущий итог» площади под кривой, начиная с некоторого произвольный левый конец и до конца до $ t = \ tau $. Мы можем вычислить площадь под $ f (t) $ между $ a $ и $ b $. посмотрев на изменение в $ F (\ tau) $ между $ a $ и $ b $. \ [ A (a, b) = F (b) – F (a). \]

Мы можем проиллюстрировать логику приведенной выше формулы графически: Площадь $ A (a, b) $ равна «промежуточной сумме» до тех пор, пока $ x = b $ минус промежуточная сумма до тех пор, пока $ x = a $.{b} f (x) \ dx = – A (a, b). \] Во всех выражениях, включающих интегралы, если вы хотите чтобы поменять границы интеграции, вам нужно добавить знак минус перед интегралом.

Площадь также может оказаться отрицательной, если мы интегрируем отрицательная функция от $ a $ до $ b $. В общем, если $ f (x) $ в некоторых местах выше оси $ x $, эти будет положительным вкладом в общую площадь под кривой, и места, где $ f (x) $ ниже оси $ x $, будут считаться отрицательными вклады в общую площадь $ A (a, b) $.c f (x) \; dx = А (а, в). \]

Линейность

Интеграция – это линейная операция: \ [ \ int [\ alpha f (x) + \ beta g (x)] \; dx знак равно \ альфа \ int f (x) \; dx + \ бета \ int g (x) \; dx, \] для произвольных констант $ \ alpha, \ beta $.

Напомним, что это было верно для дифференциации: \ [ [\ альфа f (x) + \ beta g (x)] ‘ знак равно \ альфа f ‘(х) + \ beta g ‘(х), \] так что мы можем сказать, что операции исчисления в целом – это линейные операции, операции.

Интеграл как функция

До сих пор мы рассматривали только определенные интегралы, для которых пределы интегрирования были константами $ x_i = a $ и $ x_f = b $, и поэтому интеграл был числом $ A (a, b) $.

В более общем смысле, у нас может быть один (или несколько) пределов интегрирования переменных. Например, мы можем иметь $ x_i = a $ и $ x_f = x $. Напомним, что площадь под кривой $ f (x) $ по определению равна вычисляется как разность антипроизводной функции $ F (x) $ оценивается в пределах: \ [ А (х_i, х_f) = А (а, х) = F (х) – F (а). \]

Выражение $ A (a, x) $ немного вводит в заблуждение в качестве имени функции, поскольку он выглядит как $ a $ и $ x $ – это переменная , когда на самом деле $ a $ – постоянный параметр, и только $ x $ – это переменная.х f (t) \; dt = F (x) – F (a). \]

Два наблюдения. Во-первых, обратите внимание, что $ A_a (x) $ и $ F (x) $ отличаются только константой, поэтому на самом деле антипроизводная – это интеграл с точностью до константы что обычно не важно. Во-вторых, обратите внимание, что поскольку переменная $ x $ появляется в верхний предел выражения, мне пришлось использовать фиктивную переменную $ t $ внутри интеграла. Если мы не используем другую переменную, мы можем спутать текущую переменную внутри интеграла с предел интеграции.x f (t) dt \ right] = \ frac {d} {dx} \ left [F (x) – F (0) \ right] = f (x). \]

Мы можем думать об обратных операторах $ \ frac {d} {dt} $ и $ \ int \ cdot dt $ символически на том же основании, что и другие математические операции, о которых вы знаете. Обычные методы решения уравнений могут затем применяться для решения уравнений, включающих производные. Например, предположим, что вы хотите найти $ f (t) $ в уравнении \ [ \ frac {d} {dt} \; f (t) = 100. \] Чтобы добраться до $ f (t) $, мы должны отменить операцию $ \ frac {d} {dt} $.Применяем операцию интегрирования к обеим частям уравнения: \ [ \ int \ left (\ frac {d} {dt} \; f (t) \ right) dt = f (t) = \ int 100 \; dt = 100t + C. \] Решение уравнения $ f ‘(t) = 100 $: $ f (t) = 100t + C $, где $ C $ называется постоянной интегрирования .

Дай мне немного из этого

Хорошо, хватит теории. Сделаем несколько антипроизводных. Но как делать антипроизводные? На самом деле, дело в названии. Производные и анти. Что бы ни делала производная, интеграл должен делать противоположное.4 + С. \] Каждый раз, когда вы интегрируетесь, вы всегда получаете ответ с точностью до произвольной аддитивной константы $ C $, который всегда будет отображаться в ваших ответах.

Давайте посмотрим еще на несколько примеров:

\ [ \ int \ cos \ theta \ d \ theta = \ sin \ theta + C, \]

, поскольку $ \ frac {d} {d \ theta} \ sin \ theta = \ cos \ theta $, и аналогично интеграл для $ \ sin \ theta $ равен: \ [ \ int \ sin \ theta \ d \ theta = - \ cos \ theta + C, \] поскольку $ \ frac {d} {d \ theta} \ cos \ theta = - \ sin \ theta $.{-1} = \ frac {1} {x} $ - это \ [ \ int \ frac {1} {x} \ dx = \ ln x + C, \] поскольку $ \ frac {d} {dx} \ ln x = \ frac {1} {x} $. \ pi \ nl & = [- \ cos \ pi + C] - [- \ cos (0) + C] \ nl & = \ соз (0) - \ соз \ пи \ \ = \ \ 1 - (-1) = 2.\ end {align} \]

Константа $ C $ не появляется в ответе, потому что он находится как в верхнем, так и в нижнем пределах.

Что дальше

Если интеграция - это не что иное, как обратная дифференциация и вы уже знаете дифференцирование наизнанку из дифференциального исчисления, вам может быть интересно, что вы собираетесь делать в течение всего семестра интегрального исчисления. Для всех намерений и целей, если вы понимаете концептуальную материал в этом разделе, то вы поймете интегральное исчисление.2 (х) \ dx знак равно T_1 - T_2 = \ frac {\ pi} {2} - 0 = \ frac {\ pi} {2}. \]

Вы понимаете, как быстро интеграция может стать сложной? Вам нужно изучить всевозможные уловки для решения интегралов. Я научу тебя всем необходимым трюкам, но чтобы стать опытный, вы не можете просто читать: вы должны отработать техники. Обещай мне, что будешь практиковаться! Как мой ученик, я не ожидаю меньшего чем полный набор вопросов, с которыми вы столкнетесь на выпускном экзамене. k} $$

Лимит латекса

Как писать лимиты LateX?

Определение	Латексный код	Результат
Предел на плюс бесконечности	$ \ lim_ {x \ to + \ infty} f (x) $	$$ \ lim_ {x \ to + \ infty} f (x) $$
Предел минус бесконечности	$ \ lim_ {x \ to - \ infty} f (x) $	$$ \ lim_ {x \ to - \ infty} f (x) $$
Лимит при $ \ alpha $	$ \ lim_ {x \ to \ alpha} f (x) $	$$ \ lim_ {x \ to \ alpha} f (x) $$
Инф	`$ \ inf_ {x> s} f (x)`	$$ \ inf_ {x> s} f (x) $$
Sup	$ \ sup_ {x \ in \ mathbb {R}} f (x) $	$$ \ sup_ {x \ in \ mathbb {R}} f (x) $$
Макс	$ \ max_ {x \ in \ [a, b \]} f (x) $	$$ \ max_ {x \ in [a, b]} f (x) $$
Мин. d f (x, y) dxdy $$
Двойной цельный с точками	`$$ \ idotsint $$`	$$ \ idotsint $$
Тройной интеграл	`$$ \ iiint $$`	$$ \ iiint $$
Четверной интегральный	`$$ \ iiiint $$`	$$ \ iiiint $$
Контурный интеграл	`$$ \ oint $$`	$$ \ oint $$

Латексные интегралы по замкнутой поверхности и объему

Для определения таких интегралов необходимо использовать wasysym package
$$ \ oiint \ oiiint $$

Двойной тройной циркуляционный элемент Integrale

Что такое исчисление и как с ним разобраться

Проклятие старшеклассников (а иногда и университетов), математический анализ на самом деле является благословением для человечества - сложным и довольно трудным для понимания, но все же благословением.

Исчисление - это форма продвинутой математики, которая занимается изменением вещей. По сути, это система изучения того, как одна ценность изменяется по отношению к другой; вы также можете услышать, что это называется «изучением бесконечно малых».

Например, если вы знаете, сколько денег вы получаете и тратите каждый день, расчет может помочь вам понять, сколько денег у вас будет через несколько дней. Или, как это имеет место во многих физических задачах, вы можете рассчитать, сколько времени потребуется автомобилю, чтобы остановиться, если вы знаете его скорость и замедление.Исчисление может быть неприятностью, но это очень серьезная неприятность.

Да, и да - вопреки распространенному мнению, исчисление полезно в реальной жизни либо напрямую, либо путем тренировки вашего разума смотреть на вещи с научной точки зрения.

Исчисление было открыто или изобретено?

Интересный вопрос, который иногда возникает относительно исчисления, - было ли оно открыто или изобретено. Вопрос носит скорее философский характер, поэтому на него сложно ответить так или иначе.

Вообще говоря, математики говорят об открытии доказательства или метода, и, похоже, это также относится к исчислению. Исчисление было открыто (или изобретено) в конце 17 века сэром Исааком Ньютоном в Англии и Готфридом Лейбницем. Эти двое работали по отдельности и немного соперничали между собой, вплоть до споров о том, кто заслуживает уважения к расчетам.

Ньютон, получивший поддержку британских ученых, нуждался в расчетах для изучения движения планет по небу, что было важно как с научной точки зрения (поскольку в то время область астрономии набирала обороты), так и практически потому, что она была важна для навигации. кораблей.Лейбница, которого поддерживали ученые из остальной Европы, больше интересовало вычисление площади под кривой, что в то время было сложной задачей для математиков.

Честно говоря, для нас мало важно, кто это открыл. Оба были титанами науки и математики, и оба внесли ценный вклад, который полезен и по сей день.

По правде говоря, Ньютон и Лейбниц не были первыми, кто увлекся исчислением, хотя они были первыми, кто разработал его как строгую систему.Многие идеи в области исчисления появились в Древней Греции и даже раньше. Некоторые упоминания о способах вычисления объема и площади, одной из первых целей интегрального исчисления, появляются в египетском московском папирусе более 3800 лет назад. Математик Древней Греции Евксоду обсуждал метод исчерпания в 4 веке до нашей эры, и Архимед позже основал эти методы, разработав вычисления, которые напоминают исчисление. Независимо от этого китайский математик Лю Хуэй открыл метод исчерпания (который вычисляет площадь формы, вписывая в нее последовательность многоугольников, площади которых сходятся к площади исходной формы) семь веков спустя, примерно в 300 году нашей эры.Многие математики из других частей мира внесли свой вклад в исчисление, в том числе основополагающий трактат итальянского математика Бонавентуры Кавальери, но только Лейбниц и Ньютон действительно получили исчисление.

Сущность исчисления

Существует два разных типа исчисления (дифференциальное исчисление и интегральное исчисление). Это две обратные операции (что-то вроде сложения и вычитания, но не совсем), и мы рассмотрим их чуть позже. Но перед этим давайте посмотрим, что на самом деле движет расчетом: это бесконечно малые величины.

Допустим, вы хотите вычислить площадь под кривой, как это сделал Лейбниц. Если кривая представляет собой полукруг или какую-то другую хорошо известную особенность, нам повезло - у нас есть формула для этого. Но что, если это просто случайная кривая? Что ж, давайте начнем с грубости: давайте аппроксимируем область под кривой прямоугольником. Как вы понимаете, это не очень точно. Что, если бы вместо одного мы использовали два-три прямоугольника разной высоты? Что ж, это все еще не очень хорошо, но несколько ближе к истине.

А что, если мы добавим еще несколько прямоугольников? Мы по-прежнему будем отключены, но чем больше прямоугольников мы добавим, тем ближе мы приблизимся к форме под кривой. По мере того как мы будем добавлять все больше и больше прямоугольников, мы будем приближаться к истине. В конечном итоге, если мы добавим бесконечное количество бесконечно малых прямоугольников, мы получим «бесконечно близкие», то есть наше приближение больше не является приближением, это фактическая кривая.

Анимация через Википедию.

Итак, у нас есть совершенно алгебраический способ решения сложных геометрических задач.Но это также относится к физическим величинам - кривая может, например, быть скоростью автомобиля или скоростью, с которой вы тратите деньги, и здесь могут быть полезны расчеты.

Calculus предлагает совершенно новую схему работы с физическими величинами, особенно в отношении того, как они меняются с течением времени. Мы можем изучать путь объектов, как хотел Ньютон, или смотреть на скорость или ускорение. Мы можем даже смотреть на более сложные вещи, такие как законы электромагнетизма или даже общую теорию относительности Эйнштейна - все они используют исчисление.

Этот способ работы с бесконечно малыми числами - один из фундаментальных строительных блоков исчисления. Еще один такой строительный блок - это пределы.

Предел - это значение функции (или последовательности), которое «приближается» к некоторому значению, но не достигает его. Если вы хотите сравнивать или вычислять бесконечно малые вещи, вам нужны ограничения. В приведенном выше примере кривой у вас будет бесконечное количество прямоугольников, но они будут бесконечно малыми. Пределы позволяют работать с бесконечностями и нулями без разбора математики.Возьмем простой пример.

Допустим, у вас есть функция f (x), которая определяется следующим образом:

Это все прекрасно, вы можете без проблем вычислить свою функцию почти для всех значений x. Но что происходит, когда x = 1? Итак, ваша функция становится (1-1) / (1-1), что равно 0/0, а, как мы знаем, 0/0 не определено. Но, допустим, вы очень упрямы и хотите действительно приблизиться к 1.

Давайте попробуем тот же подход, что и с кривой, и сделаем грубое приближение.Допустим, x = 0,5. Если мы сделаем расчет, f (x) будет 1,5. Если мы сделаем x = 0,75, получится 1,75. Давайте посмотрим на еще несколько значений:

9044 9044 9044 1,999

x	f (x)
0,5	1,5
0,75	1,75
0,9	1,9
0,9999	1,9999
1.0001	2.0001

Интуитивно вы уже можете видеть, что функция, когда x = 1 имеет тенденцию сходиться вокруг f (x) = 2. Мы хотим сказать, что ответ - 2, но мы не можем сказать, что это ровно 2, поэтому мы используем пределы, чтобы сказать, что когда x почти, но не совсем 1, ответ равен 2.

Технически мы можем использовать предел для вычисления, когда x бесконечно приближается к 1 через предел:

Мы также можем посмотреть на это, построив график функции со значениями x по горизонтали и значениями f (x) (или y) по вертикали.

На графике показана непрерывная линия с одним исключением, выделенным зеленым квадратом: она прерывается, когда x = 1. Таким образом, по сути, наша функция равна почти 2, когда x почти равно 1, но она не работает (не определено), когда x на самом деле 1.

Что такое интегралы и производные

Теперь у нас есть основные инструменты, необходимые для изучения производных и интегралов - основы исчисления.

Дифференциальное исчисление делит вещи на маленькие разные части (производные) и то, как они меняются от одного момента к другому, в то время как интегральное исчисление объединяет (интегрирует) части вместе и сообщает нам, насколько изменилось в целом.

Определенный интеграл функции можно представить как площадь области, ограниченную ее графиком. Изображение взято из Википедии.

Фундаментальная теория исчисления связывает их вместе. Если у вас есть непрерывная функция f , есть производная от этой функции и антипроизводная, обычно называемая неопределенным интегралом (называемая F), и эти две операции являются противоположными. Вы можете использовать одно для отмены другого, так же как вы можете использовать умножение для отмены деления и наоборот.Если наша функция привязана к интервалу [a, b], то f - производная от F, а F - интеграл от f по этому конкретному интервалу. Фактически:

Это кажется немного сложным, но хорошая новость в том, что мы уже сделали интеграл! Помните наш пример сверху с кривой и прямоугольниками? Что ж, в исчислении интеграл можно рассматривать как пространство под графиком уравнения - другими словами, площадь под кривой. В некотором смысле интеграл - это сумма; в случае площади под кривой это сумма всех маленьких прямоугольников, которые мы использовали для ее аппроксимации.

Теперь посмотрим, что означает интеграл по интервалу. В нашем предыдущем примере кривой наш интервал был «от начала кривой до конца кривой». Но это не обязательно от начала до конца - мы можем просто выбрать начальную и конечную точки и вычислить наш интеграл (площадь под кривой) для этой конкретной части кривой. Давайте посмотрим, что это означает в графической форме:

Анимация через Википедию.

Так что это значит для деривативов?

Ну, производные измеряют скорость изменения одного значения по отношению к другому - чаще всего одного значения во времени.Самый простой пример производных - это положение, скорость и ускорение.

Допустим, вы находитесь в каком-то положении и хотите рассчитать свое будущее положение. Для этого все, что вам нужно знать, это ваша скорость, поэтому скорость определяется как скорость изменения положения. Проще говоря, скорость - это изменение положения в единицу времени, будь то мили в час или метр в секунду. И наоборот, определенный интеграл скорости даст нам пройденное расстояние.

Итак, что такое ускорение?

Ну, как скорость измеряет изменение положения во времени, так и ускорение измеряет изменение скорости. Так же, как скорость - это производная от положения, ускорение - это производная от скорости или вторая производная от положения (забавные мелочи, третья производная называется рывком или толчком).

Вот простая анимация скорости изменения в зависимости от кривой, которая поможет вам представить, как эти два соотносятся:

Анимация через Википедию.

Как вычислять производные и интегралы

Теперь, когда мы, надеюсь, начали понимать, что на самом деле означают производные и интегралы, давайте посмотрим, как их можно вычислить. Это очень сложная область сама по себе, и мы рассмотрим только самые основы, чтобы вы начали.

Расчет производных

Производный финансовый инструмент обычно определяется следующим образом:

Производные часто обозначаются с помощью f (x) и апострофа после f.В некоторых случаях используется обозначение f (x) или y´. Обозначения dx / dy или d / dx также широко используются, особенно в физике (или dx / dt, если это скорость изменения во времени).

Уже можно сделать несколько выводов. Например, производная любого постоянного значения всегда будет равна 0. Поскольку производная - это скорость изменения, а константа не изменяется, скорость изменения всегда будет равна 0. Принцип прост, но вы действительно можете это доказать. Если f (x) = c:

Еще один вывод: когда f (x) = x, производная будет постоянной.Другими словами, x ’= 1; наклон линии всегда будет постоянным. И снова мы можем это доказать. Если f (x) = x:

Из этого вы, возможно, уже имеете представление, что это означает для линейных функций вида ax + b . В этой ситуации b не имеет значения, так как это будет 0, а поскольку производная x равна 1, то (ax + b) '= 1. Думайте об этом как о наклоне прямой: наклон постоянного значения всегда равно 0, наклон 2x всегда равен 2, наклон 3x всегда равен 3 и т. д.Геометрия часто помогает визуализировать математические задачи.

Производные от степени x на самом деле довольно просты, я дам вам подсказку, чтобы увидеть, сможете ли вы определить закономерность:

Вы его поймали? Для каждого числа n, производная x в степени n будет:

Существуют способы вычисления более сложных производных (включая тригонометрические функции), но мы не будем здесь вдаваться в подробности - вы найдете несколько полезных формул исчисления в следующем разделе, но это все.

Вычисление интегралов

Интегралы - это обратные производные, поэтому все, что вам нужно сделать для вычисления интеграла, - это обратить производную. Ну, технически говоря, антипроизводная - это неопределенный интеграл:

Определенные интегралы вычисляются через определенный интервал, как следует из названия, поэтому они будут выглядеть так:

В любом случае первым шагом является вычисление неопределенного интеграла. В первом случае это конец истории, тогда как во втором вам нужно сделать дополнительный шаг: мы вычисляем неопределенный интеграл как для a, , так и для b , а затем вычитаем их.Если рассматривать F как неопределенный интеграл, то:

Нет простого способа вычисления интегралов - если вы не запомните интегральные формулы или не имеете к ним доступа. Существуют правила интегрирования, о которых мы поговорим ниже, но лучше всего рассматривать интегралы как противоположность производным. Если x ’= 1, то ∫1 = x (другое обозначение будет F (1) = x). Но обратите внимание на константы! Поскольку этот пример является неопределенным, а производные исключают константы, невозможно узнать, имела ли производная константа с самого начала - так технически говоря, 1 = x + c , где c - константа.

Если бы мы преобразовали это в определенный интеграл, то он был бы целым от a до b . Приведем еще один случайный пример и скажем, что a = 7 и b = 10. Мы вычисляем F (x), когда x = a, и F (x), когда x = b, а затем вычитаем их. Поскольку наша F (x) на самом деле равна x, мы получаем b - a, или 10 - 7.

Если это звучит немного сложно, ну, в общем, так оно и есть. В исчислении, как и в жизни, нет ярлыков, и вещи могут быть как простыми, так и очень, очень сложными.

Формулы исчисления

Производные функции

В этом обозначении маленькая метка 'означает «производную от», а f и g - функции.Число e - это константа, известная как число Эйлера.

904 49 f / g

Общие функции	Функция	Производная
Константа	c	0
Линия	x	1
9048 9048 9044 9048 9044 9048 9044 9048	x ²	2x
Квадратный корень	√x	(½) x ^-½
Экспоненциальная	e ^x e 9048 x 9048 9048 9048 9048 9048	a ^x	ln (a) a ^x
Логарифмы	ln (x)	1 / x
	log _a (x) 1 ln (a))
Тригонометрия (x в радианах)	sin (x)	cos (x)
	cos (x)	−sin (x)
	tan (x)	sec ² (x)
Обратная тригонометрия	sin ^-1 (x)	1 / √ (1 − x ²)
cos ^-1 (x)	−1 / √ (1 − x ²)
	tan ^-1 (x)	1 / (1 + x ²)

Правила	Функция	Производная
Умножение на константу	cf	cf n n '
9044 9 Правило мощности 9044
Правило суммы	f + g	f '+ g'
Правило разницы	f - g	f '- g'
Правило продукта	fg '+ f' g
Правило частных	(f 'g - g' f) / g ²
Взаимное правило	1 / f	−f '/ f ²

Правило цепочки (как «Состав функций»)	f º g	(f 'º g) × g'
Правило цепочки (с использованием ')	f (g (x))	f '(g (x)) g' (x)
Правило цепочки (с использованием d dx )	dy dx = dy du du dx

Интегральные формулы

9048 2 9048 2 a )ⁿ dx

Общие функции	Функция	Интегральная
Константа	∫a dx	ax + C
Переменная	∫x dx1048	Квадрат	∫x ² dx	x ³/3 + C
Обратный	∫ (1 / x) dx	ln \| x \| + C
Экспоненциальная	∫e ^x dx	e ^x + C
	∫a ^x dx	a ^{ln (}
	∫ln (x) dx	x ln (x) - x + C
Тригонометрия (x в радианах)	∫cos (x) dx	sin (x) + C
	∫sin (x) dx	-cos (x) + C
	∫sec ² (x) dx	tan (x) + C


Правила	Функция	Интеграл
Умножение на константу	∫cf (x) dx	c∫f (x) dx
Правило мощности (n -1)	x ^{n + 1} n + 1 + C
Правило суммы	∫ (f + g) dx	∫f dx + ∫g dx
Правило разницы	∫ (f - g) dx	∫f dx - ∫g dx

Так что же для меня исчисление?

Что ж, рад, что вы спросили.Давайте посмотрим на точку зрения.

Исчисление - это форма продвинутой математики. Он вам не понадобится, когда вы пойдете в кино или выпьете с друзьями (хотя он всегда может способствовать интересным беседам). Если вы работаете в какой-либо области науки, техники, финансов или социологии, велика вероятность, что в какой-то момент вы столкнетесь с математическим расчетом. Но даже если вы этого не сделаете, вычисления могут быть полезны так же, как и все математическое образование: они помогают вам понимать вещи.

Расчет необходим для понимания таких вещей, как изменения и эволюция, для изучения таких вещей, как процентные ставки и ссуды, или даже для понимания некоторых статей, которые мы пишем здесь, в ZME Science.

Вот наглядный пример: пандемия COVID-19. Мы говорим о существующих пациентах, новых пациентах, скорости изменений, выживаемости, и, честно говоря, даже некоторые высокопоставленные политики продемонстрировали полное непонимание этих вещей. Если вы не занимаетесь наукой, вы не будете использовать вычисления, записывая что-то на бумаге, но вы примените понимание к вещам в своей повседневной жизни, и это поможет вам расти как личность.

Обзор определений производных дробного порядка и интеграла

В этой статье представлен обзор определений производных и интегралов дробного порядка, которые встречаются в математике, физике и технике.

1. Введение

В 1695 году l’Hôpital отправил письмо Лейбницу. В его сообщении возник важный вопрос о порядке производной: что может быть производной от порядка? В пророческом ответе Лейбниц предвидит начало области, которая сегодня называется дробным исчислением (ДК). Фактически, FC так же стара, как и традиционное исчисление, независимо предложенное Ньютоном и Лейбницем [1–4].

В классическом исчислении производная имеет важную геометрическую интерпретацию; а именно, это связано с концепцией касательной в противоположность тому, что происходит в случае FC.Это различие можно рассматривать как проблему медленного развития FC до 1900 г. После Лейбница именно Эйлер (1738 г.) [3] заметил проблему для производной нецелого порядка. Фурье (1822 г.) [3, 5] предложил интегральное представление для определения производной, и его версия может считаться первым определением производной произвольного (положительного) порядка. Абель (1826 г.) [3, 5] решил интегральное уравнение, связанное с проблемой таутохрон, которая считается первым применением FC.Лиувилль (1832 г.) [3, 5] предложил определение, основанное на формуле дифференцирования экспоненциальной функции. Это выражение известно как первое определение Лиувилля. Второе определение, сформулированное Лиувиллем, представлено в терминах интеграла, и теперь Лиувилль назвал его версией интегрирования нецелого порядка. После серии работ Лиувилля наиболее важная статья была опубликована Риманом [6] через десять лет после его смерти. Отметим также, что формулировки Лиувилля и Римана несут с собой так называемую дополнительную функцию - проблему, требующую решения.Грюнвальд [7] и Летников [8] независимо друг от друга разработали подход к производным нецелого порядка в терминах удобного сходящегося ряда, в противоположность подходу Римана-Лиувилля, который задается интегралом. Летников показал, что его определение совпадает с версиями, сформулированными Лиувиллем для конкретных значений порядка и Риманом при удобной интерпретации так называемой нецелочисленной разности порядков. Адамар (1892 г.) [5] опубликовал статью, в которой производная нецелого порядка аналитической функции должна быть вычислена в терминах ее ряда Тейлора.

После 1900 года FC переживает быстрое развитие, и в попытке сформулировать конкретные проблемы были предложены другие определения. Упомянем некоторые из них. Вейль [9] ввел производную, чтобы обойти проблему, связанную с конкретным классом функций, периодическими функциями. Рис [10, 11] доказал теорему о среднем значении для дробных интегралов и ввел другую формулировку, связанную с преобразованием Фурье. Маршо (1927) [3, 5] ввел новое определение нецелого порядка производных.Это определение совпадает с лиувиллевской версией для «достаточно хороших» функций. Erdélyi-Kober (1940) [3, 5] представил четкое определение нецелого порядка интегрирования, которое полезно в приложениях, включающих интегральные и дифференциальные уравнения. Капуто (1967) [12] сформулировал определение, более ограничительное, чем определение Римана-Лиувилля, но более подходящее для обсуждения проблем, связанных с дробным дифференциальным уравнением с начальными условиями [13–21].

Ввиду важности версии Капуто, мы сравним этот подход с формулировкой Римана-Лиувилля.Определение, предложенное Капуто, обращает порядок интегральных и производных операторов с производной нецелого порядка от оператора Римана-Лиувилля. Подытожим разницу между этими двумя формулировками. В Caputo: сначала вычисляем производную целого порядка, а затем вычисляем интеграл нецелого порядка. В методе Римана-Лиувилля: сначала вычислите интеграл нецелого порядка, а затем вычислите производную целого порядка. Важно отметить, что производная Капуто полезна для решения проблем, в которых начальные условия выполняются в функции и в соответствующих производных целочисленного порядка.

После первого конгресса в Университете Нью-Хейвена в 1974 году FC был разработан и появилось несколько приложений во многих областях научных знаний. Как следствие, были предложены различные подходы к решению проблем, связанных с производной, и в литературе доступны различные определения дробной производной. В статье систематизированы существующие формулировки дробных производных и интегралов. Следует также отметить, что у нас может быть несколько альтернативных выражений для одного и того же определения.Поэтому мы представляем только наиболее представительные и цитируем конкретные статьи [22–32] и книги [33–40], которые мы считаем наиболее актуальными. Кроме того, в документе не рассматриваются плюсы и минусы каждого определения и не рассматривается поддержка функции, которая должна быть дифференцирована или интегрирована.

Работа организована следующим образом. В разделе 2 представлены принятые обозначения. В разделах 3 и 4 перечислены предлагаемые определения дробных производных и интегралов соответственно.Наконец, в Разделе 5 дается несколько кратких замечаний.

2. Обозначение

Следующие примечания поясняют обозначения, используемые в дальнейшем в разделах 3 и 4. (i) Пусть,, где обозначает действительную часть комплексного числа. (Ii) Позвольте быть конечным интервалом в,,, и. (iii) нижняя функция, обозначаемая, определяется как. (iv) - это целая часть числа и дробная часть, так что. (v). (vi) - переменный дробный порядок с и. является непрерывной функцией на. (vii) является замкнутым контуром на комплексной плоскости, начиная с, обводя один раз в положительном смысле и возвращаясь в., с и. (viii) Рассмотрим и. Так называемая -гамма-функция, обозначаемая как, связана с классической гамма-функцией посредством. (Ix) Так называемый -символ Почхаммера дает. (X) -дробная производная Гильфера восстанавливает, как частные случаи, дробную Производная Римана-Лиувилля, если и, и дробная производная Капуто, если [41].

3. Определения дробных производных

Производная Лиувилля:

Левая производная Лиувилля:

Правая производная Лиувилля:

Левая производная Римана-Лиувилля:

Правая производная Римана-Лиувилля:

Левая производная Капуто:

Правая производная Капуто:

Левая производная Грюнвальда-Летникова:

Правая производная Грюнвальда-Летникова:

Производное Вейля:

Производная по Маршо:

Левая производная Маршо:

Правосторонняя производная Маршо:

Производная Адамара [42]:

Левая производная Чена:

Правая производная Чена:

Производная Дэвидсона-Эссекса [15]:

Производная Коимбры [43–45]:

Производное по канавати:

производная Джумари,:

производная Рисса:

Производная Коссара:

Локальная дробная производная Янга [40]:

Левая производная Римана-Лиувилля переменного дробного порядка:

Правая производная Римана-Лиувилля переменного дробного порядка:

Левая производная Капуто переменного дробного порядка:

Правая производная Капуто переменного дробного порядка:

Производная Капуто переменного дробного порядка:

Модифицированная дробная производная Римана-Лиувилля:

Дробная производная Ослера [46]:

-фракционная производная Гильфера [41]:

4.Определения дробных интегралов

Левосторонний интеграл Римана-Лиувилля:

Правосторонний интеграл Римана-Лиувилля:

Интеграл Адамара:

Интеграл Вейля:

Левосторонний интеграл Чена:

Правосторонний интеграл Чена:

Интеграл Коссара [47]:

Интеграл Эрдейи (левый):

Интеграл Эрдейи (правый):

Интеграл Кобера (левый):

Интеграл Кобера (правый):

Локальный дробный интеграл Яна:

Левый интеграл Римана-Лиувилля переменного дробного порядка:

Правый интеграл Римана-Лиувилля переменного дробного порядка:

-дробный интеграл Гильфера:

Замечание 1. Если - любая дробная производная, последовательная производная Миллера-Росса порядка задается формулой [3]

Замечание 2. Какое бы определение ни использовалось,.

Замечание 3. Некоторые авторы не различают используемое определение с помощью надстрочного индекса (,, и), но вместо этого используют другие шрифты для оператора (,,, и). Конкретное соответствие между шрифтами и определениями варьируется. Очень часто вообще не дается никаких указаний, за исключением, возможно, сопроводительного текста, и предполагается, что читатель понимает из контекста, какое конкретное определение имеется в виду.

Замечание 4. В литературе можно найти несколько альтернативных обозначений оператора: Только один из двух операторов должен использоваться, так как все зависит от изменения знака. На практике это один из наиболее часто используемых.

Замечание 5. В выражениях для правой и левой дробных производных Лиувилля (2) и (3), соответственно, некоторые авторы имеют несколько отличное выражение вместо просто + и на нижнем пределе.

Замечание 6. Можно упомянуть «разность дробного порядка», обсужденную Бозанке [48], и «производную Рушевея», представленную в [42, 49–51].

Замечание 7. Авторы не намерены обсуждать плюсы и минусы списка определений дробных производных и интегралов в разделах 3 и 4. Имея в виду, что читатель может найти преимущества в применении правильного определения для своего / ее особый исследовательский интерес, можно сказать, что наиболее часто используемые определения - это определения Римана-Лиувилля (т.е.g., в исчислении), Капуто (например, в физике и численном интегрировании) и Грюнвальда-Летникова (например, в обработке сигналов, инженерии и управлении). Проблема инициализации играет важную роль в прикладных науках, и, следовательно, иногда принимаются различные определения в рамках конкретных тем, но общая проблема еще предстоит прояснить.

Замечание 8. В статье не рассматриваются конкретные отношения, включающие явные параметры, интервалы или константы, связанные с различными производными.Например, можно упомянуть, что при, дробные производные Лиувилля имеют чисто мнимый порядок. Также для восстанавливаем производную целого порядка. Например, и.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.

Типы задач, поддерживаемые помощником по преобразованию в математические выражения

См.

Производные и интегралы от стационарных функций

Интерактивное пособие по алгебре для 10-11 классов

13.2: Производные и интегралы векторных функций

Производные векторных функций

Касательные векторы и единичные касательные векторы

Интегралы от векторных функций

Исчисление: дифференциалы и интегралы

Дифференциация: Насколько быстро что-то меняется?

Различные производные

Аналитические производные

Степенные члены и многочлены

Сумма сроков

Тригонометрические функции

Цепная линейка

Круговое и простое гармоническое движение

: как складываются результаты переменной ставки?

Численное интегрирование

Аналитическая интеграция

Показательная функция

1 / x и функция журнала

Интеграл синуса и cos

Способы интеграции

Частные производные

Что такое логарифм? Краткое введение.

операторов порядка матриц как расширение дробного исчисления

исчисление: интегралы

Определения

Формулы

Сумма Римана

Линейность

Интеграл как функция

Дай мне немного из этого

Что дальше

Лимит латекса

Латексные интегралы по замкнутой поверхности и объему

Что такое исчисление и как с ним разобраться

Исчисление было открыто или изобретено?

Сущность исчисления

Что такое интегралы и производные

Как вычислять производные и интегралы

Формулы исчисления

Так что же для меня исчисление?

Обзор определений производных дробного порядка и интеграла

1. Введение

2. Обозначение

3. Определения дробных производных

4.Определения дробных интегралов

Конфликт интересов

Оставить комментарий Отменить ответ