Производные и интегралы в физике: 4.3.2 Примеры применения интеграла в физике и геометрии - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Интегралы в физике как понять

Видеоурок: Применение интегралов в физике и математике

Лекция: Примеры применения интеграла в физике и геометрии

Процесс нахождение первообразной называется интегрированием.

Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.

Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.

Итак, начнем сначала. Мы помним, что скорость – это первая производная перемещения. Но так как мы знаем, что интегрирование и нахождение производной – это два взаимообратных процесса, то мы можем предполагать, что, если для нахождения скорости, нужно было найти производную от перемещения, то для нахождения перемещения по скорости, необходимо произвести интегрирование заданной функции.

Отсюда можно сделать вывод, что перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:

Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:

По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].

Итак, найдем определенный интеграл данной функции:

Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.

Точно так же можно найти скорость по заданной функции ускорения.

Еще одной физической величиной, которая находится с помощью интегрирования, является работа.

Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:

Пример: Предположим, что к некоторому телу для его передвижения прикладывают силу, которая изменяется по закону F(x) = x +3. Необходимо найти работу, которую при этом совершает сила для перемещения тела с 1 м до 2 м.

Для нахождения работы следует найти определенный интеграл заданной функции по известным пределам интегрирования:

Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.

Кроме рассматриваемых задач, интегрирование в физике используется для нахождения работы по мощности, массы по плотности, заряда по силе тока, количества теплоты по известной теплоемкости, а также многое другое.

Что же касается геометрии, то геометрическим смыслом интегрирования считается нахождение площади фигуры под графиком.

Итак, чтобы найти площадь фигуры, которая ограничена с двух сторон пределами интегрирования и с одной стороны графиком функции, то необходимо найти интеграл данной функции:

Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х 2 на пределах рассмотрения х = 0, х = 4.

Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

вычисление площади фигуры.
вычисление массы тела с неравномерной плотностью.
определение пройденного пути при движении с непостоянной скоростью.
и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком
– это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция

f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки.

Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Производная от интеграла равна подынтегральной функции:

Константу можно выносить из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

Линейность:

Знак интеграла изменяется, если поменять местами пределы интегрирования:

При любых точках a, b и с:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Исследовательская работа по теме: «Применение производных и интегралов в физике, математике и электротехнике.»

Слайд 1

ГБПОУ КНТ им. Б. И. Корнилова Исследовательская работа по теме: « применение Производных и интегралов в физике, математике и электротехнике.» Студента гр. 2014-эоп-33д иванова сергея .

Слайд 2

Содержание: 4 .Применение производной и интеграла в математике. 5 .Применение производной и интеграла в физике. 6 .Применение производной и интеграла в электротехнике. 1 .История появления производной. 2 .История появления интеграла. 3 .История появления дифференциальных уравнений.

Слайд 3

1 .История появления производной. В конце 17 века великий английский учёный Исаак Ньютон доказал что Путь и скорость связаны между собой формулой: V ( t )= S ’( t ) и такая связь существует между количественными характеристиками самых различных процессов исследуемых : физикой, ( a = V ’= x ’’ , F = ma = m * x ’’ , импульс P = mV = mx ’ , кинетическая E = mV 2 /2= mx ’ 2 /2), химией, биологией, и техническими науками. Это открытие Ньютона стало поворотным пунктом в истории естествознания.

Слайд 4

1 .История появления производной. Честь открытия основных законов математического анализа наравне с Ньютоном принадлежит немецкому математику Готфриду Вильгельму Лейбницу. К этим законам Лейбниц пришел, решая задачу проведения касательной к произвольной кривой, т.е. сформулировал геометрический смысл производной, что значение производной в точке касания есть угловой коэффициент касательной или tg угла наклона касательной с положительным направлением оси О X . Термин производная и современные обозначения y ’ , f ’ ввёл Ж.Лагранж в 1797г.

Слайд 5

2 .История появления интеграла. Понятие интеграла и интегральное исчисление возникли из потребности вычислять площади (квадратуру) любых фигур и объёмы (кубатуру) произвольных тел. Предыстория интегрального исчисления восходит к древности. Первым известным методом для расчёта интегралов является метод для исследования площади или объёма криволинейных фигур – метод исчерпывания Евдокса ( Евдокс Книдский ( ок . 408 г. до н.э. – ок . 355 г. до н.э.) – древнегреческий математик, механик и астроном), который был предложен примерно в 370 до н. э. Суть этого метода заключается в следующем: фигура, площадь или объем которой пытались найти, разбивалась на бесконечное множество частей, для которых площадь или объём уже известны.

Слайд 6

«Метод исчерпывания» Предположим, что нам надо вычислить объём лимона, имеющего неправильную форму, и поэтому применить какую-либо известную формулу объёма нельзя. С помощью взвешивания найти объём также трудно, так как плотность лимона в разных частях его разная. Поступим следующим образом. Разрежем лимон на тонкие дольки. Каждую дольку приближённо можно считать цилиндриком , радиус основания, которого можно измерить. Объём такого цилиндра вычислить легко по готовой формуле. Сложив объёмы маленьких цилиндров, мы получим приближенное значение объёма всего лимона. Приближение будет тем точнее, чем на более тонкие части мы сможем разрезать лимон.

Слайд 7

2 . История появления интеграла. Вслед за Евдоксом метод «исчерпывания» и его варианты для вычисления объёмов и площадей применял древний учёный Архимед. Успешно развивая идеи своих предшественников , он определил длину окружности , площадь круга, объём и поверхность шара. Он показал, что определение объёмов шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объёма цилиндра.

Слайд 8

Основой теории дифференциальных уравнений стало дифференциальное исчисление , созданное Лейбницем и Ньютоном. Сам термин «дифференциальное уравнение» был предложен в 1676 году Лейбницем. 3 .История появления дифференциальных уравнений. Первоначально дифференциальные уравнения возникли из задач механики, в которых требовалось определить координаты тел, их скорости и ускорения, рассматриваемые как функции времени при различных воздействиях. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи.

Слайд 9

3 .История появления дифференциальных уравнений. Из огромного числа работ XVII века по дифференциальным уравнениям выделяются работы Эйлера (1707—1783) и Лагранжа (1736—1813). В этих работах была прежде развита теория малых колебаний, а следовательно — теория линейных систем дифференциальных уравнений; попутно возникли основные понятия линейной алгебры (собственные числа и векторы в n -мерном случае). Вслед за Ньютоном Лаплас и Лагранж, а позже Гаусс (1777—1855) развивают также методы теории возмущений.

Слайд 10

4 .Применение производной и интеграла в математике : В математике производную широко используют в решениях многих задач, уравнений, неравенств, а так же в процессе исследования функции. Пример: Алгоритм исследования функции на экстремум: 1)О.О.Ф. 2) y ′=f ′(x), f ′(x)=0 и решаем уравнение. 3)О.О.Ф. разбиваем на интервалы. 4)Определяем знак производной на каждом интервале. Если f ′(x)>0 , то функция возрастает. Если f ′(x)

Слайд 11

4 .Применение производной и интеграла в математике : Интеграл (определенный интеграл) используют в математике (геометрии) для нахождения площади криволинейной трапеции. 2 , где t —время (в секундах), s(t) —отклонение точки в момент времени t (в метрах) от начального положения. Найди скорость и ускорение в момент времени t, если: t=1,5 с. 2)Материальная точка движется прямолинейно по закону x(t)= 2+20t+5t2. Найдите скорость и ускорение в момент времени t=2с (х – координата точки в метрах, t – время в секундах).

Слайд 13

Физическая величина Среднее значение Мгновенное значение Скорость Ускорение Угловая скорость Сила тока Мощность

Слайд 14

5 .Применение производной и Интеграла в физике. Интеграл также используется в задачах, например: нахождение скорости или пути. Тело движется со скоростью v(t) = t + 2 (м/с). Найти путь, который пройдет тело за 2 секунды после начала движения. Пример:

Слайд 15

6 .Применение производной и Интеграла в электротехнике. Производная также нашла применение в электротехнике. В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени . I=q ′(t ) Пример: 1)Заряд , протекающий через проводник , меняется по закону q=sin(2t-10) Найти силу тока в момент времени t=5 cек . Интеграл в электротехнике можно использовать для решения обратных задач, т.е. нахождение электрического заряда зная силу тока и т.д. 2)Электрический заряд протекающий через проводник, начиная с момента t = 0, задаётся формулой q(t ) = 3t2 + t + 2.Найдите силу тока в момент времени t = 3с. Интеграл в электротехнике можно использовать для решения обратных задач, т.е. нахождение электрического заряда зная силу тока и т.д.

Применение интеграла в физике и геометрии

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Применение интеграла в физике и геометрии

ПРИМЕНЕНИЕ
ИНТЕГРАЛА В
ФИЗИКЕ И
ГЕОМЕТРИИ
Презентацию сделал:
Кузнецов Захар

2. Краткое содержание

Что такое интеграл
История возникновения
интеграла
Применение интегралов в
физике и геометрии

3. Что такое интеграл

В высшей математике
используется такое понятие,
как интеграл или полное
название – интеграл функции.
Итак, что такое интеграл? Это
то же самое, что сумма
сложения бесконечно малых
слагаемых (точек, отрезков),
которых имеется бесконечно
огромное количество.
Обозначается интеграл
знаком «ʃ».
Упрощённо интеграл можно
представить как аналог суммы
для бесконечного числа
бесконечно малых слагаемых.
Неформально интеграл функции
можно описать как площадь
фигуры, образующейся между
осью х (ось абсцисс) и кривой
графика функции (такая фигура
называется криволинейной
трапецией).

Процесс определения
данной площади называется
интегрированием. Иногда
функция может быть задана
несколькими переменными
(неизвестными), тогда интеграл
является объемом под
поверхностью, которую образует
график данной функции.
Неформально интеграл функции можно
описать как площадь фигуры, образующейся
между осью х (ось абсцисс) и кривой графика
функции (такая фигура называется
криволинейной трапецией).
Процесс определения данной площади
называется интегрированием. Иногда функция
может быть задана несколькими переменными
(неизвестными), тогда интеграл является
объемом под поверхностью, которую образует
график данной функции.

5. История возникновения интегралов

Понятие интеграла
и интегральное
исчисление возникли
из потребности
вычислять площади
(квадратуру) любых
фигур и объёмы
(кубатуру)
произвольных тел.
Предыстория
интегрального
исчисления
восходит к
древности.

Термин «интеграл» (от лат. integer — целый, то
есть целая, вся — площадь) был предложен в 1696
г. Иоганном Бернулли.
Современное обозначение
неопределенного интеграла было
введено Лейбницем в 1675 году. Он
адаптировал интегральный символ
, образованный из буквы S —
сокращения слова
лат. summa (сумма). Современное
обозначение определенного
интеграла, с ограничениями над и
под знаком интеграла, были
впервые использованы Жаном
Батистом Жозефом Фурье в 181920.

6. . Применение интеграла

с помощью интеграла можно вычислить такие
физические величины, как работа, она равна
интегралу от силы, затраченной при
перемещении тела; масса однородного
стержня равна интегралу от линейной
плотности этого стержня; величина
заряда равна интегралу от силы
тока; количество теплоты равно интегралу
от теплоёмкости

7. . Применение интеграла в геометрии.

В геометрии понятие интеграла
используется при вычислении объёмов
тел.

Формула V=

9. Вычисление объемов тел с помощью интегралов

10. Применение интегралов в физике

В физике интеграл применяется для вычисления работы переменной силы,
вычисления массы неоднородного стержня и для вычисления расстояния по
известному закону изменения скорости.
Задача
Тело двигается прямолинейно со скоростью, которая изменяется по закону ..
Найти расстояние, пройденное телом за интервал времени от t1=1с до t2=3с
Решение

11. Применение в физике

. На вычисление пути пройденного точкой.
Путь, пройденный точкой при неравномерном
движении по прямой с переменной
скоростью
за промежуток
времени от
до
вычисляется по
формуле.

12. Решение задач с помощью интеграла

Пример 1:
Скорость движения точки
м/с.
Найти путь, пройденный точкой за 4-ю
секунду.
Решение: согласно условию:
Следовательно,

13. Решение задач с помощью интеграла

Пример 2:
Два тела начали двигаться одновременно из одной точки в
одном направлении по прямой.

Первое тело движется со
скоростью
м/с, второе — со скоростью v
= (4t+5) м/с. На каком расстоянии друг от друга они окажутся
через 5 с?
Решение: очевидно, что искомая величина есть
разность расстояний, пройденных первым и
вторым телом за 5 с:

14. вывод о применении интеграла по таблице

Математика
Физика
Вычисления S фигур.
Работа А переменной
Длина дуги кривой.
V тела на S
параллельных
сечений.
V тела вращения и т.д.
силы.
S – (путь) перемещения.
Вычисление массы.
Вычисление момента
инерции линии, круга,
цилиндра.
Вычисление координаты
центра тяжести.
Количество теплоты и т.д.

English Русский Правила

Высшая математика для начинающих физиков и техников.

Яков Борисович Зельдович, Иссак Моисеевич Яглом

М., Наука, 1982. 512 с.

Загрузить (Mb)
djvu (8. 73)	pdf (-)	ps (-)	html (-)	tex (-)

Эта книга – плод совместного труда физика и математика, поставивших своей целью написать пособие совершенно нового типа для будущих естествоиспытателей. Цель книги состоит в том, чтобы дать возможность будущему физику (химимку, инженеру и др.) использовать в своей работе высшую математику, освоив ее методы без полных логических обоснований, рассматривая ее как раздел естествознания и решая возможно большее число конкретных задач.

Содержание

Предисловие.
К читателю.
Предисловие для преподавателей.

ЧАСТЬ ПЕРВАЯ. ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ.

Глава 1. ФУНКЦИИ И ГРАФИКИ.
§ 1. Функциональная зависимость.
§ 2. Координаты. Расстояния и углы, выраженные в координатах.
§ 3. Графическое изображение функций. Уравнение прямой.
§ 4. Обратная пропорциональность и гипербола. Парабола.
§ 5. Параболы и гиперболы высших порядков. Полукубическая парабола.
§ 6. Обратная функция. Графики взаимно-обратных функций.

§ 7. Преобразования графиков функций.
§ 8. Параметрическое задание линий.
§ 9*. Некоторые дополнительные сведения из аналитической геометрии.

Глава 2. ЧТО ТАКОЕ ПРОИЗВОДНАЯ.
§ 1. Движение, путь и скорость.
§ 2*. Теплоемкость тела. Расширение тел при нагревании.
§ 3. Производная. Простейшие примеры вычисления производных.
§ 4. Первые свойства производной. Приближенное вычисление значений функции с помощью производной.
§ 5. Касательная к кривой.
§ 6. Рост и убывание функции. Максимумы и минимумы.
§ 7. Вторая производная функции. Выпуклость и вогнутость кривой.

Точки перегиба.

Глава 3. ЧТО ТАКОЕ ИНТЕГРАЛ.
§ 1. Определение пути по скорости движения и определение площади, ограниченной кривой.
§ 2. Определенный интеграл.
§ 3. Связь между интегралом и производной.
§ 4. Неопределенный интеграл.
§ 5. Свойства интегралов.
§ 6. Примеры и приложения.

Глава 4. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ.
§ 1. Дифференциал.
§ 2. Производная суммы и произведения функций.
§ 3. Сложная; функция. Производная частного двух функций.

§ 4. Обратная функция. Параметрическое задание функции.
§ 5. Степенная функция.
§ 6. Производные алгебраических функций.
§ 7. Показательная функция.
§ 8. Число е.
§ 9. Логарифмы.
§ 10. Тригонометрические функции.
§ 11. Обратные тригонометрические функции.

§ 12. Производная функции, заданной неявно.

Глава 5. ТЕХНИКА ИНТЕГРИРОВАНИЯ.
§ 1. Постановка задачи.
§ 2. Простейшие интегралы.
§ 3. Общие свойства интегралов.
§ 4. Интегрирование по частям.
§ 5. Метод подстановки.
§ 6. Замена переменной в определенном интеграле.

Глава 6. РЯДЫ. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
§ 1. Представление функций в виде рядов.
§ 2. Вычисление значений функций при помощи рядов.
§ 3. Случаи неприменимости рядов. Геометрическая прогрессия.
§ 4. Бином Ньютона для целых и дробных показателей.
§ 5. Порядок возрастания и убывания функций. Правило Бернулли-Лопиталя.
§ 6. Дифференциальные уравнения первого порядка. Случай разделяющихся переменных.
§ 7*. Дифференциальное уравнение вытекания воды.

Глава 7. ИССЛЕДОВАНИЕ ФУНКЦИЙ. НЕСКОЛЬКО ЗАДАЧ ИЗ ГЕОМЕТРИИ.
§ 1. Гладкие максимумы и минимумы.
§ 2. Негладкие максимумы и минимумы. Изломы и разрывы. Левая и правая производные функции.
§ 3*. Выпуклые функции и алгебраические неравенства.
§ 4. Вычисление площадей.
§ 5*. Оценки некоторых сумм и произведений.
§ 6*. Еще о натуральном логарифме.
§ 7. Средние значения.
§ 8. Длина кривой.
§ 9. Кривизна и соприкасающаяся окружность.
§ 10. Стереометрические приложения интегрального исчисления.
§ 11. Как строить кривые.

ЧАСТЬ ВТОРАЯ. ПРИЛОЖЕНИЯ ВЫСШЕЙ МАТЕМАТИКИ К НЕКОТОРЫМ ВОПРОСАМ ФИЗИКИ И ТЕХНИКИ.

Глава 8. РАДИОАКТИВНЫЙ РАСПАД И ДЕЛЕНИЕ ЯДЕР.
§ 1. Основные характеристики радиоактивного распада.
§ 2. Измерение среднего времени жизни радиоактивных атомов.
§ 3. Последовательный распад (радиоактивное семейство).
§ 4. Исследование решения для радиоактивного семейства.
§ 5. Цепная реакция деления урана.
§ 6. Размножение нейтронов в большой массе.
§ 7. Вылет нейтронов.
§ 8. Критическая масса.
§ 9. Подкритическая и надкритическая массы при непрерывном источнике нейтронов.
§ 10. Значение критической массы.

Глава 9. МЕХАНИКА.
§ 1. Сила, работа, мощность.
§ 2. Энергия.
§ 3. Равновесие и устойчивость.
§ 4. Второй закон Ньютона.
§ 5. Импульс силы.
§ 6. Кинетическая энергия.
§ 7. Инерwиальные и неинерциальные системы отсчета.
§ 8*. Преобразования Галилея. Энергия в движущейся системе отсчета.
§ 9*. Траектория снаряда. Парабола безопасности.
§ 10. Движение тел в космическом пространстве.
§ 11. Реактивное движение и формула К.Э.Циолковского.
§ 12. Масса, центр тяжести и момент инерции стержня.
§ 13*. Центр тяжести нити и пластинки.
§ 14. Движение тела в среде, противодействующей движению, под действием силы, зависящей только от скорости.
§ 15*. Движение тел в жидкостях и газах.

Глава 10. КОЛЕБАНИЯ.
§ 1. Движение под действием упругой силы.
§ 2. Случай силы, пропорциональной отклонению. Гармонические колебания.
§ 3. Маятник.
§ 4. Энергия колебаний. Затухающие колебания.
§ 5. Вынужденные колебания и резонанс.
§ 6. О точных и приближенных решениях физических задач.
§ 7. Сложение колебаний. Биения.
§ 8. Задача о колеблющейся струне.
§ 9. Гармонический анализ функций. Ряды Фурье.

Глава 11. ТЕПЛОВОЕ ДВИЖЕНИЕ МОЛЕКУЛ. РАСПРЕДЕЛЕНИЕ ПЛОТНОСТИ ВОЗДУХА В АТМОСФЕРЕ.
§ 1. Условие равновесия в атмосфере.
§ 2. Связь между плотностью и давлением.
§ 3. Распределение плотности.
§ 4. Молекулярно-кинетическая теория распределения плотности.
§ 5. Броуновское движение и распределение молекул по кинетической энергии.
§ 6. Скорости химических реакций.
§ 7. Испарение. Ток эмиссии катода.

Глава 12. ПОГЛОЩЕНИЕ И ИЗЛУЧЕНИЕ СВЕТА. ЛАЗЕРЫ.
§ 1. Поглощение света (постановка задачи и грубая оценка).
§ 2. Уравнение поглощения и его решение.
§ 3. Соотношение между точным и грубым расчетами поглощения.
§ 4. Эффективное сечение.
§ 5. Ослабление потока заряженных частиц α- и β-лучей.
§ 6*. Поглощение и испускание света горячим газом.
§ 7*. Термодинамическое равновесие излучения.
§ 8*. Вероятность излучения и условия термодинамического равновесия. емкости. Резонанс токов.
§ 15. Общие свойства резонанса линейной системы.
§ 16*. Ток смещения и электромагнитная теория света.
§ 17*. Нелинейное сопротивление и туннельный диод.

ЧАСТЬ ТРЕТЬЯ. ДОПОЛНИТЕЛЬНЫЕ ТЕМЫ ИЗ ВЫСШЕЙ МАТЕМАТИКИ.

Глава 14. КОМПЛЕКСНЫЕ ЧИСЛА.
§ 1. Основные свойства комплексных чисел.
§ 2. Возведение в мнимую степень и число e.
§ 3. Тригонометрические функции и логарифмы.
§ 4*. Тригонометрические функции мнимого аргумента. Гиперболические функции.

Глава 15. КАКИЕ ФУНКЦИИ НУЖНЫ ФИЗИКУ?
§ 1. Аналитические функции вещественной переменной.
§ 2. Производные функций комплексной переменной.

Глава 16. ЗАМЕЧАТЕЛЬНАЯ ДЕЛЬТА-ФУНКЦИЯ ДИРАКА.
§ 1. Различные способы определения функции.
§ 2. Дирак и его функция.
§ 3. Разрывные функции и их производные.
§ 4. Представление дельта-функции формулами.

Глава 17. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ И ДЕЛЬТА-ФУНКЦИИ.
§ 1. Комплексные числа и механические колебания.
§ 2. Интегралы в комплексной области.
§ 3. Аналитические функции комплексной переменной и течение жидкости.
§ 4. Применения дельта-функции.

ЗАКЛЮЧЕНИЕ. ЧТО ЖЕ ДАЛЬШЕ?
ЛИТЕРАТУРА.

ПРИЛОЖЕНИЯ.
I. Таблица производных.
II. Интегралы от некоторых функций.
III. Некоторые разложения функций в ряды.
IV. Некоторые числовые таблицы.
V. Международная система физических единиц СИ.
VI. Латинский и греческий алфавиты.

ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ.

Загрузить (Mb)
djvu (8. 73)	pdf (-)	ps (-)	html (-)	tex (-)

Постоянный адрес этой страницы: http://math.ru/lib/89

Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

Математический анализ. Часть II | Открытые видеолекции учебных курсов МГУ

Курс «Математический анализ. Часть II» читается студентам первого курса физического факультета МГУ имени М. В. Ломоносова во 2 семестре.

Во второй части курса лекций по математическому анализу рассматриваются следующие вопросы:

Функции многих переменных.
Производные высших порядков.
Формула Тейлора.
Локальный экстремум.
Теория неявных функций.
Условный экстремум.
Кратные и двойные интегралы. Тройные интегралы.
Криволинейные интегралы.
Формула Грина.
Поверхностные интегралы.

Понятия математического анализа используются затем во всех последующих математических дисциплинах, а также в курсах общей и теоретической физики. Поэтому активное изучение учащимися курса анализа позволяет заложить фундамент для успешного восприятия более сложных понятий и в математике, и в различных разделах современной теоретической физики.

Излагаемый в данном курсе материал полностью соответствует действующей программе по математическому анализу для физических специальностей. При рассмотрении многих вопросов особое внимание уделяется приложениям математических понятий и утверждений в физике.

Список всех тем лекций

Лекция 1. Функции многих переменных..
Основные понятия в m-мерном пространстве Последовательности точек Функции многих переменных, пределы функций

Лекция 2. Предел функции многих переменных..
Пределы функций многих переменных Непрерывность функций многих переменных Основные теоремы о непрерывных функциях

Лекция 3. Непрерывность функций многих переменных..
Непрерывность функций многих переменных Частные производные и дифференцируемость функций

Лекция 4. Дифференциал функции многих переменных..
Частные производные и дифференцируемость функций Дифференцируемость сложной функции Дифференциал функции многих переменных

Лекция 5. Геометрический смысл производной..
Геометрический смысл производной, касательная плоскость Производная по направлению, градиент функции Производные и дифференциалы высших порядков

Лекция 6. Производные высших порядков..
Частные производные высших порядков Дифференциалы высших порядков

Лекция 7. Формула Тейлора..
Дифференциалы высших порядков Формула Тейлора

Лекция 8. Локальный экстремум..
Локальный экстремум Квадратичные формы Достаточные условия экстремума

Лекция 9. Теория неявных функций..
Неявные функции Дифференцируемость неявных функций

Лекция 10. Неявные функции, определяемые системой уравнений..
Продолжение теории неявных функций Неявные функции, определяемые системой уравнений Зависимость функций

Лекция 11. Условный экстремум..
Зависимость функций Условный экстремум

Лекция 12. Кратные и двойные интегралы..
Условный экстремум Кратные интегралы, квадрируемые площади Двойные интегралы

Лекция 13. Двойные интегралы..
Двойные интегралы Вычисление двойных интегралов с помощью повторного интегрирования Замена переменных в двойном интеграле

Лекция 14. Тройные интегралы..
Замена переменных в двойном интеграле Тройные интегралы Вычисление тройных интегралов с помощью повторного интегрирования Замена переменных в тройном интеграле

Лекция 15. Криволинейные интегралы..
Криволинейные координаты Кривые, длина кривой Криволинейные интегралы первого рода Вычисление криволинейных интегралов первого рода при помощи определенных

Лекция 16. Криволинейные интегралы I и II рода..
Вычисление криволинейных интегралов первого рода при помощи определенных Криволинейные интегралы второго рода Вычисление криволинейных интегралов второго рода при помощи определенных Связь между криволинейными интегралами первого и второго рода Формула Грина

Лекция 17. Формула Грина..
Формула Грина Условия независимости криволинейного интеграла II рода от пути интегрирования

Лекция 18. Площадь поверхности..
Площадь поверхности

Лекция 19. Поверхностные интегралы I рода..
Поверхностные интегралы первого рода Вычисление поверхностных интегралов первого рода сведением к двойному Понятие стороны поверхности

Лекция 20. Поверхностные интегралы II рода..
Поверхностные интегралы второго рода Вычисление поверхностных интегралов второго рода Формула Остроградского-Гаусса Формула Стокса

Лекция 21. Геометрические приложения..
Независимость криволинейного интеграла II рода от пути интегрирования в пространстве Касание кривых Особые точки кривых Кривизна плоской кривой

26.3: Антипроизводные и интегралы – Physics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 19573

Howard Martin пересмотрено Аланом Нг
Университет Висконсин-Мэдисон

В предыдущем разделе мы занимались определением производной функции $f(x)$. Производная полезна, потому что она говорит нам, как функция $f(x)$ изменяется как функция $x$. В физике мы часто знаем, как изменяется функция, но не знаем фактическую функцию. Другими словами, мы часто сталкиваемся с противоположной проблемой: нам дана производная функции, и мы хотим определить реальную функцию. В этом случае мы ограничим наше обсуждение функциями одной независимой переменной.

Предположим, что нам дана функция $f(x)$, и мы знаем, что она является производной некоторой другой функции, $F(x)$, которую мы не знаем. Мы называем $F(x)$ антипроизводной функции $f(x)$. Антипроизводная функции $f(x)$, записанная $F(x)$, таким образом, удовлетворяет свойству: \[\begin{aligned} \frac{dF}{dx}=f(x )\end{aligned}\] Поскольку у нас есть символ, указывающий, что мы берем производную по $x$ ($\frac{d}{dx}$), у нас также есть символ, \ (\int dx\), за указание на то, что мы берем антипроизводную по $x$: \[\begin{aligned} \int f(x) dx &= F(x) \\ \therefore \ frac{d}{dx}\left(\int f(x) dx\right) &= \frac{dF}{dx}=f(x)\end{aligned}\] Ранее мы обосновали символ для производной, указав, что она похожа на $\frac{\Delta f}{\Delta x}$, но для случая, когда $\Delta x\to 0$. 2\), показанную на рисунке A2.2.1 (левая панель). Если вы представите сдвиг всей функции вверх или вниз, производная не изменится. Другими словами, если бы начало осей не отображалось на левой панели, вы все равно могли бы определить производную функции (насколько она крутая). Добавление константы $C$ к функции точно такое же, как сдвиг функции вверх или вниз, который не меняет ее производную. Таким образом, когда вы знаете производную, вы не можете знать значение $С$, если вам также не говорят, что функция должна проходить через определенную точку (так называемое начальное условие).

Чтобы определить производную функции, мы использовали Уравнение A2.2.1 . Теперь нам нужно получить эквивалентный рецепт для определения антипроизводной. Предположим, что у нас есть две части информации, необходимые для полного определения $F(x)$, а именно:

функция $f(x)=\frac{dF}{dx}$ (ее производная).
условие, что $F(x)$ должен проходить через определенную точку, $F(x_0)=F_0$.

Рисунок A2.3.1 : Определение первообразной $F(x)$ по функции $f(x) = 2x$ и начальному условию, что $F(x)$ проходит через точку $( х_{0}, F_{0}) = (1, 3)$.

Процедура определения первообразной $F(x)$ показана выше на рисунке A2.3.1. Начнем с рисования точки, которую, как мы знаем, должна пройти функция $F(x)$, $(x_0,F_0)$. Затем мы выбираем значение $\Delta x$ и используем производную $f(x)$, чтобы вычислить $\Delta F_0$, величину, на которую изменяется $F(x)$ когда $x$ меняется на $\Delta x$. Используя производную $f(x)$, оцененную в $x_0$, мы имеем: \[\begin{aligned} \frac{\Delta F_0}{\Delta x} &\ приблизительно f(x_0)\; \;\;\; (\text{в пределе} \Delta x\to 0 )\\ \следовательно \Delta F_0 &= f(x_0) \Delta x\end{aligned}\] Затем мы можем оценить значение функции $F_1 =F(x_1)$ в следующей точке, $x_1=x_0+\Delta x$, как показано черной стрелкой на рисунке A2.3.1 \[\begin{aligned} F_1&=F(x_1)\\ & =F(x+\Delta x) \\ &\приблизительно F_0 + \Delta F_0\\ &\приблизительно F_0+f(x_0)\Delta x\end{aligned}\] Теперь, когда мы определили значение функции \ (F(x)\) в $x=x_1$, мы можем повторить процедуру определения значения функции $F(x)$ в следующей точке, $x_2=x_1+\Delta x\ ). {i= N} f(x_{i-1}) \Delta x\end{aligned}\] Приведенный выше результат станет точно правильным в пределе \(\Delta x\to 0$: 9{i=N} f(x_{i-1}) \Delta x\]

Рассмотрим сумму поближе. Каждый член в сумме имеет форму $f(x_{i-1})\Delta x$ и проиллюстрирован на рисунке A2.3.2 для того же случая, что и на рисунке A2.3.1 (то есть, На рис. A2.3.2 показано известное нам $f(x)$, а на рис. A2.3.1 показано $F(x)$, которое мы пытаемся найти).

Рисунок A2.3.2 : Функция $f(x) = 2x$ и иллюстрация терминов $f(x_{0})∆x$ и $f(x_{1})∆x$ как площадь между кривой $f(x)$ и осью $x$, когда $∆x → 0$.

Как видите, каждый член в сумме соответствует площади прямоугольника между функцией $f(x)$ и осью $x$ (с отсутствующим куском). В пределе, где $\Delta x\to 0$, недостающие части (показаны заштрихованными областями на рисунке A2.3.2) исчезнут, и $f(x_i)\Delta x$ станет в точности областью между $f(x)$ и ось $x$ по длине $\Delta x$. Таким образом, сумма прямоугольных площадей будет приближаться к площади между $f(x)$ и осью $x$ между $x_0$ и $x_N$: \[\begin{aligned} \lim_ {\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x=\text{Площадь между f(x) и осью x от $x_0$ до $x_N$}\end{выровнено}\] 9{x_N}\конец{выровнено}\]

Напомним, что ранее мы писали первообразную с тем же символом $\int$: \[\begin{aligned} \int f(x) dx = F(x)\end{aligned}\] Символ \ (\int f(x) dx\) без ограничений называется неопределенным интегралом . {i=N=3} 2x_{i-1} \Delta x &=2x_0\Delta x+2x_1\Delta x+2x_2\Delta x\\ &=2\Delta x (x_0+x_1+ x_2) \\ &=2 \frac{x_3-x_0}{N}(x_0+x_1+x_2) \\ &=2 \frac{(4)-(1)}{(3)}(1+2+ 3) \\ &=12\end{aligned}\], где во второй строке мы заметили, что можем исключить $2\Delta x$, потому что он появляется в каждом термине. Поскольку мы использовали только 4 точки, это довольно грубое приближение интеграла, и мы ожидаем, что оно будет заниженным (поскольку отсутствующая область, представленная штриховыми линиями на рис. A2.3.2, довольно велика). 9{b}f(t)dt\) равно

площади между функцией $f(t)$ и осью $f$ между $t=a$ и $t= б$
сумма $f(t)\Delta t$ в пределе $\Delta t\to 0$ между $t=a$ и $t=b$
разность $f(b) – f(a)$.

Ответить

Общая первообразная и свойства

В таблице A2.3.1 ниже приведены первообразные (неопределенные интегралы) для общих функций.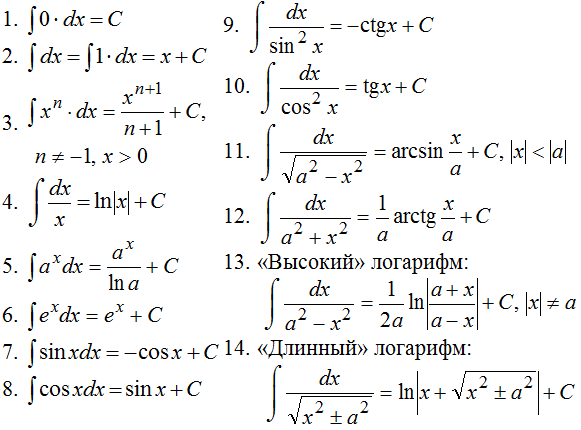 Во всех случаях $x,$ является независимой переменной, а все остальные переменные следует рассматривать как константы: 9х+С\) $f(x)=\ln(x)$ $F(x)=x\ln(x)-x+C$

Таблица A2.3.1 : Общие неопределенные интегралы функций.

Обратите внимание, что в общем случае получить первообразную функции гораздо сложнее, чем ее производную. Несколько общих свойств, помогающих вычислять неопределенные интегралы, показаны в таблице A2.3.2 ниже.

Антипроизводная	Эквивалентная антипроизводная
$\ int (f(x)+g(x)) dx$	$\int f(x)dx+\int g(x)dx$ (сумма)
$\целое (f(x)-g(x)) dx$	$\int f(x)dx-\int g(x)dx$ (вычитание)
$\int af(x) dx$	$a\int f(x)dx$ (умножение на константу)
$\целое f'(x)g(x) dx$	$f(x)g(x)-\int f(x)g'(x) dx$ (интегрирование по частям)

Таблица A2. 3.2 : Некоторые свойства неопределенных интегралов.

Обычное использование интегралов в физике — от суммы к интегралу

Интегралы чрезвычайно полезны в физике, поскольку они связаны с суммами. Если предположить, что наши друзья-математики (или компьютеры) могут определить для нас антипроизводные, использование интегралов не так сложно.

Ключевая идея в физике состоит в том, что интегралы являются инструментом для простого вычисления сумм . Как мы видели выше, интегралы соответствуют площади под кривой, которая находится путем суммирования (различных) площадей бесконечного числа бесконечно малых прямоугольников. В физике часто бывает так, что нам нужно взять сумму бесконечного числа мелких вещей, которые постоянно меняются, как площади прямоугольников.

Рассмотрим, например, стержень длиной $L$ и общей массой $M$, как показано на рисунке A2.3.3. Если стержень однороден по плотности, то если мы разрежем его, скажем, на две равные части, эти две части будут весить одинаково. Мы можем определить «линейную массовую плотность» $\mu$ для стержня как массу на единицу длины стержня: \[\begin{aligned} \mu = \frac{M}{L}\ end{aligned}\] Линейная массовая плотность имеет размеры массы относительно длины и может использоваться для нахождения массы стержня любой длины. Например, если стержень имеет массу $M=5\text{kg}$ и длину $L=2\text{m}$, то массовая плотность равна: \[\begin{ выровнено} \mu=\frac{M}{L}=\frac{(5\text{кг})}{(2\text{м})}=2,5\text{кг/м}\end{выровнено} \] Зная плотность массы, теперь мы можем легко найти массу $m$ куска стержня, длина которого, скажем, $l=10\text{см}$. Используя массовую плотность, масса стержня $10\text{см}$ определяется как: \[\begin{align} m=\mul=(2,5\text{кг/м})(0,1\ text{m})=0.25\text{kg}\end{aligned}\] Теперь предположим, что у нас есть неоднородный стержень длины $L$, как на рис. A2.3.3, и не имеющий постоянная линейная массовая плотность. Возможно, стержень становится все шире и шире, или в нем есть отверстия, которые делают его неоднородным. Представьте, что массовая плотность стержня задается функцией $\mu(x)$, которая зависит от положения вдоль стержня, где $x$ – расстояние, измеренное от одной стороны стержня. .

Рисунок A2.3.3 : Стержень с переменной линейной плотностью. Для вычисления массы стержня рассмотрим небольшой элемент массы $∆m_{i}$ длины $∆x$ в положении $x_{i}$. Суммарная масса стержня находится суммированием масс элементов малой массы.

Теперь мы не можем просто определить массу стержня путем умножения $\mu(x)$ и $L$, так как мы не знаем, какое значение $x$ использовать. Фактически, мы должны использовать все значения $x$ между $x=0$ и $x=L$.

Стратегия состоит в том, чтобы разделить стержень на $N$ частей длины $\Delta x$. Если мы пометим наши части стержня индексом $i$, мы можем сказать, что часть, которая находится в позиции $x_i$, имеет крошечную массу, $\Delta m_i$. Мы предполагаем, что $\Delta x$ достаточно мало, так что $\mu(x)$ можно считать постоянным по длине этого крошечного кусочка стержня. {i =N} \mu(x_i) \Delta x\end{aligned}\] Но это и есть определение интеграла ( 94 \\ &=78\text{g}\\\end{aligned}\]

Немного потренировавшись, вы сможете решать задачи такого типа, не записывая сумму явно. Представьте бесконечно малых кусков стержня длины $dx$ в положении $x$. Он будет иметь бесконечно малых масс, $dm$, определяемых как: \[\begin{aligned} dm = \mu(x) dx\end{aligned}\] Общая масса стержня равна тогда сумма (то есть интеграл) массы элементов \[\begin{aligned} M = \int dm\end{aligned}\], и мы действительно можем думать о знаке $\int$ как о сумме, когда суммируются вещи 9L \mu(x) dx\end{aligned}\], где мы сделали интеграл определенным, указав диапазон для суммирования, так как мы можем использовать $x$ для «пометки» элементов массы.

Следует отметить, что придумать вышеуказанный интеграл – это физика. Решение это математика. Мы будем гораздо больше беспокоиться о выписывании интеграла, чем о вычислении его значения. Вычислить интеграл всегда может друг-математик или компьютер, но определение того, какой интеграл записать, — это работа физика!

Эта страница под названием 26. 3: Анти-производные и интегралы распространяется в соответствии с лицензией CC BY-SA и была создана, изменена и/или курирована Говардом Мартином, отредактированным Аланом Нг.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
Райан Мартин и др.
Лицензия
CC BY-SA
Показать оглавление
нет
Теги

Производные для AP-физики

Введение:

AP Physics C — это курс физики, основанный на вычислениях, но факт в том, что вы можете сделать довольно хорошо, с точки зрения оценок, в AP Physics C – особенно часть механики – без знания исчисления. Конечно, вам не помешает узнать, что происходит со всеми этими странные математические символы и понятия, и обязательно будут быть задачами на тесте AP, которые требуют знания исчисления. К счастью, вы можете очень хорошо справиться даже с AP-тестом с очень элементарные навыки исчисления, которым можно научиться за несколько минут.

Вам нужно кое-что знать о:

Производные инструменты – деривативом является скорость изменения, или графически, наклон касательной к график. Хотя физика «забита» приложениями производная, нужно уметь вычислять только очень простые производные в этом курсе.
Определенные интегралы – определенный интеграл представляет собой площадь, и существует множество Применение интегралов в физике. В этом курсе вам необходимо уметь вычислять только самые элементарные интегралы.

Производные:

Производная – это скорость изменения, которая геометрически наклон графика. В физике скорость – это скорость изменения положение, поэтому математически скорость является производной положения. Ускорение — это скорость изменения скорости, поэтому ускорение равно производная скорости. Чистая сила – это скорость изменения импульса, поэтому производная импульса объекта говорит вам о чистой усилие на объект. Это лишь некоторые из приложений производная в физике.

Производные правила:

Нахождение производной функции (“дифференцирование” в язык исчисления) является операцией, основанной на правилах. Другими словами, вы необходимо распознать, какое производное правило применяется, а затем применить его. В Чтобы узнать, какое производное правило применяется, вам нужно знать некоторые производные правила. В таблицах ниже перечислены производные правила. которые вы будете использовать в этом курсе, и показывает некоторые примеры их использовать. Эти правила сформулированы с использованием «t» в качестве переменной (производная является «относительно» t на языке исчисления), так как большинство функции, которые мы будем использовать, являются функциями времени. Если вы принимаете производная, переменная которой равна “s”, просто замените “x” на “t” в производное правило.

Правила для особых функций:

Правило на английском языке	Правило в математике. Обозначение	Пример
Производная константы равна нулю.		Если x(t) = 5, то v(t) = 0. Если v(t) = -3, то a(t) = 0.
Производная от t равна единице.		Если x(t) = t, то v(t) = 1.
Производная t в степени равна степени, умноженной на t в степени. сила «одним меньше».		Если x(t) = t ² , то v(t) = 2t ¹ = 2т. (п = 2) Если v(t) = t ⁴ , то a(t) = 4t ³ . (п = 4) Если x(t) = t ^-3 , то v(t) = -3т ^-4 . (n = -3)
Производная синуса t есть косинус т.		Если x(t) = sin t, то v(t) = cos t.
Производная косинуса t является отрицательной синус т.		Если v(t) = cos t, то a(t) = -sin t.

Правила совмещения функций: В приведенных ниже правилах u и w представляют собой функции времени, t.

Правило на английском языке	Правило в математике. Обозначение	Пример
Производная константы, умноженная на функцию, равна константа, умноженная на производную функции.		Если x(t) = 3t ² , то v(t) = 3(2т ¹ ) = 6т. (с = 3 и и = т ² ) Если v(t) = 4sin t, то a(t) = 4cos t. (с = 4, и = грех т)
Производная суммы (или разности) двух функций есть сумма (или разность) их производные.		Если x(t) = t + sin t, то v(t) = 1 + cos t. (и = т, ш = грех т) Если v(t) = t ² – 4t, то a(t) = 2t ¹ – 4(1) = 2t – 4. (u = t ² , w = 4т)
Производная составного (одна функция внутри другая функция) функция равна производной “внешняя” функция, оставляя только “внутреннюю” функцию, умноженная на производную от “внутренней” функции. (Цепь Правило)		Если x(t) = (t + 2) ² , то v(t) = 2(t + 2) ¹ (1 + 0) = 2(t + 2). (и = т ² , ш = т + 2) Если v(t) = sin(2t ³ ), то a(t) = cos(2t ³)(2)(3t ²) = 6t ² cos(2t ³ ) (u = cos t, w = 2т ³ )

Правило на английском языке

Правило в математике. Обозначение

Пример

Производная константы, умноженная на функцию, равна константа, умноженная на производную функции.

Если x(t) = 3t ² , то v(t) = 3(2т ¹ ) = 6т. (с = 3 и и = т ² )

Если v(t) = 4sin t, то a(t) = 4cos t. (с = 4, и = грех т)

Производная суммы (или разности) двух функций есть сумма (или разность) их производные.

Если x(t) = t + sin t, то v(t) = 1 + cos t. (и = т, ш = грех т)

Если v(t) = t ² – 4t, то a(t) = 2t ¹ – 4(1) = 2t – 4. (u = t ² , w = 4т)

Производная составного (одна функция внутри другая функция) функция равна производной “внешняя” функция, оставляя только “внутреннюю” функцию, умноженная на производную от “внутренней” функции. (Цепь Правило)

Если x(t) = (t + 2) ² , то v(t) = 2(t + 2) ¹ (1 + 0) = 2(t + 2). (и = т ² , ш = т + 2)

Если v(t) = sin(2t ³ ), то a(t) = cos(2t ³)(2)(3t ²) = 6t ² cos(2t ³ ) (u = cos t, w = 2т ³ )

Определенные интегралы:

Определенный интеграл представляет собой площадь, и вычисление определенного интеграл («интегрирование» на языке исчисления) является обратным нахождение производной – подобное вычитанию является обратным сложением. В физике площадь под графиком зависимости скорости от времени представляет перемещение, поэтому определенный интеграл скорости дает смещение. Площадь под графиком зависимости ускорения от времени равна изменение скорости, поэтому определенный интеграл ускорения говорит вы изменение скорости. Площадь под графиком зависимости силы от положения равна работе, совершаемой силой, поэтому определенный интеграл силы (относительно положения) говорит вам о работе силы. Есть еще много, много других применений определенного интеграла в физика.

На приведенной выше диаграмме показано соотношение между определенное целочисленное обозначение и площадь, которую оно представляет. “а” и “b” – называемые “пределы интегрирования” идут внизу и вершина большой “S”. “f(t)” – это функция, интегрированный («подынтегральная функция»), а «dt» говорит, что «t» — это используемая переменная.

Обозначение читается как “определенный интеграл от a до b ф т, дт”.

Правила для определенных интегралов:

Так же, как вы можете вычесть 5 из 12, думая: “Что у меня есть? прибавить к 5, чтобы получить 12?», вы можете вычислить определенные интегралы с помощью думая: «Какую функцию я должен дифференцировать, чтобы получить функция в этом интеграле?» Эта функция называется «интегралом». или «антипроизводная». Математический символ первообразной выглядит как определенный интеграл без ограничений интеграция.

Первообразные правила для конкретных функций: если вы являетесь студент-математик, вы заметите, что мы игнорируем важный математический момент в следующих правилах.

Правило на английском языке	Правило в математике. Обозначение	Пример
Первообразная константы – это постоянные времена т.
Первообразная t в степени равна t в степени мощность плюс один, деленная на мощность плюс один.	(Это обратная производная формула)
Первообразная синуса t является отрицательной косинус т.	(Это обратная производная формула.)
Первообразная косинуса t есть синус т.	(Это обратная производная формула. )

Первообразные правила для комбинаций функций: в правила ниже, u и w представляют функции времени, т.

Правило на английском языке	Правило в математике. Обозначение	Пример
Первообразная константы, умноженная на функцию равно константе, умноженной на первообразную функция.
Первообразная суммы (или разности) двух функций равна сумме (или разности) их первообразные.

Основная теорема исчисления — расскажет, как оценить определенные интегралы на основе того, что вы знаете о первообразные.

Правило на английском языке	Правило в математике. Обозначение	Пример
Если F(t) является первообразной f(t), то определенный интеграл от a до b от f равен функции F оценивается, когда t равно b минус F оценивается, когда t равно а.

последнее обновление 26 ноября 2007 г. автор JL Стэнбро

исчисление – Задача по физике на производные и интегралы

Задавать вопрос

Спросил 6 лет, 5 месяцев назад

Изменено 6 лет, 5 месяцев назад

Просмотрено 1к раз

$\begingroup$

Итак, есть несколько основных формул, с которых я хотел бы начать: $W=\int_0^bFdx$, $F=ma$ и $a=\frac{d^2}{dt^2}x$ . 92}х\вправо)dx$$

Тут я немного запутался. Как взять интеграл по $x$, если $x$ входит в определение ускорения? Пример ситуации и как с ней справиться (предположим, что ускорение непостоянно).

Мне интересно, можно ли упростить интеграл, учитывая ускорение как функцию времени.

исчисление
интегрирование
производные
математическая физика

$\endgroup$

$\begingroup$

Причина того, что у вас есть хитрость, заключается в том, что обычно это приводит к дифференциальному уравнению в $x$. так что вы не можете вообще взять этот интеграл. Вы могли бы быть в состоянии найти некоторые тождества, но это все.

Вот пример: Если вы хотите, чтобы ускорение не было постоянным, классическим примером является пружина, где вы предполагаете, что она следует закону Гука. 2}x=-x/m$, это дифференциальное уравнение второго порядка. В этом случае довольно легко найти решение (попробуйте найти его или найти, если вы еще не знаете), как только вы его найдете, нетрудно взять интеграл. Но дело здесь в том, что вы ничего не можете сделать с тем интегралом, который вы написали в общем, потому что ускорение может быть почти любой функцией от t. 9b m\cdot a(x) dx$$

Так как $a(x)=\frac{dv(x)}{dt}=\frac{dv(x)}{dt}\frac{dx}{dt} =\frac{dv(x)}{dx}v(x)$, тогда $a(x)dx=v(x)dv(x)$

Вы можете работать с этим интегралом, но вам все равно потребуется знать актуальную информацию о занимаемой должности.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Nerdfighteria Wiki — Производные: Crash Course Physics #2

Информация
Описание
Стенограмма

Статистика

View count:	878,243
Likes:	12,720
Dislikes:	600
Comments:	2,194
Duration:	10:02
Загружено:	07.04.2016
Последняя синхронизация:	03.05.2018 11:10

ИСЧИСЛЕНИЕ! Сегодня мы делаем первые шаги на языке физики; математика. Каждая отрасль науки по-своему описывает то, что исследует. А с физикой это математика. В этом эпизоде Шини рассказывает нам о производных и о том, как исчисление помогает нам понять окружающий мир.

—

Создано в сотрудничестве с PBS Digital Studios: http://youtube.com/pbsdigitalstudios

https://pv.webbyawards.com/2016/online-film-video/video-channels-and-networks/science-education

—

Хотите найти ускоренный курс в другом месте в Интернете?
Facebook – https://www.facebook.com/YouTubeCrashCourse/
Твиттер – http://www.twitter.com/TheCrashCourse
Tumblr — http://thecrashcourse.tumblr.com

CC Дети: http://www.youtube.com/crashcoursekids

Поддержите CrashCourse на Patreon: http://www.patreon.com/crashcourse

Развернуть все | Свернуть все

Каждая научная дисциплина имеет свой особый язык, способ, которым она передает идеи, которые исследует. Например, биология находит порядок в мире, давая всему живому имя на латыни. В химии есть система префиксов, суффиксов и числительных, которые одним или двумя словами сообщают вам точный состав атома или соединения.

Физика должна по-другому выражать свои идеи. Язык физики — математика. Потому что, если вы пытаетесь описать, как устроены миры, вам действительно нужно знать, как вещи соотносятся друг с другом математически. Например, мы много говорили о положении, скорости и ускорении и о том, как они все связаны. Скорость — это мера вашего изменения положения, а ускорение — мера вашего изменения скорости. Они связаны, одно качество будет описывать, как меняется другое. И то, как мы описываем изменения в математике, — это исчисление.

Исчисление объясняет, как и почему что-то меняется, используя производные, которые помогают определить, как меняется уравнение, а также интегралы, которые можно использовать для вычисления площади под кривой. Сами производные и интегралы тесно связаны. Но начнем с производных.

Скорее всего, вы не сможете сразу перейти от этого урока к выпускному экзамену по математическому анализу. Но, надеюсь, примерно через 10 минут вы сможете понять некоторые математические расчеты, которые ученые использовали, чтобы думать о физике, по крайней мере, 400 лет или около того. И у вас также будет новый способ борьбы с штрафами за превышение скорости. Вы знаете, на всякий случай.

(Ускоренный курс физики, введение)

В прошлый раз мы говорили о том досадном происшествии, когда вы получили штраф за превышение скорости. Ваш спидометр был сломан, но поскольку мы знали ваше ускорение, мы смогли рассчитать, с какой скоростью вы ехали, когда вас остановили копы. Итак, теперь поговорим о том, что будет дальше. Скажи, что полиция уезжает. Вы готовы вернуться в путь, поэтому нажимаете на газ и мчитесь вперед, двигаясь все быстрее и быстрее. Но в этом сценарии мы не знаем вашего ускорения; мы знаем только, насколько ваша позиция меняется с течением времени.

В этом случае ваша позиция равна квадрату времени, которое вы вели за рулем. Поэтому мы запишем это как уравнение x=t ² . Через 20 секунд вы проезжаете мимо детектора со знаком, указывающим вашу скорость. Вы продолжаете движение, не отпуская педаль газа, прежде чем понимаете, какой номер вы увидели на знаке. И, о нет! В прошлом эпизоде ты получил штраф за превышение скорости за то, что разогнался до 126 км/ч в зоне 100 км/ч, а теперь детектор говорит, что ты едешь еще быстрее!

Теперь вы хотите знать, является ли число на детекторе точным, другими словами, вы хотите найти свою скорость в тот момент, когда вы ее прошли. Эта скорость — просто мера вашего изменения положения, она производная. Итак, чтобы найти вашу скорость, нам нужно найти производную от вашего положения. И чтобы определить это, нам сначала нужно поговорить о пределах.

Не ограничения скорости, я имею в виду производные. Я объясню…

Ограничения основаны на идее, что если у вас есть уравнение на графике, вы часто можете предсказать, как оно будет выглядеть в одной точке, просто зная, как оно выглядит в соседних точках. Предположим, у вас есть график x=t ² из приведенного выше сценария превышения скорости. И вы хотите узнать, как меняется ваша позиция именно в тот момент, когда время равно нулю. Это то, что мы назвали бы пределом, когда t приближается к нулю.

Итак, посмотрите, что происходит вокруг t=0. При t=1 x равно 1. При t=0,5 x равно 0,25. А при t=0,1 x равно 0,01. Вероятно, вы можете сказать, что по мере того, как мы приближаемся к t=0, ваше значение x тоже становится ближе к нулю. Вот что имеют в виду математики, когда говорят о пределе. Ограничения полезны, потому что они могут помочь предсказать, что произойдет, если вы уменьшите интервалы. Интервал — это просто диапазон на графике. Это пространство между двумя точками на горизонтальной оси.

Итак, первое, что мы можем попробовать, это вычислить вашу среднюю скорость за интервал от 15 до 20 секунд. Для этого мы используем уравнение, о котором говорили в прошлый раз, вашу среднюю скорость, которая равна изменению вашего положения, деленному на изменение во времени. Получается 35 м/с. Проблема в том, что это все еще просто среднее значение, это не точно то, как быстро вы двигались после 20 секунд ускорения, когда вы прошли детектор.

Из-за ограничений мы знаем, что вы можете немного приблизиться к правильному числу, вычисляя среднее значение для все меньших и меньших интервалов. Тогда вы бы увидели, что число все ближе и ближе приближается к 40 м/с. Это означает, что вам нужно снизить скорость, если вы не хотите получить свой второй штраф за превышение скорости в день.

Но в этом и заключается идея производных, вы можете использовать бесконечно малые интервалы, чтобы выяснить, как именно меняется уравнение в любой момент. Вы даже можете придумать уравнение, чтобы описать изменение. Это именно то, что такое скорость, уравнение, описывающее изменение положения. А ускорение описывает изменение скорости. Поэтому мы назвали бы скорость производной от положения, а ускорение — производной от скорости.

Теперь, когда дело доходит до того, как вы записываете производную, математики придумали ярлыки. Как то, что известно как правило силы. Как следует из названия, он используется для уравнений с переменными, возведенными в степень или показатель степени, если показатель степени является числом. Например, x=t ² будет работать с правилом степени, потому что t возводится в степень 2. Правило степени говорит, что для таких уравнений для вычисления производной достаточно одного странного трюка. Возьмите число этой степени, в данном случае 2, и вставьте его перед переменной. Затем вы вычитаете 1 из показателя степени. И это ваша производная.

Таким образом, производная x=t ² равна всего 2t. Это означает, что независимо от того, сколько секунд вы нажимаете на педаль газа, ваша скорость будет равна 2t, так что удвойте количество секунд. Через 5 секунд вы двигались со скромной скоростью 10 м/с. Но через 20 секунд вы двигались со скоростью 40 м/с. Что не хорошо. Мы бы написали это так: Где dx/dt (dx над dt) — это просто способ сказать, что мы берем производную той части уравнения, которая включает t. Или, как сказал бы математик, мы берем производную от x по t. Вы также иногда увидите, что это написано по-другому. Если f из t [f(t)] равно t в квадрате (t ² ), то f простое число t [f'(t)] равно 2t.

Теперь давайте попробуем найти еще пару производных, используя степенное правило: x=7t ² — еще одно уравнение в степенном стиле. В нем есть переменная t, возведенная в степень 6, с числом перед ней 7. Первое, что мы делаем, это берем показатель степени и вставляем его перед переменной. Но перед t уже стоит число; 7. Таким образом, мы умножаем их, 7 умножить на 6 — это 42. Затем мы вычитаем 1 из степени, в которую возводится t. Таким образом, мы получаем 42t ⁵ .

То же самое относится к уравнениям, в которых показатели степени представляют собой дроби или десятичные числа. Таким образом, производная от t ^½ — это половина t с минусом на половине. Это работает и для отрицательных показателей, производная от t ^-2 составляет всего -2t до отрицательной трети.

Теперь есть еще несколько уравнений, производные которых вам следует понять. Тригонометрия, которую мы используем для вычисления углов и сторон треугольников, будет широко использоваться в физике, потому что мы все время будем использовать прямоугольные треугольники. Поэтому полезно знать, как найти производные от sin(x) и cos(x). Синус говорит вам, что если у вас есть прямоугольный треугольник, и x – угол в этом треугольнике, то sin(x) будет длиной стороны, противоположной этому углу, деленной на гипотенузу. Косинус делает то же самое, только сторона рядом с этим углом делится на гипотенузу. Таким образом, их графики говорят вам, какими будут эти отношения в зависимости от угла.

На самом деле мы можем попытаться угадать производную sin(x), просто взглянув на ее график. Вы можете видеть, что кривая время от времени имеет точки поворота, при x=-90°, x=90° и т. д., повторяющиеся каждые 180°. Это означает, что в этих точках уравнения вообще не меняются, поэтому производная в этих поворотных точках также будет точно равна нулю. Давайте нарисуем еще один график, на котором мы построим производную, и поставим маленькие точки там, где мы будем знать, что она будет равна нулю.

Итак, что происходит между этими поворотными моментами? Ну, от -270° до -90°, sin(x) убывает. Другими словами, его изменение и, следовательно, его производная должны быть отрицательными. Затем, от -90° до 90°, sin(x) увеличивается, так что у него будет положительная производная. И так далее… На самом деле на этом графике гораздо больше подсказок, которые помогут нам найти производную, но мы уже знаем достаточно, чтобы сделать приличное предположение.

Если мы плавно соединим точки на графике нашей производной, помня, где кривая должна быть положительной, а где отрицательной, эй, эта производная очень похожа на график cos(x). Это потому, что это так. Производная синуса — это просто косинус, и это будет часто встречаться. То же самое можно сказать и о них, которые вы можете проработать самостоятельно, повторив то, что мы только что сделали с графиками sin(x) и cos(x).

Другая важная производная, которая часто встречается, — это очень частный случай, и это e ^x . производная e ^x равна e ^x . Да, это оно. Не важно что. На самом деле, это один из способов определить число е, которое похоже на число пи в том смысле, что это простая буква, представляющая очень конкретное иррациональное число, около 2,718, но с большим количеством цифр после запятой, которые продолжаются бесконечно. Его можно использовать в математических вычислениях, но он также проявляется, когда вы изучаете такие вещи, как финансы и вероятность.

Вооружившись всеми этими способами нахождения производных, вы можете взять практически любое уравнение своего положения и вычислить его производную и, следовательно, свою скорость. Точно так же вы можете взять производную от своей скорости и найти свое ускорение. Но есть целая другая часть исчисления, о которой мы еще не говорили, интегралы, которые позволят вам сделать это в обратном порядке. С помощью интегралов вы можете использовать свое ускорение, чтобы найти свою скорость, и свою скорость, чтобы найти свое положение. Но мы оставим это на следующий раз.

Сегодня вы узнали о пределах и о том, что производные используют их для описания того, как изменяется уравнение. Мы также говорили о нескольких различных видах деривативов; степени, константы, тригонометрия и e ^x .

Ускоренный курс физики создан совместно с PBS Digital Studios. Вы можете перейти на их канал, чтобы посмотреть потрясающие шоу, такие как Deep Look, The Good Stuff и PBC Space Time. Этот эпизод «Ускоренного курса» был снят в студии «Ускоренный курс доктора Шерил С. Кинни» с помощью этих замечательных людей, а нашей графической командой — «Кафе мысли».

Вопросы? Проблемы? Эл. адрес [email protected].
Чтобы связаться с Джоном или Хэнком, посетите hankandjohn.com.

Условия использования | Политика конфиденциальности

производных и интеграция в физике

Физика в старших классах преподает кинематические уравнения в виде набора простых формул:
v = v ₀ + а ₀ Δt
x = x ₀ + ½ (V ₀ + V) ΔT = x ₀ + V ₀ ΔT + ½ A ₀ ΔT ²
V ² = (V _{01039 0 2

V ² = (V _{0_{V ² = (V _{0
9 . ) ² + 2а ₀ Δх В большинстве школьных учебников вместо “а ₀” будет указано “а”, но смысл тот же.
К сожалению, редко упоминается, что эти упрощенные
формулы применимы только в особых случаях. Реальные формулы еще проще и их легче запомнить, чем
те, которым учат в средней школе, но они требуют немного высшей математики. Вам не нужно
быть гением исчисления, чтобы получить представление о реальных формулах.
Объект, находящийся в фиксированном положении, имеет нулевую скорость. Если вы двигаете его, то он будет иметь определенную скорость
зависит от того, как быстро он движется. Другими словами, изменение положения с течением времени равно скорости . Если вы планируете
положение x во времени, затем наклон кривой этого положения во времени представляет собой скорость .
x(t) – уравнение кривой зависимости положения от времени. Наклон кривой математически является производной функции, описывающей эту кривую. Это написано так:
∂х(т)
v(t) = -------
∂t

В краткой записи над x(t) ставится точка, обозначающая производную. Поэтому у меня нет точки в HTML
Я использую тире: ∂х(т)
v(t) = x'(t) = -------
∂t
Это просто «забавная запись», чтобы сказать: нарисуйте положение (x) как функцию времени, x (t) и измерьте наклон. Результат
скорость как функция времени. Другими словами изменение положения связано со скоростью . Для изменения скорости требуется ускорение (или торможение = отрицательное ускорение). Таким образом, наклон кривой скорости во времени равен ускорению во времени:
∂v(t) ∂ ² х(t)
a(t) = v'(t) = ------- = x"(t) = --------
∂t ∂t ² Обратная производная является интегралом. В графическом плане это площадь под кривой.
Например, автомобиль движется с постоянной скоростью 2 м/с (два метра в секунду):
v(t) = 2 м/с (синяя линия на графике ниже).
Область под этой синей линией представляет собой прямоугольник и увеличивается по мере продвижения вправо от графика. Эта область соответствует положению нашего автомобиля. При t=2с площадь равна 2с*2м/с=4м, при t=3с площадь 2м/с*3с=6м.
х(т) = 2 т
Если мы нарисуем 2*t на графике, то получим красную линию. Это положение автомобиля во времени.
Эта площадь под кривой скорости называется в математических терминах интегралом и записывается как:
х(т) = ∫v(t)∂t

Накопленная площадь за время под скоростью является положением. Это обратная сторона фразы «изменение положения — это скорость».
Изменение скорости было ускорением, а обратной функцией было бы «площадь под кривой ускорения — это скорость:v(t) = ∫a(t)∂t

Киниматические уравнения как производные и интегралы
∂х(т)
v(t) = x'(t) = -------
∂t
∂v(t) ∂ ² х(т)
a(t) = v'(t) = ------- = x"(t) = --------
∂t ∂t ²
и обратные функции:
x(t) = ∫v(t)∂t + x ₀ = ∫∫a(t)∂t ² + x ₀
v(t) = ∫a(t)∂t + v ₀

Производные и интегралы некоторых основных функций
Чтобы использовать это, мы должны знать, как вычислить производную или интеграл данной функции. За
физике на уровне средней школы вам нужно будет знать только следующее. ∂f (т)
функция: f(t) = t ² , производная: f'(t) = ------- = 2 t
∂t
∂f (т)
функция: f(t) = 2 t, производная: f'(t) = ------- = 2
∂t
функция: f(t) = константа, производная: f'(t) = 0

В общем случае производная от f(t) = t ^z равна f'(t) = z*t ^z-1 . То есть: вы ставите показатель степени впереди и уменьшаете его на 1. Интеграл — это обратная операция производной.
функция: f(t) = t, интеграл: ∫f(t)∂t = ½ t ²
функция: f(t) = константа, интеграл: ∫f(t)∂t = константа * t

В общем случае интеграл от f(t) = t ^z равен ∫f(t) = 1/(z+1) * t ^z+1 . То есть: вы увеличиваете показатель степени на единицу и делите на значение новой степени. Следующая диаграмма содержит 3 графика:
f ₁ (t) = 2 (синяя линия)
f ₂ (т) = 2 т (красная линия)
ж ₃ (т) = т ² (зеленая линия)
Графики были выбраны так, что:
∫f ₁ (t) = f ₂ (t) и ∫f ₂ (t) = f ₃ (t)
Интеграл от f ₂ (t) равен f ₃ (t), но значение f ₃ в данной точке t равно площади
под линией f ₂ (t), начиная с t=0. Если вы хотите узнать размер оранжевой области под красной линией, от t=1 до t=2, вам нужно вычесть: f ₃ (2) – f ₃ (1) = 2 ² – 1 ² = 3.
Интеграл функции f ₂ (∫f ₂ ∂t) от t=1 до t=2 равен 3.
Как перейти от общих кинематических уравнений к школьным формулам?
Формулы средней школы, упомянутые в верхней части страницы, работают только при двух предположениях: ускорение постоянное
скорость возрастает линейно от v ₀ до v за период времени Δt

Первое школьное уравнение было
v = v ₀ + aΔt
Мы получим это, если воспользуемся
v(t) = ∫a(t)∂t + v ₀
и установим a(t) = a ₀ (константа)
Интеграл константы по времени равен произведению константы на время: ∫a ₀ ∂t = a ₀ * t и мы имеем школьное уравнение. Второе уравнение средней школы было
x = x ₀ + ½ (v ₀ + v)Δt
Это можно получить из следующего уравнения:
х(т) = ∫v(t)∂t + х ₀
Предположение, при котором справедливо уравнение средней школы, следующее: скорость линейно увеличивается от v ₀ до v за период времени Δt. Мы можем сделать это предположение. Я использую «v ₁» вместо «v», чтобы было понятно
что это фиксированная точка, а не переменная.

Член ∫v(t)∂t будет областью, отмеченной оранжевым цветом. Эта область:
v ₀ Δt + ½ (v ₁ – v ₀ )Δt = ½ (v ₀ + v)Δt
Замена ∫v(t)∂t на ½ (v ₀ + v)Δt дает второе уравнение средней школы.
Это также возможно сделать чисто математически, а не графически, но это более длинный расчет, который вы можете выполнить >здесь<, если хотите.
Второе уравнение средней школы
Извините, у меня нет времени. Сделать позже.
Вернуться к: “Без консервантов”

© 2004-2022 Гвидо Сохер
Интегральный трюк Ричарда Фейнмана. Непонятная, но мощная интеграция… | от Панды Красной
Ричард Фейнман читает лекцию в 1963 году (Фото: Архив Калифорнийского технологического института) «Я научился вычислять интегралы с помощью различных методов, описанных в книге, которую дал мне мой школьный учитель физики мистер Бейдер. [Он] показал, как дифференцировать параметры под знаком интеграла — это определенная операция. Оказывается, в университетах этому не очень учат; они не подчеркивают это. Но я понял, как использовать этот метод, и я использовал этот проклятый инструмент снова и снова. [Если] у ребят из Массачусетского технологического института или Принстона возникали проблемы с вычислением определенного интеграла, [тогда] я приходил и пытался дифференцировать под знаком интеграла, и часто это срабатывало. Так что я получил прекрасную репутацию специалиста по интегральным вычислениям только потому, что мой набор инструментов отличался от всех остальных, и они опробовали на нем все свои инструменты, прежде чем ставить задачу передо мной». (Вы, конечно, шутите, мистер Фейнман!)
Сегодняшняя статья посвящена малоизвестному, но мощному методу интегрирования, более известному как дифференцирование под знаком интеграла, но иногда называемому «методом Фейнмана» из-за того, что он популяризировал этот метод в своей книге, и по праву известному как метод интегрирования. Интегральное правило Лейбница.
Одно уточнение, прежде чем мы начнем: хотя правило Лейбница иногда называют «методом Фейнмана» или подобными названиями, его не следует путать с формулировкой квантовой механики на основе интеграла по путям. Поэтому в оставшейся части этой статьи я буду обращаться к нему по его собственному имени.
Начнем с задачи вычисления следующего интеграла:
Книга, которую Фейнман упоминает в приведенной выше цитате, называется Advanced Calculus , опубликованной в 1926 году математиком Массачусетского технологического института по имени Фредерик С. Вудс. Этот интеграл взят из этой книги и равен воспроизведено на Wolfram Mathworld.
Вы можете попробовать обычные методы, которые вы изучаете в исчислении. Подстановка триггера, замена переменной, интегрирование по частям, замена подынтегральной функции рядом — ничего из этого не сработает. Вы также можете попробовать вычислить его с помощью Wolfram Alpha, и время ожидания истечет. Нам нужно будет быть более творческими.
Сначала следует заметить, что альфа является произвольной константой по отношению к интегралу. Поскольку определенный интеграл будет числом, зависящим от альфы, мы можем рассматривать этот интеграл как функцию альфы. Схема подхода выглядит следующим образом:
Рассмотрим интеграл как функцию f от альфы
Вычислим интеграл для некоторого конкретного подходящего значения альфы. В этом случае, если альфа равна единице, то интеграл равен нулю, что дает нам условие f(1) = 0, Нам это понадобится для последнего шага.
Продифференцировать интеграл по альфа.
Вычислите определенный интеграл относительно x.
Бесконечное интегрирование по отношению к альфе.
Используйте тот факт, что f(1) = 0 , чтобы вычислить значение константы интегрирования.
Что мы сделали, так это преобразовали задачу от вычисления интеграла к решению простого дифференциального уравнения. Обратите внимание:
Может показаться, что мы сделали себе только хуже. Интеграл в конце нижней строки выглядит особенно внушительно, но его можно вычислить, применив некоторую алгебраическую смекалку.
Последний интеграл проще, чем кажется. Мы должны избавиться от функции косинуса. Для этого мы можем сделать «обратную» u-подстановку.
Мы почти закончили. Сделаем замену:
Обратите внимание, что поскольку |alpha| больше или равно 1 и u положительное или нулевое значение, y находится в диапазоне от нуля до отрицательной бесконечности. Следовательно:
Таким образом, мы, наконец, имеем наше дифференциальное уравнение в альфа:
Интегрируя и используя тот факт, что f(1) = 0 , мы можем завершить вычисление интеграла:
И это завершает вычисление .
В этом первом примере параметр, по которому мы производили дифференцирование, уже присутствовал в подынтегральном выражении. Однако истинная сила дифференцирования под знаком интеграла заключается в том, что мы также можем свободно вставлять параметры в подынтегральную функцию, чтобы сделать ее более удобной. Рассмотрим следующий интеграл, взятый из математического конкурса Уильяма Лоуэлла Патнэма 2005 года.
Для тех, кто не знает, конкурс Патнэма — это соревнование по решению задач, предлагаемое студентам-математикам каждый год в декабре. Он имеет репутацию очень сложного, со средними баллами обычно от 0 до 1 из 120. Тест проводится в двух наборах по шесть задач, причем A5 и A6 обычно являются самыми сложными в первом наборе. Таким образом, этот интеграл должен быть очень сложным, несмотря на его обманчиво ручную внешность (что, кстати, является уловкой: тест ограничен по времени, так что это ловушка, чтобы заставить вас тратить время, пытаясь вычислить интеграл с помощью элементарных методов исчисления). , что не сработает). Однако, осторожно введя параметр и используя разработанную нами технику, этот интеграл можно сделать очень простым.
Для начала:
Обратите внимание, что это означает, что наш исходный интеграл равен I(1) и что I(0) = 0. Теперь продолжим как раньше:
Вторая строка была получена дробью разложение. Это элементарные интегралы, которые можно вычислить сразу, чтобы получить третью строку. Так как I(0) = 0, по Фундаментальной теореме исчисления:
Заметим, что мы могли бы действовать так же, как в первом примере, решая дифференциальное уравнение для I через a , а затем с помощью условия I(0) = 0 определить конкретное решение I(a) до подстановки a = 1 . Использование FTC делает то же самое здесь, но сокращает несколько шагов.
Это элементарный интеграл, который можно сразу вычислить стандартными методами. Результат:
Итак, решение задачи:
Какое значение интеграла указано в решениях к экзамену 2005 года. Обратите внимание, что в листе решений обсуждаются другие методы приближения к этому интегралу, но этот способ, безусловно, самый простой и элегантный, не говоря уже о самом быстром.
Одним из важнейших навыков решения математических задач является способность к обобщению. Заданная задача, такая как только что вычисленный нами интеграл, может показаться неразрешимой сама по себе. Однако, отступив назад и рассматривая проблему не изолированно, а как отдельный член целого класса смежных проблем, мы можем разглядеть факты, ранее от нас скрытые. Попытка вычислить интеграл для конкретного значения a = 1 была слишком сложной, поэтому вместо этого мы вычислили значение интеграла для каждые возможно значение a. Как это ни парадоксально, во многих ситуациях проще решить общую проблему, чем конкретную.
Я также думаю, что это подчеркивает важность готовности учиться вне класса. Часто на курсах математики и естественных наук нехватка времени и другие факторы означают, что иногда у преподавателей нет другого выбора, кроме как не включать определенные предметы в учебную программу.}}}}

Антипроизводная	Эквивалентная антипроизводная
\(\ int (f(x)+g(x)) dx\)	\(\int f(x)dx+\int g(x)dx\) (сумма)
\(\целое (f(x)-g(x)) dx\)	\(\int f(x)dx-\int g(x)dx\) (вычитание)
\(\int af(x) dx\)	\(a\int f(x)dx\) (умножение на константу)
\(\целое f'(x)g(x) dx\)	\(f(x)g(x)-\int f(x)g'(x) dx\) (интегрирование по частям)

Интегралы в физике как понять

Почему вы не знаете, как решать интегралы

Интеграл – что это?

Объясняем понятие «Интеграл»

Неопределённый интеграл

Определённый интеграл

Таблица интегралов для студентов (основные формулы)

Как вычислять интеграл правильно

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

Базовые понятия для понимания темы

Заключение

Изучаем понятие « интеграл »

Неопределенный интеграл

Полная таблица интегралов для студентов

Определенный интеграл

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Свойства определенного интеграла

Примеры решения интегралов

Исследовательская работа по теме: «Применение производных и интегралов в физике, математике и электротехнике.»

Применение интеграла в физике и геометрии

1. Применение интеграла в физике и геометрии

2. Краткое содержание

3. Что такое интеграл

5. История возникновения интегралов

6. . Применение интеграла

7. . Применение интеграла в геометрии.

9. Вычисление объемов тел с помощью интегралов

10. Применение интегралов в физике

11. Применение в физике

12. Решение задач с помощью интеграла

13. Решение задач с помощью интеграла

14. вывод о применении интеграла по таблице

Высшая математика для начинающих физиков и техников.

Содержание

Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?

Математический анализ. Часть II | Открытые видеолекции учебных курсов МГУ

26.3: Антипроизводные и интегралы – Physics LibreTexts

Общая первообразная и свойства

Обычное использование интегралов в физике — от суммы к интегралу

Производные для AP-физики

исчисление – Задача по физике на производные и интегралы

Твой ответ

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Nerdfighteria Wiki — Производные: Crash Course Physics #2

Категории

Статистика

производных и интеграция в физике

Киниматические уравнения как производные и интегралы

Производные и интегралы некоторых основных функций

Как перейти от общих кинематических уравнений к школьным формулам?

Интегральный трюк Ричарда Фейнмана. Непонятная, но мощная интеграция… | от Панды Красной

Оставить комментарий Отменить ответ