Производные и интегралы в физике: 4.3.2 Примеры применения интеграла в физике и геометрии - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

4.3.2 Примеры применения интеграла в физике и геометрии

Видеоурок: Применение интегралов в физике и математике

Лекция: Примеры применения интеграла в физике и геометрии

Процесс нахождение первообразной называется интегрированием.

Как и производная, интегралы используются и в физике, и в геометрии, а также в других областях знаний.

Сегодня же мы рассмотрим, каким образом используется интегрирование в физике и геометрии.

Итак, начнем сначала. Мы помним, что скорость – это первая производная перемещения. Но так как мы знаем, что интегрирование и нахождение производной – это два взаимообратных процесса, то мы можем предполагать, что, если для нахождения скорости, нужно было найти производную от перемещения, то для нахождения перемещения по скорости, необходимо произвести интегрирование заданной функции.

Отсюда можно сделать вывод, что перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:

Пример: Итак, предположим, что некоторое тело двигается со скоростью, заданной функцией:

V(t) = t² +1.

По условию задачи мы должны определить путь, который пройдет тело за промежуток времени [0;1].

Итак, найдем определенный интеграл данной функции:

Это означает, что за данный промежуток времени, тело прошло 1,3(3) м.

Точно так же можно найти скорость по заданной функции ускорения.

Еще одной физической величиной, которая находится с помощью интегрирования, является работа.

Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:

Пример: Предположим, что к некоторому телу для его передвижения прикладывают силу, которая изменяется по закону F(x) = x +3. Необходимо найти работу, которую при этом совершает сила для перемещения тела с 1 м до 2 м.

Для нахождения работы следует найти определенный интеграл заданной функции по известным пределам интегрирования:

Это значит, что для передвижения тела потребовалось совершить работу, равную 4,5 Дж энергии.

Кроме рассматриваемых задач, интегрирование в физике используется для нахождения работы по мощности, массы по плотности, заряда по силе тока, количества теплоты по известной теплоемкости, а также многое другое.

Что же касается геометрии, то геометрическим смыслом интегрирования считается нахождение площади фигуры под графиком.

Итак, чтобы найти площадь фигуры, которая ограничена с двух сторон пределами интегрирования и с одной стороны графиком функции, то необходимо найти интеграл данной функции:

Пример: Вычислим площадь фигуры, ограниченной графиком функции у = 4х – х² на пределах рассмотрения х = 0, х = 4.

Итак, найдем интеграл данной функции в заданных пределах и построим полученный график:

Применение интеграла в физике и геометрии

1. Применение интеграла в физике и геометрии

ПРИМЕНЕНИЕ
ИНТЕГРАЛА В
ФИЗИКЕ И
ГЕОМЕТРИИ
Презентацию сделал:
Кузнецов Захар

2.

Краткое содержание Что такое интеграл
История возникновения
интеграла
Применение интегралов в
физике и геометрии

3. Что такое интеграл

В высшей математике
используется такое понятие,
как интеграл или полное
название – интеграл функции.
Итак, что такое интеграл? Это
то же самое, что сумма
сложения бесконечно малых
слагаемых (точек, отрезков),
которых имеется бесконечно
огромное количество.
Обозначается интеграл
знаком «ʃ».
Упрощённо интеграл можно
представить как аналог суммы
для бесконечного числа
бесконечно малых слагаемых.
Неформально интеграл функции
можно описать как площадь
фигуры, образующейся между
осью х (ось абсцисс) и кривой
графика функции (такая фигура
называется криволинейной
трапецией). Процесс определения
данной площади называется
интегрированием. Иногда
функция может быть задана
несколькими переменными
(неизвестными), тогда интеграл
является объемом под
поверхностью, которую образует
график данной функции.

Неформально интеграл функции можно
описать как площадь фигуры, образующейся
между осью х (ось абсцисс) и кривой графика
функции (такая фигура называется
криволинейной трапецией).
Процесс определения данной площади
называется интегрированием. Иногда функция
может быть задана несколькими переменными
(неизвестными), тогда интеграл является
объемом под поверхностью, которую образует
график данной функции.

5. История возникновения интегралов

Понятие интеграла
и интегральное
исчисление возникли
из потребности
вычислять площади
(квадратуру) любых
фигур и объёмы
(кубатуру)
произвольных тел.
Предыстория
интегрального
исчисления
восходит к
древности.
Термин «интеграл» (от лат. integer — целый, то
есть целая, вся — площадь) был предложен в 1696

г. Иоганном Бернулли.
Современное обозначение
неопределенного интеграла было
введено Лейбницем в 1675 году.

Он
адаптировал интегральный символ
, образованный из буквы S —
сокращения слова
лат. summa (сумма). Современное
обозначение определенного
интеграла, с ограничениями над и
под знаком интеграла, были
впервые использованы Жаном
Батистом Жозефом Фурье в 181920.

6. . Применение интеграла

с помощью интеграла можно вычислить такие
физические величины, как работа, она равна
интегралу от силы, затраченной при
перемещении тела; масса однородного
стержня равна интегралу от линейной
плотности этого стержня; величина
заряда равна интегралу от силы
тока; количество теплоты равно интегралу
от теплоёмкости

7. . Применение интеграла в геометрии.

В геометрии понятие интеграла
используется при вычислении объёмов
тел. Формула V=

9. Вычисление объемов тел с помощью интегралов

10. Применение интегралов в физике

В физике интеграл применяется для вычисления работы переменной силы,
вычисления массы неоднородного стержня и для вычисления расстояния по
известному закону изменения скорости.

Задача
Тело двигается прямолинейно со скоростью, которая изменяется по закону ..
Найти расстояние, пройденное телом за интервал времени от t1=1с до t2=3с
Решение

11. Применение в физике

. На вычисление пути пройденного точкой.
Путь, пройденный точкой при неравномерном
движении по прямой с переменной
скоростью
за промежуток
времени от
до
вычисляется по
формуле.

12. Решение задач с помощью интеграла

Пример 1:
Скорость движения точки
м/с.
Найти путь, пройденный точкой за 4-ю
секунду.
Решение: согласно условию:
Следовательно,

13. Решение задач с помощью интеграла

Пример 2:
Два тела начали двигаться одновременно из одной точки в
одном направлении по прямой. Первое тело движется со
скоростью
м/с, второе — со скоростью v
= (4t+5) м/с. На каком расстоянии друг от друга они окажутся
через 5 с?
Решение: очевидно, что искомая величина есть
разность расстояний, пройденных первым и
вторым телом за 5 с:

14.

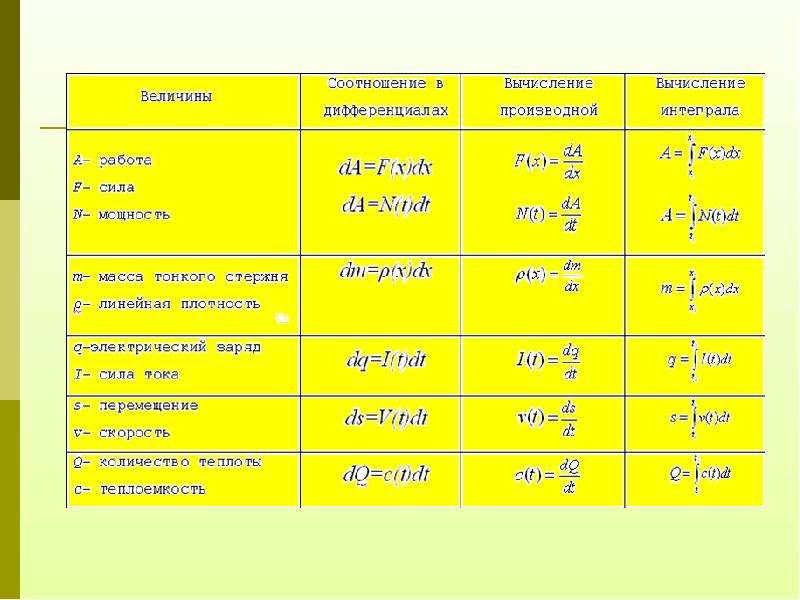вывод о применении интеграла по таблице Математика
Физика
Вычисления S фигур.
Работа А переменной
Длина дуги кривой.
V тела на S
параллельных
сечений.
V тела вращения и т.д.
силы.
S – (путь) перемещения.
Вычисление массы.
Вычисление момента
инерции линии, круга,
цилиндра.
Вычисление координаты
центра тяжести.
Количество теплоты и т.д.

Математический анализ. Часть II | Открытые видеолекции учебных курсов МГУ

Курс «Математический анализ. Часть II» читается студентам первого курса физического факультета МГУ имени М. В. Ломоносова во 2 семестре.

Во второй части курса лекций по математическому анализу рассматриваются следующие вопросы:

Функции многих переменных.
Производные высших порядков.
Формула Тейлора.
Локальный экстремум.
Теория неявных функций.
Условный экстремум.
Кратные и двойные интегралы. Тройные интегралы.
Криволинейные интегралы.
Формула Грина.
Поверхностные интегралы.

Понятия математического анализа используются затем во всех последующих математических дисциплинах, а также в курсах общей и теоретической физики. Поэтому активное изучение учащимися курса анализа позволяет заложить фундамент для успешного восприятия более сложных понятий и в математике, и в различных разделах современной теоретической физики.

Излагаемый в данном курсе материал полностью соответствует действующей программе по математическому анализу для физических специальностей. При рассмотрении многих вопросов особое внимание уделяется приложениям математических понятий и утверждений в физике.

Список всех тем лекций

Лекция 1. Функции многих переменных..
Основные понятия в m-мерном пространстве Последовательности точек Функции многих переменных, пределы функций

Лекция 2. Предел функции многих переменных..
Пределы функций многих переменных Непрерывность функций многих переменных Основные теоремы о непрерывных функциях

Лекция 3. Непрерывность функций многих переменных..
Непрерывность функций многих переменных Частные производные и дифференцируемость функций

Лекция 4. Дифференциал функции многих переменных..
Частные производные и дифференцируемость функций Дифференцируемость сложной функции Дифференциал функции многих переменных

Лекция 5. Геометрический смысл производной..
Геометрический смысл производной, касательная плоскость Производная по направлению, градиент функции Производные и дифференциалы высших порядков

Лекция 6. Производные высших порядков..
Частные производные высших порядков Дифференциалы высших порядков

Лекция 7. Формула Тейлора..
Дифференциалы высших порядков Формула Тейлора

Лекция 8. Локальный экстремум..
Локальный экстремум Квадратичные формы Достаточные условия экстремума

Лекция 9. Теория неявных функций..
Неявные функции Дифференцируемость неявных функций

Лекция 10. Неявные функции, определяемые системой уравнений..
Продолжение теории неявных функций Неявные функции, определяемые системой уравнений Зависимость функций

Лекция 11. Условный экстремум..
Зависимость функций Условный экстремум

Лекция 12. Кратные и двойные интегралы..
Условный экстремум Кратные интегралы, квадрируемые площади Двойные интегралы

Лекция 13. Двойные интегралы..
Двойные интегралы Вычисление двойных интегралов с помощью повторного интегрирования Замена переменных в двойном интеграле

Лекция 14. Тройные интегралы..
Замена переменных в двойном интеграле Тройные интегралы Вычисление тройных интегралов с помощью повторного интегрирования Замена переменных в тройном интеграле

Лекция 15. Криволинейные интегралы..
Криволинейные координаты Кривые, длина кривой Криволинейные интегралы первого рода Вычисление криволинейных интегралов первого рода при помощи определенных

Лекция 16. Криволинейные интегралы I и II рода..
Вычисление криволинейных интегралов первого рода при помощи определенных Криволинейные интегралы второго рода Вычисление криволинейных интегралов второго рода при помощи определенных Связь между криволинейными интегралами первого и второго рода Формула Грина

Лекция 17. Формула Грина..
Формула Грина Условия независимости криволинейного интеграла II рода от пути интегрирования

Лекция 18. Площадь поверхности..
Площадь поверхности

Лекция 19. Поверхностные интегралы I рода..
Поверхностные интегралы первого рода Вычисление поверхностных интегралов первого рода сведением к двойному Понятие стороны поверхности

Лекция 20. Поверхностные интегралы II рода..
Поверхностные интегралы второго рода Вычисление поверхностных интегралов второго рода Формула Остроградского-Гаусса Формула Стокса

Лекция 21. Геометрические приложения..
Независимость криволинейного интеграла II рода от пути интегрирования в пространстве Касание кривых Особые точки кривых Кривизна плоской кривой

РАЗНИЦА МЕЖДУ ПРОИЗВОДНОЙ И ИНТЕГРАЛОМ | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ – НАУКА

Производная против интегралаДифференциация и интеграция – две фундаментальные операции в исчислении. У них есть множество приложений в нескольких областях, таких как математика, инженерия и физика. И

Производная против интеграла

Дифференциация и интеграция – две фундаментальные операции в исчислении. У них есть множество приложений в нескольких областях, таких как математика, инженерия и физика. И производная, и интеграл обсуждают поведение функции или поведение физического объекта, который нас интересует.

Что такое производная?

Предположим, что y = ƒ (x) и x₀ находится в области определения ƒ. Тогда lim_{Δx → ∞}Δy / Δx = lim_Δ_{х → ∞}[ƒ (x₀+ Δx) – ƒ (x₀)] / Δx называется мгновенной скоростью изменения ƒ в точке x₀, при условии, что этот предел существует конечно. Этот предел также называется производной от at и обозначается ƒ (x).

Значение производной функции ж в произвольной точке Икс в области определения функции определяется как lim_Δ_{х → ∞}[ƒ (x + Δx) – ƒ (x)] / Δx. Это обозначается любым из следующих выражений: y, ƒ (x), ƒ, dƒ (x) / dx, dƒ / dx, D_Иксу.

Для функций с несколькими переменными мы определяем частную производную. Частная производная функции с несколькими переменными – это ее производная по одной из этих переменных, при условии, что другие переменные являются константами. Символ частной производной – ∂.

Геометрически производную функции можно интерпретировать как наклон кривой функции ƒ (x).

Что такое интеграл?

Интеграция или антидифференциация – это процесс, обратный дифференциации. Другими словами, это процесс поиска исходной функции, когда задана производная функции. Следовательно, интеграл или антипроизводная функции ƒ (x), если (x) =F(x) можно определить как функцию F(x) для всех x из области определения ƒ (x).

Выражение ∫ƒ (x) dx обозначает производную функции ƒ (x). Если ƒ (x) =F(x), то ∫ƒ (x) dx = F(x) + C, где C – константа, ∫ƒ (x) dx называется неопределенным интегралом от ƒ (x).

Для любой функции ƒ, которая не обязательно неотрицательна и определена на интервале [a, b], _а∫^бƒ (x) dx называется определенным интегралом ƒ на [a, b].

Определенный интеграл _а∫^бƒ (x) dx функции ƒ (x) можно геометрически интерпретировать как площадь области, ограниченной кривой ƒ (x), осью x и линиями x = a и x = b.

В чем разница между производной и интегралом?

• Производная – это результат дифференциации процесса, а интеграл – результат интеграции процесса.

• Производная функции представляет наклон кривой в любой заданной точке, а интеграл представляет собой площадь под кривой.

Что такое интеграл и зачем мне знать это — T&P

IMAGE 1287 NOT FOUND

Иллюстрация: Максим Чатский

Представьте, что у нас есть какая-то функция зависимости чего-то от чего-то.

Например, вот так примерно можно на графике представить скорость моей работы в зависимости от времени суток:

Скорость я измеряю в строках кода в минуту, в реальной жизни я программист.

Объем работы — это скорость работы умножить на время. То есть если я пишу 3 строки в минуту, то в час получается 180. Если у нас есть такой график, можно узнать, сколько работы я сделал за день: это площадь под графиком. Но как это посчитать?

Разделим график на столбики равной ширины величиной в час. А высоту этих столбиков сделаем равной скорости работы в середине этого часа.

Площадь каждого столбика по отдельности легко посчитать, надо умножить его ширину на высоту. Получается, что площадь каждого столбика — это сколько примерно я работы сделал за каждый час. А если просуммировать все столбики, то получится примерная моя работа за день.

Проблема в том, что результат получится примерный, а нам нужно точное число. Разобьем график на столбики по полчаса:

На картинке видно, что это уже гораздо ближе к тому, что мы ищем.

Так уменьшать отрезки на графике можно до бесконечности, и каждый раз мы все ближе и ближе будем подходить к площади под графиком. А когда ширина столбиков будет стремиться к нулю, тогда сумма их площадей будет стремиться к площади под графиком. Это и называется интегралом и обозначается вот так:

В этой формуле f(x) означает функцию, которая зависит от величины x, а буквы a и b — это отрезок на котором мы хотим найти интеграл.

Зачем это нужно?

Ученые стараются все физические явления выразить в виде математической формулы. Как только у нас есть формула, дальше уже можно при помощи нее посчитать что угодно. А интеграл — это один из основных инструментов работы с функциями.

Например, если у нас есть формула круга, мы можем при помощи интеграла посчитать его площадь. Если у нас есть формула шара, то мы можем посчитать его объем. При помощи интегрирования находят энергию, работу, давление, массу, электрический заряд и многие другие величины.

Нет, зачем мне это нужно?

Да низачем — просто так, из любопытства. На самом деле интегралы входят даже в школьную программу, но не так много людей вокруг помнят, что это такое.

Производные для AP Physics

Введение:

AP Physics C — это курс физики, основанный на вычислениях, но факт в том, что вы можете сделать довольно хорошо, с точки зрения оценок, в AP Physics C – особенно часть механики – без знания исчисления. Конечно, вам не помешает узнать, что происходит со всеми этими странные математические символы и понятия, и обязательно будут быть задачами на тесте AP, которые требуют знания исчисления.К счастью, вы можете очень хорошо справиться даже с AP-тестом с очень элементарные навыки исчисления, которым можно научиться за несколько минут.

Вам нужно кое-что знать о:

Производные инструменты – деривативом является скорость изменения, или графически, наклон касательной к график. Хотя физика «забита» приложениями производная, нужно уметь вычислять только очень простые производные в этом курсе.
Определенные интегралы – определенный интеграл представляет собой площадь, и существует множество Применение интегралов в физике. В этом курсе вам необходимо уметь вычислять только самые элементарные интегралы.

Производные:

Производная – это скорость изменения, которая геометрически наклон графика. В физике скорость – это скорость изменения положение, поэтому математически скорость является производной положения.Ускорение — это скорость изменения скорости, поэтому ускорение равно производная скорости. Чистая сила – это скорость изменения импульса, поэтому производная импульса объекта говорит вам о чистой усилие на объект. Это лишь некоторые из приложений производная в физике.

Производные правила:

Нахождение производной функции (“дифференцирование” в язык исчисления) является операцией, основанной на правилах.Другими словами, вы необходимо распознать, какое производное правило применяется, а затем применить его. В Чтобы узнать, какое производное правило применяется, вам нужно знать некоторые производные правила. В таблицах ниже перечислены производные правила. которые вы будете использовать в этом курсе, и показывает некоторые примеры их использовать. Эти правила сформулированы с использованием «t» в качестве переменной (производная является «относительно» t на языке исчисления), так как большинство функции, которые мы будем использовать, являются функциями времени.Если вы принимаете производная, переменная которой равна “s”, просто замените “x” на “t” в производное правило.

Правила для отдельных функций:

Правило на английском языке	Правило в математике. Обозначение	Пример
Производная константы равна нулю.		Если x(t) = 5, то v(t) = 0. Если v(t) = -3, то a(t) = 0.
Производная от t равна единице.		Если x(t) = t, то v(t) = 1.
Производная t в степени равна степени, умноженной на t в степени. сила «одним меньше».		Если x(t) = t ² , то v(t) = 2t ¹ = 2т. (п = 2) Если v(t) = t ⁴ , то a(t) = 4t ³ .(п = 4) Если x(t) = t ^-3 , то v(t) = -3т ^-4 . (п = -3)
Производная синуса t есть косинус т.		Если x(t) = sin t, то v(t) = cos t.
Производная косинуса t является отрицательной синус т.		Если v(t) = cos t, то a(t) = -sin t.

Правила совмещения функций: В приведенных ниже правилах u и w представляют собой функции времени, t.

Правило на английском языке	Правило в математике.Обозначение	Пример
Производная константы, умноженная на функцию, равна константа, умноженная на производную функции.		Если x(t) = 3t ² , то v(t) = 3(2т ¹ ) = 6т. (с = 3 и и = т ² ) Если v(t) = 4sin t, то a(t) = 4cos t. (с = 4, и = грех т)
Производная суммы (или разности) двух функций есть сумма (или разность) их производные.		Если x(t) = t + sin t, то v(t) = 1 + cos t.(и = т, ш = sin т) Если v(t) = t ² – 4t, то a(t) = 2t ¹ – 4(1) = 2t – 4. (u = t ² , w = 4т)
Производная составного (одна функция внутри другая функция) функция равна производной “внешняя” функция, оставляя только “внутреннюю” функцию, умноженная на производную от «внутренней» функции.(Цепь Правило)		Если x(t) = (t + 2) ² , то v(t) = 2(t + 2) ¹ (1 + 0) = 2(t + 2). (и = т ² , ш = т + 2) Если v(t) = sin(2t ³ ), то a(t) = cos(2t ³)(2)(3t ²) = 6t ² cos(2t ³ ) (u = cos t, w = 2т ³ )

Правило на английском языке

Правило в математике.Обозначение

Пример

Производная константы, умноженная на функцию, равна константа, умноженная на производную функции.

Если x(t) = 3t ² , то v(t) = 3(2т ¹ ) = 6т. (с = 3 и и = т ² )

Если v(t) = 4sin t, то a(t) = 4cos t. (с = 4, и = грех т)

Производная суммы (или разности) двух функций есть сумма (или разность) их производные.

Если x(t) = t + sin t, то v(t) = 1 + cos t.(и = т, ш = sin т)

Если v(t) = t ² – 4t, то a(t) = 2t ¹ – 4(1) = 2t – 4. (u = t ² , w = 4т)

Производная составного (одна функция внутри другая функция) функция равна производной “внешняя” функция, оставляя только “внутреннюю” функцию, умноженная на производную от «внутренней» функции.(Цепь Правило)

Если x(t) = (t + 2) ² , то v(t) = 2(t + 2) ¹ (1 + 0) = 2(t + 2). (и = т ² , ш = т + 2)

Если v(t) = sin(2t ³ ), то a(t) = cos(2t ³)(2)(3t ²) = 6t ² cos(2t ³ ) (u = cos t, w = 2т ³ )

Определенные интегралы:

Определенный интеграл представляет собой площадь, и вычисление определенного интеграл («интегрирование» на языке исчисления) является обратным нахождение производной – подобное вычитанию является обратным сложением.В физике площадь под графиком зависимости скорости от времени представляет перемещение, поэтому определенный интеграл скорости дает смещение. Площадь под графиком зависимости ускорения от времени равна изменение скорости, поэтому определенный интеграл ускорения говорит вы изменение скорости. Площадь под графиком зависимости силы от положения равна работе, совершаемой силой, поэтому определенный интеграл силы (относительно положения) говорит вам о работе силы. Есть еще много, много других применений определенного интеграла в физика.

На приведенной выше диаграмме показано соотношение между определенное целочисленное обозначение и площадь, которую оно представляет. “а” и “b” – называемые “пределы интегрирования” идут внизу и вершина большой “S”. “f(t)” – это функция, интегрированный («подынтегральная функция»), а «dt» говорит, что «t» — это используемая переменная.

Обозначение читается как “определенный интеграл от a до b ф т, дт».

Правила для определенных интегралов:

Точно так же, как вы можете вычесть 5 из 12, подумав: «Что у меня есть? прибавить к 5, чтобы получить 12?», вы можете вычислить определенные интегралы с помощью думая: «Какую функцию я должен дифференцировать, чтобы получить функция в этом интеграле?» Эта функция называется «интегралом». или «антипроизводная». Математический символ первообразной выглядит как определенный интеграл без ограничений интеграция.

Первообразные правила для конкретных функций: если вы студент-математик, вы заметите, что мы игнорируем важный математический момент в следующих правилах.

Первообразные правила для комбинаций функций: в правила ниже, u и w представляют функции времени, т.

Правило на английском языке	Правило в математике.Обозначение	Пример
Первообразная константы, умноженная на функцию равно константе, умноженной на первообразную функция.
Первообразная суммы (или разности) двух функций равна сумме (или разности) их первообразные.

Основная теорема исчисления – расскажет, как оценить определенные интегралы на основе того, что вы знаете о первообразные.

Правило на английском языке	Правило в математике.Обозначение	Пример
Если F(t) является первообразной f(t), то определенный интеграл от a до b от f равен функции F оценивается, когда t равно b минус F оценивается, когда t равно а.

последнее обновление 26 ноября 2007 г.

автор JL Стэнбро

26.3: Антипроизводные и интегралы – Physics LibreTexts

В предыдущем разделе мы занимались определением производной функции $f(x)$. Производная полезна, потому что она говорит нам, как функция $f(x)$ изменяется как функция $x$. В физике мы часто знаем, как изменяется функция, но не знаем фактическую функцию. Другими словами, мы часто сталкиваемся с противоположной проблемой: нам дана производная функции, и мы хотим определить реальную функцию. В этом случае мы ограничим наше обсуждение функциями одной независимой переменной.

Предположим, что нам дана функция $f(x)$, и мы знаем, что она является производной некоторой другой функции, $F(x)$, которую мы не знаем. Мы называем $F(x)$ антипроизводной функции $f(x)$. Антипроизводная функции $f(x)$, записанная $F(x)$, таким образом, удовлетворяет свойству: \[\begin{aligned} \frac{dF}{dx}=f(x )\end{aligned}\] Поскольку у нас есть символ, указывающий, что мы берем производную по $x$ ($\frac{d}{dx}$), у нас также есть символ, \ (\int dx\), за указание на то, что мы берем антипроизводную по $x$: \[\begin{aligned} \int f(x) dx &= F(x) \\ \therefore \ frac{d}{dx}\left(\int f(x) dx\right) &= \frac{dF}{dx}=f(x)\end{aligned}\] Ранее мы обосновали символ для производной, указав, что она похожа на $\frac{\Delta f}{\Delta x}$, но для случая, когда $\Delta x\to 0$. Точно так же мы обосновываем знак антипроизводной $\int f(x) dx$, показав, что он связан с суммой $f(x)\Delta x$, в пределе $ \Дельта х\к 0$. Знак $\int$ выглядит как «S» для суммы.

Хотя можно точно определить производную функции $f(x)$, антипроизводную можно определить только с точностью до константы. Рассмотрим, например, другую функцию $\тильда F(x)=F(x)+C$, где $C$ — константа. Производная от $\tilde F(x)$ по $x$ определяется как: \[\begin{aligned} \frac{d\tilde{F}}{dx}&=\frac{ d}{dx}\left(F(x)+C\right)\\ &=\frac{dF}{dx}+\frac{dC}{dx}\\ &=\frac{dF}{dx} +0\\ &=f(x)\end{aligned}\] Следовательно, функция $\tilde F(x)=F(x)+C$ также является антипроизводной $f(x )$.2\), показанный на рисунке A2.2.1 (левая панель). Если вы представите сдвиг всей функции вверх или вниз, производная не изменится. Другими словами, если бы начало осей не отображалось на левой панели, вы все равно могли бы определить производную функции (насколько она крутая). Добавление константы $C$ к функции точно такое же, как сдвиг функции вверх или вниз, который не меняет ее производную. Таким образом, когда вы знаете производную, вы не можете знать значение $С$, если вам также не говорят, что функция должна проходить через определенную точку (так называемое начальное условие).

Чтобы определить производную функции, мы использовали Уравнение A2.2.1 . Теперь нам нужно получить эквивалентный рецепт для определения антипроизводной. Предположим, что у нас есть две части информации, необходимые для полного определения $F(x)$, а именно:

функция $f(x)=\frac{dF}{dx}$ (ее производная).
условие, что $F(x)$ должен проходить через определенную точку, $F(x_0)=F_0$.

Рисунок A2.3.1. (x_{0}, F_{0}) = (1, 3)\).

Процедура определения первообразной $F(x)$ показана выше на рисунке A2.3.1. Начнем с рисования точки, которую, как мы знаем, должна пройти функция $F(x)$, $(x_0,F_0)$. Затем мы выбираем значение $\Delta x$ и используем производную $f(x)$, чтобы вычислить $\Delta F_0$, величину, на которую изменяется $F(x)$ когда $x$ меняется на $\Delta x$. Используя производную $f(x)$, оцененную в $x_0$, мы имеем: \[\begin{aligned} \frac{\Delta F_0}{\Delta x} &\ приблизительно f(x_0)\; \;\;\; (\text{в пределе} \Delta x\to 0 )\\ \следовательно \Delta F_0 &= f(x_0) \Delta x\end{aligned}\] Затем мы можем оценить значение функции $F_1 =F(x_1)$ в следующей точке, $x_1=x_0+\Delta x$, как показано черной стрелкой на рисунке A2.3.1 \[\begin{aligned} F_1&=F(x_1)\\ & =F(x+\Delta x) \\ &\приблизительно F_0 + \Delta F_0\\ &\приблизительно F_0+f(x_0)\Delta x\end{aligned}\] Теперь, когда мы определили значение функции \ (F(x)\) в $x=x_1$, мы можем повторить процедуру определения значения функции $F(x)$ в следующей точке, $x_2=x_1+\Delta x\ ).Опять же, мы используем производную, оцененную в \(x_1$, $f(x_1)$, чтобы определить $\Delta F_1$, и добавляем ее к $F_1$, чтобы получить $F_2=F( x_2)$, как показано серой стрелкой на рисунке A2.3.1: \[\begin{aligned} F_2&=F(x_1+\Delta x) \\ &\приблизительно F_1+\Delta F_1\\ &\приблизительно F_1+f (x_1)\Delta x\\ &\приблизительно F_0+f(x_0)\Delta x+f(x_1)\Delta x\end{aligned}\] Используя обозначение суммирования, мы можем обобщить результат и написать функцию \ (F(x)\) оценивается в любой точке, $x_N=x_0+N\Delta x$: \[\begin{aligned} F(x_N) \ приблизительно F_0+\sum_{i=1}^{i= N} f(x_{i-1}) \Delta x\end{aligned}\] Приведенный выше результат станет точно правильным в пределе $\Delta x\to 0$:

\[F(x_N) = F(x_0)+\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x\]

Рассмотрим сумму поближе. Каждый член в сумме имеет вид $f(x_{i-1})\Delta x$ и проиллюстрирован на рис. A2.3.2 для того же случая, что и на рис. A2.3.1 (то есть, На рис. A2.3.2 показано известное нам $f(x)$, а на рис. A2.3.1 показано $F(x)$, которое мы пытаемся найти).

Рисунок A2.3.2 : Функция $f(x) = 2x$ и иллюстрация терминов $f(x_{0})∆x$ и $f(x_{1})∆x$ как площадь между кривой $f(x)$ и осью $x$, когда $∆x → 0$.

Как видите, каждый член в сумме соответствует площади прямоугольника между функцией $f(x)$ и осью $x$ (с отсутствующим куском).{x_N}\конец{выровнено}\]

Напомним, что ранее мы писали первообразную с тем же символом $\int$: \[\begin{aligned} \int f(x) dx = F(x)\end{aligned}\] Символ \ (\int f(x) dx\) без ограничений называется неопределенным интегралом . Вы также можете видеть, что когда вы берете (определенный) интеграл (то есть разницу между $F(x)$, оцененную в двух точках), любая константа, добавляемая к $F(x)$, отменяется. {i=N=3} 2x_{i-1} \Delta x &=2x_0\Delta x+2x_1\Delta x+2x_2\Delta x\\ &=2\Delta x (x_0+x_1+ x_2) \\ &=2 \frac{x_3-x_0}{N}(x_0+x_1+x_2) \\ &=2 \frac{(4)-(1)}{(3)}(1+2+ 3) \\ &=12\end{aligned}\], где во второй строке мы заметили, что можем исключить $2\Delta x$, потому что он появляется в каждом термине.{b}f(t)dt\) равно

область между функцией $f(t)$ и осью $f$ между $t=a$ и $t=b$
сумма $f(t)\Delta t$ в пределе $\Delta t\to 0$ между $t=a$ и $t=b$
разность $f(b) – f(a)$.

Ответить

Общие антипроизводные и свойства

В таблице A2.3.1 ниже приведены первообразные (неопределенные интегралы) для общих функций.х+С\) $f(x)=\ln(x)$ $F(x)=x\ln(x)-x+C$

Таблица A2. 3.1 : Общие неопределенные интегралы функций.

Заметим, что в общем случае получить первообразную функции гораздо труднее, чем ее производную. Несколько общих свойств, помогающих вычислять неопределенные интегралы, показаны в таблице A2.3.2 ниже.

Антипроизводная	Эквивалентная антипроизводная
$\int (f(x)+g(x)) dx$	$\int f(x)dx+\int g(x)dx$ (сумма)
$\int (f(x)-g(x)) dx$	$\int f(x)dx-\int g(x)dx$ (вычитание)
$\int af(x) dx$	$a\int f(x)dx$ (умножение на константу)
$\целое f'(x)g(x) dx$	$f(x)g(x)-\int f(x)g'(x) dx$ (интегрирование по частям)

Таблица A2. 3.2 : Некоторые свойства неопределенных интегралов.

Общее использование интегралов в физике – от суммы к интегралу

Интегралы чрезвычайно полезны в физике, потому что они связаны с суммами. Если предположить, что наши друзья-математики (или компьютеры) могут определить для нас антипроизводные, использование интегралов не так сложно.

Ключевая идея в физике состоит в том, что интегралы являются инструментом для легкого вычисления сумм . Как мы видели выше, интегралы соответствуют площади под кривой, которая находится путем суммирования (различных) площадей бесконечного числа бесконечно малых прямоугольников.В физике часто бывает так, что нам нужно взять сумму бесконечного числа мелких вещей, которые постоянно меняются, как площади прямоугольников.

Рассмотрим, например, стержень длиной $L$ и общей массой $M$, как показано на рисунке A2.3.3. Если стержень однороден по плотности, то если мы разрежем его, скажем, на две равные части, эти две части будут весить одинаково. Мы можем определить «линейную массовую плотность» $\mu$ для стержня как массу на единицу длины стержня: \[\begin{aligned} \mu = \frac{M}{L}\ end{aligned}\] Линейная массовая плотность имеет размеры массы относительно длины и может использоваться для нахождения массы стержня любой длины.Например, если стержень имеет массу $M=5\text{kg}$ и длину $L=2\text{m}$, то массовая плотность равна: \[\begin{ выровнено} \mu=\frac{M}{L}=\frac{(5\text{кг})}{(2\text{м})}=2,5\text{кг/м}\end{выровнено} \] Зная плотность массы, теперь мы можем легко найти массу $m$ куска стержня, длина которого, скажем, $l=10\text{см}$. Используя массовую плотность, масса стержня $10\text{см}$ определяется как: \[\begin{align} m=\mul=(2,5\text{кг/м})(0,1\ text{m})=0.25\text{kg}\end{aligned}\] Теперь предположим, что у нас есть неоднородный стержень длины $L$, как на рисунке A2.3.3, и не имеет постоянной линейной плотности массы. Возможно, стержень становится все шире и шире, или в нем есть отверстия, которые делают его неоднородным. Представьте, что массовая плотность стержня задается функцией $\mu(x)$, которая зависит от положения вдоль стержня, где $x$ – расстояние, измеренное от одной стороны стержня. .

Рисунок A2.3.3 : Стержень с переменной линейной плотностью. Для вычисления массы стержня рассмотрим небольшой элемент массы $∆m_{i}$ длины $∆x$ в положении $x_{i}$.Суммарная масса стержня находится суммированием масс элементов малой массы.

Теперь мы не можем просто определить массу стержня путем умножения $\mu(x)$ и $L$, так как мы не знаем, какое значение $x$ использовать. Фактически, мы должны использовать все значения $x$ между $x=0$ и $x=L$.

Стратегия состоит в том, чтобы разделить стержень на $N$ частей длины $\Delta x$. Если мы пометим наши части стержня индексом $i$, мы можем сказать, что часть, которая находится в позиции $x_i$, имеет крошечную массу, $\Delta m_i$.Мы предполагаем, что $\Delta x$ достаточно мало, так что $\mu(x)$ можно считать постоянным по длине этого крошечного кусочка стержня. {i =N} \mu(x_i) \Delta x\end{aligned}\] Но это и есть определение интеграла ( Уравнение A2.4 \\ &=78\text{g}\\\end{выровнено}\]

Немного потренировавшись, вы сможете решать задачи такого типа, не записывая сумму в явном виде. Изобразите 90 334 бесконечно малых 90 335 куска стержня длины $dx$ в позиции $x$. Он будет иметь бесконечно малую массу , $dm$, определяемую как: \[\begin{aligned} dm = \mu(x) dx\end{aligned}\] Общая масса стержня равна сумма (т.е. интеграл) массы элементов \[\begin{aligned} M = \int dm\end{aligned}\] и мы действительно можем думать о знаке $\int$ как о сумме, когда суммируемые вещи 90 334 бесконечно малы, 90 335 малы.L \mu(x) dx\end{aligned}\], где мы сделали интеграл определенным, указав диапазон для суммирования, так как мы можем использовать $x$ для «пометки» элементов массы.

Следует отметить, что получение вышеприведенного интеграла — это физика. Решение это математика. Мы будем гораздо больше беспокоиться о выписывании интеграла, чем о вычислении его значения. Вычислить интеграл всегда может друг-математик или компьютер, но определение того, какой интеграл записать, — это работа физика!

производных и интегрирование в физике

кинематика: производные и интегрирование в физике главная | электроника | набор инструментов | научный клуб | смокинг | фото | электронные открытки | интернет магазин
Физика в старших классах преподает кинематические уравнения в виде набора простых формул:
v = v ₀ + а ₀ Δt
x = x ₀ + ½ (v ₀ + v) Δt = x ₀ + v ₀ Δt + ½ ½6 2 Δt ²4 V ² = (V ₀ ) ² + 2а ₀ Δx
В большинстве школьных учебников вместо «а ₀» будет отображаться «а», но смысл тот же.
К сожалению, редко упоминается, что эти упрощенные формулы применимы только в особых случаях. Реальные формулы еще проще и их легче запомнить, чем те, которым учат в средней школе, но они требуют немного высшей математики. Вам не нужно быть гением исчисления, чтобы получить представление о реальных формулах.
Объект, находящийся в фиксированном положении, имеет нулевую скорость. Если вы двигаете его, то он будет иметь определенную скорость зависит от того, как быстро он движется. Другими словами, изменение положения во времени равно скорости .Если вы планируете положение x во времени, затем , наклон кривой этого положения во времени – это скорость . x(t) – уравнение кривой зависимости положения от времени. Наклон кривой математически является производной функции, описывающей эту кривую. Это написано так:
∂х(т) v(t) = ------- ∂t
В краткой записи над x(t) ставится точка, обозначающая производную. Поэтому у меня нет точки в HTML Я использую тире:
∂х(т) v(t) = x'(t) = ------- ∂t
Это просто «забавная запись», чтобы сказать: нарисуйте положение (x) как функцию времени, x (t) и измерьте наклон.Результат скорость как функция времени. Другими словами изменение положения связано со скоростью .
Для изменения скорости требуется ускорение (или торможение = отрицательное ускорение). Таким образом, наклон кривой скорости во времени равен ускорению во времени:
∂v(t) ∂ ² х(t) a(t) = v'(t) = ------- = x"(t) = -------- ∂t ∂t ²
Обратная производная является интегралом.В графическом плане это площадь под кривой. Например, автомобиль движется с постоянной скоростью 2 м/с (два метра в секунду):
v(t) = 2 м/с (синяя линия на графике ниже).
Область под этой синей линией представляет собой прямоугольник и увеличивается по мере перемещения вправо от графика. Эта область соответствует положению нашего автомобиля. При t=2с площадь равна 2с*2м/с=4м, при t=3с площадь 2м/с*3с=6м.
х(т) = 2 т
Если мы нарисуем 2*t на графике, то получим красную линию.Это положение автомобиля во времени.
Эта площадь под кривой скорости называется в математических терминах интегралом и записывается как:
х(т) = ∫v(t)∂t

Накопленная площадь во времени под скоростью — это позиция. Это обратная сторона фразы «изменение положения — это скорость».
Изменение скорости было ускорением, а обратной функцией было бы «площадь под кривой ускорения — это скорость:
v(t) = ∫a(t)∂t

Киниматические уравнения в виде производных и интегралов
∂х(т) v(t) = x'(t) = ------- ∂t ∂v(t) ∂ ² х(t) a(t) = v'(t) = ------- = x"(t) = -------- ∂t ∂t ² и обратные функции: x(t) = ∫v(t)∂t + x ₀ = ∫∫a(t)∂t ² + x ₀ v(t) = ∫a(t)∂t + v ₀

Производные и интегралы некоторых основных функций
Чтобы использовать это, мы должны знать, как вычислить производную или интеграл данной функции.За физике на уровне средней школы вам нужно будет знать только следующее.
∂f (т) функция: f(t) = t ² , производная: f'(t) = ------- = 2 t ∂t ∂f (т) функция: f(t) = 2 t, производная: f'(t) = ------- = 2 ∂t функция: f(t) = константа, производная: f'(t) = 0

В общем случае производная от f(t) = t ^z равна f'(t) = z*t ^z-1 . То есть: вы ставите показатель степени впереди и уменьшаете его на 1.
Интеграл — это обратная операция производной.
функция: f(t) = t, интеграл: ∫f(t)∂t = ½ t ² функция: f(t) = константа, интеграл: ∫f(t)∂t = константа * t

В общем случае интеграл от f(t) = t ^z равен ∫f(t) = 1/(z+1) * t ^z+1 . То есть: вы увеличиваете показатель степени на единицу и делите на значение новой степени.
Следующая диаграмма содержит 3 графика:
f ₁ (t) = 2 (синяя линия)
f ₂ (t) = 2 t (красная линия)
f ₃ (t) = t ² (зеленая линия)
Графики были выбраны так, что: ∫f ₁ (t) = f ₂ (t) и ∫f ₂ (t) = f ₃ (t)
Интеграл от f ₂ (t) равен f ₃ (t), но значение f ₃ в данной точке t равно площади под линией f ₂ (t), начиная с t=0.Если вы хотите узнать размер оранжевой области под красной линией, от t=1 до t=2, вам нужно вычесть: f ₃ (2) – f ₃ (1) = 2 ² – 1 ² = 3. Интеграл функции f ₂ (∫f ₂ ∂t) от t=1 до t=2 равен 3.
Как перейти от общих кинематических уравнений к школьным формулам?
Формулы средней школы, упомянутые в верхней части страницы, работают только при двух предположениях:
ускорение постоянное
скорость возрастает линейно от v ₀ до v за период времени Δt

Первое уравнение средней школы было
v = v ₀ + aΔt
Мы получим это, если воспользуемся
v(t) = ∫a(t)∂t + v ₀
и установим a(t) = a ₀ (константа)
Интеграл константы по времени равен произведению константы на время: ∫a ₀ ∂t = a ₀ * t, и мы имеем школьное уравнение.
Второе уравнение средней школы было
x = x ₀ + ½ (v ₀ + v)Δt
Это можно получить из следующего уравнения:
x(t) = ∫v(t)∂t + x ₀
Допущение, при котором справедливо уравнение средней школы, состоит в следующем: скорость линейно увеличивается v ₀ до v за период времени Δt. Мы можем сделать это предположение. Я использую “v ₁” вместо “v”, чтобы было понятно что это фиксированная точка, а не переменная.

Терм ∫v(t)∂t будет областью, отмеченной оранжевым цветом.Эта область:
v ₀ Δt + ½ (v ₁ – v ₀ )Δt = ½ (v ₀ + v)Δt
Замена ∫v(t)∂t на ½ (v ₀ + v)Δt приводит ко второму уравнению средней школы. Это также возможно сделать чисто математически, а не графически, но это более длинный расчет, который вы можете выполнить >здесь<, если хотите.
Второе уравнение средней школы
Извините, у меня нет времени. Сделать позже.

© 2004-2022 Гвидо Сохер
Nerdfighteria Wiki – Производные: Ускоренный курс физики #2

Теперь есть еще несколько уравнений, производные которых вам следует понять.Тригонометрия, которую мы используем для вычисления углов и сторон треугольников, будет широко использоваться в физике, потому что мы все время будем использовать прямоугольные треугольники. Поэтому полезно знать, как найти производные от sin(x) и cos(x). Синус говорит вам, что если у вас есть прямоугольный треугольник, а x – угол в этом треугольнике, то sin(x) будет длиной стороны, противоположной этому углу, деленной на гипотенузу. Косинус делает то же самое, только сторона рядом с этим углом делится на гипотенузу.Таким образом, их графики говорят вам, какими будут эти отношения в зависимости от угла.
На самом деле мы можем попытаться угадать производную sin(x), просто взглянув на ее график. Вы можете видеть, что кривая время от времени имеет точки поворота, при x=-90°, x=90° и т. д., повторяющиеся каждые 180°. Это означает, что в этих точках уравнения вообще не меняются, поэтому производная в этих поворотных точках также будет точно равна нулю. Давайте нарисуем еще один график, на котором мы построим производную, и поставим маленькие точки там, где мы будем знать, что она будет равна нулю.
Итак, что происходит между этими поворотными моментами? Итак, от -270° до -90° sin(x) уменьшается. Другими словами, его изменение и, следовательно, его производная должны быть отрицательными. Затем, от -90° до 90°, sin(x) увеличивается, так что у него будет положительная производная. И так далее… На самом деле на этом графике гораздо больше подсказок, которые помогут нам найти производную, но мы уже знаем достаточно, чтобы сделать приличное предположение.
Если мы плавно соединим точки на графике нашей производной, имея в виду, где кривая должна быть положительной, а где отрицательной, эй, эта производная очень похожа на график cos(x).Это потому, что это так. Производная синуса — это просто косинус, и это будет часто встречаться. То же самое можно сказать и о них, которые вы можете проработать самостоятельно, повторив то, что мы только что сделали с графиками sin(x) и cos(x).
(PDF) Проверка способности учащихся использовать производные, интегралы и векторы в чисто математическом контексте и в физическом контексте
[12] Дж. Туминаро, Когнитивная основа для анализа и
, описывающая вводное использование и понимание учащимися
математики по физике, к. D. Thesis, University of
Maryland, 2004.
[13] L. Cui, NS Rebello, PR Fletcher, and AG Bennett,
Перенос знаний из математического анализа колледжа в курсы физики
, в Proceedings of the NARST Ежегодное собрание
, 2006 г. (2006 г.), https://web.phys.ksu.edu/papers/2006/
Cui_NARST2006.pdf.
[14] Ф. Р. Йейттс и Дж. Р. Хундхаузен, Исчисление и физика:
Проблемы на границе раздела, Am. Дж. Физ. 60, 716 (1992).
[15] Х. Т. Хадсон и В. Р. Макинтайр, Корреляция между
математическими навыками и успехами в физике, Am. Дж. Физ.
45, 470 (1977).
[16] Дж. Туминаро и Е. Ф. Редиш, Элементы когнитивной модели решения физических задач: Эпистемические игры, Phys.
Rev. ST Phys. Образовательный Рез. 3, 020101 (2007).
[17] D. Domert, J. Airey, C. Linder, and R. Lippmann Kung, An
Исследование эпистемологического
мышления студентов-физиков университетов в отношении понимания физических уравнений,
NorDiNa 3, 15 ( 2007).
[18] С. М. Барнетт и С. Дж. Сеси, Когда и где мы применяем
то, чему мы учимся? Таксономия дальней передачи, Psychol. Бык.
128, 612 (2002).
[19] А. Л. Робертс, М. Д. Шарма, С. Бриттон и П. Б. Нью, Индекс
для измерения способности студентов первого курса естественных наук к
переводу математики, Int. Дж. Матем. Образовательный науч. Технол. 38,
429 (2007).
[20] С. Бриттон, П. Б. Нью, А. Л. Робертс, М. Д. Шарма, А.
Брю и Дж. Сакс, Изучение способности студентов к
передаче математики, в Преобразовании университета:
Стипендия преподавания и обучения на практике (Sydney
University Press, Сидней, Австралия, 2007 г.).
[21] NS Rebello, L. Cui, AG Bennett, D. Zollman, and DJ
Ozimek, Перенос обучения при решении задач в контексте
математики и физики, в Learning to Solve
Complex Scientific Problems , под редакцией Д.H. Jonassen
(Routledge, New York, 2017), гл. 10.
[22] Дж. Лобато, Альтернативные взгляды на передачу
обучения: история, проблемы и задачи для будущих исследований,
поиск, Дж. Учись. науч. 15, 431 (2006).
[23] J. Lobato и B. Rhodehamel, «Замечание» как альтернатива
передачи процесса обучения, J. Learn. науч. 21, 433 (2012).
[24] J. Lobato, C. Hohensee, and B. Rhodehamel, Студенческое
математическое замечание, J.Рез. Мат. Образовательный 44, 809 (2013).
[25] А. Элби, Что учащиеся изучают представления
о конструктивизме, J. Math. Поведение 19, 481 (2000).
[26] JF Wagner, A Transfer-in-Pieces рассмотрение
восприятия структуры при передаче обучения, J. Learn.
Науч. 19, 443 (2010).
[27] А. М. Мэдсен, А. М. Ларсон, Л. С. Лошки, Н. С.
Ребелло, Различия в зрительном внимании между теми, кто
правильно и неправильно отвечает на физические задачи, Phys.
Rev. ST Phys. Образовательный Рез. 8, 010122 (2012).
[28] Дж. А. Камински, В. М. Слуцкий, А. Ф. Хеклер, Стоимость
конкретности: влияние несущественной информации на
аналоговый перенос, J. Exper. Психол. 19, 14 (2013).
[29] Л. Иванжек, А. Сусак, М. Планиник, А. Андрашевич и З.
Милин-Сипус, Студенческие рассуждения о графах в различных
контекстах, Phys. Преподобный физ. Образовательный Рез. 12, 010106 (2016).
[30] Дж.Д. Брансфорд и Д.Л. Шварц, Переосмысление передачи:
Простое предложение с многочисленными последствиями, в Обзоре
Исследования в области образования, под редакцией А. Иран-Неджада и PD
Пирсона (Американская ассоциация исследований в области образования,
Вашингтон, округ Колумбия, 1999), Том. 24, стр. 61–100.
[31] Дж. Ф. Вагнер, Передача по частям, Cognit. Инстр. 24, 1 (2006).
[32] Дж. Лобато, Перспектива переноса, ориентированная на актера, и ее
вкладов в образовательные исследования и практику, Educ.
Психолог. 47, 232 (2012).
[33] Т. Дж. Нокс, Механизмы передачи знаний, Think.
Респ. 15, 1 (2009).
[34] Н.С. Ребелло, Объединение традиционных и современных
перспектив передачи обучения: структура и последствия
, в Proceedings of the NARST 2007 Annual
Meeting (2009), https://web.phys.ksu .edu/papers/2007/
Rebello-narst.pdf.
[35] Л. Кюи, Оценка удержания студентов колледжей и перевод
с исчисления на физику, Ph.D. Thesis, Kansas State
University, 2006.
[36] Н. С. Ребелло и Д. Золман, Модель динамического переноса
обучения, в материалах ежегодного собрания NARST 2005
(2005), https: //www.researchgate.net/publication/
255580937_A_Model_for_Dynamic_Transfer_of_Learning.
[37] Д. Ху и Н. С. Ребелло, Используя концептуальное смешивание с
, описывают, как студенты используют математические интегралы в
физике, Phys. преп.СТ физ. Образовательный Рез. 9, 020118 (2013).
[38] Т. Дж. Бинг и Э. Ф. Редиш, Когнитивное смешение
математических и физических знаний, AIP Conf. проц. 883,
26 (2007).
[39] К. Бейн, Ж.-М. G. Rodriguez, A. Moon и M.H. Towns,
Характеристика когнитивных процессов, вовлеченных в
химическую кинетику, с использованием структуры смешанной обработки,
Chem. Образовательный Рез. Практика. 19, 617 (2018).
[40] Ж.-М. Г. Родригес, С.Сантос-Диас, К. Бейн и М. Х.
Таунс, Использование символических и графических форм для анализа
математических рассуждений студентов по химической кинетике,
J. Chem. Образовательный 95, 2114 (2018).
[41] PW Thompson, Развитие концепции скорости
и ее связь с концепциями скорости, в The Development
of Multipliative Reasoning in the Learning of Mathematics-
ics, под редакцией G. Harel and J. Confrey (SUNY Press,
Олбани, Нью-Йорк, 1994), стр.181–234.
[42] Д. Э. Троубридж и Л. К. Макдермотт, Исследование понимания
учащимися концепции скорости в одном
измерении, Am. Дж. Физ. 48, 1020 (1980).
[43] Д. Э. Троубридж и Л. К. Макдермотт, Исследование понимания
учащимися концепции ускорения в одном
измерении, Am. Дж. Физ. 49, 242 (1981).
[44] Л. К. Макдермотт и Э. Ф. Редиш, Информационное письмо: PER-1:
Исследования в области физического образования, Am.Дж. Физ. 67, 755 (1999).
[45] Г. Лейнхардт, О. Заславский и М. К. Штейн, Функции,
графики и графики: задачи, обучение и обучение, ред.
Educ. Рез. 60, 1 (1990).
[46] Л. К. Макдермотт, М. Л. Розенквист и Э. Х. ван Зее,
Трудности учащихся в соединении графиков и физики:
Примеры из кинематики, Am. Дж. Физ. 55, 503 (1987).
[47] Р. Дж. Бейхнер, Тестирование студенческой интерпретации кинематики
графиков, Am.Дж. Физ. 62, 750 (1994).
ТЕСТИРОВАНИЕ СТУДЕНТОВ НА СПОСОБНОСТЬ ИСПОЛЬЗОВАТЬ …PHYS. РЕВ. ФИЗ. ОБРАЗОВАНИЕ. рез. 16, 010111 (2020)
010111-15
Исчисление в физических двигателях |
Что такое физические движки?
Физические движки — это программы, которые используются для моделирования физических явлений. Эти программы десятилетиями использовались военными, метеорологами и даже разработчиками видеоигр. Диапазон их применения варьируется от определения места попадания артиллерийских снарядов на основе нескольких параметров до имитации аналогичной ситуации в игре Call of Duty или Battlefield.Видеоигры дают прекрасную возможность увидеть, как выполняются симуляции. Конечно, симуляции физики в видеоиграх не ограничиваются только милитаристскими явлениями. На самом деле, другие приложения в основном хитрые по своей природе и могут привести к совершенно захватывающим дух моментам для потребителей.
Какое отношение это имеет к Исчислению?
Различные приложения для физических движков столь же интересны, сколь и обширны, но какое это имеет отношение к исчислению и этому курсу в целом? Как оказалось, функции являются неотъемлемой частью физических движков и программирования. Первоначально исчисление физических движков в видеоиграх было делегировано обнаружению столкновений между игровыми объектами (такими как персонажи игроков, камни и частицы пыли) и выработке соответствующих ответов. Однако за последние несколько десятилетий движки были обновлены, чтобы использовать более продвинутые вычисления для более правдоподобного взаимодействия между игровыми объектами. Чтобы применить уровень исчисления, необходимый для достижения таких эффектов, физические движки используют сегмент кода, называемый интегратором.2}$
Интеграл: $\mathit{a(t)}$
Это означает, что скорость объекта может быть найдена с помощью антипроизводной его ускорения, а его положение – с помощью антипроизводной его скорости. Это также означает, что площадь, определяемая интегралом от Ускорения, представляет собой полное изменение скорости, а площадь, определяемая интегралом от Скорости, представляет собой смещение объекта. Все это важно для прогнозирования положения любого объекта с момента начала моделирования до момента его окончания. b F(x)dx$
Хотя симуляции не всегда идеальны, комбинация всех этих факторов, работающих вместе в рамках физического движка, обеспечивает опыт, который с каждым годом становится все более реалистичным до такой степени, что становится почти неотличимым от физических явлений, которые мы можем видеть в повседневной жизни.Исчисление в конечном итоге играет важную роль в том, как такой механизм интерпретирует данные моделирования и возвращает соответствующий ответ. Можно даже сказать, что без исчисления было бы невозможно предсказать исход физического явления в симуляции или даже в реальности.
Источники
Applied Calculus, 5-е издание (Hughes-Hallet, Gleason, Lock, Faith и др.): 5.1, 5.2
https://faculty.atu.edu/mfinan/2924/cal76.pdf
http://www.ugrad.math.ubc.ca/coursedoc/math203/site2012/keshet.notes/Chapter4.pdf
https://prezi.com/qicki_zqvo9v/the-calculus-of-video-games/

Но что такое «дх» на самом деле? Объяснение терминов исчисления
Символ «dx» встречается везде в исчислении. Например:
Если y является функцией x, то мы иногда записываем производную y по x следующим образом:

Когда мы записываем неопределенные интегралы, они записываются как:

Когда мы записываем определенные интегралы, они записываются как:
Но что такое «дх» на самом деле? Это больше, чем просто запись! В этом посте мы рассмотрим значение «dx» и попытаемся лучше понять некоторые символы, которые мы часто видим в исчислении.
Исчисление как исследование бесконечно малых изменений
Исчисление — это изучение непрерывных или бесконечно малых изменений. Чтобы понять, что это значит, давайте рассмотрим следующее: предположим, что вы участвуете в забеге. Вы начинаете бежать в момент времени x=0 секунд, а затем отслеживаете свое перемещение как функцию f(x). Тогда ваша функция смещения f(x) представляет собой непрерывную функцию , которая меняется со временем.
Теперь предположим, что вы хотите узнать свою скорость в момент времени x=10 секунд.Это расчетный вопрос, поскольку вы ищете скорость изменения в определенный момент времени. Как ты мог это сделать? Что ж, вы можете оценить свою скорость в момент времени t=10 как нашу среднюю скорость между моментами времени x=10 и x=11, которая может быть выражена как:
.
Но вы можете получить более точную оценку, выбрав меньший временной интервал, скажем, от x=10 до x=10,1 или, что еще лучше, от x=10 до x=10,01.
На самом деле, то, что вы хотите сделать, это взять предел, когда размер вашего временного интервала стремится к нулю.То есть вы хотите получить бесконечно малое изменение x. Тогда по определению производной ваша скорость в момент x=10 секунд будет равна:
.
Мы должны думать о том, что h стремится к нулю, как о все меньшем и меньшем увеличении x, когда мы берем среднюю скорость от времени x=10 до времени x=10+h.
Здесь на помощь приходит «dx».
“dx” — бесконечно малое изменение x. Мы можем думать о “dx” (читается как dee-ex) как о бесконечно малом изменении x. Буква «d» в «dx» должна напоминать вам о дельте ∆, которая является символом изменения.«dx не имеет численного значения. Скорее, он отражает идею, которая часто встречается в исчислении, — взять предел все меньших и меньших размеров интервалов, чтобы точно выяснить что-то о непрерывной функции.
Мы увидим это, если вернемся к нашему предыдущему примеру скорости. При вычислении нашей производной
Нижняя часть этой дроби равна (10+h)-10, когда h стремится к нулю, что является бесконечно малым изменением x. Поэтому мы могли бы думать о знаменателе при стремлении h к нулю как о dx.Если мы допустим y=f(x), то числитель этой дроби равен f(10+h)-f(10) при стремлении h к нулю, что является бесконечно малым изменением y или dy. Собрав все это вместе, мы восстанавливаем обозначение:
.
То есть производная f(x) есть отношение бесконечно малого изменения y к бесконечно малому изменению x. Точнее говоря, это как раз и есть предел изменения у над изменением х при все меньших и меньших изменениях х. Обозначения «dx» и «dy» просто фиксируют эту процедуру ограничения и вместо этого выражают ее как бесконечно малое изменение x или y.
«dx» в интегралах
Еще одно место, где часто встречается “dx”, – это интегралы. Остановимся на определенных интегралах. Что означает «dx» в определенном интеграле?
“dx” здесь по-прежнему является бесконечно малым изменением x. Чтобы понять, почему он здесь, мы должны думать об интеграле как о площади со знаком и как о пределе сумм Римана. Мы помним, что для вычисления левой суммы Римана функции f(x) от x=a до x=b с n интервалами допустимо следующее:
Тогда берем:
…где x принимает значения a, a + ∆x, a + 2∆x,…, a + (n – 1)∆x = b – ∆x.
Затем, когда мы устремляем n к бесконечности, ∆x становится все меньше и меньше, а сумма Римана сходится по значению к интегралу, который представляет собой площадь со знаком под кривой f(x) между x=a и x=b.

Антипроизводная	Эквивалентная антипроизводная
\(\int (f(x)+g(x)) dx\)	\(\int f(x)dx+\int g(x)dx\) (сумма)
\(\int (f(x)-g(x)) dx\)	\(\int f(x)dx-\int g(x)dx\) (вычитание)
\(\int af(x) dx\)	\(a\int f(x)dx\) (умножение на константу)
\(\целое f'(x)g(x) dx\)	\(f(x)g(x)-\int f(x)g'(x) dx\) (интегрирование по частям)