Производная степени | Математика
Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.
Открываем таблицу производных и правила дифференцирования.
Основная формула, по которой может быть найдена производная любой степени —
Примеры. Найти производную степени:
Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:
Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее. Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель.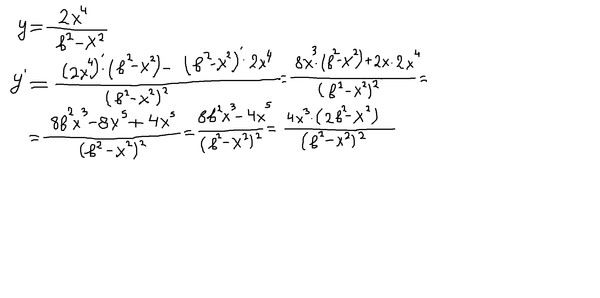
Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.
Например,
Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а далее — как обычно, производная степени.
Например,
Примеры для самопроверки. Найти производную степени:
Показать решение
Правила дифференцирования
Правила дифференцированияМатематический анализ |
2.
2. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ.
1) Производная от суммы равна сумме производных:
Доказательство:
2) Постоянный множитель выносится за знак производной: .
3) Производная произведения: .
Доказательство:
4) Производная дроби: .
Доказательство:
Вывод формул для производных.
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
Теорема о производной сложной функции.
Теорема.
Доказательство:
Это верно при условии, что каждая из функций дифференцируема.
Теорема о производной обратной функции.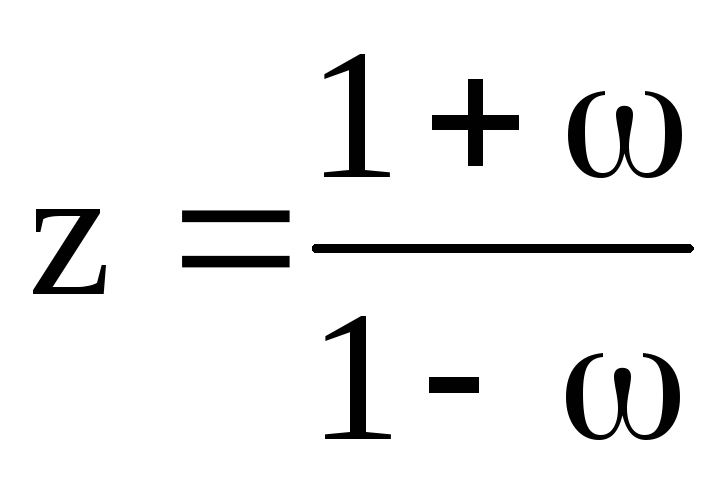
Теорема.
Доказательство:
Пусть дифференцируемая в точке (). – обратная к . Обратная функция существует если монотонная функция. Тогда
Производная сложной степенной функции.
Прием логарифмического дифференцирования.
Производная неявной функции.
– общий вид неявно заданной функции.
Производная параметрически заданной функции.
Примеры параметрических функций:
1)
2)
3)
– дифференцируемы.
Пример:
Гиперболические функции.
(гиперболический синус) | arsh x (ареа синус) |
(гиперболический косинус) | arсh x (ареа косинус) |
(гиперболический тангенс) | arth x (ареа тангенс) |
(гиперболический котангенс) | arcth x (ареа котангенс) |
Схематичные графики гиперболических функций:
Производные высших порядков.
Механический смысл второй производной – это ускорение.
назад | оглавление | вперёд
Производные. Истина в пределе [Анализ бесконечно малых]
Производные
Основное понятие дифференциального исчисления — это понятие производной. В действительности это один из краеугольных камней не только математики, но и науки в целом, ведь за ним скрываются такие фундаментальные понятия, как скорость или сила в физике, угол наклона касательной к кривой в геометрии и многие другие.
Производная функции f в точке а показывает, как изменится функция в этой точке по сравнению с тем, как изменяется значение переменной. Рассмотрим две функции из прошлых примеров: 
Однако из таблицы значений видно, что поведение функций вблизи t = 1 существенно различается:
t — s(t) — v(t)
0,8 — 0,8944… — 0,64
0,9 — 0,9486… — 0,81
1 — 1 — 1
1,1 — 1,0488… — 1,21
1,2 — 1,0954… — 1,44
Заметьте, что функция v вблизи 1 изменяется более резко, чем функция s.
Чтобы измерить эти изменения, то есть чтобы определить производную, выберем произвольное число
(f(a+h) — f(a))/h
Продолжим рассматривать функции s(t) = ?t и v(t) = t2. Вычислим значения этой дроби для а = 1:
Наибольшее значение этой дроби для функции v приближается к 2, для функции s оно примерно равно 0,5.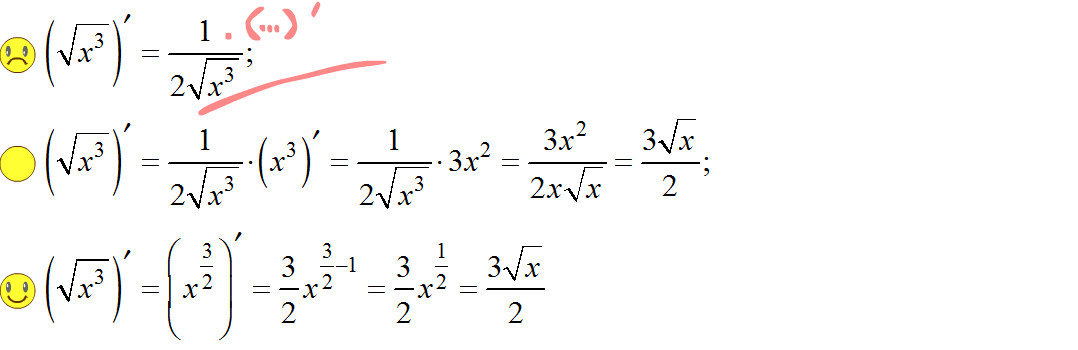
(f(a+h)-f(a))/ h
при h = 0, то есть когда числа а + h и а совпадают. Это значение мы назовем производной функции f в точке а. Будем обозначать его f’(а). Это обозначение ввел французский математик Жозеф Луи Лагранж (1736—1813) (см. главу 6). Как можно видеть, значение этой дроби равно 0/0, то есть оно не определено.
Однако это лишь кажущаяся неопределенность, поскольку, как показано в предыдущей таблице, для наших функций s(t) = ?t и
(s(l+h)-s(l))/h и (v(1+h) –v(1))/h
определены и равны соответственно 0,5 для функции s(t) = ?t и 2 — для функции v(t) = t2. Далее мы покажем, что эти значения действительно соответствуют значениям производных обеих функций в точке 1, то есть s’(l) = 0,5 и v’(l) = 2.
Деление ноля на ноль, возникающее при определении производной, представляло трудность для ученых XVII века и их предшественников всякий раз, когда они пытались рассчитать, например, угол наклона касательной к кривой или мгновенную скорость движения тела, зная пройденный им путь.
Бесконечность, основа анализа бесконечно малых, скрывается именно в этой операции деления ноля на ноль. Как мы только что сказали, нас интересует значение дроби
(f(a+h)-f(a))/ h
при h = 0, когда и числитель, и знаменатель обращаются в ноль. Подобные величины, равные нулю, отношение которых необходимо найти, математики XVII века назвали бесконечно малыми.
Анализ бесконечно малых, созданный Ньютоном и Лейбницем и усовершенствованный Леонардом Эйлером (1707—1783) и другими математиками XVIII века, можно назвать искусством манипулирования бесконечно малыми величинами. Как рассказывается в следующих главах, парадоксально, но ни один из этих гениальных математиков не определил сколько-нибудь точно понятие бесконечно малой величины, которое легло в основу математического анализа.
Ньютону и Лейбницу удалось завершить работу множества их коллег — математиков XVII века и создать анализ бесконечно малых, одним из разделов которого является дифференциальное исчисление. Ньютон и Лейбниц определили простые правила, позволявшие устранять неопределенность, которая заключается в делении ноля на ноль и возникает всякий раз, когда мы хотим вычислить производную функции. Это были правила вычисления производных элементарных функций, в частности степенной:
(xn)? = nxn-1;
тригонометрических функций:
(sin х)? = cosх, (cos x)? = -sin х;
логарифмов:
(log x)? = 1/х
показательных функций:
(ex)? = еx
а также правила вычисления производной для основных операции с функциями, в частности суммы:
(f+g)? = f? + g?;
произведения:
(fg)? = f?g + fg?;
деления:
(f/g)’ = (f’g – fg’)/g2
и для сложных функций:
(f(g))’ = f’(g)?g’.
Гордиевым узлом анализа бесконечно малых на протяжении XVII, XVIII и начала XIX века оставалось четкое определение того, как следует понимать значение дроби
(f(a+h)-f(a))/h
при h = 0. Этот гордиев узел разрубил французский математик Огюстен Луи Коши (1789—1857), применив понятие предела, которое он сам же и определил более или менее точно и которое затем улучшил немецкий математик Карл Вейерштрасс (1815—1897). Об этом рассказывается в главе 6.
Так как мгновенная скорость, с которой движется тело, является производной, то трудности при делении ноля на ноль препятствовали развитию физики, пока Ньютон не решил эту проблему, создав анализ бесконечно малых. До конца XVII века, когда был сформирован анализ бесконечно малых, ученые могли изучать только простейшие виды движения: равномерное движение, при котором пройденный путь пропорционален затраченному времени, следовательно, скорость постоянна, а ускорение отсутствует, а также равноускоренное движение, при котором пройденный путь пропорционален квадрату времени, скорость пропорциональна времени, а ускорение постоянно.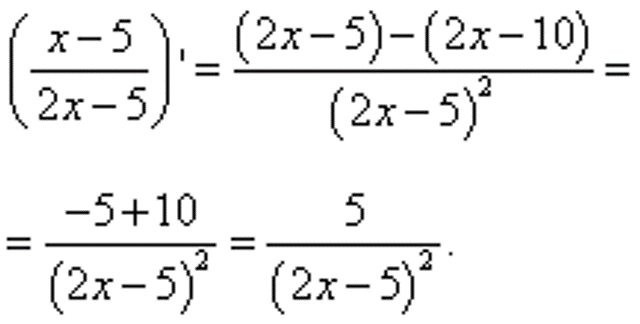
Для изучения последнего вида движения, примером которого является падение тела под действием силы тяжести, потребовался гений Галилея, который понял его суть за несколько десятков лет до того, как с помощью анализа бесконечно малых было найдено тривиальное решение этой задачи.
Проиллюстрируем это на примере. Рассмотрим, как и в прошлых примерах, движущееся тело, которое в момент времени t прошло расстояние в s(t) = ?t. Время будем измерять в секундах, расстояние — в метрах. Вычислить среднюю скорость движения тела несложно: например, в период времени с первой по четвертую секунду средняя скорость будет равна отношению пройденного пути и затраченного времени:
средняя скорость = (s(4) – s(1))/(4-1) = (2 – 1)/3 = 1/3 м/с.
Но что, если нас интересует не средняя скорость, а мгновенная скорость в конкретный момент времени? Чтобы упростить рассуждения, допустим, что мы хотим вычислить мгновенную скорость в тот момент, когда проходит ровно одна секунда от начала движения.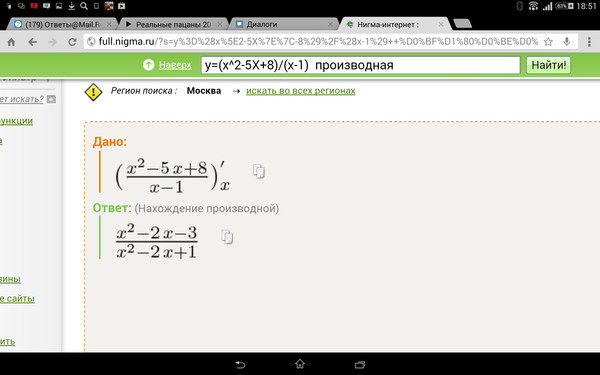
Выберем приращение времени h и вычислим среднюю скорость в интервале времени от 1 секунды до (1 + h) секунд:
Чтобы вычислить мгновенную скорость в первую секунду, достаточно свести приращение времени h к нулю. Однако в этом случае снова возникает неопределенность:
Это происходит потому, что мгновенная скорость соответствует значению производной функции пройденного пути s(t) = ?t. в момент времени t = 1.
В предыдущей таблице с числами указано, что значение этой производной должно равняться 0,5. Покажем, что это и в самом деле так, устранив неопределенность следующим способом:
Умножим числитель и знаменатель на ?(1+h) + 1 и упростим выражение:
Если в последнем выражении свести приращение времени h к нулю, то мы уже не столкнемся с неопределенностью и делением на ноль. Как и следовало ожидать, при h = 0 значение дроби будет равно 0,5. На языке физики это означает:
мгновенная скорость в момент времени 1 = 1/2 = 0,5.
Следовательно, мы устранили изначальную неопределенность, которая возникает из-за деления ноля на ноль, и получили, что если тело проходит за t секунд ?t метров, то по прошествии 1 секунды оно будет двигаться со скоростью 1/2 м/с.
2}. \ _ \ Квадрат \ end {align} dxd h (x) = (2x) 2 (2x) (9×2−1) – (3×3 − x − 2) (2) = 4x218x3−2x − 6×3 + 2x + 4 = x23x3 +1. □Дифференцирование рационального члена довольно сложно и сбивает с толку, когда выражения очень сложные. В таких случаях вы можете принять числитель как одно выражение, а знаменатель как одно выражение и найти их отдельные производные. Теперь напишите комбинированную производную дроби, используя приведенную выше формулу, и замените ее напрямую, чтобы не было путаницы и уменьшились шансы на ошибку.Следующие несколько примеров иллюстрируют, как это сделать:
Если y = a − xa + x (x ≠ −a), y = \ frac {a – x} {a + x} \ (x \ neq -a), y = a + xa − x (x = −a), затем найдите dydx \ frac {dy} {dx} dxdy.
2}.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (ax2 + bx + c) 2 (ax2 + bx + c) (0) – (2ax + b) (1) = (ax2 + bx + c) 2− (2ax + b) . □
2}.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (ax2 + bx + c) 2 (ax2 + bx + c) (0) – (2ax + b) (1) = (ax2 + bx + c) 2− (2ax + b) . □Если y = ax + bcx + d (∣c∣ + ∣d∣ ≠ 0), y = \ frac {ax + b} {cx + d} \ \ big (| c | + | d | \ neq 0 \ big ), y = cx + dax + b (∣c∣ + ∣d∣ = 0), затем найдите dydx \ frac {dy} {dx} dxdy.
Запишите u (x) = ax + b ⟹ u ′ (x) = au (x) = ax + b \, значит u ‘(x) = au (x) = ax + b⟹u ′ (x) = a и v (x) = cx + d ⟹ v ′ (x) = cv (x) = cx + d \ влечет v ‘(x) = cv (x) = cx + d⟹v ′ (x) = c, так что y = u (x) v (x): y = \ frac {u (x)} {v (x)}: y = v (x) u (x):
dydx = ddx (u (x) v (x)) = v (x) u ′ (x) −v ′ (x) u (x) (v (x)) 2 = (cx + d) (a) – (c) (ax + b) (cx + d) 2 = ad − bc (cx + d) 2.2}. \ _ \ Square \ end {align} dxdy = dxd (v (x) u (x)) = (v (x)) 2v (x) u ′ (x) −v ′ (x ) u (x) = (cx + d) 2 (cx + d) (a) – (c) (ax + b) = (cx + d) 2ad − bc. □
Если y = 1 − xx1 + xx (x> 0), y = \ frac {1 – x \ sqrt {x}} {1 + x \ sqrt {x}} \ (x> 0), y = 1 + xx 1 − xx (x> 0), затем найдите dydx \ frac {dy} {dx} dxdy.
Запишите u (x) = 1 − xx ⟹ u ′ (x) = 0 − x − x2x = −3x2u (x) = 1 – x \ sqrt {x} \, что подразумевает u ‘(x) = 0 – \ sqrt {x} – \ frac {x} {2 \ sqrt {x}} = – \ frac {3 \ sqrt {x}} {2} u (x) = 1 − xx ⟹u ′ (x) = 0− x −2x x = −23x и v (x) = 1 + xx ⟹ v ′ (x) = 0 + x + x2x = 3×2.2}. \ _ \ Квадрат \ конец {выровнено} y⇒dxdy = v (x) u (x) = (v (x)) 2v (x) u ′ (x) −v ′ (x) u (x) = (1 + xx) 2 (1 + xx) (- 23x) – (23x) (1 − xx) = 2 (1 + xx) 2−3x – 3×2− (3x −3×2) = 2 (1 + xx) 2−6x = – (1 + xx) 23x. □
Что такое дробное исчисление ?. «Парадокс, от которого однажды пригодится… | by Panda the Red
Дифференциальное исчисление было изобретено независимо Исааком Ньютоном и Готфридом Лейбницем, и было понято, что понятие производной n-го порядка, то есть применение операции дифференцирования n раз подряд, имеет смысл.В письме 1695 года Л’Опиталь спросил Лейбница о возможности того, что n может быть чем-то другим, кроме целого, например, n = 1/2. Лейбниц ответил, что «это приведет к парадоксу, из которого однажды будут извлечены полезные последствия».
Лейбниц был прав, но не пройдут века, пока не станет ясно, насколько он был прав.
В этой статье исследуется вопрос о том, что может означать выполнение чего-то вроде взятия производной 1/2 порядка, и таким образом вводится теория дробного исчисления.
Интуиция
Выражение можно интерпретировать двумя способами.
Первый – это тот, который мы все изучаем в основах исчисления: это функция, которую мы получаем, когда многократно дифференцируем f n раз. Второй вариант более тонкий: мы интерпретируем его как оператор, действие которого на функцию f (t) определяется параметром n. L’Hopital спрашивает, как ведет себя этот общий оператор, когда n не является целым числом.
Самый естественный способ ответить на этот вопрос – интерпретировать дифференцирование и интегрирование как преобразования, которые принимают f и превращают его в новую функцию.Следовательно, мы ищем оператор, который непрерывно преобразует f в свою n-ю производную или первообразную.
Дробный интеграл и производная
Наиболее естественным местом для начала поиска дифференциальных и интегральных операторов дробного порядка является формула, называемая формулой Коши для повторного интегрирования.
Если мы многократно берем первообразную n-го порядка функции, то результат будет:
Обобщение факториальной функции – это гамма-функция.Если заметить, что Γ (n) = (n-1)! тогда очевидный способ обобщить формулу Коши, чтобы включить действительный порядок α (строго больше нуля):
И действительно, это действительный оператор для интегрирования до дробного порядка. Он называется левым интегралом Римана-Лиувилля. О назначении «левого» квалификатора мы поговорим позже. На самом деле в литературе принято много различных операторов дробного интегрирования, но интеграл R-L является самым простым и легким в использовании и понимании.Обратите внимание, что α также может быть комплексным, действительная часть которого строго больше нуля, для простоты мы будем предполагать, что α является действительным. Частный случай α = 1/2 называется полуинтегралом.
Интегрирование R-L подчиняется следующим важным соотношениям:
Можно наивно предположить, что мы закончили, и что мы можем просто определить дробное дифференцирование до порядка α с помощью
Не так.
Проблема (ну, одна из проблем) в том, что гамма-функция не определена для нуля или для отрицательных целых чисел, что оставило бы нас с обобщением дифференцирования, которое не работало бы даже для обычного дифференцирования! Мы должны проявить творческий подход, чтобы найти способ обойти это.
Прежде всего отметим, что взятие производной n раз после интегрирования n раз эквивалентно операции тождества:
Это означает, что производная является левой обратной величиной интеграла. Однако интегрирование – это , а не , левая величина, обратная производной, потому что интегрирование добавляет произвольную константу. То есть, в целом неверно, что:
Имея это в виду, мы ожидаем, что дробная производная порядка α будет иметь свойство, которое:
Мы также, очевидно, хотели бы иметь возможность записать дробную производную в термины операторов, которые мы понимаем.Мы понимаем дифференциацию в целочисленном порядке и мы понимаем интеграцию в целочисленном и нецелочисленном порядке.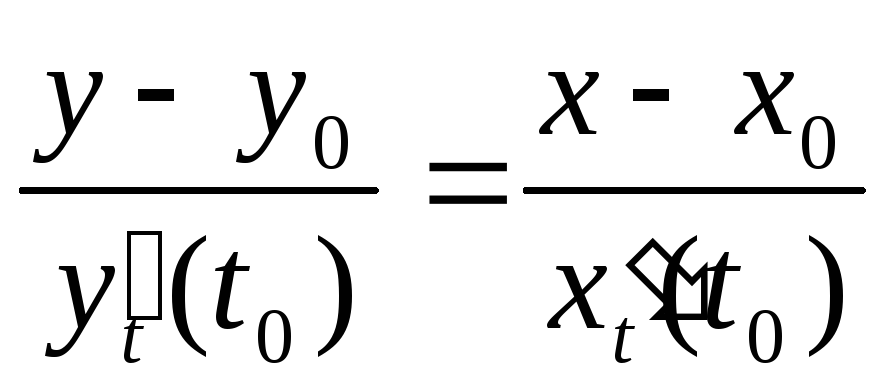
Оператор, который мы можем построить из этих составных операторов, который имеет желаемое свойство сокращения слева, это:
Где ⌈α⌉ называется функцией верхнего предела α, результатом округления α до следующего целого числа. Мы обнаруживаем, что это на самом деле правильный оператор, и полностью он выглядит так:
Это левая дробная производная Римана-Лиувилля. Глядя на этого зверя, можно ясно понять, почему этой области исследований потребовалось почти 300 лет, чтобы добиться чего-либо: большинство вычислений в дробном исчислении утомительны, если не совсем невыполнимы, если они выполняются вручную без помощи компьютера.Частный случай α = 1/2 называется полупроизводной.
Используя дробный интеграл и производную, которые мы разработали, мы теперь можем объединить их кусочно, чтобы определить дифференциальный интеграл:
Следующая анимация показывает, как дифференциальный интеграл Римана-Лиувилля непрерывно преобразуется между функциями f (x) = x, f (x) = 1 и f (x) = (1/2) x²:
Источник изображения: Wikimedia Commons.
Обратите внимание, как при значениях α в диапазоне от -1 до 1 дифференциал, показанный зеленой кривой, проходит между линией y = 1 и кривой y = (1/2) x².
Свойства
Всегда хорошо быть любопытным, что происходит, когда вы пытаетесь сделать что-то странное, например, вставить дробь для порядка дифференциации, поскольку именно так, конечно, делается много важных открытий, но когда вы отправляетесь в неизведанное На территории следует быть готовым отказаться от многого из того, что вы уже знаете и считаете само собой разумеющимся, как естественное и очевидное.
Это, по сути, банальный способ сказать, что многие из основных свойств обычных производных и интегралов, которые мы все знакомы и знакомы, такие как правила цепочки и произведения, , а не , в целом выполняются с дробными производными и интегралами, или они принимают сложные формы.Тем не менее, интеграл и производная RL, которые мы обсудили, не являются единственными возможными различными интегральными операторами, на самом деле существует целый ряд различных способов обобщения дифференцирования и интегрирования на нецелочисленные порядки, и это можно сделать способами, сохраняющими многие из классических свойств.
Однако в этой статье мы сосредоточимся на операторах R-L, потому что они, наряду с тесно связанными с ними операторами Капуто, являются наиболее простыми для понимания и наиболее распространенными в приложениях.
Еще одно интересное свойство RLFD – нелокальность. Когда мы вычисляем значение производной целого порядка в точке, результирующее значение зависит только от этой точки. Это, казалось бы, очевидное свойство называется локальностью. С дробной производной дело обстоит иначе. Дробная производная получается интегрированием по всему диапазону значений, и существует нетривиальная зависимость от нижней границы интегрирования, так что мы должны правильно записать дробную производную как:
Случай, когда a = 0 обычно при анализе физических систем, потому что часто зависимой переменной является время, а дробная производная в любой момент времени будет зависеть от состояния системы во все предыдущие моменты времени, то есть все моменты времени с момента начала эксперимента в момент времени t = 0.
Эта нелокальность является одним из основных факторов интереса к дробному исчислению в приложениях. Есть много интересных физических явлений, которые имеют так называемые эффекты памяти, означающие, что их состояние зависит не только от времени и положения, но и от предыдущих состояний. Например, можно представить себе компонент электрической цепи, сопротивление которого зависит от всего заряда, прошедшего через него за фиксированный промежуток времени. Системы с эффектами памяти могут быть очень сложными для моделирования и анализа с помощью классических дифференциальных уравнений, но нелокальность дает дробным производным встроенную способность включать эффекты памяти.Таким образом, дробное исчисление может оказаться очень полезным инструментом для анализа этого класса систем.
Нелокальность также является причиной того, почему мы должны быть осторожны при указании того, что мы обсуждаем левый RLFD. Можно также изменить порядок интегрирования, чтобы определить правую дробную производную:
Правый RLFD – это принципиально другой объект, чем левый, несмотря на схожий внешний вид.
Правые дробные производные не так хорошо изучены, и они не так полезны в прикладных условиях.Чтобы понять, почему, рассмотрим, что означало свойство нелокальности в случае левого RLFD: оно означало, что состояние физической системы зависело от ее состояния в предыдущие моменты времени. Если бы правильный RLFD описывал физическую систему, то состояние этой системы в данный момент времени зависело бы от ее будущего состояния, что не является физически разумным. Поскольку большая часть исследований дробного исчисления сосредоточена на приложениях, правые дробные производные на данный момент в основном интересны теоретикам.
Дробные производные некоторых базовых функций
Для степенных функций с n≥0 дробная производная равна:
Проверив случай n = 0, мы можем увидеть, что это означает, что дробная производная константы, как ни странно, равна не ноль.Полупроизводная f (t) = 1, константа, заслуживает запоминания и дается формулой:
Для синусоидальной функции:
Это случай, который наиболее убедительно подтверждает наше утверждение о том, что дробную производную можно рассматривать как преобразование между функциями и их производными.
Изменение α просто приводит к увеличению фазы, пока при α = 1 мы не получим функцию косинуса.
Наконец, для экспоненциальной функции:
Что, как и в случае с синусоидальной функцией, является именно тем, что мы ожидали.
Интерпретация
Пока не ясно, как мы должны интерпретировать дробные операторы геометрически и физически так же, как мы это делаем с операторами в классическом исчислении. Это область активных исследований, и когда эта проблема будет решена, это, вероятно, приведет к большим результатам в физике и технике.
А пока проще всего использовать подход, которого придерживался Оливер Хевисайд, когда он столкнулся с дробными операторами при разработке своего операционного исчисления: просто признать, что они существуют как класс объектов сами по себе и что они следуют определенному правилу. определенный набор правил, и если вам когда-нибудь случится столкнуться с чем-то, что следует этим правилам, или вам понадобится что-то, что следует этим конкретным правилам, тогда вы знаете, что искать.
Задача таутохрон
Нилс Абель (1802–1829) обычно считается первым математиком, развившим основные идеи дробного исчисления при анализе проблемы таутохрон. Задача таутохрон требует построить кривую, обладающую тем свойством, что, когда бусинка скользит по кривой, время, необходимое для достижения нижней части кривой, не зависит от начальной высоты.
Источник изображения: Wikimedia CommonsАбель использовал основные физические рассуждения, чтобы прийти к следующему интегральному уравнению, которое связывает время достижения нижней части кривой с начальной высотой:
Где s – параметризация длины дуги кривой, которая решает эта проблема.Нам нужно решить это уравнение относительно ds / dy. Мы могли бы решить эту проблему, используя свертки и преобразования Лапласа, как это сделал Абель. В качестве альтернативы мы могли бы сократить все это и признать, что выражение справа можно разделить на Γ (1/2) = √π, чтобы превратить его в полуцелый. Разделите каждую часть этого уравнения на √π и переместите √ (2g) влево, чтобы получить, и пусть T (y0) = T0, поскольку время падения является константой относительно начальной высоты:
Мы знаем, как отменить полуцелой оператор.
Просто возьмите полупроизводные каждой части этого уравнения, и задача сразу будет решена:
Кривая, описываемая этим уравнением (кстати, циклоида), называется таутохронной кривой.
Эта проблема иллюстрирует основной вариант использования дробного исчисления в нынешнем виде. Обычно при анализе системы мы случайно сталкиваемся с математическим утверждением, которое оказывается дробным оператором, и поэтому мы знаем, что можем применить правила дробных операторов к этой системе.
Заключение
Один из лучших способов сделать открытия в математике и естествознании – это увидеть, что происходит, когда мы нарушаем правила, пытаясь заставить наши существующие теории работать с крайними или необычными случаями. (Я упоминал об этом в предыдущей статье). Часто это ни к чему не приводит, потому что иногда правила существуют по какой-то причине, но иногда мы получаем отличный ответ, когда задаем нелепый вопрос. Это, безусловно, один из таких случаев.
Как всегда, я ценю любые исправления.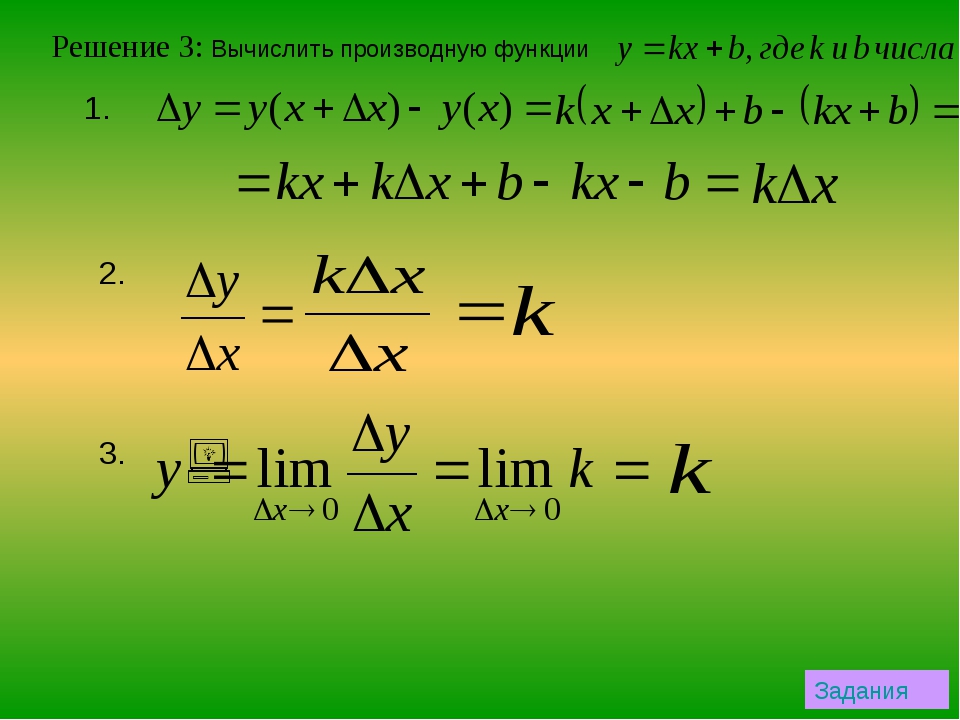
Модификация дробных производных Адамара типа Капуто | Успехи в разностных уравнениях
Пусть R (α) ≥0 и n = [R (α)] + 1. Если y (x) ∈ACδn [a, b], где 0 DαaCy (x) = aDα [y (t) −∑k = 0n − 1δky (a) k! (Logta) k ] (x), (16) и DbαCy (x) = Dbα [y (t) −∑k = 0n − 1 (−1) kδky (b) k! (Logbt) k] (x). (17) В частности, если 0 DαaCy (x) = aDα [y (t) −y (a)] (x), (18) и DbαCy (x) = Dbα [y (t) −y (b)] (x). (19) Теорема 2.1 Пусть R (α) ≥0 и n = [R (α)] + 1. Если y (x) ∈ACδn [a, b], , где 0 , если α∉N0, DαaCy (x) можно представить как DαaCy (x) = 1Γ (n − α) ∫ax (logxt) n − α − 1δny (t) dtt = aJn − αδny ( х), (20) и DbαCy (x) можно представить как DbαCy (x) = (- 1) nΓ (n − α) ∫xb (logtx) n − α − 1δny (t) dtt = (- 1) nJbn − αδny (x), (21) , если α∈N, , то DαaCy (x) = δny (x), CDbαy (x) = (- 1) nδny (x). (22) В частности, , D0aCy (x) = CDb0y (x) = y (x). (23) Доказательство Пусть α∉N0. Используя определение левой дробной производной Адамара (14) и применяя формулу интегрирования по частям u = y (t) −∑k = 0n − 1δky (a) k! (Logta) k и dv = (logxt) n − α − 1dtt в (16) получаем DαaCy (x) = (xddx) n {[- 1n − α (logxt) n − α (y (t) −∑k = 0n − 1δky (a) k! (logta) k)] | ax + 1n − α∫ax (logxt) n − α [δy (t) −∑k = 1n − 1δky (a) k! (logta) k] dtt} = (xddx) n − 1∫ax (logxt) n − α [δy (t) −∑k = 1n − 1δky (a) k! (logta) k] dtt = ⋯ = xddx1Γ (n − α) ∫ax (logxt) n − α − 1 (δn −1y (t) −δn − 1y (a)) dtt. Выполняя еще раз интегрирование по частям с тем же выбором dv , получаем уравнение (20). (21) доказывается аналогично. Теперь, когда α = n, имеем DnaCy (x) = aDn [y (t) −∑k = 0n − 1δky (a) k! (Logta) k] (x). То есть y (x) = JnaCaDny (x) + ∑k = 0n − 1δky (a) k! (Logxa) k = 1 (n − 1)! ∫ax (logxt) n − 1aCDny (t) dtt + ∑k = 0n − 1δky (a) k! (logxa) k. Из леммы 1.2 в [1] выводим DαaCy (x) = δny (x). Вторая формула в (22) доказывается аналогично. □ Теорема 2.2 Пусть R (α) ≥0 и n = [R (α)] + 1. Если y (x) ∈Cδn [a, b], , где 0 Тогда DαaCy (x) и DbαCy (x) продолжаются на [a, b] и , если α∉N0, DαaCy (x) и DbαCy (x) могут быть представлены как (20) и (21) соответственно и DαaCy (a) = 0, CDbαy (b ) = 0, (24) , если α∈N, , то формулы в (22) верны . Доказательство Представления (21) и (22) доказываются аналогично теореме 2.1. (25) (26) Когда α∈N, первая формула в (22) верна в результате леммы 1.4 в [1]. Вторая формула доказывается аналогично. □ Следствие 2.3 Пусть R (α) ≥0 и n = [R (α)] + 1. Если α∉N0, , то DαaC ограничено из пространства Cδn [a, b] в пространство Ca [a, b] = {f∈C [a, b] s.tf ( a) = 0} и DbαC ограничен из пространства Cδn [a, b] в пространство Cb [a, b] = {f∈C [a, b] s.tf (b) = 0} и (27) (28) Если α = n∈N0, , то DnaC и DbnC ограничены от Cδn [a, b] до C [a, b] и ∥aCDny∥C≤∥y ∥Cδn, ∥CDbny∥C≤∥y∥Cδn. (29) Доказательство (27) и (28) следует из оценок (25) и (26) с учетом того, что ∥δny∥C≤∥y∥Cδn (см. Формулу 1.1,28 в [1] при γ = 0). Оценки в (29) очевидны. □ DαaC и DbαC обеспечивают операции, обратные Jαa и Jbα соответственно для R (α) ≠ 0 или α∈N. Но это не так для R (α) ∈N и R (α) ≠ 0. Лемма 2.4 Пусть R (α)> 0, n = [R (α)] + 1 и y∈C [a, b]. Если R (α) ≠ 0 или α∈N, , то DαaC (aJαy) (x) = y (x), CDbα (Jbαy) (x) = y (x). (30) Если R (α) ∈N и R (α) ≠ 0 , затем (31) (32) Доказательство Из (16) имеем DαaC (aJαy) (x) = aDα (aJαy) (x) −∑k = 0n − 1δk (aJαy) (a) k! (Logxa) k. (33) Из свойств 2.28 и 2.27 в [1] имеем Dαa (aJαy) (x) = y (x) и δk (aJαy) (x) = aJα − ky (x). Легко проверить, что | aJα − ky (x) | ≤∥y∥C | Γ (α − k) | (R (α) −k) (logxa) R (α) −k, k = 0 , 1,…, n − 1, (34) , из чего заключаем, что Jα − kay (a) = 0, и, следовательно, первое тождество в (30) выполнено. Второе тождество доказывается аналогично. Если α = m + iβ, m∈N, β ≠ 0, то n = m + 1≥2 и δk (aJαy) (x) = aJα − ky (x), k = 0,1,…, m −1 и аналогично (34) имеем | aJα − ky (x) | ≤∥y∥C | Γ (α − k) | (m − k) (logxa) m − k, k = 0,1 ,…, М − 1. (35) Таким образом, Jα − kay (a) = 0, k = 0,1,…, n − 2 и, следовательно, выполняется (31). (32) доказывается аналогично. □ Лемма 2.5 Пусть y∈ACδn [a, b] или Cδn [a, b] и α∈C. Затем (36) (37) Доказательство (36) и (37) следует из тождеств DαaCy (x) = aJn − αy (x) и DbαCy (x) = Jbn − αy (x) соответственно. Модификации Капуто левой и правой дробных производных Адамара обладают одинаковыми свойствами 2.7.16 и 2.7.18. в [1], но они отличаются от приведенных в 2.7.19. Свойство 2.6 Пусть R (α) ≥0, n = [R (α)] + 1 и R (β)> 0. Тогда (38) (39) (40) В частности, имеется Дробных производных Капуто-Адамара также можно определить на положительной полуоси R +, заменив a на 0 в формуле (20) и b на ∞ в формуле (21) при условии, что y ( x) ∈ACδn (R +) (или Cδn (R +)).Таким образом получается (42) (43) Преобразования Меллина модификаций Капуто левой и правой дробных производных Адамара такие же, как преобразования Меллина левой и правой дробных производных Адамара 2. Лемма 2.7 Пусть R (α)> 0 и y (x) таковы, что преобразования Меллина (My) (s), (Mδny) (s) существуют для s∈C . Если R (s) <0, , то (MCD0 + αy) (s) = (- s) α (My) (s). (44) Если R (s)> 0, , то (MCD − αy) (s) = sα (My) (s). (45) Доказательство (44) следует из леммы 2.38 и формулу 1.4.35 в [1] (MCD0 + αy) (s) = (MJ0 + n − αδny) (s) = (- s) α − n (Mδny) = (- s) α (My ). (46) (45) доказывается аналогично. □ Сначала рассмотрим пример из механики. где – производная Римана-Лиувилля дробного порядка с нулевым начальным условием. Метод наложения 18 приводит к решению уравнения (4) следующим образом: Это согласуется с ранними наблюдениями поведения некоторых вязкоупругих материалов 19,20,21,22 . Недавно было использовано уравнение (1) 18 для соответствия данным испытания на трехточечный изгиб 13 вязкоупругой ползучести керамики SiAlYON при 1200 ° C и 240 МПа.Модель очень хорошо соответствовала тестовым данным двух образцов, но не соответствовала третьей тестовой кривой. Во-вторых, мы показываем, что уравнение (1) работает не только для моделирования вязкоупругих материалов, но и для моделирования биологической кинетики с памятью. Например, для кинетики адсорбции белка 14 , если символы концентрации c и поверхностной плотности Γ фибронектина в ней заменены на σ и ε соответственно. Используя численный метод наименьших квадратов, мы находим, что α = 0.435, μ = 6,6302 × 10 −5 см · с −α , а критическая точка равна (80, 0,109). Опять же, как показано на рис. 2, уравнение (6) очень хорошо соответствует данным испытаний. В-третьих, мы показываем, что уравнение (1) хорошо работает даже для когнитивной динамики в психологии, подгоняя данные теста на запоминание 15 , выполненного Германом Эббингаузом и представленного в 1885 году. день. Чтобы данные теста были сопоставимы, время переобучения составляет 11–12 А.До 18:00 или 18:00. был линейно преобразован в 10–11 утра. Среднее время обучения t M = 994,4 с. Проведя аналогию между обучением (забыванием) и нагрузкой (разгрузкой) и рассматривая удерживание как напряжение, мы используем уравнение (1) для соответствия данным теста Эббингауза.Здесь σ ( t ) = 1 на данном этапе обучения от 0 до t M , что означает, что для разучивания серии слогов испытуемый полностью занят, а σ ( t ) = 0, когда обучение прекращается после момента t M . Поскольку эффективность обучения меняется в течение дня, для подгонки используются тестовые данные по крайней мере за один день. Предполагается, что α дробного порядка находится между 0,5 и 1, потому что линейное преобразование, упомянутое выше, неадекватно для малого порядка. Подобно тестам по материалам, в начале обучения можно быстро запомнить несколько слогов и очень хорошо их запомнить. Это свежий этап обучения. На рабочем этапе что-то постепенно забывается после прекращения обучения. Мы предполагаем, что свежая стадия восстанавливается через сутки. В этом предположении мы используем соответствующие значения ε минус вертикальное значение критической точки, соответственно, чтобы соответствовать дробной модели. Используя численный метод наименьших квадратов и решение уравнения (5), находим, что α = 0.71, μ = 205,8 ч −α и критическая точка (0, 7.2), где время обучения новой стадии равно приблизительно 0. Кривая забывания хорошо соответствует тестовым данным, как показано на рис. 3. Кроме того, , мы рассматриваем повторный обучающий тест Эббингауза 15 , в котором выучивали 9 серий по 12 слогов, а затем в один и тот же час в последовательные дни заново выучивали до точки первого возможного воспроизведения. В последовательные 6 дней (n = 1,2,…, 6) время повторений для каждой серии в среднем составляет м n = 16. Используя уравнение (7) для рабочих этапов и принимая во внимание новый этап, кривые повторного обучения и забывания построены на рис. В этом случае получаем, что α = 0,71, μ = 264,5 h −α , а высота свежей ступени равна 8.Здесь дробный порядок такой же, как на рис. 3, как и ожидалось. Таким образом, тесты Эббингауза на обучение и забывание соответствуют уравнению (1). Таким образом, мы разделяем явления памяти на новую стадию и рабочую стадию и показываем, что дробный порядок является индексом памяти путем подбора тестовых данных феноменов памяти из разных полей. 940 1. Введение За последние несколько лет сообщество разработчиков дробного исчисления (FC) приложило немало усилий, чтобы прояснить этот вопрос. и чем они не являются ([8, 11, 14, 16, 17, 30, 31, 35, 36, 37]).Эти обсуждения в основном касались «новых дробных интегралов и производных » ([8, 11, 14, 31, 35, 36, 37]), интегро-дифференциальных операторов типа свертки с некоторыми общими ядрами ([8, 14, 22, 23, 35, 39, 40]) и абстрактные аксиомы FC ([17, 30, 33]). В этой структуре «классические» определения дробных интегралов и производных как интеграл и производная Римана-Лиувилля ([24, 34]), производная Капуто ([3, 7, 24]), обобщенная производная Римана-Лиувилля или производная Гильфера ([15, 18, 24]) и т. д., обычно считаются постулируемыми . В этой статье мы собираемся более внимательно и критически взглянуть на «правильные» определения однопараметрических семейств дробных интегралов и производных , определенных на конечном интервале. Во втором разделе мы воспроизводим результат, полученный в [4] более сорока лет назад относительно «правильных» однопараметрических семейств дробных бесконечных тегралов, определенных на конечном интервале. единственное семейство дробных интегралов на конечном интервале – это дробные интегралы Римана-Лиувилля . Вопрос о «правильных» дробных производных более конкретен и рассматривается в 3-м разделе. В исчислении производные целого порядка обычно определяются через пределы разностных коэффициентов. Определенный интеграл вводится независимо через суммы Римана или в смысле Лебега. Фундаментальная теорема исчисления устанавливает связь между этими двумя независимо определенными объектами и говорит , что производная первого порядка является оператором, обратным слева к определенному интегралу с переменным верхним пределом интегрирования в подходящем пространстве. из функций.Если мы будем следовать этому подходу, чтобы ввести «правильную» производную дроби , мы естественным образом придем к определению Грюнвальда-Летникова ([7, 13, 26, 34]). Это определение полезно и важно, например, для численного вычисления дробных производных. и обычно заменяется другими определениями, которые эквивалентны определению Грюнвальда-Летникова на некоторых подходящих пространствах функций.Скажем, для функций из Cn [a, b] при n − 1 <α≤n, n ∈N, дробная производная Грюнвальда-Летникова порядка α совпадает с дробной производной Римана-Лиувилля порядка α ( [7]). Вот почему при анализе теоретико-операторных свойств дробных производных в дробно-дифференциальных уравнениях и т. Д. Производная Грюнвальда-Летникова часто заменяется производной Римана-Лиувилля. % PDF-1.5
%
1 0 объект
>
>>
эндобдж
4 0 obj / Создатель
/ CreationDate (D: 20160928154540 + 01’00 ‘)
/ ModDate (D: 20160928154540 + 01’00 ‘)
/Режиссер
>>
эндобдж
2 0 obj
>
эндобдж
3 0 obj
>
эндобдж
5 0 obj
>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
/ XObject>
>>
/ Аннотации [28 0 R 29 0 R 30 0 R 31 0 R]
/ MediaBox [0 0 544.56 743.04]
/ Содержание [32 0 R 33 0 R 34 0 R]
/ Группа>
/ Вкладки / S
/ StructParents 0
>>
эндобдж
6 0 obj
>
/ Группа>
/ Вкладки / S
>>
эндобдж
7 0 объект
>
/ ExtGState>
/ XObject>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ Аннотации [47 0 R 48 0 R 49 0 R]
/ MediaBox [0 0 544. 2009 Rasmus ehf и Джанн Сак Урок 3 Корни, отрицательные силы,
умноженные и разделенные функции Пример
1 Найдите производную от. Используйте правило: Мы тоже можем написать так
проверим, действует ли правило дифференцирования степеней целыми числами
То, что использовалось в уроке 2, также применимо и в этом случае. Мы бы получили . Мы можем показать, что
правило f (x) = nx n1 также
применяется, когда n является
фракция Пример 2 Используйте правило, чтобы различать следующие
Например, сначала упростив корень и записав его в виде дроби с помощью
обозначение. Двигаться 7 / 6 вперед, затем уменьшите мощность на 1. Пример 3 Используйте определение производного инструмента для
дифференцировать f (x) = x 1 = 1 / х. Сначала упростите числитель, затем упростите и отмените столько, сколько
возможный. Это говорит о том, что мы
можно использовать правило
f (x) = nx n1 на отрицательных степенях Теперь докажем правило
который показывает, как различать функцию, состоящую из двух функций, умноженных
вместе. f (х) = и (х) v (х). Мы знаем, что когда h мало и , что дает нам гу (х)
u (x + h) u (x) и, следовательно, u (x + h)
ху (х) + и (х) и hv (x)
v (x + h) v (x) и, следовательно, v (x + h)
hv (x) + v (x) Ввод этих значений в
приведенное выше уравнение, упрощая, отменяя и затем принимая предел, дает нам
Правило нахождения производной при умножении двух функций: (и (х) v (х)) = и (х) v (х) +
и (х) v (х) Легче запомнить
правило, если мы опускаем x. Пример 4 Проверим правило и
убедитесь, что вы это понимаете, найдя производную от
f (x) = x 3 x 2 . Самый простой и очевидный способ
состоит в том, чтобы сначала упростить, а затем найти производную: f (x) = x 5 и f (x) = 5x 4 . Теперь воспользуйтесь правилом умножения: Положим u = x 3 дает u = 3x 2 и v =
x 2 дает v = 2x. f (x) = (УФ) = УФ + УФ = 3x 2 x 2 + x 3 2x = 3x 4 + 2x 4 = 5x 4 , который соответствует нашему первому
метод. Теперь посложнее
правило, правило дифференцирования рациональных функций
u / v, где u и v являются функциями x: Это можно доказать с помощью
определение производной так же, как правило умножения
доказано.Это также можно доказать с помощью правила, называемого цепным правилом, которое будет
представлен в 5 уроке. Даем цепное правило
доказательство здесь, вы можете вернуться к этому доказательству, когда закончите урок 5. Мы используем цепное правило (v 1 )
= v 2 v и правило (uv) = uv + uv
где u и v являются функциями от x. Это правило: Пример 5 Используйте правило деления на
дифференцировать u = x + 1, так что u
= 1 и v = x 2 давая v
= 2x. Поместив их в
формула выше дает нам Попрактикуйтесь в этих методах, а затем
пройдите тест 3 по производным. л.с. Запомните свой контрольный список.
Тогда DαaCy (x) и DbαCy (x) существуют везде на [a, b] и 
Непрерывность DαaCy (x) и DbαCy (x) следует из их представлений и леммы 2.36 в [1] с заменой f (t) = δny (t), γ = 0 и α на n − α. Тождества в (24) выполняются с
□
7.72 и 2.7.74 в [1]. Измерительная память с порядком дробной производной
Поведение вязкоупругих материалов с памятью обычно описывается с помощью модели Кевина, модели Фойгта, модели Максвелла и т. Д. С точки зрения деформации, напряжения и их производных или интегралов целого порядка 16,17 .По сравнению с дробными моделями такие модели целого порядка гораздо менее точно отражают эффекты памяти 1 . Ранние наблюдения показывают, что вязкоупругие материалы различаются по эластичности и вязкости. Следовательно, разумно предположить, что модели вязкоупругости принимают форму уравнения (1) и охватывают две крайности: α = 0 для закона упругости Гука и α = 1 для закона вязкости Ньютона. В 1979 году уравнение (1) было успешно использовано для согласования данных испытаний на ползучесть и восстановление 5 нитроцеллюлозного соединения при 90 ° C.Хотя некоторые обобщенные дробные модели, такие как дробные модели Кевина, Фойгта и Максвелла, были установлены и подтверждены экспериментами 4,12 , работ о прямой проверке уравнения (1), насколько известно авторам, немного.
Для стандартного испытания на ползучесть и восстановление образец обычно нагружают при постоянном напряжении σ ( т ) = σ 0 от 0 до т M , и нагрузка снимается в момент т = т M , тогда σ ( т ) = 0 для т ≥ т M .Пусть H ( t ) – функция Хевисайда, тогда уравнение (1) принимает следующую простую форму:
Чтобы соответствовать третьему, мы определяем свежий этап и рабочий этап. На рабочем этапе уравнение (5) идеально соответствует третьей кривой испытания образца керамики SiAlYON. С помощью численного метода наименьших квадратов мы находим, что α = 0,44, μ = 7,23 × 10 −5 (МПа −1 · с −α ), а критическая точка равна (6,1455, 0,0828), как показано на рис. 1. Новая стадия не подлежит восстановлению, поскольку уравнение (5) положительно, т.е.Т. е. восстановление всегда выше критической точки. Здесь и в следующем примере тестовые данные измеряются по цифрам соответствующих ссылок с помощью программного обеспечения Origin.
Тогда с σ ( t ) = σ 0 [ H ( t ) – H ( t – t M ) + H ( t – t N )], где σ 0 = 50 мкг / мл, t M = 240 с и t N = 1150 с, найдена поглощенная плотность быть
Коэффициенты удержания обучения ε (%) составили 58,2, 44,2, 35,8, 33,7, 27,8, 25,4 и 21,1, соответственно, через 0,33, 1, 8,8, 1 × 24, 2 × 24, 6 × 24 и 7 × 24 часа, где коэффициент удерживания был получен путем использования отношения времени повторного обучения к исходному.
5, 11, 7,5, 5, 3 и 2,5. Поскольку один слог занимает 0,4 с, время обучения равно t n = м n × 9 × 12 × 0,4 / 3600 ч. С тестовыми данными решение уравнения (1) для рабочего этапа принимает вид (PDF) Дробные производные и основная теорема дробного исчисления
что такое дробные интегралы и производные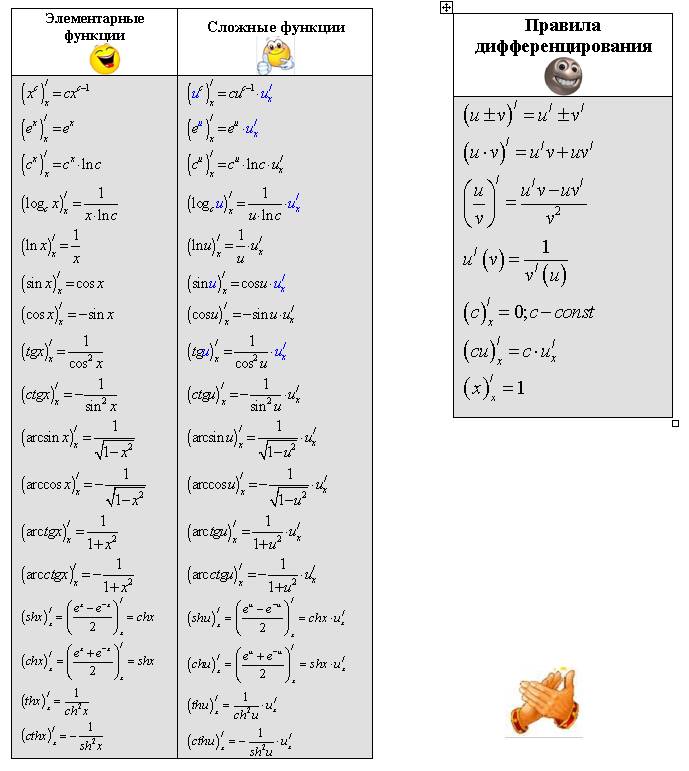
Оказывается, что при некоторых разумных условиях
Однако это непрактично для аналитических исследований
56 743,04]
/ Содержание 50 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 4
>>
эндобдж
8 0 объект
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ Аннотации [53 0 R]
/ MediaBox [0 0 544.56 743.04]
/ Содержание 54 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 8
>>
эндобдж
9 0 объект
>
/ XObject>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ Аннотации [57 0 R 58 0 R 59 0 R 60 0 R]
/ MediaBox [0 0 544.56 743.04]
/ Содержание 61 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 10
>>
эндобдж
10 0 obj
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ MediaBox [0 0 544.56 743,04]
/ Содержание 62 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 15
>>
эндобдж
11 0 объект
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ MediaBox [0 0 544.56 743.04]
/ Содержание 63 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 16
>>
эндобдж
12 0 объект
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ MediaBox [0 0 544.
56 743.04]
/ Содержание 64 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 17
>>
эндобдж
13 0 объект
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ MediaBox [0 0 544.56 743,04]
/ Содержание 65 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 18
>>
эндобдж
14 0 объект
>
/ ExtGState>
/ ProcSet [/ PDF / Text / ImageB / ImageC / ImageI]
>>
/ Аннотации [66 0 R]
/ MediaBox [0 0 544.56 743.04]
/ Содержание 67 0 руб.
/ Группа>
/ Вкладки / S
/ StructParents 19
>>
эндобдж
15 0 объект
>
эндобдж
16 0 объект
>
эндобдж
17 0 объект
>
эндобдж
18 0 объект
>
эндобдж
19 0 объект
>
эндобдж
20 0 объект
>
эндобдж
21 0 объект
>
эндобдж
22 0 объект
>
эндобдж
23 0 объект
>
эндобдж
24 0 объект
>
эндобдж
25 0 объект
>
эндобдж
26 0 объект
>
эндобдж
27 0 объект
>
транслировать
x Математическая сцена – Производные – Урок 3
Математическая сцена – Производные – Урок 3 – Корни, отрицательные степени, умноженные и разделенные функции Производные инструменты
а 2 б 2 = (ab) (a + b)
так что h можно исключить. 
